Abstract
In this study we examine the distribution of hydrophobic residues in a nonredundant set of monomeric globular single-domain proteins. We find that the total fraction of hydrophobic residues is roughly constant and has no discernible dependence on protein size. This results in a decrease of the hydrophobicity of the core as the size of proteins increases. Using a normalized measure, and by comparing with sets of randomly reshuffled sequences, we show that this change in the composition of the core is statistically significant and robust with respect to which amino acids are considered hydrophobic and to how buried residues are defined. Comparison with model sequences optimized for stability, while still required to retain their native state as a unique minimum energy conformation, suggests that the size-independence of the total fraction of hydrophobic residues could be a result of requiring proteins to be conformationally specific.
INTRODUCTION
The hydrophobic effect, i.e., the tendency for nonpolar molecules to aggregate in water, is widely believed to be the main driving force behind the folding of globular proteins (Kauzmann, 1954; Dill, 1990). When proteins fold it is thermodynamically favorable to bury the hydrophobic residues (Matsumura et al., 1988; Eriksson et al., 1992; Lumb and Kim, 1995; Waldburger et al., 1995; Malakauskas and Mayo, 1998), and as a consequence nonpolar amino acids tend to be clustered in the interior of proteins (Perutz et al., 1965; Chothia, 1976; Miller et al., 1987).
The role of polar residues in the interior of proteins is less clear. Transfer experiments of amino acids from organic solvents to water have shown that the burial of polar residues is energetically unfavorable (Radzicka and Wolfenden, 1988; Wesson and Eisenberg, 1992; Dahiyat et al., 1997). In protein structures it is indeed observed that polar residues have a preference for surface positions compared to the core (Chothia, 1976; Miller et al., 1987). However, if they are able to form intramolecular hydrogen bonds, buried polar amino acids can favorably contribute to the stability of proteins (Pace et al., 1996; Takano et al., 2001; Bolon and Mayo, 2001; Loladze et al., 2002). Furthermore, theoretical calculations (Hendsch and Tidor, 1994) and mutational studies in coiled coil systems (O'Shea et al., 1992; Lumb and Kim, 1995; Ji et al., 2000) and globular proteins (Bolon and Mayo, 2001), suggest that buried polar residues can help proteins establish conformational specificity. But database studies of related proteins (Russell and Barton, 1994; Schueler and Margalit, 1995) and mutational studies on the Arc repressor (Waldburger et al., 1995) also show that in many cases they can be replaced by hydrophobic residues without affecting the conformational specificity.
For globular proteins the relative size of the core grows with protein size (Chothia, 1975; Janin, 1976; Teller, 1976; Miller et al., 1987). With the different roles played by buried nonpolar and polar residues, it is an interesting question how this affects the balance between hydrophobic and polar residues. Indeed, studies addressing this question have been performed. A sequence-based study of the distribution of hydrophobicity in single-domain enzymes found that the relative hydrophobicity of the protein chains is essentially constant and shows no discernible dependence on protein size (Irbäck and Sandelin, 2000). This implies that the hydrophobicity of the core has to decrease as the length of the protein chains increases. Structure-based studies confirm this. Kajander et al. (2000) found that as proteins grow in size a larger and larger fraction of polar surface is buried, whereas Bolon and Mayo (2001), consistent with Kajander et al., observed an increase in the number of polar residues at core positions. Given the thermodynamically favorable effect of buried hydrophobic residues these findings might be somewhat surprising. However, as noted above, buried polar residues can contribute favorably to the formation of protein structures.
In this article we aim at improving upon the previous studies of the size-dependence of the composition of the interior of proteins. Using a normalized measure and by comparing with a background distribution of randomly reshuffled sequences, we show that the observed decrease in the hydrophobicity of the core (and the corresponding increase of buried polar residues) is statistically significant and robust as to how buried residues are defined and as to which amino acids are considered hydrophobic. Furthermore, we emphasize how this decrease is a direct consequence of the size-independence of the relative hydrophobicity of protein chains.
Finally, to explore how such a size-independence could arise, we study how requirements on stability and conformational specificity affect the distribution of hydrophobicity in a set of model sequences and structures. To this end we use the two-dimensional HP lattice model (Lau and Dill, 1989) for which it is possible to systematically explore this issue. This model contains only two types of amino acids, H (hydrophobic) and P (polar), the only interaction is pairwise attraction between hydrophobic residues, and the chain conformation is restricted to a two-dimensional lattice. Admittedly, this is a crude model of proteins which obviously has its limitations. These limitations must be carefully considered when deciding if the model is appropriate for addressing a certain question. For example, it has been shown that the additivity of the interaction scheme is insufficient to produce proteinlike thermodynamic cooperativity (Chan, 2000; Shimizu and Chan, 2002), and contributions from other types of interactions (in addition to hydrophobic) need to be incorporated to address more refined questions about the thermodynamics of protein folding (Kaya and Chan, 2000a,b). However, for studying the mapping between protein sequences and their native structures the HP model is useful. By invoking the consistency principle (Gõ, 1983) or principle of minimal frustration (Bryngelson and Wolynes, 1987), it has been argued (Chan et al., 2002; Cui et al., 2002) that for a proteinlike sequence, in the native conformation, there are no significant conflicts between the different interactions involved in the folding process, and hence it is reasonable to adopt the “working assumption” (Chan et al., 2002) that the native conformation must also be a unique or near-unique most-favored conformation when only considering its hydrophobic-polar pattern. The adoption of this working assumption is further encouraged by results from recent mutagenesis experiments (Cordes et al., 1999, 2000) which are consistent with findings from evolutionary studies of the HP model sequence-structure map (Bornberg-Bauer, 1997; Bornberg-Bauer and Chan, 1999; Chan and Bornburg-Bauer, 2002; Cui et al., 2002). Furthermore, it has also recently been found that HP model sequences exhibit the same type of hydrophobicity correlations as real proteins (Irbäck and Sandelin, 2000).
This article is organized as follows. In the next section (Methods), in the subsections Functional Protein Sequences and HP Model, we present the sequences studied. Surface Calculations describes the method used to calculate the accessible surface areas, Observables defines the observables studied, and Correlations shows the rank-order correlation method. Results and the Summary and Discussion sections follow.
METHODS
Functional protein sequences
For this study we select a nonredundant database of protein structures which we hope display statistical properties representative of functional (globular) folding units. To this end, by selecting one representative from each homologous superfamily, we start with all nonhomologous single-domain proteins from the November 2000 release of the structural classification database CATH (Orengo et al., 1997).
Using the Protein Quaternary Structure database (http://pqs.ebi.ac.uk), we select proteins classified as monomeric. This leaves us with 244 nonhomologous single-chain, single-domain, monomeric proteins. From this set we further remove proteins containing nonstandard residues in their PDB-entry (as indicated by the HETATM record).
A close inspection of the remaining proteins revealed a number of nonglobular proteins: three membrane proteins (1fio, 1vmo, and 1c4r), three ribosomal proteins (1a32, 1rss, and 1cqm), a virus capsid protein (1em9), an inhibition protein (1dvo), and a subunit fragment from RNA polymerase (1sig). Furthermore, this inspection also revealed seven proteins where CATH's single-domain classification is ambiguous (1d2p, 1cs6, 1eqf, 1eg3, 1d2o, 1dq3, and 1e4f) and four proteins which SCOP (Murzin et al., 1995) classifies as multidomain (1esl, 1ak2, 1plr, and 1eu4).
Of the remaining 127 proteins 89 had PDB-entries containing enough information to calculate their accessible surface areas (see Surface Calculations). A list of all the 89 proteins used can be found in the Appendix.
The sequences of these proteins are transformed into binary hydrophobicity strings by classifying amino acids as either hydrophobic or polar. Our calculations are performed using two different sets of hydrophobic amino acids. In the first set, referred to as Set 1, we take Leu, Ile, Val, Phe, Met, and Trp as hydrophobic, and in the second set, Set 2, in addition to the six amino acids above, we take Pro, Cys, and Ala as hydrophobic.
HP model
As mentioned in the Introduction, we want to study how requirements on stability and conformational specificity affect the balance between polar and hydrophobic residues. To this end, we need a set of protein sequences optimized for stability while still required to fold into their native state. Unfortunately, to our knowledge, existing sequence optimization methods for real proteins rely on either constraining the amino acid composition (Koehl and Levitt, 1999) or excluding polar residues from the core (Gordon et al., 1999; Marshall and Mayo, 2001), and thus they are of limited use for such a study. Instead we turn to the two-dimensional HP lattice model (Lau and Dill, 1989) for which it is possible to perform sequence optimization without any constraints on the amino acid composition.
The HP model contains only two types of amino acids, H (hydrophobic) and P (polar), and the chain conformation is represented as a self-avoiding walk of length N on a two-dimensional lattice. The formation of a hydrophobic core is favored by defining the energy as minus the number of HH pairs that form a contact, i.e., they are nearest neighbors on the lattice but not along the chain. For short chain lengths it is possible to make an exhaustive enumeration of both sequence and conformation space. Currently, the upper limit for exhaustive enumeration is N = 25 (Irbäck and Troein, 2002).
This is admittedly a coarse-grained model of proteins, but, as discussed in the Introduction, although it has its limitations it should be appropriate for the questions addressed in this article.
In this study we start with all sequences with a unique minimum energy conformation for 14 ≤ N ≤ 25. We will refer to these sequences as designing sequences and the number of sequences designing a given structure will be called the designability of that structure (Li et al., 1996). Furthermore, all structures with a designability >0 are said to be designable.
For N ≤ 18 we were able to perform the enumerations by ourselves, and for 18 < N ≤ 25 the designing sequences and their native structures were kindly provided to us by Irbäck and Troein (see Irbäck and Troein, 2002). From this set we select all structures with a designability >8 and their corresponding designing sequences. Table 1 shows the number of sequences and structures used for each N.
TABLE 1.
Number of HP model sequences used
| N | All | Maximally stable |
|---|---|---|
| 14 | 76 | 6 |
| 15 | 294 | 22 |
| 16 | 427 | 33 |
| 17 | 1450 | 99 |
| 18 | 2709 | 170 |
| 19 | 5964 | 432 |
| 20 | 12173 | 766 |
| 21 | 30576 | 545 |
| 22 | 55111 | 610 |
| 23 | 126981 | 618 |
| 24 | 219520 | 535 |
| 25 | 479310 | 626 |
To study the influence of stability and conformational specificity on the composition of the protein chains we want to select a set of designing sequences optimized for stability in their native states. To this end, for each of the designable structures in our dataset we select the designing sequence with highest folding temperature (N ≤ 18) or highest Boltzmann weight for the native state (N > 18). The folding temperature, Tf, is defined as the temperature where the probability for the sequence to visit its native state is 1/2. It was calculated by exhaustive enumeration of conformation space. For longer chains, N > 18, we were not able to perform this enumeration. Instead we applied the multisequence method (Irbäck and Potthast, 1995; Irbäck et al., 1999) to each structure to find the designing sequence with highest Boltzmann weight.
The multisequence method is a protein design method which aims at finding the sequence with largest Boltzmann weight for the target structure. Rather than estimate the Boltzmann weight by repeatedly performing Monte Carlo simulations for fixed sequence, it performs a single Monte Carlo simulation which simultaneously explores both sequence and conformation space. For coarse-grained models this method has been shown to be much more efficient than conventional protein design methods (Irbäck et al., 1999). Furthermore, if a sufficiently large number of Monte Carlo steps is used the method guarantees that for all of the surviving sequences the target structure will be a unique minimum energy conformation.
Here we apply the method in the following way. For a given structure we start with the complete set of sequences designing this structure. Then their Boltzmann weights for the native state are calculated by applying the multisequence method for 2 × 106 Monte Carlo steps at temperature, T = 1/3. This corresponds to ∼30 CPU seconds on a 1-GHz Pentium III processor. As a test, we apply the method to all the 170 N = 18 structures in our data set. For 161 of these it provides the sequence with the highest Tf and for the remaining nine structures it finds the sequence with second highest Tf. These results assure us that for the N > 18 structures it will provide us with sequences highly optimized for stability while still retaining the given structure as a unique minimum energy conformation.
For N > 20 we do not use all structures in our dataset but a random sampling of them. This sampling is performed such that we get roughly the same number of structures (∼600) for each N. Table 1 shows the number of maximally stable sequences in our dataset.
Surface calculations
The accessible surface area, ASA, of a molecule is defined by the center of a probe as it moves over the surface of the molecule. For proteins, the probe is commonly taken as a water molecule approximated as a sphere with radius 1.4 Å. Our calculations of the ASAs for our set of proteins were done using software kindly provided to us by Dr. Patrice Koehl. The procedure follows the scheme proposed by Shrake and Rupley (1973), but performs the calculation based on the Legrand and Merz algorithm (Legrand and Merz, 1993).
The degree of burial of an amino acid X in a protein is defined as the fraction of its current ASA and its ASA in a Gly-X-Gly tripeptide. A binary classification into buried and nonburied is then done by using a cutoff on the degree of burial. Four different cutoffs are used in this study: 45%, 30%, 15%, and 5%.
For HP sequences, a residue is classified as a core residue if it forms two or three contacts (it is possible for the residues at the ends of the chain to form three contacts). Furthermore, for the HP model, it is also useful to look at the set of residues forming at least one contact as this set corresponds to positions where a hydrophobic residue will always be energetically favored compared to a polar. This set of residues will be referred to as buried residues and includes core residues and residues that are partly exposed.
Observables
When establishing correlations between observables care must be taken as to how you define your observables and how you quantify the significance of the correlations. The latter problem will be addressed in the next section, whereas the former will be discussed here and in particular we will discuss areas where we believe we could improve upon previous studies.
In this study, for each protein, the N residues are classified as hydrophobic or polar and buried or nonburied. Then we count the number of buried residues, Nb, the number of hydrophobic residues Nh, and the number of buried residues that are hydrophobic, Nbh. These numbers are subsequently transformed into fractions:
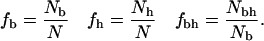 |
(1) |
When studying the distribution of polar residues in the core, Bolon and Mayo (2001) binned their data according to number of amino acids and looked at the averages for each bin. Although they this way observed an increase in the average fraction of polar residues at core positions, each average was within the standard deviations of all the other means. Thus it is difficult to quantify the significance of their observed correlation. Here, we will look at the raw fractions introduced above, quantifying the significance of observed correlations with rank-order analysis (see Correlations).
Another problem when establishing correlations is the presence of intrinsic biases in the dataset. For example, Kajander et al. (2000) found that the fraction of polar surface that is buried increases with protein size, and, in particular, they showed that the burial of charged polar surface increases faster than for uncharged polar and aromatic surfaces. However, since the relative size of the interior of globular proteins (per definition) increases with protein size, even if the different types of residues were randomly distributed in proteins, we would still expect the fractions of all types of surfaces that are buried to increase. Although Kajander et al. (2000) note that this intrinsic bias exists, it is unclear from their study how much this bias quantitatively affects their observations.
In this study we address this problem by normalizing fbh. If there were no biases present for different types of residues to reside in different parts of the protein, i.e., if polar and nonpolar residues were randomly distributed throughout the protein, we expect the hydrophobicity of the core to behave like fh. Hence, to account for possible intrinsic biases we normalize the fraction of buried residues that are hydrophobic,
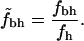 |
(2) |
Correlations
In this article we want to investigate the size-dependence of various observables. To quantify their correlations with size we use the Spearman rank-order correlation coefficient (Press et al., 1992), D. In contrast to the more commonly used linear correlation coefficient, rank correlation is not relying on any assumptions about the underlying distributions for the data points. Hence it is more robust when determining the significance of a correlation.
In rank correlation, pairs of quantities (xi, yi), i = 1, …., N, are replaced by their respective rank in the sample, i.e., xi and yi are transformed to integers Ri and Si, taking on values 1, …., N. Irrespective of the distribution of xi and yi, both Ri and Si will be distributed uniformly (Press et al., 1992). There exists several measures for detecting correlations between uniform sets of integers, and we will use one, the sum squared difference of ranks, D, defined as
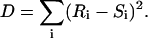 |
(3) |
To judge the significance of a correlation we will not look at the precise value of D, but rather at the two-sided significance level of how much D deviates from its null-hypothesis expected value, i.e., the expectation value of D if the data is uncorrelated. This significance level will be denoted by PD.
Furthermore, to be certain that observed correlations are not the result of intrinsic biases in the dataset we construct 1000 sets of proteins where the sequences of our original set of proteins have been randomly reshuffled. For each of these sets we calculate the rank-order correlations and count the number of times these correlations have a lower PD than the PD observed for the set of true sequences. This number is reported as ND.
RESULTS
Functional proteins
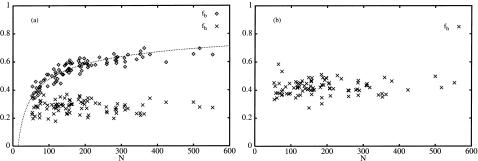
Fig. 1 shows data from the surface calculations for the proteins in our data set, with residues with ASA <30% defined as buried. The data in Fig. 1 a for the fraction of buried residues, fb, is consistent with a fit to a function with the form
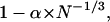 |
(4) |
with the constant α = 2.43. This behavior is expected for a set of solid objects deviating in a similar manner from a spherical shape and has been observed in monomeric proteins by several authors before (Chothia, 1975; Janin, 1976; Teller, 1976; Miller et al., 1987). Furthermore, Fig. 1 confirms the earlier finding by Irbäck and Sandelin (2000), that the fraction of hydrophobic residues, fh, is independent of chain length, with an average of 0.28 and 0.42 with six (Set 1, Fig. 1 a) and nine (Set 2, Fig. 1 b) amino acids as hydrophobic, respectively.
FIGURE 1.
(a) The fraction of buried residues, fb, and the fraction of hydrophobic residues, fh, as a function of chain length, N with Leu, Ile, Val, Phe, Met, and Trp considered hydrophobic, and residues with ASA < 30% considered buried. (b) fh with Leu, Ile, Val, Phe, Met, Trp, Cys, Pro, and Ala considered hydrophobic. The data for fb in a is fitted to a function of the form 1 − α × N−1/3 with α = 2.43.
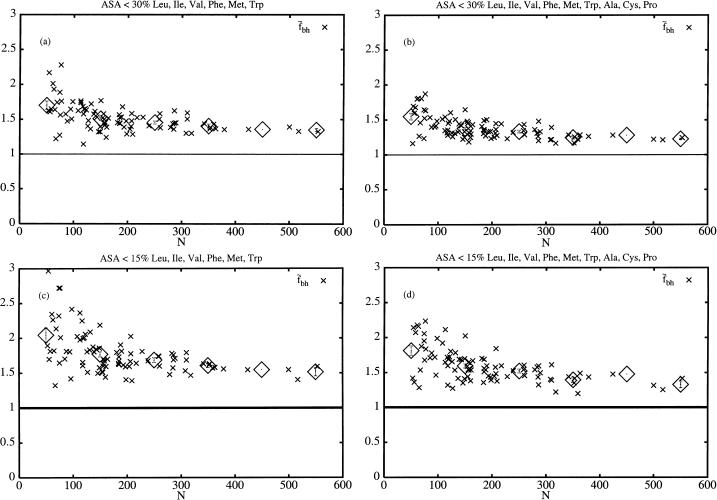
Fig. 2 shows 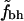 for the two different sets of hydrophobic residues and for two different definitions of buried residues. As can be seen, the hydrophobicity of the core seems to be decreasing with protein size. Furthermore, this holds true for all of the four different definitions of core residues and hydrophobic residues. We note, however, that in all four cases the core is still more hydrophobic than expected if the residues were randomly distributed in the protein, as indicated by the solid line at
for the two different sets of hydrophobic residues and for two different definitions of buried residues. As can be seen, the hydrophobicity of the core seems to be decreasing with protein size. Furthermore, this holds true for all of the four different definitions of core residues and hydrophobic residues. We note, however, that in all four cases the core is still more hydrophobic than expected if the residues were randomly distributed in the protein, as indicated by the solid line at 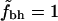 .
.
FIGURE 2.
Shown are 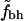 for the two sets of hydrophobic residues and for two different cutoffs for defining buried residues as indicated at the top of each figure. The ⋄ shows the averages of
for the two sets of hydrophobic residues and for two different cutoffs for defining buried residues as indicated at the top of each figure. The ⋄ shows the averages of 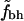 in bins of size 100.
in bins of size 100.
To quantify these observations we calculated the rank-order correlations as described in Correlations. In addition to the definitions above, these calculations were also performed, for both sets of hydrophobic residues, with buried residues defined by ASA < 15% and ASA < 5%. The results are shown in Table 2. It shows PD and ND for the rank-order correlation between fh and N, and between 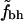 and N, for our full set of proteins and for the subset with N < 300.
and N, for our full set of proteins and for the subset with N < 300.
TABLE 2.
Rank-order correlations for fh and 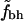 versus N
versus N
| Hydrophobic | Buried | PD | ND | PDN < 300 | NDN < 300 | |
|---|---|---|---|---|---|---|
| fh versus N | Set 1 | – | 0.98 | – | 0.59 | – |
| Set 2 | – | 0.25 | – | 0.24 | – | |
| Set 1 | ASA < 45% | 1.0 × 10−4 | 1000 | 2.1 × 10−3 | 996 | |
| Set 1 | ASA < 30% | 1.8 × 10−7 | 1000 | 2.0 × 10−5 | 1000 | |
| Set 1 | ASA < 15% | 2.9 × 10−7 | 1000 | 6.7 × 10−5 | 999 | |
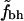 versus N versus N
|
Set 1 | ASA < 5% | 3.0 × 10−4 | 1000 | 1.3 × 10−2 | 972 |
| Set 2 | ASA < 45% | 2.5 × 10−5 | 1000 | 6.0 × 10−3 | 985 | |
| Set 2 | ASA < 30% | 8.3 × 10−8 | 1000 | 1.8 × 10−4 | 1000 | |
| Set 2 | ASA < 15% | 2.6 × 10−7 | 1000 | 1.7 × 10−4 | 1000 | |
| Set 2 | ASA < 5% | 3.7 × 10−7 | 1000 | 6.5 × 10−5 | 1000 |
Shown are PD and ND for the two different sets of hydrophobic amino acids and the four different cutoffs for defining buried residues. Data for both the full set of proteins and proteins with N < 300 is shown.
The values in Table 2 confirm the observations from Fig. 2. First we note that fh has no significant dependence on N, as indicated by the high PD-values. This is true for both sets of hydrophobic residues and also for the subset of proteins with N < 300. For all eight different definitions of burial and hydrophobicity 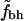 shows a significant correlation with N. In most cases the set with nine hydrophobic amino acids, Set 2, seems to have more significant correlations. We also note that the correlation is most significant when buried residues are defined as having ASA < 30% or ASA < 15%. When we restrict ourselves to shorter proteins the signal gets weaker but is still significant, except in possibly the case with Set 1 and ASA < 5% where PD is on the order of 10−2. We also note that the ND-values confirm that our observed correlations are true correlations.
shows a significant correlation with N. In most cases the set with nine hydrophobic amino acids, Set 2, seems to have more significant correlations. We also note that the correlation is most significant when buried residues are defined as having ASA < 30% or ASA < 15%. When we restrict ourselves to shorter proteins the signal gets weaker but is still significant, except in possibly the case with Set 1 and ASA < 5% where PD is on the order of 10−2. We also note that the ND-values confirm that our observed correlations are true correlations.
HP model
For the HP model sequences, with core and buried residues defined at the end of Surface Calculations, we count the number of core residues, Nc, the number of buried residues, Nb, the number of hydrophobic residues, Nh, the number of core residues that are hydrophobic, Nch, and the number of buried residues that are hydrophobic, Nbh. These numbers are subsequently transformed into fractions:
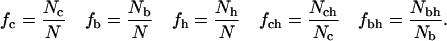 |
(5) |
Since the number of sequences for each N is large (see Table 1) it is not useful to look at the raw data. Instead we look at the averages of these fractions which we denote by 〈..〉.
From Fig. 3 a we can conclude that although both 〈fc〉 and 〈fb〉 clearly increase with protein size, 〈fh〉, just as for real proteins, has no discernible size-dependence, as noted before (Irbäck and Sandelin, 2000; Irbäck and Troein, 2002). More surprisingly, 〈fh〉 seems to be unaffected by the restriction to optimized sequences. Consequently, for both the set of all designing sequences and designing sequences optimized for stability, the average hydrophobicity of the interior is decreasing with protein size. As can be seen in Fig. 3 b both sets of sequences show this behavior, although optimized sequences on average have a more hydrophobic interior, as shown by both 〈fc〉 and 〈fb〉. However, we note that the core residues are still highly hydrophobic with <5% of the core residues polar for N = 25.
FIGURE 3.
Data for the HP model. (a) The size-dependence of the average of the fraction of hydrophobic residues, 〈fh〉, for all designing sequences and for optimized designing sequences. Also shown is the average fraction of core residues, 〈fc〉, and the average fraction of buried residues, 〈fb〉, for all designable structures. In b we show the size-dependence of the average fraction of core residues that are hydrophobic, 〈fch〉, and the average fraction of buried residues that are hydrophobic, 〈fbh〉. Shown is data for all designing sequences and for optimized designing sequences.
These results suggest that even if buried polar residues are energetically unfavorable, they still might be needed for a protein to retain its native state as a unique minimum energy structure. Consistent with this, we find that a substantial fraction of the designable HP structures have no sequence designing them with a completely hydrophobic core, i.e., a design procedure excluding polar residues from the core would fail for these structures (see Table 3, row A). For N = 25 these structures amounts to 14% of all designable structures. Furthermore, there is also a substantial fraction of designable structures for which the most stable designing sequence does not have a completely hydrophobic core, i.e., fch < 1.0 (see Table 3, row B).
TABLE 3.
Data for the HP sequences
| N | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 0% | 0% | 0% | 0% | 0% | 3% | 4% | 6% | 8% | 11% | 14% | 14% |
| B | 0% | 0% | 0% | 0% | 0% | 6% | 8% | 13% | 16% | 22% | 27% | 33% |
Row A shows the percentage of designable structures for which none of the designing sequences have a completely hydrophobic core, i.e., fch < 1.0 for all sequences. Row B shows the percentage of designable structures for which the most stable designing sequence have fch < 1.0.
SUMMARY AND DISCUSSION
Hydrophobicity plays a key role in the formation of protein structures which makes it of utmost interest to understand the distribution of hydrophobicity in protein sequences and structures. In this article we have studied the distribution of hydrophobic residues in the interior of globular proteins, and how this distribution is affected by requirements on stability and conformational specificity.
We started from the observation by Irbäck and Sandelin (2000) that the fraction of hydrophobic residues in globular proteins is roughly constant and shows no discernible dependence on protein size. This implies that for larger proteins more and more polar residues are buried, which indeed has been directly observed (Bolon and Mayo, 2001; Kajander et al., 2000). Using a nonredundant set of monomeric single-domain proteins, we reconfirmed these observations. Furthermore, using a normalized measure and by comparing with sets of randomly reshuffled sequences, we showed that this change in the composition of the core is statistically significant and robust with respect to which amino acids are considered hydrophobic and to how buried residues are defined.
Upon folding, the burial of hydrophobic residues is thermodynamically favorable for the formation of the native state. Given this it is somewhat surprising that the balance between hydrophobic and polar residues seems unaffected by the fact that the relative size of the interior of globular proteins increases with protein size. However, as mentioned in the Introduction, several experiments have shown that buried polar residues can contribute favorably to the stability of proteins and also be important for the conformational specificity of proteins.
To explore how such a size-independence of the hydrophobic/polar composition could arise, we studied how this composition is influenced by requirements on stability and conformational specificity. Although it is a well-known fact that functional proteins are only marginally stable (Dill, 1990), it is an interesting limiting case to study how the balance between hydrophobic and polar residues is affected by optimizing a set of sequences for stability under the constraint that they retain their native state as a unique most-favored conformation. Unfortunately, existing sequence optimization methods for real proteins do not allow for a freely varying amino acid composition. Instead, for this study, we used the two-dimensional HP lattice model where sequence optimization can be performed without constraining the composition. Starting with the set of all sequences which have a unique minimum energy conformation, we found that for both the set of all sequences and the subset of sequences optimized for stability the average fraction of hydrophobic residues, just as for real proteins, shows no dependence on chain length. Furthermore, the restriction to optimized sequences has very little effect on the average fraction of hydrophobic residues.
These model results suggest that conformational specificity requires a careful balance of hydrophobic and polar residues and the requirement on proteins to be conformational-specific for their native state imposes constraints on the composition of the sequences. This suggestion is further supported by the fact that the HP model sequences with unique minimum energy conformations have earlier been shown to differ significantly from random sequences in that they exhibit hydrophobicity correlations along the chain similar to what is seen in real proteins (Irbäck and Sandelin, 2000).
The HP model is obviously a coarse-grained model and care must be taken to not extrapolate these model results too far. However, as discussed in the Introduction, there are theoretical arguments, boosted by experimental observations, that this model should indeed be useful for studies, such as this, interested in the mapping between sequence and structure. Furthermore, although the HP model has its limitations, it is an interesting observation that in a simple model where conformational specificity is just a matter of counting the number of ways you can fold a self-avoiding walk to obtain a certain number of HH contacts, buried polar residues, despite being energetically unfavorable in this model, are required by a substantial number of proteins to retain their conformational specificity.
Of course, it would be interesting to see if our observations for optimized sequences persist for more realistic models and for real proteins. Hopefully, future improvements in protein design algorithms and computational power will make such a study feasible.
Acknowledgments
The authors thank Patrice Koehl for providing us with the software to perform the surface calculations, Carl Troein for sharing his HP model data for N > 18, and Anders Irbäck for valuable discussions.
E.S. acknowledges support from the Knut and Alice Wallenberg Foundation.
APPENDIX
The complete list of the 89 PDB entries used in this study is as follows:
1hst, 1enh, 1hyp, 1ycr, 1r69, 1bkr, 1maz, 2end, 1ad6, 1col, 153l, 1pbw, 1pah, 1poa, 1nfn, 1a7d, 1a0b, 2gmf, 2lis, 1dvk, 1bd8, 1cem, 1brf, 2ovo, 1abo, 1mjc, 1lop, 1dsl, 1hoe, 1noa, 1amx, 1thv, 1xnb, 1czt, 1bfg, 1rie, 1qlg, 1air, 1igd, 4fxc, 1ubi, 1mol, 2cba, 1tml, 1nar, 1tri, 1qtw, 1vcc, 1vhh, 1hka, 1a6f, 2rn2, 1fil, 1ekg, 2gar, 1chd, 1thm, 1phr, 1zon, 1tah, 2pth, 1lba, 1ovb, 1c25, 1avp, 1udg, 1uch, 2blt, 1ytn, 1vfy, 1mwp, 1gzi, 1bk7, 1mir, 1quv, 1jet, 1qgi, 1d0b, 1c1k, 1cwy, 1dde, 1psz, 1qjv, 1c44, 1f82, 1dvn, 1b04, 1qmy, 1qnx.
References
- Bolon, D. N., and S. L. Mayo. 2001. Polar residues in the core of Escherichia coli thioredoxin are important for fold specificity. Biochemistry. 40:10047–10053. [DOI] [PubMed] [Google Scholar]
- Bornberg-Bauer, E. 1997. How are model protein structures distributed in sequence space? Biochemistry. 73:2393–2403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bornberg-Bauer, E. and H. S. Chan. 1999. Modeling evolutionary landscapes: mutational stability, topology and superfunnels in sequence space. Proc. Natl. Acad. Sci. USA. 96:10689–10694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryngelson, J. D., and P. G. Wolynes. 1987. Spin-glasses and the statistical-mechanics of protein folding. Proc. Natl. Acad. Sci. USA. 84:7524–7528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan, H. S. 2000. Modeling protein density of states: additive hydrophobic effects are insufficient for calorimetric two-state cooperativity. Prot. Struct. Funct. Gen. 40:543–571. [DOI] [PubMed] [Google Scholar]
- Chan, H. S., H. Kaya, and S. Shimizu. 2002. Computational methods for protein folding: scaling a hierarchy of complexities. In Current Topics in Computational Molecular Biology. T. Jiang, Y. Xu, and M. Q. Zhang, editors. MIT Press, Cambridge, MA. 403–447.
- Chan, H. S., and E. Bornberg-Bauer. 2002. Perspectives on protein evolution from simple exact models. Appl. Bioinformatics. 1:121–144. [PubMed] [Google Scholar]
- Chothia, C. 1975. Structural invariants in protein folding. Nature. 254:304–308. [DOI] [PubMed] [Google Scholar]
- Chothia, C. 1976. The nature of the accessible and buried surfaces in proteins. J. Mol. Biol. 105:1–14. [DOI] [PubMed] [Google Scholar]
- Cordes, M. H. J., N. P. Walsh, C. J. McKnight, and R. T. Sauer. 1999. Evolution of a protein fold in vitro. Science. 284:325–327. [DOI] [PubMed] [Google Scholar]
- Cordes, M. H. J., R. E. Burton, N. P. Walsh, C. J. McKnight, and R. T. Sauer. 2000. An evolutionary bridge to a new protein fold. Nat. Struct. Biol. 7:1129–1132. [DOI] [PubMed] [Google Scholar]
- Cui, Y., W. H. Wong, E. Bornberg-Bauer, and H. S. Chan. 2002. Recombinatoric exploration of novel folded structures: a heteropolymer-based model of protein evolutionary landscapes. Proc. Natl. Acad. Sci. USA. 99:809–814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dahiyat, B. I., C. A. Sarisky, and S. L. Mayo. 1997. De novo protein design: towards fully automated sequence selection. J. Mol. Biol. 273:789–796. [DOI] [PubMed] [Google Scholar]
- Dill, K. A. 1990. Dominant forces in protein folding. Biochemistry. 29:7133–7155. [DOI] [PubMed] [Google Scholar]
- Eriksson, A. E., W. A. Baase, X. J. Zhang, D. W. Heinz, M. Blaber, E. P. Baldwin, and B. W. Matthews. 1992. Response of a protein-structure to cavity-creating mutations and its relation to the hydrophobic effect. Science. 255:178–183. [DOI] [PubMed] [Google Scholar]
- Gõ, N. 1983. Theoretical studies of protein folding. Annu. Rev. Biophys. Bioeng. 12:183–210. [DOI] [PubMed] [Google Scholar]
- Gordon, D. B., S. A Marshall, and S. L. Mayo. 1999. Energy functions for protein design. Curr. Opin. Struct. Biol. 9:509–513. [DOI] [PubMed] [Google Scholar]
- Hendsch, Z. S., and B. Tidor. 1994. Do salt bridges stabilize proteins? A continuum electrostatic analysis. Prot. Sci. 3:211–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irbäck, A., and F. Potthast. 1995. Studies of an off-lattice model for protein folding: sequence dependence and improved sampling at finite temperature. J. Chem. Phys. 103:10298–10305. [Google Scholar]
- Irbäck, A., C. Peterson, F. Potthast, and E. Sandelin. 1999. Design of sequences with good folding properties in coarse-grained protein models. Struct. Fold. Des. 7:347–360. [DOI] [PubMed] [Google Scholar]
- Irbäck, A., and E. Sandelin. 2000. On hydrophobicity correlations in protein chains. Biophys. J. 79:2252–2258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irbäck, A., and C. Troein. 2002. Enumerating designing sequences in the HP model. J. Biol. Phys. 28:1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janin, J. 1976. Surface area of globular proteins. J. Mol. Biol. 105:13–14. [DOI] [PubMed] [Google Scholar]
- Ji, H., C. Bracken, and M. Lu. 2000. Buried polar interactions and conformational stability in the simian immunodeficiency virus (SIV) gp41 core. Biochemistry. 4:676–685. [DOI] [PubMed] [Google Scholar]
- Kajander, T., P. C. Kahn, S. H. Passila, D. C. Cohen, L. Lehitö, W. Adolfsen, J. Warwicker, U. Schell, and A. Goldman. 2000. Buried charged surface in proteins. Struct. Fold. Des. 8:1203–1214. [DOI] [PubMed] [Google Scholar]
- Kauzmann, W. 1954. The Mechanism of Enzyme Action. Johns Hopkins Press, Baltimore, MD.
- Kaya, H., and H. S. Chan. 2000a. Polymer principles of protein calorimetric two-state cooperativity. Prot. Struct. Funct. Gen. 40:637–661. [DOI] [PubMed] [Google Scholar]
- Kaya, H., and H. S. Chan. 2000b. Energetic components of cooperative protein folding. Phys. Rev. Lett. 85:4823–4826. [DOI] [PubMed] [Google Scholar]
- Koehl, P., and M. Levitt. 1999. De novo protein design. I. In search of stability and specificity. J. Mol. Biol. 293:1161–1181. [DOI] [PubMed] [Google Scholar]
- Lau, K. F., and K. A. Dill. 1989. A lattice statistical model for the conformational and sequence spaces of proteins. Macromolecules. 22:3986–3997. [Google Scholar]
- Li, H., R. Helling, C. Tang, and N. Wingreen. 1996. Emergence of preferred structures in a simple model of protein folding. Science. 273:666–669. [DOI] [PubMed] [Google Scholar]
- Legrand, S. M., and K. M. Merz. 1993. Rapid approximation to molecular-surface area via the use of Boolean logic and look-up tables. J. Comput. Chem. 14:349–352. [Google Scholar]
- Loladze, V. V., D. N. Ermolenko, and G. I. Makhatadze. 2002. Thermodynamic consequences of burial of polar and non-polar amino acid residues in the protein interior. J. Mol. Biol. 320:343–357. [DOI] [PubMed] [Google Scholar]
- Lumb, K. J., and P. S. Kim. 1995. A buried polar interaction imparts structural uniqueness in a designed Heterodimeric coiled-coil. Biochemistry. 34:8642–8648. [DOI] [PubMed] [Google Scholar]
- Malakauskas, S. M., and S. L. Mayo. 1998. Design, structure and stability of a hyperthermophilic protein variant. Nat. Struct. Biol. 5:470–475. [DOI] [PubMed] [Google Scholar]
- Marshall, S. A., and S. L. Mayo. 2001. Achieving stability and conformational specificity in designed proteins via binary patterning. J. Mol. Biol. 305:619–631. [DOI] [PubMed] [Google Scholar]
- Matsumura, M., W. J. Becktel, and B. W. Matthews. 1988. Hydrophobic stabilization in T4 lysozyme determined directly by multiple substitutions of ILE-3. Nature. 334:406–410. [DOI] [PubMed] [Google Scholar]
- Miller, S., J. Janin, A. M. Lesk, and C. Chothia. 1987. Interior and surface of monomeric proteins. J. Mol. Biol. 196:641–656. [DOI] [PubMed] [Google Scholar]
- Murzin, A. G., S. E. Brenner, T. Hubbard, and C. Chothia. 1995. SCOP: a structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol. 247:536–540. [DOI] [PubMed] [Google Scholar]
- Orengo, C. A., A. D. Michie, S. Jones, D. T. Jones, M. B. Swindells, and J. M. Thornton. 1997. CATH—a hierarchic classification of protein domain structures. Structure. 5:1093–1108. [DOI] [PubMed] [Google Scholar]
- O'Shea, E. K., R. Rutkowski, and P. S. Kim. 1992. Mechanism of specificity in the Fos-Jun oncoprotein heterodimer. Cell. 68:699–708. [DOI] [PubMed] [Google Scholar]
- Pace, C. N., B. A. Shirley, M. McNutt, and K. Gaijwala. 1996. Forces contributing to the conformational stability of proteins. FASEB J. 10:75–83. [DOI] [PubMed] [Google Scholar]
- Perutz, M. F., J. C. Kendrew, and H. C. Watson. 1965. Structure and function of haemoglobin II. Some relations between polypeptide chain configuration and amino acid sequence. J. Mol. Biol. 13:669–678. [Google Scholar]
- Press, W. H., S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. 1992. Numerical Recipes in C. The Art of Scientific Computing. Cambridge University Press, UK.
- Radzicka, A., and R. Wolfenden. 1988. Comparing the polarities of the amino acids—side-chain distribution coefficients between the vapor-phase, cyclohexane, 1-octanol, and neutral aqueous-solution. Biochemistry. 27:1664–1670. [Google Scholar]
- Russell, R. B., and G. J. Barton. 1994. Structural features can be unconserved in proteins with similar folds—an analysis of side-chain to side-chain contacts secondary structure and accessibility. J. Mol. Biol. 244:332–350. [DOI] [PubMed] [Google Scholar]
- Schueler, O., and H. Margalit. 1995. Conservation of salt bridges in protein families. J. Mol. Biol. 248:125–135. [DOI] [PubMed] [Google Scholar]
- Shimizu, S., and H. S. Chan. 2002. Anti-cooperativity and cooperativity in hydrophobic interactions: three-body free energy landscapes and comparison with implicit-solvent potential functions for proteins. Prot. Struct. Funct. Gen. 48:15–30. [DOI] [PubMed] [Google Scholar]
- Shrake, A., and J. A. Rupley. 1973. Environment and exposure to solvent of protein atoms. Lysozyme and insulin. J. Mol. Biol. 79:351–371. [DOI] [PubMed] [Google Scholar]
- Takano, K., Y. Yamagata, and K. Yutani. 2001. Contribution of polar groups in the interior of a protein to the conformational stability. Biochemistry. 40:4853–4858. [DOI] [PubMed] [Google Scholar]
- Teller, D. C. 1976. Accessible area, packing volumes and interaction surfaces of globular proteins. Nature. 260:729–731. [DOI] [PubMed] [Google Scholar]
- Waldburger, C. D., J. F. Schildbach, and R. T. Sauer. 1995. Are buried salt bridges important for protein stability and conformational specificity? Nat. Struct. Biol. 2:122–128. [DOI] [PubMed] [Google Scholar]
- Wesson, L., and D. Eisenberg. 1992. Atomic solvation parameters applied to mlcular dynamics of proteins in solution. Protein Sci. 1:227–235. [DOI] [PMC free article] [PubMed] [Google Scholar]