Abstract
Coagulation factor V (FV) is a large plasma glycoprotein with functions in both the pro- and anticoagulant pathways. In carriers of the so-called R2-FV haplotype, the FV D2194G mutation, in the C2 membrane-binding domain, is associated with low expression levels, suggesting a potential folding/stability problem. To analyze the molecular mechanisms potentially responsible for this in vitro phenotype, we used molecular dynamics (MD) and continuum electrostatic calculations. Implicit solvent simulations were performed on the x-ray structure of the wild-type C2 domain and on a model of the D2194G mutant. Because D2194 is located next to a disulfide bond (S-S bond), MD calculations were also performed on S-S bond depleted structures. D2194 is part of a salt-bridge network and investigations of the stabilizing/destabilizing role of these ionic interactions were carried out. Five mutant FV molecules were created and the expression levels measured with the aim of assessing the tolerance to amino acid changes in this region of molecule. Analysis of the MD trajectories indicated increased flexibility in some areas and energetic comparisons suggested overall destabilization of the structure due to the D2194G mutation. This substitution causes electrostatic destabilization of the domain by ∼3 kcal/mol. Together these effects likely explain the lowered expression levels in R2-FV carriers.
INTRODUCTION
Coagulation factor V (FV) is the precursor of an essential procoagulant cofactor that accelerates FXa-catalyzed prothrombin activation. It is a large glycoprotein that is structurally and functionally homologous to factor VIII (FVIII), the two proteins sharing the domain organization A1-A2-B-A3-C1-C2. Activation of FV involves proteolytic removal of the large B domain, converting the procofactor into the fully active cofactor FVa (Nicolaes and Dahlback, 2002; Mann and Kalafatis, 2003). Interestingly, FV also has a reported anticoagulant function in the APC-mediated inactivation of FVIIIa (reviewed by Nicolaes and Dahlback, 2002). FV and FVIII interact with many proteins and bind to cell surfaces, essentially via the C2 domain. The three-dimensional (3D) structure of the C2 domains of FV/FVIII was initially predicted using a combination of threading and comparative modeling based on the structure of galactose oxidase (Villoutreix et al., 1998; Pellequer et al., 1998; Baumgartner et al., 1998). Despite very low sequence identity (∼10%) between the C domains of FV/FVIII and galactose oxidase, the overall 3D fold of the predicted structures was correct as seen from comparison with recently reported x-ray structures of the isolated C2 domains of FV and FVIII (Macedo-Ribeiro et al., 1999; Pratt et al., 1999). These C domains (also called discoidin domains) exhibit a distorted jelly-roll β-barrel motif, consisting of eight major antiparallel strands arranged in two β-sheets. The amino- and carboxy-terminal segments are clamped together by the only disulfide bond (S-S bond) present in this module (C2038-C2193). The modeled and experimental structures of the C2 domain of FV allowed for proposal of key regions involved in membrane binding (Nicolaes et al., 2000; Kim et al., 2000). This FV membrane-binding motif consists of several exposed hydrophobic side chains located essentially on loop structures (e.g., the 2060-loop), surrounded by a ring of basic residues. In human plasma, FV circulates as a mixture of two isoforms, FV1 (glycosylated) and FV2 (not glycosylated) that have slightly different molecular weights because of partial N-linked glycosylation at N2181. This leads to differences in membrane-binding behavior between FV1 and FV2 (Rosing et al., 1993; Hoekema et al., 1997, Nicolaes et al., 1999). Also, glycosylation at N2181 has been proposed to modulate the FV expression levels (Nicolaes et al., 1999).
The FV R2 haplotype, first described in a cohort of thromboembolic patients, encompasses several genetically linked polymorphisms, that encode amino acid substitutions (of which M385T, H1299R, M1736V, and D2194G are most likely linked to the haplotype) in different domains of the molecule (Lunghi et al., 1996; Bernardi et al., 1997; Castoldi et al., 2000). There is no consensus from epidemiogical studies if these polymorphisms are associated with venous or arterial thrombosis. Yet, in vitro studies have demonstrated that at least, the D2194G substitution in the FV C2 domain induces a substantially impaired expression due to retention of the mutant protein in the endoplasmic reticulum (ER), a place where misfolded protein tends to be trapped and degraded (Yamazaki et al., 2002). Thus the D2194G substitution appears to affect the folding/structure/stability of the C2 domains (Yamazaki et al., 2002; Van Der Neut Kolfschoten et al., 2003) via mechanisms that are not fully understood.
It is a major challenge to establish the links between point mutations, 3D structures, and disease states (Villoutreix, 2002; Bross et al., 1999; Wickner et al., 1999; Sinha and Nussinov, 2001, Hilser et al., 1998; Taverna and Goldstein, 2002). Potential impacts of mutations on protein stability, folding, and function can be investigated theoretically using a single 3D conformation of the folded native protein as a starting point (Wang and Moult, 2001) or via (short/long) molecular dynamics (MD) simulations (Cregut and Serrano, 1999; Schiffer and van Gunsteren, 1996; Kazmirski et al., 1995; Rizzuti et al., 2001). When a mutation involves a charged residue that has ionic interactions with surrounding groups, some specific electrostatic computations can also be performed to investigate the stabilizing or destabilizing roles of salt bridges on the protein stability (Kumar and Nussinov, 1999; Hendsch and Tidor, 1994; Lounnas and Wade 1997; Barril et al., 1998; Dong and Zhou, 2002).
To study the potential impacts of the D2194G mutation on the C2 domain of human FV, we used MD, electrostatic computations and site-directed mutagenesis. In the native 3D structure of the C2 domain, residue D2194 is partially solvent exposed, fully conserved in the FV species and located next to the C2038-C2193 disulfide bond. It is involved in electrostatic interactions with the side chains of K2101 and K2103. We hypothesized that the D2194G substitution could affect the stability of the molecule due to electrostatic destabilization and/or induce conformational/flexibility changes. Due to its position, directly juxtaposed to the disulfide bridge in the C2 domain, the D2194G mutation could also influence disulfide bond formation. We decided to run MD simulations with an implicit solvent model on the C2 domain of wild-type FV (WT-FV) and on the D2194G mutant, in the presence or the absence of the C2038-C2193 bond. Simulations without the S-S bond were carried out to examine some of the effects of this bond on the 3D structure of the domain. Electrostatic computations were also run on different C2 structures to further investigate the role of ionic interactions in the 2194 area. Several mutant proteins (D2194K, K2101E/K2103E, K2101E/K2103E/D2194K, and C2038A/C2193A) were produced and the final expression levels characterized to assess the overall sensitivity of this region to amino acid changes. Taken together, our data indicate that aspartate at position 2194 is important for the stability of the domain and that the above amino acid substitutions affect the stability and/or the conformation of the domain.
COMPUTATIONAL METHODS
Molecular dynamics
Molecular dynamics simulations were carried out on the high resolution x-ray structure (Macedo-Ribeiro et al., 1999) of domain C2 of WT-FV and on a model of the D2194G mutant. The x-ray structure of the human WT-FV C2 domain (Macedo-Ribeiro et al., 1999) was taken from the Protein Data Bank (Berman et al., 2000) (entry 1czt; 1.8 Å resolution). There is no experimental structure for the D2194G mutant and we have built an initial 3D model for this domain on the basis of the WT structure by simply removing the D2194 side chain. The N-terminal group was acetylated in all initial structures to account for the fact that this residue is linked to the C1 domain. MD simulations were performed: for the WT-C2 domain and the mutant D2194G, with or without the disulfide bond C2038-C2193. The same protocol for energy minimization and molecular dynamics was used for all the relevant simulations. Calculations were performed using the program CHARMm (Brooks et al., 1983) using CHARMm 22 parameters on two Silicon Graphics (IRIX 6.5) Fuel V12 single 600-MHz processor workstations (Mountain View, CA). Interactive analysis of the results was performed in InsightII (running on SGI workstations) or with ICM (Molsoft, La Jolla, CA) running on two Precision 530 Dell PC dual-2.4-GHz processors driven by Red Hat Linux 7.3.
The importance of correct accounting for solvation effects during MD simulations has been widely discussed. Because explicit treatment of solvent is very time consuming and eventually not needed, several implicit methods have been proposed for calculation of solvation effects in proteins (Bashford and Case, 2000, Feig and Brooks, 2002). We have used in our MD simulations the Generalized Born (GB) method as implemented by Dominy and Brooks (1999) into the program CHARMm to account for the electrostatic contribution to the solvation energy (Brooks et al., 1983) (version 27.b1 or 28.b1, Accelrys, San Diego, CA). The GB approximation is based on a two-dielectric model and its mathematical form, for a molecule with arbitrary shape, has been extensively parameterized (Dominy and Brooks, 1999).
The empirical Atomic Solvation Parameter (ASP) approach as proposed by Wesson and Eisenberg (1992) with parameterization by Sharp et al. (1991) was also applied to account for the nonpolar solvation energy. This method assumes that the nonpolar (considered in the present article to be the solvent-solvent cavity and solute-solvent van der Waals terms) solvation free energy of the solute can be decomposed into a sum of atomic free energy components that are proportional to the solvent accessible surface (SAS) of atoms of type k: Ghydrophobic = ∑σk SASk. Here we used σk = 12.3 cal/mol/Å2 for the hydrophobic carbon atoms and σk = 0.0 cal/mol/Å2 for the other atoms as suggested by several research groups (Qiu et al. 1997; Morozov et al. 2003).
The charge-charge interactions were treated using Coulomb law with a dielectric constant ɛ = 1 to be consistent with the GB parameterization. The GB parameters proposed in Dominy and Brooks (1999) were used and a dielectric constant of 80 was applied to represent the highly polarizable solvent medium. For all nonbonded interactions we used a cutoff of 15 Å and a switch function.
Initial hydrogen positions were calculated using the HBUILD utility of CHARMm. Definition of the charged state for the titratable groups in the x-ray structure of WT-FV and the mutant D2194G before the MD simulations was decided after electrostatic computations of the mean proton occupancy (see below for computational details). The results indicated that all Lys, Arg, Glu, Asp, and the C-terminal group are charged whereas the remaining residues including His residues were found to be neutral. Only K2148 was found not to be completely charged (calculated mean proton occupancy q = 0.4) at pH = 7.
The initial 3D structures were energy minimized (1500 steps steepest descent method or a tolerance of energy gradient of 0.15 kcal/mol/Å) and MD simulations were then performed on the minimized structures. The temperature of the system was raised gradually from 240 to 300 K in 20 ps followed by equilibration at 300 K for 50 ps. This was further continued by a 900-ps production run of NVT-MD at 300 K with the Berendsen algorithm (Berendsen et al. 1984) and the protein conformations were recorded every 1 ps. The time step was 1 fs and the SHAKE algorithm was used to eliminate the high frequency hydrogen/heavy atom bond vibrations.
Electrostatic calculations
All electrostatic calculations (pKa, electrostatic free energies of stabilization) were performed for the WT and mutants but only on the structures possessing the S-S bond. Thus, the x-ray structure of the WT, the structures with the D2194G, D2194K, K2101E/K2103E, K2101E/K2103E/D2194K substitutions (without simulations) were selected for computations. The same calculations were also carried out on the last conformations of the MD simulations for the WT and the D2194G mutant, as well as on 30 structures sampled from the MD trajectories from 670 to 970 ps of the production run (one structure selected every 10 ps).
Finite difference Poisson-Boltzmann energy calculations
For computation of electrostatic energies used in protonation states and electrostatic stabilization calculations, we used the program UHBD (Davis et al., 1991) that solves the Poisson-Boltzmann equation numerically on a grid by the finite difference method (Warwicker and Watson, 1982; Sharp and Honig, 1990; Yang et al., 1993). It has been previously proposed (Antosiewicz et al., 1994) that a better agreement between calculated and experimental pKa values of titratable groups can be obtained using a higher protein dielectric constant (e.g., ɛin = 20). However, in this work we use ɛin = 4, because accurate results for evaluation of salt-bridge energetic were obtained earlier with this value (Hendsch & Tidor, 1994; Lounnas and Wade, 1997; Barril et al., 1998). The protein atomic radii and charges were based on the CHARMm 22 parameter set. The dielectric boundary between the protein and solvent was defined using the solvent accessibility surface with probe sphere of radius 1.4 Å and 500 dots per atom for generation of the surface. Initial boundary conditions were determined by calculating the potential at each boundary point using the Debye-Huckel approximation. A salt concentration of 0.15 M and salt exclusion radius of 2.0 Å were used in the finite difference Poisson-Boltzmann (FDPB) calculations.
In the calculation of protonation states, first the protein structures were included into a grid of 45 × 45 × 45 points with a resolution of 2.5 Å. A focusing scheme proposed previously (Yang et al., 1993; Antosiewicz et al., 1994) using four successive lattices with increasing grid resolution was applied for calculation of electrostatic potentials created by every ionized group. The last focusing run was done in a 3D grid of dimension of 20 nodes and a resolution of 0.25 Å centered at the titration site. A procedure with two focusing runs in boxes of dimension of 65 with resolution of 1.5 Å, followed by a box of dimension of 70 with a 0.3-Å resolution, was applied to calculate the electrostatic energies involved in the calculation of electrostatic stabilization of the charged triads (see below).
Protonation states
The FDPB method has been widely used for calculation of protein protonation states (Bashford and Karplus, 1990; Yang et al., 1993; Antosiewicz et al., 1994). To calculate intrinsic pKa value (pKint) of a given titratable group (Tanford and Kirkwood, 1957), (the pKint is defined as the pKa that the group would have if all other titratable groups were neutral) one unit charge at the protonation site of this group and all permanent partial charges of the protein were taken into account.
The protonation state n of a protein with N titratable residues is characterized by the protonation state vector δn(i), i = 1 to N, where δn(i) = 1 when the ith group is charged and 0 when it is neutral. The free energy of the nth protonation state ΔGn is given by:
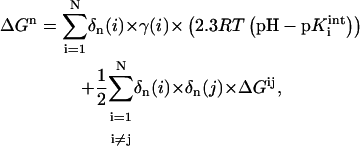 |
(1) |
where γ(i) = −1 or 1 for an acidic or basic group i, respectively, 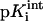 is the intrinsic pKa value of the group i, and ΔGij is the electrostatic interaction energy between groups i and j in their charged states defined by δ(i) and δ(j). In this work the protonation states of all studied structures were obtained at pH 7.0 (Antosiewicz et al., 1994).
is the intrinsic pKa value of the group i, and ΔGij is the electrostatic interaction energy between groups i and j in their charged states defined by δ(i) and δ(j). In this work the protonation states of all studied structures were obtained at pH 7.0 (Antosiewicz et al., 1994).
In the computation of electrostatic potentials φij due to the charge j at the location of the charged site i, involved in pairwise interactions calculation (ΔGij = γi·φij), only a unit charge at the protonation site was included. The protonation sites were set to the atoms: Cγ of Asp, Cδ of Glu, Cζ of Arg, Nζ of Lys, Nɛ2 of His, OH of Tyr, C atom of main-chain C-terminus. The mean proton occupancies q of titratable groups at pH 7 are computed by averaging over the protonation states sampled by the Monte Carlo method based on the ΔGn calculations (Antosiewicz and Porschke, 1989).
Electrostatic free-energy contributions to the protein stability for salt-link triads
The electrostatic free energy, ΔΔGtot, contributing to protein stability due to a triad of charged amino acid residues in a protein (WT or mutants) was calculated relative to a reference protein hydrophobic isosteres (an isostere is defined as a residue with the same conformation and position in the protein as the original residue but neutral). The term ΔΔGtot was calculated following the procedure proposed by Hendsch and Tidor (1994):
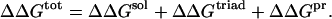 |
(2) |
The three terms ΔΔGsol, ΔΔGtriad, ΔΔGpr were computed as differences between the energies of the protein and the protein with appropriate amino acids involved into the ionic triad replaced to their respective hydrophobic isosteres.
The desolvation electrostatic energy ΔGsol of the triad in a protein was calculated as:
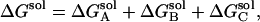 |
(3) |
and 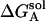 ,
, 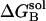 , and
, and 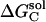 are the electrostatic desolvation free energies of each residue of the triad A, B, C, respectively. The electrostatic desolvation energy ΔGsolv for taking a residue from solvent to protein environment is given following Gilson and Honig (1988).
are the electrostatic desolvation free energies of each residue of the triad A, B, C, respectively. The electrostatic desolvation energy ΔGsolv for taking a residue from solvent to protein environment is given following Gilson and Honig (1988).
The electrostatic energy of internal interactions in the triad ΔGtriad was presented as:
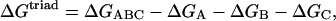 |
(4) |
where ΔGABC is the electrostatic free energy of the protein involving only the charges of the triad; ΔGA, ΔGB, ΔGC are the electrostatic free energies of the protein involving the charges of only one of the triad residues A, B, or C, respectively.
The electrostatic free energy of interactions between the triad and the rest of the protein ΔGpr is calculated by:
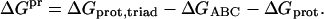 |
(5) |
The three terms in Eq. 5 correspond to electrostatic free energy of the protein when all protein charges are present (ΔGprot,triad); all charges are present excluding the charges of the triad (ΔGprot), and only the charges of the triad are present (ΔGABC).
These calculations were performed for investigation of the WT triad (D2194, K2101, K2103 versus the mutant G2194, K2101, K2103). In the calculation of these electrostatic energies of stabilization, the atomic partial charges corresponding to CHARMm22 parameters were used (such charged state of the groups is in agreement with our calculated mean proton occupancies q at pH 7 for the WT and D2194G mutant). In the modeled MD structures of WT and mutant D2194G all Lys, Arg, Glu, Asp, and C-term residues were calculated to be charged and the other groups, including the His residues were computed to be neutral.
For other C2 mutant structures (D2194K, K2101E/K2103E, K2101E/K2103E/D2194K), residue E2103 in mutants K2101E/K2103E and K2101E/K2103E/D2194K, as well as residue K2101 in mutant D2194K were taken noncharged in the calculation of triad electrostatic stabilization, as computed from the mean proton occupancies.
EXPERIMENTAL PROCEDURES
Site-directed mutagenesis
Site-directed mutagenesis was performed using the Quick Change Site-Directed Mutagenesis Kit (Stratagene, La Jolla, CA) according to the manufacturer's instructions to generate new variant FV recombinant molecules: D2194K, K2101E/K2103E, C2038A/C2193A. As a template we used the full-length cDNA of human FV, coding for the FV2 isoform (WT-N2181Q) described previously (Nicolaes et al., 1999). A fourth mutant was constructed by mutagenesis of D2194 into K, using the K2101E/K2103E plasmid as a template. The construction of an expression vector for recombinant FV containing the R2-associated D2194G mutation has previously been described (Yamazaki et al., 2002). Two complementary oligonucleotides (DNA Technology, Aarhus C, Denmark) were used as mutagenic primers for each construct, the sense oligo being:
5′-GAACTCTTTGGCTGTAAGATTTACTAGAATTG-3′ (D2194K),
5′-TTGATCTACTCGAGATCGAGAAGATAACGGC-3′ (K2101E/K2103E),
5′-TGAGGTAAATGGAGCTTCCACACCCCTG-3′ (C2038A), and
5′-CTGGAACTCTTTGGCGCTGATATTTACTAG-3′ (C2193A).
To ensure that during the mutagenesis no additional mutations were introduced, a small polymerase chain reaction (PCR) fragment containing the desired mutation(s) was cut out of the PCR product by restriction endonucleases and ligated into a new template that had been cleaved by the same restriction enzymes. The presence of only the desired mutations in each of the plasmids was checked by DNA sequencing.
Transient expression of factor V
Recombinant Factor V plasmids were transiently coexpressed with a Green Fluorescent Protein-lamin construct (GFP-lamin) in COS-1 cells using Fugene 6 Transfection Reagent (Roche Molecular Biochemicals, Indianapolis, IN). A transfection mixture was made by mixing 100 μl of Optimem serum-free medium (Optimem with Glutamax I; Gibco, Life Technologies, Gaithersburg, MD) with 7.5 μl Fugene 6 Transfection Reagent, 2 μg of mutated pMT2-FV and 0.5 μg pEGFP-lamin plasmid. This mixture was incubated at room temperature for 20 min, before adding it to ∼80% confluent monolayer of COS1 cells in 2 ml Dulbecco modified Eagle medium (DMEM), supplemented with l-glutamine. Transfection was allowed to proceed for 16 hr before replacing the transfection medium with fresh DMEM, supplemented with l-glutamine, 10% fetal calf serum, 100 IU/ml penicillin and 100 μg/ml streptomycin. After 48 h posttransfection, cells were washed with phosphate-buffered saline and after trypsinisation, 25% of the cells were harvested to quantitate the transfection efficiency by flow cytometry. The remainder of the cells was cultured for an additional 28 h in 3 ml serum-free medium supplemented with 0.1 mg/ml Albumax I (Gibco BRL; Life Technologies) and 2.5 mM CaCl2.
FV antigen measurements in media
Conditioned media were collected in prechilled tubes and centrifuged for 10 min at 200g to remove cells and cell debris. The supernatant was aliquoted and stored at −80°C. The Factor V antigen levels in the media were determined by a FV ELISA kit (Kordia, Leiden, The Netherlands). ELISA standard curves were constructed with normal pooled plasma from 81 healthy individuals.
RESULTS
Overall characteristics of the MD simulations
MD simulations were performed on the C2 domain of the WT and of the D2194G mutant with or without the C2038-C2193 S-S bond. The minimization procedure that was applied to relax the structures yielded conformations with root-mean-square deviations (RMSD) for heavy atoms between the initial WT x-ray structure and the minimized structure of 0.2 Å. With regard to MD, for all studied structures, the potential energy decreased during the first 150 ps of the simulation and then stabilized. Therefore, the entire production time interval (900 ps) was considered for the MD analysis. For the wild type, the average RMS deviations for the Cα atoms relative to the x-ray structure over the last 900 ps are 1.67 Å and 1.75 Å, in the presence or absence of the S-S bridge, respectively. For the mutant D2194G with or without the disulfide bond, RMSD were 1.86 Å and 1.76 Å, respectively. Similar RMSD for the simulated structures indicate that the mutation D2194G and the removal of the disulfide bridge do not result in large structural rearrangements (see below).
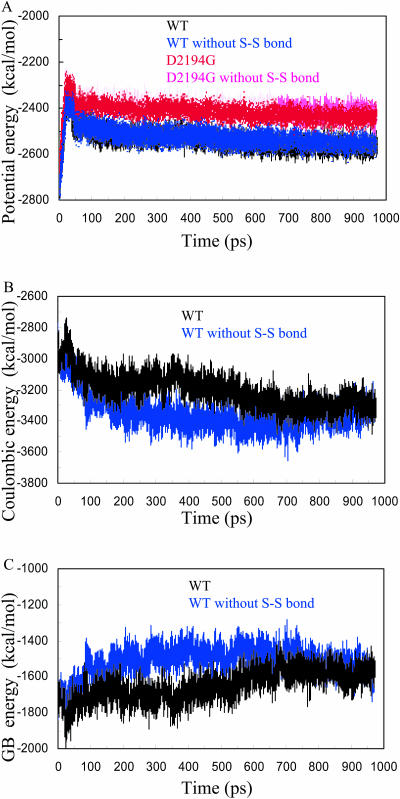
Fig. 1 A shows plots of the potential energy calculated over the trajectories. The higher potential energy observed for both mutant forms (irrespective of the presence of the S-S bond) suggests that the D2194G mutation has destabilizing effects (see below). Fig.1, B and C, show the Coulombic and GB solvation energies of both WT forms (WT with or without S-S bond) calculated during the MD trajectories. It was previously proposed by Spassov et al. (1994) that proteins containing no disulfide bonds are optimized electrostatically as compared to molecules possessing disulfide bridges. It is interesting to note that breaking the S-S bond in the FV C2 domain leads to lower Coulombic energies during the MD indicating optimization of electrostatic interactions. The lack of S-S bond apparently facilitates reorientation of charged residues and formation of stronger favorable charge-charge interactions. In contrast, more favorable Coulombic interactions lead to less-favorable solvation energies. This can be seen from the GB energies, which are higher for the WT when the structure does not have the S-S bond. The van der Waals interactions (not shown) were similar for all trajectories and remained stable during the MD simulations.
FIGURE 1.
Energetic values obtained during the MD trajectories. (A) Potential energy versus the time. The WT C2 domain is shown in black; WT without S-S bond, blue; D2194 mutant, red; and D2194G mutant without S-S bond, magenta. (B) Coulombic energy versus the time. The WT C2 domain is shown in black; WT without S-S bond, blue. (C) GB solvation energy versus the time. The WT C2 domain is shown in black; WT without S-S bond, blue.
Structural and flexibility differences between x-ray and simulated WT
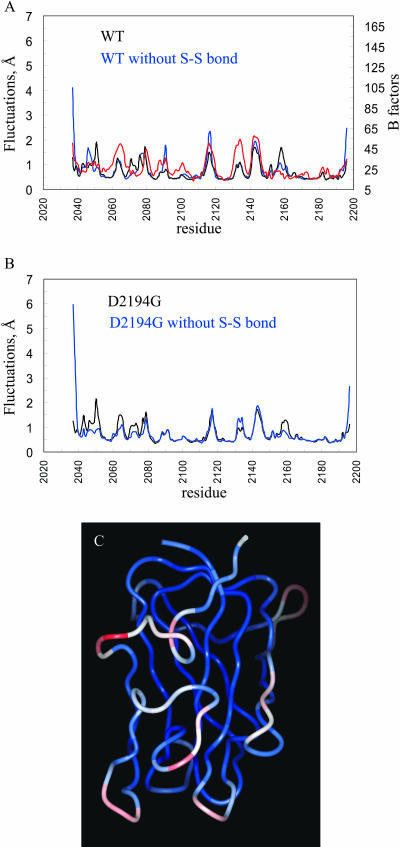
The root mean square fluctuations (RMSF) for the Cα atoms of the C2 domain per residue (sampled over 900 structures) were calculated. In Fig. 2 A the fluctuations of the simulation WT structures with and without S-S bond and the B factors (Cα atoms) of the C2 x-ray structure are presented.
FIGURE 2.
Root mean square fluctuations computed over the last 900 ps of the MD simulations. (A) RMSF of the simulated WT structures with (black) and without (blue) S-S bond and the B-factors (Cα atoms) of the C2 x-ray structure (red). (B) RMSF of the simulated mutant D2194G structures with (black) and without (blue) S-S bond, (C) Ribbon diagram for the averaged modeled structure of the D2194G mutant over the last 900 ps of the MD simulations color coded according to the calculated RMSF.
The calculated fluctuations of simulated WT (with S-S bond) are in good agreement with the B-factors. The zones of greatest flexibility in the simulated and crystal structures tend to be similar but some differences are also noted. The loop 2140-2150 is very flexible in the WT-simulated and crystal structures. The membrane-binding loop (residues 2060-2067 including two key Trp residues 2063 and 2064) and residues 2130-2139 appear to be more flexible in the crystal than in the WT-simulated structure. Some differences between the B-factors of the crystal and calculated RMSF for the WT-simulated structures are also seen for the region 2152-2162 that is found to be more rigid in the x-ray structure.
No significant structural differences are present between the x-ray and averaged simulation structure of the WT C2 domain (not shown). Important changes occur only for the loop 2060-2067 involved in membrane binding, which appears to be flexible (i.e., it adopts two different conformations in the crystal structures) (Macedo-Ribeiro et al., 1999). Some conformational changes also take place at the level of the 2074-2080 loop, which is very flexible in both the x-ray and simulated WT structures.
Structural and flexibility differences between WT and mutant D2194 with S-S bond
Fig. 2 B shows the fluctuations of modeled mutant D2194G with or without the disulfide bridge. In Fig. 2 C the averaged modeled structure for the D2194G mutant over the last 900 ps of the MD simulations is given color coded according to the calculated RMSF. Comparisons of the flexibilities in the modeled WT and the mutant indicate that the regions 2075-2085 and 2140-2150 are flexible in both WT and D2194G mutant (Fig. 2). The loop 2042-2053, situated nearby the mutated residue, is more flexible in the mutant structure. The 2060-2067 loop also becomes more flexible in the D2194G mutant. This is possibly caused by the increased mobility of the loop 2042-2053.
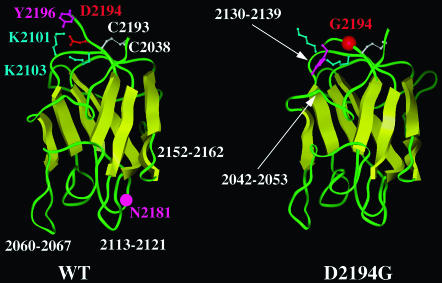
Fig. 3 shows the last structure obtained from the simulation for the WT protein domain and the D2194G mutant (S-S bond present). These structures can be considered as representative of the MD simulations in the area of residue 2194 because the calculated electrostatic stabilization energies of a set of sampled MD conformations (see below) are similar to those calculated for the last MD structure. The regions showing structural changes upon the D2194G substitution (in the presence of S-S bond) involve the loop 2130-2139 and the C-terminal residues (the N-term residues remain essentially unchanged). The D2194G mutation does not affect the dynamical properties of these two regions, which do not appear flexible in the simulated WT and D2194G mutant structures (Fig. 2), but the mutation rather causes conformational changes. In the last simulation structures (with S-S bond; Fig. 3), the loop 2130-2139 is opened in the mutant as compared to the WT, the Cα of N2132 shifts by ∼3 Å.
FIGURE 3.
Ribbon diagram of the WT and D2194G C2 domain. The last structures obtained in the simulations (with S-S bond) are shown and some key residues are labeled (see text).
We also noted that upon mutation of D2194, the nonflexible C-terminus (Tyr-2196) inserts into the structure of the domain, attempting to fill the hole created by the D2194 to G substitution, probably also trying to compensate for the missing negative charge of this mutant. These events could lead to enhanced flexibility of the loop 2042-2053 and to conformational changes of the 2130-2139 region.
Structural and flexibility differences between structures with or without disulfide bond
It is evident from Fig. 2, A and B that the N-terminal (not charged in the simulation because it is in vivo connected to the C1 domain) and C-terminal regions of the WT and mutant D2194G modeled structures become extremely mobile in the absence of the disulfide bond. As a result, important conformational changes occur at both termini. Also, the flexibility of the 2087-2093 and 2113-2121 loops in the WT is enhanced upon removal of the S-S bridge. Loss of the S-S bond also results in a decreased mobility and in structural changes of the region 2152-2162 in both the simulated WT and D2194G mutant. The observed changes in the dynamical properties of C2 domain occurring upon S-S bond disruption could influence the folding process.
Electrostatic contribution to the stability of the triad K2101-K2103-D2194/K2101-K2103-G2194
The electrostatic free energies ΔΔGtot of the triads K2101, K2103, D2194 in the WT and K2101, K2103, G2194 in the mutant, relative to their corresponding hydrophobic isoesters were computed only for the structures possessing the S-S bond. The electrostatic stabilization of the triad, taking into account the mean proton occupancies at pH 7, calculated first on the x-ray structure and on the x-ray structure with simple D2194G substitution without simulations are given in Table 1. The same calculations were also carried out on the last conformations of the MD simulations for the WT and the D2194G mutant, as well as on 30 structures sampled from the MD trajectories from 670 to 970 ps of the production run (one structure selected every 10 ps). The averaged energies for the 30 MD conformations and the term contributing to ΔΔGtot with standard deviations are reported in Table 1 .
TABLE 1.
Electrostatic free-energy contributions of the triad to the protein stability (kcal/mol)
K2101/K2103/D2194 versus K2101/K2103/G2194
| ΔΔGtot
|
ΔΔGsol
|
ΔΔGtriad
|
ΔΔGpr
|
|||||
|---|---|---|---|---|---|---|---|---|
| wt | mut | wt | mut | wt | mut | wt | mut | |
| X-ray | −2.13 | +0.93 | +1.85 | +0.72 | −3.38 | +1.23 | −0.60 | −1.02 |
| MD: last conformation | −6.34 | −4.46 | +9.41 | +5.48 | −10.62 | −0.91 | −5.13 | −9.03 |
| MD: 30 conformations | −6.81 ± 0.7* | −4.64±1.0 | +9.83±1.1 | +4.56±0.4 | −11.46±1.2 | −0.68±0.5 | −5.17±0.95 | −8.52±0.9 |
Standard deviations
Additional computations of the electrostatic stabilization of the triad 2101, 2103, 2194 and the pKa values of titratable groups were carried out for the mutants D2194K, K2101E/K2103E, and K2101E/K2103E/D2194K. The stabilization contributions and mean charges at pH 7 of the triad residues are given in Table 2.
TABLE 2.
Mutants D2194K, K2101E/K2103E/D2194K, and K2101E/K2103E
| Mean charges at pH 7 of the triad:
|
||||
|---|---|---|---|---|
| Mutants | 2101 | 2103 | 2194 | ΔΔGtot |
| D2194K | 0.00 | 0.98 | 1.00 | +3.46 |
| K2101E/K2103E/D2194K | −0.99 | 0.00 | 1.00 | −0.31 |
| K2101E/K2103E | −0.68 | 0.00 | −0.86 | +1.97 |
The ΔΔG energies are well optimized for the structures sampled from the MD simulations, relative to the x-ray structure. The electrostatic energies obtained from averaging over 30 conformations were similar to those for the final simulation structures of the WT and the mutant and the relatively small standard deviations confirm that the structures in the region of the mutation are very similar in the last 300 ps of the simulations.
In the simulated structures (30 conformations) strong favorable charge-charge interactions for the triad (ΔΔGtriad) were obtained for the WT (−11.46 kcal/mol), whereas in the mutant no significant electrostatic interactions were calculated. In all structures no large differences between the simulated WT and the mutant were found for electrostatic interactions of the triad with the rest of the protein ΔΔGpr. The averaged electrostatic stabilization due to the interactions between the triad and the protein varies between −5.17 and −8.52 kcal/mol in the WT and mutant, respectively. As can be expected, the presence of three partially buried ionized amino acid residues causes larger unfavorable desolvation energy ΔΔGsol in the WT (+9.83 kcal/mol) compared to the mutant (+4.56 kcal/mol).
The electrostatic stabilization values calculated for the triad 2101, 2103, 2194 in the mutants D2194K, K2101E/K2103E, K2101E/K2103E/D2194K demonstrate the destabilizing effect of these mutations in comparison to electrostatic stabilization energy of the triad in WT computed on the x-ray structure.
Mutagenesis
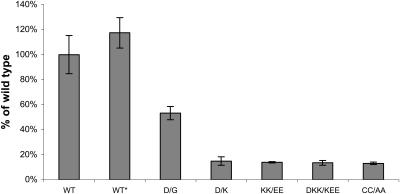
To investigate the importance of the charged triad K2101, K2103, and D2194 and of the S-S bond, several mutant FV molecules were created. These mutagenesis experiments were also performed to probe the tolerance of this region of FV to amino acid substitution. To ensure that any effects observed on expression levels of the recombinant proteins were not due to altered glycosylation of the C2 domain, which per se is a modulator of FV expression levels (Nicolaes et al., 1999), all triad mutations were constructed using a template that resulted in the production of only the FV2 isoform (lacking a glycan structure at position N2181). This construct will subsequently be called WT*. The effect of the presently studied FV mutations on the final levels of FV expression in COS-1 cells, which do not express endogenous FV, were quantitated by FV-ELISA. Results were corrected for variations in transfection efficiency by cotransfecting the pMT2-FV with a pEGFP-C1-lamin vector as described in the Materials and Methods section.
FV antigen level in serum-free media, conditioned for 28 h in cells expressing the WT FV-plasmid, ranged from 17.6 ng to 26.9 ng/35 mm well (n = 6). In conditioned media of cells transfected with the pMT2/FV-D2194G plasmid, the FV antigen level was 53% as compared to WT (Fig. 4). This is in line with previous observations by Yamazaki et al. (2002), who found that the D2194G mutation is the major determinant of low expression levels within the R2-polymorphism (Yamazaki et al., 2002). Compared to WT, a seven- to eightfold reduction in FV expression levels was observed for the mutants D2194K, K2101E/K2103E, K2101E/K2103E/D2194K, and C2038A/C2193A (Fig. 4). Together these data indicate that mutations in the C2-domain of FV that interfere with the charged triad D2194, K2101, and K2103 lower the amount of FV secreted by the cells. Mutation of the S-S bridge results in decreased final FV expression. However, expression of the mutants studied was not completely inhibited by these mutations as expression levels >13% were achieved for all constructs.
FIGURE 4.
Transient expression of FV proteins in serum-free culture medium COS-1 cells were transiently transfected to express WT-FV or the FV mutants. FV antigen levels were measured in the culture media by ELISA. Bars represent the means ± standard deviations (n = 6). The mean value of WT-FV was 23.8 ng/35 mm well and is assigned to be 100% in this figure. This WT-FV construct was used as a template for the D/G mutation and to construct the WT* plasmid (which only expresses the FV2 isoform). There was no significant difference between the expression levels of the WT FV-plasmid and the WT* plasmid, the WT* plasmid serving as a template for the other FV mutants (nomenclature: D2194G (D/G), D2194K (D/K), K2101E/K2103E (KK/EE), K2101E/K2103E/D2194K (DKK/KEE), and C2038A/C2193A (CC/AA)).
DISCUSSION
Recently, it has been proposed that ∼80% of missense mutations associated with disease states are amino acid substitutions that affect the stability of proteins by ∼1–3 kcal/mol (Wang and Moult, 2001). Stability problems can be due to loss of hydrogen bonds, of S-S bonds, overpacking, backbone strain, and/or burial of charged residues. In silico strategies can be used to investigate the potential roles of a mutation on, for instance, protein stability.
In the present study, MD simulations (970 ps) were executed on the C2 domain of WT FV and the D2194G mutant that is present in carriers of the FV-R2 gene. Because this mutation could potentially act on the formation of the nearby C2038-C2193 S-S bond and/or the conformation of the N-term/C-term residues, simulations of the WT and D2194G S-S bondless structures were compared. Electrostatic computations were performed to investigate the energetics of the WT K2101-K2103-D2194 triad and of several mutants. Mutagenesis experiments and secretion levels were also used to probe further the 2194 region of the FV C2 domain (mutants were: D2194G, D2194K, K2101E/K2103E, K2101E/K2103E/D2194K, C2038A/C2193A) because observed secretion efficiencies often relate to mutant stability in vitro. These experimental data were correlated with theoretical work while trying to include in our reasoning the fact that protein-engineering methods usually probe several physical contributions at the same time (e.g., electrostatic, steric, and entropic) (Lounnas and Wade, 1997) whereas theoretical investigations may not.
A key step after MD computations is to evaluate the accuracy of the calculations, through for instance evaluation of RMSD, potential energy versus time and others (Figs. 1 and 2). Yet, although MD simulations with implicit solvation models have been found of reasonable accuracy, some authors suggest that despite low RMSD between the simulated structures and the starting x-ray model, the conformations of the simulated molecules are of poor quality (Simonson, 2001). We thus investigated several structures of the simulated WT with the energy strain utility included in the ICM package (Molsoft) (Maiorov and Abagyan, 1998). The simulated WT and mutant C2 domains had similar structural features as the starting high-resolution x-ray structure. Secondary structure contents in the starting x-ray and simulated structures (WT or mutant) computed using the method of Kabsch and Sander (1983) were similar. Furthermore, the protein core of the WT or mutant C2 domain remained stable during the simulations performed on structures in the absence of the S-S bond, despite increased flexibility/conformational changes in some regions of the modeled structures (Figs. 2 and 3). These results as well as the low RMSD calculated between the x-ray and modeled structures together with the ICM evaluations confirm that the implicit solvation method and simulation protocol used here are appropriate.
It has been shown that physical energy functions similar to the one used in this study can identify native-like structure from misfolded protein models and that low-quality 3D structures tend to unfold during a simulation (Dominy and Brooks, 2002; Feig and Brooks, 2002). Although we did not observe unfolding of the D2194G mutant we noted that its total potential energy (with or without S-S bond) is significantly higher than the one of the WT (Fig. 1). Thus, in this specific case, investigation of the potential energy suggests overall destabilization of the protein due to the mutation.
We then analyzed trajectories obtained for the WT C2 structure (with or without S-S bond). It is known that disulfide bonds in proteins can influence the stability as well as the folding pathway and the efficiency of folding (Kowalski et al., 1998; Omura et al., 1992; Parodi, 2000). Generally, loss of a native disulfide bond reduces stability and such mutant proteins may not be able to fold; secretion can be impeded or delayed. Yet, in some situations, removal of S-S bonds does not seem to affect the 3D structure of a protein nor its function. In the simulation of the WT C2 domain with or without S-S bond, the protein core remained stable. However, the increased mobility of the two termini, in the absence of S-S bond could impair correct folding/stability of the domain and damage interaction with the C1 domain. The WT protein without S-S bond does not express well, suggesting folding/stability problems. Similar folding/stability/expression problems were also noticed when removing S-S bond(s) in retinoschisin, a discoidin-domain-containing protein (Wu and Molday, 2003).
The potential energies of the WT C2 domain (with or without S-S bond) are similar and one would not expect folding/stability problems, but S-S bond depleted 3D structures have to be analyzed with special care. It appears that removing the disulfide bond in the FV C2 domain facilitates optimization of some energy terms (thus lower the total potential energy). This hypothesis is supported by the observation that electrostatic interactions are optimized in proteins that do not contain S-S bond as compared to molecules containing S-S bonds (Spassov et al., 1994). Thus, potential energies for the WT C2 domain with or without S-S bond cannot be directly correlated with expression levels. In addition, it can be noticed in the WT and D2194G that the region 2152-2162 is less flexible in the structure without the S-S bond. This is consistent with previous MD simulations showing that removal of S-S bond can decrease the flexibility of large portions of a protein (Rizzuti et al., 2001).
The protein core of the D2194G mutant with or without the S-S bond remained also stable during the simulation. However, some regions become more rigid or more flexible due to the mutation (Fig. 2). For the mutant protein without the S-S bond we observe significantly higher flexibilities within the N-term residues as compared to the WT (simulation without S-S bond). This suggests potential folding/stability problems and/or damaged interaction with the C1 domain. Also it is probable that the increased flexibility of the N-term residues due to the D2194G mutation affects the formation of the nearby S-S bond. A possible in vivo scenario could be that mutant molecules (either D2194G or S-S bond free structure) could be marginally stable and could equilibrate between the folded state and an ensemble of unfolded conformations. This latter population could then be recognized inside the ER and be partially retained and degraded. This hypothesis would be in fact in good agreement with the observed low expression levels of these mutants.
FV C2 domain residue D2194 is involved in electrostatic interactions with the side chains of K2101 and K2103. Conservation (full or partial) of ionic interaction in this region of FV or FVIII suggests that these salt bridges could be important for the stability/structure of the C2 domain (Table 3). It has been noted that conserved salt bridges important for the stability of proteins are often buried (Schueler and Margalit, 1995) whereas in the C2 domain, the 2101-2103-2194 triad is partially exposed. However, surface salt bridges can also be important for protein stability (Strop and Mayo, 2000; Dong and Zhou, 2002). In fact, salt bridges can be stabilizing or destabilizing depending on their environment (Kumar and Nussinov, 1999, 2001; Schutz and Warshel, 2001). In the present study, we assumed that the D2194G mutation could alter the stability of the FV C2 domain. Comparison of the electrostatic free energies (ΔΔGtot) of the 2101-2103-2194 triad between the WT FV C2 domain and the D2194G mutant shows electrostatic destabilization due to the mutation by ∼3 kcal/mol. This value is in the range of what has been observed by Wang and Moult (2001). Therefore, we suggest that the D2194G mutation destabilizes the domain and that this modified structure could be detected by the proofreading apparatus inside the cells.
TABLE 3.
Multiple sequence alignment in the area of FV residue 2194 and surrounding area
| 2101 2103(buried) 2194 |
| * * * |
| hFV_C2: …ANNNKQWLEIDLLKIKKITAIIT……….LELFGCDIY |
| bFV_C2: …ANNNNQWLQIDLLKIKKITAIVT……….LELFGCDMY |
| pigFV_C2: …ANNNNQWLQIDLLKIKKITAITT……….LELFGCDIY |
| hFVIII_C2: …VNNPKEWLQVDFQKTMKVTGVTT……….MEVLGCEAQ |
| mouseFVIII_C2: …VNDPKQWLQVDLQKTMKVTGIIT……….LEILGCEAQ |
| pigFVIII_C2: …VSSAEEWLQVDLQKTVKVTGITT……….LEVLGCEAQ |
To understand better the reactions taking place at the level of residue 2194, other mutants were created in vitro and in silico. Changing the distribution of charged groups in the 2194 area could underline the importance of the salt-bridge network and could provide information about tolerance to amino acid substitutions. Computations of electrostatic energies of the 2101-2103-2194 triad in the mutants D2194K (D/K, thus three expected positive charges), K2101E/K2103E (KK/EE, thus three expected negative charges), K2101E/K2103E/D2194K (DKK/KEE, modification of the distribution of charges) calculated on the rigid structures (see Table 2) also show destabilization effects in comparison to the WT (x-ray structure). The D2194K, K2101E/K2103E, K2101E/K2103E/D2194K mutants show lower expression levels than the D2194G mutant. These experimental data correlate well with the calculated electrostatic destabilizations excluding the K2101E/K2103E/D2194K (DKK/KEE) mutant. Generally, it is expected that mutations leading to the positioning of three negatively or positively charged groups close in space will be destabilizing, as observed here in the case of the D2194K (D/K) and K2101E/K2103E (KK/EE) substitutions (Table 2). These mutants are thus predicted to be less stable than the D2194G mutant and this correlates well with the experimental expression levels. On the other hand, we initially hypothesized that the mutant K2101E/K2103E/D2194K (DKK/KEE) would form a stabilizing salt-bridge triad that could mimic the WT protein. However, the calculated proton occupancies at pH 7 show that 2103 is not charged whereas in the WT the three triad residues are ionized. This indicates that the distribution of charges in the K2101E/K2103E/D2194K mutant is not favorable as compared to the one of the WT. Although ΔΔGtot suggests that the mutated triad is slightly stabilizing, apparently, in this case, additional structural features have to be integrated in the analysis.
In summary, the D2194G substitution in the C2 domain seems to electrostatically destabilize the structure, as shown by computer calculations. Low expression levels were observed for this mutant, suggesting also potential stability and/or folding problems. Our experimental and MD/electrostatic data shows that the right distribution of charges in the 2194 region of the FV C2 domain is essential to the stability and the presence of an S-S bond is required for the stability/folding of this essential coagulation protein.
Acknowledgments
We thank Dr. Andrey Karshikoff for interesting discussions.
This work was supported by the Dutch Organization for Scientific Research (NWO to G.N.) (grant no. 902-26-227); the Netherlands Heart Foundation (grant no. 2000-021 to J.B.); and a MW-NWO/INSERM travel grant (no. 0408-023 to G.N. and B.V.). A grant from the Inserm Institute “poste-vert” is also greatly appreciated.
References
- Antosiewicz, J., J. A. McCammon, and M. Gilson. 1994. Prediction of pH-dependent properties of proteins. J. Mol. Biol. 238:415–436. [DOI] [PubMed] [Google Scholar]
- Antosiewicz, J., and D. Porschke. 1989. The nature of protein dipole moments: experimental and calculated permanent dipole of a-chymotrypsin. Biochemistry. 28:10072–10078. [DOI] [PubMed] [Google Scholar]
- Barril, X., C. Aleman, M. Orozco, and F. J. Luque. 1998. Salt bridge interactions: stability of the ionic and neutral complexes in the gas phase, in solution, and in proteins. Proteins. 32:67–79. [DOI] [PubMed] [Google Scholar]
- Bashford, D., and D. A. Case. 2000. Generalized born models of macromolecular solvation effects. Annu. Rev. Phys. Chem. 51:129–152. [DOI] [PubMed] [Google Scholar]
- Bashford, D., and M. Karplus. 1990. The pKa's of ionizable groups in proteins: atomic detail from a continuum electrostatic model. Biochemistry. 29:10219–10225. [DOI] [PubMed] [Google Scholar]
- Baumgartner, S., K. Hofmann, R. Chiquet-Ehrismann, and P. Bucher. 1998. The discoidin domain family revisited: new members from prokaryotes and a homology-based fold prediction. Protein Sci. 7:1626–1631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berendsen, H. J., J. P. Postma, A. DiNola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
- Berman, H. M., J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov, and P. E. Bourne. 2000. The protein data bank. Nucleic Acids Res. 28:235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernardi, F., E. M. Faioni, E. Castoldi, B. Lunghi, G. Castaman, E. Sacchi, and P. M. Mannucci. 1997. A factor V genetic component differing from factor V R506Q contributes to the activated protein C resistance phenotype. Blood. 90:1552–1557. [PubMed] [Google Scholar]
- Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: a program for macromolecular energy, minimization and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- Bross, P., T. J. Corydon, B. S. Andresen, M. M. Jørgensen, L. Bolund, and N. Gregersen. 1999. Protein misfolding and degradation in genetic diseases. Hum. Mutat. 14:186–198. [DOI] [PubMed] [Google Scholar]
- Castoldi, E., J. Rosing, D. Girelli, L. Hoekema, B. Lunghi, F. Mingozzi, P. Ferraresi, S. Friso, R. Corrocher, G. Tans, and F. Bernardi. 2000. Mutations in the R2 FV gene affect the ratio between the two FV isoforms in plasma. Thromb. Haemost. 83:362–365. [PubMed] [Google Scholar]
- Cregut, D., and L. Serrano. 1999. Molecular dynamics as a tool to detect protein foldability. A mutant of domain B1 of protein G with non-native secondary structure propensities. Protein Sci. 8:271–282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis, M. E., J. D. Madura, B. A. Luty, and J. A. McCammon. 1991. Electrostatics and diffusion of molecules in solution: simulations with the University of Houston Brownian dynamics program. Comput. Phys. Commun. 62:187–197. [Google Scholar]
- Dominy, B., and C. Brooks. 1999. Development of a generalized born model parameterization for proteins and nucleic acids. J. Phys. Chem. B. 103:3765–3773. [Google Scholar]
- Dominy, B., and C. Brooks. 2002. Identifying native-like protein structures using physics-based potentials. J. Comput. Chem. 23:147–160. [DOI] [PubMed] [Google Scholar]
- Dong, F., and H.-X. Zhou. 2002. Electrostatic contributions to T4 lysozyme stability: solvent-exposed charges versus semi-buried salt bridges. Biophys. J. 83:1341–1347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feig, M., and C. Brooks. 2002. Evaluating CASP4 predictions with physical energy evaluations. Proteins. 49:232–245. [DOI] [PubMed] [Google Scholar]
- Gilson, M., and B. Honig. 1988. Calculation of the total electrostatic energy of a macromolecular system: solvation energies, binding energies, and conformational analysis. Proteins. 4:7–18. [DOI] [PubMed] [Google Scholar]
- Hendsch, Z. S., and B. Tidor. 1994. Do salt bridges stabilize proteins? A continuum electrostatic analysis. Protein Sci. 3:211–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hilser, V. J., D. Dowdy, T. G. Oas, and E. Freire. 1998. The structural distribution of cooperative interactions in proteins: analysis of the native state ensemble. Proc. Natl. Acad. Sci. USA. 95:9903–9908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoekema, L., G. A. F. Nicolaes, H. C. Hemker, G. Tans, and J. Rosing. 1997. Human Factor Va1 and Factor Va2: properties in the procoagulant and anticoagulant pathways. Biochemistry. 36:3331–3335. [DOI] [PubMed] [Google Scholar]
- Kabsch, W., and C. Sander. 1983. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers. 22:2577–2637. [DOI] [PubMed] [Google Scholar]
- Kazmirski, S. L., D. O. Alonso, F. E. Cohen, S. B. Prusiner, and V. Daggett. 1995. Theoretical studies of sequence effects on the conformational properties of a fragment of the prion protein: implications for scrapie formation. Chem. Biol. 2:305–315. [DOI] [PubMed] [Google Scholar]
- Kim, S. W., M. A. Quinn-Allen, J. T. Camp, S. Macedo-Ribeiro, P. Fuentes-Prior, W. Bode, and W. H. Kane. 2000. Identification of functionally important amino acid residues within the C2-domain of human factor V using alanine-scanning mutagenesis. Biochemistry. 39:1951–1958. [DOI] [PubMed] [Google Scholar]
- Kowalski, J. M., R. Parekh, and K. D. Wittrup. 1998. Secretion efficiency in Saccharomyces cerevisiae of bovine pancreatic trypsin inhibitor mutants lacking disulfide bonds is correlated with thermodynamic stability. Biochemistry. 37:1264–1273. [DOI] [PubMed] [Google Scholar]
- Kumar, S., and R. Nussinov. 1999. Salt bridge stability in monomeric proteins. J. Mol. Biol. 293:1241–1255. [DOI] [PubMed] [Google Scholar]
- Kumar, S., and R. Nussinov. 2001. Fluctuations in ion pairs and their stabilities in proteins. Proteins. 43:433–454. [DOI] [PubMed] [Google Scholar]
- Lounnas, V., and R. C. Wade. 1997. Exceptionally stable salt bridges in cytochrome P450cam have functional roles. Biochemistry. 36:5402–5417. [DOI] [PubMed] [Google Scholar]
- Lunghi, B., L. Iacoviello, D. Gemmati, M. G. Dilasio, E. Castoldi, M. Pinotti, G. Castaman, R. Redaelli, G. Mariani, G. Marchetti, and F. Bernardi. 1996. Detection of new polymorphic markers in the factor V gene: association with factor V levels in plasma. Thromb. Haemost. 75:45–48. [PubMed] [Google Scholar]
- Macedo-Ribeiro, S., W. Bode, R. Huber, A. Quinn-Allen, W. Kim, G. P. Bourenkov, H. Bartunik, M. T. Stubbs, W. H. Kane, and P. Fuentes-Prior. 1999. Crystal structures of the membrane-binding C2 domain of coagulation factor V. Nature. 402:434–439. [DOI] [PubMed] [Google Scholar]
- Maiorov, V., and R. Abagyan. 1998. Energy strain in three-dimensional protein structures. Fold. Des. 3:259–269. [DOI] [PubMed] [Google Scholar]
- Mann, K. G., and M. Kalafatis. 2003. Factor V: a combination of Dr Jekyll and Mr Hyde. Blood. 101:20–30. [DOI] [PubMed] [Google Scholar]
- Morozov, A. V., T. Kortemme, and D. Baker. 2003. Evaluation of models of electrostatic interactions in proteins. J. Phys. Chem. B.107:2075–2090. [Google Scholar]
- Nicolaes, G. A., and B. Dahlback. 2002. Factor V and thrombotic disease: description of a janus-faced protein. Arterioscler. Thromb. Vasc. Biol. 22:530–538. [DOI] [PubMed] [Google Scholar]
- Nicolaes, G. A. F., B. O. Villoutreix, and B. Dahlbäck. 1999. Partial glycosylation of Asn2181 in human factor V as a cause of molecular and functional heterogeneity. Modulation of glycosylation efficiency by mutagenesis of the consensus sequence for N-linked glycosylation. Biochemistry. 38:13584–13591. [DOI] [PubMed] [Google Scholar]
- Nicolaes, G. A., B. O. Villoutreix, and B. Dahlback. 2000. Mutations in a potential phospholipid binding loop in the C2 domain of factor V affecting the assembly of the prothrombinase complex. Blood Coagul. Fibrinolysis. 11:89–100. [PubMed] [Google Scholar]
- Omura, F., M. Otsu, and M. Kikuchi. 1992. Accelerated secretion of human lysozyme with a disulfide bond mutation. Eur. J. Biochem. 205:551–559. [DOI] [PubMed] [Google Scholar]
- Parodi, A. J. 2000. Role of N-oligosaccharide endoplasmic reticulum processing reactions in glycoprotein folding and degradation. Biochem. J. 348:1–13. [PMC free article] [PubMed] [Google Scholar]
- Pellequer, J. L., A. J. Gale, J. H. Griffin, and E. D. Getzoff. 1998. Homology models of the C domains of blood coagulation factors V and VIII: a proposed membrane binding mode for FV and FVIII C2 domains. Blood Cells Mol. Dis. 24:448–461. [DOI] [PubMed] [Google Scholar]
- Pratt, K. P., B. W. Shen, K. Takeshima, E. W. Davie, K. Fujikawa, and B. L. Stoddard. 1999. Structure of the C2 domain of human factor VIII at 1.5 Å resolution. Nature. 402:439–442. [DOI] [PubMed] [Google Scholar]
- Qiu, D., P. S. Shenkin, F. Hollinger, and W. C. Still. 1997. The GB/SA continuum model for solvation. A fast analytical method for the calculation of approximate Born radii. J. Phys. Chem. 101:3005–3014. [Google Scholar]
- Rizzuti, B., L. Sportelli, and R. Guzzi. 2001. Evidence of reduced flexibility in disulfide bridge-depleted azurin: a molecular dynamics simulation study. Biophys. Chem. 94:107–120. [DOI] [PubMed] [Google Scholar]
- Rosing, J., H. M. Bakker, M. C. Thomassen, H. C. Hemker, and G. Tans. 1993. Characterization of two forms of human factor Va with different cofactor activities. J. Biol. Chem. 268:21130–21136. [PubMed] [Google Scholar]
- Schiffer, C. A., and W. F. van Gunsteren. 1996. Structural stability of disulfide mutants of basic pancreatic trypsin inhibitor: a molecular dynamics study. Proteins. 26:66–71. [DOI] [PubMed] [Google Scholar]
- Schueler, O., and H. Margalit. 1995. Conservation of salt bridges in protein families. J. Mol. Biol. 248:125–135. [DOI] [PubMed] [Google Scholar]
- Schutz, C. N., and A. Warshel. 2001. What are the dielectric “constants” of proteins and how to validate electrostatic models? Proteins. 44:400–417. [DOI] [PubMed] [Google Scholar]
- Sharp, K. A., and B. Honig. 1990. Electrostatic interactions in macromolecules: theory and applications. Annu. Rev. Biophys. Biophys. Chem. 19:301–332. [DOI] [PubMed] [Google Scholar]
- Sharp, K., A. Nicholls, R. Friedman, and B. Honig. 1991. Extracting hydrophobic free energies from experimental data: relationship to protein folding and theoretical models. Biochemistry. 30:9686–9697. [DOI] [PubMed] [Google Scholar]
- Simonson, T. 2001. Macromolecular electrostatics: continuum models and their growing pains. Curr. Opin. Struct. Biol. 11:243–252. [DOI] [PubMed] [Google Scholar]
- Sinha, N., and R. Nussinov. 2001. Point mutations and sequence variability in proteins: redistributions of preexisting populations. Proc. Natl. Acad. Sci. USA. 98:3139–3144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spassov, V. Z., A. D. Karshikoff, and R. Ladenstein. 1994. Optimization of the electrostatic interactions in proteins of different functional and folding type. Protein Sci. 3:1556–1569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strop, P., and S. L. Mayo. 2000. Contribution of surface salt bridges to protein stability. Biochemistry. 39:1251–1255. [DOI] [PubMed] [Google Scholar]
- Tanford, C., and J. G. Kirkwood. 1957. Theory of protein titration curves. I. General equations for impenetrable spheres. J. Am. Chem. Soc. 79:5333–5339. [Google Scholar]
- Taverna, D. M., and R. A. Goldstein. 2002. Why are proteins so robust to site mutations? J. Mol. Biol. 315:479–484. [DOI] [PubMed] [Google Scholar]
- Van Der Neut Kolfschoten, M., R. J. Dirven, H. L. Vos, and R. M. Bertina. 2003. The R2-haplotype associated Asp2194Gly mutation in the light chain of human factor V results in lower expression levels of FV, but has no influence on the glycosylation of Asn2181. Thrombo. Haemost. 89:429–437. [PubMed] [Google Scholar]
- Villoutreix, B. O., P. Bucher, K. Hofmann, S. Baumgartner, and B. Dahlbäck. 1998. Molecular models for the two discoidin domains of human blood coagulation factor V. J. Mol. Model. 4:268–275. [Google Scholar]
- Villoutreix, B. O. 2002. Structural bioinformatics: methods, concepts and applications to blood coagulation proteins. Curr. Protein Pept. Sci. 3:341–364. [DOI] [PubMed] [Google Scholar]
- Wang, Z., and J. Moult. 2001. SNPs, protein structure, and disease. Hum. Mutat. 17:263–270. [DOI] [PubMed] [Google Scholar]
- Warwicker, J., and H. C. Watson. 1982. Calculation of the electric potential in the active site cleft due to a α-helix dipoles. J. Mol. Biol. 157:671–679. [DOI] [PubMed] [Google Scholar]
- Wesson, L., and D. Eisenberg. 1992. Atomic solvation parameters applied to molecular dynamics of proteins in solution. Protein Sci. 1:227–235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wickner, S., M. R. Maurizi, and S. Gottesman. 1999. Posttranslational quality control: folding, refolding and degrading proteins. Science. 286:1888–1893. [DOI] [PubMed] [Google Scholar]
- Wu, W. W., and R. S. Molday. 2003. Defective discoidin domain structure, subunit assembly and ER processing of retinoschisin are primary mechanisms responsible for X-linked retinoschisis. J. Biol. Chem. 278:28139–28146. [DOI] [PubMed] [Google Scholar]
- Yamazaki, T., G. A. F. Nicolaes, K. W. Sørensen, and B. Dahlbäck. 2002. Molecular basis of quantitative factor V deficiency associated with factor V R2 haplotype. Blood. 100:2515–2521. [DOI] [PubMed] [Google Scholar]
- Yang, A.-S., M. Gunner, R. Sampogna, K. Sharp, and B. Honig. 1993. On the calculation of pKas in proteins. Proteins. 15:252–265. [DOI] [PubMed] [Google Scholar]