Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Jan;86(1):617–628. doi: 10.1016/S0006-3495(04)74140-5

Substrate Compliance versus Ligand Density in Cell on Gel Responses

Adam Engler *, Lucie Bacakova *, Cynthia Newman *, Alina Hategan *, Maureen Griffin *, Dennis Discher †
PMCID: PMC1303831  PMID: 14695306

Abstract

Substrate stiffness is emerging as an important physical factor in the response of many cell types. In agreement with findings on other anchorage-dependent cell lineages, aortic smooth muscle cells are found to spread and organize their cytoskeleton and focal adhesions much more so on “rigid” glass or “stiff” gels than on “soft” gels. Whereas these cells generally show maximal spreading on intermediate collagen densities, the limited spreading on soft gels is surprisingly insensitive to adhesive ligand density. Bell-shaped cell spreading curves encompassing all substrates are modeled by simple functions that couple ligand density to substrate stiffness. Although smooth muscle cells spread minimally on soft gels regardless of collagen, GFP-actin gives a slight overexpression of total actin that can override the soft gel response and drive spreading; GFP and GFP-paxillin do not have the same effect. The GFP-actin cells invariably show an organized filamentous cytoskeleton and clearly indicate that the cytoskeleton is at least one structural node in a signaling network that can override spreading limits typically dictated by soft gels. Based on such results, we hypothesize a central structural role for the cytoskeleton in driving the membrane outward during spreading whereas adhesion reinforces the spreading.

INTRODUCTION

Extracellular matrix (ECM) not only displays adhesive ligands important to anchorage-dependent cells but also presents a number of potentially influential physical properties. One such property, matrix stiffness, has become increasingly recognized as key to cellular processes ranging from motility (Lo et al., 2000; Pelham and Wang, 1997) to phagocytosis (Beningo and Wang, 2002) and differentiation (Cukierman et al., 2001; Deroanne et al., 2001). Cells display an apparent spreading preference for these stiffer substrates in cell motility—a phenomenon referred to as durotaxis (Lo et al., 2000). How matrix stiffness couples with ligand density to modulate haptotactic cellular responses has been a question raised recently with the suggestion that substrate compliance and ligand density are orthogonal determinants (Cukierman et al., 2001; Geiger, 2001) of similar importance in a host of cellular responses (Fig. 1). Here we enumerate morphological and related structural responses of aorta-derived smooth muscle cells (SMC of A7R5 lineage) under the combined effects of varied collagen density and substrate compliance. SMCs are of specific interest because of their role(s) in vascular disease, and also because two recent studies are at odds as to whether SMCs display durotaxis-like responses (Wong et al., 2003) or not (Deroanne et al., 2001).

FIGURE 1.

FIGURE 1

Open in a new tab

Ligand density and substrate compliance are postulated to influence cellular responses (Cukierman et al., 2001; Geiger, 2001). We tested that here with smooth muscle cells studied on various collagen-coated gels and glass in terms of morphological and organizational features at short times.

To a cell, an extremely soft gel could be perceived as nearly fluid and therefore inadequate for sustaining an anchorage-dependent response. This appears true even if soluble adhesive ligands are added to occupy the relevant receptors (e.g., integrins) (Frisch and Francis, 1994; Hadden and Henke, 2000; McGill et al., 1997; Meredith et al., 1993). Cells on very soft media, including “soft” gels of PA and collagen, show reduced spreading (Lo et al., 2000; Pelham and Wang, 1997) and reduced organization of actin into stress fibers (Deroanne et al., 2001). Over long times, they also show reduced expression of actin and focal adhesion proteins (Cukierman et al., 2001). Conversely, if an integrin clustering or solidifying mechanism such as an ECM-coated bead is locally provided in combination with receptor ligation, then key characteristics of the prototypical anchorage response emerge at the site: focal adhesion kinase accumulates with induction of phosphorylation, and local cytoskeletal nucleation occurs at the nascent focal adhesions (Miyamoto et al., 1995). On a suitably “stiff” gel, a more cell-wide anchorage response is similarly fortified with phosphorylation pathways and overlapping acto-myosin contractions that appear to contribute to both cell spreading (Pelham and Wang, 1997) and to the requisite cell tractions (Wang et al., 2002). One physical constant in the disparate cell on gel responses tentatively seems to be that maximum traction forces (or stresses) generated by a cell are ∼15–25% of a given substrate modulus (specifically 3T3 fibroblasts; Lo et al., 2000). These maximum stresses are always generated near the cell periphery and imply maximum substrate strains of similar magnitude there (i.e., 15–25%).

We primarily use the projected cell area of SMCs plus other cell structural measures and perturbations to elucidate the coupling between substrate stiffness and ligand density. A wide range of collagen densities on PA gels of varied stiffnesses is studied to help physically define the meaning of a “soft,” “stiff,” and “rigid” substrate to a cell. Of particular note in experiments with cells on soft gels, varying the collagen density over a wide range has minimal influence on spread cell area. We will show, however, that GFP-actin expression in SMCs on soft gels at optimal collagen density can promote strong spreading. The results highlight a dominant role for the cytoskeleton in cell spreading compared to adhesive ligands.

MATERIAL AND METHODS

Smooth muscle cells

The rat aorta-derived SMC line, A7r5, is generally known to maintain differentiation markers for smooth muscle, including α-actinin, calponin, and key myosins (Firulli et al., 1998). SMCs were cultured in polystyrene flasks in DMEM, selectively supplemented with 10% of FBS, and without antibiotics. Cell culture and transfection products were purchased from Invitrogen, Life Technologies (Carlsbad, CA), whereas all other chemicals were purchased from Sigma (St. Louis, MO) unless noted.

Transfection and weak overexpression of GFP-actin and GFP-paxillin

Plasmids for pEGFP-β-actin, pEGFP (both from BD Biosciences Clontech, Palo Alto, CA), and GFP-paxillin (Laukaitis et al., 2001), which all confer leaky resistance to geneticin for selection, were amplified in Escherichia coli (BL21) and used in separate SMC transfections 24 h after plating. Note that β-actin is a ubiquitous but nonmuscle, cytoplasmic actin. Although smooth muscle actin is a distinct isoform, Mounier et al. (1997) have shown that β-actin transfected into SMCs will express both during the transfection under control of a CMV promoter and after the transfection under very similar conditions as here (i.e., 2 μg DNA). Using a standard protocol and Lipofectamine reagent (Evans et al., 1999), DNA-lipid complexes were incubated in 1 mL of serum-free DMEM for 45 min at room temperature, mixed with 1 ml of 5% FBS containing media, and added to cultures. After 24 h, the cultures were rinsed and grown in complete growth medium with 10% FBS.

To assess expression levels of GFP-proteins, Western blots were done on SMCs grown on soft PA gels with “optimum” attached collagen (see text). The Western methods used were very similar to those described elsewhere (Massaeli et al., 1999). Briefly, cells were plated on a 35-mm dish, grown for 4 h, detached, and solubilized in detergent with protease inhibitors. Serially diluted samples and control cells were separated by SDS-PAGE with a molecular weight ladder (Invitrogen), transferred to nitrocellulose, and stained with anti-GFP (Molecular Probes, Eugene, OR) and anti-β-actin (Molecular Probes). In probing with anti-GFP, GFP-actin showed some degradation as reported by others (Choidas et al., 1998), but probing with anti-actin nonetheless proved GFP-actin to be a small percentage of cellular actin (∼5–10%). A slight overexpression proves consistent with reports of others using either CMV promoters (∼5%) (Choidas et al., 1998), as here, or actin promoters (∼10–20%) (Westphal et al., 1997). In either reference, the GFP-actin was shown to be fully functional in cells, after long-term culture, and when purified.

Collagen-coated coverslips and their characterization

Glass surfaces were prepared with either adsorbed or covalently attached collagen. Rat-tail collagen I (BD Biosciences, Bedford, MA) was adsorbed onto coverslips at 1–105 ng/cm2 (Ingber, 1990). After 24-h incubation, the 25-mm circular coverslips were rinsed in PBS to remove unbound collagen and nonspecific cell-binding sites were blocked with bovine serum albumin (2% BSA solution in PBS). Collagen was also covalently attached to aminosilanized glass coverslips (Ra et al., 1999), which were incubated overnight in collagen I and 40 mM MES containing 0.4% 1-ethyl-3-(3-dimethylamino-propyl)carbodiimide. Similarly, unbound collagen was washed and blocked with 2% BSA. The presence, as well as the possible desorption of collagen, was examined with a 9:1 mixture of collagen I to fluorescent collagen IV (Oregon Green R 488) or by immunofluorescence. Sample average intensities were calibrated against surface-bound collagen obtained without washing by flash-drying known amounts of fluorescent collagen on glass coverslips.

Collagen-coated gels and their characterization

Polyacrylamide gel samples were prepared on aminosilanized glass coverslips using published methods (Wang and Pelham, 1998). Briefly, to control or adjust the gel's stiffness, the cross-linker n,n′methylene-bis-acrylamide was varied from 0.03% to 0.3% in distilled water while holding constant the acrylamide (C3H5NO) at either 5% or 10%. Approximately 25 μl of the mixed solution was polymerized on a coverslip using 1/200 volume of 10% ammonium persulfate and 1/2000 volume of n,n,n′,n′-tetramethylethylenediamine. The polymerizing gel was covered with a second coverslip pretreated with dichlorodimethylsilane to ensure easy detachment and a uniform polymerized gel surface. Final gels were ∼70–100-μm thick as measured by microscopy. Collagen was either adsorbed to the surface of the gel in the same manner described above or more often chemically cross-linked using a photoactivating cross-linker, sulfo-SANPAH (Pierce, Rockford, IL) and attachment was confirmed by fluorescence as described above. Gel porosity, which varies with monomer and cross-linker concentrations to alter gel elasticity, can influence cell-accessible collagen by allowing protein to migrate into the gel itself where it is inaccessible. Although this creates uncertainty in the actual ligand density present on the surface, previous results (Lo et al., 2000) have shown that micron-size beads much larger than the pores and bearing anti-collagen bind almost the same to collagen-coated gels of very different porosity.

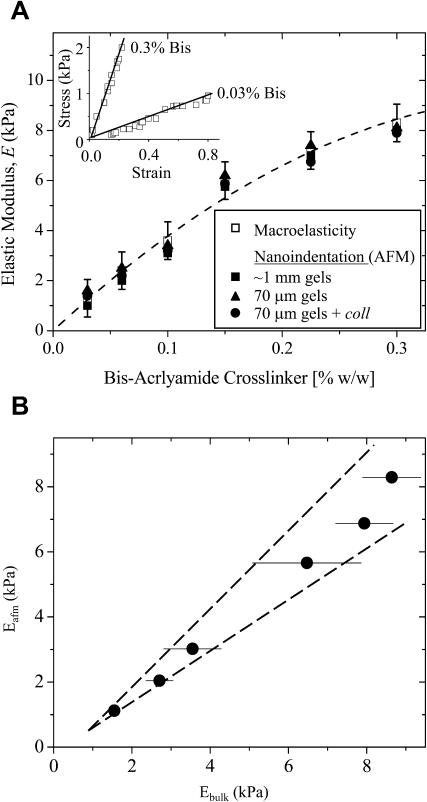
Gel stiffness was determined by two methods summarized in Fig. 2. Atomic force microscopy (AFM) was used to measure nanoscale stiffness, which is probably most relevant to actual cell sensing. The elastic modulus, E, was obtained using a Hertz cone model (Domke and Radmacher, 1998; Rotsch et al., 1999; Rotsch and Radmacher, 2000) to fit the first 5–50 nm of indentation profiles obtained from fully hydrated 1–2-mm gel samples with unsharpened, pyramid-tipped cantilevers of spring constant 60 pN/nm. Moduli measurements were performed with an Asylum Epi-Force AFM (Santa Barbara, CA) and were averaged over multiple locations per gel. Macroscopic or bulk elastic measurements were made on the same AFM-probed samples by a simple tension method (Pelham and Wang, 1997), with E calculated from the slope of the Cauchy stress, i.e., tensile force per instantaneous cross-section, versus large deformation uniaxial strain. The latter is 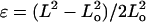Inline graphic using sample length before (Lo) and after (L) deformation (Fung, 1994) without concern for further constitutive implications. PA gels exhibit linear elasticity (Fig. 2, inset), as others have reported (Pelham and Wang, 1997), and macroscopic tests show the linearity extends over a broad range of strain measure. Importantly, the 15–25% strains typically generated by cells as cited in the Introduction are seen here to be well within the linear range of PA gel elasticity.

FIGURE 2.

FIGURE 2

Open in a new tab

Polyacrylamide gel elasticity versus bis-acrylamide cross-linker concentration (in w/w %). (A) The elastic modulus, E, was measured for multiple 5% acrylamide gels by both macroscopic tension test (n = 157) and nanoindentation with an AFM (n = 36) as detailed in Materials and Methods. The inset demonstrates the linearity of the elasticity for the highest and lowest % bis-acrylamide gels as measured by tension tests on macroscopic samples; E is the slope. Such measurements of E were made on ∼1-mm-thick gels by both tension tests and AFM, and by AFM alone on 70-μm-thick gels with and without a monolayer of collagen (coll). The best-fit (dashed) curve through the ∼1-mm gel data is E = 42.6 [bis]–48.1 [bis]2 (R2 = 0.99). For AFM, the Poisson ratio, ν—indicating how a sample shrinks laterally when extended—must be assumed, but macroscopic tension tests suggest a value near 0.4–0.45. (B) For ν = 0.45, the two methods plotted against each other are linearly correlated (R2 = 0.98) with slope nearly 1. Values of ν = 0.3–0.5 shift the cross-correlation between the two measurements methods by <±10%.

Both AFM and bulk measurements of E were made for gels with a range of concentrations of bis-cross-linker (Fig. 2 A) as well as acrylamide monomer. Fig. 2 B shows the two determinations plotted against each other with the Poisson ratio, ν, adjusted within the published range (Geissler and Hecht, 1980; Mahaffy et al., 2000) for PA gels of ν = 0.3–0.5. AFM and bulk measurements are obviously very similar.

Collagen gels and their characterization

Thick collagen gels (300 μm) were used as a gel-ECM mimic for in vivo collagen. Rat-tail collagen I (1% w/w) was treated with a 0.03% glutaraldehyde solution (Sheu et al., 2001) and covalently attached to glass. After a 24-h incubation, the cross-linked collagen was extensively rinsed with PBS to extract excess glutaraldehyde, which is known to be toxic to cells (Simmons and Kearney, 1993). The cross-linked collagen gels seemed as soft as the softest PA gels studied, with an elastic modulus measured at 2.7 ± 0.3 kPa by AFM, which was similar to previous dynamic measurements (Sheu et al., 2001).

Cell image analyses

Cell spreading, cell shape, and cytoskeletal or focal adhesion assembly and integrated fluorescent intensity were evaluated after 4 h, 24 h, or intermediate times for well-separated, viable, and spread A7r5 cells as well as transfected A7r5 cells on the three surfaces: glass, PA gels, and collagen gels. Nonviable and/or nonspread cells were not included in the analysis, but remained only a small portion of the overall cell population. Cell densities were kept at 2500 cells/cm2. Microscopy was preformed on a Nikon Eclipse TE 300 microscope equipped with liquid-nitrogen cooled CCD camera (CH 360, Photometrics Ltd., Tucson, AZ) and 20× and 60× oil-immersion Nikon objectives (0.5 and 1.4 NA, respectively). Phase contrast images of fixed cells were done after staining with hematoxylin and eosin Y (Fisher Scientific, Hampton, NH); fluorescence imaging of fixed GFP-actin or GFP-paxillin cells was done with an EGFP-HQ filter set (Chroma, Brattleboro, VT). Per 35-mm culture dish, 5 μl of a fluorescent dye, PHK 67, was used to stain cell membranes of fixed cells. Image analyses of spread cell area, cell shape, and cytoskeletal or focal adhesion assembly and integrated cell intensities were performed with Image Pro Plus 4.0 (Media Cybernetics, Carlsbad, CA). A dimensionless cell shape factor was calculated as S = 4πA/P2, where A is the projected cell area and P is the cell perimeter; S varies from 1 for a circular shape to 0 for a highly ruffled shape. Results are presented as mean ± SE. Statistical significance was evaluated by t-tests for unpaired data.

RESULTS AND ANALYSES

Spreading of cells on gels at constant collagen

SMCs were first plated on PA gels of controlled stiffness and coated with a nearly constant collagen level (∼5 × 102 ng/cm2) as assessed by fluorescent collagen intensities. Nanometer-scale gel stiffness was measured by AFM, using cantilever tips with radii of curvature <50 nm. The AFM results were confirmed by macroscopic measurements (Fig. 2 B), and prove that PA gel elasticity on the scale of molecular adhesion is not different from that at the micron or larger scale. Collagen was added to these substrates since cell spreading does not normally occur on hour timescales with either PA gels or bare glass. This is due, in part, to the lack of adhesion ligands on PAG, the relatively slow deposition of adhesion-mediating serum proteins or secreted matrix, and the antiadhesive surface chemistry presented by PA gels. To verify cell viability, for any cell on gel experiment below, parallel cultures on glass coverslips with pre-adsorbed collagen were used and found to always show strong cell spreading.

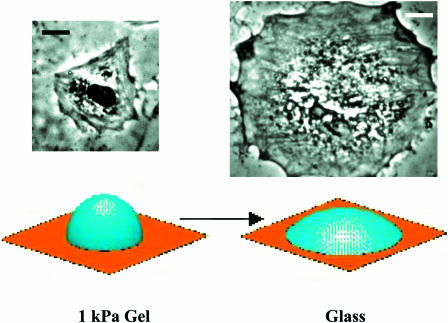
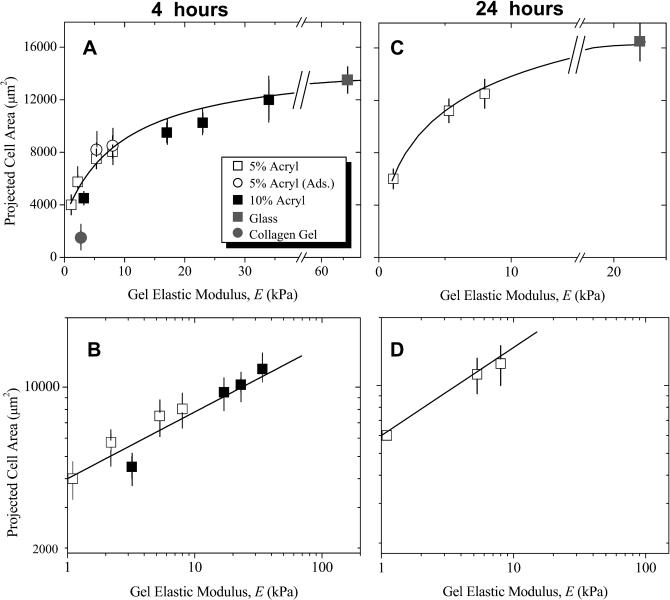
Fig. 3 illustrates typical spread cell sizes and shapes on a soft gel or glass, and Fig. 4, A and B, plot the quantitative measurements of spread cell area at 4 h after plating versus gel elastic modulus, E, or “rigid” glass. The spread cell area on glass is seen to represent a plateau or maximum in cell spreading on an infinitely rigid substrate, assuming one can ignore the minimal flexibility contribution of the thin collagen layer on glass substrates. The results appear independent of both the type of collagen attachment to PA gels (adsorbed or cross-linked as indicated). The results also appear independent of the acrylamide monomer concentration, provided that bis-acrylamide cross-linker concentration was adjusted to maintain comparable elasticity. Cells grown for 4 h on a pure collagen gel of modulus 2.7 kPa (Fig. 4 A) were mostly rounded. Others have also noted that significant morphological responses on similar collagen gels require >24 h to manifest (Sheu et al., 2001). Spreading results for PA gels and glass, however, clearly demonstrate increased cell-to-substrate contact with both substrate stiffness and time. Such observations were first made in PA gel work with epithelial cells by Pelham and Wang (1997) and quickly confirmed with work on 3T3 fibroblasts (Dembo and Wang, 1999; Pelham and Wang, 1998). Cells on gels and glass were also examined here at 24 h after plating (Fig. 4, C and D) and exhibited a similar, increasing but saturable trend with E. However, separate experiments examining collagen-dependent spreading on glass showed that, by 12 h, cell spreading is almost collagen-insensitive, suggesting that surfaces are already becoming remodeled by secreted or serum-deposited matrix by these times.

FIGURE 3.

FIGURE 3

Open in a new tab

Representative SMC spreading on substrates that range from soft PA gels to rigid glass and with an intermediate collagen density of ∼100 ng/cm2. Quantitation of cell areas is given in Figs. 4 and 5. In addition to differences in a mean spread area, the average cell shape factor tends to decrease from S = 0.49 ± 0.06 on a soft substrate (1 kPa gel) to S = 0.25 ± 0.04 for a cell on glass; the latter decreases even more with increasing collagen (see Fig. 6). The schematic depicts model spreading of a constant volume vesicle on a surface. The projected area of the spherical vesicle is just the equatorial area (πr2); when flattened, the surface area of the original sphere (4πr2) flattens to a projected area of 2πr2, which is twofold larger than the sphere (scale bar = 20 μm).

FIGURE 4.

FIGURE 4

Open in a new tab

Substrate-dependent spreading of SMCs. Projected SMC areas at 4 h (A, B) and 24 h (C, D) after plating were measured by image analysis and averaged for various PA gels or glass substrates with near-constant collagen I levels (∼5 × 102 ng/cm2) as assessed by fluorescence. Collagen I gels were also used. On a linear scale for the substrate modulus E (A, C), the results increase asymptotically toward glass, defining the saturation point of the hyperbolic fit (see Eq. 1 in text). On log-log scales (B, D), the sharp dependence of cell spreading on low modulus substrates is expanded, and plots fit a weak power law which can be used to estimate the effective gel elastic modulus that cells see when spreading on glass.

Fig. 4, A and C, clearly show that SMCs respond most strongly to changes in gel stiffness at low E whereas the response to changes in gel stiffness at high E approach saturation on rigid glass. Such presentations of the results resemble saturable binding, although at constant collagen. They therefore motivate hyperbolic fits normalized between suitable limits, as

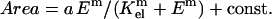graphic file with name M2.gif (1)

Fitting yields m = 0.87 − 1.0 and Kel ∼ 7.5–10 kPa (Table 1). The important, if heuristic, physiological interpretation of such an expression is that, 1), m ≈ 1 suggests minimal cooperativity, such as receptor clustering in the E-sensitive spreading response; and 2), the half-saturation constant Kel represents an intermediate set-point for the system. On matrices with E ∼ Kel, a cell can clearly either spread more if suitably stimulated or spread less if antagonized. One might therefore anticipate that tissue ECM relevant to SMCs would exhibit E ∼ Kel ≈ 8.8 ± 1.3 kPa. SMC-rich tissue such as dog ureter has a modulus of ∼5 kPa in the passive state (Fung, 1993). Regardless, the use of a hyperbolic fit certainly helps define matrices as “soft” for E ≪ Kel, “stiff” for E ∼ Kel, and “rigid” (e.g., glass) for substrates with E ≫ Kel.

TABLE 1.

Fits of SMC spread area versus substrate elasticity in Fig. 4: Area (μm2) and E (kPa)

Fits 4-h parameters 24-h parameters
Hyperbolic (Eq. 1) m = 0.87 Kel = 10 kPa m = 1.0 Kel = 7.5 kPa
Power law (Eq. 2) n = 0.29 b = 4000 n = 0.37 b = 5500
Open in a new tab

The hyperbolic fits above clearly help define soft and stiff regimes below a rigid limit, but a second phenomenological analysis using power laws proves equally insightful. Indeed, power laws are often seen in cell morphological processes, particularly when the cytoskeleton is involved. One example is the transit time of a leukocyte through a pore which is reported to depend on [F-actin]2 (Nossal, 1998). Another example is the cytoplasmic viscosity of HL-60 cells which scales as [mean shear rate]n, where n ∼ 0.5 fits normal cells and n ∼ 0.35–0.4 is found when F-actin is disrupted (Tsai et al., 1996). Zaner and Stossel (1982) were perhaps the first to suggest the power law dependence for F-actin viscosity on shear rate—a phenomenon which is typical of polymeric and complex fluids.

Log-log plots of the cell on gel data replotted in Fig. 4, B and D, are fit well by the form

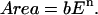graphic file with name M3.gif (2)

The exponent n = 0.29–0.37 given in Table 1 appears consistent with the discussion above of power laws in cytoskeletal response and cell morphology. Although cell spreading is a weak, nonlinear function of gel elasticity since n ≪ 1, Eq. 2 is a readily invertible function: E = (Area/b)1/n. In other words, given a cell's area, one can solve for the gel that the cell is likely spreading on. Because the spread area on glass, Area-SMCglass, is both well-defined and an effective maximum, this value can certainly be substituted and used to calculate an effective elastic modulus, Eeff, which offers at least two important insights. First, Eeff denotes a PA gel on which SMC spreading is indistinguishable from glass (if only statistically). The rigid limit is thus a finite value rather than a mathematical asymptote. Secondly, Eeff represents collective compliant features of both the ECM and the attachment apparatus of a cell (receptors, focal adhesions, actin cortex, etc.). Glass itself is far stiffer, of course, than Eeff indicates, but the body of the cell effectively perceives and responds to softer features above the glass. For context, AFM measurements of many cell types attached to rigid substrates generally reveal elastic moduli, Ecell, that are often attributable to the cytoskeleton and in a broad range of 1–100 kPa (Radmacher, 1997). By substituting Area-SMCglass, we calculate Eeff = 66 kPa at 4 h and 22 kPa at 24 h, respectively. Since Eeff is well within the range of Ecell, one might anticipate that the spreading results here correlate with cytoskeletal organization already suggested by the power law fit itself.

Cells on gels: collagen dependence of spreading

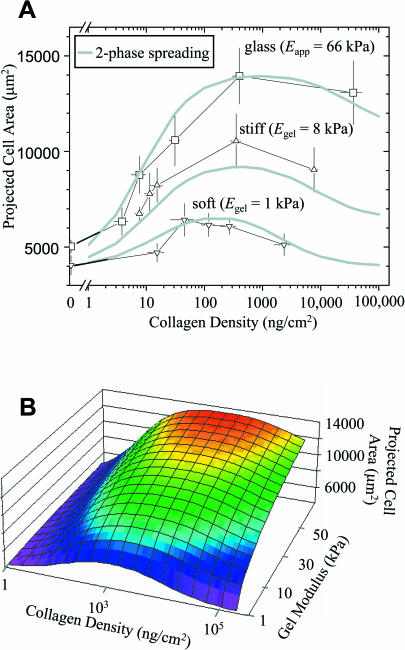
Varying the collagen density on both PA gels and glass is found to strongly modulate cell spreading (Fig. 5). For context, the previous results of Fig. 4 were performed near the “optimum” collagen concentrations of Fig. 5. At higher levels of collagen on glass, SMC spreading is minimally different, but more significant decreases in projected cell area at high collagen density are found on soft and stiff gels. Fig. 5 thus reveals the highly nonlinear, coupled effect of substrate stiffness with collagen ligand. The results clearly span the causal range of interest in substrate stiffness with a soft gel (Egel = 1 kPa), a stiff gel (Egel = 8 kPa), and a rigid substrate (glass: Eeff = 66 kPa determined above). All results in Fig. 5 were obtained from cultures grown in parallel, though in different experiments from those of Fig. 4. A comparison of the two figures proves that the trends are quantitatively reproducible.

FIGURE 5.

FIGURE 5

Open in a new tab

Spread cell area as a function of ligand density on soft, stiff, and rigid substrates. (A) The projected cell area was determined 4 h after plating (n > 10 per datapoint), giving the indicated average (mean ± SE). The smooth curves are calculated from a model for two-phase spreading (see Appendix) expressed in terms of both E (or Eapp) and collagen density. Note that cells respond strongly to increasing collagen density on glass and hardly at all on soft gels. (B) Curved surface in three dimensions that fits SMC spreading.

At near-zero ligand on any substrate studied, SMCs that are detectably spread are all still essentially round. In comparing the most rigid substrates (glass) to the soft gel at zero collagen, the cells have higher projected areas by an average spreading factor, α, of only α ∼ 1.25 (=Area-SMCglass/Area-SMCgel)|coll=0. While this appears to be within the given experimental error, addition of collagen to either a stiff or rigid substrate clearly leads to considerable cell spreading as expected. Relative to SMCs on collagen-free PA gel or glass, the 4-h spreading on glass peaks as a function of collagen at an increased area ratio, α = 2.8–3.5. On a soft substrate, a maximum spreading ratio of only α = 1.5 is attained after 4 h over a wide range of collagen density (∼50–5000 ng/cm2). The magnitude of spreading in this case is small and not very significant, and thus the dominant negative effect of a soft substrate overrides ligand density effects.

The modest peaks in spread cell area of Fig. 5 are reminiscent of the very definitive peaks in cell crawling speed versus ligand density for motile cells, notably myoblasts (Goodman et al., 1989). The accepted explanation for such biphasic phenomena (Lauffenburger and Lindermann, 1996) is that cell crawling is first limited on low ligand densities where a cell cannot form adequate attachments to pull itself forward or spread. Subsequently, at high ligand densities a cell cannot detach from enough ligand to bring its rear forward. The need for detachment in cell spreading is less obvious and thus consistent with the second phase being less pronounced here compared to cell crawling. Nonetheless, the effective peaks, or saturation, in spread cell area clearly appear shifted to lower ligand densities for decreasing substrate stiffness. The Appendix outlines a relatively simple two-reaction model that incorporates the elastic substrate dependence in two dominant association constants for spreading and its inhibition, utilizing the power law fit in Table 1 (data for Fig. 4 fits correspond to near-peak spreading levels of collagen). The single expression arrived at in the Appendix gives the three smooth curves of Fig. 5 A. These curves are cuts through a curved surface in three dimensions as shown in Fig. 5 B, and first hinted at in the simpler surface of Fig. 1.

Given the comparisons above with cell crawling, a simple estimate here of cell spreading velocity proves useful. The leading edge of a crawling cell is driven by actin polymerization to generate crawling velocities of vcrawl ∼ 1 μm/min (Carlier and Pantaloni, 1997; Mogilner and Oster, 1996). By assuming that the most spread cells on rigid substrates are circular in shape, the mean radius of such cells is ∼Rspread ∼ 70 μm, whereas the least spread cells on either soft gels or collagen-free glass have Runspread ∼ 35 μm. The difference in means, ΔR, is achieved in Δt ∼ 4 h = 240 min, and so the simplest estimate of maximum spreading velocity, vspread ∼ ΔR/Δt ∼ 0.15 μm/min. This is, of course, a time-average, and minimal additional spreading by 24 h (Fig. 4 C) suggests that initial spreading velocities are much higher. Moreover, ramified shapes described below would certainly suggest vspread is an underestimate. The fact that vcrawl and the underestimated vspread are within an order of magnitude is suggestive if not inconsistent with some shared, basic mechanisms.

Spread cell shapes

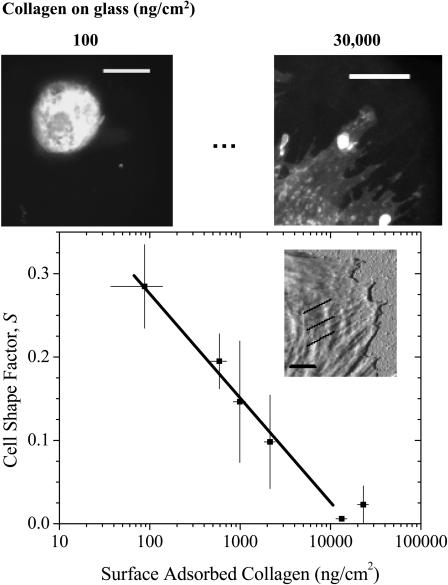
Changes in cell shape often accompany spreading (Fig. 3). Pelham and Wang (1997) reported increased ruffling of NRK epithelial cells and polarization without stress fibers in fibroblasts on their softest gels. Deroanne et al. (2001) described endothelial cells on soft gels as elongated and tubular rather than polygonal. Here, morphologies of well-separated SMCs on soft gels appear rounded and similar to those on collagen-free glass at 4 h. However, with increasing collagen on rigid glass, spreading not only increases characteristically (per Fig. 4) but the cell edge becomes considerably rougher. The shape factor, S, provides a numerical measure of cell roundness and clearly decreases with collagen surface concentration (Fig. 6), vanishing at the highest ligand densities. For the best visualization, measurements were made on cells with their plasma membrane fluorescently labeled by the cell-viable dye PKH 67 (Fig. 6, upper images). The inset AFM image (Fig. 6, plot inset) shows the leading edge of an SMC on a rigid substrate with high ligand density: it highlights distinct membrane extensions defined by organized cytoskeletal substructures that appear to drive membrane spreading.

FIGURE 6.

FIGURE 6

Open in a new tab

Cell shape-dependence on collagen density. The cell shape factor, S, for the cell periphery is high for circular shapes and low for more ramified cell boundaries. The amphiphilic, cell-viable fluorophore PKH 67 highlights the cell boundary (scale bar = 20 μm) and allows for high-resolution fluorescence imaging of cell shape. Only the results for collagen on glass at 4 h after plating are shown here, but Fig. 6 illustrates similar trends for cells on gels. The inset is an AFM tapping mode image (scale bar = 2 μm) of an SMC spread on a rigid substrate; note the filamentous cytoskeleton clearly extending up to the leading edge.

Organization of GFP-actin and GFP-paxillin

Prior cell-on-gel studies have suggested altered actin assembly on softer substrates (Deroanne et al., 2001) as well as decreased paxillin phosphorylation (Pelham and Wang, 1997). Here, GFP-β-actin- and GFP-paxillin-transfected SMCs were grown to confluency, and then replated for 4 h on a soft, stiff, or rigid substrate, first with optimum collagen densities (Fig. 5). With expression efficiencies typically >50%, the GFP chimeras allow clear identification of expressing cells as well as visualization of both assembled and diffuse, monomeric proteins. Expression levels of these GFP-proteins do add to endogenous pools, but GFP-actin in particular proved to increase overall actin levels by only ∼5–10% as is typical of GFP-based reporter studies (see Materials and Methods).

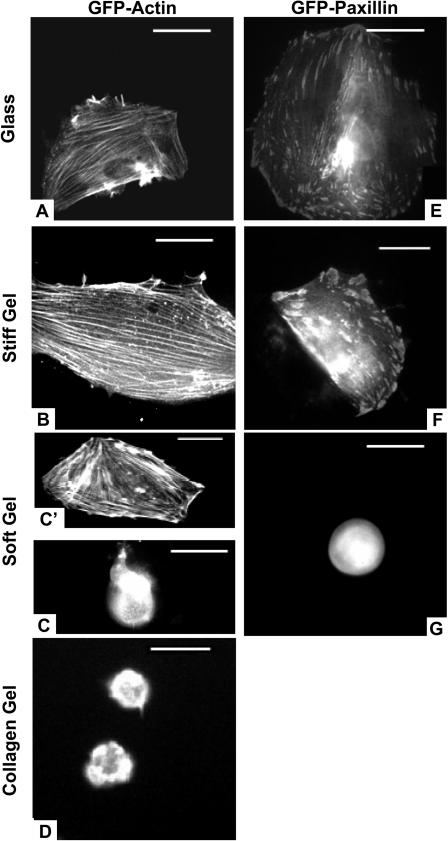
On both stiff and rigid substrates, the cells expressing GFP-actin are well-spread as above and typically show well-ordered stress fibers that span much of the cytoplasm (Fig. 7, A and B). Though such well-spread cells predominate on “optimal” collagen-coated substrates, the same substrates with low collagen densities show a majority of cells that are smaller and diffusely expressing (analogous to Fig. 7 C). However, a small subpopulation of these cells (∼20%, n = 45) proved to be highly spread with organized GFP-actin stress fibers (analogous to Fig. 7 C′). Thus, the exceptions illustrate a rule: spreading correlates well with cytoskeletal assembly.

FIGURE 7.

FIGURE 7

Open in a new tab

GFP-actin and GFP-paxillin expressing SMCs on various collagen-coated substrates. The cells had been transfected en masse at least 1 day before detachment and replating on the desired substrate. Fluorescent cells shown were imaged at 4 h after replating (scale bar = 50 μm). Cells were observed on rigid glass (A, E), stiff PA gels (B, F), soft PA gels (C, C′, and G), and cross-linked collagen I gels (D). The contrast in the images reveals the assembly within live cells in terms of a ratio of freely diffusible versus organized component (e.g., G-actin versus F-actin).

On the softest gels (Fig. 7, C and D) of either “optimally” collagen-coated PA gels or 1% pure collagen I, cells appear rounded with monomeric GFP-actin (at both 4 and 24 h). Yet on the “optimally” coated soft PA gels, a dominant fraction of expressing cells (∼70%, n = 31) not only clearly show GFP-actin stress fibers (Fig. 7 C′) but are also more spread compared to nonexpressing and untransfected spread cells. These GFP-actin-organized cells on soft gels defy the cell on gel trends above and are studied further below. They nonetheless reinforce an important correlation between spreading and cytoskeletal assembly.

GFP-paxillin focal adhesions are clearly seen—as expected, perhaps—in transfected SMCs spread on stiff or rigid substrates (Fig. 7, E and F). Such organization tends to be lost, however, on soft gels where most cells remain rounded (Fig. 7 G). These results are consistent with past studies of rhodamine-vinculin microinjected into NRK epithelial cells (Pelham and Wang, 1997). The cited studies with cells on soft gels showed no more than nascent vinculin assembly as small punctate localizations of vinculin and phosphotyrosine near the outer edge of membrane. With stiff substrates, mature elongated focal adhesions were reported, and paxillin was found to be hyperphosphorylated on these substrates. Separate studies comparing endothelial cells to fibroblasts have also shown, by Western blot, the downregulation of focal adhesion proteins (α2-integrin, vinculin, actin, etc.), though only for endothelial cells on soft gels (Deroanne et al. 2001). In the SMCs here, diffuse GFP-paxillin is clearly visible in the rounded cells on the soft substrates (Fig. 7 G), but unlike GFP-actin expression the paxillin expression here has little ability to influence spreading and overcome the dominant “soft” signal from the substrate. This is consistent with our previous finding that excess adhesive ligand (collagen) on soft gels does not override the dominant tendency for SMCs to remain rounded, unless there is a more direct cytoskeletal impetus (e.g., GFP-actin).

Ligand-dependent perturbation by GFP-actin

Though our original goal above was to use GFP-proteins merely as live reporters of both assembled and diffuse proteins, deeper study was clearly motivated by the organization and increased spreading on soft gels that emerged with GFP-actin expression (Fig. 7 C′). The differences arose even though total actin pools are only slightly increased by expression of GFP-actin (Choidas et al., 1998; see Materials and Methods). The converse experiment, for context, is the oft-repeated addition of a cytoskeleton-depolymerizing drug to cells cultured on a rigid rather than soft substrate: the actin monomer-binding drug Latrunculin A (Bar-Ziv et al., 1999) is a typical example for which the well-known consequence is cell retraction and rounding off of the surface.

On soft gels with our range of collagen densities, we sought to reproduce and extend the GFP-actin results above. In parallel with a GFP-actin transfection, SMCs were also transfected with unconjugated GFP-alone, or not transfected at all. All three cell systems were then plated on the soft PA gels of varying collagen densities and grown for 4 h before fixation and staining with rhodamine-phalloidin to label F-actin. Cells were analyzed for both spread area and phalloidin intensity integrated over the entire cell area to determine a relative level of F-actin assembly weighted by the cell size (measured as intensity a.u. × μm2).

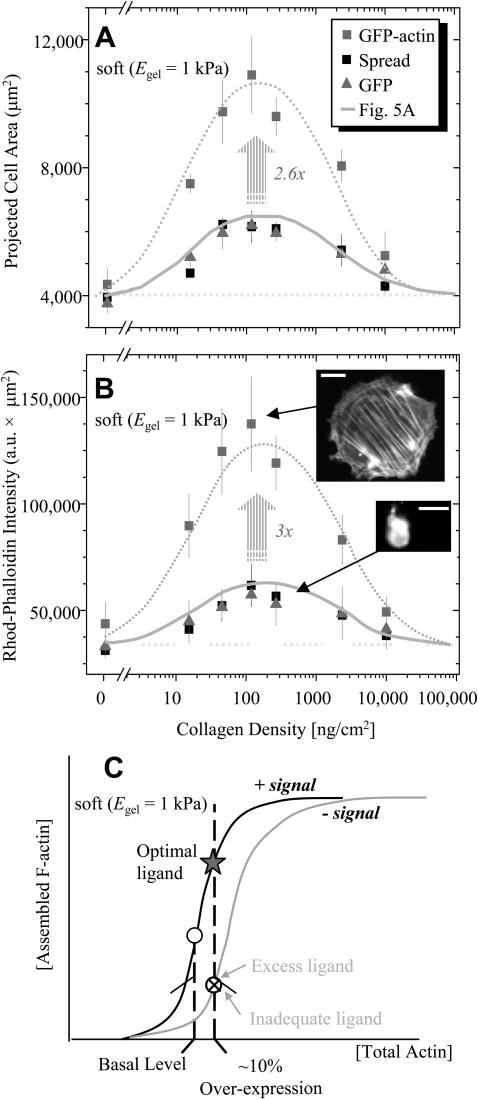
Both control cells (GFP-alone and nontransfected cells) showed minimal spreading (Fig. 8 A) as a function of collagen density. The results proved quantitatively the same as the previous determinations of Fig. 5 A, which are presented again in Fig. 8 A by the continuous, solid curve. The integrated phalloidin intensity for the control cells showed the same trend (Fig. 8 B), and the lower inset image illustrates the lack of elongated stress fibers and resolvable cytoskeletal organization in the cells even at “optimal” collagen densities.

FIGURE 8.

FIGURE 8

Open in a new tab

On soft PA gels, slight overexpression of actin with GFP-actin transfection amplifies and overrides the weak optimum seen in spread area (A) and F-actin mass (B) over a range of collagen densities. Control cells were either transfected with bare GFP or nontransfected. For spread area, the solid bell-shaped curve through the control cells is the same as in Fig. 5 A; for F-actin mass measured as the integrated intensity of rhodamine phalloidin, the same curve shape is used to fit the control cells. As explained in the text, the dotted horizontal lines define baselines and the dotted, bell-shaped curves are stretched (2.6× or 3×) forms of the respective solid curves. Nonexpressing cells are excluded from analyses, as are completely rounded cells (<30%). Scale bar is 50 μm. (C) A schematic of F-actin assembly versus total actin pool is overlaid on hypothesized signaling curves. On optimum collagen, there is an impetus to assemble F-actin, which is amplified greatly with GFP-actin expression; on high or low collagen, the signal is effectively absent or inhibitory.

As described above, GFP-actin-expressing cells spread significantly more than the control cells on optimal, intermediate collagen densities (Fig. 8 A), and yet this is not the case on either high or low collagen. At the extremes of collagen, the spreading of GFP-actin expressing cells proves more limited and tends to be the same as the control cells. This appears consistent with the lack of significant spreading of GFP-actin cells on pure 1% collagen gels. This is because collagen gels are not only soft but can also be viewed as presenting very high adhesive ligand to the cells. For purposes of a simple analysis, the extremes in Fig. 8 A define a baseline SMC area of ∼4000 μm2, which is shown as the horizontal, dotted line. Above this baseline, the solid curve for the spread area of control cells—labeled as Fig. 5 A—is stretched by 2.6× to obtain a very good fit of the bell-shaped, GFP-actin results.

The bell-shaped curve for spread area of GFP-actin SMCs is mirrored in the mean integrated intensity of rhodamine-phalloidin (i.e., F-actin) of these same cells (Fig. 8 B). Indeed, compared to control cells, GFP-actin cells on the same density of collagen exhibited 3× higher levels of phalloidin staining when integrated over the cell area. Not only is this multiplicative factor virtually the same as in Fig. 8 A, but it implies that the increase in spread area can be divided out of Fig. 8 B with the effect of proving that all of the cells, both controls and GFP-actin, on any given collagen density have nearly the same F-actin per area. This is equivalent to the same average F-actin density, but also clearly implies a greater total mass of F-actin in spread cells. The various images of Figs. 7 and 8 indicate a tendency toward longer filament length as well. Shifts from monomeric to F-actin are known to result from changes in capping protein levels (Carlier and Pantaloni, 1997), among other effectors such as ATP (Carlier et al., 1994), which are also known to have a nonlinear influence on filament length.

Regardless of detailed mechanism, the consistent amplification of the bell-shaped soft gel response stems from a relatively small perturbation to cellular actin pools with GFP-actin expression. Even with such overexpression, the persistence of an optimum in ligand density indicates that positive and negative signals underlie considerable shifts in filament assembly which we postulate drive cell spreading. An envisioned cooperativity in signaling-modulated assembly is sketched in Fig. 8 C. With optimal ligand, the signal is positive, F-actin assembly is greatly amplified, and the cell spreads. With suboptimal ligand, negative signaling works against the small perturbation of total actin and no spreading occurs. Increased cytoskeletal assembly can thus be a means of overriding by amplification the typical cell signal on a soft gel (i.e., minimal spreading). In contrast, a GFP-tagged focal adhesion protein such as paxillin does not have an effect, indicating a unique signaling node that the cytoskeleton defines in the ligand-modulated cell on gel response.

DISCUSSION

Cell spreading: wetting of a substrate or driven by internal processes and external signals?

One overly simplistic view of cell adhesion is that more ligand-receptor interactions will increase the extent of spreading (i.e., haptotaxis) in much the same way that the hydrophilicity of a surface dictates the extent that a water droplet will spread or wet the surface. Cells are obviously far more complex, and the underlying notion of durotaxis (Lo et al., 2000) is that mechanically active structures inside cells, particularly the cytoskeleton, push or pull on the substrate and respond to its compliance with some significant level of spreading, for example, that is similar to haptotactic responses. The adhesion results here support the importance of durotaxis-type response to SMCs. SMC spreading, like cell crawling in general, is thus driven by intracellular processes such as actin filament growth but modulated by external cues that include substrate stiffness as well as ligand density.

Soft or rigid is modulated by ligand density

The results here add to the central and orthogonal importance of substrate stiffness in cell attachment responses (Figs. 1, 5, and 8). A major result here is that SMC spreading on soft gels (identified as E < Kel) is relatively unresponsive to ligand density, up to the saturation point (i.e., a collagen gel). A weak optimum in collagen density for average projected cell area is suggested on soft gels, but the average stimulation on stiff or rigid (i.e., glass) substrates is far greater in comparison (Fig. 5). Thus matrix compliance and ligand density are highly coupled variables that determine mean cell responses ranging from cell spreading to cell shape and molecular organization.

Irrespective of ligand density, we show that spread SMCs grown on the softest PA (and collagen) gels are rounded although ruffled, whereas cells grown on both the stiffest gels and glass appeared more flattened and polygonal or slightly dendritic (Figs. 3 and 6). In original studies of tissue cells on soft gels (Pelham and Wang, 1997), epithelial cells were shown to have smaller, dynamically ruffled cell shapes, and fibroblasts were reported to be more polarized and clearly lacking in stress fiber expression on soft gels. In comparing the ratio of SMC spreading on glass to our softest (1 kPa) gels with optimal collagen density, we show (Fig. 5) mean area ratios that differ by a factor of α = (Area-SMCglass/Area-SMCgel) = 2.5 at 4 h (and α = 2.7 at 24 h). If these morphological differences from spreading were simply like those of a spherical vesicle that flattens out in strong adhesion from a sphere (with Projected Area = πR2) to a disk (with Projected Area = 2πR2), then the theoretical maximum spreading ratio αsphere→disc = 2. Our finding that α > 2 is consistent with a tensed smoothing, also noted by Pelham and Wang (1997), where smoothing was quantified as an approximately fivefold decrease in the amplitude of ruffling. The overall increase in SMC boundary roughness (Fig. 6) might also imply some component of membrane addition from plasma membrane “reservoirs” (Raucher and Sheetz, 1999). Such reservoirs are thought to facilitate plasmalemma addition or removal in response to a set-point such as membrane tension τo (∼0.01 mN/m typically), already established for fibroblasts, epithelial, and other cell types (Raucher and Sheetz, 1999; Reuzeau et al., 1995).

A role for cytoskeleton and, perhaps, membrane tension

Although other cytoplasmic factors (as opposed to adhesive ligands such as collagen) may be important, the cytoskeleton is clearly implicated in both spreading here on soft gels and membrane tension, τo. Talin knockout cells, for example, have been reported to have a threefold reduction in τo (Simson et al., 1998). A simple analogy seems useful here: a cell membrane is similar to a tent into which cytoskeletal “poles” are impinging as they assemble within and provide form (see Fig. 6). Poles directed centripetally outward lead to inward-directed forces or tractions where they insert into the ground (Lo et al., 2000). A higher tension generates a larger force, and softer substrates make it easier for the poles to slip and lose traction.

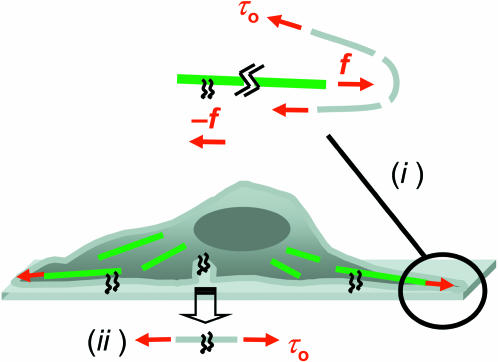
Centripetally directed traction forces exerted by cells are known to increase on stiff gels together with cell area (Lo et al., 2000). With the simple tent-poking concept in mind, such tractions should in part reflect reaction forces to cytoskeleton-driven membrane advance in cell spreading (Fig. 9 (i)). The maximum traction forces, f (as stresses typically of ∼1 kPa), reported for both 3T3 cells and airway SMCs, are always generated near the cell periphery and typically in regions of protruding membrane. Assuming quasiequilibrium with a force balance maintained between the traction forces and the membrane tension, several length scales are introduced through the focal adhesions (of length l and width w) and the curvature (R) of the distending membrane: flw = τoR. Typical values cited above for f and τo yield a nanoscopic length-scale ratio of lw/R ∼ 10 nm. The AFM image inset to Fig. 6 suggests local membrane curvatures at the leading edge with R ∼ 100 nm, and the length of many focal adhesions in Fig. 7 E is approximately l ∼ 1000 nm. These length scales then imply long and narrow focal adhesion structures (see Fig. 7 E) that can, in principle, provide insertion points for stress fibers (see Fig. 7 A) and can also, directly or indirectly, orient filaments toward the membrane. These estimations serve to illustrate the reasonableness of a protruding membrane mechanism in Fig. 9 (i) that subsumes models of motility such as polymer-rectified fluctuations (Mogilner and Oster, 1996). Cytoskeletal control of membrane τo should thus influence plasma membrane area, which can affect, in turn, accessible integrin display (Fig. 9 (ii)) and also influence net channel activity.

FIGURE 9.

FIGURE 9

Open in a new tab

Schematic of cytoskeleton-driven spreading coupled to membrane tension. F-actin is sketched as green lines which (i) drive with a force f against the membrane while being anchored by focal adhesions at the other end. Newton's law of action-reaction equates f near adhesion sites with cell tractions (Lo et al., 2000), while balancing f at the plasma membrane by the tension τo. Slight increases in this tension—driven by the cytoskeleton (see Fig. 6, inset)—will tend to reinforce spreading (ii) by driving into adhesive contact plasma membrane reservoirs such as vesicles widely known in platelets (Grouse et al., 1990). Such recruitment processes tend to relax any increases in tension back to τo.

Cell membranes and their attachment proteins are also certainly known to be compliant, leading to the idea that the compliance of any adhesive apparatus—being in series with the substrate—will ultimately define an effective gel for a cell. This limit certainly appears reasonable on a rigid substrate like glass for which we estimated a cellular Eeff in reasonable agreement with AFM-determined values for similar cells (Radmacher, 1997). The results here mean, of course, that compliant features of a cell are ultimately reflected in the cell's own attachment response. The same connection is clear from related studies on airway SMCs which show that cell stiffness is proportional to the tractions generated by a cell or, equivalently, the contractile prestress within the cell (Wang et al., 2002). Since cell stiffness is usually affected most strongly by cytoskeleton and since prestress has to at least be dynamically balanced by attachment strength, the cytoskeleton plays an obvious bridging role between contractility and adhesion. We suggest that plasma membrane tension is an important intermediary in the coupled responses of cells on gels.

Cell biological implications

Although our results indicate that the cytoskeleton is one key structural node in a signaling network, the possible role of other cytoplasmic factors altered by F-actin overexpression needs to be investigated to thoroughly understand mechanotransduction in cells on gels. Longer term studies of SMCs on soft versus stiff gels at various ligand densities are also clearly needed given the apparent lethargy of the SMCs in spreading and organization—i.e., the delayed response of cells on collagen gels versus PA gels (Sheu et al., 2001). Parallel processes might be hypothesized to result from addition of soluble versions of adhesion ligands to well-spread cells. With lung fibroblasts, soluble fibronectin peptides including RGD have been shown to disrupt adhesion and induce apoptosis with a maximal effect of almost 90% apoptosis at ∼100 h and the tell-tale proteolysis of focal adhesion kinase pp125FAK (Hadden and Henke, 2000). Similar effects have been reported previously with endothelial cells, epithelial cells, and other fibroblast types (Frisch and Francis, 1994; Hadden and Henke, 2000; McGill et al., 1997; Meredith et al., 1993). Apoptosis from soluble ligand does appear to be a component of SMC response in atherosclerotic plaque development, and it is a contributing factor to plaque rupture (Imanishi et al., 2002).

More generally, vascular SMC hypertrophy and proliferation are widely known to contribute to the development of atherosclerosis, hypertension, and restenosis where matrix remodeling occurs in parallel with perturbation of normal mechanical forces. How SMCs sense and transduce ECM signals into such altered states of expression, structure, and function is an important question recognized in the field of SMC signaling (Li and Xu, 2000). Externally imposed mechanical stress is certainly known to affect differentiation (Rowley and Mooney, 2002), probably achieving this through altered activities demonstrated for kinases and integrins (Li and Xu, 2000). Overlapping outside-in signaling pathways with growth factors have therefore been suggested to lend insight into therapeutic strategies. In these contexts, the cell-on-gel results here not only indicate that SMCs respond to ECM stiffness through intracellular stressing mechanisms (e.g., stress fibers and membrane tension), but that they do so in ways that can override matrix ligand and perhaps other outside-in signaling pathways. More generally, dose-response pharmacological agents—like the response to collagen—may prove highly dependent on the strong response of a cell to matrix stiffness. The implications of this idea extend beyond vascular disease to other matrix remodeling and detachment processes such as cancer.

Acknowledgments

The authors thank Dr. D. J. Webb for providing the GFP-paxillin DNA constructs and Dr. Makoto Funaki for the pEGFP-actin DNA constructs.

This work was supported by grants from the National Science Foundation, the National Institutes of Health, and the Muscular Dystrophy Association to D.D.

APPENDIX

The two phases of cell spreading suggested in Fig. 5 are modeled here as a single composite function of Area dependent on E (or Eeff) and [collagen] = coll. The dependence on coll is expressed in the sum of two hyperbolic terms that are typical of saturable equilibrium associations. The first hyperbolic term models the fractional association in one area-promoting reaction (with association constant K1) whereas the second term models the fractional dissociation in a separate, area-inhibiting reaction (with association constant K2). Simplicity of the model rather than uniqueness is a principal consideration here. Importantly, the power law fit of Fig. 4 B's Area (μm2) versus E (kPa) is used to scale the area-promotion reaction (see Table 1). For the cell on glass results, we use E = Eeff. A baseline projected area response appears as a constant, ao, and the association constants K1 and K2 are taken to be power laws in Eeff (kPa). The final equation defines a continuous surface for the cell Area (μm2),

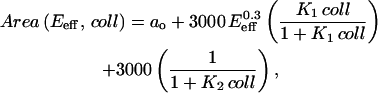graphic file with name M4.gif (A1)

where a0 = 1000, K1 = 0.07 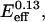Inline graphic and K2 = 0.0005/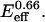Inline graphic As such, both terms involve a product of E and coll and therefore indicate mathematical coupling in a formal sense. Very good fits are also obtained with the form Area = a0 + a1exp(−γ/coll) [1/(1 +K2 coll)], which replaces the first term of Eq. A1 with a stretching penalty factor set by γ. An illustrative comparison of the two spreading phases is made by defining ψspreading ≡ K2/K1 = 0.007 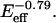Inline graphic Although the present approach is an equilibrium approach to the problem, the kinetic approach to biphasic cell motility taken by Lauffenburger and Lindermann (1996) is also parameterized by a dimensionless ratio, ψcrawling, of dissociation rate constants between the front and rear of the cell. They report ψcrawling to be from 0.5 to 0.01 in fits of a range of cell crawling results. The prefactor that we find for ψspreading is of the same order of magnitude and thus supports the idea that similar phenomena underlie the two-phase behavior in both cell spreading and cell crawling.

Adam Engler and Lucie Bacakova contributed equally to this work.

Lucie Bacakova's present address is Institute of Physiology, Acad. Sci. CR, Videnska 1083, 142 00 Prague 4-Krc.

Abbreviations used: ECM, extracellular matrix; GFP, green fluorescent protein; SMC, smooth muscle cell; FBS, fetal bovine serum; PA, polyacrylamide; DMEM, Dulbecco's Modified Eagle Medium; BSA, bovine serum albumin; PBS, phosphate buffer solution.

References

  1. Bar-Ziv, R., T. Tlusty, E. Moses, S. A. Safran, and A. Bershadsky. 1999. Pearling in cells: a clue to understanding cell shape. Proc. Natl. Acad. Sci. USA. 96:10140–10145. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Beningo, K. A., and Y. L. Wang. 2002. Fc-receptor-mediated phagocytosis is regulated by mechanical properties of the target. J. Cell Sci. 115:849–856. [DOI] [PubMed] [Google Scholar]
  3. Carlier, M. F., and D. Pantaloni. 1997. Control of actin dynamics in cell motility. J. Mol. Biol. 269:459–467. [DOI] [PubMed] [Google Scholar]
  4. Carlier, M. F., C. Valentin-Ranc, C. Combeau, S. Fievez, and D. Pantoloni. 1994. Actin polymerization: regulation by divalent metal ion and nucleotide binding, ATP hydrolysis and binding of myosin. Adv. Exp. Med. Biol. 358:71–81. [DOI] [PubMed] [Google Scholar]
  5. Choidas, A., A. Jungbluth, A. Sechi, J. Murphy, A. Ullrich, and G. Marriott. 1998. The suitability and application of a GFP-actin fusion protein for long-term imaging of the organization and dynamics of the cytoskeleton in mammalian cells. Eur. J. Cell. Bio. 77:81–90. [DOI] [PubMed] [Google Scholar]
  6. Cukierman, E., R. Pankov, D. R. Stevens, and K. M. Yamada. 2001. Taking cell-matrix adhesions to the third dimension. Science. 294:1708–1712. [DOI] [PubMed] [Google Scholar]
  7. Dembo, M., and Y.-L. Wang. 1999. Stresses at the cell-to-substrate interface during locomotion of fibroblasts. Biophys. J. 76:2307–2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Deroanne, C. F., C. M. Lapiere, and B. V. Nusgens. 2001. In vitro tubulogenesis of endothelial cells by relaxation of the coupling extracellular matrix-cytoskeleton. Cardiovasc. Res. 49:647–658. [DOI] [PubMed] [Google Scholar]
  9. Domke, J., and M. Radmacher. 1998. Measuring the elastic properties of thin polymer films with the atomic force microscope. Langmuir. 14:3320–3325. [Google Scholar]
  10. Evans, K., K. Schifferli, and P. Hawley-Nelson. 1999. High-efficiency transfection of HeLa cells. Focus. 21:15. [Google Scholar]
  11. Firulli, A. B., D. Han, L. Kelly-Roloff, V. E. Koteliansky, S. M. Schwartz, E. N. Olson, and J. M. Miano. 1998. A comparative molecular analysis of four rat smooth muscle cell lines. In Vitro Cell. Dev. Biol. Anim. 34:217–226. [DOI] [PubMed] [Google Scholar]
  12. Frisch, S. M., and H. Francis. 1994. Disruption of epithelial cell-matrix interactions induces apoptosis. J. Cell Biol. 124:619–626. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Fung, Y.-C. 1993. Biomechanics: Mechanical Properties of Living Tissues. Springer, New York.
  14. Fung, Y.-C. 1994. A First Course in Continuum Mechanics. Prentice-Hall, Englewood, NJ.
  15. Geiger, B. 2001. Encounters in space. Science. 294:1661–1663. [DOI] [PubMed] [Google Scholar]
  16. Geissler, E., and A. M. Hecht. 1980. The Poisson ratio in polymer gels. Macromolecules. 13:1276–1280. [Google Scholar]
  17. Goodman, S. L., G. Risse, and K. von der Mark. 1989. The E8 subfragment of laminin promotes locomotion of myoblasts over extracellular matrix. J. Cell Biol. 109:799–809. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Grouse, L. H., G. H. Rao, D. J. Weiss, V. Perman, and J. G. White. 1990. Surface-activated bovine platelets do not spread, they unfold. Am. J. Pathol. 136:399–408. [PMC free article] [PubMed] [Google Scholar]
  19. Hadden, H. L., and C. A. Henke. 2000. Induction of lung fibroblast apoptosis by soluble fibronectin peptides. Am. J. Respir. Crit. Care Med. 162:1553–1560. [DOI] [PubMed] [Google Scholar]
  20. Imanishi, T., D. K. Han, L. Hofstra, T. Hano, I. Nishio, W. Conrad Liles, A. M. Gorden, and S. M. Schwartz. 2002. Apoptosis of vascular smooth muscle cells is induced by Fas ligand derived from monocytes/macrophage. Atherosclerosis. 161:143–151. [DOI] [PubMed] [Google Scholar]
  21. Ingber, D. E. 1990. Fibronectin controls capillary endothelial cell growth by modulating cell shape. Proc. Natl. Acad. Sci. USA. 87:3579–3583. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lauffenburger, D. A., and J. J. Lindermann. 1996. Receptors: Models for Binding, Trafficking, and Signaling. Oxford University Press, London, UK.
  23. Laukaitis, C. M., D. J. Webb, K. Donais, and A. F. Horwitz. 2001. Differential dynamics of α-5 integrin, paxillin, and α-actinin during formation and disassembly of adhesions in migrating cells. J. Cell Biol. 153:1427–1440. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Li, C., and Q. Xu. 2000. Mechanical stress-initiated signal transductions in vascular smooth muscle cells. Cell. Signal. 12:435–445. [DOI] [PubMed] [Google Scholar]
  25. Lo, C. M., H. B. Wang, M. Dembo, and Y. L. Wang. 2000. Cell movement is guided by the rigidity of the substrate. Biophys. J. 79:144–152. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Mahaffy, R. E., C. K. Shih, F. C. MacKintosh, and J. Kas. 2000. Scanning probe-based frequency-dependent microrheology of polymer gels and biological cells. Phys. Rev. Lett. 85:880–883. [DOI] [PubMed] [Google Scholar]
  27. Massaeli, H., C. Hurtado, J. A. Austria, and G. N. Pierce. 1999. Oxidized low-density lipoprotein induces cytoskeletal disorganization in smooth muscle cells. Am. J. Physiol. 277:H2017–H2025. [DOI] [PubMed] [Google Scholar]
  28. McGill, G., A. Shimamura, R. C. Bates, R. E. Savage, and D. E. Fisher. 1997. Loss of matrix adhesion triggers rapid transformation-selective apoptosis in fibroblasts. J. Cell Biol. 138:901–911. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Meredith, I. T., T. J. Anderson, A. Uehata, A. C. Yeung, A. P. Selwyn, and P. Ganz. 1993. Role of endothelium in ischemic coronary syndromes. Am. J. Cardiol. 72:27C–32C. [DOI] [PubMed] [Google Scholar]
  30. Miyamoto, S., S. K. Akiyama, and K. M. Yamada. 1995. Synergistic roles for receptor occupancy and aggregation in integrin transmembrane function. Science. 267:883–885. [DOI] [PubMed] [Google Scholar]
  31. Mogilner, A., and G. Oster. 1996. Cell motility driven by actin polymerization. Biophys. J. 71:3030–3045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Mounier, N., J.-C. Perriard, G. Gabbiani, and C. Chaponnier. 1997. Transfected muscle and non-muscle actins are differentially sorted by cultured smooth muscle and non-muscle cells. J. Cell Sci. 110:839–846. [DOI] [PubMed] [Google Scholar]
  33. Nossal, R. 1998. Cell transit analysis of ligand-induced stiffening of polymorphonuclear leukocytes. Biophys. J. 75:1541–1552. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Pelham, R. J. Jr., and Y. L. Wang. 1998. Cell locomotion and focal adhesions are regulated by the mechanical properties of the substrate. Biol. Bull. 194:348–350. [DOI] [PubMed] [Google Scholar]
  35. Pelham, R. J., and Y.-L. Wang. 1997. Cell locomotion and focal adhesions are regulated by substrate flexibility. Proc. Natl. Acad. Sci. USA. 94:13661–13665. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Ra, H., C. Picart, H. Feng, H. L. Sweeney, and D. Discher. 1999. Muscle cell peeling from micropatterned collagen: direct probing of focal and molecular properties of matrix adhesion. J. Cell Sci. 112:1425–1436. [DOI] [PubMed] [Google Scholar]
  37. Radmacher, M. 1997. Measuring the elastic properties of biological samples with the AFM. IEEE Eng. Med. Biol. Mag. 16:47–57. [DOI] [PubMed] [Google Scholar]
  38. Raucher, D., and M. P. Sheetz. 1999. Characteristics of a membrane reservoir buffering membrane tension. Biophys. J. 77:1992–2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Reuzeau, C., L. R. Mills, J. A. Harris, and C. E. Morris. 1995. Discrete and reversible vacuole-like dilations induced by osmomechanical perturbation of neurons. J. Membr. Biol. 145:33–47. [DOI] [PubMed] [Google Scholar]
  40. Rotsch, C., K. Jacobson, and M. Radmacher. 1999. Dimensional and mechanical dynamics of active and stable edges in motile fibroblasts investigated by using atomic force microscopy. Proc. Natl. Acad. Sci. USA. 96:921–926. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Rotsch, C., and M. Radmacher. 2000. Drug-induced changes of cytoskeletal structure and mechanics in fibroblasts: an atomic force microscopy study. Biophys. J. 78:520–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Rowley, J. A., and D. J. Mooney. 2002. Alginate type and RGD density control myoblast phenotype. J. Biomed. Mater. Res. 60:217–223. [DOI] [PubMed] [Google Scholar]
  43. Sheu, M. T., J. C. Huang, G. C. Yeh, and H. O. Ho. 2001. Characterization of collagen gel solutions and collagen matrices for cell culture. Biomaterials. 22:1713–1719. [DOI] [PubMed] [Google Scholar]
  44. Simmons, D. M., and J. N. Kearney. 1993. Evaluation of collagen cross-linking techniques for the stabilization of tissue matrices. Biotechnol. Appl. Biochem. 17:23–29. [PubMed] [Google Scholar]
  45. Simson, R., E. Wallraff, J. Faix, J. Niewohner, G. Gerisch, and E. Sackmann. 1998. Membrane bending modulus and adhesion energy of wild-type and mutant cells of Dictyostelium lacking talin or cortexillins. Biophys. J. 74:514–522. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Tsai, M. A., R. E. Waugh, and P. C. Keng. 1996. Cell cycle-dependence of HL-60 cell deformability. Biophys. J. 70:2023–2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Wang, N., I. M. Tolic-Norrelykke, J. Chen, S. M. Mijailovich, J. P. Butler, J. J. Fredberg, and D. Stamenovic. 2002. Cell prestress. I. Stiffness and prestress are closely associated in adherent contractile cells. Am. J. Physiol. Cell Physiol. 282:C606–C616. [DOI] [PubMed] [Google Scholar]
  48. Wang, Y.-L., and R. J. Pelham. 1998. Preparation of a flexible, porous polyacrylamide substrate for mechanical studies of cultured cells. Meth. Enzymol. 298:489–496. [DOI] [PubMed] [Google Scholar]
  49. Westphal, M., A. Jungbluth, M. Heidecker, B. Muhlbauer, C. Heizer, J. M. Schwartz, G. Marriott, and G. Gerisch. 1997. Microfilament dynamics during cell movement and chemotaxis monitored using a GFP-actin fusion protein. Curr. Biol. 7:176–183. [DOI] [PubMed] [Google Scholar]
  50. Wong, J. Y., A. Velasco, P. Rajagopalan, and Q. Pham. 2003. Directed movement of vascular smooth muscle cells on gradient-compliant hydrogels. Langmuir. 19:1908–1913. [Google Scholar]
  51. Zaner, K. S., and T. P. Stossel. 1982. Some perspectives on the viscosity of actin filaments. J. Cell Biol. 93:987–991. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES