Abstract
A new method of direct and continuous measurement of the spring constant of single molecule or molecular complex is elaborated. To that end the standard force spectroscopy technique with functionalized tips and samples is combined with a small dithering of the tip. The change of the dithering amplitude as a function of the pulling force is measured to extract the spring constant of the complex. The potentialities of this method are illustrated for the experiments with single bovine serum albumin—its polyclonal antibody (Ab-BSA) and fibrinogen—fibrinogen complexes.
INTRODUCTION
In recent years, single molecule force spectroscopy using the atomic force microscope (AFM) has become an established technique and helped to reveal important characteristics of many proteins, DNA (RNA) molecules, polysaccharides, and other molecular complexes and/or structures of large biological importance (see, for instance, Heinz and Hoh, 1999; Zlatanova et al., 2000; Carrion-Vazquez et al., 2000; Janshoff et al., 2000; Leckband, 2001; Rief and Grubmüller, 2002 for recent reviews). Among numerous interesting results obtained using the force spectroscopy method, one could mention precise determination of the forces acting between complementary strands of DNA (Lee et al., 1994a; Cluzel et al., 1996; Essevaz-Roulet et al., 1997; Noy et al., 1997; and others). These studies seem to have attained such an excellent level that recently DNA-based systems were proposed as a “programmable force sensor” (Albrecht et al., 2003). One could mention also nanomechanical studies of single muscle protein titin molecules (Rief et al., 1997a, 1998; Marszalek et al., 1999) and chromatin fibers (Leuba et al., 2000), observation of force-induced conformational transitions of polysaccharides (Rief et al., 1997b, Marszalek et al., 1998), and so on. Probably the most informative and interesting force spectroscopy studies were the experiments revealing the specific receptor-ligand interactions including antigen-antibody (Ag-Ab) systems (Stuart and Hlady, 1995; Dammer et al., 1996; Hinterdorfer et al., 1996; Allen et al., 1997; Ros et al., 1998; Willemsen et al., 1998, 2000; Merkel et al., 1999; Harada et al., 2000; Schwesinger et al., 2000; and others), and by this reason below we will discuss the single force spectroscopy approach mainly having in mind exactly Ag-Ab system.
The method consists of functionalizing the AFM tip with the antibody and the substrate with the antigen (or vice versa). After an antibody-functionalized tip enters in contact with an antigen-functionalized sample, a specific bond between the antigen and the antibody can form. This bond will be ruptured (event) when the tip is pulled away from the substrate surface (Fig. 1). The amount by which the pulling cantilever bends before the bond ruptures is measured. From this value the specific interaction (unbinding) force is calculated using the known spring constant, k, of the AFM cantilever. It was shown that the measured unbinding force correlates with the thermal dissociation rate of the antigen-antibody (Ag-Ab) pair (Strunz et al., 2000; Schwesinger et al., 2000) and can be used for molecular recognition.
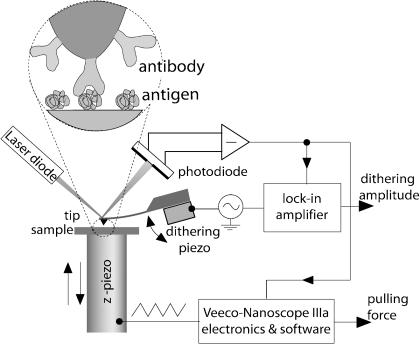
FIGURE 1.
Schematic of the experimental setup.
Very recently it was proposed to slightly modulate the distance between the cantilever and the sample at a driving frequency ω. Measuring the amplitude of the tip vibrations at this frequency leads to an improved molecule recognition fidelity (Schindler et al., 2000). The possibility to measure the dynamical properties of single molecules using this method was also demonstrated for a short polymer molecule of poly(ethylene glycol) (Kienberger et al., 2000). In the present work we report the development of this approach for direct and continuous measurement of the spring constant of a single stretched molecule or molecular complex. Mainly the complex of bovine serum albumin (BSA) with a polyclonal antibody to BSA (Ab-BSA) have been studied, additionally the potentialities of the method are illustrated also for fibrinogen-fibrinogen complex.
MATERIALS AND METHODS
AFM instrumentation
A schematic diagram of the experimental setup is given in Fig. 1. A commercially available AFM (Nanoscope IIIa Multimode Scanning Probe Microscope, Veeco Instruments, Santa Barbara, CA) and standard V-shaped Si3N4 (silicon nitride) cantilevers (Veeco) having a length of 200 μm and a nominal spring constant of 0.06 N/m were used. All experiments were performed in phosphate-buffered saline (PBS) buffer (50 mM phosphate, 150 mM NaCl, pH 7.4 at 25°C) at 25°C.
The spring constant k of each cantilever was calibrated by the resonance frequency method (Cleveland et al., 1993) and thermal fluctuations method (Hutter and Bechhoefer, 1993); variations in the spring constant of up to 30% were observed. The Nanoscope IIIa “force-volume” option was used but a small sine wave modulation voltage was applied to the piezocrystal normally used for the “tapping mode.” This dithering voltage, Umod, had a peak-to-peak amplitude of 20–80 mV at a frequency of ω = 2π × 3.2 kHz. This modulation is equivalent to the application of a driving force fω at the frequency ω onto the cantilever, which makes the tip dither with an amplitude of 0.5–2 nm. This results in the modulation of the photodiode current at the same frequency and its signal was measured using a digital lock in amplifier (SR750, Stanford Research Instruments, Sunnyvale, CA). Thus, two signals were measured simultaneously: a), standard force-distance curves, i.e., dependence of the interaction force on the z-displacement of the substrate, and b), the dependence of the amplitude of forced cantilever vibrations on the same. No noticeable dependence of the results on the dithering amplitude was observed provided that the excitation remained in the range given above. The smallest reasonable pull-off rate of 11 nm/s (0.7 nN/s) was used.
Tip and sample preparation
Tips, after initial intensive cleaning, were functionalized with polyclonal rabbit anti-bovine serum albumin antibody (270 μg/ml; Sigma, B-1520, St. Louis, MO). 1-Ethyl-3 (3-dimethylaminopropyl) carbodiimide (EDAC) was used as a coupling agent. Fibrinogen (Haemacure Corporation, Montreal, Quebec, Canada) molecules were attached to the tips by 15-min incubation in fibrinogen solution in PBS (1 mg/ml) via glutaraldehyde. The loosely attached proteins were then removed by extensive washing with PBS buffer. The protein-functionalized tips were used immediately for making measurements. Substrates (freshly cleaved muscovite mica) were functionalized first by silanization using 3-aminopropyltrimethoxysilane (APTMS) by chemical vapor deposition in a vacuum chamber. It was shown that such approach results in smooth and stable monolayer silane film without “vertical” polymerization (Jönsson et al., 1985; Vandenberg et al., 1991). This procedure was followed by processing the substrata in a 0.5% v/v glutaraldehyde solution in water for 15 min. After rinsing with deionized ultra-high-quality (UHQ) (resistivity 18 MΩ·cm) water, the samples were immersed into a solution of bovine serum albumin (BSA) (1 mg/ml, Sigma, A-3912, St. Louis, MO) or fibrinogen (1 mg/ml) in PBS for 15 min. The unreacted and loosely bond proteins were subsequently removed by extensive washing with PBS buffer. With this functionalization procedure ∼30% of all tip-sample approaches (∼1500 approach-retract cycles) present specific interactions for our Ag-Ab system.
The thickness of soft layers of linkers containing BSA molecules has been controlled by the AFM sweeping method: the sample was scanned using high loading force and afterwards a larger area was scanned at small loading force (cf., e.g., Lee et al., 1994b; You and Lowe, 1996). The thickness of APTMS+glutaraldehyde layer not exceeding 2 nm has been observed. We also recorded tapping mode AFM images in PBS of BSA molecules immobilized according to our aforementioned technique. To visualize the structure of immobilized BSA molecules, the proteins were further “frozen” with glutaraldehyde (1% v/v, 10-min incubation). An example of such image, which reveals fairly isolated BSA molecules having a globular structure with a characteristic size of 7–8 nm, is given in Fig. 2. Note the large similarity of this image with that presented earlier by Gunning et al. (1996). Using the sweeping method, an average BSA layer thickness has been estimated as 3.5 nm.
FIGURE 2.
Tapping mode AFM image in PBS buffer of BSA submonolayer prepared according to the chemical fixation procedure described in the text. Fairly isolated BSA molecules of a globular shape with the size of 7–8 nm are seen.
Control experiments
To be sure that we have measured true specific antigen-antibody forces, all possible control experiments (study of the interaction between nonfunctionalized mica and tip, mica functionalized with BSA and nonfunctionalized tip, nonfunctionalized mica and tips functionalized with Ab-BSA, etc.) have been performed. All of those gave negative results: no interactions that could be confused with specific interactions were observed. Another important control consisted in the analysis of antigen-antibody interactions in the presence of free BSA in solution (when binding sites of antibodies are blocked). Such an experiment also gave a negative result: specific unbinding forces completely disappeared; they were partially (∼50%) restored when this BSA solution was exchanged again by a PBS buffer.
Analogously, we have performed control experiments to be sure that the full extension curve (not only the value of a specific interaction) is due to the stretching of BSA–Ab-BSA system rather than the stretching of the linkers. The most convincing demonstration consists in recording a number of specific interaction events for the case when no chemical treatment of tip or substrate, or both, has been performed and the samples were prepared by a passive adsorption from solutions of BSA or Ab-BSA for a few hours. Of course, specific interaction events were really rare for such a case (essentially <1% of all approach curves), but for a few tens of events recorded, both the characteristic tip displacement at bond rupture and the form of the extension curve were similar to those obtained using the samples prepared as described above.
RESULTS AND DISCUSSION
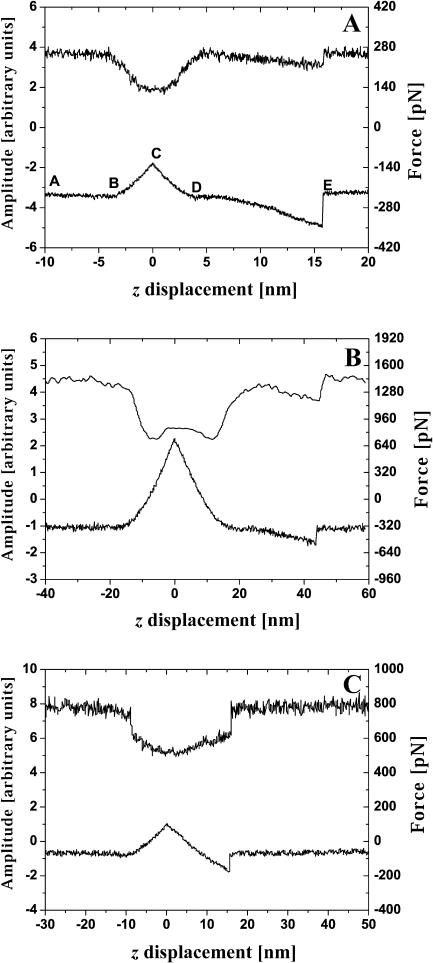
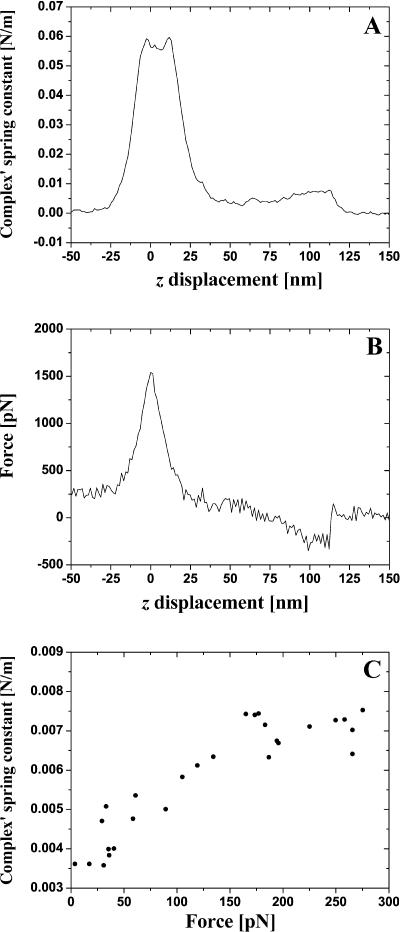
Typical experimental results obtained for BSA–Ab-BSA complex are shown in Fig. 3. The recording of the data starts when the tip and sample are far apart (A–B in Fig. 3 A). Then, as the tip approaches, it enters into contact with the substrate (segment B–C). At point C the tip is retracted until point D where it loses contact with the substrate. Between D and E the tip is further retracted from the substrate with the Ag-Ab complex extended. Point E corresponds to the rupture of a BSA–Ab-BSA bond and the unbinding force is measured at this moment. Calibration of the absolute value of the force has been performed based on the linear part of the contact line (B–C and C–D) using the known tip spring constant.
FIGURE 3.
Experimental dependencies of the pulling force (lower curves) and lock in output signal used to measure the spring constant (upper curves) on the sample stage z-displacement. Dithering peak to peak amplitude is 2 nm. See text for the classification of the presented events.
Calculation of spring constant of tip-sample complex
The following procedure was used to extract the value of the spring constant for the tip-sample complex kcomplex from the recorded data.
The process of excitation of cantilever vibrations in a liquid is very complicated to describe and is not yet fully understood. Nevertheless, for small amplitudes of vibration, it still can be described as forced vibrations of a nonlinear oscillator (Sarid, 1991; Sader, 1998; Schindler et al., 2000; Kienberger et al., 2000). Introducing the variable δz, which describes the deviation of the cantilever from its equilibrium position, z0, produced by a (quasi)static pulling force fpul, one can write down:
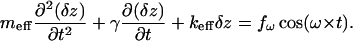 |
(1) |
Here, the parameters meff and γ characterize the vibrations of the cantilever in liquid and keff is the sum of the spring constant of the cantilever and that of the stretched complex. Note that the differential spring constant of the complex 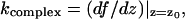 rather than its static spring constant f/z0, is of importance for this equation, containing δz as a variable. (Here f(z) is the force-extension characteristic of the BSA–Ab-BSA complex; see below.)
rather than its static spring constant f/z0, is of importance for this equation, containing δz as a variable. (Here f(z) is the force-extension characteristic of the BSA–Ab-BSA complex; see below.)
Solution of Eq. 1 is well known (Sarid, 1991, or any textbook with an introduction to oscillatory motion); this equation describes the forced vibrations 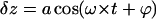 with an amplitude
with an amplitude
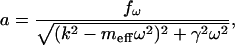 |
(2) |
and a phase shift
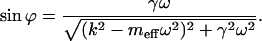 |
(3) |
If the driving frequency ω is much smaller than the value of 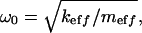 which, for the rather small quality factor Q ≥ 2 is already very close to the resonance frequency of the system
which, for the rather small quality factor Q ≥ 2 is already very close to the resonance frequency of the system 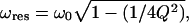 then, evidently, the vibration amplitude can be well approximated by the value of
then, evidently, the vibration amplitude can be well approximated by the value of
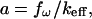 |
because 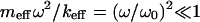 and
and 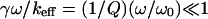 for this case. The amplitude of the forced oscillation is measured with a lock in amplifier while recording force-distance curves. Three intervals are interesting for the force-distance curve as indicated in Fig. 3 A: 1), A–B where the lever oscillates freely; 2), D–E where the antigen-antibody complex is extended under the action of the pulling force fpul; 3), after E where the specific bond is ruptured and the cantilever oscillates again freely. From the oscillation amplitude in these three regions one obtains the reciprocal spring constants k−1, (k + kcomplex)−1 and k−1, respectively. The value of k is known, which makes it possible to determine the spring constant kcomplex of the single Ag-Ab complex as a function of z and fpul.
for this case. The amplitude of the forced oscillation is measured with a lock in amplifier while recording force-distance curves. Three intervals are interesting for the force-distance curve as indicated in Fig. 3 A: 1), A–B where the lever oscillates freely; 2), D–E where the antigen-antibody complex is extended under the action of the pulling force fpul; 3), after E where the specific bond is ruptured and the cantilever oscillates again freely. From the oscillation amplitude in these three regions one obtains the reciprocal spring constants k−1, (k + kcomplex)−1 and k−1, respectively. The value of k is known, which makes it possible to determine the spring constant kcomplex of the single Ag-Ab complex as a function of z and fpul.
In principle, the measured value of kcomplex can be further refined if the parameters of the oscillatory system (meff and γ) are well known. This is, however, a very difficult problem, especially given the fact that the acting force value fω in itself depends on the frequency for our excitation method because the piezodriver is a source of displacement (of the cantilever base) rather than directly the force.
For our case, the resonant frequency of the cantilevers in liquid was measured and found to be in the range from 8.5 to 10 kHz. The driving frequency of 3.2 kHz is a trade-off between the necessity to have this value as small as possible for the better interpretation of data as discussed above and the necessity to have a sufficient number of oscillations per averaging time for the proper functioning of a lock in amplifier.
BSA–Ab-BSA complex
We can classify events presented in Fig. 3 as follows: single bond rupture (Fig. 3 A; the value of the unbinding force is 130 pN), double bond rupture (Fig. 3 B; 295 pN), and “no specific event” (Fig. 3 C). The last example is a demonstration of the utility of the measurement of the spring constant for the interpretation of results of pulling-off experiments. Although the standard force-distance curve (lower) in Fig. 3 C looks like a single bond rupture event, the upper curve has no peculiarities (that is no decrease of dithering amplitude during the pulling off) and clearly demonstrates that nonspecific interactions take place here. This is a really useful addition to all approaches designed to distinguish between different events in the experiments of this type; see e.g., Kasas et al. (2000) and references cited therein. In some experiments forces larger than 1 nN were observed. These events are believed to be due to the multiple ruptures of glutaraldehyde-amine bonds, and we will not discuss them below.
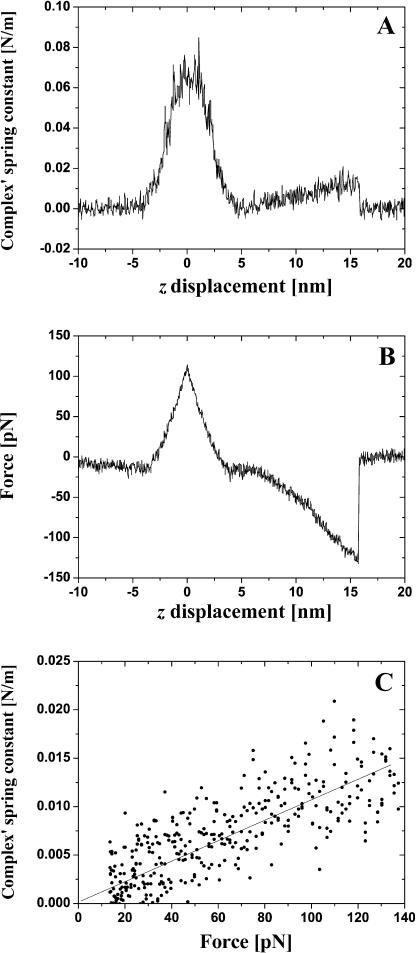
In Fig. 4 we present typical experimental dependencies kcomplex(z) (A) and fpul(z) (B) for the case of single bond rupture. The linear approximation of the experimental dependence kcomplex(f) derived from Fig. 4, A and B is given in Fig. 4 C. Before plotting Fig. 4 C we fitted Fig. 4 A to a straight line in the region from 4.23 nm to 15.72 nm and fitted Fig. 4 B to a second-degree polynomial in the same interval. The spring constant of an individual (and double) BSA–Ab-BSA complex always increases together with the increase of the pulling force and attains the maximal value at a moment of the bond rupture. A good correlation between the value of the specific interaction force, the simultaneously measured spring constant of the complex, and the value of tip-sample distance at this moment is observed. The average value of the complex's spring constant at the moment of the single antigen-antibody bond rupture was measured to be 0.017 ± 0.003 N/m (average over ∼50 events). The majority of the events corresponding to the double bond rupture gives kcomplex values ranging from 0.03 to 0.04 N/m (10 events). However, values as large as 0.053 N/m were sometimes observed.
FIGURE 4.
Typical dependence of the antigen-antibody complex's spring constant kcomplex (A) and pulling force f (B) for a single specific bond rupture event on the sample stage z-displacement. In C we present a dependence kcomplex(f) derived from A, B, and its linear approximation.
For the interpretation of the experimental results (only the case of single bond rupture is considered here) we should take into account the following. The force f is the derivative of the free energy of the system with respect to the value of the distance between the molecule's endpoints, i.e., the fragments of a BSA–Ab-BSA complex that are fixed on the tip and sample surface (Doi and Edwards, 1992). The sample stage displacement z is an evident measure of such a distance. It can be argued that the complex's extension is given by the difference of z and cantilever displacement y. The latter can be determined from the fpul(z) curve, y = fpul/k, and, thus, the value of z can be corrected, which we did whenever relevant. Note that this correction is of only minor importance for our experiments. For example, for the typical one bond rupture event (fpul = 130 pN) y = 2.4 nm and, thus, is essentially smaller than the characteristic (uncorrected) z-value of 16 nm.
Molecular dynamics calculations of the extension curves for antigen-antibody complexes (Grubmüller et al., 1996; Balsera et al., 1997; Izrailev et al., 1997; Strunz et al., 2000; Heymann and Grubmüller, 1999a,b, 2000, 2001) show that the range of extension during which the details of the antigen-antibody interaction are important is of a few Ångströms very close to the point of rupture. For typical experimental conditions this corresponds to a characteristic timescale of the order of a few milliseconds or less. These values are beyond the reach of our experimental technique, so only the usual “entropy-related” contribution to the antigen-antibody complex's spring constant (Doi and Edwards, 1992; Marko and Siggia, 1995) was measured.
It is well known that BSA is a globular protein “stiffened” by 17 disulfide bonds, and that this protein has different conformational forms (N, F, B, A, and E) characterized by different contents of helical β-sheets and other structures (Carter and Ho, 1994). Transitions between these forms can be caused either by a stretching (“mechanical denaturation”) or pH change. Earlier it was argued by Pereira et al. (2003) that expanded, E, BSA form (35% helix) corresponds to the “full extent allowed by the disulfide bond structures.” For our experiments, the possibility of BSA–Ab-BSA complex stretching should be limited exactly by attaining this “disulfide bond structures limited” E-form; relatively weak antigen-antibody bond will be ruptured before the rupture of disulfide bonds, which would allow further stretching, will occur. (For different experimental conditions, where essentially larger forces could be applied, the stretching of human serum albumin molecule until “the full contour length” of ∼200 nm has been observed by Rixman et al. (2003).) Using the data about the sizes of antibody and relevant conformational forms of BSA molecules together with the ≤2-nm thickness of linker layers, one could anticipate the maximal attainable stretching of the BSA–Ab-BSA complex of roughly 15 nm. This value is very close to that which has been indeed observed in our experiments: we have determined an average extension z = 14 ± 3 nm (correction for the cantilever displacement y is taken into account) at the moment of specific bond rupture.
Detailed interpretation of our data using worm-like chain (WLC) or some other more sophisticated statistical polymer model would be somewhat premature at the current stage of experiments, because such a detailed interpretation seems to require a comparison of analogous data for different Ag-Ab complexes and (possibly) careful characterization of the protein binding sites. Nevertheless, we would like to underline the following. For long flexible molecules having numerous conformational degrees of freedom (linear polymers, DNA, etc.) force-extension dependence is given by a quasiuniversal function relatively insensitive to the chemical composition of the molecule. In the frame of WLC model, it was shown that such a force can be expressed by the formula (Marko and Siggia, 1995):
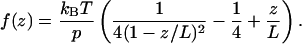 |
(4) |
Here kB is the Boltzmann constant, T, the temperature, p, the persistence length, and L, the maximal attainable length of a stretched polymer. Of course, a polypeptide chain is not a good linear polymer in the sense that there is not a single monomer unit and, hence, a well-defined persistence length. Moreover, the WLC model does not allow for the secondary and tertiary structure of the complex. Nevertheless, Eq. 4 is often used to approximate experimental data of single protein stretching (Rief et al., 1997a; Mueller et al., 1999; Minajeva et al., 2001; Zhou, 2001; Round et al., 2002; Liu and Pollack, 2002). For our case, where both the force f and the spring constant are simultaneously and independently measured, the following consideration seems to be of interest. The value of the spring constant for the WLC model is given by the derivative of Eq. 4
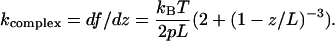 |
(5) |
For the case of z = 0 in this model one has 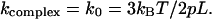 Now it is worthwhile to note that in the frame of the WLC model a simple analytical dependence between the pulling force and spring constant can be given. For this, one needs to solve Eq. 5 for z/L and then to insert the obtained expression in Eq. 4, which results in
Now it is worthwhile to note that in the frame of the WLC model a simple analytical dependence between the pulling force and spring constant can be given. For this, one needs to solve Eq. 5 for z/L and then to insert the obtained expression in Eq. 4, which results in
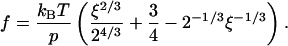 |
(6) |
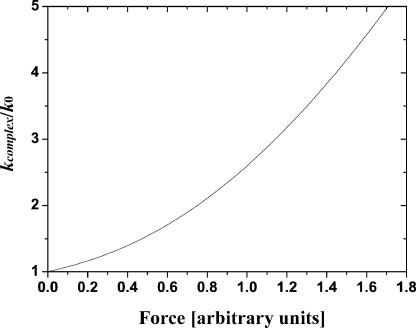
Here ξ ≥ 0.5 is a dimensionless parameter, 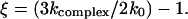 The inverse function, i.e., the dependence kcomplex(f), can be derived from Eq. 6 but this requires a solution of cubic equation that renders the resulting expression not so practical. The inverse function of Eq. 6 is plotted in Fig. 5.
The inverse function, i.e., the dependence kcomplex(f), can be derived from Eq. 6 but this requires a solution of cubic equation that renders the resulting expression not so practical. The inverse function of Eq. 6 is plotted in Fig. 5.
FIGURE 5.
Universal dependence of the spring constant kcomplex of a polymer molecule (measured in units of the spring constant k0 of this molecule at z = 0) on the pulling force for the worm-like chain model of polymer elasticity. Here shown for 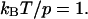
Thus, the WLC model predicts a monotone increase of the single polymer molecule spring constant with the increase of the pulling force and extension. As it was mentioned before, only such monotone increase has been observed for all single bond rupture events in our experiments. (Note that a nonmonotone dependence kcomplex(f) was observed in our experiments for some multiple glutaraldehyde-amine bonds rupture events; this data is not considered here and will be published elsewhere.) At the current stage of experimental precision and statistics we were not able to approximate the observed dependencies kcomplex(f), similar to the one shown in Fig. 4 C by this function; only a linear approximation turns out to be sufficiently reliable and statistically sound. Nevertheless, we are sure that this will be very interesting to do in the near future.
The lack of direct measurements of spring constants of stretching antigen-antibody complexes in the literature makes the comparison of our data with other experiments rather difficult. First, usually it is not possible to determine reliably the relevant differential df/dz from the published results (see the next section for a brief discussion). Surprisingly, even to simply calculate the characteristic force-displacement ratio f/z at the moment of rupture of the antigen-antibody bond turned out to be virtually impossible because the average value of the complex extension at the moment of rupture, z, is rarely accurately reported in the literature. In some cases it also turns out that this is the stretching of linkers rather than of an Ag-Ab complex, which is responsible for observed z and k values. This takes place, for example, for Hinterdorfer et al. (1996) experiments with the complex of a human serum albumin (HSA) and polyclonal antibody to HSA (Ab-HSA), which have been performed using 8-nm poly(ethylene glycol) linkers. No correlation between z and specific interaction value has been reported. This observation is opposite to our data, where, as it was stated above, good correlation between the values of unbinding force, force constant k and extension z has been obtained.
Essentially different values of df/dz have been measured for systems other than antigen-antibody complexes. We can use sufficiently detailed data of Sakai et al. (2002) to estimate the possible effect of the linkers on our k-measurements. Sakai et al. (2002) worked with polystyrene molecules whose stretching data could be a model for the chemicals used to attach the protein molecules onto the tip and sample surface in our experiments. (All our chemicals are simple short molecules for which, as for the polystyrene, ordinary C–C, Si–C, and similar bonds are the only component.) For long polystyrene molecules (L = 50 nm, that is ∼200 styrene monomers and 400 C–C bonds) Sakai et al. (2002) obtained for stretching forces of 100–140 pN (this is exactly the forces that are of interest to us) a value of k = df/dz close to 0.02–0.03 N/m (see Fig. 1 of Sakai et al., 2002). For our linkers, which contain around 10 C–C bonds and have a length L1 ∼ 1.5 nm, we have from WLC model the value of k, which is L/L1 times larger (see Eq. 5), that is ∼0.8 N/m. This value is much larger than the spring constant of 0.017 N/m measured for Ag-Ab complex, thus we believe that the elasticity of linkers does not contribute significantly to the measured value.
Fibrinogen-fibrinogen complex
For comparison and further illustration of our method of spring constant measurement, in Fig. 6 we present typical experimental dependencies of the spring constant (Fig. 6 A) and pulling force (Fig. 6 B) on the sample stage z-displacement for fibrinogen-fibrinogen complex. The protocol of fixation of fibrinogen molecules on the AFM tip and sample surfaces is briefly discussed above in the Materials and Methods section; all other experimental details are the same as for BSA–Ab-BSA complex. Hence, Fig. 6 contains a data analogous to that of Fig. 4 but obtained for a completely different system.
FIGURE 6.
Typical experimental dependence of the fibrinogen-fibrinogen complex's spring constant kcomplex (A) and pulling force f (B) on the sample stage z-displacement. Dithering peak-to-peak amplitude is 2 nm; single bond rupture event is shown. In C we present a dependence kcomplex(f) derived from A and B.
Fibrinogen-fibrinogen interaction is obviously a nonspecific one, which defines much broader distribution of the value forces at the moment of the bond rupture, frupt, and corresponding values of z at this moment, zrupt, in comparison with the single BSA–Ab-BSA complex. Indeed, experimentally obtained values of frupt ranges from 50 to 250 pN whereas the corresponding values of zrupt ranges from 50 to 130 nm for fibrinogen-fibrinogen complex. Accordingly, much broader distribution of the spring constant at the moment of the bond rupture also has been observed: such a value varies from 0.003 to 0.008 N/m for different events. (Only single fibrinogen-fibrinogen bond rupture events are considered here and below; for rupture events involving multiple bonds as large forces as 2–3 nN and spring constants up to 0.055 N/m have been observed. At the same time the distribution of zrupt does not essentially depend on the number of bonds involved.) Correlation between the values of frupt and zrupt measured for one concrete event was also rather poor, contrary to the BSA–Ab-BSA case.
Thus, the prominent difference between the experimental data concerning fibrinogen-fibrinogen and BSA–Ab-BSA complexes is evident. Especially we would like to underline an enormous difference between attainable complex extensions. As large zrupt values as 100–130 nm (simply unimaginable for antigen-antibody experiments) have been often observed for fibrinogen-fibrinogen rupture events. These values are consistent with the known long and well-stretchable molecular structure of fibrinogen (Doolittle, 1973, 1981). This circumstance, given all the precautions used by us to eliminate possible effects of linkers for the fibrinogen-fibrinogen case, similar to that of BSA–Ab-BSA (see Material and Methods section), should be considered as an additional proof of utility and reliability of the presented method of direct and continuous measurement of the spring constant for single molecules and molecular complexes. Detailed discussion of fibrinogen-fibrinogen complex stretching experiments will be published elsewhere.
CONCLUSION
In this article the new method of direct and continuous measurement of the spring constant of single molecule or molecular complex is presented and illustrated for the cases of complexes formed by specific BSA–Ab-BSA and nonspecific fibrinogen-fibrinogen interactions.
Finally, we would like to underline the following. In principle, one could speculate that similar information can be obtained by analyzing only standard force-distance curves f(z) and calculating the derivative df/dz from them. Albeit this is formally true, in practice such a procedure leads to very poor results due to unavoidable experimental noises: with a closer look, each real experimental curve contains a large number of “noise-induced” local maxima and minima. Hence, its derivative will have the corresponding large number of zeroes and the outcome of the procedure only rarely approaches the “real” values. If, trying to avoid this, one will first process the experimental curve to make it smooth, the derivative will strongly depend on the details of such a processing and hence, again, will be unreliable. Indeed, the necessity and utility to measure the derivative of some function directly (even if it is formally possible to derive it from some other data) is very well known in experimentation. It is sufficient to give here only one example—tunneling spectroscopy. Based on small modulation of the applied voltage, U, together with the measuring of modulation of a tunneling current, I, such an approach readily enables to observe characteristic vibrations of molecules located in the interelectrode spacing. This is the data practically unobservable when only the dependence U(I) is measured.
Acknowledgments
We are grateful to Dmitrii A. Lapshin for useful suggestions and help during the work with fibrinogen, and to André Haeberli for kindly supplying fibrinogen.
This study was supported by the Swiss National Science Foundation (grant Nos. 2000-065160.01, 2000-61751.00, and 7SUPJ062202).
George T. Shubeita's present address is Dept. of Developmental and Cell Biology, School of Biological Sciences, University of California, Irvine, 2302 Natural Sciences I, Irvine, CA 92697-2300.
References
- Albrecht, C., K. Blank, M. Lalic-Mülthaler, S. Hirler, T. Mai, I. Gilbert, S. Schiffmann, T. Bayer, H. Clausen-Schaumann, and H. E. Gaub. 2003. DNA: a programmable force sensor. Science. 301:367–370. [DOI] [PubMed] [Google Scholar]
- Allen, S., X. Y. Chen, J. Davies, M. C. Davies, A. C. Dawkes, J. C. Edwards, C. J. Roberts, J. Sefton, S. J. B. Tendler, and P. M. Williams. 1997. Detection of antigen-antibody binding events with atomic force microscopy. Biochemistry. 36:7457–7463. [DOI] [PubMed] [Google Scholar]
- Balsera, M., S. Stepananits, S. Izrailev, Y. Oono, and K. Schulten. 1997. Reconstructing potential energy functions from simulated force-induced unbinding processes. Biophys. J. 73:1281–1287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrion-Vazquez, M., A. F. Oberhauser, T. E. Fisher, P. E. Marszalek, H. Li, and J. M. Fernandez. 2000. Mechanical design of proteins studied by single-molecule force spectroscopy and protein engineering. Prog. Biophys. Mol. Biol. 74:63–91. [DOI] [PubMed] [Google Scholar]
- Carter, D. C., and J. X. Ho. 1994. Structure of serum albumin. Adv. Protein Chem. 45:153–203. [DOI] [PubMed] [Google Scholar]
- Cleveland, J. P., S. Manne, D. Bocek, and P. K. Hansma. 1993. A nondestructive method for determining the spring constant of cantilevers for scanning force microscopy. Rev. Sci. Instrum. 64:403–405. [Google Scholar]
- Cluzel, Ph., A. Lebrun, C. Heller, R. Lavery, J.-L. Viovy, D. Chatenay, and F. Caron. 1996. DNA: an extensible molecule. Science. 271:792–794. [DOI] [PubMed] [Google Scholar]
- Dammer, U., M. Hegner, D. Anselmetti, P. Wagner, M. Dreier, W. Huber, and H.-J. Güntherodt. 1996. Specific antigen/antibody interactions measured by force microscopy. Biophys. J. 70:2437–2441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doi, M., and S. F. Edwards. 1992. The Theory of Polymer Dynamics. Clarendon, Oxford, UK.
- Doolittle, R. F. 1973. Structural aspects of the fibrinogen to fibrin conversion. Adv. Protein Chem. 27:1–109. [DOI] [PubMed] [Google Scholar]
- Doolittle, R. F. 1981. Fibrinogen and fibrin. Sci. Am. 245:92–101. [DOI] [PubMed] [Google Scholar]
- Essevaz-Roulet, B., U. Bockelmann, and F. Heslot. 1997. Mechanical separation of the complementary strands of DNA. Proc. Natl. Acad. Sci. USA. 94:11935–11940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grubmüller, H., B. Heymann, and P. Tavan. 1996. Ligand binding: molecular mechanics calculation of the streptavidin-biotin rupture force. Science. 271:997–999. [DOI] [PubMed] [Google Scholar]
- Gunning, A. P., P. J. Wilde, D. C. Clark, V. J. Morris, M. L. Parker, and P. A. Gunning. 1996. Atomic force microscopy of interfacial protein films. J. Colloid Interface Sci. 183:600–602. [DOI] [PubMed] [Google Scholar]
- Harada, Y., M. Kuroda, and A. Ishida. 2000. Specific and quantized antigen-antibody interaction measured by atomic force microscopy. Langmuir. 16:708–715. [Google Scholar]
- Heinz, W. F., and J. H. Hoh. 1999. Spatially resolved force spectroscopy of biological surfaces using the AFM. Trends Biotechnol. 17:143–150. [DOI] [PubMed] [Google Scholar]
- Heymann, B., and H. Grubmüller. 1999a. AN02/DNP-hapten unbinding forces studied by molecular dynamics atomic force microscopy simulations. Chem. Phys. Lett. 303:1–9. [Google Scholar]
- Heymann, B., and H. Grubmüller. 1999b. Elastic properties of poly(ethylene)-glycol studied by molecular dynamics stretching simulations. Chem. Phys. Lett. 307:425–432. [Google Scholar]
- Heymann, B., and H. Grubmüller. 2000. Dynamic force spectroscopy of molecular adhesion bonds. Phys. Rev. Lett. 84:6126–6129. [DOI] [PubMed] [Google Scholar]
- Heymann, B., and H. Grubmüller. 2001. Molecular dynamics force probe simulations of antibody/antigen unbinding: entropic control and nonadditivity of unbinding forces. Biophys. J. 81:1295–1313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinterdorfer, P., W. Baumgartner, H. J. Gruber, K. Schilcher, and H. Schindler. 1996. Detection and localization of individual antibody-antigen recognition events by atomic force microscopy. Proc. Natl. Acad. Sci. USA. 93:3477–3481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutter, J. L., and J. Bechhoefer. 1993. Calibration of atomic force microscope tips. Rev. Sci. Instrum. 64:1868–1873. [Google Scholar]
- Izrailev, S., S. Stepaniants, M. Balsera, Y. Oono, and K. Schulten. 1997. Molecular dynamics study of unbinding of the avidin-biotin complex. Biophys. J. 72:1568–1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janshoff, A., M. Neitzert, Y. Oberdörfer, and H. Fuchs. 2000. Force spectroscopy of molecular systems—single molecule spectroscopy of polymers and biomolecules. Angew. Chem. Int. Ed. 39:3212–3237. [DOI] [PubMed] [Google Scholar]
- Jönsson, U., G. Olofsson, M. Malmqvist, and I. Rönnberg. 1985. Chemical vapor deposition of silanes. Thin Solid Films. 124:117–123. [Google Scholar]
- Kasas, S., B. M. Riederer, S. Catsicas, B. Cappella, and G. Dietler. 2000. Fuzzy logic algorithm to extract specific interaction forces from atomic force microscopy data. Rev. Sci. Instrum. 71:2082–2086. [Google Scholar]
- Kienberger, F., V. P. Pastushenko, G. Kada, H. J. Gruber, C. Riener, H. Schindler, and P. Hinterdorfer. 2000. Static and dynamical properties of single poly(ethylene glycol) molecules investigated by force spectroscopy. Single Mol. 1:123–128. [Google Scholar]
- Leckband, D. 2001. Force as a probe of membrane protein structure and function. Curr. Opin. Struct. Biol. 11:433–439. [DOI] [PubMed] [Google Scholar]
- Lee, G. U., L. A. Chrisey, and R. J. Colton. 1994a. Direct measurement of the forces between complementary strands of DNA. Science. 266:771–773. [DOI] [PubMed] [Google Scholar]
- Lee, G. U., D. A. Kidwell, and R. J. Colton. 1994b. Sensing discrete steptavidin-biotin interactions with atomic force microscopy. Langmuir. 10:354–357. [Google Scholar]
- Leuba, S. H., J. Zlatanova, M. A. Karymov, R. Bash, Y.-Z. Liu, D. Lohr, R. E. Harrington, and S. M. Lindsay. 2000. The mechanical properties of single chromatin fibers under tension. Single Mol. 1:185–193. [Google Scholar]
- Liu, X. M., and G. H. Pollack. 2002. Mechanics of F-actin characterized with microfabricated cantilevers. Biophys. J. 83:2705–2715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marko, J. F., and E. D. Siggia. 1995. Stretching DNA. Macromolecules. 28:8759–8770. [Google Scholar]
- Marszalek, P. E., A. F. Oberhauser, Y. P. Pang, and J. M. Fernandez. 1998. Polysaccaride elasticity governed by chair-boat transitions of the glucopyranose ring. Nature. 396:661–664. [DOI] [PubMed] [Google Scholar]
- Marszalek, P. E., H. Lu, H. Li, M. Carrion-Vazquez, A. F. Oberhauser, K. Schulten, and J. M. Fernandez. 1999. Mechanical unfolding intermediates in titin modules. Nature. 402:100–103. [DOI] [PubMed] [Google Scholar]
- Merkel, R., P. Nassoy, A. Leung, K. Ritchie, and E. Evans. 1999. Energy landscapes of receptor-ligand bonds explored with dynamic force microscopy. Nature. 397:50–53. [DOI] [PubMed] [Google Scholar]
- Minajeva, A., M. Kulke, J. M. Fernandez, and W. Linke. 2001. Unfolding of titin domains explains the viscoelastic behavior of skeletal myofibrils. Biophys. J. 80:1442–1451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mueller, H., H. J. Butt, and E. Bamberg. 1999. Force measurements on myelin basic protein adsorbed to mica and lipid bilayer surfaces done with the atomic force microscope. Biophys. J. 76:1072–1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noy, A., D. V. Vezenov, J. F. Kayyem, T. J. Meade, and C. M. Lieber. 1997. Stretching and breaking duplex DNA by chemical force microscopy. Chem. Biol. 4:519–527. [DOI] [PubMed] [Google Scholar]
- Pereira, L. G. C., O. Théodoly, H. W. Blanch, and C. J. Radke. 2003. Dilatational rheology of BSA conformers at the air/water interface. Langmuir. 19:2349–2356. [Google Scholar]
- Rief, M., M. Gautel, F. Oesterhelt, J. M. Fernandez, and H. E. Gaub. 1997a. Reversible unfolding of individual titin immunoglobulin domains by AFM. Science. 276:1109–1112. [DOI] [PubMed] [Google Scholar]
- Rief, M., F. Oesterhelt, B. Heymann, and H. E. Gaub. 1997b. Single molecule force spectroscopy of polysaccarides by atomic force microscopy. Science. 276:1295–1297. [DOI] [PubMed] [Google Scholar]
- Rief, M., J. M. Fernandez, and H. E. Gaub. 1998. Elastically coupled two-level systems as a model for biopolymer extensibility. Phys. Rev. Lett. 81:4764–4767. [Google Scholar]
- Rief, M., and H. Grubmüller. 2002. Force spectroscopy of single biomolecules. Chemphyschem. 3:255–261. [DOI] [PubMed] [Google Scholar]
- Rixman, M. A., D. Dean, C. E. Macias, and C. Ortiz. 2003. Nanoscale intermolecular interactions between human serum albumin and alkanethiol self-assembled monolayers. Langmuir. 19:6202–6218. [Google Scholar]
- Ros, R., F. Schwesinger, D. Anselmetti, M. Kubon, R. Schäfer, A. Plücktun, and L. Tiefenauer. 1998. Antigen binding forces of individually addressed single-chain Fv antibody molecules. Proc. Natl. Acad. Sci. USA. 95:7402–7405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Round, A. N., M. Berry, T. J. McMaster, S. Stoll, D. Gowers, A. P. Corfield, and M. J. Miles. 2002. Heterogeneity and persistence length in human ocular mucins. Biophys. J. 83:1661–1670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sader, J. E. 1998. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 84:64–76. [Google Scholar]
- Sakai, Y., T. Ikehara, T. Nishi, K. Nakajima, and M. Hara. 2002. Nanorheology measurement on a single polymer chain. Appl. Phys. Lett. 81:724–726. [Google Scholar]
- Sarid, D. 1991. Scanning Force Microscopy. Oxford University Press, London, UK.
- Schindler, H., D. Badt, P. Hinterdorfer, F. Kienberger, A. Raab, S. Wielert-Badt, and V. P. Pastushenko. 2000. Optimal sensitivity for molecular recognition MAC-mode AFM. Ultramicroscopy. 82:227–235. [DOI] [PubMed] [Google Scholar]
- Schwesinger, F., R. Ros, T. Strunz, D. Anselmetti, H.-J. Güntherodt, A. Honegger, L. Jermutus, L. Tiefenauer, and A. Plücktun. 2000. Unbinding forces of single antibody-antigen complexes correlate with their thermal dissociation rates. Proc. Natl. Acad. Sci. USA. 97:9972–9977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strunz, T., K. Oroszlan, I. Schumakovitch, H.-J. Güntherodt, and M. Hegner. 2000. Model energy landscapes and the force-induced dissociation of ligand-receptor bonds. Biophys. J. 79:1206–1212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart, J. K., and V. Hlady. 1995. Effects of discrete protein-surface interactions in scanning force microscopy adhesion force measurements. Langmuir. 11:1368–1374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandenberg, E. T., L. Bertilsson, B. Lieberg, K. Uvdal, R. Erlandsson, H. Elwing, and I. Lundström. 1991. Structure of 3-aminopropyl triethoxy silane on silicone oxide. J. Colloid Interface Sci. 147:103–118. [Google Scholar]
- Willemsen, O. H., M. M. E. Snel, K. O. van der Werf, B. G. de Grooth, J. Greve, P. Hinterdorfer, H. J. Gruber, H. Schindler, Y. van Kooyk, and C. G. Figdor. 1998. Simultaneous height and adhesion imaging of antibody-antigen interactions by atomic force microscopy. Biophys. J. 75:2220–2228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willemsen, O. H., M. M. E. Snel, A. Cambi, J. Greve, B. G. De Grooth, and C. G. Figdor. 2000. Biomolecular interactions measured by atomic force microscopy. Biophys. J. 79:3267–3281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- You, H. X., and C. R. Lowe. 1996. AFM studies of protein adsorption. 2. Characterization of immunoglobulin G adsorption by detergent washing. J. Colloid Interface Sci. 182:586–601. [Google Scholar]
- Zhou, H. X. 2001. Loops in proteins can be modeled as worm-like chains. J. Phys. Chem. B. 105:6763–6766. [Google Scholar]
- Zlatanova, J., S. M. Lindsay, and S. H. Leuba. 2000. Single molecule force spectroscopy in biology using the atomic force microscope. Prog. Biophys. Mol. Biol. 74:37–61. [DOI] [PubMed] [Google Scholar]