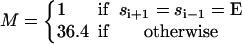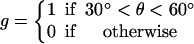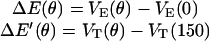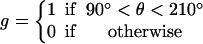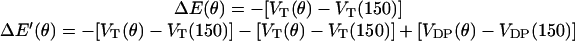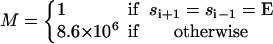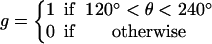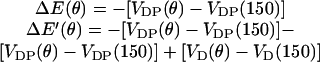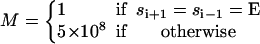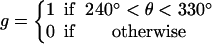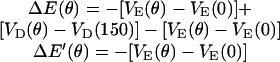Asymmetry in the F₁-ATPase and Its Implications for the Rotational Cycle

Abstract

ATP synthase uses a rotary mechanism to carry out its cellular function of manufacturing ATP. The centralγ-shaft rotates inside a hexameric cylinder composed of alternating α- and β-subunits. When operating in the hydrolysis direction under high frictional loads and low ATP concentrations, a coordinated mechanochemical cycle in the three catalytic sites of the β-subunits rotates the γ-shaft in three 120° steps. At low frictional loads, the 120° steps alternate with three ATP-independent substeps separated by ∼30°. We present a quantitative model that accounts for these substeps and show that the observed pauses are due to 1), the asymmetry of the F₁ hexamer that produces a propeller-like motion of the power-stroke and 2), the relatively tight binding of ADP to the catalytic sites.

INTRODUCTION

ATP synthase consists of two rotary motors connected by an elastic shaft (the γ-subunit). The F_o subunit is driven by a transmembrane proton-motive force that, under normal circumstances, drives the rotation of the γ-shaft to release newly synthesized ATP from the three catalytic sites in the F₁ hexamer. Figs. 1 a and 2 a show the F₁ hexamer in cross-section and top views.

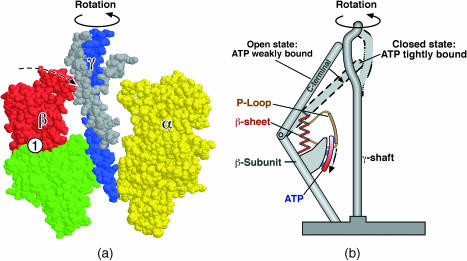
FIGURE 1.

Schematic of ATP synthase. (a) Cross section of the F1 assembly showing the β-subunit bending to turn the γ-shaft. (b) Cartoon showing the escapement for the F₁ motor. Bending of the β-subunits is driven by the sliding of the P-loop over the ATP phosphates. The helix-turn-helix at the C-terminal tip of the β-subunit pushes on the eccentric γ-shaft to produce the rotary torque.

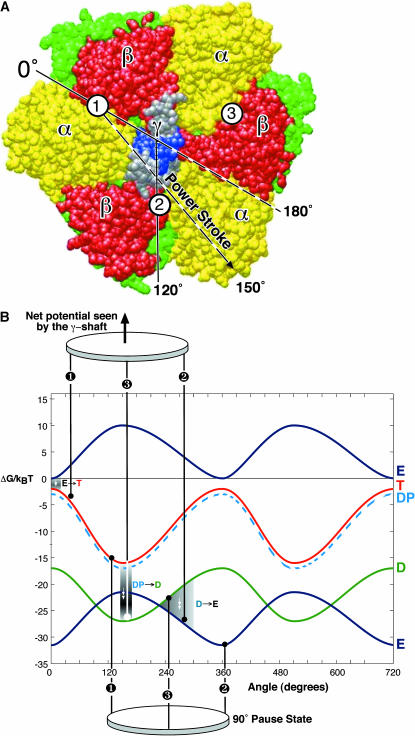
FIGURE 2.

(A) Top view of the F1 hexamer showing the alternating α- and β-subunits encircling the central γ-shaft. The catalytic sites are numbered. Sequential bending of each β-subunit toward a point ∼150° across the diameter drives the rotation of the γ-shaft. (B) The γ-shaft is driven by the coordinated bending of the three β-subunits, each of which could be one of four potentials, one for each occupancy state, V_E, V_T, V_DP, and V_D. The total torque is given by the sum of the potentials at the three leg positions spaced 120° apart. The first set of legs shows the system just after ATP binding in site 1 at the beginning of its power-stroke. Site 3 has just released its Pi, site 2 is empty and aiding site 1 during its recoil power-stroke. The second set of legs shows the system at a pause position just before ADP release from site 3. Site 2 is empty and has finished its recoil power-stroke. Site 1 is near the end of its primary power-stroke and contributes a positive driving torque; it is balanced by the negative torque from site 3 in D state. The positive torque from site 1 drives the opening of site 3, which promotes ADP release from site 3. Upon the ADP release from site 3, site 1 finishes its primary power-stroke and drives the system to a position where site 2 waits ATP binding. The separations between the curves corresponds to the experimental conditions: [ATP] = 2 × 10⁻³ M, [ADP] = 1 × 10⁻⁷ M, and [Pi] = 1 × 10⁻⁴ M.

Rotation of the F₁ motor was first visualized by attaching a fluorescent actin filament to the γ-shaft (Noji et al., 1997; Adachi et al., 2000). More recent experiments reduced the frictional drag on the rotation by using 40-nm gold beads to tag the γ-shaft (Yasuda et al., 2001). These experiments revealed that each 120° rotation was broken into a 90° substep followed by a 30° substep. Moreover, the dwell time between the 90° and 30° substeps was independent of ATP concentration, but the dwell time between the 30° and 90° substeps was ATP-concentration dependent. Here we describe a new mathematical model that quantitatively explains these new observations.

The mechanical escapement that drives rotation of theγ-shaft could only be deduced after Walker's group succeeded in capturing the atomic structure of the F₁ motor in several chemical states along the hydrolysis pathway (Abrahams et al., 1994; Shirakihara et al., 1997; Menz et al., 2001). Interpolating between the crystal structures demonstrated that the eccentric γ-shaft was driven by sequential hinge-bending motions of the β-subunits, in which the upper part of the β-subunit bent ∼30° with respect to the lower part (Wang and Oster, 1998; Oster and Wang, 2000a). A helix-turn-helix (HTH) motif at the tip of the β-subunit pushes against the eccentric γ-shaft, rotating it much like turning the crank on an automobile jack (see Fig. 1 b).

A striking feature of the F₁ motor was its extremely high efficiency (Yasuda et al., 1998; Wang and Oster, 2001). This can only be achieved if the torque generated by the motor is nearly constant, a deduction consistent with direct observations (Kinosita et al., 1999). Further analysis, coupled with molecular dynamics studies, led to the conclusion that the power-stroke that drives the bending of the β-subunit is driven mostly, if not entirely, by the progressive binding of ATP to the catalytic site (Wang and Oster, 1998; Oster and Wang, 2000a; Antes et al., 2003; Sun et al., 2003). The hydrolysis step weakens the binding of products to the catalytic site sufficiently for them to be released so that the cycle can be repeated. The unisite kinetics, coupled with the high efficiency, suggested that the power-stroke proceeded in two steps. Nucleotide binding drives the primary power-stroke to bend the β-subunit. But during that motion, elastic energy is stored in the β-sheet whose loops grasp the nucleotide (Sun et al., 2003). A secondary recoil power-stroke releases this stored energy to aid the primary power-stroke of the adjacent β-subunit.

A MODEL FOR THE F₁ MOTOR

To formulate the model quantitatively, the nucleotide hydrolysis cycles must be coupled to the conformational motions of the protein. Each of the three catalytic sites progress through four occupancy states (Wang and Oster, 1998; Oster and Wang, 2000a), as

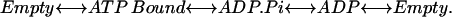(1)

At any instant, the α₃β₃ hexamer is in one of 4³ = 64 possible states. The progress of the three reactions can be pictured as hopping in a 4 × 4 × 4 periodic lattice according to the Markov model, where

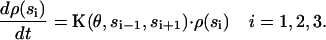(2)

Here s_i denotes the occupancy state of β-subunit i; ρ(s_i) denotes a vector containing the probabilities of subunit i being in states s_i = E, T, DP, and D; θ is the rotational angle of the γ-shaft; and K is the transition matrix. The transition rates in K are obtained by modifying the unisite kinetics to their multisite values as described in the Appendix.

The rotation of the γ-shaft plays a central role in coordinating the chemical states, and its motion can be described by a collection of Langevin equations of the form

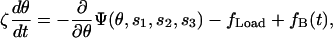(3)

where ζ is the viscous drag coefficient on the γ-shaft (ζ is large for the actin filament experiments and small for the bead experiments); f_Load is the load torque from an external conservative force (e.g., a laser trap); f_B(t) is the Brownian torque due to thermal fluctuations; and Ψ(θ,s₁,s₂,s₃) is the potential driving rotation of the γ-shaft (i.e., −∂Ψ/∂θ is the motor driving torque). The driving potential is the sum of the potentials from the three β-subunits as

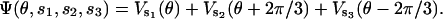The potential caused by one β is one of the four potentials (V_E, V_T, V_DP, and V_D). Thus at any instant, the composite potential Ψ(θ,s₁,s₂,s₃) is one of 64 possible functions.

The four potentials characterizing each β are shown in Fig. 2, and the regions where the chemical transitions between potentials can occur are shown as shaded contour paths. The details of the driving potentials are given in the Appendix, along with the complete forms of the equations and the numerical method of solution. Briefly, the functional forms of the potentials are obtained by invoking the high efficiency of the F₁ motor (Kinosita et al., 2000; Oster and Wang, 2000b) to model each β as a constant force elastic element in the bending angle, φ. The high efficiency of the F₁ motor also implies a tight mechanical coupling between β and γ. A simple mechanical linkage gives a function that relates φ with the rotation angle, θ. In this fashion, the bending force generated at the catalytic site of each β is converted into potentials driving the rotation of γ. It is important to point out that the actual functional form of the potentials is not critical so long as their relative depths and general shape are similar to the form we propose.

The general shapes of the individual potentials from each β can be understood by considering the β-subunits as elastic bodies with their equilibrium positions dictated by the identity of the nucleotides in the binding pocket. For V_T, V_DP, and V_D, the nucleotides interact strongly with the pocket so that the lowest energy configuration is the closed position. For V_E, i.e., without the nucleotide closing the pocket, the β-subunit prefers to be in the open position. Furthermore, inasmuch as the escapement tightly couples the bending of the β-subunit to the rotation of the γ-subunit and the position of γ uniquely defines the conformation of β, all the potentials are 2π-periodic.

The asymmetry of the power-stroke arises because of the asymmetric construction of the hexamer subunits. Each catalytic site lies at the interface between α- and β-subunits and the locus of the hinge-bending motion is around the β-sheet whose loops grasp the nucleotide (Sun et al., 2003). Consequently, the bending motion of each β-subunit is not directed toward the center axis of the hexamer, but has a small propeller component of its motion toward the adjacent α-subunit. We have deduced from the interpolated structures that the bending motion of each β is directed slightly off center, at an angular position 150° when β is completely closed. Thus the maxima of V_E and the minima of V_T are at 150° rather than at 180°.

We obtain the depth of V_E from the free energy computed from the unisite kinetics (Weber and Senior, 1997; Al-Shawi et al., 1989). There are two free energy drops: ΔG = 14 k_BT upon ATP binding and 10 k_BT upon product release. We attribute the first drop to the power-stroke driven by ATP binding (see below), and the second drop to the recoil power-stroke as the β-subunit unbends to its open configuration. During ATP binding, 14 k_BT of the 24 k_BT ATP-binding free energy is delivered directly to turn the γ-shaft and the remaining 10 k_BT is stored as elastic energy when the β-subunit is maximally bent. Thus the depth of V_T(θ) is 14 k_BT and the depth of V_E(θ) is 10 k_BT. The bending of the β-subunit is driven by the progressive annealing of hydrogen bonds between ATP and the catalytic site. This generates a nearly constant bending torque on the β-subunit (Oster and Wang, 2000a,b; Antes et al., 2003; Lutkenhaus and Sundaramoorthy, 2003). The high efficiency of the motor requires that the motor torque in Eq. 3 is nearly constant (Wang and Oster, 2001; Oster and Wang, 2000b). Therefore, the slope of V_T(θ) is nearly constant over most of its descent. The shapes of potentials are determined by the crankshaft escapement that converts the bending of the β into the rotation of the γ-shaft. In the Appendix we give the trigonometric forms of the potentials plotted in Fig. 2.

The complete shape of V_DP(θ) corresponding to bound products in the catalytic site is unknown. However, we need only consider its shape near the minima of V_T (see Fig. 2 B) because transitions between the T and DP states can only take place when ATP is tightly bound (i.e., at the minima of V_T). Moreover, the equilibrium constant between T ↔ DP is close to unity. Therefore, V_DP lies very close to V_T near its minimum. We have approximated V_DP by a curve that nearly coincides with V_T near its minimum. The exact shape of V_DP away from this segment does not affect any of our conclusions. Finally, we estimate the depth of V_D by scaling V_T by a factor, V_D(θ) = aV_T(θ), where a is approximately two-thirds, since the interaction of ADP with the catalytic site should be weaker than ATP due to one less phosphate, so the total number of hydrogen bonds is reduced from ≈18 to ≈12 (Antes et al., 2003). Thus, after hydrolysis, ADP is still held rather tightly; we will see that this leads to one of the pauses observed experimentally.

At any position during the rotation, the total driving potential in Eq. 3 is the sum of the individual contributions from three β-subunits. This is represented schematically in Fig. 2 as three legs, spaced 120° apart, moving on one set of four potentials. The model Eqs. 2 and 3 are solved numerically where all parameter values are determined from the experimental data and tabulated as described in the Appendix.

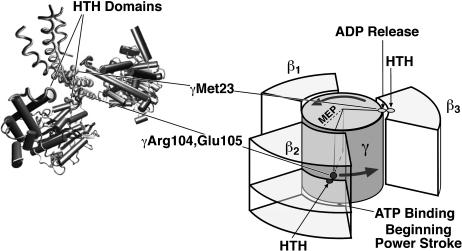
Finally, specific interactions between the rotating γ-shaft and the β-subunits are required to regulate binding of nucleotide and release of products, analogous to the camshaft on a gasoline engine. We refer to these interactions as binding and release gates. They are achieved via several critical residues on the γ, found in mutation experiments (Nakamoto et al., 2000, 1999). In Fig. 3 we show the spatial relationships of these critical residues with β-subunits. The critical residues are in two groups separated in angular position by ∼100°. The residues make contact with two HTH domains in different regions of the β-subunit. These HTH domains are connected to the catalytic site via the β-sheet so that when they interact with the γ-shaft, ADP release and ATP binding can occur. From the mutation studies and the predictions of our model, we believe that γMet-23 is critical for triggering ADP release; γArg-104 and γGlu-105 are critical for triggering ATP binding as shown in Fig. 3. We now demonstrate that the model reproduces virtually all of the available experimental data.

FIGURE 3.

The γ-shaft triggers ATP binding and ADP release via specific interactions with two HTH domains (in red) of β. The residue γMet-23 is 100° (in angular position) ahead of the residues γArg-104 and γGlu-105. Therefore, we infer that γMet-23 triggers ADP release, and γArg-104 and γGlu-105 trigger ATP binding.

RESULTS

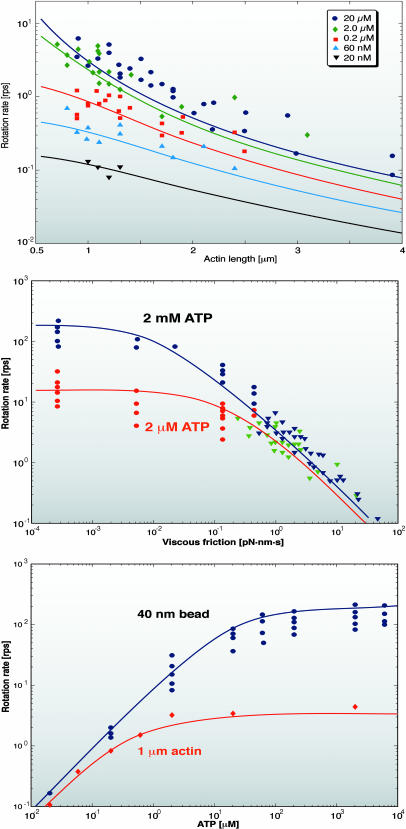
We first calculated the rotational speed of the F₁ motor under various load conditions and nucleotide concentrations. Fig. 4, top, shows the model results compared to the experiments when an actin filament is attached to the γ-shaft (Yasuda et al., 1998). Subsequent experiments employed a small bead attached to the γ-shaft (Yasuda et al., 2001). As the drag coefficient is reduced dramatically (with small beads), the rotational speed saturates even for high ATP concentrations, as shown in Fig. 4, middle. At 2 μM ATP, the rotation is limited by ATP binding; at 2 mM ATP, it is limited by ADP release. Fig. 4, bottom, shows the rotation rate as a function of ATP concentration for a 40-nm bead and for a 1-μm actin filament. The rate-limiting process at high viscous loads is the mechanical step of completing the power-stroke, whereas at low viscous loads, chemical steps are rate-limiting—i.e., waiting for ATP to bind (at low ATP concentration) or waiting for ADP release (at high ATP concentration). Next we show how the interplay between these two rate-limiting chemical steps is responsible for the observed rotational substeps.

FIGURE 4.

(Top) Model predictions for the actin filament rotation experiments at various ATP concentrations. The theoretical results are the solid lines and the experimental measurements are the symbols. (Lines and symbols of the same color are for the same ATP concentration.) In these experiments the rotational speed is limited by the viscous drag force on the actin filament. (Middle) Nanometer-sized beads have very small drag coefficients, close to the unloaded conditions. The model prediction (solid lines) and the experimental results (symbols) show that the rotational speed saturates to a maximum speed at very small friction coefficients. The rotational speed at these conditions is limited by the kinetics of ATP binding and ADP release. (Bottom) Rotational speed versus ATP concentration for actin (red lines and symbols) and 40-nm beads (blue line and symbols). The lines are model results. The symbols are experimental results. The model correctly predicts the rotational speed over the range of ATP concentrations in experiments.

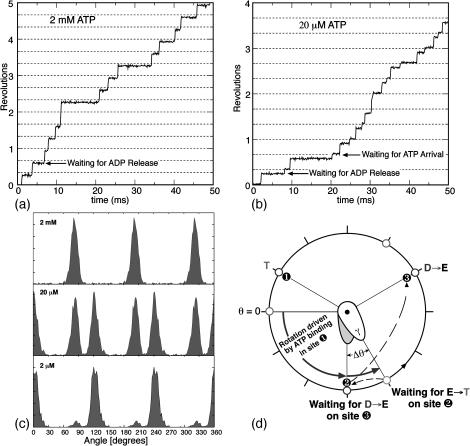
The substeps observed under low viscous loading provide important new insights into the operation of the F₁ motor. Fig. 5, a and b, shows two typical trajectories at high and low ATP concentrations. At 2 mM ATP, the rate-limiting step of ADP release gives rise to pauses in the rotation of the γ-shaft at relative angles of 90°, 210°, and 330°, whereas at 20 μM ATP additional pauses appear at 0°, 120°, and 240°, as catalytic sites await the arrival of ATP. Since the experiments only give the relative positions of the pauses, we redefine the θ = 0° position as the (most likely) beginning position of power-stroke as shown in Fig. 5 d (θ = 0° in Fig. 5 corresponds to θ = 30° in Fig. 2). Fig. 5c shows computed histograms of the pauses at several ATP concentrations. At 2 mM ATP the pauses are centered at 90°; at 20 μm ATP there are two peaks at 90° and 120°; and at 2 μM, the pauses are centered at 120°. Both the trajectories and the histograms agree with the experimental results (Yasuda et al., 2001).

FIGURE 5.

(a) A computed 50-ms time-trace of the angular position of the γ-shaft at 2 mM ATP concentration showing pauses at 90°, 210°, and 330° due to the delay in ADP release from site 3 (see d). (b) Time-trace of the angular position of the γ-shaft at 20 μM ATP. A substep appears at 120° in addition to the pause at 90° that was present at 2 mM ATP. The new pause arises as site 2 awaits a successful ATP binding event (see d). (c) Computed angular histograms of the time-traces at various ATP concentrations reproduce those measured by Yasuda et al. (2001). At 2 mM, one pause is seen at 90°. At 20 mM, two pauses are seen at 90° and 120°. At 2 μM, again only one pause is seen at 120°. (d) A cartoon diagram illustrating the sequence of events that produce the rotational pauses. Define the rotational angle of the γ-shaft measured from θ = 0° as shown. Site 1 waits for ATP binding when γ is at θ = 0° (pause one if ATP concentration is low, circles at 1 and 9 o'clock). Upon ATP binding, the power-stroke of site 1 tries to turn γ to θ = 120°, but it stalls at θ = 90° by the resisting torque (slope of the V_D curve in Fig. 2 B) of site 3 with ADP bound (pause two, circles at 2, 6 and 10 o'clock). Upon the ADP release from site 3, site 1 completes its power-stroke to θ = 120°.

Fig. 5 d summarizes the sequence of events responsible for the pauses; their mechanical basis can be understood from Fig. 2 B. First consider the case when the ATP concentration is high. When the γ-shaft is at θ = 0°, the progressive binding of ATP at site 1 is driving a power-stroke that, if unhindered, would turn the γ-shaft to θ = 120° (150° across the diameter from site 1, which is at θ = −30° in Fig. 5). However, ADP bound at site 3 stalls out the power-stroke at θ = 90°. (Fig. 2 B, the second set of three legs, shows when the slope of V_T is equal to the negative slope in V_D.) When the ADP is released, the driving potential for site 3 switches from V_D→V_E and site 1 can complete the power-stroke to θ = 120°, now assisted by site 3's recoil power-stroke. At θ = 120° ATP immediately binds to site 2 commencing its power-stroke. When the ATP concentration is low, an additional pause takes place at θ = 120° whereas site 2 waits for ATP binding. This sequence of events completely explains the observed pauses in the γ-shaft's rotation. At 2 mM ATP, the timescale for ATP binding is very short and only the ADP release step is observed (Fig. 5 c, top panel). At 20 μM ATP, the timescales for ATP binding and ADP release are comparable, and two pauses appear in the histogram (Fig. 5 c, middle panel). At 2 μM ATP the pause is dominated by the waiting time for ATP binding.

The complete agreement between the predictions of the model and the experiments demonstrates that the observed pauses are due to the asymmetry in the structure of the β-subunits. Because the bending motion is off-center, the minima of the elastic energy potentials for the T, DP, and D states are offset from 180°, to ∼150° (Fig. 2). If the bending motion were toward the center of the hexamer, then the minima of the elastic potentials would be at 180° and the double peaks in the histogram at 20 μM would be absent. The angular position where the motor is awaiting ATP binding and the position where it is waiting for ADP release would be indistinguishable, leaving but a single peak at all ATP concentrations.

Before ADP is released, the pause at θ = 90° corresponds to an occupancy state of (T, E, D) in sites (1, 2, 3) as shown in Fig. 5 d. This occupancy state corresponds precisely to Walker's original F₁-ATPase structure. Our model suggests that Walker's structure corresponds to the 90° paused configuration in the Kinosita/Yoshida single molecule experiments. The model agrees completely with recent fluorescence resonance energy transfer measurements of F₁ by Yasuda and co-workers, where they concluded that the γ-shaft in the ATP-waiting state is ∼30–40° (in the direction of rotation) from that in Walker's structure (Yasuda et al., 2003). The combined experimental and theoretical evidence indicate that Walker's structure corresponds to the pre-ADP release state.

DISCUSSION

Recent molecular dynamics studies reinforce the major assumptions of the model:

1. The power-stroke is generated by progressive binding of ATP to the catalytic sites that drives the hinge-bending motion of the β-subunits that in turn drive the rotation of the γ-shaft (Oster and Wang, 2000a; Antes et al., 2003).

2. At the same time, the bending of the β-subunit deforms the β-sheet adjacent to the catalytic site. This deformation stores elastic energy in the sheet that is released to drive a recoil power-stroke. This accounts for the two free energy drops observed in the unisite kinetics.

The model demonstrates that the rotational pauses observed in the Yasuda and co-workers' experiments are quantitatively explained by the tight binding of ADP and two intrinsic asymmetries in the F₁ motor (Yasuda et al., 2003). First, the catalytic site and the power-stroke motion in the α₃β₃ hexamer have an inherent handedness such that the power-stroke driven by the bending β-subunit has an offset of ∼30°. This biases the direction of rotation because the bending motion of each β-subunit is tightly coupled to the eccentric γ-shaft. Second, the γ-shaft itself must regulate the binding and release of nucleotides via asymmetric interactions with β.

In summary, the mechanochemical model presented here quantitatively explains all of the mechanochemical behavior of the F₁ motor. We have emphasized that asymmetry inherent in the structure of F₁ and the power-stroke is the explanation for the observed pauses. The nearly constant torque generated by the motor requires ADP release and subsequent ATP binding to only occur at specific angular positions of γ relative to β, and in the correct direction of rotation. Thus the rotating γ-shaft acts as a timing cam ensuring that the exhaust and intake parts occur in the right phase of the hydrolysis cycle. Our model should be contrasted with the kinetic model of Gao et al. (2003) where a different set of kinetic states are considered. Our model is consistent with the kinetic data on F₁ as well as single molecule measurements. When driven in reverse by the F_o motor, F₁ synthesizes ATP from ADP and phosphate. By adding an external load torque to the model, it is possible to drive F₁ in reverse and synthesize ATP. However, there is evidence that the ɛ-subunit changes conformation significantly under these conditions (Cipriano et al., 2002; Kato-Yamada and Yoshida, 2003). Consequently, the driving potentials we have used in the model are not applicable in the reverse direction. Our analysis of ATP synthesis will be presented elsewhere.

APPENDIX A: MATHEMATICAL MODELING OF THE F₁ MOTOR

We model the rotational dynamics of the F₁ motor by a high friction Langevin equation coupled to Markov equations describing chemical transitions in the catalytic site. These equations generate individual trajectories of the F₁ motor, i.e., time series of the angular position of the shaft, θ, and the sequence of chemical changes in the three β-subunits. Each of the β-subunits in the α₃β₃ hexamer can be in any of four occupancy states (E, T, DP, or D). Thus the composite F₁ motor can be in any one of 4³ = 64 ≡ N occupancy states. We label the composite chemical state using the index σ. Transitions between these states are modeled as Markov processes governed by transitions rates k_σσ′. (Note k_σσ′ is related to but not the same as the measured reaction rates such as k_E→T. The relationship is given in Eq. B11.) We write the Markov equations describing the transitions as

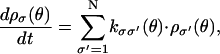(A1)

where ρ_σ(θ) denotes the population density in the σ-th chemical state when the γ-shaft is fixed at rotational position θ. The sequence of chemical states is specified by a triplet of occupancy states. For example,

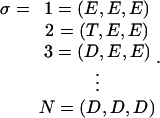(A2)

The time-evolution of Eq. A1 can be solved using kinetic Monte Carlo. The system progresses through a 4 × 4 × 4 periodic cubic lattice where each vertex labels one of the 64 possible states. The kinetic transition matrix k_σσ′ determines the stochastic trajectories through this lattice. In our model, each transition step involves a change in only one of the catalytic sites. For example, (E, DP, E) → (E, D, E) can be achieved in one transition step, but (E, DP, E)→(E, D, T) requires at least two transition steps.

The evolution in chemical state-space is coupled to the Langevin equation governing the rotation of the γ-shaft,

(A3)

where σ is the composite chemical state of F₁ (i.e., the states of three catalytic sites). ζ is the apparent viscous drag on the γ-shaft that is varied to model different attached objects. (See Appendix B, Kinetics, for a more detailed discussion.) ∂Ψ(θ,σ)/∂θ is the total motor torque driving the rotation of the γ-shaft, where Ψ(θ;σ) is the potential corresponding to chemical state σ. The total driving potential consists of contributions from three β-subunits. In our model, the angular position of the γ-shaft determines uniquely the bending angles of the three β-subunits, and the three β-subunits are 120° apart. Therefore, the total elastic potential can be written as

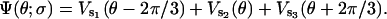(A4)

Here s₁, s₂, and s₃ are the chemical states of three catalytic sites, i.e., σ = (s₁, s₂, s₃). For example, if σ = (E, T, D), then

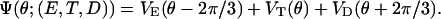(A5)

Ensembles of stochastic angular trajectories from Eqs. A1 and A3 can be averaged to obtain the rotational speed of F₁ motor. Alternatively, one can directly solve for the probability density of the γ-shaft position, ρ_σ(θ). The governing equation for the probability density is the high-friction limit of the Fokker-Planck equation (Risken, 1989). The time-evolution of the probability density is given by

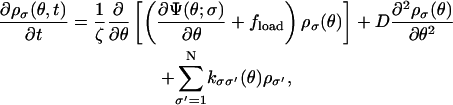(A6)

where ρ_σ(θ,t),σ = 1, 2, ··· 64 is the angular probability density for the σ^th state. D is the diffusion constant given by D = k_BT/ζ. The transition matrix k_σσ′ is the same matrix appearing in Eq. A1.

In most instances, we are interested in the steady-state situation where ρ_σ(θ, t) is not changing in time. This is obtained from the solution of Eq. A6 with the time-derivative set to equal zero. Quantities such as the average rotational speed, fluxes between different states, and site occupancies all can be computed from the steady-state probability densities ρ_σ(θ).

The method of solution for Eq. A6 has been published elsewhere (Mogilner et al., 2002; Wang et al., 2003); here we summarize the method. Since Eq. A6 is invariant under a rotation that permutes the labels on the sites, it is sufficient to solve for ρ_σ(θ) only in the interval from 0 to 120°. We discretize the angular interval in increments of size Δθ. We label the probability density of the σ^th chemical state at n^th angular interval as ρ_σ,n. Eq. A6 can be discretized as

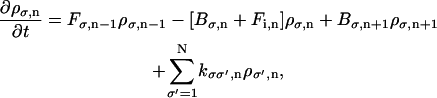(A7)

where F_σ,n is the forward transition rate from interval n to n + 1 and B_σ,n is the reverse transition rate from interval n to n − 1. Since these transition rates obey detailed-balance, we have the condition

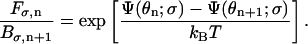(A8)

The jump rates F_σ,n and B_σ,n, determined from detailed-balance condition and local approximate solutions (Mogilner et al., 2002), are given by

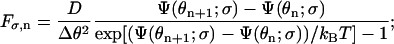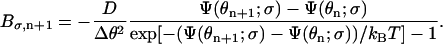(A9)

Eq. A7 has the form

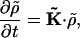(A10)

where 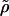is a vector containing ρ_σ,n. The matrix 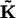contains chemical transition rates k_σσ′ and the angular jump rates, F_σ,n and B_σ,n. The steady-state solution for ρ_σ,n is the nontrivial solution of Eq. A10 with the left-hand side set to zero. To obtain individual trajectories of the F₁ system progressing through (σ,θ) space, we perform a kinetic Monte Carlo simulation in (σ,n) state-space. Starting at state (σ,n), random numbers are drawn from an exponential distribution

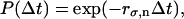(A11)

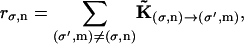(A12)

where r_σ,n is the rate of jumping out of state (σ,n). The random number Δt is the time needed to make a transition from state (σ,n) to a different state. An additional random number determines the identity of the destiny state from the ratio

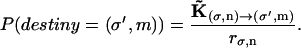(A13)

Iteration of this process gives a trajectory through the (σ,θ) space.

Experiments measure θ as a function of time. The experimental apparatus has finite time resolution ranging from 0.0001 s to 0.004 s (Noji et al., 1997; Yasuda et al., 2001). We mimic the experimental time-trace by averaging the Monte Carlo trajectory over intervals corresponding to the experimental time resolution. The time-traces displayed in the main text are determined in this fashion.

For a given set of driving potentials, 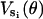, and kinetic transition rates, k_σσ′, the mathematical steps outlined here give the measurable quantities such as time-traces and rotational speeds. The remaining sections describe how structural and physical considerations fix the model parameters.

APPENDIX B: CONSTRUCTION OF THE MODEL

The kinematics of F₁

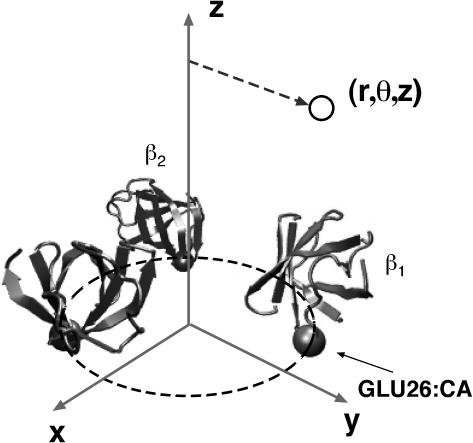
The mechanical motion of F₁ during the power-stroke was analyzed by Wang and Oster (1998). Here, we summarize their interpolation procedure. The structures of Walker (Abrahams et al., 1994) show that the F₁ hexamer is approximately sixfold symmetric at the N-terminal end. C_α atoms ofβ-GLU26 (Bovine convention) from the bottom portion of the subunits provide a fixed frame from which a cylindrical coordinate system can be constructed as shown in Fig. 6. Every atom in the α₃β₃ hexamer is assigned a coordinate in the cylindrical coordinate system. The hydrolysis cycle in each catalytic site proceeds through the states E→T→DP→D→E. Walker's structures for the β-subunits are configurations along this cycle. To find the conformational change connecting one configuration to the next, the positions of the atoms are linearly interpolated within the cylindrical coordinate system. For example, since β_E goes to β_T, coordinates of atoms in β_E and β_T are endpoints of interpolation from E→T. Similar procedure is carried out for all the other subunits within the Walker structures.

FIGURE 6.

The cylindrical coordinate system used for interpolation. The N-terminal portion of chains D–F (from PDB 1BMF) is nearly sixfold symmetrical. C_α atoms from Glu-26 are used to define a cylindrical coordinate system depicted in the graph. Each atom in the β-subunit is assigned a coordinate (r, θ, z) in this coordinate system.

The interpolation reveals that the β-subunits undergo a hinge-bending motion during the transition from E to T. The bend is centered at a β-sheet directly behind the catalytic site (Sun et al., 2003). The α-subunits remain relatively stationary during the interpolated motion. During the bending motion, the helix-turn-helix (HTH) motif at the C-terminal end of the β-subunit impacts the eccentric γ-shaft so that a torque is applied to the shaft. In contrast, when β proceeds from T→D (bypassing DP for the moment), very little conformational change is observed. This suggests that the chemical changes in the catalytic site from T→DP→D do not directly contribute to the power-stroke. The final step from D→E again produces a conformational change resembling the reverse of E→T. We interpret this motion as a recoil step where the deformed β-sheet acts as a spring tending to restore the β-subunit to its open conformation after the hydrolysis products are released (Sun et al., 2003). These conformational motions constitute the kinematic basis for our dynamical model.

Dynamics of F₁ motor

Elastic potentials

The elastic potential functions that drive the bending motion of theβ-subunits are derived from free energy changes of the complete hexamer (Sun et al., 2003). In principle, these functions could be obtained from molecular dynamics simulations. However, without resorting to this level of detail, we derive the elastic potentials from a simple mechanical model that satisfies certain structural constraints. First, we assume that the bending motion of the β-subunit is tightly coupled to the rotational angle of the γ-shaft. This ensures that the bending coordinate, φ, maps one-to-one onto the rotational angle, θ. Fig. 7 shows the relationship between the bending angle φ and the shaft rotation angle θ. Second, in accord with the assumptions in the Binding Zipper model (Oster and Wang, 2000a), the power-stroke is driven by the progressive formation of hydrogen-bonds between the catalytic site and the nucleotide. Therefore, we take the elastic potential as a function of the bending angle φ to be (see Fig. 7)

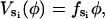(B1)

where 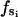is the force constant with respect to φ for the occupancy state s_i. The sign of 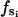determines whether the β-subunit prefers to be closed or open. When β is closed, the angle φ is ∼50°; when β is open, the angle φ is ∼80°. Thus, the allowed range, Δφ, is ∼30°. When s_i is equal to T, DP, or D state, the β-subunit prefers to be closed. When s_i = E, the β-subunit prefers to be open. That is, f_T > 0, f_DP > 0, f_D > 0, and f_E < 0.

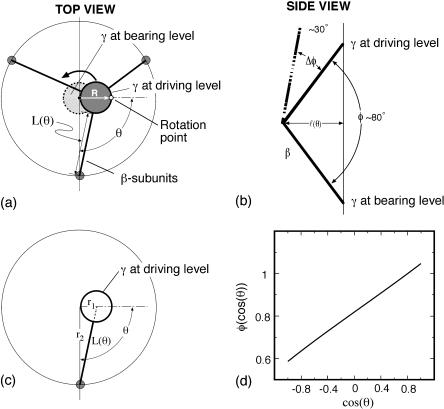
FIGURE 7.

(a) Diagram of the F₁ subunit viewed from the top (membrane side) showing the three β-subunits whose bending drives the rotation of the γ-shaft. The β-subunits are shown schematically as three rods. (b) A stick model illustrating the geometric relationship between the angle, φ, of the bending of theβ-subunit and the length, L, of the HTH lever arm on β. (c) The relationship between L and θ as the power-stroke goes from 0 to π. The perspective is from the top of F₁ so that the axis in the z direction is out of the figure. Each bending β-subunit, viewed from above, acts like a radial driving piston on the eccentric portion of the γ-shaft. (d) The bending angle φ is nearly a linear function of cos(θ).

To transform the elastic potentials in φ into potentials as functions of the shaft angle θ, a mechanical escapement is required, i.e., a geometric relationship between φ and θ. This is obtained as follows. In Fig. 7 the three driving pistons representing the β-subunits are 120° apart. The upper portion of the piston represents the C-terminal domain of the β-subunit that impacts the γ-shaft. The length of this piston, R, is assumed to be fixed. As the β-subunit bends, the projection of R in the plane perpendicular to z is L(θ). The geometric relationship between L and θ is

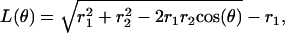(B2)

where r₁ = 5 nm and r₂ = 1 nm. (In this equation, L increases as θ goes from 0 to π.) But, from Fig. 7 b, we have

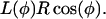(B3)

Setting Eq. B2 equal to Eq. B3 gives the desired relationship between θ and φ. Fig. 7 d is a plot of φ vs. cos(θ), showing that φ is a nearly linear function of cos(θ). Thus, we shall set φ = c₁ cos(θ) and write 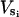as a linear function of cos(θ),

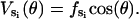(B4)

We use f_T = f_DP = 7 k_BT, f_D = 5 k_BT, and f_E = −5 k_BT. This set of values is selected so that the depth of V_T and V_DP is 14 k_BT and the depth of V_D and V_E is 10 k_BT, in accordance with the Binding Zipper model (Oster and Wang, 2000a). For ATP binding, 15–17 hydrogen bonds are eventually formed between ATP and the binding pocket (Antes et al., 2003). The free energy change for forming these hydrogen bonds is ≈24 k_BT. In the bending motion of the β-subunit, 10 k_BT of the 24 k_BT-binding free energy is stored as elastic strain energy in the deformed β-sheet. The remaining 14 k_BT directly drives the rotation of γ. The 10 k_BT stored elastic energy drives the recoil power-stroke after ADP release when the catalytic site is empty. Thus, the depth of V_T is 14 k_BT and the depth of V_E is 10 k_BT.

The transitions between the T and DP states can only take place when ATP is tightly bound (i.e., at the minima of V_T). Thus, we need only the shape of V_DP near the minima of V_T. The equilibrium constant between states T and DP is close to unity (Boyer, 1993). V_DP should be very close to V_T near its minima. We choose f_DP = f_T. The shape of V_DP away from its minima is irrelevant. Because the interaction of ADP with the catalytic site is weaker than that of ATP, we make the depth of V_D 10 k_BT. This completely specifies the elastic potentials for the four occupancy states.

Asymmetry of the power-stroke

Closer examination of the power-stroke motion reveals that the motion of the C-terminal HTH domain that drives the γ-shaft is not directed along the diameter toward 180°. Rather, the propeller-like motion of the power-stroke is directed slightly off center, toward ≈150°. To model this effect in the elastic potential, the same functional form for the 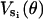values are taken, with θ replaced by u(θ) where u(θ) models the propeller bias:

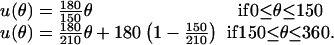(B5)

The elastic potentials 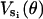are replaced by 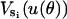. By scaling the angles linearly, the minimum (and maximum) of the elastic potential is constructed to be at 150°. This completely specifies the elastic potential for a single β-subunit as a function of the γ-shaft angle θ. No additional modifications in the potential are necessary to produce the correct hydrolysis and synthesis rates.

Since there is a one-to-one mapping between the angle φ of β and the angular position θ of γ, the location of the shaft completely specifies the mechanical state of the F₁ motor. Of all the different states of each β-subunit, the conformation is most open near θ = 0° and most closed near θ = 150°.

By the threefold symmetry of the α₃β₃ hexamer, the total elastic potential on the γ-shaft due to the action of all three β-subunits is the sum of the individual contributions

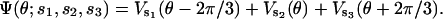(B6)

The actual potentials of the individual β-subunits are plotted in the main text. It is important to note that the power-stroke experienced by γ is a combination of two contributions. The main contribution comes from the bending β-subunit after binding ATP. Additional contributions come from the recoil of the E state after ADP is released. Furthermore, if a β-subunit is in the D state, it resists the rotation of γ. The resistance from the D state is the origin of one of the pauses seen in the experiments.

Kinetics

The reaction rates for the hydrolysis cycle are denoted as k_E→T, etc. The transition rates depend on the mechanical state of the β-subunit, φ(θ), and the chemical state of the adjacent catalytic sites. The exact dependence of the transition rates are not available, and so our parameters derive from several experimental observations.

First, experiments show that the hydrolysis and synthesis rates are enhanced by many orders of magnitude when more than one catalytic site is occupied by nucleotides (Senior, 1992; Weber and Senior, 1997). Thus, there is a cooperative effect during the F₁ chemical cycle such that the reaction rates in each catalytic site is effected dramatically by adjacent sites. The exact mechanism of this enhancement is uncertain. To model this rate enhancement, we take several factors into consideration. Since chemical transition rates are inversely proportional to the exponential of the free energy difference between the reactant and the transition state, these rates may be enhanced by either a lowering of the transition state free energy or a raising of the reactant free energy. We write the multisite rates as

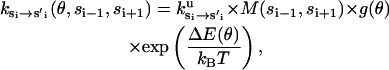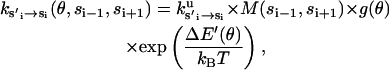(B7)

where k^u is the unisite reaction rate measured by Senior (1992) (see Table 1). The dependence of M, g(θ), ΔE(θ), and ΔE′(θ) on (s_i+1, s_i−1) is shown in Table 2. The exponential factors ΔE(θ) and ΔE′(θ) are the elastic energy contributions to the rate; they account for increase/decrease in the reaction rates as functions of θ. For example, ATP release rate increases as β becomes open. ΔE(θ) and ΔE′(θ) satisfy

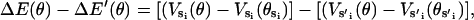(B8)

where θ_E = 0° and θ_T = θ_DP = θ_D = 150°. Eq. B8 fixes the energetic differences between the driving potentials to approximately satisfy unisite kinetics

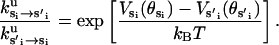(B9)

TABLE 1.

Unisite reaction rate measured by Senior (1992) for Escherichia coli

Unisite rates of E. coli	Value
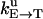	[ATP] × 1.1 × 105 s−1
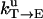	2.5 × 10−5 s−1
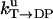	1.2 × 10−1 s−1
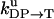	4.3 × 10−2 s−1
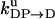	1.2 × 10−3 s−1
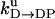	[Pi] × 4.8 × 10−4 s−1
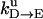	1.6 × 10−3 s−1
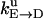	[ADP] × 1.8 × 102 s−1

TABLE 2.

Parameters for the kinetic rates list the multisite enhancement factors and elastic contributions to the transition rates

Rate	M(si−1,si+1)	Switches	Elastic contribution
kE→T
kT→E
kT→DP
kDP→T
kDP→D
kD→DP
kD→E
kE→D

Together, Eqs. B7–B9 ensure that the reaction rates satisfy the detailed-balance condition,

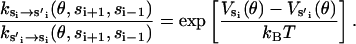(B10)

Several critical residues for the rate enhancement have been identified. It appears certain residues on the γ-shaft and the α-subunit side of the binding pocket are critical for achieving the observed rate enhancement (Nakamoto et al., 2000, 1999). The enhancement must involve elastic strains induced by nucleotide binding and rotation of the γ-shaft. Without detailed information on the exact function of these residues, the enhancement factors M are phenomenological and are made to agree with available experimental results.

The transition rates appearing in Eq. A1 are directly related to the rates defined in Table 2. Since chemical changes can only occur in one site at a time, we have

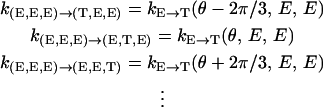(B11)

This completely specifies our transition matrix, k_σσ′.

Gates

The assumptions stated above specify the approximate dependence of transition rates on θ. To achieve the correct rotation speeds, the binding of ATP and release of ADP must be triggered at specific positions of the γ-shaft. For ATP binding, the transition from E→T does not become appreciable until slightly after θ = 0°. If binding occurred at θ = 0°, there is appreciable probability that the power-stroke would be reversed. Thus, binding and release gates are necessary to ensure the asymmetry of the power-stroke. Similarly, for ADP release, the transition rates must not become appreciable until the catalytic site is sufficiently strained. The effect of switches on the transition rates is contained in the function g(θ) in Eq. B7 for the transition rate derived from the V_D elastic potential.

There is experimental evidence that the position of the γ-shaft is crucial in the enhancement of hydrolysis rates. Mutation studies of amino acid residues along γ have identified several critical positions (Nakamoto et al., 2000, 1999). Substitution of these critical amino acids results in a dramatic reduction in the overall hydrolysis rate. Examining the sequence of interpolated structures reveals that these critical residues make contact with two regions on the β-subunit. The first region is the HTH domain at the C-terminal end of β; this is the place where β impacts the γ-shaft. Clearly, disturbing this region affects the power-stroke motion. The second region is another HTH domain directly behind the ATP binding pocket. Both of these HTH domains lie within loops emanating from the same β-sheet whose loops grasp the nucleotide (Sun et al., 2003). Thus, chemical transitions in the binding pocket are directly coupled to the angular position of the γ-shaft primarily through elastic stress passing these contact regions. Our model takes this structural information into account.

Mechanism of multisite rate enhancement

An interesting aspect of the model is that to reproduce the experimental rotation rates, all of the chemical transition rates must be enhanced by at least 10³, and some steps are enhanced by 10⁸! These enhancement factors are necessary so that no one chemical step is rate-limiting. (Senior, in 1992, first estimated the enhancement factors and pointed out that the rate of all chemical steps are increased.)

In addition to the requirement that more than one catalytic site must be occupied, two additional ingredients are necessary. First, the presence of the γ-shaft is necessary for the multisite rate enhancement. Second, an arginine residue from the α-subunit part of the binding pocket is also crucial. Mutation of this particular residue reduces the overall rate to unisite conditions. The enhancement factors in Table 2 implicitly take these two factors into account. First, the angular switches that determine where the chemical transition can occur reflect of the influence of γ. Thus if γ is not in the correct position relative to the β-values, the chemical transition cannot occur. Second, the enhancement factor M is a crude model for the effect of the arginine residue on the catalytic site. When the catalytic site is occupied, stress from binding of nucleotide radiates out through the adjacent α-subunit to the adjacent site. The path of this stress must pass through the essential α-arginine. The net effect of this stress is to lower the barrier for hydrolysis and enhance the rate by a factor represented by M. The nature of the reaction barrier and a detailed account of the reaction mechanism will be discussed in a forthcoming article.

The viscous drag coefficient on γ

We assume that the viscous drag coefficient in Eq. A3 is dominated by the viscous friction experience by the objects attached to the γ-shaft. For example, when an actin filament is attached,

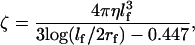(B12)

where l_f and r_f are the length and radius of the actin filament, respectively, and η is the viscosity of water. For fluorescent beads we use

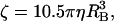(B13)

where R_B is the radius of the bead. For beads of 40 nm in diameter, ζ = 2.56 × 10⁻⁴ pN nm s (Yasuda et al., 2001). Experimental measurements of the rotation speed are also reported as a function of this external drag.

The actual drag experienced by the γ-shaft is a sum of the external drag from the attached objects and the internal friction from the motion of γ relative to β. Thus, neglecting any hydrodynamic coupling, we may write

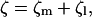(B14)

where ζ_l is the drag from the external load coming from the attached actin or gold beads, and ζ_l varies with the size of the attached load; and ζ_m is the internal friction of the motor, and ζ_m is a constant during changing experimental conditions. When actin filaments are attached, the external drag is much larger than the internal friction, i.e., ζ_l ≫ ζ_m. Therefore, the total drag experienced by γ is dominated by ζ_l. However, for small gold beads, it is not clear that the external friction is much greater than internal friction. Perhaps for the smallest beads, ζ_m ≈ ζ_l. In this case, the total drag coefficient must include contributions from both. In Fig. 4 of the main text, the rotational speed levels off as a function of the external drag. However, it is not correct to explain this behavior by assuming ζ_m ≫ ζ_l, so that the total friction is essentially constant in this region. The leveling-off behavior has more to do with the chemical reaction rates being the rate-limiting steps.