Abstract
When mouse embryonic fibroblasts in suspension contact a matrix-coated surface, they rapidly adhere and spread. Using total internal reflection fluorescence microscopy of dye-loaded fibroblasts to quantify cell-substrate contact, we found that increasing the surface matrix density resulted in faster spreading initiation whereas lamellipodial dynamics during spreading were unaltered. After spreading initiation, most cells spread in an anisotropic manner through stochastic, transient extension periods (STEPs) with ∼30 STEPs over 10 min to reach an area of 1300 μm2 ± 300 μm2. A second mode of spreading, increased in serum-deprived cells, lacked STEPs and spread in a rapid, isotropic manner for 1–4 min. This isotropic mode was characterized by a high rate of area increase, 340 μm2/min with 78% of the cell edge extending. Anisotropic cells spread slower via STEPs, 126 μm2/min with 34% of the edge extending. During the initial 2–4 min of fast, isotropic spreading, centripetal flow of actin was low (0.8 μm/min) whereas in anisotropic cells it was high from early times (4.7 μm/min). After initial isotropic spreading, rearward actin movement increased and isotropic cells displayed STEPs similar to anisotropic cells. Thus, the two cell states display dramatically different spreading whereas long-term motility is based on STEPs.
INTRODUCTION
Cell adhesion and spreading on extracellular matrix (ECM) substrata are critical for cell motility, cell growth, and organization of tissues (Aplin et al., 2002; Gumbiner, 1996; Parker et al., 2002). The signaling events following the interaction of integrins with ECM constitute a major stimulus for spreading, motility, and viability (Geiger et al., 2001). In the spread state, cells exert contractile forces on the substrate and sense stresses from the surface through integrin attachments (Galbraith et al., 2002; Riveline et al., 2001; Schwartz and Ginsberg, 2002). As cells adhere to matrix-coated surfaces, integrin binding to matrix molecules activates cell spreading, and subsequent spreading enables additional matrix-integrin interactions to form (Maheshwari et al., 2000). Thus, cell-matrix adherence is a complex function of the density of ECM bonds, force generation on these bonds, and cell-matrix contact area.
Cell spreading is an actin- and myosin-dependent process of membrane extension along the ECM-coated surface. Actin filament assembly at the cell's leading edge mechanically extends the membrane and the cell transforms from a spheroidal to nearly discoidal conformation over the course of spreading. Similar to cell migration, spreading is dependent on the regulation of actin filament dynamics (Cunningham et al., 2001; Pollard and Borisy, 2003) as well as on other aspects of motility including focal contact dynamics (Potter et al., 1998) and force generation through these contacts onto the surface (Pelham and Wang, 1997). After spreading, polarization requires spatial coordination dependent on microtubule organization and actomyosin contractility (Omelchenko et al., 2002). Diminished cortical tension has been correlated to the active, rapidly fluctuating leading edges of motile 3T3 fibroblasts (Rotsch et al., 1999).
To understand the underlying nature of the signaling events controlling and coordinating motility, a detailed analysis of the activity of the cell periphery is useful. The benefit of such analysis is exhibited in the recent study of the role of Ena/VASP proteins in actin filament regulation (Bear et al., 2002) where changes in the capping function of Ena/VASP are correlated to changes in motility as represented in one-dimensional kymographs of the cell edge. Other experiments following motility in one spatial dimension and on timescales of 1 min have suggested that cells migrate via short-lived extension and retraction events (<1 min) which, over the course of many minutes, result in net movement of the cell's leading and trailing edges (Dunn et al., 1997). The theoretical and experimental underpinnings of computer-assisted motility analysis in two spatial dimensions have existed for over a decade (Dunn and Brown, 1987; Soll, 1988, 1995). With decreasing cost of high performance computers, quantitative analysis of the cell edge has reached ever-higher resolutions. In a two-dimensional study conducted in 1990, 3-s time-lapse recordings of migrating fibroblast lamellipodia were made using video-enhanced differential interference microscopy (Felder and Elson, 1990). This study revealed that protrusion initiation is a stochastic process in the segments of the cell edge studied.
To explore the motility dynamics of entire cells, we have devised a simple method for quickly quantifying edge dynamics on short timescales (<10 s) and with submicron precision (<300 nm). This is achieved by exploiting the high contrast between contact and noncontact regions in images obtained using total internal reflection fluorescence (TIRF) microscopy (Axelrod et al., 1983).
Combining this high resolution analysis of whole-cell edge dynamics in spreading cells with the details of actin filament centripetal flow, we reveal fundamental characteristics of motility during cell spreading. We explore the role of ECM molecules in spreading, showing that a decrease in matrix density increases the lag time between cell contact with the matrix and spreading initiation whereas spreading dynamics after initiation were not altered. In addition, we define two fundamental modes of spreading, the predominant form, anisotropic spreading, and a second form, isotropic spreading. Isotropic spreading is increased in serum-deprived populations. In anisotropic spreading cells we identify spatially and temporally limited protrusions whose direction is randomly determined. We propose that these stochastic transient extension periods (STEPs) underlie most motile processes. Finally, we correlate the anisotropic mode of spreading and its associated STEPs with increased contractility in the lamellipodium as indicated by the rearward movement of the cytoskeletal GFP-α-actinin. The anisotropic mode of motility is seen in all cells after completion of spreading and is the basis for other cell motility processes such as polarization and migration.
METHODS AND MATERIALS
Reagents
Calcein AM was purchased from Molecular Probes (Eugene, OR). Cell culture reagents and 120 KDa human fibronectin fragments were purchased from GibcoBRL (Carlsbad, CA). Hexamethyl disilazane (HMDS), GRGDTP peptides, soybean trypsin inhibitor, and fibronectin-like engineered protein (pronectin) were purchased from Sigma (St. Louis, MO). The Cy-5 labeling kit was purchased from Amersham Biosciences (Piscataway, NJ). The GFP-α-actinin construct was the generous gift of Carol Otey, and is characterized elsewhere (Edlund et al., 2001).
Fibroblast culture
Immortalized mouse embryonic fibroblast cells were obtained from Jan Sap (New York University, New York, NY) and cultured in DMEM (Gibco, Carlsbad, CA) with 10% FBS. One day before experiments, cells were sparsely plated to minimize cell-cell interactions before replating for experiments. For serum-deprivation experiments, experimental cells were cultured in DMEM containing no serum.
Cover glass preparation
Cover glasses were acid-washed and treated with hexamethyl disilazane, creating a highly hydrophobic surface that prevents nonspecific receptor activation and adhesion (Groth and Altankov, 1996). 3.1 cm2 sections of the surface were subsequently exposed to 200 μl of 6.6 μg/ml fibronectin solution or 6.6 μg/ml pronectin solution for 1 h at 37°C. The uniformity of the protein coating was confirmed by observation of Cy-5 labeled ECM. Experiments using higher and lower coating concentrations are denoted by multiples of the standard 6.6 μg/ml, i.e., 2 × FN refers to a coating concentration of 13.2 μg/ml.
Sample preparation
Cells were washed with 200 μl of 0.25% trypsin and 1 mM EDTA solution for 2 min. Trypsin was neutralized with serum or soybean trypsin inhibitor (for serum starvation experiments) followed by centrifugation. Resuspension proceeded in culture media containing 0.2 μM of the fluorescent cytoplasmic dye, calcein AM. Labeling proceeded for 15 min at 37°C. Next, cells were again centrifuged and resuspended in serum-free media immediately before the spreading assay. For actin filament speckle analysis and focal contact identification, GFP-α-actinin was transiently expressed in fibroblast cultures.
Microscopy
We built a custom-designed prism-based TIRF microscope using an upright Olympus (Melville, NY) BX-50 microscope as a starting point. We replaced the standard stage with a sample holder situated above a dove prism. Guiding the 488-nm excitation light from a Melles Griot (Carlsbad, CA) argon-ion laser through telescoping lenses and then into the beveled side of the prism, we were able to control both the angle of incidence and diameter of the beam. A rotating diffuser was placed in the beam path to blur out laser interference patterns. Adjusting the angle that the beam made with the top surface of the prism to be less than the critical angle of incidence resulted in the laser rising through the prism, totally reflecting at its top surface, and creating an evanescent wave that penetrated upwards out of the top surface for 100 nm. ECM-coated cover glass was placed on a motorized sample holder so that the cover glass was suspended above the prism. Coupling the prism to the cover glass using standard immersion oil resulted in a refractive interface between the top of the borosilicate cover glass and our aqueous sample (situated atop the cover glass), causing the reflection of the laser beam to occur at the surface onto which the cells spread and exposing the cells to the evanescent wave.
An Olympus 20× 0.95-NA water immersion objective was then lowered into the aqueous sample. The field of view through this objective was 400-μm across, and the diameter of the laser beam (and resulting evanescent wave) was adjusted to these dimensions by adjusting the magnification of the laser telescope. 37°C temperature control of the sample was achieved by constructing a Plexiglas box around the sample holder, stage, and objective which was heated remotely via flexible tubing connected to a fan heater. Major sources of vibration, such as the heater, were mechanically isolated from the vibration isolation air table upon which the microscope sat to reduce sample movement during measurement.
At the start of an experiment, fluorescently labeled cells suspended in serum-free media were added to the cover glass on the TIRF microscope and allowed to sediment onto the coated surface. A Roper Scientific (Trenton, NJ) CoolSnap FX cooled charge-coupled device camera captured 12-bit digital 1300 × 1030 pixel grayscale images from the TIRF-illuminated cells every 5 s for 30 min. These images were stored to a computer hard disk drive running custom image capture software operating as a plug-in from within the open-source ImageJ software package (developed at the United States National Institutes of Health by Wayne Rasband and available on the Internet at http://rsb.info.nih.gov/ij/). Exposure time for each image was typically 250 ms and the TIRF laser was shuttered with a Uniblitz (Rochester, NY) shutter between exposures to mitigate photodamage and photobleaching effects.
Image analysis
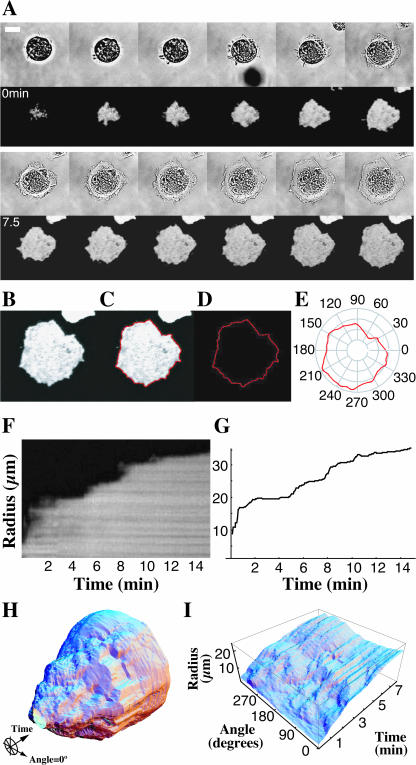
Cells were chosen for analysis if they initiated and completed spreading during the observation period of 30 min after plating. These cells were cropped from the full-size images (Fig. 1 A) and a median filter with a radius of 1 pixel was applied frame-by-frame to the images to reduce noise without altering the position of the cell edge (Yang and Huang, 1981). We extensively modified an existing open source Java image segmenter (source code available via the ImageJ website, see above) to process individual fluorescent TIRF images of a spreading cell (Fig. 1 B) resulting in a curve differentiating the edge of the cell from the background (Fig. 1 C).
FIGURE 1.
Computer visualization of spreading in space and time. A time-lapse series of bright-field (A, upper series) and total internal reflection fluorescence (TIRF) microscope images (A, lower series) of a calcein AM-loaded fibroblast spreading from suspension onto a fibronectin-coated substrate (scale bar = 20 μm, 75 s between frames, 15 min total length). Individual TIRF images (B) were analyzed via a program that found the border between fluorescent cell and background (C and D) and then expressed this border in polar coordinates (E). F shows the traditional method for measuring motility via a kymograph that gives a plot of radius as a function of time along a single line perpendicular to the cell edge. Our method reproduces data in this single spatial dimension (G). Our technique allows us to easily visualize the time course of cell spreading in two spatial dimensions by displaying the entire sequence in cylindrical coordinates with radius as a function of angle and time (H). To view spreading of an entire cell at the same time, we express radius as a function of angle and time in Cartesian coordinates (I).
Polar coordinate representation of cell edge
The cell outline (Fig. 1 D) was processed via a custom C program that calculated the distance from the centroid of the outline to the outline edge along rays pointing outwards at evenly spaced angles using a cubic spline interpolation package (Press, 1988; Fig. 1 E). We sampled 360 such rays for each outline, which gives a sampling resolution of 0.22 μm for a spreading cell with diameter of 25 μm whereas our pixel resolution was 0.33 μm. This process was repeated for each frame in the time-lapse sequence, using the centroid of the first outline in the sequence as the origin of the polar coordinate system to maintain a fixed reference frame throughout time. Choosing a coordinate system with a lab reference frame (defined by the origin of our polar coordinate system) allowed us to measure velocities relative to the cover glass, a measurement that would be nontrivial to make if, for example, we chose to parameterize the cell outline in terms of arc length. A significant drawback of choosing a polar coordinate system is that one cannot describe regions of the cell that double back on the outline because this creates multiple values for a single angle. Cell spreading data, however, lends itself to a polar coordinate description, since most motion is radial and most cell contours approximate a circle. To eliminate situations where the outlines did indeed produce multivalued functions of angle, we simply dropped all but the largest values for the distance to the outline at a given angle. Further visualization and analyses were carried out using Mathematica (Wolfram Research, Champaign, IL) software. By arranging successive outlines in a column (Fig. 1 H), we created a surface that shows all outlines for a particular time-sequence of spreading. To view the entire surface at once (as one uses a Mercator projection to observe the entire Earth at once), we plot the angle coordinate in a rectilinear coordinate system by cutting the surface and flattening it such that the z axis represents radius as a function of angle and time (Fig. 1 I).
It should be noted that our representation in Fig. 1 I distorts distances just as a Mercator projection of a globe distorts real distances on the surface of the resulting two-dimensional map. This effect is greatest at the poles, in our case corresponding to early spreading where the cell's radius is small. Thus, when interpreting spreading results in polar coordinates, one must be careful not to interpret angular separation with a measure of arc length along the cell edge. These two quantities are related simply by arc length = radius × angular separation, and when quantifying spreading behavior we use arc length as a measure of separation between two points. An additional technical consequence of this relation arises from the fact that, in this case where the number of sampling points in the angular coordinate is fixed, one will have a much higher sampling rate per pixel when the radius is small as compared to when the cell is large. Our image resolution is sufficiently high such that even for a cell with an area of 100 μm2, the smallest that we typically analyze, there will still be roughly 100 pixels in this outline and we will, at most, oversample 4:1 when using 360 divisions in our angular coordinate.
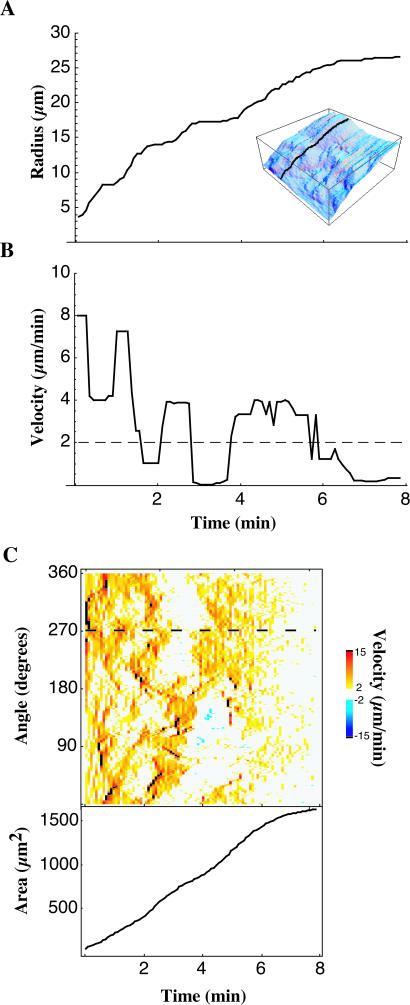
The value of the centroid/edge distance for a given angle over time (Fig. 2 A) details the dynamics of a particular ray (black line in Fig. 2 A, inset, shows the slice in angle taken). The derivative of radius with respect to time gives the velocity of the cell edge as a function of time (Fig. 2 B). We eliminated high frequency noise in velocity data by applying a moving median filter with a width of three frames to the velocity time-sequence at each angle.
FIGURE 2.
Spreading proceeds by stochastic, transient extension periods (STEPs). The early spreading of the lamellipodia is characterized by these STEPs, apparent when examining radius as a function of time along a given ray (A, inset indicates angle shown with respect to Fig. 1 I). STEPs are interspersed with periods of quiescence of the cell periphery. Edge velocity at a given time is measured by taking the derivative of radius with respect to time (B). Applying a threshold on the velocity (horizontal dashed line, B), individual STEPs can be isolated. In C, color codes for the velocity of a spreading cell (top) are shown along with the area of the cell (bottom). The horizontal dashed line in C shows the angle at which the radius versus time curve (A) and velocity versus time curve (B) are taken.
Cell area used to define time of active spreading
Cell areas were numerically calculated using the Gauss-Green formula (Wagon, 1999). By summing the areas of regions of the cell that extended (or retracted) with an above- (or below-) threshold radial velocity we calculated the thresholded area. By taking the percentage of total area that we accounted for after applying a given velocity threshold, we ensured that our analysis was indeed taking into account most of the activity of the cell. Our 2-μm/min threshold gave an average 85% of the total area being accounted for by above-threshold protrusions and retractions during spreading.
Because, in this study, we are interested in exploring primarily the dynamics of cells during spreading, we limited our quantitative analysis to the times during which the cells were actually spreading and did not include in our analysis the period of time leading up to spreading nor any activity such as polarization, migration, or quiescence that followed the cells reaching their fully spread state. To achieve this in a systematic way, we automatically limited our region of analysis with a simple algorithm. First, we only analyzed cells that could be followed through the entire course of spreading. Cells that were already partially spread at the start of measurement were excluded along with cells that interacted with other cells before they completed spreading or cells that did not complete spreading by the end of the sequence. Next, we recorded the maximum area to which the cell spread. We restricted our quantification of edge dynamics for a cell to the times during which its area was between 20% and 80% of its eventual maximum area. With the exception of measurements of spreading initiation, time 0 refers to the moment after spreading initiation at which the contact region of the cell was large enough to be tracked, normally corresponding to an area of 100 μm2.
STEP analysis and quantifying motility
After applying a threshold equal to the smallest observable velocity per frame (1 pixel/frame, shown as dashed line in Fig. 2 B) and encoding the velocity in color (Fig. 2 C), patterns of protrusion and retraction activity emerge. We consider these regions of the cell the active regions of protrusion and retraction. For some cells (anisotropic spreading cells) we were able to assign contiguous protrusive active regions to discrete groups called STEPs. We were able to characterize each STEP separately in terms of their average velocity, duration, length along the perimeter, and area change. Together, these quantities form a quantitative description of a cell's behavior.
More general analyses were used when exploring the behavior of isotropic cells or when comparing isotropic cells to anisotropic cells. Summing the contour length of active regions at a given time and dividing this sum by the total contour length of the cell at that time determined the percent of the cell edge active as a function of time. To measure the lifetimes of active regions of protrusion, we measured the lengths over which the velocity at a given angle remained above threshold. Fits to this data were made using Mathematica's Non-Linear Fit package.
We used autocorrelation functions to investigate spatial patterns in the velocity of spreading. Correlations were averaged over many cells to identify the presence of emerging patterns. We utilized a discrete autocorrelation function based on the fast Fourier transform (Eq. 1; Press, 1988) normalized for unity at zero-lag (Eq. 2):
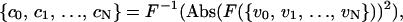 |
(1) |
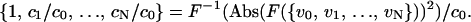 |
(2) |
Measure of spreading initiation
Cells plated for the spreading assay were generally surveyed 30 min after plating. The calcein AM-loaded cells as seen in bright-field and TIRF images captured at this time point were identified as either spread or not spread. Cells exhibiting a TIRF footprint >200 μm2 as measured using the techniques described above were considered to be spread. The number of spread cells was then compared against the total number of cells that appear in the bright-field images.
Analysis of α-actinin dynamics
The movement of GFP-labeled α-actinin during spreading was analyzed using a technique similar to fluorescence speckle microscopy as has previously been described (Waterman-Storer et al., 1998). Kymographs were constructed as described above and the slopes of fluorescent bands in these kymographs were measured and converted to corresponding velocities. The slope of the cell edge was measured from the same kymograph, allowing us to correlate cell edge dynamics with rearward movement of the cytoskeleton.
Statistical analysis
The statistical testing of distributions was performed using analysis of variance and Bonferroni post hoc tests with significance levels as indicated in text. Correlations were calculated using Spearman's Rank Correlation. All errors refer to the standard deviation of a distribution.
RESULTS
Contact area increases with time
Utilizing TIRF microscopy, we observed cell-substrate contact from the time of first contact with the surface. Spreading behavior after settling onto fibronectin-like (fibronectin fragment or a synthetic fibronectin molecule, pronectin) matrices depended upon the prior culture conditions of the cells; therefore the conditions were standardized. In these studies, mouse fibroblasts (NIH 3T3 and several primary and immortalized lines) were cultured to 70% confluence, released by 2 min trypsinization at 37°C, washed with media containing serum and incubated at 37°C with calcein AM to label the cytoplasm. No cytotoxic effect of calcein AM was observed based on cell morphology and spread area when compared to unlabeled controls, consistent with past use of this dye as a measure of cellular adhesion (Braut-Boucher et al., 1995; Goligorsky and DiBona, 1993). When labeled cells, resuspended in serum-free DMEM, contacted a fibronectin- or pronectin-coated surface at 37°C, they rapidly increased their area of contact with the surface (Fig. 1 A; see also Supplemental Materials for anisotropic cell movie). This rapid spreading was dependent upon fibronectin- or pronectin-coating of the cover glass: >80% of cells spread within 30 min at optimum ECM-coating concentrations for both fibronectin and pronectin. In contrast, uncoated hydrophobic surfaces (glass treated with HMDS; see Methods and Materials) or BSA-coated HMDS surfaces did not support spreading on the glass; <20% of cells spread in 1 h on BSA-coated substrates. We did, however, observe extensions of membrane processes above the BSA surface and the velocity of membrane protrusion was similar to that of cells on ECM-coated glass. These extensions were quickly retracted and did not contribute to a net increase in cell area. Thus, spreading involves a matrix-dependent signal that allows extensions to proceed along the surface.
Cell spreading is discontinuous
To quantify the spreading process, the digital TIRF images were analyzed to give a mathematical description of the cell periphery in polar coordinates (Fig. 1, B–E). A traditional kymograph (Fig. 1 F) reveals the edge at one point over time. Fig. 1 G is a similar plot of cell edge distance with respect to time except that this plot is calculated based on our computerized, polar coordinate representation of the cell. Both of these plots show the transient nature of extension events that most cells display and serve to introduce the concept of stochastic, transient, extension periods, or STEPs. We refer to this discontinuous mode of spreading as anisotropic spreading. To determine the global structure of these discontinuities, we used a technique that allows the entire cell edge to be analyzed at once, effectively giving a global, two-dimensional kymograph of the cell. The periphery of the spreading cell over time served as the initial numeric data for our analysis (Fig. 1, H and I). The radius of an individual angle over time (Fig. 2 A) illustrates that increases in radius over the course of spreading were separated by stationary periods. To calculate the velocity of protrusion, we determined the rate of radius change over time for a given angle (Fig. 2 B), as one would take the slope of features in a one-dimensional kymograph to measure velocity. The power of our technique is demonstrated when we look at the global pattern of spreading events by visualizing the velocity of the entire cell edge simultaneously. Using color to designate the velocity of extension, the radial edge velocity was plotted as a function of time and angle (Fig. 2 C). These velocity maps confirmed that cell spreading occurs discontinuously over the entire cell periphery and that this discontinuous behavior of STEPs is a global property of anisotropic spreading cells.
Matrix concentration affects the time of onset but not the rate of spreading
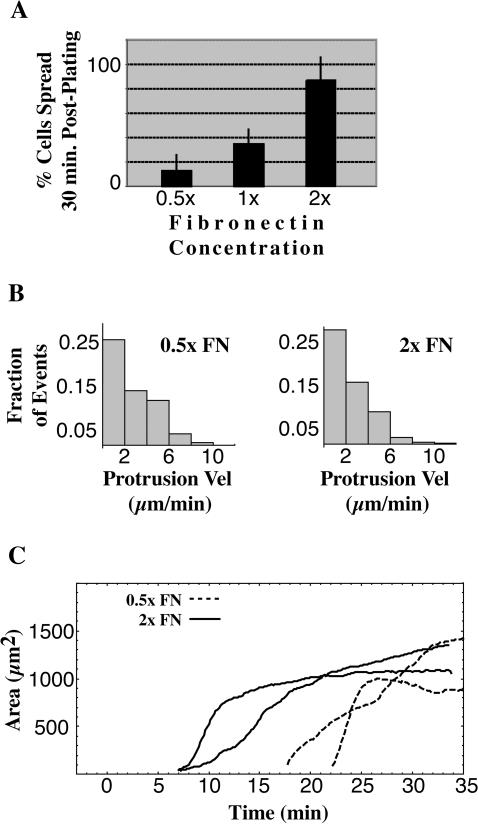
To determine the dependence of spreading on ECM density, we coated the glass with a range of fibronectin densities. There was an eightfold increase in the percentage of spread cells after 30 min with a fourfold increase in fibronectin-coating concentration (Fig. 3 A, n = 103 cells from three experiments at each condition, p < 0.05, Bonferroni post hoc test, all pairings significantly different). However, neither the velocity of edge protrusions (Fig. 3 B) nor rate of increase in contact area for individual cells (Fig. 3 C) correlated significantly with fibronectin concentration. Instead, the time of onset of spreading was dramatically delayed with decreasing concentration of ECM. In plots of spread area versus time, the delay in onset of spreading was ∼7 min at 2× concentration of fibronectin (Fig. 3 C, solid black lines) whereas the delay increased to ∼20 min at 0.5× (Fig. 3 C, dashed black lines). At both matrix concentrations, individual cells spread rapidly or slowly depending upon the cell state (Fig. 3 C, black solid and dashed curves; see below for description of slow, anisotropic versus fast, isotropic spreading). Thus, the major effect of ECM stimulation on spreading was not through changes in the rate of the spreading events but rather through a delay in spreading initiation.
FIGURE 3.
Fibronectin concentration modulates spreading initiation. The percent of spread cells at 30 min is an increasing function of fibronectin (FN) concentration up to a peak concentration (A, bars indicate SD). This increase in number of spread cells does not correlate with an increase in the velocity of protrusions of the spreading cells (B). This suggests that whereas FN catalyzes spreading initiation, it does not play a role in regulating the velocity of the spreading edge. The two representative cells spreading on 2× fibronectin (C, solid curves) and two representative cells on 0.5× fibronectin (C, dashed curves) show the time delay caused by decreasing fibronectin concentration.
Matrix binding is needed continuously
To determine if binding to a matrix-coated surface was continuously needed for spreading, we replaced the media with media containing high (0.1–1 mM) concentrations of a synthetic polypeptide with the amino acid sequence GRGDTP. This polypeptide competes with the RGD domains of fibronectin and binds to integrins with an affinity of 0.4 mM (Dedhar et al., 1987; Gehlsen et al., 1988). All cells stopped spreading within 3 min after exposure to 0.1 mM GRGDTP (n = nine cells, two repetitions) as compared to the continued spreading of all cells in the control where we simply replaced the media with new media (n = six cells, one repetition). At 1 mM of peptide, cessation of spreading was followed by a rapid loss of surface contacts and the cells retracted (n = five cells, one repetition). Thus, integrin-matrix bonds are highly dynamic and the continued binding of new matrix sites is required for continued spreading.
Isotropic versus anisotropic spreading
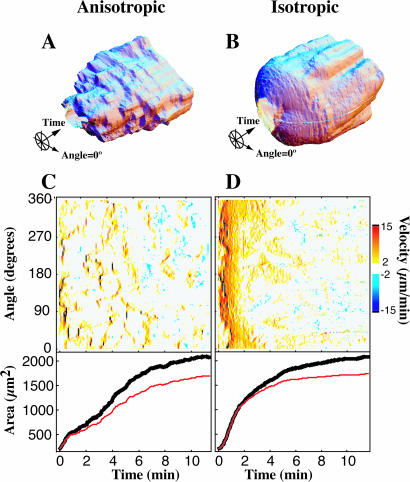
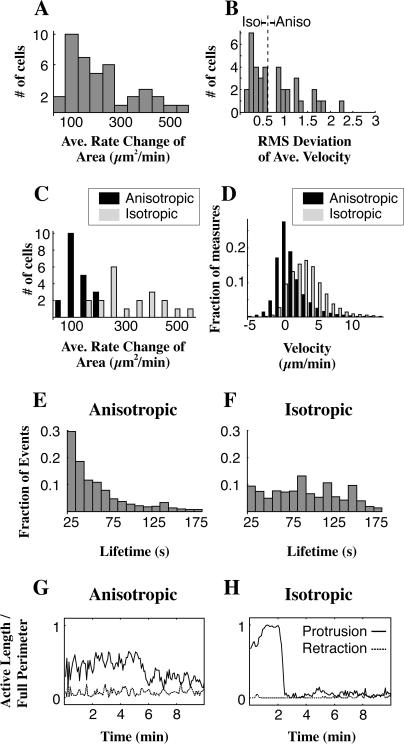
There were two modes of spreading, anisotropic (nonuniform, uneven) and isotropic (uniform, even). Radius versus time plots (Fig. 4, A and B) and velocity plots (Fig. 4, C and D, upper panel) show the discontinuous nature of anisotropic spreading compared with the continuous extension in isotropic spreading during the first minutes of spreading. The more rapid increase in area of isotropic versus anisotropic spreading is also evident from these representative cells (Fig. 4, C and D, lower panel). To explore the differences between these two spreading types while ensuring that we were comparing cells at the same point in the spreading process, we limited further analysis to a restricted window in time during which the cell completed the middle 60% of its area increase (see Methods and Materials). By focusing on the most active time of spreading, we were able to discern a bimodal distribution in the rate of change in total cell area during peak spreading (Fig. 5 A). The slower mode corresponded to cells that we had visually identified as anisotropic spreading cells and the faster mode corresponded to the cells identified as isotropic. However, a more general method of differentiating between isotropic and anisotropic spreading is to calculate the average root-mean squared (RMS) deviation of the velocity over all angles for a given time (Fig. 5 B). It is clear that a cell that spreads isotropically (by definition, equally in all directions at the same time) will have much lower variation in velocity with respect to angle than a cell that is extending in a directed manner, and the RMS deviation (Fig. 5 B) is simply a measure of this variation. We chose a cutoff RMS deviation of 0.6 μm2/min; if a cell's average RMS deviation during the middle 60% of spreading was <0.6 μm2/min it was classified isotropic, otherwise the cell was classified as anisotropic. Replotting the rate of change of area keyed for the isotropic and anisotropic populations (Fig. 5 C) reveals a satisfying separation between the two modes that we had originally observed, justifying the cutoff RMS deviation we chose. Isotropic cells increased their area >2.5 times faster at 340 ± 101 μm2/min than anisotropic at 126 ± 60 μm2/min (p < 0.001, n = 40 cells).
FIGURE 4.
Two modes of spreading: anisotropic and isotropic. Comparing the three-dimensional time plots of the spreading cell edge of a typical anisotropic spreading cell (A) versus a typical isotropic spreading cell (B) reveals spreading by STEPs throughout anisotropic spreading, although STEPs appear in the isotropic cell only after 2 min. Above-threshold edge velocities of the anisotropic (C, top) and isotropic cells (D, top) clearly display these two modes. Both cells reach the same total area (C and D, bottom, black curves) and the majority (>75%) of the spreading is accounted for by the above-threshold regions (C and D, bottom, red curves).
FIGURE 5.
Bimodal distribution of spreading characteristics. The rate of area change for a population of cells (A, n = 40) shows a bimodal distribution; we find two peaks in the distribution near 100 and at 400 μm2/min. The average root mean-squared (RMS) deviation of the velocity over angle for the same population of cells (B) reveals a cluster of values <0.6 μm/min. When cells are grouped based on the value of their RMS deviation, either above or below 0.6 μm/min (B, vertical dashed line shows cutoff at 0.6 μm/min), the rate change of area plot (C) is divided into the two separate modes that we observed. The distribution of the average velocities of the membranes of these cells (D) shows that anisotropic spreading cells are significantly shifted toward lower velocities when compared with the velocities of the edge in the isotropic spreading cells. Measuring the duration of continuous, above-threshold protrusive regions in a group of 20 anisotropic cells (E) reveals a fast decay in lifetimes of spreading events for anisotropic spreading cells that is fit well by an exponential decay. Duration measurement in 20 isotropic cells (F) reveals a much broader distribution caused by the 1- to 3-min-long burst of continuous spreading characteristic of isotropic spreading cells. The fraction of the edge protruding in a representative anisotropic cell (G, solid curve) lacks the early peak in protrusion activity seen in the isotropic cell (H, solid curve). In the anisotropic cell, retraction and quiescence of the cell edge is seen from the onset of spreading (G, dashed curve), whereas for the representative isotropic spreading cell there is little detectable retraction of the cell edge until 6 min after the onset of spreading (H, dashed curve). Activity is measured as the quotient of the contour length of above-threshold regions along the edge and the total contour length along the edge.
To further quantify the differences between the two modes, we measured velocity, duration, and arc length of protruding motile regions. We found that increased velocity, a longer persistence of protrusions, and a higher total length of edge extension combined with a general lack of retraction, all contributed to isotropic spreading cells' faster rates of area increase. We measured an average protrusion velocity of 4.2 ± 1.7 μm/min for isotropic versus 2.3 ± 1 μm/min for anisotropic (p < 0.001, n = 40, velocity distributions shown in Fig. 5 D).
When we analyzed the lifetimes of extension events for both spreading modes, anisotropic cells (Fig. 5 E, 20 cells) showed a steeply decreasing distribution whereas isotropic cells (Fig. 5 F, 20 cells) displayed a high number of extensions in the 40–180 s range. The distribution of lifetimes of active regions (see Methods and Materials) in anisotropic spreading cells is described by a mean lifetime of 33 s and exhibits sharp dropoff with an exponential decay constant of 26 ± 6 s (95% confidence interval, the domain of the fit was limited to 25 s < duration < 180 s). In contrast, the mean lifetime of events for isotropic spreading cells is 111 s and this population exhibits a broader distribution of event durations, with many events lasting as long as 1–3 min. These longer persistence times correspond to the sustained period of high velocity spreading associated with early isotropic spreading. After their early rapid spreading phase, however, isotropic cells showed a steep decay in extension lifetime at later times and became similar to the distribution for the anisotropic population of spreading cells.
Finally, there was a lower fraction of the edge extending at a given time in anisotropic cells, on average 34% ± 16% for early anisotropic versus 78% ± 20% for early isotropic spreading cells (p < 0.001, n = 40, representative examples in Fig. 5, G and H, solid curves). Though low in both cases, retractions were also significantly different between the two cell types in terms of the percent of active edge with 0.0% ± 0.5% in isotropic cells retracting on average as compared to 2% ± 3% in anisotropic spreading cells (p < 0.001, n = 40, representative examples in Fig. 5 G and H, dashed curves). Interestingly, the average velocities of retractions were statistically indistinguishable from one another, both being near −0.8 μm/min. However, retraction events may have been too slow to be efficiently detected with our resolution.
Bright-field images (data not shown) revealed further differences, showing a total lack of membrane ruffles during isotropic spreading as well as no new formation of filopodia, whereas anisotropic cells demonstrated membrane ruffles and filopodia formation throughout spreading. Thus, the characteristics of isotropic spreading are easily differentiable from those associated with anisotropic spreading both by edge dynamics and the overall characteristics of the cell.
In most cell populations, there was a mixture of cells spreading in the isotropic and anisotropic modes; indeed, individual cells displayed mixtures of anisotropic and isotropic spreading phenotypes. These mixed cells could spread in what resembled an isotropic fashion in one section while at the same time in another region exhibit anisotropic spreading. Another mixed phenotype was observed when a cell would begin spreading in an anisotropic manner and then suddenly transition to an isotropic spreading state, its lamellipodia free of ruffles and extending beyond nascent filopodia. These mixed populations contributed to middle values in the measure of RMS deviation, and these cells were the most difficult to classify in terms of this measure.
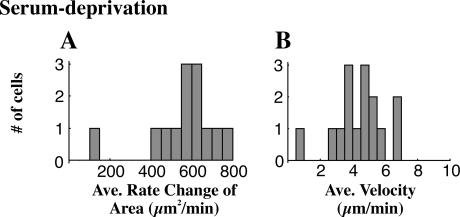
In populations grown with normal serum levels (10% calf serum), 50% of the cells spread in a purely anisotropic manner, whereas 30% spread displaying some of both phenotypes and 20% of cells spread purely in the isotropic mode (n = 33 cells). Serum deprivation caused the fraction of purely isotropic cells to increase with >70% of cells spreading in the isotropic mode after 48 h of starvation (two experiments, n = 44 cells, p < 0.05). Indeed, these cells exhibited a higher level of isotropism than isotropic cells in serum-fed samples, with an average RMS deviation of only 0.25 ± 0.15 μm/min as compared to isotropic serum-fed cells that exhibited an RMS deviation of 0.34 ± 0.14 μm/min or anisotropic serum-fed cells with an average RMS deviation of 1.9 ± 1.8 μm/min (p < 0.05, all pairings significantly different). In addition, the average rate of area change was high compared to serum-fed isotropic cells, 662 ± 111 μm2/min (Fig. 6 A). This increased rate was partially due to the more consistent isotropic extension and partly due to a higher velocity of protrusion (4.7 ± 1.2 μm/min, Fig. 6 B).
FIGURE 6.
Serum deprivation promotes isotropic spreading. Serum deprivation induces the population to behave isotropically in terms of the rate of area change (A, notice peak at 600, mean of 15 cells) although this population shows only a slight shift in its velocity as seen in a histogram of average velocities for each cell (B, mean of 15 cells).
Once isotropic cells were nearly spread, they displayed behavior similar to anisotropic spreading cells. The periphery became uneven, extension events were limited in size and duration, and edge retraction and ruffling was observed. At late times both isotropic and anisotropic spreading cells had similar morphologies and spread areas, and no significant difference between the final spread areas of the two modes was observed.
Finally, both modes of spreading behaved similarly with respect to the effect of matrix concentration: at all matrix concentrations we tested there was a similar delay for both isotropic and anisotropic spreading cells. However, once they initiated spreading, both spread at their normal rates (Fig. 3 C).
Extension events are stochastically distributed in anisotropic cells
The spreading patterns of normal, anisotropic cells were composed of many separate extension and retraction events (see Fig. 2 C, 4 A, and 7 A, as well as http://sheetzlab.bio.columbia.edu for unpublished data). We defined discrete events of extension in time and space as STEPs (stochastic, transient extension periods; see Methods and Materials). We found 33 ± 21 individual STEPs during spreading in anisotropic cells (n = 21 cells) with a STEP being classified as a region of contiguous, above-threshold protrusion. The number of STEPs was confirmed through visual examination since in many instances it was impossible for the computer to differentiate what were visually distinct STEPs due to the overlapping of activity. Over 21 cells, we measured an average extent of protrusion along the perimeter of the cell of 2.5 ± 2.7 μm. We found no significant correlation between the STEP extent and time after spreading initiation. Our quantification of STEPs was limited by the inability of the computer to separately analyze what were, to the eye, distinct protrusion events.
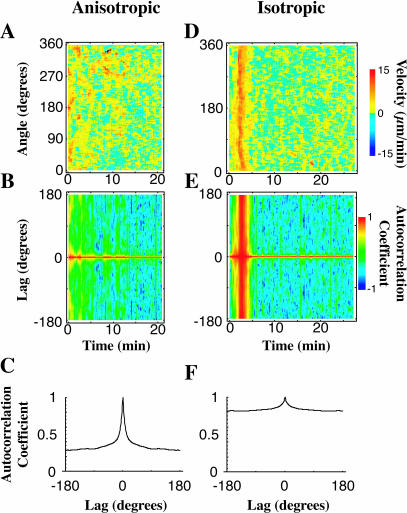
FIGURE 7.
Cross-correlation analysis suggests the stochastic nature of spreading. A velocity map for an anisotropic cell displays distinct regions of protrusion activity (A). Angular correlations of velocity at a given time (B) reveal favored angles (positive correlation) or disfavored angles (negative correlation) between regions of similar activity. Although peaks are often revealed for individual cells, the average of the autocorrelation functions for the initial spreading of 20 anisotropic cells (C) shows no discernable correlation length apart from 0 lag. Thus we surmise that protrusion initiation is randomized in space and is the result of a stochastic process. An isotropic cell's velocity map (D) exhibits a characteristic high velocity, 3-min-long isotropic expansion of the membrane onto the substrate. The corresponding autocorrelation map (E) of this cell shows a band of high correlation coinciding with the isotropic expansion. Uniformly high autocorrelation is simply a restatement of the definition of isotropism—the cell's movement is the same (is highly correlated) in all directions at the same time. An average of the autocorrelation functions of the initial spreading regions of 20 isotropic cells (F) shows no preferred angle of correlation in the population but tells us that the overall correlation is large.
To investigate whether there was an angular correlation in activity in anisotropic extensions, we looked at the autocorrelation of velocity with respect to a lag in angle for a given time during spreading. Anisotropic cells extend in several directions at a time via STEPS, as is evident in velocity plots of their spreading activity (Fig. 7 A). An autocorrelation map of the cell (Fig. 7 B) shows transient peaks, simply giving the angle between the dominant STEPs at that frame. By averaging the autocorrelation function during spreading for an individual cell and then averaging an ensemble of these average autocorrelations, we see that there are no peaks indicating preferred angles between STEP initiation at a given time (Fig. 7 C, average over 20 cells). The rapid decay of the autocorrelations (∼10° for 50% decrease) further indicates that the regions of correlated spreading were not large. The autocorrelations did not decay to zero because there was very little retraction. This supports the hypothesis that the initiation of STEPs around the cell during spreading is a random-event-driven process, or, in another word, is stochastic.
The velocity map of a highly isotropic spreading cell (Fig. 7 D) has a region of high angular correlation (Fig. 7 E) that corresponds perfectly in time with the highly isotropic times. This is as expected since high angular correlation is essentially just a restatement of the definition for isotropic. After averaging, isotropic cells continue to show a peakless angular correlation function (Fig. 7 F, n = 20 cells) during isotropic expansion, confirming that there is no preferred direction of spreading in isotropic cells.
Actin filament centripetal flow is greatest in anisotropic and late isotropic spreading
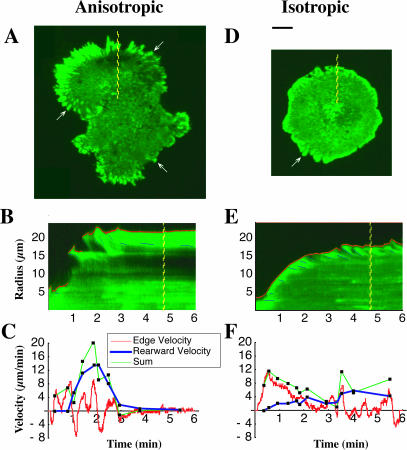
Breaks in extension could be caused either by the cessation of polymerization or by increased centripetal flow of actin filaments. To determine if breaks in edge extension were correlated with an increase in the velocity of actin rearward transport, we analyzed the rearward movement of aggregates of GFP-tagged α-actinin in isotropic and anisotropic cells (Fig. 8, A and D). The α-actinin is used as a marker for focal contact formation as well as for actin fibers (Edlund et al., 2001). During early isotropic spreading (50–1000 μm2 of contact area, 0–2 min), the velocity of rearward movement of actin was low (Fig. 8, E and F, show a representative time course; 0.8 ± 0.5 μm/min, average of 12 measurements from three cells) and the formation of focal contacts was absent. As the isotropic cell approached maximal area (2–5 min), α-actinin retraction rates increased nearly sixfold (4.7 ± 2.2 μm/min, average of 14 measurements from three different cells, p < 0.001 between early and late isotropic retraction rates) and stable (persisting >1 min) focal contacts formed (Fig. 8 D). In contrast, anisotropic cells displayed α-actinin retraction rates at the start of spreading that were indistinguishable from those at later times (Fig. 8, B and C, show a representative time course; 4.5 ± 1.3 μm/min for the first 2 min of spreading, 4.4 ± 1.2 μm/min for the last 2 min of spreading, average of 14 measurements from four cells, p = 0.78, F = 0.08). Furthermore, anisotropic cells form focal contacts from the beginning of spreading (data not shown). In anisotropic spreading, large regions of the edge were inactive, showing neither actin filament retraction nor edge extension.
FIGURE 8.
Low actin rearward movement in isotropic spreading cells. Time-lapse TIRF microscopy of the spreading of transiently transfected GFP α-actinin-labeled cells revealed further information regarding the nature of the difference between anisotropic (A–C) and isotropic (D–F) cells. As an indicator of focal contacts, α-actinin labeling shows that in anisotropic spreading cells (A, arrows), focal contacts matured more quickly than in isotropic cells (D, arrow). GFP α-actinin is also used as an indicator of the rearward movement of the actin cytoskeleton. Using kymographs (time-space plots in which the spatial axis is perpendicular to the cell's edge) of fluorescent time-lapse sequences for both anisotropic (B) and isotropic (E) cells, we computed the velocity of the rearward movement of α-actinin, the edge velocity, and the sum of the two in anisotropic spreading (C) and isotropic spreading (F). Rearward movement in anisotropic cells (C, blue curve) was much higher at early times compared to that of isotropic spreading cells (F, blue curve).
In late isotropic spreading cells (t > 3 min), breaks in fast, isotropic extension and the transition to anisotropic spreading correlated with an increase in rearward transport of actin filaments. In anisotropic cells, actin filament retraction was observed in most protrusions and these cells transitioned more quickly than isotropic cells into a state characterized by stable focal adhesions and a quiescent cell margin (Fig. 8 A). Anisotropic motility was always concomitant with the centripetal flow of actin filaments.
Cell migration seen as directed anisotropic motility and retractions
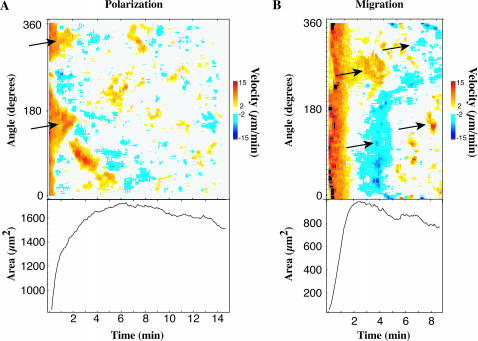
When cells were observed for longer periods, they would often polarize and/or start to migrate across the surface. Isotropic cells polarized as exhibited by extension and retraction on opposite sides of the cell (Fig. 9 A, arrows indicate regions of extension leading to polarization). Lamellipodial velocities could also be tracked during cell migration (Fig. 9 B). In migrating cells, STEPs and, in some cases, more broad extensions were concentrated on one side of the cell (Fig. 9 B, 2–8 min). Retraction of the edge (blue regions) occurred on the other side of the cell such that the spread area stayed roughly constant. Often there was a slight decrease in spread area as the cell polarized (Fig. 9 A, bottom) and migrated (Fig. 9 B, bottom) and the area fluctuated since STEPs were not always coincident with retraction events. Both of these examples exhibit how subsequent motility processes can be based on STEPs.
FIGURE 9.
Quantitative view of migration and polarization. Our quantitative measure of cell edge movement is applicable to motility generally and not just cell spreading. Cells were often seen to polarize after spreading and this polarization can be seen clearly in a velocity plot (A, top, arrows) as protrusions occurring on opposite sides of the cell, and proceeded in moving via STEP-based motility. Some cells were observed to migrate soon after spreading (B, left two arrows), indicated by retracting regions of the cell 180° away from the protruding region of the cell as seen in a velocity plot for such a cell. This cell quickly began migrating in the opposite direction via STEPs (B, right two arrows). Cell area often decreased after the cell reached its fully spread area and polarized (A, bottom) or migrated (B, bottom). Both A and B show examples of how cells, including isotropic cells, eventually display STEPs in later motility processes.
DISCUSSION
We have found that cell spreading can be classified into two distinct modes, isotropic or anisotropic. Isotropic spreading is promoted in serum-deprived populations and protrusions occur over a large, continuous segment of the cell edge, giving the appearance of pancake batter spreading on a griddle. During this rapid spreading phase, cells exhibited little or no rearward actin flow, filopodia formation, ruffling, or retraction of the lamellipodia. As isotropic spreading cells approached their maximal area, actin retraction rates increased, the fraction of the edge that was extending decreased, and the periphery demonstrated increased ruffling and retraction. Other cells from the same population spread in a slower, anisotropic mode, exhibiting filopodial protrusions, greater membrane ruffling, edge retraction, and centripetal flow of actin filaments. These differences were not due to different cell types; a population of cells could switch from primarily anisotropic to primarily isotropic spreading upon serum deprivation. At later times all cells were observed to move in an anisotropic manner via STEPs.
Relevance of ECM in cell spreading
Ligand concentration, either fibronectin or pronectin, correlates with the fraction of spread cells at early times. Protrusion velocities during spreading, however, were not correlated with ligand concentration. Instead, the length of the time lag between contact with the ECM and spreading initiation were inversely related to ECM concentration.
Spreading requires continued integrin binding. After initiation of spreading, blocking integrin binding with soluble RGD arrested spreading within 2 min for both isotropic and anisotropic spreading cells. It follows that spreading requires the continued integrin signaling from the substrate, which stimulates further extension events. In anisotropic spreading, when STEPs turn off, matrix binding is critical for initiating the next STEP. Thus, once a cell initiates spreading, binding of an above-threshold number of integrins to new matrix sites sustains spreading. Above the threshold binding level, however, the rate of spreading is independent of number of ligand-bound integrins and is instead dependent on the cell's state, either isotropic or anisotropic.
Together these two pieces of evidence suggest that spreading initiation is a type of cellular phase change, with the cell requiring a certain threshold of an ECM-dependent signal after which its dynamic state is radically altered. Such changes have been theoretically predicted for bundles of polar filaments (Kruse et al., 2001) and these considerations may extend to the polar actin bundles found in the lamellipodia. After this phase change, integrin binding to ligand simply sustains the change but does nothing to alter the dynamics (i.e., the velocity) of spreading. For cells to follow gradients of bound ECM, this model suggests that the cell would sense the differential and not the absolute level of bound ECM.
Isotropic versus anisotropic spreading
We propose that the highly activated state of spreading corresponds to activation of the signaling pathways leading to activation of motility. Serum deprivation withdraws from the cell a variety of receptor ligands such as growth factors and soluble matrix molecules. In the transition to the STEP-based motility after the initial first phase of fast spreading in isotropic cells, we suggest that these signaling pathways, after 1–3 min of rapid spreading, enter a refractory period.
Anisotropic spreading has many characteristics of general cell migration and motility as evidenced by the rapid actin filament retraction rates, limited extension areas, and the development of α-actinin containing focal contacts. Myosin-dependent filament retraction and force generation may be a major signal for the stabilization of the spread state through focal contact formation, which is consistent with other effects of force in stabilizing cell-matrix contacts (Choquet et al., 1997; Liang et al., 2002; Riveline et al., 2001; Wang et al., 1993) and the subsequent loss of spreading on substrates that do not support force generation (Pelham and Wang, 1997). In summary, both the stochastic nature of the initiation of extensions and their limited lifetimes are consistent with cell migration (Hinz et al., 1999).
In isotropic spreading, retraction of α-actinin is limited until cells are over half spread. With the activation of actin centripetal flow, isotropic cells begin irregular extension and transition into STEPs, and can polarize and generate longer-lived focal complexes in the periphery. Thus, actin filament retraction is a consistent feature of anisotropic and late isotropic spreading and may contribute to the activation of further spreading by the generation of force on integrin-cytoskeleton linkages.
STEP duration
Distinct extension events (STEPs) form the basis of anisotropic spreading and are observed in all migrating cells (even fish keratocytes show limited extensions lasting 10–20 s; M. P. Sheetz, unpublished results). We observed that the speed of rearward movement and the speed of edge protrusion do not sum to a constant value, implying that actin polymerization at the leading edge is not constant through time. This assumes the membrane edge is tightly coupled to the actin filaments (no blebbing) and thus the speed of protrusion is given by the difference in the speed of actin tip polymerization and the speed of rearward actin movement. Evidence for this nonblebbing model of fibroblast motility has been seen in migrating 3t3 fibroblast cells (Rotsch et al., 1999). Given this model, after the initiation of a STEP, there are two potential mechanisms to arrest extension; either actin polymerization stops or the rate of actin retraction is equal to or greater than the rate of actin polymerization. In anisotropic spreading cells, large regions of the cell edge are inactive with no extension or retraction. In active lamellipodia, extensions can slow or stop for brief periods due to an increase in the rate of retraction. All STEPs have relatively short durations given by a half-life on the order of 25 s for anisotropic and late isotropic cells. The exponential decay of the lifetime of STEPs suggests regulation by a first order process such as in the random initiation of a retraction event caused by the decay of substrate-enzyme complex, e.g., a small G-protein with bound GTP, although several other mechanisms could give similar kinetics. We suggest STEPs are internally controlled after initiation. Similar STEP behavior in migrating cells is sensitive to actin-binding proteins like Ena/VASP (Bear et al., 2002) and growth factors affect the frequency of activation of protrusions in keratinocytes (Galiacy et al., 2003).
Relevance to cell migration and other motility processes
The primary difference between spreading and migration is the polarization of extension and retraction events. After initial spreading, some cells in these studies have migrated when STEPs are polarized to one side and retractions to the other side of the cell. Therefore, we suggest that the STEP constitutes a basic unit of extension in both spreading and migration. In contrast, isotropic spreading appears similar to hormone activation of motility since both demonstrate acute phases of activity that last for 1–2 min (Bailly et al., 1998) and turn off as the pathway enters a refractory period. The integrated motility of anisotropic cells is the result of the combination of many small STEPs and retractions. Cell motility is not continuous but rather it involves many distinct events that are independently initiated.
The coordination of a 3-μm-wide STEP would involve >750 growing actin filament ends (Abraham et al., 1999), presumably supported by a local increase in Arp2/3 as well as a local increase in the concentration of G-actin, relying on a complex signaling network for regulation (Pollard and Borisy, 2003). Further studies using this system of spreading and quantitative analysis (Giannone et al., 2004) will aid in understanding the dynamics of the proteins involved in the regulation of spreading dynamics.
SUPPLEMENTAL MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
The authors acknowledge Jana Gruenewald and Mike Castleman for modifying the ImageJ ImageSegmenter Java plug-in, Mike Lehman for modifying our camera acquisition software, and Adam Meshel for valuable input and proofreading of the manuscript.
Funding for this study was provided by the National Institutes for Health and by Columbia University Startup monies.
References
- Abraham, V. C., V. Krishnamurthi, D. L. Taylor, and F. Lanni. 1999. The actin-based nanomachine at the leading edge of migrating cells. Biophys. J. 77:1721–1732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aplin, A. E., B. P. Hogan, J. Tomeu, and R. L. Juliano. 2002. Cell adhesion differentially regulates the nucleocytoplasmic distribution of active MAP kinases. J. Cell Sci. 115:2781–2790. [DOI] [PubMed] [Google Scholar]
- Axelrod, D., N. L. Thompson, and T. P. Burghardt. 1983. Total internal inflection fluorescent microscopy. J. Microsc. 129:19–28. [DOI] [PubMed] [Google Scholar]
- Bailly, M., J. S. Condeelis, and J. E. Segall. 1998. Chemoattractant-induced lamellipod extension. Microsc. Res. Tech. 43:433–443. [DOI] [PubMed] [Google Scholar]
- Bear, J. E., T. M. Svitkina, M. Krause, D. A. Schafer, J. J. Loureiro, G. A. Strasser, I. V. Maly, O. Y. Chaga, J. A. Cooper, G. G. Borisy, and F. B. Gertler. 2002. Antagonism between Ena/VASP proteins and actin filament capping regulates fibroblast motility. Cell. 109:509–521. [DOI] [PubMed] [Google Scholar]
- Braut-Boucher, F., J. Pichon, P. Rat, M. Adolphe, M. Aubery, and J. Font. 1995. A non-isotopic, highly sensitive, fluorimetric, cell-cell adhesion microplate assay using calcein AM-labeled lymphocytes. J. Immunol. Methods. 178:41–51. [DOI] [PubMed] [Google Scholar]
- Choquet, D., D. P. Felsenfeld, and M. P. Sheetz. 1997. Extracellular matrix rigidity causes strengthening of integrin-cytoskeleton linkages. Cell. 88:39–48. [DOI] [PubMed] [Google Scholar]
- Cunningham, C. C., R. Vegners, R. Bucki, M. Funaki, N. Korde, J. H. Hartwig, T. P. Stossel, and P. A. Janmey. 2001. Cell permeant polyphosphoinositide-binding peptides that block cell motility and actin assembly. J. Biol. Chem. 276:43390–43399. [DOI] [PubMed] [Google Scholar]
- Dedhar, S., E. Ruoslahti, and M. D. Pierschbacher. 1987. A cell surface receptor complex for collagen type I recognizes the Arg-Gly-Asp sequence. J. Cell Biol. 104:585–593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunn, G. A., and A. F. Brown. 1987. A unified approach to analysing cell motility. J. Cell Sci. Suppl. 8:81–102. [DOI] [PubMed] [Google Scholar]
- Dunn, G. A., D. Zicha, and P. E. Fraylich. 1997. Rapid, microtubule-dependent fluctuations of the cell margin. J. Cell Sci. 110:3091–3098. [DOI] [PubMed] [Google Scholar]
- Edlund, M., M. A. Lotano, and C. A. Otey. 2001. Dynamics of α-actinin in focal adhesions and stress fibers visualized with α-actinin-green fluorescent protein. Cell Motil. Cytoskeleton. 48:190–200. [DOI] [PubMed] [Google Scholar]
- Felder, S., and E. L. Elson. 1990. Mechanics of fibroblast locomotion: quantitative analysis of forces and motions at the leading lamellas of fibroblasts. J. Cell Biol. 111:2513–2526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galbraith, C. G., K. M. Yamada, and M. P. Sheetz. 2002. The relationship between force and focal complex development. J. Cell Biol. 159:695–705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galiacy, S., E. Planus, H. Lepetit, S. Fereol, V. Laurent, L. Ware, D. Isabey, M. Matthay, A. Harf, and M. P. d'Ortho. 2003. Keratinocyte growth factor promotes cell motility during alveolar epithelial repair in vitro. Exp. Cell Res. 283:215–229. [DOI] [PubMed] [Google Scholar]
- Gehlsen, K. R., W. S. Argraves, M. D. Pierschbacher, and E. Ruoslahti. 1988. Inhibition of in vitro tumor cell invasion by Arg-Gly-Asp-containing synthetic peptides. J. Cell Biol. 106:925–930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geiger, B., A. Bershadsky, R. Pankov, and K. M. Yamada. 2001. Transmembrane crosstalk between the extracellular matrix–cytoskeleton crosstalk. Nat. Rev. Mol. Cell Biol. 2:793–805. [DOI] [PubMed] [Google Scholar]
- Giannone G., B. J. Dubin-Thaler, H. G. Döbereiner, N. Kieffer, A. R. Bresnick and M. P. Sheetz. 2004. Periodic lamellipodial contractions correlate with rearward actin waves. Cell. 116. [DOI] [PubMed]
- Goligorsky, M. S., and G. F. DiBona. 1993. Pathogenetic role of Arg-Gly-Asp-recognizing integrins in acute renal failure. Proc. Natl. Acad. Sci. USA. 90:5700–5704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groth, T., and G. Altankov. 1996. Studies on cell-biomaterial interaction: role of tyrosine phosphorylation during fibroblast spreading on surfaces varying in wettability. Biomaterials. 17:1227–1234. [DOI] [PubMed] [Google Scholar]
- Gumbiner, B. M. 1996. Cell adhesion: the molecular basis of tissue architecture and morphogenesis. Cell. 84:345–357. [DOI] [PubMed] [Google Scholar]
- Hinz, B., W. Alt, C. Johnen, V. Herzog, and H. W. Kaiser. 1999. Quantifying lamella dynamics of cultured cells by SACED, a new computer-assisted motion analysis. Exp. Cell Res. 251:234–243. [DOI] [PubMed] [Google Scholar]
- Kruse, K., S. Camalet, and F. Julicher. 2001. Self-propagating patterns in active filament bundles. Phys. Rev. Lett. 87:138101. [DOI] [PubMed] [Google Scholar]
- Liang, W., L. Licate, H. Warrick, J. Spudich, and T. Egelhoff. 2002. Differential localization in cells of myosin II heavy chain kinases during cytokinesis and polarized migration. BMC Cell Biol. 3:19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maheshwari, G., G. Brown, D. A. Lauffenburger, A. Wells, and L. G. Griffith. 2000. Cell adhesion and motility depend on nanoscale RGD clustering. J. Cell Sci. 113:1677–1686. [DOI] [PubMed] [Google Scholar]
- Omelchenko, T., J. M. Vasiliev, I. M. Gelfand, H. H. Feder, and E. M. Bonder. 2002. Mechanisms of polarization of the shape of fibroblasts and epitheliocytes: separation of the roles of microtubules and ρ-dependent actin-myosin contractility. Proc. Natl. Acad. Sci. USA. 99:10452–10457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker, K. K., A. L. Brock, C. Brangwynne, R. J. Mannix, N. Wang, E. Ostuni, N. A. Geisse, J. C. Adams, G. M. Whitesides, and D. E. Ingber. 2002. Directional control of lamellipodia extension by constraining cell shape and orienting cell tractional forces. FASEB J. 16:1195–1204. [DOI] [PubMed] [Google Scholar]
- Pelham, R. J., Jr., and Y. Wang. 1997. Cell locomotion and focal adhesions are regulated by substrate flexibility. Proc. Natl. Acad. Sci. USA. 94:13661–13665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollard, T. D., and G. G. Borisy. 2003. Cellular motility driven by assembly and disassembly of actin filaments. Cell. 112:453–465. [DOI] [PubMed] [Google Scholar]
- Potter, D. A., J. S. Tirnauer, R. Janssen, D. E. Croall, C. N. Hughes, K. A. Fiacco, J. W. Mier, M. Maki, and I. M. Herman. 1998. Calpain regulates actin remodeling during cell spreading. J. Cell Biol. 141:647–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press, W. H. 1988. Numerical Recipes in C: The Art of Scientific Computing. Cambridge University Press, New York, Cambridge, UK.
- Riveline, D., E. Zamir, N. Q. Balaban, U. S. Schwarz, T. Ishizaki, S. Narumiya, Z. Kam, B. Geiger, and A. D. Bershadsky. 2001. Focal contacts as mechanosensors: externally applied local mechanical force induces growth of focal contacts by an mDia1-dependent and ROCK-independent mechanism. J. Cell Biol. 153:1175–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rotsch, C., K. Jacobson, and M. Radmacher. 1999. Dimensional and mechanical dynamics of active and stable edges in motile fibroblasts investigated by using atomic force microscopy. Proc. Natl. Acad. Sci. USA. 96:921–926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz, M. A., and M. H. Ginsberg. 2002. Networks and crosstalk: integrin signalling spreads. Nat. Cell Biol. 4:E65–E68. [DOI] [PubMed] [Google Scholar]
- Soll, D. R. 1988. DMS, a computer-assisted system for quantitating motility, the dynamics of cytoplasmic flow, and pseudopod formation: its application to Dictyostelium chemotaxis. Cell Motil. Cytoskeleton. 10:91–106. [DOI] [PubMed] [Google Scholar]
- Soll, D. R. 1995. The use of computers in understanding how animal cells crawl. Int. Rev. Cytol. 163:43–104. [PubMed] [Google Scholar]
- Wagon, S. 1999. MATHEMATICA in Action. Springer-TELOS, New York.
- Wang, N., J. P. Butler, and D. E. Ingber. 1993. Mechanotransduction across the cell surface and through the cytoskeleton. Science. 260:1124–1127. [DOI] [PubMed] [Google Scholar]
- Waterman-Storer, C. M., A. Desai, J. C. Bulinski, and E. D. Salmon. 1998. Fluorescent speckle microscopy, a method to visualize the dynamics of protein assemblies in living cells. Curr. Biol. 8:1227–1230. [DOI] [PubMed] [Google Scholar]
- Yang, G. J., and T. S. Huang. 1981. Effect of median filtering on edge location estimation. Comp. Graphics Image Proc. 15:224–245. [Google Scholar]