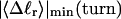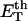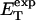Monte Carlo Simulations of Locally Melted Supercoiled DNAs in 20 mM Ionic Strength

Abstract

Mesoscopic models of unmelted and locally melted supercoiled DNAs in 20 mM ionic strength are simulated over a range of linking difference from Δℓ = 0 to −26 turns, or superhelix density from σ = 0 to −0.062. A domain containing m = 0, 28, or 56 melted basepairs (out of 4349 total) is modeled simply by a region of suitable length with substantially reduced torsion and bending elastic constants. Average structural properties are calculated from the saved configurations, and a reversible work protocol is used to calculate the supercoiling free energy, 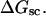The cross-writhe between duplex and melted regions (defined herein) is found to be negligibly small. The total writhe, radius of gyration, and ordered elements of the diagonalized inertial tensor are found to be nearly universal functions of the residual linking difference (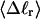) associated with the duplex region, independent of m. However, deformability of the tertiary structure, as manifested by the variance of those same properties, is not a universal function of 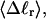but depends upon m. 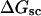varies with 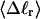more strongly than 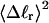due to the low ionic strength. The twist energy parameter, 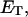obtained from the simulated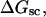 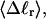and net twisting strain of the melted region, 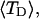is found to be independent of m, hence also of the torsion and bending elastic constants of the melted region. However, 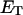increases linearly with 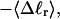which leads to 1), a small overestimation of 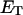for any giv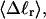en when 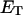is determined from the observe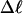d and 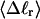by the protocol of Bauer and Benham; and 2), a significant enhancement of the apparent slope, 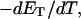obtained via the protocol of Bauer and Benham, relative to the actual slope at fixed 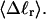After taking these two effects into account, the theoretical and experimental 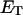values and 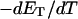values agree rather well. For the larger 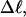the melted regions are found preferentially in the linker domains between interwound arms, rather than in the apical regions at the ends of interwound arms.

INTRODUCTION

Negative supercoiling generally raises the free energy of a duplex circular DNA relative to that of its melted intertwined single strands. In sufficiently low ionic strength (≲20 mM) at 37°C, supercoiled DNAs with sufficient superhelix density (σ) in the range 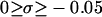(native) will locally melt to an extent that depends upon the sequence (Benham, 1990, 1992; Bauer and Benham, 1993; Bauer et al., 1995). Even at higher, more physiological ionic strengths, where stable local melting is not observed up to native superhelix density (−0.05) (Kowalski et al., 1988), the free energy change required to locally melt the DNA is substantially reduced. This supercoiling-induced destabilization of duplex with respect to local melting has been suggested to facilitate certain biological processes, wherein melted regions are involved, such as the initiation of transcription, replication, and recombination (Benham, 1990; Bauer and Benham, 1993; Bauer et al., 1995; Sheridan et al., 1998).

A quantitative understanding of supercoiling-induced local melting requires knowledge of 1), the decrease (ΔΔG_sc)in deformational supercoiling free energy (ΔG_sc) upon melting a sequence of m basepairs, which depends upon the unknown effective elastic constants for torsion and bending of the melted regions, and 2), the free energy increase upon melting m basepairs far below their normal melting temperature, T_M. Until now, neither direct experimental measurements nor simulations of ΔG_sc for a locally melted DNA have been reported. Likewise, direct experimental or theoretical assessments of ΔΔG_sc for local melting of an initially unmelted supercoiled DNA are lacking. Nonetheless, the phenomenon of supercoiling-induced local melting has been extensively analyzed by Benham (1990, 1992)), who employed some of the known statistical thermodynamics of DNA melting together with several untested assumptions regarding both the structural properties of partially melted supercoiled DNAs and the thermodynamics of their supercoiling. After invoking an additional untested assumption pertaining to the gel mobilities of locally melted and unmelted supercoiled DNAs, Bauer and Benham (1993) and Bauer et al. (1995) investigated the magnitude and temperature dependence of the supercoiling free energy. We believe that it is now essential to address several questions pertaining to the structures and supercoiling thermodynamics of locally melted DNAs, and to test certain of the assumptions invoked by Benham and co-workers. This is done via Monte Carlo simulations of mesoscopic models of locally melted supercoiled DNAs, wherein the denatured (melted) regions are modeled simply as regions with much reduced torsion and bending elastic constants. The assumptions invoked by Benham and Bauer and Benham would be expected to be more applicable to our simple model molecules than to real DNAs. The results in this work significantly increase our knowledge regarding the structural properties and supercoiling thermodynamics of model circular DNAs with fixed numbers (28 or 56) of melted basepairs, and significantly deepen the level of analysis. Hopefully, our findings will lead to a further refinement of Benham's model, and ultimately lead to the extraction of increasingly reliable and accurate estimates of certain unknown quantities, including the effective elastic constants of the melted regions, by fitting various experimental data.

Topological and geometrical aspects of supercoiling

Every DNA topoisomer is characterized by its integral linking number 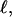the number of turns of each single strand around the other. ℓ is a topological invariant that is unaltered by any change in tertiary or secondary structure of the DNA, including local melting. The extent of deformation of the DNA is characterized by the linking differenc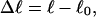e, where 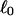is the intrinsic twist of the unstrained DNA. For an unmelted supercoiled DNA comprising M basepairs (bp), 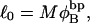where 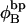((1/10.45) turns/bp) is the intrinsic succession angle between basepairs of the duplex DNA. 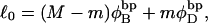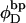For a locally melted DNA comprising M basepairs, of which m are melted, where is the intrinsic succession angle between (open) basepairs of the melted, or denatured, DNA. Although 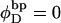for a real DNA, it typically does not vanish for our simulated molecules, so is introduced at this point and carried along through the subsequent development. In the sequel, when a distinction is necessary, the properties of unmelted DNAs will be denoted by an overbar (e.g., 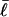) and those of locally melted DNAs will be denoted by a tilde (e.g., 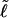). When considering unmelted and locally melted forms of the same molecule, 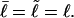Then the change in linking difference upon local melting is

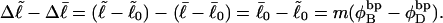(1)

For unmelted and locally melted molecules, the superhelix density is defined by 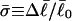and 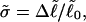respectively. 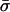is generally negative for native supercoiled DNAs, since 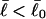in that case.

We assume that the linking number is partitioned between twist (t) and writhe (w) according to (White, 1969; Fuller, 1971):

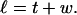(2)

Equation 2 was proved for ribbons of infinitesimal width with smooth edges. Its validity for ribbons of finite width might be restricted to the case of smooth inextensible edges. Moreover, its applicability to partially denatured DNAs is far from obvious. However, for the DNAs considered here, which exhibit a large linking difference and only a small locally denatured region, a large amount of linking difference is typically absorbed into the latter, which would be expected to wind that denatured DNA into a left-handed helical bundle, wherein the space curves of the single strands are reasonably smooth, and for which Eq. 2 is either valid or a good approximation.

The DNA is here regarded as a chain of N = M/ν subunits, each containing ν basepairs. These subunits are labeled consecutively by the index j, j = 1, … N. In each subunit (j) is fixed a coordinate frame (x_j,y_j,z_j), the z_j axis of which lies along the bond vector (b_j) that extends from the origin of the jth frame to the origin of the succeeding (j + 1)th frame. The Euler rotation that carries a coordinate frame from coincidence with the jth frame to coincidence with the (j + 1)th frame is 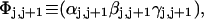where the component rotations, 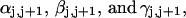are taken sequentially around the body-fixed z, new body-fixed y′, and final body-fixed z″ axes (Edmonds, 1974). The net twist of the DNA is given by

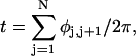(3)

where 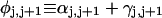(radians) is the net twist of the Euler rotation from the jth to the (j + 1)th frame (Schurr, 1985). For a partially melted molecule, in which the N − n subunits, j = 1,2, … N − n, are B-helical duplex, but the n = m/ν subunits, j = N − n + 1, … ,N, are melted, the net twist can be partitioned among the two regions according to

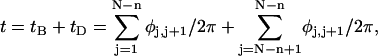(4)

where the first term on the far right-hand side (rhs) constitutes the twist (t_B) of the B-helical duplex region and the second term constitutes that (t_D) of the denatured (melted) region.

The writhe is commonly approximated by the discretized Gauss integral,

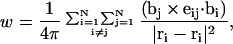(5)

where the 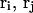denote the positions of the origins of the ith and jth subunit frames, respectively, in the laboratory frame, and 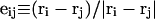denotes a unit vector along r_i − r_j (Hao and Olson, 1989). We imagine that the single strands in a locally melted region are smoothly wound in such a way that their midline is well-defined, and can be taken as a line of discretized bond vectors for the purpose of a calculating w according to Eq. 5. It is useful to partition the writhe among the B-helical duplex and denatured regions according to

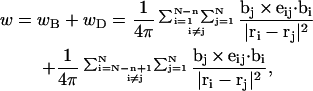(6)

where the first term on the far rhs constitutes the writhe (w_B) associated with the B-helical duplex region and the second term constitutes the writhe (w_D) associated with the denatured region. The writhe w_B of the duplex region contains (N − n)² self-terms in which both i and j lie within that same region (1, … N − n), plus (N − n)n cross-terms in which i lies within the duplex region but j lies within the denatured region (N − n + 1, … N). The writhe w_D of the denatured region similarly contains n² self-terms in which both i and j lie within the denatured region plus n(N − n) cross-terms in which i lies within the denatured region, but j lies within the duplex region. The number of cross-terms in w_B and in w_D is identical. Moreover, because 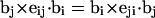is invariant to interchange of i and j, every cross-term in w_B has an identical counterpart in the cross-terms of w_D. Thus, the entire cross-term contribution of the total writhe is divided evenly between the two regions, regardless of their relative sizes.

The linking number of locally melted DNA can be partitioned as 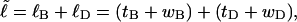where 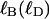corresponds to the first (second) term on the far rhs. The intrinsic twist can also be partitioned as 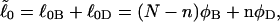where 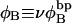is the intrinsic succession angle (turns/subunit) between subunits of unmelted DNA and 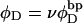is that for melted DNAs, and 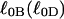corresponds to the first (second) term on the far rhs. Finally, the linking difference, 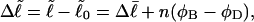can be partitioned between the duplex and melted regions according to

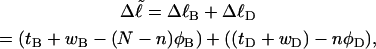(7)

where the first term on the rhs constitutes the linking difference 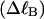of the duplex region and the second term constitutes that 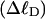of the melted region. Although 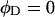for a real DNA, it typically does not vanish for our model DNAs.

Questions pertaining to locally melted supercoiled DNAs

The following questions are relevant to the characterization and analysis of supercoiling-induced local melting:

1. How are the writhe, twisting strain, and linking difference of a locally melted topoisomer distributed between its duplex and melted regions, the latter of which exhibits much weaker torsional and bending rigidities than the former?

2. How does the presence of the elastically soft denatured region affect the structure (e.g., writhe and radius of gyration (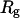)), and fluctuations in structure of the molecule? In particular, how do such properties of a locally melted DNA compare with the corresponding properties of an unmelted topoisomer whose total 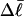matches the 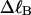of the locally melted DNA?

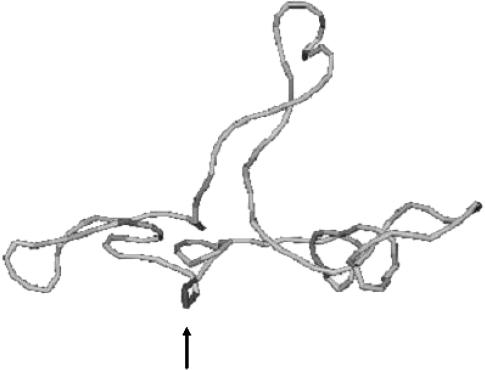
3. Are the more flexible melted regions found preferentially at certain locales or instead more or less uniformly distributed throughout all regions of the tertiary structure of the supercoiled DNA? Intrinsically curved sequences with normal duplex rigidity are found preferentially at the external ends, or apices, of interwound superhelical branches or domains (Bussiek et al., 2002; Pfannschmidt and Langowski, 1998; Chirico and Langowski, 1996). Supercoiled plasmids containing the SCA10 repeats, (ATTCT)_n.(AGAAT)_n, n = 5, … 29, were deposited on a mica surface treated with 3-aminopropyltriethoxysilane (APS) (Lyubchenko and Shlyakhtenko, 1997), rinsed, dried, and scanned by atomic force microscopy (AFM) in air (Potaman et al., 2003). Open regions were observed in these DNAs, and found not to be associated with apices. However, the extensive flattening, low prevailing water activity, and certain peculiarities in the data suggest that these are not equilibrium structures typical of normal locally melted supercoiled DNAs in solution. The open regions in the AFM images are specific to the SCA10 sequences, and are not observed for other DNAs with (A + T)-rich regions of comparable length, which also exhibit stable melting in two-dimensional gels. They also do not show the expected negative interwinding of the two single strands. Hence, the location(s) of locally melted regions in normal equilibrium supercoiled DNAs in solution remains an open question.

4. How does the (deformational) supercoiling free energy ΔG_sc of a locally melted DNA vary with the linking difference of its unmelted parent topoisomer 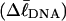and with the number m of its melted basepairs, or equivalently the number n = m/ν of its melted subunits? From such information, the difference in supercoiling free energy, ΔΔG_sc, between an unmelted parent topoisomer with linking difference 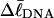and its partially melted daughter molecule with m melted basepairs can be estimated. This latter quantity is important, because the reduction in supercoiling free energy upon partial melting provides the driving “force” for supercoiling-induced partial melting.

5. Can the total supercoiling free energy, including the configurational entropy contribution, be partitioned between the duplex and melted regions and, if so, how does it vary with the average linking difference 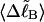of the duplex region, and the average twisting strain of the melted region, ?

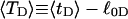6. When the supercoiling free energy of the duplex region of a locally melted DNA is expressed in terms of the square of its associated linking difference, 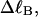how does its effective torque constant, or equivalently its twist energy parameter (E_T), compare with the E_T for the corresponding unmelted DNA in regard to both magnitude and variation (if any) with linking difference?

With the answers to these questions in hand, one could combine the estimated reduction in supercoiling free energy upon opening a region containing m basepairs with an estimate of the free energy increase upon melting m basepairs (below T_m) to estimate m for any given linking difference and temperature. By explicitly or implicitly assuming the answers to certain of the preceding questions, Benham (1990, 1992) formulated a protocol to do essentially that for sufficiently supercoiled DNAs in low ionic strength (≤20 mM) at temperatures 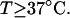(There is currently no evidence for stable opening of a supercoiled DNA with 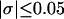at 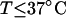in ionic strengths ≥30 mM (Kowalski et al., 1988)). After invoking an additional assumption pertaining to the gel mobilities of unmelted and locally melted species, Bauer and Benham formulated and applied a protocol to analyze two-dimensional gels of an ensemble of topoisomers of supercoiled PBR322 DNA in ∼20 mM ionic strength at various temperatures, 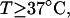to estimate several quantities, including E_T and the free energy, enthalpy, and entropy of supercoiling.

The primary objectives of this work are to address questions 1–6 above for a simple mesoscopic model of a locally melted DNA, to test or partially test certain assumptions of Bauer and Benham (1993), and to understand why such assumptions are, or are not, valid. It is first necessary to clarify those assumptions somewhat.

Assumptions in the model of Benham

Benham (1990, 1992) introduced a new quantity, called the residual linking difference (ΔLk_r), for a locally denatured molecule. Bauer and Benham (1993) described ΔLk_r as “that portion of the initial linking difference (i.e., of the unmelted parent) that is not accommodated either by local strand separation or by subsequent interstrand twisting in the denatured regions”. They further state that denaturation of a run of m basepairs leads to a change in the magnitude of ΔLk_r equal to 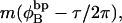where τ is the “helicity” (i.e., twist) of the denatured regions in radians per basepair. Keeping our notation to distinguish denatured and nondenatured forms of the same molecule, we express the above statement as

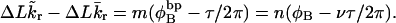(8)

This description of 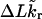is incomplete, because Benham and Bauer and Benham did not consider the possibility that the denatured region might, owing to its rather low bending rigidity, absorb linking difference not only in the form of twist, but also in the form of writhe, perhaps by tight toroidal winding of the axis (i.e., midline) of the denatured region.

If the convex volume that just envelopes the minor denatured domain (D) is sufficiently small in all of its physical dimensions compared to that of the major unmelted domain (B), then in the vast majority of two-dimensional projections of the molecule taken from all orientations, the axis of the unmelted region will have no intersections with the axis of the unmelted region, so there will be no significant cross-term contributions to the total writhe. It will be explicitly demonstrated below that such a circumstance prevails for the relatively small denatured regions considered here. In this case, any significant writhe w_D associated with the minor denatured domain D must stem primarily from its self-writhe 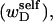and would therefore be predominantly local. Unfortunately, such a local writhe, 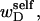cannot be distinguished from local twist, t_D, of that same region without some means of resolving the structure of the locally denatured region. Currently, there is no experimental method to ascertain unequivocally whether the linking difference associated with a small denatured region is present in the form of twist 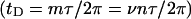or self-writhe 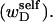In any event, it will be shown rigorously below that Eq. 8 is incomplete whenever either 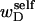or the cross-writhe term 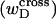associated with the denatured region is nonvanishing.

Benham (1990, 1992) and Bauer and Benham (1993) also assumed that the total supercoiling free energy, ΔG_sc, of a single partially melted DNA consists of only two terms,

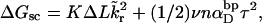(9)

where K is an effective torque constant for supercoiling of the duplex region and 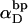is the effective torsion elastic constant of each of the m = νn “torsion” springs between (open) basepairs of the denatured region. It is implicitly assumed in Eq. 9 that the intrinsic twist, 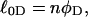of the denatured regions vanishes, as it does for real DNAs. Our objective here is not to assess the validity of the assumed Hooke's law behavior of the melted region, but instead to assume such behavior to address other questions and test other assumptions. The quantity K in Eq. 9 is related to the twist energy parameter, E_T, used previously in our laboratory by K = kT(E_T/M), where k is Boltzmann's constant, T the absolute temperature, and M = νN the number of (duplex) basepairs (Wu et al., 1988; Clendenning and Schurr, 1994; Clendenning et al., 1994; Gebe et al., 1995, 1996; Schurr et al., 1995; Delrow et al., 1997a,b; Naimushin et al., 2001). For sufficiently large DNAs (M ≥ 2000 bp) E_T is practically independent of M. (Bauer and Benham used the symbol q(T) instead of E_T, and C_τ instead of α_D). The partitioning of ΔG_sc into separate contributions from the duplex and denatured regions, which is implied by Eq. 9, suggests that for a partially melted DNA, one should employ K = kT(E_T/(M − m), where M is replaced by the number (M − m) of basepairs in the duplex region. However, both in the experiments of Bauer and Benham and in these simulations, m is only a tiny fraction of M (m/M ≲ 0.013), so the error in ΔG_sc resulting from use of M in place of M − m in the expression for K is smaller than either the experimental or simulation errors. We test the assumption (Eq. 9) that was originally stated by Benham.

Another crucial assumption employed by Benham (1990, 1992) and Bauer and Benham (1993) is that the same value of K (or E_T) applies to both the unmelted DNAs and the duplex regions of partially melted DNAs. Because K (or E_T) sensitively reflects the bending rigidity and also the partitioning of 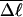between twist and writhe in an unmelted supercoiled DNA, its use in Eq. 9 can be justified only if 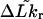pertains exclusively to the unmelted region B, and contains no contribution from the torsionally and flexurally softer denatured region D.

To better illuminate the assumptions of Benham (1990, 1992) and Bauer and Benham (1993) that are implied by Eqs. 8 and 9, we begin with 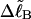in Eq. 7, which is rigorously given by

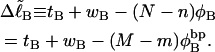(10)

We now define an alternative residual linking difference, 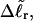of the partially melted DNA as that part of the total linking difference that is associated with the unmelted duplex region. That is, 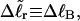which gives exactly

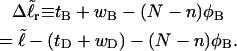(11)

For the unmelted parent molecule with the same linking number, 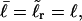the residual linking difference is

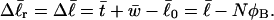(12)

After subtracting Eq. 12 from Eq. 11, and setting t_D = νnτ/2π, we obtain

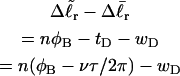(13)

for the change in 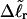upon local melting of m = νn basepairs. Our Eq. 13 differs from the corresponding relation of Bauer and Benham (our Eq. 8) by the term, −w_D. Our definition of the residual linking difference in Eq. 11 is complete and is the most appropriate choice for two main reasons. i), The value of our 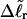is unaffected by any interconversion between t_D and 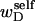in the denatured region. This is important, because the exact form of the linking difference in that region is not known, and could well be self-writhe instead of twist. ii), 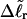pertains only to the duplex region, and is therefore the appropriate quantity to employ in Eq. 9 for the supercoiling free energy, given that the same value of K (or E_T) is assumed to apply for both unmelted DNAs and the duplex regions of locally melted DNAs. Consequently, we believe that Bauer and Benham either intended, or should have intended, to adopt our choice of the residual linking difference in Eq. 11. Thus, their adoption of Eq. 8 instead of Eq. 13 involves the implicit assumption that 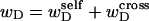is negligibly small. Because 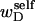and the cross-writhe term 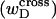associated with the denatured region are expected to have the same sign, the assumption that w_D is negligibly small is equivalent to assuming that 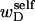and 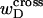are both negligibly small.

A possible alternative interpretation of the ansatz of Benham (1990, 1992) and Bauer and Benham (1993), contained in Eqs. 8 and 9, is that the total “helicity” of the denatured region (in turns) is actually the sum of the twist (t_D) and the self-writhe 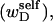rather than simply the twist, so that 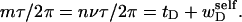Then, if the ratio 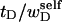were to remain constant with increasing linking difference (as is the case for t_B/w_B in an unmelted DNA), then the free energy associated with the superhelicity in the denatured region could conceivably be quadratic in the sum, 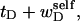(as it is for an unmelted DNA). Because the effective torque constant α_D is taken as an unknown adjustable parameter characteristic of denatured regions, it could conceivably apply as well to the square of 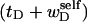as to the square of t_D. In this case, Eq. 13, which applies in all events, could be written as

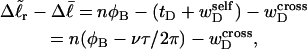(14)

where 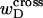denotes the cross-writhe of the denatured region. Equation 8 is identical to Eq. 14 if, and only if, 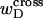is negligibly small. In this interpretation, the implicit assumption of Benham is that 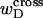is negligibly small.

One might also ask whether Eqs. 8 and 9 would be reasonable assumptions, if the total “helicity” of the denatured region, nντ/2π turns, were taken to be its associated linking difference in turns, 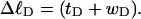This would cause Eq. 8 to coincide with the first line of Eq. 13. However, 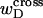depends strongly on the space curve of the duplex B region, as well as that of the locally melted D region, and those regions have very different elastic constants. Consequently, it seems most unlikely that t_D/w_D would remain constant with increasing linking difference, or that the free energy of the denatured region would vary simply quadratically with 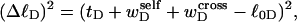unless 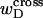were negligibly small. Indeed, one cannot expect to decompose the supercoiling free energy of the entire molecule into separate local contributions of its unmelted and denatured domains, whenever cross-writhe terms make a significant contribution to eithe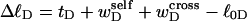r or 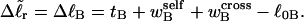Hence, this interpretation would be sensible only if the identical cross-writhe terms, 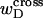and 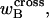were negligibly small.

Thus, under any interpretation of the meaning of the “helicity” ascribed to the denatured region, an additional assumption is required, namely that 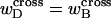is negligibly small.

The assumptions of Benham's model that are tested in this work are summarized in our notation as follows:

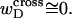
1. (15)
2. (16)

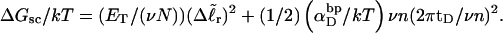
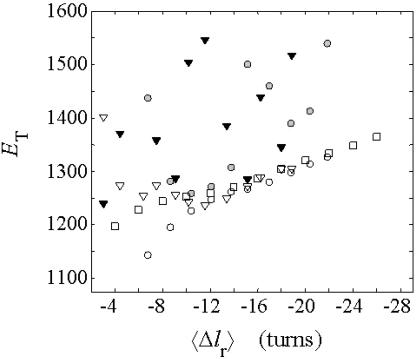
3. E_T is the same for unmelted and partially melted DNAs.

4. E_T is a constant, independent of

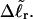
Our simulations of model DNAs containing m = 28 or 56 contiguous melted basepairs indicate that Assumption 1 above is an excellent approximation. However, the assumed quadratic variation of ΔG_sc with 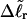appears to be somewhat inaccurate, even for the unmelted DNA, at the prevailing low (20 mM) ionic strength. For the unmelted DNA, n = 0 and 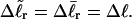For the same value of 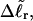the same value of E_T is obtained for all three DNAs (m = 0, 28, 56), so Assumption 3 appears to be surprisingly accurate. Assumption 4 is found to be somewhat inaccurate, again due to the nonquadratic variation of ΔG_sc with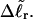

The final term in Eq. 16 reflects the assumption that the intrinsic twist of the melted region vanishes. Although that is indeed true for a real DNA, in our simulations the intrinsic twists of both duplex and melted regions are varied to alter the linking difference, as described below. In that case, the t_D in Eq. 16 must be replaced by the net twisting strain of the melted region, 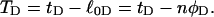It is implicit in Benham's analysis that 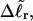t_D, and T_D must all be regarded as ensemble average values.

Additional assumptions in the protocol of Bauer and Benham

Bauer and Benham (1993) created a collection of topoisomers of pBR322 containing every linking difference from ∼+10 to −24 at an ionic strength ∼20 mM and investigated these at 40, 45, 50, 55 and 60°C. These topoisomers were analyzed by two-dimensional gels, where the prevailing temperatures for the first dimension were one or another of those just noted, which caused partial melting of the more negatively supercoiled topoisomers. The second dimension was run at 25°C in the presence of sufficient chloroquine to relieve the negative superhelical strain of every topoisomer, so that it is no longer locally melted, regardless of whether or not it was melted in the first dimension.

In addition to the assumptions implicit in their model, Bauer and Benham (1993) invoked an additional crucial assumption to interpret their two-dimensional gels, namely that any two topoisomers, one partially melted and the other unmelted, with the same gel mobility in the first dimension, have the same residual linking difference, 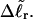Under this gel mobility assumption, the residual linking difference 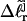of the jth locally melted topoisomer can be equated to the interpolated 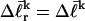of the (hypothetical) unmelted topoisomer with the same mobility in the first dimension. The 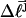of the unmelted parent of the jth topoisomer, and the 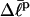of all the other unmelted topoisomers, are obtained from their positions in the second dimension. Specifically, 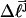is reckoned by counting the sequence of (unmelted) topoisomers in the second dimension that extends from the topoisomer with the slowest mobility in the first dimension up to that with the mobility of the jth topoisomer in the first dimension. In the computational protocol of Benham and Bauer and Benham, the experimental value of 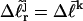becomes the “target” for a statistical thermodynamic calculation conducted for the jth topoisomer with unmelted linking difference 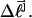The relative probabilities for various partially melted states are calculated for a nearest-neighbor two-state (i.e., unmelted or melted) melting model that takes account of the supercoiling (deformational) free energy in a parameterized way, based upon Eq. 18 below. The calculation ideally treats all possible numbers, 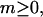of open basepairs, which are arranged in all compatible numbers of melted domains of various sizes, but takes no direct account of the actual tertiary structures or fluctuations in tertiary structure that determine the thermodynamics of supercoiling and the reduction in supercoiling free energy upon melting. In each iteration, the three adjustable parameters, E_T, 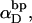and an opening initiation free energy a, are fixed at appropriate trial values. For any given value of m, 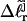is eliminated in favor of τ and 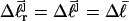by using Eq. 13 with w_D = 0. In the general case, where 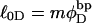does not vanish, τ is related to the twisting strain of the denatured region, 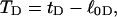according to 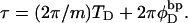Using this relation in Eq. 13 with w_D = 0 gives 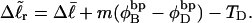When this expression for 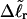is substituted into Eq. 16, and t_D in the final term of that equation is replaced by T_D, then T_D can also be eliminated in favor of 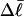by minimizing ΔG_sc with respect to T_D, which gives (at the minimum)

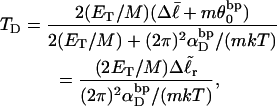(17)

where 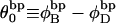is the difference in the intrinsic succession angle between the duplex and denatured regions ( 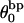vanishes for our model filaments.)

Now the supercoiling free energy in Eq. 16 can be written as

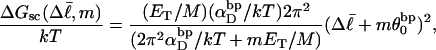(18)

which depends only on the fixed (known) 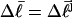and the specified value of m. The total free energy of each state consists of 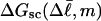plus a free energy of melting term, which also depends upon m. The average value of 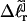for the set of partially melted topoisomers with the same 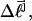but different values of m, is computed by averaging the quantity

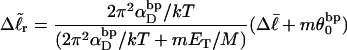(19)

from Eq. 17 over all of the various partially melted states, each of which is weighted according to the exponential function of its total free energy divided by −kT. In Benham's analysis, 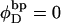and 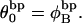The experimental estimate of the average 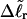and its corresponding 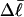are fitted by Eq. 19, and the disposable parameters, E_T, 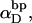and a are adjusted until the computed average value of 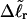matches the experimental value. By simultaneously fitting the observed 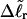values for several (≥3) partially melted topoisomers at a given temperature, Bauer and Benham obtained a unique optimum fit for all three parameters at each temperature. Clearly, the gel mobility assumption that 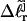of the jth partially melted topoisomer is identical to the interpolated 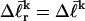of the (hypothetical) unmelted topoisomer with the same gel mobility provides the crucial experimental estimate of 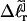upon which the entire subsequent analysis is based.

We wish to test this crucial gel mobility assumption insofar as possible. Unfortunately, a complete test is not possible, because we do not know how to calculate gel mobilities for individual topoisomers. Nevertheless, we can calculate equilibrium tertiary structural properties, such as the principal components of the inertial tensor, the radius of gyration Rg, and writhe w_B, of the duplex region, upon which the gel mobility might depend, and with which it might be expected to vary in some smooth and continuous way. We then plot the average value of each structural property versus 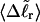for each of our model DNAs, which contain m = 0, 28, or 56 melted basepairs, and compare the resulting “curves” to see whether they are superimposable. Coalescence of all three curves for each equilibrium tertiary structural property is regarded as a necessary, though not sufficient, condition for validity of the gel mobility assumption of Bauer and Benham. In fact, for several structural properties examined, all three curves for m = 0, 28, and 56 melted basepairs do coincide within the simulation error. Evidently, the global equilibrium tertiary structural properties of our model DNAs with very small denatured regions are determined almost entirely by the average residual linking difference, 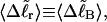of the duplex region. The gel mobility assumption of Bauer and Benham clearly passes this test. However, it remains doubtful that these conclusions will extend to situations, wherein a much larger fraction of the total sequence is melted.

Electrophoretic migration of large supercoiled and linear DNAs in dilute agarose gels involves periodic extension of the DNA to highly elongated states far outside the normal equilibrium range, as it becomes temporarily trapped in extended hairpin configurations while sliding over physical constraints within the gel, followed by contraction to more normal dimensions, as it finally slides past those constraints (Smith et al., 1989; Song and Maestre, 1991). Hence, the gel mobility presumably reflects also the deformability of the DNA. In regard to small displacements from the average value of any particular structural property, the corresponding deformability is linearly related to the equilibrium variance of that same property (Kubo, 1957). Hence, we calculate the variance of each tertiary structural property and plot its standard deviation ((variance)^1/2) versus 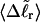for each of our model DNAs with m = 0, 28, and 56 melted basepairs. Whenever the standard deviation is not negligibly small compared to the mean value, the coincidence of such curves for all three DNAs is regarded as a necessary, though probably still not sufficient, condition for validity of the gel mobility assumption of Bauer and Benham. In our simulations, the standard deviations in every tertiary structural property at the same value of 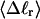are found to be significantly larger for DNAs with 56 melted basepairs than for those with zero basepairs. In the case of R_g and principal moments of the inertial tensor, the standard deviations are negligibly small compared to the mean values, even for the partially melted DNA, and probably have an insignificant effect on the gel electrophoretic mobility. However, in the case of the writhe, the standard deviation is significant compared to its mean value, so the greater deformability of the writhe in the case of the partially melted DNA may well endow that DNA with a different gel electrophoretic mobility even at the same value of 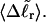Thus, insofar as deformability of the writhe, or fluctuations therein, contributes significantly to the gel electrophoretic mobility, the gel mobility assumption of Bauer and Benham might be somewhat inaccurate.

The analysis of experimental data by Bauer and Benham (1993) relies primarily on Eq. 18 for ΔG_sc and Eq. 19 for 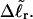Both of these expressions were derived from Eq. 16 by minimizing ΔG_sc with respect to T_D (or τ) to eliminate T_D in favor of 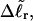and ultimately to determine how the total linking difference 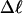is apportioned between T_D (or τ) and 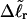(i.e., between the melted and duplex regions). The specific protocol adopted by Benham to perform the minimization involves yet another assumption, namely that E_T is a constant independent of 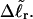As described below, this assumption is found to be inaccurate at the prevailing relatively low ionic strength.

The plan of the article

In this work, we simulate supercoiled mesoscopic model DNAs with m = 0, 28, or 56 melted basepairs and selected linking differences over the range from 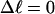to −26 turns. The supercoiling free energies, ΔG_sc, are reckoned as a function of 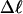for each molecule with fixed m via a reversible work protocol. In addition, for each molecule at a given 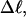the ensemble average residual linking difference of its duplex region, 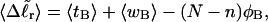and net twisting strain of its melted region, 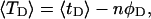are calculated. 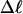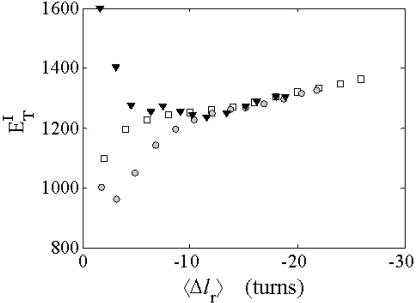Hence, we can directly assess the variation of ΔG_sc with for each molecule, and for each value of 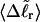we can determine the effective E_T value, since that is the only unknown quantity in Eq. 16, and examine its variation with 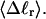In addition, we can extract E_T values from Eq. 19 by using the simulate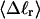d and 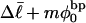in a manner directly analogous to the way in which Bauer and Benham obtained E_T. E_T values can also be estimated from 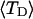and the corresponding 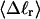via Eq. 17 or from ΔG_sc and the corresponding 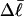via Eq. 18. E_T values obtained by these different methods are critically compared. The E_T values determined from Eq. 16 are not necessarily identical to those extracted from Eq. 19, because the minimization protocol used to obtain the latter rests upon an additional assumption, as noted above, namely that E_T does not vary with 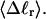In fact, a nonquadratic variation of ΔG_sc with 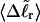would imply a (possibly modest) variation of E_T with 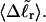Because E_T was assumed to be constant, when performing the minimization with respect to T_D (or τ), Eqs. 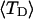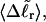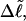17–19 will be somewhat inaccurate, whenever E_T actually does vary with (or with or or 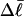). Fortunately, the errors in the extracted E_T values that are associated with this minimization protocol are found to be relatively small (5–7%).

THE MODEL

Our mesocopic model of a circular DNA comprises N = 155 rigid-rod subunits, each connected to its neighbors at either end by Hookean torsion and bending springs. The subunit length, b = 95.4 Å, corresponds to ν = 28.06 bp, and the overall chain length corresponds to 4349 bp, which is similar in size to the pBR322 plasmid DNA (4363 bp) investigated by Bauer and Benham (1993). The total potential energy is given by

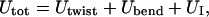(20)

where U_twist is torsion potential energy, U_bend is the bending potential energy, and U_I is the repulsive potential energy of interaction between nonnearest-neighbor subunits. Expressions for U_twist, U_bend, and U_I, and the selections of input parameters therein, are presented and discussed in the Appendix.

In this work, we simulate model DNAs containing small torsionally and flexurally weak regions. This is done by designating n = 0, 1, or 2 consecutive springs as weak. We take the (155,1) spring for n =1, and the (154,155) and (155,1) springs for n = 2 as weak springs, which are assigned reduced torque constants for torsion and bending. For melted regions comprising only one or two rigid-rod subunits, 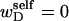(see Appendix), so 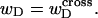With a subunit length of 95.4 Å, the n = 0, 1, and 2 weak springs correspond to denatured regions with m = 0, 28.06, and 56.12 bp. For convenience, these m values are rounded to the nearest integer in the text, though not in the data analysis. The torsion elastic constant for a duplex subunit corresponds to a torsional rigidity, C = 2.0 × 10⁻¹⁹ dyne cm², and its bending elastic constant is chosen to yield a persistence length, P = 500 Å, after taking account of the intersubunit repulsions. The torsion elastic constant of a melted subunit was determined by extrapolating the corresponding results of Bauer and Benham to 37°C, and is 54.6-fold smaller than that for the duplex region. The bending elastic constant of a melted subunit was taken to be 10-fold smaller than for a duplex subunit, and yields a 2.9-fold smaller persistence length after taking account of the intersubunit repulsions. The intersubunit potential consists of a screened Coulomb interaction plus a hard-cylinder interaction with a 24 Å diameter. The locations and magnitudes of the effective charges appropriate for the prevailing ionic strength are described in the Appendix. The simulation temperature is 298 K.

SIMULATION PROTOCOLS

Our simulation protocols, relevant computational procedures, and statistical methods are described in the Appendix. Average values of the various quantities are plotted versus 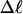or 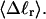Typically, either straight lines or quadratic polynomials are fitted to the data to guide the eye.

RESULTS AND DISCUSSION

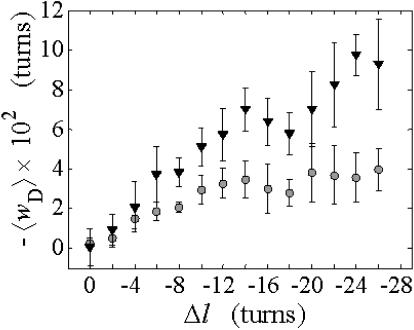
The calculated 〈w_D〉 are negligibly small for n = 1, 2

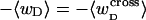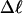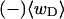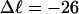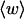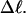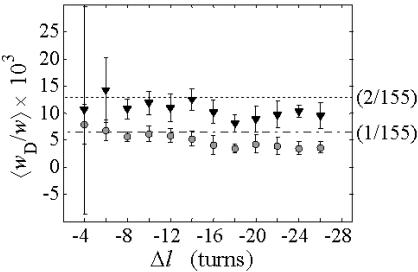
The ensemble average value is plotted versus for n = 1 and 2 in Fig. 1. Although increases overall between and turns, it never exceeds 0.05 turns for n = 1 or 0.10 turns for n = 2, even though the total writhe rises from −0 to −13 turns over the same range of The average fraction, 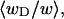of the total writhe contained in w_D is plotted versus 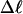in Fig. 2. Clearly, 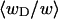is typically less than or equal to the fraction of bond vectors, 1/155 or 2/155, that are contained in the weak region. Consequently, 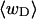can be regarded as negligibly small compared to 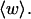Thus, the implicit assumption of Benham that 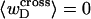is a rather good approximation, and our Eq. 13 becomes practically identical to the relation assumed by Benham and Bauer and Benham (our Eq. 8). Because the fraction of cross-writhe in the melted region evidently increases with size of that region, this approximation very likely fails for much larger melted regions.

FIGURE 1.

Negative writhe of the melted region, 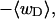versus linking difference of the entire molecule, 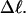Simulated molecules have either n = 1 (shaded circles) or n = 2 (▾) contiguous melted subunits out of 155 total subunits. In both cases, 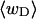is purely cross-writhe between the melted and duplex regions.

FIGURE 2.

Ratio 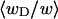of the writhe of the melted region, w_D, to the total writhe of the entire molecule, 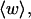versus linking difference of the entire molecule, 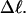Simulated molecules have either n = 1 (shaded circles) or n = 2 (▾) contiguous melted subunits out of 155 total subunits. The dashed lined has the value 1/155, and the dotted line has the value 2/155.

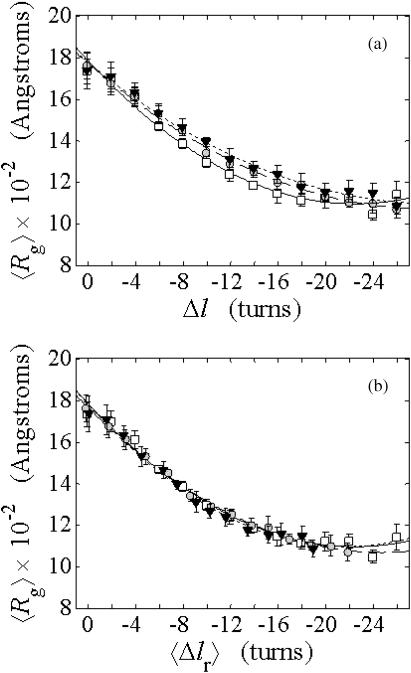
The mean tertiary structural properties are nearly universal functions of 〈Δℓ_r〉

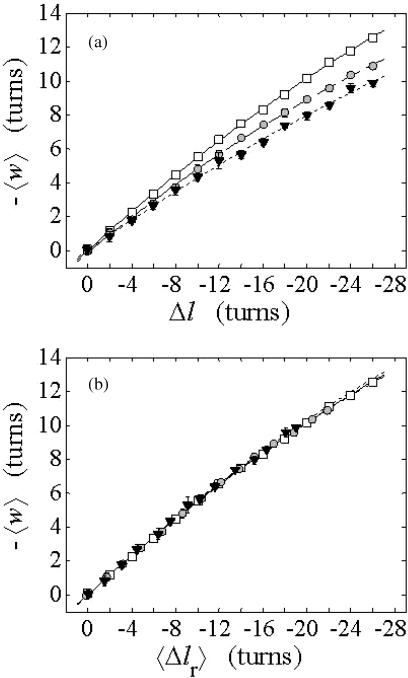
The total mean writhe 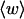for n = 0, 1, and 2 is plotted versus 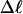in Fig. 3 a and versus 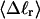in Fig. 3 b. The three separate curves in Fig. 3 a have coalesced to a single curve in Fig. 3 b, which indicates that 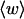is a nearly universal function of 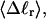independent of n. The evident curvature shows that this universal relation is not strictly a proportionality.

FIGURE 3.

(a) Negative total writhe, 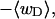versus linking difference of the entire molecule, 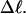(b) 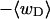versus residual linking difference associated with the duplex region, 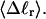Simulated molecules have n = 0 (□), n = 1 (shaded circles), or n = 2 (▾) melted subunits out of 155 total subunits. 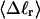is calculated according to the first line of Eq. 11.

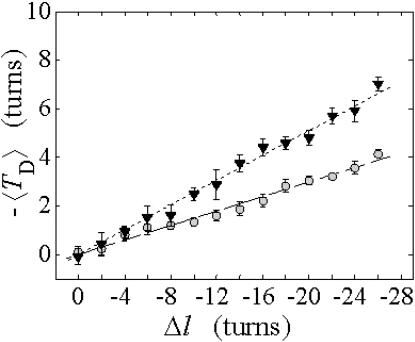
The net twisting strain in the melted region, 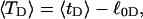is plotted versus 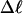for n = 1 and 2 in Fig. 4. These two data sets do not coalesce even when plotted versus 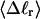(not shown), so 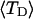is not a universal function of 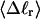independent of n. Of course, 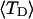is also not a tertiary structural property. Within simulation error, 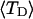is proportional to both 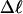and 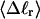(not shown) in agreement with Eq. 17, when 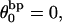as it does here. This simultaneous proportionality of 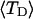to both 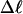and 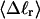implies that 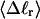is also proportional to 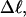in agreement with Eq. 19 (when 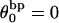). Because 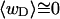for n = 1 and 2, Eq. 7 gives 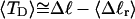for our model DNAs.

FIGURE 4.

Negative twisting strain per subunit of the melted region, 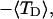versus linking difference, 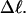Simulated molecules have either n = 1 (shaded circles) or n = 2 (▾) melted subunits out of 155 total. The dashed and dotted lines are the respective best-fit proportionality relations.

The fraction of the total linking difference that resides in the melted region is approximately 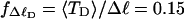for m = 1 and 0.26 for m = 2. These values apply over the full range of 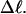When an unmelted parent DNA with σ = −0.05 and 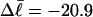turns melts 56 bp, then its linking difference drops to 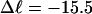turns, of which −4.0 are contained in the melted region. The −4.0 turns are −0.75 times the intrinsic twist of that same region, when it is present as duplex. Thus, very substantial negative interwinding of the single strands of the melted region is expected, whenever the molecule is at least moderately supercoiled, provided Benham's torsion elastic constant for the melted region applies, as assumed here. The fraction of the total twisting strain in the denatured region is 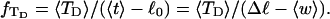Because w is not strictly proportional to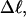 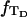is not independent of 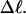However, for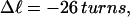 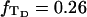for n = 1 and 0.42 for n = 2.

The mean radius of gyration, 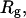for n = 0, 1, and 2, is plotted versus 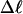in Fig. 5 a and versus 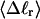in Fig. 5 b. Again, the three curves in Fig. 5 a have largely coalesced in Fig. 5 b. The ensemble average values of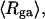 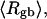and 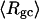for n = 0, 1, and 2 also do not coalesce when plotted versus 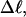but are significantly more coalesced, when plotted versus 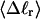(not shown) (Sucato, 2001). This coalescence is most pronounced for the largest element, 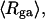which is most sensitive to n at fixed 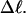The values of the smaller elements, 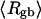and 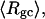are considerably less sensitive to n at fixed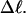

FIGURE 5.

(a) Radius of gyration, R_g, versus linking difference of the entire molecule, 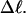(b) R_g versus residual linking difference associated with the duplex region, 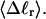Simulated molecules have n = 0 (□), 1 (shaded circles), or 2 (▾) melted subunits out of 155 total subunits. 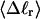is calculated according to the first line of Eq. 11.

These results indicate that 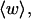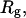and 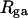depend primarily upon the residual linking difference of the duplex region, 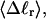independent of the size of the melted region. This conclusion most likely does not extend to DNAs with very much larger melted regions, for reasons noted above.

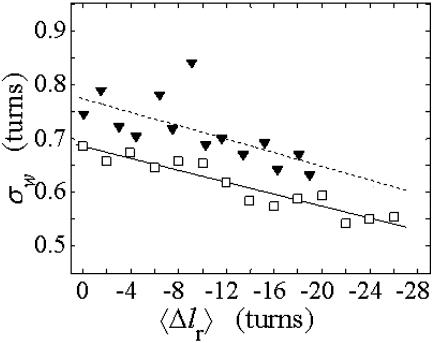
The fluctuations in structural properties are not universal functions of 〈Δℓ_r〉

The standard deviation of the total writhe, σ_w, is plotted versus 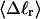in Fig. 6 for n = 0 and 2. σ_w clearly depends upon n even at the same 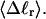Specifically, at the same 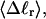σ_w increases with the size of the melted region. In addition, σ_w declines with increasing 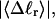which presumably reflects the diminished deformability of the more tightly writhed structures prevailing at larger 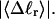For the molecule with n = 2 melted subunits, σ_w exceeds 10% of 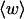at all 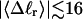turns. These fluctuations in the writhe imply an enhanced deformability of the writhe that increases with size of the melted region at constant 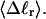To the extent that such writhe deformability affects the gel mobility, the latter will not be a universal function of 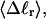independent of n. This finding leaves open the possibility that the gel mobility assumption of Bauer and Benham is not entirely correct, despite the fact that the average structural properties of the unperturbed DNAs are universal functions of 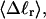independent of n.

FIGURE 6.

Standard deviation of the writhe, σ_w, versus linking difference associated with the duplex region, 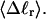Simulated molecules have n = 0 or 2 melted subunits out of 155 total subunits.

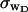for the denatured region increases with increasing 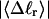(data not shown). This trend is in the opposite direction to that for σ_w. Because 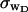pertains only to the cross-writhe, 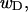which is the same as the cross-writhe in w_B, we conclude that fluctuations in cross-writhe increase with increasing 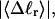whereas fluctuations in self-writhe of the B-helix region decrease with increasing 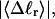as expected. The increase in cross-writhe fluctuations with increasing 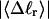may simply be a consequence of compaction of the dimensions of the B-helical region, which may allow greater fluctuations in cross-writhe for the same range of variations in local structure. In any case, 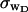is much smaller than σ_w, and is insignificant compared to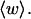

It was similarly found that 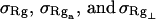vary significantly with n at constant 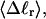but these standard deviations are negligibly small compared to the corresponding average values (data not shown). Hence, their effect on the gel mobility is probably negligible.

Results pertaining to the supercoiling free energy

When a real unmelted supercoiled DNA with linking difference 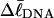undergoes melting of m basepairs, its linking difference becomes 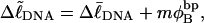and the supercoiling free energy declines due to both the decline in magnitude of the (negative) linking difference and the presence of elastically weak regions. However, for our model molecules, 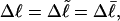because in our simulations we have for convenience taken 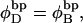as noted above. Nevertheless, for each of our simulated molecules, we can reckon the linking difference 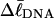of that real unmelted DNA, whose linking difference after melting m basepairs, 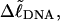is precisely equal to the linking difference of our simulated molecule, 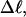by setting 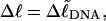which gives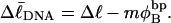

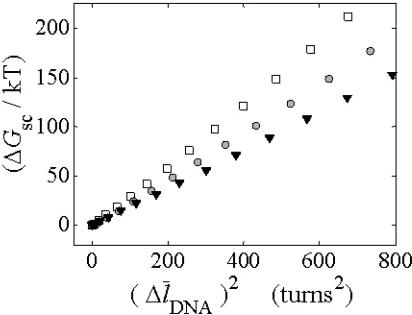
Computed values of ΔG_sc/kT are plotted versus 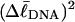in Fig. 7. The drop from the top curve (n = 0) to the middle (n = 1) or lower (n = 2) curve at fixed 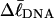gives the decrease in supercoiling free energy, 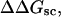upon opening m = 28 or 56 basepairs, respectively. The evident curvature indicates that ΔG_sc is not a quadratic function of 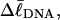even for n = 0 (m = 0), where 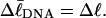This curvature far exceeds that (negligibly small curvature) predicted and observed for 0.1 M ionic strength (Gebe et al., 1995), and is attributed to the greater magnitude and range of the electrostatic repulsions prevailing at this lower ionic strength. 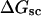rises more rapidly than the second power of 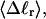because at 20 mM ionic strength the intersubunit electrostatic repulsions not only contribute significantly to the supercoiling free energy, but also contribute a larger fraction of the total at the larger 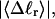where the DNA is more compact. When plotted versus 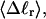the ΔG_sc/kT values do not coalesce to a single curve (not shown). Hence, ΔG_sc/kT is not a universal function of 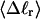independent of n, nor was it expected to be so.

FIGURE 7.

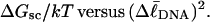
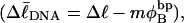is the supercoiling free energy of a simulated molecule with linking difference, and is the linking difference of the unmelted real DNA that would have the linking difference of the simulated molecule after melting m basepairs and 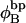is the intrinsic twist per basepair of the duplex region. Simulated molecules contain n = 0 (□), n = 1 (shaded circles), or n = 2 (▾) melted subunits out of 155 total melted subunits.

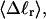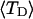Values of E_T that are determined directly from the simulated ΔG_sc, and via Eq. 16 (with 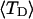in place of 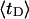) are denoted by 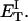In Fig. 8, 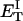is plotted versus 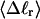for m = 0, 28, and 56. Although the 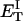values are very noisy at small 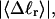they nearly coalesce at large 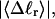where the simulate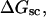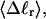d and 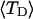are better converged. This coalescence confirms that E_T is independent of n, as assumed by Benham (1990, 1992). However, the upward slope of 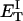with 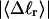implies a nonquadratic variation of ΔG_sc/kT with 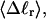which was not anticipated by Benham (1990, 1992) or Bauer and Benham (1993).

FIGURE 8.

Twist energy parameter, 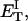versus residual linking difference of the duplex region,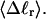 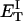is determined directly from the simulate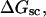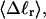d and 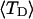via Eq. 16 with 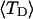in place of 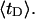Simulated molecules have n = 0 (□), n = 1 (shaded circles), or n = 2 (▾) melted subunits out of 155 total subunits.

E_T values can also be determined from Eq. 19 by using the values of 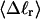and 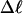from the simulations in each case. This corresponds most closely to the protocol of Bauer and Benham (1993). These values are denoted by 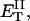and are coplotted with the 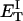values versus 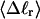in Fig. 9. These 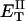values are much noisier than the 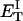values. This is due to the fact that modest relative errors in 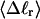produce five- to sixfold larger relative errors in E_T via Eq. 19 and in 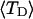via Eq. 17. For the larger 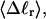where the relative errors in 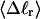are smallest, the 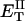values systematically exceed the corresponding 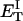values. This systematic overestimation of 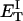by 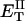at the larger 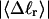arises because the variation of E_T with 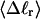(or 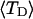) was neglected, when taking the derivative of ΔG_sc/kT with respect to 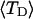in the minimization step. When the simulated slope, 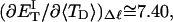is actually taken into account in the minimization step for n = 1, the corrected 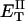values lie 5–7% lower than those obtained directly from Eq. 19, and are in reasonable, if noisy, accord with the 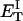values in Figs. 8 and 9. These observations indicate that the E_T values obtained by Bauer and Benham from Eq. 19 are likely to be systematically several percent too large, and to be quite sensitive to errors in the experimental estimates of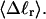

FIGURE 9.

Twist energy parameter, E_T, versus residual linking difference of the duplex region. The solid or shaded symbols apply to 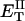values that are determined from the 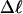and 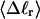of the simulated molecules according to Eq. 19. These 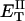values apply for n = 1 (shaded circles) or n = 2 (▾) melted subunits. The open symbols represent the same 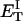values that appear in Fig. 8 for n = 0 (□), n = 1 (○), or n = 2 (▿) melted subunits out of 155 total subunits.

E_T values obtained from the simulate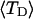d and 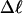via Eq. 17 are similar to, and behave like, those from Eq. 19. This is expected, because Eqs. 17 and 19 are simply two different realizations of the same equation. In contrast, E_T values reckoned from Eq. 18 (with the simulated ΔG_sc/kT and 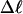) lie much closer to the corresponding 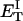values. It is unfortunate that the particular expression (Eq. 19) required to analyze the 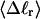versus 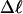data of Bauer and Benham manifests to a much greater extent the effects of the unexpected slope,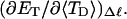

A systematic error in the apparent slope, −dE_T/dT, obtained by the protocol of Bauer and Benham

With increasing temperature, the spans of the experimental 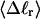versus 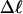data that are fitted by Bauer and Benham (1993) are centered about progressively smaller 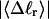values. This is because topoisomers with lower 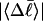undergo melting at higher temperature. If 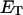decreases with decreasing 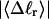at fixed temperature, as predicted by the present simulations, then the decrease in typical 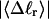values that are sampled with increasing T should act to enhance the slope, 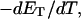above the intrinsic value that would apply, if 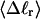were held constant. The magnitude of this enhancement can be estimated in the following way. First, we note that the simulated 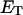values in Fig. 8 for 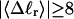can be satisfactorily approximated by the empirical linear relation, 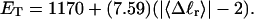The 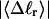values at each temperature in Fig. 4 of Bauer and Benham can be characterized by the minimum value, 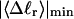in each case. These 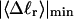values range from 13.25 turns at 313 K to 4.5 turns at 333 K. We now assume that the simulated slope, 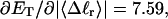is independent of T. The simulated 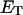value at 298 K for 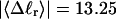is 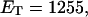and that for 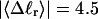is 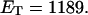The shift in 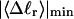from 13.25 to 4.5, as T increases from 313 to 333 K, then contributes to the apparent slope, 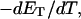a term −(1189 − 1255)/20 = 3.3 K⁻¹. This value should be subtracted from the negative slope of the E_T values reported by Bauer and Benham, which are given in Table 1. A least-squares fit of a straight line 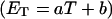to those data yields the experimental slope, −a = −dE_T/dT = 9.36 K⁻¹. After subtracting the preceding correction, 3.3 K⁻¹, we obtain 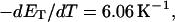which should apply to any fixed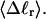

TABLE 1.

Comparison of theoretical and experimental E_T values

T (K)		*	†
313	13.25	1141	1160
318	11.0	1086	1125
323	8.8	1032	1085
328	6.8	978	1035
333	4.5	923	973

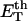^* is calculated for the appropriate 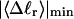according to Eq. 21.

^†Reported as q by Bauer and Benham.

Statistical errors in E_T and −dE_T/dT

Bauer and Benham (1993) reported no standard deviations for E_T. Determinations of E_T by the topoisomer distribution method require typically 10 replicate measurements of E_T to reduce the standard deviation of the mean to the 3% level, or ±30, when E_T is ∼1000. This 3% uncertainty is comparable to the spacing between reported E_T values at the different temperatures in the study of Bauer and Benham. In addition, problems with reproducibility of E_T measurements and slow temporal shifts in behavior of pBR322 have been noted previously (Song et al., 1990; Naimushin et al., 1994). Although the protocol of Bauer and Benham is a very different approach to E_T measurements that is possibly less prone to statistical and reproducibility errors, in the absence of any evidence to support such a conjecture, that must be regarded as unlikely. Indeed, in a subsequent application of the same protocol to pSM1 DNA, the scatter in the plot of E_T versus 1/T is ∼±30 around the best-fit curve (Bauer et al., 1995). If we assume a standard deviation of ±30 in the E_T measurements, then a routine error propagation analysis yields a standard deviation, 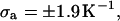for the best-fit slope, a = −9.36 K⁻¹, of the experimental data. The above corrected experimental slope for fixed 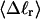can now be restated as 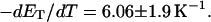The 31% relative uncertainty in the corrected slope is considerably greater than that (∼8%) reported for the uncorrected slope by Bauer and Benham, who evidently assumed much smaller relative errors, 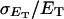<1%, in their measurements. We suspect that the fourfold larger relative errors in both E_T and 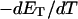found for pSM1 are more realistic.

The predicted variation of E_T with 〈Δℓ_r〉 and T

The present simulations for n = 0 were performed using a torsion elastic constant, 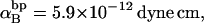between basepairs, a persistence length, P = 500 Å, and repulsive interactions for 20 mM ionic strength at 298 K. The line defined by the linear parts of the coalesced E_T versus 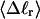curves in Fig. 8 is empirically given by 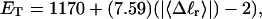as noted above, and takes the value 1170 at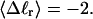

Previously, E_T values at various temperatures were simulated for a model unmelted DNA in a 55 mM ionic strength buffer containing 5 mM Mg²⁺ by using the measured temperature dependent torsion elastic constants of an 1876 bp pBR322 fragment under those same conditions (Delrow et al., 1997b). In addition, the persistence length was taken as 500 Å, and the intersubunit repulsions were appropriate for the 55 mM ionic strength buffer containing 5 mM Mg²⁺. Simulations were performed only for 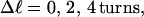so any variation of with 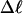was not discernible. Although the presence of the Mg²⁺ significantly raised the torsion elastic constant to 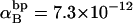dyne cm at 293 K, it also significantly decreased the repulsive interactions in comparison to those in the present simulation. The best-fit line of the simulated E_T versus T, namely 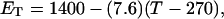takes the value E_T = 1187 at 298 K, which is close to the corresponding value, E_T = 1170, obtained from the empirical line of E_T versus 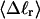for 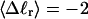at 298 K in our simulations. Evidently, for small 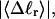the differences in torsion elastic constant and intersubunit repulsions between the two simulations have almost exactly canceling effects on E_T. The slope of the torsion elastic constant, 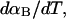was previously found to be insensitive to either removal of the 5.5 mM Mg²⁺ or an increase in ionic strength. We now assume that the temperature dependence of E_T at small fixed 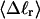under conditions of these simulations would be practically the same as found in the previous simulations. Then the combined variation of the simulated E_T with both T and 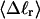in 20 mM ionic strength should be closely approximated by the relation,

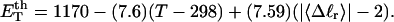(21)

The theoretical slope, 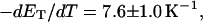agrees with the above corrected experimental slope, 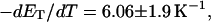within their combined uncertainties.

Equation (21) enables theoretical predictions of the absolute magnitude of E_T for arbitrary T and 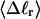for pBR322 in 20 mM ionic strength.

A test of the theory versus experiment

We assume that the minimum value, 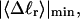of the fitted data at each temperature in Fig. 4 of Bauer and Benham carries the most weight in their fitting procedure, and is maximally responsible for determining the best-fit value of E_T. If we further suppose that their protocol yields reliable values of both 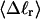and E_T, then the experimental E_T values reported by Bauer and Benham should match the theoretical values computed from Eq. 21 by using the various 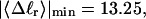11.0, 8.8, 6.8, and 4.5 turns at T = 313, 318, 323, 328, and 333 K, respectively. This comparison is given in Table 1. The experimental values exceed the theoretical values by ∼2–5%. As noted above, a ∼5% overestimation of the experimental E_T values is expected due to the use of Eq. 19, when E_T increases with 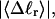as predicted in 20 mM ionic strength. After scaling the experimental values by 0.95 to compensate for their overestimation, the agreement is remarkably good, with discrepancies of 3.4, 1.6, 0.1, −0.5, and −0.1% between the theoretical and the downward scaled experimental values (not shown) at, respectively, 313, 318, 323, 328, and 333 K. Such good agreement argues for the approximate validity of both Eq. 21 and the 0.95 scaling of the experimental E_T values.

To what extent does Eq. 21 depend upon parameters of the melted region, such as its torsion and bending elastic constants? The coalescence of the E_T versus 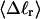curves in Fig. 8 establishes that E_T is independent of n (or m). Because E_T for n = 0 is necessarily independent of the torsion and bending elastic constants of the melted region, it must be presumed that E_T depends only on parameters of the duplex region, even in locally melted DNAs. Thus, the slope, 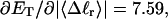in Eq. 21 should be practically independent of the values of the torsion and bending elastic constants of the melted region. Equation 21 may prove useful in the prediction of E_T values at various temperatures for the duplex regions of both unmelted and locally melted supercoiled DNAs with lengths comparable to 4349 bp in 20 mM ionic strength.

A possible enhancement of the slope, −dα_D/dT, in the protocol of Bauer and Benham

It seems likely that the elastic constant for interwinding single strands, corresponding to 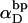in our model, increases with increased interwinding, or linking difference, 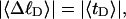in the melted region. 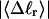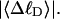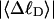This phenomenon should be similar to the increase in E_T with of the duplex region, and should occur for a similar reason, namely an increase in electrostatic free energy relative to the interwinding free energy for a hard filament upon increasing If this conjectured increase of with increasing were true, that would provide an additional contribution to 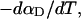because the typical 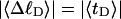(or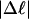) of the topoisomer with a given fixed number of melted basepairs decreases with increasing T. Such an artifactual enhancement of 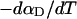may be partly responsible for the extrapolation of the experimental 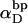to unphysical negative values for temperatures above 79°C, as discussed in the Appendix.

Locations of the melted regions

More than 100 configurations were examined visually with the aid of a modeling program. The writhe was found predominantly in interwound domains, as expected, and the superhelix axis was commonly branched especially at the larger 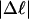values. To determine where the melted regions occurred, each molecule was subdivided into the following four rough categories:

1. An arm domain, which is the interior of a well-defined interwound superhelix.

2. An apex domain, which is the external end loop of an interwound superhelix.

3. A linker domain at a “node”, where two or more superhelix branches, or arms, meet.

4. Other domains not easily characterized.

Detailed inspections were carried out for randomly chosen configurations from three regular simulations:

1. n = 0,

2. n = 2,

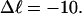
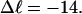
3. n = 2,

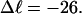
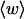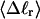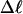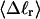Subsets a and b have very similar and values despite the difference in n, whereas subsets b and c have the same n, but very different and values. Twenty configurations were inspected in each case to determine the locations of subunits 154 and 155, which are those possessing the weak bending and torsion springs. The numbers of occurrences in each kind of domain are shown in Table 2. For n = 0, there are no elastically weak regions, and the results simply provide a noisy sampling of the fraction of the molecule within each kind of domain. For the n = 2 molecules with intermediate linking difference (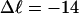), the melted regions occupy about equally the apex and linker domains, both of which are apparently preferred to arms. However, at larger linking difference (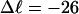), where more superhelix branching is evident, the melted regions strongly prefer linker and to a lesser extent arm domains to apex domains. A typical location for a melted domain is shown in Fig. 10. Substantial bends are typically associated with the melted regions in the linker domains. This behavior contrasts sharply with that found for directional permanent bends (Bussiek et al., 2002; Pfannschmidt and Langowski, 1998; Chirico and Langowski, 1996), which strongly prefer apex domains. The strong preference of a melted region for linker domains in the typically branched molecules at large 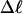is likely due in part to the entropy associated with the ability of the molecule to bend in any direction at that point, which allows for many relative orientations of the two superhelix branches that are connected by that linker domain.

TABLE 2.

Numbers of occurrences of subunits 154 and 155 in different regions for various simulated molecules

	Simulated molecules
	n = 0	n = 2	n = 2	n = 1*	n = 1*
Domain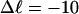
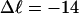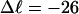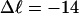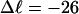Arm	8	0	5	2	3
Apex	2	5	2	5	1
Linker	2	6	11	6	10
Other	8	9	2	7	6

^*The (154,155) spring has the weak bending elastic constant of a melted subunit, but also has the torsion elastic constant of a normal duplex subunit.

FIGURE 10.

Typical structure of a simulated model DNA with n = 2 melted subunits and 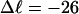turns. The location of the melted region is indicated by the arrow, and lies in the linker region between interwound arms.

To determine whether the softer bending potential or instead the softer torsion potential was primarily responsible for the preference of the melted regions for linker regions at large two additional simulations were performed for models containing a single subunit with a weak bending spring typical of a melted region, but also a normal duplex torsion spring. The results for this model are presented in the fourth and fifth columns of Table 2. These results are very similar to those in columns three and four, respectively. We conclude that the softer torsion elastic constant contributes little or nothing to the preference of melted regions for linker domains.

The contrasting preferences of flexurally weak melted regions for linker domains on one hand and of intrinsically curved duplex sequences for apex regions on the other may stem largely from the strong directionality of the latter bends, which would prevent such a region from realizing the full entropy of bending in different directions, if it were to occupy a linker domain. This interpretation is supported by the fact that the strong preference of flexurally weak regions for linker domains over apex regions occurs only at the larger linking differences, where superhelix branching is both more common and more extensive.

APPENDIX: POTENTIALS, INPUT PARAMETERS, SIMULATION PROTOCOLS, AND STATISTICAL METHODS

Potential functions

The torsion potential is given by

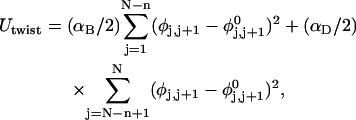(A1)

where N − n and n are the numbers of subunits in the duplex and melted regions, respectively, α_B is the torsion elastic constant of those springs for which 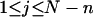lies in the duplex region, 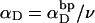is the torsion elastic constant of those springs for which 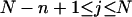lies in the melted region, 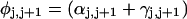is the sum of the first and last angles of the Euler rotation, 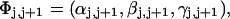which orients the (j + 1)th subunit in the frame of the jth subunit, and 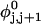(radians) is the intrinsic twist from the jth to (j + 1)th subunit. In this study, 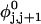is not identified with the intrinsic subunit succession angle, 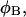of a real DNA, but instead is a parameter that is employed to continuously vary the linking difference from 0 to −26 turns, whereas the linking number remains fixed at zero turns.

The simulation temperature is taken to be 298 K. For duplex regions, we take 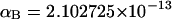dyne cm, which corresponds to a torsional rigidity, 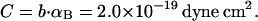Numerous measurements of the torsional rigidities of pBR322 and other plasmids of comparable size by time-resolved fluorescence polarization anisotropy yielded values in the range (1.9–2.2) × 10⁻¹⁹ dyne cm² in the ionic strength range 10–100 mM at ambient temperature (Schurr et al., 1992; Heath et al., 1996; Naimushin et al., 2000, 2001). When such measured values of C were employed along with a persistence length, P = 500 A, and appropriate intersubunit repulsions in simulations of supercoiled p30δ DNA (4752 bp) in 0.1 M ionic strength, the predicted values of the twist energy parameter (E_T), structure factor (S(q)) over a range of scattering vectors from q = 0 to 2.4 × 10⁵ cm⁻¹, and translational diffusion coefficient (D_T) agreed well with the corresponding measured values over a wide range of superhelix density from zero to native (Gebe et al., 1995, 1996; Clendenning et al., 1994). Likewise, simulations of surface-flattened pSA509 DNA (3760 bp) in 161 mM ionic strength, using C = 2.0 × 10⁻¹⁹ dyne cm², yielded structures similar to those seen in AFM (Fujimoto and Schurr, 2002; Lyubchenko and Shlyakhtenko, 1997).

The torsion elastic constant between subunits (containing 28.06 bp/subunit) for locally melted regions is here taken to be 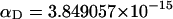dyne cm, which is 54.5-fold smaller than α_B for the duplex regions at 298 K. This choice of 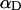corresponds to 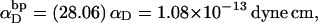which is obtained by extrapolating the results of Bauer and Benham to 37°C. A longer extrapolation to 25°C, some 15° below their lowest measurement, cannot be justified, because unphysical negative values of 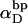are predicted by their best-fit straight line 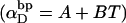for T ≥ 79°C, and presumably arise from an overestimated negative slope (−B), as noted in the main text.

The electrostatic part of the nonnearest-neighbor interaction energy is reckoned by placing three spheres, each containing Z electronic charges, on the axis of each subunit rod. These charged spheres are spaced (95.4)/3 = 31.8 Å apart and are centered at positions r_j, r_j + (1/3)b_j, and r_j + (2/3)b_j, where r_j is the position of the coordinate frame of the jth subunit at the end of the (j − 1)th rod, and b_j is the bond vector from the jth frame to the (j + 1)th frame. The electrostatic interaction energy is taken over all pairs of charged spheres that do not lie on the same or adjacent subunit rods. The subunit interaction energy also includes a hard-cylinder repulsion energy, U_HC, between nonnearest neighbor units. The total interaction energy between two charged spheres, i and j, on nonadjacent subunits is taken as (Fujimoto and Schurr, 2002; Delrow et al., 1997a)

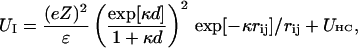(A2)

where e is the electronic charge, ɛ is the dielectric constant, r_ij is the distance between charge centers, d is the charged sphere radius, and κ(cm⁻¹) is the Debye-Hückel screening parameter, given in cgs units by 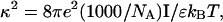where N_A is Avogadro's number, 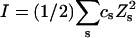is the ionic strength, c_s is the concentration (mole/L), and Z_s is the valence of the sth kind of ion. The dielectric constant is taken to be ɛ = 78.54 at 25°C. The radius of the charged spheres is taken as d = 12 Å. U_HC is infinite, when the axes of the two subunit rods approach more closely than 24 Å (corresponding to a hard-cylinder diameter, 2d = 24 Å), and zero otherwise. Screened Coulomb interactions are ignored, when 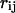exceeds a cut-off distance, which is chosen so that the first term on the right-hand side of Eq. A2 equals (7.3 × 10⁻⁴)kT at the cut-off distance. U_HC is implemented by a protocol that performs the test and rejects any Monte Carlo move leading to a configuration that violates the minimum distance of closest approach (Gebe et al., 1995).

The screening parameter κ is calculated from the prevailing ionic strength in the 90 mM Tris-borate solution of Bauer and Benham (1993). The reckoning of this ionic strength is complicated, because the measured pH of the 90 mM Tris-borate solution (8.4 at 25°C) differed from that expected (8.65) from the pK_a's of Tris·H⁺ (8.069) and boric acid (9.236) alone. This discrepancy is presumably attributable to the formation of complexes between the neutral Tris and borate anion (Taylor et al., 1996). Three different approximate estimates of the ionic strength clustered around 20 mM, which is the value adopted here. Finally, the effective valence of the charged spheres, Z = −9.19, was chosen so that the electrostatic potential surrounding the middle of a linear array of 2001 charged spheres with 31.8 Å spacing closely matched the solution of the nonlinear Poisson-Boltzmann equation for a uniformly charged cylinder with 12 Å radius and the linear charge density of DNA at all distances beyond the hard-cylinder diameter, d = 24 Å, as described by Delrow et al. (1997a).

The bending potential energy is given by

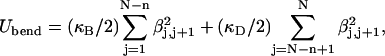(A3)

where κ_B and κ_D are the torque constants for bending of the duplex and denatured regions, respectively. β_j,j+1 is the second rotation in the composite Euler rotation, 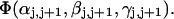The value of κ_B was chosen to yield a persistence length, P = 500 Å, in the following manner. Simulations of both 10- and 20-subunit (b = 95.4 Å) chains were performed (10 million attempted moves per simulation) with several different values of 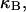but using always the same values of the parameters in U_twist and U_I that were discussed above. For each simulation, the persistence length was calculated according to 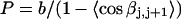for each model, where the average, 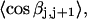was taken over all subunits, j = 1, … ,N − 1, in all configurations. The value κ_B = 1.806 × 10⁻¹³ dyne cm was found to yield P = 500 Å (within the simulation errors) for both 10- and 20-subunit chains, and was adopted for the simulations reported here.

To our knowledge, the effects of flexurally soft regions on the tertiary structure and energetics of supercoiled DNAs have not previously been simulated. In the absence of any precedent, we choose 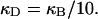However, due to the large size and valence of the charged spheres, the electrostatic interactions make an overly large contribution to the persistence length (Delrow et al., 1997a). Thus, despite the fact that 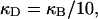the persistence length associated with κ_D is ∼175 Å, which is only ∼2.9-fold smaller than that associated with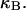

Calculation of t_B, w_B, t_D, T_D, w_D, and Δℓ̃_r

For each selected configuration, the net twist, t, is calculated according to Eq. 3), and t_B and t_D are reckoned from the first and second terms, respectively, on the far right-hand side of Eq. 4. Finally, T_D = t_D − nφ_D.

Due to the long subunit length in this work, the writhe computed according to Eq. 5 is insufficiently accurate, and leads to fluctuations in the computed linking difference, 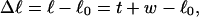of as much as 4% around the starting value. To improve the accuracy of the writhe calculations, each subunit rod is subdivided into 10 coaxial subrods of equal length, b/10. The total writhe is now calculated according to

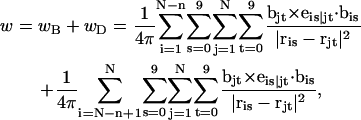(A4)

where 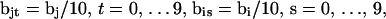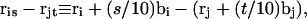and 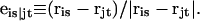w_B and w_D correspond to the first and second terms, respectively, in Eq. A4. Use of this higher-resolution writhe calculation reduced the fluctuations in computed linking difference around the starting value to less than one part in 10³. The writhe is calculated for only one configuration in every 10,000 moves.

Nonvanishing self-writhe requires a minimum of three bond vectors, sufficient to create a nonplanar bend. In these models, wherein the denatured region contains only n = 1 or 2 rigid-rod subunits, 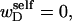so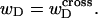

The total linking difference of any simulated DNA, whether partially melted or not, is reckoned according to 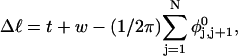where 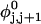is the intrinsic twist of the torsion spring between the jth and(j + 1)th subunits, and is defined explicitly below.

The residual linking difference of the duplex region in a partially melted molecule is calculated by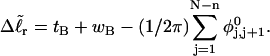

Models with total linking differences of {0, −2, −4, −6, … , −26} turns are simulated by using the corresponding uniform values of 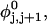namely 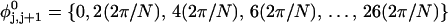for all j = 1, … , N, together with a starting configuration that is a planar polygon with initial twist angles, φ_j,j+1 = 0, so w = 0 and t = 0. In this convention, 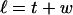remains at the value 0 in all of our simulations, but the linking difference is decreased stepwise, as 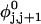is raised from each step to the next. In other words, the actual DNA comprising a duplex region with intrinsic subunit succession angle, 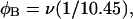a melted region with intrinsic succession angle, φ_D = 0, and a nonvanishing linking number, 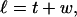is replaced by a model that exhibits a linking number, 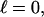and a uniform intrinsic twist, 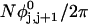(turns), that is chosen to yield the desired linking difference. Although the intrinsic twist is chosen to be uniform over the entire molecule, the torsion and bending elastic constants differ greatly between duplex and melted regions. Such a procedure is valid because the state of torsional strain of the molecule depends only upon the difference between the actual twist 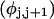and intrinsic twist 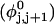of each spring, not upon either value separately. In principle, the 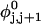for a given subunit could be assigned any value, provided that 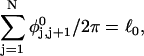the total intrinsic twist of our model DNA. Here, 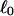is used as an adjustable parameter to vary the linking difference, so for each of our DNAs with n = 0, 1, or 2 weak springs (i.e., “melted” subunits), the initial value is taken to be 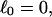and 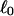is increased stepwise to 2, 4, … , 26 turns to generate total linking differences, 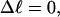−2, −4, … , −26 turns, respectively. The unmelted parent of a locally melted model molecule is not simulated. However, its linking difference 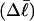is reckoned from the 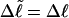of its locally melted model daughter DNA via Eq. 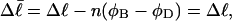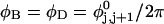1, since in these simulations. For our simulated molecules, then, it is always true that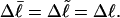

Calculation of the inertial tensor elements and the radius of gyration

The squared radius of gyration of a single configuration is calculated according to 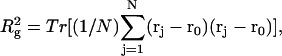where 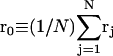is the center of “mass”. The quantity in square brackets is the dyadic inertial tensor, which can be expressed as a 3 × 3 symmetric matrix. This symmetric matrix is diagonalized to yield its three positive eigenvalues, which are designated in order from largest to smallest as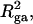 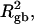and 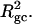Each of these three quantities and also 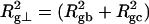is averaged over the saved molecular configurations. Invariance of the trace to similarity transformation gives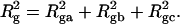

Simulation protocols

The Metropolis Monte Carlo protocol is similar to that described previously by Schurr et al. (1995). In particular, the full potential energy function, rather than just the reduced potential energy function, is evaluated on every step and used in the Metropolis acceptance criterion. Moreover, the 3N Euler angles that orient each subunit in the laboratory frame are kept to define each configuration. The topological constraint in Eq. 2 is never explicitly enforced, except for the initial configuration, but instead is automatically obeyed to acceptable numerical accuracy (better than 1 part in 10³). Our protocol employs the sampling, ring closure, hard-cylinder exclusion, knot detection, and reversible work algorithms of Gebe et al. (1995), Gebe and Schurr (1996), and Schurr et al. (1995), and the electrostatic interaction algorithm of Delrow et al. (1997a). When supplied with appropriate input parameters, simulations using these algorithms satisfactorily reproduce experimental values of the supercoiling free energy, translational diffusion coefficient, and structure factor of the p30δ DNA over a wide range of superhelix density in 0.1 M ionic strength, and also yield typical observed structures of a surface-flattened native supercoiled plasmid in 0.161 M ionic strength, as noted above. However, these same protocols and potentials are known not to work so well at lower ionic strength, specifically at 0.01 M (Gebe et al., 1996; Fujimoto and Schurr, 2002). There is considerable evidence that certain supercoiled DNAs in 0.01 M ionic strength undergo one or more long-range allosteric transitions in secondary structure with increasing superhelix density (Shibata et al., 1984; Wu et al., 1988, 1991; Song et al., 1990; Schurr et al., 1992, 1997; Heath et al., 1996; Delrow et al., 1997b; Naimushin et al., 2000). This phenomenon may be at least partially responsible for the observed shortcomings of these protocols and potentials for 0.01 M ionic strength. Such complications are ignored here to assess the properties of the very simplest idealized model of a supercoiled DNA.

The starting configuration for the simulation of each model supercoiled DNA with n = 0, 1, or 2 weak springs was taken to be a planar polygon with zero intrinsic twist, 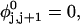j = 1, … , N, and zero actual twist, 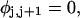j = 1, … , N. Thus, the initial values of the writhe, w; net twist, t; linking number, 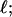intrinisic twist, 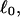and linking difference all vanish. The system was then “equilibrated” for 12 million attempted moves before saving any configurations. The final configuration at the end of this “equilibration” period was used as the initial configuration for eight additional runs of 4 million attempted moves, totaling 32 million attempted moves. During these latter data collection runs, a configuration was saved once every 10,000 moves (3200 saved configurations for each linking difference). 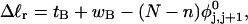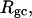From these saved configurations, the average values and variances are calculated for t, t_B, t_D, T_D, w, w_B, w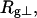_D, and 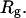The total linking difference 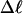is initially selected in the simulation. The values of 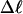computed according to Eq. A5 fluctuate only very slightly (by less than 1 part in 10³) from the initial value, due to numerical errors primarily in the writhe calculation. The ensemble average values 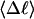lie even closer to the initially selected values. For that reason, we take 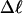as the initially selected value, rather than the practically identical average value, 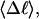in the discussion of results.

The squared standard deviation (variance) of each property, x, is calculated in the usual way, 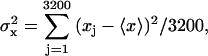where the average value, 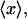is reckoned from all 3200 sample values.

The squared standard deviation of the mean of each property is estimated according to 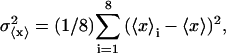where 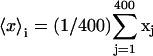is the average over individual values of the ith data collection run, of which there are eight (for each selected value of 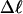and n). This relation provides an accurate estimate, when the system relaxes well within the 4 million moves of each data collection run, which is the case here.

After completion of the data collection runs, the intrinsic succession angle, 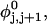is incremented by 4π/N for all j = 1, … , N, which decreases the linking difference by two turns. The starting configuration for this new linking difference is taken to be the final configuration at the end of the “equilibration” period for the previous linking difference. The system is then “equilibrated” at the new linking difference for 12 million attempted moves. Again, the final configuration at the end of the “equilibration” period was taken as the starting configuration for each of eight additional runs of 4 million moves, and the entire procedure outlined above is repeated.