Dynamic Elastic Modulus of Porcine Articular Cartilage Determined at Two Different Levels of Tissue Organization by Indentation-Type Atomic Force Microscopy

Abstract

Cartilage stiffness was measured ex vivo at the micrometer and nanometer scales to explore structure-mechanical property relationships at smaller scales than has been done previously. A method was developed to measure the dynamic elastic modulus, |E^*|, in compression by indentation-type atomic force microscopy (IT AFM). Spherical indenter tips (radius = ∼2.5 μm) and sharp pyramidal tips (radius = ∼20 nm) were employed to probe micrometer-scale and nanometer-scale response, respectively. |E^*| values were obtained at 3 Hz from 1024 unloading response curves recorded at a given location on subsurface cartilage from porcine femoral condyles. With the microsphere tips, the average modulus was ∼2.6 MPa, in agreement with available millimeter-scale data, whereas with the sharp pyramidal tips, it was typically 100-fold lower. In contrast to cartilage, measurements made on agarose gels, a much more molecularly amorphous biomaterial, resulted in the same average modulus for both indentation tips. From results of AFM imaging of cartilage, the micrometer-scale spherical tips resolved no fine structure except some chondrocytes, whereas the nanometer-scale pyramidal tips resolved individual collagen fibers and their 67-nm axial repeat distance. These results suggest that the spherical AFM tip is large enough to measure the aggregate dynamic elastic modulus of cartilage, whereas the sharp AFM tip depicts the elastic properties of its fine structure. Additional measurements of cartilage stiffness following enzyme action revealed that elastase digestion of the collagen moiety lowered the modulus at the micrometer scale. In contrast, digestion of the proteoglycans moiety by cathepsin D had little effect on |E^*| at the micrometer scale, but yielded a clear stiffening at the nanometer scale. Thus, cartilage compressive stiffness is different at the nanometer scale compared to the overall structural stiffness measured at the micrometer and larger scales because of the fine nanometer-scale structure, and enzyme-induced structural changes can affect this scale-dependent stiffness differently.

INTRODUCTION

Stiffness is the mechanical parameter describing the relation between an applied, nondestructive load and resultant deformation of a material. It can be determined at all scales of a material's internal structure, and will vary if the measuring device addresses different structural elements rather than their aggregation. It also often varies with the nature of the load (e.g., tension, compression, and shear), the rate of deformation, and whether deformation is monotonic or cyclic.

Additionally, stiffness can be sensitive to the internal structural details of heterogeneous materials and thus can be used as a probe of hierarchical structure-property relationships. A large body of data is available describing the compressive stiffness of articular cartilage at the millimeter scale. These stiffness values have often been measured in situ by indentation testing using clinical millimeter-scale indentation devices during arthroscopic surgery. The purpose of such studies is to help surgeons assess and map the loadbearing capacity or “health” of the cartilage, and to better understand how cartilage pathology affects this key mechanical property.

Mechanical properties of cartilage

Because of its composition and structure, cartilage behaves mechanically as a viscoelastic solid (Cohen et al., 1998; Lai et al., 1991; Mow et al., 1980). Therefore, its mechanical properties (e.g., stiffness, strength) depend on the rate of strain or the rate of stress - depending on which parameter is controlled. Also, under cyclic loading, the applied stress and the resulting strain are not in phase. For compressive or tensile strains, the ratio of stress to strain is the dynamic elastic modulus, |E^*|, which is the vector sum of the storage modulus E′ (the in-phase, elastic component) and the loss modulus E″ (the out-of-phase, viscous component). In contrast, for solid materials that behave elastically (e.g., steel), cyclic stress and strain are in phase, i.e., no energy dissipation occurs in the elastic range and all applied energy is stored, not lost, and the ratio of stress to strain is the elastic modulus, E (also having units of force/area). The general term stiffness is used to describe the relation between stress and strain determined under various loading modes below the stress level which causes permanent deformation. In tension and compression, the quantities are E and |E^*| as described, whereas in shear, the analogous quantities are G and |G^*|.

Two mechanisms are responsible for the viscoelastic behavior of cartilage: 1), a flow-independent mechanism, intermolecular friction, exhibited in all polymeric materials, and 2), a flow-dependent mechanism that is present if loading conditions allow water to move through the structure. However, in ambulation (i.e., walking, running), loading and unloading are transient events, occurring in <1 s. Under these conditions, essentially no motion of water through the structure occurs, due to the high drag coefficient (∼10¹⁴ Ns/m⁴; Mankin et al., 1994). Hence, the mechanical response of cartilage should be measured under dynamic cyclic conditions at a functionally relevant frequency, i.e., in the range of 0.5–3 Hz. The value of the dynamic shear modulus |G^*| for human articular cartilage was found to increase with cyclic frequency, and for a frequency range of 0.01–20 Hz, it varied from ∼0.1 to 2.5 MPa (Mankin et al., 1994). In contrast, when cartilage was placed under a constant compressive load for a few hours (i.e., with the interstitial fluid allowed to escape freely), the swelling pressure vanished and the quasistatic compressive modulus was determined to be ∼0.4–1.5 MPa (Mankin et al., 1994).

For clarification, the shear modulus G and the extensional modulus E are related for homogenous, isotropic materials by E = 2 G (1 + ν), where ν is Poisson's ratio, so for ν = 0.5, E = 3 G. The indentation modulus is usually an extensional modulus, E or |E^*|, although the state of stress is primarily a mixture of compression and shear. In the work presented here, a dynamic indentation modulus, |E^*|, using a microspherical probe and a modulus value, E, from a calibration curve based on quasi-static compression testing were measured (see Materials and Methods, Table 2). Because the measurements presented here are dynamic, the use of |E^*| in place of E is appropriate, and for the materials presented here, with ν = 0.5, it should be appropriate to assume that |E^*| = 3 |G^*| so the measurements can be related to the results of Mankin et al. (1994).

TABLE 2.

Comparison of the dynamic elastic modulus |E^*| of a 2.5% agarose gel and for native, cathepsin D digested and elastase-digested articular cartilage

Sample	Indenter shape radius (nominal values)	Spring constant [N/m] (nominal values)	Method	(Dynamic) Elastic modulus ± variation [MPa]/number of measurements (n)
Agarose gel 2.5%	Flat punch cylindrical r > 3 cm	—	Compression tester	E = 0.022 ± 0.002/3
	Spherical r = 2.5 μm	k = 0.06	Modeling	|E*| = 0.036 ± 0.005/3
	Pyramidal r = 20 nm	k = 0.06	Blind calibration	|E*| = 0.022 ± 0.003/5
Articular cartilage (native)	Spherical r = 2.5 μm	k = 13	Modeling	|E*| =2.6 ± 0.05/4
	Pyramidal r = 20 nm	k = 0.06	Modeling	|E*| = 0.027 ± 0.003/5
	Pyramidal r = 20 nm	k = 0.06	Blind calibration	|E*| = 0.021 ± 0.003/5
Articular cartilage cathepsin D digestion	Spherical r = 2.5 μm	k = 13	Modeling	|E*| = 2.6 ± 0.05/4	0*
				|E*| = 2.6 ± 0.05/4	2*
	Pyramidal r = 20 nm	k = 0.06	Blind calibration	|E*| = 0.021 ± 0.003/5	0*
				|E*| = 0.032 ± 0.006/5	1*
				|E*| = 0.054 ± 0.010/5	2*
Articular cartilage elastase digestion	Spherical r = 2.5 μm	k = 13	Modeling	|E*| = 2.6 ± 0.05/4	0*
				|E*| = 0.877 ± 0.05/4	2*
	Pyramidal r = 20 nm	k = 0.06	Blind calibration	†

Note: The compression tester performed a quaisi-static compression testing, therefore an elastic modulus E instead of a dynamic elastic modulus |E*| was measured.

Values are shown for nanometer-sized sharp pyramidal tips and micrometer-sized spherical tips employed for the IT AFM measurements, along with values determined for the agarose gel with a millimeter-sized compression tester. For IT AFM measurements, modulus values were determined from the slopes of the load-displacement curves using either an elasticity-based indentation model (modeling) or a calibration curve based on compression testing of agarose gels (blind calibration). The data on articular cartilage are the result of measurements on articular cartilage that came from pig knees of several different animals. The number of data sets, n, averaged to produce a given tabulated value is shown.

^*Elasticity measurements done after 0, 1, or 2 days of cathepsin D or elastase digestion.

^†After digestion of the sample with elastase, it became very sticky so that reliable measurements of the modulus were not possible.

Determining cartilage mechanical properties by indentation testing

Well-established indentation testing procedures are available for estimating mechanical properties, typically stiffness and strength. These tests were originally developed in the material sciences for both hard solids (e.g., ceramics and metals) with more recent application to polymeric materials and are increasingly being applied to studies of biological tissues. Clinical indentation testing devices used for evaluating the mechanical properties of articular cartilage typically employ flat-end cylindrical or spherical probes, a few millimeters in diameter (Appleyard et al., 2001; Shepherd and Seedhom, 1997; Lyyra et al., 1995; Aspden et al., 1991; Tkaczuk, 1982). Such large-scale clinical indenters average the mechanical properties of the biological tissue over a large volume, i.e., over several mm³ of material. Hence the sensitivity of resolving local variations in cartilage properties is quite limited, such that, for example, no statistically significant difference was found between clinically healthy and unhealthy types of arthritic cartilage (Tkaczuk, 1986).

As the lateral size of the indentation probe decreases, lower forces and penetration depths can often be used, resulting in the measurement of biomechanical properties of a smaller volume of material, potentially with improved sensitivity to local property variations. Thus, when articular cartilage tissue is tested mechanically at the millimeter and micrometer scales, the nanoscale structural components share the task of load bearing, resulting in aggregate mechanical properties that are distinctly different from those of the individual nanoscale components. In contrast, a nanometer-sized AFM tip, being smaller than the diameter of a collagen fiber, can be expected to reveal stiffness variations that are related to the three-dimensional organization of collagen fibers and proteoglycan chains. Therefore, the combination of micrometer-sized and nanometer-sized AFM tips can be used to measure the aggregate stiffness of articular cartilage as well as the stiffness related to the tissue's fine structure.

Other considerations in tissue indentation testing

The onset of tip-sample contact in indentation testing is difficult to detect for soft biological tissues, because, compared to hard materials, biological tissues are 4–6 orders-of-magnitude lower in stiffness and can have more irregular surfaces. These characteristics result in load-displacement data with no abrupt increase in load to mark the point of physical contact. This difficulty was overcome by calculating the area under the load-displacement curves that corresponds to the work done by the cantilever (A-Hassan et al., 1998). Using this approach, a method was established for relative microelastic mapping of living cells.

Because tissues are highly anisotropic and inhomogeneous and thus exhibit site- and direction-specific mechanical properties, single-location measurements may yield a significantly biased view of the mechanical properties of a given tissue. Thus, quantitative estimation of any mechanical property is best based on statistical analysis of many repeated measurements. Nevertheless, most published indentation measurements to date of the elastic properties of tissue have been based on the manual selection of one or only a few load-displacement curves. For example, Weisenhorn et al. (1993b) employed this approach in indentation-type atomic force microscopy (IT AFM) measurements to determine the elastic modulus of cells and cartilage. Radmacher and co-workers (Randall et al., 1998; Radmacher, 1997) and A-Hassan et al. (1998) provided information about the contribution of the cytoskeleton to the local cell stiffness of living cells by recording single load-displacement curves at only a few different cell surface locations. Some investigations have also evaluated the effect of drugs on the local stiffness of living cells in this manner (Rotsch and Radmacher, 2000; Hoh and Schoenenberger, 1994).

VanLandingham et al. (1999, 1997a) used the AFM for characterizing the nanometer-scale properties of the interphase regions of fiber-reinforced polymers. These authors clearly stated that in these systems the nanometer-scale properties can be significantly different from the bulk properties of one and the same sample. Along the same lines, Rho et al. (1997) and Turner et al. (1999) measured the elastic properties of human cortical and trabecular lamella bone by nanoindentation using tissue sections dehydrated in a graded series of alcohol solutions. They proposed that the elastic properties of the microstructural components of bone might not be the same as the corresponding macroscopic values. Moreover, they stated that a technique by which elastic properties of the individual microstructural components can be measured would be of great value in understanding the microstructural mechanical behavior of bone. A further step in this direction was made by Hengsberger et al. (2002), who applied a combination of AFM and a commercial nanoindenter device to measure the influence of the lamella type on the mechanical behavior of cortical and trabecular bone. These measurements, which were performed both under dry and more physiological conditions, revealed a clear dependence on lamella thickness, with thin and thick lamella exhibiting a different mechanical behavior.

The potential for elucidating the changes in structure-mechanical property relationships of cartilage from the millimeter to the micrometer to the nanometer scale motivated us to develop and scrutinize an AFM-based approach (Stolz et al., 1999) to image cartilage and measure its stiffness. We refer to our method as indentation-type AFM (IT AFM). More specifically, we have established and used a protocol for absolute measurements of |E^*|, the dynamic elastic modulus, of articular cartilage at two different length scales of tissue organization - micrometer and nanometer - and related our findings to those reported at the millimeter scale.

MATERIALS AND METHODS

Chemicals

Unless specified otherwise, all chemicals used were of analytical or best grade available and purchased from one source (Fluka Chemie, Buchs, Switzerland). For all experiments, ultrapure deionized water was used (18 MΩ/cm, Branstead, Boston, MA).

Agarose gel preparation

Gels were prepared with 0.75%, 2.0%, 2.5% and 3.0% (w/w) agarose (AGAR Noble, DIFCO Laboratories, Detroit, MI) in water. For testing agarose gels using IT AFM, plastic rings, used to reinforce paper-punch holes (inner ring diameter ∼5 mm; outer ring diameter ∼12 mm; thickness ∼0.08 mm), were glued onto 10-mm-diameter stainless steel disks used as specimen supports for mounting samples magnetically in the AFM. An aliquot of melted agarose was then poured into the center of the plastic ring and allowed to spread and solidify. The agarose gel was covered with a droplet of water to avoid dehydration. For macroscale calibration studies described later, gels were poured into cylindrical wells (43-mm diameter × 82-mm height). The hardened gels were removed from the wells immediately before measuring their stiffness.

Cartilage sample preparation

Porcine articular cartilage was obtained from freshly slaughtered pigs and kept on ice until use. It was prepared from disarticulated knee joints within 1–2 h post mortem. The cartilage was harvested from the medial and lateral femoral knee condyles by cutting samples off the underlying bone with a sharp razor blade, yielding ∼5 mm × 5 mm pieces that were ∼2 mm in thickness. The specimens, usually harvested from several animals at once, were stored at room temperature in PBS (2.6 mM NaH₂PO₄, 3 mM Na₂HPO₄, 155 mM NaCl, 0.01% NaN₃ w/v, pH 7.0) supplemented with a protease inhibitor cocktail (Complete, Boehringer-Mannheim, Mannheim, Germany).

Fresh cartilage samples were embedded in Tissue-Tek (Tissue-Tek, 4583 Compound, Sakura Finetek Europe, Zoeterwoude, Netherlands) and sectioned with a cryostatic microtome (SLEE, Mainz, Germany) at −15°C. From the ∼5 mm × 5 mm pieces, ∼2 mm in thickness, the outermost (∼1-mm thick) layer of the cartilage surface was discarded to minimize surface irregularities and tilt. Then, 20-μm-thick frozen sections were allowed to adhere to glass coverslips (6-mm diameter) that had been coated with a 0.01% poly-l-lysine solution (P8920, Sigma, St. Louis, MO) and dried in an oven at 60°C.

In preparing cartilage samples for stiffness measurements, a Teflon disk (11 mm diameter × 0.25-mm thick) was first fixed onto a 10-mm diameter stainless steel disk with fast-setting glue (Loctite 401, Henkel KG, Düsseldorf, Germany). Subsequently, the pieces of cartilage described above (∼5 mm × 5 mm × 2 mm) were glued onto the Teflon disc with Histoacryl tissue glue (B. Braun Surgical, Melsungen, Germany). The mounted specimens were then placed in a vibratory microtome (752 M Vibroslice, Campden Instruments, Loughborough, UK) to trim off the outermost, ∼1-mm-thick cartilage layer parallel to the support surface. These trimmed cartilage samples were kept in PBS at 4°C until further use.

Enzymatic digestion of articular cartilage

For enzymatic digestion of the proteoglycan moiety, a 10-μl droplet of cathepsin D solution (10 U/100 μl diluted in water; Sigma C3138) was applied to a mounted cartilage sample that had been prepared for stiffness measurements and covered with 50 μl of PBS to prevent drying. Similarly, for enzymatic digestion of the collagen fibers, a 10 μl droplet of elastase solution (Leukocyte; 1 U/100 μl diluted in water; Sigma E8140) was applied to a mounted cartilage sample that has been prepared for stiffness measurements and covered with 50 μl of PBS to prevent drying. The specimen was then placed in a petri dish at saturated humidity and incubated for ∼24 h at 37°C. Three samples were treated and measured independently. Also, three independent controls without enzyme were prepared in parallel. After 24 h, the enzyme solution was replaced by a drop of PBS. Before stiffness measurements, samples were left to equilibrate in PBS for at least 30 min in the fluid cell of the AFM. After completion of the AFM measurement, the 50-μl aliquot of the originally used buffer-enzyme solution was added back to the sample for another ∼24-h incubation before a second AFM measurement.

Atomic force microscopy imaging and indentation

All AFM experiments were carried out with a Nanoscope III (Veeco, Santa Barbara, CA) equipped with a 120-μm scanner (J-Scanner) and a standard fluid cell. Images of articular cartilage topography were obtained in AFM contact mode at a scanning rate of ∼2 Hz, either in air on dehydrated thin-sectioned samples, or in the same PBS buffer solution used for the stiffness measurements but before indentation testing. For nanometer-scale experiments, oxide-sharpened, square-based pyramidal silicon-nitride tips with a nominal tip radius ∼20 nm on V-shaped 200-μm-long silicon nitride cantilevers with a nominal spring constant of 0.06 N/m (Veeco) were employed. For micrometer-scale experiments, spherical tips were prepared by gluing borosilicate glass spheres (radius = 2.5 μm; SPI Supplies, West Chester, PA) with epoxy resin (Epicote 1004, Shell Chemicals, London, UK) onto the end of V-shaped tipless silicon nitride cantilevers having nominal spring constants of 0.06 N/m (Veeco) or 13 N/m (Ultralevers, ThermoMicroscopes, Sunnyvale, CA), using a three-dimensional microtranslation stage as described in more detail by Raiteri et al. (1998).

AFM stiffness measurements were based on recording the elastic response of the material by using the AFM tip as either a micro- or nanoindenter, depending on which tips were used. Cyclic load-displacement curves (Cappella et al., 1997; Weisenhorn et al., 1993a, 1992) were recorded at different sites on the sample surface at a vertical displacement frequency of 3 Hz. To achieve a constant and well-defined maximum applied load, a maximum tip deflection value (in units of photodiode voltage) was set, where this value (the so-called trigger voltage) indicates the desired increase in photodiode voltage beyond that for the undeflected cantilever probe. To get the deflection value in nanometers, the optical lever system had to be calibrated for a given tip. For this calibration, load-displacement curves were recorded with the same cantilever on a mica surface, which acted as an infinitely stiff sample, i.e., a sample that the tip of a low-stiffness cantilever probe cannot penetrate or deform in any way. The resulting slope obtained for the region of linear compliance provided the sensitivity factor, i.e., the factor relating photodiode voltage to nanometers of displacement, for the optical lever system (Gibson et al., 1996; Torii et al., 1996; Cleveland et al., 1993). This sensitivity value was used to correct the load-displacement data to obtain load-indentation data (Weisenhorn et al., 1993b).

The load-displacement curves were recorded at different trigger deflections for the two types of indenter tips: at 30 nm for the sharp pyramidal tips, and at 250 nm for the microspherical tips. A trigger deflection of 30 nm with the sharp tips corresponded to an applied load of ∼1.8 nN (with k = 0.06 N/m) and maximum penetration depth of e.g., ∼550 nm in 0.75% agarose gel and ∼300 nm in articular cartilage. A trigger deflection of 250 nm with the spherical tips corresponded to an applied load of ∼15 nN (with k = 0.06 N/m) or ∼3.3 μN (with k = 13 N/m) and maximum penetration depth of e.g., ∼250 nm in 2.5% agarose gel or ∼600 nm in cartilage. In all cases, the penetration depths were <1% of the sample thickness and thus well below Bueckle's indentation depth limit, i.e., 10% of specimen thickness (Persch et al., 1994; Bueckle, 1973).

Data acquisition and processing

The AFM was operated in the force-volume mode for recording a set of loading/unloading load-displacement curves dynamically at a frequency of 3 Hz. In these measurements, an individual set of data consisted of 1024 load-displacement curves recorded at a given sample site. Each curve consists of 256 data points. To exclude any possible contribution from plastic (i.e., permanent) deformation, only data from the unloading curves were employed.

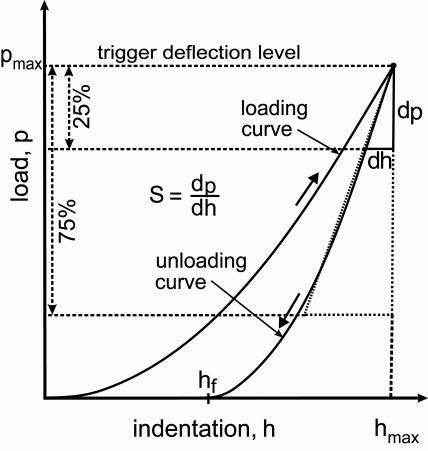
Software was developed to estimate a linear slope for each curve by fitting a 90°-angle triangle to the unloading part of the load-displacement curve and using its hypotenuse (i.e., the slope of the unloading curve) as a measure of stiffness, S (see dashed line in Fig. 1). The calculated slopes from a given set of 1024 measurements were plotted as a histogram to which a Gaussian curve was fit (see Fig. 7 A). The maximum of the Gaussian curve represents the most frequent S, i.e., S_max. Curves within a surrounding interval of S_max ± 1% (typically 100–200 load-displacement curves) were selected and arithmetically averaged to yield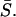

FIGURE 1.

Schematic representation of a load-indentation curve during the first complete cycle of loading and unloading. p_max is the maximum applied load, p, at maximal indentation depth, h_max, and S = dh/dp is the slope of the hypotenuse. In IT AFM measurements of cartilage, the slope of the upper 75% of the unloading curve (dashed line) was used for the analysis of the unloading data recorded by employing a sharp pyramidal tip. When employing a micrometer-sized spherical indenter, S was the slope of the upper 25% of the unloading curve (bold line).

FIGURE 7.

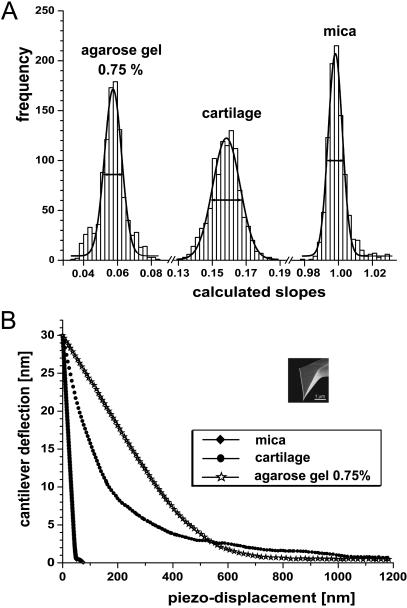
(A) Histograms and corresponding Gaussian distribution curves for repeated stiffness measurements on mica, agarose gel, and articular cartilage. Each histogram was based on 1024 load-displacement curves and was taken at a single site. (B) Averaged unloading load-displacement curves for the three different materials corresponding to the curves within ±1% of the frequency peak in A.

Determining stiffness using microspherical tips

For data collected with the microspherical tips, the dynamic elastic modulus |E^*| was computed from the average slope 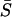(see Fig. 1) from a set of cyclic load-displacement curves according to the modeling method developed by Oliver and Pharr (1992). In this approach, the upper part of the unloading data can be fitted using a simple power-law equation,

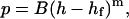where p is the indenter load, h is the vertical displacement of the indenter, and h_f represents the final unloading depth, although it is typically used as a fitting parameter along with B and m (Oliver and Pharr, 1992; Sneddon, 1965). For spherical indenters, m = 1.5, and for pyramidal tip geometries, m = 2 (VanLandingham et al., 1997b).

The load was obtained by simple multiplication of the cantilever deflection with the spring constant k. Next, a power-law fit to the average load-indentation curve was determined using the Levenberg-Marquardt algorithm and the stiffness was calculated by linear regression of the upper 25% of this fit. For calculating the dynamic elastic modulus |E^*|, we assumed that |E^*| ≈ E where the indentation modulus, E, is given by

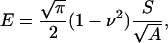where ν is the Poisson's ratio, S the contact stiffness, and A an area function related to the effective cross-sectional or projecting area of the indenter. The Poisson's ratio for agarose gels is ν = 0.5 (Matzelle et al., 2002; Mak et al., 1987; Vawter, 1983). The contact stiffness S = dp/dh has the dimension of force per unit length and is calculated as the derivative of the upper 25% of the unloading part of the load-indentation curve (see Fig. 1).

Determining stiffness using nanometer-scale sharp pyramidal tips

Rather than modeling the pyramidal tip data, the slope of the unloading part of the IT AFM load-displacement curve was directly converted into a dynamic elastic modulus by means of a calibration curve recorded from agarose gels. To generate this calibration curve, macroscale measurements of agarose gel stiffness were performed in unconfined compression by following a standard protocol for polymer testing, using a universal mechanical testing apparatus (Zwick Z010; Zwick GmbH, Ulm, Germany). As shown in Fig. 2 A, agarose gels exhibit a virtually linear stress-strain behavior over a wide range of applied load. By varying the amount of agarose in the gel (see above) the modulus can be adjusted so as to match the biological tissue of interest (Fig. 2 B). Based on the results displayed in Fig. 2, a calibration curve was generated as depicted in Fig. 2 C that was used to directly determine the dynamic elastic modulus at the nanometer scale based on the averaged load-displacement curve measured by IT AFM.

FIGURE 2.

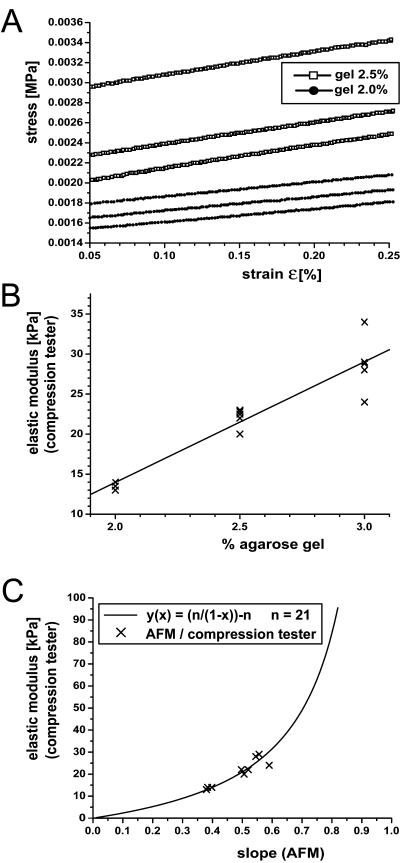
Plots of representative data used to develop a calibration curve for the direct conversion of IT AFM load-displacement curves into modulus values. (A) Stress-strain data for two agarose gels with n = 3 measurements each that are exhibiting the same slope (2.0 lower data sets and 2.5 upper data sets) in compression; (B) modulus values for three agarose gels (2.0%, 2.5%, and 3.0%) measured by compression testing, showing a linear trend with respect to the percent agarose in the gels; (C) the final calibration curve relating the slope of IT AFM load-displacement curves to a corresponding elastic modulus for the three agarose gels (2.0%, 2.5%, and 3.0%). The simplest functional relationship was y(x) = (n/(1–x))−n, where n = 21 is the fitting parameter, as indicated by the solid curve. A gel with a modulus approaching zero will not bend the cantilever, so the calibration curve must go through the origin, and for an “infinitely” hard sample, the slope is 1; thus the asymptotic behavior.

RESULTS

Agarose stiffness was equivalent at both the micrometer and nanometer scales

The modulus was determined from indentation testing of agarose gels at the nanometer scale with sharp pyramidal tips (radius = ∼20 nm) based on the calibration curve (Fig. 2 C), whereas the modulus determined at the micrometer scale with spherical tips (radius = 2.5 μm) was computed from the load-indentation geometry, as described previously. For a 2.5% agarose gel, the maximum penetration depth reached for the sharp pyramidal tip was ∼300 nm and for the microsphere, it was ∼250 nm. The resulting values of the dynamic elastic modulus were of 0.022 MPa and 0.036 MPa, respectively. The accuracy of these modulus determinations depends on the accuracy of the values of the cantilever spring constant and the sphere size used in the calculations. According to the supplier, the cantilever spring constants have an uncertainty of up to 50%, even for cantilevers on the same wafer, and the sphere size measurements are only accurate within ∼5%. Hence the agarose gel moduli determined at the nanometer and micrometer scales were indistinguishable within the range of error.

Cartilage stiffness was ∼100-fold lower at the nanometer scale than at the micrometer scale

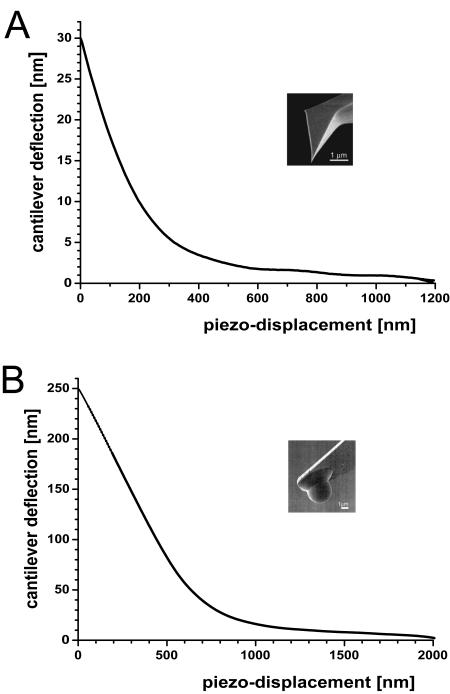
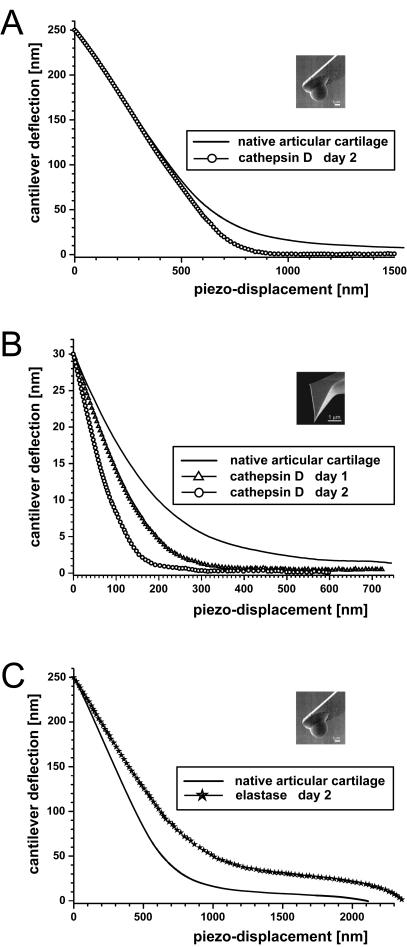
In Fig. 3, load-displacement curves are shown for articular cartilage indented with a sharp AFM tip with a nominal tip radius of 20 nm (Fig. 3 A), and with a spherical tip radius of 2.5 μm glued to an AFM cantilever (Fig. 3 B). The indentation depths were ∼300 nm for the sharp pyramidal tip and ∼600 nm for the microsphere, and the resulting modulus values were 0.021 MPa and 2.6 MPa, respectively. For comparison to the values obtained by the calibration curve, the averaged unloading load-indentation curve for the sharp pyramidal tip was also modeled according to the Oliver and Pharr model and a dynamic elastic modulus of 0.027 MPa was calculated for articular cartilage (see Tables 1 and 2 and Fig. 3 A). With the uncertainty of the spring constant mentioned above, this calculated value of 0.027 MPa is in good agreement to the 0.021 MPa obtained by the calibration curve. The micrometer-scale value of 2.6 MPa is comparable to literature values corresponding to millimeter-scale measurements (Shepherd and Seedhom, 1997; Swanepoel et al., 1994; Aspden et al., 1991; Popko et al., 1986; Hori and Mockros, 1976), but is two orders-of-magnitude larger than the nanometer-scale value of 0.021 MPa.

FIGURE 3.

Load-displacement curves of articular cartilage recorded with (A) a sharp AFM tip with a nominal tip-radius ∼20 nm and (B) a spherical tip glued to an AFM-cantilever (radius = 2.5 μm). Load-displacement curves shown are each based on 1024 measurements taken at a single site.

TABLE 1.

Comparison of test parameters between the nanometer- and the micrometer-scale modulus measurements of soft biological materials by IT AFM

	Nanoregime	Microregime
Radius of the tip	Several nm (i.e., ∼20 nm)	Few μm (i.e., ∼2.5 μm)
Applied load	NanoNewton (i.e., ∼1.8 nN)	MicroNewton (i.e., 15 nN–3.3 μN)
Indentation depth	Several 10 to a few 100 nm (i.e., 300–550 nm)	Several 100 nm (i.e., 250–600 nm)

Comparison of the structure of agarose gels and articular cartilage

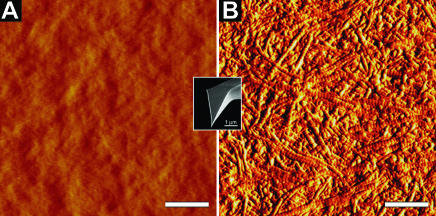
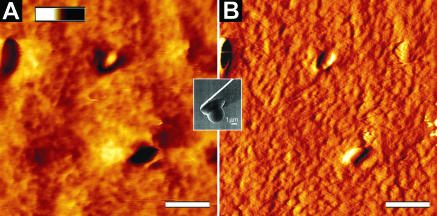
In Fig. 4, AFM images recorded with a sharp pyramidal tip are shown for a 2.5% agarose gel (Fig. 4 A) and articular cartilage (Fig. 4 B). The agarose gel image exhibits almost no structural details. In contrast, the surface of the articular cartilage is highly structured with the collagen fibers being randomly oriented. The 67-nm axial repeat of individual collagen fibers is clearly resolved. In Fig. 5, AFM height (Fig. 5 A) and deflection (Fig. 5 B) images of native articular cartilage imaged with a microspherical tip are shown. The color-graded scale bar displayed in Fig. 5 A represents a height range of 10 μm between black and white. In contrast to Fig. 4 B, the microspherical tip was not capable of resolving individual fibers, causing the surface to appear relatively homogenous. The dimensions suggest that the structures visible are chondrocytes. Note that imaging of articular cartilage tissue was much more reproducible compared to imaging the agarose gels.

FIGURE 4.

Comparison of the structure of (A) an agarose gel (2.5% agarose) with that of (B) articular cartilage as imaged using a sharp AFM tip with a nominal tip radius of ∼20 nm. The images demonstrate what the indentation tip “sees” at the nanometer scale. The agarose gel was imaged under aqueous solution, whereas the articular cartilage was imaged both under buffer solution and after cryo-thin-sectioning in air. Because of the higher resolution the image in air is presented here. The scale bars represent a distance of 1 μm.

FIGURE 5.

AFM images of native articular cartilage imaged in buffer using the microspherical tip: (A) topographic or height image and (B) deflection image. The height range (bar from white to black in A) is 10 μm and the scale bars represent a distance of 20 μm.

Enzymatic digestion of articular cartilage

Additional indentation tests were performed at the nanometer and micrometer scales on native articular cartilage to study the effects of the enzymes cathepsin D and elastase. The results are summarized in Table 2. The same protocol as discussed with Fig. 3 was followed, but additionally the articular cartilage was treated with the enzyme cathepsin D for two days. As shown in Fig. 6 A, no change in stiffness was measured as a result of cathepsin D treatment when employing the microspherical indenter. In contrast, measurements at the nanometer scale revealed stiffening from 0.021 MPa (before treatment) to 0.032 MPa after one day, and to 0.054 MPa after two days for the same samples (Fig. 6 B). In contrast, elastase digestion of collagen significantly reduced the stiffness of cartilage measured at the micrometer scale (Fig. 6 C). Articular cartilage samples treated with elastase exhibited a decrease in stiffness from 2.6 MPa (before treatment) to 0.877 MPa after two days of exposure. Measurements at the nanometer scale of elastase-treated articular cartilage were not possible, because the sample became so sticky that tip-sample adhesion dominated the load-displacement data.

FIGURE 6.

Load-displacement curves comparing the response of articular cartilage before and after enzymatic digestion with cathepsin D (A and B) and elastase (C). In A and C, measurements were made using the microsphere tip, whereas in B, measurements were made using the sharp pyramidal tip. The same samples (n = 3) were evaluated using both indenter sizes; however, measurements on elastase-digested cartilage using the sharp pyramidal tip were not feasible, due to the tip sticking in the digested cartilage.

Assessment of IT AFM stiffness measurements

To assess the sensitivity and reproducibility of stiffness measurements made using IT AFM, large numbers of load-displacement curves were made on three different materials—mica, agarose gels, and cartilage. Mica, a stiff, structurally simple material, is an aluminosilicate mineral that is readily cleaved into thin sheets with almost atomically smooth surfaces having little in-plane structural variation above the atomic crystalline level over relatively large areas (millimeter scale or greater). Although mica is softer than many minerals, its stiffness is orders-of-magnitude higher than the IT AFM cantilever spring constant of k = 0.06 N/m, and therefore essentially no penetration of the indenter into the surface occurs. Agarose gels, representing a soft, simple material, have little structure above the atomic scale but are orders-of-magnitude softer than mica. Cartilage, representing a soft, structurally complex material, is similar in stiffness to agarose gel but exhibits a well-known complex, hierarchical structure, starting at the molecular level and culminating in bundling of matrix-embedded collagen fibers that are even visible by conventional light microscopy.

A set of 1024 load-displacement curves were recorded at a single site and the slopes put into a histogram for each of these materials, as shown in Fig. 7 A. The width of the Gaussian distributions of calculated slopes was smallest for mica, larger for the agarose gel, and largest for the articular cartilage tissue. The corresponding histograms for the digested articular cartilage (i.e., with cathepsin D or elastase; see above) typically were even wider (not shown) than that for the native cartilage. In Fig. 7 B, the unloading part of the averaged load-displacement curves is shown as calculated from the curves within a surrounding interval of S_max ± 1% from each of the histograms in Fig. 7 A. The averaged load-displacement curve as shown in Fig. 7 B obtained on the hard mica surface exhibits a clear point of tip-sample contact, i.e., a sharp transition between the data before contact and after contact. In contrast, the transitions of the averaged unloading load-displacement curves of the agarose gel and cartilage do not exhibit a clear point of contact. The three different unloading load-displacement curves also demonstrate the wide range of indentation depths (i.e., the piezo displacements in Fig. 7 B) that may be obtained for the same maximum load (i.e., the maximal cantilever deflection in Fig. 7 B) for materials having different stiffnesses.

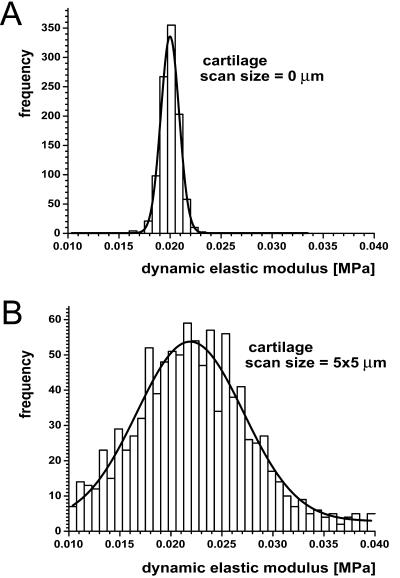
In addition to single measurements on different materials, IT AFM measurements were made to compare single site measurements to multiple site measurements on cartilage. First, 1024 unloading load-displacement curves were recorded at a single site of the cartilage tissue; the resulting histogram is shown in Fig. 8 A. Then, the AFM scan size was changed from 0 × 0 μm (collection of unloading load-displacement curves at a single site) to 5 × 5 μm (collection of 1024 unloading load-displacement curves in a two-dimensional regular array, i.e., at 156-nm spatial intervals in x and y). More specifically, the AFM tip was advanced to its new position after each loading/unloading cycle so that 32 lines of 32 unloading load-displacement curves per line were recorded for a total of 1024 multiple-site curves; the resulting histogram is shown in Fig. 8 B. Comparing these two histograms, the width is much larger for the multiple-site histogram, and the peak of the corresponding Gaussian distribution curve occurred at a slightly higher modulus value compared to the single-site distribution curve, although the difference in mean values was not statistically significant. The stiffness distribution for cartilage is also wider than for agarose gels (data not shown), reflecting the less-uniform structure of cartilage. Additionally, kinks were often observed in the load-displacement curves for cartilage, apparently due to changes in the local deformation process related to the heterogeneous structure. Repeated multiple-site measurements at a scan size 5 × 5 μm revealed that the most frequent modulus and the shape of the Gaussian distribution were highly reproducible (data not shown).

FIGURE 8.

Histograms and corresponding Gaussian distribution curves for (A) 1024 stiffness measurements at a given site, i.e., at scan size 0, and (B) 1024 stiffness measurements at multiple sites spaced evenly over a 5 × 5 μm area. The data were taken at the nanometer scale on porcine articular cartilage.

DISCUSSION

Indentation testing of soft biological materials

This study represents the first exploratory investigation of dimensional scale on the measured stiffness of soft biological tissues by IT AFM. Our goal was to make indentation testing of soft biological tissues both more reproducible and also capable of evaluating the effects of changes in fine structure on tissue stiffness - both mean values and site-to-site variability. These considerations resulted in a new protocol for preparing and mechanically testing articular cartilage in a mode that maintains its bona fide structure and its biological functioning. Because articular cartilage is a loadbearing tissue, our protocol for measuring its dynamic elastic modulus includes physiologically relevant loading rates.

Because of the considerable differences in the mechanical responses compared to hard solids, different testing and analysis protocols must be used to extract meaningful indentation data from soft biological specimens. First, some traditional indentation testing protocols include the use of preloads before loading and/or long hold periods before unloading to reduce time-dependent effects on the resulting data. However, preloading of soft biological tissue would inevitably move the water within the tissue. Also, because articular cartilage is a highly viscoelastic material, its functional stiffness, the dynamic elastic modulus |E^*|, is most appropriately determined from either stress relaxation as a function of time or cyclic load-displacement data as a function of frequency. For providing stiffness data relevant to the function of, for example, the knee joint, the cyclic rate employed should reflect the transient loading/unloading time of normal ambulation (walking, running). For articular cartilage this is in the range of a few hundred milliseconds (Shepherd and Seedhom, 1997; Popko et al., 1986). Therefore, we performed indentation testing at 3 Hz (three complete loading/unloading cycles per second), corresponding to an indenter unloading time of ∼150 ms.

Oliver and Pharr and co-workers have demonstrated that the elastic modulus of solid materials can be derived by modeling load-indentation curves (as illustrated in Fig. 1) within a few percent (Hay and Pharr, 2000; Oliver and Pharr, 1992; Pharr and Oliver, 1992; Pharr et al., 1992). In determining of the elastic modulus of hard solid materials, indentation depths are extremely low and consequently sharp tips are mostly preferred to other geometries to ensure that measurable indentation occurs. However, from our experience, a spherical tip shape produces results that are more consistent and easier to model and interpret in testing soft biological specimens. Unfortunately, there are no well-defined spherical indenters available for indentation tests at the subcellular level.

To date, stiffness measurements by AFM on biological samples have been most commonly interpreted based on the Hertz model (Walch et al., 2000; Rotsch et al., 1999; Vinckier and Semenza, 1998; A-Hassan et al., 1998; Radmacher, 1997; Radmacher et al., 1995). Although the Hertz model analyzes the problem of the elastic contact between two spherical surfaces with different radii and elastic constants (Hertz, 1882), most AFM-based indentation experiments have been performed with sharp pyramidal tips (radius = ∼5–30 nm). Further, inherent in these analyses is the need to precisely locate the initial point of contact between the tip and the specimen surface. However, for soft biological tissues, the accurate determination of the point of contact was recently described to be “one of the most vexing problems” (A-Hassan et al., 1998). Compared to hard materials, soft biological tissues are several orders-of-magnitude lower in stiffness and can have more irregular surfaces due to the lack of sample preparation, so that there is no abrupt increase in load to mark the point of physical contact. To achieve meaningful data for soft biological tissues, higher depth/width ratio indents need to be made with sharp pyramidal tips compared to e.g., spherical tips to minimize effects of tip-sample adhesion forces. Unfortunately, sharp tip indentation (tip radius ≪ indentation depth) causes complicated stress-strain fields in the tissue under the tip that is not accounted for by the Hertzian model.

To avoid some of these issues, calibration with reference materials can be used. In fact, calibration procedures for indentation of hard materials typically include indentation of reference samples. Whereas hard materials can be cut and machined to produce specimens suitable for indentation testing at different dimensional scales, biological tissues are limited in their dimensions by anatomic location and function. Therefore, agarose gels can be used as a tissue-like reference material because they 1), represent a high-water-content organic material, which is readily modeled as a mechanically isotropic structure at the length scales of interest (i.e., at the nanometer and micrometer scales); 2), can be prepared in a standard and reproducible manner; and 3), are available in bulk quantities. Further, because the gel properties vary as a function of gel content, a calibration curve can be created such that the local geometry of the tip and the profile of the sample deformation does not need to be known. The disadvantage of a calibration curve is that the sample measurement is only accurate for exactly the same set of parameters, and the same tip with the same cantilever spring constant as were used for determining the calibration curve. Hence, every time a new tip shape, cantilever spring constant, indentation speed, or indentation depth is employed, a new calibration curve must be determined.

In IT AFM determination of the elastic properties of biological materials, extraneous phenomena such as adhesion forces between the tip and sample or electrostatic interactions may cause irregularities in the lower part of the load-displacement curve (i.e., at low physical contact of the tip with the surface), thereby adding substantial noise to the recorded signal. To derive as much reliable information from the load-displacement curves as possible, the data from the upper 75% (percentage relative to the maximum force) of the unloading curves were used, because they were essentially noise-free and appeared reproducible over many indentation and retraction cycles on different biological samples. Also, no post-indentation deformation was evident that could have compromised the upper portion of the unloading curve.

Specimen stability and integrity

A prerequisite for performing of IT AFM on soft biological tissues is the stable immobilization of the sample on a solid support in a close-to-native state. Because specimens can easily deteriorate during preparation or inspection, the protocol devised has to maintain the integrity of the biological structure upon immobilization. Immobilization of the specimens on a solid support must be stable, yet the chemistry of the adhesive or glue should not alter the structural and/or functional properties of the specimen.

For indentation tests using nanometer-sized indenters on hard solids, ultrasmooth surfaces can often be prepared by finely polishing the sample with abrasive compounds of decreasing grain sizes in liquid suspensions. In contrast, for indentation testing of soft biological tissues their natural surfaces are often intrinsically neither smooth nor homogeneous at the nanometer scale. For assessing inner zones of a tissue, the outer layer can be removed by sectioning, but this still does not ensure a smooth surface at this scale. In IT AFM, a rough surface in combination with the low cantilever spring constants required for low-stiffness materials inevitably adds more noise to the measurement. To compensate, much larger indentation depths (producing longer load-displacement curves) were needed for indentation-testing the agarose gels or articular cartilage compared to the measurement of hard solids. Moreover, biological specimen surfaces are typically charged. The electrostatic interactions between the surface and the tip and local variations in the ion content of the buffer at the nanometer scale add more noise to the measurement. This is another reason why deeper indents are required.

The use of relatively large penetration depth might have caused fluid flow within or out of the cartilage during the dynamic tests. However, load-displacement curves obtained during unloading and recorded at 3 Hz using either microsphere or the sharp pyramidal tip on both agarose gels and articular cartilage did not change over the course of our multiple cycle protocol. Even after hundreds of loading and unloading cycles, no changes were observed in the load-displacement behavior, nor were any persistent residual indentations (which would be indicative of yield and plastic flow) or any mechanical effects or imaging appearance changes indicative of material fatigue. Given this lack of change in mechanical properties, the hypothesis regarding the absence of fluid flow within or out of the cartilage during the dynamic tests appears sufficiently correct. Also, given the absence of signs of structural damage and the apparently complete dimensional recovery of the samples, the use of elastic contact theory for the data analysis appears to be at least a good first approximation (Oliver and Pharr, 1992).

Determining representative load-displacement curves

The IT AFM stiffness measurements at the nanometer scale were compared for three different materials exhibiting different combinations of hierarchical structural complexity and stiffness - mica, an agarose gel, and articular cartilage. Comparison between the histograms as documented in Fig. 7 A of the slopes of individual load-displacement curves of the hard mica, the homogeneous agarose gels, and the multiphasic cartilage biocomposite reveals a broadening of the distribution with decreasing stiffness and increasing complexity of the sample. The widths of the Gaussian distributions in Fig. 7 A also demonstrate the difficulty of selecting a representative load-displacement curve for a given sample. Indentation testing of articular cartilage tissue exhibited a much larger variation in the stiffness values as usually performed by the collection of only a few unloading load-displacement curves for characterizing a homogenous hard solid, such as mica.

The width of the stiffness histogram broadens considerably when the 1024 load-displacement curves are recorded from multiple sample sites (Fig. 8 B) rather than measured at a single sample site (Fig. 8 A). This result could indicate either an increase in noise or an actual variation in modulus due to the sharp tip encountering slightly different arrangements of the complex cartilage structure. However, a tip with a nominal radius of ∼20 nm can, in principle, be positioned on top of a collagen fiber of ∼50-nm diameter, in between two fibers, or the tip might interact in many different ways with the collagen fibers. Because of the variety of difficulties related to indentation testing of soft biological tissues that potentially can lead to large variations of the data, we based our results by IT AFM on a large enough number of unloading load-displacement curves followed by statistical analysis.

Comparison of modulus values at the micrometer and nanometer scales

Indentation testing of a cultured cell that has a thickness of a few micrometers or the articular cartilage in a human knee joint of ∼1–4-mm thickness is often limited by the performance of the instrument. However, IT AFM, which is based on piezoelectric actuators, has far greater dimensional sensitivity compared to conventional clinical indentation testing devices for mechanical testing of small samples (see the Appendix for further discussion). Whatever instrumentation is employed for indentation testing, the rule of Bueckle (1973) specifies a maximum indentation depth of 10% of the overall thickness of a sample having the same structure throughout. Otherwise, the results vary with the ratio of depth to thickness. Hence for articular cartilage (∼1–4-mm thick), the overall z-range (i.e., 0.1–0.4 mm) that remains for testing a specimen often is close to the resolution capability of clinical indentation testing devices. Moreover, some published data might be biased by the presence or absence of an underlying bone or other substrate of different stiffness.

In contrast to clinical indenters that probe cartilage at the millimeter scale, a sharp AFM tip with a radius typically ∼20 nm, which is smaller than an individual collagen fiber having a diameter of ∼50 nm, was used. With this nanometer-scale indenter, a dynamic elastic modulus of 0.021 MPa was obtained. This value is ∼100-fold lower than reported values obtained with millimeter-sized clinical indenters (Shepherd and Seedhom, 1997; Mankin et al., 1994; Popko et al., 1986; Hori and Mockros, 1976; Kempson et al., 1971, 1970; Linn, 1967). For example, Hori and Mockros (1976) measured the short-time elastic modulus for human articular cartilage, including both healthy and diseased samples, to vary over 0.4–3.5 MPa and the short-time bulk elastic modulus over the range 9–170 MPa. Popko et al. (1986) reported a dynamic elastic modulus for human knee cartilage of 1.5–9.7 MPa, i.e., with the areas of highest weight-bearing being characterized by a higher dynamic elastic modulus. Aspden et al. (1991) measured a strain-rate dependency for bovine knee articular cartilage from 0.58 MPa to 1.63 MPa, and Swanepoel et al. (1994) determined a mean stiffness of healthy human lumbar apophyseal cartilage of 2.8 MPa. Finally, Shepherd and Seedhom (1997) reported values of the compressive elastic modulus of human articular knee cartilage under physiological loading rates between 4.4 and 27 MPa. Interestingly, using a micrometer-size (2.5-μm radius) spherical tip (see Table 2 and Fig. 3 B), a dynamic elastic modulus of 2.6 MPa was obtained, a value in close agreement with clinical indenter measurements.

Employing sharp pyramidal tips similar to those used in our measurements, Weisenhorn et al. (1993b) performed AFM measurements on bovine articular cartilage of the proximal head of the humerus. By modeling the stress-strain curves, an elastic modulus of 0.16–0.6 MPa was calculated (Weisenhorn et al., 1993b). The difference between these stiffness values and those obtained by clinical indenter measurements was explained as being caused by the inhomogeneity of the elastic response. However, the more general relevance of relating the biomechanical properties to the hierarchical architecture of cartilage tissue was not realized by these authors. Because cartilage is not a homogenous material, the macroscale stiffness represents an average of the elastic response of the various structural elements comprising the tissue, whereas at the nanometer scale, the stiffness of the individual structural elements is measured.

To explore this hypothesis that the ∼100-fold modulus difference is due to the measurement of the molecular and supramolecular cartilage components at the nanometer and micrometer scales, respectively, the influence of the tip size on image resolution was explored using agarose gels and articular cartilage. As expected, the agarose gels appear amorphous not only at the micrometer scale but also at the nanometer scale (see Fig. 4 A). After all, a 2.5% agarose gel consists of 97.5% water with the 2.5% supporting gel structure being a relatively simple cross-linked galactose polymer. Hence, the agarose gel exhibits a similar stiffness at both the micrometer and nanometer scales. In contrast, the articular cartilage surface imaged at the nanometer scale appears distinctly structured with individual collagen fibers and even their characteristic 67-nm axial repeat length being resolved (see Fig. 4 B). In our attempt of imaging articular cartilage under buffer solution we could also resolve individual collagen fibers in a similar quality as previously obtained by Jurvelin et al. (1996). However, because of the significant lower resolution obtained under buffer conditions, we only present images in air. In Fig. 4 B, the collagen fibers appear relatively loosely packed against each other with a random orientation. However, when articular cartilage is imaged with a micrometer-sized spherical tip, its surface topography appears rather featureless (see Fig. 5) - i.e., similar to an agarose gel - except for some chondrocytes that are just barely resolved. These results appear to support the assertion that the ∼100-fold difference in articular cartilage stiffness between measurements at the micrometer or nanometer scale is meaningful and reflects differences in the level of structure that is probed - i.e., the cartilage structural elements acting in concert at the supramolecular level versus distinct entities of the molecular level cartilage structure.

Effects of enzymatic digestion on cartilage stiffness

As might be expected, the chemical and physical states of the proteoglycan (PG) moiety play an important role in defining cartilage pathology. For example, osteoarthritic cartilage exhibits a distinct loss of the PG content (Maroudas, 1976). Ex vivo, such changes can be induced in a controlled way by specific enzymatic digestion of some components of the PG moiety. To assess the contribution of the PG moiety to the stiffness of articular cartilage, specimens were incubated with cathepsin D (Bader and Kempson, 1994) and their stiffness was measured at different time points at both the nanometer and micrometer scales. The stiffness determined at the micrometer scale did not exhibit any significant change even after 40 h of enzyme treatment (see Fig. 6 A). This result is consistent with the results obtained by Bader and Kempson (1994), who followed the course of a similar cathepsin D digestion experiment of articular cartilage with a macroscopic indenter. Evidently, digestion of the PGs does not significantly affect the bulk elastic properties of articular cartilage. This suggests that although the PGs are fragmented by the enzyme, the PG remnants still foster the ionic imbalance and charge repulsion phenomena that lead to water retention and the swelling that takes place in the collagen matrix in tension. This result obviously bears further study. In contrast, when measured at the nanometer scale, the stiffness of articular cartilage gradually increased with progressive cathepsin D digestion (see Fig. 6 B). Thus, stiffness measurements with a sharp nanometer-sized pyramidal tip appear to be a sensitive means for assessing the structural degradation of the proteoglycan moiety, which intersperses with the fibrous collagen network (see Table 2).

In a related experiment, articular cartilage was incubated for two days with the enzyme elastase, which specifically digests the collagen fibers. In this case, the dynamic elastic modulus measured at the micrometer scale decreased substantially, i.e., from 2.6 MPa to 0.877 MPa (see Table 2 and Fig. 6 C), which can clearly be attributed to the destruction of the collagen fibers. Reproducible measurements at the nanometer scale on elastase-digested cartilage were not feasible, because the tip became readily contaminated by the digested products and often stuck to the sample surface.

CONCLUSIONS

We have established a method, which we refer to as IT AFM, for directly measuring the stiffness of cartilage at length scales of both a few nanometers and several micrometers that span much of the range of the hierarchically organized structure of articular cartilage. This method should be applicable to other tissues also. The IT AFM dynamic elastic modulus of articular cartilage determined with micrometer-sized spherical tips is in good agreement with values obtained by clinical indenters which typically determine stiffness at the millimeter scale. In contrast, stiffness values measured with IT AFM using nanometer-sized sharp pyramidal tips were typically 100-fold lower. Comparison of the size of the indenters relative to the structural building blocks of cartilage led to the conclusion that this stiffness difference was due to the two distinct levels of tissue organization at these scales. In contrast, when agarose gels, which are more amorphous and elastically isotropic than cartilage, were measured by the same IT AFM method, the stiffness was the same at the micrometer and nanometer scales within the range of error.

Articular cartilage is a complex composite material, principally comprised of a collagen fiber network placed under tension by the swelling pressure of the proteoglycan gel interspersed within it. The resulting structure is actually mostly water - i.e., 60–80 wt %. Consequently, the observed mechanical properties of cartilage depend highly on the dimensional level at which they are investigated. Based on our measurements, we conclude that a 2.5-μm radius spherical tip is still large enough to yield information about the bulk elastic behavior of cartilage. In contrast, nanometer-sized tips enable us to observe mechanical properties and structure at the nanometer scale. For example, although not detectable at the micrometer or millimeter scale, digestion of the cartilage proteoglycan moiety with the enzyme cathepsin D increased the dynamic elastic modulus significantly when measured with nanometer-sized sharp pyramidal tips. In contrast, digestion of the collagen fiber network by elastase decreased the tissue stiffness drastically at the micrometer scale. (Collagen digestion products prevent attempts to make measurements at the nanometer scale.)

More detailed information about the mechanical properties of articular cartilage, including changes that might be triggered by physical and chemical stimuli, may be of practical importance for a better understanding of both cartilage mechanics and cartilage disease progression. Measurements at the nanometer scale provided by sharp pyramidal tips may open the possibility for either early diagnosis of proteoglycan changes related to the onset of cartilage diseases such as osteoarthritis or the effects of pharmaceutical agents on the tissue. Ultimately, this study may be a step toward developing an arthroscopic IT AFM for direct in vivo inspection of the articular cartilage at the nanometer scale in a knee or hip joint in a clinical environment (Stolz et al., 2003; Hunziker et al., 2002). Finally, IT AFM measurements of the functional stiffness of articular cartilage with micrometer-sized spherical tips may also be of clinical interest. Potentially, this method would allow investigations of joint surfaces such as those in the fingers or ankles, where joint surfaces are small and the cartilage is much thinner, i.e., where current clinical millimeter-scale indenters are too big.

APPENDIX: INDENTATION TESTING DEVICE RESOLUTION CAPABILITY

For accurate determination of the stiffness of a sample, its mechanical response should be independent of the mechanical property response of the underlying substrate or support. According to the rule of Bueckle (Persch et al., 1994; Bueckle, 1973), the depth of indentation should therefore be no more than 10% of the sample thickness. Because most biological specimens are limited in their size, only small indentation depths are possible. For example, the thickness of cartilage covering the articulating surfaces of human joints is typically 1–4 mm (Swanepoel et al., 1994) and consequently the maximal indentation depth is between 0.1 and 0.4 mm. To achieve such small indentation depths, high resolution monitoring of the z displacement of the indenter is required.

The accuracy of the z displacement can be characterized by the signal/quantization-noise ratio (SQNR), which is the ratio between the z-displacement signal in the load-displacement curve and the noise due to the approximation or quantization error in the z position of the indenter. Clinical indentation testing devices typically have a z-position resolution of ∼±10 μm (Aspden et al., 1991). Thus, the true z-position values are within intervals of ±10 μm and are assumed to be Gaussian distributed (Lueke, 1991). When employing such a clinical testing device for testing articular cartilage (assuming a 4-mm thickness), optimally N = 40 sample points can be taken over the entire range of indentation, i.e., 0.4 mm, while recording a single loading/unloading data set. Then the SQNR can be calculated (Lueke, 1991),

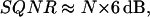(1)

where N is an integer number to quantify the system, and

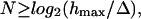(2)

where log₂ = logarithm to basis 2, h_max = maximal depth of indentation, and Δ = z-positioning uncertainty, where this uncertainty could include contributions from the device, the measurement itself, and the signal detection and processing. Synonyms often used instead of the term “uncertainty” are resolution (device), accuracy (measurement) and positioning error (signal processing theory for signal detection) depending on the perspective.

For such a clinical indentation testing device with a z-positioning accuracy of ±10 μm, one obtains a SQNR_clinic of ≈ 36 dB. A similar calculation of the SQNR for IT AFM that has a z-positioning accuracy of ±0.1 nm (Hues et al., 1993) results to SQNR_AFM ≈ 132 dB. Because a specific indentation testing device has a limited and fixed z-resolution capability, Δ, a higher SQNR thus can only be obtained by increasing the depth of indentation, h_max, which then increases the number of sample points N (see Eq. 1). However, an increase of the depth of indentation then violates the rule of Bueckle (1973).