A Structural Model of EmrE, a Multi-Drug Transporter from Escherichia coli

Abstract

Using a recently reported computational method, we describe an approach to model the structure of EmrE, a proton coupled multi-drug transporter of Escherichia coli. EmrE is the smallest ion-coupled transporter known; it functions as an oligomer and each monomer comprises four transmembrane segments. Because of its size, EmrE provides a unique experimental paradigm. The computational method does not afford a unique solution for the monomer. The experimental constraints available were used to select the most likely structure and to dock two monomers together to yield a dimer. The model is further validated by modeling of Hsmr, an EmrE homolog with a remarkable amino acid composition with over 40% of Ala and Val. The Hsmr model is similar to that of EmrE, with the majority of the Ala or Val residues facing the lipid. In addition, the model of EmrE features a putative substrate-binding site very similar to that observed in BmrR, a transcription activator of multi-drug transporters, with a similar substrate profile. The two crucial residues that couple proton fluxes with substrate binding in the homo-dimer of EmrE, Glu-14, have a spatial arrangement that agrees with proposed molecular mechanisms of transport.

INTRODUCTION

Extensive crystallographic, biophysical, and theoretical studies have provided an in-depth understanding of the mechanism of ion channels and redox, light and ATP-driven ion pumps (Capaldi and Aggeler, 2002; Chung and Kuyucak, 2002; Booth et al., 2003). A different, yet highly important group of membrane proteins is the family of transporters. Multi-drug and drug-specific efflux systems are responsible for clinically significant resistance to chemotherapeutic agents in pathogenic bacteria, fungi, parasites, and in human cancer cells (Nikaido, 1994; Paulsen et al., 1996a,b; Van Bambeke et al., 2000). However, the scarcity of structural information for ion-coupled transporters has impeded our understanding of the mechanism of these important proteins. Only recently, high-resolution structures of ion-coupled transporters are becoming available (Chang and Roth, 2001; Locher et al., 2002; Murakami et al., 2002; Abramson et al., 2003). However, our structural knowledge of these proteins is still very scarce and other approaches to obtain structural information are needed.

Computational searches of the conformational space of helix bundles have been used to model aspects of membrane protein structure and function. Due to the complexity of the problem, most approaches either focused on membrane proteins featuring just two helices, or on homo-oligomeric bundles, for which symmetry considerations can reduce the conformational space to be searched (Adams et al., 1995, 1996; Grice et al., 1997; Forrest et al., 1999; Briggs et al., 2001; Fleming and Engelman, 2001; Betanzos et al., 2002; Kim et al., 2003). Recently, a new method has been introduced (Gottschalk, 2004) that allows the modeling of small, nonsymmetrical helical bundles. The method distinguishes itself from the earlier method in two ways: a), it does not regard the total interaction energy as scoring function, but instead focuses on individual helices in the bundle, and b), reduces the computational effort by regarding the backbone of the helices as rigid bodies, while allowing the side chains to be flexible. This approximation reduces the computational effort significantly and has been demonstrated to give reliable results (Gottschalk, 2004).

Phylogenetic studies show that efflux systems are associated with five superfamilies of transporters (Chung and Saier, 2001). One of these includes a family of small multi-drug resistance (SMR) conferring proteins. The SMR family consists of small hydrophobic proteins of ∼100 amino acid residues with four transmembrane α-helical spanners (Paulsen et al., 1996a,b). These proteins function as oligomers (Yerushalmi et al., 1996; Rotem et al., 2001) and remove cationic drugs from the cytoplasm using a drug/H⁺ antiport mechanism (Paulsen et al., 1996a,b; Schuldiner et al., 2001a,b). The most extensively characterized SMR protein is EmrE, from Escherichia coli. The secondary structure of EmrE was determined by a variety of methods including high-resolution NMR studies (Fig. 1 A) (Schwaiger et al., 1998). The four transmembrane segments in EmrE are tightly packed in the membrane without any continuous aqueous domain, as was shown by FTIR and cysteine scanning experiments (Arkin et al., 1996; Steiner Mordoch et al., 1999). These results suggest the existence of a hydrophobic pathway through which the substrates are translocated. Glu-14, the only membrane-embedded charged residue is highly conserved in the SMR family (Ninio et al., 2001). This residue has an unusually high pK and is an essential part of the binding domain, shared by substrates and protons (Muth and Schuldiner, 2000; Yerushalmi and Schuldiner, 2000a,b,c).

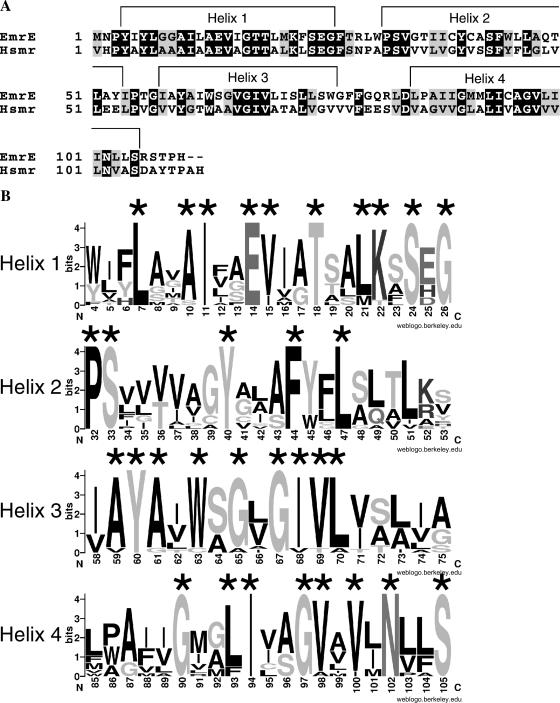
FIGURE 1.

Sequences and secondary structure of EmrE and Hsmr. (A) The sequences of EmrE and Hsmr are shown, with identical residues having a black background and similar residues a gray background. The shown secondary structure has been determined for EmrE using high-resolution NMR experiments. (B) Information content of a multiple alignment of 14 highly homologous sequences including EmrE and Hsmr is shown as sequence logos, generated with the web-based application WebLogo (http://weblogo.berkeley.edu). The overall height of each logo indicates the conservation at this position, whereas the height of each individual residue indicates the frequency of occurrence of this particular amino acid at this position. The topmost amino acid at each position corresponds to the consensus sequence.

Cross-linking experiments with EmrE provided important structural constraints. These studies suggest that helix 1 and helix 4 of the homo-dimer are at the interface in a crossover fashion (Soskine et al., 2002). Also a loop between helices 2 and 3 has been shown to cross-link. The location of helix 1 at the dimer interface has been further corroborated by spin-labeling experiments (Koteiche et al., 2003). Additionally, these experiments provided information about the rotational orientation and tilt of helix 1.

Here, we describe a structural model of EmrE, which has been obtained by generating a large library of random conformations as described earlier (Gottschalk, 2004). For validation of the model of EmrE, we additionally calculated a model of an archaeal homolog of EmrE, Hsmr. Hsmr displays a remarkable amino acid composition of over 40% valine and alanine residues (Fig. 1 A) (Ninio and Schuldiner, 2003). The distribution of valine and alanine residues within the trans-membrane domains of Hsmr is not random. Many of these abundant residues appear to be clustered in structural domains that are not essential for activity (Ninio and Schuldiner, 2003). This resembles the result of an alanine scan mutagenesis experiment, pointing out instantaneously the residues that are important for the function of the protein, and therefore cannot be replaced with valine or alanine. Mutational studies that identify important residues are commonly used to validate structural models. Furthermore it has been shown that a parallel search of homologous sequences can serve to discriminate between near-native and nonnative structural models (Briggs et al., 2001). Since the amino acid composition of Hsmr resembles the result of an extensive alanine scan and the Hsmr sequence is homologous to the EmrE sequence, modeling of Hsmr provides a combination of mutational validation and validation by means of homology considerations. For further validation using homology considerations, fourteen highly homologous sequences—including EmrE and Hsmr—have been aligned and the conservation grade has been visualized with Sequence Logos (Fig. 1 B).

The monomeric models for both homologous proteins, EmrE and Hsmr, are very similar. The monomeric model of EmrE has been dimerized using cross-linking constraints. The dimeric model of EmrE provides novel insight for the understanding of the function of these proteins at an atomic level.

METHODS

All the calculations have been performed with the molecular modeling and manipulation program CNS, version 1.1 (Brunger et al., 1998). The OPLS force field parameters were used (Jorgensen and Tirado-Rives, 1988).

Firstly the monomer of EmrE was modeled and secondly dimerized based on cross-linking results. This two-step procedure emulates the two-step model of membrane protein folding. Two topological models of the monomer with different relative helix orientations (helix-order of model 1: 1 2 3 4, counting clockwise; helix-order of Model 2: 1 4 3 2 counting clockwise) had to be tested. Other possibilities like helix order “1 3 4 2” could be excluded due to the shortness of the helix-connecting loops. The starting structure was a bundle of four canonical α-helices. The helices ranged from residues 4–26 (helix 1), 32–53 (helix 2), 58–76 (helix 3), and 85–105 (helix 4) as determined by NMR studies (Schwaiger et al., 1998) (see also Fig. 1). The initial tilt of the helices was set to 27°, which was obtained as the average helix tilt angle by FTIR studies (Arkin et al., 1996). Only left-handed crossing angles have been assigned during the search procedure as suggested earlier (Torres and Arkin, 2000).

Generation of canonical helices

As input for the library generation served a bundle of four caconical α-helices. The helices were built one by one as follows:

First the backbone was built so that the C_α-atoms rotated by 98.99° per residue and had a rise of 1.5 Å per residue. The generated helix was initially minimized with 3000 steps of Powell minimization with fixed C_α-atoms. Then 500 steps of a molecular dynamics simulation in Cartesian space with NOE restraints of 2.8 Å between N_i and O_i+4 and of 1.8 Å between H_i and O_i+4 with the temperature bath set to 300 K, and a time step of 0.5 fs followed. This was followed by 3000 steps of Powell minimization with the van der Waals repel term set to 1.5, followed by 3000 steps of Powell minimization using the standard van der Waals term, followed by another 3000 steps of Cartesian dynamics at a temperature of 300 K with 3000 steps and a time step of 0.5 fs. During all these steps up to now the C_α-atoms were kept fixed at their position. Then the helices were minimized with 1000 steps of Powell minimization releasing the C_α-atoms, using NOE restraints of 2.8 Å between N_i and O_i+4 and of 1.8 Å between H_i and O_i+4 , followed by 1000 steps of a Cartesian dynamics calculation coupled to a temperature bath at 300 K with a step size of 0.5 fs, followed by another 1000 steps of Powell minimization. The applied building scheme assures that the χ1 angles are in accordance with an α-helical secondary structure. This restricts the rotamers of β-branched side chains like I or V to a single value, but does not determine the rotamers of all the side chains unambiguously. The single helices were then put together to form a bundle by separating the helix centers to 10.4 Å at the appropriate angle (90° between three neighboring helix centers for a 4-helix bundle). No further minimization was applied for the start structure. Only the random conformations generated in the next step were further minimized.

Library generation

In a helix bundle, each helix has four degrees of freedom: the rotation angle around the long axis of the helix, the tilt relative to the membrane normal, a vertical translation in the direction of the membrane normal, and a lateral translation perpendicular to the membrane normal. A structure library of the monomer consisting of 200,000 different conformations was generated by assigning random values to each of the four structural parameters as described elsewhere (Gottschalk, 2004). The assigned tilt angle had a range of 27° ± 20° (in accordance with FTIR studies), the rotation angle of 360°, the horizontal shift of 3 Å toward the helix center and 5 Å away from the helix center, and the vertical shift 0 ± 4 Å. After assignment of the structural parameters, a brief Powell minimization with 50 steps was performed keeping the backbone restraint, and the interaction energies between each single helix with the rest of the bundle helices were calculated.

Library evaluation

For the evaluation of the random structure library, only the nonbonded terms (electrostatic and van der Waals terms) of the force field energy were used. The membrane was not included explicitly or by using solvation terms, but membrane effects were implicitly included by setting the dielectric constant ɛ of the surrounding medium to ɛ = 1. For each individual helix, the nonbonded interaction energy between the designated helix and the rest of the bundle has been calculated for all structures. The 1000 lowest energy structures of each helix were further evaluated using a frequency analysis of the structural parameters, assuming that native like values should be predominant in the ensemble of low-energy conformations. A three-dimensional histogram for each of the four structural parameters (tilt angle, rotation angle, vertical shift, and horizontal shift) was generated, with the structural parameter on the x axis, the energy on the y axis and the frequency on the z axis. Peaks in each distribution of the structural parameter were determined by visual inspection from these histograms. These peaks relate to the predominant value of the respective structural parameter in the low-energy ensemble. We assume that native like values are predominant at low energies. From the obtained values the structures were combinatorially generated by applying the respective geometric operation (like rotation by 20°, if the peak in the distribution is at 20°) to the respective helices. These generated structures were compared to experimental data.

Inclusion of loop

To use the cross-linking data available, the loop between helix 2 and helix 3 had to be included. The loop consists of just four residues, I⁵⁴PTG⁵⁷. Out of these residues, only G⁵⁷, which is directly at the beginning of helix 3, has been tested and shown to cross-link. The inclusion of the loop was performed in two steps: first the loop was interactively put into place using SwissPdbViewer. This program generates a combinatorial list of φ-ψ-angles. The corresponding loop conformations are then evaluated with an energy function based on the Gromos 96 force field (van Gunsteren, 1996). The lowest energy conformation was chosen as initial loop conformation. In a second step, the initial loop conformation was minimized with 5000 steps of Powell minimization, using again the OPLS force field and keeping backbone of the rest of the protein fixed during minimization. No further simulation was performed in this step, since the loop was only included for the next step, the formation of a dimer. During dimerization, the loop was subjected to a slow cool molecular dynamics protocol.

The other loops are longer and we therefore refrain from trying to predict their structure without inclusion of explicit solvents and/or the membrane environment. As mentioned before, the complex environment of the lipid-water interface certainly influences the loop conformation, so that for longer loops standard procedures such as the one used by the SwissPdbViewer will hardly produce reliable results.

Dimerization

For dimerization, a slow cool-simulated annealing/molecular dynamics protocol was used, which is similar to reported protocols for docking dimers using experimental restraints. To get an initial structure, the two monomers were separated by 12 Å with the interfacial helices 1 and 4 facing each other, forming a symmetrical dimer. The dimer was then subjected to a molecular dynamics calculation in Cartesian space, first heating the system to 1000 K by assigning random velocities to each atom according to a Maxwell distribution. The system was simulated in vacuo for 5000 steps with a step size of 0.5 fs and then gradually cooled down to 0 K in 25 K steps with 100 time steps per temperature step with a step size of 1 fs. The calculated forces were acting on all atoms, but certain NOE-like constraints restrained the conformational space of the system. Three sets of constraints have been used: the first two sets are supposed to prevent the helices from unfolding and the bundle from floating apart at the high temperatures of the initial step, whereas the remaining set includes the cross-linking data. The first set restrained N_i and O_i+4 to 2.8 Å to maintain the helical conformation, the second set restrained the maximal distance between two neighboring helices to 12 Å, the third set comprised the cross-linking data (Table 1) and restrained the C_β-atoms (which correspond to the S_β in cystein) of the affected residues to 9.5 Å ± 0.5 Å. 9.5 Å ± 0.5 Å is the distance the rigid cross-linker used can span. 50 structures were generated with this molecular dynamics protocol using CNS version 1.1, applying noncrystallographic symmetry restraints with each monomer being a symmetry-related group. The resulting structures were clustered using NMRclust (Kelley et al., 1996). The highest populated cluster entails 23 structures with a spread of 1.3 Å within the cluster. Although standard docking algorithms normally use rigid bodies, sometimes with certain side-chain flexibility, the applied molecular dynamics scheme allows conformational modifications during dimerization.

TABLE 1.

Cross-linking residues^* used for dimerization

Monomer 1	Monomer 2
14	14
22	22
57	57
88	88
92	92
95	95
14	88
14	95
88	14
95	14

^*Distance between the C_β-atoms of the cross-linking residues was set to 9.5 ± 0.5 Å.

RESULTS

Model of the monomer of EmrE

The aim of this study is to provide a structural model of EmrE, which is in agreement with all biochemical and biophysical experiments. To this end, the EmrE monomer was modeled using the computational approach described elsewhere (Gottschalk, 2004). Although the computational search did not lead to a unique solution, the biochemical data available allowed us to discriminate the models. Only one topological model has peaks at the rotation angle distribution for helices 1 and 4 that is compatible with the cross-linking results (Fig. 2).

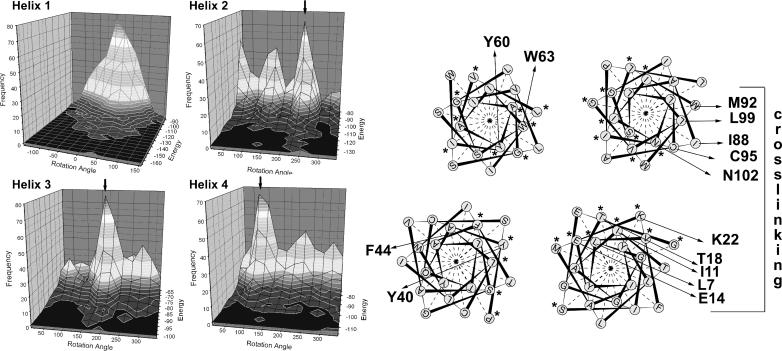
FIGURE 2.

Rotational orientation of the EmrE monomer. (Left) The energy-dependent rotation angle distributions of the 1000 lowest energy conformations are shown. From peaks in these distributions, the rotational orientation of the helices was determined (right). If more than one maximum in the rotation-angle distribution exists, the chosen maximum is depicted by an arrow. Important residues are marked with an arrow. The cross-linking interfaces of helix 1 and helix 4 are oriented so that they can cross-link in a crossover fashion. The highly conserved residues are marked with an asterix and tend to accumulate at the core of the protein.

In this model, helix 4 is oriented in accordance with the cross-linking data, whereas helix 1 might have to rotate on the order of 30° to be in accord with the cross-linking data. The rotation angle distribution for the low energy structures of helix 1 is rather broad, indicating a certain rotational flexibility of this helix in the monomer. A 30° rotation is therefore in line with the observed rotation-angle distribution. As Glu-14 is the only charged residue in the membrane, it appears reasonable that it is shielded from the membrane and becomes exposed to a putative binding domain shared with the neighboring monomer in the dimer.

Helix 3 has one predominant peak in the rotation-angle distribution. This rotation angle places Tyr-60 in the center of the bundle and Trp-63 at the interface between helix 3 and helix 4. Both residues are evolutionary conserved (Ninio and Schuldiner, 2003) and have been shown by mutational work to be essential for functional or structural integrity (Yerushalmi et al., 1995).

Helix 2 has one predominant peak in the rotation angle distribution, but two smaller peaks are also detectable. The predominant angle places Tyr-40 and Phe-44 in the middle of the bundle. Mutation of these residues significantly decreases expression levels of the protein, indicating an important structural role (Steiner Mordoch et al., 1999). This structural role would be explained by the obtained rotation angle, as the residues are involved in key contacts in middle of the helix bundle. Nevertheless, the data are not sufficient to clearly distinguish between different rotation angles of helix 2.

It has been observed earlier that lipid exposed residues of GPCRs, the photosynthetic reaction center and of ion channels are poorly conserved, whereas the protein core is much higher conserved (Stowell and Rees, 1995; Baldwin et al., 1997; Durell et al., 1999). To test whether a similar pattern can be observed for this family of transporters, fourteen highly homologous sequences, including EmrE and Hsmr, have been aligned and the conservation grade has been visualized using sequence logos (Fig. 1 B). Although helices 1, 2, and 4 show a clear helical pattern of conservation, helix 3 deviates from this pattern. In our model, the highly conserved residues (marked with an asterisk in Fig. 1 B and in Fig. 2) tend to cluster at the core of the bundle, whereas the nonconserved residues are the lipid-facing residues.

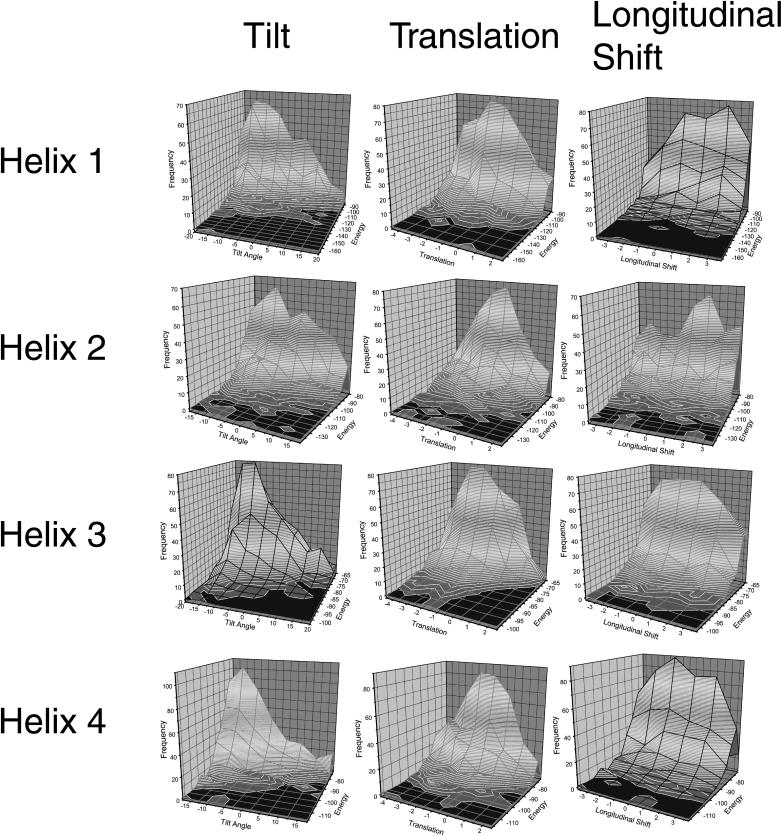
The other structural parameters (tilt angle, lateral translation, and vertical shift) were also determined from the energy-dependent distributions (Fig. 3). Most of the parameters are well-defined by the distributions, whereas the longitudinal shift of helix 3 has a rather broad plateau instead of a peak. This structural parameter is not well-defined by the experimental data available and therefore error-prone.

FIGURE 3.

Tilt, translation, and longitudinal shift of EmrE. For each of the helices, the 1000 lowest energy conformations were further evaluated by a frequency analysis. For this analysis, a three-dimensional histogram with the frequency on the z axis, the energy on the y axis, and the respective structural parameter on the x axis has been generated. The distribution for tilt angle, lateral translation, and longitudinal shift for each of the helices are shown here. The maximum values were assumed to be near-native values. The conformation of the respective helix was then changed according to these values.

As an additional test for the correctness of the obtained model, we repeated the modeling procedure for the extremophilic EmrE-homolog Hsmr. To save computer time, only one topological model was tested for Hsmr. We could narrow down the search to this topological model, as the purpose of the parallel modeling was to test whether or not a structure similar to the model of EmrE can be found for Hsmr. Since only one topology of EmrE is in accord with the biochemical and structural data available, only this topology had to be tested for Hsmr.

The generation and evaluation of the random structure library for Hsmr using the same method as for EmrE yielded 36 possible models, much more than for EmrE. The high content of Ala and Val leads to a diminished discrimination between the rotation angles, since whole patches of the helix-faces are looking virtually identical. One of these possible models has an orientation very similar to EmrE. Helices 1, 3, and 4 have approximately the same rotational orientation in both models, but the rotational orientation of helix 2 differs by ∼90°. Whereas for EmrE, the residues 40 and 44 face directly into the interior of the four-helix bundle, they are involved in contacts to helix 3 in the model of Hsmr. The experimental data available do not allow us to distinguish between these two possibilities of helix 2. In both cases the residues appear to be involved in key contacts.

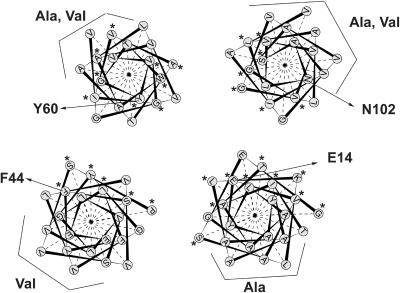
Closer analysis of the model of Hsmr reveals that the majority of Ala and Val face the outside (Fig. 4). An extreme example of the natural Ala scan is helix 1. Whereas one face of the helix features a sequence homologous to EmrE, the other face of the helix is nearly solely composed of Ala (Ninio and Schuldiner, 2003). In our model all the helix surfaces that predominantly feature Ala or Val face the lipid. Mutational studies in EmrE demonstrate that replacement of residues facing the side that is rich in Ala in Hsmr has no functional consequences (Gutman et al., 2003), whereas replacement of the residues which are on the conserved face of helix 1 leads to changes in affinity to TPP+ or impairment in transport activity (Gutman et al., 2003). These data strongly suggest that the Ala/Val side of the helix indeed faces the lipid in the protein, as it does in our model. Also the other helices display a strong tendency to accumulate either Ala or Val on one face of the helix. The Ala or Val rich faces coincide with the poorly conserved regions of the protein. The highly conserved regions (marked with an asterisk in Fig. 4) are—as in the case of EmrE—clustered at the protein core. In each case the Ala/Val rich side of the helix faces the lipid in our model, indicating that a), a model of Hsmr which is energetically favored is very similar to our model of EmrE, b), that in this model of Hsmr nearly all the Ala or Val face the lipid, and c), that therefore the rotational orientation of the helices in our model is in agreement with the basic assumed explanation for the richness in Ala and Val, namely that some evolutionary pressure forced the organism to replace all nonessential (here, lipid-facing) residues of the protein by either Ala or Val.

FIGURE 4.

Rotational orientation of Hsmr. The rotational orientation of Hsmr is shown as a helical wheel projection. The Ala,Val-rich faces are exposed to the lipid, whereas the highly conserved faces (depicted with an asterisk) are at the core of the bundle. Whereas helix 1, helix 3, and helix 4 are oriented as in EmrE, helix 2 is rotated at around 100°. The residue numbering of the marked residues relates to EmrE.

Dimerization of EmrE

For the dimerization of the monomeric structures the cross-linking data obtained by Soskine et al., were used as NOE-like constraints (Soskine et al., 2002). Cross-linking was performed on single Cys mutants using the N,N-1,2-phenylene dimaleimide OPDM or mercury as cross-linker. Most of the mutants used for cross-linking have been shown to be active, indicating that the Cys-replacement had little or no consequences on the structure (Soskine et al., 2002). Cross-linking studies sample the whole conformational space available for the protein. Thus no single structure does necessarily fulfill all constraints obtained by cross-linking, especially if one is dealing with highly dynamical systems like the transporter EmrE. To ensure that all constraints relate to a single structure, we excluded those from cross-linking of residues, which are strongly affected by ligand binding (Soskine and Schuldiner, unpublished results). It is more likely that these constraints should correspond to a single conformation, since conformational changes of the protein upon ligand binding should affect certain cross-links, but not those that correspond to the ligated structure.

As cross-linking has been observed between a Cys-replacement at position 57 in the loop connecting helix 2 with helix 3, the loop has to be included for dimerization of the two monomers. The loop consists of only four residues. Despite the shortness of the loop it does fit to the helix orientation without causing any strain.

The distances of the residues cross-linking with OPDM were set to 9.5 + 0.5 Å between the C_β-atoms of the involved residues. OPDM is a rigid cross-linker, and the distance is therefore well-defined. This does not imply that the dynamical movements of the protein are restricted to this distance range. A total number of 10 intermonomer constraints was used (Table 1). It has been shown in computational docking studies that five constraints are sufficient to reliably dock two proteins. The number of constraints here should therefore suffice to obtain a well-defined model (Roisman et al., 2001).

Fifty dimeric structures were calculated starting from the monomer (including the loop between helix 2 and helix 3) with different initial velocities assigned to the atoms of the start structure. These fifty dimers were clustered according to structural similarity. The highest populated cluster contains 23 structures with a spread of 1.3 Å in the cluster. This points to a well-defined structure with enough constraints to dock the two monomers. The representative of this cluster was chosen for further interpretation of the model (Fig. 5).

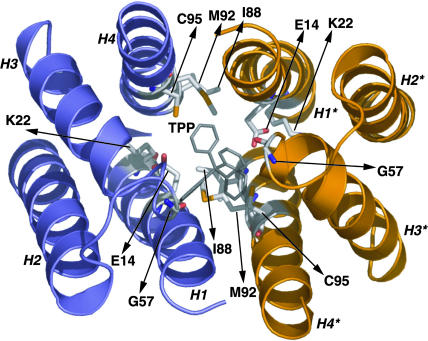
FIGURE 5.

Dimeric structure of EmrE. The model of EmrE as a dimer is depicted together with the predicted binding site. One monomer is blue, the other orange. The cross-linking side chains used for dimerization are shown.

The rotational orientation of the helices remains virtually unchanged after dimerization (Fig. 6 A).

FIGURE 6.

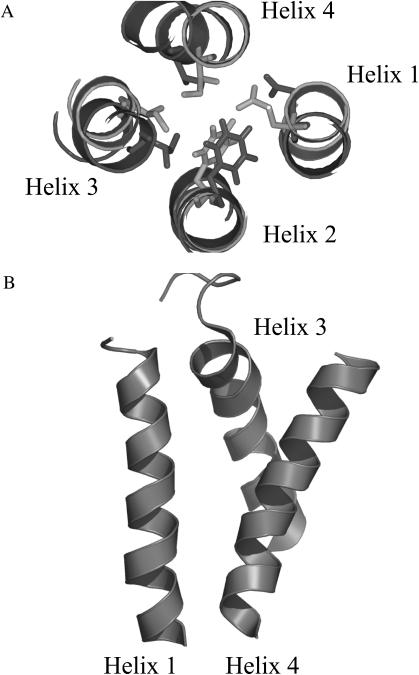
Effect of dimerization on EmrE. (A) The rotation of each helix before dimerization (light gray) and after dimerization (dark gray) is virtually unchanged, even for helix 1. To demonstrate the rotation of each helix before and after dimerization, one arbitrary residue per helix is shown. (B) Due to the restraint between the Gly-57 in the loop connecting helix 2 with helix 3, helix 3 inserts between helix 1 and helix 4, increasing the tilt angle of the latter and exposing the negative charge of Glu-14 to the intracellular space.

The tilt angle of some of the helices changes significantly. The restraint between position 57 placed at the short loop between helix 2 and helix 3 of both monomers leads to an insertion of the N-terminal end of helix 3 between helix 1 and helix 4 and a separation of the latter two helices (Fig. 6 B). In our model of the dimer, helix 1 and helix 4 form a V-shaped unit, which is open at the N-terminus of helix 1. This V-shaped conformation of helix 1 and helix 4 in our model implies that the N-terminus of helix 1 and the C-terminus of helix 4 are inside the cell, exposing the negative charge of Glu-14 to the ligand.

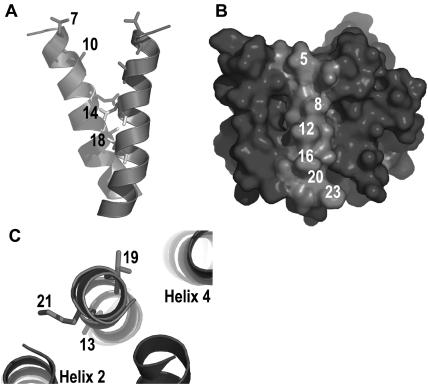
In spin-labeling experiments, it has been demonstrated that Leu-7 and Ala-10 of helix 1 are solvent-exposed, whereas Glu-14 and Thr-18 are restricted in their mobility and close to the respective residues in the other monomer (Koteiche et al., 2003). This is also true for our model (Fig. 7 A). It has further been observed that residues 5, 8, 12, 16, 20, and 23 face the lipid, as they do in our model (Fig. 7 B). Strikingly, five of these residues are Ala in the Hsmr homolog and are not evolutionary conserved. In addition, it was shown that residues 13, 19, and 21 have a restricted mobility. This fact was interpreted as stemming from contacts to neighboring helices. In our model, residues 13 and 21 face helix 2, whereas residue 19 faces helix 4 (Fig. 7 C). Hence, our model is in complete accordance with the data from the spin labeling experiments, even though these data have not been used in the modeling process, as they were published only after the model was completed. Thus they provide an independent and unbiased test of the modeling success.

FIGURE 7.

Comparison with spin-labeling results. (A) Spin-labeling experiments showed that Leu-7 and Ala-10 do not have restricted mobility and are solvent exposed, as opposed to Glu-14 and Thr-18, which have restricted mobility due to interaction with the corresponding residue in the homodimer. This is in line with our model. (B) Surface of EmrE is shown. The labeled residues have been shown to face the lipid by spin-labeling experiments. (C) Contacts to other helices as predicted by our model are corroborated by the spin-label results.

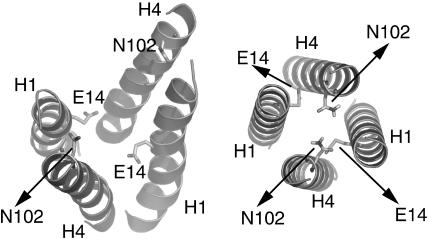
The four interfacial Helices 1 and 4, which line the translocation pathway, were also subject to a conformational search. The result of this conformational search demonstrates that although the rotational orientation of the helices is virtually identical in both cases, the tilt angle differs significantly (Fig. 8). Although the computational search keeps the helices canonical throughout the process, the slow cool molecular dynamics protocol used allows deviations from ideal geometry. The conformation obtained by dimerizing the two monomers features a central four helix bundle that is composed of helices 1 and 4 and is open at the cytoplasmic face. The separation of the helices causes Asn-102 to be separated by more that 10 Å, although Asn-102 has been shown to cross-link to itself when no ligand is present. The cross-linking data at this part of the bundle have been excluded from the dimerization calculation, since adding ligand strongly reduces the cross-linking ability of Asn-102 and the residues in its vicinity.

FIGURE 8.

Central dimer-interface. (Left) Central dimer interface after dimerization of the monomers. (Right) Central dimer interface as obtained through conformational search of helices 1 and 4. The rotational orientation between the two different conformations is identical, but the tilt is different. Whereas the left conformation should correspond to a ligand binding conformation, the right conformation might represent the unligated conformation. This would indicate a change of the tilt upon complexation. Whereas in the right conformation all cross-linking data between helices 1 and 4 are fulfilled, some cross-linking data have been excluded to obtain the left conformation as described in the text.

The conformation of the four central helices after the conformational search on the other hand is a closed 4-helix bundle, which is in accord with all cross-linking data between helices 1 and 4. This difference in the tilt angle can have different reasons. One reason might be that the applied modeling scheme is not very accurate in describing the tilt angle of the helices. A more intriguing interpretation is that the closed bundle obtained by the conformational search of the translocation pathway-lining helices 1 and 4 corresponds to an unligated state, and that upon ligation the tilt of the helices changes, exposing the charge of Glu-14 to the ligand. If this is true, one might speculate about the function of Asn-102. Not only is it highly conserved (Fig. 1 B), it also seems to be involved in helix-helix contacts. In model helices, Asn has been shown to be able to drive TM helix association (Gratkowski et al., 2001; Lear et al., 2003), as does Glu (like Glu-14 of helix 1). Thus there are two residues at the dimer interface, Asn-102 and Glu-14, which are highly conserved and which can drive helix-helix association. One can speculate that Asn-102 is therefore important for correct dimer formation and might even have a functional significance: upon ligand binding, helices 4 and 4* separate according to our model. Asn-102 might drive reassociation of helix 4 after ligand release.

Ligand binding

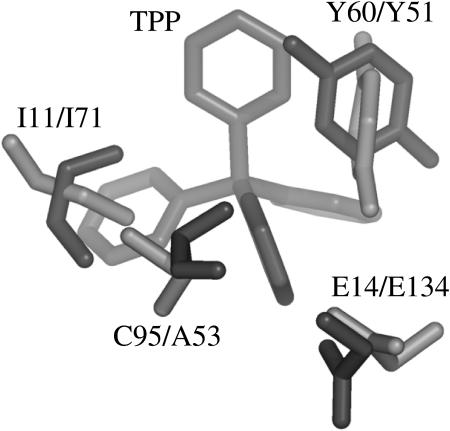
One pivotal residue in EmrE is Glu-14. It is the only charged residue that is irreplaceable. Glu-14 binds ligand and hydrogens mutually exclusively (Muth and Schuldiner, 2000; Yerushalmi and Schuldiner, 2000; Yerushalmi et al., 2001). Even the conservative mutation E14D inhibits transport, although not binding of substrate. In our model, Tyr-60 is close to Glu-14. Also Tyr-60 has been shown to be an essential residue (Lebendiker and Schuldiner, 1996). Even a Y60F mutant is inactive. The biochemical data together with the spatial closeness of the two residues in the model imply an active involvement of both residues in ligand binding. This implication can be corroborated by a comparison of our model with the structure of BmrR (Zheleznova et al., 1999). BmrR is a transcription activator for Bmr, a Bacillus subtilis multi-drug transporter. BmrR and EmrE share a very similar substrate profile, and both bind TPP+. The crystal structure of the BmrR/TPP+ complex is known. BmrR adopts a unique fold which resembles the β-barrel motif and has no similarity to the all-helical EmrE-model. An unusual feature of the unligated BmrR structure is the buried Glu-134. Glu-134 turns out to be the central binding residue for TPP+ and becomes exposed after a short helix, which masks the binding site in the nonligated state, unfolds upon ligation. The binding site of BmrR is dominated by the negative charge of Glu-134, by the residues Tyr-51, Ala-53 of the β3-strand and Tyr-68, Ile-71 of the β4-strand. The structure of BmrR in complex with TPP+ allows us to compare the predicted binding site of EmrE with the structurally determined binding site of BmrR. A comparison shows that the spatial correlation of Glu-14 and Tyr-60 in our model and E 134 and Y 51 of BmrR is very similar (Fig. 9). Not only Glu-14 and Tyr-60, but also Ile-11 and Cys-95 of our model structure have a counterpart in the x-ray structure of the BmrR/TPP+ complex: Ile-71 of BmrR relates structurally to Ile-11 in our EmrE model, Ala-53 of BmrR relates to Cys-95 in our EmrE model (Fig. 8). Ile-11 is relatively conserved within the family of SMR and mutation to Cys reduces the affinity to TPP+ 10-fold. The observed differences in side-chain conformation between the EmrE model and the BmrR structure are within the error of the model. Apparently half of the binding site of EmrE emulates BmrR and is duplicated in the dimer.

FIGURE 9.

Binding pocket of EmrE and BmrR. (Top) EmrE emulates half of the binding pocket of BmrR. The main interaction partners in BmrR have a counterpart in EmrE. In EmrE, this half of the binding pocket is duplicated in the dimer.

The similarity between the two binding sites allows us to manually dock TPP+ into the EmrE model. The predicted binding mode is in agreement with observed cross-linking behavior. Ligand binding inhibits cross-linking between Cys-replacement at positions 102 and 99 in different monomers (Soskine and Schuldiner, unpublished results). Although the conformation of helices 4 and 4* obtained by the conformational search of the central helices allows cross-linking between these helices, the distance in the ligand binding conformation is too large. According to our model TPP binds between these residues and the distance between helices in two monomers may change upon binding. Adding ligand inhibits labeling of Leu-7 and Ala-10 with water-soluble substrates. In our model, ligand binds between these residues, blocking the access of the labeling compounds (Schuldiner, unpublished results).

Proton binding

Recently, the crystalline structure of the proton-coupled transporter AcrB of the RND family has been reported (Murakami et al., 2002). In the case of AcrB, as in the case of EmrE, binding is mainly performed by hydrophobic or π-stacking interactions in addition to charged interactions. A structural comparison on top of this functional similarity between the binding sites of the two proteins is not possible.

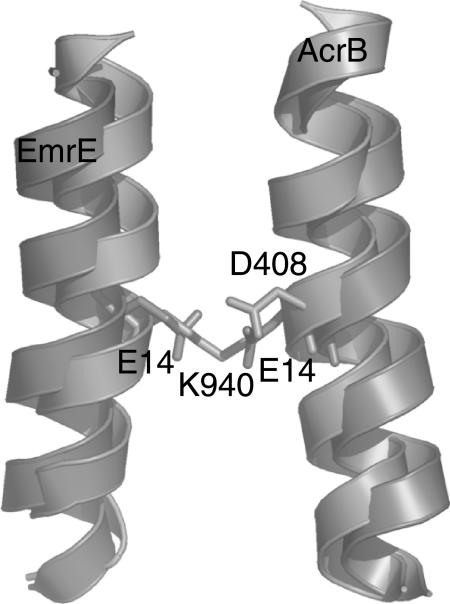
Although EmrE and AcrB do not share detectable sequence homology, have a structurally dissimilar binding site, and are comprised of different numbers of helices (AcrB of 12 helices and EmrE of 8 helices in the functional dimer), it would be interesting to see whether still certain similarities in crucial parts of the proteins can be detected between the crystal structure and our model. In AcrB, three charged residues (Asp-407, Asp-408 and Lys-940) in the center of the membrane have been implicated with proton binding. For EmrE it has been shown that protons and substrate both bind mutually exclusively Glu-14, which is also near the middle of the membrane. Thus Glu-14 is not only the central residue in substrate binding, but also the central proton-binding site. It is interesting to note that the central helices of AcrB, namely helix 4 and helix 10, and in our model of EmrE (both times helix 1), which in both cases entail the proton-binding sites and are symmetry related, are oriented in a nearly identical way (Fig. 10). Thus it seems as if not only the ligand binding site of EmrE—as described in our model—is very similar to a protein of known structure (BmrR), but also the proton-binding site.

FIGURE 10.

Superposition of central helices of EmrE and AcrB. Although there is no significant sequence similarity between the two proteins, the proton-binding site as described by our model and found in the x-ray structure of AcrB is remarkably similar. In both cases, the central, symmetry-related helix constitutes the proton-binding site, although with different residues: EmrE uses two Glu, whereas Acrb uses a Lys and two Asp (only one shown).

Comparison with 2D projection maps

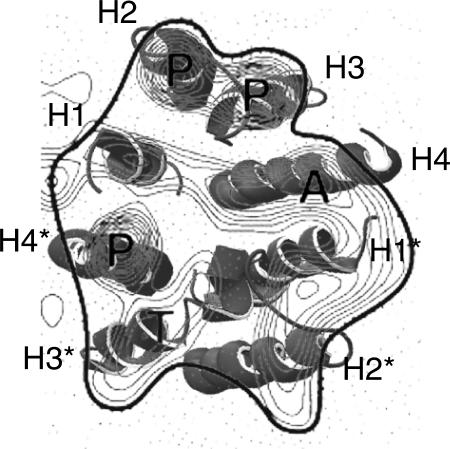
Recently, 2D projection maps of EmrE with and without ligand have been published (Tate et al., 2001,2003). The projection maps show an asymmetric dimer of EmrE with the proposed binding site nearly in the middle of the dimer. The source of the asymmetry is unclear; the other structural data available appear to be symmetric. Symmetry considerations therefore guided our dimerization scheme. The discrepancy between our symmetric model and the asymmetric projection map is reflected by the different degrees of fit between our model and the projection maps. An excellent agreement of one monomer of our model with the projection map is obtained and allows a putative assignment of the projected helices (Fig. 11). The symmetry-related second monomer of the model does not match the projection images to the same extent.

FIGURE 11.

Comparison with two two-dimensional projection map reveals an excellent fit of one monomer with the obtained densities (H1–H4). The symmetry-related second monomer (H1^*–H4^*) fits less well. This might be caused by the asymmetry of the projection map.

DISCUSSION

During the modeling procedure, the influence of the membrane has been treated only implicitly by setting the dielectric constant ɛ of the surrounding medium to ɛ = 1. Although this is an approximation, it has been applied before with success. A global conformational search in vacuo of the TM homo-dimeric protein glycophorin A resulted in a near-native conformation (Adams et al., 1996). A global search of the tilt- and rotation-angle of a number of oligomeric proteins, considering just the force field energy and treating the membrane as a medium with a dielectric constant of ɛ = 1, demonstrated that the native conformation is at an energy minimum (Torres et al., 2001). The here applied modeling and evaluation scheme has been shown to give reliable results for two 4-helix bundles with known structure (Gottschalk, 2004). Furthermore, Duneau and co-workers compared simulations of TM helices in vacuo with ɛ = 1 and in explicit lipid bilayer and concluded that the lipid bilayer has only little influence on the configurational space available to a transmembrane peptide (Duneau et al., 1999). Therefore, for a rapid scan of the conformational space available, it is sufficient to perform the calculations in vacuo. The success in predicting helical transmembrane bundles without including membrane components is a direct consequence of the two-state character of membrane protein folding: the formation and insertion of the helices is governed by helix-lipid interactions, whereas the bundle formation is governed by helix-helix interactions (Popot et al., 1987; Popot and Engelman, 1990,2000). It has been demonstrated experimentally that indeed helix-helix interaction terms can be separated from helix-lipid interaction terms, underlining the correctness of the assumption that the bundle formation is determined by helix-helix interactions. Therefore, as opposed to soluble proteins, for which solvation terms are crucial for a correct description of the energy landscape, membrane proteins can be described with sufficient accuracy excluding terms that describe helix-membrane interactions. This is probably not true for helix-connecting loops, as these are at the membrane-water interface, which is a complex environment with strong influence of the charged lipid-headgroups and the water. Therefore we did not attempt to model the structure of the loops with the exception of the very short loop between helix 2 and helix 3. This loop had to be modeled to be able to use all the cross-linking data.

The applied modeling scheme suffers from the fact that the correct side-chain configuration is not known. Preliminary attempts to more rigorously refine the side-chain conformation for each of the 200,000 members of the structure library turned out to be too time-consuming to be practical. Therefore, it cannot be ruled out that the initial side-chain conformation influences the final result. But it has been demonstrated that β-branched or small residues are likely to be at the helix-helix interface (MacKenzie et al., 1997; MacKenzie and Engelman, 1998). This also appears to be true for EmrE (Fig. 2, bottom), although not exclusively. For β-branched or small residues, the side-chain conformation is fixed due to possible side-chain/backbone clashes (for the β-branched residues like V or I) or due to the existence of just a single rotamer (as for A and G). Also for Ser and Thr, it is rather likely that hydrogen bonds with the backbone of the same helix are formed, reducing the rotameric space to just one rotamer. Large unbranched side chains like Met or to a lesser extent Leu are nevertheless a possible source of error. Yet, the applied minimization should reduce artificially high energies if these side chains overlap. Furthermore, it has been suggested that TM helices pack in a knob-into-hole fashion (Dunker and Jones, 1978; Langosch and Heringa, 1998). This way of packing will be favored by the applied scheme, since knobs-into-holes packing effectively reduces the danger of overlapping side chains. Therefore, one might think that the approximation used here, namely to allow the side chains to adapt to the conformation during a brief minimization, but not to perform a complete search of the rotameric space, is a valid approximation. This is demonstrated by the success of the applied method to predict the conformations of 4-helix bundles with known structures (Gottschalk, 2004).

In our opinion, different parts of the model have different degrees of reliability. The position and rotational orientation of helix 1 and helix 4 are supported by the following points:

1. Cross-linking studies, which provide very good structural constraints.

2. The structural homology of the binding site of our model with the binding site of the BmrR structure.

3. The similarity of the proton-binding site of our model and of the proton-coupled transporter AcrB.

4. Identical orientations of these helices in the monomeric model of Hsmr.

5. Recent spin-labeling experiments on helix 1.

Thus, we have high confidence in the correct position of these two helices. Helix 3 is not supported by cross-linking constraints to the same extent as are helix 1 and helix 4. However, cross-linking between Gly-57Cys in each monomer, which is very close to helix 3, the involvement of helix 3 in ligand binding, which has been suggested based on mutational data, and the spatial correlation of Tyr-60 to Glu-14, which reflects a similar orientation in BmrR, all support the assumption that helix 3 is also oriented correctly. This is underlined by an identical orientation of the homologous helix in the model of the monomer of Hsmr. The least data are available for helix 2. In addition, the largest discrepancy between the models of EmrE and Hsmr can be found for helix 2. Thus we are least confident in the correct orientation of this helix. However, based on the comparison between the EmrE and Hsmr models and on the standard deviations of the respective rotation-angle distributions, the error should be within the order of 100° rotation angle. As a consequence of the applied modeling scheme, the rotation angles are probably modeled with a higher accuracy than the tilt angles of the helices.

The modeling study describes EmrE as a transporter that can couple two fluxes, substrate and proton, with a minimal number of essential residues due to fine-tuning of electrostatic attraction and repulsion. The binding site in our model is dominated by two stabilizing mechanisms, π-stacking and electrostatic attraction. Both mechanisms of stabilization, electrostatic attraction as well as π-stacking interactions, are less dependent on changes in the geometry of the substrate than tightly fitting pockets dominated by van der Waals interactions. Thus, EmrE can transport a large variety of substrates, provided that they are positively charged and aromatic. This is in accordance with the profile of substrates transported by EmrE.

Transport of solutes across the cell membrane is a very basic phenomenon that enables life. Our modeling studies enhance the understanding of the transport mechanism at an atomic level. The results reported here integrate data from many different sources and combine different experimental procedures to obtain a single, consistent model. The calculations provide a good starting point for further studies, which can test the presented hypothesis about ligand binding and the role of different amino acids in the transport cycle.