Dynamics of Molecular Motors and Polymer Translocation with Sequence Heterogeneity

Abstract

The effect of sequence heterogeneity on polynucleotide translocation across a pore and on simple models of molecular motors such as helicases, DNA polymerase/exonuclease, and RNA polymerase is studied in detail. Pore translocation of RNA or DNA is biased due to the different chemical environments on the two sides of the membrane, whereas the molecular motor motion is biased through a coupling to chemical energy. An externally applied force can oppose these biases. For both systems we solve lattice models exactly both with and without disorder. The models incorporate explicitly the coupling to the different chemical environments for polymer translocation and the coupling to the chemical energy (as well as nucleotide pairing energies) for molecular motors. Using the exact solutions and general arguments, we show that the heterogeneity leads to anomalous dynamics. Most notably, over a range of forces around the stall force (or stall tension for DNA polymerase/exonuclease systems) the displacement grows sublinearly as t^μ, with μ < 1. The range over which this behavior can be observed experimentally is estimated for several systems and argued to be detectable for appropriate forces and buffers. Similar sequence heterogeneity effects may arise in the packing of viral DNA.

INTRODUCTION

The dynamics of many single molecule experiments can be described in terms of a “particle” moving along a one-dimensional substrate. For example, polymer translocation through a narrow pore can be parameterized by the number of monomers threaded through the pore. The motion of molecular motors such as kinesins, dyneins, myosin, helicase, DNA polymerase, exonuclease, and RNA polymerase can be described by the location of the motor on the one-dimensional substrate (microtubules, actin filaments, DNA, and mRNA) on which they move. Similarly, the packing of a newly replicated DNA or RNA in viruses may be described by the molecular weight of the packed genome. These systems have been a subject of much experimental (Bates et al., 2003; Henrickson et al., 2000; Howard, 2001; Kasianowicz et al., 1996; Maier et al., 2000; Meller, 2003; Meller et al., 2001; Smith et al., 2001; Visscher et al., 1999; Wang et al., 1998; Wuite et al., 2000;) and theoretical attention (Bhattacharjee and Seno, 2003; Bustamante et al., 2001; Chuang et al., 2002; Fisher and Kolomeisky, 1999; Flomenbom and Klafter, 2003, 2004; Goel et al., 2003; Jülicher et al., 1997; Jülicher and Bruinsma, 1998; Kolomeisky and Fisher, 1999; Lattanzi and Maritan, 2001a,b; 2002; Lubensky and Nelson, 1999; Magnasco, 1993; Muthukumar, 2001; Prost et al., 1994; Sung and Park, 1996; Zandi et al., 2003).

Under most conditions, the motion of the coordinate describing the system is biased in one direction. The bias in the case of molecular motors and packing of newly replicated viral genomes is due to a chemical process such as ATP (or more generally, NTP) hydrolysis, whereas for polymer translocation it can be generated by the different chemical environments on the two sides of the pore. For translocating single-stranded DNA, such a bias could be provided by adding, for example RecA (Hegner et al., 1999) or other single-stranded binding proteins (which do not pass through the pore) to the solution on one side of the membrane. Single-molecule experiments allow another source of bias to be introduced into the system, namely an externally applied force F. This has been done, for example, by attaching a bead to a molecular motor (Visscher et al., 1999) or to the end of the genome that is packed into the viruses (Smith et al., 2001) and pulling on it using optical tweezers. Similarly, charged polymers have been translocated using an externally applied electric field (Meller et al., 2001). An interesting variant on these experiments is the single-molecule measurements of Wuite et al. (2000) on DNA polymerase, which converts NTPs (nucleotide triphosphates) into a ligated chain of nucleotides via complementary basepairing (Maier et al., 2000). Wuite et al. apply a force F′ not to the motor itself, but instead across the ends of the ssDNA/dsDNA complex to create a tension across the substrate on which the molecular machine operates. Beyond a critical tension 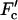of order of 40 pN, the motor goes backward and turns into an exonuclease. The severe stretching of the backbone of the complementary DNA strand for 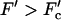presumably makes further conversion of NTPs unfavorable and causes removal of nucleotides by the motor to be favored. Forward and reverse motion of this enzyme are believed to be associated with different active sites (Doublié et al., 1998).

Most theoretical treatments of these systems have assumed homogeneous (or at least periodic) systems. Independent of the microscopic details, such problems can be described at long times by a random walker moving along a tilted potential or, equivalently, a biased random walker. For molecular motors such as kinesins, dyneins, or myosins, the assumption of homogeneity is indeed, in most experiments, entirely appropriate. However, in other cases the motion is along a one-dimensional disordered substrate. This is the case, for example, for RNA polymerases, exonuclease and DNA polymerases, helicases, the motion of ribosomes along mRNA, the translocation of RNA or DNA through a pore, and the packing of a viral genome. In all these systems, the one-dimensional substrate reflects the heterogeneity of DNA or RNA, and leads to a modification of the coarse-grained effective potential in which the random walker describing the system moves. The potential now depends in a complicated way on the location along the substrate. Two examples of potential energy landscapes of particular interest to us here are random energy and random forcing energy landscapes. We define a random energy landscape to be any effectively one-dimensional potential with a mean slope and fluctuations in the value of the potential with a finite variance about this linear tilt. A random forcing energy landscape has an overall mean slope but with energy fluctuations that are themselves described by a random walk. In this case, the energy fluctuations about a linear tilt grow as the square root of the distance along the substrate. These two types of energy landscapes have been studied in detail in the statistical mechanics literature (Bouchaud et al., 1990; Derrida, 1983) and lead to strikingly different long time dynamics. In particular, the random forcing energy landscape leads to behavior quite different from diffusion with drift when the overall tilt of the landscape is small, as discussed in detail below.

Recently, the effect of disorder in the form of defect sites in a ratchet model that locally reverse the bias of molecular motors has been considered (Harms and Lipowsky, 1997), using the methods of Jülicher et al. (1997). It was suggested that even though fluctuations in the microscopic potential are bounded, the resulting effective energy landscape is random forcing. Specifically, it was argued that when the defect concentration was large enough, anomalous random force dynamics would appear. As pointed out in Lubensky and Nelson (2002), heterogeneity in basepairing energies also leads to a random force landscape in the context of DNA unzipping.

In this article we study the effect of sequence heterogeneity in both polymer translocation and molecular motors in detail for an exactly solvable class of simple lattice models. We consider both systems in the context of single-molecule experiments that apply an external force pulling back on the polymer or the motor, which in the absence of this force are biased to move in one direction. We introduce microscopic models for both systems that can be solved exactly both with and without disorder. A generalization of our motor model, discussed in “Experimental Considerations” and Appendix D, can also be used as a very simple model of the DNA polymerase/exonuclease experiments of Wuite et al. (2000). One can also consider closely related models of the packing of a viral genome. In this case there is an extra source of bias due to the energetic cost of packing the DNA inside the virus. The externally applied force acts in conjunction with this bias whereas the motor acts against both. The details are very similar to the cases discussed here, with the exception that the energy cost of forcing the DNA into the capsid does not necessarily vary strictly linearly with the amount of DNA that has entered. We do not include a separate discussion of this interesting system.

We show that sequence heterogeneity of single-stranded DNA or RNA and heterogeneous basepairing energies have a dramatic effect on the dynamics of both systems. For a homogeneous substrate and no chemical bias, the average velocity changes monotonically through zero as the external force is varied, changing sign as the force reverses direction (see Fig. 1 a). When a chemical bias (which we take to act in the direction opposing the force) is present, the scenario is similar with the velocity changing sign at a stall force, F_s, which depends on the degree of chemical bias (see Fig. 1 b). In contrast, the combination of a disordered substrate and a chemical bias produces very different behavior for both systems. In this case we show that generically, disorder introduces a random forcing effective energy landscape, which is responsible for the anomalous dynamics. Similar to the observation of Harms and Lipowsky (1997), a random forcing landscape is generated even if we neglect an explicit contribution (Lubensky and Nelson, 2002) from random basepairing energies. We discuss three different dynamical regimes that arise due to this landscape as the externally applied force is varied. The most notable transition arises in the velocity of the random walker describing the system. Specifically, we find that there are critical values of the force 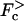and 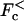such that for any force between these values, the velocity is zero in the sense that the average particle position 〈x(t)〉, where 〈…〉 denotes an average over thermal fluctuations, increases as a sublinear power of time. We also discuss an even broader range of forces where the diffusion is anomalous (see Fig. 1 b). The transition points between the different types of long time dynamics can be calculated exactly for the simple models studied here.

FIGURE 1.

Schematic behavior of the drift velocity at long times for homogeneous and heterogeneous systems as a function of the applied force, where a positive force resists the chemically favored direction of motion. It is assumed that chemical forces (such as ATP hydrolysis or chemical binding on one side of a pore) lead to a positive velocity in the absence of a force. (a) No externally applied chemical bias (Δμ = 0). (b) A finite chemical bias (Δμ > 0), where the shaded line corresponds to homogeneous or periodic environments and the solid line refers to heterogeneous environments. The anomalous dynamics (〈x(t)〉 ∼ t^μ, with μ < 1) arises in the vicinity of what would be the stall force, F_s, for the homogeneous system. For 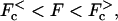the effective velocity depends on the width of the time averaging window, and tends to zero as the width of the window goes to infinity. The dashed line denotes the region where anomalous diffusion is also present.

Under special conditions, a random energy landscape is also possible. In this case the expected behavior as a function of force is similar to a homogeneous system: The potential fluctuations simply renormalize the drift velocity and diffusion constant at long times. That is, as the applied force is varied, the behavior is similar to that of a homogeneous system with no chemical bias. Provided that random contributions to the energy landscape not associated with simple conversion of chemical energy can be neglected, random energy models describe the dynamics in the absence of chemical bias (see Fig. 1 a) on heterogeneous substrates.

An alternative way to observe the anomalous dynamics is by holding the external force constant and varying the chemical bias. This can be done by changing the concentration of, say, nucleotide triphosphates for molecular motors, or by changing the concentration of the polymer-binding protein in one chamber for polymer translocation experiments. In this case, when the force is held at zero, the velocity changes monotonically in tandem with the chemical bias (see Fig. 2 a). However, when the external force is held constant at a nonzero value, a region with anomalous dynamics appears as the chemical bias is varied (see Fig. 2 b). Between two values of the chemical bias 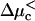and 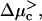the displacement of the particle with time is again sublinear, in contrast to the same experiment performed on a homogeneous substrate. As illustrated in Fig. 2 b, the velocity is then a monotonic function of the chemical bias, changing sign at a stalling chemical bias Δμ_s. A summary of the qualitative behavior of the velocity as function of both the chemical bias Δμ and the external force F is shown in Fig. 3. It is worth noting that there is no region of sublinear displacement when Δμ = 0 because the energy landscape is then random energy rather than random forcing, whereas when F = 0, there is still a random forcing landscape everywhere except exactly at stalling, but the randomness is too small in the vicinity of Δμ = 0 to cause anomalous dynamics.

FIGURE 2.

Schematic behavior of velocity for homogeneous and heterogeneous systems as a function of the chemical bias Δμ. (a) No externally applied force. (b) A finite externally applied force for homogeneous (shaded line) and heterogeneous (solid line) substrates. The anomalous dynamics arises in the vicinity of what would be the stall chemical bias, Δμ_s, for the homogeneous system. As in Fig. 1, the dashed line denotes the region where anomalous diffusion is present.

FIGURE 3.

Dependence of the velocity on the chemical bias Δμ and the external force F. We neglect for simplicity contributions to a random force landscape (such as fluctuations in basepairing energies) that may be present even for Δμ = 0. Here it is assumed that the chemical bias always acts in the direction opposing the force. The black wedge denotes a region of sublinear drift with time, i.e., effectively zero velocity.

To keep the discussion simple, Fig. 3 neglects contributions to a random forcing landscape other than those produced by the simple conversion of chemical energy along an inhomogeneous track. Additional random forcing contributions will arise from, e.g., basepairing energies in the case of helicases, which open up DNA strands or DNA polymerases and exonucleases, which add or delete complementary basepairs. Motors, such as RNA polymerases and ribosomes, produce trailing strands of mRNA and protein, respectively. Since these products are themselves heteropolymers, composed of monomers that interact differently with the solvent, here too we would expect additional contributions to a random forcing landscape. Such effects will only accentuate the anomalous dynamics, which is the subject of this article.

Before concluding this introduction, we should emphasize our perspective on the models of polynucleotide translocation and molecular motors studied here. In an effort to obtain simple, soluble models that incorporate heterogeneity, we intentionally neglect important molecular details such as those that describe the detailed pore interactions of the translocating nucleotides or distinguish the biological role of motors such as helicases, DNA polymerase and exonucleases, RNA polymerases, etc. The motors mentioned above perform important specialized functions such as opening double-stranded DNA, polymerization and depolymerization, or creating messenger RNA while moving along heterogeneous tracks. Such functions are incorporated into our model simply by adding an explicit (position-dependent) chemical force to the energy landscape. More sophisticated attempts to get molecular details right (see, e.g., Goel et al., 2003; Simon et al., 1992; and Betterton and Jülicher, 2003) serve a valuable purpose, which can be important for modeling some aspects of the dynamics on various timescales. However, incorporation of sequence heterogeneity, neglected in most previous modeling efforts, is nevertheless crucial to correctly describe the anomalous long time dynamics (e.g., 〈x(t)〉 ∼ t^μ with μ < 1) near the stall forces in these systems. Otherwise, we expect simple diffusion with drift (similar to what we find here for homogeneous models or a random energy landscape) at long times. We do not expect the multiple intermediate states and numerous rate constants of more sophisticated models to change our predictions of heterogeneity-induced anomalous dynamics at long times.

The article is organized as follows: In the next section, to establish notation and provide a context for the rest of the article, we discuss the homogeneous models for polymer translocation and molecular motors is some detail. Then the effect of heterogeneity on the energy landscape is introduced. “Dynamics in Heterogeneous Environments” discusses the resulting dynamical behavior and the exact location of the transition points within the models. Finally, “Experimental Considerations” estimates the experimental range over which the anomalous dynamics may be observed for a few representative biological systems and discusses the effect of finite time experiments on the shape of the velocity-force curve.

HOMOGENEOUS MODELS

Before turning to heterogeneous systems, we first define microscopic models for both homogeneous polymer translocation and molecular motors. The simplicity of both models allows for their exact solution. Dynamics in heterogeneous systems will be treated in “The Effect of Heterogeneity on the Energy Landscape” and “Dynamics in Heterogeneous Environments”.

Polymer translocation

An idealized experimental setup is shown schematically in Fig. 4. A polymer is threading through a narrow pore located on a two-dimensional membrane that separates two chemically distinct solutions. For concreteness we consider the right side as containing a polymer-binding protein that is absent in the left-hand side. In addition, a bead, through which a resisting force is exerted on the polymer, is connected to the left end of the polymer. A model of this kind has been discussed by P. Nelson (Nelson, 2003) as a simple example of stochastic ratchet-like dynamics in biological systems (see also Peskin et al., 1993). Alternatively a force could be applied via an external electric field acting across the pore on a charged polymer (Kasianowicz et al., 1996).

FIGURE 4.

Schematic picture of the polymer translocation experimental setup considered. A polymer is biased to move through the pore by a solution of binding proteins in the right chamber. A bead exerts a force in the opposite direction. The arrows reflect the lack of inversion symmetry in, e.g., single-stranded DNA or RNA.

A convenient representation of the system is through a one-dimensional random walker located at a coordinate x that represents the length of the polymer that has translocated to the right-hand side. The conditions under which the full three-dimensional, multispecies problem can be simplified are reviewed below. The dynamics of the random walker is governed by the interaction of the polymer with the pore, the binding of the protein in the right chamber, and the externally applied force.

Before turning to a specific microscopic model, consider the general form of the potential experienced by the random walker due to all these interactions. Because we neglect sequence heterogeneity in this section, the energy due to interactions with the pore, U(x), is some periodic function with a period given by the size of a monomer. An example is the sawtooth or ratchet potential shown in Fig. 5 a. This type of potential accounts for an energetic barrier for translocation through the pore. The lack of inversion symmetry reflects, for example, the difference in passing single-stranded DNA or RNA in the 3′ → 5′ direction through the pore as opposed to the reverse. The energy due to the interaction with the polymer-binding protein is, however, very different and has the form −F_μx, growing linearly with x. Thus the energy decreases as the polymer translocates to the right-hand side. The value of F_μ is governed by the chemical potential difference per monomer, Δμ, of the polymer in the solutions on the right-hand and left-hand sides. This chemical potential difference is a function of the protein concentration and its binding energy to the polymer (a more detailed description of F_μ for the microscopic model discussed below is presented in Appendix A). Finally, the backward force applied on the bead leads to a contribution to the energy of the form Fx. Upon collecting together these contributions, the total potential experienced by the random walker, Φ(x), is given by

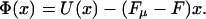(1)

As is evident from the effective energy landscape shown in Fig. 5 b, the random walker is moving in a periodic potential with an overall slope that depends on the protein concentration and binding energy as well as the external force. Such a potential leads on long time scale and large length scales to motion that is diffusion superimposed on an overall drift velocity. Thus, the average location of the particle 〈x〉 behaves as 〈x〉 = vt whereas the mean-square fluctuations about this drift behave as 〈x²〉 − 〈x〉² = 2Dt, where v and D depend on F_μ − F and the details of the ratchet potential (see, e.g., Lubensky and Nelson, 1999). Here, the brackets 〈…〉 represent an average over thermal fluctuations.

FIGURE 5.

(a) The periodic potential due to pore interactions with a translocating polymer without inversion symmetry. (b) The tilt of this potential generated by a combination with the binding protein and the external force.

We emphasize that our simplified description in terms of a single coordinate x that diffuses and drifts in a one-dimensional energy landscape is valid only when the translational motion of the polymer backbone through the pore is the slowest process in the problem (Lubensky and Nelson, 1999). In particular, this model assumes that the translocating polymer is not so long that the relaxation times in the cis (left) or trans (right) chambers exceed the diffusion time for the backbone through the pore. This simplified model is also inadequate if the polymer can become bound to the pore interior for long periods, as recent experiments suggest occurs for one of the best studied polymer-pore systems (Bates et al., 2003). In this case, x will still undergo biased diffusion on long enough timescales, but its velocity and diffusion coefficient will no longer be determined by a simple potential U(x). Finally, the effect of binding proteins can be captured by a single free-energy parameter Δμ only when their binding and unbinding kinetics are sufficiently fast. The opposite limit, in which proteins bind irreversibly, but slowly, to the polymer, has also received attention (Peskin et al., 1993; Simon et al., 1992; Sung and Park, 1996), but we will not consider it further here.

We now define a simplified microscopic model for the motion of a random walker in such a potential. Our model is in the spirit of those analyzed for motor proteins in Fisher and Kolomeisky (1999) and Kolomeisky and Fisher (1999) (see also “Molecular motors” in this section), and allows exact results for the diffusion and drift on long times. In the language of Fisher and Kolomeisky (1999) and Kolomeisky and Fisher (1999), our model is an n = 2 model corresponding to a motor with just two internal states. More importantly, our model generalizes naturally to a heterogeneous version (see “The Effect of Heterogeneity On The Energy Landscape”) for which exact results are also possible. We allow x to assume a discrete set of values x_m, where m = 0, 1, 2 … labels distinct a (even) and b (odd) sites. We can allow different distances between x_m+1 − x_m, and x_m+2 − x_m+1 but require x_m+2 − x_m = 2a₀, which we assume for simplicity is the size of the polymer unit that accommodates a single adsorbed protein. For a homopolymer, the interactions with the pore are some periodic function with a period that we can take to be 2a₀. To model this situation, we take odd-labeled sites to have a higher energy than even-labeled sites. The arrangement is shown schematically in Fig. 6. Even sites have an energy ɛ = 0 whereas odd sites (corresponding roughly to the peaks in the ratchet potential of Fig. 5) have a higher energy ɛ = Δɛ. Also, indicated in the Figure are the hopping rates that describe the dynamics of the random walker. The detailed balance condition (in temperature units such that k_B = 1) is satisfied by

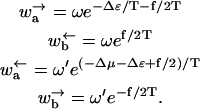(2)

Because of the lack of reflection symmetry in the translocating DNA or RNA (for our model this asymmetry could be represented by taking x₁ − x₀ ≠ x₂ − x₁), we expect the intrinsic hopping rates to be unequal, ω ≠ ω′. The bias induced by the interaction of individual monomers with the reservoir of proteins on one side of the pore has been accounted for by the chemical potential difference Δμ. A more detailed discussion of the dependence of Δμ on the protein-binding energy and its concentration is given in Appendix A. The effect of the applied force is included through the parameter f = Fa₀. Note that the bias controlled by Δμ > 0 arises only for steps from odd to even sites since a protein is assumed to bind only to a whole monomer. As pointed out, in Kolomeisky and Fisher (1999), other f-dependences of the rates consistent with detailed balance are possible. We shall be content with the simple one displayed in Eq. 2 that corresponds to choosing x₁ − x₀ = x₂ − x₁.

FIGURE 6.

Graphical representation of a simplified model for polymer translocation or molecular motors. These two cases are distinguished by the choice of rate constants (see text). The distinct even and odd sublattices are denoted by a and b, respectively.

To show that this microscopic model embodies an effective potential of the form Eq. 1, we eliminate the odd-numbered sites. This elimination can be accomplished by formally solving the equations of motion for the odd sites, substituting into the remaining even site equations, and taking the long time limit (see Appendix B). Alternatively we can invoke detailed balance and consider an effective energy difference ΔE = E(m + 2) − E(m) between site m + 2 and m, where m is even. Upon setting

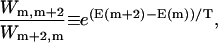(3)

where W_n,m is the effective transition rate between site m and n, we have

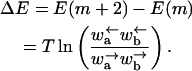(4)

Use of the rates Eq. 2 leads to

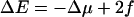(5)

as one would expect. Note that when the force vanishes (f = 0) and the chemical potential gradient Δμ = 0, one has ΔE = 0 and no net motion is generated. More generally, an effective tilted potential of the form Eq. 1 is generated, with Δμ > 0 causing a drift of the polymer to the right. The external force on the left can reduce or even reverse the overall slope. Such a potential inserted into microscopic rate equations for the even sites (see Appendix B) is well known to lead to diffusion with drift on long timescales and large length scales.

In fact, for this model using the results of Derrida (1983) and following Fisher and Kolomeisky (1999) and Kolomeisky and Fisher (1999), one can calculate the velocity and diffusion constant exactly. After some lengthy calculations, one obtains for the velocity

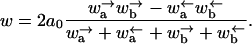(6)

The diffusion constant of the model is given by

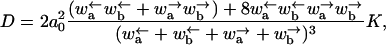(7)

with

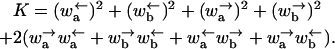(8)

It is interesting to set f = 0 and consider the limit of 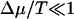(small chemical bias, no external force) and the limit Δμ/T → ∞ and 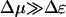(large chemical bias, no external force). When , the velocity takes the linear response form

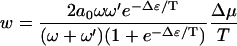(9)

In the limit of Δμ/T → ∞ and , the velocity saturates at v_max, with

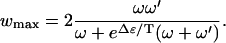(10)

In both cases the velocity is a decreasing function of Δɛ, as one might expect because the rate-limiting step in this simple polymer translocation model is the energetic barrier as each successive segment passes through the pore potential.

For the diffusion constant, one finds similarly in the limit :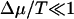

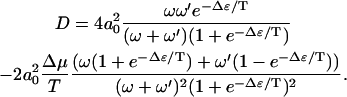(11)

Like the velocity, in this regime the diffusion constant decreases as Δɛ increases. Note that the diffusion constant deceases when Δμ increases. This behavior arises since the rate of backward steps decreases as Δμ increases. In the limit Δμ/T → ∞, and 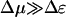, we find that the diffusion constant saturates at

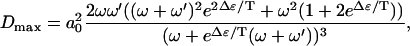(12)

which also decreases with Δɛ. The diffusion constant again decreases as a function of Δɛ due to the rate-limiting step of the passage through the pore.

Molecular motors

A typical experimental setup is shown in Fig. 7. The motor attempts to move from the plus end to the minus end by utilizing the chemical energy stored in ATP or some other source of chemical energy. For RNA polymerase, this energy source would be the nucleotide triphosphates, which are converted into mRNA (not shown). A force (say from an optical tweezer) pulls in the opposite direction to the motion generated by the ATP. In this section, we focus primarily on models of relatively simple motors as in Fig. 7 and mention only in passing more complicated effects associated with motors such as helicases or RNAp.

FIGURE 7.

Setup modeled. The motor is moving from the “plus” end to the “minus” end. A force is pulling on the motor in the opposite direction. Note that some of the specific biological examples considered in the text are more complicated and may be driven by energy sources other than ATP.

Theoretical models of molecular motors (Jülicher et al., 1997) have demonstrated how an effective potential of the form Eq. 1 is generated as a result of the coupling to an energy source like ATP for a general class of periodic substrate potentials that lack inversion symmetry. Here we again introduce a simple model for a two-level ratchet that is amendable to an exact solution, similar to an n = 2 version of the models of Fisher and Kolomeisky (Fisher and Kolomeisky, 1999; Kolomeisky and Fisher, 1999). Like the model for polymer translocation in the previous section, this motor model will allow us to study the effect of heterogeneity. We first consider the homogeneous motor model in some detail.

We again consider a one-dimensional lattice where even sites have energy ɛ = 0 and odd sites have an energy ɛ = Δɛ. The odd sites represent an “inchworm”-like walking that is facilitated by chemical energy released by, e.g., hydrolysis of ATP. The transition rates depicted in Fig. 6 now take a different form, namely

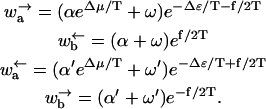(13)

Note that there are two parallel channels for the transitions (Jülicher et al., 1997). The first, represented by contributions containing α and α′, arise from utilization of chemical energy. The second channel, represented by the terms containing ω and ω′, correspond to thermal transitions unassisted by the chemical energy. Δμ is given by the standard relation (Howard, 2001),

(14)

where the square brackets […] denote concentrations under experimental conditions and the […]_eq denote the corresponding concentrations at equilibrium. We have again assumed the external applied force f biases the motion in a particularly simple way. If the substrate lacks inversion symmetry, we have α′ ≠ α and ω′ ≠ ω. As discussed in the Introduction, in some cases an additional force arises from, e.g., basepairing energies in the case of helicases, DNA polymerases, and exonucleases. Similarly, an addition force arises also for motors such as RNA polymerase and ribosomes, which produce trailing strands of mRNA or protein, respectively. Here we ignore such contributions, although they could easily be added in a simple way to the model through a redefinition of f through f → f + f_μ, where f_μ is the additional force. The model is formally similar to the model of polymer translocation, although the different functional form of 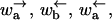and 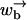has important consequences.

First we consider the effective energy landscape. To this end, we again eliminate the odd sites and describe the remaining dynamics in terms of an effective potential. This is the effective potential under which a random walker satisfying detailed balance would exhibit the same dynamics. From a formula similar to Eq. 3, one finds that ΔE = E(m + 2) − E(m), where m is an even site, is given by

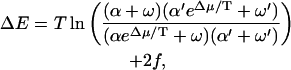(15)

where we have used the rates Eq. 13.

Note that when the external force f = 0 and the ATP/ADP + P chemical potential difference Δμ = 0, one has ΔE = 0 and no net motion is generated. Also, when there is directional symmetry in the transition rates α = α′, ω = ω′, and f = 0, one has ΔE = 0, even when Δμ ≠ 0. Absent this symmetry, chemical energy can be converted to motion and an effective tilted potential is generated. Although these conditions are equivalent to those presented in Jülicher et al. (1997) and Prost et al. (1994) for continuum models, it is interesting to see them at work in the “minimal” model studied here (see also Fisher and Kolomeisky, 1999, and Kolomeisky and Fisher, 1999). The effect of the externally applied force is simply to change the overall tilt in the potential.

For a motor on a homogeneous or periodic substrate, the effective potential generated by the coupling to the chemical potential is thus qualitatively the same as that of a polymer translocating through a pore. Again, on long timescales and large length scales, the dynamics is just diffusion with drift. The equation for the velocity and diffusion constant are given by Eqs. 6, 7 and 8 together with the rates displayed in Eq. 13.

As for the polymer translocation problem, it is interesting to consider various limits for the case f = 0. Using Eq. 13, we find in the limit of 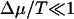a drift velocity

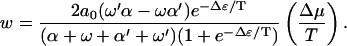(16)

Therefore, for small Δμ/T, the velocity decreases as Δɛ increases. Note that even when Δμ ≠ 0, v vanishes for a symmetric substrate, i.e., for ω′ = ω and α′ = α. A natural measure of the asymmetry of the potential is ω′α/ωα′. When this quantity is >1 (<1), a positive Δμ induces a motion to the right (left). This result remains valid to any order in Δμ.

The maximum possible motor velocity v_max is obtained in the limit Δμ/T → ∞ and 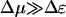, where

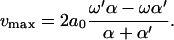(17)

In contrast to the previous regime and the polymer translocation problem, the velocity is insensitive to Δɛ. Because of the injection of large amounts of external chemical energy, the barrier Δɛ no longer controls a rate-limiting step.

For the diffusion constant of this model of molecular motors in the limit 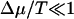, we find

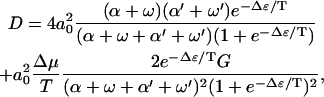(18)

with

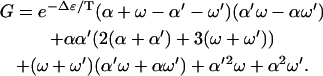(19)

Like the velocity, the diffusion constant decreases as Δɛ increases in this regime. Note that the diffusion constant increases as Δμ increases, because Δμ enhances the rates of motion in both directions. In the limit Δμ/T → ∞, one obtains

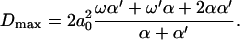(20)

Again, for large chemical potential differences, the result is independent of Δɛ.

THE EFFECT OF HETEROGENEITY ON THE ENERGY LANDSCAPE

Next we discuss the effect of heterogeneity on the effective energy landscape experienced by motors or translocating polymers. The detailed dynamics that results will be considered in the next section. As we shall see, heterogeneity has dramatic consequences over a range of parameters close to the stall force.

We first consider the somewhat simpler problem of heterogeneity and polymer translocation. We then show that a similar picture arises for motor proteins on heterogeneous substrates like DNA or RNA.

Polymer translocation

Two sources of heterogeneity affect polymer translocation. Both arise for polymers composed of different types of monomer. We assume for simplicity that the monomers composing the polymer are drawn from some random distribution with a finite variance. Provided the correlations along the backbone are short range, our results are insensitive to the exact nature of the distribution. The effect of sequence heterogeneity corresponding to a particular nucleotide sequence could easily be incorporated into a numerical analysis of the dynamics.

We first consider general features of the potential for a model with sequence heterogeneity. Randomness in the composition of the polymer will, of course, modify the interaction potential between the polymer and pore, U(x). It is easy to see that this leads to a random potential component with a finite variance around its mean value, i.e., a random energy landscape. The second, more striking, effect arises from the randomness in the binding energy of the proteins. The associated force depends specifically on the location x along the polymer. In a convenient continuum notation, the total energy gained by attaching to the monomers has the form 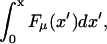where F_μ(x) represents the different binding energies associated with the sequence of the polymer. If the sequence is random, the fluctuations around the mean slope of the potential grow like 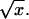The effective potential experienced by the random walker is therefore

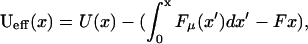(21)

where we have included the externally applied force, F. A schematic representation of the potential is shown in Fig. 8. Since 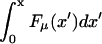has fluctuations that grow as 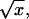the sequential binding of proteins to a translocating polymer creates a random forcing landscape, in contrast to the landscape defined by Eq. 1. Because the energy landscape itself can be viewed as a simple random walk about a linear landscape, the random force contribution to U_eff(x) (an integrated random walk) dominates the random energy term arising from interactions with the pore. As will be discussed in the next section, this results in unusual behavior if the externally applied force lies in a certain range of values near the stall force.

FIGURE 8.

Graphical representation of the energy landscape in the case of heterogeneous polymer translocation when the chemical environments on both sides of the pore are different. Potential fluctuations about the mean slope scale like 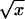for large x. The same picture holds for molecular motors moving on a heterogeneous substrate powered by a finite chemical potential difference.

Note that it is also possible to obtain a purely random energy landscape in polymer translocation. When the chemical environments on both sides match (e.g., for identical concentrations of binding proteins) one has F_μ(x) = 0. The only random component of the energy landscape is due to the potential for translocating through the pore that has bounded fluctuations about its mean value. For this energy landscape, the dynamics at long times and large length scales is then biased diffusion, with a drift velocity and diffusion constant renormalized by the heterogeneous interactions with the pore (Alexander et al., 1981).

We now explore these effects within our microscopic model of polymer translocation. The heterogeneity is introduced into the model through the rates Eq. 2. Imagine drawing the set of parameters {p} = {ω, ω′, Δɛ, Δμ} from random distributions (corresponding to various nucleotide sequences) with a finite variance. According to Eq. 5, the total change in energy after m monomers translocate is given by

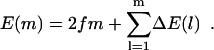(22)

Here the ΔE(m) are effective energy differences between two even sites corresponding to the set of values of the set {p} drawn randomly. Since the energy is a sum of independent random variables, a random forcing landscape is developed.

We expect that a simple random energy landscape results if we turn off the protein binding by setting Δμ = 0. However, because the energy at even sites is always E = 0 in our simple model, the landscape is just a uniform tilt in this limit. A more realistic model would allow additional energy variations at these sites. If we assign an energy ɛ(m) to these even sites, it is straightforward to show that the total change in energy after m monomers have translocated takes the form

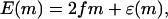(23)

corresponding to a random energy landscape.

Molecular motors

We now turn to the effect of heterogeneity on molecular motors. Here, as for polymer translocation, we select the set of parameters {p} = {α, α′, ω, ω′, Δɛ} from a random distribution with a finite variance. For some motors and enzymes (for example, RNA polymerase, helicases, and DNA polymerases and exonucleases—see Introduction and below), Δμ may also be random. This clearly only adds an additional contribution to the random forcing landscape. Using the results presented above, it is easy to see from Eq. 15 that the total effective energy change after m monomers is given by

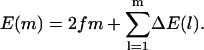(24)

Here, each ΔE(m) corresponds to an independent set of values of {p} drawn randomly. Thus, as in the polymer translocation problem, the potential is random forcing.

For motors such as helicases, DNA polymerases and exonucleases, and RNA polymerase and ribosomes, an additional contribution to the random energy arises due to the force associated with, e.g., basepairing energies or the trailing strand that is produced. The effect of this would be to modify the expression above to

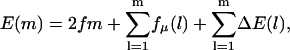(25)

where f_μ is the additional contribution of the explicit random forcing from monomer m. The resulting random forcing landscape is even more pronounced.

The above scenario applies as long as the chemical potential difference Δμ ≠ 0. In the case when Δμ = 0, it is easy to see that ΔE(m) = 0 unless we allow, as in the polymer translocation problem, for the energy at even sites also to vary and take the value ɛ(m). In this case we obtain

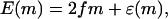(26)

corresponding to a random energy landscape provided ɛ(m) has only short range correlations. Although we could write the energy in the form of Eq. 24, now ΔE(m) = ɛ(m) − ɛ(m − 1), so ΔE(m) is effectively the gradient of a random potential with bounded fluctuations. Note, however, that for motors with an f_μ contribution (as in Eq. 25), it is not possible to obtain a random energy landscape.

The energy landscape for both polymer translocation and molecular motors is therefore qualitatively identical. Generically, in both cases, a random forcing energy landscape develops. However, if the motor model without the applied external force has no bias (i.e., if Δμ = 0), we recover the diffusion with drift dynamics associated with a random energy potential.

DYNAMICS IN HETEROGENEOUS ENVIRONMENTS

In this section we discuss in detail the dynamics of translocating polymers and motor proteins with heterogeneity for the model depicted schematically in Fig. 6. We describe four distinct cases with different dynamical behaviors as the externally applied force is varied. The critical forces for the transition between the regimes can be calculated exactly in terms of the rates 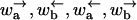averaged over their heterogeneous generalization with f = 0. The explicit expressions for polymer translocation and molecular motors can be easily obtained by using the rates in Eqs. 2 and 13, respectively. We assume throughout that Δμ ≠ 0, as the case Δμ = 0 leads only to a random energy model and biased diffusion. Also, contributions to the random forcing energy landscape of the form of Eq. 25 are omitted for simplicity. Their addition is straightforward and can be easily seen to enhance the region of anomalous dynamics.

The dynamical behaviors of random walkers in random forcing or random energy landscapes have been studied in detail in the statistical mechanics literature (Bouchaud et al., 1990; Derrida, 1983). Unusual dynamical behavior arises for random walkers in a random forcing energy landscape. Using the results of Derrida (1983), one can calculate the transition points between the different regimes including the effect of randomness. Parts of the calculation are outlined in Appendix C along with the different regimes in terms of the transition rates . Here we consider the experimental setup in Figs. 4 and 6 where the external force is varied. Denoting spatial averages by an overline and using the results of Appendix C, one finds the following regimes.

Regime I

The velocity v and diffusion constant D of the model are finite when

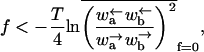(27)

or

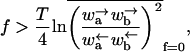(28)

where the subscript f = 0 denotes that f has been set to zero in the average. In this regime 〈x〉 = vt and 〈x²〉 − 〈x〉² = 2Dt for long times, where the angular brackets denote an average over different thermal histories of the system. Simpler conditions can be obtained by assuming that has a Gaussian distribution about the mean 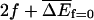(see Eqs. 5 and 15) and a variance 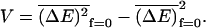Here again the subscript f = 0 denotes that averages are taken with the value of the force set to zero. In this case one has

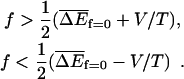(29)

Note that the force does not contribute to the variance so that .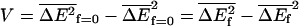

Regime II

The velocity v is finite but the diffusion constant is infinite. Thus, in this region 〈x〉 = vt and 〈x²〉 − 〈x〉² ∼ t^2/μ, where 1 < μ < 2. The relevant force ranges are

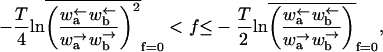(30)

and

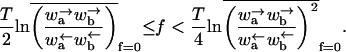(31)

Provided that ΔE has a Gaussian distribution, the conditions reduce to

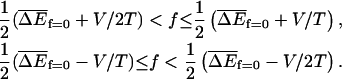(32)

For a Gaussian distribution, it is known (Bouchaud et al., 1990) that the exponent μ is given by

(33)

Regime III

The velocity v is zero in the sense that 〈x〉 ∼ t^μ, where μ < 1. The exponent μ also controls the variance, 〈x²〉 − 〈x〉² ∼ t^2μ. This behavior occurs when

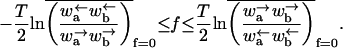(34)

When ΔE has a Gaussian distribution, these conditions reduce to

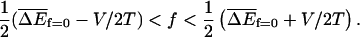(35)

Sinai diffusion

Here 〈x 〉 = 0 and 〈x²〉 ∼ (ln(t/τ))⁴, where τ is the microscopic time needed to move across one monomer. This regime appears precisely at the “stall force” corresponding to a disordered substrate, namely

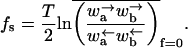(36)

If ΔE has a Gaussian distribution, this condition yields

(37)

The resulting behavior as the force is varied is summarized qualitatively in Fig. 1.

It is interesting to consider the location of the stall force, f_s, as well as the range of forces over which the displacement is anomalous, namely the region where 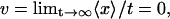in some more detail for both polymer translocation and molecular motors in some simple scenarios. These quantities characterize how the location and width of the anomalous displacement region develops as a function of temperature and chemical forces. We assume ΔE(m) with a Gaussian distribution about 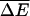with a variance V, although it is straightforward to extend the results to non-Gaussian distributions with no change of the qualitative behavior. It is straightforward to show using Eq. 35 that the range of forces, Δf, over which the velocity is zero satisfies

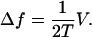(38)

For polymer translocation using Eqs. 5 and 37 implies that Sinai diffusion occurs for the force

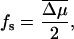(39)

whereas Eq. 38 implies that the range of forces around f_s where the displacement is anomalous is given by

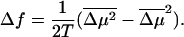(40)

If there are no proteins on left-hand side (cis chamber), and a small concentration, P, of protein is added to the right-hand side (trans chamber) one can show using Eq. A3 that f_s ∝ P whereas Δf ∝ P². Thus, as the chemical bias increases, both f_s and Δf grow. Note that in general, one may consider proteins in both the left and right chambers. In this case even when the average chemical bias 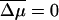, one may still have V > 0 giving rise to anomalous dynamics even when the external bias F = 0.

For molecular motors, the situation is more interesting. The results presented above for the transition points between the different regimes hold even when Δμ is also random. However, here we restrict ourselves to the simpler case when Δμ is constant. In this case, Eq. 15 implies that for small chemical potential (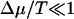), the chemical energy difference ΔE_f=0 = qΔμ, where q is the coefficient in the Taylor expansion of Eq. 15 in Δμ, which is independent of T. Therefore, in this limit, the stall force is

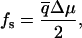(41)

and

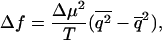(42)

where we have assumed the purpose of a rough estimate that the chemical potential difference does not depend on the type of monomer. Similarly to polymer translocation, as the system is driven out of chemical equilibrium, both f_s and Δf grow. However, in the limit of 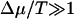, one obtains ΔE_f=0 = pT, where p is obtained by taking the appropriate limit in Eq. 15 and is independent of T. We then have

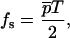(43)

and

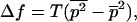(44)

implying that both quantities increase with increasing temperature.

Note that if the force applied to the polymer or motor is held constant and the chemical parameters (e.g., ATP or protein concentration) are varied from their equilibrium value, one should also observe a region of anomalous displacement (see the general expressions in Appendix C). These conclusions are summarized qualitatively in Figs. 1, 2, and 3.

EXPERIMENTAL CONSIDERATIONS

As discussed in the previous section, the important quantity for deciding if anomalous dynamics is present is the variance 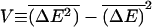of ΔE(m), where the overbar represents an average over the ensemble of random sequences. Effects related to sequence heterogeneity dominate when V is large compared to 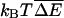. Here we estimate the ranges over which anomalous dynamics may be observed in experiments as well as other preconditions needed to observe this behavior. We also discuss the effect of finite time experiments on the shape of the velocity-force curve. In this section, we reintroduce Boltzmann's constant k_B.

Polymer translocation

For polymer translocation, whether the variance V is large compared to 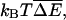of course, depends on a number of factors, including the base composition of the polynucleotide passing through the pore, the particular protein whose binding drives translocation, and the concentration of the binding protein. Nonetheless, it is instructive to consider an example to get some sense of the orders of magnitude involved. We focus on DNA binding proteins. Note that, like those of most such proteins, the binding sites are several nucleotides long; unlike in previous sections, unless stated otherwise, we will give values of V and other parameters normalized per nucleotide rather than per bound protein.

The bacteriophage T4-coded gene 32 protein (gp32) is a monomeric single-stranded DNA (ssDNA) binding protein that is implicated in DNA replication and related processes (Coleman and Oakley, 1980). When it associates with ssDNA cooperatively in the “polynucleotide” mode (Kowalczykowski et al., 1981), its net affinity K_net can vary by as much as a factor of 10 depending on the polymer's base composition; in physiological salt concentrations, a typical range is K_net ∼2 × 10⁸ − 2 × 10⁹ M⁻¹ (Newport et al., 1981). (The net affinity is the affinity of an additional protein molecule for a growing chain of cooperatively bound monomers; it differs from the affinity of an isolated protein molecule for ssDNA by an enhancement factor arising from the cooperative interactions.) In this binding mode, the binding site of each gp32 monomer is seven nucleotides long. For a micromolar protein concentration, K_net is large enough that almost all sites on the translocated ssDNA will be occupied. Upon assuming that V is determined entirely by the base dependence of K_net, we then estimate that V ∼0.1 − 0.2(k_BT)² for a “generic” DNA molecule in which each of the bases appears with roughly equal frequency. Here T is room temperature, 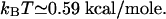In this case, the change in free energy of a nucleotide moved from a buffer without any gp32 to one where the protein is present is Δμ ∼ k_BT (see Eq. 2). Upon taking the ssDNA to be a freely jointed chain with Kuhn length 1.5 nm (Smith et al., 1996), one finds that a force of ∼10–15 pN on the polymer is required to cancel the effects of the protein binding. To have 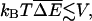so that disorder effects can be detected, the value of the force must be controlled to ∼10% or better accuracy.

Molecular motors

To be able to measure the motion of a motor along a substrate, it must remain attached long enough to be able to perform many moves across monomers. In other words, if the rate at which the motor leaves the substrate is γ and the rate of crossing a monomer to the right or left is 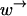or 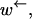respectively, then 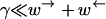must hold. In the regime of anomalous dynamics, 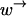is of the same order of 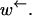Therefore, the condition will not be fulfilled in this regime when the rate of hopping against the chemical bias is always very small.

There are, however, experiments where such a restriction does not hold. For example, the experiment by Wuite et al. (2000) on the DNA polymerase/exonuclease system (see also Maier et al., 2000) monitors not the displacement of a single motor but the location of the junction between the ssDNA and the dsDNA. Therefore, it is more natural to model the dynamics of the ssDNA/dsDNA junction and not of the motor. A motor that leaves the ssDNA/dsDNA junction is eventually replaced by a motor from the solution. Within our models, this can be represented by an internal state of the junction (similar in spirit to Fisher and Kolomeisky, 1999, and Kolomeisky and Fisher, 1999). A model of this type for the DNA polymerase/exonuclease has been studied in Goel et al. (2003). However, the disorder in the transition rates, present due to the heterogeneity of the DNA, has been neglected. In Appendix D we analyze in some detail a simple model of the DNA polymerase/exonuclease system. As shown in the appendix it is straightforward to show that the presence of heterogeneity (for example, in the energy gained from the hydrolysis of the different NTPs) leads to a random forcing energy landscape. One therefore expects a region of anomalous dynamics near where the external stretching force F′ causes a change in direction. We stress that more realistic models with many intermediate states can by analyzed similarly without affecting the existence of the region with anomalous dynamics. Unfortunately, for this experiment an estimation of the width of the region is not straightforward.

Estimates, similar to those above for polymer translocation, can be obtained for the random force landscapes for a number of molecular motors that operate on DNA or RNA. Two examples of interest are RNA polymerases (RNAps) (Davenport et al., 2000; Gelles and Landick, 1998; Jülicher and Bruinsma, 1998; Wang et al., 1998) and helicases acting on double-stranded DNA (dsDNA) (Bianco et al., 2001; Dohoney and Gelles, 2001; Lohman and Bjornson, 1996; von Hippel and Delagouette, 2001). An RNAp's function is to transcribe DNA—that is, to synthesize an RNA “copy” with the same sequence as a DNA molecule. To do so, it walks along dsDNA trailing a growing RNA strand. The RNAp motor is powered entirely by the energy gained from the hydrolysis of successive NTPs as they are added to the RNA molecule. Although the mechanism of RNAp motion is still the subject of debate (Jülicher and Bruinsma, 1998; von Hippel and Pasman, 2002), many models suggest that at low enough NTP concentrations, its ability to move forward will be limited by the rate at which NTPs arrive at the catalytic site. A straightforward way to force RNAp into a regime in which its motion is dominated by a random force energy landscape is thus to place it in a buffer with different concentrations of each of the four NTPs. The motor's ability to take a forward step is dependent on the incorporation of the appropriate NTP, and the rate of that incorporation is proportional to that NTP's concentration. Thus, one can in principle make V arbitrarily large and satisfy the criterion 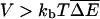for significant random force effects. Each factor of 10 difference between the concentrations of two nucleotide triphosphates, and hence in the rates to make a forward step, translates into a difference of k_BT ln(10) ≈ 2.3k_BT in ΔE(m). Of course, in practice, other factors—for example the possibility that the RNAp might fall off its DNA track before the needed NTP arrives—will limit how large a range of concentration differences can be achieved experimentally. It will be interesting to see whether strong disorder effects can be observed.

Another class of motors that use DNA as their track are helicases, which are needed to separate the two strands of dsDNA to facilitate various processes in the cell such as cell division in prokaryotes. Helicases move along the DNA by consuming energy from NTPs. Although some helicases only break a few basepairs at a time, others can move substantial distances along their tracks (Bianco et al., 2001; Dohoney and Gelles, 2001). Recent modeling of certain monomeric helicases (Betterton and Jülicher, 2003) suggests that disordered DNA sequences affect helicase motion primarily through the different energies required to open different basepairs. Random sequences thus lead to anomalous helicase motion in much the same way they do anomalous dynamics of mechanical unzipping (Lubensky and Nelson, 2000, 2002). In the simplest case of “passive” opening, one finds that ΔE(m) ≈ ΔE_motor + ΔE_DNA(m), where ΔE_motor, which summarizes the forward force exerted by the helicase motor, is negative and has magnitude at least ∼2k_BT, and ΔE_DNA is simply the thermodynamic free-energy cost of opening each successive basepair, with size roughly between 1 and 3 k_BT (SantaLucia, 1998). One thus has V ∼1(k_BT)². This large variance means that it should be relatively easy to observe anomalous, disorder-dominated dynamics in helicases as predicted earlier for DNA unzipping. If, for example, one assumes that the magnitude of ΔE_motor is near its lower bound of 2k_BT, then, in the passive opening model, disorder effects should begin to appear for a mechanical load opposing the motor's motion of as little as 7 pN and should persist up to at least 20 pN.

Finite time effects

All calculations of quantities such as the velocity have been done by taking the limit of very large times and averaging over thermal realizations with the same heterogeneous sequence. For experiments done over finite times, the velocity will not be strictly zero in the regime of anomalous dynamics. Instead, the velocity decays to zero as 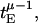where t_E is the experimental averaging time used to define v as 〈x(t_E) − x(0)〉/t_E. The closer μ is to zero, the faster the decay will be. Therefore, the curve of the velocity as a function of the external force or chemical potential (see Figs. 1 and 2) will be rounded, becoming sharper and sharper as t_E → ∞. To illustrate this, we have carried out simulations of model Eq. 13 on a single realization of the disorder averaging over thermal realizations and measured the v − F curve. The results are shown in Fig. 9. As can be seen, the longer t_E, the closer is the v − F curve to that shown in Fig. 1. The convex shape of the curve near the stall force is clear already for averaging times t_E ∼ 10⁵, corresponding to motors that transverse distances of O(1000) at f/T = 0. Note that, if one looks at the displacement of a single motor (i.e., without averaging over thermal realizations), the regime of anomalous dynamics will be characterized by long pauses at localized regions (corresponding to deep minima of the effective potential) with fast transitions between the localized regions (corresponding to overcoming the barrier associated with the minima). The inset of Fig. 9 shows a single trajectory as a function of time for a given realization of disorder. The value of f/T was chosen to be in the region close to the anomalous velocity regime but not inside it (the point is at the edge of the anomalous diffusion region close to the normal diffusion region). As can be seen, the motion of the motor is characterized by long pauses at specific locations along the track, with quick jumps between the pause points. The location of the pause points is reproducible for the same spatial disorder and different thermal realizations, although their duration varies from simulation to simulation. Note that since the velocity is finite in this regime, over large length scales the effect of the jumps becomes unimportant. These pauses correspond to local minima of the effective potential and as such are inherently correlated with the structure of the track. Such pauses and jumps have been observed in recent experiments (Danilowicz et al., 2003) on DNA unzipping.

FIGURE 9.

The velocity as a function of f/T for different values of t_E. Here Δμ/T = 3 and parameters were chosen with equal probability to be either {p} = {5, 1, 0.3, 1, 0} or {p} = {4, 0.1, 0.7, 1, 0} (see text for notation). The calculated regime of anomalous velocity is 0.5116 < f < 0.699. Data were averaged over 100 thermal realizations. (Inset) A single trajectory shown for the same parameters at f/T = 0.45.

SUMMARY

We have studied the effect of sequence heterogeneity on both polymer translocation and the motion of molecular motors within simple models. The models were solved exactly both with and without disorder. It was shown that these systems can be represented on large length scales and long timescales by a random walker moving along a random forcing energy landscape. Thus, in a range of forces near the stall force, we expect anomalous dynamics where the displacement grows as a sublinear power of time. We stress again that such results also apply to more sophisticated models that include many internal states of the motor (see the discussion of the DNA polymerase/exonuclease system in Appendix D). Several systems in which the regime of anomalous dynamics might be wide enough to be observable were considered.

APPENDIX A: THE CHEMICAL POTENTIAL DIFFERENCE FOR TRANSLOCATING POLYMERS

Here we discuss the dependence of the chemical potential difference Δμ for a translocating polymer between the right-hand (trans) and left-hand (cis) sides of Fig. 4 on the protein concentrations and its binding energy to the polymer. Consider first a denatured polymer in a solution with a concentration c_p of proteins that can bind to its monomers with a binding energy E_b < 0. We neglect cooperativity in the binding of the proteins to the polymer, although this effect could easily be included. Assuming an ideal solution theory, the protein chemical potential is given 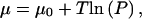where P = c_p/c and c are the concentration of the solvent. Here we take the free-energy change due to an addition of one isolated protein to the solvent to be μ₀ − T ln n, where n is the number of solvent molecules (Landau and Lifshitz, 1963). Next, we take the energy function of a polymer of length N inside the solution to be

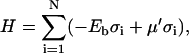(A1)

where σ_i = 1(0) if a protein is bound (unbound) to monomer i and μ′ is a chemical potential that controls the density of proteins bound to the polymer. In thermal equilibrium μ = μ′, which gives for the free energy of a polymer monomer in the solution

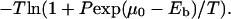(A2)

The change in the free energy of the polymer, which occurs as a result of a monomer passing from the left (cis) chamber to the right (trans) chamber, with ratios of protein/solvent concentrations P_L and P_R, respectively, is given by

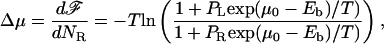(A3)

where ℱ is the total free energy of the polymer and N_R is the number of monomers in the right chamber. It is straightforward to see that this result implies that for proteins with different binding energy to different types of monomers, Δμ will depend on the type of monomer.

APPENDIX B: DERIVING THE EFFECTIVE POTENTIAL FROM THE MASTER EQUATION

In this appendix we show that the equations for the probability P_n(t) of being at site n at time t are equivalent in the long time limit (to be specified more exactly below) to a random walker moving in an energy landscape constructed using Eq. 4. We demonstrate this by eliminating the even sites from the equations of motion (see Lattanzi and Maritan, 2002, for similar ideas).

First, consider the equations governing the evolution of the probability, i.e., the master equation. For odd n one has (see Fig. 6)

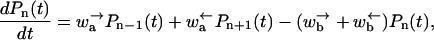(B1)

whereas for even n

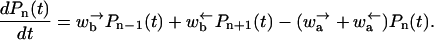(B2)

Next, we solve the equation for the odd sites and substitute into that for the even sites. The solution of the equation for the odd sites is

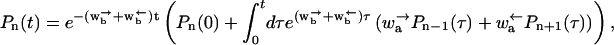(B3)

where P_n(0) is the probability distribution at the initial time t = 0. Substituting this into the equation for the even sites yields

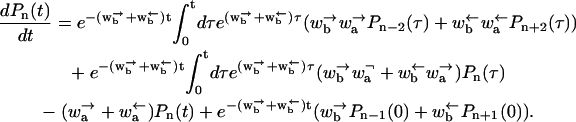(B4)

At times 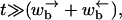one can neglect the two last terms in Eq. B4 and approximate the integrals as follows:

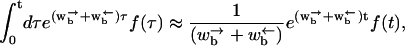(B5)

where f(τ) is assumed to vary slowly with τ. In this long time approximation, Eq. B4 reduces to

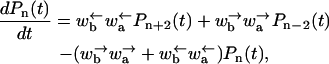(B6)

where we have rescaled times such that 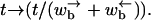As expected, this equation corresponds to a random walker moving in a potential constructed using Eq. 4.

APPENDIX C: DERIVATION OF THE DIFFERENT DYNAMICAL REGIMES

In this appendix the expressions for the different dynamical regimes in terms of the hopping rates 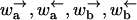are given. These general equations allow a straightforward derivation of the expressions in the text. However, before turning to the results, we outline the derivation of the regime where the displacement is anomalous. The derivation of the other regimes is much lengthier, so we only sketch the main results.

Unless stated otherwise, we assume throughout this appendix that

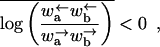(C1)

where, as in the main text, we denote spatial averages by an overbar. Because 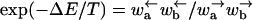in our notation, this condition is equivalent to assuming an overall bias to the right

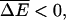(C2)

where ΔE arises from the generalization of Eqs. 5 and 15 to heterogeneous systems. The other opposite regime, 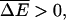can be treated similarly. As shown by Derrida (1983), the velocity of a random walker on an infinite lattice model in this case is given by

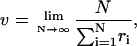(C3)

where

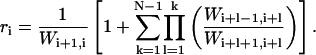(C4)

Here, W_i,j is the hopping rate from site j to i. The denominator of Eq. 3 can be simplified by replacing the sum by an average of r_i:

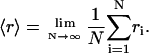(C5)

Using the rates 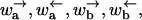one finds that the average 〈r〉 is finite only if

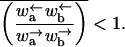(C6)

In this case the velocity is finite. However, when the inequality is reversed, 〈r〉 = ∞ and the velocity is zero.

A much lengthier calculation along somewhat similar lines can be done to derive the other dynamical regimes. One obtains the following results.

Regime I

When

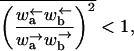(C7)

the velocity v and diffusion constant D of the model are finite. Namely, 〈x〉 = vt and 〈x²〉 − 〈x〉² = 2Dt for long times, where the angular brackets denote an average over different thermal histories of the system. Assuming for simplicity that ΔE(m) is distributed around 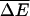with a Gaussian distribution with a variance 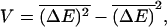this condition reduces to

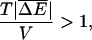(C8)

i.e., the variance of the energy fluctuations must not be too large. Here we have used the fact that 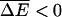and the relation 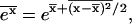which holds for Gaussian distributions.

Regime II

When

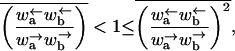(C9)

the velocity v is finite but the diffusion constant is infinite. It can be shown (Bouchaud et al., 1990) that in this region the long time behavior is 〈x〉 = vt and 〈x²〉 − 〈x〉² ∼ t^2/μ, where 1 < μ < 2. If we assume a mean value of ΔE with a Gaussian distribution about the mean, the condition reduces to

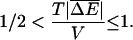(C10)

We have again used 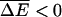. For this case it is known (Bouchaud et al., 1990) that the exponent μ is given by .

Regime III

When

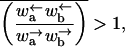(C11)

the velocity v is zero. More precisely, 〈x〉 ∼ t^μ, where μ < 1. The diffusion about this drift is anomalous in the sense that 〈x²〉 − 〈x〉² ∼ t^2μ. Assuming again a mean value of ΔE with a Gaussian distribution about the mean leads to the condition

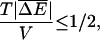(C12)

where again we have used the fact that .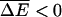

Sinai diffusion

When the average bias is exactly zero,

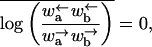(C13)

the system exhibits Sinai diffusion (Sinai, 1982) with 〈x〉 = 0 and 〈x²〉 ∼ (ln(t/τ))⁴, where τ is the microscopic time needed to move one monomer. Thus, we are now considering the case .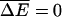

Note that when

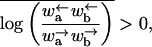(C14)

namely a reversed bias where 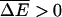, similar regions can be found by interchanging and . For example, when

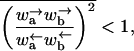(C15)

the velocity v and diffusion constant D of the model are finite. Such results, of course, require that the molecular motors remain attached when they reverse direction.

Note also that the three regimes may be identified (Bouchaud et al., 1990) according to the parameter μ. In particular, we identify μ > 2 with regime I, 1 < μ < 2 with regime II, μ < 1 with regime III, and μ = 0 with Sinai diffusion.

APPENDIX D: SIMPLE MODEL FOR THE DNA POLYMERASE/EXONUCLEASE SYSTEM

In this appendix, a model of the DNA polymerase/exoneclease system is studied. It is shown how a more detailed microscopic model than those studied in the main text also leads to an effective random forcing energy landscape. However, in contrast to these models, the location of the transition points into the anomalous dynamics regime cannot be calculated exactly in a straightforward manner.

The model we consider is a simplified version of the model studied by Goel et al. (2003). The model takes into account the two active sites of the motor, one acting as a polymerase with the other acting as an exonuclease. The system can be in one of five state denoted in Fig. 10 by a–f. The Figure represents only transitions that differ by a motion of the motor over a distance of one base. The full model along with an illustration of the experiment is shown in Fig. 11. In state a, the motor is attached to the ssDNA/dsDNA junction with the polymerase active site. In state b, the motor uses the energy from the hydrolysis of NTP to be able to extend the dsDNA. States c and d represent similar states but now with the motor connected to the junction using the exonuclease active site. Here the motor does not utilize energy from the hydrolysis of NTP but instead uses the binding energy of the NMP. State f represents the motor unbound from the junction. One of the motors in the solution can bind to the junction in through either the polymerase or exonuclease active site. Clearly, the model is not a strictly one-dimension model but corresponds to a random walker moving on two lanes.

FIGURE 10.

The possible states of the DNA polymerase/exonuclease model. Each pair of either a, f, or c states differ by an addition (or removal) of one base from the dsDNA.

FIGURE 11.

The full model on the two-lane lattice. The inset on the top depicts a cartoon of the experimental system.

The rates of transitions between the states are denoted in the Figure. Explicit expressions similar to Eq. 13 can easily be written down. The effect of the external stretching force F′ acting on the ssDNA/dsDNA complex will cause transitions through the cycle 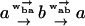to be less favorable with transitions through the cycle to be more favorable.

To show that the energy landscape corresponding to the model in the presence of disorder is indeed a random forcing energy landscape, we first calculate the landscape for the homogeneous model. Using the results of Derrida (1983), we study one cycle of the model (see Fig. 10) and calculate the ratio of the probabilities P_a(n) and P_a(n + 2) of being in the two a states that differ by a translation of one base. Similarly, the effective energy difference between any two other sites can be calculated. With the help of Eq. C4, this ratio can be shown to be given by

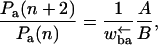(D1)

with

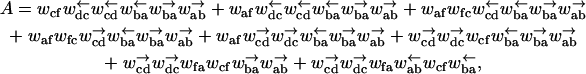(D2)

and

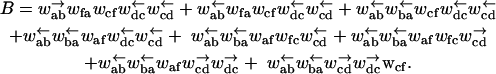(D3)

The effective energy landscape can be inferred by assuming an equilibrium distribution so that

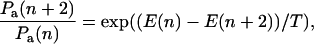(D4)

and the effective energy difference is given by

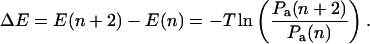(D5)

It is now clear, using Eq. D1 and arguments similar to those in “Dynamics of Heterogeneous Environments” that if the set of rates becomes site-dependent, a random forcing energy landscape will develop. The only difference from the simple soluble models studied in the main text is that the random walker representing the system is moving on a two-lane lattice. On general grounds (Fisher, 1984), this will not make a difference on the long timescales and large length scales behavior of the system. Again, one expects a region when the velocity is anomalous. The expected behavior of the velocity as a function of the external force F′ is sketched in Fig. 12. Again, we expect that the singularities at F′_< and F′_> become rounded when v is defined by a finite experimental time window t_E, with a plateau at zero velocity becoming more and more pronounces as t_E → ∞.

FIGURE 12.

The expected behavior of the velocity as a function of the external force F of the DNA polymerase/exonuclease system. The striped line represents the region over which the diffusion is expected to be anomalous.