Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Jun;86(6):3993–4003. doi: 10.1529/biophysj.103.038422

Automatic and Quantitative Measurement of Protein-Protein Colocalization in Live Cells

Sylvain V Costes *,†, Dirk Daelemans ‡, Edward H Cho *, Zachary Dobbin *, George Pavlakis ‡, Stephen Lockett *
PMCID: PMC1304300  PMID: 15189895

Abstract

We introduce a novel statistical approach that quantifies, for the first time, the amount of colocalization of two fluorescent-labeled proteins in an image automatically, removing the bias of visual interpretation. This is done by estimating simultaneously the maximum threshold of intensity for each color below which pixels do not show any statistical correlation. The sensitivity of the method was illustrated on simulated data by statistically confirming the existence of true colocalization in images with as little as 3% colocalization. This method was then tested on a large three-dimensional set of fixed cells cotransfected with CFP/YFP pairs of proteins that either co-compartmentalized, interacted, or were just randomly localized in the nucleolus. In this test, the algorithm successfully distinguished random color overlap from colocalization due to either co-compartmentalization or interaction, and results were verified by fluorescence resonance energy transfer. The accuracy and consistency of our algorithm was further illustrated by measuring, for the first time in live cells, the dissociation rate (kd) of the HIV-1 Rev/CRM1 export complex induced by the cytotoxin leptomycin B. Rev/CRM1 colocalization in nucleoli dropped exponentially after addition of leptomycin B at a rate of 1.25 × 10−3 s−1. More generally, this algorithm can be used to answer a variety of biological questions involving protein-protein interactions or co-compartmentalization and can be generalized to colocalization of more than two colors.

INTRODUCTION

Spatial colocalization between two fluorescently labeled molecular species (typically between proteins) is a common question in optical microscopy. However, existing colocalization techniques are generally visual-based and therefore highly prone to random error and bias. We introduce here a novel statistical approach that automatically quantifies colocalization in any region of an image without the bias of visual interpretation. Two proteins are considered colocalized if they bind to the same spatial compartments (i.e., the same as co-compartmentalized). If the compartments are well-separated spatially, then typical visual approaches might be sufficient to discriminate those that are colocalized. On the other hand, if the compartments are not visually distinct, then real quantitative tools are needed. In addition, the random localization of two free proteins in the same compartment does not imply actual colocalization. This definition of colocalization also requires that spatial variation of intensity is necessary for colocalization to be measurable.

Several approaches have been proposed before for colocalization using cross-correlation analysis (Akner et al., 1991; Barbarese et al., 1995; Grande et al., 1997; Lynch et al., 1991; Manders et al., 1993; Rubbi and Milner, 2000; van Steensel et al., 1996), or cluster analysis of the two-dimensional histogram (Demandolx and Davoust, 1997). However, most of those approaches are either qualitative (only proving existence of colocalization, e.g., cross-correlation analysis) or subjective (due to manual identification of clusters in two-dimensional histograms). The most quantitative estimate of colocalization is the Pearson's correlation coefficient, (r) (Manders et al., 1992), which depends on the amount of colocalized signals in both channels in a nonlinear manner. A more biologically meaningful set of coefficients are the colocalization coefficients (Manders et al., 1993). They quantify the colocalized fraction of each molecular species, but they also require a threshold value for each channel, which is then used as a cutoff between specific staining versus nonspecific. The overlapping regions between both channels that are above cutoff are then considered as colocalized regions, and the proportions of signal for each channel inside those areas are defined as colocalization coefficients. A problem with this technique is that the thresholds are typically based on visual estimation of the images or the performance of a segmentation algorithm leading to inconsistent and irreproducible results. Our approach solves this problem by taking into account the amount of correlation in different regions of the two-dimensional histogram to automatically estimate the thresholds. This automatic procedure, based on spatial statistics, makes our approach unique and robust.

In this article, we further describe how protein interactions can sometimes be concluded indirectly from quantitative colocalization given prior knowledge of the biological system. Although other microscopy techniques exist for detecting interaction directly, our method has fewer limitations. Fluorescence resonance energy transfer (FRET; Herman, 1989) only detects interaction of proteins <10 nm apart, generally restricting it to small and directly bound proteins. Methods based on monitoring over time intensity fluctuation of each protein simultaneously (i.e., fluorescence cross-correlation spectroscopy, image cross-correlation spectroscopy, photon counting histogram, and fluorescence intensity distribution analysis) are restricted to live samples with only a few labeled proteins per confocal volume. With the exception of image cross-correlation spectroscopy, they are also limited to single point measurements (Checovich et al., 1995; Chen et al., 1999; Jameson and Sawyer, 1995; Kask et al., 1999; Petersen et al., 1993; Winkler et al., 1999; Wiseman et al., 2000). Fluorescence recovery after photobleaching (FRAP) offers another method to measure protein interactions, which does not have the limitations of the above methods, but still requires live samples. It evaluates binding kinetics of a protein by measuring the rate of fluorescence recovery after photobleaching (McNally et al., 2000) and interpreting slow recovery as the signature of bound proteins. As with fluorescence cross-correlation spectroscopy (FCS) using one labeled protein only, FRAP measurements only gives information about the binding constant of the labeled protein to a cellular site and not to any other particular protein. Advantages of our colocalization approach over these dynamic measurements are that an arbitrary volume in the cell can be selected for measurement and fixed samples may be employed.

We first validated our approach on simulated data, identifying its limits of detection and showing its ability to detect and quantify colocalization in images where colocalization was not obvious visually. We then tested our algorithm on diffuse protein nucleolar patterns. This was done on a large series of three-dimensional images of fixed HeLa cells looking at known protein-protein interactions, co-compartmentalization, or random overlap. Results correlated well to FRET measurements of the same groups. Finally, we used colocalization measurements to calculate the dissociation rate of HIV-Rev and CRM1 induced by the drug leptomycin B (LMB) in live HeLa cells (Kudo et al., 1999). This is the first in situ measurement of the kd of HIV-Rev and CRM1 and it shows that our colocalization algorithm can return an accurate evaluation of the proportions of interacting proteins.

MATERIAL AND METHODS

Cell culture

To visualize the HIV-1 Rev-CRM1 interaction, HeLa cells in glass-bottom plates were cotransfected with pRev-CFP expressing HIV-1 Rev N-terminally fused to cyan fluorescent protein (CFP) and pYFP-CRM1 expressing the human CRM1 protein C-terminally fused to yellow fluorescent protein (YFP, Effectene; Qiagen, Valencia, CA). For the three-dimensional control imaging of fixed cells, we used different combinations of cotransfection with pRev-CFP, pRev-YFP, pTat-YFP, or pYFP. One day after transfection cells were washed with PBS, colorless medium was added and cells were analyzed by microscopy. During microscope image acquisition, cells were maintained at 37°C and at 5% CO2 in a heating chamber (20/20 Technology, Wilmington, NC). Leptomycin B (LMB, a generous gift from Dr. Wolff, Sandoz Research Institute, Vienna, Austria) was added in the media after taking two images of the same cell at a 5-min time interval. The final concentration of LMB in the media was 50 nM, enough to saturate all CRM1 protein in the cell (Daelemans et al., 2002).

Microscopy and image analysis tools

There are several requirements to have accurate colocalization measurements (and this is true for any method). In brief, one must make sure that the images acquired have low noise levels and no bleedthrough, and that the optical setup used for each color leads to the same point spread functions (PSFs) and is free of registration errors. For this, we used the following instruments and protocols. Images were acquired with a Zeiss LSM 510 confocal microscope equipped with an Axiovert 200 microscope (Carl Zeiss, Thornwood, NY) and a 40× 1.3 NA plan-NEOFLUAR oil differential interference contrast objective lens. CFP and YFP were excited with Argon laser lines at 458 and 514 nm and by using a dichroic beam splitter (HFT 458/515). Emissions were collected as follows: emitted beam was split by a beam splitter (NFT 490), and light below 490 nm was collected by a bandpass filter (BP 480–520) leading to a collection from 480 to 490 nm for CFP. Light above 490 nm was collected by a bandpass filter (BP 565–615) leading to a collection from 565 to 615 nm for YFP. (Digital images consist of a chessboard-like array of elements, called pixels for two-dimensional images and voxels for three-dimensional images. Each pixel or voxel is assigned one intensity value. For simplification in this article, both pixels and voxels are referred to as pixels.) The pixel sizes were 0.15 × 0.15 × 0.4 μm3 and pinholes were set to one Airy unit (i.e., 63 and 74 μm for CFP and YFP, respectively). We verified the three-dimensional PSFs were the same for different excitation and emission wavelengths, and there was no registration shift between images. This was done by imaging 0.5-μm diameter multicolor fluorescent beads with the previously described CFP/YFP setup. No significant difference was observed in the X, Y, or Z directions. Background levels were obtained by measuring the mean intensity of each stain outside the cells. Bleedthrough was checked by taking images of cells with a single transfection (either Rev-CFP or YFP-CRM1) or no transfection and acquiring dual channel images with the same setup used for the cotransfected cells. Laser power and detection gains were adjusted so that the mean pixel intensity in singly transfected cells acquired with the filter set used for the nontransfected fluorophore was equal (i.e., within 1 SD) to the mean pixel intensity of cells without transfection (i.e., levels of autofluorescence, which were actually insignificant). In this manner, bleedthrough could be neglected. The amount of noise in a region of interest was determined by measuring the Pearson correlation coefficient (Manders et al., 1992) of two consecutive acquisitions of the same channel. In our case, we tried to keep this correlation above 90%. The image and statistical analysis was performed with Matlab (MathWorks, Natick, MA) and DIPimage (image processing toolbox for Matlab, Delft University of Technology, The Netherlands).

Colocalization concept

When two proteins are spatially distributed over the region of the cell being analyzed, no specific colocalization exists between the two proteins when their spatial distributions are independent of each other, although some amount of random overlap will be present between the two images. Conversely, if the two proteins have some specific colocalization, then the overlay of the two spatial distributions will show a level of correlation that is in excess of the random overlap. To express this concept mathematically, let protein type 1 and type 2 be acquired in channels 1 and 2 with intensity value arrays I1 and I2, respectively. In all our derivations, intensities are background-subtracted. Each channel is then the summation of a colocalized component C and a random component R1 and R2, respectively. This can be written as

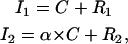graphic file with name M1.gif (1)

where the stoichiometry coefficient α takes into account the possibility that proteins 1 and 2 may not colocalize in a 1:1 ratio. The value α is also dependent on the microscope settings of each channel.

The Pearson correlation coefficient (r) is then defined by

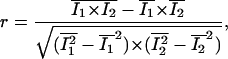graphic file with name M2.gif (2)

where averages over the region of the image being analyzed are indicated by a bar above the variables. Substituting the expressions in Eq. 1 into Eq. 2 and noting that the mean of the product of two uncorrelated signals is approximately equal to the product of the means of the individual signals, r can be written as a function of C, R1, and R2 only:

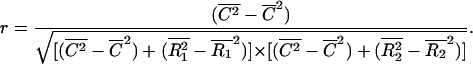graphic file with name M3.gif (3)

One can observe from Eq. 3 that r ranges from −1 to 1, and is equal to 1 for 100% colocalization (i.e., R1 and R2 are null images) and 0 for random overlap of proteins (i.e., C is null). (Negative values of r are not used for colocalization, since they indicate an anti-colocalized situation where a pixel is bright in one channel and dim in the other.) One can also note that r is invariant to background or intensity scales (i.e., if I1 is substituted by aI1 + b in Eq. 2, r remains unchanged). This makes the correlation coefficient a robust estimator for colocalization (Manders et al., 1992), but a major drawback of r is the lack of a biological meaning and its quadratic dependence to the colocalized signal.

Finally, a more biologically meaningful set of coefficients are the proportion of each protein colocalized with the other (Manders et al., 1993). We define them as

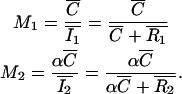graphic file with name M4.gif (4)

Note that M1 and M2 are not necessarily the same for the two proteins.

Test of significance of true colocalization

Before evaluating the amounts of colocalization M1 and M2 in a region of the image, we first check that true colocalization in present. This cannot be determined directly from the value of r since intermediate positive values are difficult to interpret. Therefore a statistical significance test was derived to evaluate the probability (P-value) that the measured value of r from the two colors (robs) is significantly greater than values of r that would be calculated if there was only random overlap. This test (Lifshitz, 1998) is performed by randomly scrambling the pixels in one image, and then measuring the correlation (r) of this image with the other (unscrambled) image. Since scrambling the pixels in one image will make the two spatial distributions independent, then only the contribution to the correlation of the random overlap will be measured. By repeatedly scrambling and measuring the amount of random overlap, the probability distribution of the amounts of random overlap specifically for these two proteins in the region of interest is generated (i.e., distribution centered on 0). Comparing the amount of correlation measured from the unscrambled image with this distribution determines whether significant colocalization exists for a predefined probability for significance. See Fig. 1S in the in the Supplementary Material Appendix for an illustration.

The above procedure, however, assumes that each pixel's intensity is uncorrelated with its neighboring pixels when generating the distribution of the amounts of random overlap. This is not actually the case in optical images, because either the texture of the object or the point spread function (PSF) leads to correlations in the intensities of adjacent pixel intensities. To take this into account, images are divided into independent blocks which are approximately the size of the texture or the PSF, in the case that the texture is below the resolution as measured by the smaller of the widths of the autocorrelations for the two images. Then instead of scrambling individual pixels, the blocks are scrambled. The consequence of this is that there are significantly fewer independent data points in the image, which in turn leads to a significantly broader distribution of random overlap measurements. See Fig. 2S in the Supplementary Material Appendix for further explanation and an illustration.

The reason for the broader distribution when pixel intensities are correlated can be explained theoretically for binary images as follows. Assume an image region has N pixels, of which a random subset of a pixels contain protein type 1 in one image and a random subset of b pixels contain protein type 2 in the other image; then the probability, p, of x pixels containing both proteins 1 and 2 is given by

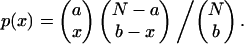graphic file with name M5.gif (5)

To illustrate the point, we apply the following values of 60, 15, and 9 for N, a, and b, respectively, which leads to p(0,1,2,3,4,5,6,7,8,9) = (0.06, 0.22, 0.32, 0.25, 0.11, 0.03, 0.005, 0.0004, 0.00, 0.00). For simplicity we assume that the image is one-dimensional and that pixel intensities are correlated with their nearest neighbors (in other words, positive and negative signals come in sets of three), then the number of independent points is reduced by 3 to N = 20, and then similarly a and b reduce to 5 and 3, respectively. Using these values, p(0, … ,3, … .6, … .9) = (0.4, 0.46, 0.13, 0.01), which is a much broader distribution.

We performed 200 randomizations for each region being analyzed and chose a P-value of >95% to indicate significant true colocalization. For these values, <11 out of the 200 randomizations would be expected to produce Pearson correlation coefficients higher than the value measured for the unscrambled images.

Quantification of colocalization and identification of colocalized pixels

Colocalization in a two-color image (e.g., red and green) can be visualized in a two-dimensional histogram, where the number of pixels with red and green intensities IR, IG is plotted as a scattergram with each axis representing the intensity of each color (see Fig. 1). Based on the expressions in Eq. 1, pixels with significant colocalization (i.e., C ≫ (R1, R2/α)) should be very close to a line IG = aIR + b, where a is the stoichiometry constant α in the expressions in Eq. 1, and b reflects the difference of mean random overlap between the green and red channels after correction for α. We approximate this linear behavior by a least-square fit in the two-dimensional histogram based on orthogonal regression. The slope derived from the least-square fit is directly proportional to the Pearson correlation coefficient r, and therefore takes into account the overall correlation present in the image.

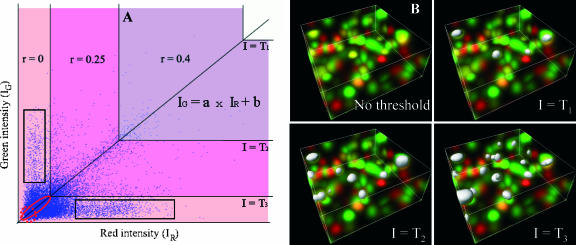
FIGURE 1.

FIGURE 1

Open in a new tab

The automatic threshold search is done in a two-dimensional histogram (shown on left graph) along a line whose slope and intercept (a and b) are obtained by linear least-square fit of the red and green intensities (IR and IG) over all pixels in the image (i.e., IG = a × IR + b). The threshold (T) corresponds to two intensity values (T and a × T + b) applied simultaneously to the red and green channels, respectively. Any pixel with red intensities >T and green intensity >a × T + b is said to be above the threshold. Starting with the highest intensity value, the algorithm reduces the threshold value incrementally and computes the correlation coefficient of the image using only pixels with intensities below the threshold. The algorithm continues reducing the threshold until r reaches 0. The corresponding three-dimensional color image for this simulation is shown on the right of the graph (noted No threshold) and the pixels above different threshold are shown as white surfaces. In this simulation, r is 0.4 for threshold T1, 0.25 for lower threshold T2, and 0 for threshold T3. Thus, T3 is the automatic threshold our algorithm will return for the red channel and a × T3 + b for the green channel. As further discussed in the main text, some pixels are still colocalized (i.e., ellipse shown in red) and some pixels are anti-colocalized (i.e., one channel dim, the other one bright, shown as rectangles) in the r = 0 region (light pink area). However, trying to include the dim colocalized pixels is a difficult task since, as they become dimmer, they are most likely background noise (i.e., shown in dotted circle).

Typically, colocalized areas are defined by regions where both channels are above a red and green threshold, TR and TG, respectively. In other studies these thresholds are defined visually or via a separate segmentation algorithm for the two-dimensional histogram. We propose here an algorithm that determines automatically these thresholds based on a simple statistical criterion. If one assumes that a pixel is the summation of a colocalized component and a random component (see the expressions in Eq. 1), then there is a higher probability to have colocalization in pixels that are brighter in both channels than in dim pixels. In addition, those bright pixels have a significant positive contribution to the overall correlation coefficient of the image. Hence, our approach for identifying colocalized pixels proceeds by successively classifying pixels as being colocalized if their intensities, IR, IG are both above the threshold pair T (TG) and aT + b (TR), respectively. The approach starts with the maximal value of T and incrementally lowers T until the correlation coefficient of remaining pixel intensities below T and aT + b equals zero. The method is illustrated and further described in Fig. 1. This approach leads to the approximation of the colocalization coefficients (Eq. 4) as

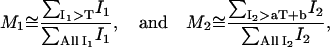graphic file with name M6.gif (6)

where T is the automatic threshold below which the Pearson correlation coefficient becomes negative. There is no formal mathematical proof that this approach always leads to accurate values for M1 and M2. However, intuitively, based on Eq. 3, pixels below the threshold pair will have an overall correlation of 0, indicating that on average there is no colocalization present. To test the validity of this approach we thus tested our algorithm on a variety of computer three-dimensional-color simulated images and real biological samples, as will be described in Results.

A general problem that is inherent to all known methods is the classification of pixels as either colocalized or non-colocalized, when all pixels are actually the sum of colocalized and non-colocalized signals (see expressions in Eq. 1). However, we show in simulations that the overall amount of colocalization remains very accurate in our method, although errors are made in the classification of individual pixels. For instance, very low intensity colocalized pixels are often not detected by our method (solid ellipse in Fig. 1). This is because for the same colocalization thresholds there are also regions that contain pixels that contribute negatively to the correlation coefficient r (located in rectangles in Fig. 1), resulting in an overall correlation of zero. These undetected colocalized pixels have a small contribution to the total amount of colocalization and have intensities close to background. Also our method can wrongly classify pixels that are way off the diagonal of the two-dimensional histogram but which have fairly large intensities for both channels as colocalized. However, these pixels typically represent a very low proportion of the image.

Another approach was tested for the selection of colocalized pixels in the two-dimensional histogram to help distinguish between low intensity colocalized pixels and background. We selected pixels closest to the diagonal line in the two-dimensional histogram (see Fig. 1 A). However, when testing this approach, typically a large number of background noise pixels ended up being identified as colocalized (e.g., circled by dashed line, Fig. 1 A) and most intense pixels that deviated from the diagonal were missed. Another issue with this alternative was the need for much more accurate determination of the diagonal line than our method requires.

RESULTS

Simulated data

Simulations covering different amounts of colocalization were performed, from 100% of green pixels colocalized to red pixels to no colocalized pixels. Fig. 2 shows one set of simulations where each three-dimensional image had more positive red pixels than green, leading to a systematically larger amount of colocalization in the green channel than in the red. Fig. 2 shows good agreement between the known amounts of colocalization and the amounts automatically detected by the algorithm, with most of the data lying on a diagonal of slope 1. The method's accuracy was confirmed by the closeness of the true and measured colocalization (1.5% deviation). On the other hand, Pearson's correlation coefficient (asterisks and pluses) sometimes considered as a direct measure of colocalization (Barbarese et al., 1995), only equaled the amount of colocalization at low values (i.e., 0%). This simulation illustrates well the performance of our method in dealing with the difficult case of unbalanced colocalization where the proportion of each protein colocalized with the other is not the same. In this case, colocalization can only be fully described by the measurement of the two colocalized fractions for each protein which are two different values (i.e., M1 different from M2), and not by a single measurement, such as the correlation coefficient. Furthermore, it is noteworthy in this simulation that for low amounts of colocalization which are not visible (i.e., a few percent), the algorithm could still compute accurate amounts.

FIGURE 2.

FIGURE 2

Open in a new tab

In this simulation pixel-sized objects were generated with random positions and colocalized pixels had identical nonzero intensities in both colors. The intensity distribution of all pixels was uniform with a range 100–255 in both channels. A test series of 100 three-dimensional images (30 × 30 × 30) was generated with different fractions of colocalization by controlling the percentage of identical objects in both channels. The choice of the density of each object was set deliberately low and different (i.e., 6% of the area is covered by green objects and 9% by red) to force the amount of red and green colocalization to be different. Simulations covering the full range of possible colocalization were performed, from all green objects colocalized (i.e., 100% and 67% colocalized green and red objects, respectively) to no colocalization. Finally, noise with intensity distributed uniformly between 10 and 30 was added to both channels. The Pearson's correlation coefficient, r, is plotted twice for the same image, once against the real amount of green colocalization (green +) and once against the red amount of colocalization (red *). We can see that r (* or +) evaluates inaccurately either amount of colocalization in comparison to our current algorithm (○ or □). The P-value (not shown) remained above the 95% significance level as long as >1% of the green objects were colocalized. For all test images, measured amounts of colocalization were accurate with <2% deviation, as is observed with most points close to the diagonal of slope 1 (dashed line). Finally, the two dashed curves show the fractions of pixels without colocalization that were incorrectly classified as being colocalized. This was worst for intermediate amount of colocalization, where up to 5% of pixels were misclassified.

Our algorithm resulted in a small proportion (∼5%) of pixels being misclassified as false-positives and false-negatives (see Fig. 2), but these errors were balanced, thus the overall measure of colocalization remained accurate.

The subvisual capability of our algorithm was also illustrated in another simulation (Fig. 3) where individual pixels contained colocalized signals that were not significantly above the mean intensity of the full image. In such cases, it was impossible to identify the colocalization by eye. However, the algorithm was able to detect it unequivocally for amounts of colocalization as low as 3% (Fig. 3 D).

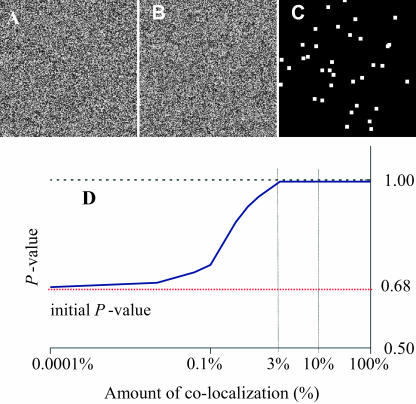
FIGURE 3.

FIGURE 3

Open in a new tab

Detection of nonrandom colocalization that is not visible. A and B are two independent computer-generated 256 × 256 images with pixel intensities randomly distributed between 0 and 255 except for 3% of the pixels (shown in image C) having the same intensity for both channels. Even though one cannot see which pixels are identical between A and B, our algorithm could identify this difference unequivocally with a true colocalization significance test above the significant threshold of 0.95. D shows the sensitivity of the algorithm as a function of the proportion of colocalization by repeating the process described above for different colocalized images going from 0% to 100% colocalization. This graph shows P-values >95% for colocalized amounts as low as 3%. If there is <3% of the image being colocalized, the algorithm returns an inconclusive answer about the existence of colocalization; i.e., P-value is <95%. Note on D: if no colocalization was deliberately inserted, i.e., image C was blank, the P-value of the two initial uncorrelated images used for this simulation was 0.68. This value has no meaning in itself and could be anywhere between 0 and 1 for two uncorrelated images, with a most probable value ∼0.5 (see Fig. 1s of Supplementary Material for distribution of r).

Biological data

A first set of analyses was performed successfully (Costes et al., 2002) on simple positive and negative biological controls, consisting of fixed cells stained for the same protein with two different fluorophores or for two different cellular compartments, i.e., lysosome and mitochondria, respectively (see Supplementary Material).

We then tested the algorithm on a large set of three-dimensional images of fixed HeLa cells cotransfected with different fluorescent proteins. Three groups of 40 cells each were analyzed for colocalization. The first group was a negative control and was cotransfected with free YFP and HIV-1 Rev protein fused with CFP. Free YFP fills uniformly the whole cell, whereas wild-type Rev is localized in the nucleoli of the cell (see Fig. 4 A). The second group was a positive control with cells cotransfected with the two nucleolar proteins Tat fused to YFP and HIV-1 Rev fused to CFP. In this group, Rev and Tat do not interact directly but bind to ribosomal RNA (rRNA) in an unrelated manner in the nucleoli (see Fig. 4 B). Thus, those two proteins co-compartmentalize into submicron regions of the nucleoli probably smaller than the PSF of the microscope. The third group consisted of cells cotransfected by HIV-1 Rev CFP and HIV-1 Rev YFP, both localizing in the nucleoli (see Fig. 4 C). Wild-type Rev is known to multimerize and therefore the colocalization in this last group is still representative of the co-compartmentalization to rRNA, but should be higher since Rev is expected to also bind indirectly to rRNA via its multimerization with other Rev proteins directly bound to rRNA. The analysis showed a clear statistical separation of the amount of colocalization between each group (Fig. 4 D). The negative controls had an average of 5% colocalization for both Rev and free YFP and an average P-value of 0.7 indicating that this colocalization was likely the result of random overlap. On the other hand, the co-compartmentalization of Rev and Tat on rRNA gave a very wide distribution of colocalization with an average of 60% and a P-value >95%. Note on the two-dimensional histogram in Fig. 4 E it would be impossible to determine manually where the thresholds for each channel should be placed. In the Rev-Rev case, a skewed distribution toward 100% colocalization was measured (Fig. 4 D) with an average colocalization of 98% and a P-value >95%. This trend was confirmed by measuring the FRET efficiency in each group with the acceptor photobleaching method (manuscripts in preparation). The comparison between the mean amount of colocalization for HIV-Rev and the FRET efficiencies in each group is shown in Table 1 and reinforce the fact that Rev-Rev are much closer spatially than Rev-Tat (i.e., 25% vs. 5% efficiency).

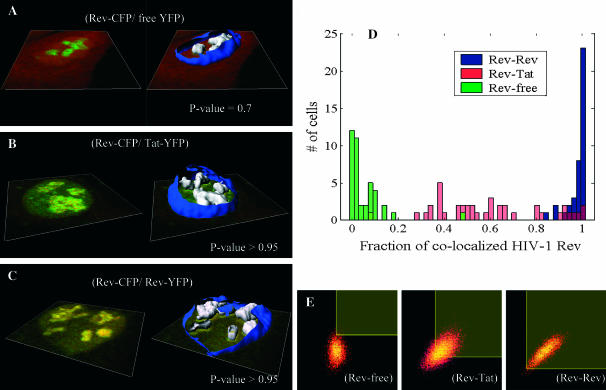
FIGURE 4.

FIGURE 4

Open in a new tab

Colocalization control study. A–C show representative confocal slices of the analyzed HeLa cells (CFP shown in green and YFP in red). On the left of these panels, one center slice is shown and on the right a reconstructed surface of the nuclear membrane is shown in blue. The nucleoli where colocalization was computed are shown as white surfaces. Each group analysis was performed on a population of 40 cells. Group A focused on colocalization of free YFP and Rev-CFP in the nucleoli and had very little colocalization, as shown by the green distribution in D with an average colocalization of 5% for both signals and a P-value of 0.7 indicating the random aspect of that colocalization. Group B focused on colocalization of Tat-YFP and Rev-CFP, two proteins known to bind to rRNA. This co-compartmentalization led to an average colocalization of 60% for both signals with a P-value >0.995. Finally, group C focused on colocalization of Rev-YFP and Rev-CFP, a protein known to multimerize in addition to binding to rRNA. This combination of co-compartmentalization and interaction led to a very narrow distribution of colocalization in the nucleoli ∼98% for both signals with a P-value >0.95. E shows a representative two-dimensional histogram of those different groups within the nucleoli. The red channel (Rev, Tat, or free YFP) is on the x axis and the green (Rev) is on the y axis in the two-dimensional histograms. Automatic selected colocalized areas are shown by a rectangular yellow overlay in the two-dimensional histogram. One can appreciate, in the Rev-Tat case, how difficult it would be to decide manually what threshold levels to use.

TABLE 1.

FRET versus colocalization

Group % Rev colocalization % FRET efficiency
Rev-free 5 ± 8 (40) 0 ± 2 (6)
Rev-Tat 60 ± 23 (40) 5 ± 4 (10)
Rev-Rev 98 ± 4 (40) 25 ± 3 (14)
Open in a new tab

Mean ± SD (number of cells).

The consistency and accuracy of simulations and fixed specimens led us to believe our algorithm could quantify accurately the dissociation of two proteins in a live system. To test our hypothesis, we applied our method on a system where, to our knowledge, only interaction takes place. We looked at HeLa cells cotransfected with HIV-1 Rev fused to CFP and its nuclear export factor CRM1 fused to YFP. In contrast with the Rev-Rev case, FRET was negative for this complex, presumably due to the large size of CRM1 (130 kDa). The HIV-1 Rev protein is an essential regulator of the HIV-1 rRNA expression that promotes the export of unspliced and partially spliced rRNAs from the nucleus to the cytoplasm of the cell (Felber et al., 1989; Malim et al., 1988; Sodroski et al., 1986; Terwilliger et al., 1988). In cells expressing Rev, CRM1 colocalizes in the nucleolus due to its interaction with Rev (Zolotukhin and Felber, 1999). The cytotoxin LMB inhibits the CRM1/Rev association by binding irreversibly to CRM1 (Kudo et al., 1999). Therefore, addition of LMB to cells coexpressing Rev and CRM1 induces the dissociation of the Rev/CRM1 complex in the nucleolus leading to the diffusion in the nucleus of CRM1 bound to LMB while Rev stays localized in the nucleolus (Daelemans et al., 2002). After LMB addition into the cell media, the equilibrium between association and dissociation of the CRM1/Rev complex is broken, only allowing dissociation. Thus, the complex concentration is expected to decay at an exponential rate after addition of the drug at a rate equal to the dissociation rate constant kd of the CRM1/Rev complex. Mathematically,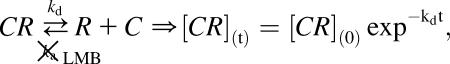Inline graphicwhere [C], [R], and [CR] are the concentrations in the nucleolus of CRM1, Rev, and the CRM1/Rev complex respectively. For mathematical clarification, we denote concentrations with [ ], the volumes by V, and the nucleolus and the full cell compartments as nucleo and cell, respectively. Assuming only interaction takes place (co-compartmentalization only due to interaction), the percent colocalization for each protein in the nucleolus (i.e., MRev and MCRM1) can be expressed as

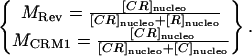graphic file with name M7.gif (8)

Assuming there is no loss or gain of proteins in the whole cell, then

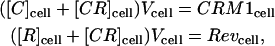graphic file with name M8.gif (9)

where CRM1cell and Revcell are the constant total amounts of CRM1 and Rev proteins in the cell. The amounts of CRM1 and Rev in the nucleolus can be similarly defined as

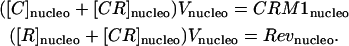graphic file with name M9.gif (10)

However, CRM1nucleo and Revnucleo will not be constant once LMB is added to the media. On the other hand, the ratio with CRM1cell and Revcell, respectively, can be evaluated by the ratio of the integrated intensity of CRM1 and Rev in the nucleolus over the full cell as shown in the expressions in Eq. 11,

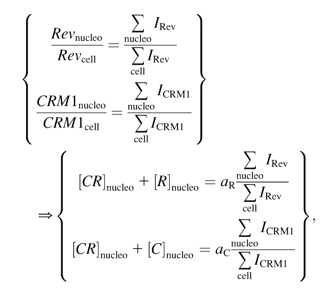graphic file with name 3993e11.jpg (11)

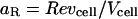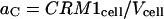where Inline graphic and Inline graphic are proportionality constants and I is the pixel intensity in the image. Note aR and aC remain the same over the full time course of the decay (see Eq. 9). We can then express the concentration of CRM1/Rev bound complex as a function of intensity ratios and percent colocalization by substituting the expressions in Eq. 11 in Eq. 8:

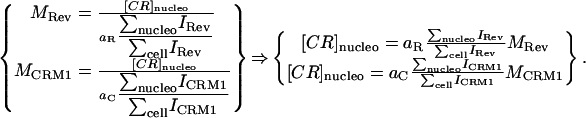graphic file with name M12.gif (12)

MRev and MCRM1 are returned by our colocalization algorithm for each time point, and aR and aC do not need to be evaluated if we normalize the time response by setting the first time point to 1. In this case, using this mathematical model in conjunction with our colocalization algorithm, we should be able to measure for the first time in live cells the dissociation rate of the HIV-1 Rev/CRM1 complex.

Images were collected with a confocal microscope and background-corrected, showing Rev-CFP and YFP-CRM1 with green and red pseudo colors, respectively. With this choice of colors, the exit of CRM1 from the nucleolus can be visualized clearly, with the initial yellow color due to the green-red overlap turning to green, 33 min after addition of LMB (Fig. 5 A). In the experiment, we first controlled the consistency of our measurements for each cell by computing the amount of colocalization of two images acquired before LMB addition. If the two measurements differed by >10%, the cell was not used for computation (three out of 11 cells were rejected). An average lag of ∼6 min was observed before decays commenced. Thus, for all cells, the commencement time for dissociation was corrected for this lag and concentrations were normalized such that decays started at time 0 with a relative complex concentration of 1. This enabled all cell measurements to be taken together (Fig. 5 D). Using the test of significance, true colocalization was observed from the start time until ∼20 min later. In the quantification of the corrected colocalization (i.e., the expressions in Eq. 2), the exponential decay was found to be statistically the same for both Rev and CRM1 decays. Therefore, measurements for both proteins were taken and fitted together to a decreasing exponential by the nonlinear least-squares Gauss-Newton method (Dennis, 1977), to return a kd of (1.25 ± 0.31) × 10−3 s−1 (95% confidence interval) with a goodness for the fit of R2 = 0.96. The corresponding colocalized pixels and thresholded two-dimensional histograms at different time points in the decay curve are also shown in Fig. 5, B and C, respectively. The loss of colocalization is reflected by a change of slope of the two-dimensional histograms, becoming more and more vertical as colocalization drops (i.e., x axis is CRM1). This change also indicates the diminution of CRM1 proteins in the nucleolus as it fills the entire nucleus and the nuclear membrane, which reduces the overall intensity range on the x axis of the two-dimensional histogram.

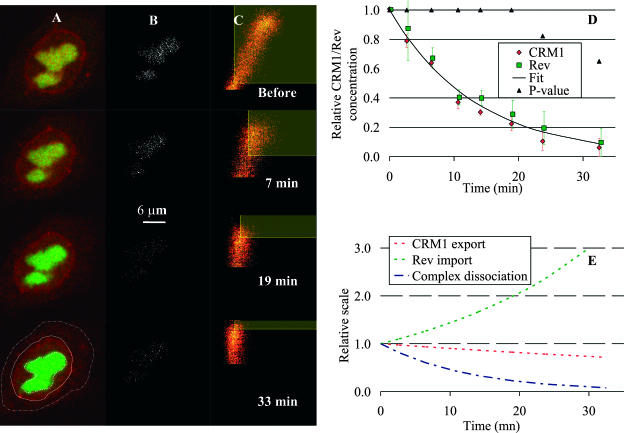
FIGURE 5.

FIGURE 5

Open in a new tab

Rev-CRM1 dissociation. (A) Time series of two-dimensional confocal sections of a cell cotransfected with CRM1 and Rev fused to YFP (red) and CFP (green), respectively. (B) The corresponding estimate of colocalized pixels (shown in white). (C) The corresponding two-dimensional histograms for each image in A. The red channel (CRM1) is on the x axis and the green one (Rev) on the y axis in the two-dimensional histogram. Selected colocalized areas are also shown by yellow transparent rectangular areas. Initially, CRM1 colocalized with Rev in the nucleolus. Thirty-three minutes after addition of leptomycin B, an inhibitor of the CRM1-cargo binding, most of the CRM1 has dispersed in the nucleus. The last image of the color sequence indicates the region of the nucleolus in which the amount of colocalization is computed (bold dashed line in A). The nucleus and cell limits are also shown (solid and light dashed lines, respectively, in A). (D) The graph shows the relative concentration of the bound complex Rev/CRM1 derived from the amount of colocalization of each protein (expressions in Eq. 12) as a function of time after the end of the lag period. The dissociation rate constant kd was found to be (1.25 ± 0.31) × 10−3 s−1 (fit shown by solid line). Error bars are standard errors based on all cells averaged for each time point. Average P-values for colocalization significance test are also plotted as ▴ and confirm Rev/CRM1 interaction for at least the first 20 min of dissociation (at a 95% significance level). These results match very well the two-dimensional histogram shown in C, where the linear behavior goes from a clear inclined line to a vertical line at 33 min, indicating no more colocalization. E shows the least-square fits of the import rate of Rev into the nucleolus and the diffusion of CRM1 out of the nucleolus after injection of LMB versus the dissociation rate obtained in D, which clearly indicates that simply measuring the loss of CRM1 outside the nucleolus after injection of LMB had nothing to do with measuring the dissociation of Rev/CRM1.

In CRM1/Rev dissociation, the proportion of Rev in the nucleolus increased after addition of LMB, whereas the proportion of CRM1 decreased in the nucleolus and diffused into the whole nucleus (see Fig. 5 E). Thus, the rate of decrease of Rev colocalization in the nucleolus was faster than the actual dissociation rate of the CRM1/Rev complex. The import of Rev from the cytoplasm to the nucleolus accelerated the drop of colocalization by increasing the concentration of unbound Rev in the nucleolus (see expressions in Eq. 2). Conversely, the diffusion of unbound CRM1 into the nucleus reduced the concentration of unbound CRM1 in the nucleolus, slowing down the measured colocalization decay. This was observed on uncorrected colocalization data where the rate of decay of Rev colocalization was found to be 1.3 ± 0.05 times faster than the rate for CRM1.

DISCUSSION

We developed an automatic algorithmic method to measure the amount of colocalization in two-color three-dimensional microscopic images. Our algorithm has been commercialized by Bitplane AG (Zurich, Switzerland) and made available to the intramural National Institutes of Health research community as part of the software MIPAV (McAuliffe et al., 2001). This method first measures the probability (P-value) that true colocalization is present in a selected region of the image. We opted to use a P-value >95% to indicate true colocalization. As a second step, colocalized pixels in the selected region are identified using a statistical criterion based on the two-dimensional histogram of both channels allowing the computation of the overall fraction of each proteins being colocalized (i.e., colocalization coefficients, Eqs. 4 and 6).

Simulations (Figs. 2 and 3) showed that the method was able to accurately quantify as little as 3% true colocalization in images where visual examination would not be conclusive. This subvisual feature was also apparent on biological cases we tested. For example, it clearly separated groups of cells where we had pure random colocalization with a P-value ≪95%, from groups where we had co-compartmentalization or interaction with a P-value >95% (Fig. 4). This result indicates the novelty and value of our method given the fact that both proteins of interest had a diffuse pattern in the region of interest (i.e., nucleoli) for all cases (Fig. 4, A–C). Finally, the P-value also confirmed the loss of Rev/CRM1 interaction in the nucleolus (Fig. 5 D), by dropping below the 95% cutoff value 20 min after injection of a drug-inducing dissociation of the Rev/CRM1 complex.

On the quantitative side, the strength of the algorithm comes from the use of a statistical criterion that makes detection automatic and completely reproducible. This is clearly demonstrated in Fig. 4 on the large fixed cell study. In the case of Rev and Tat, both proteins localize in the nucleoli by binding to rRNA. The algorithm was able to select automatically a threshold value which would have been impossible to find manually based on the two-dimensional histogram (Fig. 4 E). Fortuitously, the quantification of colocalization for this test was accurate enough to distinguish co-compartmentalization alone from combined co-compartmentalization and interaction with statistically different averages of 60% and 98%, respectively. This difference was confirmed by FRET where the corresponding efficiency measurements were 5% and 25%, respectively. The sensitivity of the method is impressive considering the fact that Tat and Rev co-compartmentalization occurred on a target that cannot be resolved by light microscopy (i.e., rRNA). This indicates that rRNA concentration probably varies on a scale close to the size of the PSF.

To further illustrate the quantitative strength of the algorithm, we demonstrated its ability on a biological test where we could model and predict what we should measure. Measuring a dynamic event in live cells offered such a possibility. By blocking the CRM1-Rev association with leptomycin B (Daelemans et al., 2002), one would expect to see an exponential decay by measuring the concentration of CRM1/Rev complex. This concentration could be evaluated in a relative manner by a mathematical model linking it to the colocalization coefficients of Rev and CRM1 (see Eqs. 7–12). The corrected colocalization data (Fig. 5 D) correlated well with the prediction of the expressions in Eq. 12 as shown by the goodness of the fit (dashed line, R2 was 0.96) to the measurements, suggesting the algorithm detected real protein interaction. In addition, our mathematical model showed that the dissociation rate could not have been obtained solely by measuring the rate of nucleolar relocation of Rev or CRM1 (Fig. 5 E). This led to the measurement for the first time in live cells of the dissociation rate constant of the HIV-Rev/CRM1complex in the nucleolus with kd = 1.25 × 10−3 s−1.

Colocalization is often quantified by computing the Pearson's correlation coefficient (Manders et al., 1992). However, this approach only reports one measurement per image. This coefficient has sometimes been interpreted as the percent amount of colocalization in the image (Barbarese et al., 1995), which is clearly not the case based on Eqs. 3 and 4. This interpretation can be misleading when the relative amounts of the two species are different (Fig. 2). In comparison, our method quantifies colocalization coefficients for each color separately. It is done automatically and results are approximately invariant to the relative amounts of the two proteins (Fig. 2). This is an important feature in the Rev/CRM1 study, where the relative amounts of the two species changes because of Rev import and CRM1 export from the nucleolus (Fig. 5).

One could argue that a similar and simpler approach could be thresholding each channel separately, based on some automatic threshold algorithm (e.g., isodata, skewed bimodality, unimodal background symmetry, etc.). These algorithms are typically optimized to identify background or objects (i.e., segmentation). In case of a diffuse pattern, such as the Rev study shown in Fig. 4, these algorithms will typically split equally the image into a brighter region and a dimmer one. Thus, when using such algorithms on the negative controls of Rev CFP and free YFP (Fig. 4 A), high levels of colocalization are falsely computed (data not shown). The main reason for this approach to fail in this case is the fact that the correlation between each channel is not used as a criterion for threshold. Finally, if one decides to use manual threshold instead, this becomes very difficult and poorly reproducible when colocalization is not visible in the images or in the two-dimensional histogram (e.g., group B, Fig. 4).

The automatic approach for quantifying colocalization that we employed has the advantage of being simple and intuitive. Similar analysis would have taken much longer using approaches based on visual interpretation which would also be highly prone to random error and bias. Furthermore, the approach can be extended to evaluation of the colocalization of three or more molecular species, which would be much harder to do visually or with other analytical techniques (e.g., FRET, FCS, PCH, FIDA, or FRAP). Note that our method is not a substitute for those other techniques, but is a complementary approach. For example, our approach can be readily combined with FRET to clarify co-compartmentalization, direct, or indirect binding. FRET alone would only detect interaction if the average distance between the binding proteins is <10 nm. Colocalization alone would be unable to distinguish binding proteins from nonbinding proteins located within a cellular compartment smaller than the resolution of light microscopes (∼200 nm).

Another caveat of our approach is that it is forcing each pixel to be classified as either entirely colocalized or entirely non-colocalized signals. All other current colocalization methods also make the same assumption. However, this is clearly not the case in reality since, in general, a pixel's intensity is the result of the sum of hundreds of labeled proteins either binding to the substrate or free-convolved by the PSF. In fact, assuming that the selected points in the two-dimensional histogram are entirely colocalized, this can actually lead to overprediction of the amount of colocalization (data not shown). This is due to the fact that the colocalization coefficients computation (Eq. 6) includes contribution of random overlap. Overpredictions are, however, fairly small as long as colocalized pixels are fairly sparse in the image (see simulations of Fig. 2). This is due to the fact that, inasmuch as the search for the colocalization threshold leads to lower values in the algorithm, the positive contribution of the colocalized pixels left below the thresholds are compensated by an increasing negative contribution of random overlap (rectangular regions in Fig. 1). Thus, our method is best used to compute the colocalization coefficients and not so much in identifying specific colocalized pixels.

Ideally one would like a method that treats each pixel as the sum of colocalized and non-colocalized signals, as our colocalization model suggests in the expressions in Eq. 1. This could be done in many ways. One could try to establish a better fit for the linear pattern in the two-dimensional histogram than the orthogonal linear regression. This could lead to the identification of the mean intensities of colocalization as well as of the two random populations. This in turn could be used to assign to each pixel a proportion of colocalization based on their relative position to the identified linear pattern. One could also try to directly deconvolve the two-dimensional histogram into the colocalized contribution and the two random contributions. Finally, it would be interesting to actually approach the problem at the image level, using the neighbor intensity pixel as an indicator of colocalization itself. In brief, there is still a lot of work to be done in the field of quantitative colocalization.

In conclusion, rapid and reliable measurements of protein interactions in the cell are becoming essential for the understanding of many cellular processes. The simple procedure described here allows extraction of quantitative information about molecular interactions or localization from two or more color images. Our method can also analyze anti-colocalization by colocalizing the presence of one protein with the absence of the other. With further extension, a more general analysis of spatial organization of proteins in cells could be performed. Such microscopic measurements are becoming more readily accessible. With the appropriate imaging algorithms, optical hardware, and mathematical modeling, optical microscopy will increasingly provide quantitative information about protein chemistry inside live cells that currently can only be obtained outside the cell by in vitro assays.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Supplementary Material

[Supplemental Material]
biophysj_86_6_3993__index.html (726B, html)

Acknowledgments

The authors thank Dr. Ruth Redman and Aboubaker Elkharroubi from the National Cancer Institute for their useful scientific advice.

This project has been funded in part with federal funds from the National Cancer Institute, National Institutes of Health, under contract No. NO1-CO56000. The content of this publication does not necessarily reflect the views of the Department of Health and Human Services, nor does mention of trade names, commercial products, or organizations imply endorsement by the U.S. government.

References

  1. Akner, G., K. Mossberg, A. C. Wikstrom, K. G. Sundqvist, and J. A. Gustafsson. 1991. Evidence for colocalization of glucocorticoid receptor with cytoplasmic microtubules in human gingival fibroblasts, using two different monoclonal anti-GR antibodies, confocal laser scanning microscopy and image analysis. J. Steroid Biochem. Mol. Biol. 39:419–432. [DOI] [PubMed] [Google Scholar]
  2. Barbarese, E., D. E. Koppel, M. P. Deutscher, C. L. Smith, K. Ainger, F. Morgan, and J. H. Carson. 1995. Protein translation components are colocalized in granules in oligodendrocytes. J. Cell Sci. 108:2781–2790. [DOI] [PubMed] [Google Scholar]
  3. Checovich, W. J., R. E. Bolger, and T. Burke. 1995. Fluorescence polarization—a new tool for cell and molecular biology. Nature. 375:254–256. [DOI] [PubMed] [Google Scholar]
  4. Chen, Y., J. D. Muller, P. T. So, and E. Gratton. 1999. The photon counting histogram in fluorescence fluctuation spectroscopy. Biophys. J. 77:553–567. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Costes, S., E. Cho, M. Catalfamo, T. Karpova, J. McNally, P. Henkart, and S. Lockett. 2002. Automatic three-dimensional detection and quantification of colocalization. Proc. Microsc. Microanal. 8:S2-1040CD–S2-1048CD. [Google Scholar]
  6. Daelemans, D., E. Afonina, J. Nilsson, G. Werner, J. Kjems, E. De Clercq, G. Pavlakis, and A.-M. Vandamme. 2002. A synthetic inhibitor of the HIV-1 Rev CRM1-mediated export. Proc. Natl. Acad. Sci. USA. 99:14440–14445. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Demandolx, D., and J. Davoust. 1997. Multicolour analysis and local image correlation in confocal microscopy. J. Microsc. Oxford. 185:21–36. [Google Scholar]
  8. Dennis, J. E., Jr. 1977. Nonlinear least squares. In State of the Art in Numerical Analysis. D. Jacobs, editor. Academic Press. New York, NY. 269–312.
  9. Felber, B. K., M. Hadzopoulou-Cladaras, C. Cladaras, T. Copeland, and G. N. Pavlakis. 1989. Rev protein of human immunodeficiency virus type 1 affects the stability and transport of the viral mRNA. Proc. Natl. Acad. Sci. USA. 86:1495–1499. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Grande, M. A., I. van der Kraan, L. deJong, and R. van Driel. 1997. Nuclear distribution of transcription factors in relation to sites of transcription and RNA polymerase II. J. Cell Sci. 110:1781–1791. [DOI] [PubMed] [Google Scholar]
  11. Herman, B. 1989. Resonance energy transfer microscopy. Methods Cell Biol. 30:219–243. [DOI] [PubMed] [Google Scholar]
  12. Jameson, D. M., and W. H. Sawyer. 1995. Fluorescence anisotropy applied to biomolecular interactions. Methods Enzymol. 246:283–300. [DOI] [PubMed] [Google Scholar]
  13. Kask, P., K. Palo, D. Ullmann, and K. Gall. 1999. Fluorescence-intensity distribution analysis and its application in biomolecular detection technology. Proc. Natl. Acad. Sci. USA. 96:13756–13761. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kudo, N., N. Matsumori, H. Taoka, D. Fujiwara, E. P. Schreiner, B. Wolff, M. Yoshida, and S. Horinouchi. 1999. Leptomycin B inactivates CRM1/exportin 1 by covalent modification at a cysteine residue in the central conserved region. Proc. Natl. Acad. Sci. USA. 96:9112–9117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Lifshitz, L. M. 1998. Determining data independence on a digitized membrane in three dimensions. IEEE Trans. Med. Imaging. 17:299–303. [DOI] [PubMed] [Google Scholar]
  16. Lynch, R. M., K. E. Fogarty, and F. S. Fay. 1991. Modulation of hexokinase association with mitochondria analyzed with quantitative three-dimensional confocal microscopy. J. Cell Biol. 112:385–395. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Malim, M. H., J. Hauber, R. Fenrick, and B. R. Cullen. 1988. Immunodeficiency virus Rev trans-activator modulates the expression of the viral regulatory genes. Nature. 335:181–183. [DOI] [PubMed] [Google Scholar]
  18. Manders, E. M. M., J. Stap, G. J. Brakenhoff, R. Vandriel, and J. A. Aten. 1992. Dynamics of three-dimensional replication patterns during the s-phase, analyzed by double labeling of DNA and confocal microscopy. J. Cell Sci. 103:857–862. [DOI] [PubMed] [Google Scholar]
  19. Manders, E. M. M., F. J. Verbeek, and J. A. Aten. 1993. Measurement of colocalization of objects in dual-color confocal images. J. Microsc. 169:375–382. [DOI] [PubMed] [Google Scholar]
  20. McAuliffe, M. J., F. M. Lalonde, D. McGarry, W. Gandler, K. Csaky, and B. L. Trus. 2001. Medical Image Processing, Analysis and Visualization In Clinical Research. IEEE Computer-Based Medical Systems. New York, NY. 381–386.
  21. McNally, J. G., W. G. Muller, D. Walker, R. Wolford, and G. L. Hager. 2000. The glucocorticoid receptor: rapid exchange with regulatory sites in living cells. Science. 287:1262–1265. [DOI] [PubMed] [Google Scholar]
  22. Petersen, N. O., P. L. Hoddelius, P. W. Wiseman, O. Seger, and K. E. Magnusson. 1993. Quantitation of membrane receptor distributions by image correlation spectroscopy: concept and application. Biophys. J. 65:1135–1146. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Rubbi, C. P., and J. Milner. 2000. Non-activated p53 colocalizes with sites of transcription within both the nucleoplasm and the nucleolus. Oncogene. 19:85–96. [DOI] [PubMed] [Google Scholar]
  24. Sodroski, J., W. C. Goh, C. Rosen, A. Dayton, E. Terwilliger, and W. Haseltine. 1986. A second post-transcriptional trans-activator gene required for HTLV-III replication. Nature. 321:412–417. [DOI] [PubMed] [Google Scholar]
  25. Terwilliger, E., R. Burghoff, R. Sia, J. Sodroski, W. Haseltine, and C. Rosen. 1988. The art gene product of human immunodeficiency virus is required for replication. J. Virol. 62:655–658. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. van Steensel, B., E. P. van Binnendijk, C. D. Hornsby, H. T. van der Voort, Z. S. Krozowski, E. R. de Kloet, and R. van Driel. 1996. Partial colocalization of glucocorticoid and mineralocorticoid receptors in discrete compartments in nuclei of rat hippocampus neurons. J. Cell Sci. 109:787–792. [DOI] [PubMed] [Google Scholar]
  27. Winkler, T., U. Kettling, A. Koltermann, and M. Eigen. 1999. Confocal fluorescence coincidence analysis: an approach to ultra high-throughput screening. Proc. Natl. Acad. Sci. USA. 96:1375–1378. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Wiseman, P. W., J. A. Squier, M. H. Ellisman, and K. R. Wilson. 2000. Two-photon image correlation spectroscopy and image cross-correlation spectroscopy. J. Microsc. 200:14–25. [DOI] [PubMed] [Google Scholar]
  29. Zolotukhin, A. S., and B. K. Felber. 1999. Nucleoporins nup98 and nup214 participate in nuclear export of human immunodeficiency virus type 1 Rev. J. Virol. 73:120–127. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplemental Material]
biophysj_86_6_3993__index.html (726B, html)
biophysj_86_6_3993__1.pdf (1.1MB, pdf)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES