Information Bounds and Optimal Analysis of Dynamic Single Molecule Measurements

Abstract

Time-resolved single molecule fluorescence measurements may be used to probe the conformational dynamics of biological macromolecules. The best time resolution in such techniques will only be achieved by measuring the arrival times of individual photons at the detector. A general approach to the estimation of molecular parameters based on individual photon arrival times is presented. The amount of information present in a data set is quantified by the Fisher information, thereby providing a guide to deriving the basic equations relating measurement uncertainties and time resolution. Based on these information-theoretical considerations, a data analysis algorithm is presented that details the optimal analysis of single-molecule data. This method natively accounts and corrects for background photons and cross talk, and can scale to an arbitrary number of channels. By construction, and with corroboration from computer simulations, we show that this algorithm reaches the theoretical limit, extracting the maximal information out of the data. The bias inherent in the algorithm is considered and its implications for experimental design are discussed. The ideas underlying this approach are general and are expected to be applicable to any information-limited measurement.

INTRODUCTION

The greatest advantage of optical single-molecule spectroscopy—elimination of the ensemble average—is also its greatest fault. Elimination of the ensemble average allows unprecedented opportunities for observation of rare events and the distributions that underlie the ensemble average. These observations are near the limits of optical detection, however, such that raw experimental data are inundated with Poissonian photon counting noise. For instance, as pointed out by Köllner and Wolfrum (1992), at least 185 photons are required to measure with 10% accuracy a static, monoexponential fluorescence lifetime from a single molecule.

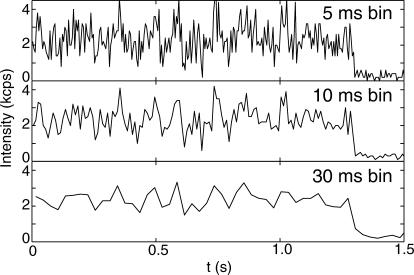
Eliciting quantitative dynamical information from these noisy trajectories is still one of the major challenges in single-molecule spectroscopy. The problem is illustrated by the simulated single-molecule traces displayed in Fig. 1. As the bin time is increased from 5 to 30 ms (lowering the time resolution), the noise subsides, but the dynamics are obscured as well. On the other hand, very small bin widths (high time resolution) lead to very large statistical errors. What is the correct balance between these competing factors? Single-molecule spectroscopy will not reach its full potential until this question is thoroughly explored. In this report, we derive the basic equations that relate time resolution to measurement uncertainties. Maximum likelihood estimators, which achieve the theoretical limits of accuracy, are also presented. Finally, a data analysis algorithm is proposed to take advantage of these expressions. We begin with a brief overview of recent developments in dynamic single-molecule measurements.

FIGURE 1.

Simulated single-molecule trajectories where the number of detected photons within certain bin times (5, 10, and 30 ms) is recorded as a function of chronological time. The simulation assumes a FRET configuration in which the donor-acceptor distance follows Langevin dynamics evolving on a parabolic potential (see main text for details). Only the donor intensity is shown. The simulation also assumes a confocal optical detection scheme with which the number of detected fluorescence photons from a single molecule is recorded as a function of time. The signal level is set to 3000 counts per second (kcps) and the background level 0.4 kcps. The molecule undergoes an irreversible photochemical reaction (photobleaching) at ∼1 s such that it no longer fluoresces.

Since the pioneering experiments by Moerner and Kador (1989) and Orrit and Bernard (1990), optical single-molecule spectroscopy has gained great momentum both in technology development (Moerner and Fromm, 2003) and in applications (Nie and Zare, 1997; Weiss, 1999; Xie and Trautman, 1998). It is particularly suited for the investigation of biological systems because it probes dynamics on the enzymatically relevant submicrosecond-to-second timescales. Using this technique, for example, enzymatic reaction rates of cholesterol oxidase (Lu et al., 1998) and horse radish peroxidase (Edman et al., 1999) were found to fluctuate with time; previously unreported folding intermediates were directly observed in RNA molecules (Tan et al., 2003; Zhuang et al., 2000) and their transition states characterized (Bokinsky et al., 2003); the detailed dynamics of F₁-ATPase rotation were revealed (Adachi et al., 2000; Yasuda et al., 1998); and the timescales of protein conformational fluctuations were quantitatively characterized and modeled (Yang et al., 2003). Not only have single-molecule experiments contributed to our fundamental understanding of biomolecular function, they have also stimulated much theoretical work that provides physical insights into such processes as dynamic disorder, conformational fluctuations, and photon statistics (Jung et al., 2002).

Monitoring biochemical events in real-time utilizing optical single-molecule spectroscopy can in principle establish a quantitative relationship between the static structure and the dynamic function of a biomolecule. Structural changes in a single molecule can be probed using Förster-type resonance energy transfer (FRET) (Ha et al., 1996). Although FRET allows studies of structural changes on the length scale of an entire biomolecule (20–80 Å) (Stryer, 1978), the minutiae of conformational fluctuations that accompany or facilitate the functioning of a biomolecule can be examined by utilizing excited-state electron transfer (ET) quenching of fluorescence. By virtue of the exponential distance dependence of the quenching rate, ET is sensitive to distance variations on the Ångström length scale and is a probe of conformational fluctuations at the catalytically active site (Yang et al., 2003). In addition, fluorescence polarization experiments can yield information about the orientational dynamics of a molecule (Adachi et al., 2000; Bartko et al., 2002; Yasuda et al., 1998).

A disadvantage of single molecule spectroscopy is that the organic dyes commonly used as fluorescent probes eventually undergo irreversible photodegradation, limiting the length of recordable single-molecule trajectories (Deschenes and Vanden Bout, 2002; Eggeling et al., 1998b). Consequently, it is not always guaranteed that the molecular system under investigation explores all possible configurations during the measurement period, as the ergodic principle would have dictated. Such non-ergodic conditions are expected to be encountered experimentally in a reactive system such as a single enzyme molecule. Despite the conviction that all dynamical information is contained in single molecule trajectories, these practical matters inevitably hamper the experimentalist's ability to quantitatively characterize the fast conformational motions that critically influence the function of a biomolecule. The challenge thus lies in the efficient extraction of the maximal amount of dynamic information from short, noisy single-molecule traces.

Many theoretical tools for the analysis of single molecule systems already exist. In the context of room-temperature time-resolved studies, for example, the correlation method (Onuchic et al., 1999; Wang and Wolynes, 1995)—which is a very sensitive probe of the memory of a system—has been used to analyze the dynamics of a single enzyme molecule (Agmon, 2000; Schenter et al., 1999) and conformational fluctuations (Chen et al., 2003; Edman et al., 1999; Yang et al., 2003; Zhuang et al., 2002). In principle, more features can be revealed using higher order correlations (Yang and Xie, 2002b) or event echo analysis (Cao, 2000; Yang and Cao, 2001). These methods are applicable to systems that exhibit stationarity and ergodicity. In cases where the measurement period is commensurate with the interconversion timescale between states (Edman et al., 1996; Jia et al., 1997), kinetic parameters can be deduced by applying the motional narrowing concept originally developed for lineshape analysis (Berezhkovskii et al., 1999, 2000, 2001; Geva and Skinner, 1997). However, due to nonideal experimental conditions—namely, short trajectories and the non-ergodic conditions typically seen in a reactive setting—it may prove difficult to use these powerful theoretical tools on experimental data.

Recent advances in experimental data registering, originally developed for time-correlated single photon counting (TCSPC) (Becker et al., 1999; Böhmer et al., 2001), allow the chronological arrival time of each detected photon to be recorded. This has stimulated new experimental schemes such as multiparameter fluorescence spectroscopy (Kuhnemuth and Seidel, 2001) and photon-by-photon correlation (Yang et al., 2003). For ergodic systems, the latter method allows detailed examination of conformational dynamics that covers a wide range of timescales from submicroseconds to tens of seconds. Advanced statistical methods that rely on stationarity and ergodicity have also been developed to elicit physical parameters from such time-stamped data streams (Novikov et al., 2001; Yang and Xie, 2002a;b). Most recently, photon by photon approaches assuming certain Bayesian prior models have been proposed for time-dependent ET (S. C. Kou, X. S. Xie, and J. S. Liu, unpublished) and FRET distance measurements (Schröder and Grubmüller, 2003).

Despite these exciting new developments, a general, nonparametric method that allows in-depth studies of a reactive, non-ergodic, single molecule system to relate its dynamics to its biochemical function is still lacking. In particular, such methods should allow one to accurately determine the conformational state of a single enzyme molecule with a temporal resolution that is better than its catalytic timescale (microseconds to seconds), while simultaneously addressing the problems of background photons, cross talk between multiple data acquisition channels, and error analysis of the results obtained. The outcome of such model-free analyses will allow an experimentalist to construct a quantitative model that extracts the dynamics underlying the motions of a complex biological macromolecule.

With the ultimate goal of developing general methods to build a quantitative dynamic structure-function relationship in biological macromolecules, in this report we first address the theoretical limits of time and distance resolution in time-resolved single-molecule measurements. We utilize principles from information theory (Cover and Thomas, 1991), specifically the Fisher information (Fisher, 1925), to quantify the knowledge that can be drawn from experimental data.

As an example, consider the task of estimating an experimental parameter q from a measurable quantity λ. Note that the only restriction on the parameter q is that the value of λ must in some way be dependent on it. Otherwise q may represent any property of the experimental system, including distance, orientation (Osborn et al., 2003), and oxidation state. The distribution of experimentally observed λ is given by the likelihood function f(λ; q): the probability, given that the value of the parameter is q, that the observable will be λ. The Fisher information about q is given by

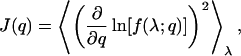where 〈⋯〉_λ denotes the expectation value weighted by the likelihood f(λ; q) over all possible λ. One may expect that uncertainties in measuring q are related to the Fisher information because, intuitively, q can be determined more accurately if more information about q can be obtained. This qualitative understanding can be quantitatively expressed by the Cramér-Rao-Fréchet inequality (Cramér, 1946; Fréchet, 1930; Rao, 1949), 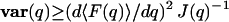, where 〈F(q)〉 is the expectation value of q from the estimator F. For an unbiased estimator, 〈F(q)〉 = q. The Cramér-Rao-Fréchet inequality then states that the variance of the best possible estimator of q is given by the inverse of its Fisher information matrix. In general, the maximum likelihood estimator (MLE)—which is determined by maximizing f(λ; q) as a function of q given the experimental observation λ—is a good starting point because it is asymptotically normal (Gaussian) under most conditions. (We would like to point out that, during the review process, an article was published in this Journal detailing the maximum likelihood determination of the positions of single molecules; see Ober et al., 2004.)

Based on these information-theoretical considerations, we derive the basic equations that determine the best achievable time resolution in a single molecule fluorescence experiment. In this context, the measurable quantity λ will be the arrival times of individual photons. The general expression is given in Eq. 3, and special cases are listed in Eqs. 22–25 for FRET, and Eq. 40 for ET. These equations allow us to propose a data reduction algorithm to extract, photon by photon, the maximum amount of information in distance measurements as a function of time. We then use computer simulations to show that the algorithm extracts distance and time information at resolutions that achieve the theoretical limit. Potential complications in applying this new method such as fluorophore blinking and bias are also considered. We note that the concept and approach presented here are general and their applications are not limited to the examples discussed.

THEORY

The experimentalist conducting a time-resolved single-molecule fluorescence measurement wishes to measure some parameter q as a function of time. In general, q is a dynamic variable that changes with time as the molecular conformation undergoes thermal fluctuations. If fluctuations in q cause corresponding fluctuations in the emitted fluorescence intensity of the molecule, then the dynamics of q can in principle be followed in real time by recording the arrival times of the emitted photons. If the photons can be meaningfully separated based on wavelength, polarization, or some other property, they may be detected and analyzed on separate channels.

It is not immediately clear how to analyze the data thus acquired, nor is it clear exactly how much that data will mean. For example, an observer may measure the donor-acceptor distance of a single-molecule to be 4 nm with a time resolution of 100 μs but with a 68% confidence interval σ(x(t)) = 10 nm. This datum, although measured at a very high time resolution, is not very meaningful; the 10-nm uncertainty is most likely greater than the size of the molecule. Some averaging will thus be required before a meaningful value can be obtained

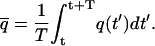(1)

The time interval T is chosen so that the uncertainty associated with this measurement, 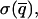is less than some predefined value. Further time averaging, thus reducing 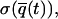will improve the accuracy in 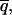but at the expense of time resolution. The following discussions are based on a coarse-grained picture in which the parameter q is assumed to remain constant during the time required to reduce the standard deviation below a certain threshold. The rationale behind this assumption is that an observer has no knowledge, a priori, of the true value q̃(t) until an accurate measurement can be made.

To determine the proper averaging time T, the Fisher information matrix is calculated and then inverted to find the covariance matrix for the parameters of interest. This gives us the Cramér-Rao-Fréchet bound for the variance of an estimator. The MLE, which approaches the Cramér-Rao-Fréchet bound, is then constructed.

Fisher information

Suppose the variables of interest, q = {q_i}, are being measured on m independent channels. Typically, q are chosen such that they are relevant as an indicator of the molecular state on the single-molecule level, for example, the FRET efficiency or the distance between a fluorescent donor and acceptor. Since the exact arrival times of the photons on these channels will be uncorrelated from one another, the Fisher information of these independent channels will be additive. The Fisher information can be computed for each of these channels individually. The observed intensity at a detector can be written as I(q). The intensity on the channel is generally measured relative to some constant reference intensity I⁰. We can write I(q) as I⁰ζ(q), with the dimensionless scaling factor ζ(q) containing all of the q-dependence of the detected intensity. The probability density function for observing n photons at the detector for this channel in time T is Poisson,

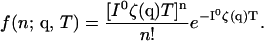(2)

Based on this probability density, the Fisher information matrix elements for a single channel are

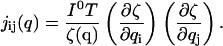(3)

This form makes it clear that information is acquired at a rate proportional to I⁰/ζ(q) through the course of the measurement.

The information from independent channels may be combined. The total information matrix is just the sum of the information matrices for each of the m channels, as

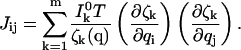(4)

Adding the effects of a detected background intensity B, the total detected intensity is

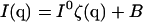(5)

(6)

where the signal/background ratio (I⁰ + B)/B has been written as β and the maximum observed intensity in the presence of background is I^β = I⁰/(1–β⁻¹). Finally, then, the total m-channel information is

(7)

The inclusion of background photons on a detection channel thus degrades the information that can be collected.

Covariance matrix

The Cramér-Rao-Fréchet bound states that the covariance (σ_ij) between the estimated parameters q_i and q_j is bounded by the inverse of the information matrix,

(8)

where the approximation is true when the bias of the estimator F(q) approaches 0. The bias of an estimator depends on the probability density function of the parameter to be measured. The estimators proposed in this work can be shown to meet the consistency condition lim_T→∞F(q)→q (Schervish, 1997). Therefore, the subsequent derivations will assume the use of unbiased estimators, and bias in the short-time limit will be discussed case by case in the Appendix.

Given p parameters to estimate, the information matrix will be of order p. The form of the matrix given in Eq. 7 makes it clear that p channels are required to form an invertible matrix. If multiple parameters are to be estimated simultaneously, the entire information matrix must be inverted to find the variances of the individual parameters and their covariances, so at least p independent sources of information are required to estimate p different parameters.

Concentrating on the estimation of one variable, q_i, the variance of that measurement is simply (J_ii)⁻¹. If the variable q is to be measured to a relative accuracy of α ≡ δq/q, the requirement is σ(q) ≤ α. The best possible time resolution will be

(9)

Estimators

Again concentrating on the estimation of one variable, given expressions for ζ₁(q) through ζ_m(q), the total probability density for observing n₁…n_m photons on channels 1…m is

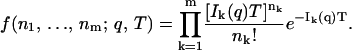(10)

The maximum likelihood estimator is the value of q for the observed T and n₁, … , n_m that maximizes f (n₁, … , n_m; q, T). This value of q is given by

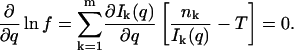(11)

The solution to this equation gives the maximum likelihood estimator in terms of T and n₁, … , n_m.

From another point of view, each photon can be regarded as an instantaneous measurement of the state of the system under observation. Then a photon will be detected on channel k with probability

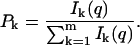(12)

The probability distribution for observing n_k photons on channel k, with N being the total number of photons, is

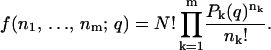(13)

The maximum likelihood estimator for q will thus be given by the solution to this equation:

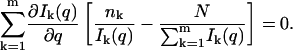(14)

The Poisson (Eq. 11) and the multinomial (Eq. 14) approaches are equivalent since the former can be derived as a limiting case of the latter. The only differences are practical. First, the multinomial approach cannot be used with a single-channel measurement. Second, the multinomial approach generally yields simpler maximum likelihood estimators for multiple channel measurements.

Having derived the basic information theoretical expressions for estimating parameters from single photon counting single-molecule measurements, it is of interest to apply these general formulae to some special cases.

FÖRSTER RESONANCE ENERGY TRANSFER

A variety of measures have been proposed and implemented to quantify the extent to which resonance energy transfer occurs from an energy donor to an acceptor (Berney and Danuser, 2003). Here, the energy transfer efficiency, E, is used because it has been widely adopted in single-molecule experiments (Ha, 2001). It is defined as the fraction of photon energy absorbed by the donor that is transferred to the acceptor. In cases where the acceptor is a nonfluorescent quencher, the transfer efficiency is measured by the donor fluorescence intensity alone (single-channel detection) and is expressed as

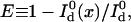(15)

where 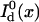is the detected background-free donor intensity and 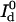is the detected background-free donor intensity in the absence of the quencher. 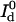can be measured in a separate control experiment. For simultaneous detection of donor and acceptor fluorescence, the transfer efficiency is given by

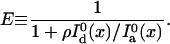(16)

I_a and I_d are the detected background-free fluorescence intensities (number of photons per second) of the acceptor and donor channels, respectively. ρ ≡ φ_aη_a/φ_dη_d, to be determined experimentally, is a scaling factor that corrects for differences in fluorescence quantum yields of the donor (φ_d) and acceptor (φ_a) probes, as well as those in detection (η_d for the donor channel and η_a for the acceptor channel).

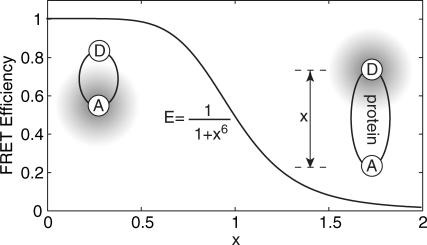
Within the framework of orientation-randomized dipole-dipole coupling between the donor and acceptor probes (Förster, 1949), the energy transfer efficiency can be related to the distance between the donor and acceptor probes,

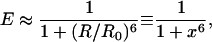(17)

where x is the normalized donor-acceptor distance, x ≡ R/R₀ R is the center-to-center distance of the donor and acceptor probes, and R₀ is the Förster radius—the distance at which energy transfer efficiency is 0.5 (see Fig. 2). For a given donor-acceptor pair, the corresponding Förster radius can be calculated from the donor fluorescence and acceptor absorption spectra, and the orientation factor can be calculated from fluorescence anisotropy measurements (Yasuda et al., 2003). Alternatively, one may construct a series of polypeptides of different length to calibrate the effective R₀ for tethered, gyrating fluorescent probes (Schuler et al., 2002). Here, it is assumed that both fluorescent probes gyrate around the tethered point on a timescale much shorter than the achievable experimental time resolution T, which can be verified experimentally. Information on slow orientation-dependent dynamics can be acquired by considering additional polarization-dependent channels.

FIGURE 2.

Energy transfer efficiency as a function of normalized donor (D) acceptor (A) distance x, defined by x ≡ R/R₀.

Fisher information and maximum likelihood estimators

A FRET measurement consists of observation of fluorescence from a donor fluorophore and/or from an acceptor chromophore. The E- and x-dependence of the intensities on these channels is

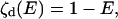(18)

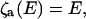(19)

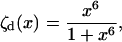(20)

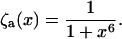(21)

Note that with these definitions, 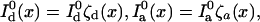and 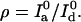Using Eq. 7 to calculate the information, one has

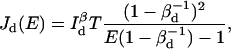(22)

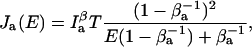(23)

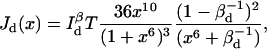(24)

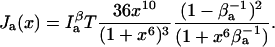(25)

For one-channel measurements, the only possible MLE is that given by the Poisson distribution, Eq. 11, as

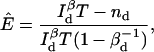(26)

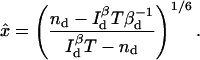(27)

For two-channel measurements, the multinomial estimator given by Eq. 14 is used. The equations for the maximum likelihood estimators are

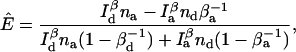(28)

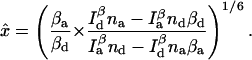(29)

Cross talk and cross-excitation between donor and acceptor channels

Due to spectral overlap and other experimental considerations, there is often cross talk between the donor and acceptor channels. Also, if the absorbance spectrum of the acceptor overlaps with that of the donor, the acceptor may be excited directly. As will be shown below, cross talk and cross-excitation simply change the effective signal/background ratio. As such, Eqs. 22–29 still apply.

Cross-talk coefficients from the donor and acceptor channels are denoted χ_d and χ_a, respectively. The cross-excitation coefficient is denoted χ_x. All three of these coefficients may be measured experimentally. For instance, χ_d can be measured by recording the acceptor channel intensity at different excitation power levels for donor probes whereas χ_a can be measured by recording the donor channel intensity at different excitation power levels for a control system where donor and acceptor probes are in juxtaposition so that E → 1. χ_x may be measured by recording the acceptor channel intensity in the absence of the donor. With these notations, the distance-dependent photon intensities become

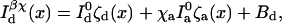(30)

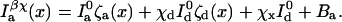(31)

Expanding the intensity terms, one has

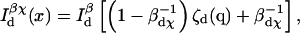(32)

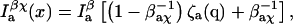(33)

with

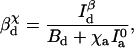(34)

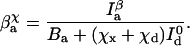(35)

The crests and troughs in one channel correspond with the valleys and peaks in the other, so the only effect of the cross talk is to decrease the apparent signal/background ratio. The expressions given for J(x) and x̂ in the previous section still hold, using the new β_dχ and β_aχ in place of β_d and β_a, respectively.

Distance and time resolution

One channel

When measuring FRET efficiency on only the donor channel, the total information is

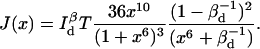(36)

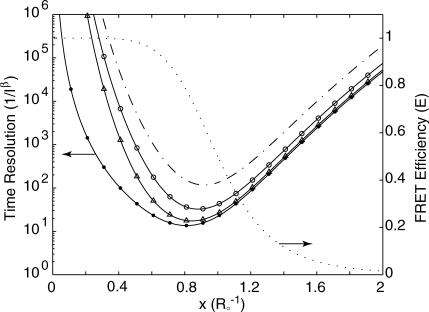
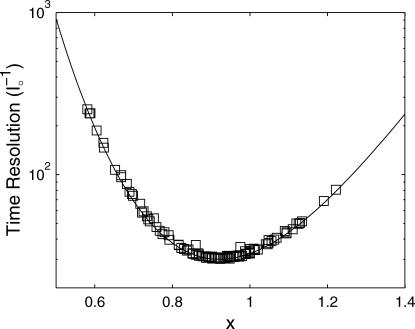
This suggests that time resolution T is a function of donor-quencher distance. Fig. 3 shows the theoretical minimum observation time period (T, in units of 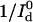) required to achieve a relative measurement error δR/R₀ less than a preset value α = 0.1. Given α, the theoretically achievable time resolution at various donor-quencher distances can be found under the ideal condition that there are no background photon counts (solid circle in Fig. 3). The time resolution worsens sharply at both large and small x. This is not surprising; the energy transfer efficiency E does not vary much with x for donor-quencher distances that are significantly larger or smaller than R₀ (compare to overlaid FRET efficiency curve in Fig. 3). Consequently, it will take a large number of photons to measure x at these distances to within this error tolerance. At distances closer to R₀ the efficiency is very sensitive to changes in x, so fewer photons are required to obtain the desired tolerance.

FIGURE 3.

Observation time, in units of 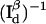required to achieve a relative measurement uncertainty α = 0.1 as a function of normalized donor-quencher distance δR/R₀ < α. Shown in the figure are expected time resolutions under various signal/background ratios in the donor channel: β_d = 2 (–·), β_d = 5 (○), and β_d = 20 (▵), which are compared to that under background-free conditions, β_d → ∞ (•). Overlaid is a FRET efficiency curve for comparison (⋯), referenced to the ordinate on the right.

In practice, one cannot avoid recording background photons. In these cases, the curve remains U-shaped, but is shifted to longer observation times. This is because the information of x is degraded by a factor of x⁶(1–β⁻¹)²/(x⁶ + β⁻¹) < 1 in the presence of background photons.

These equations can be used to understand the time and distance resolution limits of a single molecule experiment. For example, for a single molecule labeled with a donor-quencher pair that exhibits a Förster radius of 50 Å and whose fluorescence can be measured with a signal/background ratio of 10, the highest time resolution achievable for measuring this donor-quencher distance is achieved at R = ∼43 Å with 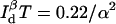photons required to achieve the desired accuracy of α. To measure R within a standard deviation of 5 Å, then, one must collect 22 photons.

Two channels

Time resolution in the two-channel detection scheme is also a function of normalized donor-acceptor distance. The total information for this scheme is

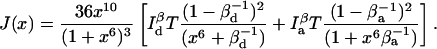(37)

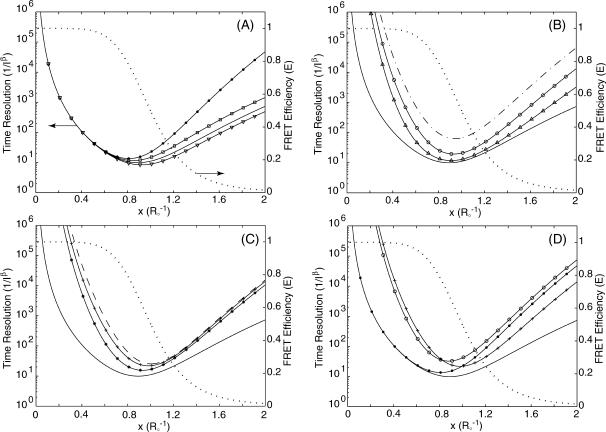
A comparison of background-free single-channel and two-channel detection schemes is displayed in Fig. 4 A. Although both detection schemes behave similarly at short distances, the two-channel detection scheme clearly delivers better performance. This is expected since more information about x is gathered with two channels. Furthermore, better time resolution can be achieved for larger x in cases where ρ > 1, compared to the ρ = 1 case where the emission/detection efficiencies are the same for both donor and acceptor channels. This is because in the ρ > 1 cases, the acceptor probe emits more photons than it would have if ρ = 1, to give more information about x. Information degradation due to various degrees of background and cross talk in the two-channel detection scenario is depicted in Fig. 4, B and C. Fig. 4 D illustrates a more realistic situation in which the signal/background ratio is 5. The performance of the two-channel scheme is generally better than the single-channel scheme for large x. Using the same example as in the last section, for a single molecule labeled with a donor-quencher pair that exhibits a Förster radius of 50 Å and whose fluorescence can be measured with a signal/background ratio of 10, the highest time resolution achievable for measuring this donor-quencher distance is achieved at R = ∼43 Å with 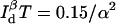photons required to achieve the desired accuracy of α. To measure R within a standard deviation of 5 Å, then, one must collect a total of 15 photons.

FIGURE 4.

Observation time T, in units of 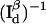, as a function of normalized donor-acceptor distance x = R/R₀ to achieve a relative measurement error of σ(x) < α = 0.1 in two-channel detection. (A) Background-free scenario when ρ = 1.5 (▿), ρ = 1.0 (—), and ρ = 0.5 (□). Background-free, single-channel detection (•) is also included for comparison. (B) Background emission is present, but no cross talk between the donor and acceptor channels. The background levels are β = 2 (– ·), β = 5 (○), and β = 20 (▵). The background-free case is also plotted (—) for comparison. In all plots on this panel, the background levels are the same for both the donor and acceptor channels. (C) Both background, β_d = β_a = 5, and cross talk, χ_d = χ_a = 0 (*), χ_d = χ_a = 0.25 (+), and χ_d = χ_a = 0.5 (– –), are present for two-channel detection. The background- and cross-talk-free, two-channel detection curve (—) is also plotted for comparison. (D) Comparison of background-free single-channel detection (•), single-channel with a signal/background ratio of 5 (○), background- and cross-talk-free two-channel detection (—), and two-channel detection with signal/background ratio of β_d = β_a = 5 and cross-talk coefficient of χ_d = χ_a = 0.25 (+). On A–D, FRET efficiency E as a function of x is overlaid (⋯) and referenced to the ordinate to the right.

ELECTRON TRANSFER

Recently, excited-state electron transfer has been used as a probe for investigation of conformational changes in individual molecules (Eggeling et al., 1998a; Jia et al., 1997; Sauer et al., 1998). In most cases, emission intensity or florescence lifetime of the probe is quenched via electron transfer to or from a nearby quencher. Due to the exponential distance dependence, ET can also be used as a spectroscopic ruler to measure distances on the Ångström scale under such conditions that chromophore-quencher distance variation is the sole source for changes in ET rate. These conditions include, for instance, barrierless excited-state ET so that thermal fluctuation in the relative free-energy levels ΔΔG is negligible, rapidly randomized, or fixed relative to orientation of chromophore and quencher. The timescale of protein conformational motions must also be separated from that of probe rotation and facile electron back transfer so that repetitive excitation of a single molecule is achievable. Therefore, ET allows investigation of minute changes of biomolecular conformation (Yang et al., 2003) and serves as a complementary method to FRET which, as discussed in earlier sections, is sensitive to distance changes on the 20–80 Å scale. In the following discussion, we assume that ET is primarily dominated by chromophore-quencher distance. That is, the quenching rate k_q is

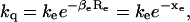(38)

where k_e is the ET rate when chromophore and quencher are in van der Waals contact, β_e is the distance parameter in ET and varies from 1.0 to 1.4 Å⁻¹ for proteins (Gray and Winkler, 1996; Moser et al., 1992), R_e is the edge-to-edge distance between chromophore and quencher, and x_e = β_eR_e is the normalized chromophore-quencher distance.

Fisher information and maximum likelihood estimators

Let the radiative and nonradiative decay rates of a fluorescent probe in its excited state be k_r and k_nr, respectively. The total decay rate and emission intensity of the probe in the absence of quenchers is k₀ ≡ k_r + k_nr < k_e and I₀, respectively. In the presence of a quencher, the excited-state decay rate becomes k_x = k₀ + k_q. If ET is the sole mechanism that increases the excited-state decay rate of a chromophore, the emission intensity of the chromophore is inversely proportional to its excited-state decay rate: I_x ∝ (k_x)⁻¹. The total detected emission intensity becomes 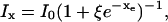where ξ = k_e/ k₀ > 1. The x-dependent part of the intensity is thus

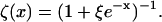(39)

Using Eq. 7, the Fisher information is calculated to be

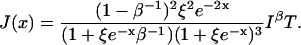(40)

The MLE can be determined using the Poissonian formula, Eq. 11:

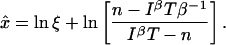(41)

Distance and time resolution

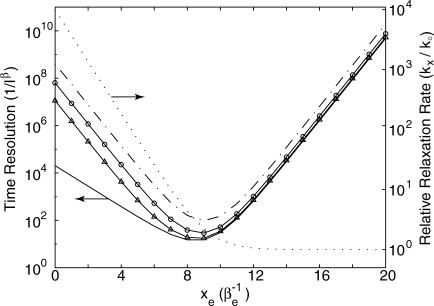
The expression for information in an electron transfer experiment, Eq. 40, makes it clear that time resolution T at a given detected photon flux is a function of chromophore-quencher distance x and background level β. The information of x degrades by a factor of (1 − β⁻¹)²/(1 + ξe^−xβ⁻¹) ≤ 1 in the presence of background photons. The condition for measuring x_e to a relative error α is

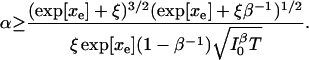(42)

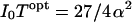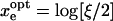Note that whereas time resolution in general is related to ξ, the ratio of maximum ET rate (k_e) to the excited-state decay rate of the chromophore (k₀), the best possible time resolution is independent of ξ. In fact, the best possible time resolution becomes at under the ideal background-free condition when β → ∞. In other words, under such ideal conditions, ∼6.8/α² photons are needed on average to measure x_e to a relative error α. For example, if one is interested in measuring R_e to an absolute error of 0.5 Å within a protein having β_e = 1.4 Å⁻¹, which corresponds to a relative error α = 0.5, β_e = 0.7, at least ∼14 photons will be needed in the ideal background-free condition. (See Fig. 5.)

FIGURE 5.

Observation time, in units of (I₀)⁻¹ under background-free conditions, or in units of 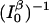when there is background, required to achieve a relative measurement uncertainty α = 0.7 as a function of normalized donor-quencher distance x_e = R_eβ_e. This confidence interval corresponds to an absolute error of ∼0.5 Å if the distance dependence of electron transfer β_e is 1.4 Å⁻¹. The value ξ in these plots are set to 10,000, corresponding to k_e = 10¹³ and k₀ = 10⁹. Shown in the figure are expected time resolutions under various signal/background ratios: β = 2 (– ·), β = 5 (○), and β = 20 (▵), which are compared to that under the background-free condition, β → ∞ (–). Overlaid is excited-state lifetime relative to the quencher-free case for comparison (⋯), referenced to the ordinate on the right.

In addition, the optimal chromophore-quencher distance becomes greater in the presence of background photons, but decreases asymptotically to log[ξ/2] = log[k_e/2 k₀] as β → ∞. This suggests that one may choose probes of different fluorescent lifetime k₀ for different systems so the best time resolution will be achieved at an experimentally relevant distance. This is analogous to choosing donor and acceptor pairs by their spectral overlaps for optimal measurements in FRET applications.

APPLICATION

The above analysis focuses on information-theoretic results about photon counting in general and discusses a number of special cases. Now the practical application of these results is considered. In this section, an algorithm is given to convert a list of measured photon arrival times to a distance trajectory. This algorithm is general for the experimental methods described and reaches the information theoretic limit. Since it applies equally to all approaches, it is discussed only in the context of two-channel FRET. Similar considerations apply for the measurement of any other parameter that can be understood in the context of the previous theoretical discussion, including single-channel FRET and ET measurements.

Maximum information data analysis algorithm

The data analysis algorithm that follows is predicated on accurate detection of the arrival times of individual photons. Experimentally, this is typically accomplished by a single-photon avalanche photo diode (Li and Davis, 1993). It is also assumed that the fluorophores used as probes are excited by a light source that provides constant illumination on the timescale of photon detection. The molecules under observation must be well enough separated that any electronic interactions between fluorophores on different molecules may be neglected. Any experimental configuration that satisfies these criteria may be used to generate the single molecule trajectories whose analysis is described.

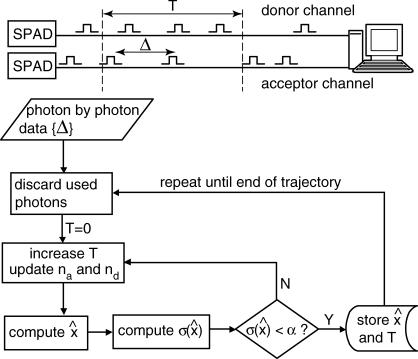
An algorithm for obtaining distance measurements of predefined precision α is prescribed as follows (see Fig. 6). Each measurement consists of a chronological time t, a time uncertainty δt, a distance x̂, and a distance uncertainty σ. With the first measurement starting at time T = 0, find the minimum block length that will give 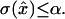Set the chronological time t for that data point to the middle of the time block, time resolution T(t) to its length, and calculate x̂ and 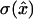, according to the formulae given above. This algorithm achieves the limit of maximum information. Other termination conditions are possible as well, but only the constant 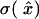method is treated here, as it is the most practically applicable.

FIGURE 6.

Flowchart of the maximum information algorithm.

Simulation details

This algorithm was validated using simulated single molecule trajectories for which the donor-acceptor coordinate is exactly known as a function of time. Motion on the x-coordinate is modeled according to a discretized Langevin equation in the limit of large, fast friction with potential of mean force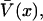

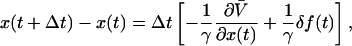(43)

where Δt is the propagation time of the simulation, and γ is a frictional coefficient representing velocity-dependent dissipation. δf(t) is a Gaussian-distributed random force with 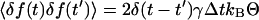in which δ(t − t′) is the Dirac δ-function, k_B is Boltzmann's constant, and Θ is the absolute temperature.

At each time step the emission and intersystem crossing rates are calculated and the system tested to see if either fluorophore has emitted a photon or entered the triplet state. Both photon emission and intersystem crossing are distance-dependent according to the FRET efficiency relation, Eq. 17. Relaxation from the triplet state is treated as exponential in time. If a photon is emitted on either channel, the x-coordinate of the simulation is recorded. Photon data is recorded as interphoton timings on donor and acceptor channels and subsequently analyzed according to the prescribed algorithm.

Example trajectories

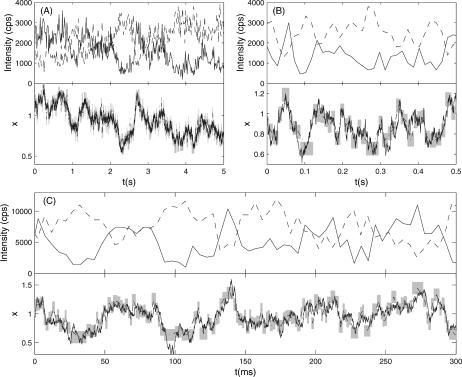
Evolution of the x-coordinate was simulated according to Eq. 43 on a parabolic potential (see Fig. 7). The performance of this algorithm for a sample x(t) trajectory is analyzed in Fig. 8. Eq. 37 gives a lower bound for the time resolution T(t). The maximum information algorithm achieves this lower bound and is thus the optimal data analysis algorithm for extraction of x-trajectories from this kind of data.

FIGURE 7.

Sample FRET trajectories analyzed according to the maximum information algorithm. The top half of each panel shows the simulated intensities on the donor (—) and acceptor (– –) channels as a function of time. The bottom half of each panel compares the analysis of the given FRET trajectory with the simulated trace corresponding to the true trajectory (—). The dashed black line (– ·) is the trajectory recovered by the maximum information method, and shaded areas outline the standard deviations calculated from the information analysis. All trajectories were generated according to Eq. 43 on the potential 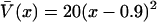at a temperature of Θ = 1/k_B. Trajectories A and B were simulated with γ = 10 and γ = 1, respectively, 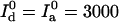cps and 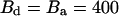cps, and analyzed with α = 0.07. Their intensity trajectories were calculated with 15-ms bins. C was simulated with γ = 0.3, 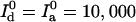cps, and B_d = B_a = 1200 cps, and analyzed with α = 0.1. Its intensity trajectory was calculated with 5-ms bins.

FIGURE 8.

The theoretical limit of the time resolution as a function of x, calculated using Eq. 37 with parameters determined by the simulation parameters for the trajectory in Fig. 7 B (—) is compared with the δt values from the maximum information algorithm (□).

Analysis with the maximum information algorithm yields the trajectories shown in Fig. 7. Fig. 7, A and B, were simulated with 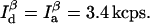The maximum time resolution is 8.8 ms (see Fig. 7). The maximum information algorithm can detect any conformational changes happening on this timescale or longer.

Since the analysis is primarily based on the number of photons detected, this resolution scales exactly as the inverse of the average count rate. If one were to measure a single molecule FRET trajectory at an experimentally realizable average count rate of 10 kcps, the maximum time resolution would improve to 2.6 ms. Also, the value of the accuracy cutoff, α, makes a significant difference. Analysis of the trajectory in Fig. 7 C with α = 0.1 improves the maximum time resolution to 1.2 ms.

If donor-acceptor distance fluctuations in the experimental system are large and fast, measured distance trajectories may not represent the full conformational flexibility of the experimental system. In this case, spatial resolution may be sacrificed for time resolution, allowing the full conformational distribution to be observed. In this way the analysis can be tailored to the experimental system and conditions.

Bias in distance measurements and effects of fluorophore intermittency

The maximum likelihood estimator is asymptotically unbiased when measuring a single distance in the limit of long measurement time. It is, however, slightly biased at small time intervals. In the cases we have studied, this bias is always much lower than the standard deviation given by the Fisher information (see Fig. 9 and numerical studies of bias in the Appendix). If the inherent bias becomes significant, many methods exist to generate estimators that correct for the bias while simultaneously approaching the Cramér-Rao-Fréchet bound (Voinov and Nikulin, 1993), or the bias can be corrected empirically by numeric simulations such as those presented in Appendix.

FIGURE 9.

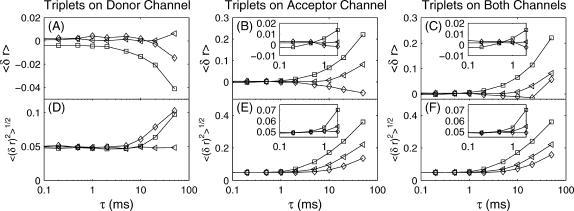
(A–C) Mean error and (D–F) root mean-square error as a function of acceptor-donor distance triplet lifetime (Eq. 44). Only donor triplet states are allowed in A and D; only acceptor triplet states in B and E; and both acceptor and donor triplet states are allowed in C and F. Trajectories were simulated at constant x-values of 0.8 (□), 1.0 (◃), and 1.2 (⋄) with effective φ_isc = 1 × 10⁻². The trajectories were analyzed by the maximum information algorithm with α = 0.05. Under typical experimental conditions the triplet lifetime τ will not exceed 1–2 ms. At these lifetimes, there is no significant effect on the accuracy of the algorithm.

Intensity blinking due to triplet state trapping or other mechanisms has the potential to cause inaccuracies in distance measurements. The algorithm given above does not take these intensity intermittency effects into account. Here we use simulations to show that our algorithm is robust against such blinking behavior up to a few microseconds of nonfluorescent state lifetime. Without loss of generality, we use triplet-state blinking as an example and consider typical dye molecules that exhibit S₁ → T₁ intersystem crossing quantum yields on the order of φ_isc = 5 × 10⁻⁴ and triplet lifetimes of 500 μs (Hübner et al., 2001). Using these typical values, and assuming a collection efficiency of 5% (giving an effective φ_isc of 10⁻²), simulations were carried out at constant x-values.

To make a quantitative evaluation of the accuracy of the analysis under these conditions, we consider the error parameter 〈(δr)^s〉 as a measure of the closeness of a particular analysis 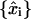to the true data x(t),

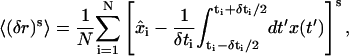(44)

where x̂_i is the maximum-information estimate of x(t) at time t_i and N the total number of estimates at given α. Therefore, bias (mean error) is represented by s = 1 and mean-square error by s = 2. Fig. 9 shows the results of this analysis.

For experimentally relevant triplet lifetimes, there is no significant error. This is because—although the analysis is done on a photon-by-photon basis—generally >10 photons are included in each box. As long as the triplet lifetime and intersystem crossing quantum yield are such that the total time spent in the triplet state is not a large fraction of the width of the box, the analysis will not be adversely affected.

In the case that only donor triplets are allowed, there is no significant increase in bias due to the triplet state even at very long triplet lifetimes. This is due to the multinomial nature of the analysis—the time taken to acquire photons is not important, only the channel they arrive on. Since donor triplets states prevent photon emission from both the donor and the acceptor, the only effect is that the time resolution will be decreased.

This is not the case with acceptor triplet states. Bias due to acceptor triplet states is very distance-dependent. At large x, even with very long acceptor triplet lifetimes, there will be no effect on the accuracy of distance measurements: the acceptor simply will not enter the triplet state. As x decreases, the probability that the acceptor will enter the triplet state increases, and the bias becomes more significant.

Experimental considerations

The formulas presented here are ready for immediate use in many experimental setups that have already been reported in the literature. In addition, these results are applicable to other, time-independent measurements. For example, the maximum likelihood estimators for determining distance from the numbers of photons measured on the donor and acceptor channels can be used in any situation where all of the calibration numbers (B_d, B_a, 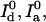χ_d, and χ_a) are known. It is important to note that, although formulas regarding FRET efficiency are also given in this report, the use of FRET efficiency as an indicator of molecular state may be misleading as it is not a linear function of donor-acceptor distance; small distance changes may be amplified as a result.

The number of photons that may be collected from a single molecule is heavily dependent on experimental conditions and the particular fluorophores used. On the order of 10⁸ photons may be collected from a single molecule of Rhodamine 6G under vacuum in a poly (methylacrylate) film at low excitation intensities (Deschenes and Vanden Bout, 2002). This means that on the order of 10⁶ independent distance measurements may be made if the molecule is part of a FRET pair between 0.4 R₀ and 1.6 R₀. To study fast dynamics, one may wish to excite the single molecules at higher intensities, but the detected time trace will also be shorter. Currently, for example, using the Alexa-555/Alexa-647 dyes (Molecular Probes), photon arrival rates on the order of 5 × 10⁴ photons per second are experimentally feasible in water solution, giving time resolutions better than 1 ms (L.P.W. and H.Y., unpublished data).

Several detection methods exist that are compatible with the maximum information method. Avalanche photodiodes, photomultiplier tubes, and multichannel plates may all be used to detect and count single photons. The dark counts on high quantum efficiency (QE > 60%) Peltier-cooled, avalanche photodiodes range from 25–500 cps, whereas the dark counts on uncooled, single photon-counting photomultiplier tubes and multichannel plates (QE < 20%) are similar, ranging from 10–1500 cps. At high excitation intensities, the detection device is not the primary source of background; dark counts from the detector are miniscule compared to other sources including Raman scattering and autofluorescence in cells, both of which are difficult to suppress using spectral filters. These background contributions, however, do play a role in determining the lowest possible excitation intensities and thus the longest possible trajectories. The maximum information method will work at almost any signal/background ratio; but as this ratio approaches 1, the required number of photons to make a particular distance measurement increases without bound. It should be stressed that, although the proposed method has in mind the use of detectors capable of single photon counting, the concepts and ideas that underlie the development of maximum information method is general and should be applicable to any measurements that are information-limited.

The preceding discussions suggest that, when choosing a FRET dye pair to measure a distance of ∼R, the most effective dyes will be those that exhibit a R₀ = ∼1.1–1.3 R (or R = ∼0.8–0.9 R₀), instead of the commonly used ∼R = R₀ condition. The options available, in dye and filter selection, are much broader. Since cross talk and cross-excitation are now recognized as merely contributions to the background, the filter set may be chosen with this in mind. Bandpass filters may be made as wide as possible to collect as many photons as possible. Also, the excitation wavelength may be chosen to be the maximum absorbance of the donor, even if that would generate some direct acceptor excitation.

CONCLUSION

A detailed and quantitative study of reactive dynamics in biomolecular systems will require both an accurate way to measure the biomolecular conformation and a reliable estimate of the errors involved in the experiment. We have presented a general method, using the maximum likelihood estimator, to analyze experiments using detectors capable of single photon detection. The Fisher information was used to demonstrate that our analysis achieves the best possible resolution given the constraints of the experimental system.

The accuracy of a single photon counting experiment is determined by Poisson statistics. For example, if one is trying to measure the distance between two fluorophores in an experimental system, the distance information that one seeks is carried by each detected photon and is acquired at a constant rate in time, as shown in Eqs. 7, 24, 37, and 40, and the actual rate will vary depending on the experimental configuration. Any measurement of these parameters will be limited in precision by the amount of information obtained, as specified by the Crámer-Rao-Fréchet bound. By choosing the proper analysis, one that achieves these limits of precision, one can assure that the maximum information is extracted from the data.

We have presented a method that achieves this, yet allows great flexibility in determining the relative values of the temporal and spatial resolutions. This concept is: 1), generally applicable to a variety of systems; 2), independent of kinetic models; 3), easy to implement in practical experiments; 4), efficient, since it extracts information photon by photon; 5), quantitative; and 6), most importantly, applicable to reactive systems.

Experimentally, it is helpful to remember that this algorithm is based on the detection of individual photons. The maximum information method of analysis relies upon the Poisson noise inherent in photon counting applications. Arbitrary subtraction of background from the measured signal obscures these statistics. Also, to increase experimental time resolution, all that must be done is to increase the excitation power, and thus the average detected intensity. Conversely, one can choose the intensity based on the desired time resolution. This allows one to take into account other experimental limitations, such as fluorophore photobleaching and triplet blinking.

For two-channel FRET measurements, if cross talk between the donor and acceptor channels is ignored, one would naturally excite the donor at the maximum in its absorption spectrum to give the highest signal/background ratio in a single molecule experiment. But the acceptor in a FRET pair will frequently absorb at that wavelength, producing cross talk between the two channels. Since we now recognize cross talk as just another contribution to the background—its only effect is to decrease the ratio of signal/background—it is no longer necessary to ensure that the acceptor is perfectly transparent at the excitation wavelength. With our information analysis, the excitation wavelength can be adjusted intelligently and the optimal signal/background ratio can be achieved.

All of these issues arise from the central idea of an information-based analysis. In any experiment the fundamentally limited parameter is information. Since the amount of information does not increase, it is to the advantage of the experimentalist to be as flexible as possible in choosing where to allocate that information. With our maximum information analysis the experimentalist is given optimal control over the information.

APPENDIX

Maximum likelihood estimators are not guaranteed to be unbiased. In this section we calculate the bias in the estimators we have given and consider the effects it might have on the results obtained by the maximum information algorithm discussed in the body of this article.

In general, the bias b_n in an estimator F_n of some parameter x is

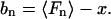(45)

Here n is the number of observations in the data set and 〈⋯〉 indicates an average over all possible n-point datasets, weighted by the probability density of the observation of that dataset.

In the cases considered in this article, the probability density to observe a particular data set is Poisson. In the context of dynamic measurement, however, we are concerned more with the time in photon acquisition rather than the number of photons in a certain observation interval as indicated by the Fisher information. The bias in our estimators will therefore by given by

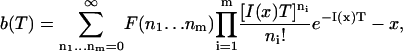(46)

where, as before, m denotes the number of channels.

The estimators of FRET efficiency given in Eqs. 26 and 28 can be analytically shown to be unbiased. The sums for the estimators of distance in FRET and ET (given in Eqs. 27, 29, and 41) was evaluated numerically. A photon trajectory was generated at constant x, the photons were binned into time intervals T, and the appropriate estimator was applied. When negative, infinite, or imaginary distances were generated, the data point was discarded, just as in the maximum information algorithm in which T is increased until the set uncertainty level α is reached.

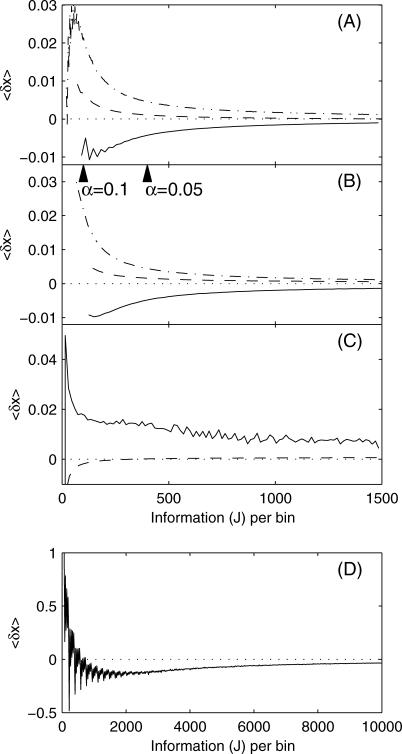
These calculations were performed at a variety of constant x-values. The results, plotted as a function of the information per bin, can be seen in Fig. 10. Information per bin is the most natural coordinate for the bias plot in the context of the maximum information algorithm. As an example, if a trajectory is analyzed at α = 0.07 (as in Fig. 7, A and B), the information per bin is 204. To convert to units of bin time, simply use the appropriate information equation: Eq. 36 for one-channel FRET, Eq. 37 for two-channel FRET, or Eq. 40 for ET.

FIGURE 10.

Bias in estimators of x based on simulations of (A) one-channel FRET and (B) two-channel FRET at distances of 0.8 (—), 1.0 (– –), and 1.2 (– · –) and electron transfer at distances of (C) x = 9 (– –), 12 (—), and (D) x = 6 (- - -). Wedges are placed to indicate the values of the information (J) which satisfy the cutoff values of α = 0.1 and α = 0.07, as discussed in the main text.

There are strong fluctuations in the bias at extreme values of x in single-channel FRET and electron transfer. These arise as a consequence of the discrete nature of photons. Because photons are quantized, the possible values of the estimator at a given bin time are quantized. Since the estimator is highly nonlinear, the possible values of the estimator are also highly oscillatory as a function of the bin time. This oscillatory effect is most pronounced for the extreme values of the estimator. At extreme values of x, the average that is calculated to determine the bias is heavily influenced by the extreme value of the estimator. This produces the oscillations in bias. As the bin time increases, the number of possible values of the estimator also increases, and the oscillations damp out. For two-channel FRET, the estimator is not a function of bin size, so there are no oscillations.

For both one- and two-channel FRET, bias is smallest when x = 1.0. In all the curves the bias approaches zero as the information increases, confirming the asymptotic unbiasedness of these estimators. For ET at x = 6, the estimator is quite biased. At larger distances for ET, and at all distances for FRET measurements, the bias is at least an order-of-magnitude smaller than the standard deviation (J^–1/2).

This work was supported by the Office of Science, U.S. Department of Energy, under contract DE-AC03-76SF00098, and by the University of California at Berkeley. L.P.W. acknowledges a graduate research fellowship from the National Science Foundation.