The Proton-Driven Rotor of ATP Synthase: Ohmic Conductance (10 fS), and Absence of Voltage Gating

Abstract

The membrane portion of F₀F₁-ATP synthase, F₀, translocates protons by a rotary mechanism. Proton conduction by F₀ was studied in chromatophores of the photosynthetic bacterium Rhodobacter capsulatus. The discharge of a light-induced voltage jump was monitored by electrochromic absorption transients to yield the unitary conductance of F₀. The current-voltage relationship of F₀ was linear from 7 to 70 mV. The current was extremely proton-specific (>10⁷) and varied only slightly (≈threefold) from pH 6 to 10. The maximum conductance was ≈10 fS at pH 8, equivalent to 6240 H⁺ s⁻¹ at 100-mV driving force, which is an order-of-magnitude greater than of coupled F₀F₁. There was no voltage-gating of F₀ even at low voltage, and proton translocation could be driven by ΔpH alone, without voltage. The reported voltage gating in F₀F₁ is thus attributable to the interaction of F₀ with F₁ but not to F₀ proper. We simulated proton conduction by a minimal rotary model including the rotating c-ring and two relay groups mediating proton exchange between the ring and the respective membrane surface. The data fit attributed pK values of ≈6 and ≈10 to these relays, and placed them close to the membrane/electrolyte interface.

INTRODUCTION

ATP synthase or F₀F₁-ATPase, a key enzyme of bioenergetics, is present in the photosynthetic and respiratory coupling membranes of eubacteria, mitochondria, and chloroplasts. The enzyme is bipartite. Its membrane-embedded F₀-portion transports protons down the electrochemical gradient (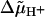) and generates torque. The peripheral F₁-portion synthesizes ATP at the expense of this mechanical energy. Both F₀ and F₁ are rotary motors/generators and steppers. They are mechanically coupled by a central rotary shaft and held together by a peripheral stator (for general reviews, see Senior et al., 2002; Noji and Yoshida, 2001; Leslie and Walker, 2000; Boyer, 1997; Junge et al., 1997; and for the sodium ATP synthase, see Dimroth, 2000; Dimroth et al., 1999). By its rotary mechanism F₀ is distinguished from most other proton or cation transporters with the exception of the structurally unrelated ionic drive of the bacterial flagellar motor.

F₀ is composed of three types of subunits in a stoichiometry of a₁b₂c_10–14. All three types of subunits are required for proton conduction (Schneider and Altendorf, 1987; Altendorf et al., 2000). Multiple copies of the hairpin-shaped c-subunit form a ring in the membrane to which subunits a and b are attached from the outer side (Lightowlers et al., 1988; Angevine and Fillingame, 2003; Fillingame and Dmitriev, 2002; Jiang et al., 2001; Muller et al., 2001; Seelert et al., 2000; Stock et al., 1999). ATP hydrolysis in F₀F₁ is coupled to the rotation of the c-ring (Pänke et al., 2000; Sambongi et al., 1999; Tsunoda et al., 2000, 2001), and power is elastically and without slip transmitted between the drive in F₁ and the ring of F₀ (Cherepanov et al., 1999; Cherepanov and Junge, 2001; Pänke et al., 2001).

The currently favored mechanism of torque generation by proton flow (Junge et al., 1997; Elston et al., 1998) has been based on the following assumptions: Brownian rotary motion of the c-ring relative to subunit a, two non-co-linear access channels for protons from either side, and two electrostatic constraints, namely the acid Glu residue (Asp in Escherichia coli) in the middle of the hairpin of c being deprotonated when in contact with subunit a and protonated when facing the core of the membrane (Junge et al., 1997; Elston et al., 1998). Modifications to this basic scheme have been formulated to account for Na⁺-translocation in F₀ from Propionigenium modestum (Dimroth et al., 1999) or to account for internal librational motion in the ring (Fillingame et al., 2000). The basic principle of this rotary mechanism of proton conduction—Brownian fluctuations and two electrostatic constraints—has remained (see Junge, 1999). It is obvious that a comprehensive understanding of rotary proton conduction requires both structural and kinetic information.

Most recent studies on this enzyme have focused on the F₁-portion, whereas most studies on the mechanism of proton conduction by F₀ date back by more than one decade. The assessment of the conductance of F₀ has been hampered by complications:

1. The conductance is too small for the single-molecule patch-clamp approach; see below for one report to the contrary.

2. Studies with large ensembles suffer from the difficulty in determining the proportion of F₀ that is actually conducting.

3. Studies with reconstituted F₀ using glass electrodes for recording pH transients have often lacked sufficient time resolution.

Thus it is not surprising that the reported values for the conductance at neutral pH diverged by four orders of magnitude. Some studies on the conductance of F₀ have yielded rather low values in the range of 0.1 fS, which is equivalent to a rate of 62 s⁻¹ at a driving force of 100 mV (Negrin et al., 1980; Friedl and Schairer, 1981; Schneider and Altendorf, 1982; Sone et al., 1981; Cao et al., 2001). This value would be insufficient to cope with the turnover rate of the coupled F₀F₁ enzyme. For chloroplast CF₀ we have found a 100-fold-higher figure, 9 fS (or 5600 s⁻¹ at 100 mV) under the assumption that all exposed F₀ molecules contributed to the relaxation of the transmembrane voltage (Schönknecht et al., 1986). This conductance is compatible with the maximum proton turnover rate of the coupled enzyme, ≈1000 s⁻¹. Later we obtained circumstantial evidence for a majority of inactivated F₀, which raised the conductance to a value of 1 pS (Lill et al., 1986; Althoff et al., 1989). Such high rates by far exceeded the diffusive proton supply to F₀, as then noted, and it has remained questionable whether the underlying assumption was correct. This work has also provided evidence for an extreme proton specificity of the conductance (>10⁷ over other cations), small pH-dependence between 5.5 and 8, a H/D-kinetic isotope effect of 1.7, and an activation energy of 42 kJ/mol in H₂O and 47 in D₂O. The latter data were not affected by the above ambiguity over the absolute magnitude of the conductance (Althoff et al., 1989).

A conductance of similarly high magnitude was reported for CF₀CF₁ in a lipid bilayer formed by the dip-stick technique, which is related to patch-clamp (Wagner et al., 1989). Gated single channel currents were observed. They peaked at 0.55 pA at 180 mV, implying a conductance of 0.4 pS, and channels were gated open with a sharp activation above 100 mV. The authors attributed this voltage-gated conductance to the proton (Wagner et al., 1989). Whether this attribution was correct has remained an open question, in particular because proteoliposomes, which contained the purified c-subunit alone, have revealed unspecific cation channels (Schönknecht et al., 1989; for the proton conduction at pH 2 of the purified c-subunit see Schindler and Nelson, 1982).

The lack of information on the number of active F₀ “motors” per membrane area was a major obstacle for obtaining a reliable estimate of its proton conductance. Our recent studies on isolated chromatophore vesicles from the photosynthetic bacterium Rhodobacter capsulatus (Feniouk et al., 2001, 2002) have paved a way to overcome the ambiguity over the proportion of active and inactive F₀. The key was to prepare vesicles of such small size as to contain less than one copy of F₀ on the average. Then, any rapid relaxation of the transmembrane voltage could be attributed to the subset of vesicles containing mainly a single F₀ molecule.

In this work we prepared vesicles with 28-nm mean diameter as checked by transmission electron microscopy (TEM). Excitation of a suspension of such vesicles with a flash of light generated a voltage step across the membrane. The magnitude of the initial voltage jump after a saturating flash of light (70 mV) was calibrated by comparison with electrochromic absorption transients that were induced by submitting vesicles from the same batch to a salt-jump. The relaxation of the voltage was monitored by electrochromic absorption transients of intrinsic carotenoids, and the proton flow by pH-indicating dyes. The relaxation was biphasic. The fast phase (25%) was mediated by F₀ as evident from its sensitivity to the F₀-inhibitor oligomycin. It was mainly attributable to proton conduction in the subset of vesicles containing a single copy of F₀.

MATERIALS AND METHODS

Cell growth and preparation of stock chromatophores

Cells of Rb. capsulatus (wild-type, strain B10) were grown photoheterotrophically on malate as the carbon source at +30°C (Lascelles, 1959) as described elsewhere (Feniouk et al., 2001). The cells were disrupted by sonication with a W-250 Branson Sonifier (Branson, Soest, The Netherlands); the relative power output was set at 35%. The material was exposed to one series of five exposures for 20 s with 1-min incubation on ice in between. Large cell fragments were removed by centrifugation (20,000 × g, 20 min, 4°C). The supernatant was collected and centrifuged again (180,000 × g, 90 min, +4°C). The pellet was resuspended in 20 mM glycylglycine-KOH (pH 7.4), 5 mM MgCl₂, 50 mM KCl, 10% sucrose. It contained chromatophores at a bacteriochlorophyll concentration of 0.3–1.0 mM. These stock chromatophores were stored at −80°C until use. The concentration of bacteriochlorophyll in the samples was determined spectrophotometrically in acetone-methanol extract at 772 nm according to Clayton (1963). The amount of functionally active photosynthetic reaction centers (RCs) was estimated from the extent of flash-induced absorption changes at 603 nm (Mulkidjanian et al., 1991). The above protocol was used throughout the experiments, except for the data shown in Fig. 4 B and Fig. 5, where chromatophores from another stock prepared with a weaker sonifier were used. However, the F₁ depletion was performed in the same way as for the other batches. The smallness of the F₁-depleted vesicles (see below) resulted from the sonication during the F₁ depletion.

FIGURE 4.

Effect of pH on the H/D-isotope effect and on the Arrhenius activation energy of the charge transfer through F₀. (A) H/D isotope effect was calculated as the ratio of the rate constants in H₂O and D₂O (data taken from Fig. 3). (B) The pH-dependence of the Arrhenius activation energy (E_a). Measurements were done in the presence of 3 μM myxothiazol in the temperature interval from 3°C to 40°C. A single experiment was done at pH 9; other points are the average of at least three experiments.

FIGURE 5.

Transient charge transfer through F₀ in the presence of 3 μM myxothiazol as inhibitor of cytochrome-bc₁. (A) Two transients of charge flow through F₀, both electrochromic differences (± oligomycin) as the bottom trace in Fig. 2 B. ○, the transient recorded under excitation with a flash of saturating energy. Noisy line, the transient recorded at attenuated excitation flash energy to produce 33% signal saturation. The extent after the flash was normalized to unity. The insert maps allowed (uncolored) and forbidden (hatched) area in the parameter-field of α and β (see details in the text). (B) The noisy line represents the difference between the original transients shown in A; a histogram of the deviations is shown in the insert. The thick solid line is the same difference calculated according to the model with the parameters α = 0.05, β = 0.71, γ = 10 (other parameters are listed in Table 2; see details in the text). It is consistent with the experimental error of 3%. The dashed curve was calculated with the same set of parameters except that γ = 1, and the dotted curve was calculated for another set of parameters, namely α = 0.1, β = 0.71, and γ = 10.

Preparation of F₁-depleted chromatophores

Chromatophores from the stock were thawed, diluted 25-fold with 1 mM EDTA, and titrated with KOH to pH 8, in daylight (Melandri et al., 1970, 1971; Baccarini-Melandri et al., 1970). The suspension was submitted to another series of sonications (W-250 Branson, relative output 35%), five times for 20 s each with 1-min pausing on ice, and centrifuged at 180,000 × g, 90 min, +4°C. The pellet was resuspended in a medium containing 20 mM glycylglycine-KOH (pH 7.4), 5 mM MgCl₂, 50 mM KCl to yield a bacteriochlorophyll concentration of 0.3–1.0 mM and stored at −80°C until use. For measurements of the pH transients F₁-depleted chromatophores were prepared without glycylglycine-KOH.

Chromatophore size determination by TEM

Chromatophores were suspended in a medium with 100 mM KCl, 20 mM glycylglycine, 5 mM MgCl₂, pH 8.0 to yield a bacteriochlorophyll concentration of 5 μM. A drop of the suspension was applied on the carbon-coated grid, stained with 3% uranyl acetate, washed with water, dried and examined in a Zeiss 902 transmission electron microscope (Carl Zeiss, Oberkochen, Germany). F₁-depleted chromatophores appeared as disks with diameters of 39.7 ± 1.0 nm (SD 7.9 nm; see Results; also see Discussion).

Flash spectrophotometry

The kinetic flash-spectrophotometer was described elsewhere (Feniouk et al., 2001). The bandwidth of the measuring beam, 8 nm, was set by interference optical filters (Schott, Mainz, Germany). Changes in transmitted light intensity (ΔI) were monitored by a photomultiplier (Thorn EMI, 9801B, UK) shielded from the actinic flash with two blue filters (BG 39, 4 mm, Schott). The electrical bandwidth was 3 kHz and the digital time-per-address of the averager was 200 μs. The optical path was 1 cm, both for the exciting and for the measuring beam. The final concentration of bacteriochlorophyll in the cuvette was 8–12 μM.

Transient signals were generated by flashing light at a repetition rate of 0.08 Hz. Eight signals at 522 nm were averaged in recordings of the electrochromism and 32 in measurements with pH indicators. During the dark time (12.5 s) between flashes the electrochromic signal decayed to <5% of its initial value after the flash of light, even if the conductance of F₀ was blocked by oligomycin (not documented). The actinic flashes were provided by a xenon flash lamp (full-width at half-maximum = 10 μs) with a red optical filter (RG 780, Schott); the total energy density on the cuvette (not attenuated) was 12 mJ cm⁻². The peaks of the xenon emission spectrum (e.g., 825 and 875 nm) overlap with regions of low absorption of the chromatophores (their peaks are at 800 and 850 nm). We calculated an effective optical density for the excitation by convoluting the xenon emission and chromatophore absorption. With the highest concentration (12 μM bacteriochlorophyll) in the cuvette it was 0.6 OD, one-half of the value (1.2 OD), which was calculated for the peak absorption at 850 nm. In control experiments with lower bacteriochlorophyll concentration (6 μM), the effective optical density was 0.3, which provided a rather homogenous excitation profile over the thickness of the optical cell. Neutral density filters were used to attenuate the actinic light flash when indicated (see Fig. 5 legend).

Electrochromic carotenoid bandshifts at 522 nm were used as a molecular voltmeter to monitor Δψ (Junge and Witt, 1968; Clark and Jackson, 1981; Symons et al., 1977; Jackson and Crofts, 1971).

Transients of the pH inside chromatophores (ΔpH_in) were monitored by absorption changes of the amphiphilic pH indicator Neutral red at 545 nm as in Ausländer and Junge (1975) and Mulkidjanian and Junge (1994). In these experiments 0.3% BSA was used as an impermeable buffer to quench pH changes in the suspending medium (Ausländer and Junge, 1975). pH transients in the outer medium (ΔpH_out) were monitored by absorption changes of the hydrophilic pH indicator Cresol red at 575 nm (Saphon et al., 1975) and calibrated in pH units. For each pH indicator, control traces without the indicator were recorded and subtracted.

Calibration of the carotenoid bandshift in millivolts of transmembrane electrical potential difference

Chromatophores were suspended in a medium containing 20 mM glycylglycine (pH 8.0), 5 mM MgCl₂, 2 mM NaCN, 3 μM myxothiazol, 3 μM oligomycin, and KCl. The KCl concentration was varied, and NaCl was added to keep the total concentration of KCl+NaCl constant at 250 mM. Valinomycin (1 mM stock solution in EtOH, final concentration in the cuvette 1.6 μM) was added to induce a diffusion potential of K⁺; the resulting absorption transients at 522 nm were recorded in the same instrument used for flash spectrophotometry.

RESULTS

Vesicle diameter and transmembrane voltage of F₁-depleted chromatophores

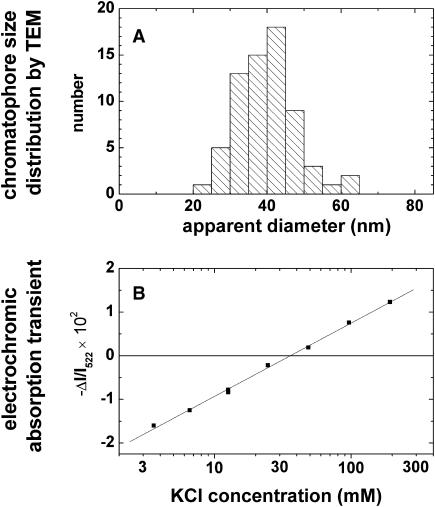
Fig. 1 A shows the size-distribution of F₁-depleted chromatophores as obtained by TEM. The diameter of the circular spots, 39.7 ± 1.0 nm (SD 7.9 nm), was attributable to vesicles that were flattened by drying on the microscope grid. If these were swollen to spherical shape the expected diameter was 28.1 ± 0.7 nm (SD 5.6 nm).

FIGURE 1.

(A) Size distribution of F₁-depleted chromatophores by transmission electron microscopy (TEM). Because of drying on the microscope grid the originally spherical particles appeared as flat disks (see text). (B) Absorption transients attributable to carotenoid bandshifts of electrochromic origin as function of the K⁺ concentration in the suspending medium. These transients were caused by a diffusion potential that was generated by submitting chromatophores to a K⁺-concentration jump in the presence of the K⁺-ionophore valinomycin. F₁-depleted chromatophores (940 μM bacteriochlorophyll) were preincubated with 45 mM KCl, 205 mM NaCl, 5 mM MgCl₂, 20 mM glycylglycine-NaOH, pH 7.9. The final bacteriochlorophyll concentration in the samples was 12 μM.

Fig. 1 B shows the extent of the absorption transients at a wavelength of 522 nm, the peak of the electrochromic transient, as a function of the KCl concentration in the suspending medium. These transients represent the electrochromic response of intrinsic pigments to the diffusion potential of K⁺, which was generated by suspending F₁-depleted and KCl-loaded chromatophores in a KCl-containing buffer and adding the potassium-specific ionophore valinomycin. The photometric response was linearly related to the logarithm of the KCl concentration over two decades. In the experiment documented in Fig. 1 B there was no electrochromic transient induced at a K⁺ concentration of 35 mM. Apparently, 35 mM was the effective concentration of KCl in the chromatophore lumen in this particular experiment. The linear dependence on the ambient KCl concentration was perfectly reproducible, whereas the crossover point and the slope varied slightly between experiments. We took the variation of the intensity jump over one decade of KCl as representing 58 mV, as usual.

If the transmembrane voltage jump was generated by the photosynthetic reaction centers (RCs) in response to a single saturating flash of light, the electrochromic absorption transient was composed of two contributions, one being the response to the delocalized and transmembrane field and the other to the local electric field originating from the oxidized primary electron donor. In the calibration procedure, only the first component had to be considered. We eliminated the delocalized transmembrane component by adding valinomycin, 1 μM, and estimated its magnitude (see Fig. 2). The residual valinomycin-insensitive absorption changes (≈5% of the total flash-induced jump in our sample, see Fig. 2) relaxed in the range of 100 ms, following the reduction of the primary electron donor in the RC. Although the relative extent of this component was only 5% in the samples studied in this work, it can reach 15% if no redox mediator is present in the medium.

FIGURE 2.

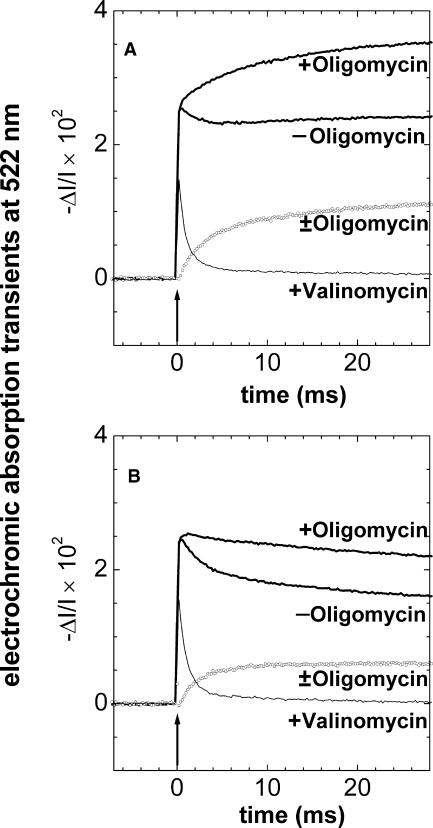
Electrochromic absorption transients at a wavelength of 522 nm in F₁-depleted chromatophores as caused by a short flash of light. The upper traces were obtained without and with blocking of F₀ by 3 μM oligomycin, respectively. The difference trace (± oligomycin) represents the charge flow across F₀ (A) without and (B) with 3 μM myxothiazol added to deactivate the electrogenic and proton pumping activity of the cytochrome bc₁ complex. The actinic flash is indicated by an arrow. The bottom traces were obtained in the presence of 1 μM valinomycin to enhance the ion conductance of all chromatophores in the sample. It was apparent that absorption transients not originating from electrochromism as well as any electrochromic responses to localized electric fields were negligible under our conditions. The suspending medium contained: 100 mM KCl, 5 mM magnesium acetate, 2 mM K₄[Fe(CN)₆], 5 μM 1,1′-dimethylferrocene (DMF), 2 mM KCN, 20 mM glycylglycine-KOH, pH 7.9; chromatophores were added to 12 μM bacteriochlorophyll.

With the above correction, the calibration yielded 70 ± 15 mV for the RC-generated transmembrane voltage jump after a saturating flash of light (seven calibration experiments on three different preparations of F₁-depleted chromatophores).

We estimated the number of RCs in these vesicles. The estimate was based on the voltage of 70 mV, on the usual figure for the specific capacitance of biomembranes, Ĉ = 1 μF cm⁻² (Hille, 1984), and on the mean vesicle radius of 14 nm, as determined by TEM. The capacitor equation reads: n × e_o = A × Ĉ × ΔU, wherein n denotes the number of RCs per vesicle, e_o, the elementary charge, A the vesicle area, and ΔU the transmembrane voltage. We obtained a value of n = 11 as the mean number of RCs in our preparation of F₁-depleted vesicles. This number implied a surface density of 7.3 × 10⁻⁹ mol m⁻², ≈40% larger than the previously determined 5.3 × 10⁻⁹ mol m⁻² (Packham et al., 1978).

Electrochromic absorption transients with and without active cytochrome bc₁ complex

Fig. 2 A shows flash-induced absorption transients at 522 nm in F₁-depleted chromatophores. The rapidly decaying lower traces were obtained with valinomycin. Their decay reveals the magnitude of the electrochromic response to the transmembrane and delocalized electric field. The upper traces were obtained with and without added oligomycin (Linnett and Beechey, 1979) as an inhibitor of proton conduction through F₀. The slowly rising lower traces give the difference between the upper two, corresponding to the cumulative charge flow through F₀. The rise of absorption after the actinic flash was biphasic (see Fig. 2 A, trace with oligomycin added). The sharp (here not time-resolved) increase is attributable to the charge separation in the RC. Its magnitude is fairly independent of pH, redox potential, and temperature (Jackson, 1988). We used the extent of the fast rise to normalize transients that were obtained in different samples. In Fig. 2 A the fast onset was followed by a slowly rising phase. It was attributable to the electrogenic reaction in the cytochrome bc₁ complex (bc₁; Crofts and Wraight, 1983; Jackson, 1988). This slow phase was abolished upon the addition of the bc₁-inhibitor myxothiazol (see Fig. 2 B).

The decay of the electrochromic transient was rapid if F₀ was conducting and slow if it was blocked. The latter proved the low leak conductance of the membrane. A clear-cut interpretation of the difference trace in Fig. 2 A was hampered by the activity of the cytochrome bc₁ complex for two reasons: 1), bc₁ translocates electrons and protons, and thereby generates a transmembrane pH jump in addition to a voltage jump; and 2), the turnover of bc₁ is hindered by a large 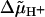. In other words, the turnover of bc₁ is not independent of the presence of the F₀-inhibitor oligomycin. These effects were eliminated by inactivating the bc₁-complex with myxothiazol, which abolished the slow rise of the electrochromic transient as documented in Fig. 2 B. The RCs generated a voltage step of the same magnitude as when bc₁ was active (compare Fig. 2, A and B; also see Mulkidjanian and Junge, 1994). Only in this case does the difference trace (± oligomycin) reflect the relaxation of the transmembrane voltage step in those vesicles that have a single or, in a minor fraction only, several F₀ complexes. Comparison of the relaxation times in Fig. 2, A and B, revealed the systematic error when assessing the voltage relaxation with active bc₁ (the apparent relaxation time was 7–11 ms as compared with 2–4 ms in the presence of myxothiazol). In the first case, F₀ first transferred the protons driven by the RC-generated Δψ and then “waited” for the protons that were ejected by the cytochrome bc₁-complex. The rate of proton transfer through F₀ in the presence of myxothiazol was almost independent of the presence of a penetrating pH-buffer glycylglycine (see Table 1).

TABLE 1.

Apparent relaxation time constants of transmembrane proton flow through F₀ at pH 8 (average values from four different trials)

Experimental conditions	Time constant, ms
Control (no additions)	8.6 ± 1.4
3 μM myxothiazol	3.8 ± 1.1
20 mM glycylglycine, Na2HPO4, MES, glycine each, and 3 μM myxothiazol	3.1 ± 0.9

The medium contained 100 mM KCl, 2 mM KCN, 5 μM 1,1′-dimethylferrocene (DMF), 2 mM K₄[Fe(CN)₆].

To avoid complications coupled with slow proton release from bc₁, all subsequent studies were carried out in the presence of the bc₁-blocker myxothiazol (conditions as in Fig. 2 B). The relative extent of the rapid proton transfer represented the fraction of vesicles containing at least one copy of active F₀. In the preparations used in this work this fraction was 26%. According to Poisson's distribution, ≈22% of total contained a single copy of F₀, and ≈3% two copies.

The discharge time of the vesicles' electric capacitance by F₀ was then apparent as the relaxation time of the difference trace (± oligomycin) as in Fig. 2 B. The alternative interpretation of the biphasic decay of the voltage, the discharge of the membrane's electric capacitance by a voltage-gated channel, was ruled out by the observation of the same biphasic behavior after a lower starting voltage (nonsaturating energy of the exciting flash; see Fig. 3 in Feniouk et al., 2002).

FIGURE 3.

The rate constant of charge flow through F₀ (see Fig. 2 B) as a function of the pH and the isotope composition of the medium (H₂O: ○, D₂O: •). Medium contained 20 mM glycylglycine, 20 mM sodium phosphate, 20 mM 4-morpholinepropanesulfonic acid (MES), 20 mM glycine, 50 mM KCl, 2 mM K₄[Fe(CN)₆], 5 μM DMF, 2 mM KCN, 3 μM myxothiazol. The solid line was calculated by the kinetic model of F₀ conductance as described in the text with the parameters listed in Table 2.

The pH-dependence, H/D-kinetic isotope effect, and Arrhenius activation energy of proton conduction by F₀

Fig. 3 shows the variation of the rate constant of the electric relaxation via F₀ (in the presence of myxothiazol) as function of the pH and the pD. The pD was determined as pH-meter reading plus 0.4 (Glasoe and Long, 1960). Magnesium acetate was omitted from the measuring medium because of precipitation at pH values >8.5. However, up to pH 8.5 the presence of magnesium cations had no detectable effect on the pH-dependence (data not shown). The highest rate constant, 350 s⁻¹, was observed at pH 8. The small variation of the rate in the wide pH range from 6 to 10 was astounding. The rate constant was decreased only threefold at both the acid and alkaline end of the pH range. The H₂O/D₂O-kinetic isotope effect was as large as two at acid pH and decreased to ≈1 above pH 8 (Fig. 4 A). The extent of the charge flow via F₀ was pH-independent within the experimental error (when care was taken to avoid the aging of the preparation). The Arrhenius activation energy of the electric relaxation was 57 ± 4 kJ mol⁻¹ at pH 8, and increased to 72 ± 3 kJ mol⁻¹ upon acidification (Fig. 4 B).

It was noteworthy that the changes of the conductance by 60 min exposure to acid (e.g., pH 5.5) and alkaline pH (pH 10.5) were reversible. The electric relaxation time constant changed by <10% after back-titration into the neutral pH range.

The Ohmic behavior of F₀

The following data on the electric conductance of F₀ were obtained in the presence of myxothiazol, to avoid the complications caused by the electrogenic and proton pumping activity of bc₁. We changed the initial voltage jump by varying the flash energy. With a mean number of RCs per vesicle of 11 (see above) the initial extent of the voltage could be varied over one order of magnitude.

Fig. 5 shows two difference transients (± oligomycin) reflecting the charge transfer through F₀. These transients were obtained at 100% and 33% saturation (judging from the initial extent of the absorption jump at 522 nm), respectively. The extent of the initial step of absorption was normalized. It was obvious that the two transients perfectly superimposed. The transient at nonsaturating flash energy was only discernible by greater noise from the one obtained at saturating flash energy (circles). The relaxation was almost perfectly monoexponential (fit curve not shown in Fig. 5) and independent of the initial voltage jump. The same relaxation time was found when the flash intensity was attenuated to yield 10% saturation (not documented).

The original traces in Fig. 5 were obtained at a bacteriochlorophyll concentration of 12 μM where the effective optical density of the sample in the excitation region was 0.6 (see Materials and Methods). It caused a drop of the flash energy from the entry to the exit of the cuvette (1-cm thickness) from 100% to 25%. This did not matter for the traces with 100% signal saturation, because the flash energy was far-oversaturating, but it did matter for the traces at 33%. In this respect, it was noteworthy that we obtained the same relaxation times both in samples with halved bacteriochlorophyll concentration (6 μM, optical density 0.3, flash energy drop across the cuvette from 100% to 50%) and in samples with 10% saturation. It justified the neglect of the saturation profile in the following interpretation of our data.

The traces at the bottom of Fig. 5 show the difference between the normalized 100% and 33% transients; the deviation between them was very small indeed. Such a voltage-independent relaxation characterizes the discharge of a capacitor (area-specific capacitance = Ĉ/AsV⁻¹ m⁻²) by an Ohmic resistor (area-specific conductance = Ĝ/AV⁻¹ m⁻²). It yields a voltage-independent relaxation time, τ = Ĉ/Ĝ. F₀ behaved as an Ohmic resistor, and it showed no voltage-gating.

The rapid relaxation of the voltage (relaxation time = ≈2.9 ms at pH 8; see Fig. 3) was only observed in the small subset of vesicles containing F₀ (26% of total). The electric capacitance of vesicles Ĉ was calculated by their size using the usual figure for biological membranes, 1 μF cm⁻² (Hille, 1984). The conductance of F₀, g, was calculated according to g = A × Ĝ with Ĝ = Ĉ/τ. Herein A denotes the vesicle area, τ the electric relaxation time, and Ĝ and Ĉ are the area-specific conductance and electric capacitance of the membrane, respectively.

The shortest relaxation time observed, 2.3 ms, gave rise to a calculated conductance of 10.5 fS. It implied the transport of 6500 protons/s at 100-mV steady driving force or of 13,000/s at 200 mV.

It was noteworthy that the proton-transporting properties of the Rb. capsulatus F₀ were robust against the changes of the concentration of K⁺, Na⁺, Cl⁻, of various permeating and nonpermeating buffers, and redox mediators (not documented).

The proton specificity of F₀

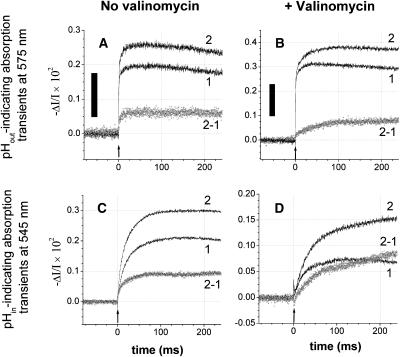
We complemented measurements of the electric relaxation with measurements of the pH transients in both phases—the suspending medium (hydrophilic indicator Cresol red, wavelength 575 nm) and the interior of chromatophores (amphiphilic indicator Neutral red, 545 nm, with BSA as a nonpermeating buffer). The results are documented in Fig. 6. The data were obtained with active bc₁, to demonstrate the proton uptake from the bulk medium by the RC and by bc₁ (Fig. 5, A and B) and the proton release into the interior of chromatophores by bc₁ (Fig. 5, C and D). The alkalization of the bulk and the acidification of the interior were fully apparent when F₀ was blocked by oligomycin (traces 2), and both were diminished when F₀ was conducting (traces 1). The respective difference traces gave the F₀-related pH-relaxation, however, with somewhat distorted kinetics because of the slow proton-pumping activity of bc₁ (see above discussion in the context of Fig. 2, A and B). Ignoring the complex kinetics of these difference transients, they proved that the major ion transported by F₀ was the proton at an ambient pH 7.9 against a background of 100 mM KCl. Similar results were observed with NaCl and LiCl (data not shown). In other words, the proton selectivity of F₀ was at least 10⁷.

FIGURE 6.

Proton transfer through F₀ as monitored by two pH indicators reporting pH transients from either side of the chromatophore membrane, (A, B) from the n-side (Cresol red, 90 μM, at a wavelength of 575 nm), and (C, D) from the p-side (Neutral red, 26 μM plus 0.3% w/v BSA, at 545 nm). Traces in parts A and C were recorded in the absence, and traces B and D in the presence of the ionophore valinomycin (2 μM). In the latter case the transmembrane voltage was collapsed by the valinomycin-mediated K⁺ current in <3 ms (see Fig. 2). The relaxation of the pH difference was then entirely due to the entropic driving force (ΔpH). The proton release from bc₁ was slower in the presence of valinomycin (compare to traces 2 in Figs. 6 C and 5 D). The medium contained 50 mM KCl, 5 mM MgCl₂, 2 mM K₄[Fe(CN)₆], 2 mM KCN, 5 μM dMF; pH was 7.9. Chromatophore stock was in 5 mM MgCl₂, 50 mM KCl, 10% sucrose. Traces 1 without, and traces 2 with 3 μM oligomycin added; traces 2-1 = difference trace ± oligomycin. Actinic flashes are marked by arrows; black bars correspond to 0.002 pH units.

ΔpH as the only driving force for proton transport: further evidence for the absence of voltage-gating

Dimroth and co-workers have recently shown that the operation in the synthesis direction of both the Na⁺-ATP synthase of P. modestum and the H⁺-ATP synthase of E. coli cannot be driven by an ion gradient alone but requires a transmembrane voltage exceeding a certain threshold (Kaim and Dimroth, 1998b, 1999; Dimroth et al., 2000). This paralleled the previous observation of a voltage threshold of the (oxidized) chloroplast enzyme (Junge, 1970; Junge et al., 1970; Gräber et al., 1977; Witt et al., 1977; Schlodder and Witt, 1980), which could be replaced by chemical driving force, ΔpH (Schlodder and Witt, 1981; Schlodder et al., 1982). The latter now seems controversial. The data in Fig. 5, B and D, clearly showed that proton-transfer through F₀ driven by a pH difference persisted, even after the electric potential difference was dissipated in <1 ms by the addition of valinomycin. There was no voltage requirement and no threshold for proton conduction by F₀ itself. This was in line with the above observation of the same electric relaxation time observed with 100%, 33%, and 10% of the initial voltage.

It was obvious that F₀ was not, by itself, voltage-gated. The observed electrical gating in the intact enzymes from E. coli and P. modestum was likely attributable to the interaction of F₁ with F₀.

A kinetic model for proton conduction by F₀

We investigated whether the magnitude, the Ohmic behavior, and the weak pH-dependence of proton conduction by F₀ could be accommodated within the framework of the presently assumed rotary mechanism of proton conduction (Junge et al., 1997; Elston et al., 1998). The proton transfer through the bare chloroplast F₀ has been explained elsewhere by a model where two proton-conducting half-channels were connected by a (horizontally) rotating carrier (see Fig. 7 A for an illustration). The fit of experimental data yielded a low pK of 5–6 for the proton-accepting group of the input half-channel and an alkaline pK of 8 for the output group (Cherepanov et al., 1999). The weak pH-dependence between these two pK values follows from this model. The proton-transfer rate is determined by the probability of proton binding to group A and proton release from group B. When the ambient pH inside and outside are the same, as in our experiments, the product probability is constant in this interval. This feature explained the observed weak pH-dependence of proton transfer through the bare F₀. In energized membranes, on the other hand, the pK values of the relay groups tend to match the ambient pH at the p- and n-sides of the coupling membrane. This allows higher turnover numbers of F₀ even against backpressure (Cherepanov et al., 1999).

FIGURE 7.

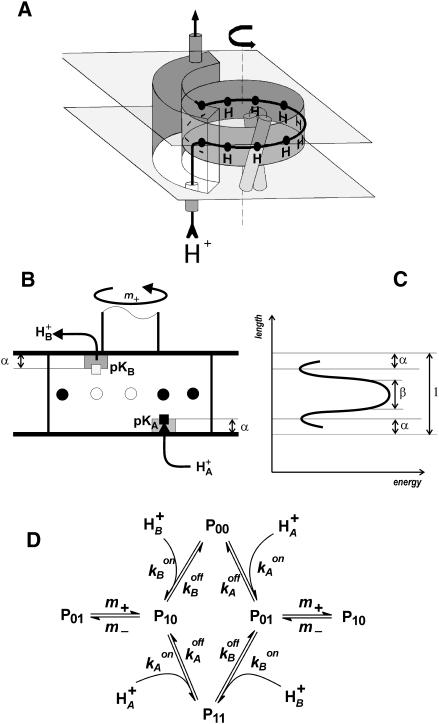
Functional model of F₀. (A) Schematic illustration of F₀ operation. (B) Simple model for proton transfer; see text for details. (C) Hypothetical energy profile for proton transfer; see text for details. (D) Kinetic scheme.

In an extension of the previous model (Cherepanov et al., 1999), we assumed here that the pK values of the input and output groups, located within the dielectric inside noncoaxial proton-conducting half-channels as illustrated in Fig. 7 B, are sensitive to the membrane voltage in proportion to their (dielectrically weighted) z-position in the membrane dielectric. The respective potential profile of proton transfer is schematically shown in Fig. 7 C.

The main elements of the model were two noncoaxial proton-conducting half-channels both considered to rapidly equilibrate with their adjacent bulk phase. In the simplest case, each half-channel contained only one proton-binding relay group (A at the acidic side of the membrane and B at the basic side). In the absence of a transmembrane voltage, the rate of proton binding to the groups A and B was assumed to depend on the pH in the respective bulk phase in accordance with the equations

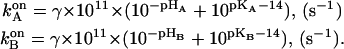The first term in each equation denotes the proton flux owing to the diffusion of H₃O⁺ ions and the second term describes the hydrolysis of neutral water (see Eigen, 1963). The factor γ was introduced to account for the accelerated proton supply from surface buffering groups. The addition of penetrating pH buffer—glycylglycine was tested at concentration up to 0.02 M—caused no further acceleration of proton transfer through F₀; see Table 1. This implies a rapid proton delivery along the inner chromatophore surface to F₀ from many ionizable groups acting as proton antennae. (See e.g., Zhang and Unwin, 2002, for a quantitative examination of surface proton conduction.) The estimate of γ was obtained by considering the strictly Ohmic behavior of F₀ with accuracy >3% (See Fig. 4). Because the overall rate of proton transfer through F₀ after a saturating flash was ≈ 3.5 × 10³ s⁻¹ (see above), the linear relationship implied that at neutral pH the rate constant 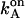(which was independent of 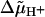) was >10⁵ s⁻¹, which corresponds to the γ-factor >10 (see also the discussion below). We used the latter value of γ in the modeling.

The rate constants of the reverse reactions (see the kinetic scheme in Fig. 7 D) were calculated by the thermodynamic equilibria of

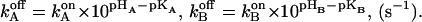The rate of proton exchange between F₀ and the bulk solutions was high and not limiting to the overall reaction rate. The forward and reverse rate constants of the proton transfer in the middle of membrane (m₊ and m₋) were interconnected by the thermodynamic constraint of

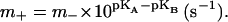Thus, there were only three independent kinetic parameters in the model: the pK values of buffer groups in each of the two half-channels, and the rate constant of the elementary rotary step (the rotation of the c_n-ring by the angle 2π/n), which brings one proton into and another one off the ring in contact with its respective access channel.

The potential energy of a transferred proton within F₀ is schematically plotted in Fig. 7 C. The transmembrane electric field affects both the protonation state of the two relay groups (A and B) in the two half-channels, and the rate of proton transfer over the center of the membrane. The magnitude of the first effect depends on the (dielectrically weighted) relative depth of groups A and B in the membrane (denoted α in Fig. 7 C, L is the full and 1 the relative thickness of the membrane). The second effect depends on the effective width of the barrier, denoted β in Fig. 7 C. The absolute height of the barrier is not important, if it is much greater than the thermal energy k_BT.

A step of the transmembrane electric potential, magnitude ϕ (in Volts, positive at the A-side) shifts the pK values as

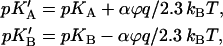where q is the charge of proton. The electric field also changes the proton transfer rate across the middle of the membrane, which is treated by the Nernst-Planck model according to Hladky (1974) as

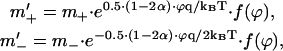where the function F(ϕ) depends on the shape of potential barrier, which for a rectangular profile is

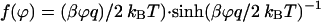(see e.g., Bihler and Stark, 1997, for details). The kinetic model shown in Fig. 7 B gives rise to a system of four differential equations. Three equations describe the changes of the population of the various states of the enzyme as

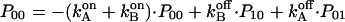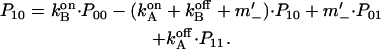These three differential equations have to be completed by the normalizing condition

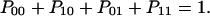P_ij denotes the probability of protonation (index 1) and deprotonation (index 0) of the relay groups in contact with the left (left index) and the right (right index) access channel.

The fourth differential equation describes the membrane recharging

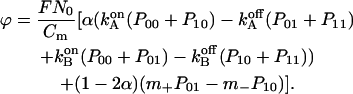The solution of this system of four differential equations was obtained by numerical integration.

Herein F denotes the Faraday constant, N₀ the surface density of F₀ in the membrane (mol m⁻²), and C_m the electric capacitance of membrane (F m⁻²). Because the average diameter of chromatophores was ≈28 nm and they contained a mean of ≈0.3 copies of F₀ per vesicle, the mean surface density of F₀ in vesicles, which contained enzyme N₀, was ≈6.6 × 10⁻¹⁰ mol m⁻². The membrane's specific capacitance was taken as 10⁻² F m⁻². On modeling we took a value of 70 mV for the average Δψ jump in response to a single saturating flash with the blocked bc₁ complex. The fit parameters pK_A, pK_B, and m₊ were determined from the pH-dependence of the F₀ conductance by nonlinear minimization. The final set of model parameters is summarized in Table 2. The resulting theoretical pH-dependence of the proton transfer rate in H₂O is plotted in Fig. 3 by the solid line. The obtained values pK_A = 6.1, pK_B = 10.0, and m₊ = 1 × 10⁷ s⁻¹ corresponded to the overall F₀ turnover rate .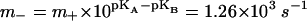

TABLE 2.

The kinetic and geometric fit parameters to the data in Fig. 3 by the model illustrated in Fig. 7

pKA	pKB	m+	α	β	γ
6.1	10.0	1.0×107 s−1	≤0.08	≥0.6	10

Fig. 5 A shows the normalized transients of the transmembrane voltage at pH 8.0 after a saturating (100%) and an attenuated (33%) flash, the difference between them is plotted in Fig. 5 B by the thin noisy line. This difference, which is very small, characterizes the deviation from the Ohmic behavior. The insert to Fig. 5 B shows the distribution of the deviation between two traces, which did not reveal a systematic bias from zero. The calculated mean root-square dispersion of the difference was 3%.

The high signal/noise ratio of the traces allowed us to impose constraints on the possible values of the parameters a, b, and γ. Generally, the greater was α and the smaller β, the faster was proton transfer at a given value of the transmembrane voltage, so the relaxation dynamics was faster after saturating and slower after nonsaturating flashes (positive nonlinearity). The effect of the parameter γ was opposite: because the diffusion of protons outside F₀ was voltage-independent, the proton diffusion at small values of γ slowed down the overall proton transfer (diffusional control of the reaction) and caused thereby a negative nonlinearity in the relaxation kinetics.

The dashed curve in Fig. 5 B shows the difference between the transmembrane voltage decay after a saturating and an attenuated flash calculated with the parameter γ = 1. This curve revealed a substantial deviation from the Ohmic behavior, which exceeded the experimental error. The minimal value of γ consistent with the experimental data was ≈10, and this value was used in the following modeling.

The dotted curve in Fig. 5 B was calculated for a set of parameters α = 0.1, β = 0.8, and γ = 10. It illustrates the positive nonlinearity in the relaxation owing to the accelerating effect by the transmembrane voltage. The deviation again exceeded the experimental error, but had the opposite sign.

We calculated the membrane discharge dynamics after saturating and attenuated flashes using the kinetic model described above and determined the range of possible values of α and β consistent with an experimental error of <3%. Generally the relaxation rate was 10-fold more sensitive to the variation of α (the buried position of groups A and B inside the membrane) than to the variation of β (the form of the potential barrier in the middle of the membrane). In the two-dimensional phase space (α and β correspond to the abscissa and ordinate axes of the insert to Fig. 5 A, respectively) we determined the area where the maximal deviation between the discharge curves after saturating and attenuated flashes was being <3% consistent with the experimental error. The allowed space found by this method is shown in the insert to Fig. 5 A by the uncolored upper-left area, and the forbidden area inconsistent with the experimental data is hatched. An example of the calculated difference between two recharging traces with the maximal deviation of 3% is shown in Fig. 5 B by the thick dashed line (the parameters chosen were α = 0.04, β = 0.64, and γ = 10).

In practice, these findings implied that both proton-conducting groups A and B were placed at the membrane/water interface. The dielectrically weighted distance between them had to be >0.86 (the maximal allowed value of α is 0.07). This maximal value of α corresponded, however, to an infinitely sharp rectangular barrier in the middle of the membrane (β = 1), physically unfeasible. A realistic value of β is 0.6; it corresponds to an upper limit of α of ≈0.04. It is worth noting, however, that the positive nonlinearity of the electric field inside the membrane could be partially compensated by the negative nonlinearity of the voltage-independent diffusion outside the membrane, so we used the value α = 0.07 as an estimate of the buried position of groups A and B inside the membrane. If the dielectric permittivity was constant over the full width of the membrane, say of 4 nm, the topological distance between A and B would be >3.4 nm. The dielectric permittivity of the water-filled cavities in membrane proteins may, however, strongly differ from that in the membrane interior (see, e.g., a value of 30 in the ubiquinone binding pocket of bacterial reaction center versus the value of 4 in the middle of membrane; Cherepanov et al., 2000). In this case, the distance between groups can be substantially smaller, on the order of 1.8 nm (45% of the geometrical membrane thickness). It was obvious though, that if either group was embedded more deeply in the membrane dielectric, one had to expect a marked deviation from an Ohmic behavior.

Our analysis reveals that the proton transfer to the conserved carboxyl residue of subunit c, which is topologically located in the middle of the membrane, is mediated by at least two residues located close to the membrane surface. It remains open how this finding relates to the recent Cys-mapping experiments of Angevine and Fillingame (2003), which led these authors to postulate two water-accessible half-channels in the F₀F₁-ATP synthase of E. coli. The relay groups A and B may be found among those residues lining these half-channels.

DISCUSSION

The Ohmic conductance of F₀, its pH-dependence, kinetic H/D-isotope effect, and the absence of voltage-gating

In F₀F₁-ATP synthase the membrane-embedded F₀ portion conducts protons, and thereby it generates torque for the synthesis of ATP by the F₁ portion. We studied proton conduction by F₀ in chromatophores isolated from the purple bacterium Rb. capsulatus. Rapidly rising voltage and/or pH steps were generated by a flash of light. The subsequent electric relaxation and the pH relaxation mediated by F₀ were detected by absorption transients of intrinsic (electrochromic) pigments and of added pH-indicating dyes, respectively. The vesicle size was so small that vesicles contained less than a single conducting F₀ molecule on the average, namely 0.3. This was apparent from the fact that the electrochemical relaxation was rapid only in a subset of vesicles (26%); see Fig. 2. It was straightforwardly interpreted in terms of a Poisson distribution of F₀ over vesicles with a mean of 0.3 and a frequency of 22% vesicles containing one and 3% containing two copies of F₀. This notion was corroborated by the observation that the relative magnitude of the rapid relaxation was larger in a preparation of chromatophores with larger radius (see Feniouk et al., 2002, and the text relating to Fig. 2 A of this article). When the small contribution of vesicles containing more than one single copy of F₀ was neglected, we determined a unitary conductance of 10.5 fS for the bacterial F₀, which was equivalent to the translocation of 6500 H⁺/s at 100-mV driving force.

In our related previous studies the average number of F₀ per vesicle was also small but larger than in this work (Feniouk et al., 2002). Those particular preparations were, however, prepared with a sonifier of smaller output power (Branson W-15, Soest, The Netherlands). The average diameter of the chromatophores used in the previous work determined by TEM was 62.8 nm (data not shown), 1.6-fold larger than that of the F₁-depleted ones used here (see Fig. 1 A). The larger chromatophores contained approximately one copy of F₀F₁ on the average, in good correspondence with the F₀ mean surface density calculated here.

We found that the electric relaxation through F₀ was almost mono-exponential and that the relaxation time was practically independent of the magnitude of the initial voltage step up to 70 mV. F₀ behaved as an Ohmic conductor with a linear current-voltage relationship. There was no voltage-gating of F₀. The conductance varied little (less than threefold) as function of the pH over the wide range from 6 to 10. The specificity for protons over other cationic species was very high (>10⁷).

There was no kinetic H/D-isotope effect at pH above 8, and an isotope effect of ≈2 was observed at pH 6 (Fig. 4 A). The appearance of the isotope effect could be attributed to protonation of a group with the apparent pK of 7–8. A possible candidate for this titratable group might be Glu⁶¹ of the c-subunit. The pK of its counterpart in the E. coli enzyme (cAsp⁶¹) has the apparent pK of 8 (Valiyaveetil et al., 2002). An alternative explanation could be secondary isotope effects: the general conformation of the enzyme might be slightly altered by pH, and the H/D-isotope effect could be inherent to the acidic conformation only. In this case a smooth pH-dependence of the H/D isotope effect like that in Fig. 4 A could be expected. The pH-dependence of both the isotope effect and the Arrhenius activation energy (Fig. 4 B) points out that the rate-limiting step of proton transport through F₀ is different at pH 6 and 8. Further experiments are necessary to clarify this point.

The above properties of the bacterial F₀—the high specificity, the weak pH-dependence, and the kinetic isotope effect—were in a good agreement with those of the chloroplast counterpart, where data were obtained over a narrower pH interval, of 5.5 < pH < 8. (Althoff et al., 1989). The very high proton specificity of F₀ was attributable to proton binding by acid/base group(s) as selectivity filter. It excluded models with a contiguous water-wire without such groups. The same property favored a Grotthuss-type mechanism of proton transport, and it excluded the self-diffusion of the proton in the form of H₃O⁺ or OH⁻.

These properties of F₀ were simulated based on the current rotary mechanism with the multicopy c-ring carrying one essential acid residue (Glu or Asp) in the middle of the membrane and with one access channel at each side. We assumed one proton relay group in each channel. The fit to the data attributed pK values of ≈6 and ≈10, respectively, to these relay groups because of the low dependence on the pH. The Ohmic behavior called for a location of the relays very close to their respective membrane/bulk interface. F₀ conducted protons irrespective of the nature of the driving force, whether of electric (transmembrane voltage) or entropic origin (pH difference): Both this property and the Ohmic behavior under an electric driving force proved the absence of voltage gating of F₀. The -gating of the coupled enzyme in chloroplasts (Junge, 1970, 1987; Junge et al., 1970; Gräber et al., 1977; Witt et al., 1977; Schlodder and Witt, 1980, 1981; Schlodder et al., 1982) and the voltage-gating in E. coli and P. modestum (Kaim and Dimroth, 1998a, 1999; Dimroth et al., 2000) is attributable to the interaction of F₁ with F₀, but not to F₀ proper.

The straightforward method used to obtain the unitary conductance of one single copy of F₀ in this work resolved the discrepancy between previous reports from our lab. In studies with spinach thylakoids we arrived at a similar magnitude for the conductance (9 fS) under the then-unproven assumption that any exposed F₀ was conducting (Schönknecht et al., 1986). Circumstantial evidence for only a minority of conducting F₀, which had led us to claim a much higher conductance of up to 1 pS (Lill et al., 1986; Althoff et al., 1989), can now be rejected. It also appears conceivable that the similarly high conductance of 0.4 pS as attributed to whole F₀F₁ in one study with bilayers formed by the dip-stick technique (Wagner et al., 1989) might have involved unspecific cation channels as observed with the purified subunit c of F₀ (Schönknecht et al., 1989).

Extrapolating the data in this work on F₀ to a driving force of 200 mV (nearly sufficient for the maximum rate of ATP synthesis by the coupled enzyme), one expects a transport rate by F₀ of 13,000 s⁻¹. ATP synthesis by the E. coli enzyme can reach a turnover number of 270 s⁻¹ (Etzold et al., 1997), with coupled ATP hydrolysis in Rhodospirillum rubrum at 320 s⁻¹ (Slooten and Nuyten, 1984), and ATP synthesis in Rb. capsulatus at 250 s⁻¹ (calculated from 900 μmol/mg BChl·h, Casadio et al., 1978, if there was one ATPase per 1000 BChl; Packham et al., 1978; Feniouk et al., 2002, and with a proton/ATP stoichiometry of 3.3). Taking the proton/ATP stoichiometry into account, which is probably 3.3 for yeast F_oF₁ (Stock et al., 1999) and 4 (van Walraven et al., 1996; Turina et al., 2003) or 4.7 (Seelert et al., 2000) for spinacia, these figures imply the turnover of only ≈1000 H⁺/s by the coupled enzyme, F₀F₁. This is one order-of-magnitude lower than that of the exposed F₀.

Comparison with the proton conductance of gramicidin

Gramicidin is perhaps the best studied cation channel and proton conductor. It is gated open when its two half-spanning helices join tail-to-tail to fully span the membrane. Cations are conducted along and with the internal water wire. This is well established by studies on electro-osmosis and streaming potentials. The proton, on the other hand, bypasses the single-file transport (see Finkelstein and Andersen, 1981; Levitt et al., 1978; for molecular dynamics simulation see (Skerra and Brickmann, 1987; Schumaker et al., 2000). The proton conductance of the covalently linked gramicidin A channels is proportional to the H⁺ concentration in the pH range from 0 to 4 (Cukierman, 2000). Extrapolation to pH 8 yields a H⁺ conductance of 1 fS, 10-fold smaller than the H⁺ conductance of F₀. In simulating the data on F₀ we had to assume that the supply of protins to F₀ was not rate-limiting, i.e., it was by order-of-magnitude faster than expected by bulk diffusion from a half-space to the channel mouth. It implied supply from several buffering groups at the membrane surface acting as proton donors. Recently, the lateral diffusion coefficient along the lipid/water interface has been determined to be 5.8 × 10⁻⁹ m² s⁻¹ (Serowy et al., 2003), only twofold lower than in the bulk (9.3 × 10⁻⁹ m² s⁻¹), but greater than for any other ion in the bulk phase and thus compatible with a Grotthuss-mechanism involving surface water (see Gutman and Nachliel, 1997). Proton supply in the alkaline range is not critical, because water then acts as the proton donor (see Kasianowicz et al., 1987; Gopta et al., 1999). These features have been considered in the above simulation.

CONCLUSIONS

The membrane portion, F₀, of the F₀F₁-ATP synthase is a ion-driven rotary engine. For the first time, its unitary electric conductance was determined without ambiguity concerning active and inactive copies of F₀. We used F₁-depleted chromatophore vesicles from Rb. capsulatus that were so small as to contain only 0.3 copies of F₀ on the average. The conductance was constant as function of the voltage, extremely proton-specific (>10⁷), but only mildly pH-dependent. The maximum conductance of 10.5 fS was observed at pH 8 implying the translocation of 6500 H⁺ s⁻¹ at 100-mV electric driving force and 13,000 at 200 mV. Hence, F₀, when operating without F₁, turns over >10-fold faster than it does in the coupled enzyme, F₀F₁. In other words, F₀ is not rate-limiting for the operation of F₀F₁, as technically desirable. We found that F₀, by itself, was not voltage-gated. The observed electrical gating in the intact enzymes from P. modestum and E. coli was likely attributable to the interaction of F₁ with F₀. The nature of the gating charge/dipole is still unknown.

In F₀ the selectivity filter for protons over other cations is highly specific, >10⁷, both in the purple bacterium used in this work and in thylakoids from green plants, as previously studied. The selectivity is still present but less pronounced in organisms that operate on Na⁺ instead of H⁺.

We interpreted the properties of F₀ in terms of the current rotary model for proton conduction. This model is based on two proton-conducting half-channels linking the rotating ring of 10–14 copies of subunit c with the respective bulk phases. The observed Ohmic conduction implies that the relay groups for protons that are involved in rate limitation sample only a small fraction of the transmembrane voltage. We simulated such a behavior by two relay groups located close to the respective membrane/water interfaces. The slight variation of the conductance as function of the pH implied a large difference between the pKs of these groups (≈6 and ≈10, respectively). This is a testable prediction for structural studies aiming at high resolution of the c-ring and its partners in the membrane, the a- and b-subunits. That the proton conductance of F₀ was not limited by the supply of protons to the entrance channel implied supply from buffers at the membrane surface and from bulk water.

APPENDIX

The proton buffering capacity of chromatophores

If the electrical and chemical components of 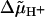, Δψ and ΔpH, were discharged via F₀ in isolation of each other, we observed different relaxation times (see Fig. 5). This phenomenon has been previously observed in studies on chloroplast F₀ in spinach thylakoids (Schönknecht et al., 1986) and has been interpreted as follows (Junge et al., 1992a,b). If Δψ is the major driving force of proton conduction, one observes the discharge of the electric capacitance (C_el), whereas the chemical capacitance (C_chem) of vesicles is discharged if ΔpH is the major driving force. Presenting both in the same physical dimensions, namely Farad × m⁻², C_chem is related to the specific proton buffering capacity of the vesicle, 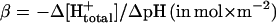as

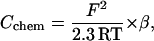wherein F denotes the Faraday constant, R the gas constant, T the temperature, and β the specific buffering capacity, as defined above.

We described the proton flux through F₀ by a two-step sequential kinetic mechanism: A → B → C. The first step was the proton release by the bc₁ complex (in the presence of valinomycin, its relaxation time was 37 ± 1 ms as detected by Neutral red, see Fig. 6 D). The second step (occurring with the unknown time τ₂) was the proton entry/escape through F₀. The overall rate of pH transients, as measured both by Cresol red outside and by Neutral red inside chromatophores, was characterized by the summed time τ₁ + τ₂ = 52 ± 5 ms. The proper time of ΔpH relaxation τ₂ was estimated thereby as 15 ± 5 ms. This implied that the proton buffering capacitance of the vesicles at pH 8.0 was ≈3.5-fold greater than the electrical one. Taking the electric capacitance of 1 μF cm⁻², we calculated the specific proton buffering capacitance of the internal surface of chromatophores β = 2.1(±0.7) × 10⁻⁸ mol m⁻². Because the surface density of RC in chromatophores is ≈5.3 × 10⁻⁹ mol m⁻² (Packham et al., 1978), this value corresponds to eight buffer groups with pK = 8 per RC. Assuming that all electron equivalents, which were generated by the excited RCs after a saturating light flash were completely utilized by the bc₁ complexes, we calculated a pH jump per saturating flash of 0.36 pH units. This estimate is in the range of earlier ones, as obtained with 9-aminoacridine as a pH dye for chromatophores of Rb. sphaeroides (0.32 pH unit; Saphon and Gräber, 1978) and with Neutral red for chromatophores of Rb. capsulatus (0.8 ± 0.2 pH unit; Mulkidjanian and Junge, 1994). The flash-induced pH jump in bacterial chromatophores is by one order-of-magnitude greater than in thylakoid membranes of green plants (0.06 units; Hong and Junge, 1983; Junge et al., 1979). The difference could be attributed to the lower density of proton pumps and larger amount of pH-buffering groups in thylakoids as compared to the situation in bacterial chromatophores.