Database-Derived Potentials Dependent on Protein Size for In Silico Folding and Design

Abstract

Knowledge-based potentials are widely used in simulations of protein folding, structure prediction, and protein design. Their advantages include limited computational requirements and the ability to deal with low-resolution protein models compatible with long-scale simulations. Their drawbacks comprehend their dependence on specific features of the dataset from which they are derived, such as the size of the proteins it contains, and their physical meaning is still a subject of debate. We address these issues by probing the theoretical validity of these potentials as mean-force potentials that take the solvent implicitly into account and involve entropic contributions due to atomic degrees of freedom and solvation. The dependence on the size of the system is checked on distance-dependent amino acid pair potentials, derived from six protein structure sets containing proteins of increasing length N. For large inter-residue distances, they are found to display the theoretically predicted 1/N behavior weighted by a factor depending on the boundaries and the compressibility of the system. For short distances, different trends are observed according to the nature of the residue pairs and their ability to form, for example, electrostatic, cation-π or π−π interactions, or hydrophobic packing. The results of this analysis are used to devise a novel protein size-dependent distance potential, which displays an improved performance in discriminating native sequence-structure matches among decoy models.

INTRODUCTION

A wide range of methods have been developed in view of predicting the folding, structure, and stability of proteins from their amino acid sequence and conversely, with significant but limited success (for reviews, see e.g., Takada, 1999; Hansmann and Okamoto, 1999; Moult et al., 2001; Bonneau and Baker, 2001; Al-Lazikani et al., 2001; Shea and Brooks, 2001; Guerois and Serrano, 2001; Gilis et al., 2001; Dehouck et al., 2002; Hardin et al., 2002). The performance of these methods heavily relies on the adequacy of the energy functions used to evaluate sequence-structure compatibility. Although the interactions ruling protein folding and stability are known in principle, the challenge resides mainly in the complexity of the systems and the huge number of their possible conformations.

Two main types of energy functions have been explored in the context of in silico protein studies. Semiempirical potentials are derived from analytical expressions, describing the different interactions encountered in proteins, whose parameters are obtained by fitting experimental data on small molecules and/or from quantum mechanical calculations (Halgren, 1995; Moult, 1997; Lazaridis and Karplus, 2000). They present the incontestable advantage of corresponding to well-defined interactions, with a clear physical basis. Delicate aspects of this approach include the parameterization of the functions and the inclusion of solvent and other entropic effects. The use of such potentials is generally very expensive in terms of computer time, as they require a full atomic protein representation and, preferentially, explicit solvent molecules.

An attractive alternative is provided by statistical or knowledge-based potentials, derived from datasets of known protein structures. They can be easily adapted to simplified protein models, taking the solvent implicitly into account and including some entropic contributions (Sippl, 1995; Jernigan and Bahar, 1996; Moult, 1997; Lazaridis and Karplus, 2000). However, their physical significance is less straightforward, basically because they are mean-force potentials, usually residue-based, in which different kinds of atom-atom interactions and entropic effects are mixed. These potentials are either obtained by optimization of the parameters of a predefined analytical form by requiring them to yield a large energy gap between the native and unfolded states (e.g., Crippen, 1991; Goldstein et al., 1992; Mirny and Shakhnovich, 1996; Tobi et al., 2000; Vendruscolo et al., 2000), or derived from observed frequencies of association of specific sequence and structure elements (e.g., Tanaka and Scheraga, 1976; Miyazawa and Jernigan, 1985; Kang et al., 1993; Kocher et al., 1994; Sippl, 1995; Simons et al., 1997; Melo and Feytmans, 1997; Lu et al., 2003). Energy functions describing different types of interactions are obtained according to the kind of structure elements considered, the assumptions made, and the reference state used (Godzik et al., 1995; Du et al., 1998; Rooman and Gilis, 1998).

When this approach is performed in a statistical mechanics framework, the frequencies of sequence and structure elements in native proteins can be related to Helmholtz free energies. The formalism underlying this relation has repeatedly been investigated and questioned (Rooman and Wodak, 1995; Thomas and Dill, 1996; Bahar and Jernigan, 1997; Rooman and Gilis, 1998; Zhang and Skolnick, 1998; Furuichi and Koehl, 1998; Koppensteiner and Sippl, 1998; Shan and Zhou, 2000; Russ and Ranganathan, 2002). Indeed, it relies on approximations whose incidence on the extracted potentials is difficult to estimate. Among these is the assumption that structural elements, such as inter-residue distances or torsion angles, follow a Boltzmann-type distribution in native proteins (Janin et al., 1978; Miller et al., 1987), and the approximation of expressing the folding free energy as a sum of (pairwise) free energies.

Another controversial aspect resides is what may be called the memory of the potentials on the dataset from which they are extracted. The influence of the length of the dataset proteins is a particularly delicate issue. On the one hand, two-dimensional lattice simulations of pseudoproteins composed of two types of residues (hydrophobic and polar) indicated that pair energies, derived from a dataset containing large chains, are shifted compared to those derived from small chains (Thomas and Dill, 1996). In the same line of thought, a scaling factor inversely proportional to the number of residues has been introduced in contact potentials with reduced amino acid encoding, to account for the variation in the number of contacts in proteins of different sizes (Hardin et al., 2000). On the other hand, contact potentials extracted from datasets including real proteins of different sizes showed no significant dependence on protein length (Bahar and Jernigan, 1997). Protein size dependence also appeared to be negligible for interactions between residues separated by <∼10 Å (Furuichi and Koehl, 1998), and for a special kind of pair potentials in which the implicit effect of the solvent is eliminated (Vijayakumar and Zhou, 2000). Other analyzes led to less clearcut conclusions—in particular, that distance-dependent pair potentials derived from datasets composed of small or large proteins are highly correlated, but that the slope of the regression line is different from 1 (Rooman and Gilis, 1998).

In light of these apparent contradictions, we further investigate the statistical mechanical background of pair potentials and their dependence on the size of the proteins from which they are derived. Such potentials have already been extensively studied on simple nonprotein systems. In particular, it was shown that for finite systems of N particles, the pair distribution functions present a 1/N correction for large inter-residue distances, which is especially significant in compressible systems or systems with boundaries (Hill, 1956; Lebowitz, 1960; Lebowitz and Percus, 1961). When mean-force potentials are derived from real proteins, another type of size effect arises, since some properties of native proteins, such as their stability or their secondary structure content, may depend on their size. The interior-exterior partitioning of amino acids plays a major role at this level (Thomas and Dill, 1996; Janin, 1979). For example, two hydrophobic residues separated by a distance of 20 Å in a small protein will most likely be at its surface, which is very unfavorable for them, whereas they can be buried in a large protein. A potential derived on small proteins will thus be different from that derived on large proteins. We analyze here in detail the dependence of the short- and long-range components of pair potentials. Finally, we propose a solution to generate potentials that adapt to the size of the protein on which they are applied.

FORMALISM AND METHODS

Knowledge-based mean-force potentials

We first recall briefly the statistical mechanics derivation of mean-force potentials and apply them to proteins, before tackling their dependence on the size of the systems. In an isotropic fluid-like system of volume V containing N particles at temperature T, the mean-force potential w⁽²⁾(r₁,r₂) acting on the two particles located at r₁ and r₂ is defined as (Hill, 1956)

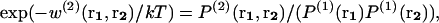(1)

where k is the Boltzmann constant. 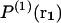denotes the probability of finding a given particle at position r₁, and 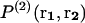the joint probability of finding a particle at position r₁ and another at position r₂. These probabilities are expressed as a function of the potential energy U and the partition function Z as

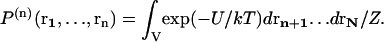(2)

It is straightforward to see that w⁽²⁾ is a potential of mean force. Indeed,

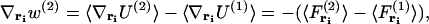(3)

where 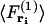is the force acting on a particle at r_i averaged over the configurations of the N−1 other particles of the system, and 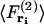is the force acting on a particle at r_i, knowing that there is a particle at r_j (with j ≠ i), averaged over the configurations of the N−2 others. The mean-force potential w⁽²⁾ has the nature of a free energy because of the statistical averaging. In the case of an independent distribution, we have 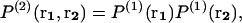and 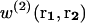vanishes.

When different types of particles s_i coexist in the same system, Eqs. 1–3 need to be generalized. The mean-force potential 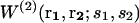acting on the particles of type s₁ and s₂ located at r₁ and r₂ is then given by Hill (1956) as

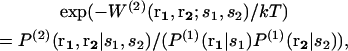(4)

where 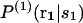is the conditional probability of finding a given particle of type s₁ at a given position r₁ and 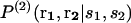the conditional probability of finding a given particle of type s₁ at position r₁ and a given particle of type s₂ at position r₂. The difference ΔW⁽²⁾ between the mean-force potentials W⁽²⁾ and w⁽²⁾

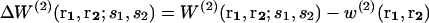(5)

measures the mean-force potential in a system containing several types of particles compared to a reference system with only one type of particles. For isotropic fluid-like systems, ΔW⁽²⁾ is direction-independent and relies only on the distance between r₁ and r₂.

Usually, mean-force potentials W⁽ⁿ⁾ and w⁽ⁿ⁾ describing the simultaneous interaction of n particles can, to a good approximation, be expressed in terms of pair potentials. In particular, the difference in mean-force potential ΔW⁽ⁿ⁾, which takes n particles explicitly into account and averages over the N−n others, can be approximated as the sum of all possible pairwise mean-force potential differences ΔW⁽²⁾,

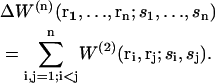(6)

To obtain this relation, the superposition approximation is used, which consists of assuming that the probability P⁽ⁿ⁾ of finding n particles in a given configuration r₁, r₂, … ,r_n is proportional to the product of all possible pairwise probabilities P⁽²⁾.

In the case of proteins, s₁ and s₂ are amino acid types separated by the spatial distance r₁₂; the primary structure is overlooked and the solvent molecules are not taken into account explicitly, they are included in the statistical averaging. The reference state mean-force potential w⁽²⁾ can be considered as representing an average, nonspecific, globular state with nondifferentiated amino acids, and can be taken to model the denatured state. ΔW⁽²⁾ represents thus the folding free energy. It can be evaluated from the relative frequencies F(r₁₂) of arbitrary amino acid pairs separated by a distance comprised between r₁₂ and r₁₂ + Δr₁₂ in native protein structures, and from the corresponding relative frequencies F(r₁₂|s₁,s₂) of specific amino acid pairs. Indeed, assuming the system to be fluid-like and isotropic and overlooking any dependence on the specific positions r₁ and r₂, we obtain the relations

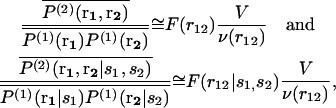(7)

where the average is over all positions r₁ and r₂ such that |r₁₂| = r₁₂; v(r₁₂) is the volume of the shell of inner radius r₁₂ and outer radius r₁₂ + Δr₁₂. For systems without boundaries, 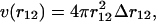whereas for systems with boundaries such as proteins the shell is incomplete when approaching these boundaries. Proteins can indeed be viewed as systems with boundaries when the solvent molecules are not taken into account explicitly. The volume accessible to residues located at a distance between r₁₂ and 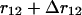from a given residue is thus equal to 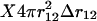on the average, where X depends on r₁₂ but also on the shape of the protein and is comprised between 0 and 1. If we assume that the proteins are spheres of radii R, which is a relatively good approximation in the case of globular proteins, a straightforward calculation shows that

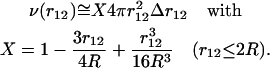(8)

Finally we find, using Eqs. 1, 4, 5, 7, that ΔW⁽²⁾ can be approximated as

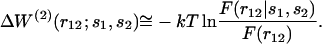(9)

In principle, the frequencies should be computed from systems containing exactly N particles. This is not feasible in proteins, where N is relatively small, especially considering the 20 different amino acid types. Therefore, the frequencies are computed from a set containing several native protein structures of different N.

In practice, the inter-residue distances r₁₂ are computed between average side-chain centroids, noted C^μ. These centroids correspond to the geometric center of heavy side-chain atoms of a given amino acid type, averaged over all side-chain conformations in a dataset of known structures (Kocher et al., 1994); the C^μ pseudoatoms thus have a well-defined position for each amino acid type, which means that side-chain degrees of freedom are neglected. Distances are divided into bins of 0.2 Å width. To smooth the potentials, the frequencies computed for each distance bin are combined with those computed for the 10 neighboring bins on both sides, weighted by a factor inversely proportional to their separation with respect to the central bin (Kocher et al., 1994). Residue pairs separated by <15 residues along the chain are overlooked to minimize the effect of the constraint induced by the polypeptide chain. This effect is indeed important for sequence separations of <∼10 residues and then strongly decreases. Furthermore, potentials for r₁₂ values between 3 and 8 Å are qualified as short range, and those for r₁₂ values >15 Å as long range. The choice of these cutoffs is based on the observations that, on the one hand, the predictive power of distance potentials increases only slightly for distances >8–10 Å (Furuichi and Koehl, 1998; Melo et al., 2002) and that, on the other hand, the correlation length of mean-force pair potentials is ∼15 Å (Bahar and Jernigan, 1997).

Size dependence at large distances

It has been shown (Lebowitz and Percus, 1961; Hill, 1956) that when the distance r between two particles tends to infinity, in a system of volume V containing N identical particles, the probability P⁽²⁾ goes like

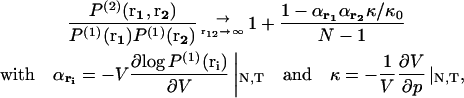(10)

where κ is the isothermal compressibility, κ₀ the compressibility in an ideal gas, and p the pressure. For a uniform fluid-like system without boundaries, 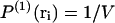and α_ri = 1. In this case, Eq. 8 means that for an ideal gas the probability of finding two particles far apart is equal to 1/V², whereas it is smaller than 1/V² for a system more compressible than an ideal gas and larger than 1/V² for a system less compressible than an ideal gas. In the case of a system with boundaries, there are additional corrections encoded in α_ri (Lebowitz, 1960; Lebowitz and Percus, 1961).

Equation 10 can be easily generalized to systems containing N particles of different types. We find

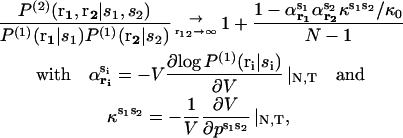(11)

where p^s₁s₂ is the specific pressure due to the particles of types s₁ and s₂ and κ^s₁s₂ the corresponding compressibility.

In proteins, which can be considered as having water-induced boundaries, the asymptotic behaviors (Eqs. 10–11) can be approximated in terms of frequencies of amino acid pairs, using Eq. 7, as

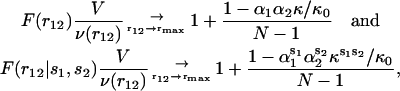(12)

where r_max denotes large distances that do not exceed the protein diameter, and α_i and 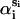correspond to α_ri and 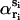values averaged over possible r_i positions. In the protein core, assuming a uniform distribution of the amino acids, α_ri is approximately equal to 1, whereas it can be different from 1 near the boundaries, because of the spatial extent of the amino acids and the departure from spherical shape. In contrast, 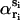usually also differs from 1 in the protein interior, because of the nonuniform distribution of specific amino acid types. Furthermore, the relative compressibility κ/κ₀ is expected to be smaller than 1, due to the close packing of the residues and the repulsive interatomic forces at short distances. As for κ^s₁s₂/κ₀, it should be larger than κ/κ₀ for amino acid pairs having the tendency of being buried in the protein interior, and smaller than κ/κ₀ for hydrophilic pairs. The volume V is set equal to N times the mean volume per residue, which is estimated to be 190 ų by computing the volumes of different proteins with the SurVol program (Alard, 1991).

Protein structure datasets

The database used in this study for deriving the potentials consists of 735 high-resolution (≤2 Å) x-ray structures of protein chain with <20% sequence identity. They were extracted from the website “Culling the PDB by Resolution and Sequence Identity” (the new version of this server can be found at the address: http://www.fccc.edu/research/labs/dunbrack/pisces/culledpdb.html) (Wang and Dunbrack, 2003). Note that when a chain is part of a multichain protein, only residue pairs in which at least one of the residues belongs to the considered chain are taken into account in the derivation of the short-range potentials, but the size is defined by the total number of residues of the whole protein.

The structure dataset was divided into six nonoverlapping subsets that include approximately the same number of residues, but contain proteins of increasing sizes. Details on the complete dataset, noted 𝒟ℬ₀, and on the six subsets, noted 𝒟ℬ_i with i from 1 to 6, are given in Table 1. The number of subsets was chosen so as to maximize the range of protein sizes without introducing too much noise in the potentials due to sparse data. Another way of dividing the dataset would be to construct subsets including the same total number of residue pairs rather than the same number of residues. However, this alternative definition entails two problems: the subset including small proteins covers a much wider range of protein sizes while the subset including large proteins contains only a few proteins. Although the same general trends can be observed, the results are less significant (data not shown), due to the high level of noise in the potentials derived from the set of large proteins and to the lack of differentiation between small- and medium-sized proteins.

TABLE 1.

Characteristics of the datasets

Dataset	𝒟ℬ0	𝒟ℬ1	𝒟ℬ2	𝒟ℬ3	𝒟ℬ4	𝒟ℬ5	𝒟ℬ6
Number of proteins	735	243	137	116	86	80	73
Neff (short range)	603	146	257	344	476	700	1475
Neff (long range)	1890	160	259	348	481	709	2448

𝒟ℬ₀ represents the whole dataset and 𝒟ℬ_i, with 1 ≤ i ≤ 6, the different subsets. N^eff is the effective number of residues of the proteins included in each set, computed using Eq. 13.

Since these subsets contain proteins of similar but different sizes, we need to define an effective number of residues, noted N^eff, for each dataset. The choice of a relevant definition of N^eff is delicate: theoretically, its value depends indeed on both r₁₂ and (s₁,s₂). As a first approximation, we can, however, average over all (s₁,s₂) pairs, the relative frequencies F(s₁,s₂) being rather well conserved between proteins of different sizes. We may thus define the effective number of residues for a given protein set 𝒟ℬ as a linear combination of the number of residues (N) of all proteins included in the dataset as

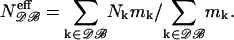(13)

The weighting factor m_k corresponds to the number of residue pairs in protein k, which are taken into account while deriving the potentials; this number is different for short- and long-range interactions. The computed N^eff values, for each dataset, are given in Table 1.

Performances of the potentials

To assess the performances of the potentials, we evaluate their ability of singling out the native sequence-structure match out of a set of 1000 decoy models, obtained by maintaining the structure and randomizing the amino acid sequence with fixed amino acid composition. Note that we keep the amino acid composition conserved upon randomization because folding free energies are defined with respect to a reference (unfolded) state which is, according to the approximations used, identical for sequences with the same amino acid composition (Rooman and Wodak, 1995).

The chosen performance measure is the energy Z-score,

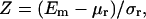(14)

where E_m is the energy computed on the correct sequence-structure association, and μ_r and σ_r are the average and standard deviation of the distribution of energies computed on the decoy models. This procedure is repeated with each protein of 𝒟ℬ₀.

The jackknife procedure is applied when comparing the performances of the potentials derived from 𝒟ℬ₀ with those derived from 𝒟ℬ_i; that is, we remove the tested protein from the datasets before deriving the potentials. We did not apply this procedure when comparing the performance of the potentials derived from 𝒟ℬ₀ with and without the corrections for protein size, since recalculating the corrective functions for each test case is too computer time-consuming. This should not have any significant effect as both types of potentials are extracted from the same dataset, and as we focus only on their relative performances.

Note that there are several reasons that led us to prefer decoy models build by shuffling the amino acid sequence of a fixed protein structure, over those obtained by maintaining the sequence and modifying the conformation. Firstly, the use of decoys with altered structures offers limited possibilities of comparative tests on proteins of different sizes. Most available sets of alternative structures, obtained by various types of simulation or modeling approaches, have indeed been designed on the basis of small proteins (see for instance Park and Levitt, 1996; Samudrala et al., 1999; Tsai et al., 2003). Considering substructures of larger known folds, as used in threading procedures, suffers from a similar shortcoming: long sequences can only be compared with a very limited number of conformations. Secondly, structural modification usually affects the compactness of the protein, and the ability of energy functions to enumerate inter-residue contacts might in some cases overrule the evaluation of the specificity of these contacts. In contrast, sequence shuffling appears as a convenient way to produce different sets of specific amino acid interactions, while keeping the global distribution of inter-residue distances (mostly) fixed. It presents the advantage of being equally applicable to small and large proteins and has been shown to be slightly more efficient than structural modification in assessing the performances of distance-dependent statistical potentials (Melo et al., 2002).

RESULTS

General size dependence

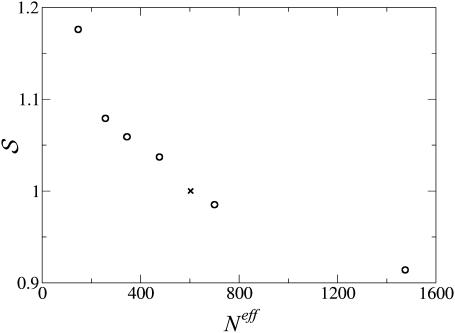
To probe the dependence of distance potentials on the size of the proteins from which they are derived, we used six subsets characterized by increasing protein sizes (see Formalism and Methods). The short-range distance potentials derived from each subset were compared to those derived from the complete dataset. A very good correlation between these potentials was found, with linear correlation coefficients between 0.92 and 0.96. However, the slope of the regression line decreases from >1.15 to ∼0.9, when the protein sizes increase from ∼150 to 1500 (Fig. 1). Note that the potentials derived from the complete dataset 𝒟ℬ₀ behave approximately as if they were derived from proteins of size equal to N^eff (𝒟ℬ₀), which confirms our definition of N^eff (Eq. 13).

FIGURE 1.

S as a function of the average number of residues in each subset (N^eff). S is the slope of the regression line obtained by plotting the values of the short-range potentials derived from each protein subset 𝒟ℬ_i against those derived from the complete set 𝒟ℬ₀. The X symbol marks the coordinates (603,1) corresponding to the regression 𝒟ℬ₀ vs. 𝒟ℬ₀.

The observed variation of the slope means that the absolute values of the interaction free energies are, on average, smaller when derived from a set of larger proteins. It denotes, to a certain extent, that larger proteins can tolerate higher levels of frustration. This general trend, which has already been noted in a previous study (Rooman and Gilis, 1998), is to be related to the more extended core of large proteins and to the inhomogeneous partitioning of hydrophobic and hydrophilic residues between the surface and the core of the proteins. A more detailed interpretation of this effect is given in the following section.

This result suggests that overlooking the dependence on protein size might be a relatively good approximation when focusing on a single protein or considering similar-sized proteins, but not when comparing proteins of different sizes.

Size dependence for specific residue pairs

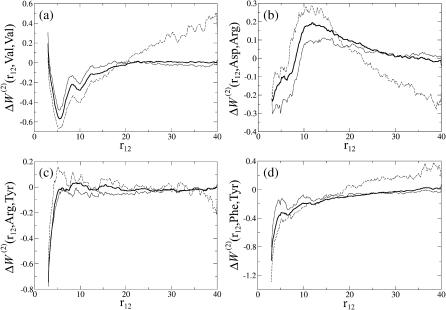
Although the correlation between potentials derived from proteins of different sizes is quite high, different behaviors are observed when considering each amino acid pair separately. A few examples are displayed in Fig. 2.

FIGURE 2.

The mean-force potential 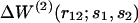as a function of r₁₂, for various amino acid pairs (s₁,s₂). The potentials derived from the whole dataset (𝒟ℬ₀) are depicted by bold curves; the dashed and continuous thin curves delineate those derived from the set of small (𝒟ℬ₁) and large (𝒟ℬ₆) proteins, respectively. (a) Val-Val; (b) Asp-Arg; (c) Arg-Tyr; and (d) Phe-Tyr.

The Val-Val free energy profile (Fig. 2 a) is characteristic of most hydrophobic pairs: it presents a deep minimum at short distance followed by a second minimum, reflecting the close packing of hydrophobic residues in the protein interior. The second minimum is similar to that observed in ordinary liquids and means that the configuration with two hydrophobic residues separated by a third (hydrophobic) residue is also favorable. However, the minima are more pronounced for small than for large proteins. At the origin of this phenomenon is the surrounding presence of water, that induces an inhomogeneous partition of amino acids between the protein surface and the protein core. As a result, the hydrophobic cores of the proteins become less and less hydrophobic when we consider proteins of increasing sizes. Indeed, the smaller surface/volume ratio is not (or only partially) compensated by variations in the amino acid composition. For example, valines represent 6.8% of all residues and buried valines 10.9% of all buried residues in 𝒟ℬ₁, while these values are 7.4% and 9.5%, respectively, in 𝒟ℬ₆. Since the majority of short-range interactions are established between core residues, this decrease in the concentration of hydrophobic residues in the protein core generates short-range potentials that are computed as less favorable in the case of hydrophobic pairs.

Another noticeable feature of these curves is the sudden variation in free energy for distances close to the average protein diameter (which is ∼20 Å for the subset including small proteins and >40 Å for the subset including large proteins as well as for the whole dataset): two residues separated by such a distance are very likely to be situated near the surface, which is quite unfavorable in the case of hydrophobic residues.

Oppositely charged residue pairs are represented here by the Asp-Arg profile (Fig. 2 b). In this case, the energy is negative at very short distances, which results from the favorable electrostatic interaction energy upon formation of a salt bridge. The free energy becomes positive after 10 Å, due to the energetic cost of burying individual charged residues. In the case of small proteins, the energy becomes favorable again at distances >20 Å, as both residues become accessible to the solvent. Protein size has here an opposite effect than in the case of hydrophobic residues: the energy minimum at short distances is deeper, and the energy maximum at medium distances is less pronounced for large than for small residues. This effect is mainly due to an increase in the proportion of buried hydrophilic residues.

Another way to understand the effect of protein size is to consider that larger proteins can tolerate higher levels of frustration. Such frustration results at least in part from the necessity to accommodate similar fractions of hydrophilic and hydrophobic residues in a protein that contains a more extended hydrophobic core. As a consequence, the potentials between hydrophobic (hydrophilic) residues are computed as less (more) favorable in large proteins. The general size dependence depicted above is explained by the fact that, in addition to specific interactions that can be either favorable or not, a significant contribution to the potentials comes implicitly from the presence of water and is favorable between hydrophobic residues and unfavorable between hydrophilic residues. Therefore, increasing protein size results on average in a decrease, in absolute value, of the computed interaction free energies.

These examples clearly show that database-derived potentials are mean-force potentials, including a coupling between different types of interactions. Indeed, we would not expect a “true” Asp-Arg potential to be unfavorable at distances between 10 and 20 Å. Similarly, the favorable “interaction” energy displayed here by hydrophobic residues reflects implicitly the fact that they avoid contact with water molecules. This kind of coupling has sometimes been invoked to demonstrate that statistical potentials are not valid (Thomas and Dill, 1996). We do not agree with this statement, in accord with several authors (Moult, 1997; Koppensteiner and Sippl, 1998; Shan and Zhou, 2000). Statistical potentials do not try to mimic the potential energy U, but correspond to statistical averages of these potentials, as visible in Eqs. 2 and 3. They define a limited set of mean-force energy functions that embody the complex ensemble of interactions ruling protein folding and stability.

Fig. 2, c and d, show two other types of interactions and dependencies on protein size. The Arg-Tyr profile (Fig. 2 c) presents a very deep minimum at very short distances. This minimum reflects the favorable nature of cation-π interactions between an aromatic ring (here of Tyr) and a positive charge (here carried by Arg) located above it (Ma and Dougherty, 1997). The free energy essentially vanishes for all distances >5–6 Å. More precisely, it remains slightly negative in large proteins and has a positive maximum near 5–6 Å for small proteins. These somewhat different behaviors are probably due to the competing individual tendencies of Tyr and Arg: the former is hydrophobic and likes to be packed in the protein interior whereas the latter prefers to be at the surface.

The Phe-Tyr energy profile (Fig. 2 d) shows a free energy minimum at short distances, reflecting the favorable interaction free energy between aromatic side chains. Note that, as side-chain degrees of freedom are neglected, the energies of the conformations in which the aromatic moieties are parallel (π−π stacking) or orthogonal (T-shaped conformation) are mixed. The free energy increases for distances >5–6 Å but remains slightly negative, because the hydrophobic nature of aromatic residues renders their burial in the protein core favorable. In this distance range the dependence on protein size therefore resembles that of hydrophobic residues.

Size dependence for large inter-residue distances

The size effects determining the long-range behavior of the sequence-specific and nonspecific potentials can be investigated with the help of Eq. 12. The correlation length of mean-force potentials is in general larger than that of ordinary potentials (e.g., a value of 7.0 Å is commonly used with Lennard-Jones potentials). For example, in the case of lattice systems with an attractive nearest-neighbor potential, the mean-force potential has a second minimum for particles separated by one lattice site. In proteins, the correlation length is observed to be ∼15 Å (Bahar and Jernigan, 1997). Hence, the condition r₁₂→ r_max is taken here to be fulfilled when r₁₂ > 15 Å (without exceeding the protein diameter).

To check the predicted behavior of F(r₁₂) V/v(r₁₂) as a function of 1/(N^eff−1) (see Eq. 12), we computed it, from each 𝒟ℬ_i, for r₁₂ values equal to 15, 20, 25, and 30 Å (with Δr₁₂ = 1 Å). To limit the errors due to v(r₁₂), proteins with a radius of gyration deviating by >10% from that corresponding to a perfect sphere were excluded. Some other proteins had to be excluded for being too small, when considering large r₁₂ values. Strikingly, the theoretically derived relation is rather well verified for proteins. Indeed, the linear correlation coefficients range from −0.67 for r₁₂ = 15 Å to −0.96 for r₁₂ = 25 Å. Moreover, the regression lines have intercepts close to unity (between 0.95 and 1.07). The slopes vary from −5.2 (r₁₂ = 15 Å) to −19.8 (r₁₂ = 30 Å), and the factor α₁α₂ κ/κ₀ representing the compressibility and boundaries of the system increases thus from 6.2 at r₁₂ = 15 Å to 20.8 at r₁₂ = 30 Å. The dependence of α_i on r₁₂ is due to the fact that it corresponds to averages of α_ri over different positions r_i (see Eqs. 11 and 12) and that the proportion of residues close to the boundary increases with r₁₂. On the other hand, the departure from the spherical shape used to compute v(r₁₂) is likely to result in an overestimation of V/v(r₁₂) at large distances that do not exceed the protein diameter, and therefore in a larger effective α₁α₂κ/κ₀ value. The magnitude of this effect is also likely to depend on r₁₂.

For the sequence-specific potentials 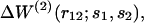the imprecision issue on v(r₁₂) vanishes. Eq. 12 then becomes

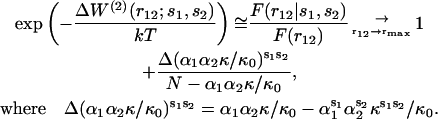(15)

To maintain a reasonable signal/noise ratio, given the 210 amino acids pairs, we compute frequencies over all bins corresponding to distances >15 Å. In Fig. 3, F(r₁₂|s₁,s₂)/F(r₁₂) with r₁₂ > 15 Å, is plotted as a function of 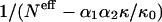for a few pairs (s₁,s₂). A remarkable qualitative agreement with the theoretical relationship is observed: in all cases the dependence on 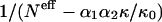is linear, with a very good correlation and an intercept close to unity.

FIGURE 3.

The frequency ratio F(r₁₂|s₁,s₂)/F(r₁₂), extracted from the subsets 𝒟ℬ_i with r₁₂ > 15 Å, as a function of 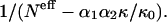On the basis of the observed long-range behavior of the nonspecific potential, α₁α₂ κ/κ₀ is taken to be 15. The imprecision of this value is not very important, since α₁α₂ κ/κ₀ is small in regard with N^eff.

According to Eq. 15, the slopes of these lines correspond to Δ(α₁α₂ κ/κ₀)^s₁s₂. Hydrophobic pairs are expected to be more compressible than the average, and indeed display a negative slope (e.g., Δ(α₁α₂ κ/κ₀)^Val,Val = −26). In contrast, Δ(α₁α₂ κ/κ₀)^s₁s₂ values are positive when considering pairs of charged residues (e.g., Δ(α₁α₂ κ/κ₀)^Asp,Arg = 12). It is, however, interesting to note that oppositely charged residues are only slightly more compressible than equally charged residues, because the dominating effect is that charged residues like to be in contact with water molecules, and thus to be situated at the surface. The excess in the number of charged residue pairs at long distance appears thus to result mostly from the partitioning of hydrophobic and hydrophilic residues between the surface and the protein core, and to a lesser extent from specific short-range interactions.

Size-dependent distance potentials

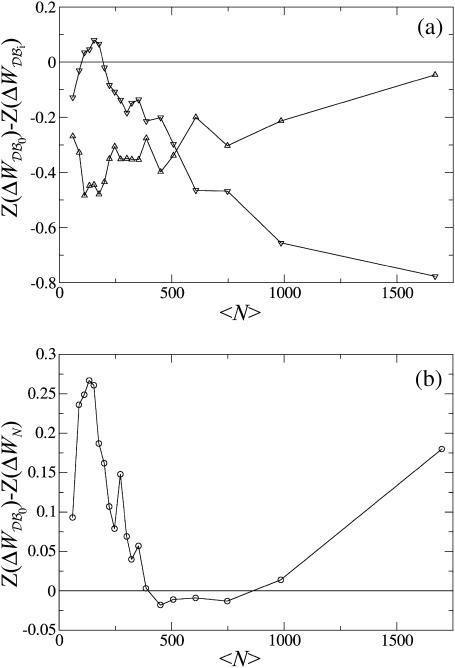
The results obtained in the previous sections indicate that the dependence of knowledge-based potentials on the size of the proteins from which they are derived is specific to each amino acid pair and may be quite important. A straightforward solution to this problem is to define several datasets 𝒟ℬ_i, each including only proteins whose sizes are similar to the size of the protein studied, and to derive mean-force potentials 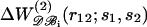on each of these subsets. However, this solution has the drawback that the potentials corresponding to protein subsets are generally much more noisy than those corresponding to the whole dataset; this is visible in Fig. 2 but is even more problematic for seldom-seen residue pairs. This drawback entails that the performance of such potentials is not better than that of the potentials derived from the whole dataset. In particular, we analyzed their relative performances in discriminating correct sequence-structure associations out of sets of decoy models (see Formalism and Methods). As expected (Furuichi and Koehl, 1998; Melo et al., 2002), we found that the potentials derived from subsets of proteins of similar size perform better on proteins of such size than on proteins of other sizes (Fig. 4 a). However, they yield poorer discrimination on proteins of any size than the potential derived from the whole dataset. The only exception is the potential derived from the subset including the smallest proteins, which performs slightly better over a limited range of protein sizes.

FIGURE 4.

Relative performances of different pair potentials ΔW as a function of the average number of residues in the test proteins. The discriminative power of potential ΔW is monitored by the Z-score Z(ΔW) (see Eq. 14). A positive value of the difference Z(ΔW_x)−Z(ΔW_y) means that ΔW_y performs better than ΔW_x. Each plotted value corresponds to an average over 35 proteins of similar sizes. (a) Comparison of the efficiency of the potentials derived from subsets of the database 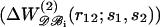and from the complete dataset 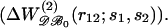Overall, the potentials derived from small (ΔW_𝒟ℬ1, ▿) and large (ΔW_𝒟ℬ6, ▵) proteins are less effective than ΔW_𝒟ℬ0. (b) Comparison of the performance of the size-corrected potentials ( 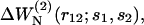see Eq. 16) and those derived from the complete dataset 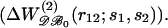ΔW_N is globally more efficient than ΔW_𝒟ℬ0, especially when applied to small or large proteins.

We thus propose an alternative solution, based on the observation that, for short inter-residue distances, the general shape of the pair energy profile is usually conserved when derived from proteins with varying sizes. This leads us to devise a procedure where the interaction energy corresponding to a given protein size is expressed as a simple function of the energy derived from the whole dataset and of the number of residues of the target protein. This procedure allows us to take into account protein length while still keeping the advantages of a large dataset.

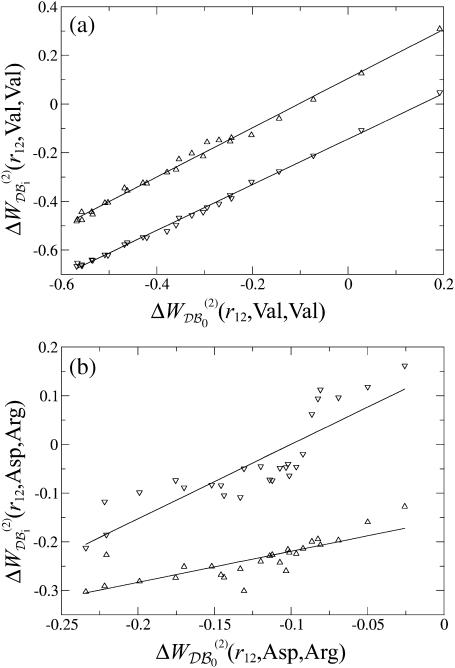
As illustrated in Fig. 5 for Asp-Arg and Val-Val, the correlation between the free energy values corresponding to different protein sizes described above for all amino acid types taken together still holds, to a good extent, when focusing on a single amino acid pair. The free energy corresponding to a given protein size N, which is estimated by 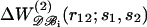for 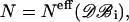can thus be approximated by 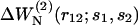defined as

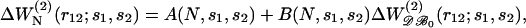(16)

where r₁₂ is restricted to values comprised between 3 and 8 Å, because the shapes of the energy profiles are more variable for larger inter-residue distances. We found that for many pairs, A(N,s₁,s₂) and B(N,s₁,s₂) can be expressed as 1/N series truncated at the second order,

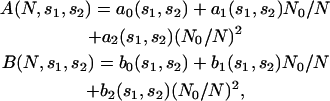(17)

where N₀ = 603 is the effective number of residues of the proteins included in 𝒟ℬ₀ (see Eq. 13). The parameters a_i(s₁,s₂) and b_i(s₁,s₂) are obtained by least-square fittings, so as to minimize the difference between 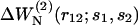and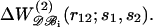

FIGURE 5.

Pair potential 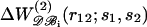derived from the subsets 𝒟ℬ₁ (▿) and 𝒟ℬ₆ (▵) versus the potential derived from the whole database. The regression lines are depicted. (a) Val-Val pair; the correlation coefficients are >0.99 (b) Asp-Arg pair; the correlation coefficients are comprised between 0.80 and 0.98.

For some pairs, however, the absence of a significant dependence of the potential on protein size or high noise levels in the curves, in particular for the less frequent amino acids, leads to unreliable A(N,s₁,s₂) and B(N,s₁,s₂) functions. Therefore, to avoid any artificial N-dependence, we chose to keep only the most efficient corrective functions. To identify these, we evaluated the average quadratic errors q_i as

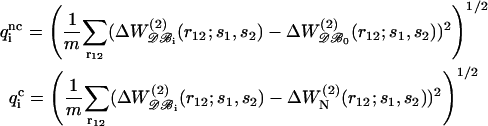(18)

where the sums extend over the m distance bins r₁₂, and 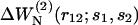is defined in Eq. 16, with 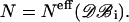To be considered reliable, the corrective functions associated with a given amino acid pair must fulfill the following conditions: 1), 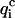< 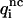for at least four of the six subsets 𝒟ℬ_i and 2), 〈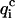〉, the value of 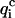averaged over all subsets 𝒟ℬ_i, must be <0.8 × 〈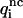〉. The corrective functions corresponding to the Cys-Cys pair were also excluded for being strongly affected by the large variations in Cys composition in small proteins. Within these constraints, 108 out of 210 pair potentials are successfully corrected. For the others, the direct use of 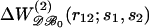is preferred over the application of corrective functions suspected to be unreliable. The parameters of 10 of the most efficient corrective functions are given in Table 2. The complete set of corrective functions is available as Supplementary Material.

TABLE 2.

Parameters of 10 of the most efficient corrective functions A(N,s₁,s₂) and B(N,s₁,s₂)

Amino acid pair	a0	a1	a2	b0	b1	b2
Val-Val	0.153	−0.134	0.015	1.033	−0.011	−0.003
Phe-Ile	0.357	−0.327	0.062	1.321	−0.379	0.096
Leu-Val	0.144	−0.131	0.016	1.032	−0.044	0.011
Ile-Val	0.116	−0.076	0.005	1.004	0.019	−0.008
Ile-Ile	0.241	−0.276	0.064	1.184	−0.364	0.107
Gly-Ser	−0.041	0.028	0.007	1.004	0.106	−0.026
Phe-Val	0.211	−0.135	0.017	1.134	0.029	−0.007
Ala-Val	0.055	−0.064	0.007	0.946	0.059	−0.007
Leu-Trp	0.105	−0.096	0.011	0.940	0.031	0.006
Pro-Ser	−0.110	0.120	−0.017	0.614	0.394	−0.050

These functions, defined by Eqs. 16–17, allow us to express the pair potential corresponding to a given protein size as a function of the pair potential derived from the complete dataset.

To compare the performances of the size-corrected potentials with the original ones, we evaluated their ability to discriminate correct sequence-structure associations from large decoy sets of incorrect ones (see Formalism and Methods). We found that these potentials lead, on average, to a sizable improvement of the performances (Fig. 4 b). More precisely, the corrected potentials always perform better than the usual potentials except when applied to proteins whose size is close to the average size of the proteins in the full dataset—in the latter case, the introduction of corrective functions is obviously unnecessary. We may hence conclude that, overall, our novel potential is quite successful in extracting pertinent information on the influence of protein size, without being corrupted by the higher noise levels in the subset-derived potentials.

As discussed above, an important part of the dependence on protein size can be accounted for by a global scaling factor of the potentials, and does not have any influence on the computed Z-scores since we compare native proteins with decoys models of the same length. The observed improvement of the performances must therefore be imputed solely to the amino acid-specific part of the size corrections. Size-dependent potentials can thus be expected to outperform ordinary potentials even more markedly in studies that compare proteins of various sizes.

DISCUSSION

Database-derived mean-force potentials are widely used in the field of protein structure prediction and design. They are able to deal with simplified representations of protein structures, with the uncontestable advantage of limiting calculation times. It can moreover been argued that such simplified representations reflect a certain reality of protein folding. Indeed, since the high folding rates prevent exhaustive conformational searches, protein residues probably do not “see” the full atomic details of the other residues in their vicinity, but are more likely simply “aware” of atom groups or complete amino acids, at least in the first stages of the folding process until a compact low-resolution or molten globule-like structure is reached.

The formalism underlying the derivation of mean-force potentials has originally been developed for fluid-like systems (Hill, 1956) and has only recently been adapted to proteins. The difference between fluids and protein systems gives rise to legitimate questioning about the validity of this formalism for proteins. In consequence, although mean-force potentials have already provided many valuable insights into protein folding and stability, studies intending to clear their physical basis are still of prime relevance.

We investigated one of the most controversial limitations of database-derived potentials: their dependence on the size of the proteins included in the dataset. In fluid-like systems, the size effects determining the long-range behavior of pair potentials have been theoretically described (Hill, 1956; Lebowitz, 1960; Lebowitz and Percus, 1961). We showed here that the relative frequencies of amino acid pairs separated by a large distance, computed from our protein datasets, follow quite remarkably the predicted 1/N behavior. This result indicates that mean-force potentials derived from protein datasets stand not so far from the firm theoretical background of their fluid-like ancestors, and supports the validity of the formalism for proteins.

In addition to the influence of protein size on the long-range components of the potentials, our analysis also revealed peculiarities of the short-range components for certain amino acid pairs, resulting mainly from the partitioning of hydrophobic and hydrophilic residues between the surface and the protein core. For instance, the interaction free energies between hydrophobic residues are computed to be less favorable in large than in small proteins. This is related to the facts that the amino acid composition is more or less identical in proteins of different sizes, that larger proteins have a smaller surface/core ratio, and that hydrophobic amino acids are more diluted both in the core and on the surface of large proteins.

This result raises the question of why evolution has not further adapted amino acid composition, so as to maintain a similar fraction of hydrophobic residues in the core of large and small proteins. The answer can probably be found in the necessity of a compromise between opposing effects. Indeed, increasing the hydrophobic content of the protein core should have a stabilizing impact, and in some cases generate a higher folding rate (Calloni et al., 2003). But it can also be expected to affect the solubility, and induce an excessive rigidity likely to hamper proper functioning and degradation.

We have tested two different solutions to overcome the problem of the dependence of the potentials upon protein size. The most straightforward procedure consists of restricting the dataset to proteins similar in size to the one studied. However, this does not lead to improvements in the performances of the potentials, because of the small number of proteins in the subsets. This procedure might gain relevance in the future, as the sizes of the datasets increase.

The second solution is based on the observation that the shapes of the energy profiles are mostly conserved when derived from proteins of different sizes. This allows us to express the potentials corresponding to a given protein size N as a function of the potentials derived from the whole dataset, through parametric corrective functions of 1/N. This novel potential is found to be advantageous in applications focusing on a single protein, in particular to single out native sequence-structure matches from decoy models. It is expected to be even more useful in studies comparing proteins of various sizes, such as the prediction of their relative stabilities, where the different characteristics of small and large proteins may play a crucial role. Actually, our potential has the double advantage of including explicitly the dependence on protein size and of being derived from a large dataset with limited noise level. It appears therefore as a more efficient utilization of the available protein structure information.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.