Molecular Dynamics Simulations of Guanine Quadruplex Loops: Advances and Force Field Limitations

Abstract

A computational analysis of d(GGGGTTTTGGGG)₂ guanine quadruplexes containing either lateral or diagonal four-thymidine loops was carried out using molecular dynamics (MD) simulations in explicit solvent, locally enhanced sampling (LES) simulations, systematic conformational search, and free energy molecular-mechanics, Poisson Boltzmann, surface area (MM-PBSA) calculations with explicit inclusion of structural monovalent cations. The study provides, within the approximations of the applied all-atom additive force field, a qualitatively complete analysis of the available loop conformational space. The results are independent of the starting structures. Major conformational transitions not seen in conventional MD simulations are observed when LES is applied. The favored LES structures consistently provide lower free energies (as estimated by molecular-mechanics, Poisson Boltzmann, surface area) than other structures. Unfortunately, the predicted optimal structure for the diagonal loop arrangement differs substantially from the atomic resolution experiments. This result is attributed to force field deficiencies, such as the potential misbalance between solute-cation and solvent-cation terms. The MD simulations are unable to maintain the stable coordination of the monovalent cations inside the diagonal loops as reported in a recent x-ray study. The optimal diagonal and lateral loop arrangements appear to be close in energy although a proper inclusion of the loop monovalent cations could stabilize the diagonal architecture.

INTRODUCTION

Guanine quadruplex (G-DNA) molecules as a family represent the most important noncanonical DNA structural motif. G-DNA is involved in a wide range of biological and biochemical processes and holds significant promise as a pharmacological target. An example is the role of G-DNA in telomeres. Telomeres are protein-DNA complexes located at the end of chromosomes where the DNA sequences are particularly guanine-rich and readily form quadruplexes in vitro. The length of the telomere is maintained by the enzyme telomerase. As this enzyme shows significantly increased activity in cancer cells, and is implicated in aging, the telomeres represent potentially significant targets for cancer therapy and aging research. G-DNA quadruplexes have been shown to inhibit the action of telomerase. Additional biological roles of G-DNA have been suggested in recent years (Balagurumoorthy and Brahmachari, 1994; Fedoroff et al., 1998; Gowan et al., 2002; Han et al., 1999; Kang and Henderson, 2002; Neidle and Parkinson, 2003; Neidle and Read, 2000; Parkinson et al., 2002; Phan and Mergny, 2002; Riou et al., 2002; Sen and Gilbert, 1988; Schaffitzel et al., 2001; Williamson et al., 1989).

The basic structural unit of a G-DNA molecule is a quartet of cyclically hydrogen-bonded guanines. Several consecutive quartets stack to form the G-DNA stem. The G-DNA stem is a structurally rigid molecular assembly that is stabilized by monovalent cations residing in its central channel interacting with the guanine carbonyl groups between the quartet planes. The strands forming the guanine quadruplex stem can run parallel as well as antiparallel, and the quadruplexes can be assembled as monomolecular hairpin folds, hairpin dimers, or by four separate strands (Bouaziz et al., 1998; Haider et al., 2002; Hardin et al., 2000; Horvath and Schultz, 2001; Hud et al., 1999; Chowdhury and Bansal, 2001a,b; Marathias and Bolton, 2000; Parkinson et al., 2002; Phillips et al., 1997; Schultze et al., 1999; Smirnov and Shafer, 2000; Smith and Feigon, 1992; Spackova et al., 1999, 2001; Stefl et al., 2001, 2003; Strahan et al., 1998; Wang and Patel, 1992). The stem may also incorporate other bases in the stem leading to noncanonical quartets such as mixed GCGC (Bouaziz et al., 1998); however, these provide only limited contribution to the G-DNA stem stability (Spackova et al., 2001). Formation of guanine stems is a long process that may take hours to days and involves a wide range of intermediates (Hardin et al., 2000; Stefl et al., 2003).

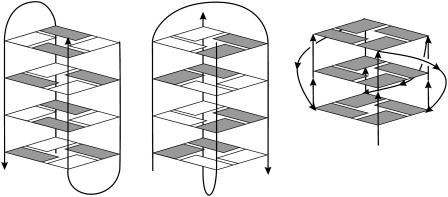
G-DNA stem forming sequences often contain single-stranded connecting loop regions (Fig. 1). Although there is a high degree of sequence and length variability, these looping regions typically contain thymine bases (Balagurumoorthy and Brahmachari, 1994; Bouaziz et al., 1998; Haider et al., 2002; Horvath and Schultz, 2001; Marathias and Bolton, 2000; Parkinson et al., 2002; Sen and Gilbert, 1988; Smirnov and Shafer, 2000; Strahan et al., 1998; Williamson et al., 1989). The flexibility of the loops contrasts sharply with the rigid G-DNA stems. This combination of rigid and flexible segments could be important for the biological and biochemical roles of G-DNA molecules.

FIGURE 1.

Depictions of lateral (left), diagonal (middle), and groove or propeller-like (right) G-DNA loop arrangements are shown. The strand directions are indicated by arrows, and anti and syn bases are indicated by solid and open boxes, respectively. All three loop types are common in G-DNA. Lateral (edge) and diagonal loops are attached to one of the terminal quartets. The lateral loops are positioned across the stem grooves, whereas diagonal loops extend across the channel entry. Finally, the loops may also connect quartets on the opposite side of the stem (bulged-out loops) leading to a propeller-type shape of the whole molecule (Parkinson et al., 2002). One base sequence can lead to several distinct quadruplex arrangements, depending on the environment.

X-ray and NMR studies have provided detailed atomic insight into G-DNA quadruplex structure (Bouaziz et al., 1998; Haider et al., 2002; Horvath and Schultz, 2001; Hud et al., 1999; Marathias and Bolton, 2000; Parkinson et al., 2002; Phillips et al., 1997; Schultze et al., 1999; Smirnov and Shafer, 2000; Smith and Feigon, 1992; Strahan et al., 1998; Wang and Patel, 1992). Molecular dynamics (MD) simulations (Chowdhury and Bansal, 2001a,b; Spackova et al., 1999, 2001; Stefl et al., 2001, 2003) and other computational methods (Balagurumoorthy et al., 1992; Meyer et al., 2001; Mohanty and Bansal, 1993, 1994; Ross and Hardin, 1994; Suhnel, 2001) complement these experiments and have been particularly informative in studies of G-DNA stems (Chowdhury and Bansal, 2001a,b; Spackova et al., 1999, 2001; Stefl et al., 2001, 2003). Flexible loop regions still represent a major challenge in these types of computational studies. For example, our earlier MD studies localized several loop geometries of quadruplex molecules with lateral loops that were stable and did not interconvert on the timescale of simulations (Spackova et al., 1999, 2001). At that time, no conclusions regarding the global minimum could be made. In this work, we show that we can overcome these limitations.

One of the most widely studied quadruplex molecules is that formed by the sequence d(GGGGTTTTGGGG) from the 3′ overhang of the Oxytricha telomere (Haider et al., 2002; Horvath and Schultz, 2001; Hud et al., 1996, 1999; Schultze et al., 1999; Smith and Feigon, 1992). NMR and high-resolution x-ray experiments show that the d(GGGGTTTTGGGG)₂ molecule forms an antiparallel four quartet quadruplex with two diagonal four-thymidine loops. An alternative arrangement with two lateral (edge) loops was reported in an earlier 2.3-Å resolution x-ray structure of d(GGGGTTTTGGGG)₂ (Kang et al., 1992). This particular structure is now considered unlikely (Haider et al., 2002; Horvath and Schultz, 2001; Spackova et al., 1999) and may have the incorrect overall topology. Nevertheless, lateral loops do commonly exist in quadruplexes of different sequences and have been seen in atomic resolution experiments (Bouaziz et al., 1998; Crnugelj et al., 2002; Marathias and Bolton, 2000; Smirnov and Shafer, 2000; Strahan et al., 1998).

In this article, we provide computational analysis of the d(GGGGTTTTGGGG)₂ quadruplex. The aim of this article is to obtain a general characterization and comparison of the conformational properties of both lateral and diagonal four-thymidine loop arrangements attached to G-DNA stems. Our study is based on all-atom MD simulations in explicit solvent that have in recent years been successfully used to characterize a wide range of nucleic acid structures (Beveridge and McConnell, 2000; Cubero et al., 2000, 2002; Giudice and Lavery, 2002; Cheatham, 2004; Cheatham et al., 1995; Cheatham and Young, 2000; Kollman et al., 2000; Lankas et al., 2002; MacKerell et al., 2000; Norberg and Nilsson, 2002; Orozco et al., 2003; Shields et al., 1997; Strahs and Schlick, 2000; Varnai and Lavery, 2002; Yang and Pettitt, 1996; Young and Beveridge, 1998; Young et al., 1997). Besides the conventional MD simulations, we utilize the locally enhanced sampling (LES) approach in explicit solvent (Cui and Simmerling, 2002; Elber and Karplus, 1990; Roitberg and Elber, 1991; Simmerling et al., 1998). LES splits the loop regions of the simulated molecules in several independently moving copies and reduces barriers between different conformations of the loop regions. In addition, the conformational space of loops is investigated via a systematic conformational search using CICADA (Koca, 1994). This approach identifies conformational families of the loops over the whole potential energy surface. This study thus investigates multiple loop conformations over a large portion of the available loop conformational space including interconversions between different loop arrangements.

Finally, the relative free energies of all the loop geometries that are stable in conventional nanosecond-scale MD simulations are estimated using the molecular-mechanics, Poisson Boltzmann, surface area (MM-PBSA) approximation (Honig and Nicholls, 1995; Jayaram et al., 1998; Sitkoff et al., 1994; Srinivasan et al., 1998). This technique extracts estimates of the free energies from the MD trajectories based on averages of the gas phase molecular mechanical energy of the solute with an estimate of solvation free energies from a Poisson Boltzmann continuum solvation model. Although the LES MD approach is designed to localize the global minima of the loops, the CICADA → MD → MM-PBSA investigations are aimed at exposing alternative accessible conformations of the loops. Alternative loop conformations may be, for example, involved in interactions with proteins and drugs.

Prior MD simulation studies were limited to straightforward investigation of the G-DNA loop geometries observed in the atomic resolution experiments. In contrast, the results of this investigation are largely independent of the starting conformation of the loop and allow the comparison of multiple loop geometries. The methodology tested here can be applied to other types and sequences of G-DNA molecules. The simulations predict that the optimal diagonal loop arrangement of d(GGGGTTTTGGGG)₂ has a similar free energy as the optimal lateral loop one. Although the free energy results (neglecting the solute entropy) favor the diagonal loop arrangement, inclusion of the solute entropy (which however is a possible source of errors) favors the lateral loop arrangement. Nevertheless, all these differences are within the error margins of the applied techniques, and thus we conclude that these two arrangements are rather close in energy. Unfortunately, our study also suggests previously unnoticed deficiencies in the force field approximation. Specifically, the optimal diagonal loop geometry predicted by the simulation techniques differs rather substantially from the experimental one. This limitation was entirely hidden in preceding molecular mechanical studies of G-DNA molecules due to insufficient sampling. This provides important new information for further refinement and development of computational methods and force fields for nucleic acids.

METHODS

Starting geometries

The initial structures were taken from the 2.3-Å crystal structure of lateral-loop d(GGGGTTTTGGGG)₂ quadruplex (Kang et al., 1992; PDB: 1D59) and the NMR structure of the diagonal loop quadruplex form of the same molecule (Schultze et al., 1994; Smith and Feigon, 1992; PDB: 156D). Subsequently, many computations were initiated with these structures and those obtained from a variety of MD, LES, or CICADA investigations. After this study began, two diagonal loop x-ray structures of d(GGGGTTTTGGGG)₂ appeared (Haider et al., 2002; Horvath and Schultz, 2001) with PDB codes 1JRN and 1JB7, and both are in reasonable agreement with the NMR structure. The recent x-ray structures were also simulated in this study.

Force field

The calculations were carried out either with the original Cornell et al. force field (Cornell et al., 1995) parm94 or its recent modification parm98/99 (Cheatham et al., 1999) as will be specified in the text. The results are not substantially affected by the choice between these two force fields, thus we consider both variants to be roughly equivalent.

Molecular dynamics simulations

Explicit solvent simulations were performed with AMBER (Case et al., 1997). The simulation cell was extended ∼10 Å in each direction from the solute with TIP3P water (Jorgensen et al., 1983), and 22 counterions (Na⁺) were included to neutralize the system. Three of the cations were positioned in the quadruplex channel, and the remaining were assigned via the LEAP module of AMBER. As specified in the text, some additional simulations were carried out with different cation distributions. All simulations were run with the SHAKE algorithm (Ryckaert et al., 1977) (with a tolerance of 0.0005 Å) to constrain covalent bonds involving hydrogens, with periodic boundary conditions, a 2-fs time step, and a temperature of 300 K (Berendsen temperature coupling algorithm (with a time constant of 0.2 ps); Berendsen et al., 1984). The nonbonded list was updated every 10 steps, and a 9-Å cutoff was applied to the Lennard-Jones interactions. As shown in recent work, this simulation protocol proves reliable for the simulation of G-DNA (Stefl et al., 2003). The equilibration started with 1000 step minimization with the solute constrained (solvent and ions allowed to move). All the equilibration steps after this were run with the particle mesh Ewald (PME) method. The first step was followed by dynamics for 25 ps with the solute position fixed. Equilibration continued with a 1000 step minimization, followed by a 3-ps MD, with harmonic restraints of 25 kcal/(mol Ų) on the G-DNA to relax water around the solute. This equilibration was followed by five rounds of 1000 step minimizations where the solute restraints were reduced by 5 kcal/(mol Ų) in each round. Finally, a 20-ps unrestrained MD simulation was performed, during which the system was heated from 100 K to 300 K in the initial 2 ps, and then production runs were initiated with an equivalent simulation protocol without any restraints.

CICADA computations

Single coordinate driving combined with MD simulated annealing (MDSA) as implemented in the CICADA program (Koca, 1994) is used to search conformational space. To do this, selected dihedral angles are systematically rotated and constrained, and then simulated annealing is applied to relax the remainder of the molecule at each step of rotation. This search methodology has been described in detail previously (Fadrna and Koca, 1997; Koca, 1994). CICADA calculations were run for systems including the loop and the adjacent quartet. The quartet geometry was frozen for the CICADA search. The size of the G-DNA loop and quartet fragment was eight residues with 259 atoms. The backbone torsions ξ and α and base rotation angles χ of the loop thymines were considered as active (driven). Two conformers were considered to be different if at least one of the torsion angles (ɛ, ξ, α, β, γ, and χ) differed by more than 30°.

The annealing protocol is as follows: the structure was heated slowly from 10 K to 50 K in 5-ps MD steps, then a 15-ps MD trajectory was run at 50 K after which the structure was cooled to 10 K in 10 ps. CICADA was interfaced with AMBER-4.1 (for technical reasons), and all MD simulated annealing as well as minimizations were performed with the SANDER module. The all-atom Cornell et al. force field (Cornell et al., 1995), parm94, was used. MD simulations were run with SHAKE on hydrogens and a 2-fs time step. A 9-Å cutoff, nonbonded pairlist update value of 100 steps was applied. As for minimization, the steepest descent method was switched to conjugate gradient after 50 cycles of minimization, and the maximum of the minimization cycles was set to 2200. Calculations were performed with the distance-dependent dielectric constant (ɛ = 4r) that crudely mimics the presence of a high dielectric solvent. No explicit cations or water molecules were included.

The CICADA analysis results in a large number of conformers that were then clustered into conformational families. The clustering was performed by the FAMILY program (Imberty and Perez, 1994) based on the root-mean-square deviation (RMSD) distances between conformers.

Molecular dynamics: locally enhanced sampling simulations

MD-LES simulations were performed with AMBER-5.0 and parm98/99 force field (Cornell et al., 1995; Cheatham et al., 1999). As shown below, both parm94 and parm98/99 versions of the force field provide similar results for this system. The ADDLES module of AMBER was used to divide the structure into three regions (stem and two loops) and each of the loops was split into five independent copies. Force field parameters for the copies were adjusted, which finally resulted in the lowering of the energy barriers on the potential energy surface (Simmerling et al., 1998).

To provide an initial kick to the five copies, the structure was heated to 500 K. Moreover a long relaxation phase appears vital to provide sufficient freedom for the copies to settle in different regions of conformational space. To allow for this, the temperature was gradually decreased from 500 K to 300 K over 1.5 ns (during the first 750 ps, the pressure was set to 100 atm), and guanine quartets were maintained with flatwell restraints (R1 = 0.0, R4 = 6.0, RK2 = 5.0, and RK3 = 10.0; R2 and R3 depend on the actual distance R between the restrained atoms (R2 = R − 0.5 Å, R3 = R + 0.5 Å)) on the N7-N2 and O6-N1 virtual bonds in neighboring guanines. The five independent loop trajectories were separated using the Moil-view software (Simmerling et al., 1995).

MM-PBSA calculations

PB analysis was performed using a modified MM-PBSA script distributed with AMBER-6.0. The Cornell et al. (parm94) charge set, PARSE van der Waals radii (Sitkoff et al., 1994) and a dielectric constant of 1 were used. The final 2-ns or 0.5-ns portions of the trajectories were examined at 10-ps intervals. The three cations present in the channel were considered explicitly in the MM-PBSA calculations. These cations represent an integral part of the structure and their inclusion is necessary in the MM-PBSA analysis to obtain meaningful numbers (Stefl et al., 2003).

In some of the MM-PBSA calculations, we separated the G-DNA molecule into three segments: the stem and each of the two stem-loop fragments. This partitioning is useful for separating the loop free energy contributions from stem free energies. In one of the cases, specifically when the MD trajectory was performed in the presence of K⁺ ions, the K⁺ ions were replaced by Na⁺ to carry out the MM-PBSA analysis.

Solute entropic contributions were estimated using a subset of these structures (at 250-ps intervals) based on a harmonic approximation to the normal modes and standard (quantum) formulas at 300 K (McQuarrie, 1976). Only a subset of the configurations was minimized due to the relatively high computational cost as described in our previous work (Stefl et al., 2003). Although this minimization causes the structures to distort somewhat, the calculated entropy is not tremendously sensitive to small structural perturbations. Moreover, very similar vibrational entropy estimates were obtained from quasiharmonic estimates from the covariance matrix of multinanosecond portions of the MD trajectories using Schlitter's formalism implemented in ptraj (Cubero et al., 2001; Schlitter, 1993).

Abbreviations

The model structures investigated are identified using a concatenation of the following abbreviations: K refers to the 2.3-Å lateral loop crystal structure by Kang (Kang et al., 1992), whereas F_diag, H_diag, and N_diag refer to the diagonal loop structures by Feigon (Schultze et al., 1994; Smith and Feigon, 1992), Horvath (Horvath and Schultz, 2001), and Neidle (Haider et al., 2002), respectively. C1-C4 refer to the lateral loop structures generated by the CICADA method (see below). L means that the structure was subjected to the locally enhanced sampling run, whereas M means that conventional PME MD was carried out. Finally (K⁺) means that the simulation was carried out in the presence of K⁺. If not specified otherwise, Na⁺ was utilized. For example, the abbreviation C1-L-M means that the CICADA C1 lateral structure was subjected to a LES run followed by conventional PME MD. Table 1 summarizes abbreviations of all structures investigated in this study.

TABLE 1.

Summary of abbreviations of all structures analyzed in this study

Abbreviation	Description	Trajectory length
Lateral loops
K	X-ray structure by Kang (Kang et al., 1992), PDB code 1D59
K-M	Conventional MD simulation started from K, Na+ ions	2.5 ns
K-M(K+)	Conventional MD simulation started from K, K+ ions	2.5 ns
C1	Conformational search CICADA structure 1 (the lowest energy one)
C2	CICADA structure 2
C3	CICADA structure 3
C4	CICADA structure 4, with MD-relaxed quartet geometry
C1-M	Conventional MD simulation started from structure C1	3 ns
C2-M	Conventional MD simulation started from structure C2	3 ns
C3-M	Conventional MD simulation started from structure C3	3 ns
C4-M	Conventional MD simulation started from structure C4	3 ns
C1-L	LES simulation started from structure C1, parm99	6 ns
C1-L-M	Conventional MD simulation started from the C1-L structure (last 0.5-ns average)	3 ns
K-M-L	LES simulation started from structure K-M, parm99	6 ns
K-M-L-M	Conventional MD simulation started from K-M-L structure (last 0.5-ns average)	3 ns
Diagonal loops
Fdiag	NMR structure by Feigon (Schultze et al., 1994; Smith and Feigon, 1992), PDB code 156D
Ndiag	X-ray structure by Neidle (Haider et al., 2002), PDB code 1JRN
Hdiag	X-ray structure by Horvath (Horvath and Schultz, 2001), PDB code1JB7
Fdiag-M	Conventional MD started from structure Fdiag	10 ns
Hdiag-M	Conventional MD started from structure Hdiag with four integral Na+ cations	5 ns
Ndiag-M	Conventional MD started from structure Ndiag with five integral Na+ cations	5 ns
Ndiag-M(K+)	Conventional MD started from structure Ndiag, with five integral cations, in presence of K+	5 ns
Fdiag-L	LES run started from structure Fdiag, parm99	6 ns
Fdiag-L-M	Conventional MD simulation started from the Fdiag-L structure (last 0.5-ns average)	3 ns

MD simulations were performed with parm94 parameter set if not specified otherwise.

RESULTS

Structural families of lateral four thymidine loops

A CICADA systematic conformational search was initiated from the 2.3-Å lateral loop crystal structure (K) (Kang et al., 1992) using the upper loop T5-T8 and the adjacent guanine quartet to generate a wide range of geometries of the loops. The search uncovered 2108 different loop conformers that were clustered into conformational families by RMSD values (see Table 2).

TABLE 2.

Main conformational families of lateral loops found by the first CICADA search (distance dependent dielectric constant ɛ = 4r) with x-ray quartet geometry

Family ID	No. of conformations	%	Thy geometry	Relative energy (kcal/mol)
As (C1)*	546	26	T7=T5-T8*	0.0
Ab (C2)*	376	18	T7=T5⊥T8*	1.7
B (C3)*	956	45	T5=T8*	9.7
Rest	230	11
All	2108	100

An additional CICADA search with MD-relaxed G-quartet provided a similar outcome, though the pairing in the lowest energy family changed to T5-T7=T8 (structure C4 in the following).

^*Signs =, -, and ⊥ represent two hydrogen bonds, single hydrogen bond, or T-shape (perpendicular) interaction between the thymines, respectively. C1, C2, and C3 are designations of representative loop geometries for each family.

The conformational search was terminated when no new conformations with lower energy could be detected and when the energies of newfound conformers remained at least 5 kcal/mol above the lowest energy conformer found so far. Two main conformational families (denoted as A and B in Table 2) were observed. The family A forms a T5=T7 asymmetric basepair with T5(O4)…T7(N3) and T5(N3)…T7(O2) H-bonds, whereas family B results in a T5=T8 basepair with T5(O2)…T8(N3) and T5(N3)…T8(O4) H-bonds.

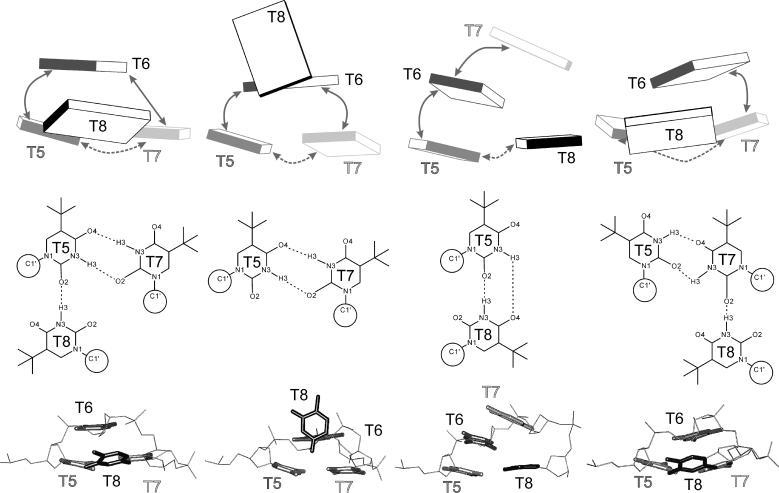
Family A consists of two subfamilies differing by the T8 base position. In the As family, the base T5 is connected by a H-bond T5(O2)…T8(N3) to T8 making a well organized planar thymine triad that interacts via stacking with the remaining T6 base. In the Ab family, the T8 base is perpendicular to the T5=T7 basepair (see various representations of the loop structures in Fig. 2, first three columns).

FIGURE 2.

Base positions and H-bonding in loop arrangements from C1 (outer left column) to C4 (outer right column) in several representations: bricks scheme (top) showing mutual positions of the bases with stacking and H-bonding interactions marked by solid and dashed arrows, respectively; H-bonding arrangements (middle), and stick representation of the loop geometry with bases highlighted (bottom).

Relative to the lowest energy conformation of the As family, the best conformations of the Ab and B families are 1.7 and 9.0 kcal/mol higher, respectively (evaluated with a distance dependent dielectric function). The best representatives of Ab, As, and B families are marked as the C1, C2 and C3 structures in this article and are utilized as starting points for further simulations (Fig. 2).

As the original x-ray structure possesses distorted G-quartets adjacent to the loops, we carried out a second CICADA search utilizing the relaxed quartet-loop starting geometry obtained previously by MD simulation (Spackova et al., 1999) augmented by the C1, C2 and C3 loop structures. In the second search, a counterrotation of the bases from the T5=T7 basepair was observed away from the C1 geometry in such a way that they established new H-bonds, T5(N3)…T7(O4) and T5(O2)…T7(N3). T8 then moved to a position suitable to establish a T8(N3)…T7(O2) H-bond, since T5 no longer presents a H-bond acceptor suitable for T8. Nevertheless, the N3-O2 separation remained out of hydrogen bonding range at a distance of ∼3.8 Å. This new geometry is designated as C4 throughout this article and is very similar to the C1 geometry except that the roles of T5 and T7 are interchanged (see Fig. 2 for comparison). The second CICADA search indicates that the loop geometry is sensitive to changes of the pertinent G-quartet. Nevertheless, both CICADA searches have qualitatively similar outcomes.

The most significant drawback of the CICADA predictions in their current form is the use of the distance-dependent dielectric model. As we discuss later, the CICADA search with this simple potential incorrectly ranks the different conformational families (as compared with the MM-PBSA data). This has been shown previously in other nucleic acid systems (Zacharias, 2000). Although it would be more appropriate to use a more realistic continuum solvation representation, such as a generalized Born approximation (GB), the CICADA code has not yet been coupled with the generalized Born approximation method (work in progress). Nevertheless, the use of the distance-dependent dielectric constant in the CICADA run has no effect on any key conclusion of this article, as our aim was to quickly identify distinct conformational families of the loops over a wide range of the conformational space. An important advantage of the CICADA method, in this regard, is that it provides (in contrast to simple model building) loop structures that are well relaxed intramolecularly. This allows initiation of smooth LES or MD runs even when the initial structure is relatively high in free energy. Our intent was not to validate the relative importance of these conformational families using a simple potential but to perform validation of the particular geometries by conventional MD simulations and LES in explicit solvent. With the LES method, we were able to move away from the starting geometries and converge to common low energy structures (see below). In fact, the use of the distance-dependent dielectric constant in the CICADA run had the additional benefit of producing a rather poor initial geometry for the sampling by LES. This harder test case demonstrates the power of the LES method.

Locally enhanced sampling PME MD explicit solvent simulation, the lateral loop

The lateral (edge) loop LES simulation was initiated with the CICADA geometry C1 for both loops and was extended to 6 ns with temperature relaxation from 500 K to 300 K during the first 1.5 ns. The LES PME MD simulation results in two independent loop trajectories, T5-T8 and T17-T20. This LES simulation is abbreviated as C1-L throughout this article.

All five copies of each loop follow essentially the same path in the LES run and do not diverge into markedly different geometries. This is not surprising since, although the copies move independently, they are enveloped by explicit solvent that tends to push the copies together. When one of the copies tests a markedly different geometry, either the remaining copies swiftly interconvert to this new geometry, or the first copy bounces back. The individual loop trajectories nevertheless differ (Cui and Simmerling, 2002). The LES run visited very different parts of the conformational space and finished a fair distance from the initial structure C1 (Figs. 3 and 4). The LES procedure allows major structural changes that are not seen in conventional PME MD simulations, including anti to syn conversions of the bases.

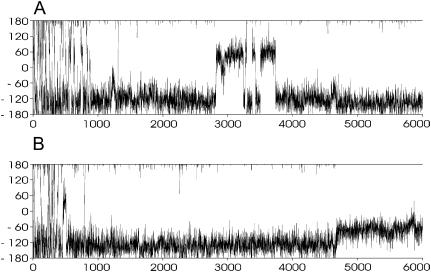
FIGURE 3.

Development of χ-angle of nucleotides T6 (A) and T7 (B) as a function of time (ps) during the LES run C1-L, second copy (see Supplementary Material for behavior of the remaining copies). Note the back and forth χ-switch of T6 ∼2.8–3.7 ns that is essential to allow further changes of the structure and the χ-adjustment of T7 at ∼4.7 ns leading to the final base rearrangement.

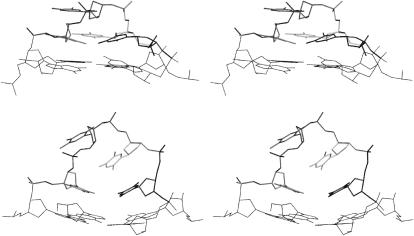
FIGURE 4.

Stereoview of the C1 lateral loop geometry (top) and averaged C1-L-M geometry (bottom). PDB files are available in the Supplementary Material. The LES procedure completely changed the loop structure.

The geometries of the two initially identical loops (T5-T8 at the top and T17-T20 at the bottom) in the C1-L simulation substantially diverged during the extended 1.5-ns LES equilibration but finally end up in equivalent geometries. Whereas the bottom loop essentially adopts its final geometry during the equilibration phase, the top loop continues to sample different conformations even during the production phase. However, by the end of the LES simulation, this loop finally converges to a geometry equivalent to the bottom loop (RMSD of 0.47 Å between the two loops).

During the C1-L run, the RMSD between the two loops was as high as 2.8 Å. The top loop (residues T5-T8) converts to a structure very similar to the C3 structure in the middle of the simulation via formation of a T5=T8 basepair with T5(O2)…T8(N3) and T5(N3)…T8(O4) H-bonds. The most significant conformational change was an anti to syn flip around the glycosidic torsion angle χ of residue T6. This transition is highlighted in Fig. 3 A. The χ-switch occurred in all copies, starts at ∼2800 ps, and ends between 3400 and 3800 ps. In some copies, repeated attempts to complete the structural transition are observed as the syn period is broken by short anti periods. Interestingly, the T6 anti-syn transition does not lead to immediate changes of the overall loop geometry as the T5=T8 basepair and base stacking are almost unchanged. However, a subsequent smaller change in residue T7's χ-angle (see Fig. 3 B) from ∼−120° to −60° at ∼4.7 ns is accompanied by a large rearrangement of the base stacking that effectively exchanges the positions of the middle bases (T6 and T7). After that, residue T6 moves on the top of the stack replacing the T7 base. Similar changes occurred in the bottom (T17-T20) loop during the later phases of the equilibration. Again, the middle bases (T18 and T19) exchanged their stacking positions and this arrangement persists until the end of the LES simulation. Note that although the C1-L geometry is different from any geometry identified by the CICADA search, it resembles the C3 structure due to the presence of the same T5=T8 basepair. However, the stacking of bases T6 and T7 is interchanged. The common convergence to near equivalent structures in both the top and bottom loops, given the different paths sampled, suggests that the LES run was sufficiently long. It is safe to assume that we localized a minimal energy geometry of the loop as determined by the current force field.

We carried out an additional LES simulation starting from the very different x-ray geometry of Kang and co-workers (K) (Kang et al., 1992). The LES simulation followed 2.5 ns conventional MD (simulation K-M), and thus the LES run is marked K-M-L (see the Methods section and Table 1 for the abbreviations). In this simulation, one of the loops adopted a geometry that is identical to both of the converged loop geometries from the C1-L LES run. The other loop, on the other hand, finished the simulation in a more open geometry that is characterized by significant exposure of the bases to the solvent (Fig. 5). The MM-PBSA analysis (see below) indicates that this open geometry is somewhat less stable.

FIGURE 5.

T5-T8 (top) and T17-T20 (bottom) loops localized by the second LES MD run K-M-L. Note that although the T17-T20 loop has essentially the same geometry as in the C1-L-M structure (Fig. 4), T5-T8 is different with one thymine looped into the solution.

Conventional PME MD explicit-solvent simulations, the lateral loops

The conformational searching with CICADA and subsequent LES simulations provided a wide range of lateral loop structures of d(GGGGTTTTGGGG)₂. These, along with the crystal structure, were subsequently used in conventional MD simulations. More specifically, simulations were performed with the CICADA geometries C1, C2, C3, and C4, the final LES geometries, and the crystal geometry designated as K. The corresponding MD structures are denoted C1-M, C2-M, C3-M, C4-M, C1-L-M, K-M, K-M-L-M, and K-M(K⁺). The last simulation, K-M(K⁺), is the only one that was run in the presence of K⁺. The C1-L-M simulation was initiated using LES MD structure C1-L (where all copies of both loops were averaged over the last 0.5 ns to obtain the starting geometry).

The 3.0-ns conventional MD simulations C1-M–C4-M sample geometries that largely conserve the structural features of their respective starting CICADA structures. All of the individual hydrogen bonds present in the initial loop structures are ∼80–100% conserved in each of the trajectories with a single exception. The T17=T20 basepair in the bottom loop of the C1-M simulation is perturbed after ∼0.8 ns. Breaking of one of the initial three hydrogen bonds causes the loop structure to shift away from the starting triad structure (not shown). This is not surprising as the thermodynamics analysis (shown below) suggests that the triad arrangement C1 is relatively high in energy. The instability of C1 arrangement is also due to a relaxation of the adjacent G-DNA quartet away from the strained crystal geometry used in the CICADA search (see above). The top (T5-T8) loop, on the other hand, did not change. Taken together, the results suggest that conventional MD, in contrast to LES, does not lead to transitions between conformational families on this timescale.

The LES averaged structure C1-L remained essentially unchanged during 3 ns additional conventional molecular dynamics (C1-L-M). In the top (T5-T8) loop, the T5 and T8 bases maintained the T5=T8 basepair (H-bonds T5(O2)…T8(N3) and T5(N3)…T8(O4)). In the bottom loop, the T17=T20 basepair formed at the beginning of the MD run but broke in the last third of the MD with no marked structural change. The RMSD between the two loops is only ∼0.6 Å, which does not represent a significant conformational transition. It should be noted that the C1-L loop conformation (and likely other loop conformations) are not rigid entities and offer local structural variations due to the subtle competition between base H-bonding and hydration that are detectable on the nanosecond timescale. A comparison of different loop topologies is summarized in Fig. S1 in the Supplementary Material section. In all simulations, the three integral cations remained inside the channel. We did not notice any substantial interaction with external bulk cations.

In contrast to the above simulations where little structural change was observed, the 2.5-ns K-M and K-M(K⁺) simulations starting from the incorrect x-ray geometry show major changes of the loops including syn ↔ anti transitions (see Spackova et al., 1999, for further details). The significant conformational changes observed in the MD simulations are indicative of major structural stress in the starting structures.

Structures of the diagonal loops, LES, and MD analysis

Given our ability to converge to common lateral geometries in the LES simulations, partially as a control case we also investigated the well-characterized diagonal loop quadruplex structures. As the correct (experimental) diagonal loop geometry is well established, we did not carry out a CICADA search on this geometry. To our surprise, the experimental loop arrangement is unstable in the LES simulation (structure F_diag-L), and both loops show marked structural rearrangements. In addition, at the end of the LES procedure, the upper and lower loops show markedly different geometries (see Fig. 6).

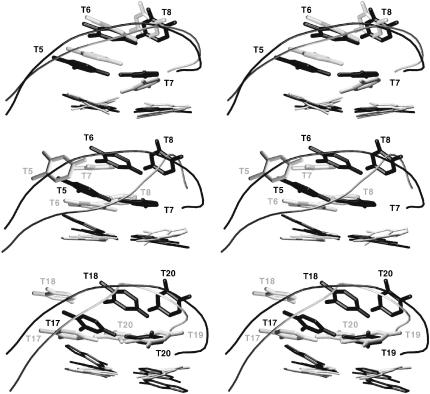
FIGURE 6.

Comparison of x-ray (N_diag), NMR (F_diag), and LES-MD (F_diag-L-M) diagonal loop geometries. (Top) The x-ray (solid) and NMR (shaded) structures. (Middle) T5-T8 loop, x-ray (solid) and F_diag-L-M (shaded). (Bottom) T17-T20 loop, x-ray (solid) and F_diag-L-M (shaded).

An additional 3 ns conventional MD simulation using the F_diag-L structure (marked as F_diag-L-M) displayed no additional changes to the loop geometries.

There are several available experimental structures of the diagonal loop complex of d(GGGGTTTTGGGG)₂. They include the original solution NMR structure in the presence of K⁺ by Feigon (PDB code 156D; Schultze et al., 1994; Smith and Feigon, 1992) and then two crystal structures, one by Horvath (Na⁺, 1.86 Å, PDB code 1JB7; Horvath and Schultz, 2001), where the quadruplex coexists with a protein-DNA single strand complex, and the other by Neidle (K⁺, 2.0 Å, orthorhombic space group, PDB code 1JRN, and 1.49 Å, trigonal space group, PDB code 1JPQ; both structures are close to identical; Haider et al., 2002). The two crystal structures are very similar. The x-ray structure by Horvath (H_diag) indicates possibly one Na⁺ cation in the loop region, above the channel entry, though no definitive conclusion could be made due to the limiting resolution. The x-ray structure by Neidle (N_diag), on the other hand, shows clearly a K⁺ cation in each loop above the channel entrance. This effectively results in five consecutive cations lining up inside the structure.

All three experimental structures (abbreviated as F_diag, H_diag, and N_diag) show essentially the same diagonal loop architecture. The RMSD of the loop regions between the H_diag and N_diag structures is 0.4 Å, and the NMR loop F_diag differs from the x-ray ones by ∼1 Å. In a sharp contrast, the two F_diag-L-M loop structures from the LES simulation show an RMSD of 4.2–4.3 Å and 2.4–2.7 Å with respect to the experimental structures F_diag, N_diag, and H_diag. The mutual RMSD between the two computed loops is 4.6 Å.

It is to be noted that a more recent NMR study indicates a different loop geometry in the presence of K⁺ (PDB code 1K4X; Schultze et al., 1999). This structure differs from both x-ray structures and older NMR data by 2.4–2.6 Å due to accumulated base position shifts. This structure is also far from both LES structures (4.0 Å and 2.5 Å). Thus we did not use this experimental structure for simulations. An additional structure of d(GGGGTTTTGGGG)₂ in the presence of Na⁺ in solution was reported, but the coordinates were not released. However, by visual inspection of the published figure, it appears to be rather similar to the F_diag, H_diag, and N_diag structures (Schultze et al., 1999). A final and relevant diagonal loop is that of a related monomolecular quadruplex NMR structure with PDB code 230D (Smith et al., 1995) that has loop geometries very similar to the F_diag, N_diag, and H_diag loops (RMSD of 1–1.3 Å).

The x-ray structures show a clear H-bonded basepair, T5(17)-T7(19), with a single T5(O2)…T7(N3) H-bond. In contrast, the T5-T8 F_diag-L-M simulated structure shows two H-bonds, T6(N3)…T8(O4) and T6(O2)…T8(N3), with significant stacking between the T6=T8 basepair and T7, whereas the T17-T20 loop has only a single H-bond, T17(N3)…T20(O4). In addition, the methyl groups of T19 and T20 contact the O2 atom of T17 due to a coplanar arrangement of these three bases (Fig. 6).

In addition to the LES simulations, we carried out conventional MD simulations using three of the experimental structures F_diag, N_diag, and H_diag. In all simulations, the loops were stable and show no interconversion. The NMR structure was simulated for 10 ns in the presence of Na⁺ with initially three cations in the channel (F_diag-M simulation). The x-ray structure by Horvath was simulated for 5 ns with initially four Na⁺ inside the structure (H_diag-M simulation). In this particular case, we used a somewhat reduced Na⁺ radii. This reduced radius was used to minimize the possibility that the ion is expelled from the in-loop position due to its size; this follows from our preceding study that suggests that the commonly used Na⁺ is slightly oversized (see Spackova et al., 1999, for details). The four cations remained stably coordinated in the quadruplex during the simulation but relocated in such a way that each was in a plane of one of the quartets. We observed essentially no interaction of the cations with the loops. The x-ray structure by Neidle (PDB code 1JRN) was simulated for 5 ns in the presence of Na⁺ cations (standard radius, simulation N_diag-M) and K⁺ (N_diag-M(K⁺) simulation) with initially three cations in the channel and two in the loops, as seen in the experiment. Notably, in both simulations, the loop-coordinated cations were unstable and left the loops within 1 ns (N_diag-M(K⁺)) and 3 ns (N_diag-M). The instability of the cations in the loop is not in agreement with the experimental structure. The cations do not return back to the loops and are not replaced by other cations. Since the x-ray structure by Neidle shows a stable in-loop coordination of large K⁺ cations, we have to conclude that the force field is unable to reproduce this feature of the quadruplex architecture.

Overview of all available structures

We investigated a wide range of lateral and diagonal loop arrangements of d(GGGGTTTTGGGG)₂. Additional information about the structures including PDB files of well-sampled configurations can be found in the Supplementary Material section.

Free energy calculations

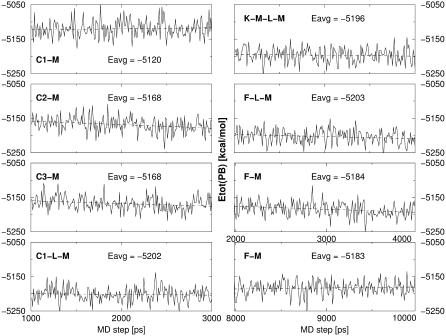
The MM-PBSA method was applied (Honig and Nicholls, 1995; Jayaram et al., 1998; Sitkoff et al., 1994; Srinivasan et al., 1998) to all models investigated in the MD simulations in presence of Na⁺. The three cations residing in the channel of the stem were explicitly included in the MM-PBSA analysis (Stefl et al., 2003). Free energies of the whole simulated systems are denoted as G(TOTAL) in Tables 3 and 4. We also attempted to separate the loop free energies from the stem free energies by formally splitting the systems into three parts: Loop1-Stem, Loop2-Stem, and the Stem (L1S, L2S, and S). Due to the importance of the outer quartet-loop interaction, it is not possible to calculate the loop free energy in the absence of the adjacent quartet. Although it is fair to assume that the splitting procedure may bring some additional errors into the calculations, we can extrapolate free energies of both loops by the following relationship: G(L1) = G(S + L1) − G(S) and G(L2) = G(S + L2) − G(S). The free energies are calculated for the last 2.0-ns (Table 3) and 0.5-ns (Table 4) portions of each trajectory.

TABLE 3.

Free energies (G total taken from MM-PBSA analysis, last 2-ns snapshots average) were calculated for the whole system (TOTAL) and various combinations of guanine stem (S) and both loops (L1 and L2) to distinguish upper and lower loop contributions

Simulation	G(TOTAL)	G(S + L1)	G(S + L2)	G(S)	G(L1)*	G(L2)*
Lateral
K-M	−5167	−4521	−4518	−3871	−650	−647
K-M(K+)	−5148	−4504	−4498	−3854	−650	−644
C1-M	−5120	−4479	−4489	−3848	−631	−641
C2-M	−5168	−4523	−4520	−3874	−649	−646
C3-M	−5168	−4511	−4511	−3853	−658	−658
C1-L-M	−5202	−4544	−4541	−3882	−662	−659
C4-M	−5167	−4524	−4523	−3880	−644	−643
K-M-L-M	−5196	−4538	−4548	−3888	−650	−660
Diagonal
Fdiag-L-M	−5203	−4541	−4549	−3886	−655	−663
Fdiag-M†	−5183	−4533	−4532	−3881	−652	−651
Ndiag-M	−5188	−4534	−4536	−3882	−652	−654

^*Contributions of L1 and L2 are extracted from the preceding four columns as specified in the text. Solute entropy term is not included in this table.

^†8.0–10.0 ns.

TABLE 4.

Free energies (G total taken from MM-PBSA analysis, last 0.5-ns snapshots average) were calculated for the whole system (TOTAL) and various combinations of guanine stem (S) and both loops (L1 and L2) to distinguish upper and lower loop contributions

Simulation	G(TOTAL)	G(S + L1)	G(S + L2)	G(S)	G(L1)*	G(L2)*
Lateral
K-M	−5167	−4523	−4518	−3872	−651	−646
K-M(K+)	−5146	−4504	−4496	−3853	−651	−643
C1-M	−5122	−4480	−4491	−3849	−631	−642
C2-M	−5176	−4528	−4528	−3878	−650	−650
C3-M	−5174	−4514	−4515	−3856	−658	−659
C1-L-M	−5206	−4550	−4543	−3887	−663	−656
C4-M	−5172	−4528	−4528	−3884	−644	−644
K-M-L-M	−5198	−4539	−4549	−3889	−650	−660
Diagonal
Fdiag-L-M	−5210	−4548	−4553	−3890	−658	−663
Fdiag-M†	−5181	−4532	−4531	−3881	−651	−650
Fdiag-M‡	−5180	−4528	−4528	−3876	−652	−653
Ndiag-M	−5189	−4536	−4536	−3882	−654	−654

^*Contributions of L1 and L2 are extracted from the preceding four columns as specified in the text. Solute entropy term is not included in this table.

^†9.5–10.0 ns.

^‡2.5–3.0 ns.

The estimated free energies from the final 0.5-ns portions of the MD trajectories, compared to the final 2.0-ns portions, are more favorable. This indicates that the quadruplex structures are relaxing as the simulations proceed. This is not surprising given that the majority of the simulations are rather short (only 3 ns). Nevertheless, despite the lack of complete convergence, the analysis of the free energy over the final 0.5 ns of simulation (see Fig. 7 for selected examples) indicates that no major drifts of free energies are seen. This suggests that the final part of the trajectory samples reasonably stable and relaxed structures. Further, in the longer 10-ns simulation F_diag-M, no significant changes in the free energies are observed after 3 ns. The observation that the free energy improves during the initial part of the simulations is an encouraging indication that the continuum solvent MM-PBSA free energy properly parallels the true free energy in presence of the explicit solvent.

FIGURE 7.

Selected developments of the MM-PBSA free energies along the trajectories over intervals 1–3 ns (except of the F_diag-M simulation). The dashed line shows the linear regression over the trajectory portion shown. Note that after 2.5 ns the free energy values are largely stabilized.

Lateral loop arrangement

The best total free energy, omitting the solute entropy term, was achieved in the C1-L-M LES trajectory. The second (control) LES/MD run, K-M-L-M, is 8 kcal/mol less stable. As discussed above, in this LES run, one of the loops did not locate to the presumably optimal arrangement and finished with bases protruding into solvent. Based on the MM-PBSA free energy estimates, no other lateral loop structure is close to the structures localized by LES. The C2-M and C3-M arrangements are ∼30 kcal/mol away, whereas the C1-M structure (global minimum with the distance dependent dielectric model conformational search) is more than 80 kcal/mol away. This confirms that the simple distance dependent screening method is not realistic. Taking into consideration that the initial LES search was initiated using the poor C1 geometry, our simulation results suggest that the LES method is indeed capable of initiating and achieving large-scale conformational transitions in the various G-DNA quadruplex loop structures. The incorrect x-ray structure K-M is (even after the significant conformational transitions seen in the MD run) 40 kcal/mol away the C1-L-M minimum.

Comparison of lateral and diagonal loop arrangements

One of the key aims of this article is to compare the relative stability of models of the d(GGGGTTTTGGGG)₂ structure with lateral and diagonal loop arrangements. Although the F_diag-M and N_diag-M simulations maintain the experimentally observed diagonal loop arrangements over a 3-ns timescale in the simulation, the free energy estimates suggest that these structures are nearly 25 kcal/mol less stable than the best lateral loop arrangement C1-L-M. In contrast, the alternate diagonal loop structure found in the F_diag-L-M (Feigon → LES → MD) enhanced sampling simulation appears to be the most stable arrangement among all structures studied (by ∼4 kcal/mol). However, this difference of only 4 kcal/mol with respect to the best lateral loop arrangement C1-L-M is within the error margin of the MM-PBSA method. Overall, the results suggest that the optimal diagonal and lateral loop arrangements are close in energy. At this point, it is difficult to judge the reliability of the estimates in relation to the true stability since our predicted optimal diagonal loop architecture is in disagreement with the x-ray and NMR structures (see above). What we can state with certainty is that the MM-PBSA and LES results are mutually consistent. This strongly implicates the force field and deficiencies within (and not the LES procedure) are responsible for the failure to predict the correct diagonal loop geometry. We note that the LES simulations were carried with the parm99 force field version, whereas the conventional MD simulations and MM-PBSA calculations were carried out with the parm94 parametrization. Despite this minor force field change (relating to small changes in the dihedral potential), the MM-PBSA calculations with the parm94 force field still predict that the LES structure is favored over the experimental one. As part of the Supplementary Material, we compare the MM-PBSA free energy estimates with parm94 and parm99 force fields and conclude that they provide comparable results. Rerunning the LES simulation with the parm94 parameterization would not alter the results, and we conclude that both the parm94 and parm99 parameter sets consistently disfavor the experimental geometry under the applied simulation conditions.

Separation of stem and loop free energies

Tables 3 and 4 show that the individual simulations differ markedly in the estimated free energies of the stem. Overall, the range of estimated stem free energies is on the order of 40 kcal/mol. The best stem free energies are seen for the three structures based on the LES loop geometries (lateral C1-L-M, lateral control simulation K-M-L-M, and diagonal F_diag-L-M). The greater sampling and more significant loop relaxation during the LES procedure not only improve the loop geometries but lead to improvement of the stem free energies. Similarly, the worst stem free energy is indicated for the C1-M simulation of the poor distance dependence derived geometry, and this simulation also has the worst total free energy. Taken in the context of all the simulations performed, the results suggest that there is a direct interrelationship (structural communication) between the stem and the loop. The LES method, even when only applied to the loop regions, is able to optimize the stem-loop junction, as it allows very large loop rearrangements not seen in conventional MD.

The estimated free energies of the top (L1, T5-T8) and bottom (L2, T17-T20) loops are equivalent (within a few kcal/mol) in most simulations. The main exception is the least stable structure C1-M, where one of the loops shows a large structural change during the MD simulation, resulting into a free energy improvement. A similar explanation could also be used to explain the G(L1)/G(L2) difference in the K-M-L-M simulation, as in this particular case the LES simulation resulted in a partially unfolded geometry for the T5-T8 lateral loop. This loop is less stable than the best lateral loop structure predicted by LES. In general, except for the T5-T8 loop of K-M-L-M, all five other loop structures obtained by LES have very good free energies (656–663 kcal/mol). C1-L-M and C3-M structures have isoenergetic loop geometries, and yet the C3 structure is less stable due to a poor stem energy. It is fair to assume (see above) that at least part of the stem free energy penalty in C3-M is due to conflicts between the stem and loop geometries.

Inclusion of the solute entropy

The thermodynamic data above do not include the solute entropy. This is because the evaluation of the solute entropy term (see the Methods section) is the least reliable component of the MM-PBSA free energy estimation. The solute entropy terms are given in Table 5.

TABLE 5.

Solute entropy terms derived via the harmonic vibration analysis

Simulation	−TS, 300 K (kcal/mol)
K-M	−641
C1-M	−705
C2-M	−703
C3-M	−714
C4-M	−714
C1-L-M	−718
K-M-L-M	−718
Fdiag-L-M	−706

See the text for data by the method of Schlitter.

Regarding the lateral loop models, the entropy term further stabilizes the C1-L-M structure over all the others, thus the basic results presented in Tables 3 and 4 are not significantly altered. The simulations based on the incorrect x-ray lateral loop structure give very unfavorable entropic contributions. On the other hand, when the solute entropy term is added to the data in Tables 3 and 4, the best lateral loop arrangement C1-L-M is 7 kcal/mol more stable than the best diagonal loop F_diag-L-M. Nevertheless, the difference is still quite small and within the error bars of the computations. We interpret the results to suggest that the C1-L-M and F_diag-L-M structures are rather close in free energy.

To verify the entropy results, we reevaluated the entropy data for key structures with quasiharmonic estimates of the entropy using Schlitter's method. The entropy terms were calculated by the covariance matrix from 2 to 3 ns, 1.5 to 3 ns, and 1 to 3 ns (2000 frames) portions of the simulations. We obtained the following numbers for the three periods. Simulation C1-L-M: 606.4, 656.1, and 681.8 kcal/mol; simulation F_diag-L-M: 594.8, 644.2, and 670.0 kcal/mol; and their difference: −11.0, −11.9, and −11.8 kcal/mol. The absolute entropy values obtained by the Schlitter analysis are not converged even after the 2-ns period. However, the relative values for the C1-L-M and F_diag-L-M structures are insensitive to the period of calculations, and the difference value of −11.6 kcal/mol obtained by harmonic vibrational analysis is identical to that predicted by the covariance matrix analysis.

DISCUSSION AND CONCLUSIONS

In this study, we report an extensive computational analysis of lateral and diagonal four-thymidine loops of d(GGGGTTTTGGGG)₂ guanine quadruplex molecules. This study provides, within the approximation of the force field, a qualitatively complete analysis of the loop conformational space of d(GGGGTTTTGGGG)₂, and the results are independent of the starting structures.

We have utilized a combination of four computational approaches including nanosecond-scale MD simulation in explicit solvent, LES, and systematic conformational search. Finally, the MM-PBSA method was used to evaluate the relative free energies including the three integral monovalent cations residing in the quadruplex channel (Stefl et al., 2003).

The lateral loops in d(G₄T₄G₄)

The systematic conformational search of the loops in absence of solvent (with just a simple distance dependent dielectric screening function) provides a set of possible lateral loop conformational types, marked as C1-C4, that were utilized as starting structures for further investigations. Although the simple model of solvent screening is not capable of reliably estimating the correct rank of the structures, this drawback is overcome by the subsequent MD and LES simulations. All four structure classes found in the systematic search appear to be stable in 3-ns length conventional MD simulations. In contrast, a LES run initiated with the structure C1 achieved major conformational changes absent from the (short) conventional MD simulations. Convergence was seen to a structure denoted as C1-L (C1 → LES) in this article. The C1-L structure is rather different from the starting C1 geometry. Both loops adopt the same geometry in the course of the LES run, with a mutual heavy atom RMSD of ∼0.4 Å, and all of the geometrical features appear identical. A second LES run was initiated from a different starting structure. It sampled the C1-L loop arrangement for one of its loops, whereas the second loop substantially unfolded toward the solvent. This study confirms that the LES method is capable of achieving major conformational changes within flexible loop regions, independent of the starting structure. However, multiple LES runs starting from different structures are advised to check the reproducibility of the results.

The LES result is consistent with the MM-PBSA free energy analysis. The C1-L structure is superior to all other loop arrangements. The best loop structure indicated by the conformational search with a distance dependent dielectric constant (C1) is actually the least stable arrangement according to the MM-PBSA approach. Thus, the LES procedure was capable of finding a new and more favorable geometry even when started from the least stable structure C1, with MM-PBSA free energy improvement of 80 kcal/mol.

Separation of the free energies into the stem and loop parts shows that the stem and loops are structurally interconnected. Changes of the loop geometry exert effects on the stem energetics and vice versa. This is also demonstrated by the CICADA conformational search with different quartet geometries.

The calculated free energy differences for the various loop geometries sampled, ranging from the best lateral loop arrangement C1-L to the other lateral loops, are very significant. Thus, these results do not support earlier suggestions that multiple loop geometries would coexist for lateral four-thymidine loops of G-DNA molecules (Spackova et al., 1999). Nevertheless, the C1-L loop arrangement (as well as the others) is not rigid and shows nanosecond-scale dynamics (substates) in the course of the simulations with evident competition between the interthymine hydrogen bonds and hydration.

The computations predict lateral loop geometries that are substantially different from those in the 2.3-Å x-ray study in presence of K⁺ (Kang et al., 1992). The crystal geometry is highly unstable, and the MM-PBSA method predicts that it is more than 40 kcal/mol away the global minimal C1-L. It is to be noted that this particular crystal structure is in disagreement with all other NMR and x-ray studies showing a diagonal type of quadruplex, even in case of a recent high-resolution structure crystallized in the presence of K⁺ (Haider et al., 2002).

Diagonal loop arrangement: failure to predict the correct structure

The structure of the diagonal loop arrangement of d(GGGGTTTTGGGG)₂ has been well characterized (Haider et al., 2002; Horvath and Schultz, 2001; Schultze et al., 1994, 1999; Smith and Feigon, 1992). Unfortunately, in our simulations this structure is unstable. The LES simulation leads to a major conformational transition of this diagonal loop arrangement away from that suggested by experiment. Thus in contrast to preceding attempts to use LES for nucleic acids (Simmerling et al., 1998), we witnessed a transition from the correct structure to an incorrect one. This is a significant setback for molecular modeling of the G-DNA loop structure. The subsequent free energy MM-PBSA analysis predicts the rearranged (incorrect) diagonal loop topology to be considerably more stable than the correct loop geometry. In other words, the LES and MM-PBSA data are mutually consistent, and we thus suggest that the inability of the computations to predict the correct diagonal loop arrangement originates primarily in some previously unknown imbalances of the force field. A significant issue (or warning) is that when conventional MD is applied to the experimental geometries, the loop structures are stable on a nanosecond timescale. This suggests that stability in nanosecond-scale MD simulation is not a reliable indicator of structural stability. The MD and LES results provide a consistent prediction of the loop geometry that is at odds with the experimental results. Ironically, even though the experimental studies were carried out under different conditions and environments, their results are very consistent. Thus, although we cannot ultimately rule out that, for example, crystal packing, different ion conditions, and other interactions may be responsible for the differences discussed above, this possibility is rather unlikely.

It is very difficult at this stage to pinpoint the actual origin of the misbalance of the force field that leads to the incorrect diagonal loop topologies. One of the reasons could be the imbalance of the solute-cation and solvent-cation interactions caused by pair additivity of the force field (Spackova et al., 1999). The recent x-ray studies show that the diagonal loops of d(GGGGTTTTGGGG)₂ host monovalent cations residing inside the loop and outside the channel. Such arrangements, however, are unstable in our simulations. It is to be noted that subtle conformational defects in the stem area (bifurcated G-quartets) were reported in our earlier study of G-DNA molecules and were tentatively attributed to the lack of polarization in the force fields (Spackova et al., 1999). Treatment of cations represents one of the most severe approximations in contemporary molecular modeling of nucleic acids (Cheatham, 2004; Reblova et al., 2003; Spackova et al., 1999). It is to be noted that the wrong diagonal loop topology appears to be predicted by both currently available variants of the Cornell et al. force field, which is parm94 and parm98/99 that differ in the tuning of the sugar parameters. The LES runs were carried out with the later parametrization, whereas the MD and MM-PBSA analysis was done with parm94. All computations favor the incorrect loop arrangement.

Despite the evident setback of the simulations to correctly predict the G-DNA loop geometry, we still suggest that the simulation technique represents a useful tool to study many aspects of the G-DNA and other nucleic acids forms. Correct description of the flexible loop region interacting with monovalent cations represents an exceptional challenge for the accuracy and balance of the force fields. Thus, problems with loop description do not necessarily mean that other structural aspects of nucleic acids are not properly reflected by the simulations. Specifically, in case of the G-DNA molecules, we have so far carried out extensive MD analyses of the G-DNA stems, and for this part of the quadruplex molecules the force field appears to work properly (Chowdhury and Bansal, 2001a; Spackova et al., 1999, 2001; Stefl et al., 2001, 2003). The simulations provided some unique insights into the G-DNA stem structure, dynamics, and stability. In a sharp contrast to problems with the loops, for the stem part of G-DNA, the MM-PBSA procedure correctly predicts the experimentally observed arrangement (full cation-stabilized stem) as the global free energy minimum (Stefl et al., 2003), with close to quantitative structural agreement with high-resolution x-ray structural data. Further work is however evidently needed to improve the accuracy of the quadruplex modeling, primarily with respect to the force field description of the loops.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.