Abstract
The energy of intermediates in fusion of phospholipid bilayers is sensitive to 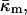 the saddle splay (Gaussian curvature) elastic modulus of the lipid monolayers. The value
the saddle splay (Gaussian curvature) elastic modulus of the lipid monolayers. The value 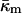 is also important in understanding the stability of inverted cubic (QII) and rhombohedral (R) phases relative to the lamellar (Lα) and inverted hexagonal (HII) phases in phospholipids. However,
is also important in understanding the stability of inverted cubic (QII) and rhombohedral (R) phases relative to the lamellar (Lα) and inverted hexagonal (HII) phases in phospholipids. However, 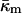 cannot be measured directly. It was previously measured by observing changes in QII phase lattice dimensions as a function of water content. Here we use observations of the phase behavior of N-mono-methylated dioleoylphosphatidylethanolamine (DOPE-Me) to determine
cannot be measured directly. It was previously measured by observing changes in QII phase lattice dimensions as a function of water content. Here we use observations of the phase behavior of N-mono-methylated dioleoylphosphatidylethanolamine (DOPE-Me) to determine 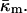 At the temperature of the Lα/QII phase transition, TQ, the partial energies of the two phases are equal, and we can express
At the temperature of the Lα/QII phase transition, TQ, the partial energies of the two phases are equal, and we can express 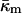 in terms of known lipid monolayer parameters: the spontaneous curvature of DOPE-Me, the monolayer bending modulus κm, and the distance of the monolayer neutral surface from the bilayer midplane, δ. The calculated ratio
in terms of known lipid monolayer parameters: the spontaneous curvature of DOPE-Me, the monolayer bending modulus κm, and the distance of the monolayer neutral surface from the bilayer midplane, δ. The calculated ratio 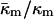 is −0.83 ± 0.08 at TQ ≈ 55°C. The uncertainty is due primarily to uncertainty in the value of δ for the Lα phase. This value of
is −0.83 ± 0.08 at TQ ≈ 55°C. The uncertainty is due primarily to uncertainty in the value of δ for the Lα phase. This value of 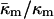 is in accord with theoretical expectations, including recent estimates of the value required to rationalize observations of rhombohedral (R) phase stability in phospholipids. The value
is in accord with theoretical expectations, including recent estimates of the value required to rationalize observations of rhombohedral (R) phase stability in phospholipids. The value 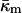 substantially affects the free energy of formation of fusion intermediates: more energy (tens of kBT) is required to form stalks and fusion pores (ILAs) than estimated solely on the basis of the bending elastic energy. In particular, ILAs are much higher in energy than previously estimated. This rationalizes the action of fusion-catalyzing proteins in stabilizing nascent fusion pores in biomembranes; a function inferred from recent experiments in viral systems. These results change predictions of earlier work on ILA and QII phase stability and Lα/QII phase transition mechanisms. To our knowledge, this is the first determination of the saddle splay (Gaussian) modulus in a lipid system consisting only of phospholipids.
substantially affects the free energy of formation of fusion intermediates: more energy (tens of kBT) is required to form stalks and fusion pores (ILAs) than estimated solely on the basis of the bending elastic energy. In particular, ILAs are much higher in energy than previously estimated. This rationalizes the action of fusion-catalyzing proteins in stabilizing nascent fusion pores in biomembranes; a function inferred from recent experiments in viral systems. These results change predictions of earlier work on ILA and QII phase stability and Lα/QII phase transition mechanisms. To our knowledge, this is the first determination of the saddle splay (Gaussian) modulus in a lipid system consisting only of phospholipids.
INTRODUCTION
It is now fairly clear that fusion in lipid membranes occurs via the stalk mechanism (Kozlov and Markin, 1983; Siegel, 1993; Kuzmin et al., 2001; Kozlovsky and Kozlov, 2002; Kozlovsky et al., 2002; Markin and Albanesi, 2002; May, 2002), which is related to the mechanism of lamellar/inverted phase transitions in phospholipids (Siegel and Epand, 1997; Siegel, 1999; Kozlovsky et al., 2002; Y. Kozlovsky, D. P. Siegel, and M. M. Kozlov, unpublished results). When stalks or fusion pores form between membrane vesicles, there is a change in topology that decreases the Gaussian curvature integrated over the surface. The same changes in the integrated Gaussian curvature occur when fusion pores form between flat lipid bilayers during the lamellar/inverted cubic (Lα–QII) phase transition of membrane-forming lipids. Fusion pores are also known as “passages” (Harbich et al., 1978) or interlamellar attachments (ILAs; Siegel, 1999). Related changes in the integrated Gaussian curvature must also accompany formation of stalks during formation of the recently discovered rhombohedral (R) phase (Yang and Huang, 2002, 2003; Yang et al., 2003) from the Lα phase.
Differences in free energy between such structures have usually been described in terms of the curvature elastic energy of membranes (Helfrich, 1973), with emphasis placed on changes in the bending (e.g., Siegel, 1999; Markin and Albanesi, 2002) or, more generally, splay elastic energy (Hamm and Kozlov, 1998, 2000; Kozlovsky and Kozlov, 2002; Kozlovsky et al., 2002). However, changes in the integrated Gaussian curvature also influence the free energy of fusion or phase transition intermediates. In treatments of intermediate energies, these contributions to the total curvature energy have usually been either neglected (Markin and Albanesi, 2002; Kozlovsky and Kozlov, 2002; Kozlovsky et al., 2002; May, 2002) or treated with simple models (Siegel, 1999). Recent work suggests that the Gaussian curvature elastic energy is one of the major contributions to the energy of fusion stalks for lipids that are near the Lα/inverted hexagonal (HII) phase boundary (e.g., lipid compositions rich in phosphatidylethanolamine), and plays an important role in determining the stability of the R phase (Y. Kozlovsky, D. P. Siegel, and M. M. Kozlov, unpublished results).
One reason that the Gaussian curvature elastic energy has been neglected is that it is proportional to an elastic modulus, 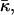 that cannot be directly measured. Previously, this modulus was estimated by analysis of the dependence of QII phase unit cell dimensions on the water content (Turner et al., 1992; Chung and Caffrey, 1994; Templer et al., 1994, 1995, 1998). This analysis is complex and inaccurate for QII phases with small unit cell constants (Templer et al., 1995), and can be hampered by the coexistence of different QII phases (Templer et al., 1998). Here, we use another approach, based on detailed observations of the Lα–QII phase transition in DOPE-Me (Siegel and Banschbach, 1990; Cherezov et al., 2003). We determine a value of the Gaussian curvature elastic modulus for DOPE-Me monolayers that is within the range expected by theory. To our knowledge, this is the first measurement of this modulus in a lipid system composed only of phospholipids, as opposed to mixtures of phospholipids with monoglycerides or fatty acids or in glycolipids. The results have a substantial impact on the theories of membrane fusion and lamellar/nonlamellar transition mechanisms.
that cannot be directly measured. Previously, this modulus was estimated by analysis of the dependence of QII phase unit cell dimensions on the water content (Turner et al., 1992; Chung and Caffrey, 1994; Templer et al., 1994, 1995, 1998). This analysis is complex and inaccurate for QII phases with small unit cell constants (Templer et al., 1995), and can be hampered by the coexistence of different QII phases (Templer et al., 1998). Here, we use another approach, based on detailed observations of the Lα–QII phase transition in DOPE-Me (Siegel and Banschbach, 1990; Cherezov et al., 2003). We determine a value of the Gaussian curvature elastic modulus for DOPE-Me monolayers that is within the range expected by theory. To our knowledge, this is the first measurement of this modulus in a lipid system composed only of phospholipids, as opposed to mixtures of phospholipids with monoglycerides or fatty acids or in glycolipids. The results have a substantial impact on the theories of membrane fusion and lamellar/nonlamellar transition mechanisms.
THEORY
Criterion for Lα/QII phase transition
DOPE-Me has a fairly well-defined Lα–QII phase transition temperature, TQ (Siegel and Banschbach, 1990; Cherezov et al., 2003). The chemical potentials for the Lα and QII phase must be equal at TQ. The difference in chemical potential can be expressed in terms of the curvature energy of the bilayers in the two phases. We base our consideration on the Helfrich elastic model (Helfrich, 1973). The local membrane shape is determined at each point by two principal curvatures, c1 and c2, or alternatively, by the total curvature, J = c1 + c2 and Gaussian curvature, K = c1c2. The membrane structure is characterized by the spontaneous curvature, Js, whereas the membrane elasticity is determined by the bending modulus, κ, and the Gaussian elastic modulus, 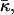 which is also referred to as the saddle splay modulus. We do not include the effects of hydration energy and consider only systems in excess water.
which is also referred to as the saddle splay modulus. We do not include the effects of hydration energy and consider only systems in excess water.
The curvature elastic energy per unit area of a membrane is given by
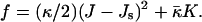 |
(1) |
The total curvature energy is obtained by integration of Eq. 1 over the membrane area A.
The elastic model Eq. 1 can be used to calculate the elastic energy of a whole lipid bilayer. In this case the total and Gaussian curvatures describe the bilayer midsurface, whereas the elastic constants characterizing the bilayer are denoted by κb, 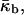 and
and 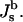 The same model determines the curvature energy of each of the two monolayers. Then it is convenient to relate the curvatures to the so-called neutral surface of the monolayer (Kozlov and Winterhalter, 1991), which is shifted by distance δ from the bilayer midplane toward the lipid-water interface. The elastic characteristics of a monolayer will be denoted by κm,
The same model determines the curvature energy of each of the two monolayers. Then it is convenient to relate the curvatures to the so-called neutral surface of the monolayer (Kozlov and Winterhalter, 1991), which is shifted by distance δ from the bilayer midplane toward the lipid-water interface. The elastic characteristics of a monolayer will be denoted by κm, 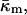 and
and 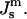
Both the Lα and QII phases are composed of lipid bilayers, which are assumed to have the same lipid composition in both monolayers. Although each monolayer is characterized by a certain spontaneous curvature 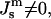 the spontaneous curvature of the bilayer vanishes for symmetry reasons (
the spontaneous curvature of the bilayer vanishes for symmetry reasons (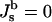 ). The bilayers of the Lα phases are flat and, consequently, characterized by J = 0 and K = 0. The QII phases formed by DOPE-Me (Gruner et al., 1988; Siegel and Banschbach, 1990; Cherezov et al., 2003) have the geometry of infinite periodic minimal surfaces (IPMS): the midplanes of the bilayers lie on surfaces which have, similarly to the Lα phase, a zero total curvature, J = 0, at each point. At the same time, and in contrast to the lamellar phase, the Gaussian curvature of the minimal surfaces is different from zero and negative at each point, K < 0. Hence, the difference in curvature energy between the two phases, ΔF, is due solely to the Gaussian curvature of the cubic phase and given by
). The bilayers of the Lα phases are flat and, consequently, characterized by J = 0 and K = 0. The QII phases formed by DOPE-Me (Gruner et al., 1988; Siegel and Banschbach, 1990; Cherezov et al., 2003) have the geometry of infinite periodic minimal surfaces (IPMS): the midplanes of the bilayers lie on surfaces which have, similarly to the Lα phase, a zero total curvature, J = 0, at each point. At the same time, and in contrast to the lamellar phase, the Gaussian curvature of the minimal surfaces is different from zero and negative at each point, K < 0. Hence, the difference in curvature energy between the two phases, ΔF, is due solely to the Gaussian curvature of the cubic phase and given by
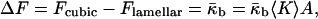 |
(2) |
where 〈K〉 is the average of the bilayer Gaussian curvature K over the membrane area. There is an additional contribution to the free energy of the QII phase relative to the Lα phase due to the frustration energy (Anderson et al. 1988). We will neglect this contribution because it is small for the swollen QII phases, whereas the unit cell is large with respect to the monolayer thickness (Templer et al., 1998).
〈K〉 is negative in the QII phase. Thus, according to Eq. 2, the QII phase is energetically more favorable than the Lα phase, ΔF < 0, if the Gaussian curvature elastic modulus is positive, 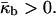 For
For 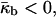 the Lα phase is energetically more favorable than the QII phase, ΔF > 0.
the Lα phase is energetically more favorable than the QII phase, ΔF > 0.
The Gaussian curvature modulus of the bilayer can be expressed in terms of the properties of the lipid monolayers. This is important because the monolayer spontaneous curvature and bending elastic modulus of many phospholipids have been measured by x-ray diffraction experiments. It can be shown (Helfrich and Rennschuh, 1990; Ljunggren and Erikkson, 1992; Templer et al., 1994; Schwarz and Gompper, 2001; see also Appendix A) that
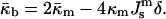 |
(3) |
The monolayer Gaussian curvature modulus should be negative, 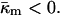 This is predicted based on the inferred lateral stress profiles as a function of depth within lipid monolayers (Ben-Shaul, 1995) and on the measured positions of pivotal planes within phospholipid monolayers (Templer et al., 1998). Since the monolayer spontaneous curvature is a function of temperature,
This is predicted based on the inferred lateral stress profiles as a function of depth within lipid monolayers (Ben-Shaul, 1995) and on the measured positions of pivotal planes within phospholipid monolayers (Templer et al., 1998). Since the monolayer spontaneous curvature is a function of temperature, 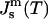 (Tate and Gruner, 1989; Kozlov et al., 1994), the Gaussian curvature modulus of the bilayer,
(Tate and Gruner, 1989; Kozlov et al., 1994), the Gaussian curvature modulus of the bilayer, 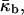 also becomes a function of temperature,
also becomes a function of temperature, 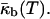 Thus, the temperature TQ at which IPMS-based QII phases can form must be the temperature at which the monolayer spontaneous curvature reaches a value that makes the bilayer Gaussian curvature modulus equal to zero (Schwarz and Gompper, 2002),
Thus, the temperature TQ at which IPMS-based QII phases can form must be the temperature at which the monolayer spontaneous curvature reaches a value that makes the bilayer Gaussian curvature modulus equal to zero (Schwarz and Gompper, 2002),
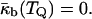 |
(4) |
Using Eqs. 3 and 4 and the experimentally found function 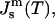 the Gaussian curvature modulus of the monolayers,
the Gaussian curvature modulus of the monolayers, 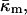 can be determined at the temperature TQ.
can be determined at the temperature TQ.
Free energy of fusion pores (ILAs)
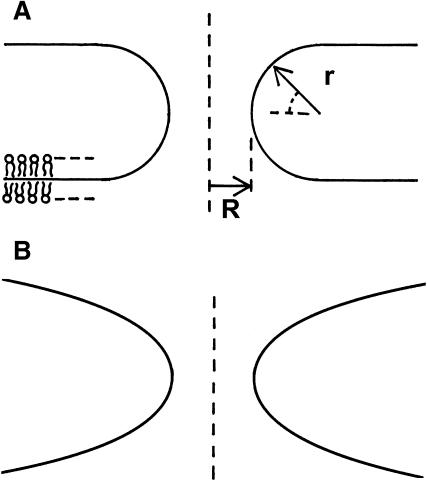
An elementary step of Lα–QII transition must be formation of a bilayer passage between two flat membranes, which is also referred to as fusion pore or ILA (Siegel et al., 1989a; Siegel, 1986, 1999). The energy of these structures can be also determined by Eq. 1. Provided that fusion pores (ILAs) are minimal surface-based structures (J → 0), with vanishing bending energy (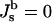 ), ILA formation is determined by the criterion Eq. 4. ILAs were formerly assumed to be circular toroids (Siegel, 1986, 1993, 1999; Nanavati et al., 1992; Chizmadzhev et al., 1995; Kuzmin et al., 2001; see Fig. 1 A). However, these structures have lower free energies if the midplanes of the bilayers of the pore lie on an axisymmetric surface with zero mean curvature at all locations (Harbich et al., 1978), referred to as catenoid (do Carmo, 1976). The infinite periodic minimal surface resembling an array of ILAs in a lamellar phase (Thomas et al.,1988) also fulfills this condition and represents one possible shape of a bicontinuous cubic phase. There must be a narrow region of membrane with nonvanishing curvature around the periphery of the catenoid-like ILA, to connect it to the flat bilayers of the Lα phase. It has been shown (Petrov and Kozlov, 1984; Kozlov and Chernomordik, 1998) that such regions can have negligibly small bending energies ≪ kBT. Markin and Albanesi (2002) modeled fusion pores as surfaces of constant curvature with Jb approaching zero, which can also have negligible bending energies ≪ kBT. An example is shown in Fig. 1 B. Since the bending energies of ILAs and the flat bilayers of the Lα phase are practically equal, the energy difference between the two structures is due to the Gaussian curvature.
), ILA formation is determined by the criterion Eq. 4. ILAs were formerly assumed to be circular toroids (Siegel, 1986, 1993, 1999; Nanavati et al., 1992; Chizmadzhev et al., 1995; Kuzmin et al., 2001; see Fig. 1 A). However, these structures have lower free energies if the midplanes of the bilayers of the pore lie on an axisymmetric surface with zero mean curvature at all locations (Harbich et al., 1978), referred to as catenoid (do Carmo, 1976). The infinite periodic minimal surface resembling an array of ILAs in a lamellar phase (Thomas et al.,1988) also fulfills this condition and represents one possible shape of a bicontinuous cubic phase. There must be a narrow region of membrane with nonvanishing curvature around the periphery of the catenoid-like ILA, to connect it to the flat bilayers of the Lα phase. It has been shown (Petrov and Kozlov, 1984; Kozlov and Chernomordik, 1998) that such regions can have negligibly small bending energies ≪ kBT. Markin and Albanesi (2002) modeled fusion pores as surfaces of constant curvature with Jb approaching zero, which can also have negligible bending energies ≪ kBT. An example is shown in Fig. 1 B. Since the bending energies of ILAs and the flat bilayers of the Lα phase are practically equal, the energy difference between the two structures is due to the Gaussian curvature.
FIGURE 1.
Fusion pore structures, seen in cross section in the plane of the cylindrical axes. The curves represent the midplane of the bilayers. (A) Fusion pores were formerly modeled as circular toroids (see text), defined by two radii, r and R. (B) However, fusion pores probably adopt shapes where the mean curvature of the bilayers is zero everywhere, and the bending energy is minimized. Shown here is a geometry with constant curvature Jb approaching zero, which has a bending energy < kBT (Markin and Albanesi, 2002).
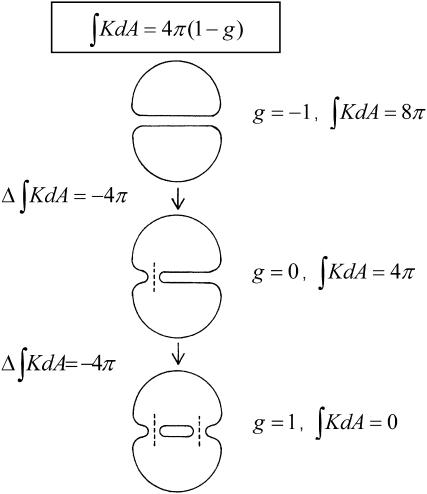
ILAs have 〈K〉 < 0 (the two principal radii of curvature have opposite signs at all points). According to the Gauss-Bonnet theorem, the integral of the Gaussian curvature of a closed surface over the area, dA, is
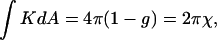 |
(5) |
where g is genus and χ is the Euler characteristic of the surface (do Carmo, 1976). The genus is zero, g = 0, for a sphere, whereas a torus, which is a sphere with one “handle,” has genus g = 1, and the genus increases by one for every additional handle (do Carmo, 1976). Formation of an ILA is equivalent to a handle formation (Δg = 1), so the change in the integrated Gaussian curvature on formation of an ILA is −4π (Eq. 5, Fig. 2). Thus the difference in energy between an ILA and an equivalent area of Lα phase lipid is
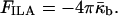 |
(6) |
Eq. 6 shows that ILAs formation is also favored for 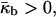 as is QII phase formation.
as is QII phase formation.
FIGURE 2.
The change in the integrated Gaussian curvature accompanying ILA formation. The integrated Gaussian curvature of a closed bilayer structure is given by Eq. 5 (reproduced at the top of the figure). (Top) Two closed liposomes each have a genus g = 0 and 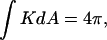 for a total
for a total 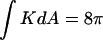 that is equivalent to genus g = −1. (Middle) Formation of a single ILA between the two liposomes (the ILAs are shown in cross section, with the axis indicated by dashed line). The result is a single liposome, with g = 0, and
that is equivalent to genus g = −1. (Middle) Formation of a single ILA between the two liposomes (the ILAs are shown in cross section, with the axis indicated by dashed line). The result is a single liposome, with g = 0, and 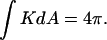 (Bottom) Formation of another ILA between the same two liposomes results in the topological equivalent of a sphere with one “handle” (g = 1), with
(Bottom) Formation of another ILA between the same two liposomes results in the topological equivalent of a sphere with one “handle” (g = 1), with 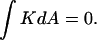 For formation of each ILA, the reduction in K of the total system is −4π. This would occur if the ILAs formed between liposomes, as indicated, or between concentric shells of a multilamellar structure (i.e., in MLVs of bulk Lα phase).
For formation of each ILA, the reduction in K of the total system is −4π. This would occur if the ILAs formed between liposomes, as indicated, or between concentric shells of a multilamellar structure (i.e., in MLVs of bulk Lα phase).
Lamellar-bicontinuous cubic-inverted hexagonal phase diagram
The criterion for QII phase formation (Eq. 4), accounting for Eq. 3, can be presented in the form
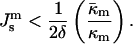 |
(7) |
At T = TQ, where FILA = 0, and the monolayer spontaneous curvature is 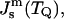 the ratio of the moduli can be presented as
the ratio of the moduli can be presented as
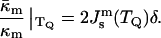 |
(8) |
By comparison, the free energy difference between the HII phase and Lα phase per lipid molecule is (Hamm and Kozlov, 1998)
 |
(9) |
where κt is the chain tilt modulus and a is the area/lipid molecules at the neutral plane. Since the free energy difference must vanish at the Lα–HII phase transition temperature, 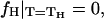 we can use Eq. 9 to express κt through the spontaneous curvature at the transition point,
we can use Eq. 9 to express κt through the spontaneous curvature at the transition point, 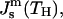 and present the energy of the HII phase in the form
and present the energy of the HII phase in the form
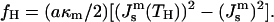 |
(10) |
Based on Eq. 10, the criterion of the Lα/HII transition, fH ≤ 0, is
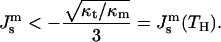 |
(11) |
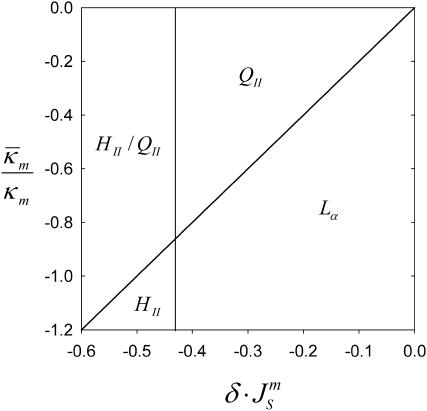
Thus, using Eqs. 7 and 11, a simple phase diagram can be presented in terms of the ratio 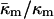 and
and 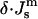 (Fig. 3). Systems with the ratio above the slanted line will form QII phases with decreasing
(Fig. 3). Systems with the ratio above the slanted line will form QII phases with decreasing 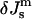 until the HII phase boundary is encountered. At lower values of
until the HII phase boundary is encountered. At lower values of 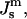 either a mixture of HII and QII phases, or pure HII phase, will be found. Whether or not QII phase will appear or predominate in the region indicated as HII–QII (Fig. 3) will depend on the specific values of the unit cell parameters and the space group of the QII phases that form. More accurate models for ΔF are needed to predict the diagram in this region.
either a mixture of HII and QII phases, or pure HII phase, will be found. Whether or not QII phase will appear or predominate in the region indicated as HII–QII (Fig. 3) will depend on the specific values of the unit cell parameters and the space group of the QII phases that form. More accurate models for ΔF are needed to predict the diagram in this region.
FIGURE 3.
Phase diagram showing the phases expected to be most stable as a function of the product 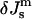 and the ratio of the monolayer Gaussian curvature elastic and bending elastic moduli,
and the ratio of the monolayer Gaussian curvature elastic and bending elastic moduli, 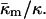 The present model cannot predict which phase will predominate in the HII/QII region.
The present model cannot predict which phase will predominate in the HII/QII region.
The tilt modulus appears in the expression for HII lipid free energy (Eqs. 9 and 10), and not in the expression for the free energy of QII phase lipid (Eq. 2). The reason for that is tilt deformation of the hydrocarbon chains, which is generated within the nonbilayer structural defects forming unavoidably in the HII phase and referred to as hydrophobic interstices (Hamm and Kozlov, 1998, 2000). In contrast, the bicontinuous cubic phases (QII) consist of intact lipid bilayers, which do not include nonbilayer structures and, hence, do not require tilt deformation.
Data from the phase behavior of DOPE-Me and related phospholipids
Several properties of the Lα/QII phase transition in DOPE-Me, and some properties of related lipids, are relevant to our calculations.
With increasing temperature, QII phase is first observed in a narrow band of temperature at ∼60°C (Siegel and Banschbach, 1990; Cherezov et al., 2003). Careful observations indicate that it first forms in DOPE-Me at 55°C, although only after a delay of several hours (Cherezov et al., 2003). The transition is very slow in the heating direction, with considerable scan rate dependence, and is extremely hysteretic in the cooling direction. HII phase first forms (after long incubations at constant temperature) at ∼61°C.
ILAs have been observed in DOPE-Me at temperatures below TQ, via electron microscopy and 31P NMR; most of the time via NMR. This is often reported to start at ∼40°C (Gagné et al., 1985; Ellens et al., 1989; Siegel et al., 1989a,b; Yeagle et al., 1991; Epand et al., 1994), although it is occasionally observed starting at temperatures of 50°C or above (van Gorkum et al., 1992; Epand and Epand, 1994; Davies et al., 1998). However, the isotropic resonance characteristic of ILAs and QII phase can be detected when it constitutes as little as 1% of the total resonance intensity (Ellens et al., 1989; Yeagle et al., 1991). Typically <10% of the intensity is present in the isotropic component when the temperature reaches 50°C (Yeagle et al., 1991). Therefore, the temperature at which the free energy of lipid in ILAs and flat bilayers is equal, where we would expect coexistence of the two types of structure, is probably close to the observed value of TQ of 55°C.
The lattice parameter of the first QII phases to form in DOPE-Me is on the order of 30 nm (Cherezov et al., 2003), and the first QII phase to form is almost always QII (Pn3m). The large lattice parameter is significant because chain stretching contributions to the free energy of minimal surface-based ILAs and the QII phase should be negligible under these circumstances (Schwarz and Gompper, 2001), and higher-order Gaussian curvature effects are likely to be small. Therefore, the model we use here should give a reasonably accurate account of the threshold value of
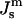 for ILA and QII phase formation.
for ILA and QII phase formation.Js is measured by x-ray diffraction experiments on HII phases as a function of osmotic pressure. This has not been done for DOPE-Me, although
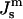 has been measured at one temperature for DOPE and a DOPE/DOPC mixture (Rand et al., 1990; Leikin et al., 1996; Chen and Rand, 1997).
has been measured at one temperature for DOPE and a DOPE/DOPC mixture (Rand et al., 1990; Leikin et al., 1996; Chen and Rand, 1997). 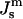 values can be obtained for DOPE-Me if we assume that the distance between the neutral plane and the periphery of the HII tube is the same for DOPE-Me as in these two lipid systems, which have similar lipid headgroups and the same acyl chains. Then
values can be obtained for DOPE-Me if we assume that the distance between the neutral plane and the periphery of the HII tube is the same for DOPE-Me as in these two lipid systems, which have similar lipid headgroups and the same acyl chains. Then 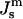 of DOPE-Me in excess water can be obtained as a function of temperature using measurements of the lattice parameter of the HII phase of DOPE-Me in the presence of dodecane (Gruner et al., 1988). Values of
of DOPE-Me in excess water can be obtained as a function of temperature using measurements of the lattice parameter of the HII phase of DOPE-Me in the presence of dodecane (Gruner et al., 1988). Values of 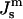 obtained in this manner are given in Table 1.
obtained in this manner are given in Table 1.The value of κm has not been determined for DOPE-Me, but it has been measured for DOPE and for DOPC at 22°C (Chen and Rand, 1997) as 11 and 9 kBT, respectively, where kB is Boltzmann's constant. Since DOPC is triply methylated DOPE, we assume that the value for DOPE-Me is intermediate between the values for DOPE and DOPC, and use the value 10 kBT.
We assume that the neutral plane is near the interface between the hydrophilic and hydrophobic regions of the monolayer. Using data from Rand and Parsegian (1989) for monomethylated egg PE, we estimate δ = 1.3 nm. This value is uncertain to within ∼10%.
TABLE 1.
Values of spontaneous curvature for DOPE-Me at relevant temperatures
| Temperature (°C) |
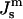 (nm−1) (nm−1) |
|---|---|
| 50 | −0.316 |
| 55 | −0.322 |
| 60 | −0.328 |
| 65 | −0.334 |
| 70 | −0.341 |
| 75 | −0.347 |
Temperatures were calculated using data from Gruner et al. (1988), as described in the text. Js was calculated at temperatures between 20 and 75°C, and can be fitted with the equation 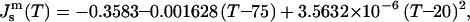 where T is in °C. The error with respect to the derived values is 0.3% or less, which is within the error of the measurements themselves.
where T is in °C. The error with respect to the derived values is 0.3% or less, which is within the error of the measurements themselves.
The Gaussian curvature elastic modulus of DOPE-Me
With TQ for DOPE-Me = 55°C, we find from Table 1 that 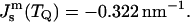 With δ = 1.3 nm, we find from Eq. 8 that
With δ = 1.3 nm, we find from Eq. 8 that
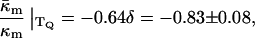 |
(12) |
where the uncertainty is due to the uncertainty in δ (±10%). In comparison, a 10° error in TQ changes the ratio of the constants by only 4–5%. With κm = 10 kBT, 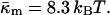 It should be noted that this value is measured at T = TQ ≈ 55°C. The temperature dependence of
It should be noted that this value is measured at T = TQ ≈ 55°C. The temperature dependence of 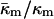 (i.e., the value at temperatures far from TQ) is unknown.
(i.e., the value at temperatures far from TQ) is unknown.
Free energy of QII phase as a function of Js and temperature
The free energy of QII phases is a complicated function of the unit cell parameter c, details of the geometry of the IPMS that is the basis of the particular QII phase, and the lipid volume fraction, as well as 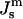 and the values of the elastic constants (Schwarz and Gompper, 2001, 2002). A detailed analysis of the temperature-dependent free energy of the QII phase in DOPE-Me is beyond the scope of this work. However, we would like to estimate the free energy of lipid in the first QII phase to form as a function of decreasing
and the values of the elastic constants (Schwarz and Gompper, 2001, 2002). A detailed analysis of the temperature-dependent free energy of the QII phase in DOPE-Me is beyond the scope of this work. However, we would like to estimate the free energy of lipid in the first QII phase to form as a function of decreasing 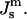 The first QII phase to form in DOPE-Me during temperature-scan or constant-temperature incubation experiments is almost always the Pn3m phase, and c is initially 30 nm or more (Cherezov et al., 2003). The c values generally decrease rapidly after formation (e.g., in one case, c decreases from almost 35 nm to 28 nm in 20 min, and then to 26 nm over the next 1.5 h). The equilibrium values of c are smaller than the initial values observed at any temperature, and the equilibrium values fall rapidly with increasing temperature. For the large value of c corresponding to the initial lattice, the density of Gaussian curvature will be comparatively low. Accordingly, using Eqs. 2 and 5, we estimate the free energy fQ per lipid molecule in this initial lattice relative to the Lα phase,
The first QII phase to form in DOPE-Me during temperature-scan or constant-temperature incubation experiments is almost always the Pn3m phase, and c is initially 30 nm or more (Cherezov et al., 2003). The c values generally decrease rapidly after formation (e.g., in one case, c decreases from almost 35 nm to 28 nm in 20 min, and then to 26 nm over the next 1.5 h). The equilibrium values of c are smaller than the initial values observed at any temperature, and the equilibrium values fall rapidly with increasing temperature. For the large value of c corresponding to the initial lattice, the density of Gaussian curvature will be comparatively low. Accordingly, using Eqs. 2 and 5, we estimate the free energy fQ per lipid molecule in this initial lattice relative to the Lα phase,
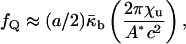 |
(13) |
where a is the area per lipid molecules at the neutral plane; χu and A* are the Euler characteristic of the unit cell, and the surface area of the unit cell (for unit lattice parameter), respectively, of the IPMS that is the structural basis of the QII. For QII–Pn3m, this is the D surface, for which A* = 3.838 and χu = −16 (Schwarz and Gompper, 2001). The term inside the brackets is the area average of the Gaussian curvature in the QII–Pn3m phase for which χu < 0. Eq. 13 cannot describe the free energy of the equilibrium phase, because it indicates that c would shrink indefinitely. The rapid decrease of c after QII phase formation is as expected because, initially, 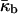 must be positive. However, c stabilizes at an equilibrium value. The increase of the frustration elastic energy (Anderson et al., 1988) at small c is, probably, the factor that halts the collapse of the unit cell in practice (Schwarz and Gompper, 2002). Using κm = 10 kBT and
must be positive. However, c stabilizes at an equilibrium value. The increase of the frustration elastic energy (Anderson et al., 1988) at small c is, probably, the factor that halts the collapse of the unit cell in practice (Schwarz and Gompper, 2002). Using κm = 10 kBT and 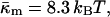 the free energy of an ILA in DOPE-Me, FILA (Eq. 6), is plotted as a function of Js in Fig. 4. The values of
the free energy of an ILA in DOPE-Me, FILA (Eq. 6), is plotted as a function of Js in Fig. 4. The values of 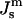 corresponding to TQ and TQ ± 10°C are indicated, to emphasize the slow change in FILA with temperature in the lamellar/nonlamellar phase transition interval. The values fQ (Eq. 13) and fH (Eq. 10) are plotted as a function of
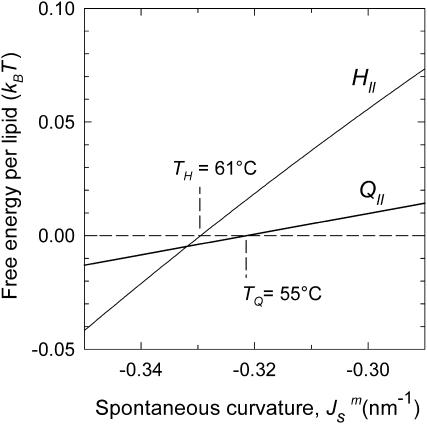
corresponding to TQ and TQ ± 10°C are indicated, to emphasize the slow change in FILA with temperature in the lamellar/nonlamellar phase transition interval. The values fQ (Eq. 13) and fH (Eq. 10) are plotted as a function of 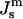 in Fig. 5. The rate of change with temperature of fQ is smaller than for fH.
in Fig. 5. The rate of change with temperature of fQ is smaller than for fH.
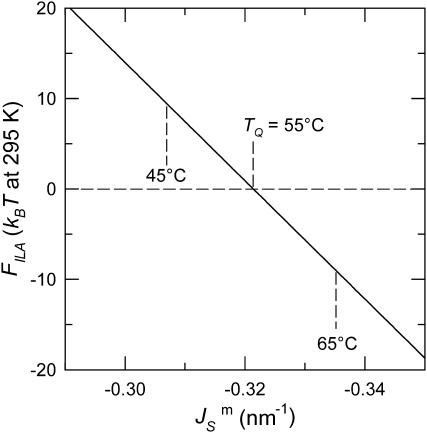
FIGURE 4.
Plot of the free energy of an ILA with respect to an equivalent amount of Lα phase lipid as a function of 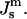 The values of
The values of 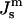 corresponding to temperatures 10 K above and below TQ are indicated by dashed vertical lines. The unit of energy is kBT evaluated at 295 K.
corresponding to temperatures 10 K above and below TQ are indicated by dashed vertical lines. The unit of energy is kBT evaluated at 295 K.
FIGURE 5.
Comparison of the driving force for formation of the initial QII phase lattice and bulk HII phase as a function of 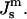 The
The 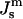 values corresponding to TQ and TH are indicated. The driving force for HII phase formation increases with decreasing
values corresponding to TQ and TH are indicated. The driving force for HII phase formation increases with decreasing 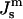 (increasing T) much faster than the QII phase.
(increasing T) much faster than the QII phase.
DISCUSSION
The value of 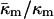 derived here from TQ is in accord with theoretical expectations. The value required for stability of lamellar and QII phases is −2 <
derived here from TQ is in accord with theoretical expectations. The value required for stability of lamellar and QII phases is −2 < 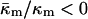 (Schwarz and Gompper, 2001, 2002), and it has been argued that there is the further restriction −1 <
(Schwarz and Gompper, 2001, 2002), and it has been argued that there is the further restriction −1 < 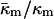 (Templer et al., 1998). The value of
(Templer et al., 1998). The value of 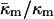 determined here for DOPE-Me, −0.83 ± 0.08, is also comparable to the value for DOPE estimated from studies of R phase stability (Y. Kozlovsky, D. P. Siegel, and M. M. Kozlov, unpublished results). It is also close to the value of −0.75 ± 0.08 calculated from a study of the swelling of a QII phase of monoolein/DOPC/DOPE = 58/38/4 (Templer et al., 1998). To our knowledge, the value determined in this study is the first measurement in a system consisting only of phospholipid.
determined here for DOPE-Me, −0.83 ± 0.08, is also comparable to the value for DOPE estimated from studies of R phase stability (Y. Kozlovsky, D. P. Siegel, and M. M. Kozlov, unpublished results). It is also close to the value of −0.75 ± 0.08 calculated from a study of the swelling of a QII phase of monoolein/DOPC/DOPE = 58/38/4 (Templer et al., 1998). To our knowledge, the value determined in this study is the first measurement in a system consisting only of phospholipid.
The present analysis is possible because DOPE-Me, a single lipid component system, has a well-defined TQ. To our knowledge, TQ values have not been reported for other phospholipids. Multicomponent lipid systems that form QII phases would be difficult to analyze in this way because of possible differences in lipid composition of the two phases at the transition temperature.
Is the value of 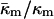 determined here relevant to biomembrane lipids? PE is the most abundant inverted phase-forming lipid in mammalian cell membranes. The values of
determined here relevant to biomembrane lipids? PE is the most abundant inverted phase-forming lipid in mammalian cell membranes. The values of 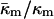 for PEs, PE-rich mixtures of PE and PC, and PE/PC/cholesterol mixtures should be similar to the value determined here for DOPE-Me. PE/PC mixtures form ILAs at temperatures 10–15° below TH (e.g., up to a DOPC/DOPE ratio of 1:2 mol/mol; Ellens et al., 1989). Mixtures of DOPE, DOPC, and cholesterol form ILAs and/or QII phases below TH across a wide range of PE/PC ratio (Tilcock et al., 1982). This is the same behavior observed in DOPE-Me. As with DOPE-Me, this means that TQ ≈ TH. Hence
for PEs, PE-rich mixtures of PE and PC, and PE/PC/cholesterol mixtures should be similar to the value determined here for DOPE-Me. PE/PC mixtures form ILAs at temperatures 10–15° below TH (e.g., up to a DOPC/DOPE ratio of 1:2 mol/mol; Ellens et al., 1989). Mixtures of DOPE, DOPC, and cholesterol form ILAs and/or QII phases below TH across a wide range of PE/PC ratio (Tilcock et al., 1982). This is the same behavior observed in DOPE-Me. As with DOPE-Me, this means that TQ ≈ TH. Hence 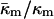 should have approximately the same value as for DOPE-Me. Pure PEs (DOPE, DiPoPE, and DEPE) do not form QII phase upon heating through TH, but they do form QII phases when the temperature is cycled repeatedly between temperatures ∼10°C below and above TH (Shymasunder et al., 1988; Erbes et al., 1994; Tenchov et al., 1998). This implies that TQ is greater than TH, but not much greater. Using Eqs. 8, 10 and 11, the expected value for
should have approximately the same value as for DOPE-Me. Pure PEs (DOPE, DiPoPE, and DEPE) do not form QII phase upon heating through TH, but they do form QII phases when the temperature is cycled repeatedly between temperatures ∼10°C below and above TH (Shymasunder et al., 1988; Erbes et al., 1994; Tenchov et al., 1998). This implies that TQ is greater than TH, but not much greater. Using Eqs. 8, 10 and 11, the expected value for 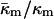 when TQ = TH is
when TQ = TH is
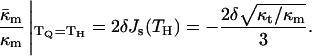 |
(14) |
Using 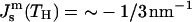 for PEs near TH (e.g., Gruner et al., 1988; Tate and Gruner, 1989), or alternatively κt = 0.04 N/m (Hamm and Kozlov, 1998) and κm = 4 × 10−20 J, we estimate the value of the ratio for pure PEs to be
for PEs near TH (e.g., Gruner et al., 1988; Tate and Gruner, 1989), or alternatively κt = 0.04 N/m (Hamm and Kozlov, 1998) and κm = 4 × 10−20 J, we estimate the value of the ratio for pure PEs to be
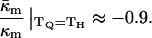 |
(15) |
Note that for any given PE, Eq. 15 is strictly valid only at TQ ≈ TH. The value in Eq. 15 is more negative than the range −0.6 to −0.3 predicted by Y. Kozlovsky, D. P. Siegel, and M. M. Kozlov (unpublished results) for DOPE at room temperature. This may be due partly to the temperature dependence of 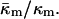 The TH of DOPE (3°C; Toombes et al., 2002) is substantially different from room temperature. It is not known how rapidly
The TH of DOPE (3°C; Toombes et al., 2002) is substantially different from room temperature. It is not known how rapidly 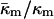 changes with temperature away from TQ. Also, the fact that κm has most often been measured near room temperature makes it difficult to estimate
changes with temperature away from TQ. Also, the fact that κm has most often been measured near room temperature makes it difficult to estimate 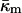 itself via Eq. 15 for lipids with TQ far away from room temperature.
itself via Eq. 15 for lipids with TQ far away from room temperature.
Eq. 15 shows that the stability of QII phases is in sensitive balance in PEs, their derivatives, and their mixtures with PC and PC/cholesterol. For example, if a change in system composition slightly increases 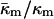 in a pure PE, QII phases may appear spontaneously where none did before. The value
in a pure PE, QII phases may appear spontaneously where none did before. The value 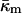 is the second moment of the lateral pressure profile in the lipid monolayer (Helfrich, 1990). As such, it might be very sensitive to small changes in the effective volume of, or interactions between, lipid (or lipid and peptide) moieties at different planes in the monolayer. This might explain the surprisingly large effect of hydrophobic or transmembrane peptides on QII phase stability (Keller et al., 1996; Morein et al., 2000; Liu et al., 2001; D. P. Siegel, V. Cherezov, D. V. Greathouse, R. E. Koeppe, J. A. Killian, and M. Caffrey, unpublished observations). It might also explain the effects of aqueous solutes on the kinetics of QII phase formation in temperature-cycled DEPE (Tenchov et al., 1998). The lipid compositions of some biomembranes may be close to the Lα–QII phase boundary. For example, cholesterol, a ubiquitous membrane constituent, induces QII phases in POPE (Wang and Quinn, 2002). Moreover, recently it has been found that mixtures of PC and cholesterol (i.e., with no inverted phase-preferring lipid) form numerous ILAs at ∼40°C, as determined via 31P NMR (Epand et al., 2003, 2004).
is the second moment of the lateral pressure profile in the lipid monolayer (Helfrich, 1990). As such, it might be very sensitive to small changes in the effective volume of, or interactions between, lipid (or lipid and peptide) moieties at different planes in the monolayer. This might explain the surprisingly large effect of hydrophobic or transmembrane peptides on QII phase stability (Keller et al., 1996; Morein et al., 2000; Liu et al., 2001; D. P. Siegel, V. Cherezov, D. V. Greathouse, R. E. Koeppe, J. A. Killian, and M. Caffrey, unpublished observations). It might also explain the effects of aqueous solutes on the kinetics of QII phase formation in temperature-cycled DEPE (Tenchov et al., 1998). The lipid compositions of some biomembranes may be close to the Lα–QII phase boundary. For example, cholesterol, a ubiquitous membrane constituent, induces QII phases in POPE (Wang and Quinn, 2002). Moreover, recently it has been found that mixtures of PC and cholesterol (i.e., with no inverted phase-preferring lipid) form numerous ILAs at ∼40°C, as determined via 31P NMR (Epand et al., 2003, 2004).
Implications for membrane fusion intermediates
The Gaussian curvature energy term in Eqs. A8 and A9 has usually been neglected in computing the energies of fusion intermediates on the basis of the monolayer curvature elastic energies (Siegel, 1999; Kozlovsky and Kozlov, 2002; Kozlovsky et al., 2002; Markin and Albanesi, 2002). However, recent work on the stability of the stalk phase has shown that Gaussian curvature elastic energies can make substantial contributions to stalk stability (Y. Kozlovsky, D. P. Siegel, and M. M. Kozlov, unpublished results). The value measured here for a phospholipid is comparable to the value of bending modulus, κm, and confirms that this is true. The Gaussian curvature elastic energy has a very substantial affect on the stability of fusion pores. Previous authors (Siegel, 1993, 1999; Markin and Albanesi, 2002) calculated the energy of the fusion pore on a monolayer basis (Eqs. A8 and A9) with the assumption that 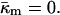 For a fusion pore with minimal curvature (zero bilayer curvature; Jb = 0), comparison with Eqs. 1, 3, A8, and A9 show that this approach underestimates the energy by
For a fusion pore with minimal curvature (zero bilayer curvature; Jb = 0), comparison with Eqs. 1, 3, A8, and A9 show that this approach underestimates the energy by 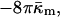 or 200 kBT, if we use the value of
or 200 kBT, if we use the value of 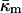 for DOPE-Me. Thus, fusion pores are much higher in energy than estimated solely on the basis of the monolayer bending elastic energy. The data in Fig. 4 show that phospholipid fusion pores can be higher in energy than an equal amount of lamellar phase lipid at physiological temperatures, depending on the values of the elastic moduli and the monolayer spontaneous curvature
for DOPE-Me. Thus, fusion pores are much higher in energy than estimated solely on the basis of the monolayer bending elastic energy. The data in Fig. 4 show that phospholipid fusion pores can be higher in energy than an equal amount of lamellar phase lipid at physiological temperatures, depending on the values of the elastic moduli and the monolayer spontaneous curvature 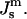 An important function of fusion proteins in biomembranes may be to stabilize nascent fusion pores. This is an activity inferred by others from recent experimental studies of viral fusion proteins (Markosyan et al., 2000). It has been proposed that protein coats of viruses act cooperatively to stabilize an expanding fusion pore (Kozlov and Chernomordik, 2002). The transmembrane domains of fusion-catalyzing proteins may play a similar role, based on their ability to lower TQ. The measurement of
An important function of fusion proteins in biomembranes may be to stabilize nascent fusion pores. This is an activity inferred by others from recent experimental studies of viral fusion proteins (Markosyan et al., 2000). It has been proposed that protein coats of viruses act cooperatively to stabilize an expanding fusion pore (Kozlov and Chernomordik, 2002). The transmembrane domains of fusion-catalyzing proteins may play a similar role, based on their ability to lower TQ. The measurement of 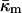 in the present work emphasizes the potential importance of such an effect.
in the present work emphasizes the potential importance of such an effect.
Implications for the mechanism of transitions between Lα, QII, and HII phases
Siegel and Epand (1997) and Siegel (1999) proposed a stalk-based mechanism for the transitions between lamellar and nonlamellar phases. The theory neglected the effects of the Gaussian curvature energy, and hence estimated ILA energies that are far too low. This resulted in a prediction that ILAs should be thermodynamically stable in the temperature interval between the chain-melting (gel/liquid crystalline transition) temperature, Tm, and some temperature >TH. Siegel (1999) did estimate the size of the effect of Gaussian curvature energy on ILA stability, but used a value estimated for monoglycerides by Chung and Caffrey (1994) from studies of QII phase swelling in water. The procedure used to calculate this value of 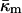 has been questioned (Templer et al., 1995), and the value is much smaller than the present value for DOPE-Me. Siegel (1999) proposed that ILAs, and perhaps QII phase, did not form at temperatures far below TH because some other factor, like the membrane rupture tension, inhibited ILA formation under these circumstances. In view of the large value of
has been questioned (Templer et al., 1995), and the value is much smaller than the present value for DOPE-Me. Siegel (1999) proposed that ILAs, and perhaps QII phase, did not form at temperatures far below TH because some other factor, like the membrane rupture tension, inhibited ILA formation under these circumstances. In view of the large value of 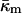 measure here, a better explanation is that ILAs do not become thermodynamically stable until the temperature reaches the vicinity of TH in DOPE-Me. Presumably, small numbers of ILAs can form at temperatures as low as 40°C or 50°C because the ILA free energy is within 13 kBT or 4 kBT, respectively, of the free energy of an equivalent amount of Lα phase lipid (Fig. 4). This may also be another reason why temperature cycling through TH has been observed to produce QII phases in PEs that do not form them during temperature ramp experiments (Shyamsunder et al.; 1988; Veiro et al., 1990; Tenchov et al., 1998). According to Eqs. 3 and 6, ILAs may not be stable at
measure here, a better explanation is that ILAs do not become thermodynamically stable until the temperature reaches the vicinity of TH in DOPE-Me. Presumably, small numbers of ILAs can form at temperatures as low as 40°C or 50°C because the ILA free energy is within 13 kBT or 4 kBT, respectively, of the free energy of an equivalent amount of Lα phase lipid (Fig. 4). This may also be another reason why temperature cycling through TH has been observed to produce QII phases in PEs that do not form them during temperature ramp experiments (Shyamsunder et al.; 1988; Veiro et al., 1990; Tenchov et al., 1998). According to Eqs. 3 and 6, ILAs may not be stable at 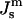 values corresponding to temperatures lower than TH, but a few accumulate each time the temperature exceeds TH. These persist below TH because ILAs are kinetically trapped, and are present unless the lipid composition is frozen below the main transition temperature Tm (Cullis et al., 1978; Ellens et al., 1986, 1989).
values corresponding to temperatures lower than TH, but a few accumulate each time the temperature exceeds TH. These persist below TH because ILAs are kinetically trapped, and are present unless the lipid composition is frozen below the main transition temperature Tm (Cullis et al., 1978; Ellens et al., 1986, 1989).
In DOPE-Me, TQ and TH are close together (Siegel and Banschbach, 1990; Cherezov et al., 2003). The rates of the Lα–HII and Lα–QII phase transitions are in kinetic competition in the temperature interval above TQ (Cherezov et al., 2003), with the rate of HII phase formation predominating at higher temperatures. Cherezov et al. (2003) explained this in terms of the transition mechanism. The HII phase nucleates from clusters of ILA precursors, which subsequently grow rapidly by diffusion. In contrast, the QII phase accrues by formation of individual ILAs and slow subsequent arrangement of these structures into arrays and then QII phase. This is still a reasonable explanation. The data in Fig. 5, however, provide an additional explanation for the preponderance of the HII phase formation rate at higher temperatures: the thermodynamic driving force for HII phase formation increases more rapidly than the driving force for formation of the initial QII lattice in this temperature interval. Note that the free energy fQ (Eq. 13) plotted in Fig. 5 refers to the initial QII phase lattice. The free energy of the equilibrium QII phase, which has a smaller lattice constant (Cherezov et al., 2003), may be quite different. It remains to be seen why the QII lattice constant is initially so much larger than the equilibrium values.
Siegel and Epand (1997) and Siegel (1999) proposed that transitions between Lα, QII, and HII phases occur via formation of stalks and transmonolayer contacts (TMCs). The latter structures are similar to the early stages of growth of the hemifusion diaphragms described by Kozlovsky et al. (2002). Siegel (1999) pointed out that TMCs appeared to have too high an energy to form in large enough numbers to mediate the lamellar/nonlamellar phase transitions. The work of Kozlovsky et al. (2002) shows that the bending and interstitial energies of such structures are much lower than calculated by Siegel (1999); so much so that they would have been thermodynamically stable under conditions where no such phases are observed. The large negative value of 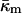 determined here increases the predicted energies of these structures to values roughly consistent with both the observations of rhombohedral phase formation in phospholipids (Y. Kozlovsky, D. P. Siegel, and M. M. Kozlov, unpublished results) and with observed rates of membrane fusion. We are approaching an understanding of the energetics of lipid intermediates in membrane fusion and lipid phase transitions.
determined here increases the predicted energies of these structures to values roughly consistent with both the observations of rhombohedral phase formation in phospholipids (Y. Kozlovsky, D. P. Siegel, and M. M. Kozlov, unpublished results) and with observed rates of membrane fusion. We are approaching an understanding of the energetics of lipid intermediates in membrane fusion and lipid phase transitions.
Acknowledgments
We are grateful to Leonid Chernomordik for useful comments.
M.M.K. thanks the Human Frontier Science Program Organization, the Israel Science Foundation (grant 75/03), and the Binational USA-Israel Science Foundation for financial support.
APPENDIX A
Let us assume that the bilayer is symmetric, i.e., each monolayer has the same spontaneous curvature, 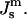 The bending modulus of a monolayer is κm and the Gaussian modulus of a monolayer is
The bending modulus of a monolayer is κm and the Gaussian modulus of a monolayer is 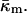 We describe the bilayer in terms of the area A of its midplane. The mean and Gaussian curvatures of the bilayer midplane are denoted by J and K, respectively. The neutral surface of each of the monolayers (Kozlov and Winterhalter, 1991) is shifted by a distance δ from the bilayer midplane.
We describe the bilayer in terms of the area A of its midplane. The mean and Gaussian curvatures of the bilayer midplane are denoted by J and K, respectively. The neutral surface of each of the monolayers (Kozlov and Winterhalter, 1991) is shifted by a distance δ from the bilayer midplane.
The areas of the neutral surfaces of the outer and inner monolayers corresponding to the area A of the bilayer midplane are (do Carmo, 1976)
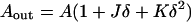 |
(A1) |
and
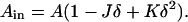 |
(A2) |
The total and Gaussian curvatures of the two monolayers are (do Carmo, 1976)
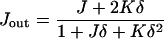 |
(A3) |
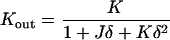 |
(A4) |
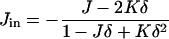 |
(A5) |
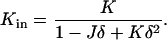 |
(A6) |
The energy of the bilayer in terms of the bending energy of the constituent monolayers is
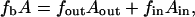 |
(A7) |
where fout and fin are the curvature energies of the outer and inner monolayers, respectively, and
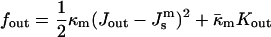 |
(A8) |
 |
(A9) |
where κm and 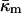 are the bending elastic modulus and Gaussian curvature modulus, respectively, of the lipid monolayers. We insert Eqs. A1–A6 into Eqs. A7–A9. If we make the approximation that
are the bending elastic modulus and Gaussian curvature modulus, respectively, of the lipid monolayers. We insert Eqs. A1–A6 into Eqs. A7–A9. If we make the approximation that
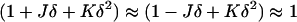 |
(A10) |
and retain terms only up to the first power of δ, we obtain
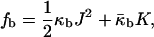 |
(A11) |
where the bilayer elastic coefficients are
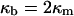 |
(A12) |
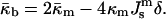 |
(A13) |
In deriving Eqs. A11–A13, the bilayer spontaneous curvature vanishes, 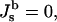 because the spontaneous curvatures of the monolayers are equal. The bilayer bending modulus is twice that of the monolayer (assuming that the monolayers can slide with respect to each other). Retaining terms with δ2 in Eq. A11 produces a term = 4κm δ2K2. Retaining this term has a negligible effect on the calculated value of
because the spontaneous curvatures of the monolayers are equal. The bilayer bending modulus is twice that of the monolayer (assuming that the monolayers can slide with respect to each other). Retaining terms with δ2 in Eq. A11 produces a term = 4κm δ2K2. Retaining this term has a negligible effect on the calculated value of 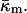 Eq. A10 is correct to within 3% for the QII phases dealt with in the present work.
Eq. A10 is correct to within 3% for the QII phases dealt with in the present work.
References
- Anderson, D. M., S. M. Gruner, and S. Leibler. 1988. Geometrical aspects of the frustration in the cubic phases of lyotropic liquid crystals. Proc. Natl. Acad. Sci. USA. 85:5364–5368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ben-Shaul, A. 1995. Molecular theory of chain packing, elasticity and lipid-protein interaction in lipid bilayers. In Structure and Dynamics of Membranes. R. Lipowsky, and E. Sackmann, editors. Elsevier, Amsterdam, The Netherlands.
- Chen, Z., and R. P. Rand. 1997. The influence of cholesterol on phospholipid membrane curvature and bending elasticity. Biophys. J. 73:267–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cherezov, V., D. P. Siegel, W. Shaw, S. W. Burgess, and M. Caffrey. 2003. The kinetics of non-lamellar phase formation in DOPE-Me: relevance to biomembrane fusion. J. Membr. Biol. 195:165–182. [DOI] [PubMed] [Google Scholar]
- Chizmadzhev, Y. A., F. S. Cohen, A. Shcherbakov, and J. Zimmerberg. 1995. Membrane mechanics can account for fusion pore dilation in stages. Biophys. J. 69:2489–2500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung, H., and M. Caffrey. 1994. The curvature elastic-energy function of the lipid-water cubic mesophases. Nature. 368:224–226. [DOI] [PubMed] [Google Scholar]
- Cullis, P. R., P. W. M. van Dijck, B. de Kruijff, and J. de Gier. 1978. Effects of cholesterol on the properties of equimolar mixtures of synthetic phosphatidylethanolamine and phosphatidylcholine. Biochim. Biophys. Acta. 513:21–30. [DOI] [PubMed] [Google Scholar]
- do Carmo, M. P. 1976. Differential Geometry of Curves and Surfaces. Prentice-Hall, Englewood Cliffs, New Jersey.
- Davies, S. M. A., R. F. Epand, J. P. Bradshaw, and R. M. Epand. 1998. Modulation of lipid polymorphism by the feline leukemia virus fusion peptide: implications for the fusion mechanism. Biochemistry. 37:5720–5729. [DOI] [PubMed] [Google Scholar]
- Ellens, H., J. Bentz, and F. C. Szoka. 1986. Fusion of phosphatidylethanolamine liposomes and the mechanism of the Lα-HII phase transition. Biochemistry. 25:4141–4147. [DOI] [PubMed] [Google Scholar]
- Ellens, H., D. P. Siegel, D. Alford, P. L. Yeagle, L. Boni, L. J. Lis, P. J. Quinn, and J. Bentz. 1989. Membrane fusion and inverted phases. Biochemistry. 28:3692–3703. [DOI] [PubMed] [Google Scholar]
- Epand, R. M., and R. F. Epand. 1994. Relationship between the infectivity of influenza virus and the ability of its fusion peptide to perturb bilayers. Biochem. Biophys. Res. Commun. 202:1420–1425. [DOI] [PubMed] [Google Scholar]
- Epand, R. F., I. Martin, J. M. Ruysschaert, and R. M. Epand. 1994. Membrane orientation of the SIV fusion peptide determines its effect on bilayer stability and ability to promote membrane fusion. Biochem. Biophys. Res. Commun. 205:1938–1943. [DOI] [PubMed] [Google Scholar]
- Epand, R. M., D. W. Hughes, B. G. Sayer, N. Borochov, D. Bach, and E. Wachtel. 2003. Novel properties of cholesterol-dioleoylphosphatidylcholine mixtures. Biochim. Biophys. Acta. 1616:196–208. [DOI] [PubMed] [Google Scholar]
- Epand, R. M., R. F. Epand, A. D. Bain, B. G. Sayer, and D. W. Hughes. 2004. Properties of polyunsaturated phosphatidylcholine membranes in the presence and absence of cholesterol. Magn. Res. Chem. 42:139–147. [DOI] [PubMed] [Google Scholar]
- Erbes, J., C. Czeslik, W. Hahn, R. Winter, M. Rappolt, and G. Rapp. 1994. On the existence of bicontinuous cubic phases in dioleoylphosphatidylethanolamine. Ber. Bunsenges. Phys. Chem. 98:1287–1293. [Google Scholar]
- Gagné, J., L. Stamatatos, T. S. Diacovo, W. Hui, P. L. Yeagle, and J. R. Silvius. 1985. Physical properties and surface interactions of bilayer membranes containing N-methylated phosphatidylethanolamines. Biochemistry. 24:4400–4408. [DOI] [PubMed] [Google Scholar]
- Gruner, S. M., M. W. Tate, G. L. Kirk, P. T. C. So, D. C. Turner, D. T. Keane, C. P. S. Tilcock, and P. R. Cullis. 1988. X-ray diffraction study of the polymorphic behavior of N-methylated dioleoylphosphatidylethanolamine. Biochemistry. 27:2853–2866. [DOI] [PubMed] [Google Scholar]
- Hamm, M., and M. M. Kozlov. 1998. Tilt model of inverted amphiphilic mesophases. Eur. Phys. J. B. 6:519–528. [Google Scholar]
- Hamm, M., and M. M. Kozlov. 2000. Elastic energy of tilt and bending of fluid membranes. Eur. Phys. J. E. 3:323–335. [Google Scholar]
- Harbich, W., R. M. Servuss, and W. Helfrich. 1978. Passages in lecithin-water systems. Z. Naturforsch. 33A:1013–1017. [Google Scholar]
- Helfrich, W. 1973. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. 28C:693–703. [DOI] [PubMed] [Google Scholar]
- Helfrich, W. 1990. Elasticity and thermal undulations of fluid films of amphiphiles. In Liquids at Interfaces. J. Charvolin, J. F. Joanny, and J. Zinn-Justin, editors. Les Houches, France. 212–237.
- Helfrich, W., and H. Rennschuh. 1990. Landau theory of the lamellar-to-cubic phase transition. J. Phys. 51:C7189–C7195. [Google Scholar]
- Keller, S. L., S. M. Gruner, and K. Gawrisch. 1996. Small concentrations of alamethicin induce a cubic phase in bulk phosphatidylethanolamine mixtures. Biochim. Biophys. Acta. 1278:241–246. [DOI] [PubMed] [Google Scholar]
- Kozlov, M. M., and V. S. Markin. 1983. Possible mechanism of membrane fusion. Biofizika. 28:255–261. [PubMed] [Google Scholar]
- Kozlov, M. M., and M. Winterhalter. 1991. Elastic moduli for strongly curved monolayers. Position of the neutral surface. J. Phys. II France. 1:1077–1084. [Google Scholar]
- Kozlov, M. M., S. Leikin, and R. P. Rand. 1994. Bending, hydration and interstitial energies quantitatively account for the hexagonal-lamellar-hexagonal reentrant phase transition in dioleoylphosphatidylethanolamine. Biophys. J. 67:1603–1611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozlov, M. M., and L. V. Chernomordik. 1998. A mechanism of protein-mediated fusion: coupling between refolding of the influenza hemagglutinin and lipid rearrangements. Biophys. J. 75:1384–1396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozlov, M. M., and L. V. Chernomordik. 2002. The protein coat in membrane fusion: lessons from fission. Traffic. 3:256–267. [DOI] [PubMed] [Google Scholar]
- Kozlovsky, Y., L. V. Chernomordik, and M. M. Kozlov. 2002. Lipid intermediates in membrane fusion: formation, structure, and decay of the hemifusion diaphragm. Biophys. J. 83:2634–2651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozlovsky, Y., and M. M. Kozlov. 2002. Stalk model of membrane fusion: solution of energy crisis. Biophys. J. 82:882–895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuzmin, P. I., J. Zimmerberg, Y. A. Chizmadzhev, and F. S. Cohen. 2001. A quantitative model for membrane fusion based on low-energy intermediates. Proc. Nat. Acad. Sci. USA. 98:7235–7240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leikin, S., M. M. Kozlov, N. L. Fuller, and R. P. Rand. 1996. Measured effects of diacylglycerol on structural and elastic properties of phospholipid membranes. Biophys. J. 71:2623–2632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, F., R. N. A. H. Lewis, R. S. Hodges, and R. N. McElhaney. 2001. A differential scanning calorimetry and 31P NMR spectroscopic study of the effect of transmembrane α-helical peptides on the lamellar-reversed hexagonal phased transition of phosphatidylethanolamine model membranes. Biochemistry. 40:760–768. [DOI] [PubMed] [Google Scholar]
- Ljunggren, S., and J. C. Erikkson. 1992. Minimal surfaces and Winsor III microemulsions. Langmuir. 8:1300–1306. [Google Scholar]
- Markin, V. S., and J. P. Albanesi. 2002. Membrane fusion: stalk model revisited. Biophys. J. 82:693–712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markosyan, R. M., F. S. Cohen, and G. B. Melikyan. 2000. The lipid-anchored ectodomain of influenza virus hemagglutinin (GPI-HA) is capable of inducing nonenlarging fusion pores. Mol. Biol. Cell. 11:1143–1152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- May, S. 2002. Structure and energy of fusion stalks: the role of membrane edges. Biophys. J. 83:2969–2980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morein, S., R. E. Koeppe, II, G. Lindblom, B. de Kruijff, and J. A. Killian. 2000. The effect of peptide/lipid hydrophobic mismatch on the phase behavior of model membranes mimicking the lipid composition in Escherichia coli membranes. Biophys. J. 78:2475–2485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nanavati, C., V. S. Markin, A. F. Oberhauser, and J. M. Fernandez. 1992. The exocytotic fusion pore modeled as a lipidic pore. Biophys. J. 63:1118–1132 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrov, A. G., and M. M. Kozlov. 1984. Curvature elasticity and passage formation in lipid bilayer lattice of passages. Comptes Rendu Bulg. Acad. Sci. 1191.
- Rand, R. P., and V. A. Parsegian. 1989. Hydration forces between phospholipid bilayers. Biochim. Biophys. Acta. 988:351–376. [Google Scholar]
- Rand, R. P., N. L. Fuller, S. M. Gruner, and V. A. Parsegian. 1990. Membrane curvature, lipid segregation, and structural transitions for phospholipids under dual-solvent stress. Biochemistry. 29:76–87. [DOI] [PubMed] [Google Scholar]
- Schwarz, U. S., and G. Gompper. 2001. Bending frustration of lipid-water mesophases based on cubic minimal surfaces. Langmuir. 17:2084–2096. [Google Scholar]
- Schwarz, U. S., and G. Gompper. 2002. Bicontinuous surfaces in self-assembling amphiphilic systems. Lect. Notes Phys. 600:107–151. [Google Scholar]
- Shymasunder, E., S. M. Gruner, M. W. Tate, D. C. Turner, P. T. C. So, and C. P. S. Tilcock. 1988. Observation of inverted cubic phase in hydrated dioleoylphosphatidylethanolamine membranes. Biochemistry. 27:2332–2336. [DOI] [PubMed] [Google Scholar]
- Siegel, D. P. 1986. Inverted micellar intermediates and the transitions between lamellar, inverted hexagonal, and cubic lipid phases. III. Formation of isotropic and inverted cubic phases and fusion via intermediates in transitions between Lα and HII phases. Chem. Phys. Lipids. 42:279–301. [DOI] [PubMed] [Google Scholar]
- Siegel, D. P. 1993. Energetics of intermediates in membrane fusion: comparison of stalk and inverted micellar intermediate mechanisms. Biophys. J. 65:2124–2140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel, D. P. 1999. The modified stalk mechanism of lamellar-to-inverted phase transitions and its implications for membrane fusion. Biophys. J. 76:291–313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel, D. P., J. L. Burns, M. H. Chestnut, and Y. Talmon. 1989a. Intermediates in membrane fusion and bilayer/non-bilayer phase transitions imaged by time-resolved cryo-transmission electron microscopy. Biophys. J. 56:161–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel, D. P., J. Banschbach, D. Alford, H. Ellens, L. J. Lis, P. J. Quinn, P. L. Yeagle, and J. Bentz. 1989b. Physiological levels of diacylglycerols in phospholipid membranes induce membrane fusion and stabilize inverted phases. Biochemistry. 28:3703–3709. [DOI] [PubMed] [Google Scholar]
- Siegel, D. P., and J. L. Banschbach. 1990. Lamellar/inverted cubic (Lα/QII) phase transition in N-methylated dioleoylphosphatidylethanolamine. Biochemistry. 29:5975–5981. [DOI] [PubMed] [Google Scholar]
- Siegel, D. P., and R. M. Epand. 1997. The mechanism of lamellar-to-inverted hexagonal phase transitions in phosphatidylethanolamine: implications for membrane fusion. Biophys. J. 73:3089–3111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tate, M. W., and S. M. Gruner. 1989. Temperature dependence of the structural dimensions of the inverted hexagonal (HII) phase of phosphatidylethanolamine-containing membranes. Biochemistry. 28:4245–4253. [DOI] [PubMed] [Google Scholar]
- Templer, R. H., J. M. Seddon, and J. M. Warredner. 1994. Measuring the elastic parameters for inverse bicontinuous cubic phases. Biophys. Chem. 49:1–12. [Google Scholar]
- Templer, R. H., D. C. Turner, P. Harper, and J. M. Seddon. 1995. Corrections to some models of the curvature elastic energy of inverse bicontinuous cubic phases. J. Phys. II France. 5:1053–1065. [Google Scholar]
- Templer, R. H., B. J. Khoo, and J. M. Seddon. 1998. Gaussian curvature modulus of an amphiphile monolayer. Langmuir. 14:7427–7434. [Google Scholar]
- Tenchov, B., R. Koynova, and G. Rapp. 1998. Accelerated formation of cubic phases in phosphatidylethanolamine dispersions. Biophys. J. 75:853–866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas, E. L., D. M. Anderson, C. S. Henkee, and D. Hoffman. 1988. Periodic area-minimizing surfaces in block copolymers. Nature. 334:598–601. [Google Scholar]
- Tilcock, C. P. S., M. B. Bally, S. B. Farren, and P. R. Cullis. 1982. Influence of cholesterol on the structural preferences of dioleoylphosphatidylethanolamine-dioleoylphosphatidylcholine systems: a phosphorous-31 and deuterium nuclear magnetic resonance study. Biochemistry. 21:4596–4601. [DOI] [PubMed] [Google Scholar]
- Toombes, G. E. S., A. C. Finnefrock, M. W. Tate, and S. M. Gruner. 2002. Determination of Lα-HII phase transition temperature for 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine. Biophys. J. 82:2504–2516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner, D. C., Z.-G. Wang, S. M. Gruner, D. A. Mannock, and R. N. McElhaney. 1992. Structural study of the inverted cubic phases of di-dodecyl alkyl-β-D-glucopyranosyl-rac-glycerol. J. Phys. II France. 2:2039–2063. [Google Scholar]
- van Gorkum, L. C. M., S. Q. Nie, and R. M. Epand. 1992. Hydrophobic lipid additives affect membrane stability and phase behavior of N-monomethyldioleoylphosphatidyl-ethanolamine. Biochemistry. 31:671–677. [DOI] [PubMed] [Google Scholar]
- Veiro, J. A., R. G. Khalifaj, and E. S. Rowe. 1990. 31P nuclear magnetic resonance studies of the appearance of an isotropic component in dilauroylphosphatidylethanolamine. Biophys. J. 57:637–641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, X., and P. J. Quinn. 2002. Cubic phase is induced by cholesterol in the dispersion of 1-palmitoyl-2-oleoyl-phosphatidylethanolamine. Biochim. Biophys. Acta. 1564:66–72. [DOI] [PubMed] [Google Scholar]
- Yang, L., and H. W. Huang. 2002. Observation of a membrane fusion intermediate structure. Science. 297:1877–1879. [DOI] [PubMed] [Google Scholar]
- Yang, L., and H. W. Huang. 2003. A rhombohedral phase of lipid containing a membrane fusion intermediate structure. Biophys. J. 84:1808–1817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang, L., L. Ding, and H. W. Huang. 2003. New phases of phospholipids and implications to the membrane fusion problem. Biochemistry. 42:6631–6635. [DOI] [PubMed] [Google Scholar]
- Yeagle, P. L., R. M. Epand, C. D. Richardson, and T. D. Flanagan. 1991. Effects of the “fusion peptide” from measles virus on the structure of N-methyl dioleoylphosphatidylethanolamine membranes and their fusion with Sendai virus. Biochim. Biophys. Acta. 1065:49–53. [DOI] [PubMed] [Google Scholar]