Folding λ-Repressor at Its Speed Limit

Abstract

We show that the five-helix bundle λ_6–85 can be engineered and solvent-tuned to make the transition from activated two-state folding to downhill folding. The transition manifests itself as the appearance of additional dynamics faster than the activated kinetics, followed by the disappearance of the activated kinetics when the bias toward the native state is increased. Our fastest value of 1 μs for the “speed” limit of λ_6–85 is measured at low concentrations of a denaturant that smoothes the free-energy surface. Complete disappearance of the activated phase is obtained in stabilizing glucose buffer. Langevin dynamics on a rough free-energy surface with variable bias toward the native state provides a robust and quantitative description of the transition from activated to downhill folding. Based on our simulation, we estimate the residual energetic frustration of λ_6–85 to be δ² G ≈ 0.64 k²T². We show that λ_6–86, as well as very fast folding proteins or folding intermediates estimated to lie near the speed limit, provide a better rate-topology correlation than proteins with larger energetic frustration. A limit of β ≥ 0.7 on any stretching of λ_6–85 barrier-free dynamics suggests that a low-dimensional free-energy surface is sufficient to describe folding.

INTRODUCTION

It is quite remarkable that the folding reaction of many small proteins can be described by a single rate coefficient (Jackson, 1998), much like an ordinary unimolecular reaction. On a small scale along the reaction coordinate, the energy landscape is multidimensional and rough (Bryngelson and Wolynes, 1987), potentially leading to complicated kinetics. On a larger scale, the decrease of configurational entropy hinders folding, whereas the simultaneous decrease in energy assists folding (Bryngelson et al., 1995). The resulting bottleneck synchronizes the folding reaction, and a single activated timescale 1/k_a can be observed.

In one dimension, the two-state scenario is represented by a double-well free-energy profile with a dominant folding barrier. Kramers' activated rate model can be used when the barrier is sufficiently high (Kramers, 1940). The model's prefactor ν^† introduces an additional timescale for crossing the activated region. It has been measured directly for downhill reactions of small molecules, where the prefactor ranges over a factor of 100 from 10 fs to 1 ps (Gruebele and Zewail, 1990). Many efforts have been made to estimate the prefactor for protein folding reactions. First contact times of nonfolding peptides or proteins provide a lower limit on the time 1/ν^† (Bieri et al., 1999; Chang et al., 2003; Hagen et al., 1996; Lapidus et al., 2000; Qiu et al., 2003). Upper limits can be set by fast two-state (Zhu et al., 2003) or single molecule data (Schuler et al., 2002).

The “speed limit”—the fastest an optimally designed sequence can fold into a specified structure—could be rather short (<1 μs) for small proteins (Yang and Gruebele, 2003) or quite long (>10 μs) for larger proteins. A universal “speed limit” will not apply to all polypeptide chains, just as all small molecules do not have the same prefactor. For a protein, the minimal time required to cross the activated region depends critically on residual nonnative interactions that roughen up the free-energy landscape even in the absence of a major barrier (Bryngelson et al., 1995).

To observe the speed limit, one needs to lower the folding barrier so the activated region is populated. This causes the observed rate coefficient k_a(t) to increase beyond the unimolecular rate “constant” k_a below the “molecular timescale” 1/k_m (Berne, 1993). k_m provides a natural value for the prefactor in activated rate models, as it is the shortest timescale where these models remain valid. We therefore proposed the molecular timescale as a measure for the minimal activation barrier of protein relaxation during folding and unfolding (Yang and Gruebele, 2003):

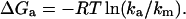(1)

Usually time-varying rate coefficients and the molecular timescale cannot be observed because the barrier is large: preactivated populations are negligible when k_a ≪ k_m. Protein folding reactions, however, have very small barriers compared to most chemical reactions: unfolded proteins react in microseconds to seconds under native conditions, compared to the indefinite shelf life of most organic chemicals. Moreover, a protein's molecular timescale could be rather longer than a nanosecond because of the large amplitude motions through a viscous solvent required to make contacts among amino acid residues. This diffusional motion is further slowed down by residual roughness of the free-energy profile (caused, for example, by nonnative contacts or protein-solvent interactions) (Bryngelson and Wolynes, 1987).

We recently demonstrated that through site-directed mutagenesis, it is possible to lower the folding barrier of the λ-repressor N-terminal domain λ_6–85 so that the molecular timescale can be observed (Yang and Gruebele, 2003). The measured 2 μs molecular timescale for λ_6–85 is significantly slower than collapse or loop formation on smooth free-energy surfaces under nonfolding conditions (Bieri et al., 1999; Chang et al., 2003; Lapidus et al., 2000; Sadqi et al., 2003), indicating that under native conditions the protein free-energy surface has considerable residual roughness that slows down the kinetics. This result is in good agreement with folding calculations for λ_6–85 (Portman et al., 2001b), with general models for kinetic prefactors (Camacho and Thirumalai, 1993, Camacho and Thirumalai, 1995), and with molecular dynamics simulations that have indicated very low folding barriers (Shea and Brooks, 2001).

In this article, we provide new experimental observations and calculations to support these results in more detail. We show that the observation of the molecular timescale is not uniquely associated with the specific mutations used to speed up the λ_6–85 folding rate: equilibrium activated populations disappear again when further mutations that slow down folding are applied. In addition, we demonstrate that the molecular timescale, unlike the activated kinetics, scales inversely with bulk solvent viscosity because it is not sensitive to the change of the free-energy barrier that occurs as a side effect of viscogenic agents (Jacob et al., 1999). This allows a rigorous determination of the role of solvent viscosity in protein folding reactions. The results are explained in terms of Langevin simulations on a rough free-energy surface, to which a native bias is applied by mutations or temperature changes. Finally we discuss that λ_6–85 has important implications for the application of topological folding models based on contact order (Plaxco et al., 1998) for the dimensionality of the folding free-energy surface, and for the origins of energetic frustration (Clementi et al., 2000; Gruebele, 2002).

EXPERIMENTAL METHODS

λ-repressors used in this study

λ_6–85 is an 80-residue, five-helix globular protein whose fold is shown in Fig. 1. The different λ-repressor mutants used here are abbreviated according to Table 1. All six proteins contained the mutations Tyr22Trp and Glu33Tyr. The tryptophan mutation in helix 1 provides a fluorescent probe for folding (Ghaemmaghami et al., 1998), whereas the tyrosine mutation replaces a charged residue by a less polar side chain. These mutations speed up folding and provide a large tryptophan fluorescence-lifetime increase upon unfolding (Yang and Gruebele, 2003). The distinguishing mutations fall into two categories. The first category speeds up folding. S45A, Gly46Ala/Gly48Ala, and S79A increase the helix propensity in helices 3, 4, and 5, respectively. In particular, the Gly→Ala mutations also reduce backbone flexibility required by the protein's DNA binding function. Asp14Ala, which removes a hydrogen bond between positions 14 and 77, also speeds up folding (Myers and Oas, 1999). The second category slows down folding. Ala37Gly and Ala49Gly decrease helix propensity and enhance flexibility in helices 2 and 3, respectively. They cause only small changes to the protein folding rates while destabilizing the protein (low φ-values) (Burton et al., 1997). Combinations of these mutations allow us to speed up and slow down the fast folding λ_6–85 variants.

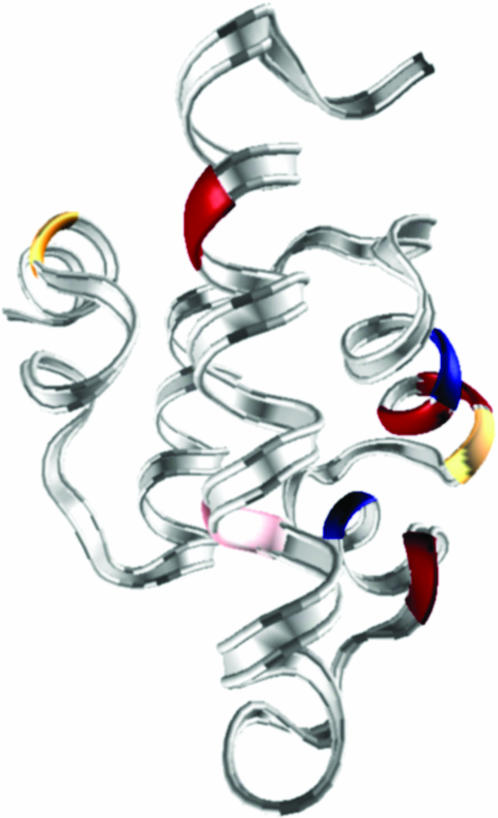
FIGURE 1.

Ribbon structure of λ_6–85 based on the PDB structure 1LMB. D14, Q33, A46, and A48 (rate-accelerating) residues are shown in red, G37 and G49 (rate-decelerating) in blue, and A45 and A79 (rate-accelerating only at high temperature) in yellow. The chromophore W22 is shown in pink. See also Hecht et al. (1984) for early mutant studies.

TABLE 1.

Mutants used in this study, and their maximum activated relaxation rates

Name	Mutations to the protein	Maximum 1/ka and T
λD14A	D14A Y22W Q33Y G46A G48A	9 μs (79°C)
λQ33Y	Y22W Q33Y G46A G48A	20 μs (61°C)
λA37G	Y22W Q33Y A37G	42 μs (56°C)
λS45A	Y22W Q33Y G46A S45A G48A	25 μs (56°C)
λS79A	Y22W Q33Y G46A S45A G48A S79A	24 μs (59°C)
λA49G	D14A Y22W Q33Y A37G G46A G48A A49G	29 μs (54°C)

λ-repressor expression and purification

The λ-repressor N-terminal domain gene provided by Terry Oas, who predicted very fast folding based on NMR line shape analysis (Huang and Oas, 1995), was inserted into the PET-15b vector (Novagen, San Diego, CA) between the NdeI and BamHI cutting sites, allowing for histidine-nickel binding binding-based purification to be carried out. Point mutations were done using the QuickChange site-directed mutagenesis kit (Stratagene, La Jolla, CA) and plasmids were verified by DNA sequencing. Proteins were expressed in Rosetta (DE3) pLysS (Novagen) cells with the media: 20 g/L tryptone, 10 g/L yeast- extract, 5 g/L NaCl, 200 mg/L ampicilin, 35 mg/L chloramphenicol, and 4 g/L glucose at pH 7.4 (2 mM isopropyl-ß-d-thiogalactopyranoside induction after cell density reached OD₆₀₀ = 0.8–1, and grew overnight at 28°C). Harvested cells were lysed by passing through a French press twice at >12,000 psi, and λ-repressor was normally found to exist in the soluble fraction. Purification was first done using a Ni-NTA column (QIAGEN, Tokyo, Japan) with imidazole as the eluting reagent. Further purification was done by running a size-exclusion column, such as a Sephacryl S-200 HR column (Amersham Pharmacia, Uppsala, Sweden) at pH 8, in 20 mM Tris and 500 mM NaCl. Histidine tags were removed by thrombin cleavage (Novagen), using 1 Unit of thrombin per mg of λ-repressor. The cleavage time was 16 h at room temperature. Histidine tags were then separated from the protein solution by dialysis or running through the Ni-NTA column. Pure proteins were dialyzed extensively against doubly deionized water and lyophilized for storage at −20 °C. Low resolution electro-spray-ionization mass spectrometry was used to confirm that the proteins contain the correct mutations. Expression levels of proteins were inversely related to the mutant stabilities.

λ-Repressor measurements

Protein concentrations in all measurements were estimated using 280 nm absorption of the protein solution, assuming an extinction coefficient of 5600 cm⁻¹ M⁻¹ for tryptophans and 1300 cm⁻¹ M⁻¹ for tyrosines. Concentrations were chosen so the observed kinetics were concentration-independent, as described previously (Yang and Gruebele, 2003). Steady-state circular dichroism measurements were carried out in a Jasco (Easton, MD) J-715 equipped with a Peltier temperature controller (Jasco). Protein thermal denaturation curves are nominally analyzed using a two-state approximation with linear folded and unfolded circular dichroism (temperature) baselines. Temperature jump folding kinetics (Ballew et al., 1996b) were induced by a 10 ns Raman-shifted Nd:YAG laser pulse. Folding was probed by a continuous pulse train of 280 nm, 200 fs duration Ti:sapphire laser pulses spaced by 14 ns to excite tryptophan 22, tyrosine 33, and tyrosine 60. Changes in the overall fluorescence emission lifetime were used to track the protein folding kinetics, which were fitted to single- or double-exponential decays. Following the notation used in the previous publication on λ-repressor (Yang and Gruebele, 2003), observed rates from single-exponential relaxations are termed k_a; in double-exponential relaxations, the faster rate constant is termed k_m and the slow one k_a.

RESULTS

Speeding up and slowing down λ_6–85

Except for the very fast mutants, the relaxation kinetics of λ_6–85 are described by a single rate constant. For example, the Y22W pseudo wild-type folds with a maximal rate of k_a = (31 μs)⁻¹, and can be fitted by a single exponential decay (data not shown). Two mutants, λD14A and λQ33Y, were previously identified as deviating from this behavior. Both fold faster than k_a = (20 μs)⁻¹ (Table 1). Below 4 μs they exhibit a speedup of the kinetics, which could be fitted with a second rate coefficient k_m = (2 μs)⁻¹ (Yang and Gruebele, 2003). Here and elsewhere in this article, nominal values of the folding rate k_f are obtained from the “slow” exponential component k_a and from the equilibrium constant derived by temperature titrations using the two-state assumption k_f = k_aK_eq/(K_eq+1). This is only approximately correct for the fastest folders, where the two-state approximation breaks down.

It was also demonstrated that slowing λQ33Y back down to k_a < (30 μs)⁻¹ by adding mutations Ala37Gly, Ala46Gly, and Ala48Gly (resulting in λA37G) restores single-exponential kinetics. Here we investigate the folding kinetics of a slowed-down version of λD14A, namely λA49G. λA49G incorporates mutations Ala37Gly and Ala49Gly onto λD14A, resulting in a decreased melting point (by 10°C; Fig. 2) and reduced k_a ((29 μs)⁻¹ at 54°C; Table 1). Thus λA49G's k_a lies between those of λQ33Y (30% fast phase) and λA37G (<5% fast phase). Decreasing the folding rate of λD14A reduces the fast phase amplitude to <20% (depending on temperature; Fig. 3), compared to the 20–40% observed for λD14A at various temperatures. As shown in Fig. 4, the maximum relative amplitude of the fast phase decreases smoothly as k_a decreases, and becomes too small to accurately determine beyond k_a ≈ (30 μs)⁻¹: there is no correlation of the fast phase amplitude with the nature of the mutations, only with the speed of the slow phase.

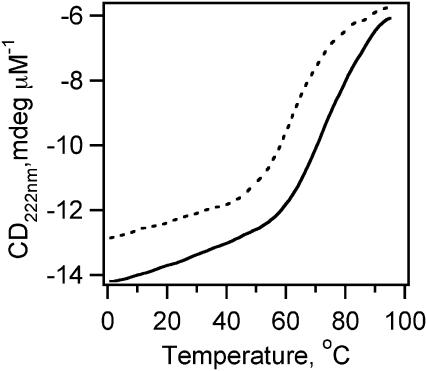
FIGURE 2.

λA49G thermal denaturation curve (dashed line). Its T_m lies 10 °C lower than that of λD14A (solid line). Data were obtained at pH 7 with 2 μM protein for λA49G and 5 μM for λD14A.

FIGURE 3.

λA49G folding kinetics as a function of temperature. The observed relative fast phase is <20% at all temperature/GuHCl/glucose, in contrast to the >20% fast phases seen for λD14A (e.g., Figs. 7, 9, and Yang and Gruebele (2003). Fits to a double exponential are shown in blue, and fits to a single exponential that best fits the data at t > 10 μs are shown in red.

FIGURE 4.

Correlation between the size of the fast phase amplitude, and the ratio of the main folding rate coefficient to the molecular rate coefficient. This is the only clear correlation observed in our fast folding data for the early speedup of the kinetics. The curve is a guide for the eye.

The relative amplitude of the λA49G speedup was largest near the midpoint of the unfolding equilibrium, allowing the most accurate determination of its fast phase timescale. A double-exponential fit yielded k_m = (2.0 ± 0.5 μs)⁻¹, similar to λD14A and λQ33Y. The temperature dependence of the relative fast phase amplitude has been discussed previously (Yang and Gruebele, 2003).

Effect of increased helix propensities on λQ33Y

Myers and Oas (1999) showed that the folding rates of λ-repressor mutants correlate well with the helix-forming propensities of their five individual helices (Myers and Oas, 1999). Helices 3 and 5 have the lowest helix-forming propensities according to the AGADIR algorithm (Lacroix et al., 1998) (Table 2). The mutation G46A, G48A present in λQ33Y already greatly increases the helix-forming propensity in helix 3 (Table 2). The additional mutation S45A increases the helix 3 propensity by another 26%, and S79A increases helix 5's overall propensity by 20% (Table 2). The two mutations increase the folding rate slightly at higher temperature, but not at the lower temperatures, where folding conditions are more optimal. In addition, the value of k_m remains unchanged (Fig. 5). The folding time has reached a limit that cannot be pushed by further enhancing helix stability.

TABLE 2.

Helix content at 298 K (%) predicted by the AGADIR algorithm, using pH 7, 0.1 M ionic strength, an amidated C-terminus, and an acetylated N-terminus as the input parameters

Helix number	Amino acid sequence	% helix at 298 K
Helix 1	QEQLEDARRLKAIWEKKKNELG	34.73
Helix 2	QESVADK	1.16
Helix 3 wild-type	QSGVGALFN	0.21
Helix 3 G46A G48A	QSAVAALFN	1.66
Helix 3 S45A G46A G48A	QAAVAALFN	2.09
Helix 4	AYNAALLAKI	17.31
Helix 5 wild-type	SIAREIR	0.90
Helix 5 S79A	AIAREIR	1.08

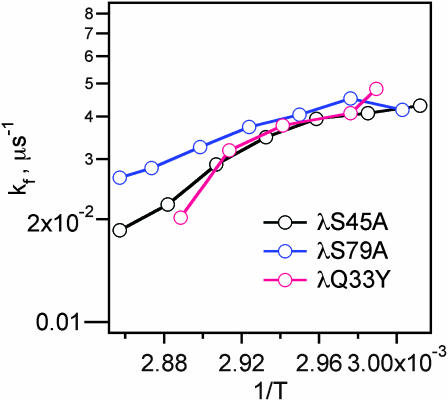
FIGURE 5.

Arrhenius plot of λS45A, λS79A, and λQ33Y folding rates. The rates differ significantly only at the highest temperatures, where proteins with higher helix propensity fold slightly faster.

Effect of GuHCl on the λD14A folding kinetics

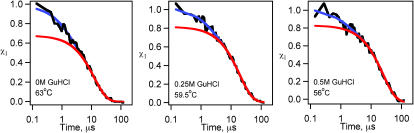
We explored the effect of GuHCl on the fast and slow phases observed during the folding λD14A. GuHCl decreases the folding rate of most small proteins by increasing the folding free-energy (Creighton 1993) and folding barrier height. Indeed, the folding rate for slower single-exponential folding mutants, such as λA37G, simply slows down in GuHCl. For λD14A, we carried out folding experiments in 0 M, 0.25 M, and 0.5 M GuHCl, under “isotability” conditions: the temperature was lowered to compensate for the destabilizing effect of GuHCl, keeping the free-energy difference between the folded and unfolded states constant (Fig. 6). In addition to seeing the expected slowdown of the k_a folding phase, we find a steady decrease in the percentage of fast phase amplitudes as the GuHCl concentration increases (Fig. 7). Yet the timescale for the fast relaxations decreases slightly as its amplitude decreases, from 2 μs in 0 M GuHCl to 1 μs in 0.5 M GuHCl.

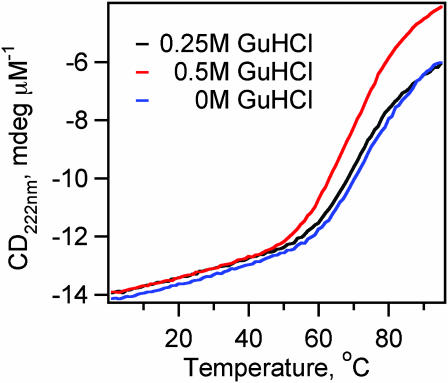
FIGURE 6.

Thermal denaturation curves in 0 M, 0.25 M and 0.5 M GuHCl. T_ms are shifted lower by ∼3.5°C/0.25M of GuHCl. Protein concentrations are 5 μM.

FIGURE 7.

λD14A folding kinetics at the same stability condition as in 0M GuHCl at 63°C. The relative fast phase amplitudes decrease as the GuHCl concentrations are increased. Percentage fast phase: 0 M GuHCl, > 30%; 0.25 M GuHCl, 20%, and 0.5 M GuHCl, 15%. The blue curves are double exponential fits; the red curves are best single exponential fits at t > 10 μs.

Solvent viscosity and λ_6–85 folding kinetics

Viscogenic agents affect folding kinetics by changing viscosity as well as folding barriers (Jacob et al., 1999). The activated folding rate k_a of variants of λ₆₋₈₅ is not greatly altered by the presence of glucose. This is illustrated by comparing the folding rates of the slower folding λA37G in 0 M and 1 M glucose solutions (Fig. 8). For λD14A, which has a large initial speedup, the effect on both k_a and k_m can be determined. The slower phase (k_a) is again unaffected by glucose, but the fast phase (k_m) is slowed down in proportion to the viscosity change (a factor of 1.8 upon adding 1 M glucose (Jas et al., 2001)).

FIGURE 8.

Folding kinetics in 0 and 1 M glucose buffers. (Left) Folding rate of λA37G obtained from single exponential fits in 0 M glucose (magenta) and 1 M glucose (cyan). (Black line) Expected slowdown from a ×1.8 increase in bulk viscosity; the rate in 1 M glucose slows down only minimally. (Right) λD14A folding rates. (Upper curves) k_m in 0 M glucose (magenta) and 1 M glucose (cyan). (Lower curves) k_a. The molecular timescale tracks viscosity fully, whereas the activated folding rate again changes only minimally because barrier decrease and viscosity increase compensate.

The fast phase of both λD14A and λQ33Y increases compared to the slow phase as glucose is added (Fig. 9). In 1 M glucose at temperatures above 67 °C, the slow phase has disappeared, and the kinetics are again well fitted by a single exponential (≈9 μs for λD14A). The fluorescence lifetime signature at the end of the fast phase corresponds to the native state.

FIGURE 9.

λD14A folding in 1 M glucose at different temperatures. At 67°C, the two timescales merge into a single fast timescale of ∼9 μs. This merger does not go to completion in aqueous buffer.

Glucose also induces interesting thermodynamic behavior in the fast folding λD14A. Normally, glucose stabilizes folded proteins; the same happens here, judging from the small T_m increase for λD14A in glucose (Fig. 10). With increasing glucose concentration, the transition broadens, starting earlier despite the increase in T_m. The thermal denaturation curve gradually loses its cooperative folding behavior. This effect is even more apparent when using 50% ethylene glycol instead of glucose (data not shown). Ethylene glycol has also been widely observed to enhance protein stabilities.

FIGURE 10.

(Left) λA37G in 1 M glucose (thicker curve). The melting point in increased by 2°C compared to aqueous solution (thin curve). (Right) λD14A thermal denaturation in 0 (thin curve), 1 (medium curve), and 2 M (thick curve) glucose solutions. The transitions increases T_m, but starts earlier at higher glucose concentration. Native baselines are shown in red. A similar but even more dramatic effect is observed with ethylene glycol (not shown).

Initial phase can be fitted to a single exponential

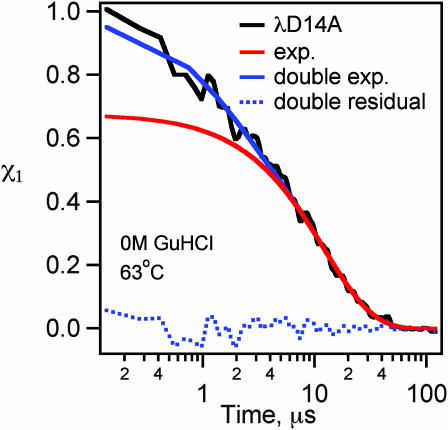
So far, we have discussed the early speedup below a few microseconds in terms of its own rate constant k_m, implying that it can be fitted by a single exponential exp[−k_mt]. This corresponds to fitting the overall kinetics with a biexponential function. In our previous report, we also used a stretched exponential to fit the overall kinetics (Yang and Gruebele, 2003). Our higher signal/noise remeasurements of λD14A and λQ33Y (Fig. 11) in this report show that the fast phase can be fitted by a single exponential within the signal/noise of our data. We can set a lower limit of 0.7 on any stretching factor β (in exp[−(k_mt)^β]) of the initial speedup fitted by itself.

FIGURE 11.

The λD14A fast phase is well described by a single exponential within the signal/noise of our data under all conditions we have been able to access.

DISCUSSION

Sequence-specific calculations using energy landscape theory have been carried out for λ_6–85 in the past. They show that the energy landscape is rough (Portman et al., 1998), and obtain a value for the molecular timescale of 0.5 μs (Portman et al., 2001a,b), compared to our measured result of 1–2 μs (in GuHCl or aqueous buffer). A very recent off-lattice study shows a similarly rough landscape without a significant barrier for the λQ33Y mutant (Pogorelov and Luthey-Schulten, 2004). General considerations also lead to values for the speed limit around 1 μs (Camacho and Thirumalai, 1993; Hagen et al., 1996). We discuss our results in terms of energy landscape theory, how our results demonstrate folding at the speed limit, and how they compare with Langevin simulations on a rough free-energy surface. Finally, we discuss some broader implications for rate-topology relationships and the dimensionality of the folding free-energy surface needed to describe the dynamics.

In the linear response limit, the rate coefficient is time-dependent according to the formula (Berne, 1993)

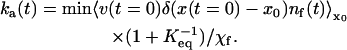(2)

Here, v is the velocity of the molecule in the free-energy double well, x is its position, x₀ is the location of the bottleneck (usually at or near the top of the barrier,; Fig. 12), and χ_f is the mole fraction of folded protein. n_f(t) = 1 if the molecule is on the folded side of the bottleneck, and 0 if it is on the unfolded side. 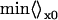indicates that an average over a full ensemble of initial conditions (“the unfolded state”) is to be made, and x₀ is to be moved until k_a(t) is minimized. It has been shown that when t > 1/k_m, the rate coefficient approaches the phenomenological rate constant used in two-state kinetic models. Single-exponential kinetics are recovered (Berne, 1993). When t < 1/k_m, the rate coefficient increases toward the bare transition state theory value, which exceeds k_a(∞) by the average number of recrossings (which can be large in proteins because of surface roughness). A brief and very readable description of the rate theory in a double-well potential is given in the last chapter of (Chandler, 1989).

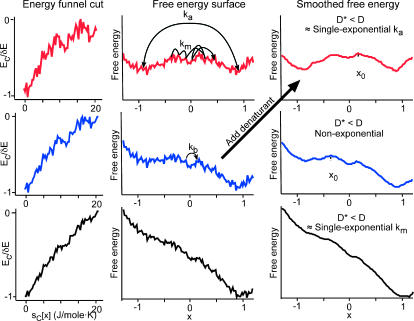
FIGURE 12.

Cut through of a multidimensional energy landscape (left column), corresponding free-energy plot along the reaction coordinate x (middle column), and smoothed free-energy plot (right column). Native bias increases from top to bottom. Transitions corresponding to the activated rate coefficient k_a, to the molecular rate k_m, and to the rate coefficient k_b for a single loop contact are shown. On a smoothed surface, the diffusion coefficient must be renormalized to D* < D to take into account roughness. Smoothing is accomplished experimentally (large arrow) by denaturant or cold denaturation (Sabelko et al., 1999). This creates a barrier even if there is none under native conditions, as long as ∂ΔG/∂[denaturant] = m > 0 in the activated region. Thus denaturant titrations always appear cooperative, even when folding is actually downhill under native conditions.

The speedup of the rate coefficient below t = 1/k_m is connected to the energy landscape picture in Fig. 12, and explains all of our experimental observations. The three columns of Fig. 12 plot a cut through a multidimensional folding funnel, a rough free-energy surface that includes some of the “transverse” roughness along coordinates other than the chosen folding coordinate “x”, and a smoothed free-energy surface. The bias toward the native state increases from top to bottom.

The top row corresponds to two-state folding, although free-energy roughness contributes high energy intermediates (Feng et al., 2003; Pappenberger et al., 2000). The plot of energy versus configurational entropy s_C has an overall funnel shape because making favorable contacts requires making the protein more compact. Cuts through a multidimensional folding funnel are rough because the protein can make nonnative contacts or interact with the solvent, leading to fluctuations in the energy (Bryngelson et al., 1995). Experiments are carried out at constant temperature, not at constant entropy, so it is more useful to compute a free-energy F[x] = E[x] − TS[x] from the energy, as shown in the middle. Because of incomplete compensation of energy and entropy as the protein compactifies, the free energy has a barrier at x = 0. Motions corresponding to the timescales 1/k_a and 1/k_m are shown. When the barrier is large, the population in the activated region is small, and only k_a can be observed. λA37G is an example of this case, and λA49G (Fig. 3) is nearly such a case. The value of k_m was calculated by Portman et al. (2001b) for those conditions. The predicted value of 1/k_m on this rough surface is much larger than 1/k_b ≈ 10–100 ns, the timescale for diffusion to form a single loop (Bieri et al., 1999; Lapidus et al., 2000). On the right of Fig. 12, a smoothed free-energy surface is shown. On such a smooth surface, the diffusion coefficient D must be rescaled to a smaller value D* to account correctly for diffusion in unproductive “transverse” modes and hence for the observed kinetics. The smaller diffusion coefficient effectively takes over the role of multidimensional surface roughness, and we previously estimated D/D* ≈ 40 for λ_6–85 (Yang and Gruebele, 2003).

In the middle row, the native bias of the funnel is increased, so the free-energy barrier decreases. The small local minima causing free-energy roughness are now comparable to the barrier. This allows the “activated” population to climb to a significant level, causing the speedup of kinetics predicted by linear response theory and observed for λQ33Y and λD14A in aqueous solvent. Two timescales may be observable for proteins in this regime. Two kinetic timescales for fast two-state folders have also been found in funneled master equation models (Ozkan et al., 2002).

In the bottom row of Fig. 12, the native bias is increased further, so residual roughness dominates completely over the barrier. Now only k_m can be measured. This corresponds to λQ33Y and λD14A in viscous solvents, where the added viscogen slows down the diffusive dynamics and at the same time decreases the barrier, so only the fast timescale remains. Under certain conditions, the fast timescale is again described by a single rate constant (Zwanzig, 1988).

We now discuss in detail the experimental evidence that λ₆₋₈₅ folds over a low barrier or even downhill under some conditions, and that k_m probes the surface roughness that reduces the effective diffusion constant. A Langevin model calculation supports this picture further, as do some observations made earlier that we reiterate (Yang and Gruebele, 2003).

λ_6–85 folds near the speed limit

Is the energy already maximally biased for low barrier folding? The result from adding the two helix-enhancing mutations S45A and S79A to λQ33Y suggests that the answer is yes. These mutations have very little effect on the folding kinetics of λQ33Y at the lower end of the temperature range (Fig. 5). The ability for forming helices and subsequently the native state is nearly saturated at those temperatures. At higher temperatures, the mutants are faster, indicating that additional mutations do stabilize helices against thermal melting within the unfolded ensemble.

k_m is robust

No matter what temperature or mutant are is used, the initial speedup ranges from 1 to 2 μs (measured with 30 ns dead time) whenever it has an observable amplitude. Only viscogenic agents and denaturants have a significant effect on its duration or amplitude (discussed below). In particular, no specific mutation correlates uniquely with the observed speedup, i.e., no intermediate stabilized only by specific mutations is responsible. We investigated this by testing whether mutations such as Q33Y and D14A, can be engineered into versions of λ-repressor that give normal exponential kinetics. The mutants λA37G and λA49G present two such examples. We find that both have diminished or absent fast phase amplitudes, indicating that Q33Y and D14A do not induce specific intermediates that account for the observation of the fast phase. The only correlation of the fast phase with mutation we could find was that mutants with larger k_a also had a larger fast phase amplitude, irrespective of the exact mutation (Fig. 4).

k_m originates from roughness of the activated region

The effect of denaturants on protein folding has long been investigated (Pace, 1986; Tanford, 1968). Denaturants destabilize the folded state and smooth the free-energy surface. The activated region is also destabilized by denaturants when the transition state has some native-like properties; this is shown experimentally for λ_6–85 in Fig. 7 and in much greater detail in previous experiments (Burton 1997, 1998). In our rate measurements, we utilized isostability conditions (G_folded − G_denatured = constant) at low GuHCl concentrations. This preserves the relative population distribution between the two wells. Any signal originating from reequilibration within the two wells should therefore remain unchanged. Any signal from the activated region should decrease because GuHCl raises the barrier free energy and decreases the activated population.

In the 0–0.5 M GuHCl measurements, we clearly see this decrease of the fast phase amplitude as the GuHCl concentration is raised (Fig. 7), confirming that k_m originates from the activated region. Therefore GuHCl titrations cannot be used to establish two-state folding: GuHCl induces a barrier even when there is none under native conditions (Yang et al., 2004).

In 0.5 M GuHCl, we also observe the fastest initial phase (≈1 μs), compared to ≈2 μs fitted in 0 M GuHCl (Fig. 7). GuHCl increases solvent viscosity, which should actually slow down diffusional kinetics (see below), so a factor of two increase in k_m upon addition of a small amount of GuHCl corresponds to a reduction of the free-energy surface roughness by at least k_BT ln(2). Denaturant smoothes out the roughness of the free-energy surface.

Closely related to this argument is the observation that k_m does not decrease at the lower temperatures, even though solvent viscosity slightly increases. Lower temperatures reduce the hydrophobic interaction, and the resulting decrease of free-energy roughness compensates for viscosity. A clear example of this kinetic effect is phosphoglycerate kinase, which switches to less stretched kinetics at lower temperatures where cold denaturation sets in (Sabelko et al., 1999).

k_m tracks solvent viscosity

Whether folding folding-rate coefficients k_a scale with bulk solvent viscosity or not is a longstanding debate (Klimov and Thirumalai, 1997). Some rates scale as η⁻¹ (overdamped Kramers' regime) upon addition of viscogens (Jacob et al., 1999; Jacob and Schmid, 1999; Plaxco and Baker, 1998), whereas others are less sensitive or insensitive to the change in solvent conditions (Jas et al., 2001; Ladurner and Fersht, 1999). The reason is that viscogens tend to compensate reduced diffusion constants by also lowering activation barriers (Jacob et al., 1999).

Because we measure both k_m and k_a, we can separately determine the effects of bulk viscosity on the prefactor and on the folding free-energy barrier. Variation in k_m signals a change of the prefactor, while the ratio k_a/k_m tracks the change of the folding free-energy barrier. This allows an unambiguous investigation of the role that solvent viscosity plays in protein folding.

Folding rates k_a of λ-repressor remain almost unaffected when the solvent viscosity is changed. In the single exponential folder λA37G, or in the “slow” phases of λQ33Y and λD14A, we see no obvious rate change when 1 M glucose is added to the solution, which represents a 1.8 times change in bulk viscosity. However, the fast phases of λQ33Y and λD14A slow down proportionally to the bulk viscosity (Fig. 8). Thus λ_6–85 folds in the overdamped Kramers regime (Klimov and Thirumalai, 1997), and the reason that k_a does not scale with bulk viscosity is because the folding free-energy barrier is lowered by the introduction of viscogens. This observation fits well with literature data that viscogens oftentimes stabilize folded states (Jacob et al., 1999; Jas et al., 2001). The general intuition that increasing the bulk solvent viscosity slows down folding reactions by slowing down diffusive motions of the chain therefore holds for λ-repressor.

Thermal denaturation of λD14A in glucose-containing buffer supplies additional evidence that its folding barrier is low, and that viscogens reduce folding barriers. In proteins where activated populations exist, lowering (stabilization) of the barrier region will lead to a loss of apparent cooperativity in thermal unfolding transitions. Upon the addition of 1–2 M glucose or 50% ethylene glycol, the λD14A melting curve is broadened, indicating that partially folded states are stabilized. This effect is only seen in the fastest folding λ-repressors, not in the ones with higher barriers, such as λA37G.

The molecular phase can take λ_6–86 to the native state

Upon addition of glucose, the fast phase amplitude increases until it comprises the entire folding process. No further kinetics are observed at longer times, and the fluorescence signature achieved by λ_6–85 corresponds to the native fluorescence signature.

A rough downhill surface describes both k_m and k_a

Although simple transition-state theory does not describe the two timescales we observe, Langevin dynamics simulating Eq. 2 on a rough free-energy surface G quantitatively describes the biexponential folding dynamics and its temperature dependence. The solvent is simulated by a time-dependent random force that equilibrates the population distribution of λ_6–85, and by a diffusion constant D (Chandler, 1989):

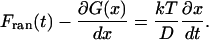(3)

We previously showed that a smoothed surface (such as Fig. 12, left column, middle) can describe both timescales 1/k_a and 1/k_m if the diffusion coefficient is rescaled by a factor of 40. Fig. 13 shows a similar surface with added roughness. This roughness has to account for both “longitudinal” roughness along x, and for “transverse roughness” along coordinates left out of our one-dimensional model. The surface was constructed by adding a linear bias and Gaussian noise to a double-well potential

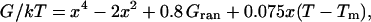(4)

where G_ran is random Gaussian noise with a root mean-square value of 1 kT. The actual shape of the roughness cannot be determined from these experiments, so Gaussian noise was chosen for simplicity. When the linear bias is large enough, Eq. 4 switches from a double to a single minimum. The x scale is in nanometers and D = 0.05 nm²/ns was used, to provide realistic values for free diffusion of helices over the length scale of a protein.

FIGURE 13.

(Top) Rough nearly downhill free-energy surface in blue; the same surface with an added linear free-energy bias for a 10°C temperature jump is shown in red. The root mean-square roughness (δ²G ≈ 0.64 k²T²) is comparable to the barrier height and to a recent experimental estimate for trpzip2 (Yang and Gruebele, 2004). The length scale of the roughness will be larger for real folding surfaces, and more than one coordinate is required for a full description (Yang and Gruebele, unpublished). (Middle) Langevin dynamics on the model surface quantitatively reproduces the fast and slow timescales, as well as the amplitudes for the λD14A mutant at 63°C (black); the populations at x < 0.83 and x > 0.83 were assigned different spectroscopic signals to compute a signal change from the population change. (Bottom) Residuals of the single and double-exponential fits to the simulation.

The smooth surface in Yang and Gruebele (2003) required D* = D/40. The surface in Fig. 13 and Eq. 4 directly reproduces the biexponential data observed experimentally with the correct timescale and free-diffusion coefficient D, by adjusting the roughness. When the surface is less biased toward the native state, a double well with single exponential kinetics results. When the surface is more biased toward the folded state, only the fast phase is observed. This models the single-double-single exponential transition observed experimentally as protein stability is increased by mutation (λA37G versus λQ33Y), followed by addition of glucose (Fig. 9). The nice feature of this model is its robustness: the results only depend on the size of the roughness and the ratio of roughness to barrier height; no fine tuning of many kinetic parameters is required to reproduce the smooth trend in Fig. 4. We found that a roughness of δ²G ≈ 0.64 k²T² reproduces the experimental timescale and amplitude for λD14A at 63°C using the one-dimensional model. Finally, the residual error for the biexponential fit to the calculation in Fig. 13 falls within the noise, also in agreement with experiment: the fast component can be fitted by a single exponential within computational and measurement uncertainty, ruling out stretched exponentials exp[−(kt)^β] with β > 0.7.

Downhill folding free-energy surfaces consisting of a roughened shelf with a dip for the native state have been computed by molecular dynamics simulations. Specific examples include the trpzip2 peptide (Yang et al., 2004), and G simulations on λQ33Y by Pogorelov and Luthey-Schulten (2004). For the trpzip2 peptide, a δ²G similar to the above has been measured (Yang and Gruebele, 2004). A downhill free-energy surface also has been invoked for the formation of a folding intermediate of phosphoglycerate kinase (PGK) (Osváth et al., 2003; Sabelko et al., 1999).

We also performed a fit to the three-well potential described in Yang and Gruebele (2004, supplementary information); for the fastest folding in 1 M glucose;, that model has a maximum barrier of 4.5 kT for the intermediate well, but only with the unrealistic assumption of an otherwise completely smooth free-energy surface. The model does not provide a satisfactory explanation for the lack of a rollover as [GuHCl] is reduced to 0 M, of the correlation shown in Fig. 4, and of the transition from single to double back to single exponential as the protein is stabilized.

In addition to the points outlined above, it is worth reiterating several others already discussed in our earlier report. These are (Yang and Gruebele, 2003): 1), The observed relaxation rates are as fast as or faster than the extrapolations of k_a from high denaturant concentrations, so there is no “roll-off” in the Chevron plot that can be attributed to a folding intermediate. 2), The fastest mutants are most prone to aggregation. Fast folding proteins have low barriers, so their activated populations are larger, and they switch back and forth between the native and denatured states more rapidly. This increases the probability of a temporarily unfolded protein aggregating (Jacob et al., 1997). And 3), we also confirmed the arguments made in our earlier letter (Yang and Gruebele, 2003): no significant 2 μs phase is observed when λ_6–86 is jumped under fully denatured or fully native conditions, and of course the slow mutants have no fast phase, although their folded and unfolded populations should relax just the same as the fast mutants. This rules out explanations such as that put forth in Mayor et al. (2003).

Our results for λ_6–85 have broader implications for protein folding. The first and foremost conclusion is that a two-state barrier is not obligatory for the folding of λ_6–85 under the most optimal folding conditions. If barriers turn out not to be obligatory for other globular proteins, this would leave us with an “anti-Levinthal paradox” (Levinthal 1969): why don't all wild-type proteins fold at the speed limit? There are now several examples of small globular proteins or domains of globular proteins folding to native structures or compact globules in 0.5–10 μs (Ballew et al., 1996a; Mayor et al., 2003; Qiu et al., 2002; Wittung-Stafshede et al., 1997; Yang and Gruebele, 2003; Zhu et al., 2003), but the majority of wild-type proteins certainly do not.

To answer this question, we propose a slightly different connection between folding rates and “topological frustration” (Clementi et al., 2000). It has been found that ln(k_f) of two-state folders is inversely correlated with contact order, an order parameter that measures the average sequence separation between contacting amino acids (Baker, 2000; Plaxco et al., 1998). The rate at which proteins fold decreases with increasing complexity of their folds, a “topological” effect. Nonetheless, k_f for different sequences with the same fold still range over several orders of magnitude about the linear ln(k_f) versus contact-order relationship. This is true even when sequence length corrections are added (Koga and Takada, 2001), or other measures of fold complexity are used. This variation is caused by “energetic frustration” (Clementi et al., 2000) from nonnative contacts and protein-solvent interactions, which differ from sequence to sequence. We propose that the best correlation with topology occurs when plotting ln(k_m) versus contact order because k_m corresponds to the folding rate of a minimally frustrated protein where the effects of topology are maximized.

Currently only λ_6–85 has an independently determined k_m. However, several very fast folders of different sizes have been identified, and rapidly formed folding intermediates provide another estimate of how fast a protein could fold. When six such proteins and peptides covering a wide range of contact order (CO) are put on a ln(k) versus CO plot (Fig. 14), a much better correlation than with the general ln(k_f) versus CO curve from Ivankovet al. (2003) emerges. We predict that folds whose fastest-folding known sequences lie well below our speed limit line can be sped up further by mutation, whereas those sequences whose rates lie near our speed limit line are limited by small traps and solvent interactions inherent in a 20-amino acid design. Very importantly, there is not a universal speed limit because topological frustration grows with sequence length and fold complexity. The speed limit slows down faster with sequence length N than expected from homopolymer theory (N), as expected if topological details play a role. We predict k_m ≈ 0.5 μs for 2–3 helix bundles, ≈ 2 μs for typical 5-helix bundles, ≈ 10 μs for an 8-helix bundle such as myoglobin, and ≈ 90 μs for a 200-residue protein such as the C-terminal domain of PGK, where nonexponential kinetics have been resolved during formation of a compact intermediate (Osváth et al., 2003). It may turn out that the rate of formation of fast-folding “burst phase” intermediates with near-native topology accurately estimates the “speed limit”, but much more data is required to test this conjecture.

FIGURE 14.

Logarithm of the folding rate correlated with the contact order according to Ivankov et al. (2003) (red circles, measured; red line, fitted correlation). The black line goes through very fast folders. The molecular rate k_m leading to the native state has been observed directly only for λ_6–85 (3). Other speed limit candidates include a single helix (1) (Thompson et al., 1997), the three-helix bundle α-3D (2) (Zhu et al., 2003), and the large protein cyclophilin A (6) (Ikura et al., 2000). Speed limits estimated from fast-forming intermediates include apomyoglobin (4) (Ballew et al., 1996a) and phosphoglycerate kinase (5), which has nonexponential folding kinetics (Osváth et al., 2003). Other proteins close to the speed limit include the 20-residue Trp cage, observed at 4 μs, and with a speed limit probably near 0.5 μs based on our plot (Qiu et al., 2002).

It has been suggested that protein function is an important cause of energetic frustration that produces a folding barrier (Gruebele, 2002). Functional residues are not necessarily optimal for folding; they increase protein flexibility or add unfavorable interactions from the point of view of the folding free energy. Examples include loop 1 of Pin WW domain, which can be shortened to speed up folding by a factor of 10 at the expense of its binding affinity (M. Jäger, H. Nguyen, J. Kelly, and M. Gruebele, unpublished results); the very different folding rates of the AGH core (∼10 μs) and DEF core (∼1 s) of apomyoglobin (Ballew et al., 1996a; Jennings and Wright, 1993), where the latter binds heme and can be folded more speedily when the heme binding histidine 64 is replaced by a phenylalanine (Garcia et al., 2000), and perhaps helix 3 of λ-repressor, whose wild-type contains two glycines that decrease stability but may increase flexibility for induced-fit DNA binding. (It remains to be shown whether the faster G46A/G48A mutant has reduced binding affinity despite its increased stability, as we predict here.) If any globular fold can be pushed near its speed limit, then the investigation of large folding barriers by φ-value analysis (Jackson et al., 1993) would mainly tell us about the energetic frustration induced by functional and other constraints on the amino amino-acid sequence. The folding barrier then becomes a biological instead of a physical problem.

Another reason for the existence of barriers has been suggested by Jacob et al. (1997); and Silow et al. (1999): barriers decrease the available native configuration space by confining the protein in a narrower well. Without a barrier, partially unfolded structures are more likely to be populated, and this would lead to an increased probability of aggregation or proteolysis in vivo. Our measurements of λ_6–85 agree with this view because we found a direct correlation of aggregation and folding rate: the fastest-folding mutants λQ33Y and λD14A are also most prone to aggregation (Yang and Gruebele, 2003).

A final important result concerns the dimensionality of the free-energy surface required to provide a faithful description of the experimental data. As detailed in the Results section, the initial speedup of λD14A and λQ33Y can be fitted by a single exponential exp[−k_mt] without any significant residuals (Fig. 11); a one-dimensional Langevin model agrees with this observation (Fig. 13). There is no reason a priori why diffusive hopping on a rough free-energy surface should fit to a single exponential. One important assumption that goes into deriving exponential diffusion on a rough surface is a one-dimensional reaction coordinate with uncorrelated roughness (Zwanzig, 1988). In higher dimensions, the diffusing molecules are less restricted and have more options of taking longer paths to the folded state, leading to a stretching of the diffusive dynamics (Metzler et al., 1999, 1998). Our result shows that the assumption of a single reaction coordinate (one-dimensional plots such as Fig. 12) is a reasonable approximation for λ₆₋₈₅, and that the actual dimensionality of the coordinate space required to provide a satisfactory description of its folding cannot be very large. It has been shown by landscape analysis (Socci et al., 1998) and for small peptides by enumeration of minima and saddle points (Becker and Karplus, 1997) that a few coordinates (but more than one) can describe the folding landscape. We are in agreement with these results. Even the much larger C-terminal domain of PGK can be fitted about equally well by stretched and double exponentials (Osváth et al., 2003), pointing toward a small number of reaction coordinates.

Clearly, many questions remain to be answered in connection with our findings: Can α-helical bundles and more general folds always be redesigned to fold downhill, or nearly downhill? The speed limit decreases faster than linearly with protein size, but does it slow down exponentially or polynomially? What number of coordinates is required to represent folding at low resolution? Indications are the number is >1, but not by much, according to our measurements. How does the roughness of the free energy depend on these coordinates? In this study we treated roughness as uniformly distributed along the reaction coordinate (Fig. 13), yet thermodynamic tuning studies and MD simulations of the designed peptide trpzip2 indicate that the unfolded region of the free-energy surface is quite rough (Yang et al., 2004), whereas the folded region is smoother. Very recent simulations by Luthey-Schulten and co-worker show a similar result for λQ33Y (Pogorelov and Luthey-Schulten, 2004). It will be interesting to see if other proteins behave in the same way.