Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Aug;87(2):1378–1391. doi: 10.1529/biophysj.103.037184

Impedance Analysis of the Organ of Corti with Magnetically Actuated Probes

Marc P Scherer 1, Anthony W Gummer 1
PMCID: PMC1304476  PMID: 15298940

Abstract

An innovative method is presented to measure the mechanical driving point impedance of biological structures up to at least 40 kHz. The technique employs an atomic force cantilever with a ferromagnetic coating and an external magnetic field to apply a calibrated force to the cantilever. Measurement of the resulting cantilever velocity using a laser Doppler vibrometer yields the impedance. A key feature of the method is that it permits measurements for biological tissue in physiological solutions. The method was applied to measure the point impedance of the organ of Corti in situ, to elucidate the biophysical basis of cochlear amplification. The basilar membrane was mechanically clamped at its tympanic surface and the measurements conducted at different radial positions on the reticular lamina. The tectorial membrane was removed. The impedance was described by a generalized Voigt-Kelvin viscoelastic model, in which the stiffness was real-valued and independent of frequency, but the viscosity was complex-valued with positive real part, which was dependent on frequency and negative imaginary part, which was independent of frequency. There was no evidence for an inertial component. The magnitude of the impedance was greatest at the tunnel of Corti, and decreased monotonically in each of the radial directions. In the absence of inertia, the mechanical load on the outer hair cells causes their electromotile displacement responses to be reduced by only 10-fold over the entire range of auditory frequencies.

INTRODUCTION

Magnetically coated cantilevers are typically used either for so-called magnetic force microscopy, where a magnetic sample surface (e.g., a computer hard disk) is scanned in noncontact mode and differently magnetized domains lead to a detectable change in force on the cantilever (e.g., Hartmann, 1999), or in force modulation mode with the probe being actuated by a magnetic field rather than a piezoelectric actuator (e.g., Florin et al., 1994). Mechanical properties of biological samples have also been studied by applying a magnetic force or torque to magnetic beads adhering to the sample surface (e.g., Freeman et al., 2003a; Mijailovich et al., 2002). These methods are used: 1), statically, where the force on the probe at one scanning location is time-independent; 2), at low frequencies of a few hundred Hz; or 3), at the resonance frequency of the cantilever.

Broadband impedance measurements are complicated, however, by the necessity to calibrate the impedance of the magnetic probe. Here we present a technique to calibrate a ferromagnetically coated atomic force cantilever in fluid up to 40 kHz. Then we used the magnetically actuated cantilever to determine the point impedance of a biological sample—specifically, the organ of Corti—over its entire, physiologically relevant frequency range.

In auditory research a point has been reached (for review see Robles and Ruggero, 2001) where focus has turned to the local nanomechanics of the cochlear partition, especially for the following.

  1. The interplay between basilar membrane, organ of Corti, and tectorial membrane (Allen, 1980; Cai et al., 2003; Cooper and Rhode, 1995; Dallos, 2003; Freeman et al., 2003a; Gummer et al., 1996; Hemmert et al., 2000; Hubbard, 1993; Hubbard et al., 2003; Kolston, 1999; Mammano and Nobili, 1993; Mammano and Ashmore, 1993; Neely and Kim, 1986; Nobili and Mammano, 1996; Richter and Dallos, 2003; Steele and Puria, 2003; Zwislocki, 1980).

  2. The deformation of the organ of Corti itself (Fridberger and de Monvel, 2003; Fridberger et al., 2002; Hu et al., 1999; Karavitaki and Mountain, 2003; Naidu and Mountain, 1998, 2001; Richter and Dallos, 2003; Scherer et al., 2003; Ulfendahl et al., 2001, 2003).

  3. The generation of electromechanical force by outer hair cell somata (Ashmore, 1987; Brownell et al., 1985; Dallos et al., 1993; Frank et al., 1999; Hallworth, 1995; Iwasa and Adachi, 1997; Mountain and Hubbard, 1994; Russell and Schauz, 1995) and their stereocilia (Hudspeth, 1997; Hudspeth et al., 2000; Martin and Hudspeth, 1999, 2001; Martin et al., 2000, 2001, 2003; Zweig, 2003).

These processes are thought to form the basis of the so-called cochlear amplifier, the correct function of which is a prerequisite for the extraordinary sensitivity, frequency selectivity, and dynamic range of the mammalian auditory system.

To elucidate the biophysical basis of cochlear amplification, the point impedance of the organ of Corti in situ was measured over the entire auditory frequency range. An innovative technique using a ferromagnetically coated atomic force cantilever to deliver a calibrated mechanical force was developed for this purpose. The technique yielded the viscoelastic properties of the organ of Corti.

MATERIALS AND METHODS

Measurement principle

For sufficiently small displacement amplitudes it is reasonable to assume a linear relationship between a point force F on the organ of Corti and the resulting displacement x (or velocity v) of that point in the same direction as the force (linearity was confirmed experimentally; see Discussion); that is, F = Kx or F = Zv, where K is the generalized complex stiffness, and Z is the impedance. For a harmonic time dependency, v = iωx and, thus, K = iωZ, with 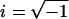Inline graphic and ω the radial frequency. To find Z, or equivalently K, we determined experimentally the mechanical impedance: 1), of the free swinging tip of an atomic force cantilever, Zeq, at a short distance (13 μm) from the preparation and 2), of a system consisting of the same cantilever with its tip in contact with the specimen, Zcont (Fig. 1). The impedances were found by applying a magnetic force to a ferromagnetic cantilever and simultaneously measuring the velocity of the cantilever tip. From the difference in impedance between the noncontact and the contact modes, we calculated the point impedance of the organ of Corti at the point of contact. In general, Z and K will depend on the frequency of the applied force—measurements were made in the range from 480 Hz–40 kHz. Above 40 kHz, standing acoustic waves formed between the measuring chamber and the objective, leading to an uncontrollable additional force on the cantilever.

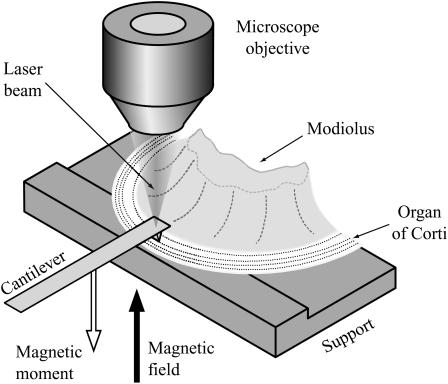
FIGURE 1.

FIGURE 1

Open in a new tab

The sample consisted of approximately one half of a cochlear turn, including modiolus bone, basilar membrane, and overlying organ of Corti. The tectorial membrane was removed and the preparation was placed on a plastic support in such a way that the basilar membrane was lying flat on the support. The modiolar bone was fixed to the support with vaseline. The (atomic force) cantilever, with its tip in contact with the upper surface of the organ of Corti, was used to determine the point impedance of the organ at the contact point. The laser beam was used for measuring cantilever velocity. A microscope objective located above the measurement site enabled the laser beam to be focused on the cantilever at the same time as observing the sample. The focus of the laser beam was in the focal plane of the microscope. Both experimental chamber and cantilever could be moved independently with motorized micromanipulators (Luigs and Neumann, Ratingen, Germany), to establish contact between organ of Corti and cantilever. The (inhomogeneous) magnetic field was generated by a coil (shown in Fig. 2) below the preparation and acted upon the magnetic moment of the cantilever to deliver a mechanical point force to the organ of Corti.

Atomic force cantilevers with a ferromagnetic cobalt coating are available commercially (type SC-MFM, Team Nanotec, Villingen-Schwenningen, Germany). The cantilevers, which were made of silicon, have a rectangular shape with length 215 μm, width 35 μm, and thickness ∼2 μm; the Co-coating has a thickness of 50 nm. The tip-diameter of the cantilever was enlarged from the typical value of ∼10 nm to ∼0.5–2 μm by scratching the tip over a glass surface. The profile of the tip was examined in a separate set of experiments using an electron microscope (LEO 912, Oberkochen, Germany); the reproducibility of the profile and diameter of the enlarged tip was ensured by the crystalline structure of the Si; surface irregularities in the profile were less than 10 nm in magnitude. The cantilevers were slightly transparent when illuminated with white light in the experimental setup (Fig. 1), so that the tip appeared as a dark spot when viewed from the reverse side. This was used to position the tip precisely on the desired place.

The organ of Corti was described mechanically by an equivalent (Norton) point impedance, ZOC, between the measured point on its upper surface and ground. In the absence of electrical stimulation, the outer hair cells do not produce electromechanical force and, therefore, the organ of Corti does not contain a force source.

The mechanical stimulus with a magnetic area force applied to the cantilever was described by an equivalent point force source, Feq, and an equivalent point impedance, Zeq, connected between the tip of the cantilever and ground. A calibration procedure for Feq and Zeq is described in the next section.

Since the cantilever tip is in contact with the organ of Corti at only one point, namely at the point for which the equivalent impedances and force are considered, Zeq and ZOC are independent of each other and do not change when contact is established. Therefore, the total impedance that is driven when the magnetic force is applied while the cantilever tip is in contact with the organ of Corti is Zcont = Zeq + ZOC. Since Feq and Zeq are known and Zcont = Feq/vcont can be found by measuring the velocity vcont of the cantilever tip in the contact mode, ZOC was calculated as ZOC = Zcont–Zeq.

The signal/noise ratio (SNR) for ZOC is largest when the cantilever is soft compared with the sample; that is, when Zeq is much smaller than Zcont, because then the difference Zcont–Zeq is large. In contrast, for a hard cantilever with Zcont ≈ Zeq, the difference becomes small while the noise remains the same, and consequently the SNR is poor. Therefore, we used the softest cantilevers that we could obtain: one with a spring constant of 1.20 N/m for the first 21 preparations (first and second cochlear turns) and one with a spring constant of 1.59 N/m for the remaining nine preparations (third cochlear turn).

Determination of contact

Contact between the cantilever and the sample was established by bringing the reticular lamina—the upper surface of the organ of Corti—into microscope focus and then approaching the cantilever until a visible deformation of the reticular lamina had occurred. Typically, the indentation had a depth of 1 μm, as measured from a direction perpendicular to the laser beam with a self-made second microscope; the objective was a W25×/∞ with NA of 0.45 described in Maier et al. (1997); the tubus lens had f = 160 mm, and the ocular was 12.5× with f = 20 mm. This allowed the sample indentation to be visualized while establishing contact. We attempted a second method to determine the instant of contact, namely by stimulating the cantilever magnetically and monitoring the velocity phase while the cantilever was approached. However, it was difficult to clearly identify the instant of contact by this method because there was no obvious phase-jump upon contact; instead, because of fluid coupling to the surface of the organ of Corti, the phase changed only gradually as the surface was approached (<0.5°/μm over a distance of ∼17 μm before contact).

Equivalent impedance and force calibration

In the following, reference is repeatedly made to equations given in Scherer et al. (2000), which are denoted here as Eq. S-n, where n is the number of the equation; these are reproduced in the Appendix. The theory of cantilever vibrations is taken from Sader (1998).

The magnetic force is an area force, because the ferromagnetic coating covers the entire tip side of the cantilever. The inhomogeneity caused by the tip coating was neglected. Calibration was carried out after blunting the tip. In the case of a harmonic magnetic field with angular frequency ω, the force per unit length is given by

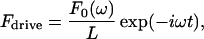graphic file with name M2.gif (1)

where F0 is the total magnetic force on the magnetic moment of the entire cantilever, L is the length of the cantilever, and t is time. Introducing the Fourier-transformed Eq. 1 into Eqs. S-18 and S-19 and inverse-Fourier transforming Eq. S-19, gives the deflection velocity v of the cantilever tip as

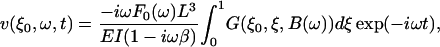graphic file with name M3.gif (2)

where ξ is the scaled coordinate along the cantilever, ξ0 the location of the tip, E the Young's modulus of the cantilever material, I the area moment of inertia, and β the internal damping factor of the cantilever and G(ξ,ξ′,B(ω)) is Green's function, Eq. S-20, to the differential equation of the cantilever, Eq. S-16. B(ω) includes the fluid, inertial, and elastic forces on the cantilever and is given by Eq. S-17. The equivalent point impedance of the cantilever at its tip is given by Eq. S-27 as

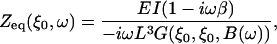graphic file with name M4.gif (3)

and the equivalent point force is

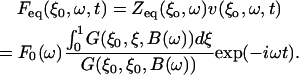graphic file with name M5.gif (4)

This means that Zeq(ω) and Feq(ω) can be calculated if F0(ω) and B(ω) are known for the situation where the cantilever is near the organ of Corti. However, B(ω) is known from theory only if the cantilever is in air or is in an infinitely extending fluid. In our case, the organ is in a solution (Hanks' balanced salt solution) and the cantilever is near the sample. Therefore, a calibration procedure was developed to establish F0(ω) and B(ω).

To find F0(ω), the magnetically induced velocity of the cantilever tip in air was measured with the cantilever in its usual position within the experimental chamber (200 μm above the support). This velocity spectrum, vair(ω), together with the theoretical Bair(ω), were substituted into Eq. 2, which was then solved for F0(ω). F0(ω) depends only on the magnetic moment of the cantilever and on the magnetic field. Since the magnetic field does not change in the solution (see Magnetic Force Generation), F0(ω) is the same in fluid and air.

To find B(ω) in the actual measurement situation, the velocity spectrum of the noncontact mode in fluid was measured (cantilever 13 μm above the sample). This velocity spectrum, vfree(ω), together with F0(ω) as determined above, were substituted into Eq. 2, which was then solved numerically for B(ω).

Finally, the equivalent impedance and force in the measurement situation were calculated from Eqs. 3 and 4.

Velocity measurement

Velocity was measured with a laser Doppler vibrometer (LDV, OFV-302, wavelength 633 nm, power 1 mW) equipped with a demodulator (OFV-3000, bandwidth 100 kHz), both from Polytech (Waldbronn, Germany). The laser beam was focused on the sample by coupling it into the optical path of an upright microscope (Axioskop 2FS, Zeiss, Jena, Germany) via a beam splitter (AHF Analysentechnik, Tübingen, Germany), which was highly reflective only above 590 nm, but transparent for shorter wavelengths (Fig. 2). This allowed microscopic observation while the laser was focused on the sample. Since the reflectivity of the beam splitter for the laser wavelength was <100%, the laser spot could be seen through the ocular. The microscope objective was a water-immersion objective with magnification 40×, numerical aperture 0.8, and working distance 3.61 mm (Zeiss Achroplan, Jena, Germany). The laser spot had approximately a Gaussian profile, with full-width at 1/e2 of maximum power of 0.63 μm (quantified with a knife-edge method). From the measured velocity, v(t), the velocity spectrum v(ω) was obtained via fast Fourier transformation and the displacement spectrum calculated as a(ω) = v(ω)/iω. The velocity spectrum was corrected for the measured transfer function of the LDV. The noise floor of the measurement system, quantified as displacement amplitude, was derived from the cantilever velocity measured with the tip in contact with the support. The noise floor decreased from 10−2 nm at 480 Hz to 10−4 nm at 76 kHz (effective averaging time: 25 s).

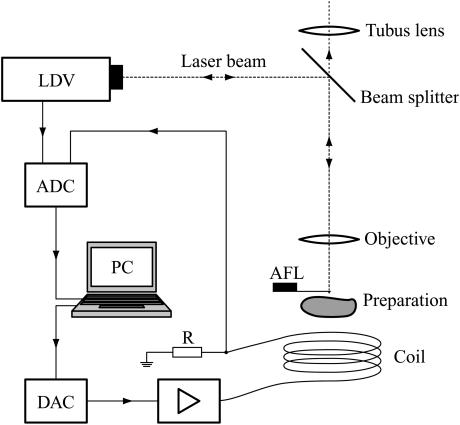
FIGURE 2.

FIGURE 2

Open in a new tab

The beam from the laser Doppler vibrometer (LDV) was coupled into an upright microscope via a beam splitter, transparent below 590 nm, and focused on the atomic force cantilever (AFL). The tip of the AFL could be seen as a dark spot through the slightly transparent AFL, allowing the tip to be accurately positioned on its target. The digital-to-analog converter (DAC) is for the driving voltage for the coil, amplified with a wide-band audio amplifier. A 0.9 Ω-resistor (R) was inserted between the coil and ground to monitor current. Analog-to-digital converters (ADC) are for velocity and current data. Not illustrated is the second microscope used for measuring the indentation of the organ of Corti resulting from contact with the tip of the AFL; its optical axis was directed orthogonal to the direction of the laser beam.

Magnetic force generation

The cantilever was magnetized with a strong NdFeB permanent magnet in the direction of its deflection (Fig. 1). The magnetic field was generated by a cylindrical coil (length 3 mm, diameter 4–10 mm, 120 windings of 0.22-mm varnished Cu wire), with the cantilever tip placed near the central axis of the coil at a distance of 2 mm from the end of the coil (Fig. 2). The magnetic moment of the cantilever thus experiences a dipole force in the magnetization direction.

The coil was driven by an audio amplifier (Onkyo A-905X, ONKYO Europe Electronics, Gröbenzell, Germany) with a 3-dB bandwidth of 100 kHz. The RMS-current through the coil was set to 600 mA, corresponding to a peak current of 2 A, with the standard multitone driving voltage (see next section). Since the magnetic field strength is proportional to the coil current, the latter was measured via a 0.9-Ω resistor in the current path (Fig. 2). The voltage at the resistor was recorded simultaneously with the velocity signal (voltage output) of the LDV, so that the measured velocity could be normalized to coil current (and thus field strength). In this way, all measurements were truly comparable, irrespective of the amplifier gain. By placing a second coil on top of the stimulation coil and monitoring the induced voltage, it was confirmed that filling the chamber with Hanks' balanced salt solution did not affect the frequency response of the generated magnetic field.

Signal processing

Magnetically induced displacement amplitudes of the cantilever were on the order of 1 nm and, therefore, a linear relationship between force and displacement (or velocity) could be safely assumed; this was also verified experimentally (Discussion). Consequently, instead of stimulating with a single frequency, the coil current (and thus the magnetic force) was chosen to be a multitone signal. It contained 81 frequency components between 480 Hz and 70 kHz, which were spaced almost logarithmically with a ratio of 1.07 between adjacent frequencies. The frequencies were shifted somewhat to exclude the coincidence of a stimulation frequency with one of the first four harmonics of a lower frequency, thereby reducing contamination of the measured velocity spectrum with harmonic distortion products. If the frequency components of the driving voltage Udrv for the coil were each chosen to have unity amplitude, but random phase, then

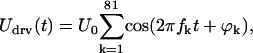graphic file with name M6.gif (5)

where t is time, fk is the kth frequency, U0 is a scaling factor, and ϕk is the randomly distributed phase of the kth frequency component.

The cantilever exhibits a resonance at 10–20 kHz in fluid. Therefore, to maximize the SNR for the measured velocity at all frequencies, the cantilever response was compensated for by weighting the stimulus with a function W(ω), which was approximately the inverse of the cantilever response at

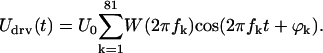graphic file with name M7.gif (6)

For our cantilevers, the equation

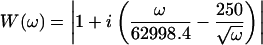graphic file with name M8.gif (7)

yielded a measured velocity that remained within one order-of-magnitude over the entire frequency range. The minimum value of W = 1 is at ω = 2π × 104 rad/s, the approximate resonance frequency of the cantilever in fluid. With this stimulus, the peak amplitude of the voltage signal was a factor-of-53 greater than the amplitude of the frequency component with W = 1. U0 was chosen so that the displacement amplitude per spectral point was ∼1 nm.

The stimulus voltage was generated with an arbitrary waveform generator (AWG; Hewlett-Packard E1445A, Böblingen, Germany).

The voltage output of the LDV coding the cantilever velocity and the voltage across the 0.9-Ω resistor coding the coil current were digitized simultaneously with a 4-channel, 16-bit resolution, 196-kHz sample rate analog-digital converter (Hewlett-Packard E1433A). The data blocks had a size of 8192 samples. The beginning of data input and output was synchronized via trigger lines so that multiple data blocks could be averaged in the time domain.

Both averaged input data blocks (velocity and current) were fast-Fourier-transformed and saved to files. Velocity data were corrected off-line for the measured frequency response of the LDV and normalized to the coil current. The impedance Z was then calculated from the velocity v (per unit coil current) and the force Feq, which was also calibrated relative to the coil current (see Equivalent Impedance and Force Calibration, above), according to Z = Feq/v, so that the coil current cancels out.

The measurement software was written in VEE (Hewlett-Packard) and the off-line data processing software in Mathematica (Wolfram Research, Champaign, IL). Nonlinear least mean-square fitting was performed with the Levenberg-Marquardt algorithm. Fit parameters are given as mean ± SD. Tests of statistical significance were performed at the 95% confidence level.

Animal preparation

Preparations were made from the first three turns of the adult, pigmented guinea-pig cochlea, corresponding to distances of 3.8–13 mm from the round window (Fernández, 1952; von Békésy, 1960). Young female animals were used, weighed 300–400 g, had a positive Preyer's reflex, and were killed by rapid cervical dislocation. The preparation included the modiolar bone, basilar membrane, and overlying organ of Corti of a half to a full turn (Figs. 1 and 3). The tectorial membrane was removed with an ultrafine needle. Care and maintenance of the guinea pigs was in accordance with institutional and state guidelines. During preparation and experiment the sample was kept in Hanks' balanced salt solution (Sigma, supplemented with 4.1 mM NaHCO3 and 10 mM HEPES buffer, adjusted to 310 ± 10 mOsm and pH 7.38 ± 0.02).

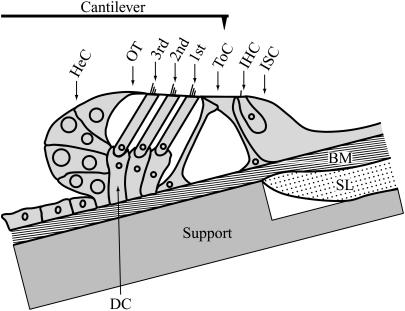
FIGURE 3.

FIGURE 3

Open in a new tab

Cross section of the organ of Corti (schematic, from the second cochlear turn) showing the eight recording positions in the radial direction. ISC, inner sulcus cells; IHC, inner hair cell; ToC, tunnel of Corti; 1st–3rd, rows of outer hair cells; OT, outer tunnel; and HeC, Hensen's cells. The basilar membrane (BM) lies flat on the support, and is held in place by hydrodynamic forces. The support was tilted, so that the reticular lamina was approximately parallel to the focal plane of the microscope and the long axis of the cantilever. Cells within the ISC are not depicted. SL, spiral lamina; DC, Deiters' cells. Nonshaded areas depict fluid spaces. The cantilever is drawn approximately to scale.

The organ of Corti was mounted on a custom-made support within the experimental chamber (Fig. 1). The design of the support was such that the basilar membrane was lying on its tympanic surface. Relative motion between basilar membrane and support was negligible, as ascertained by measurements of basilar membrane velocity with the LDV in response to cantilever stimulation—velocity was below the noise floor at all frequencies. The mechanically clamped configuration of the basilar membrane allowed the impedance of the organ of Corti to be investigated without the influence of the basilar membrane.

Impedance measurements typically began 40 min after sacrifice of the animal. An impedance measurement at one radial position required ∼4 min; 40 min were required for measurements at all radial positions. In control experiments, the impedance was repeatedly measured during a time span of 80 min—no significant change in impedance was observed. All experiments were carried out at controlled room temperature (20–22°C).

RESULTS

Impedance was measured from 30 cochleae, each from a separate animal. One longitudinal location was examined in each cochlea. Measurements were made at up to eight radial positions (Fig. 3). Data were pooled from three longitudinal regions along the cochlea: 3.8–4.5 mm (N = 9), 7–8 mm (N = 12), and 12–13 mm (N = 9) from the round window. Figs. 4–6 show typical examples from these three longitudinal regions for impedances measured at three different radial positions on the reticular lamina.

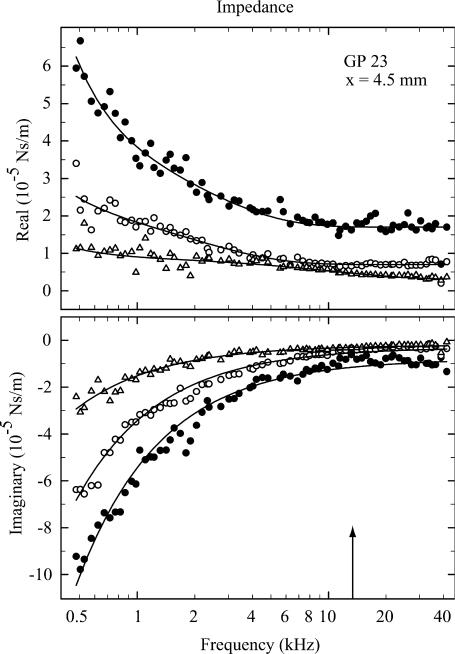
FIGURE 4.

FIGURE 4

Open in a new tab

Real and imaginary parts of the impedance of a preparation 4.5 mm from the round window at three radial locations: tunnel of Corti (•), inner hair cell (○), and first-row outer hair cell (▵). Notice that the magnitude of the impedance is greatest at the tunnel of Corti. The arrow indicates the characteristic frequency according to the map of Tsuji and Liberman (1997). The fit functions are given by Eq. 8. Parameters are (mean ± SD). tunnel of Corti, k = 0.292 ± 0.005; c1 = 237 ± 27; c2 = (1.75 ± 0.03) × 10−5; c3 = (2.38 ± 0.28) × 10−5; c4 = (7.11 ± 0.95) × 10−5; and c5 = (7.92 ± 0.61) × 10−6. Inner hair cell, k = 0.197 ± 0.003; c1 = 49.5 ± 19.3; c2 = (7.00 ± 0.23) × 10−6; c3 = (1.56 ± 0.21) × 10−5; c4 = (7.39 ± 1.10) × 10−5; and c5 = (3.13 ± 0.34) × 10−6. First-row outer hair cell, k = 0.082 ± 0.002; c1 = 23.7 ± 8.0; c2 = (3.21 ± 0.46) × 10−6; c3 = (6.03 ± 0.47) × 10−6; c4 = (1.53 ± 0.38) × 10−5; and c5 = (1.94 ± 0.25) × 10−6. Stiffness of cantilever, 1.20 N/m. All units are SI.

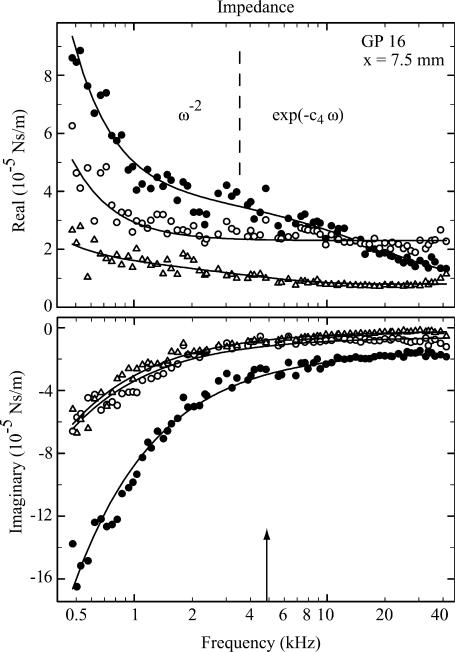
FIGURE 5.

FIGURE 5

Open in a new tab

Real and imaginary parts of the impedance of a preparation 7.5 mm from the round window at three radial locations: tunnel of Corti (•), inner hair cell (○), and first-row outer hair cell (▵). Dashed line separates the regions where the ω−2 and exponential terms of Eq. 8 dominate—at lower frequencies for ω−2 and at higher frequencies for the exponential. The arrow indicates the characteristic frequency according to the map of Tsuji and Liberman (1997). Fitted parameters are tunnel of Corti, k = 0.456 ± 0.009; c1 = 502 ± 29; c2 = (9.57 ± 3.20) × 10−6; c3 = (2.86 ± 0.27) × 10−5; c4 = (8.52 ± 2.17) × 10−6; and c5 = (1.46 ± 0.10) × 10−5. Inner hair cell, k = 0.176 ± 0.005; c1 = 253 ± 17; c2 = (2.35 ± 0.04) × 10−5; c3 = 0; c4 is not used; and c5 = (5.65 ± 0.54) × 10−6. First-row outer hair cell, k = 0.179 ± 0.004; c1 = 53.7 ± 20.5; c2 = (7.68 ± 0.39) × 10−6; c3 = (9.01 ± 1.65) × 10−6; c4 = (4.57 ± 1.33) × 10−5; and c5 = (1.54 ± 0.48) × 10−6. Stiffness of cantilever, 1.20 N/m. All units are SI.

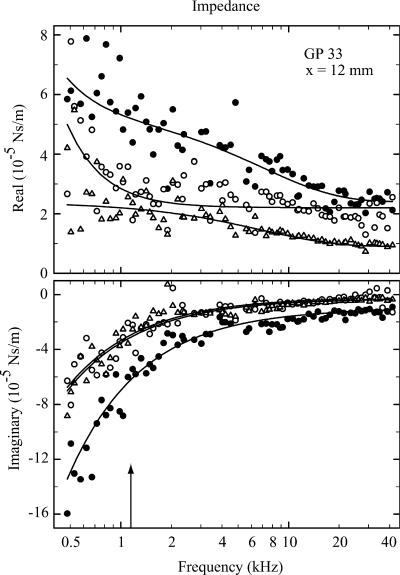
FIGURE 6.

FIGURE 6

Open in a new tab

Real and imaginary parts of the impedance of a preparation 12 mm from the round window at three radial locations: Tunnel of Corti (•), inner hair cell (○), and first-row outer hair cell (▵). The arrow indicates the characteristic frequency according to the map of Tsuji and Liberman (1997). Fitted parameters are tunnel of Corti, k = 0.375 ± 0.010; c1 = 122 ± 48; c2 = (2.41 ± 0.16) × 10−5; c3 = (2.96 ± 0.28) × 10−5; c4 = (2.22 ± 0.52) × 10−5; and c5 = (1.04 ± 0.11) × 10−5. Inner hair cell, k = 0.198 ± 0.009; c1 = 254 ± 36; c2 = (2.19 ± 0.08) × 10−5; c3 = 0; c4 is not used; and c5 = (2.37 ± 1.01) × 10−6. First-row outer hair cell, k = 0.202 ± 0.008; c1 = 0; c2 = (9.39 ± 1.15) × 10−6; c3 = (1.47 ± 0.15) × 10−5; c4 = (2.29 ± 0.68) × 10−5; and c5 = (2.68 ± 0.88) × 10−6. Stiffness of cantilever, 1.59 N/m. At frequencies below ∼2 kHz, the SNR was approximately half that for the more basal recordings in Figs. 4 and 5, because the cantilever was stiffer and, in addition, the magnetic force was 70% of that for the softer cantilever. All units are SI.

A Voigt-Kelvin viscoelastic description of impedance

Data from the organ of Corti could be consistently described by the impedance of a generalized Voigt-Kelvin viscoelastic material; that is with spring in parallel with a dashpot, for which Z = k/(iω) + μ, with spring constant k and viscosity μ. The generalization was obtained by choosing the viscosity to be complex-valued, μ = μ′ – iμ″, such that real, ℜ, and imaginary, ℑ, components of Z have the frequency dependence of

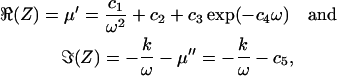graphic file with name M9.gif (8)

where c1…c5 and k are real-valued parameters, independent of frequency.

Obviously, the organ of Corti at any place along the cochlea is not as homogeneous as implied by this model: it is a mechanically complicated biological structure with fluid-filled channels (Fig. 3). Instead, the model is empirical, intended to mathematically describe the data in an analytical form, suitable for future development of biophysical models of the entire cochlea.

In the first step of the fitting procedure, the model Eq. 8 was fitted to the data with all parameters free. If one or more of the parameters c1, c2, k, or c5 were not statistically significant, they were successively set to zero and the fitting algorithm repeated. If either or both c3 or c4 were not statistically significant, the exponential term was removed from the model in Eq. 8, and the fitting algorithm then repeated. This procedure prevented the occurrence of physically meaningless parameters. The values k and c2 were always significant; c1 and c5 were significant with a few exceptions; and c3 and c4 were significant in approximately half of the cases around the tunnel of Corti, but zero otherwise. In the collated data given in Tables 1–3, the parameters that were not significant were treated as zero with the exception of c4: if the exponential term was not used, c3 was set to zero, but c4 was excluded from the estimation of mean values. Average values of the fitted parameters for the three cochlear turns are plotted in Fig. 7.

TABLE 1.

Averaged fitted parameter values from nine preparations from the region 3.8–4.5 mm from the round window—the basal turn of the cochlea

N c1 c2 c3 c4 k c5
ISC 3 15.2 2.15 × 10−6 0 * 0.0281 1.16 × 10−7
IHC 11 180 1.39 × 10−5 1.22 × 10−5 1.174 × 10−4 0.219 3.94 × 10−6
ToC 11 491 2.96 × 10−5 8.44 × 10−6 8.044 × 10−5 0.478 8.43 × 10−6
1st OHC 9 168 9.72 × 10−6 3.82 × 10−6 2.823 × 10−5 0.195 3.99 × 10−6
2nd OHC 9 57.1 6.54 × 10−6 6.74 × 10−7 3.371 × 10−5 0.112 1.42 × 10−6
3rd OHC 9 59.6 5.27 × 10−6 3.59 × 10−7 3.721 × 10−5 0.0670 1.52 × 10−6
OT 8 57.4 4.68 × 10−6 0 * 0.0534 8.50 × 10−7
HeC 6 40.0 1.33 × 10−6 0 * 0.0354 0
Open in a new tab

Radial locations are: inner sulcus cells (ISC), inner hair cells (IHC), tunnel of Corti (ToC), first to third row outer hair cells (OHC), outer tunnel (OT), and Hensen's cells (HeC). N gives the number of measurements used for calculating the average. The subscript on the value of c4 gives the number of measurements, for which both c3 and c4 were significantly different from zero, and the exponential term was consequently included. If the exponential term in Eq. 8 had to be omitted, c4 is meaningless, which is indicated by *; c3 was set to zero in this case. All units are SI.

TABLE 2.

Averaged fitted parameter values from 12 preparations from the region 7–8 mm from the round window—the second turn of the cochlea

N c1 c2 c3 c4 k c5
ISC 10 45.8 5.99 × 10−6 6.98 × 10−7 1.181 × 10−4 0.0197 1.31 × 10−6
IHC 13 194 1.76 × 10−5 3.59 × 10−6 3.341 × 10−4 0.174 5.46 × 10−6
ToC 14 416 2.61 × 10−5 1.04 × 10−5 8.494 × 10−6 0.428 9.24 × 10−6
1st OHC 13 90.7 8.69 × 10−6 5.11 × 10−6 3.136 × 10−5 0.149 2.52 × 10−6
2nd OHC 15 20.8 6.59 × 10−6 8.34 × 10−7 5.432 × 10−5 0.0480 5.82 × 10−7
3rd OHC 15 23.5 4.44 × 10−6 1.00 × 10−6 1.551 × 10−4 0.0326 5.92 × 10−7
OT 10 16.1 4.47 × 10−6 0 * 0.0296 5.44 × 10−7
HeC 17 26.0 3.27 × 10−6 0 * 0.0361 3.22 × 10−7
Open in a new tab

Acronyms and notations as in Table 1.

TABLE 3.

Averaged fitted parameter values from nine preparations from the region 12–13 mm from the round window: the third turn of the cochlea

N c1 c2 c3 c4 k c5
ISC 6 16.3 1.01 × 10−5 0 * 0.0255 0
IHC 7 118 1.95 × 10−5 0 * 0.191 3.46 × 10−6
ToC 7 321 3.35 × 10−5 4.23 × 10−6 2.221 × 10−5 0.307 9.92 × 10−6
1st OHC 7 99.3 1.36 × 10−5 6.02 × 10−6 2.502 × 10−5 0.201 3.54 × 10−6
2nd OHC 7 51.4 8.35 × 10−6 0 * 0.0795 1.02 × 10−6
3rd OHC 6 11.6 6.84 × 10−6 0 * 0.0551 1.25 × 10−7
OT 6 0 6.22 × 10−6 0 * 0.0190 − 3.83 × 10−7
HeC 7 47.1 4.81 × 10−6 0 * 8.59 × 10−3 − 2.37 × 10−7
Open in a new tab

Acronyms and notations as in Table 1. Notice the negative values for c5 on the outer tunnel and Hensen's cells—this indicates a measurable inertial component.

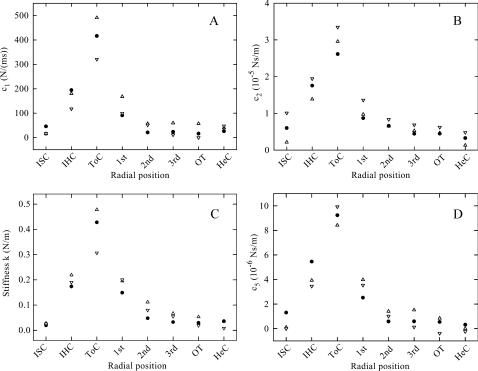
FIGURE 7.

FIGURE 7

Open in a new tab

Mean parameter profiles across the organ of Corti for the three longitudinal regions of the cochlea: ▵, 3.8–4.5 mm; •, 7–8 mm; and ▿, 12–13 mm. (A) c1, the proportionality constant describing the quadratic decrease of ℜ(Z) at low frequencies; (B) c2, the high-frequency value of ℜ(Z); (C) k, the stiffness; (D) c5, the high-frequency value of – ℑ(Z). To make the different regions comparable, the radial positions are set to equidistant intervals rather than true distance. Notice that the tunnel of Corti presents the stiffest component, and that its stiffness becomes progressively larger toward the base of the cochlea. Error bars are not shown because the standard deviations were in most cases smaller than the radius of the plot symbols. Acronyms as in Table 1.

In general, the impedance results can be characterized as follows. The real (or frictional) part exhibits a monotonic decrease proportional to ω−2, followed by a region of reduced slope between 2 and 5 kHz (particularly evident in Fig. 5), and asymptotes to a constant positive value toward 40 kHz. (Here it should be emphasized that we use the word “asymptote” rather liberally—it simply refers to the observation that the impedance component is constant at high frequencies, up to at least the maximum measurement frequency of 40 kHz. Assertions about a true asymptote would require measurements to at least an octave above the highest physiologically relevant frequency for the tissue; namely, at least 90 kHz for the extreme basal region of the guinea-pig cochlea.) The exponential term in ℜ(Z) was introduced to model the region of reduced slope. Both the quadratic decrease and the region of reduced slope were most prominent at the tunnel of Corti and the adjacent positions (inner hair cells and first-row outer hair cells), and were less obvious for recording locations away from the tunnel of Corti. The imaginary (or storage) part exhibits a decrease proportional to ω−1, which asymptotes to a constant, (usually) negative offset at high frequencies. The proportionality constant of the former is equivalent to the spring constant k, and the latter represents the imaginary component, μ″, of the viscosity.

Dominance of the real component near CF

At low frequencies, the magnitude of the imaginary component was larger than the real component; on average, a factor of 2.5, 2.8, and 2.9 larger at 500 Hz for outer hair cells of the first, second, and third turns, respectively. However, the ratio eventually reversed with increasing frequency, so that in the first and second turns, at the characteristic frequency (CF) of the recording location, the real part was greater than the imaginary part; on average, 1.7 and 1.5 for outer hair cells of the first and second turns, respectively. In the third turn, at CF, the real part remained smaller than the imaginary part by a factor of 0.8. The crossover frequency, where both have equal magnitude, was located 2.9 and 0.9 octaves below CF for the first and second turns, respectively, and 0.8 octave above CF for the third turn.

This experimental result compares with a model by Nobili and Mammano (1996), which proposes that enhanced frequency selectivity, particularly in the basal half of the cochlea, requires that at CF the viscous forces transmitted by the Deiters' cells and outer hair cells are greater than the elastic forces.

Absence of an inertial component

Positive values for the imaginary component, which are indicative of an inertially dominated impedance at high frequencies, were found only in two cases: on the outer tunnel and Hensen's cells in the third turn of the cochlea (Table 3). In all other cases, ℑ(Z) ≤ 0 up to 40 kHz. To verify that the measurement method can actually detect an inertial component, the impedance of a second cantilever was measured in place of the organ of Corti. The expected impedance with a positive imaginary (inertial) part at high frequencies was found. Therefore, we conclude that, except for the outer tunnel and Hensen's cells in the third turn, the mass of the organ of Corti has physically insignificant effect on its dynamical behavior in the transverse direction up to at least 40 kHz.

Spatial dependence of the mechanical parameters

The magnitudes of both the real and the imaginary parts of the impedance were greatest above the tunnel of Corti and decreased toward the Hensen's cells and the inner sulcus (Fig. 7). This radial position of maximum stiffness is consistent with the triangular structure of the pillar cells spanning the region between basilar membrane and reticular lamina, with their cytoskeletons reinforced by microtubules (Slepecky, 1996). The stiffness of the basilar membrane is also known to be largest at the outer pillar cell (Naidu and Mountain, 1998).

The stiffness of the organ of Corti decreased from base to apex of the cochlea; the ratio of the stiffnesses was less than a factor of 2 (Fig. 7). This relatively small longitudinal variation of the compressional stiffness of the organ of Corti contrasts with the situation for the basilar membrane, where the (bending) stiffness decreases by two orders of magnitude from base to apex (von Békésy, 1960; Naidu and Mountain, 1998). The stiffness of the organ of Corti measured at the tunnel of Corti (0.3–0.5 N/m in Fig. 7) is comparable to basilar membrane stiffness at the outer pillar cells reported by Naidu and Mountain (1998) for the apical region of the (gerbil) cochlea. In other words, the compressional stiffness of the organ of Corti does not contribute significantly to the mechanical impedance of the cochlear partition in the basal region of the cochlea. This result supports an assumption in a viscoelastic model by Nobili and Mammano (1996)—namely that the cochlear amplifier stiffness, km, defined in that article, which is equivalent to the stiffness, k, measured by us at the outer hair cells, appreciably contributes to the cochlear partition stiffness only in the apical region of the cochlea.

When mean parameter values at different radial positions of one longitudinal region are compared, all pairs of c1, c2, k, and c5 are highly correlated (Table 4). This implies that they might not be as independent as our empirical viscoelastic model suggests, but could be derived instead from a suitable physical model of the organ.

TABLE 4.

Pearson's correlation coefficients for the mean values of c1, c2, k, and c5

3.8–4.5 mm
7–8 mm
12–13 mm
c1 c2 k c5 c1 c2 k c5 c1 c2 k c5
c1 1.00 0.987 0.989 0.979 1.00 0.982 0.982 0.991 1.00 0.960 0.911 0.986
c2 1.00 0.992 0.981 1.00 0.957 0.994 1.00 0.928 0.974
k 1.00 0.990 1.00 0.968 1.00 0.957
c5 1.00 1.00 1.00
Open in a new tab

Pairs were taken from one longitudinal region and the correlation coefficient calculated for the eight radial positions. Correlation matrices from all three longitudinal regions are included in this table. The values c3 and c4 are omitted because they describe a region of reduced slope, which was found mainly, although not exclusively, for recordings at the tunnel of Corti. All correlation coefficients are significantly different from zero.

There was no significant correlation between parameter pairs from different preparations at the same radial and longitudinal recording locations. This is simply explained by the observation that the inter-animal scatter of parameter values was of the order of the standard deviations of the parameter estimates, which in turn were also small (e.g., for k, the coefficient of variation was typically 2–4% at the outer hair cells).

Qualitative observations

Apart from the quantitative results, the following qualitative observations were made. When the tunnel of Corti was compressed in the transverse direction by moving the tip of the cantilever 10 μm beyond the point of initial contact, the visually observable deformation of the reticular lamina extended radially from the inner hair cells to the third row outer hair cells, and longitudinally along the tunnel of Corti for at least 50 μm. Since this is a static displacement, the coupling cannot be mediated by the fluid, but represents a property of the solid structure. This is in agreement with findings of other authors: Naidu and Mountain (2001) displaced the basilar membrane with a point probe and measured deflection in the neighborhood of the probe. They found space constants for the longitudinal coupling of 16.7–56.9 μm from base to apex, respectively. Richter et al. (1998) measured the response of the basilar membrane to a displacement pulse applied on a certain longitudinal position in the so-called hemicochlea preparation. They found a longitudinal decrease in basilar membrane vibration amplitude of 58 dB/mm, which corresponds to a space constant of 150 μm. Moreover, in our preparation, the further away the cantilever tip was situated from the pillar heads, the more local the deformation was. Inner sulcus and Hensen's cells were so soft that pushing the cantilever so far toward the reticular lamina that its tip penetrated the cell membrane and its flat part touched the cells, still led to an extremely localized deformation, extending <15 μm around the cantilever, whereas the cells appeared to wrap around it. Therefore, it seemed as if the pillar cells form a rigid longitudinal beam, surrounded by tissue, which becomes increasingly softer in the radial direction.

DISCUSSION

The impedance measured in this study is the compressional impedance of the organ of Corti. It is compressional because the basilar membrane was mechanically clamped, the velocity of the reticular lamina being measured in response to an applied (point) force. These are the first measurements of its kind.

The expression describing the frequency dependence of the impedance (Eq. 8) was empirically chosen to reproduce mathematically the data in analytical form. Only the stiffness parameter, k, can be interpreted physically. The other parameters, ci (i = 1,…,5), define the so-called viscous element of the Voigt-Kelvin model. It should be emphasized, however, that the ci will not necessarily be defined by viscous material properties alone, but also by other material properties, such as Young's moduli and fluid density, as well as geometry. The usefulness of this empirical description lies in its ability to supply components for and properties of biophysical models of the organ of Corti. For example, one of the salient features of the data, or equivalently of the analytical expression, was that the point impedance is purely viscoelastic; that is, for force applied at a point on the organ of Corti, there is no inertial component of vibration. The biophysical consequence of zero inertia, together with the magnitudes of the viscous and stiffness components, is the subject of the last section of the Discussion.

Stiffness

The compressional impedance measured in these experiments should not be confused with the impedance of the cochlear partition, or as it is sometimes called, the impedance of the basilar membrane. That impedance is derived from the displacement (or velocity) of the basilar membrane in response to an applied force (or pressure) at its tympanic surface, without mechanical constraint of the upper (vestibular) surface of the partition. The stiffness component of the cochlear partition impedance has been numerously measured since the original work of von Békésy (1960), both in vitro (Gummer et al., 1981; Miller, 1985; Naidu and Mountain, 1998) and in vivo (Olson and Mountain, 1991; Olson, 2001); it appears to derive from the bending stiffness of the cochlear partition, as originally postulated by von Békésy (1960). This stiffness is reduced after removal of the organ of Corti (Naidu and Mountain, 1998). The compressional stiffness of the organ of Corti decreases by a factor of two from base to apex (Fig. 7), whereas the stiffness of the cochlear partition decreases by two orders of magnitude (von Békésy, 1960; Naidu and Mountain, 1998); the two impedances are of similar magnitude only in the apical part of the cochlea. The compressional impedance is an important component of the “cochlear amplifier impedance” (Nobili and Mammano, 1996): these authors predicted that only in the apical region is the compressional stiffness of the organ of Corti comparable in size to the bending stiffness of the cochlear partition. Our experiments support this prediction.

The stiffness measured at the second row outer hair cells was a factor 4–10 larger than that of isolated outer hair cells (Adachi and Iwasa, 1997; Frank et al., 1999; Hallworth, 1995; Iwasa and Adachi, 1997). That is, the mechanical components and structure of the organ of Corti appear to increase the stiffness at the outer hair cells relative to that for the isolated cell.

The stiffness measured at the tunnel of Corti was at least a factor of 40 smaller than the axial stiffness of isolated outer pillar cells estimated from the data of Tolomeo and Holley (1997), and at least a factor of 400 larger than their measured (midpoint) bending stiffness. (Tolomeo and Holley found the outer pillar cell to be composed of approximately equal numbers of cross-linked microtubules and actin filaments extending along the length of the cell. Based on 2000 microtubules, on average, with inner and outer diameters, respectively, of 17 nm and 30 nm, they estimate Young's modulus from bending experiments to be ∼2 GPa for the microtubules. Assuming that the microtubules are isotropic and uncoupled, and obey Hooke's law, with each extending along the entire length of the cell (92 μm) and undergoing equal axial strain, then we estimate that a compressive uniaxial force experiences an axial stiffness of 21 N/m. This estimate may be taken as a lower limit for the axial stiffness. Inclusion of an equal number of actin filaments, with a diameter approximately one-fifth that of microtubules (Tolomeo and Holley, 1997), and Young's modulus of ∼3 GPa (Gittes et al., 1993), would contribute an additional 2 N/m. Cross-linking might further increase the axial stiffness.) Due to the similar microstructure of outer and inner pillar cells (Tolomeo and Holley, 1997), their corresponding axial stiffnesses are likely to be comparable. Therefore, the deformation of the triangular structure of the tunnel of Corti by a point load on the pillar heads, as was the situation in our experiments, appears to cause mainly bending of the pillar cells, rather than compression. This is consistent with the more general observation in the literature, that microtubules are almost inextensible, the compliance of cells being due primarily to filament bending or sliding between filaments (Gittes et al., 1993). Finally, resistance to bending by this triangular structure appears to be greater than for the isolated pillar cells.

Contact versus noncontact impedance measurements

The distance between sample and cantilever in the noncontact case has consequences for the in situ calibration: if it is too large, the hydrodynamics of the fluid surrounding the cantilever will be that of an infinitely extending fluid rather than that with a nearby surface, and the calibration procedure of Equivalent Impedance and Force Calibration (see above) becomes obsolete. On the other hand, as the cantilever approaches the sample, surface fluid coupling between the two increases gradually rather than abruptly, so that the impedance (and we looked especially at the phase) changed only gradually from the noncontact value to the contact value. This meant that according to the continuous monitoring of impedance phase, there was no definite point of contact. Indeed, the contact condition was defined visually as the point at which the surface was depressed ∼1 μm by the cantilever tip (see Materials and Methods). For the purpose of determining the noncontact impedance, we found that a distance of ∼13 μm between sample surface and cantilever tip yielded a fluid coupling that was strong enough for the in situ calibration, but small compared with the coupling in the contact case.

The question arises as to what extent the pre-stress of the preparation due to the presence of the cantilever tip (1-μm compression) has significant consequences for the results. To resolve this issue, we conducted a series of measurements at different distances from the sample. The result was that once a reliable contact had been established, a further approach (meaning stronger pre-stress) of up to 3 μm did not change the measured impedance. This suggests that the experiments were conducted under linear mechanical conditions. Further evidence for linearity derives from the velocity spectra: second and higher order harmonics were always at least 30 dB below the fundamental amplitude and disappeared in the noise for most frequencies. Linear conditions are also consistent with the small standard deviations of the stiffness estimates and the small standard deviations of the stiffness populations at given radial and longitudinal positions. The latter are not shown in Fig. 7, because in most cases they were smaller than the radius of the plot symbols. Finally, with a total sample thickness of ∼100 μm in the first cochlear turn, a compression of 1 μm yields a strain of 1%. (Using confocal microscopy of unfixed preparations, we found distances between basilar membrane and reticular membrane at the tunnel of Corti of ∼100 μm both in the first and second turn, and 180 μm in the third turn. This distance increases toward Hensen's cells in the second and third turns.) From experiments with isolated outer hair cells, inner and outer pillar cells, and Deiters' cells, we have found that these cells do not exhibit buckling for strains up to at least 10% (data from a separate set of experiments, not illustrated here). Furthermore, when the cantilever tip is retracted, the upper surface of the organ returns to its original position. It is, therefore, unlikely that this relatively small pre-stress of the organ of Corti caused buckling or strain-hardening. In summary, we can safely conclude that the required pre-stress was sufficiently small to ensure linear mechanical conditions and that the measured impedances represent those of the unloaded organ of Corti.

Biophysical significance for cochlear amplification

It is noteworthy that the imaginary part of the impedance almost never became positive, not even at the highest frequency of 40 kHz. This means that the inertial component in the transverse direction was overwhelmingly dominated by the stiffness and/or by the negative imaginary part of the viscosity, so that most of the organ of Corti moved like a purely viscoelastic material at all physiologically relevant frequencies. The only exceptions to this rule were the outer tunnel region and the Hensen's cells in the third turn of the cochlea.

This has important consequences for cochlear amplification: displacement x of the cuticular plates is related to the electromechanical force F generated by the outer hair cells by x = F/(iωZ), where Z is the impedance of the organ of Corti, which we have presented here. If Z were dominated by an inertial term due to mass, m, at high frequencies Z ≈ iωm, then for constant force stimulation the displacement amplitude would decrease in proportion to ω−2, or equivalently with 12 dB/octave. However, if the load impedance driven by the electromechanical force of the outer hair cells is purely viscoelastic, then Z ≈ μ at high frequencies. Since μ decreased only slightly above 6 kHz (1.2 dB/octave), this means that the displacement amplitude decreases by only 4.8 dB/octave.

Indeed, for the basal region of the cochlea, where frequency selectivity and sensitivity are greatest (for review see Robles and Ruggero, 2001), we found that between 480 Hz and 40 kHz the magnitude of the complex compliance 1/(iωZ), which is the transfer function between force and displacement, decreased by only 20 dB and the phase shifted from ∼−25° to only −70° for all rows of outer hair cells (calculated as the phase of Z using Eq. 8, with parameters from Table 1). That is, without tectorial membrane, the mechanical load on the outer hair cells causes only a 10-fold decrease in their electromechanical displacement responses between low and high frequencies.

The tectorial membrane constitutes an additional point load on the stereocilia of the outer hair cells. What effect does this have on the interpretation of our results? To answer this we note that this load will be elastic at low frequencies and either frictional or inertial at high frequencies. For the second cochlear turn of the gerbil in vivo, Zwislocki and Cefaratti (1989) find a transverse stiffness of a 200-μm-long piece of tectorial membrane of 0.125 N/m. (Note that here we only consider a stiffness defined by the ratio of force to transverse displacement of the whole tectorial membrane in situ, attached to the spiral limbus, and detached from the stereocilia. Zwislocki and Cefaratti (1989) consider their previous results in Zwislocki (1988) as “qualitative.” Abnet and Freeman (2000) measured the longitudinal and radial, but not the transverse, stiffness. In the results of von Békésy (1960), the physiological state of the tectorial membrane is questionable, because it is known to be sensitive to the ionic environment; see Edge et al., 1998; Freeman et al., 2003b; Kronester-Frei, 1979; Shah et al., 1995.) The load is inertial above its resonant frequency—∼2.5 kHz in the transverse direction for the second cochlear turn of the gerbil. (The inertial impedance of a cuboid piece of tectorial membrane of length 200 μm, width 112 μm, and thickness 22 μm—see Zwislocki and Cefaratti, 1989—with a density of 1 g/cm3—that is, if the gel matrix is neglected; see Freeman et al., 2003a—was set equal to the elastic impedance of a spring of stiffness 0.125 N/m, to calculate the resonant frequency.) In this turn of the gerbil cochlea, the characteristic frequency is 3–8 kHz (Müller, 1996), implying that the transverse impedance of the tectorial membrane is inertial for the frequency selective region of basilar membrane motion. Moreover, due to the flat geometry of the tectorial membrane, the fluid forces acting upon it in the transverse direction will be much larger than in the radial direction. Therefore, using this gerbil data as an indicator and the fact that the density of the tectorial membrane and the surrounding fluid are similar, it is conceivable that for frequencies of cochlear amplification the tectorial membrane follows the motion of the surrounding fluid in the transverse direction. Consequently, if the pressure on the tectorial membrane toward scala tympani is in phase with a contractile force of the outer hair cells, the impedance of the organ of Corti could be (partially) compensated by the force of the tectorial membrane on the stereocilia of the outer hair cells.

The finding that in the first two cochlear turns the real part of the impedance is larger than the imaginary part at CF nicely concurs with the viscoelastic model proposed by Nobili and Mammano (1996) for cochlear amplification. Their hypothesis is that the attenuation and phase delay of the receptor potential relative to stereocilia displacement, and consequently of the electromechanical force, caused by the electrical time constant of the basolateral membrane of the outer hair cell, is compensated by the combined viscoelastic action of the outer hair cell and its supporting Deiters' cell. Indeed, the Mammano group (Lagostena et al., 2001) has since shown that the electromechanical action of the outer hair cell causes motion of its supporting Deiters' cell (together with its nearest neighbors). To compensate for the electrical time constant, their model requires that the viscous force be greater than the elastic force at CF; the required ratio is ∼33 at the 4.5-mm point, 16 at the 7.5-mm point, and 8 at the 12-mm point. (Note we calculated these ratios as follows: Using the notation of Nobili and Mammano (1996), we denote the combined viscosity of the outer hair cell and its Deiters' cell by hm(x), and their combined stiffness by km(x). The resulting mechanical filter is highpass with 3-dB (radial) frequency of ωm(x) = km(x)/hm(x). The electrical filter, whose time constant is to be compensated, is lowpass with 3-dB (radial) frequency denoted by ωc(x). The dependence of this latter frequency on cell-length was determined directly by Preyer et al. (1996) from the frequency spectrum of the whole-cell receptor potential in response to displacement of the stereocilia; it decreases by 0.058 octave/μm cell-length, beginning with a value of 546 Hz for a length of 20 μm. Then we invoke the assumption made by Nobili and Mammano (1996) that ωm(x) = ωc(x); that is, the highpass filter completely compensates the lowpass filter. Then, at CF the magnitude ratio of the viscous force to the elastic force must be equal to CF/fc, where fc = ωc/(2π). Using the tonotopy measured by Tsuji and Liberman (1997), the required ratios at the 4.5-mm, 7.5-mm, and 12-mm points are, respectively, 33, 16, and 8.)

Experimentally, we found the real part of the impedance to be approximately twice the imaginary part at CF in the first two cochlear turns; they were approximately equal in the third turn. The discrepancy between experiment and model is mainly due to the model values of stiffness assumed for the combination of outer hair cell and Deiters' cell being approximately an order-of-magnitude smaller than our experimentally observed stiffness values for the organ of Corti. Thus, using their assumed values of cochlear-partition viscosity, h(x), with hm(x) ≈ h(x)/1.33, we calculate viscosities of 0.27 × 10−5 Ns/m at all points along the cochlea; this is a factor of 2–3 smaller than our measured values (mean c2-data at the second row outer hair cell in Fig. 7). Fluid viscosity within the organ of Corti, which was not included in their model, might account for the difference between theory and experiment. The stiffness values derived from the assumption that ωm(x) = ωc(x), with km(x) = ωm(x)hm(x), are factors-of-9 and -17 smaller than our measured values at the 7.5-mm and 4.5-mm points, respectively (mean k-data at the second row outer hair cell in Fig. 7). Again, embedding of the cells within the structure of the organ of Corti might explain this difference, the experimentally observed stiffness at the outer hair cell in situ being larger than expected from model calculations with an isolated combination of outer hair cell and Deiters' cell.

Given all the assumptions involved in the theoretical and experimental analyses of this complicated system, the agreement between theory and experiment is encouraging; namely, that viscoelasticity at CF is of paramount importance for cochlear amplification.

CONCLUSION

We have demonstrated that this novel measurement technique works reliably up to at least 40 kHz, yielding reproducible results for a biological structure surrounded by fluid. The technique allows determination of the compressional mechanical impedance of the organ of Corti at all auditory frequencies. An empirical model yielded parameters relevant for a biophysical understanding of cochlear amplification.

Acknowledgments

We appreciate helpful discussions with Ernst Dalhoff. The bath chamber was machined by Klaus Vollmer. The electron microscope, in the Institute of Anatomy, University of Tübingen, was made available by Andreas Mack and operated by Ulrich Mattheus and Uta Paulsen.

This work was supported by a grant from the Federal Ministry of Education, Science, Research and Technology (Fö. 01KS9602), the Interdisciplinary Center of Clinical Research, Tübingen, and the Deutsche Forschungsgemeinschaft, DFG Gu 194/5-1 and SFB 430 TPA4.

APPENDIX

Equations describing the cantilever vibration (from Sader, 1998 and Scherer et al., 2000), which are used in Materials and Methods, are reproduced here for completeness.

The Fourier-transformed differential equation for the cantilever in fluid relates the deflection of the cantilever, Ŵ, with the scaled external forces, ŝ. Both depend on the scaled coordinate along the cantilever, ξ, and the radial frequency, ω, as

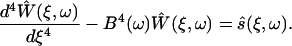graphic file with name M10.gif (S-16)

The coefficient B(ω) includes the cantilever and fluid parameters,

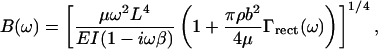graphic file with name M11.gif (S-17)

where μ is the mass per unit length, L the length, E the Young's modulus, I the area moment of inertia, b the width, and β the internal friction coefficient of the cantilever, ρ is the density of the surrounding fluid and Γ(ω) is the “hydrodynamic function” for the rectangular cantilever,

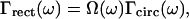graphic file with name M12.gif (S-15)

where Ω(ω) is an empiric correction function found by Sader (1998) and

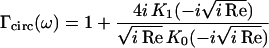graphic file with name M13.gif (S-13)

is the hydrodynamic function of a beam with circular cross section in terms of the Reynold's number

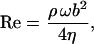graphic file with name M14.gif (S-14)

where η is the viscosity of the fluid.

The scaled driving force is a modified version of the driving force F̂drive,

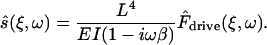graphic file with name M15.gif (S-18)

The solution to the differential equation S-16 is given in terms of its Green's function G(ξ,ξ′,ω),

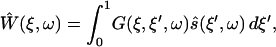graphic file with name M16.gif (S-19)

where the Green's function is given by

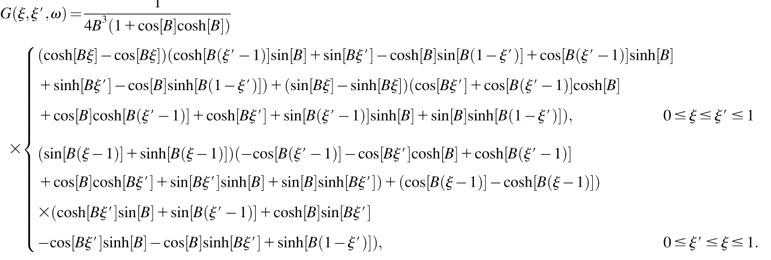graphic file with name 1378eqs20.jpg (S-20)

Finally, the point impedance of the cantilever upon a load at position ξ0 is

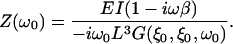graphic file with name M17.gif (S-27)

References

  1. Abnet, C. C., and D. M. Freeman. 2000. Deformations of the isolated mouse tectorial membrane produced by oscillatory forces. Hear. Res. 144:29–46. [DOI] [PubMed] [Google Scholar]
  2. Adachi, M., and K. H. Iwasa. 1997. Effect of diamide on force generation and axial stiffness of the cochlear outer hair cell. Biophys. J. 73:2809–2818. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Allen, J. B. 1980. Cochlear micromechanics—a physical model of transduction. J. Acoust. Soc. Am. 68:1660–1670. [DOI] [PubMed] [Google Scholar]
  4. Ashmore, J. F. 1987. A fast motile response in guinea-pig outer hair cells: the cellular basis of the cochlear amplifier. J. Physiol. 388:323–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Brownell, W. E., C. R. Bader, D. Bertrand, and Y. de Ribaupierre. 1985. Evoked mechanical responses of isolated cochlear outer hair cells. Science. 227:194–196. [DOI] [PubMed] [Google Scholar]
  6. Cai, H., C. P. Richter, and R. S. Chadwick. 2003. Motion analysis in the hemicochlea. Biophys. J. 85:1929–1937. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cooper, N. P., and W. S. Rhode. 1995. Nonlinear mechanics at the apex of the guinea-pig cochlea. Hear. Res. 82:225–243. [DOI] [PubMed] [Google Scholar]
  8. Dallos, P. 2003. Organ of Corti kinematics. J. Assoc. Res. Otolaryngol. DOI:10.1007/s10162–002– 304:1–18. [DOI] [PMC free article] [PubMed]
  9. Dallos, P., R. Hallworth, and B. N. Evans. 1993. Theory of electrically driven shape changes of cochlear outer hair cells. J. Neurophysiol. 70:299–323. [DOI] [PubMed] [Google Scholar]
  10. Edge, R. M., B. N. Evans, M. Pearce, C.-P. Richter, X. Hu, and P. Dallos. 1998. Morphology of the unfixed cochlea. Hear. Res. 124:1–16. [DOI] [PubMed] [Google Scholar]
  11. Fernández, C. 1952. Dimensions of the cochlea (guinea pig). J. Acoust. Soc. Am. 24:519–523. [Google Scholar]
  12. Florin, E. L., M. Radmacher, B. Fleck, and H. E. Gaub. 1994. Atomic force microscope with magnetic force modulation. Rev. Sci. Instrum. 65:639–643. [Google Scholar]
  13. Frank, G., W. Hemmert, and A. W. Gummer. 1999. Limiting dynamics of high-frequency electromechanical transduction of outer hair cells. Proc. Natl. Acad. Sci. USA. 96:4420–4425. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Freeman, D. M., C. C. Abnet, W. Hemmert, B. S. Tsai, and T. F. Weiss. 2003a. Dynamic material properties of the tectorial membrane: a summary. Hear. Res. 180:1–10. [DOI] [PubMed] [Google Scholar]
  15. Freeman, D. M., K. Masaki, A. R. McAllister, J. L. Wei, and T. F. Weiss. 2003b. Static material properties of the tectorial membrane: a summary. Hear. Res. 180:11–27. [DOI] [PubMed] [Google Scholar]
  16. Fridberger, A., and J. B. de Monvel. 2003. Sound-induced differential motion within the hearing organ. Nat. Neurosci. 6:446–448. [DOI] [PubMed] [Google Scholar]
  17. Fridberger, A., J. Boutet de Monvel, and M. Ulfendahl. 2002. Internal shearing within the hearing organ evoked by basilar membrane motion. J. Neurosci. 22:9850–9857. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gittes, F., B. Mickey, J. Nettleton, and J. Howard. 1993. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J. Cell Biol. 120:923–934. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gummer, A. W., W. Hemmert, and H.-P. Zenner. 1996. Resonant tectorial membrane motion in the inner ear: its crucial role in frequency tuning. Proc. Natl. Acad. Sci. USA. 93:8727–8732. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Gummer, A. W., B. M. Johnstone, and N. J. Armstrong. 1981. Direct measurement of basilar membrane stiffness in the guinea pig. J. Acoust. Soc. Am. 70:1298–1309. [Google Scholar]
  21. Hallworth, R. 1995. Passive compliance and active force generation in the guinea pig outer hair cell. J. Neurophysiol. 74:2319–2328. [DOI] [PubMed] [Google Scholar]
  22. Hartmann, U. 1999. Magnetic force microscopy. Ann. Rev. Mater. Sci. 29:53–87. [Google Scholar]
  23. Hemmert, W., H.-P. Zenner, and A. W. Gummer. 2000. Three-dimensional motion of the Organ of Corti. Biophys. J. 78:2285–2297. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Hu, X., B. N. Evans, and P. Dallos. 1999. Direct visualization of Organ of Corti kinematics in a hemicochlea. J. Neurophysiol. 82:2798–2807. [DOI] [PubMed] [Google Scholar]
  25. Hubbard, A. 1993. A traveling-wave amplifier model of the cochlea. Science. 259:68–71. [DOI] [PubMed] [Google Scholar]
  26. Hubbard, A. E., D. C. Mountain, and F. Chen. 2003. Time-domain responses from a nonlinear sandwich model of the cochlea. In Biophysics of the Cochlea: From Molecules to Models. A. W. Gummer, editor. World Scientific, New Jersey, London, Singapore, Hong Kong. 351–358.
  27. Hudspeth, A. J. 1997. Mechanical amplification of stimuli by hair cells. Curr. Opin. Neurobiol. 7:480–486. [DOI] [PubMed] [Google Scholar]
  28. Hudspeth, A. J., Y. Choe, A. D. Mehta, and P. Martin. 2000. Putting ion channels to work: mechanoelectrical transduction, adaptation, and amplification by hair cells. Proc. Natl. Acad. Sci. USA. 97:11765–11772. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Iwasa, K. H., and M. Adachi. 1997. Force generation in the outer hair cell of the cochlea. Biophys. J. 73:546–555. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Karavitaki, K. D., and D. C. Mountain. 2003. Is the cochlear amplifier a fluid pump? In Biophysics of the Cochlea: From Molecules to Models. A. W. Gummer, editor. World Scientific, New Jersey, London, Singapore, Hong Kong. 310–311.
  31. Kolston, P. J. 1999. Comparing in vitro, in situ, and in vivo experimental data in a three-dimensional model of mammalian cochlear mechanics. Proc. Natl. Acad. Sci. USA. 96:3676–3681. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Kronester-Frei, A. 1979. The effect of changes in endolymphatic ion concentrations on the tectorial membrane. Hear. Res. 1:81–94. [DOI] [PubMed] [Google Scholar]
  33. Lagostena, L., A. Cicuttin, J. Inda, B. Kachar, and F. Mammano. 2001. Frequency dependence of electrical coupling in Deiters' cells of the guinea pig cochlea. Cell Commun. Adhes. 8:393–399. [DOI] [PubMed] [Google Scholar]
  34. Maier, H., C. Zinn, A. Rothe, H. Tiziani, and A. W. Gummer. 1997. Development of a narrow water-immersion objective for laser interferometric and electrophysiological applications in cell biology. J. Neurosci. Methods. 77:31–41. [DOI] [PubMed] [Google Scholar]
  35. Mammano, F., and J. F. Ashmore. 1993. Reverse transduction measured in the isolated cochlea by laser Michelson interferometry. Nature. 365:838–841. [DOI] [PubMed] [Google Scholar]
  36. Mammano, F., and R. Nobili. 1993. Biophysics of the cochlea: linear approximation. J. Acoust. Soc. Am. 93:3320–3332. [DOI] [PubMed] [Google Scholar]
  37. Martin, P., and A. J. Hudspeth. 1999. Active hair-bundle movements can amplify a hair cell's response to oscillatory mechanical stimuli. Proc. Natl. Acad. Sci. USA. 96:14306–14311. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Martin, P., and A. J. Hudspeth. 2001. Compressive nonlinearity in the hair bundle's active response to mechanical stimulation. Proc. Natl. Acad. Sci. USA. 98:14386–14391. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Martin, P., A. J. Hudspeth, and F. Jülicher. 2001. Comparison of a hair bundle's spontaneous oscillations with its response to mechanical stimulation reveals the underlying active process. Proc. Natl. Acad. Sci. USA. 98:14380–14385. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Martin, P., F. Jülicher, and A. J. Hudspeth. 2003. The contribution of transduction channels and adaptation motors to the hair cell's active process. In Biophysics of the Cochlea: From Molecules to Models. A. W. Gummer, editor. World Scientific, New Jersey, London, Singapore, Hong Kong. 3–15.
  41. Martin, P., A. D. Mehta, and A. J. Hudspeth. 2000. Negative hair-bundle stiffness betrays a mechanism for mechanical amplification by the hair cell. Proc. Natl. Acad. Sci. USA. 97:12026–12031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Mijailovich, S. M., M. Kojic, M. Zivkovic, B. Fabry, and J. J. Fredberg. 2002. A finite element model of cell deformation during magnetic bead twisting. J. Appl. Physiol. 93:1429–1436. [DOI] [PubMed] [Google Scholar]
  43. Miller, C. E. 1985. Structural implications of basilar membrane compliance measurements. J. Acoust. Soc. Am. 77:1465–1474. [DOI] [PubMed] [Google Scholar]
  44. Müller, M. 1996. The cochlear place-frequency map of the adult and developing Mongolian gerbil. Hear. Res. 94:148–156. [DOI] [PubMed] [Google Scholar]
  45. Mountain, D. C., and A. E. Hubbard. 1994. A piezoelectric model of outer hair cell function. J. Acoust. Soc. Am. 95:350–354. [DOI] [PubMed] [Google Scholar]
  46. Naidu, R. C., and D. C. Mountain. 1998. Measurements of the stiffness map challenge a basic tenet of cochlear theories. Hear. Res. 124:124–131. [DOI] [PubMed] [Google Scholar]
  47. Naidu, R. C., and D. C. Mountain. 2001. Longitudinal coupling in the basilar membrane. J. Assoc. Res. Otolaryngol. 2:257–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Neely, S. T., and D. O. Kim. 1986. A model for active elements in cochlear biomechanics. J. Acoust. Soc. Am. 79:1472–1480. [DOI] [PubMed] [Google Scholar]
  49. Nobili, R., and F. Mammano. 1996. Biophysics of the cochlea. II. Stationary nonlinear phenomenology. J. Acoust. Soc. Am. 99:2244–2255. [DOI] [PubMed] [Google Scholar]
  50. Olson, E. S. 2001. Intracochlear pressure measurements related to cochlear tuning. J. Acoust. Soc. Am. 110:349–367. [DOI] [PubMed] [Google Scholar]
  51. Olson, E. S., and D. C. Mountain. 1991. In vivo measurement of basilar membrane stiffness. J. Acoust. Soc. Am. 89:1262–1275. [DOI] [PubMed] [Google Scholar]
  52. Preyer, S., S. Renz, W. Hemmert, H.-P. Zenner, and A. W. Gummer. 1996. Receptor potential of outer hair cells isolated from base to apex of the adult guinea-pig cochlea: implications for cochlear tuning mechanisms. Aud. Neurosci. 2:145–157. [Google Scholar]
  53. Richter, C.-P., and P. Dallos. 2003. Micromechanics in the gerbil hemicochlea. In Biophysics of the Cochlea: From Molecules to Models. A. W. Gummer, editor. World Scientific, New Jersey, London, Singapore, Hong Kong. 278–284.
  54. Richter, C.-P., B. N. Evans, R. Edge, and P. Dallos. 1998. Basilar membrane vibration in the gerbil hemicochlea. J. Neurophysiol. 79:2255–2264. [DOI] [PubMed] [Google Scholar]
  55. Robles, L., and M. A. Ruggero. 2001. Mechanics of the mammalian cochlea. Physiol. Rev. 81:1305–1352. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Russell, I., and C. Schauz. 1995. Salicylate ototoxicity: effects on the stiffness and electromotility of outer hair cells isolated from the guinea pig cochlea. Aud. Neurosci. 1:309–319. [Google Scholar]
  57. Sader, J. E. 1998. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 84:64–76. [Google Scholar]
  58. Scherer, M. P., G. Frank, and A. W. Gummer. 2000. Experimental determination of the mechanical impedance of atomic force microscopy cantilevers in fluids up to 70 kHz. J. Appl. Phys. 88:2912–2920. [Google Scholar]
  59. Scherer, M. P., M. Nowotny, E. Dalhoff, H.-P. Zenner, and A. W. Gummer. 2003. High-frequency vibration of the Organ of Corti in vitro. In Biophysics of the Cochlea: From Molecules to Models. A. W. Gummer, editor. World Scientific, New Jersey, London, Singapore, Hong Kong. 271–277.
  60. Shah, D. M., D. M. Freeman, and T. F. Weiss. 1995. The osmotic response of the isolated, unfixed mouse tectorial membrane to isosmotic solutions: effect of Na+, K+, and Ca2+ concentration. Hear. Res. 87:187–207. [DOI] [PubMed] [Google Scholar]
  61. Slepecky, N. B. 1996. Structure of the mammalian cochlea. In The Cochlea. P. Dallos, A. N. Popper, and R. R. Fay, editors. Springer, New York. 44–129.
  62. Steele, C. R., and S. Puria. 2003. Analysis of forces on inner hair cell cilia. In Biophysics of the Cochlea: From Molecules to Models. A. W. Gummer, editor. World Scientific, New Jersey, London, Singapore, Hong Kong. 359–367.
  63. Tolomeo, J. A., and M. C. Holley. 1997. Mechanics of microtubule bundles in pillar cells from the inner ear. Biophys. J. 73:2241–2247. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Tsuji, J., and M. C. Liberman. 1997. Intracellular labeling of auditory nerve fibers in guinea pig: central and peripheral projections. J. Comp. Neurol. 381:188–202. [PubMed] [Google Scholar]
  65. Ulfendahl, M., J. Boutet de Monvel, and A. Fridberger.2003. Visualizing cochlear mechanics using confocal microscopy. In Biophysics of the Cochlea: From Molecules to Models. A. W. Gummer, editor. World Scientific, New Jersey, London, Singapore, Hong Kong. 285–291.
  66. Ulfendahl, M., Å. Flock, and E. Scarfone. 2001. Structural relationships of the unfixed tectorial membrane. Hear. Res. 151:41–47. [DOI] [PubMed] [Google Scholar]
  67. von Békésy, G. 1960. Experiments in Hearing. McGraw-Hill, New York.
  68. Zweig, G. 2003. Cellular cooperation in cochlear mechanics. In Biophysics of the Cochlea: From Molecules to Models. A.W. Gummer, editor. World Scientific, New Jersey, London, Singapore, Hong Kong. 315–329.
  69. Zwislocki, J. J. 1980. Five decades of research on cochlear mechanics. J. Acoust. Soc. Am. 67:1679–1685. [DOI] [PubMed] [Google Scholar]
  70. Zwislocki, J. J. 1988. Mechanical properties of the tectorial membrane in situ. Acta Otolaryngol. (Stockh.). 105:450–456. [DOI] [PubMed]
  71. Zwislocki, J. J., and L. K. Cefaratti. 1989. Tectorial membrane. II. Stiffness measurements in vivo. Hear. Res. 42:211–227. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES