Coupling of Protein Relaxation to Ligand Binding and Migration in Myoglobin

Abstract

Protein relaxation, ligand binding, and ligand migration into a hydrophobic cavity in myoglobin are unified by a bounded diffusion model which produces an accurate fit to complex ligand rebinding data over eight decades in time and a 160 K temperature range, in qualitative agreement with time-resolved x-ray crystallography. Protein relaxation operates in a cyclic manner to move the ligand away from the binding site.

INTRODUCTION

Myoglobin (Mb), a small protein specialized for the binding of small ligands, has been studied extensively as a model for the possible coupling of ligand binding to ligand migration and protein relaxation. Early measurements by Austin et al. (1975), of CO rebinding to Mb after MbCO laser photolysis, revealed complex nonexponential temporal behavior. It has been interpreted as sequential ligand migration within the protein,

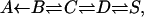(1)

which slows down the recombination process at the longer times. Here A is the bound Fe-CO state, in B the unbound ligand is within the “distal heme pocket” close to iron, and in C and D it has migrated to some other locations within the protein matrix whereas in state S it has escaped to solution. In addition it was shown that at low temperatures the B → A kinetics involves a distribution of barrier heights, which makes it highly nonexponential.

A subsequent theoretical model by Agmon and Hopfield (1983b) suggested that protein relaxation slows down geminate ligand rebinding, giving rise to nonexponential kinetics. In this approach, simple two-state kinetics was utilized for the ligand

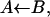(2)

but state B was assumed to consist of many protein conformations. These constituted a coordinate “perpendicular” to the AB reaction coordinate. Its diffusive relaxation dynamics was depicted by a Smoluchowski equation (Agmon and Hopfield, 1983a). The relaxation scenario was subsequently corroborated by several authors (Steinbach et al., 1991; Petrich et al., 1991; Tian et al., 1992; Ansari et al., 1992, 1994; Lim et al., 1993), but has not become universally accepted (Frauenfelder et al., 2002).

Despite the long time which has elapsed since these observations, it was thus far not possible to fit the full time and temperature dependence to any kinetic model (Frauenfelder et al., 2002). In the usual chemical kinetic approach, one solves a set of coupled ordinary differential equations depicting the assumed reaction scheme. Due to the distributed kinetics and relaxation it was not possible to explain the data this way.

For example, the horse-MbCO data by Post et al. (1993), analyzed below, was previously treated in either of two ways. The first (Post et al., 1993; Kleinert et al., 1998) is an empirical superposition of three time-dependent functions: A distribution of barrier heights for the short time component, a stretched exponential for the intermediate times, and a hyperbolic function depicting bimolecular rebinding from solution for the longest times.

The second approach extended the model of Agmon and Hopfield (1983b) by constructing a temperature-dependent potential for the protein coordinate (Agmon and Sastry, 1996, 1997). Since ligand escape from the pocket (state B) was not accounted for, this approach allowed us to fit the data only up to intermediate times, when the ligand exits from the heme pocket. The purpose of the present work is to extend the model so that it includes also a state C, enabling one to analyze the data up to longer times. This extension is timely, because more knowledge has accumulated on the ligand migration path in recent years.

Molecular-dynamics simulations were successful in mapping ligand escape pathways through the protein matrix (Case and Karplus, 1979; Elber and Karplus, 1990). Some of these pathways involve the hydrophobic “xenon cavities” discovered by Tilton et al. (1984). Binding kinetics for different Mb mutants and under Xe pressures (Scott and Gibson, 1997; Scott et al., 2001; Tetreau et al., 2004) suggest that the ligand may migrate to the Xe1 cavity on the proximal side (the opposite side of the porphyrin ring from which it has detached), possibly via the Xe4 cavity on the distal side. Indeed, recent cryogenic x-ray studies (Ostermann et al., 2000; Chu et al., 2000) have located the dissociated CO in these cavities. Most notable are pioneering time-resolved x-ray crystallography studies (Šrajer et al., 2001; Schotte et al., 2003) that follow, in real time, the ligand rebinding, ligand migration, and structural changes in the protein.

Despite this progress, the actual exit point of the ligand to solution remains controversial. Many years ago, Perutz and Matthews (1966) have suggested that the ligand escapes via the distal histidine (His-64) gate. This was observed in earlier molecular-dynamics simulations (Case and Karplus, 1979), but later abandoned in favor of the multiple-pathway scenario (Elber and Karplus, 1990). Today, some authors (Frauenfelder et al., 2002) believe that the ligand escapes from the Xe1 cavity, in line with Eq. 1. In contrast, extensive mutagenesis work (Scott and Gibson, 1997; Scott et al., 2001) found a prominent effect on the rate constant for O₂ entry when the distal histidine (His-64) was mutated, but little or no effect of mutations near the xenon cavities. The conclusion was therefore that the ligand exits/enters directly from state B.

Other authors (Tetreau et al., 2004) suggest that the first scenario holds below 250 K, whereas the histidine gate becomes the dominant pathway near room temperature. Another possibility (Radding and Phillips, 2004) is that the Xe cavity pathway is more important for CO than for O₂, helping in discriminating against CO. The branched kinetic scheme sends the CO preferentially into the Xe1 cavity, functioning much like the Hopfield (1974) proofreading mechanism.

The present work builds on the insight gained from such studies to construct a kinetic model that can explain quantitatively the laser photolysis data over wide time and temperature ranges. To avoid the exit pathway controversies, we focus on low temperature data (120–250 K), where contributions from the solvent process are small. Since the x-ray data suggest that in wild-type Mb only the Xe1 cavity (and not Xe4) is appreciably populated, the kinetic scheme in Eq. 2 is extended by adding a single state, C. At higher temperatures and long times the migration path may be more complex, but the kinetics also becomes more closely exponential, thus containing less information to help unravel the kinetics.

The Agmon and Hopfield (1983b) model is therefore extended into two coupled Smoluchowski equations, for the B and C states, respectively. As recently observed for other problems, such as single molecule enzymology (Agmon, 2000) and diffusion-influenced reactions (Gopich and Szabo, 2002), models based on two coupled Smoluchowski equations are already sufficiently powerful to reproduce a wide range of kinetic phenomena. With the extended approach presented below, it will be possible not only to fit, for the first time, all of the kinetic data by an equation of motion, but also to gain insight into the various stages of this fundamental biophysical process.

THE MODEL

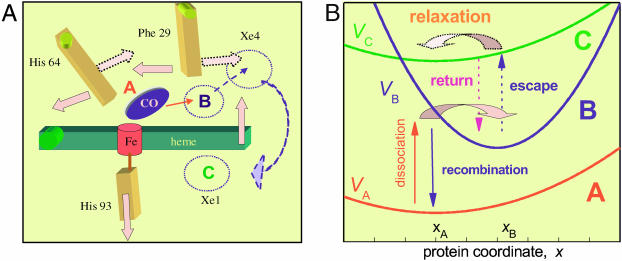
Fig. 1 A shows schematically some major protein motions after the dissociation of the Fe–CO bond, as revealed in the recent time-resolved x-ray study of a L29F Mb mutant by Schotte et al. (2003). As the bound state A disappears, dissociated CO appears in the distal pocket above the heme plane (state B). Concomitantly, the proximal His-93 moves away from the heme plane, which tilts toward the distal side with a hinge point near the propionate side chains. At the same time, the distal His-64 and Phe-29 (Leu-29 in the wild-type) swing sideways. These (and other) protein relaxation events apparently open a pathway for the CO ligand, which escapes out of the pocket. After a short residence near the Phe-29 residue on the distal side (it is not clear whether this step occurs also in the wild-type), the CO moves into the Xe1 cavity on the proximal side of the heme plane (state C).

FIGURE 1.

The coupling of ligand binding and migration to conformational change in Mb. (A) Schematics of some heme and distal pocket motions as observed in the recent time-resolved crystallographic study of Schotte et al. (2003). Full arrows represent motions immediately after photolysis, whereas the dotted arrows are motions occurring later, after CO expulsion from the heme pocket. (B) Schematics of the corresponding multi-tier diffusion model. Effective potentials for tiers A, B, and C are the three parabolas. Vertical arrows symbolize the coordinate-dependent rate functions. Fat horizontal arrows depict the downhill protein relaxation in these two tiers. They correspond to the early and late relaxation phases depicted in A.

After the ligand exit from the heme pocket, the two side chains relax back to their original orientation (though nearer to the heme plane). Interestingly, nonmonotonic relaxation was previously observed in the spectral shifts of the heme Soret band by Eaton and collaborators (Ansari et al., 1992, 1994), and it plays an important role in the extended model presented below. Cyclic relaxation may also explain the rather small structural difference between MbCO and deoxyMb, as observed in x-ray studies of near-atomic resolution (Kachalova et al., 1999).

The model outlined in Fig. 1 B captures these relaxation events qualitatively, although allowing for a quantitative computation of the rebinding kinetics. It is an extension of the Agmon and Hopfield (1983b) model along similar lines used to describe the conformational cycle of a single working enzyme (Agmon, 2000). The model involves three discrete ligand states, A, B, and C; A represents the bound Fe-CO state, B is the nascent photodissociated state, and C depicts the ligand in a more remote protein cavity, which in wild-type Mb appears to correspond to the Xe1 cavity (Chu et al., 2000). In the time-resolved kinetics, B is the initial state whereas A serves as the final trap for the ligand.

The three states are coupled to a single conformational coordinate, denoted by x. It corresponds to the concerted motion of the iron center, the heme plane tilt and the distal pocket changes discussed above. Conformational changes are subject to effective harmonic potentials, e.g., V_A(x) = a_A(x−x_A)², and similarly for the other two ligation states. (These potentials are given here in units of the thermal energy, k_BT). The rate of conformational relaxation is determined by diffusive motion on these effective potentials. Because of the bounded potentials for the protein mode, such a model was termed by Agmon and Hopfield (1983b) a “bounded diffusion” model.

As the ligand dissociates, the protein is out of equilibrium in the nascent B-state potential, V_B(x). It relaxes to its new equilibrium value, x_B. During this process, the iron out-of-plane motion and heme plane tilt make ligand rebinding less probable, so that the recombination rate coefficient, k_BA(x), decreases. At the same time, distal relaxation (such as the tilt of His-64 and Leu-29) make the ligand escape out of the heme pocket more probable. Hence the escape rate coefficient, k_BC(x), increases. After the expulsion of the ligand into state C, the distal pocket is again out of equilibrium in the new potential field, V_C(x). It thus relaxes back, e.g., by reorienting His-64 and Leu-29 to block the return pathway and thus decrease the return rate coefficient, k_CB(x). From the time-resolved crystallographic data, this reverse distal relaxation does not seem to couple to a corresponding reverse heme relaxation, yet both are depicted by the same coordinate in our model. To decouple the two motions on the long timescale, we allow for different “diffusion constants,” D_B and D_C, for the B and C states, respectively. These determine the protein relaxation rates in these two states.

METHODS

The mathematical implementation of the model involves two coupled Smoluchowski equations for the conformational distribution functions in states B and C, denoted p_B(x,t) and p_C(x,t), respectively:

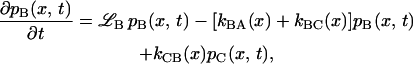(3)

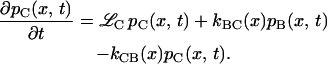(4)

The Smoluchowski operators, 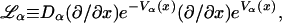produce diffusive relaxation in the two states, α = B or C. The rate functions coupling these partial differential equations describe ligand binding and migration,

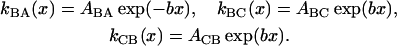(5)

With increasing x, k_BA(x) decreases whereas k_BC(x) and k_CB(x) increase exponentially (b is positive). In the following we assume, for simplicity, that in Eq. 5 only A_BA, A_BC, and A_CB vary with temperature.

Initially, only state B is populated, and its conformational distribution is assumed identical to that which prevailed in state A before photodissociation,

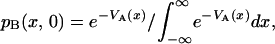(6)

whereas p_C(x,0) = 0. Starting from this initial condition, the above partial differential equations are solved with the user-friendly Windows application for solving the Spherically Symmetric Diffusion Problem (SSDP, ver. 2.66), developed by Krissinel' and Agmon (1996) and available for general use.

The total occupation of states A, B, and C is denoted by P_A(t), P_B(t), and P_C(t), respectively. The latter two are given by the respective integrals over the conformational space,

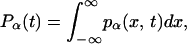(7)

where α = B or C. Assuming that a single ligand resides within the protein, P_A(t) + P_B(t) + P_C(t) = 1, whereas initially P_B(0) = 1 and P_A(0) = P_C(0) = 0. The survival probability of the unbound protein, S(t), is thus

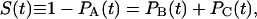(8)

and this is compared with the experimental transient absorption data, which is sensitive to the binding state of the heme.

We note that the above equations may be extended to include ligand exchange with solution (state S). Escape to solution from state B (Scott et al., 2001) will add a term −k_BS(x) p_B(x, t) to Eq. 3. Similarly, if ligand escape occurs from state C (Frauenfelder et al., 2002), a term −k_CS(x) p_C(x, t) can be added to Eq. 4. CO entry through the distal histidine can be treated approximately by adding the term k_SB(x)[CO] [1 − P_B(t)] to Eq. 3 (and similarly if entry is to state C). Here [CO] is the CO concentration in solution (which, unfortunately, is seldom determined in a quantitative manner). The term 1 − P_B(t) accounts for saturation of the distal pocket by preventing the entry of more than one ligand.

Present experimental data does not contain sufficient information to determine these additional parameters. Therefore we focus on analyzing the low temperature data (250 K and below), where the solvent process may be either less prominent or nonexistent.

RESULTS

The model is applied to the kinetics of CO binding to horse-Mb in 75% glycerol-water solutions, investigated by Post et al. (1993; see also Agmon et al., 1994). Their time-resolved absorption measurements provide accurate kinetic data over eight orders-of-magnitude in time, four orders-of-magnitude in S(t), and an extensive temperature range. As mentioned in the Introduction, this time-behavior was previously fitted to a superposition of time-dependent functions (Post et al., 1993; Kleinert et al., 1998), or to the simpler model of Agmon and Hopfield (1983b), which does not include state C (Agmon and Sastry, 1996).

Fig. 2 shows a fit of the complete temporal behavior to the solution of the bounded diffusion model described above. The parameters used in the fits are collected in Table 1. To reduce the number of adjustable parameters, some of them were held fixed over the whole temperature range. For example, the exponent b in the rate functions of the expressions in Eq. 5 was assigned a universal (positive) value. The parabolic potentials were assumed to be identical for the A- and C-states, hence a_A = a_C and x_A = x_C. Thus we adjust only a_A/a_B and x_A−x_B (fixing a_B and x_B). We find that a_B ≫ a_A , which may be understood if the CO ligand docked in state B limits the fluctuations of the heme plane adjacent to it.

FIGURE 2.

CO rebinding to horse-Mb in glycerol-water solution, at 120–280 K, after photodissociation of horse-heart MbCO with a nanosecond laser and monitoring the transient absorption in the Soret band. Data (circles) were obtained by Doster and co-workers (Post et al., 1993; Agmon et al., 1994). The bold lines are fit to Eqs. 3 and 4 using SSDP ver. 2.66 (Krissinel' and Agmon, 1996), with parameters summarized in Table 1.

TABLE 1.

Temperature-dependent parameters used in fitting horse-MbCO kinetics in Fig. 2 to Eqs. 3 and 4

T, K	−xA, Å	aB/aA	ABA, s−1	ABC, s−1	ACB, s−1	DB, Å2/ms	DC, Å2/ms
120	2.1	80	6 × 10−10	–	–	8 × 10−6	–
150	2.1	65	1.6 × 10−8	1.7 × 10−9	5 × 10−10	1.4 × 10−4	1 × 10−5
180	2.1	50	1.1 × 10−7	2.0 × 10−8	5 × 10−9	3.1 × 10−3	1.5 × 10−4
200	2.1	50	4.0 × 10−7	9.0 × 10−8	3 × 10−8	2.6 × 10−2	5 × 10−4
220	1.7	60	1.0 × 10−6	1.0 × 10−7	1.5 × 10−7	0.11	0.021
230	1.2	50	2.4 × 10−6	2.6 × 10−7	1.7 × 10−7	0.24	0.11
250	0.65	50	8.0 × 10−6	2.5 × 10−6	3.5 × 10−7	1.0	0.9
280	0.2	50	3.5 × 10−5	3.2 × 10−5	1.2 × 10−6	6	6

The temperature-independent parameters are as follows: x_B = 0.2 Å, b = 4 Å⁻¹, a_B = 50 Å⁻², a_A = a_C, and x_A = x_C. Distance units are determined only up to a scaling factor. The quality of the fits deteriorates if parameters are changed arbitrarily by >10%. However, it is possible to obtain comparable fits by a concerted variation of several parameters. In particular, the reliability of the kinetic parameters at 280 K is low, because the kinetics become nearly exponential, whereas the model does not include the solvent process.

The value of x_A−x_B determines the short-time slope of the data. It is insensitive to temperature below T ≈ 200 K (roughly the solvent glass transition, T_g), and diminishes above this temperature, “collapsing” nearly to zero as room temperature is approached. This operates to slow down the short-time rebinding kinetics above 200 K (the “inverse temperature effect”), in agreement with earlier work (Agmon and Sastry, 1996; Sastry and Agmon, 1997).

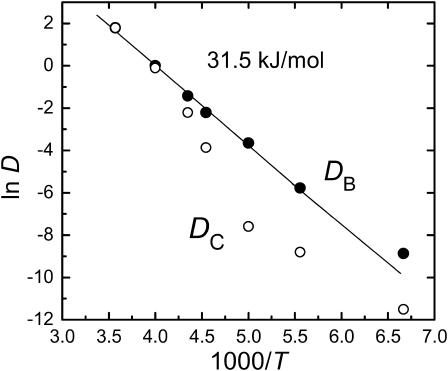
In contrast to x_A, D_B appears to be insensitive to T_g, as it follows a simple Arrhenius behavior (Fig. 3), with ln D_B being linear in 1/T over the whole temperature range (120–280 K). From the slope, one obtains an activation energy of 31.5 kJ/mol. The linearity of this plot suggests that the relaxation of the heme plane is insensitive to the dynamics in the external solvent (Agmon and Sastry, 1996). Considering the relaxation in the C-state, D_C is indeed smaller than D_B (except near room temperature, but there the fitting procedure may be nonunique), possibly showing an abrupt change around T_g. We conclude that 1), the distal pocket relaxation after ligand escape is slower than the heme relaxation after the photolysis event and 2), unlike the heme relaxation which is largely decoupled from the external solvent, the distal pocket relaxation is much more sensitive to the solvent.

FIGURE 3.

The temperature dependence of the two diffusion coefficients depicting protein relaxation in states B and C. Obtained by fitting Eqs. 3 and 4 to the time-resolved data in Fig. 2 (see Table 1).

The elementary relaxation and migration steps

What can be learned from the kinetic model about the various steps after ligand dissociation? Whereas only some of these steps occur at the highest and lowest temperatures, at intermediate temperatures (e.g., 220 K) one observes the most intricate kinetics, when all these steps come into play. The value of x_A at 220 K, which is similar to its temperature-independent value observed at 200 K and below, suggests that solvent effects are negligible. Thus the observed kinetic features at 220 K may be attributed mainly to ligand migration within the protein.

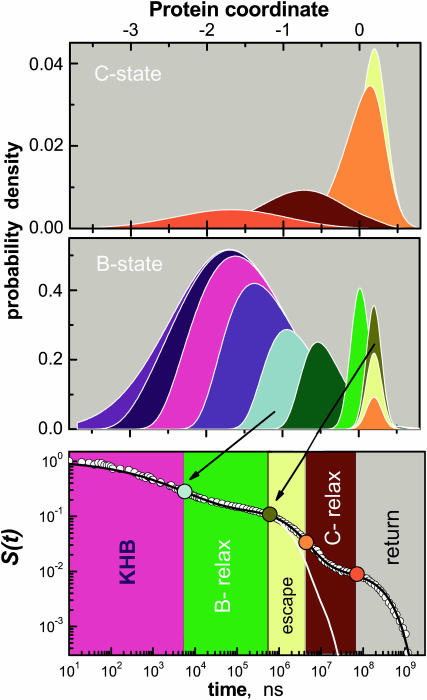
Fig. 4 shows the two distributions, p_B(x, t) and p_C(x, t), and the sum of their areas, S(t), which is compared to the experimental kinetics at 220 K. The initial phase is due to static inhomogeneity, with more reactive conformations (for x ≪ 0) rebinding first and disappearing from the ensemble. This “kinetic-hole burning” effect (KHB, Campbell et al., 1987; Agmon, 1988) gives rise to an initial power-law phase in S(t). It prevails until protein relaxation commences (∼5 μs), and p_B(x, t) moves out of its initial profile, p_B(x, 0). This slows down the B → A rebinding, giving rise to the first undulation in S(t). Because a_A ≪ a_B, p_B(x, t) also narrows appreciably during this relaxation phase. When the B-state relaxation ends (∼600 μs), p_B(x, t) centers around x_B and continues to decay only in amplitude.

FIGURE 4.

The coupling of ligand binding and migration to conformational change in Mb, as calculated by the present model at 220 K. Relaxation and migration are depicted by the probability densities for levels B and C, p_B(x, t) and p_C(x, t), top two panels. Matching colors correspond to matching times after photolysis. From blue to red: t = 0, 5.0 ns, 53 ns, 554 ns, 5.8 μs (cyan, roughly when B-state relaxation commences), 28 μs, 134 μs, 640 μs (dark yellow, roughly when B-state relaxation ends), 1.4 ms, 3.1 ms (orange, roughly when C-state relaxation begins), 15 ms, and 71 ms (red, roughly when C-state relaxation ends). The bottom panel shows the corresponding kinetics, S(t), with its different phases (see text) indicated by the color code.

Around this time the B → C migration commences, and we observe an increase in the amplitude of the C-state distribution, p_C(x, t). As a result, the rebinding kinetics slows down. Subsequent protein relaxation in state C moves p_C(x, t) back to the left, from which the return rate is slower. The rebinding kinetics slows down even further, leading to the second undulation in S(t). At the termination of this second relaxation phase the kinetics tend to an ultimate exponential decay.

Ligand excursion to the Xe cavities

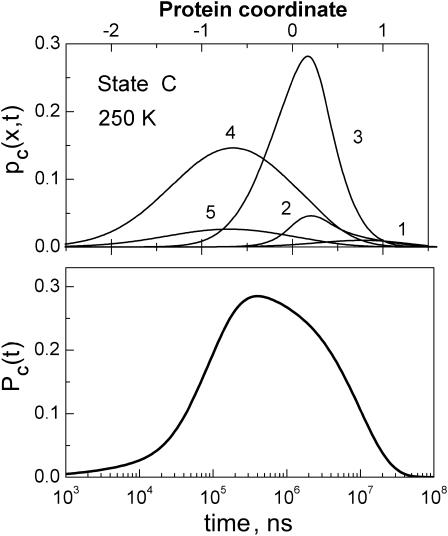
The kinetics of the CO excursion into state C (which we identify predominantly with Xe1) is depicted by the spatial integral over the C-state conformational manifold (see Eq. 7). As an example, Fig. 5 shows both p_C(x, t) and P_C(t) at 250 K. The population of state C (bottom panel) peaks ∼3 × 10⁻⁴ s and disappears by 3 × 10⁻² s. It has a long tail into short times.

FIGURE 5.

Ligand excursion into the Xe pocket (state C) at 250 K, as predicted by the model which was previously adjusted to fit the horse-Mb data in Fig. 4. p_C(x, t) (upper panel) is shown at times t_i = 3 × 10³, 1.5 × 10⁴, 1.6 × 10⁵, 1.7 × 10⁶, and 1.9 × 10⁷ ns (for i = 1–5). The shift in its peak is due to relaxation in state C. Their areas give the cavity occupation function, P_C(t).

Recently, Tetreau et al. (2004) have reported a rebinding experiment under Xe pressures (see the upper panel of their Fig. 5 for data at 250 K). Xe is expected to partially block the Xe1 cavity, so that the difference in the measured S(t) with and without Xe should peak approximately when P_C(t) does (see Fig. 5, this article). Although their experiment was performed on a sample of sperm whale (rather than horse) Mb, the similarity is indeed evident. To obtain a S(t) curve similar to their high Xe-pressure experiment, we need to decrease the rate constants k_BC and k_CB in the model by approximately a factor of 2.

One also notes (in the bottom panel of their Fig. 5) that the effect of Xe pressure on O₂ binding is much smaller than on CO binding. This agrees with the assessment of Radding and Phillips (2004), that migration into the Xe cavities is more prominent for CO (their estimated k_BC is five-times larger for CO as compared with O₂).

CONCLUSION

The diffusive-kinetic theory presented here is of intermediate complexity, between simple chemical kinetics and atomic-detail molecular dynamics. To date, it is the only kinetic model successful in fitting and explaining MbCO rebinding kinetics over wide time and temperature ranges. This model singles out one functionally important protein mode, which couples to ligand binding and migration. From its analysis, the role of protein relaxation emerges.

Firstly, the relaxation in both the B and C states operates to reduce the probability of geminate CO rebinding, and enhance the probability of its escape from the immediate vicinity of the heme iron. Whereas the nonexponential slowing-down of ligand rebinding is due to both protein relaxation and ligand migration, relaxation is more effective in slowing down the rebinding than ligand escape. It leads to the cascade-like time dependence of the survival probability (Fig. 2), with two conspicuous “steps” corresponding to the two relaxation processes. The complete sequence of events influencing the progress of geminate rebinding, as emerging from our analysis, is: inhomogeneous kinetics (kinetic-hole burning); B-relaxation; BC-escape; C-relaxation; and finally return from the cavity to state B (see bottom panel of Fig. 4, this article).

The second characteristic of protein relaxation is that it operates in a cyclic manner, relaxing in one direction in the B state and the opposite direction in the C state. In the photodissociation experiment, it operates like a microscopic cyclic engine, utilizing the photolyzing energy to move the ligand away from the heme, and dumping the remainder into the heat bath of all other protein modes.

When Agmon and Hopfield (1983b) first put forward the idea that protein relaxation participates in the binding kinetics, the scenario could have been criticized based on the relatively small structural differences between MbCO and deoxy-Mb observed in the steady-state x-ray diffraction data. Time-resolved x-ray measurements (Schotte et al., 2003) now reveal that the transient structural changes are actually much larger, but they occur in a cyclical manner so that their accumulated effect is rather small. The present model not only describes the laser photolysis kinetics quantitatively, but also produces this cyclic conformational change.

An important question concerns the biological significance of a mechanism which utilizes both cavities and protein conformations, particularly if the O₂ ligand enters mainly through the histidine gate (Scott et al., 2001). A possible conjecture is that Mb acts to preferentially move CO into the Xe cavities (Radding and Phillips, 2004). If so, the conformational cycle may be instrumental in facilitating this outcome.

For ligands such as NO, Mb may function also as an enzyme (Frauenfelder et al., 2001), catalyzing the reaction 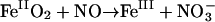(Eich et al., 1996; Møller and Skibsted, 2002). This reaction may be important in regulating NO levels in the brain or in the heart (Garry et al., 2003). If NO is also preferentially channeled into the Xe1 cavity like CO, one may envision protein relaxation delaying its return for sufficiently long times, allowing for concomitant O₂ binding to the heme iron. As the NO subsequently returns to state B, it collides with the iron-bound oxygen, leading to its rapid oxidation.