Influence of the Solvent Structure on the Electrostatic Interactions in Proteins

Abstract

The proper estimation of the influence of the many-body dynamic solvent microstructure on a pairwise electrostatic interaction (PEI) at the protein-solvent interface is very important for solving many biophysical problems. In this work, the PEI energy was calculated for a system that models the interface between a protein and an aqueous solvent. The concept of nonlocal electrostatics for interfacial electrochemical systems was used to evaluate the contribution of a solvent orientational polarization, correlated by the network of hydrogen bonds, into the PEI energy in proteins. The analytical expression for this energy was obtained in the form of Coulomb's law with an effective distance-dependent dielectric function. The asymptotic and numerical analysis carried out for this function revealed several features of dielectric heterogeneity at the protein-solvent interface. For charges located in close proximity to this interface, the values of the dielectric function for the short-distance electrostatic interactions were found to be remarkably smaller than those determined by the classical model, in which the solvent was considered as the uniform dielectric medium of high dielectric constant. Our results have shown that taking into consideration the dynamic solvent microstructure remarkably increases the value of the PEI energy at the protein-solvent interface.

INTRODUCTION

Electrostatic interactions play an important role in protein-protein complex formations, molecular recognitions, conformational adaptabilities, stabilities, and the function of proteins (Perutz, 1978; Warshel, 1981; Warshel and Russell, 1984; Russell et al., 1987; Hendsch and Tidor, 1994; Honig and Nicholls, 1995; Sheinerman et al., 2000; Drozdov-Tikhomirov et al., 2001; Heifetz et al., 2002; Sinha and Smith-Gill, 2002; Kumar and Nussinov, 2002a). Despite a large number of studies focused on the evaluation of electrostatic interactions in proteins (Tanford and Kirkwood, 1957; Warshel and Levitt, 1976; Gilson et al., 1985; Rogers, 1986; Nakamura et al., 1988; Gilson and Honig, 1988; Schaefer and Froemmel, 1990; Rashin and Bukatin, 1994; Smith and Pettitt, 1994; Gilson, 1995; Luo et al., 1997; Papazyan and Warshel, 1997; Levy and Gallicchio, 1998; Sham et al., 1998; Schutz and Warshel, 2001; Simonson, 2001; Wisz and Hellinga, 2003), there are still many questions that have been poorly explored. Levy and Gallicchio formulated some of the questions, the answers of which are only beginning to emerge (Levy and Gallicchio, 1998). The major two questions are following: i), “how can the dielectric properties of boundary layer solvent that behaves differently from the bulk be most accurately captured in a continuum model?”; and ii), “what is the spatial variation of the dielectric response in a protein and is there a simple way to capture that variation within the framework of continuum models?” We believe that developing some treatment of the dielectric response of the protein-solvent interface, which would consider the solvent and protein as condensed polar media with inherent many-body dynamic properties, may help to answer the aforementioned questions and perhaps some other questions associated with the electrostatic estimations in biomolecules.

One of the methods that is most often used to calculate a pairwise electrostatic interaction (PEI) energy in protein (or other macromolecule) is the macroscopic continuum model (Gilson et al., 1985; Papazyan and Warshel, 1997). In the framework of this model, the protein is frequently considered as a uniform low-dielectric medium with a value of the dielectric constant between two and four. These values of the dielectric constant were estimated by experimental data on the dried protein films and powders, and were also predicted by a variety of theoretical estimations based on the theory of dielectrics (see Gilson and Honig, 1986; Nakamura et al., 1988; Simonson and Perahia, 1995; Simonson, 2001; and references cited there). The protein's low-dielectric response could in principle be larger, depending upon the extent to which the protein dipoles are free for reorientation (Gilson et al., 1985). One of the molecular mechanisms rationalizing conclusions on the high dielectric constant at the protein exterior was proposed in the framework of the Frölich-Kirkwood theory of dielectrics and takes into account the fluctuation of charged side chains of the residues concentrated at the protein-solvent interface (Simonson and Perahia, 1995; Simonson and Brooks, 1996). The local high dielectric constant at the protein interior was estimated by experimentally obtained pK_a values of buried groups (see Dwyer et al., 2000; and references cited there). The microscopic and semimicroscopic models for calculating the effective dielectric constant in protein, which considers the reorientation effects of protein and solvent dipoles (as the Langevin dipoles) as well as effects of the solvent penetration into protein, was developed by Warshel and his associates (Warshel and Levitt, 1976; Warshel and Russell, 1984; Cutler et al., 1989; Papazyan and Warshel, 1997; Sham et al., 1998; Schutz and Warshel, 2001). The results obtained in these works suggest that proteins cannot be treated as a low-dielectric medium (Warshel et al., 1984). It was also suggested that the fluctuations and reorganization of the protein dipoles, but not the solvent effect, are the major factor that determines the dielectric response in proteins. This concept, however, was discussed critically and in great detail in several other works (see Gilson et al., 1985; Rogers, 1986; Nakamura et al., 1988; Levy and Gallicchio, 1998; Simonson, 2001; and references cited there). The strong argument for the low-dielectric protein model is that the protein dipoles, which are in a favorable but more or less rigid orientation, actually cannot be significantly reoriented in response to an externally applied electric field, and as a result, the medium cannot be viewed as having a high dielectric constant (Gilson et al., 1985). The same point of view that “the highly organized spatial structure of the proteins' polar groups results in the existence of a permanent intraprotein electric field and in proteins' weak dielectric response, i.e., its low dielectric constant,” is one of the basic concepts of the insightful model for studying the kinetics of charge transfer in enzymatic reactions (Cannon and Benkovic, 1998; Krishtalik and Topolev, 2000; Mertz and Krishtalik, 2000). In another microscopic model, proposed by Simonson and his co-workers (Simonson et al., 1991), the local dielectric properties of a protein were investigated by the calculation of a generalized susceptibility, which determines the macroscopic susceptibility of continuum electrostatics. The obtained susceptibilities were consistent with values of the macroscopic dielectric constants of ∼2–4. Thus, different theoretical and experimental approaches reveal the heterogeneous nature of the protein dielectric properties. The results obtained by these approaches are not simply reconciled with each other and some of them are inconsistent with the results of continuum electrostatic models for proteins.

The uniform low-dielectric model for the whole protein suggests that screening by the surrounding high dielectric solvent is negligible. This model is reasonably accurate for determining the electrostatic interactions between the charges on short distances (short-distance interactions) within the interior of proteins. The use of a low-dielectric constant to calculate the PEI energy between distantly remote charges (long-distance interactions), however, can result in an inaccurate estimation of these interactions within any region of a protein. This is especially obvious in the case of arbitrary distance for interactions within the exterior of a protein.

A geometrical description of the electrostatic field by the field lines gives a simple physical explanation for the inaccuracy of the PEI energy estimation, when the uniform dielectric model of a protein is used. In fact, when the force lines between charges of interest in a protein cross over the solvent, the corresponding electrostatic field undergoes an additional screening by high solvent permittivity. The more the force lines cross over the solvent, the bigger electrostatic screening takes place. It suggests that the effective protein permittivity should depend on the distance between the interacting charges of interest, their submergence in the protein interior, and orientation relative to the protein surface. It also suggests that the corresponding value of the effective dielectric constant for two interacting charges at the interface should depend on heterogeneity of the solvent dielectric properties that differ significantly on the protein surface and in the bulk phase (see Edsall and McKenzie, 1983 and references cited therein).

To take into account the solvent effects and evaluate the electrostatic interactions in biopolymers, the linear and nonlinear distance-dependent dielectric functions were used in the framework of the concept of the effective dielectric constant (Warshel et al., 1984; Hingerty et al., 1985; Rogers, 1986; Buravtsev et al., 1989; Smith and Pettitt, 1994; Mehler, 1996). In particular, the nonlinear sigmoidal functions that approximate the low-dielectric constant (∼4) characteristic for biopolymers at short distances and approach bulk dielectric constant of water (∼80) at large distances between charges were used (Hingerty et al., 1985; Ramstein and Lavery, 1988; Mehler, 1996; Hassan and Mehler, 2002; Wang et al., 2002). The other sigmoidal function approximates the value of the dielectric constant in proteins between 20 (at short distances) and 80 (at long distances) (Warshel et al., 1984; Schutz and Warshel, 2001). In principal, the aforementioned functions, however, can be incorrect because they ignore a dielectric boundary between a biopolymer and solvent.

The Tanford-Kirkwood theory (Tanford and Kirkwood, 1957) and its modifications (see, for instance, Gilson et al., 1985; Rogers, 1986; and references there) provide means to calculate the effect of the dielectric boundary on the PEI within proteins. It was shown that this effect is significant (Gilson et al., 1985). These approaches consider a protein medium as a spherical region of low-dielectric constant surrounded by a solvent of high-dielectric constant. Numerical methods were used to extend this approach for the native-like geometries of proteins and to solve the linearized Poisson-Boltzmann equation (Warwicker and Watson, 1982; Klapper et al., 1986; Sharp, 1991; Bharadwaj et al., 1995; Gilson, 1995; Baker and McCammon, 2003; Bordner and Huber, 2003). These calculations take into account the ionic strength effects of the solution, as well as the effects of the reaction field appearing due to the induced surface charges at the interface between two uniform dielectric media with high (∼80) and low (∼2–4) dielectric constants.

Dielectric models, utilized in the most aforementioned approaches, represent the solvent and solute as homogeneous dielectric continuums. In these models, in each point, r, of the space filled out by a medium, the electric induction vector D(r) and electric field vector E(r) are related by a simple linear equation:

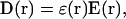(1)

where ɛ(r) is a dielectric function of the medium. The potential of the electric field, ϕ(r), produced by the charge density of external field sources, ρ(r), over the medium is determined by solving the first Maxwell equation:

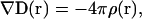(2)

where ∇ is the divergence operator. After the substitution of Eq. 1 with E(r) = −∇ϕ(r), Eq. 2 has the form of the Poisson equation:

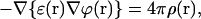(3)

or, in the case of the uniform dielectric, ɛ(r) = ɛ = const, transforms into the simplest one:

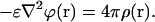(4)

Equations 3 and 4 can be modified into linear or nonlinear Poisson-Boltzmann equations (Robinson and Stokes, 1955; Bharadwaj et al., 1995; Baker and McCammon, 2003; Bordner and Huber, 2003) to model the ionic strength effects of the solution.

It should be noted, however, that Eq. 1 is only a particular case of the dielectric response for the homogeneous dielectric medium. In a more general case, the linear dielectric response for infinite homogeneous dielectric medium can be presented by an integral relationship between the electric induction D and the electric field E (Landau and Lifschitz, 1980):

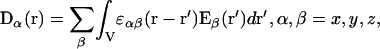(5)

where the integration is taken over the volume V of the medium and the function ɛ_αβ(r − r′) is the static permittivity tensor determined by the spatial correlation of the polarization of the medium in the space. Equation 5 allows one to introduce the influence of the microstructure of the dielectric medium, ɛ_αβ(r − r′), on the value of the electric induction D_α(r) (Dogonadze et al., 1977). It should be emphasized that the integral relationship, Eq. 5, is required to study the electric field, which is changing on the scale of the characteristic dynamic-structure distances of the system. For example, the Debye length in electrolyte solutions, as well as the characteristic length of several hydrogen bonds, at which the bound charge density fluctuations are correlated in solvent within the orientational Debye polarization mode, may determine the scale (Kornyshev, 1981).

According to Eq. 5, the values of the field E at point r and in some region around this point (in different points r′) determine the induction D at point r. This is significantly different from Eq. 1, where the electric field E in point r determines the electric induction D at the same point. In this work, we are using a model based on Eq. 5. This model will be referred to as a nonlocal model for nonlocal dielectric to distinguish it from the models utilizing Eq. 1; models utilizing Eq. 1 will be referred to as local models for local dielectrics. Dependence of the dielectric function ɛ_αβ(r − r′) upon r − r′ is associated with an assumption on the continuous translational invariance of the infinite homogeneous dielectric medium, and is referred to as spatial dispersion of the dielectric function (Dogonadze et al., 1977).

In contrast to Eq. 1, which is determined by differential equations (Eqs. 3 and 4), Eq. 5 (after the substitution in Eq. 2) determines the integro-differential equation for potential of the electric field, ϕ(r) (Kornyshev et al., 1978; Kornyshev, 1981):

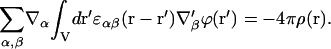(6)

For charge q located at point r₀ in the dielectric medium

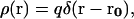(7)

where δ(r − r₀) is the Dirac δ-function, the electrostatic potential ϕ(r) can be found by solving the integro-differential Eq. 6 using a Fourier transform. This solution can be presented by an analytical expression in the form of Coulomb's law with an effective distance-dependent dielectric function ɛ_eff (R) (Kornyshev, 1985):

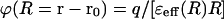(9)

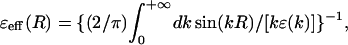(10)

where ɛ(k) is the longitudinal wavenumber static dielectric function that is the Fourier component

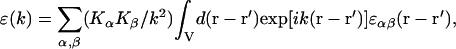and k = {K_x, K_y, K_z}.

In the case of the homogeneous isotropic infinite medium with uniform dielectric constant ɛ,

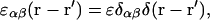(11)

where δ_αβ is the Kronecker δ: δ_αβ = 1 if α = β, and δ_αβ = 0 if α ≠ β, Eq. 9 can be reduced to the classical coulombic form:

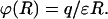(12)

According to this example, analytical properties of the dielectric function ɛ(k) determine the electrostatic screening in a condensed media (see Kornyshev and Vorotyntsev, 1980; Kornyshev, 1981; for more complicated dielectric functions). Such an approach demonstrates the so-called “dielectric formalism”. This formalism, in particular Eqs. 9–10, was widely used in solid-state physics (Harrison, 1970), for the cases when the dielectric function ɛ(k) can be calculated on the basis of rather realistic micromodels. For more complicated systems, such as water, electrolyte solutions and other associated polar liquids, the corresponding calculations of ɛ(k) on the basis of microscopic (“first-principle”) statistical-mechanic models are impeded. It is due to an absence of a self-consistence theory of polar liquids that would take into account not only electrostatic interdipole interactions but also quantum-mechanical short-range interactions, in particular, hydrogen bonding between water molecules (Dogonadze et al., 1977). That is why the microscopic models for polar liquids are rather simplified. Nevertheless, some common properties of spatial dispersion of the dielectric function ɛ(k) for homogeneous isotropic polar media can be revealed on the basis of a phenomenological theory of the polar solvent, which has been developed by R. R. Dogonadze and his associates (Dogonadze and Kornyshev, 1972, 1974; Dogonadze et al., 1977, 1985). In the framework of this theory, the relationship between ɛ(k) and the Fourier transform of the correlation function determined for the longitudinal polarization fluctuation in space (r) and time (t)—the dynamic structure factor S(ω, k)—was stated by an effective Hamiltonian formalism and the fluctuation-dissipation theorem (see Zubarev, 1974; Kornyshev, 1981; and references cited therein):

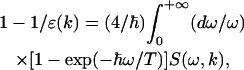(13)

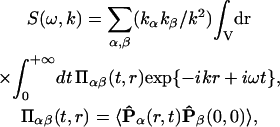(14)

where ℏ is the Planck constant; T is the absolute temperature in energetic units, 〈…〉 means quantum-statistical average, and 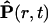is the Heisenberg operator for the dynamic variable P(r, t): a position- and time-dependent medium polarization. In such an approach, the dielectric function ɛ(k) is a result of averaging of all possible (long- and short-range) interactions that take place in medium undergoing an external electric field, and that are very difficult to be fully taken into account in microscopic models. For an associated polar liquid, such as water, it is possible to select three major zones of the frequencies (ω) of the electromagnetic absorption separated by transparency zones where the structure factor S (ω, k) ∼ 0. These absorption zones are associated with the specific polarization modes that have inherent distinguished frequencies of motions (Fröhlich, 1958; Dogonadze and Kornyshev, 1974; Kornyshev and Vorotyntsev, 1980), namely: 1), high-frequency electronic transitions changing the dipole moment; 2), fast oscillations due to infrared intramolecular vibration of dipoles; and 3), Debye fluctuations of the dipole orientations—hindered rotation of dipoles. Thus, total polarization of the medium is a result of superposition of these polarization modes. Each type of polarization is correlated in space with some effective correlation radius due to strong nonelectrostatic interactions. In the framework of this approach, the effect of the spatial dispersion was estimated, and the dielectric function, ɛ (k), was expressed through a set of the spectral functions of spatial correlation of polarization fluctuations determined for each of the corresponding three modes, f(kL_i) (Dogonadze and Kornyshev, 1974; Kornyshev, 1981, 1985):

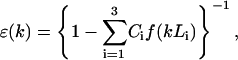(15)

where C₁ = 1 − 1/ɛ₁, C₂ = 1/ɛ₁ − 1/ɛ₂, C₃ = 1/ɛ₂ − 1/ɛ₃; ɛ_i denotes the frequency-dependent dielectric constants in the different transparency regions, corresponding to electronic, infrared, and orientational (Debye) polarization modes, respectively; and L_i denotes the typical correlation length of each mode. The expression for the f(kL_i) can be approximated by some functions (Dogonadze and Kornyshev, 1972; Kornyshev, 1981; Kornyshev et al., 1982; Kornyshev and Sutmann, 1996). In the simplest case, this function is 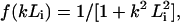(i = 1,2,3). The analysis of the experimental data and theoretical consideration allowed for the estimation of the distinguished values L_i (L₁ ≈ 0.5 Å, L₂ ≈ 1 Å, and L₃ ≈ 3–5 Å) and the dielectric constants ɛ_i (ɛ₁ ≈ 2, ɛ₂ ≈ 5–6, and ɛ₃ ≈ 80) for water solvent (see Dogonadze and Kornyshev, 1974; Kornyshev, 1981, 1985; Kornyshev and Volkov, 1984; Kornyshev and Ulstrup, 1986; and references cited therein). For the “pole” approximation, when the spatial dispersion in the high-frequency modes (electronic and infrared) may be neglected (L₁ = L₂ = 0), the dielectric function ɛ(k) for water has a simpler expression compared to Eq. 15, and substituted into Eq. 10, gives (see Kornyshev, 1985):

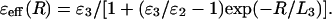(16)

The obtained expression for the effective dielectric function has a simple feature: the function ɛ_eff(R) increases from the low value ∼ɛ₂ (at small distances) to bulk water dielectric constant ɛ₃ (at large distances R ≫ L₃). The physical origin of this effect was explained by a feature of the distribution of the induced bound charge in the effective spherical layer (thickness ∼L₃) around the charge of interest (Kornyshev, 1985; Kornyshev and Sutmann, 1996).

The nonlocal electrostatics in the bulk of a homogeneous infinite medium (Eqs. 5–10) was extended for interfacial electrochemical systems (Dogonadze et al., 1977; Kornyshev et al., 1977, 1978; Kornyshev and Vorotyntsev, 1980; Rubinshtein, 1981, 1983; Kornyshev, 1985). An interfacial system should be referred to as a heterogeneous one because the translational invariance of the bulk phase (if it exists) is broken down in the direction normal to the interface (Dogonadze et al., 1977; Kornyshev and Vorotyntsev, 1980). In other words, the medium structure on the interface is distorted significantly in comparison with the bulk phase. Information about this breach stretches from the interface to the depth of the medium (at least for the spatial dispersion scales) (Dogonadze et al., 1977). Consideration of this effect is very important in electrostatics, when the electric field is changing on the same scales. In this case, the kernel of the integro-differential Eq. 6, the permittivity tensor, becomes dependent upon r and r′ separately (ɛ_αβ(r − r′) becomes ɛ_αβ(r, r′)). To solve Eq. 6, this tensor has to be determined at the interface. To do this, the tensor ɛ_αβ(r, r′) can be expressed through the bulk dielectric function ɛ_αβ(r − r′) of the given phase. This can be done in the framework of the so-called “sharp boundary model” that was previously used in the electrodynamics of semiinfinite plasma-like systems (Heinrichs, 1973; Platzman and Wolf, 1973). In the framework of this model, the so-called “specular-diffuse reflection approximation” was adapted to the dielectric medium (Dogonadze et al., 1977; Kornyshev et al., 1977, 1978; Kornyshev and Vorotyntsev, 1980). This approximation allows one to express the electrostatic potential through the bulk dielectric functions of the contacting media and, thereby, reveals the influence of the nonlocal bulk dielectric functions of the component on the distribution of the potential at the interface with different geometries (see Kornyshev and Vorotyntsev, 1980; and references cited therein).

The aforementioned nonlocal electrostatics developed for the bulk phase and a polar solvent interface led to the revision of some basic concepts of electrolyte solutions' properties and allowed one to explain several experimental data in the electrolyte theory (Dogonadze and Kornyshev, 1974; Kornyshev, 1981, 1985; Kornyshev and Sutmann, 1996) and interfacial electrochemistry (Kornyshev and Vorotyntsev, 1980; Rubinshtein, 1985, 1986; Kornyshev et al., 2002). The nonlocal electrostatic approach was effectively applied to solve several problems in the computational biophysics (Buravtsev et al., 1989; Leikin and Kornyshev, 1990; Kornyshev and Leikin, 2001; Rubinstein and Sherman, 2001).

In this work, a concept of nonlocal (NL) electrostatics for interfacial electrochemical systems was used to estimate the influence of the orientational Debye polarization of an aqueous solvent on the PEI energy in proteins. The effects of the electrolyte solution associated with Debye-Hückel screening by the mobile counterions were not considered in this work. The major goal of our work is to capture (in the continuum model) the dielectric properties of boundary layer solvent that behaves differently from the bulk phase and estimates the spatial variation of the dielectric response in a protein. The effects of protein structural reorganization were factored out of the continuum electrostatic model. Protein was considered as the uniform low-dielectric medium, in accordance with the classical theory of dielectrics. The general integral expression for the PEI energy at the interface between protein and solvent was obtained in the form of Coulomb's law with an effective distance-dependent dielectric function. It was demonstrated for short-distance electrostatic interactions between the charges, located in close proximity to the interface, that the values of the effective dielectric function were greater than the bulk dielectric constant in proteins, but were remarkably smaller than those determined by the classical model of the solvent (without consideration of the nonelectrostatic solvent dipole spatial correlations). This suggests that the spatial correlation effects of the solvent dipoles can make significant contributions into the PEI energy on the exterior of proteins. These contributions, however, have been underestimated in classical electrostatic approaches.

METHODS

In this work, the concept of NL electrostatics previously developed for arbitrary interfacial electrochemical system (Dogonadze et al., 1977; Kornyshev et al., 1977, 1978, 2002; Kornyshev and Vorotyntsev, 1980; Kornyshev, 1981; Rubinshtein, 1983, 1986) was used. The linear dielectric response for each of the media in contact was presented by the nonlocal relationship, Eq. 5, between the electric induction D and the electric field E:

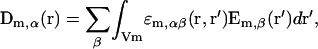(17)

where m = 1, 2 is the number of the medium; the function ɛ_m,αβ(r, r′) is the static permittivity tensor typical for each medium m.

To describe the interface between protein and water, the “sharp-boundary model” was utilized. In this model, the function ɛ_m,αβ(r, r′) is nonzero only for points r and r′ belonging to the same medium, m. Each medium was considered as a homogeneous isotropic one; the corresponding function of the medium was determined as:

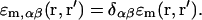(18)

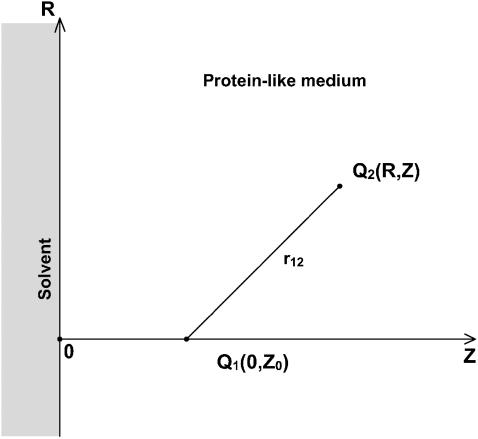
The simple case of the planar dielectric boundary that models the local regions of the interface between protein and solvent was considered, and a model system of two semi-infinite media was used (Fig. 1). The cylindrical coordinate system, (R, Z), was introduced for this boundary, where Z is the axis perpendicular to the plane passing through the boundary, and R is the two-dimensional radius vector in this plane. The semi-infinite region Z > 0 was assigned for the protein-like medium with an immersed charge Q₁ located at point (0, Z₀), and the region Z < 0 was assigned for the solvent.

FIGURE 1.

Schematic presentation of the interface between solvent (Z < 0) and protein-like medium (Z > 0) in the cylindrical coordinate system (R, Z). Charge Q₁ is located at the point (0, Z₀), charge Q₂-at the point (R, Z); r₁₂ is the distance between charges Q₁ and Q₂.

To solve the electrostatic problem (Eq. 2 subject to the usual boundary conditions and Eqs. 17 and 18) and to find the electrostatic potential ϕ (R, Z, Z₀) created by the charge Q₁ in the point R, Z of the protein-like medium, the approach, based on the “specular reflection approximation” (Heinrichs, 1973; Kornyshev et al., 1977; Kornyshev and Vorotyntsev, 1980), was utilized. In this approximation, the desired potential can be presented in terms of the Fourier-transform ɛ₁(k) and ɛ₂(k) of the dielectric functions, ɛ₁(r − r′) and ɛ₂(r − r′), that characterize the bulk properties of the media in contact (Kornyshev and Vorotyntsev, 1980; Rubinshtein, 1981). Thus, if the dielectric bulk functions of the protein-like medium and the solvent given as ɛ₁(r − r′) and ɛ₂(r − r′), respectively, the general expression for the potential can be presented as:

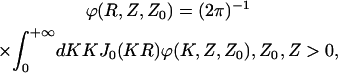(19)

where:

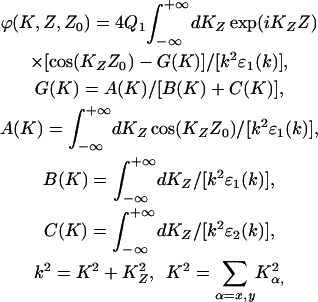(20)

and J₀ (KR) is the Bessel function of the first kind.

In this work, the orientational polarization, determined by the rotations of the dipoles in water, which, in turn, are hindered by the hydrogen-bonding chains, was considered by the phenomenological theory of the polar solvent (Dogonadze et al., 1977, 1985). In the framework of this theory the dielectric function for water, ɛ₂(k), was presented by the simple Lorentzian form utilized in several electrochemical and biophysical applications of the NL electrostatic approach (Kornyshev et al., 1978; Kornyshev, 1981; Rubinshtein, 1983, 1986; Buravtsev et al., 1989; Leikin and Kornyshev, 1990; Kornyshev and Sutmann, 1996):

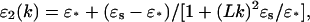(21)

where ɛ_* = 6 and ɛ_s = 78.3 are short- and long-wavelength dielectric constants of the solvent at room temperature; L is the correlation length of the water dipoles, which is proportionate to the characteristic length (∼3–5 Å) of the hydrogen-bonding network of water molecules (Kornyshev, 1985; Kornyshev and Ulstrup, 1986). This dielectric function, which is used for modeling the aqueous solvent as a system of rigid and strongly correlated dipoles (Kornyshev, 1981), gives the macroscopic (bulk) dielectric constant, ɛ_s, for the small k-limit (distances much larger than L) and the short-wavelength dielectric constant, ɛ_*, for the large k-limit (distances much smaller than L). In fact, at large wave vectors, k, the spatial dispersion of the dielectric function ɛ₂ (k) can be neglected: ɛ₂ (k → ∞) = 1. In this case, the macroscopic theory is actually inapplicable. Therefore, the utilized model of the dielectric response for water assumed that the function ɛ₂(k) in Eq. 21 changes from long wavelengths, ɛ_s, to some value (ɛ₂ (∞) = ɛ_* > 1), corresponding to distances smaller than the parameter L, but still exceeding interatomic distances (Rubinshtein, 1983; Kornyshev and Sutmann, 1996). Such peculiarities of spatial dispersion of the dielectric function ɛ₂ (k) with inherent key parameters L and ɛ_*, Eq. 21, resemble the effective distance-dependent dielectric function that can be estimated from experimental data interpreted as the free energy of interaction between protonated amino groups in dibasic amines (Kornyshev and Ulstrup, 1986). The protein-like medium was presented as a uniform dielectric with a low-dielectric constant: ɛ₁(k) = ɛ₁ = 4.

In the protein-like medium the PEI energy between the point partial charges Q₁ = ξ₁e and Q₂ = ξ₂e (ξ₁, ξ₂—parts of the electron charge e) was calculated as the product of the electrostatic potential, Eq. 19, created by the charge Q₁ at point (R, Z) and the charge Q₂, which is located at this point (Fig. 1). All integrals in Eq. 20 were calculated as in the work (Rubinshtein, 1983), where the method of complex contour integration in the complex plane K_Z was utilized. Omitting cumbersome computations, the PEI energy can be written in the form of:

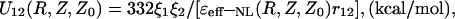(22)

where: r₁₂ = [R² + (Z − Z₀)²]^1/2 is the distance between charges Q₁ and Q₂ in the cylindrical coordinate system,

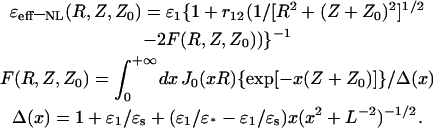(23)

RESULTS AND DISCUSSION

As one can see from Eq. 22, the PEI energy, U₁₂(R, Z, Z₀), looks similar to the expression for Coulomb interactions with the NL effective (distance-dependent) dielectric function, ɛ_eff-NL(R, Z, Z₀). The second and third terms in Eq. 23 mean that, in addition to the direct Coulomb interaction between charges, there is a contribution associated not only with the distance-dependent density distribution of the surface-induced bound charges (σ_b(R)), but also with the space-induced bound charges of the solvent (ρ_b(R, Z)) in close vicinity to the interface (Rubinshtein, 1983, 1985). The contribution to the direct coulombic interactions in proteins associated with the reorganization effects of the surrounding environment (due to reorientation of the protein and the solvent dipoles) was also considered in the framework of the microdielectric model (Warshel et al., 1984; Sham et al., 1998). When the correlations between the water dipoles are not considered (L = 0 or ɛ_* = ɛ_s = 78.3), the NL effective dielectric function, ɛ_eff-NL(R, Z, Z₀), is transforming into the limit expression for the classical dielectric function, ɛ_eff-CL(R, Z, Z₀):

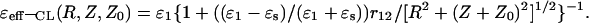(24)

This function can be easily obtained from the corresponding expression for the PEI energy in the case of the classical model of two uniform dielectrics (ɛ₂(k) = ɛ_s and ɛ₁(k) = ɛ₁) with a flat interface (Jackson, 1975). The effective dielectric functions, given by Eqs. 23 and 24, approach the value ɛ₁ at limiting large distances Z, Z₀ → + ∞ and finite R: ɛ_eff-CL (R, Z, Z₀) = ɛ_eff-NL(R, Z, Z₀) = ɛ₁. According to Eq. 23, ɛ_eff-NL(R, Z, Z₀) depends upon the distance, r₁₂ = [R² + (Z − Z₀)²]^1/2, between the interacted charges as well as upon their orientation relative to the interface and remoteness, Z₀, from the interface. The ɛ_eff-NL(R, Z, Z₀) function also depends upon the correlation length of the water dipoles, L, which is the spatial parameter for R and Z.

To simplify the analysis of the ɛ_eff-NL(R, Z, Z₀) function, two extreme orientations of the charged couple were considered: i), parallel, (‖), to the interface, (R = r₁₂, Z = Z₀), and ii), perpendicular, (⊥), to the interface, (R = 0, Z = Z₀ + r₁₂). An asymptotic expansion of the integral in Eq. 23 was performed for limiting large and small values of Z₀/L, Z₀/r₁₂, and r₁₂/L. This asymptotic analysis suggests that the values r₁₂, Z₀, and L are expended (in some cases outside of the physical scales) to select small parameters for corresponding expansions and to reveal the major features of the ɛ_eff-NL(R, Z, Z₀) as a formal function of two variations, r₁₂ and Z₀, and one parameter of the system, L. Simple estimations of the behavior of ɛ_eff-NL(R, Z, Z₀) were carried out considering only the first terms of the expansions. As is demonstrated below by numerical analysis, the behavior of the NL dielectric function in the field of physically applicable distances (r₁₂ and Z₀), comparable with the correlation length L (∼5 Å), is consistent with the behavior of this function revealed by the asymptotic analysis.

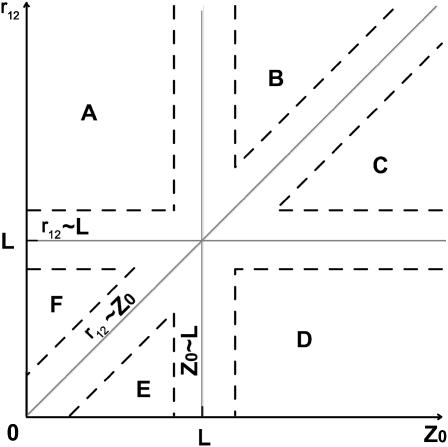
In the (‖) case, the limiting (asymptotic) values for 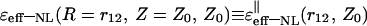were obtained for six spatial regions (A, B, C, D, E, F), each of which is characterized by a unique relationship between distances Z₀, r₁₂, and the correlation length of the water dipoles, L. Parametrical characteristics of these regions and obtained estimations of the 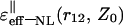values in these regions are shown in Table 1 and Fig. 2. It is necessary to note that similar asymptotic solutions in A and B regions (as well as in C, D, and E regions) are slightly different in the higher order terms of the expansions.

TABLE 1.

Asymptotic values of the NL dielectric function, 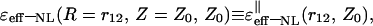in the (‖) case for six spatial regions of the variables r₁₂ and Z₀

r12	Z0		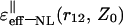Spatial region
r12 ≫ L	Z0 ≪ L ≪ r12	(ɛ1 + ɛs)/2	A
	L ≪ Z0 ≪ r12	(ɛ1 + ɛs)/2	B
	Z0 ≫ r12 ≫ L	ɛ1	C
r12 ≪ L	Z0 ≫ L ≫ r12	ɛ1	D
	L ≫ Z0 ≫ r12	ɛ1	E
	Z0 ≪ r12 ≪ L	(ɛ1 + ɛ*)/2	F

FIGURE 2.

Schematic presentation of the spatial regions A, B, C, D, E, and F of the limiting values obtained for ɛ_eff-NL(r₁₂, Z₀) (Table 1) in the coordinate system (plane r₁₂, Z₀). The areas inside of the dashed lines denote zones where r₁₂ ∼ L, Z₀ ∼ L and/or r₁₂ ∼ Z₀.

Asymptotic expressions for the classical dielectric function, ɛ_eff-CL (R, Z, Z₀), described by Eq. 24, were also obtained. Table 2 presents the limiting values for this function obtained for the (‖) case, 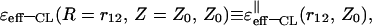when only the first terms of the expansions were taken into consideration.

TABLE 2.

Asymptotic values of the classical dielectric function, 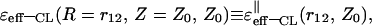in the (‖) case for two spatial regions of the variables r₁₂ and Z₀

r12		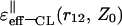Spatial region
r12 ≫ Z0	(ɛ1 + ɛs)/2	A
r12 ≪ Z0	ɛ1	B

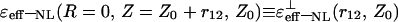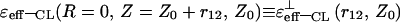In the (⊥) case, the asymptotic expressions for and were also obtained. Restricting the use of the first terms of expansions, these expressions were found to be similar to the expressions presented in Tables 1 and 2, respectively.

As can be seen from Table 2, there is a spatial scale, r₁₂ ∼ Z₀, at which the estimated value for the classical dielectric function is significantly changing. This scale divides the space of the parameters in two parts, r₁₂ ≫ Z₀ and r₁₂ ≪ Z₀, where the corresponding asymptotic solutions are significantly different from each other: ɛ_eff-CL (r₁₂ ≫ Z₀, Z₀) / ɛ_eff-CL (r₁₂ ≪ Z₀, Z₀) ≫ 1. It is necessary to note that the corresponding values ∼(ɛ₁ + ɛ_s)/2 for r₁₂ ≫ Z₀ and ∼ɛ₁ for r₁₂ ≪ Z₀ are the classical limiting values obtained in the continuum electrostatics for the effective dielectric constant at the interface between two uniform dielectric media with dielectric constants ɛ₁ and ɛ_s (Gilson et al., 1985; Rogers, 1986).

In the case of the NL electrostatic approach, an additional scale, the dimensional parameter L, arises (see Table 1 and Fig. 2). This scale determines the behavior of the function ɛ_eff-NL(r₁₂, Z₀) in protein-like medium with changing Z₀ and r₁₂ for both extreme orientations of the interacted charges. More specifically, the correlation length L of the solvent determines an additional spatial scale of dielectric heterogeneity at the interface of the protein-like medium. As a result, the specific spatial region F is arising (Table 1; Fig. 2), where the limiting value of ɛ_eff-NL(r₁₂, Z₀) is much smaller compared to the value ∼(ɛ₁ + ɛ_s)/2 obtained in the classical (local) case (Table 2, spatial region A) and the values predicted by the Tanford-Kirkwood theory for surface groups (Tanford and Kirkwood, 1957; and relevant calculations carried out by Gilson et al., 1985).

Overall, the asymptotic solutions shown in Table 1 and Fig. 2 allow for the formulation of the following heterogeneity features of the NL dielectric function:

1. For the region Z₀ ≪ L, an increase of the distance r₁₂ leads to an increase of the function ɛ_eff-NL (r₁₂, Z₀) starting from the values ∼ɛ₁ (for r₁₂ ≪ Z₀) passing through the values ∼(ɛ₁ + ɛ_*)/2 in the intermediate region Z₀ ≪ r₁₂ ≪ L and reaching the values ∼(ɛ₁ + ɛ_s)/2 (for r₁₂ ≫ L). Because the value ∼(ɛ₁ + ɛ_*)/2 is slightly different from the value ∼ɛ₁, it suggests that the NL dielectric function, Eq. 23, in close proximity to the interface has low values of ∼ɛ₁ in the more extended region when r₁₂ ≪ L, in contrast to the classical case, when the corresponding dielectric function, Eq. 24, is restricted by the values ∼ɛ₁ in the region where r₁₂ ≪ Z₀ (Table 2, region B). The “classical” behavior of the NL dielectric function takes place only for Z₀ ≫ L (regions B, C, and D in Table 1; Fig. 2).

2. For the region r₁₂ ≪ L, a decrease of the Z₀ values leads to an insignificant increase of the function ɛ_eff-NL (r₁₂, Z₀) from the values ∼ɛ₁ (for Z₀ ≫ L) to values ∼(ɛ₁ + ɛ_*)/2 (for r₁₂ ≪ Z₀ ≪ L). It is different from the classical case, when the function ɛ_eff-CL (r₁₂, Z₀) is approximately equal to (ɛ₁ + ɛ_s)/2 for r₁₂ ≫ Z₀ (Table 2). The ɛ_eff-NL (r₁₂, Z₀) has “classical” behavior only for r₁₂ ≫ L (regions C, B, and A in Table 1; Fig. 2).

In the asymptotic analysis, the values r₁₂, Z₀, and L were expanded to reveal peculiarities in the behavior of the NL dielectric function described by Eq. 23. Because the correlation length L in the considered aqueous solvent model, Eq. 21, is ∼3–5 Å, it is obvious that for distances r₁₂, much smaller than L, the function ɛ_eff-NL (r₁₂ → 0, Z₀) does not have physical meaning and is restricted by some values on the distances that exceed interatomic distances. Therefore, the ɛ_eff-NL(R, Z, Z₀) function was analyzed for values r₁₂ that are ≥1.5 Å. For a model of the planar interface between solvent and protein-like media the applicability of Eqs. 22 and 23 for the accurate estimation of the electrostatic interactions in proteins is restricted by a range of distances r₁₂, which are smaller than a radius of curvature for the local region of the interface. Such a restriction can be satisfied in globular proteins and membranes. For the intercharge distances, when this restriction is not implemented, the corresponding estimation is less accurate because it is impossible to neglect the curvature of the interface. The lowest limit for Z₀ was considered as the van der Waals radius of the aromatic hydrogen in proteins (∼1 Å).

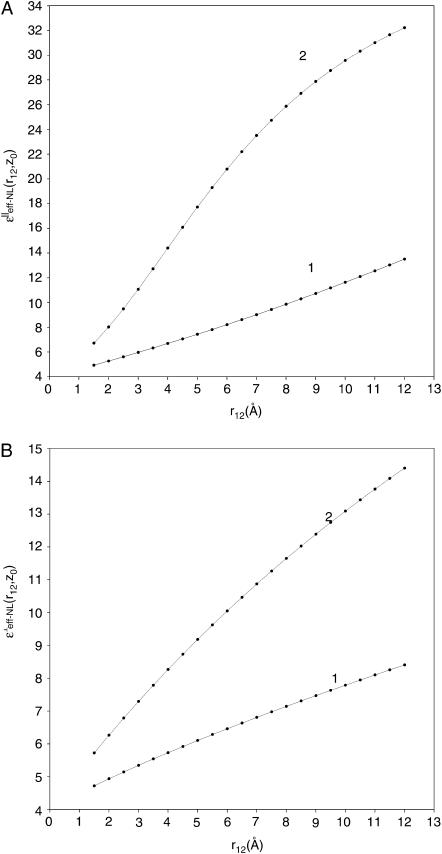
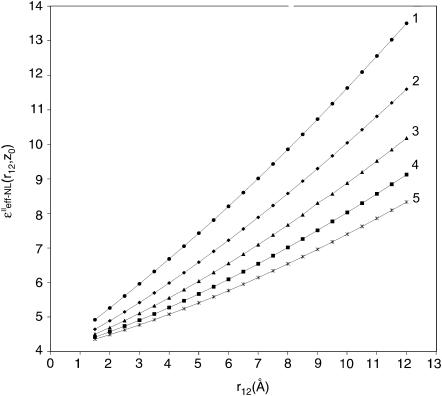
Numerical calculations of the ɛ_eff-NL(r₁₂, Z₀) and ɛ_eff-CL(r₁₂, Z₀) functions were performed using Eqs. 23 and 24, respectively. The calculations were made for the charged couple having two extreme orientations relative to the interface, (‖ and ⊥). Dependence of the dielectric function upon the distance Z₀ was analyzed for several intercharge distances, r₁₂, taken in the interval of ∼3–6 Å (Figs. 3 and 4). This interval is typical for distances between partial charges within amino acid residues as well as for protein salt bridges (Kumar and Nussinov, 2002a). For charges located in close proximity to the interface (Z₀ within range ∼5 Å), dependence upon the intercharge distance r₁₂ was also analyzed (Figs. 5 and 6). Figs. 3–6 present behavior of the effective dielectric function for the classical local model (ɛ_* = ɛ_s = 78.3), ɛ_eff–CL(r₁₂, Z₀), and for the NL model (ɛ_* = 6.0, ɛ_s = 78.3, L = 5.0 Å), ɛ_eff–NL(r₁₂, Z₀), of the aqueous solvent for both (‖ and ⊥) extreme orientations.

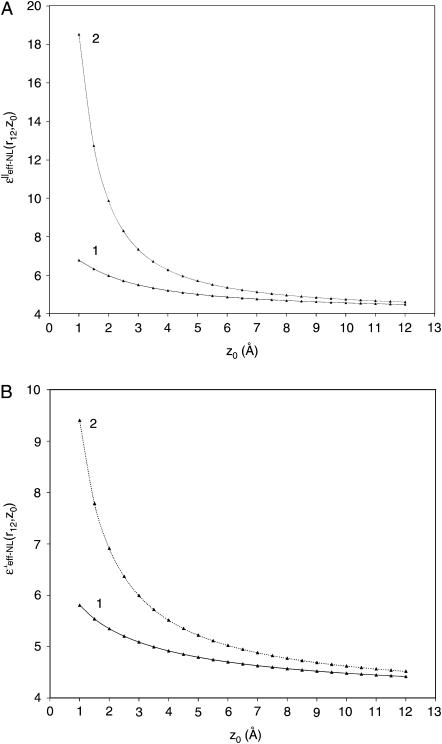
FIGURE 3.

Behavior of the effective dielectric functions, ɛ_eff-NL(r₁₂, Z₀) and ɛ_eff-CL(r₁₂, Z₀), for the NL and classical solvent models, correspondingly, depending on distances Z₀ from the protein interface for two charges of interest. (A) The charge orientations are parallel (‖) and (B) perpendicular (⊥) to the interface. Curve 1 indicates the ɛ_eff-NL(r₁₂, Z₀) function. Curve 2 indicates the ɛ_eff-CL(r₁₂, Z₀) function. Calculations were made for the fixed intercharge distances r₁₂ = 3.5 Å.

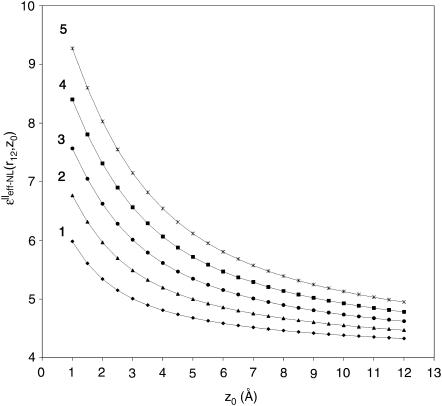
FIGURE 4.

Behavior of the effective dielectric function 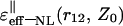depending on the distances Z₀ from the interface in the case of parallel (‖) orientation of two charges of interest with fixed intercharge distances r₁₂: 2.5, 3.5, 4.5, 5.5, and 6.5 Å—the curves 1, 2, 3, 4, and 5, respectively.

FIGURE 5.

Behavior of the effective dielectric functions, ɛ_eff-NL(r₁₂, Z₀) and ɛ_eff-CL(r₁₂, Z₀), for the NL and classical solvent models, correspondingly, depending on distance r₁₂ between two charges of interest. (A) The charge orientations are parallel (‖) and (B) perpendicular (⊥) to the interface. Curve 1 indicates the ɛ_eff-NL(r₁₂, Z₀) function. Curve 2 indicates the ɛ_eff-CL(r₁₂, Z₀) function. The calculations were made for the fixed value Z₀ = 1.5 Å.

FIGURE 6.

Behavior of the effective dielectric function 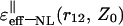depending on distance r₁₂ in the case of parallel (‖) orientation for two charges of interest with five fixed values Z₀: 1.5, 2.5, 3.5, 4.5, and 5.5 Å—the curves 1, 2, 3, 4, and 5, respectively.

As can be seen from Figs. 3 and 4, the value of the ɛ_eff–NL(r₁₂, Z₀) function for both extreme orientations is changing from the values ∼4–5 (for large Z₀ > r₁₂) and reaching the values ∼6–9 (for small Z₀ < r₁₂). For both (‖ and ⊥) orientations, such an increase in the value of ɛ_eff–NL(r₁₂, Z₀) for the small Z₀ is much smaller than the increase suggested by the classical dielectric function (see Fig. 3, A and B). The same tendency was observed for all other intercharge distances (data are not shown). Fig. 4 shows the greater the distance between the charges, the greater the value of the effective dielectric constant at the interface, and the greater the distances Z₀ when dielectric function approaches the bulk value ∼4.

Our analysis has shown that for the given parameter r₁₂, in the cases when the charged couples are located in close proximity to the interface (i.e., Z₀ is small) and when the distances between the charges are short, the NL effective dielectric function determined by Eq. 23 varies within a narrow interval of values. This interval is limited by the values within the area between the 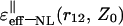and 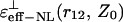curves. For example, when r₁₂ is equal to 3.5 Å, for any orientation of two charges, the ɛ_eff–NL(r₁₂, Z₀) function for the small Z₀ adopts the values within the interval ∼5–7 (Fig. 3). Analogously, when r₁₂ is equal to 5.5 or 6.5 Å, the ɛ_eff–NL(r₁₂, Z₀) function for the same Z₀ adopts the values within the interval ∼6–9 (Fig. 4, data for the 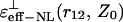are not shown).

Figs. 5 and 6 demonstrate the strong dependence of the ɛ_eff–NL(r₁₂, Z₀) function upon the distances r₁₂ between two interacting charges. According to Fig. 5, there is a significant difference between the values of the classical (local), ɛ_eff–CL(r₁₂, Z₀), and the NL, ɛ_eff–NL(r₁₂, Z₀), dielectric functions. This is especially clear in the case of the parallel orientation to the interface (Fig. 5 A), when the value of parameter r₁₂ is increasing. Fig. 6 shows that the greater the remoteness of the charged couple from the interface, Z₀, the smaller the value of the effective dielectric constant, and the greater the distance r₁₂ when ɛ_eff–NL(r₁₂, Z₀) approaches rather large values that are comparable with the value ∼(ɛ₁ + ɛ_s)/2 ≫ 1. This limiting value obtained by the asymptotic analysis (Fig. 2) is the maximum of the ɛ_eff–NL(r₁₂, Z₀) function at the interface, and it is smaller than the value of the long-wavelength dielectric constant (ɛ_s) of the solvent. Such behavior of the ɛ_eff–NL(r₁₂, Z₀) function differs essentially from the behavior of the sigmoidal functions previously used (Warshel, et al., 1984; Ramstein and Lavery, 1988; Buravtsev et al., 1989; Hassan and Mehler, 2002; Wang et al., 2002) that ignore the presence of a dielectric interface between the protein and solvent.

As can be seen in Table 1 and Figs. 2–6, the data of the numerical analysis are in agreement with the solutions of the asymptotic analysis. For example, in Fig. 4, at the small distances Z₀ (Z₀ < L) and r₁₂ (r₁₂ < L, curves 1 and 2), the values of the NL dielectric function are ∼5–6 that are comparable with the values ∼(ɛ₁ + ɛ_*)/2 estimated by the asymptotic analysis in the region F (Fig. 2; Table 1). In Fig. 6 the similar behavior of the NL dielectric function for the same Z₀ and r₁₂ is exhibited. Thus, this suggests that the asymptotic solution in the region F (Table 1; Fig.2) may be extended into the broader region: Z₀ < r₁₂ < L.

Our numerical calculations have shown (see Figs. 3–6) that, in close proximity to the interface, the value of the effective NL dielectric function determined by Eq. 23 is bigger than the bulk dielectric constant ɛ₁ = 4 of a protein, but much smaller than the values predicted by the use of Eq. 24 for the classical dielectric function. It is necessary to note that with an increase in the distance between charges, r₁₂, the value of the effective NL dielectric function in close proximity to the interface is increasing more significantly in comparison with the values when these charges are located on large distances Z₀ from the interface (Fig. 4). As a result, the PEI energy for the short distances between charges located near the protein surface is less than twice weaker than the PEI energy calculated for the protein interior. In particular, these estimations show that the difference between values of the effective dielectric function in the protein interior and exterior is significantly smaller than one estimated by the classical (local) approach (Eq. 24). It should be emphasized that these estimations for the value of the effective NL dielectric function (∼6–9) for short interchange distances in close proximity to the interface is consistent with estimations of the effective static dielectric constant (ɛ_s ≈ 9) in the active site of α-chymotrypsin (independent of ionic strength effects) obtained from direct spectroscopic measurements of the reorganization energy at this site (Mertz and Krishtalik, 2000).

The revealed influence of the spatial dispersion of the solvent permittivity on the features of the dielectric heterogeneity in proteins has a simple explanation. The results of the asymptotic analysis (taken together with the numerical analysis) show that in protein-like media, the function ɛ_eff-NL(R, Z, Z₀) for the small distances r₁₂ and Z₀ compared with the correlation length L, Z₀ < r₁₂ < L, approaches the value ∼(ɛ₁ + ɛ_*)/2 (Fig. 2; Table 1, region F; Figs. 4 and 6). From a physical standpoint, it suggests that this rather low value (compared with the limiting value (ɛ₁ + ɛ_s)/2 for the large distances, r₁₂ ≫ L) is a result of the arising effective layer of the boundary water, nonevidently presented in our model system on the interface between a protein and solvent. A thickness of this layer is comparable with the correlation length L (∼5 Å). The dielectric constant of the layer is determined by the short-wavelength dielectric constant of the bulk phase of the solvent (ɛ_* = 6), which is much smaller in comparison with the bulk value (ɛ_s = 78.3). It is consistent with results of the previous study of spatial dispersion of the electrolyte solution permittivity at the interface of the electrochemical systems (Rubinshtein, 1985). These results show that an effective low-dielectric boundary water layer arises at the interface between water and any contacting medium (including the gas phase with dielectric constant that is equal to one), and this arising is unrelated to the possible effects of dielectric saturation or other nonelectrostatic effects at the interface.

The data obtained in this work also suggest an arising of the boundary low-dielectric water layer on the protein surface. It should be noted that this effect was predicted without consideration of any specific interactions between water molecules and the protein. In the case of the native proteins, the arising of a boundary layer on the protein surfaces are caused by specific and nonspecific (in particular, electrostatic) effects that provide partial structurization and immobilization of the boundary water. Because the dominant contribution to the high water permittivity under room temperature is due to the reorientation of water dipoles, the restricted rotations of the dipoles within the boundary layer should determine a low-dielectric constant of this layer. The NL electrostatics allows one to capture some general properties of the boundary layer (such as thickness and dielectric constant) and mimic this layer. It is evident that consideration of this layer, with inherent physical properties, is an important factor for correct electrostatic estimations at the protein-solvent interface. The asymptotic and numerical analysis performed in this work suggest that this low-dielectric boundary water layer is the major factor that determines the values of the effective dielectric function for the short-distance electrostatic interactions in close proximity to the protein-solvent interface.

There are several convincing experimental data that point to the existence of the boundary water layer on the protein surface. A partially structured water layer (“dynamically ordered water” within ∼4-Å distance shell) was experimentally observed by the direct study of the dynamics of hydration at the surface of the enzyme protein (Pal et al., 2002). Results obtained by the use of a time domain reflectometry for several globular proteins in solvent revealed a dielectric relaxation peak that was associated with the orientation of bound water molecules on the protein surface (Miura et al., 1994). The dynamic properties of the bound water layer on the protein surface were clearly demonstrated by Rocchi et al. (1998). In that work, the average rotational reorientation time of the water molecules in close proximity to the protein surface (within distance ∼7 Å) was shown to be significantly longer than one in bulk water. The use of an accurate simulation of protein dynamics in solution (Levitt and Sharon, 1988; Lounnas et al., 1994) has also shown the existence of a layer of the bound water molecules around a protein (within distance ∼5 Å from the surface).

The consideration of the mobile-free counterions in the solvent by the use of the simple approximation for the dielectric function for a dilute solution of a strong electrolyte (Kornyshev et al., 1978; Rubinshtein, 1983, 1986) can amplify the electrostatic screening (Rubinstein and Sherman, 2001) and leads to an increase in values of the effective dielectric function near the protein exterior. The detailed analysis of this effect will be described elsewhere.

The high values of the PEI energy at the protein-solvent interface estimated in the framework of the NL electrostatic approach, Eqs. 17–23, compared to the classical approach suggest that salt bridges and their complexes as well as other polar side-chain–side-chain interactions at the protein surface, including cation-π interactions, may provide significantly more contributions to the protein and the secondary structure stabilization than was previously assumed (Hendsch and Tidor, 1994; Luo et al., 1999; Vijayakumar and Zhou, 2001; Shi et al., 2001; Kumar and Nussinov, 2002a; Alexov, 2003). In fact, our analysis has shown that the PEI energy for the short-distance charges located in close proximity to the protein-solvent interface adopts the values, which are not more than twice weaker than the analogous values for the same charges deeply buried within the protein-like medium. It suggests that the electrostatic interactions at the protein interface can be bigger than it was previously assumed. Thus, it is reasonable to assume that distribution of the charged groups on the protein surface, which determine a number of salt bridges, is not random and is a result of the favorable electrostatic interactions associated with an additional driving force in protein folding. This assumption is consistent with data obtained in several works (Sundaralingam et al., 1987; Shi et al., 2001; Kumar and Nussinov, 2002a), particularly, with an observation that thermophilic enzymes are much more stable compared with mesophilic enzymes, which have a significantly smaller number of salt bridges at their surface (Perutz, 1978; Sinha and Smith-Gill, 2002; Kumar and Nussinov, 2002b).

CONCLUSIONS

In this work, the NL electrostatic concept, previously used for electrochemical systems, has been utilized for the estimation of the PEI energy in proteins. This approach allowed us to calculate the PEI energy at the protein-solvent interface in terms of the Fourier-transform ɛ₁(k) and ɛ₂(k) of the dielectric functions characterizing the bulk properties of the contact media and to carry out the electrostatic calculations at the interface for arbitrary media types by adequately representing the dielectric bulk properties. Using this approach, it is possible to analyze the contribution of the various modes of the solvent polarization (orientational, infrared, and electronic) and intrinsic protein polarization to the PEI energy at the protein-solvent interface. In this way, the NL electrostatics concept can be used for a better understanding of the nature of interactions at the protein-solvent interface and employed for more accurate energy calculations and the molecular modeling of proteins.

The NL electrostatic concept allowed us to reveal some features of spatial heterogeneity of the protein dielectric properties (at the scale ∼L) and show that this heterogeneity can be determined by the spatial dispersion of the solvent dielectric function. In this work, we have shown that the nonlocal effects of the solvent microstructure are appreciable and can be significant in the electrostatic calculations at the rather small distances r₁₂ and Z₀, compared with correlation solvent length L (r₁₂ < L and Z₀ < L). The results obtained in our work also suggest that, when the strong spatial dipole correlation in solvent is taken into account (Eq. 21), the electrostatic estimations of the PEI energy in proteins captures the effect of the presence of the partially structured water layer on the protein surface. Physical peculiarities of this boundary water layer are reflected in the framework of the NL approach without consideration of the specific interactions of the water molecules with the protein surface. Our results suggest that this layer, which is called “dynamically ordered water” or “biological water” (Pal et al., 2002), can be the major factor determining the value of the PEI energy between short-distance charges located in close proximity to the protein interface. This energy has a value comparable with the PEI energy value when the analogous charges are deeply buried in protein.

Overall, our results suggest that the electrostatic interactions can play a significantly larger role in the protein folding than previously thought, providing additional support to the assumption that specific distribution of the charged and polar amino acid residues along polypeptide chains of the globular proteins may be responsible for the relative uniqueness of their folding (Paul, 1982; Hendsch and Tidor, 1994).