A Structural Model of Polyglutamine Determined from a Host-Guest Method Combining Experiments and Landscape Theory

Abstract

Modeling the structure of natively disordered peptides has proved difficult due to the lack of structural information on these peptides. In this work, we use a novel application of the host-guest method, combining folding theory with experiments, to model the structure of natively disordered polyglutamine peptides. Initially, a minimalist molecular model (C_αC_β) of CI2 is developed with a structurally based potential and captures many of the folding properties of CI2 determined from experiments. Next, polyglutamine “guest” inserts of increasing length are introduced into the CI2 “host” model and the polyglutamine is modeled to match the resultant change in CI2 thermodynamic stability between simulations and experiments. The polyglutamine model that best mimics the experimental changes in CI2 thermodynamic stability has 1), a β-strand dihedral preference and 2), an attractive energy between polyglutamine atoms 0.75-times the attractive energy between the CI2 host Go-contacts. When free-energy differences in the CI2 host-guest system are correctly modeled at varying lengths of polyglutamine guest inserts, the kinetic folding rates and structural perturbation of these CI2 insert mutants are also correctly captured in simulations without any additional parameter adjustment. In agreement with experiments, the residues showing structural perturbation are located in the immediate vicinity of the loop insert. The simulated polyglutamine loop insert predominantly adopts extended random coil conformations, a structural model consistent with low resolution experimental methods. The agreement between simulation and experimental CI2 folding rates, CI2 structural perturbation, and polyglutamine insert structure show that this host-guest method can select a physically realistic model for inserted polyglutamine. If other amyloid peptides can be inserted into stable protein hosts and the stabilities of these host-guest mutants determined, this novel host-guest method may prove useful to determine structural preferences of these intractable but biologically relevant protein fragments.

INTRODUCTION

Understanding the fundamental physics of protein folding is a goal of both experimentalists and theoreticians. Guided by landscape theory (Onuchic et al., 1997), an understanding of the fundamental principles of protein folding has recently advanced due to the development of 1), small fast-folding peptide systems (Blanco et al., 1994; Krieger et al., 2003; Marqusee et al., 1989; Munoz et al., 1997; Neidigh et al., 2002; Thompson et al., 2000; Yang et al., 2004) which are tractable to study by all-atom simulation (Bursulaya and Brooks, 1999; Daggett and Levitt, 1992; Garcia and Sanbonmatsu, 2001, 2002; Hansmann et al., 1999; Okur et al., 2003; Pitera and Swope, 2003; Shirley and Brooks, 1997; Wang and Sung, 1999; Yeh and Hummer, 2002; Zagrovic and Pande, 2003) and 2), minimalist simulation models which can effectively sample the dynamics of larger protein systems (Chan and Dill, 1993; Cheung et al., 2003; Clementi et al., 2000a; Ding et al., 2002; Klimov and Thirumalai, 2000; Shea et al., 1999). Although these research efforts are increasing our understanding of protein folding, many challenges remain. One significant goal is connecting the physical principles learned from protein folding studies to multiprotein interactions, such as binding and aggregation. Developing a theory consistent with both folding and binding processes is particularly crucial in understanding natively unfolded proteins which fold upon binding to other molecules (Guo et al., 2002).

An important disease pathology which can be addressed with protein folding theory is the assembly of unfolded protein monomers into β-sheet amyloid fibers. In many amyloid diseases, mutations in genes which enhance the disease symptoms also result in increased amyloid fiber formation from the gene's protein product, both in vivo and in vitro. One prominent example of this phenomenon is found in Huntington's Disease (HD), where aggregation of the protein huntingtin is dependent on the length of a polyglutamine region within the huntingtin protein sequence (Zoghbi and Orr, 2000). Patients with longer huntingtin polyglutamine regions (>35 glutamines) demonstrate increased huntingtin amyloid fiber formation as well as an increased risk of neuron death, cognitive dysfunction, and atrophy of motor functions (Zoghbi and Orr, 2000). One major difference between HD and other amyloid diseases is that polyglutamine length is the only genetic factor needed to determine a patient's risk of developing disease symptoms whereas other non-polyglutamine amyloid diseases involve multiple genetic and behavioral determinants (Hardy and Gwinn-Hardy, 1998). Polyglutamine length has also been shown to be the sole risk factor of developing symptoms in other diseases as well (Zoghbi and Orr, 2000).

In individuals whose huntingtin gene exceeds the polyglutamine threshold, the likelihood of acquiring HD each year does not increase with age, indicating that age-related impairment of aggregate clearance is not a cause of the disease (Perutz and Windle, 2001). A second inference of this work is that a nucleation-initiated process, such as protein aggregation, is responsible for the onset of the disease (Perutz and Windle, 2001). The polyglutamine aggregation-disease link is further supported by studies showing that simple polyglutamine peptides will assemble into amyloid fibers (Chen et al., 2002a) and are toxic to cells when delivered to the nucleus as aggregates, but not monomers (Yang et al., 2002). Polyglutamine, both as a monomer and aggregate, offers a simple molecular system to explore amyloid formation and its role in polyglutamine disease.

Although the correlation between polyglutamine length and disease is straightforward, understanding the molecular events involved in polyglutamine disease remains unclear (Temussi et al., 2003). An increase in detailed molecular information on polyglutamine has been limited by the fact that structural information on polyglutamine has been difficult to obtain (Temussi et al., 2003). A detailed structure of unaggregated polyglutamine has not been determined, possibly due to the fact that monomeric polyglutamine is natively disordered (Altschuler et al., 1997; Bennett et al., 2002; Chen et al., 2002a, 1999; Gordon-Smith et al., 2001; Masino et al., 2002). As polyglutamine aggregates, an increase in β-sheet spectroscopic structural indicators is observed (Chen et al., 2002b). However, even these polyglutamine aggregates can only be probed with low-resolution structural methods, such as circular dichroism (Altschuler et al., 1997; Bennett et al., 2002; Chen et al., 2002a; Masino et al., 2002), Fourier-transform infrared, and x-ray diffraction (Perutz et al., 2002, 1994), such that detailed information on this β-sheet structure is limited.

The present study combines molecular dynamics, energy landscape theory, and experimental protein stability information to determine structural parameters for a minimalist model of polyglutamine. Reminiscent of earlier host-guest studies (Lotan et al., 1966; Wojcik et al., 1990), increasing lengths of the inserted polyglutamine “guest” into the “host” chymotrypsin inhibitor 2 mutants show increasing destabilization to the host CI2 protein (Ladurner and Fersht, 1997). Unfortunately, crystal structures and NMR structures of polyglutamine inserts into CI2 are disordered and do not show a discrete structure such as polyglutamine adopts in the context of the CI2 host (Chen et al., 1999; Gordon-Smith et al., 2001). However, thermodynamic stability and kinetic folding rates of these polyglutamine insert mutants can be used to determine the structural preferences of the polyglutamine insert (Ladurner and Fersht, 1997).

First, a minimalist molecular model (C_αC_β) of the CI2 host is developed with a Go-potential and is shown to capture many of the folding properties of CI2 determined from experiments. Second, polyglutamine guests are inserted into the CI2 Go-model host and polyglutamine parameters are selected which best agree with host-guest thermodynamic results: a β-strand dihedral and an attractive energy between polyglutamine atoms equaling 0.75 the Go-contact energy. Third, using this potential in the polyglutamine guest, kinetic folding rates of the host-guest mutants, structural perturbation of the CI2 host by the polyglutamine guest, and the structure of the inserted polyglutamine guest are shown to agree well with experiments.

Despite the good agreement between experiments and simulations for the CI2-polyglutamine host-guest system, it is unclear whether the polyglutamine energy potential will also accurately characterize the polyglutamine guest in the absence of the CI2 host. Although minimalist models may capture the essential physics of funneled energy landscapes, such as those observed in protein folding (Onuchic et al., 2000), the frustrated energy landscapes of natively disordered proteins may require a more detailed molecular model. To validate the minimalist host-guest approach used in the present study, the polyglutamine parameters determined in the present study will used in future studies to directly simulate polyglutamine chains, either as isolated monomers or as an aggregating system of multiple chains.

MATERIALS AND METHODS

Molecular dynamics

Molecular dynamics (MD) simulations were carried out using AMBER 6 software, compiled on a Linux platform, employing the sander_classic program as an integrator for initial energy minimization and subsequent molecular dynamics (Pearlman et al., 1995). Simulations were performed on the wild-type protein chymotrypsin inhibitor 2 as well as CI2 insert mutants with MG₃SG₄SG₃M, MGQ₄GM, and MGQ₁₀GM inserted in substitution for methionine 40 (Ladurner and Fersht, 1997). The initial structure used for MD was determined by simulated annealing which used the 2CI2.pdb coordinates as an initial structure. For each protein studied, six simulations were run for 120 ns at the folding temperature (350 K for wild-type, 333 K for mutants) and the first 30 ns of MD was discarded as equilibration.

The following describes the AMBER sander_classic molecular dynamics parameters used in this study. The specific parameter values are listed in parentheses. The time step was 0.001 ps (DT = 0.001). Translational and rotational motion was removed at the beginning of each run and every 1000 time steps thereafter (NTCM = 1, NSCM = 1000, NDFMIN = 0). Initial velocities were randomly selected (INIT = 3, IG = random). If the absolute value of the velocity of any atom exceeded 500 Å/timestep, velocities are scaled such that the absolute value of the velocity of that atom = 500 Å/timestep (VLIMIT = 500). Temperature was maintained with external bath using the method of Berendsen (1984) with a coupling constant of 0.2 ps (NTT = 5, TAUTP = 0.2, TAUTS = 0.2). If the simulation temperature T_sim exceeds the average temperature T by >10 K, velocities are scaled such that T_sim = T. SHAKE was not used. The particle-mesh Ewald method was not used (IEWALD = 0). During each integration step, interactions between all atom pairs were calculated and this contact pair-list only update once at the beginning of the simulation (CUT = 9999, NSNB = 9999). No periodic boundary and pressure regulation were used (NTB = 0, NTP = 0). Structures and energies were saved every 1.5 ps (NTPR = 1500, NTWR = 1500, NTWX = 1500, NTWV = 1500, NTWE = 1500).

Go-model of CI2 host

In minimalist MD simulations of the host CI2 protein, each amino acid in CI2 is reduced to the backbone C_α atom and a single C_β atom located at each side chain's center of mass (Cheung et al., 2003; Ding et al., 2002; Irback et al., 2000; Klimov and Thirumalai, 2000; Liwo et al., 2002; Takada et al., 1999; Vieth et al., 1995). For wild-type CI2, the overall potential energy for a given protein conformation is given by Eq. 1 as

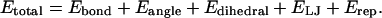(1)

Consistent with the original Go-model (Go, 1983), the minimum energy of each energy term is obtained when the protein is in the native folded state. For covalent bond distance terms,

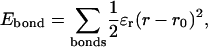(2)

where ɛ_r = 100 kcal/mol is the bond energy, r is the bond distance in the simulation, and r₀ is the native bond distance, summed over all bonds in 2CI2.pdb.

For the bond-angle term,

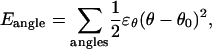(3)

where ɛ_θ = 20 kcal/mol is the bond angle energy, θ is the bond angle in the simulation, and θ₀ is the native bond angle, summed over all bond angles in 2CI2.pdb (C_αC_αC_α, C_βC_αC_α, C_αC_αC_β).

For dihedral energies,

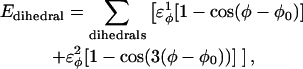(4)

where 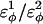are the dihedral energies, φ is the dihedral angle in the simulation, and φ₀ is the native dihedral angle, summed over all dihedral angles in 2CI2.pdb (C_αC_αC_αC_α, C_βC_αC_αC_β, C_αC_αC_αC_β, C_βC_αC_αC_α). For backbone dihedrals (C_αC_αC_αC_α) dihedrals, 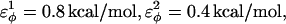and for side-chain dihedrals (C_βC_αC_αC_β/C_αC_αC_αC_β/C_βC_αC_αC_α),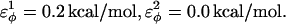

In the Go-model of the CI2 host, two C_α atoms were selected as attractive if they fall within 7.5 Å in the crystal structure 2CI2.pdb and within an angular definition described by Veith et al. (1995). A C_β–C_β pair was determined to be attractive if they are separated by three or more residues and are indicated to be in contact using CSU analysis on 2CI2.pdb (Sobolev et al., 1999). No attractive contacts are allowed between C_α and C_β atoms. Each attractive C_α–C_α and C_β–C_β contact is described by an attractive Lennard-Jones potential as

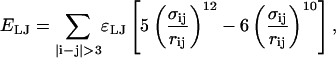(5)

where ɛ_LJ = 0.8 kcal/mol is the contact energy, σ_ij is the native distance between the two contact atoms, i and j, given from the crystal structure, and r_ij is the distance between the two contact atoms, i and j, determined for a given iteration of the simulation.

If any two atoms are not determined to be attractive or fall within two residues of each other (i, i + 2), then their interaction is defined by a repulsive term

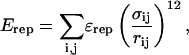(6)

where ɛ_rep = 0.8 kcal/mol is the repulsive energy, σ_ij is the hard-sphere distance between the two repulsive atoms, i and j, and r_ij is the distance between the two repulsive atoms, i and j, determined for a given iteration of the simulation. In the simulations, σ_ij = r_i + r_j, where r_i, r_j = 1.9 Å (if atom i,j is C_α) or native C_α–C_β bond distance (if atom i,j is C_β).

A list of the parameters used in the CI2 host Go-model is shown in Table 1.

TABLE 1.

CI2 host parameters and Model polyglutamine guest parameters

		Polyglutamine guest
Parameter	CI2 host Energy ɛ	Value	Energy ɛ
Bonds	(kcal/mol)	(Å)	(kcal/mol)
CαCα	100	3.81	100
CαCβ	100	3.45	100
Angles	(kcal/mol)	(°)	(kcal/mol)
CαCαCα	20	109.5	20
CβCαCα	20	109.5	20
CαCαCβ	20	109.5	20
Dihedrals	(kcal/mol)	(°)	(kcal/mol)
CαCαCαCα	0.8 ()	−330	0.8 ()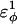
	0.4 (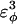)	−330	0.4 ()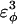
CβCαCαCβ	0.2 (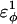)	−0	0.2 ()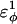
CβCαCαCα	0.2 (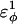)	−180	0.2 ()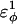
CαCαCαCβ	0.2 (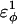)	−140	0.2 ()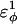
10–12 contacts	ɛLJ (kcal/mol)	(i, i + 3 contacts)	ɛQQ (kcal/mol)
CαCα	0.8 (i, i + 3)	all Q–Q pairs	0.6
CβCβ	0.8 (i, i + 3)	all Q–Q pairs	0.6

Go-model parameters of the CI2-host are shown as normal text. Assumed Model parameters of the polyglutamine guest are shown as italicized text. Fitted Model parameters of the polyglutamine guest, determined in the present study, are shown in bold.

Model of polyglutamine guest

As with the CI2 host, each polyglutamine guest residue is approximated by the backbone C_α atom and a single C_β atom located at the polyglutamine side chain center of mass (3.45 Å). Insertion of the guest adds an additional potential energy contribution to the host potential energy, comprised of the same energy terms as the CI2 host described in Eq. 1. However, since polyglutamine does not have a discrete structure, the polyglutamine potential is not a Go-model. The energy parameters for polyglutamine must be determined without the knowledge of a discrete structure. As such, it is unclear whether a “frustrated” non-Go model of polyglutamine will be physically relevant without an all-atom representation of polyglutamine and solvation. As was done with early protein folding Go-models (Onuchic et al., 1997), the present study is a first attempt to determine whether minimalist models can also address the dynamics of natively disordered proteins and protein aggregation phenomenon.

For bond distance energies in polyglutamine, Eq. 2 is used. For polyglutamine, ɛ_r = 100 kcal/mol is the assumed bond energy, r is the bond distance in the simulation, and r₀ = 3.81 Å (assumed if C_α–C_α bond) or 3.45 Å (assumed if a glutamine C_α–C_β bond), summed over all bonds in the polyglutamine guest.

For bond-angle energies in polyglutamine, Eq. 3 is used. For polyglutamine, ɛ_θ = 20 kcal/mol is the bond energy, θ is the bond angle in the simulation, and θ₀ = 109.5° (assumed preferred polyglutamine bond angle), summed over all bond angles in the polyglutamine guest (C_αC_αC_α, C_βC_αC_α, C_αC_αC_β).

For dihedral energies in polyglutamine, Eq. 4 is used. For polyglutamine, where 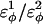are assumed dihedral energies, φ is the dihedral angle in the simulation, and 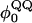is a varied parameter in the present study, summed over all dihedral angles in the polyglutamine guest (C_αC_αC_αC_α, C_βC_αC_αC_β, C_αC_αC_αC_β, C_βC_αC_αC_α). The values of 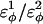are assumed to be similar to the CI2 host: for backbone dihedrals (C_αC_αC_αC_α), 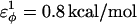and 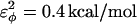; and for side-chain dihedrals (C_βC_αC_αC_β/C_αC_αC_αC_β/C_βC_αC_αC_α), 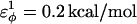and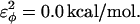

In the model of the polyglutamine guest, the interaction between all nonlocal (i, i + 3 or greater) C_α atoms in the guest polyglutamine is attractive to approximate a fundamental propensity for polyglutamine chains to form backbone hydrogen bonds (Chen et al., 2002a). Similarly, the interaction between all nonlocal (i, i + 3 or greater) C_β atoms in the guest polyglutamine is attractive to approximate a fundamental propensity for polyglutamine side chains to form stable bonds (Chen et al., 2002a). As with the CI2 host, no attractive contacts were allowed between C_α and C_β atoms and the energy of the C_α–C_α and C_β–C_β contacts were equal, for simplicity. Each attractive C_α–C_α and C_β–C_β contact between residues within the polyglutamine guest is described by Eq. 5 and the total attractive contact energy is the sum of all attractive contacts in the polyglutamine guest. To distinguish between the Lennard-Jones energy between contacts in the CI2 host, ɛ_LJ = 0.8 kcal/mol, the contact energies in the polyglutamine guest are denoted with polyglutamine contact energy, ɛ_QQ, which is a varied parameter in the present study. For attractive contacts between nonlocal atoms in the polyglutamine guest, σ_ij is assumed to be 4.6 Å for C_α–C_α contacts or 5.2 Å for C_β–C_β contacts, consistent with distances observed between hydrogen bonded glutamine residues in β-sheets, and r_ij is the distance between the two contact atoms, i and j, in the simulation. Using these assumptions, the only contact parameter to determine is the attractive Lennard-Jones potential between the polyglutamine atoms, ɛ_QQ.

As with the CI2 host, it is assumed that all local (i, i + 2 or less) Lennard-Jones interactions in the polyglutamine guest are repulsive since their conformations are defined by the dihedral parameters. Furthermore, since the crystal structure and NMR studies of CI2-polyglutamine host-guest mutants shows the polyglutamine guest residues as disordered (Chen et al., 1999; Gordon-Smith et al., 2001), it is also assumed that the Lennard-Jones interactions between atoms in the polyglutamine guest and the CI2 host are repulsive. Eq. 6 is used to determine the total repulsive contact energy as the sum of all repulsive contacts in the polyglutamine guest. For repulsive contacts involving atoms in the polyglutamine guest, ɛ_rep = 0.8 kcal/mol is the assumed repulsive energy, r_ij is the distance between the two repulsive atoms (i and j) in the simulation, and σ_ij = r_i + r_j, where r_i, r_j = 1.9 Å (if atom i,j is C_α) or native C_α–C_β bond distance (if atom i,j is C_β).

A list of the parameters used in the polyglutamine guest model is shown in Table 1.

Analysis of simulations

Thermodynamic quantities, such as free energy (G), energy (E), and entropy (S), are determined using the weighted histogram analysis method (WHAM) (Ferrenberg and Swendsen, 1988; Kumar et al., 1992). For each reported CI2 free energy, six MD simulations are sampled for 120 ns, with 90 ns used for WHAM analysis and the initial 30 ns discarded. The free energies are reported as an average and standard deviation of the WHAM-calculated free energy of each of the six 90-ns trajectories.

For kinetic refolding studies of CI2, 60 kinetic trajectories are collected to obtain statistically significant reaction rate measurements. The initial unfolded coordinates of each refolding trajectory are obtained from the final structure of a short simulation at 999 K of a randomly determined length (500–1500 ps) and random initial velocities. For each refolding trajectory, these initial coordinates are subjected to 300 K and random initial velocities and followed for 9000 ps, a sufficient amount of computational steps to refold all CI2 trajectories. For each trajectory, the average value of Q, the number of native contacts formed is determined at each MD iteration. From the 60 trajectories, six groups of 10 trajectories are averaged together and each group fit using the Marquardt algorithm with in-house software to Eq. 7 (Marquardt, 1963),

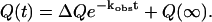(7)

In Eq. 7, Q(t) is the average number of native contacts Q at time t, k_obs is the observed kinetic rate, ΔQ is the change in the number of native contacts Q between native and unfolded CI2, and Q(∞) is the equilibrium average native value of Q. The average and standard deviation of the rate constants k_obs are calculated from the six groups for each value of k_obs.

RESULTS

Wild-type CI2

Minimalist models of chymotrypsin inhibitor 2 were examined to determine whether a minimalist CI2 model can capture experimentally determined properties and therefore be suitable for use in this study. CI2, denoted “Wild-Type CI2” in Fig. 1, is a small protein but contains many different types of secondary structures:

1. Alpha-helix (residues 12–24).

2. Parallel β-sheet between β-strands: three (residues 28–34) and four (residues 45–52).

3. Antiparallel β-sheets between β-strands, one (residues 3–5) and six (residues 60–64); two (residues 5–8) and five (residues 55–58); four and six.

4. Extended loop (residues 35–44).

FIGURE 1.

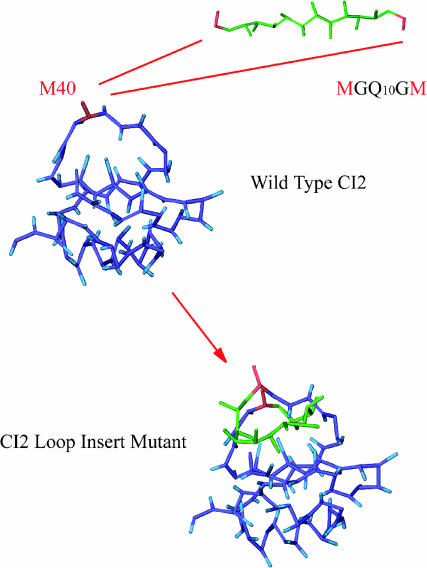
Schematic of polyglutamine residues MGQ₁₀GM inserted into the CI2 host. Wild-type CI2 host residues are labeled in blue, the insertion residue site, Met-40, is labeled in red, and the 10Q polyglutamine guest insert is labeled in green.

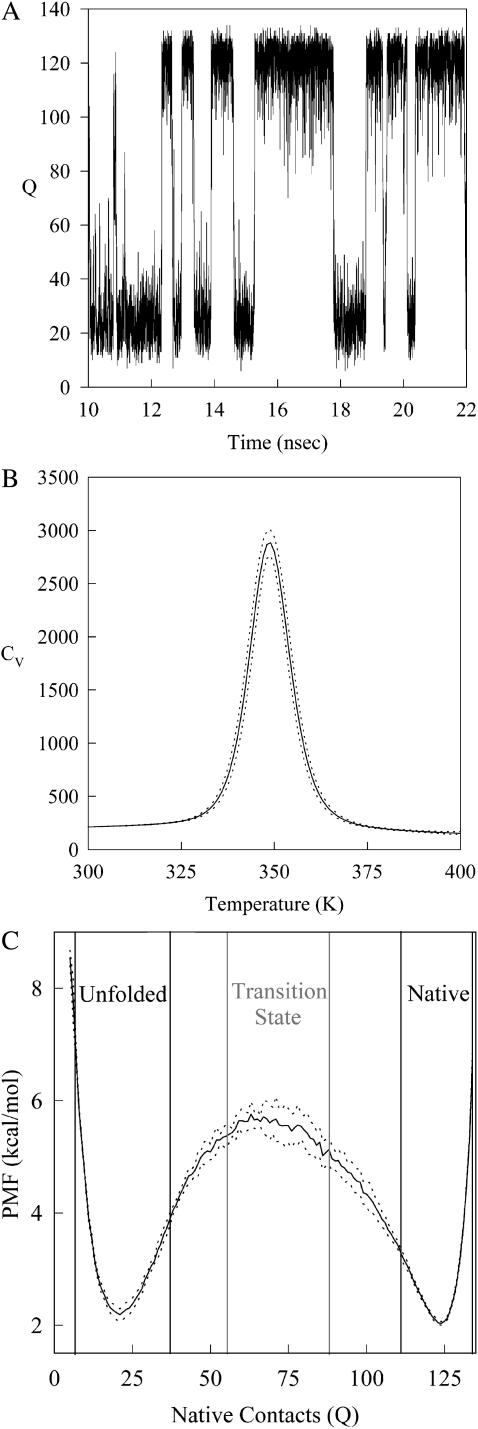
A two-state folding mechanism of CI2 has been determined rigorously with both bulk and single molecule experiments (Deniz et al., 2000; Jackson and Fersht, 1991). In simulations, CI2 folding should also be absent of folding intermediates. Fig. 2 A shows the number of CI2 native contacts (Q) present in a representative wild-type CI2 simulation between 10 and 22 ns at the folding temp of CI2, T_f = 350 K. In Fig. 2 A, Q occupies native (Q ∼ 125) or unfolded (Q ∼ 20) conformations without populating intermediates states. The lack of intermediate states observed in Fig. 2 A is consistent with previous simulations of both C_α and C_αC_β representations of CI2 (Cheung et al., 2003; Clementi et al., 2000b).

FIGURE 2.

Wild-type CI2 demonstrates two-state folding behavior. (A) The number of native contacts (Q) between 10 and 22 ns in a simulation of wild-type CI2 at T_f = 350 K predominantly samples native (Q ∼ 125) or unfolded (Q ∼ 20) conformations. (B) A single peak is observed in the plot of the specific heat (C_V) versus temperature (T), indicating two-state folding behavior. A 1-SD error of C_V is shown with dashed lines (- - -). (C) A plot of potential mean force (PMF) versus native contacts (Q) at the wild-type CI2 T_f = 350 K shows two free-energy minima at the native (Q ∼ 125) and unfolded (Q ∼ 20) ensembles and a single free-energy maxima at the transition state (Q ∼ 70). 1 SD of PMF is shown with dashed lines (- - -).

In Fig. 2 B, the two-state mechanism of CI2 is further demonstrated in a WHAM calculation of the specific heat, C_V(T) versus temperature, T near the folding temperature, T_f ∼350 K, where

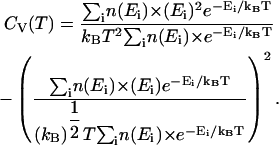(8)

In Eq. 8, E_i is the potential energy of each conformation in the simulation, k_B is the Boltzmann constant, and n(E_i) is the density of states, or number of iterations, of the simulation. In Fig. 2 B, a single specific heat peak is observed in wild-type CI2 simulations, consistent with a two-state mechanism and no stable intermediates. The error boundary of one standard deviation for C_V(T), determined from six independent simulations, is indicated in Fig. 2 B by dashed lines above and below the C_V(T) trace. The specific heat plot in Fig. 2 B is consistent with previous simulations of both C_α and C_αC_β representations of CI2 (Cheung et al., 2003; Clementi et al., 2000b).

In Fig. 2 C, only two free-energy minima, corresponding to native (Q ∼125) and unfolded (Q ∼20) ensembles, are in a WHAM calculation of the number of native contacts (Q) versus potential mean force (PMF) for a representative wild-type CI2 simulation at T_f = 350 K, where

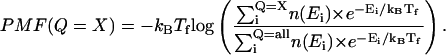(9)

In Eq. 9, k_B is the Boltzmann constant, n(E_i) is the density of states in the simulation with the indicated value of Q, Q = X denotes all simulation configurations with X native contacts, and Q = ALL denotes all simulation configurations. Although PMF is not a direct measure of free-energy, differences in PMF are equivalent to the difference in free energy (ΔG). For example, the free-energy difference between a native (Q = 125) and unfolded (Q = 20) ensembles (ΔG_NU) can be estimated by Eq. 10 as

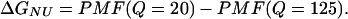(10)

The two free-energy minima observed in Fig. 2 C demonstrates the two-state folding of the C_αC_β CI2 Go-model, in agreement with experimental results (Jackson and Fersht, 1991) as well as previous simulation studies (Cheung et al., 2003, 2000b). Also indicated in Fig. 2 C are boundaries inclusive of the unfolded, native, and transition state ensembles. The error boundary of 1 SD, determined from six independent simulations in the PMF shown in Fig. 2 C, is indicated by dashed lines above and below the PMF trace.

Confirming two-state folding is the first step toward a successful computational model of CI2. The second step is to ensure that the transition state in simulations is in agreement with experimental φ-values. In a typical φ-value measurement, a CI2 mutant is made which removes the wild-type side chain at a single residue site i (i.e., wild-type side chain to alanine). To determine the degree to which, between 0 and 1, a side chain is structured in the transition state, the φ-value is calculated using Eq. 11,

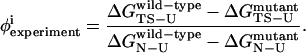(11)

It is important to note that interpretation of φ-values is complicated by alterations in the folding mechanism from the mutation and sampling of non-native contacts in the transitions state ensemble, which can lead to φ-values <0 and >1. Furthermore, φ-values derived from a single-site mutation cannot distinguish which additional residue contacts are involved in the transition state structuring, although these interactions can be measured with double mutants (Itzhaki et al., 1995). Also, the correlation between free energy and the formation of native side-chain structure may not be straightforward in all proteins (Bulaj and Goldenberg, 2001).

Despite these caveats, φ-value analysis remains an invaluable method to study the transition state structure and compare experimental and simulation results. In the low-resolution C_αC_β model employed in the present study, a residue-to-residue φ-value comparison between simulation and experiment is not used. Instead, the accuracy of the CI2 model is evaluated on whether it predicts the predominant CI2 secondary structure elements involved in the transition state. In simulations, the free-energy perturbation method is used to calculate the φ-value of each contact from the wild-type simulation without actually having to simulate each mutation separately or conduct kinetic simulations (Clementi et al., 2000b). Using free-energy perturbation, the φ-value of each contact, i, is calculated by removing the energy of each contact from the wild-type energy function, effectively producing a deletion mutant at that contact. The φ-value itself is calculated using the energy difference between the wild-type and mutant energies (ΔE) of the unfolded, native, and transition state thermodynamic ensembles through Eq. 12,

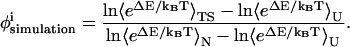(12)

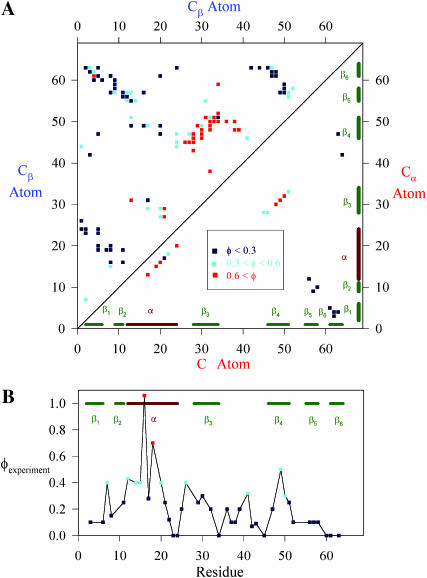
As with experimental φ-values, the free-energy perturbation method assumes that the folding mechanism will be unchanged when each contact is removed. Fig. 3 A presents each residue-residue wild-type CI2 contact with the simulated transition state φ-value of each contact indicated by its color. The upper left corner of Fig. 3 A indicates C_β–C_β contacts and the lower right corner indicates C_α–C_α contacts. Both the C_α–C_α and C_β–C_β φ-values are high in the α-helix (residues 12–24), β-strand β₃ (residues 28–34), and β-strand β₄ (residues 46–52). These results are consistent with earlier results on a C_α model of CI2 (Clementi et al., 2000b). Standard deviations of simulated φ-values are no greater than ±0.05, indicating a high degree of confidence in the magnitudes of the simulated φ-values.

FIGURE 3.

Simulation φ-values agree with experimental φ-values. The magnitude of the φ-values is indicated by color: φ < 0.3 (black square), 0.3 < φ < 0.6 (light-blue square), and φ > 0.6 (red square). Secondary structure elements of CI2 are shown for reference: β₁, β₂, α, β₃, β₄, β₅, and β₆. (A) A contact map showing the simulation φ-values of the wild-type CI2 transition state for C_β–C_β contacts (upper left) and C_α–C_α contacts (lower right). The maximum standard deviation error of any simulation φ-value listed is ±0.05. (B) Experimental φ-values are shown for each residue (Itzhaki et al., 1995).

For comparison, Fig. 3 B shows the values of φ_experiment for CI2 as listed in Itzaki et al. (1995). Values of φ_experiment were selected with preference for side-chain deletion mutations instead of mutations which introduce new side-chain atoms. High (φ > 0.6) and medium (0.6 > φ > 0.3) φ-values are found in the regions of α-helix, and β-strands β₂, β₃, and β₄. Outside these regions, only low φ-values are found (φ < 0.3). When compared to the regions exhibiting high φ-values by simulation in Fig. 3 A, it is shown that the simulation captured the higher φ-value regions of α-helix and β-strands β₃/β₄. Although it is true that β₂ is not a high φ-value region in the simulation and that the φ-values magnitude can differ between simulation and experiment, the simulation largely captures the high φ-value regions found in experiments. Given the uncertainty in experimental φ-value measurements, this Go-model of CI2 appears to qualitatively capture the transition state ensemble properties and the two-state folding behavior of CI2. This agreement shows that the C_αC_β CI2 model can be used as an accurate wild-type “host” to examine the effects of introducing “guest” polyglutamine inserts into CI2.

Polyglutamine insertion mutants of CI2

Fig. 2, A–C, and Fig. 3, A and B, have indicated that the C_αC_β Go-model of CI2 used in this study captures the observed properties measured with experiments. As such, further studies involving more complex mutations involving significant amino acid inserts can be conducted. The present study focuses on the insertion of polyglutamine residues into the CI2 loop at residue methionine 40, as in the experimental work (Ladurner and Fersht, 1997). A schematic for this mutational method is shown in Fig. 1. The rational for examining these mutants is to determine the preferred polyglutamine dihedral, 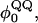and Lennard-Jones energetic parameters, ɛ_QQ, and to later use these parameters in the simulation of polyglutamine chains in the absence of the CI2 host protein.

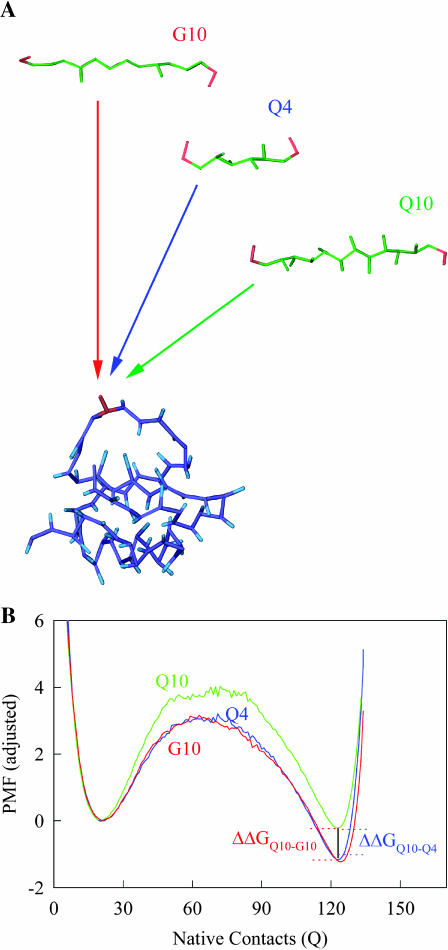
The present study focuses on three loop insertion mutants of CI2: 1), MG₃SG₄SG₃M (G10); 2), MGQ₄GM (Q4); and 3), MGQ₁₀GM (Q10). A schematic of these insert mutations is shown in Fig. 4 A. The Q4 and Q10 mutants were selected since, of the mutants studied, the length difference and therefore free-energy difference were the largest and most statistically significant (Ladurner and Fersht, 1997). The G10 insert mutant is simulated for reference as a random coil insert. Different polyglutamine dihedral parameters, 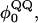and Lennard-Jones energetic parameters, ɛ_QQ, are imposed upon the polyglutamine guest inserts within the CI2 host Go-model, and the best match with experimental results is tentatively proposed as the “correct” polyglutamine computational model. Comparison of this model with experiments on the CI2-polyglutamine host-guest mutants is conducted in the present study. Comparison of this model with experiments on isolated polyglutamine chains will be the subject of future studies.

FIGURE 4.

Schematic of the computational host-guest method. (A) Guest inserts MG₃SG₄SG₃M (G10), MGQ₄GM(Q4), and MGQ₁₀GM (Q10) are inserted into the CI2 host at residue Met-40. (B) The free-energy difference between host-guest mutants CI2–Q10 and CI2–G10, ΔΔG_Q10–G10, and between CI2–Q10 and CI2–Q4, ΔΔG_Q10–Q4, is calculated directly from differences in PMF at Q = 120.

Thermodynamics

Using the simulation data, the free-energy difference between each pair of mutants, ΔΔG_Q4–G10, ΔΔG_Q10–G10, and ΔΔG_Q10–Q4, is calculated. In Fig. 4 B, a plot of PMF versus Q is calculated for each mutant at T_f = 333K and the PMF values linearly corrected so the unfolded ensemble (Q = 20) PMF is zero. The PMF of the native ensemble basin (Q = 120) used to determine ΔG_G10, ΔG_Q4, and ΔG_Q10 as indicated in Fig. 4 B. As shown in Fig. 4 B, free energies ΔG_G10, ΔG_Q4, and ΔG_Q10 are simply the PMF of the native ensemble basin at Q = 120 and free-energy differences are simply calculated by subtraction. For example,

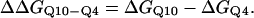(13)

It should be noted that, for the CI2-polyglutamine host-guest mutants shown in Fig. 4 B, the number of native contacts present in the native state (Q ∼120) is slightly less than the wild-type CI2 in Fig. 2 C (Q ∼125). Nonetheless, the structure of the transition state of the CI2-polyglutamine host-guest mutants is essentially the same as the wild-type CI2 transition state shown in Fig. 3 A (data not shown). Thus, as suggested from experiments (Ladurner and Fersht, 1997), the folding mechanism of CI2 host is relatively unchanged by insertion of polyglutamine guests.

To model the guest inserts in the CI2 host, it is important to consider the necessary parameters to modulate. For the CI2 host, the minimum energy bond lengths, angles, dihedrals, and pairwise contacts for the CI2 residues are parameters biased to the values obtained from the crystal structure 2CI2.pdb. For the inserted polyglutamine guest residues, bond length and angle parameters are assumed to be similar to the values observed in proteins (see Table 1); bond lengths are 3.81 Å for C_αC_α bonds, 3.45 Å for C_αC_β bonds, and all bond angles are set to 109.5°. Due to their large energy (ɛ_r, ɛ_θ) constraints, bond lengths and angles largely remain constant between folded and unfolded conformations of CI2 and therefore do not affect protein stability. However, protein stability does depend on dihedrals and Lennard-Jones contacts which will adopt non-native conformations at higher temperatures due to their small energy constraints (ɛ_φ, ɛ_LJ).

Initially, different dihedral parameters in the polyglutamine guest insert are examined. Dihedral angles are set to values biasing the insert to different secondary structures of random coil, α-helix, polyproline helix (PPII), and β-strand. A random coil dihedral is achieved by setting the dihedral energy within the loop insert at 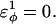For α-helix, polyproline II helix, and β-strand dihedrals, the dihedral energies are equal to the CI2 host dihedral energies (see Table 1). The atoms in the polyglycine insert G10 (MG₃SG₄SG₃M) are modeled with random coil dihedrals and hard-sphere repulsive interactions with all other atoms in the protein.

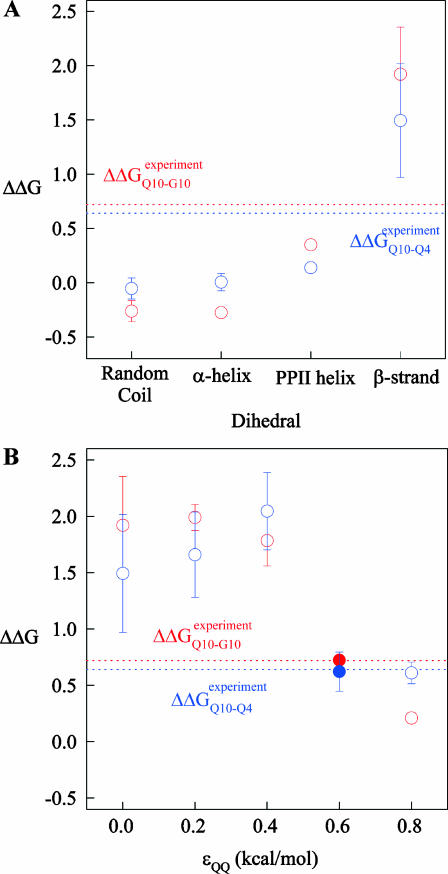
Fig. 5 A shows the values of ΔΔG_Q10–G10 and ΔΔG_Q10–Q4 for polyglutamine models with random coil, α-helix, PPII, and β-strand dihedral preferences. The ΔΔG_Q10–G10 value is the free-energy difference between the CI2 host with a random coil glycine insert and CI2 with a polyglutamine insert in a particular secondary structure. The value of ΔΔG_Q10–Q4 is the difference between two CI2 hosts, each with a different length of polyglutamine insert in a particular secondary structure. In Fig. 5 A, no polyglutamine insert dihedral parameter destabilizes the CI2 host exactly at the experimental values of ΔΔG_Q10–G10 = 0.72 kcal/mol and ΔΔG_Q10–Q4 = 0.64 kcal/mol. However, the β-strand parameters produce the only model resulting in destabilization larger than experimental values. The PPII parameters slightly destabilize ΔΔG_Q10–G10 but not ΔΔG_Q10–Q4. The random coil and α-helix models do not destabilize either ΔΔG_Q10–G10 or ΔΔG_Q10–Q4. In Fig. 5 A, error bars show standard deviations determined from six independent simulations, indicating that simulated ΔΔG_Q10–G10 and ΔΔG_Q10–Q4 are statistically significant measurements.

FIGURE 5.

Simulated free-energy differences match experimental host-guest free-energy differences when the polyglutamine guest favors a β-strand dihedral and ɛ_QQ = 0.6 kcal/mol. (A) The stability difference between CI2–G10 and CI2–Q10, ΔΔG_Q10–G10 (red open circle), and between CI2–Q4 and CI2–Q10, ΔΔG_Q10–Q4 (blue open circle), is shown for a random coil, α-helical, PPII strand, and β-strand dihedral preference in the polyglutamine guest. (B) The stability difference between CI2–G10 and CI2–Q10, ΔΔG_Q10–G10 (red open circle), and between CI2–Q4 and CI2–Q10, ΔΔG_Q10–Q4 (blue open circle), is shown for a β-strand dihedral + increasing values of the attractive contact energy between guest polyglutamine atoms, ɛ_QQ. The best match between simulation and experiment is shown for ΔΔG_Q10–G10 (red solid circle) and ΔΔG_Q10–Q4 (blue solid circle) when the dihedral is β-strand and ɛ_QQ = 0.6 kcal/mol. For comparison in A and B, the experimentally measured free-energy differences are shown between CI2–G10 and CI2–Q10, 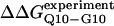(red dashed line), and between CI2–Q4 and CI2–Q10, 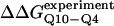(blue dashed line). Error bars on simulated values of ΔΔG_Q10–G10 (O) and ΔΔG_Q10–Q4 (O) shown in A and B are standard deviations calculated from six independent simulations.

β-strand parameters were assumed to be the most reasonable dihedral parameters for polyglutamine secondary structure, since β-strand polyglutamine is the only model which destabilizes the CI2 host sufficiently close to the experimental values ΔΔG_Q10–G10 and ΔΔG_Q10–Q4. However, the long-range attractive force, or Lennard-Jones energy, between polyglutamine atoms (ɛ_QQ) remained to be determined. With the dihedral parameters as β-strand, the stability of the CI2 host, ΔΔG_Q10–G10 and ΔΔG_Q10–Q4, was examined as ɛ_QQ is varied between 0 and 0.8 kcal/mol in Fig. 5 B. In Fig. 5 B, the value of ɛ_QQ which matches experimental values is ɛ_QQ = 0.6 kcal/mol. Values of ɛ_QQ <0.6 kcal/mol overestimate ΔΔG_Q10–G10 and ΔΔG_Q10–Q4 relative to the experimental values. The value ɛ_QQ = 0.8 kcal/mol fits the experimental value of ΔΔG_Q10–G10 but underestimates ΔΔG_Q10–Q4. Thus, the best parameters for polyglutamine are β-strand dihedral parameters combined with a Lennard-Jones energy ɛ_QQ = 0.6 kcal/mol. In Fig. 5 B, error bars show standard deviations determined from six independent simulations, indicating that simulated ΔΔG_Q10–G10 and ΔΔG_Q10–Q4 are statistically significant measurements.

Kinetics

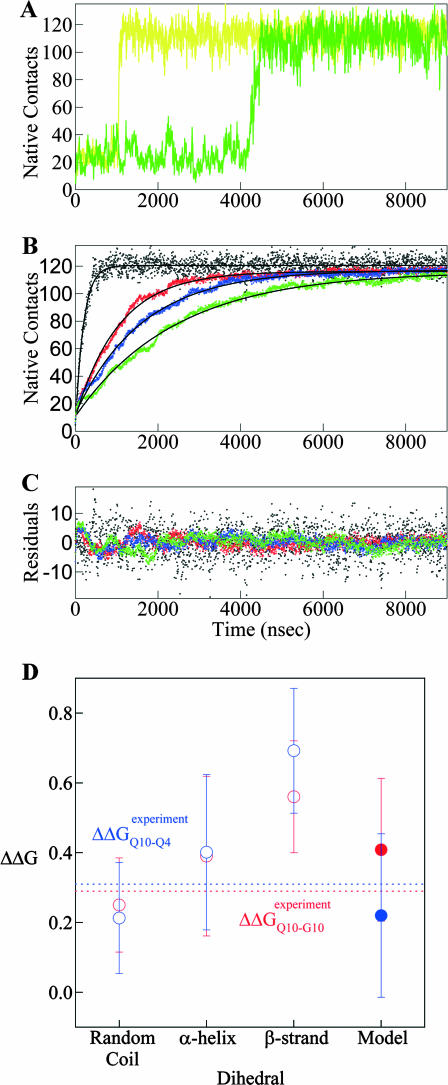
Having determined parameters which produce agreement between simulation and experimental thermodynamics, agreement is expected between simulation and experimental kinetic results with these parameters. Fig. 6 A shows two sample “Q versus time” trajectories for the CI2–10Q insert mutant, one indicating a fast refolding trajectory (yellow) and the second indicating a slower refolding trajectory (green). In agreement with experiments, the transitions from unfolded to native CI2 occur in a single discrete step and do not significantly populate kinetic intermediates (Jackson and Fersht, 1991; Ladurner and Fersht, 1997). Fig. 6 B shows “Q versus time” averaged over all 60 kinetic refolding trajectories for wild-type CI2 (black), the 10G insert mutant (red), the 4Q insert mutant (blue), and the 10Q insert mutant (green). For the 10G insert mutant, the insert dihedral is random coil and ɛ_QQ = 0. For the 4Q and 10Q insert mutants, the insert dihedral favors β-strand and ɛ_QQ = 0.6 kcal/mol. All trajectories in Fig. 6 B are shown to fit successfully with a single exponential equation, consistent with experiments (Jackson and Fersht, 1991; Ladurner and Fersht, 1997). This is also evident in Fig. 6 C, which shows that residuals of the fit are randomly dispersed for all trajectories. It should be noted that the average value of Q for the native state of the CI2-polyglutamine mutants in Fig. 6 B (Q ∼120) is slightly lower than that observed for wild-type CI2 in Fig. 2 A (Q ∼125). Nonetheless, the single exponential kinetic fits of both wild-type CI2 and all host-guest mutants in Fig. 6 B demonstrate that the basic folding mechanism remains unchanged.

FIGURE 6.

Simulated folding kinetics using the calibrated model parameters of a β-strand dihedral and ɛ_QQ = 0.6 kcal/mol agree with experiments. (A) Two representative kinetic “Q versus time” trajectories for the CI2–10Q insert mutant are shown for a fast refolding trajectory (yellow line) and a slower refolding trajectory (green line). (B) The average “Q versus time” for all 60 kinetic refolding trajectories for wild-type CI2 (black points), the random coil 10G insert mutant (red points), the model parameter 4Q insert mutant (blue points), and the model parameter 10Q insert mutant (green points). Lines through each trajectory show a single exponential fit of the data. (C) Residuals of the single exponential fit through each trajectory are randomly dispersed for wild-type CI2 (black points), the random coil 10G insert mutant (red points), the Model parameter 4Q insert mutant (blue points), and the Model parameter 10Q insert mutant (green points). (D) The transition state stability differences between CI2–G10 and CI2–Q10, ΔΔG_Q10–G10 (red open circle), and between CI2–Q4 and CI2–Q10, ΔΔG_Q10–Q4 (blue open circle), are shown when random coil, α-helical, and model (red solid circle/blue solid circle) parameters, and β-strand parameters are applied to the polyglutamine guest insert. For comparison, the experimentally measured transition state free-energy differences are shown between CI2–G10 and CI2–Q10, 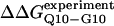(red dashed line), and between CI2–Q4 and CI2–Q10, 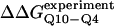(blue dashed line). Error bars on simulated values of ΔΔG_Q10–G10 (red open circle) and ΔΔG_Q10–Q4 (blue open circle) are standard deviations calculated from six independent simulations.

The free-energy difference between the unfolded and transition state ensemble, ΔΔG^TSsim, is calculated using Eq. 14,

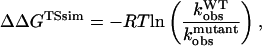(14)

where R = 0.002 kcal/(mol * K) and T = 300 K. Shown in Fig. 6 D is a comparison of 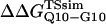and 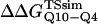with the experimental values of 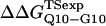and 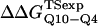(Ladurner and Fersht, 1997). In Fig. 6 D, the x-axis labels stating “random coil,” “α-helix,” and “β-strand” denote a guest insert model with dihedral parameters only (ɛ_QQ = 0 kcal/mol) whereas the x-axis label stating “Model” denotes β-strand dihedral parameters combined with ɛ_QQ = 0.6 kcal/mol. In Fig. 6 D, the random coil, α-helix, and Model parameters result in 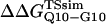and 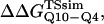which agree with experimental 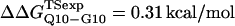and 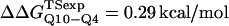within the simulation error. The β-strand parameters result in 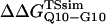and 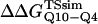significantly larger than experimental 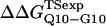and 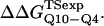In Fig. 6 D, error bars show the standard deviation of 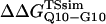and 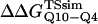as determined by six independent averages of 10 simulation traces.

Structural perturbation of CI2 host by polyglutamine guest inserts

In Fig. 5 A, β-strand dihedral parameters for guest insert polyglutamine residues destabilize the CI2 host when the insert is lengthened (ΔΔG_Q10–Q4 ∼ 1.5 kcal/mol). Also in Fig. 5 A, random coil parameters for guest insert polyglutamine residues do not destabilize the CI2 host when the insert length is increased (ΔΔG_Q10–Q4 ∼ 0). This fact suggests that the increase in chain entropy between a 4Q and 10Q guest insert is negligible (ΔΔS_Q10–Q4 ∼ 0). Thus, the free-folding energy differences from lengthening the β-strand guest insert (ΔΔG_Q10–Q4 ∼ 1.5 kcal/mol) result from changes in the host energy, not entropy, as the stiffness of the guest insert will compete with the native contacts of the CI2 host near the insertion site. This loss of native state energy of the CI2 host can be observed between Fig. 2 A, where native wild-type CI2 has Q ∼ 125, and Fig. 6 A, where the CI2–10Q host-guest mutant has Q ∼ 120. Thus, increasing the β-strand dihedral energy parameters 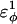for the guest insert polyglutamine should highlight structural perturbations in the CI2 host which account for the loss in CI2 free energy.

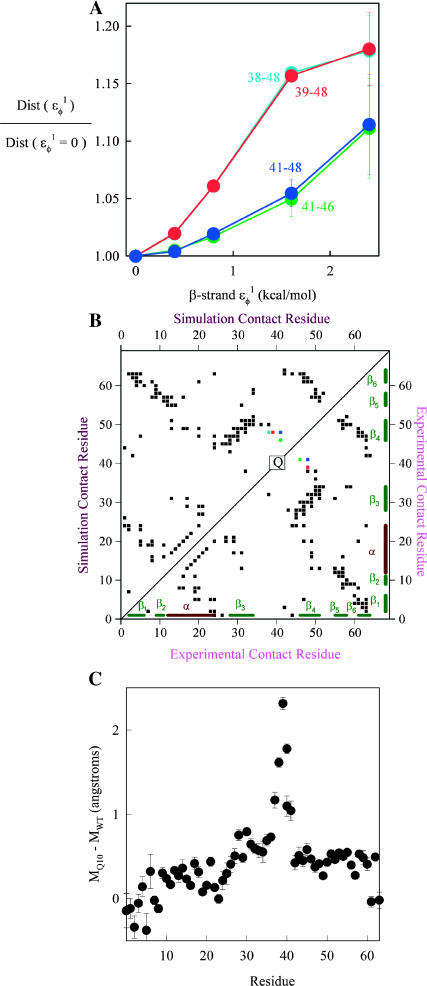
As 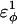is increased in the 10Q guest insert, 4 of the 134 native contacts in the CI2 host are perturbed in the native ensemble: 1), 38–48 spanning the insert; 2), 39–48 spanning the insert; 3), 41–48 C-terminal of the insert; and 4), 41–46 C-terminal of the insert. All other contacts do not show significant perturbation at increasing β-strand dihedral energies. Fig. 7 A shows, for each of these four contacts, the normalized contact distance, 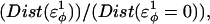increases as β-strand dihedral energy (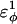) is increased. The increase in 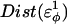accounts for the increase in CI2 host energy as 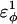is increased in the 10Q guest. It should be noted that the parameter 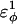refers to the first energy parameter of the C_αC_αC_αC_α dihedral in Eq. 4. The second dihedral energy parameter of the C_αC_αC_αC_α dihedral, 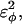scales at 0.5-times the C_αC_αC_αC_α value of 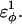The energies of the C_βC_αC_αC_β, C_βC_αC_αC_α, C_αC_αC_αC_β dihedral values of 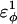scale at 0.25 the C_αC_αC_αC_α value of 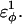In Fig. 7 A, error bars show the standard deviation of 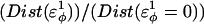as determined by six independent simulations.

FIGURE 7.

Native ensemble simulations (300 K) of the CI2-polyglutamine host-guest mutants, using the model parameters (β-strand dihedral and ɛ_QQ = 0.6 kcal/mol) for the polyglutamine guest, agree with experiments where insertion of the polyglutamine guest induces minor structural perturbations of the CI2 host located near the loop insert region. (A) A normalized plot of the distance increase 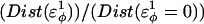in four CI2 host contacts involving residues 38–48 (light-blue solid circle), 39–48 (red solid circle), 41–46 (dark-blue solid circle), and 41–48 (green solid circle) as β-strand dihedral energy (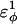) is increased in the polyglutamine guest region of the CI2–10Q host-guest mutant. (B) A contact map shows perturbed CI2 host contacts in the native ensemble between wild-type CI2 and the CI2–4Q host-guest mutant with Model parameters applied to the 4Q insert. Contacts perturbed >2 Å between wild-type CI2 and CI2–4Q in simulations are shown in color in the upper left corner, 38–48 (light-blue solid square), 39–48 (red solid square), 41–46 (dark-blue solid square), and 41–48 (green solid square), and unperturbed contacts (black solid square). Wild-type CI2 crystal structure (2CI2.pdb) contacts absent in the CI2–4Q insert mutant crystal structure (1CQ4.pdb) are shown in color in the lower right corner, 39–48 (red open circle), 41–46 (red open circle), and 41–48 (red open circle), whereas unperturbed contacts are black (red open circle). For reference, the 4Q insert region is indicated by “Q” on the diagonal, and secondary structure elements of CI2 are shown along the x and y axes: β₁, β₂, α, β₃, β₄, β₅, and β₆. (C) The mobility difference between each CI2 host C_α atom in the Model 10Q host-guest mutant versus the wild-type CI2, M_Q10–M_WT. Error bars shown in A and C are standard deviations calculated from six independent simulations.

In Fig. 7 B, native ensemble contact differences between simulated WT CI2 and CI2–4Q were compared to contact differences between the WT CI2 crystal structure (2CI2.pdb) and CI2–4Q crystal structure (1CQ4.pdb). For simulations, the upper left corner of Fig. 7 B shows CI2 contacts with >2 Å difference between native wild-type CI2 and native CI2–4Q mutant with the Model polyglutamine parameters for the guest insert (β-strand dihedral, ɛ_QQ = 0.6 kcal/mol), each at 333 K. The perturbed contacts measured from simulation are the same as those studied in Fig. 7 A: 1), 38–48; 2), 39–48; 3), 41–48; and 4), 41–46. For experiments, the lower right corner of Fig. 7 B shows wild-type CI2 crystal structure contacts absent in the 4Q insert mutant structure. Three of the four contacts perturbed in simulation are found disrupted between the two crystal structures: 1), 39–48; 2), 41–48; and 3), 41–46, whereas 38–48 is not shown to be disrupted. Nonetheless, good agreement exists between the simulation and experiment.

In Fig. 7 C, native ensemble residue mobility differences between simulated WT CI2 and CI2–10Q were compared to experimental residue mobility differences between WT CI2 and the CI2–10Q mutant. Short 300 K simulations (30 ns) were run to compare residue mobility between simulation and experiment in stable folded wild-type CI2 and the CI2–10Q insert mutant using model β-strand dihedral parameters + ɛ_QQ = 0.6 kcal/mol. Fig. 7 C shows the mobility difference, M_Q10–M_WT, between each WT CI2 C_α atom and the corresponding C_α atom in the CI2–10Q insert mutant, where the mobility of a C_α atom is calculated by Eq. 15:

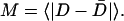(15)

In Eq. 15, D is the distance between the residue C_α atom and the protein center of mass at one simulation time step and 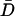is the average value of D over all simulation time steps. In Fig. 7 C, insertion of the 10Q polyglutamine guest increases mobility in the CI2 loop residues immediately proximal to the insert site. Error bars in Fig. 7 C show the standard deviation of M_Q10–M_WT as determined by six independent simulations.

Polyglutamine loop insert structure

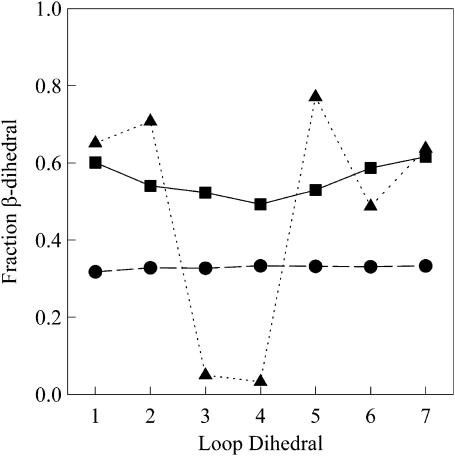
To determine the conformational preferences in the 10Q loop guest insert, consisting of the seven backbone dihedrals from Q₁Q₂Q₃Q₄ to Q₇Q₈Q₉Q₁₀, 30-ns simulations of wild-type CI2 and CI2–10Q were run at 300 K. Fig. 8 shows the probability of a β-strand dihedral conformation at each backbone dihedral in the 10Q insert for three different parameter assumptions for the 10Q guest insert: 1), random coil dihedral parameters + ɛ_QQ = 0 kcal/mol (circles); 2), model β-strand dihedral parameters + ɛ_QQ = 0.6 kcal/mol (squares); and (3), β-hairpin dihedral parameters + contact parameters derived from residues 44–53 of the protein GB1 crystal structure 2IGD.pdb (triangles) (Blanco et al., 1994). A backbone dihedral was determined to be β-strand if it falls within ±45° of the expected C_αC_αC_αC_α β-strand dihedral. Random coil parameters produce equal dihedrals throughout the insert near 0.3 probability. Model parameters produce dihedrals ∼0.6 probability, with a slightly lower probability (0.5) near the center of the guest insert. For comparison, β-hairpin parameters result in dihedrals characteristic of a β-hairpin—high β-strand dihedral probability (0.7) at the N-/C-termini and low β-dihedral probability (0.03) in the central turn region.

FIGURE 8.

Model polyglutamine parameters support an extended β-strand model of the 10Q polyglutamine guest in the CI2–10Q host-guest mutant. The probability of a β-strand dihedral conformation at each backbone dihedral in the 10Q insert of the CI2–10Q host-guest mutant are shown for three parameter assumptions in the polyglutamine guest: 1), random coil dihedral parameters + ɛ_QQ = 0 kcal/mol (•); 2), Model β-strand dihedral parameters + ɛ_QQ = 0.6 kcal/mol (▪); and 3), 2IGD.pdb (residues 44–53) β-hairpin dihedral + contact parameters (▴).

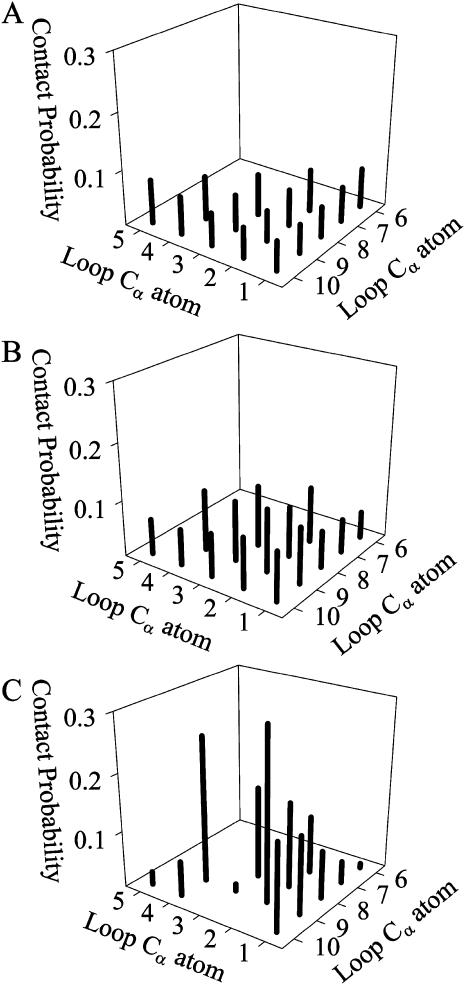
To measure contact probabilities, Fig. 9, A–C, show the C_α–C_α contact map for three different parameter assumptions for the 10Q guest insert in CI2–10Q: 1), random coil dihedral parameters + ɛ_QQ = 0 kcal/mol (Fig. 9 A); 2), model β-strand dihedral parameters + ɛ_QQ = 0.6 kcal/mol (Fig. 9 B); and 3), β-hairpin dihedral parameters + contact parameters derived from residues 44–53 of the protein GB1 crystal structure 2IGD.pdb (Blanco et al., 1994) (Fig. 9 C). A C_α–C_α pair is considered “in-contact” if within 6.1 Å, 1.3 × C_α–C_α distance in antiparallel β-sheets. In Fig. 9 A, random coil insert parameters produce contact probability between 0.05 and 0.08 for all C_α–C_α pairs in the 10Q insert, with slightly lower contact probabilities in the loop end contacts. In Fig. 9 B, model parameters produce contact probability between 0.05 and 0.10 for all C_α–C_α pairs in the 10Q insert, with slightly higher contact probabilities in the loop end contacts. Fig. 9 C shows the β-hairpin parameters produce contact probabilities characteristic of a β-hairpin. All nonhairpin contacts are <0.10 with the exception of 4–9 (probability 0.25). Expected hairpin contact probabilities are 3–8 (probability 0.16), 2–9 (probability 0.30), and 1–10 (probability 0.15).

FIGURE 9.

Model polyglutamine parameters support homogeneous contact probabilities between residues in the 10Q polyglutamine guest in the CI2–10Q host-guest mutant. Contact probabilities in the 10Q insert (C_α of any i, i + 5 residue pair within 6.1 Å) are shown for three parameter assumptions in the polyglutamine guest: (A) Random coil dihedral parameters + ɛ_QQ = 0 kcal/mol; (B) Model β-strand dihedral parameters + ɛ_QQ = 0.6 kcal/mol. (C) 2IGD.pdb (residues 44–53) β-hairpin dihedral + contact parameters.

DISCUSSION

Theory and simulation of amyloid peptides

Simulations of protein aggregation were initially studied using lattice models (Gupta et al., 1998; Istrail et al., 1999), which have also been used to model prion propagation (Dima and Thirumalai, 2002; Harrison et al., 1999, 2001). More recently, all-atom simulations have been used to study monomeric Aβ (Klimov and Thirumalai, 2003; Massi et al., 2001), aggregated polyalanine (Ma and Nussinov, 2002a), and aggregated Aβ (Klimov and Thirumalai, 2003; Ma and Nussinov, 2002b). In one study of aggregated Aβ_10–35, good qualitative agreement with experiments has been shown (Ma and Nussinov, 2002b), although it remains to be determined whether future all-atom studies will prove as successful. The present study is the first study of polyglutamine combining molecular dynamics with experimental constraints to 1), determine dihedral and contact parameters for a C_αC_β model of polyglutamine and 2), study the conformational thermodynamics of this polyglutamine model as an insert in CI2. This study is important in the continual development of a structural understanding of polyglutamine structure and a theoretical understanding of protein aggregation (Guo et al., 2002).

A number of computational studies have proposed different structural models of the polyglutamine monomer. The AGADIR algorithm suggests that polyglutamine is at least 95% random coil at all polyglutamine lengths (Munoz and Serrano, 1997). Molecular modeling studies have hypothesized that polyglutamine could be a β-hairpin (Perutz, 1996), a μ-helix (Monoi, 1995), or a β-helical nanotube (Perutz et al., 2002). Homology modeling predicts the polyglutamine region of ataxin-3 to be an α-helix (Albrecht et al., 2003). A Flory-Huggins mean-field lattice model predicts that polyglutamine increasingly prefers a β-hairpin state over an extended state as the polyglutamine length is increased (Starikov et al., 1999). Finally, all-atom energy minimization studies of polyglutamine with implicit solvation show that CHARMM parameters produce a β-hairpin structure whereas the AMBER parameters produce a random coil structure (Starikov et al., 1999). Given the large discrepancy between the polyglutamine structures hypothesized by these different studies, it is important to conduct simulations based on known experimental constraints, which is the purpose of the present study.

Unstructured guest peptides can be modeled within a Go-model host protein

In the original host-guest experiments, introduction of guest amino acids into large synthetic helical host polymers and the free-energy cost of forming helices with the inserted guest amino acids is calculated using helix-coil theory (Lotan et al., 1966; Wojcik et al., 1990). A modern version of the original host-guest study uses site-directed mutagenesis where the free energy of the insertion mutants can be used to infer the structure preferences of the inserted residues (Iwakura and Nakamura, 1998; Ladurner and Fersht, 1997; Nagi et al., 1999; Nagi and Regan, 1997; Tanaka et al., 2001; Viguera and Serrano, 1997). Unlike the original large polymer host systems, complete thermodynamics of protein hosts can be simulated in minimalist models (Cheung et al., 2003; Clementi et al., 2000b). In the present study, CI2 is the host protein and polyglutamine is the guest. However, wild-type CI2 protein folding simulations must agree with protein folding experiments before any host-guest studies.

Fig. 2, A–C, and Fig. 3, A and B, showed that the Go-model of CI2 captures the known experimental properties of CI2 (Itzhaki et al., 1995; Jackson and Fersht, 1991). Fig. 2, A–C, clearly showed that the folding of CI2 occurs in a two-state manner, with no population of folding intermediates. Fig. 3, A and B, shows that the dominant regions of CI2 structured in the folding transition state were the α-helix, β-strand 3, and β-strand 4, consistent with experiments (Itzhaki et al., 1995). As such, the CI2 Go-model was suitable for use as a host to accept guest peptides for which limited structural information exists. This study aims to directly compare the simulated CI2 thermodynamic stability change from inserting polyglutamine peptides into CI2 with the corresponding thermodynamic stability change measured from experimental CI2 loop insert mutants. Finding the polyglutamine energy parameters which match simulation and experimental values, in effect, calibrates these energy parameters for the polyglutamine model.

Fig. 5 A demonstrates that only an extended β-strand dihedral parameter results in ΔΔG destabilization comparable to the experimental values and is therefore the dihedral used to model polyglutamine. Other dihedrals do not produce destabilization consistent with the experimental values. With β-strand selected as the preferred polyglutamine dihedral, the remaining parameter to be tuned is the attractive contact energy, ɛ_QQ, between all nonlocal atoms in the polyglutamine chain. In Fig. 5 B, the β-strand dihedral combined with ɛ_QQ = 0.6 kcal/mol agrees best with experimental values, and these are designated the “Model” parameters for polyglutamine, shown in Table 1. Simulations of CI2 host-guest mutants using random coil, α-helical, and PPII helix polyglutamine insert dihedral parameters with varying values of ɛ_QQ never show ΔΔG destabilization comparable to the experimental values (data not shown).

Fig. 5, A and B, demonstrate that short polyglutamine guest inserts can destabilize the CI2-host without any Lennard-Jones interactions between the guest and the host residues, as has been proposed for longer polyglutamine inserts (Tanaka et al., 2001). Fig. 7 A shows that destabilization of the CI2 host correlates with the degree of forced extension, or persistence length, of the inserted guest residues. To characterize this inherent stiffness of the inserted peptide chains, the Flory characteristic ratio, C_n, is used,

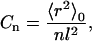(16)

where 〈r²〉₀ is the mean-square end-to-end distance of the polyglutamine guest insert, n is the number of segments (residues) of the insert, and l is the length of each segment (3.81 Å) (Flory, 1969; Krieger et al., 2003). Ideally, a range of guest lengths are simulated and the value of C_n increases with insert length n if residual stiffness exists in the chain. Eventually, an asymptotic value of C_n is reached above a certain length n (C_∞). Above this length, a stiff chain will act like a random coil chain except that the effective segment length is given by C_∞ and not l, as in a random coil chain (Flory, 1969).

Values of C_n were determined for the 4Q and 10Q inserts within the CI2 host, for each dihedral model of polyglutamine at 333 K. For the 4Q insert, C_4Q ∼ 2 for the random coil dihedral, the extended β-strand dihedral, the α-helix dihedral, the PPII helix dihedral, and the Model polyglutamine (β-strand dihedral, ɛ_QQ = 0.6 kcal/mol). For the 10Q insert, the values of C_n differed significantly depending on the dihedral model used. For the random coil dihedral, C_10Q ∼ 2, indicating that C_4Q ∼ C_10Q ∼ C_∞ ∼ 2, a value predicted for polyglycine (Miller et al., 1967). For the α-helix dihedral, C_10Q ∼ 2, also indicating that C_4Q ∼ C_10Q ∼ C_∞ ∼ 2. For the PPII helix dihedral, C_10Q ∼ 3, suggesting that C_∞ > 3 since C_10Q > C_4Q. For the β-strand dihedral, C_10Q ∼ 3.6, suggesting that C_∞ > 3.6 since C_10Q > C_4Q. For the model polyglutamine, C_10Q ∼ 3.2, suggesting that C_∞ > 3.2 since C_10Q > C_4Q, a value consistent with experimental measurements (Krieger et al., 2003). Thus, the characteristic ratio of polyglutamine C_∞ is found to correlate with ΔΔG_Q10–G10/ΔΔG_Q10–Q4 (Fig. 5, A and B) and the displacement of native contacts in the vicinity of the insert site (Fig. 7 A). A more extensive assessment of the characteristic ratio for longer lengths of polyglutamine will be the subject of future work.

An unusual secondary structure proposed for polyglutamine which was not explicitly simulated as a guest was the μ-helix (Monoi, 1995). In Figs. 5 A and 7 A, it is apparent that destabilization of the CI2 host correlates with the degree of forced end-to-end extension, or characteristic ratio, of the inserted residues. The μ-helix (φ = 81°, ψ = 98°) is considerably less extended than either the PPII helix (φ = −80°, ψ = 150°) or an extended β-strand (φ = −140°, ψ = 135°). Since the PPII helix dihedral did not successfully reproduce the experimental values of ΔΔG_Q10–G10 and ΔΔG_Q10–Q4, it is unlikely that a μ-helix dihedral in the polyglutamine guest would match ΔΔG_Q10–G10 and ΔΔG_Q10–Q4 in simulations as well.

Polyglutamine parameters calibrated with experimental CI2 thermodynamic values agree with experimental CI2 kinetic and structural results

In Fig. 6, A–C, the Go-model of CI2 demonstrates single exponential kinetic refolding behavior, consistent with experimental results (Jackson and Fersht, 1991; Ladurner and Fersht, 1997). Introducing polyglutamine inserts into the CI2 host slows the folding rate but does not alter single exponential refolding behavior (Ladurner and Fersht, 1997). Fig. 6 D shows that the model parameters produce kinetic ΔΔG values consistent with experimental values (Ladurner and Fersht, 1997). However, the relative error of simulated kinetics is higher than simulated thermodynamics and does not distinguish whether random coil, α-helix, or Model parameters best match the experimental results. The β-strand dihedral (ɛ_QQ = 0) produces kinetic ΔΔG values significantly higher than experimental values indicating that β-strand dihedral parameters alone should not be used to model polyglutamine.

In Fig. 5 A, polyglutamine β-strand dihedral parameters destabilize (ΔΔG_Q10–Q4 ∼ 1.5 kcal/mol) whereas polyglutamine random coil parameters do not destabilize (ΔΔG_Q10–Q4 ∼ 0.0 kcal/mol) the CI2 host when the polyglutamine guest insert length is increased. The small entropy change from lengthening the random coil guest insert (ΔΔS_Q10–Q4 ∼ 0) suggests that free-folding energy difference from lengthening the β-strand guest insert is due to changes in the energy, not entropy, of the CI2 host-guest system. Destabilization of the CI2 host results from “energetic frustration” between β-strand dihedral preferences in the polyglutamine guest insert competing with the attractive Go-contacts in the host. Since CI2 host energy is primarily determined from C_α–C_α and C_β–C_β contacts, it was useful to determine which disrupted CI2 host contacts account for the loss of CI2 host energy as the β-strand guest insert length is increased. As β-strand dihedral energy parameter, 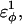was increased in the 10Q polyglutamine guest insert, the distance between each of the 134 CI2 host contact pairs in the folded CI2–10Q insert mutant was measured. Of the 134 contacts, four contacts around the guest insertion site (Met-40) increased in distance as guest polyglutamine insert β-strand dihedral energy strength 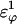was increased: 1), 38–48; 2), 39–48; 3), 41–48; and 4), 41–46. In Fig. 7 A, contacts bridging the loop insert, 38–48 and 39–48, are disrupted at low values of 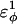whereas contacts at C-terminal to the loop insert, 41–48 and 41–46, are disrupted at higher values of 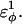These results highlight the local energetic frustration in this loop region of the CI2–10Q host-guest system, where β-strand dihedral preferences in the polyglutamine guest compete with native contacts in the CI2 host.

Evidence of this energetic frustration was observed experimentally in crystal structures of wild-type CI2 (2CI2.pdb) and CI2–4Q (1CQ4.pdb), which are similar except in the loop region where T39, M40, E41, and the loop insert are disordered. All contacts made by residues T39, M40, and E41 (39–48, 41–48, 41–46) are shown as colored contacts in the lower right corner of Fig. 7 B and indicate experimental disrupted contacts. Also, in upper right of Fig. 7 B are four contacts disrupted in simulations of native CI2–4Q with model polyglutamine parameters for the 4Q guest insert when compared to native wild-type CI2. Of these four disrupted contacts in simulations, three are found to be disrupted in the CI2–4Q crystal structure. One contact, 38–48, is not disrupted in the CI2–4Q crystal structure. Nonetheless, both simulation and experiment show that disrupted contacts immediately near the loop can account for CI2 host destabilization by polyglutamine guest insertion.

Evidence of energetic frustration near the loop insert region has also been observed in multidimensional NMR studies on CI2–10Q. {¹H}-¹⁵N NOE enhancement measurements show increased mobility near the loop insert is increased between wild-type CI2 and the CI2–10Q mutant in residues I37, V38, T39, M40, E41, and Y42 (Gordon-Smith et al., 2001; Shaw et al., 1995). For comparison, the mobility of each CI2 host residue is calculated from simulations of wild-type CI2 and CI2–10Q and the mobility difference between the two, M_Q10–M_WT, is compared with experimental {¹H}-¹⁵N NOE enhancements. In Fig. 7 C, residues with increased mobility difference between simulated CI2–10Q and wild-type CI2 are E37, V38, T39, M40, and E41. The residue Y42, showing a mobility difference between wild-type CI2 and CI2–10Q in experiments (Gordon-Smith et al., 2001; Shaw et al., 1995), is not found to increase in mobility from simulations. Nonetheless, simulations have captured the increased in mobility which occurs in residues near the loop insert. Thus, selecting polyglutamine guest parameters which match experimental free energies also produces an accurate structural model of the CI2-polyglutamine host-guest system.

Polyglutamine guest insert is an extended random coil

Experiments support a random coil model of monomeric polyglutamine. Experimental {¹H}-¹⁵N NOE enhancement studies on the CI2–10Q insert mutant show that the inserted guest glutamine residues are much more mobile than the host CI2 residues. This same NMR study shows that all polyglutamine insert residues have ¹H-¹⁵N and ¹⁵N chemical shifts consistent with random coil conformations. The crystal structure of the CI2–4Q insert mutant (1CQ4.pdb) shows that the inserted guest glutamine residues are highly disordered and lack electron density. Circular dichroism spectra of monomeric polyglutamine are consistent with random coil conformations (Altschuler et al., 1997; Bennett et al., 2002; Chen et al., 2002b; Masino et al., 2002). Although β-hairpin structures of polyglutamine have been proposed (Perutz, 1996; Sharma et al., 1999; Tanaka et al., 2001), convincing evidence for a monomeric polyglutamine β-hairpin has not been demonstrated yet.

This study shows that experimental results are best modeled when the dihedral parameters are β-strand and ɛ_QQ = 0.75ɛ_LJ. Such parameters might conceivably stabilize a β-hairpin at longer polyglutamine lengths if the contact energy (ɛ_QQ) from end residues in the β-strands of the hairpin compensates for the high energy dihedral conformations required to form the turn in the center of the peptide. To determine whether the model polyglutamine parameters produce random coil or β-hairpin configurations in the CI2-polyglutamine host-guest system, structural properties of the polyglutamine insert are compared to structural properties of 1), a random coil insert and 2), a β-hairpin insert.

The first structural property to compare is the backbone dihedral angles in the polyglutamine guest. Fig. 8 shows the fraction of insert conformations found in the β-strand conformation for each dihedral in the 10Q polyglutamine insert region using random coil parameters, model polyglutamine parameters, and β-hairpin parameters derived from GB1 2IGD.pdb (residues 44–53). The β-hairpin parameters produce high β-strand probability in the N- and C-terminal residues of the insert (0.7) and low β-strand probability in the central turn region (0.03), as expected for a β-hairpin. The random coil parameters produce a β-strand dihedral probability expected for a random coil at all dihedrals in the polyglutamine guest (0.30). The model parameters produce a high β-strand probability throughout the insert with a slightly higher β-strand probability in the N- and C-terminal residues (0.6) than the center residues (0.5). However, the β-strand probability difference between the terminal and central residues with the model parameters is only ∼10% of that observed in the β-hairpin. Based on dihedral probabilities, model polyglutamine does not resemble a β-hairpin conformation and resembles an extended version of the random coil model.

A second structural property to compare is the probability of each nonlocal C_α–C_α atomic contact between nonlocal loop insert residues. Fig. 9 A shows a nearly equal probability of all nonlocal contacts in the 10Q polyglutamine insert using random coil polyglutamine parameters. Fig. 9 B also shows nearly equal probability of all nonlocal contacts in the 10Q using model polyglutamine parameters. Fig. 9 C shows a highly heterogeneous distribution of nonlocal contacts using β-hairpin parameters. The probabilities of C_α–C_α atom contacts 3–8, 2–9, and 1–10, expected in a β-hairpin, are significantly higher than other nonhairpin contacts, with the exception of 4–9. Thus, the contact map produced by model parameters appears to resemble that of the random coil parameters, not the β-hairpin parameters. Together, the polyglutamine structural properties of dihedrals and contact probabilities indicate that the model polyglutamine parameters produce an extended β + random coil structural ensemble, consistent with observed random coil properties in experiments (Altschuler et al., 1997; Bennett et al., 2002; Chen et al., 2002b; Masino et al., 2002).

It is important to note that Model polyglutamine parameters that favor a β-strand dihedral do not preclude the transient formation of other secondary structures. For example, the PPII helix dihedrals are quite close to those of the β-strand and are occupied with a probability of 0.3 by model polyglutamine. Even the α-helix is sampled with a 0.1 probability in any given dihedral by model polyglutamine. Thus, the PPII helix and α-helix conformations may be sampled regularly in any given dihedral although it is highly unlikely that the entire 10Q polyglutamine guest will be a full PPII helix or α-helix.

Comparison with experiments

Although x-ray diffraction and solid-state NMR may prove useful in studying aggregated polyglutamine (Balbach et al., 2000; Perutz et al., 1994), these methods are not practical for studying the initial stages of polyglutamine aggregation. To determine if intramolecular folding steps precedes intermolecular aggregation steps, circular dichroism (CD) studies have probed the conformation of monomeric polyglutamine different constructs and conditions to determine if a partially folded monomeric intermediate can be detected (Altschuler et al., 1997; Bennett et al., 2002; Bevivino and Loll, 2001; Chen et al., 2002b; Masino et al., 2002, 2003; Perutz et al., 1994; Sharma et al., 1999; Stott et al., 1995; Tanaka et al., 2001). The CD spectra of polyglutamine, either as a peptide or a protein insert, is a characteristic random coil spectra in many studies (Altschuler et al., 1997; Bennett et al., 2002; Chen et al., 2002b; Masino et al., 2002). Some CD studies show a polyglutamine CD spectra consistent with a β-hairpin structure (Perutz et al., 1994; Sharma et al., 1999), although it is unclear whether these CD spectra are acquired on monomeric polyglutamine since these studies did not use a crucial polyglutamine disaggregation procedure (Chen and Wetzel, 2001). Subtracted CD spectra of polyglutamine in monomeric protein insert mutants indicate the possibility of both random coil and β-hairpin polyglutamine conformations (Bevivino and Loll, 2001; Masino et al., 2003; Stott et al., 1995; Tanaka et al., 2001). Although CD spectra are sensitive to conformational changes, structure determination from CD spectra is unreliable since CD spectra does not easily distinguish random coil with β-sheet in metastable β-hairpins (Blanco et al., 1994; Ramirez-Alvarado et al., 1996; Sieber and Moe, 1996). As a result, additional methods are required to study polyglutamine.

X-ray crystallography, NMR, and antibody binding experiments provide additional structural information on polyglutamine (Bennett et al., 2002; Chen et al., 1999; Gordon-Smith et al., 2001; Masino et al., 2002, 2003). The lack of electron density in the polyglutamine insert region of the CI2–4Q insert mutant is indicative of a random coil ensemble. The random coil model of polyglutamine is further supported by random coil chemical shifts and low NOE enhancements of the polyglutamine region in the CI2–10Q insert mutant (Gordon-Smith et al., 2001), polyglutamine-GST fusion protein (Masino et al., 2002), and ataxin-3 (Masino et al., 2003). Binding studies have shown that longer polyglutamine chains strongly bind polyglutamine-specific antibodies, whereas shorter polyglutamine chains are not observed to bind, suggesting a change in conformation to account for the increased affinity at longer lengths (Huang et al., 1998; Klement et al., 1998; Persichetti et al., 1999; Tanaka et al., 2001; Trottier et al., 1995). However, polyglutamine has been shown to bind more antibodies at increased lengths instead of a single antibody with higher affinity, reinforcing the random coil model for monomeric polyglutamine (Bennett et al., 2002). The consensus of these biophysical studies favors a random coil polyglutamine structure at all monomeric polyglutamine lengths and is in agreement with the results of the present study. As a contribution to these experimental studies, the present study offers a detailed description of individual polyglutamine conformations.

A second experimental host-guest study has been conducted using sperm whale myoglobin as a host and polyglutamine inserts between 12 and 50 residues as guests (Tanaka et al., 2001). Although this myoglobin-polyglutamine host-guest system does investigate longer lengths of polyglutamine, the CI2-polyglutamine host-guest system was selected for initial study with simulations, since it has been rigorously investigated with folding kinetics (Ladurner and Fersht, 1997) and structural studies (Chen et al., 1999; Gordon-Smith et al., 2001). Having determined a polyglutamine model in the present study which accurately characterizes the CI2-polyglutamine host-guest system, this model of polyglutamine will be studied in the myoglobin-polyglutamine host-guest system in future work. The authors of the myoglobin-polyglutamine host-guest system propose that the polyglutamine guest forms a β-hairpin which destabilizes the myoglobin host by inserting itself between myoglobin native contacts (Tanaka et al., 2001). Although this mechanism does not occur in the CI2-polyglutamine host-guest system in the present study with relatively short polyglutamine guests, it may well be observed with guests of longer polyglutamine lengths.

CONCLUSIONS

Peptides and proteins which are disordered under biologically relevant conditions present a challenge for structural modeling due to the lack of high-resolution structural information. To produce a realistic structural model of model of natively disordered polyglutamine peptides, a novel host-guest method is used which combines folding theory and protein folding experiments. Experimentally, the structurally ambiguous peptide of interest, polyglutamine, is inserted into a protein of known structure, CI2, and the resulting change in CI2 stability is measured at different polyglutamine insert lengths (Ladurner and Fersht, 1997). The same procedure is used in simulation, with the CI2 host modeled using a Go-model whereas the parameters of the polyglutamine insert are varied to best match the experimental stability changes. In the first step of the method, a minimalist molecular model (C_α–C_β) of CI2 is developed and shown to capture many of the folding properties of CI2 determined from experiments. In the second step, polyglutamine inserts are introduced into this CI2 model and the polyglutamine model selected which best agrees with the corresponding changes in experimental CI2 thermodynamic stability resulting from these same polyglutamine insert lengths. The polyglutamine model which best mimics experimental results has 1), an extended β-strand dihedral preference and 2), an attractive energy (ɛ_QQ) between polyglutamine atoms 0.75-times the attractive energy between the CI2 Go-contact energies (ɛ_LJ).

Having optimized the structural parameters of the polyglutamine model to match the thermodynamic stabilities of the different polyglutamine loop length guest inserts into the CI2 host, these Model polyglutamine parameters reproduce the relative kinetic rate differences between the CI2 loop host-guest mutants. Also, the increase in native-state flexibility and structural disruption in the CI2 host resulting from incorporating the polyglutamine guest inserts is limited to the immediate residues near the loop insert, in agreement with experimental results. Finally, the structure of the polyglutamine loop corresponds to an ensemble of extended random coil conformations, also in qualitative agreement with low resolution experimental methods. Having shown that these Model parameters correctly predict the properties of polyglutamine guests inserted into the CI2 protein host, these Model parameters will be used to simulate the guest polyglutamine chains in future studies in the absence of the CI2 host.

As a general principle, the study of natively disordered amyloid proteins should combine all available information to produce physically meaningful models of their structural ensembles. The rational design of polyglutamine aggregation inhibitors, which act through 1), competitive binding to an aggregation-competent conformation of polyglutamine or 2), noncompetitive binding (trapping) of polyglutamine in an aggregation-incompetent state, will be enhanced by accurate models of polyglutamine structure. The present study is a first step toward a complete structural characterization of monomeric and oligomeric polyglutamine, which will be conducted in subsequent work. It should be noted that it has not been rigorously demonstrated whether minimalist non-Go models are capable of capturing the correct physical properties of natively disordered proteins and protein aggregation. Nonetheless, the success of the present approach in capturing experimentally measured properties of CI2-polyglutamine host-guest mutants suggests that minimalist protein models will be a valuable tool in the structural modeling of other natively disordered peptides.