Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Sep;87(3):2086–2097. doi: 10.1529/biophysj.104.042960

Microscopic Kinetics of DNA Translocation through Synthetic Nanopores

Aleksij Aksimentiev 1, Jiunn B Heng 1, Gregory Timp 1, Klaus Schulten 1
PMCID: PMC1304610  PMID: 15345583

Abstract

We have previously demonstrated that a nanometer-diameter pore in a nanometer-thick metal-oxide-semiconductor-compatible membrane can be used as a molecular sensor for detecting DNA. The prospects for using this type of device for sequencing DNA are avidly being pursued. The key attribute of the sensor is the electric field-induced (voltage-driven) translocation of the DNA molecule in an electrolytic solution across the membrane through the nanopore. To complement ongoing experimental studies developing such pores and measuring signals in response to the presence of DNA, we conducted molecular dynamics simulations of DNA translocation through the nanopore. A typical simulated system included a patch of a silicon nitride membrane dividing water solution of potassium chloride into two compartments connected by the nanopore. External electrical fields induced capturing of the DNA molecules by the pore from the solution and subsequent translocation. Molecular dynamics simulations suggest that 20-basepair segments of double-stranded DNA can transit a nanopore of 2.2 × 2.6 nm2 cross section in a few microseconds at typical electrical fields. Hydrophobic interactions between DNA bases and the pore surface can slow down translocation of single-stranded DNA and might favor unzipping of double-stranded DNA inside the pore. DNA occluding the pore mouth blocks the electrolytic current through the pore; these current blockades were found to have the same magnitude as the blockade observed when DNA transits the pore. The feasibility of using molecular dynamics simulations to relate the level of the blocked ionic current to the sequence of DNA was investigated.

INTRODUCTION

Silicon nanotechnology makes it possible to manufacture electronic circuits with features comparable in size to the building blocks of life, i.e., proteins and DNA. A semiconductor device can be integrated around a nanometer-diameter pore in a thin (2–5 nm) synthetic membrane for electrical recordings while DNA molecules transit the pore. In principle, the sequence of a DNA strand can be discerned by such a device.

To relate the DNA sequence to the measured electrical signals it is essential to characterize DNA conformations inside the pore in atomic detail. Presently, sequences of DNA during pore translocation cannot be resolved experimentally yet, because A, C, G, and T DNA nucleotides differ from each other by only a few atoms. However, the entire translocation process can be investigated at atomic resolution through molecular dynamics (MD) simulations that can test the resolution of existing devices and guide development toward higher resolution. In such simulations, a molecular system is approximated by an ensemble of virtual atoms interacting with each other according to a molecular force field (Allen and Tildesley, 1987), which has been developed and calibrated to reproduce quantitatively physical properties of the simulated system. Here we report for the first time MD simulations of a nanopore device, linking an all-atom description of a DNA translocation through a pore to experimentally measured ionic currents induced along with the DNA translocation.

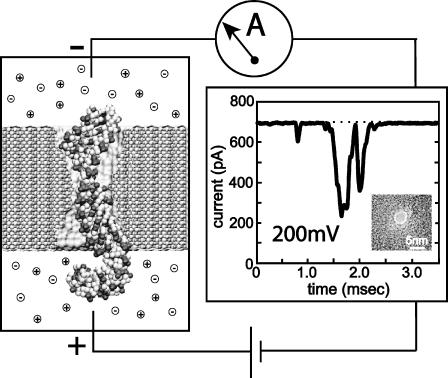
Fig. 1 illustrates schematically a system for measuring characteristic ionic currents for a pore that conducts DNA. A single nanopore separates two compartments filled with salt buffer and connected to Ag-AgCl electrodes. A constant voltage bias is applied between the two electrodes, inducing a steady-state ionic current through the pore, which is measured by the amplifier. Adding DNA to the negatively biased compartment is observed to cause transient reductions of the ionic current, like the one shown in Fig. 1. This reduced conductance is associated with the translocation of DNA through the pore, which partially blocks the ionic current.

FIGURE 1.

FIGURE 1

Open in a new tab

Experimental setup for measuring DNA electrical signatures. Driven by the electrical field between two electrodes, DNA transits a pore in a thin, synthetic membrane, inducing a transient blockade of the ionic current, measured by the amplifier. (Left) Snapshot of DNA transiting the pore. (Right) An exemplary ionic current signature registered by an Axopatch 200B amplifier, when 600-basepair double-stranded DNA transits the 2.4 ± 0.2-nm diameter pore in a 30-nm thick Si3N4 membrane (Heng et al., 2004). The inset shows a transmission electron micrograph of the pore sculptured by a highly focused electron beam (C. Ho, unpublished data).

Using a similar setup, Kasianowicz and co-workers (Kasianowicz et al., 1996) measured, for the first time, the blockage currents of single-stranded RNA and DNA electrophoretically driven through the transmembrane pore of an α-hemolysin channel (Song et al., 1996), which was suspended in a lipid bilayer. Statistical analysis of many blockage currents allowed the researchers to discriminate different sequences of RNA (Akenson et al., 1999), of DNA (Meller et al., 2000) homopolymers, and of segments of purine or pyrimidine nucleotides within a single RNA molecule (Akenson et al., 1999). Single nucleotide resolution has been demonstrated for individual Watson-Crick basepairs at the termini of single DNA hairpins (Vercoutere et al., 2001, 2003; Howorka et al., 2001), raising the prospect of creating a nanopore sensor capable of reading the nucleotide sequence directly from a DNA or RNA strand.

Recent advances in semiconductor nanotechnology allow one to manufacture pores with nanometer-size diameters using highly focused ion (Li et al., 2001) and electron (Heng et al., 2003, 2004; Storm et al., 2003) beams. These nanopores have been used as Coulter counter devices for detecting single DNA molecules (Li et al., 2001, 2003; Heng et al., 2004; Mara et al., 2004), resolving their length (Heng et al., 2003; Mara et al., 2004) and diameter (Heng et al., 2003, 2004). So-called ionic current blockades measured for synthetic nanopores differ from their α-hemolysin analogs. For synthetic nanopores observed blockades presently show irregular shapes (see Fig. 1) due to fluctuations of the reduced current within one blockade event; some blockades have a positive spike of the ionic current above the open pore level at the end of the blockade. The measurements also revealed a dependence of the duration τ of the current blockades on the applied voltage V, τ increasing with V (Heng et al., 2004).

To provide a theoretical account of the measurements, several models of nucleotide transport through nanopores have been proposed (reviewed by Meller, 2003). Describing DNA as an ideal polymer chain, one can compute the free-energy barrier for the DNA translocation caused by the pore restricting DNA conformations (Sung and Wu, 1996; Muthukumar, 1999), the average translocation time as a function of pore dimensions and length of DNA (Slonkina and Kolomeisky, 2003; Muthukumar, 2003), as well as the total polymer flux induced by the external electrical field (Ambjörnsson et al., 2002). Mathematical models describing diffusion of polymers through the pores have been deployed to investigate the origin of the measured non-Gaussian distributions of DNA passage times (Lubensky and Nelson, 1999; Matzler and Klafter, 2003). Transport of polymers through the pores has been studied also computationally in Monte Carlo (Muthukumar, 2001; Chern et al., 2001; Loebl et al., 2003) and Brownian dynamics (Chuang et al., 2001; Kong and Muthukumar, 2002) simulations, which examined the distribution of the polymer transit times and its scaling with polymer length. Due to the over-idealized description of DNA, nanopore, and electrolyte in both theoretical and computational studies so far, the microscopic kinetics of the DNA translocation could not be addressed. Moreover, the inability to connect to the microscopic structure of the pore and DNA prevents these approaches from relating the sequence of DNA to the electrical current signatures measured by the nanopore device.

Here, we investigate the kinetics of DNA transport through large-scale molecular dynamics simulations, accounting for atomic level detail in the system. We focus on DNA translocation through artificial pores in Si3N4 as these pores have become well characterized (C. Ho, unpublished data). To reproduce the experimental setup, we apply an electrical field to all atoms in the simulated system (water, DNA, ions, and Si3N4 membrane), inducing a capture and the subsequent translocation of DNA through the pore. Below we describe in detail how the electrical field drives single- and double-stranded DNA through the pore, causing partial unzipping of double-stranded DNA and hydrophobic adhesion of the nucleotide bases to the Si3N4 surface. We relate the microscopic conformation of DNA to the ionic current through the pore and estimate the minimum time required for the DNA transit. In conclusion, we discuss the implications of this study for analysis of ionic current signatures and design of the nanopore DNA sequencing device. In a subsequent article we will provide the same analysis for DNA transport through α-hemolysin.

METHODS

To simulate the DNA/nanopore system, we adapted the methodology of microscopic simulations developed for membrane proteins (Gullingsrud et al., 2001; Berneche and Roux, 2001; de Groot and Grubmüller, 2001; Beckstein et al., 2001; Hummer et al., 2001; Tajkhorshid et al., 2002; Pomès and Roux, 2002; Beckstein and Sansom, 2003; Lopez et al., 2004) and DNA (Beveridge and Ravishanker, 1994; Wong and Pettitt, 2001; Yeh and Hummer, 2004). A molecular force field describing water, ions, and nucleic acids (Cornell et al., 1995) was combined with the MSXX force field developed for silicon nitride (Wendel and Goddard, 1992).

Force field

To perform MD simulations on the system containing both DNA and Si3N4, the force field describing Si3N4 (Wendel and Goddard, 1992) was transcribed in terms of the potential functions used with the CHARMM27 force field (MacKerell et al., 1998). The Morse bond stretch potential between silicon and nitrogen was approximated by the harmonic potential; the parameters were transcribed by expanding the Morse potential around its minimum. The parameters describing the angular bonds between three atoms, the van der Waals interactions, and the charges of silicon and nitrogen in Si3N4 were taken from (Wendel and Goddard, 1992), which supposedly, but not necessarily, reflect the atomic arrangement in the amorphous Si3N4 membrane.

Other potential energy terms considered by Wendel and Goddard (1992) were not included in our force field, because the electrophoretic transport of ions and DNA through the pore is not expected to alter or deform the structure of the Si3N4 membrane significantly. Finally, the transcribed MSXX force field was combined with the AMBER95 force field describing DNA and with the CHARMM27 force field (MacKerell et al., 1998) describing TIP3 water as well as K+ and Cl− ions.

System setup

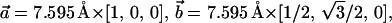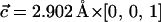A unit cell of the β-Si3N4 crystal was constructed according to the interatomic distances and bond angles resolved by x-ray crystallography (Grün, 1979). The unit cell was replicated in three dimensions along the unit cell vectors Inline graphic and Inline graphic to produce a hexagonal patch of Si3N4 membrane oriented perpendicular to the z axis. To accommodate pores of different diameters, two hexagonal patches of the same thickness (5.2 nm) were built with their sides equal to 30.38 Å and 45.57 Å.

Every two atoms in the Si3N4 membrane located <2 Å apart were assigned a covalent bond. The covalent bonds were also defined over the adjacent boundaries of the hexagon (but not in the z direction) to realize the hexagonal prism periodic boundary conditions.

To create a pore, the atoms satisfying one of the following geometrical conditions,

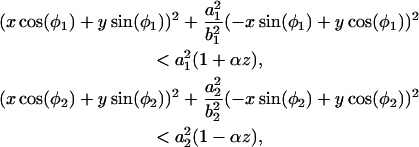graphic file with name M3.gif (1)

were removed from the membrane. The resulting pore has a shape of two intersecting cones, resembling the pores sculptured in silicon nitride by the high-energy electron beam (C. Ho, unpublished data; Heng et al., 2004) (see also Fig. 2). The elliptic intersections of the cones with the xy plane define the geometry of the pore through the two pairs of half axes a1, b1 and a2, b2, and two angles φ1 and φ2. The angle that the cones form with the z axis is controlled by the parameter α.

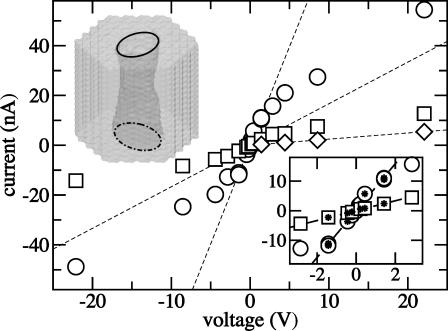
FIGURE 2.

FIGURE 2

Open in a new tab

Open pore ionic currents. Symbols indicate three geometrically different nanopores. Dashed lines interpolate the linear current-voltage dependences observed at small voltages. The inset shows ionic currents at small voltages; stars indicate the points used to draw the linear interpolation. The geometry of the pores is defined through Eq. 1 as: (circles) a1 = a2 = 14.4 nm, b1 = b2 = 12.2 nm, φ1 − φ2 = 0, α = 0.039; (squares) a1 = a2 = 1.0 nm, b1 = b2 = 0.7 nm, φ1 − φ2 = π/2, α = 0.02; (diamonds) a1 = a2 = 0.67 nm, b1 = b2 = 0.55 nm, φ1 − φ2 = π/6, α = 0.02. All pores were made in a 5.2-nm-thick Si3N4 membrane.

When a pore is created by the method described above, the total charge of Si3N4 becomes noninteger, along with the charges of silicon and nitrogen atoms. To perform MD simulation with full electrostatics, the total charge of the simulated system was adjusted to zero. This was done by tuning the charge assigned to all silicon atoms, ensuring an overall electrical neutrality of the Si3N4 membrane. For all pores considered, the adjustment made to the charge was <0.1% of its absolute value. We note, though, that the recent measurements of the concentration dependence of the ionic conductivity (C. Ho, unpublished data) suggest that the pores produced in Si3N4 may possess a fixed negative charge.

To disorder the crystalline structure of Si3N4, the temperature was increased to 6000 K in a 5-ps MD simulation by reassigning velocities of all atoms. The membrane was annealed at 6000 K for 60 ps followed by a rapid cooling to 310 K. This procedure reduced, but did not eliminate, the overall crystalline arrangement of the atoms because the melting of Si3N4 was suppressed by the harmonic potentials describing the covalent bonds between the atoms.

A straight double-stranded (ds) helix of 20 C-G pairs was built from individual basepairs in the geometry suggested by Quanta (Polygen, 1988). Single-stranded (ss) poly(dC)20 DNA was obtained from that structure by removing the G strand. The helix was oriented along the z axis, its center of mass was aligned with the geometrical center of the pore. Subsequently, the helix was placed in front of the pore such that the distance between the DNA end and the atomic plane of Si3N4 nearest to it was zero.

The Si3N4/DNA complex was then solvated in a volume of preequilibrated TIP3 water molecules. Potassium and chlorine ions were added, corresponding to a concentration of 1 M. The final system measured ∼165 Å in the z direction; the other dimensions were equal to the dimensions of the Si3N4 patch. Systems included from 38,000 to 85,000 atoms, depending on the size of the hexagonal patch used.

We performed 2000 steps of minimization followed by gradual heating from 0 to 310 K in 3 ps, equilibration for 5 ps with the DNA backbone atoms constrained, and equilibration for another 75 ps without any constraints in the NpT ensemble (i.e., with particle number N, pressure p, and temperature T fixed). After 75 ps, the system acquired a constant volume, and we continued the equilibration in the NVT ensemble (i.e., with particle number N, volume V, and temperature T fixed) for another ns, keeping the temperature constant at 310 K.

MD methods

All our MD simulations were performed using the program NAMD2 (Kalé et al., 1999), hexagonal prism boundary conditions, and particle mesh Ewald full electrostatics (Batcho et al., 2001). The temperature was kept at 310 K by applying Langevin forces (Brünger, 1992) to all heavy atoms; the Langevin damping constant was set to 0.2 ps−1. The integration time step chosen was 1 fs. The equilibration in the NpT ensemble was performed using the Nosé-Hoover Langevin piston pressure control (Martyna et al., 1994). Van der Waals energies were calculated using a smooth (10–12 Å) cutoff. To induce a translocation of DNA through the pore, a uniform electrical field was applied to all atoms in the system. To prevent the Si3N4 membrane from drifting, a 10-Å slab of atoms forming a belt around the pore was restrained by harmonic forces; the force constants were set to 10 kcal/(Å2mol).

Coordinates of all atoms were recorded every picosecond. The ionic current was computed as

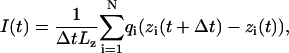graphic file with name M4.gif (2)

where zi and qi are the z coordinate and the charge of atom i, respectively; we chose Δt = 1 ps; Lz is the length of the simulated system in the z direction; the sum runs over all ions.

RESULTS AND DISCUSSION

The timescale covered by molecular dynamics simulations is currently limited to ∼100 ns. To accelerate events that normally could take milliseconds, like the permeation of a nanopore by a DNA segment, most of the MD simulations were performed at a higher applied voltage than 100–200 mV, applied typically in experiments. Because the silicon nanopores can withstand higher voltages than the α-hemolysin channel, direct comparison between experiments and simulations was possible.

Open pore ionic current

When a uniform electrical field is applied to all atoms of the simulated system, it induces, at the beginning of the simulation, a rearrangement of the ions that focuses the electrical field to the vicinity of the membrane, neutralizing the field in the bulk. The resulting voltage bias V across the simulated system depends both on the magnitude of the applied field E and the dimension LZ of the system in the direction of the field (Crozier et al., 2001), i.e., V = ELz; the electrostatic potential near the pore is not uniform.

To assess the level of ionic current through an open pore, MD simulations were performed first on a system without DNA. The applied electrical field was observed to induce displacements of Cl− and K+ ions, forcing them to move through the pore in opposite directions. The average total current was computed by plotting a cumulative sum of the instantaneous currents I(t) (Eq. 2) versus time and applying a linear regression fit to the last, linear (saturated) part of the curve, which was at least 1-ns long.

Fig. 2 illustrates the current-voltage relationship computed for three geometrically different pores. The narrowest part of the largest pore (circles) has 2.2 × 2.6 nm2 cross section. The cross section of the second pore (squares) is 1.3 × 1.5 nm2 (this pore is shown in Fig. 2), and the smallest pore (diamonds) is a cylinder of 0.9 × 1.1 nm2 cross section (the exact geometries are defined in the figure caption). The open pore current depends strongly on the diameter of the pore, decreasing rapidly as the pore diameter approaches the size of a hydrated ion. At small voltages (V < 1.4 V), the current increases linearly with the voltage for all three pores; the pore conductance in this regime was estimated to be 7.93 nS, 1.67 nS, and 0.25 nS for the pores of 2.2 × 2.6 nm2, 1.3 × 1.5 nm2, and 0.9 × 1.1 nm2 cross section, respectively. At higher voltages, the current becomes limited by the diffusion of ions into the capturing aperture of the pore and the linear current-voltage dependence breaks down. The crossover voltage depends on the pore geometry, and is higher for a smaller pore.

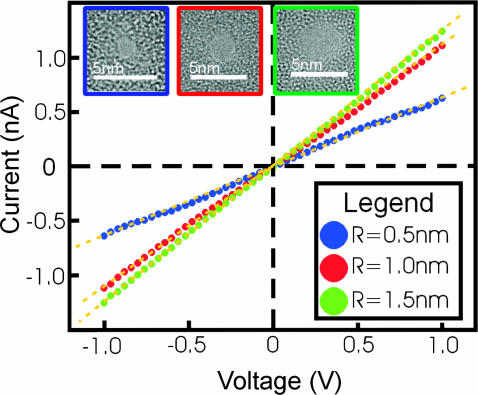
Fig. 3 on the other hand shows the experimental result of the current-voltage relationship for three Si3N4 pores. In the inset to Fig. 3 is shown the top-down transmission electron micrographs (TEM) of three pores with effective diameters of 2.90 ± 0.2 nm, 2.00 ± 0.2 nm, and 0.95 ± 0.2 nm, respectively, in Si3N4 membranes that we estimate to be 10 ± 2-nm thick (the effective diameter is taken from the geometric mean of the major and minor axes of the pore). The images represent a two-dimensional projection through the membrane; the shot noise observed in the area identified as the pore is indicative of perfect transmission of the electron beam through the membrane and reflects the minimum unobstructed diameter of the pore. We measured the ionic current through these nanopores by placing the membrane between two separate chambers each containing solutions of KCl in contact with a Ag-AgCl electrode. A constant voltage bias is applied between the electrodes and then a steady-state current is measured using an Axopatch 200B amplifier (Axon, Union City, CA) with a 10-kHz bandwidth. The figure shows the corresponding I-V characteristics measured at 23.5 ± 1°C in the range ±1 V in 1 M KCl electrolyte after >29h of immersion in deionized water. The current is approximately a linear function of the voltage over the range of actually applied voltages. The linear slope of a least-squares fit through the data (yellow dashed lines) yields a conductance of 1.23 ± 0.03 nS, 1.09 ± 0.03 nS, and 0.64 ± 0.03 nS through pores with an effective diameter of 2.9 nm, 2 nm, and 0.95 nm, respectively. In general, we do not find a simple relationship between the electrolytic conductance obtained from the slope and the nanopore geometry inferred from TEM. The discrepancies are attributed to: 1), a fixed (negative) volume charge in the pore (∼0.6 Faraday/dm3 for the pore of a 0.95-nm diameter shown in the inset of Fig. 3); and 2), a reduced ion mobility in the pore from the bulk due to size effects (C. Ho, unpublished data).

FIGURE 3.

FIGURE 3

Open in a new tab

Experimental measurements show the corresponding current-voltage characteristics measured at 23.5 ± 1°C in the range ±1 V in 1 M KCl electrolyte after >29 h of immersion in deionized water. The linear slope of a least-squares fit (yellow dashed lines) through the data yields a conductance of 0.64 ± 0.03 nS, 1.09 ± 0.03 nS, and 1.23 ± 0.03 nS for pores with an effective diameter of 0.95 nm, 2 nm, and 2.9 nm, respectively. The insets are top-down transmission electron micrographs of three pores with effective diameters of 0.95 ± 0.2 nm, 2.0 ± 0.2 nm, and 2.9 ± 0.2 nm in Si3N4 membranes that we estimate to be 10 ± 2-nm thick.

The simulation and measurement data presented in Figs. 2 and 3, respectively, are in good agreement with each other. Simulated and measured current-voltage relationships are both linear up to applied voltages of 1 V; the values of the ionic conductance are found to be in the same range. A direct quantitative comparison between experiments and simulations, however, cannot be made, because the charge distribution at the pore surface and the exact shape of the pores are not experimentally known; also, the experimental and simulated silicon nitride membranes had different thickness. Once the pore geometry and the charge distribution are well characterized, one can expect a close agreement between experiment and simulations, as it was demonstrated for ion- and water-conducting membrane proteins (Berneche and Roux, 2001; de Groot and Grubmüller, 2001; Tajkhorshid et al., 2002; Zhu et al., 2002) and electrophoretic transport of RNA (Yeh and Hummer, 2004).

Electrophoresis of DNA by strong electrical fields

The linear current-voltage characteristic of the nanopore and the high breakdown field of the membrane dielectric indicate that large electric fields can be employed to either induce a faster DNA translocation by increasing the longitudinal field along the axis of the pore, or to retard translocation by increasing the transverse field perpendicular to the pore axis (Chen and Coalson, 2003). To investigate what consequences a high electrical field along the pore axis would have on the kinetics of DNA transport through the pore, we performed simulations applying voltage biases in a range much higher than the ones routinely used in experiments (although there is some overlap between the lowest field simulated and the highest fields measured, as shown below).

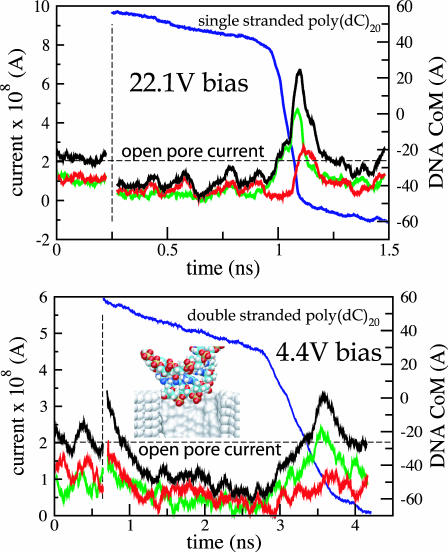
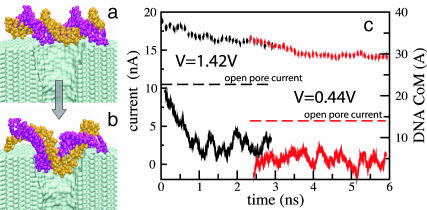
Fig. 4 (top) illustrates translocation of a short segment of single-stranded DNA through the pore of 1.3 × 1.5 nm2 cross section (shown in Fig. 2). The left vertical axis of this figure indicates the ionic current through the pore, whereas the right vertical axis indicates the z coordinate of the DNA center of mass (CoM) relative to the center of the Si3N4 membrane. The first part of the figure (time < 0.25 ns) corresponds to a simulation, in which DNA does not block the ionic current. The figure compares the total ionic current, with separate currents of Cl− and K+ ions. When DNA is placed in front of the pore (vertical dashed line in Fig. 4 (top)), it is rapidly captured by the pore. Driven by a very strong, 22.1-V bias, DNA transits the pore in ∼1 ns, as shown in Fig. 4 (top). The presence of DNA in the pore reduces on average the level of ionic current by 60%. When DNA rapidly exits the pore, the clouds of Cl− and K+ ions that were accumulating near the pore's mouths are released, resulting in a transient increase of the total ionic current above the open pore level.

FIGURE 4.

FIGURE 4

Open in a new tab

Electrophoresis of DNA through nanopores. Green, red, and black lines indicate Cl−, K+, and total ionic currents, respectively, which are shown at the left vertical axes. Blue lines represent the position of the DNA center of mass relative to the center of the Si3N4 membrane, which is shown at the right vertical axes. Vertical dashed lines mark the moment when DNA is placed in front of the pore (see Methods); horizontal dashed lines indicate the open pore currents. (Top) Electrophoresis of single-stranded DNA through a 1.3 × 1.5 nm2 pore. (Bottom) Electrophoresis of double-stranded DNA through a 2.2 × 2.6 nm2 pore. The exact geometry of both pores is defined in the caption to Fig. 2. Rapid translocation of DNA is facilitated by its stretching. The transient increase of the ionic current above the open pore level results from clouds of Cl− and K+ ions that are released when DNA exits the pore rapidly. The inset shows a typical DNA conformation at the moment when DNA enters the pore.

Translocation of double-stranded DNA through a bigger, 2.2 × 2.6 nm2, pore is illustrated in Fig. 4 (bottom). Driven by a strong, 4.4-V bias, the double-stranded DNA transits the pore in 3.5 ns. At the end of the translocation the DNA molecule partially unzips.

Electrophoresis of single- and double-stranded DNA exhibits qualitatively similar kinetics (c.f. Fig. 4 (top and bottom)), because, in both cases, the cross section of the pore matches the diameter of the DNA moving through it. At the beginning of the simulation, the end of DNA nearest to the Si3N4 membrane is captured by the pore, reducing the ionic current. Moving down the pore, DNA stretches under the influence of the focused electrical field (see, for example, Fig. 1). This stretching decreases the effective diameter of DNA, triggering its rapid exit from the pore, accompanied by a transient increase of the total ionic current above the open pore level. The supplied movies (see Supplementary Material) and at http://www.ks.uiuc.edu/research/nanopore/movies/ illustrate translocation of both single- and double-stranded DNA.

Slow electrophoresis of double-stranded DNA

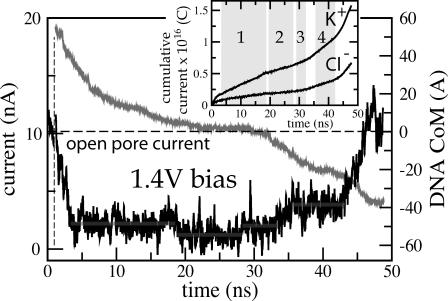
Due to the timescale limitations of our microscopic simulations, 1.4 V is the smallest voltage bias, at which we observed a full translocation of DNA from one side of the membrane to the other. Fig. 5 shows the level of the total ionic current during the translocation (left vertical axis), and together with the location of the DNA CoM (right vertical axis). Snapshots of the DNA conformations are shown in Fig. 6.

FIGURE 5.

FIGURE 5

Open in a new tab

Slow electrophoresis of double-stranded DNA. The black line indicates the total ionic current (left axis); the gray line depicts the position of the DNA center of mass relative to the center of the Si3N4 membrane. The inset shows a cumulative current of Cl− and K+ ions. The highlighted regions correspond to the four plateaus in the ionic current signature (see text). The cross section of the narrowest part of the pore is 2.2 × 2.6 nm2. Snapshots from this simulation are shown in Fig. 6.

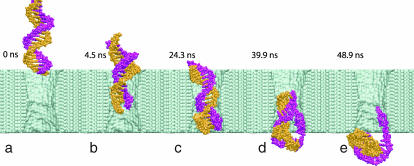
FIGURE 6.

FIGURE 6

Open in a new tab

Snapshots of DNA conformations during slow electrophoresis. (a) Beginning of the simulation. (b) The moment when the terminal Watson-Crick basepair splits at the narrowest part of the pore. (c) A moment during the time interval of 8 ns that DNA spends in the conformation shown without moving. (d) The moment when DNA exits the pore while one base at the DNA end remains firmly attached to the surface of the nanopore. (e) End of the simulation, when most of the DNA has left the pore and the ionic current has returned to the open pore level. Fig 5 illustrates the ionic currents and defines conditions of this simulation.

At the beginning of the simulation, double-stranded poly(dC)20·poly(dG)20 is placed in front of the 2.2 × 2.6 nm2 pore, as shown in Fig. 6 a. Within the first 2 ns, the end of DNA nearest to the pore is pulled into the pore by its charged backbone, forming a “sail”, like the one shown in Fig. 4 (bottom). The rest of the molecule follows that end, which, after 4 ns, encounters the narrowest part of the pore. At this point, the terminal Watson-Crick basepair splits, and the freed nucleotides adhere with their bases to the surface of the pore, as shown in Fig. 6 b. The translocation proceeds further until it halts after 20 ns in the conformation similar to the one shown in Fig. 6 c. At this point, the three Watson-Crick basepairs that were first to enter the pore are split; one of the terminal bases continues to adhere strongly to the pore surface. The system is driven out of this metastable conformation by increasing the voltage bias from 1.4 to 4.4 V for 0.3 ns (approximately after 30 ns from the beginning of the simulation). Subsequently, the simulation was continued at a 1.4-V bias. DNA slowly exits the pore, while one of the bases holds firmly to the surface of the pore (Fig. 6 d). After ∼50 ns, most of the DNA has left the pore, but a few bases remain attached to the pore surface (Fig. 6 e); nine of 20 basepairs are split. This simulation is illustrated by the supplied movies (see Supplementary Material) and at http://www.ks.uiuc.edu/research/nanopore/movies/.

According to the MD simulations, the level of the total ionic current measured during the translocation event appears to be correlated with the DNA velocity inside the pore: the faster DNA moves, the less it blocks the ionic current. In Fig. 5, we highlighted four plateaus in the ionic current trace. The first plateau (3.5–18 ns) reflects a gradual entry of DNA into the pore; 80% of the current is blocked. When DNA translocation halts, one observes a second plateau (19.5–28 ns), characterized by the highest, 88%, reduction of the total ionic current. A third plateau (28.3–32.9 ns, 82% current reduction) develops when DNA resumes its translocation, and the last plateau (35.5–42.9 ns, 64% current reduction) reflects a gradual exit of DNA from the pore. Note, that although some DNA remains inside the pore at the end of the simulation (Fig. 6 e), the current returns to the open pore level. The ionic current signature has a positive spike above the open pore level, which develops when the last basepairs exit the pore. Similar spikes at the end of current blockades have been observed experimentally with Si3N4 nanopores (Heng et al., 2004). However, the interpretation of the observed spikes is complicated by the frequency response of the membrane-pore system due to the measurement apparatus.

The cumulative currents of Cl− and K+ ions are plotted in the inset of Fig. 5. On average, the current of K+ ions through the pore blocked by DNA is twice as high as that due to Cl− ions. Such selectivity is introduced by the negative charge of DNA, as the simulated pore itself exhibits no selectivity to K+ ions over Cl−. On the other hand, the actual pores in Si3N4 may be ion-selective due to a fixed charge in the pore (C. Ho, unpublished data). If that fixed charge is negative as indicated by Ho et al., then the K+ to Cl− selectivity would be even higher. During our 50-ns simulation, ∼1500 ions have moved through the pore from one side of the membrane to the other.

DNA-nanopore interaction

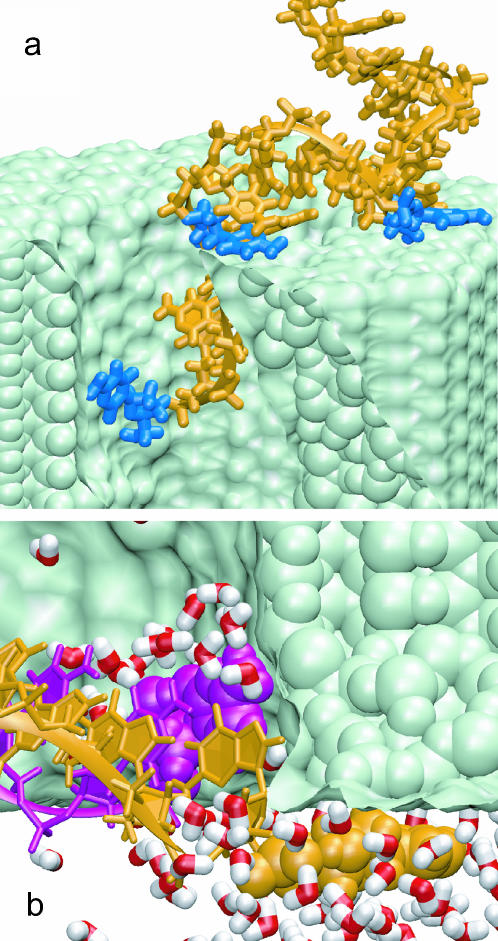
A strong interaction between DNA nucleotides and the surface of the Si3N4 pore was observed in all simulations conducted at moderate and small applied voltages (V ≤ 4.4 V). For example, driven by a 4.4-V bias, single-stranded DNA moved 15 Å down the 1.3 × 1.5 nm2 pore in 3 ns, but could not transit any further within the next 5 ns because several nucleotides adhered to the surface of Si3N4. Fig. 7 a illustrates the conformation of DNA at the end of this simulation; three bases interacting with Si3N4 are highlighted in mauve: one inside the pore, and two at the surface of the Si3N4 membrane. Visual inspection with the program VMD (Humphrey et al., 1996) revealed a very tight contact between the three bases and the surface of the pore, the contact apparently excluding water. To test the hydrophobic nature of the adhesion, we set the charges of all silicon and nitrogen atoms comprising Si3N4 to zero and resumed the simulation for 1 ns. The bases first slid by several Ångströms along the Si3N4 surface (reacting to the change of the electrostatic field), but continued to hold firmly to the surface, halting the DNA translocation as efficiently as before. Thus, we concluded that the adhesion of the DNA bases is not induced by the charge of the Si3N4 surface, but rather seems to be due to a purely entropic, hydrophobic effect.

FIGURE 7.

FIGURE 7

Open in a new tab

DNA-nanopore interaction. (a) Single-stranded poly(dC)20 adheres with three nucleotide bases to the Si3N4 surface; the interacting bases are shown in mauve. (b) The terminal Watson-Crick basepair of double-stranded poly(dC)20·poly(dG)20 splits spontaneously inside the pore; the freed bases adhere to the Si3N4 surface. Two strands of DNA are shown in different colors; the bases interacting hydrophobically with the Si3N4 surface are shown in vdW representation; only water molecules within 5 Å of the terminal nucleotides are shown explicitly. Water molecules are found to be excluded from the sites where DNA bases adhere to the nanopore wall.

In the case of double-stranded DNA, adhesion of DNA bases to the Si3N4 surface and an applied electrical field can cause unzipping of the terminal Watson-Crick basepair. We observed two types of such events. First, a terminal basepair unzipped when it reached the narrowest part of the pore, like in the 50-ns simulation performed at 1.4-V bias (see Figs. 5 and 6). The unzipping of this basepair did not occur within 5 ns when we restarted the simulation at a smaller, 0.44-V bias from the moment right before the unzipping, although the DNA translocation halted. After the rupture, one of the bases moved down the pore by several Ångströms, lowering its electrostatic energy by Vlz/L, where lz is the distance traveled along the electrostatic field and L is the membrane thickness. For lz = 5 Å, a 1-V bias across a 5.2-nm membrane creates an electrical field sufficient to rupture two hydrogen bonds and, thereby, can initiate DNA unzipping. Adhesion of DNA bases to the pore surface prevents restoration of the double helical structure after DNA has passed the narrowest part of the pore. Although this type of unzipping was not observed at 0.44-V or smaller biases, we cannot rule out the possibility of DNA unzipping at such fields on timescales longer than 10 ns.

We also observed “spontaneous” unzipping of the terminal basepair when DNA, which had been threaded through the pore by a 4.4-V bias (all basepairs remained intact) and equilibrated for 1.5 ns to release the strain introduced by the threading, was subject to a very small field (140 mV) for an extended period of time, namely 26 ns. The unzipping occurred after DNA spent 9 ns inside the pore, and was followed by adhesion of the terminal bases to the surface of the pore, as shown in Fig. 7 b (see also Fig. 9). A movie (see Supplementary Material) illustrates this simulation and can be also found at http://www.ks.uiuc.edu/research/nanopore/movies/. In this case, a terminal basepair was cleaved at the edge of the pore by strong hydrophobic interactions between the bases and the pore surface.

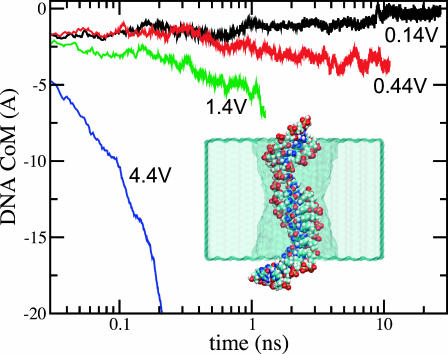
FIGURE 9.

FIGURE 9

Open in a new tab

DNA electrophoresis at different voltage biases. Four simulations were conducted starting from the conformation shown in the inset. The lines indicate the location of the DNA center of mass. At 1.4-V bias, spontaneous unzipping of the terminal basepair (at 9 ns) shifts the DNA CoM by 1 Å up.

Blocking current without translocation

As the electrical field in the bulk of the electrolyte is zero, one can assume that DNA approaches the pore by diffusion, and, hence, the conformation in which DNA collides with the pore for the first time is random. The starting configuration in which DNA is placed in front of the pore normal to the surface of the Si3N4 membrane shown in Fig. 6 a might not be representative.

We simulated electrophoresis of DNA and ions starting from the conformation shown in Fig. 8 a, in which a double poly(dC)20·poly(dG)20 strand is placed parallel to the surface of the Si3N4 membrane (12 Å away from the membrane). By applying a 1.4-V bias, DNA was pulled inside the pore in a 2.5-ns simulation, as illustrated in Fig. 8, b and c. Although the DNA molecule cannot be driven through the pore in the conformation shown in Fig. 8 b, its presence above the pore blocks the ionic current by 75%, which is comparable to the level of the current blockade induced by DNA transiting the pore (compare Fig. 8 c to Fig. 5). After 2.5 ns, we reduced the applied bias to 0.44 V. The double strand continued to deform, rotating by ∼30° around the z axis (normal to the Si3N4 surface). The average reduction of the ionic current approached 85%, which makes it practically indistinguishable from the current reduction induced by the DNA actually translocating through the pore. Both simulations are illustrated by the supplied movies (see Supplementary Material) and at http://www.ks.uiuc.edu/research/nanopore/movies/.

FIGURE 8.

FIGURE 8

Open in a new tab

Blocking current without translocation. (a) Double-stranded poly(dC)20·poly(dG)20 is placed in front of the pore. (b) Driven by a 1.4-V bias, DNA enters the pore blocking the ionic current. (c) The ionic current (solid line) and the DNA center of mass (dashed line) as a function of time. Black and red traces correspond to the applied biases of 1.4 V and 0.44 V. Although the DNA molecule cannot transit the pore, the blockage induced is comparable to that when DNA transits the pore (c.f. Fig. 5). The pore has the same dimensions as in Fig. 5.

Observed deformations in the DNA structure as seen in Fig. 8 are consistent with known elastic properties of DNA. To demonstrate this consistency we assume that a DNA strand undergoes a conformational change from a straight rod into a semicircle of radius R = 12 Å. The elastic energy required for such a deformation is

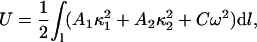graphic file with name M5.gif (3)

where A1, A2, and C are the bending and twisting rigidities, κ1 and κ2 are the principal curvatures, and w is the local twist (Balaeff et al., 2004). Neglecting DNA anisotropy and twist contributions to the elastic energy, one can estimate the energy required for the conformational change in question to be 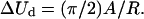Inline graphic Assuming A = kBTlp, where kB is the Boltzmann constant, T the absolute temperature, and lp the persistence length of DNA (∼50 nm), one estimates the value ΔUd ≈ 65 kBT.

While deforming, DNA is pulled inside the pore by a fraction f of the membrane thickness. Assuming that the electrical field is zero in the bulk and varies linearly across the membrane, the DNA strand acquires a change in electrostatic energy during the deformation measuring ΔUE = fVQ, where Q is the total charge of the DNA fragment that is exposed to the electrical field. For f = 0.2, V = 0.44 V, and Q = 16, one obtains, accordingly, ΔUE ≈ 70 kBT. The electrostatic energy of the DNA strand monitored in our simulation was found to be lowered by about ΔUS ≈ 100 kBT during the transformation shown in Fig. 8. Because the energy ΔUd required to deform DNA is close to the energies ΔUE and ΔUS, we conclude that the electrical bias can indeed deform DNA as seen in Fig. 8.

Single-stranded DNA is more flexible than double-stranded DNA, and can be expected to transit wide pores starting from the conformations similar to the one shown in Fig. 8 a. The DNA strand would bend first, as shown in Fig. 8 b, and then move down the pore blocking the current. When one of the DNA ends exits the pore, the current reduction decreases by a factor of two. Ionic current signatures of this kind have been observed experimentally (Li et al., 2003; Mara et al., 2004), although the reduction levels of the ionic current (10–20% reported by Li et al.) suggest that the pores used were significantly wider than the DNA strand.

Translocation times

To assess a typical translocation time of a long, double-stranded DNA through a 2.2 × 2.6 nm2 pore at small voltage biases, we set up the following simulation. A double poly(dC)20·poly(dG)20 strand was pulled by a 4.4-V bias halfway through the pore, such that the two DNA ends were found at different sides of the Si3N4 membrane, as shown in Fig. 9. An artificial harmonic bond, applied to the nucleotides forming the terminal basepair, prevented DNA from unzipping. By inducing DNA displacement by several angstroms, we could mimic translocation of a fairly long segment of DNA, assuming that the friction between DNA and the pore is the dominant factor determining the timescale of the translocation.

After DNA had been pulled halfway through the pore, the external forces were switched off for ∼1.5 ns. Within this time interval, the strain introduced into the DNA conformation by pulling subsided and the end-to-end distance of the DNA strand returned to its equilibrium value of 6.6 ± 0.2 with all Watson-Crick basepairs remained intact. The DNA molecule was then subject to four different electrical fields equivalent to 4.4-, 1.4-, 0.44-, and 0.14-V biases. Fig. 9 illustrates the resulting displacements of the DNA center of mass versus time (logarithmic scale).

The DNA center of mass moved by 20, 5.5, 2, and −1.0 Å in 0.2, 1.3, 11, and 26 ns, for the four bias values above.

The negative displacement in case of the 0.14-V bias is due to a spontaneous unzipping of the DNA terminal basepair, which was not restrained in this simulation (see also Fig. 7).

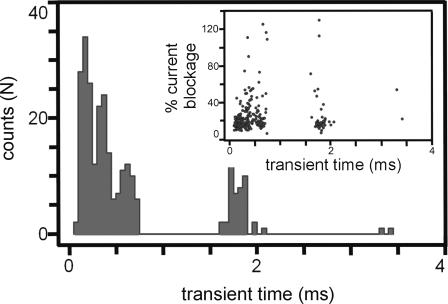
Not taking into account the possibility of DNA unzipping during the translocation, one would estimate the translocation time for 100-basepair double-stranded DNA to be a few microseconds at 0.44-V bias. However, the duration of the ionic current blockades experimentally measured at similar conditions (1 V/10 nm) exhibits a distribution of times ranging from near zero to several milliseconds as shown in Fig. 10 (Heng et al., 2004). The histogram shown in Fig. 10 is a compilation of events categorized according to the number and duration of the transients associated with 58-mer single-stranded DNA interacting with the pore. The distribution shown involves two main contributions: one at ∼200 μs and one at ∼1.8 ms. Each contribution exhibits a variety of blocking current values as indicated in the inset. Overall, the observed translocation times are clearly much longer than suggested by our simulations.

FIGURE 10.

FIGURE 10

Open in a new tab

Histogram of transient times when a 58-mer of single-stranded DNA interacts with a 2.0 nm ± 0.2 nm diameter pore in a Si3N4 membrane at a voltage of 1 V. There are two peaks associated with the histogram centered at transit times of 0.2 ms and 1.8 ms. The inset shows the current reduction percentage versus duration of the current blockades of the same events.

Naturally, the strong adhesion between DNA and the Si3N4 surface would prolong translocation of DNA. However, if the sole reason for the timescale discrepancy between our simulations and experiments would be DNA-nanopore interactions, one would observe shorter current blockades at higher voltages. The experimental data suggest the opposite: increasing the applied voltage bias usually increases the duration of the current blockades (Heng et al., 2004). A possible resolution could be associated with the initial orientation of the molecule relative to the pore axis. As demonstrated in Fig. 8, DNA can effectively block the ionic current through the pore without translocating through it. Consequently, the field dependence of the distribution of transient width may not solely reflect translocation of DNA through the pore. Increasing a voltage bias could lead to a stronger binding of DNA to the pore mouth and/or extend the time required for the DNA to search via diffusion for an orientation that would facilitate translocation.

Sequence dependence of the current blockades

It has been demostrated that purine and pyrimidine DNA strands can be distinguished from each other by measuring ionic currents through an α-hemolysin channel blocked by DNA (Kasianowicz et al., 1996; Akenson et al., 1999; Meller et al., 2000; Vercoutere et al., 2001; Howorka et al., 2001). We conducted MD simulations to investigate the feasibility of differentiating nucleotides through nanopores in Si3N4.

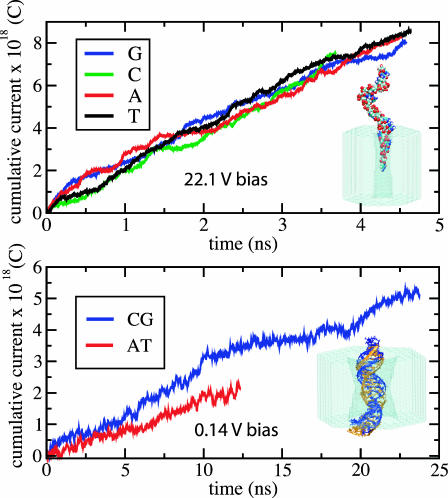
First, a single poly(dC)20 strand was pulled inside a 0.9 × 1.1 nm2 pore by applying an external force to one of the DNA's ends. The strand was only partially introduced into the pore, such that only four nucleotides obstructed the ionic current, as shown in Fig. 11 (top). Within the next 1.5 ns, the system was simulated without applying any external forces on DNA, dissipating the strain introduced by the pulling. Next, all bases of the original DNA strand were mutated into poly(dA)20, poly(dG)20, and poly(dT)20 strands, producing four systems different only in their nucleotide composition. These systems underwent energy minimization followed by 100 ps equilibration in the NVT ensemble (see Methods). An electrical field equivalent to 22.1 V was applied normal to the Si3N4 membrane, inducing ionic currents through the pores blocked by the nucleotides. We chose to apply such a strong field to collect a statistically significant number of ion permeation events within the time interval covered by MD. The resulting cumulative currents are plotted in Fig. 11 (top). The data indicate no sequence specificity of the ionic current within the time interval studied. The presence of the DNA strands in the pores made the ionic currents highly selective (∼90% of the total current) to K+ ions.

FIGURE 11.

FIGURE 11

Open in a new tab

Sequence dependence of current blockades. (Top) Cumulative ionic currents through a 0.9 × 1.1 nm2 pore blocked by homopolymers of A, C, G, and T nucleotides. The traces show no sequence specificity. (Bottom) Cumulative ionic currents through a 2.2 × 2.6 nm2 pore blocked by poly(dC)20·poly(dG)20 and poly(dA)20·poly(dT)20 double strands. The AT strand blocks the current 25% less than does the CG strand. The fluctuations of the ionic current in the CG trace are larger than the sequence-dependent difference of the ionic currents.

The second system included a fragment of double-stranded DNA inserted halfway through a 2.2 × 2.6 nm2 pore. CG and AT double strands were pulled into the pore by applying an electrical field equivalent to 4.4 V. Next, both systems were simulated for 1.5 ns without applying external forces on DNA; the end-to-end distances of both CG and AT strands shrunk by 15%, reaching a constant value of 6.6 ± 0.2 nm. At the end of the equilibration, the CG and AT strands assumed an overall similar shape (a superposition of the CG and AT strands is shown in Fig. 11 (bottom)); the root-mean-square deviation (RMSD) between the backbone atoms of the CG and AT strands for a fragment of five consecutive nucleotides was below 3.5 Å; the overall RMSD between the backbone atoms of the CG and AT strands was 7.9 Å.

A weak electrical field equivalent to 0.14 V was applied then to induce ionic currents. The resulting cumulative currents are shown in Fig. 11 (bottom). The data indicate that the AT strand blocks the ionic current 25% less then the CG strand does. The difference, however, is comparable with the fluctuations of the ionic current due to the changes of DNA conformation as revealed by the CG current trace shown in Fig. 11 (bottom).

Our data do not rule out the possibility of experimentally distinguishing different sequences in DNA strands with Si3N4 nanopores. They indicate, however, that, on the timescale of tens of nanoseconds, conformational changes in the DNA structure cause large fluctuations of the blocked ionic current that are comparable to the sequence-dependent difference of the ionic conductance.

CONCLUSIONS

Molecular dynamics simulations provide unequivocal insights into the atomic level dynamics of DNA translocation through artificial nanopores in Si3N4 membranes. Under experimental conditions, translocation of double-stranded DNA inside the pore can proceed at a rate of 10–100 basepairs per microsecond depending on the electric field along the pore axis (see Figs. 5 and 9). This suggests that a bioelectrical sensor should have nanosecond resolution to detect DNA sequences. However, portions of DNA that are transverse to the pore axis and the interactions between the pore wall and DNA basepairs can slow translocation through the pore. A strong hydrophobic interaction of the DNA bases with the surface of the pore (Fig. 7) favors an unzipped conformation of a double-stranded DNA inside the pore (Figs. 6 and 9). A significant reduction of the ionic current can be observed even when DNA is not transiting the pore (Fig. 8), such that only part of the ionic current blockade measured experimentally reflects actual DNA translocation events.

The results of the simulations and experiments presented in this article suggest that we have reached a quantitative understanding of DNA translation through nanopores. The manufacturing of actual nanopores and electrical recordings are still at an early stage that needs guidance toward optimal strategies toward the ultimate goal of sequencing DNA. We conclude from our rather successful simulation efforts that the computation approach permits one now to investigate such optimal strategy. In future work we will simulate supposedly ideal nanopore shapes, coatings of nanopore walls, application of mechanical forces on one or both sides of the nanopore to translocate DNA in a more controlled way, as well as the application of various types of electrical field, e.g., alternating fields. The future simulations will also study the signatures in various electrical recordings that can be obtained in principle, along with the error bars expected.

We finally note that this investigation demonstrates that MD simulations cannot only furnish detailed descriptions of natural biomolecular systems, but are rather ideally suited to simulate artificial nanosize systems, except for the method's present limitation to 10-ns timescales. Molecular dynamics simulations can provide dynamical images of nanodevices as a computational microscope, probe as well as analyze physical properties, alter and test designs, and thereby contribute to the development of some of the most promising measuring techniques in modern biophysics.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Supplementary Material

[Supplemental Material]
biophysj_87_3_2086__index.html (1.1KB, html)

Acknowledgments

This work is supported by grants from the National Science Foundation (CCR-02-10843), National Aeronautics and Space Administration (NAG2-1626), and the National Institutes of Health (PHS-5-P41-RR05969 and 1-RO1-GM067887). The authors gladly acknowledge supercomputer time provided by Pittsburgh Supercomputer Center and the National Center for Supercomputing Applications via National Resources Allocation Committee grant MCA93S028.

References

  1. Akenson, M., D. Branton, J. J. Kasianowicz, E. Brandin, and D. W. Deamer. 1999. Microsecond timescale discrimination among polycytidylic acid, polyadenylic acid, and polyuridylic acid as homopolymers or as segments within single RNA molecules. Biophys. J. 77:3227–3233. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Allen, M. P., and D. J. Tildesley. 1987. Computer Simulation of Liquids. Oxford University Press, New York.
  3. Ambjörnsson, T., S. P. Apell, Z. Konkoli, E. A. D. Marzio, and J. J. Kasianowicz. 2002. Charged polymer membrane translocation. Biophys. J. 117:4063–4073. [Google Scholar]
  4. Balaeff, A., C. R. Koudella, L. Mahadevan, and K. Schulten. 2004. Modeling DNA loops using continuum and statistical mechanics. Philos. Trans. R. Soc. Lond. A. In press. [DOI] [PubMed]
  5. Batcho, P. F., D. A. Case, and T. Schlick. 2001. Optimized particle-mesh Ewald/multiple-time step integration for molecular dynamics simulations. J. Chem. Phys. 115:4003–4018. [Google Scholar]
  6. Beckstein, O., P. C. Biggin, and M. S. P. Sansom. 2001. A hydrophobic gating mechanism for nanopores. J. Phys. Chem. B. 105:12902–12905. [Google Scholar]
  7. Beckstein, O., and M. S. P. Sansom. 2003. Liquid-vapor oscillations of water in hydrophobic nanopores. Proc. Natl. Acad. Sci. USA. 100:7063–7068. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Berneche, S., and B. Roux. 2001. Energetics of ion conduction through the K+ channel. Nature. 414:73–77. [DOI] [PubMed] [Google Scholar]
  9. Beveridge, D. L., and G. Ravishanker. 1994. Molecular dynamics studies of DNA. Curr. Opin. Struct. Biol. 4:246–255. [Google Scholar]
  10. Brünger, A. T. 1992. X-PLOR, Version 3.1: A System for X-ray Crystallography and NMR. The Howard Hughes Medical Institute and Department of Molecular Biophysics and Biochemistry, Yale University, New Haven, CT.
  11. Chen, C.-M., and E.-H. Coalson. 2003. Nanopore sequencing of polynuclueotides assisted by a rotating electric field. Appl. Phys. Lett. 82:1308–1310. [Google Scholar]
  12. Chern, S. S., A. E. Cárdenas, and R. D. Coalson. 2001. Three-dimensional dynamic Monte Carlo simulations of driven polymer transport through a hole in a wall. J. Chem. Phys. 115:7772–7782. [Google Scholar]
  13. Chuang, J., Y. Kantor, and M. Kardar. 2001. Anomalous dynamics of translocation. Phys. Rev. E. Stat. Nonlin. Soft Matter. 65:011802. [DOI] [PubMed] [Google Scholar]
  14. Cornell, W. D., P. Cieplak, C. I. Bayly, I. R. Gould, J. K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell, and P. A. Kollman. 1995. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 117:5179–5197. [Google Scholar]
  15. Crozier, P. S., D. Henderson, R. L. Rowley, and D. D. Busath. 2001. Model channel ion currents in NaCl-extended simple point charge water solution with applied-field molecular dynamics. Biophys. J. 81:3077–3089. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. de Groot, B. L., and H. Grubmüller. 2001. Water permeation across biological membranes: mechanism and dynamics of aquaporin-1 and GlpF. Science. 294:2353–2357. [DOI] [PubMed] [Google Scholar]
  17. Grün, R. 1979. The crystal structure of β-Si3N4: structural and stability considerations between α- and β-Si3N4. Acta Crystallogr. B35:800–804. [Google Scholar]
  18. Gullingsrud, J., D. Kosztin, and K. Schulten. 2001. Structural determinants of MscL gating studied by molecular dynamics simulations. Biophys. J. 80:2074–2081. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Heng, J. B., V. Dimitrov, Y. V. Grinkova, C. Ho, T. Kim, D. Muller, S. Sligar, T. Sorsch, R. Twesten, R. Timp, and G. Timp. 2003. The detection of DNA using a silicon nanopore. IEDM '03 Technical Digest. IEEE International, 8–10 Dec. 2003. 32.2.1–32.2.4.
  20. Heng, J. B., C. Ho, T. Kim, R. Timp, A. Aksimentiev, Y. V. Grinkova, S. Sligar, K. Schulten, and G. Timp. 2004. Sizing DNA using an artificial nanopore. Biophys. J. In press. [DOI] [PMC free article] [PubMed]
  21. Howorka, S., S. Cheley, and H. Bayley. 2001. Sequence-specific detection of individual DNA strands using engineered nanopores. Nat. Biotechnol. 19:636–639. [DOI] [PubMed] [Google Scholar]
  22. Hummer, G., J. C. Rasaiah, and J. P. Noworyta. 2001. Water conduction through the hydrophobic channel of a carbon nanotube. Nature. 414:188–190. [DOI] [PubMed] [Google Scholar]
  23. Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD: visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
  24. Kalé, L., R. Skeel, M. Bhandarkar, R. Brunner, A. Gursoy, N. Krawetz, J. Phillips, A. Shinozaki, K. Varadarajan, and K. Schulten. 1999. NAMD2: greater scalability for parallel molecular dynamics. J. Comp. Phys. 151:283–312. [Google Scholar]
  25. Kasianowicz, J. J., E. Brandib, D. Branton, and W. Deamer. 1996. Characterization of individual polynucleotide molecules using a membrane channel. Proc. Natl. Acad. Sci. USA. 93:13770–13773. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kong, C. Y., and M. Muthukumar. 2002. Modeling of polynucleotide translocation through protein pores and nanotubes. Electrophoresis. 23:2697–2703. [DOI] [PubMed] [Google Scholar]
  27. Li, J., M. Gershow, D. Stein, E. Brandin, and J. A. Golovchenko. 2003. DNA molecules and configurations in a solid-state nanopore microscope. Nat. Mater. 2:611–615. [DOI] [PubMed] [Google Scholar]
  28. Li, J., D. Stein, C. McMullan, D. Branton, M. J. Aziz, and J. A. Golovchenko. 2001. Ion-beam sculpting at nanometre length scales. Nature. 412:166–169. [DOI] [PubMed] [Google Scholar]
  29. Loebl, H. C., R. Randel, S. P. Goodwin, and C. C. Matthai. 2003. Simulation studied of polymer translocation through a channel. Phys. Rev. E. Stat. Nonlin. Soft Matter. Phys. 67:041913. [DOI] [PubMed] [Google Scholar]
  30. Lopez, C. F., S. O. Nielsen, P. B. Moore, and M. L. Klein. 2004. Understanding nature's design for a nanosyringe. Proc. Natl. Acad. Sci. USA. 101:4431–4434. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Lubensky, D. K., and D. R. Nelson. 1999. Driven polymer translocation through a narrow pore. Biophys. J. 77:1824–1838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. MacKerell, A. D., Jr., B. Brooks, C. L. Brooks III, L. Nilsson, B. Roux, Y. Won, and M. Karplus. 1998. CHARMM: the energy function and its parameterization with an overview of the program. In The Encyclopedia of Computational Chemistry. P. Schleyer, editor. John Wiley & Sons, Chichester, UK. 271–277.
  33. Mara, A., Z. Siwy, C. Trautmann, J. Wan, and F. Kamme. 2004. An asymmetric polymer nanopore for single molecule detection. Nano. Lett. 4:497–501. [Google Scholar]
  34. Martyna, G. J., D. J. Tobias, and M. L. Klein. 1994. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 101:4177–4189. [Google Scholar]
  35. Matzler, R., and J. Klafter. 2003. When translocation dynamics becomes anomalous. Biophys. J. 85:2776–2779. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Meller, A. 2003. Dynamics of polynucleotide transport through nanometre-scale pores. J. Phys. Condens. Matter. 15:R581–R607. [Google Scholar]
  37. Meller, A., L. Nivon, E. Brandin, J. Golovchenko, and D. Branton. 2000. Rapid nanopore discrimination between single polynucleotide molecules. Proc. Natl. Acad. Sci. USA. 97:1079–1084. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Muthukumar, M. 1999. Polymer translocation through a hole. J. Chem. Phys. 111:10371–10374. [Google Scholar]
  39. Muthukumar, M. 2001. Translocation of a confined polymer through a hole. Phys. Rev. Lett. 86:3188–3191. [DOI] [PubMed] [Google Scholar]
  40. Muthukumar, M. 2003. Polymer escape through a nanopore. J. Chem. Phys. 118:5174–5184. [Google Scholar]
  41. Polygen. 1988. Quanta. Polygen Corporation, Waltham, MA.
  42. Pomès, R., and B. Roux. 2002. Molecular mechanism of H+ conduction in the single-file water chain of the gramicidin channel. Biophys. J. 82:2304–2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Slonkina, E., and A. B. Kolomeisky. 2003. Polymer translocation through a long nanopore. J. Chem. Phys. 118:7112–7118. [Google Scholar]
  44. Song, L., M. R. Hobaugh, C. Shustak, S. Cheley, H. Bayley, and J. E. Gouaux. 1996. Structure of staphylococcal α-hemolysin, a heptameric transmembrane pore. Science. 274:1859–1866. [DOI] [PubMed] [Google Scholar]
  45. Storm, A. J., J. H. Chen, X. S. Ling, H. W. Zandergen, and C. Dekker. 2003. Fabrication of solid-state nanopore with single-nanometre precision. Nat. Mater. 2:537–540. [DOI] [PubMed] [Google Scholar]
  46. Sung, S.-S., and X.-W. Wu. 1996. Molecular dynamics simulations of synthetic peptide folding. Proteins Struct. Func. Genet. 25:202–214. [DOI] [PubMed] [Google Scholar]
  47. Tajkhorshid, E., P. Nollert, M. Ø. Jensen, L. J. W. Miercke, J. O'Connell, R. M. Stroud, and K. Schulten. 2002. Control of the selectivity of the aquaporin water channel family by global orientational tuning. Science. 296:525–530. [DOI] [PubMed] [Google Scholar]
  48. Vercoutere, W. A., S. Winters-Hilt, V. S. DeGuzman, D. Deamer, S. E. Ridino, J. T. Rodgers, H. E. Olsen, A. Marziali, and M. Akeson. 2003. Discrimination among individual Watson-Crick basepairs at the termini of single DNA hairpin molecules. Nucleic Acids Res. 31:1311–1318. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Vercoutere, W., S. Winters-Hilt, H. Olsen, D. Deamer, D. Haussler, and M. Akeson. 2001. Rapid discrimination among individual DNA hairpin molecules at single-nucleotide resolution using an ion channel. Nat. Biotechnol. 19:248–252. [DOI] [PubMed] [Google Scholar]
  50. Wendel, J. A., and W. A. Goddard, Iii.1992. The Hessian biased force-field for silicon nitride ceramics: predictions of the thermodynamic and mechanical properties for α- and β-Si3N4. J. Chem. Phys. 97:5048–5062. [Google Scholar]
  51. Wong, K. Y., and B. M. Pettitt. 2001. A study of DNA tethered to a surface by an all-atom molecular dynamics simulation. Theo. Chem. Accounts. 106:233–235. [Google Scholar]
  52. Yeh, I. C., and G. Hummer. 2004. Diffusion and electrophoretic mobility of single-stranded RNA from molecular dynamics simulations. Biophys. J. 86:681–689. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Zhu, F., E. Tajkhorshid, and K. Schulten. 2002. Pressure-induced water transport in membrane channels studied by molecular dynamics. Biophys. J. 83:154–160. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplemental Material]
biophysj_87_3_2086__index.html (1.1KB, html)
biophysj_87_3_2086__1.pdf (27.9KB, pdf)
Download video file (1.1MB, mpg)
Download video file (2.2MB, mpg)
Download video file (2.8MB, mpg)
Download video file (1.6MB, mpg)
Download video file (1.5MB, mpg)
Download video file (1.8MB, mpg)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES