Abstract
Recent experiments focusing on the function of the immunological synapse formed between a T cell and an antigen-presenting cell raise many questions about its purpose. We examine the proposal that the close apposition of the cell membranes in the central region of the synapse acts to focus T-cell secretions on the target cell, thus reducing the effect on nearby cells. We show that the efficiency of targeted T-cell responses to closely apposed cells is only weakly dependent on the distance between the cells. We also calculate effective (diffusion-limited) rates of binding and unbinding for molecules secreted within the synapse. We apply our model to the stimulation of B cells by secreted interleukin-4 (IL-4), and find that very few molecules of IL-4 need be released to essentially saturate the IL-4 receptors on the B-cell surface.
INTRODUCTION
A recurrent theme in T-cell-mediated immune responses is the directed transfer of effector substances from the T cell to a target cell in close proximity. For example, after stimulation of a cytotoxic T cell by a cell presenting viral proteins, the cytotoxic T cell will secrete a variety of cytoplasmic toxins—perforin and granzymes—to kill the virus-infected cell (Janeway et al., 1999). Similarly, for B cells to be stimulated by helper T cells, interleukin-4 (IL-4) and interleukin-5 (IL-5) must be transferred (Janeway et al., 1999). In most cases, it is important that the secreted molecules are directed toward the target cell to prevent unwanted effects on bystander cells and the diversion of these molecules away from the target cell.
The contact regions formed between T cells and antigen-presenting cells (APCs) (termed “immunological synapses”) have been a subject of extensive experimental work (Monks et al., 1998; Grakoui et al., 1999; Delon and Germain, 2000; Lee et al., 2002; van der Merwe and Davis, 2002) as well as theoretical considerations (Qi et al., 2001; Burroughs and Wülfing, 2002; Coombs et al., 2004). After a period of rearrangement, cell surface proteins segregate into a central region containing signaling molecules, surrounded by a peripheral region dense in adhesion molecules. This topological arrangement is found to be stable for several hours and may be necessary for T-cell activation through sustained signaling. Subsequent experiments (Lee et al., 2002, 2003), however, show that certain signaling events precede the full rearrangement and segregation of cell surface molecules that form the immunological synapse and indicate a balance between signaling and TCR degradation. The question arises: what biological functions does the long-lived immunological synapse help facilitate? Recent reviews addressing this question include Huppa and Davis (2003), Davis and Dustin (2004), and Jacobelli et al. (2004). We shall focus on the suggestion that synapse formation helps to ensure that soluble effector molecules are confined to the interface and their effects on bystander cells are minimized (van der Merwe and Davis, 2002; van der Merwe, 2002). It is known that cytokines produced during helper T cell–B cell association and cytoplasmic toxins produced during cytotoxic T-cell–target-cell association localize to the contact region between the cells before being released (Kupfer et al., 1991, 1994; Yannelli et al., 1986). Furthermore, experiments using cytotoxic T cells (Stinchcombe et al., 2001) show that the granules release their contents at a particular point on the contact region, within the outer ring of adhesion molecules but separate from the inner zone of signaling molecules.
In this article we will examine effects of immunological synapse geometry on the delivery of diffusing effector molecules to target cells. We illustrate our method using the specific example of the transfer of IL-4 molecules from T cells to B cells, within the context of an immunological synapse. The majority of our results apply to all immunological synapses with similar geometry. However, in some sections we use parameters measured for the IL-4 system; these results will not generally hold in other situations.
RESULTS
Details of intermembrane attachment weakly affect the fraction of effector molecules reaching the target cell
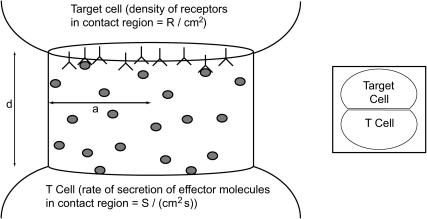
Once secreted molecules leave the cell, they must diffuse across the contact region to reach their target. We estimate the fraction of the molecules that escape from the synapse before reaching the target cell surface (and may potentially interact with cells other than the target) by solving a diffusion equation as follows. We model the cell contact region as a squat cylinder of radius a and height d, and the release of effector molecules as a constant, uniform rate of release S molecules/(cm2 s) over the base of the cylinder (Fig. 1). The effector molecules diffuse with coefficient D (cm2/s), and we assume that molecules reaching the boundary of the cylinder are lost. We then solve the steady diffusion problem D∇2C = 0 for the concentration C of effector molecules within the cylinder with perfectly absorbing boundaries at the top of the cylinder (corresponding to the target cell) and on the sides (corresponding to escape from the synapse volume), and calculate the flux of molecules into the top of the cylinder. (For details, see the appendix.) The solution is
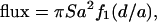 |
(1) |
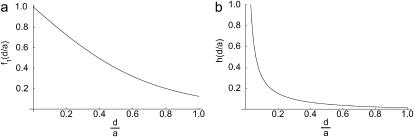
and we plot the function f1(d/a) as Fig. 2 a.
FIGURE 1.
The model geometry. Two cells are held together by ligand-receptor bonds (not shown) at a distance d (tens of nanometers). The radius of the tight contact region is a (a few microns). Not to scale. (Inset) Scale drawing to indicate actual aspect ratio of contact region.
FIGURE 2.
(a) Fraction of dimensionless flux of effector molecules f1(d/a) reaching the target cell at steady state. (b) Dimensionless mean concentration h(d/a) of effector molecules at the target cell surface at steady state.
We can now compare: a), a contact region held together by TCR–peptide-MHC bonds (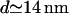 from Wild et al., 1999), with b), a contact region held together by nonspecific adhesion molecules (
from Wild et al., 1999), with b), a contact region held together by nonspecific adhesion molecules (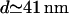 also from Wild et al., 1999). Taking the radius of the contact region to be a = 2 μm (Grakoui et al., 1999) we find that in case a 98.9% of the available effector molecules reach the target cell, compared to 97.0% in case b. We note that these figures are mild underestimates: some molecules that leave the synapse volume will return, and in any case some of the escaped molecules might bind with the target cell at a point outside our computational region.
also from Wild et al., 1999). Taking the radius of the contact region to be a = 2 μm (Grakoui et al., 1999) we find that in case a 98.9% of the available effector molecules reach the target cell, compared to 97.0% in case b. We note that these figures are mild underestimates: some molecules that leave the synapse volume will return, and in any case some of the escaped molecules might bind with the target cell at a point outside our computational region.
This result shows that molecular rearrangements in the synapse do not significantly improve effector transfer by bringing the two cells closer together; the aspect ratio of the synapse volume is already sufficiently small that most molecules reach their target. From the point of view of diffusion, the timescale for transport across the contact volume scales as d2/D, whereas the timescale for lateral diffusion scales as a2/D. The dimensionless ratio of these times is thus (d/a)2. Because this ratio of diffusion times depends on the square of the aspect ratio, we see that the details of the synapse separation should indeed be unimportant. (Choosing d = 14 nm, the ratio of timescales is 0.01%. For d = 41 nm, it is 0.04%.)
Saturation of target-cell receptors
We now calculate the release rate S that is sufficient to ensure that a substantial fraction of the receptors on the target cell will be bound at steady state. At equilibrium, for monovalent ligands binding to receptors, half the receptors will be bound to ligand when the free ligand concentration is equal to the equilibrium dissociation constant, Kd. To find the concentration of effector molecules over the cylinder in this case, we must solve the steady diffusion equation with a reflecting boundary at z = d and an absorbing boundary at r = a.
At steady state the concentration of secreted effector molecules at the target cell will have its highest concentration in the center of the synapse (r = 0) and drop off radially as one moves away from the center of the synapse. (In our calculations the concentration is set to zero at r = a, the outer boundary of the synapse. This ignores the small concentration that will build up outside the contact region.) The mean concentration of effector molecules at the target cell,  i.e., the concentration of effector molecules averaged over the contact surface of the target cell, is given by (see Appendix)
i.e., the concentration of effector molecules averaged over the contact surface of the target cell, is given by (see Appendix)
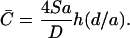 |
(2) |
The dimensionless function h(d/a) is plotted in Fig. 2. For a = 2 μm and d = 14 nm and 41 nm, h(d/a) = 4.46 and 1.52, respectively.
Low IL-4 release rates saturate the IL-4 receptor at equilibrium
To illustrate, we consider the secretion of IL-4 by helper T cells held in close proximity to B cells. IL-4 binds to its cell surface receptor (IL-4Rα) and the bound complex associates with a common signaling unit, γc, the latter being required for signaling transduction (Kondo et al., 1993; Hoffman et al., 1995). The forward and reverse rate constants for binding of human IL-4 to its receptor have been determined (Shen et al., 1996; Wang et al., 1997) and their values are given in Table 1.
TABLE 1.
Parameters for IL-4–IL-4R interaction
| Parameter | Symbol | Estimate |
|---|---|---|
| Dissociation constant | Kd | 100 pM = 6 × 1010 cm−3 |
| Forward binding constant | kon | 2 × 107 M−1s−1 = 3.3 × 10−14 cm3s−1 |
| Unbinding rate | koff | 2 × 10−3 s−1 |
| Receptor density | R | 107–109 cm−2 |
| Diffusion constant for IL-4 | D | 10−6 cm2s−1 |
Rate and dissociation constants were determined at 25°C (Table 1 of Wang et al., 1997). Receptor density is estimated from measurements of receptor number of 50–5000 receptors/cell (Lowenthal et al., 1988; Galizzi et al., 1989) uniformly distributed over a cell of surface area 5 × 10−6cm2.
Solving 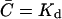 and taking D = 10−6cm2/s, we find that a release rate (πa2S) of between 2.1 (at d = 14 nm, corresponding to the length of a TCR-pMHC bond) and 6.2 (at d = 41 nm, the length of a LFA-1–ICAM-1 bond) molecules per second at the T cell is sufficient to fill half the IL-4 binding sites on the B-cell surface in the contact area, in the steady state.
and taking D = 10−6cm2/s, we find that a release rate (πa2S) of between 2.1 (at d = 14 nm, corresponding to the length of a TCR-pMHC bond) and 6.2 (at d = 41 nm, the length of a LFA-1–ICAM-1 bond) molecules per second at the T cell is sufficient to fill half the IL-4 binding sites on the B-cell surface in the contact area, in the steady state.
Diffusion-limited reaction rates
When receptors are confined to a surface the system is intrinsically not well mixed and the transport of ligands to the surface can influence the kinetics of binding and dissociation. If transport is slow compared to the ligand-receptor binding kinetics then as binding proceeds there will be competition among receptors for ligand. Transport effects can be accounted for in the binding kinetics by introducing effective rate coefficients. If we call the average concentrations of secreted molecules between the cells C, free receptors on the target cell surface R, and their bound complex B, we can write
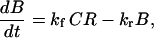 |
(3) |
where kf and kr are effective rate coefficients for the forward and reverse reactions. We may express these coefficients as (Eigen, 1974; Shoup and Szabo, 1987; Goldstein, 1989):
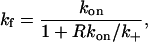 |
(4) |
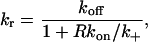 |
(5) |
where k+ is the diffusion-limited forward rate constant averaged over the area of the target cell within the contact region. For our geometry, k+ is obtained by setting up a steady state and calculating the mean flux into a perfectly absorbing disc, the contact region of the target cell. The fraction 1/(1 + Rkon/k+) is the reduction in the forward rate constant due to competition among the free receptors on the surface for ligand (Goldstein and Dembo, 1995).
We write k+ in the form
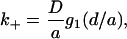 |
(6) |
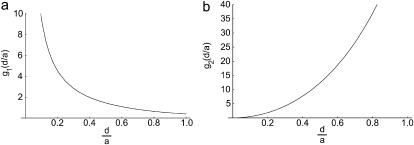
where g1(d/a) is a dimensionless function that depends only on the ratio of the height of the cylinder to its radius. We plot g1(d/a) in Fig. 3 a and present the details of the calculation in the appendix.
FIGURE 3.
(a) Dimensionless diffusion-limited forward rate constant g1(d/a) for the association problem. (b) Dimensionless diffusion-limited reverse rate constant g2(d/a) for the dissociation problem.
Competition among receptors for IL-4 is weak
Returning to the T-cell–B-cell interface where a = 2 μm, for d = 14 nm we find g1 = 142.6 whereas when d = 41 nm, g1 = 48.4. Taking the diffusion coefficient for IL-4 to be D = 1 × 10−6 cm2/s we find from Eq. 6 that if d = 14 nm, 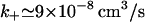 whereas if d = 41 nm,
whereas if d = 41 nm, 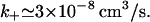 From Eq. 4 we see that transport will have a strong influence on the binding kinetics when konR/k+ ≥ 1. We can estimate how many free receptors must be in the contact region for competition among receptors for free IL-4 to become important. For d = 41 nm and kon = 3.3 × 10−14 cm3/s, we would have to have 9.1 × 105 IL-4 receptors in the contact area whereas for d = 14 nm the number would even be higher. Because the number of IL-4 receptors expressed on B cells has been found to be in the range of 50–5000 receptors per cell (Lowenthal et al., 1988; Galizzi et al., 1989) it is clear that during binding, transport by diffusion is rapid and binding is as if the system is well mixed. However, during dissociation the situation is quite different.
From Eq. 4 we see that transport will have a strong influence on the binding kinetics when konR/k+ ≥ 1. We can estimate how many free receptors must be in the contact region for competition among receptors for free IL-4 to become important. For d = 41 nm and kon = 3.3 × 10−14 cm3/s, we would have to have 9.1 × 105 IL-4 receptors in the contact area whereas for d = 14 nm the number would even be higher. Because the number of IL-4 receptors expressed on B cells has been found to be in the range of 50–5000 receptors per cell (Lowenthal et al., 1988; Galizzi et al., 1989) it is clear that during binding, transport by diffusion is rapid and binding is as if the system is well mixed. However, during dissociation the situation is quite different.
Diffusion-limited dissociation
Consider a situation where secretion is turned off and bound ligand-receptor complexes begin to dissociate with the ligand diffusing away. Because the area in which the ligand diffuses is so confined we expect a ligand that dissociates from a receptor to return to the surface many times before it manages to diffuse out of the contact area. The binding kinetics are described by Eq. 3 where at time t = 0, C = C0, the average ligand concentration in the region between the two cells at the start of the experiment. With time this concentration decays to zero. The effective rate constants have the same form as Eqs. 4 and 5 with the diffusion-limited forward rate constant k+ replaced by the diffusion-limited rate constant for leaving the surface 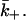 In the most familiar case where ligands bind to or dissociate from a single isolated spherical cell of radius a,
In the most familiar case where ligands bind to or dissociate from a single isolated spherical cell of radius a, 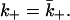 However, in general,
However, in general, 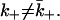 That is the case here.
That is the case here.
In a dissociation experiment the effective dissociation rate constant is
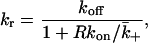 |
(7) |
where 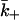 is the diffusion-limited rate constant for leaving the surface, averaged over the area of the target cell within the contact. The fraction
is the diffusion-limited rate constant for leaving the surface, averaged over the area of the target cell within the contact. The fraction 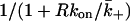 is the reduction in the off-rate constant due to rebinding to free receptors on the surface, i.e., it is the probability that a dissociation will lead to the ligand escaping into the bulk solution rather than rebinding back to the surface (Berg, 1978; Goldstein and Dembo, 1995).
is the reduction in the off-rate constant due to rebinding to free receptors on the surface, i.e., it is the probability that a dissociation will lead to the ligand escaping into the bulk solution rather than rebinding back to the surface (Berg, 1978; Goldstein and Dembo, 1995).
We write 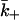 in the form
in the form
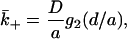 |
(8) |
where g2(d/a) is the dimensionless function plotted in Fig. 3 b. For a = 2 μm and d = 14 nm, we find g2 = 2.6 × 10−3 whereas if d = 41 nm then g2 = 1.9 × 10−2. Therefore, using a diffusion coefficient of 1 × 10−6 cm2s−1 and taking d = 14 nm, 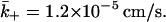 Further,
Further, 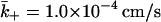 when d = 41 nm.
when d = 41 nm.
Rebinding substantially delays the loss of IL-4 from the synaptic volume
We can now estimate how many IL-4 receptors must be on the B-cell surface in the contact region for rebinding to be significant. As we discussed after introducing Eq. 7, when 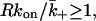 the probability of rebinding to the surface rather than escaping from the contact region is 0.5 or greater. Using the forward rate constant for IL-4 binding to its receptor (Table 1), we find that if d = 14 nm then 46 IL-4 receptors in the contact area are sufficient to satisfy
the probability of rebinding to the surface rather than escaping from the contact region is 0.5 or greater. Using the forward rate constant for IL-4 binding to its receptor (Table 1), we find that if d = 14 nm then 46 IL-4 receptors in the contact area are sufficient to satisfy 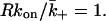 If d = 41 nm then 381 IL-4 receptors are required. In other words, when d = 14 nm the probability of an IL-4 molecule rebinding will be 0.5 when ∼50 IL-4 receptors are in the contact region. Even though the numbers of IL-4 receptors are small on B cells (Table 1), if they move to the contact region when a synapse is established, the half-life for dissociation of an IL-4 molecule from the contact volume will be significantly increased. In the usual case of receptors on a surface of a cell, if there is no competition for ligand among receptors during binding then rebinding is negligible as well. Here, because of the geometry of the synapse, competition during binding can be negligible but can be significant during dissociation. This reflects the fact that a large fraction of diffusive paths that start on one surface lead directly to the second surface without ever encountering the side of the cylinder whereas only a small fraction of paths that start on one surface and end by reaching the side of the cylinder do so without returning to the starting surface many times. It appears that this effect depends on the details of the intermembrane separation. Given present uncertainties in the number of IL-4 receptors expressed by B cells (Lowenthal et al., 1988; Galizzi et al., 1989) and the open question of whether they relocate to the synapse region upon signaling, however, we should not overstate this difference. The key conclusion is that the synapse geometry may promote rebinding, and hence, efficient delivery of IL-4.
If d = 41 nm then 381 IL-4 receptors are required. In other words, when d = 14 nm the probability of an IL-4 molecule rebinding will be 0.5 when ∼50 IL-4 receptors are in the contact region. Even though the numbers of IL-4 receptors are small on B cells (Table 1), if they move to the contact region when a synapse is established, the half-life for dissociation of an IL-4 molecule from the contact volume will be significantly increased. In the usual case of receptors on a surface of a cell, if there is no competition for ligand among receptors during binding then rebinding is negligible as well. Here, because of the geometry of the synapse, competition during binding can be negligible but can be significant during dissociation. This reflects the fact that a large fraction of diffusive paths that start on one surface lead directly to the second surface without ever encountering the side of the cylinder whereas only a small fraction of paths that start on one surface and end by reaching the side of the cylinder do so without returning to the starting surface many times. It appears that this effect depends on the details of the intermembrane separation. Given present uncertainties in the number of IL-4 receptors expressed by B cells (Lowenthal et al., 1988; Galizzi et al., 1989) and the open question of whether they relocate to the synapse region upon signaling, however, we should not overstate this difference. The key conclusion is that the synapse geometry may promote rebinding, and hence, efficient delivery of IL-4.
DISCUSSION
In this article we performed an analysis of the effects of synaptic geometry on the diffusive transport of effector molecules between immune cells. We showed that, from this point of view, fine details of attachment (such as differences of a few tens of nanometers in the separation of the two cells) are qualitatively unimportant. Whether the region of contact between the regions is in the form of a bull's eye pattern with the short (TCR) bonds in the central core surrounded by longer (ICAM) bonds (Monks et al., 1998; Grakoui et al., 1999) or the other way around as is observed in NK cells (Davis et al., 1999), or more complex patterns, the delivery of effector molecules is highly efficient. This result is intuitively clear when we realize that the aspect ratio of the synapse volume is large: the cylinder is very flat. The hypothesis that the much-studied details of the immunological synapse play an important role in signaling mediated by transfer of soluble molecules may therefore be discarded, but the function of the immunological synapse will continue to generate much discussion from the point of view of signaling (Huppa and Davis, 2003; Davis and Dustin, 2004; Jacobelli et al., 2004).
We applied our model to the example of T-cell–B-cell signaling moderated by IL-4, and showed that a release rate of just a few IL-4 molecules per second is sufficient to essentially saturate the IL-4 receptors on the B cell. Two further related effects were that during binding the receptors essentially do not compete for IL-4 but that during dissociation, an IL-4 molecule will rebind with high probability to an IL-4 receptor in the contact region when there are as few as 30 free IL-4 receptors available. This raises the possibility that a single IL-4 could serially bind a number of IL-4 receptors. This is conceptually similar to serial engagement of multiple T-cell receptors within the immunological synapse by a single membrane-bound peptide-MHC (Valitutti et al., 1995; Wofsy et al., 2001).
In drawing these conclusions we used a simple cylindrical geometry. Clearly, natural synapses are considerably more complex, in that a ring of bound adhesion molecules surround the shorter TCR-pMHC bonds in the synapse center. We assumed that effector molecules leaving the cylinder are irreversibly lost. Of course, these molecules may bind the target cell outside the synapse region, and may return to the cylinder. Given the lack of sensitivity of our conclusions to the exact cellular separation in the synapse volume, we do not think that these assumptions are qualitatively important.
Finally, we note that the problem we have considered is interesting in that the diffusion-limited forward rate constants during the binding and dissociation phases (k+ and 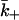 ) are different. This is the generic case, but many of the simple cases commonly studied (such as diffusion to a spherical particle) have
) are different. This is the generic case, but many of the simple cases commonly studied (such as diffusion to a spherical particle) have 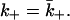
Acknowledgments
This work was supported by National Institutes of Health grant R37-GM35556 and by the United States Department of Energy through contract W-7405-ENG-36. D.C. acknowledges support from the National Science and Engineering Research Council of Canada.
APPENDIX
We are interested in the steady diffusion problem D∇2C = 0 in a squat cylinder of radius a and height d, that is d ≤ a. We shall always assume that the sides of the cylinder are perfect absorbers, but we will consider different boundary conditions at the top and bottom of the cylinder. We will use the usual cylindrical coordinate system (r, θ, z). So throughout, C(r = a) = 0; and in these coordinates, the problem becomes
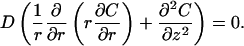 |
(9) |
In computing the diffusion-limited forward rate constant, we need to impose a constant flux at the lower boundary (z = 0) and a perfectly absorbing boundary at the top (z = d). Mathematically, this means
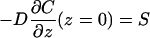 |
(10) |
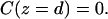 |
(11) |
By inspection (of Carslaw and Jaeger (1959)), we find that
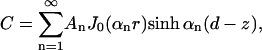 |
(12) |
satisfies Eq. 9 and the boundary conditions at z = 0 and z = d, where we choose the αn to satisfy J0(αna) = 0. The coefficients An are chosen to satisfy the boundary condition (Eq. 10). This is a standard problem, solved by multiplying by a particular Bessel function J0(αmr) and integrating both sides over r. In summary,
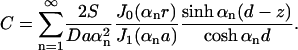 |
(13) |
The flux through the top surface z = d is found to be
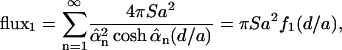 |
(14) |
(where 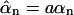 ). The dimensionless flux f1(d/a) is plotted as Fig. 2 a.
). The dimensionless flux f1(d/a) is plotted as Fig. 2 a.
We also calculate the concentration of effector molecules in the synapse at steady state. This is achieved by solving the diffusion equation with boundary conditions (Eq. 10) and ∂C/∂z|z=0 = 0. The method is exactly the same and the solution is
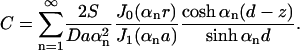 |
(15) |
We use this formula to find the mean concentration of effector molecules at z = d:
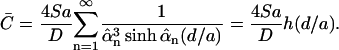 |
(16) |
Fig. 2 b plots h(d/a). The diffusion-limited forward rate constant k+ is computed as the ratio of flux1 to the mean concentration at z = 0 averaged over the contact area:
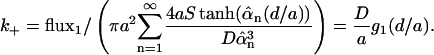 |
(17) |
Fig. 3 a plots g1(d/a). We now move to computing the diffusion-limited off-rate constant, 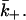 For convenience, we shall invert the cylinder so the target cell is now at z = 0. We consider the problem where effector molecules dissociate from the target cell, and calculate the escaping flux through the sides of the cylinder. The T cell (at z = d) is taken as a reflecting boundary. We therefore have
For convenience, we shall invert the cylinder so the target cell is now at z = 0. We consider the problem where effector molecules dissociate from the target cell, and calculate the escaping flux through the sides of the cylinder. The T cell (at z = d) is taken as a reflecting boundary. We therefore have
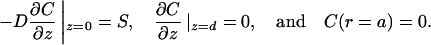 |
(18) |
The mathematical problem is identical to the problem previously considered so the concentration at z = 0 is given by Eq. 15 (with 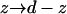 ). The flux leaving the cylinder through its sides is flux2 = πSa2 − flux1. Dividing flux2 by the mean concentration at z = 0 and averaging over the contact area, we get the diffusion-limited off rate,
). The flux leaving the cylinder through its sides is flux2 = πSa2 − flux1. Dividing flux2 by the mean concentration at z = 0 and averaging over the contact area, we get the diffusion-limited off rate,
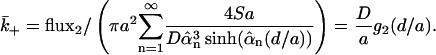 |
(19) |
Fig. 3 b shows g2(d/a).
References
- Berg, O. G. 1978. On diffusion-controlled dissociation. Chem. Phys. 20:47–57. [Google Scholar]
- Burroughs, N. J., and C. Wülfing. 2002. Differential segregation in the cell-cell contact interface: the dynamics of the immunological synapse. Biophys. J. 83:1784–1796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carslaw, H. S., and J. C. Jaeger. 1959. Conduction of Heat in Solids, 2nd Ed. Oxford University Press, Glasgow, UK.
- Coombs, D., M. Dembo, C. Wofsy, and B. Goldstein. 2004. Equilibrium thermodynamics of cell-cell adhesion mediated by multiple ligand-receptor pairs. Biophys. J. 86:1408–1423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis, D. M., I. Chiu, M. Fassett, G. B. Cohen, O. Mandelboim, and J. L. Strominger. 1999. The human natural killer cell immune synapse. Proc. Natl. Acad. Sci. USA. 96:15062–15067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis, D. M., and M. L. Dustin. 2004. What is the importance of the immunological synapse? Trends Immunol. 25:323–327. [DOI] [PubMed] [Google Scholar]
- Delon, J., and R. N. Germain. 2000. Information transfer at the immunological synapse. Curr. Biol. 10:R923–R933. [DOI] [PubMed] [Google Scholar]
- Eigen, M. 1974. Diffusion control in biochemical reactions. In Quantum Statistical Mechanics in the Natural Sciences. S. L. Minz and S. M. Weidermayer, editors. Plenum, New York, NY. 37–61.
- Galizzi, J. P., C. E. Zuber, H. Cabrillat, O. Djossou, and J. Banchereau. 1989. Internalization of human interleukin-4 and transient down-regulation of its receptor in the CD23-inducible jijoye cells. J. Biol. Chem. 264:6984–6989. [PubMed] [Google Scholar]
- Goldstein, B. 1989. Diffusion-limited effects of receptor clustering. Comments Theor. Biol. 1:109–127. [Google Scholar]
- Goldstein, B., and M. Dembo. 1995. Approximating the effects of diffusion on reversible reactions at the cell surface: ligand-receptor kinetics. Biophys. J. 68:1222–1230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grakoui, A., S. K. Bromley, C. Sumen, M. M. Davis, A. S. Shaw, P. M. Allen, and M. L. Dustin. 1999. The immunological synapse: a molecular machine controlling T cell activation. Science. 285:221–227. [DOI] [PubMed] [Google Scholar]
- Hoffman, R. C., H. Schalk, B. J. Castner, M. Grtjsty, M. G. Gibson, B. D. Rasmussen, C. J. March, J. K. Weatherbee, M. Tsang, A. Gustchina, H. Schalk, L. Reshetnikova, and A. Wlodawer. 1995. Direct evidence of a heterotrimeric complex of human interleukin-4 with its receptors. Protein Sci. 4:382–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huppa, J. B., and M. M. Davis. 2003. T-cell-antigen recognition and the immunological synapse. Nat. Rev. Immunol. 3:973–983. [DOI] [PubMed] [Google Scholar]
- Jacobelli, J., P. G. Andres, J. Boisvert, and M. F. Krummel. 2004. New views of the immunological synapse: variations in assembly and function. Curr. Opin. Immunol. 16:345–352. [DOI] [PubMed] [Google Scholar]
- Janeway, C. A., P. Travers, M. Walport, and J. D. Capra. 1999. Immunobiology, 4th Ed. Elsevier, London, UK.
- Kondo, M., T. Takeshita, N. Ishii, M. Nakamura, S. Watanabe, K. Arai, and K. Sugamura. 1993. Sharing of the interleukin-2 (IL-2) receptor γ chain between receptors for IL-2 and IL-4. Science. 262:1874–1877. [DOI] [PubMed] [Google Scholar]
- Kupfer, H., C. R. F. Monks, and A. Kupfer. 1994. Small splenic B cells that bind to antigen-specific T helper (Th) cells and face the site of cytokine production in the Th cells selectively proliferate: immunofluorescence microscopic studies of Th-B antigen-presenting cell interactions. J. Exp. Med. 179:1507–1515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kupfer, A., T. R. Mosmann, and H. Kupfer. 1991. Polarized expression of cytokines in cell conjugates of helper T cells and splenic B cells. Proc. Natl. Acad. Sci. USA. 88:775–779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee, K. H., A. R. Dinner, C. Tu, G. Campi, S. Raychaudhuri, R. Varma, T. N. Sims, W. R. Burack, H. Wu, J. Wang, O. Kanagawa, M. Markiewicz, P. M. Allen, M. L. Dustin, A. K. Chakraborty, and A. S. Shaw. 2003. The immunological synapse balances T cell receptor signaling and degradation. Science. 302:1218–1222. [DOI] [PubMed] [Google Scholar]
- Lee, K. H., A. D. Holdorf, M. L. Dustin, A. C. Chan, P. M. Allen, and A. S. Shaw. 2002. T cell receptor signaling precedes immunological synapse formation. Science. 295:1539–1542. [DOI] [PubMed] [Google Scholar]
- Lowenthal, J. W., B. E. Castle, J. Christiansen, J. Schreurs, D. Rennick, N. Arai, P. Hoy, Y. Takebe, and M. Howard. 1988. Expression of high-affinity receptors for murine interleukin-4 (BSF-1) on hematopoietic and nonhemopoietic cells. J. Immunol. 140:456–464. [PubMed] [Google Scholar]
- Monks, C. R., B. A. Freiberg, H. Kupfer, N. Sciaky, and A. Kupfer. 1998. Three-dimensional segregation of supramolecular activation cluster in T cells. Nature. 395:82–86. [DOI] [PubMed] [Google Scholar]
- Qi, S. Y., J. T. Groves, and A. K. Chakraborty. 2001. Synaptic pattern formation during cellular recognition. Proc. Natl. Acad. Sci. USA. 98:6548–6553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen, B.-J., T. Hage, and W. Sebald. 1996. Global and local determinants for the kinetics of interleukin-4/interleukin-4 receptor α chain interaction: a biosensor study employing recombinant interleukin-4 binding protein. Eur. J. Biochem. 240:252–261. [DOI] [PubMed] [Google Scholar]
- Shoup, D., and A. Szabo. 1987. Role of diffusion in ligand binding to macromolecules and cell-bound receptors. Biophys. J. 40:33–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stinchcombe, J. C., G. Bossi, S. Booth, and G. M. Griffiths. 2001. The immunological synapse of CTL contains a secretory domain and membrane bridges. Immunity. 15:751–761. [DOI] [PubMed] [Google Scholar]
- Valitutti, S., S. Müller, M. Cella, E. Padovan, and A. Lanzavecchia. 1995. Serial triggering of many T-cell receptors by a few pMHC complexes. Nature. 375:148–151. [DOI] [PubMed] [Google Scholar]
- van der Merwe, P. A. 2002. Formation and function of the immunological synapse. Curr. Opin. Immunol. 14:293–298. [DOI] [PubMed] [Google Scholar]
- van der Merwe, P. A., and S. J. Davis. 2002. The immunological synapse: a multitasking system. Science. 295:1479–1480. [DOI] [PubMed] [Google Scholar]
- Wang, Y., B.-J. Shen, and W. Sebald. 1997. A mixed-charge pair in human interleukin 4 dominates high-affinity interaction with the receptor α chain. Proc. Natl. Acad. Sci. USA. 94:1657–1662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wild, M. K., A. Cambiaggi, M. H. Brown, E. A. Davies, H. Ohno, T. Saito, and P. A. van der Merwe. 1999. Dependence of T cell antigen recognition on the dimensions of an accessory receptor-ligand complex. J. Exp. Med. 190:31–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wofsy, C., D. Coombs, and B. Goldstein. 2001. Calculations show substantial serial engagement of T cell receptors. Biophys. J. 80:606–612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yannelli, J. R., J. A. Sullivan, G. L. Mandell, and V. H. Engelhard. 1986. Reorientation and fusion of cytotoxic T lymphocyte granules after interaction with target cells as determined by high resolution cinemicrography. J. Immunol. 136:377–382. [PubMed] [Google Scholar]