Stalk Phase Formation: Effects of Dehydration and Saddle Splay Modulus

Abstract

One of the earliest lipid intermediates forming in the course of membrane fusion is the lipid stalk. Although many aspects of the stalk hypothesis were elaborated theoretically and confirmed by experiments it remained unresolved whether stalk formation is always an energy consuming process or if there are conditions where the stalks are energetically favorable and form spontaneously resulting in an equilibrium stalk phase. Motivated by a recent breakthrough experiments we analyze the physical factors determining the spontaneous stalk formation. We show that this process can be driven by interplay between two factors: the elastic energy of lipid monolayers including a contribution of the saddle splay deformation and the energy of hydration repulsion acting between apposing membranes. We analyze the dependence of stalk formation on the saddle splay (Gaussian) modulus of the lipid monolayers and estimate the values of this modulus based on the experimentally established phase boundary between the lamellar and the stalk phases. We suggest that fusion proteins can induce stalk formation just by bringing the membranes into close contact, and accumulating, at least locally, a sufficiently large energy of the hydration repulsion.

INTRODUCTION

Membrane fusion is the merger of two membranes into one. Elucidation of the fusion mechanism is indispensable for understanding such fundamental biological processes as intracellular protein trafficking, secretion, fertilization, and viral infection (Jahn and Grubmuller, 2002; Jahn et al., 2003; Skehel and Wiley, 2000), and for biotechnological applications involving formation of liposomes (Lasic, 1995; Lichtenberg and Barenholz, 1988). Fusion of cell membranes is mediated and controlled by fusion proteins (Gibbons et al., 2004; Jahn et al., 2003; Modis et al., 2004; Skehel and Wiley, 2000). At the same time, feasibility and kinetics of membrane merger are largely determined by the architecture and energy of the intermediate structures emerging in the course of this process (Chernomordik and Kozlov, 2003).

Although proteinaceous fusion intermediates have been suggested for specific cell systems (Mayer, 2002), there is an accumulating evidence (Chernomordik et al., 1995; Chernomordik and Kozlov, 2003) that in many cases biological fusion and fusion of purely lipid synthetic membranes share at least one intermediate structure called the fusion stalk (Kozlov and Markin, 1983; Markin et al., 1984). The stalk is a first lipid connection emerging at the early stage of the fusion reaction between the contacting (proximal) lipid monolayers of two apposing membranes. Stalk is the earliest hemifusion intermediate (Chernomordik et al., 1998, 1987; Kemble et al., 1994; Melikyan et al., 1995b), which further evolves to fusion pore (Melikyan et al., 1995a; Zimmerberg et al., 1994), completing the fusion process.

The fusion stalk has been suggested as a transient structure determining an energy barrier of the fusion reaction and, hence, limiting the fusion rate. Analysis of the physical factors determining the stalk energy is absolutely necessary for understanding the mechanisms by which the fusion proteins mediate the membrane merger (Chernomordik and Kozlov, 2003). An extensive theoretical work has been devoted to modeling the lipid arrangement within the stalk intermediate and calculations of its energy (Kozlov et al., 1989; Kozlov and Markin, 1983; Kozlovsky et al., 2002; Kozlovsky and Kozlov, 2002; Kuzmin et al., 2001; Malinin and Lentz, 2004; Markin and Albanesi, 2002; Markin et al., 1984; May, 2002; Siegel, 1993, 1999), as well as to numerical simulations of stalk formation (Marrink and Mark, 2003; Muller et al., 2002). One of the major results of these theoretical efforts was a conclusion that the stalk energy can be strongly modulated by lipid composition of the fusing membranes (Kozlov et al., 1989; Kozlov and Markin, 1983; Kozlovsky et al., 2002; Kozlovsky and Kozlov, 2002; Marrink and Mark, 2003). This prediction has been verified successfully in a series of experimental investigations of membrane fusion kinetics, which provided confidence in the adequacy of the stalk mechanism (Chernomordik et al., 1995; Chernomordik and Kozlov, 2003). At the same time, a direct experimental evidence for stalk formation was lacking and, hence, the stalk intermediate remained hypothetical. An experimental breakthrough has been reached recently by Huang's group, which was able to observe for the first time formation of stalks by electron density reconstruction of lipid mesophases (Yang et al., 2003; Yang and Huang, 2002, 2003). An important outcome of these works was a demonstration that the conditions exist where the stalk energy becomes lower than that of the flat lipid bilayer so that the first stage of membrane fusion does not represent an energy barrier and proceeds spontaneously.

In this work we analyze the factors required to enable a spontaneous formation of fusion stalks. We demonstrate that, in addition to the lipid spontaneous curvature, the stalk energy can be strongly influenced by the saddle splay (Gaussian) modulus of the lipid monolayers (Helfrich, 1973) and by the hydration repulsion acting between the apposing membranes (Leikin et al., 1993; Marcelja and Radic, 1976; Rand and Parsegian, 1989). We show that interplay between these three factors within the realistic parameter ranges can determine the observed spontaneous stalk formation, and compute the relationships between the values of the membrane elastic moduli and the hydration repulsion parameters necessary to interpret the experimental phase diagrams (Yang et al., 2003; Yang and Huang, 2002, 2003). Based on the obtained results, we suggest that the hydration repulsion can contribute to the mechanism by which fusion proteins that bring the apposing membranes into close contact can drive the first stages of the fusion reaction.

Phenomenology of spontaneous stalk formation

Phospholipids in aqueous solutions exhibit a rich mesophasic behavior (Luzzati, 1968; Seddon and Templer, 1995). The most common phases formed by phospholipids present in cell membranes are the lamellar (L_α) and the inverted hexagonal (H_II) phases. The L_α phase consists of a stack of flat lipid bilayers separated by 2–3 nm-thick water layers (Rand and Parsegian, 1989), whereas the H_II phase has a completely different nonbilayer topology (Epand, 1997; Rand and Fuller, 1994; Seddon, 1990). It is represented by water cylinders of ∼2 nm radius wrapped by lipid monolayers and packed in a way that their cross sections form a two-dimensional hexagonal array (Rand and Fuller, 1994). Transition between the L_α and H_II phases can be driven by changes in temperature, hydration (Gawrisch et al., 1992; Kozlov et al., 1994), and lipid composition (Chen and Rand, 1997; Fuller et al., 2003; Leikin et al., 1996; Szule et al., 2002). It has been suggested that transformation of the flat bilayers of the L_α phase into the cylinders of the H_II phase proceeds via spontaneous stalk formation (Siegel and Epand, 1997).

The experiments by Huang's group have been performed with the phospholipid diphytanoylphosphatidylcholine (DPhPC) (Yang and Huang, 2002, 2003) and with mixtures of dioleoylphosphatidylcholine (DOPC) and dioleoylphosphatidylethanolamine (DOPE) (Yang et al., 2003). The lipids were spread on a flat substrate producing an oriented sample exposed to air with controlled temperature and relative humidity denoted by ζ. Changes of ζ resulted in variation of the amount of water within the lipid phase referred to as lipid hydration (see e.g., Gawrisch et al., 1992). The goal was to explore transitions between lipid phases resulting from changes of temperature, sample hydration and lipid composition. In the present study we will focus on the two latter factors and address the representative experimental results obtained for a fixed temperature of 35°C.

At full hydration DPhPC formed the lamellar L_α phase (Yang and Huang, 2002). When the relative humidity in contact with the sample was reduced to a critical value, ζ*, of ζ* ∼80%, the lamellar phase converted into a phase of stalks arranged in a rhombohedral lattice and connecting the proximal monolayers of the apposing bilayers. The intermembrane distance of the lamellar phase at the transition point was ∼1 nm. The three-dimensional electron density distribution constructed from the complete diffraction pattern of the stalk phase showed an hourglass-like shape of individual stalks, similar to the hypothesized structure of the stalk intermediate (Kozlov and Markin, 1983; Kozlovsky and Kozlov, 2002; Markin and Albanesi, 2002). When the relative humidity was further reduced to below ∼70%, the lipid formed the inverted hexagonal H_II phase. Clearly, the stalks observed in these experiments were not transient intermediate structures, but rather formed an equilibrium phase located in the phase diagram between the L_α and H_II phases.

The phases adopted by DOPC/DOPE mixtures upon the humidity changes were similar to those of DPhPC. However, the phase boundaries were dependent on the lipid composition. Pure DOPC formed the L_α phase at full hydration but formed the stalk phase when the relative humidity decreased below ζ* ∼45%. The values of ζ* for different lipid compositions, as taken from Yang et al. (2003) are presented in Table 1. The data shows a trend of increasing ζ* as the DOPC content decreases, although the two mixtures with DOPC/DOPE ratio of 3:1 and 2:1 have almost the same ζ*. For lower DOPC contents the system behavior became more complex and for mixtures with DOPC/DOPE ratio of 1:3 or smaller, the stalk phase did not form at all, and the lamellar phase transformed directly into the hexagonal phase.

TABLE 1.

DOPC/DOPE	1:0	3:1	2:1	1:1	1:2	1:3
λ[nm]	0.210	0.190	0.183	0.170	0.157
ζ*	45%	67%	68%	76%	83%	no stalks
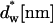	0.748	0.808	0.786	0.787	0.786
β*[nm]	−0.01	−0.19	−0.20	−0.25	−0.29

THEORETICAL MODEL

Outline of analysis

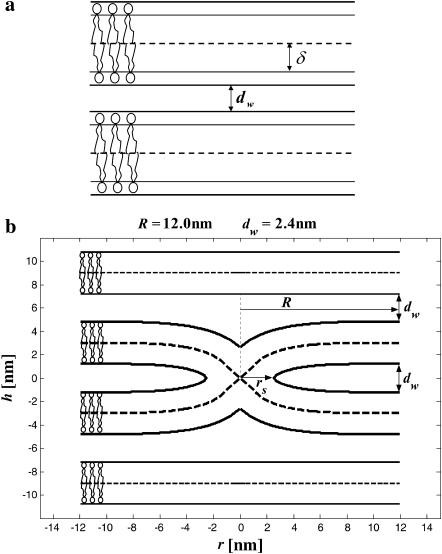
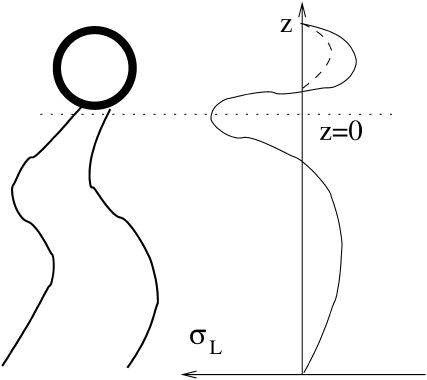
Our goal is to analyze the conditions of stalk formation in lipid lamellar phase upon changes in the system hydration and lipid composition. To this end we consider two parallel adjacent membranes within the lamellar phase, which are separated by a water layer with thickness depending on the relative humidity, ζ, of the surrounding air. In the initial state the monolayers are flat and the water layer between them is continuous (Fig. 1 a). In the final state a lipid connection—a fusion stalk—is formed between the apposing membrane monolayers (Fig. 1 b). The energy of stalk formation consists of two major contributions: 1), the change of the elastic energy of membrane monolayers, which is caused by their deformation from the initial flat shape into the stalk configuration and 2), the change of the energy of the intermembrane interactions. The former contribution has been analyzed partially in the previous studies (Kozlov et al., 1989; Kozlov and Markin, 1983; Kozlovsky et al., 2002; Kozlovsky and Kozlov, 2002; Kuzmin et al., 2001; Markin and Albanesi, 2002; Markin et al., 1984; May, 2002; Siegel, 1993, 1999). In the present work we will extend this consideration by taking into account the effects of the saddle splay (Gaussian) elasticity of membrane monolayers (Helfrich, 1973) and the varying intermembrane distance. The reason for the latter contribution is that the membrane area subject to the intermembrane interaction in the initial state is reduced when stalk forms and fills a part of the intermembrane gap by lipid material.

FIGURE 1.

Stalk formation within a lamellar phase. The dashed lines represent the midsurface separating lipid monolayers within a bilayer. The thicker solid lines represent membrane-water boundaries. (a) Initial state of two parallel flat membranes separated by a water distance d_w. The neutral surface (thinner solid lines) is lying at the interface between the polar heads and the hydrocarbon chains (Leikin et al., 1996) at a distance δ from the bilayer midsurface. (b) Cross section of the stalk (neutral surface not shown). The stalk radius, R, is the distance from its center at which all elastic stresses vanish. The radius r_s, defines the area that contributes the most to the stalk elastic energy. The stalk profile is calculated for d_w = 2.4 nm by minimizing the elastic energy of stalk monolayers and the hydration energy of the stalk wings. The hydration parameters used are P₀ = 10^10.6 dyn/cm² and λ = 2.1 Å. The values of the spontaneous curvature and the Gaussian modulus are taken to be zero, J_s = 0, and 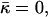and the elastic moduli are κ = 4 × 10⁻²⁰ J and κ_t = 0.04 N/m, while δ = 1.3 nm.

In the following we first introduce the way and assumptions we use to calculate each of the energy contributions. We then compute the total energy of stalk formation as a function of the elastic parameters of the lipid monolayers, lipid composition, and hydration of the lipid sample, the latter related to the relative humidity of the air. We determine the relationship between these parameters, corresponding to formation of an equilibrium stalk and present the results in the form of a phase diagram.

Elastic energy of stalk formation

We calculate the elastic contribution to the stalk energy by using the model for tilt and splay deformations of lipid monolayers (Hamm and Kozlov, 1998, 2000). Below we sketch this approach, whose major part has been presented in detail by Kozlovsky and Kozlov (2002) and some mathematical details are given in Appendix A.

We consider, separately, each monolayer of the lipid bilayer. The monolayer shape is described by the shape of its neutral surface lying at the interface between the polar heads and the hydrocarbon chains (Leikin et al., 1996) at a distance δ from the bilayer midsurface (Fig. 1 a). Average orientation of the hydrocarbon chains of lipid molecules is described by the effective chain director, Three deformations contribute to the monolayer elastic energy. The first is tilt of the chain director with respect to the normal to the monolayer surface 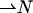(Appendix A). The second and third are splay, 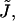and saddle splay, 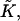of the hydrocarbon chains. The latter deformations include additive contributions from the monolayer bending and tilt variation along the monolayer surface (Hamm and Kozlov, 2000). They can be expressed as the first- and second-order invariants of the tensor n_ij, which is a gradient of the chain director 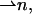calculated along the monolayer surface (Appendix A). The splay is the two-dimensional divergence of the chain director, 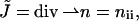whereas the saddle splay is the determinant of the director gradient, 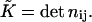In the case of a bent monolayer with vanishing tilt, 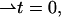the splay and saddle splay reduce to the total, J, and Gaussian, K, curvatures of the monolayer surface (Hamm and Kozlov, 2000).

The structure of the monolayer is characterized by its spontaneous curvature, J_s, and by its saddle splay modulus, 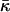(Helfrich, 1973). The resistance of the monolayer to deformation is accounted by the monolayer bending, κ, and tilt, κ_t, moduli (Hamm and Kozlov, 1998, 2000). The elastic energy per monolayer unit area, related to the initial state of a flat monolayer, is given by

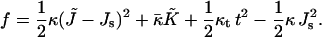(1)

The elastic energy of the stalk, F_e, is determined by integrating Eq. 1 over the area A of the two monolayers,

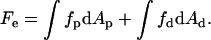(2)

Here and below, the subscripts p and d denote the proximal and distal monolayers, respectively.

We consider a single stalk formed between two parallel membranes in the L_α phase, with the intermembrane distance d_w. The lamellar phase imposes two structural constraints on the stalk membranes. The first is that far from the stalk the two membranes become flat and adopt the initial parallel orientation with separation d_w. The second constraint is that near the stalk, membranes are confined from above and below by the adjacent membranes of the L_α phase. The exact character of these limitations depends on the intermembrane interactions and the deformations of the neighboring membranes. We assume that the neighboring membranes remain flat and their interaction with the stalk wings (Kozlovsky et al., 2002) determines the shape of the latter.

The tilt deformation of the stalk monolayers is generated by packing the hydrocarbon chains in the nonbilayer structural defect (Kozlovsky and Kozlov, 2002), which unavoidably emerges in the middle of the stalk intermediate and is referred to as the hydrophobic interstice (Siegel, 1993). The tilt relaxes along the monolayer surface resulting in a contribution to the splay. A smooth connection between the interstice and the undisturbed flat membrane surrounding the stalk generates bending of the stalk monolayers (Fig. 1 b).

Contribution of the intermembrane interaction to the energy of stalk formation

Interaction between electrically neutral membranes in the lamellar phase includes several competing forces such as van der Waals attraction, undulation force, and repulsive hydration force (Safran, 1994), which result in an equilibrium intermembrane distance of 2–3 nm (Rand and Parsegian, 1989). Stalk formation has been observed when the intermembrane distance was reduced to ∼1 nm (Yang and Huang, 2002). At such small distances, the major energy contribution arises from hydration forces (Rand and Parsegian, 1989) and the two other interactions can be neglected (Kozlov et al., 1994).

The pressure generated by the hydration interaction between two parallel flat membranes separated by a water layer of thickness d_w is given by

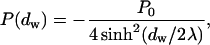(3)

where P₀ and λ are hydration force parameters (Leikin et al., 1993; Rand and Parsegian, 1989). The energy of the hydration interaction between two such membranes of area A is thus given by

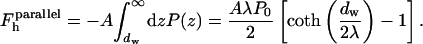(4)

The contribution to the energy of stalk formation due to the hydration interaction, ΔF_h, can be separated into two parts.

The first contribution, denoted as ΔF_h1, is related to the fact that the stalk fills a part of the gap between the membranes with lipid material. As a result, the membrane area exposed to the hydration repulsion is reduced by 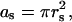where r_s ≈ 2.5 nm is the radius of the stalk base (Fig. 1 b), so that

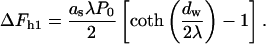(5)

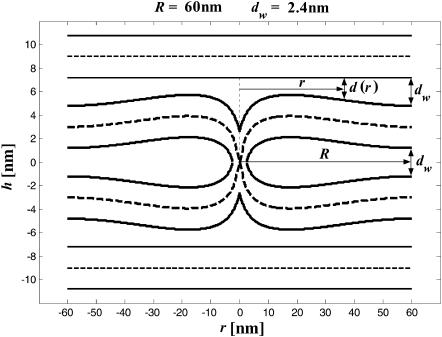
The second contribution, ΔF_h2, comes from the effect of the hydration repulsion on the shape of stalk monolayers. As shown in Kozlovsky et al. (2002), minimization solely of the elastic energy predicts formation of stalk “wings” bulging out of the planes of the fusing membranes as illustrated in Fig. 2 (note that the apparent narrowing of the membranes at the center of the stalk results solely from the different scales along the r and h axes). The outer monolayers of the wings tend to approach the upper and lower adjacent membranes in the lamellar phase to distances, d, smaller than the average water spacing in the lamellar phase d_w. Obviously, this results in additional energy of the hydration repulsion, ΔF_h2, which must reduce the amplitudes of the stalk wings as compared to the case where the hydration repulsion is not taken into account explicitly (Kozlovsky et al., 2002). We account for this effect by calculating the hydration energy of the wing formation as the work produced against the hydration repulsion in the course of changing the distance between the membranes relative to the equilibrium spacing,

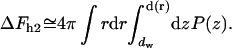(6)

The internal integration in Eq. 6 provides the hydration energy of the elements of the wing surface, which possess the radial coordinate r and approach the adjacent membranes from the distance d_w to the distance d(r) (Fig. 2). The external integration is performed over the area of the stalk wings bulging toward the adjacent membranes.

FIGURE 2.

Stalk cross section in a case where the hydration repulsion between the stalk wings and the adjacent membranes is not taken into account. The apparent narrowing of the membranes at the center of the stalk results from the different scales along the r and h axes. As in Fig. 1 b, the values of the spontaneous curvature and the Gaussian modulus are taken to be zero, J_s = 0, and 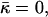and the elastic moduli are κ = 4 × 10⁻²⁰ J and κ_t = 0.04 N/m, while δ = 1.3 nm. The stalk radius is chosen to be R = 60 nm.

In addition to the two hydration effects above, another contribution to the energy has to be discussed, arising from the hydration interaction between the portions of the same monolayer in the course of membrane bending. We assume that the latter energy is, effectively, accounted for by the monolayer bending energy (Eq. 1), where the hydration interaction determines, in addition to other factors, the membrane elastic moduli. The same assumption has been used in a model for the L_α–H_II phase transition (Kozlov et al., 1994), which succeeded to describe delicate features of this process. (A more detailed discussion of this issue has been presented in Appendix C of Kozlovsky and Kozlov, 2002.)

For the purposes of the following analysis of the experimental data, it is convenient to express the energy given by Eq. 5 through the relative humidity of the air surrounding the lipid sample, ζ, which is controlled experimentally (Yang and Huang, 2002). Using the relationships of Rand and Parsegian (1989), we obtain

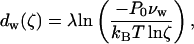(7)

and thus

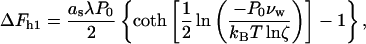(8)

where v_w ≈ 0.03 nm³ is the volume of a water molecule.

Method of solving the problem

The mathematical problem is to find the shape of the stalk monolayers and the distribution of the tilt along the monolayer surfaces, which minimize the sum of the elastic energy, Eq. 1, and the energy due to the intermembrane interactions, Eq. 6. The solution must satisfy the boundary conditions of filling the hydrophobic interstices by the hydrocarbon chains and matching the surrounding membranes. The explicit expressions for the splay 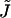and saddle splay 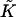of a monolayer with radial symmetry are presented in Appendix A. We solve this problem numerically by minimizing the elastic energy of the lipid bilayer and determining the shape of stalk monolayers and distribution of tilt by the method of finite elements (Prenter, 1975) using the MATLAB software (The MathWorks, Natick, MA), as described in detail in Appendix B.

RESULTS

Stalk elastic energy and the hydration energy of the wings

The numeric analysis shows that the curvatures of the stalk monolayers and the distribution of tilt of the lipid chains along the monolayer surfaces are largely determined by the boundary conditions in the hydrophobic interstice and the ratio between the elastic moduli of tilt and splay, κ/κ_t. At the same time, the stalk structure, practically, does not depend on the values of the spontaneous curvature, J_s, and the saddle splay modulus, 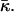This property allows presenting the stalk elastic energy in the form

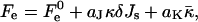(9)

where 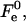a_J, and a_K are independent of J_s and 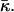The value 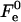has a meaning of the stalk elastic energy for J_s = 0 and 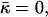and is given, according to Eqs. 1 and 2, by

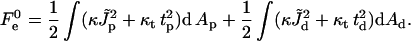(10)

The dimensionless coefficients a_J and a_K are given by

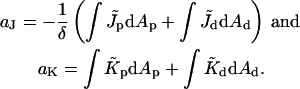(11)

The elastic energy, Eq. 9, depends linearly on J_s and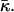

The other parameters determining the stalk energy are the elastic moduli κ and κ_t, the intermembrane separation d_w, and the distance between the neutral surface of each of the monolayers and the bilayer midsurface, δ (the latter value is taken as a positive value for both monolayers). We obtained that a_J and a_K are almost independent of these parameters and within a realistic range of κ and κ_t, they have practically constant values: a_J = 26.1 and a_K = −11.8. Therefore, Eq. 9 can be written as

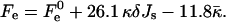(12)

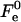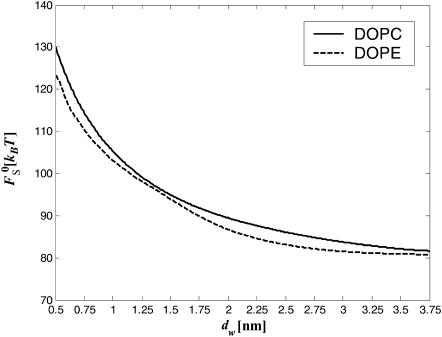
The value of depends considerably on the moduli κ and κ_t, and on the shape of the stalk membrane. The latter, as mentioned above, is strongly influenced by the hydration repulsion between the stalk wings and the adjacent membranes. Therefore, calculation of 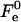required concurrent determination of the optimal shape of the stalk monolayers which minimizes the sum of the elastic energy and the hydration energy of the wings, ΔF_h2. According to our analysis, the hydration forces result in almost complete flattening of the stalk wings as compared to the case where the hydration interaction is not taken into account (Fig. 2). This is illustrated in Fig. 1 b presenting the calculated stalk configuration for d_w = 2.4 nm.

The results of the numerical calculations of the sum of the elastic contribution 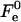and the hydration energy of the wings,

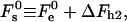(13)

for the optimal membrane shape and for the hydration parameters of DOPC and DOPE membranes, are presented in Fig. 3 as functions of the water distance, d_w. In this figure and in all the calculations below, the energy is presented in the unit of k_BT ≈ 4 × 10⁻²¹ J (where k_B is the Boltzmann constant and T = 308°K is the absolute temperature) and the values of the two elastic moduli are taken to be κ ≈ 4 × 10⁻²⁰ J (see e.g., Niggemann et al., 1995) and κ_t = 0.04 N/m (Hamm and Kozlov, 1998), whereas δ = 1.3 nm (Rand and Parsegian, 1989). For large values of d_w, the energy 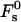becomes practically constant, adopting a value of 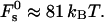The total energy of the stalk, restricted by the membranes of the lamellar phase, is thus given by

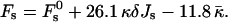(14)

To proceed, it is convenient to define an effective parameter β, which is a linear combination of the monolayer spontaneous curvature J_s and the saddle splay modulus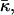

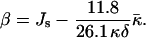(15)

The energy (Eq. 14) depends on J_s and 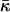only through β, whereas the dependence on the intermembrane distance d_w is accounted for only by :

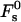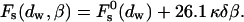(16)

The effective parameter, β, has the same physical dimensions as the spontaneous curvature, J_s, and characterizes the tendency of lipids to form stalks.

FIGURE 3.

The stalk energy 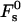for J_s = 0 and 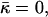as a function of the intermembrane distance d_w. It includes both elastic contribution and hydration energy of the stalk wings. The hydration force parameters used are P₀ = 10^10.6 dyn/cm², λ = 2.1 Å for DOPC, and λ = 1.3 Å for DOPE. The elastic moduli are κ = 4 × 10⁻²⁰ J and κ_t = 0.04 N/m, while δ = 1.3 nm.

Total energy and conditions for spontaneous stalk formation

The energy of a single stalk formation between two parallel membranes of the lamellar phase is the sum of the energy F_s, Eq. 16, and the hydration energy ΔF_h1, Eq. 5, released due to stalk formation

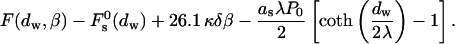(17)

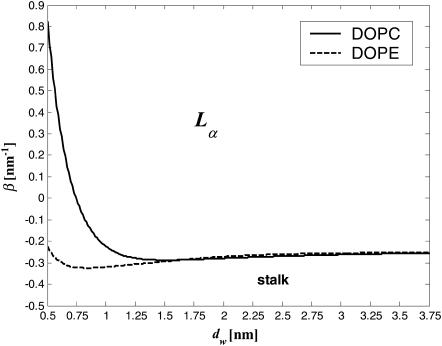
The conditions for spontaneous stalk formation corresponding to negative energy, Eq. 17, can be represented as a phase diagram expressed in terms of d_w and β (Fig. 4). The phase boundaries are determined by the condition F = 0, for the measured hydration force parameters, P₀ = 10^10.6 dyn/cm², λ = 2.1 Å for DOPC, and λ = 1.3 Å for DOPE (Rand and Parsegian, 1989). The region below the phase boundary is characterized by negative energy, F < 0, and describes the parameter range of spontaneous stalk formation. For the parameters from the region above the phase boundary the energy is positive, F > 0, and the flat membranes are stable with respect to stalk formation. According to this phase diagram, for the practically important intermembrane distances d_w, the larger the parameter β is, the smaller is the d_w (and the lower ζ) that has to be reached to make the stalk formation energetically favorable. Note that a re-entrant lamellar-stalk-lamellar transition can be driven by changing d_w, as predicted by the nonmonotonous character of the curves in Fig. 4. This prediction holds, however, only if the combination of the membranes parameters, β, does not change with dehydration (see Discussion below).

FIGURE 4.

Phase diagram of stalk formation as a function of the intermembrane distance d_w and the effective parameter β. The lines indicate the phase boundaries for DOPC (solid line), for which λ = 2.1 Å, and DOPE (dashed line), for which λ = 1.3 Å. The other parameters determining the phase boundary are κ = 4 × 10⁻²⁰ J, κ_t = 0.04 N/m, δ = 1.3 nm, and P₀ = 10^10.6 N/m².

Lamellar-stalk phase transition: comparison with the experimental results

Transition from the lamellar to stalk phase mediated by variations of the relative humidity, ζ, can be seen as initiated by formation of single stalks. Taking into account Eq. 8, the energy of one stalk, Eq. 17, expressed through ζ is

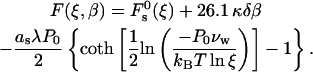(18)

When the stalk energy (Eq. 18) becomes negative, spontaneous formation of multiple stalks is expected to result in transformation of the lamellar to the stalk phase. However, the energy of a stalk within such phase may differ from the energy (Eq. 18) of an isolated stalk because of the membrane-mediated stalk-stalk interaction. To estimate this interaction energy, we investigated in further detail the energy of a single stalk formed in the lamellar phase. We found that the elastic stresses are concentrated in a compact region near the stalk center. This region extends up to a radial distance of ∼3.5 nm from the stalk center. Our computation for a characteristic intermembrane separation of d_w = 2.4 nm (Rand and Parsegian, 1989) shows that the elastic energy of the stalk portions outside this compact region amounts to <1.5 k_BT. As long as the distance between centers of two stalks within the stalk phase constitutes 7 nm or more, only the outside region of each stalk is perturbed so that the resulting energy change should not exceed 1.5 k_BT. For reduced d_w ≈ 1 nm, this energy slightly increases but does not exceed several k_BT, which is negligible compared to the corresponding change of the hydration energy. According to the experimental information (Yang et al., 2003; Yang and Huang, 2003), the unit cells of the rhombohedral lattice of stalks form two-dimensional hexagonal arrays stacked in layers. The characteristic side-length of a hexagonal unit cell of this lattice is 6.84 nm, which corresponds to the distance of 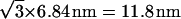between the adjacent stalks in the same layer and to the separation of 6.84 nm between the neighboring stalks in two consecutive layers. The smaller of these two distances is very close to our criterion of 7 nm, so that we neglect the stalk interaction energy and describe the energy of a stalk within the rhombohedral phase by Eq. 18.

The condition of the lamellar-stalk phase transition, F < 0, will be expressed in terms of the lipid parameter β, Eq. 15, whose critical value, β*(ζ), depends on the relative humidity, ζ, and determines the phase boundary between the lamellar and the stalk phases in the β–ζ phase diagram. It can be determined, based on Eq. 18, from the condition F < 0.

Stalk formation by DPhPC

The physical properties of DPhPC have been scarcely investigated (Hung et al., 2000) and its elastic constants have not been measured. Because DPhPC has the same headgroup as DOPC, the two lipids can be expected to have the same hydration force decay length, λ = 2.1 Å (Rand and Parsegian, 1989). We also assume that DPhPC has the same bending modulus and tilt modulus as DOPC. At relative humidity of 80%, DPhPC underwent a phase transition from the lamellar into the stalk phase. Based on this value, we estimate the critical parameter of this lipid to be β* = −0.23 nm⁻¹.

Stalk phase formation by DOPC/DOPE mixture

The value of the lipid parameter β, which, as defined by Eq. 15, is a linear combination of the monolayer spontaneous curvature J_s and the saddle splay modulus 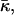depends on the lipid composition of the DOPC/DOPE mixture. In the Discussion we show the effective parameter of DOPE is expected to be smaller than that of DOPC, β^DOPE < β^DOPC. Therefore, β should increase monotonically as the membrane fraction of DOPC increases.

Other elastic constants characterizing DOPC and DOPE monolayers have similar values for the two lipids. We will take the monolayer splay (bending) and tilt moduli to be κ = 4 × 10⁻²⁰ J (Leikin et al., 1996) and κ_t = 0.04 N/m (Hamm and Kozlov, 1998), respectively. The neutral surface lies at a distance δ = 1.3 nm (Rand and Parsegian, 1989) from the bilayer midsurface.

The phase boundary β*(ζ) depends also on the decay length of the hydration forces, λ, Eq. 18. The decay length of DOPC is λ^DOPC = 2.1 Å, whereas the decay length of DOPE, which is assumed to be equal to that of egg PE, is λ^DOPE = 1.3 Å (Rand and Parsegian, 1989). We are not aware of a model allowing calculation of the parameters of the hydration repulsion of a mixture based on those of individual components. Therefore, we plot two phase boundaries between the lamellar and stalk phases (Fig. 5), one corresponding to λ = λ^DOPC (Fig. 5, curve 1, solid line) and the other to λ = λ^DOPE (Fig. 5, curve 2, dashed line). For a mixture of DOPC/DOPE, the decay length should be between those of the pure lipids, λ^DOPE < λ < λ^DOPC. Therefore, we can only say that the phase boundary of a mixture is bounded by the two curves (Fig. 5, curves 1 and 2). The phase transition of pure DOPC (Table 1) is represented in Fig. 5 a.

FIGURE 5.

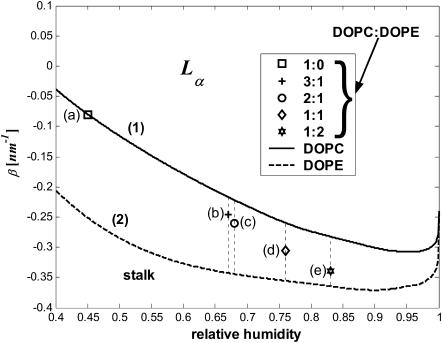
The lamellar-stalk phase diagram as a function of the relative humidity and the effective parameter β. The two thick lines indicate the boundaries for phase transition from the lamellar to the stalk-phase of 1), DOPC (solid line) and 2), DOPE (dashed line). The vertical dashed lines represent the ranges of β* values for mixtures with DOPC/DOPE ratios: (a) 1:0, (b) 3:1, (c) 2:1, (d) 1:1, and (e) 1:2.

The range of the critical parameter β*(ζ), as computed for the values of the relative humidity ζ* mediating the phase transition of the several lipid mixtures (Yang et al., 2003), are shown in the phase diagram, Fig. 5, by the dotted vertical lines (Fig. 5, b–e). The marked point on each of those dotted lines is the result of choosing a linear approximation for the decay length λ^X of a mixture, DOPC/DOPE, in the form

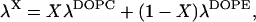(19)

where X is the mole fraction of DOPC.

Parameters of the lamellar-stalk phase transition at T = 35°C are presented in Table 1. For different ratios of the DOPC/DOPE mixture, we give the relative humidity, ζ*, of the transition as extracted from Fig. 2 of Yang et al. (2003). The presented values of the hydration force parameter, λ, are within the linear approximation of Eq. 19.

Fitting the values of the saddle splay modulus

The values obtained for the critical parameters β* allow us to estimate the saddle splay modulus, 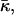of DOPC and DOPE, fitting the experimental observations. Note that 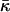can only be measured in certain circumstances, by Q_II lattice swelling experiments (e.g., Templer et al., 1998), or in one-component lipid systems with sharp thermotropic L/Q_II phase transitions (Siegel and Kozlov, 2004).

We obtained that the critical parameter of DOPC satisfying the condition that the L_α-stalk phase transition of this lipid occurs at the relative humidity ζ* = 45%, has the value β*^DOPC = −0.01 nm⁻¹ (Fig. 5 a). Neglecting the possible effects of dehydration on the effective parameter β (see below) and taking into account that at full hydration the spontaneous curvature of DOPC has been measured, 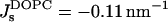(Chen and Rand, 1997), we obtain, based on Eq. 15, the value of the saddle splay modulus of this lipid:

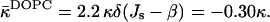(20)

The value of the saddle splay modulus of DOPE can be estimated in a different way. A critical observation is that at full hydration the temperature change drives a direct transition of DOPE between the L_α and H_II phases without formation of an equilibrium stalk phase (Yang et al., 2003). This means that the stalk energy is positive compared to both the lamellar and H_II phases. On the other hand, the stalks serve as intermediate structures of the transition from the lamellar into nonlamellar phases (Siegel and Epand, 1997) and their formation represents an energy barrier of the process. Estimations based on the experimental investigations of the electrical breakdown of membranes (Chernomordik and Abidor, 1980; Kuzmin et al., 2001; Weaver and Mintzer, 1981) show that an upper bound to the energy barrier the membrane can overcome to form a stalk within an experimental timescale is ∼40 k_BT. The latter estimation, which is not crucial for the present analysis, implies that the characteristic frequency of formation of nonbilayer structures driven by the thermal fluctuation does not depend on the specific architecture of the structure, but is determined by the characteristic number of lipid molecules involved and the membrane area available for fluctuations. The stalk energy should, therefore, be in the range

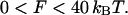(21)

Taking the limit of 100% humidity, ζ → 1, we obtain from Eqs. 7 and 8 that d_w → ∞ and ΔF_h1 → 0. In that case, Eq. 18 is reduced to Eq. 16 so that F → F_s. Also, note that, as mentioned above, for large values of d_w, the energy 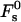becomes independent of d_w, adopting the value of 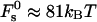(Fig. 3). Based on that we get

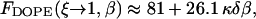(22)

and substituting it into the inequality expression Eq. 21, we obtain the range for the effective parameter of DOPE,

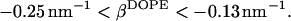(23)

Using Eq. 15 and the measured value of the spontaneous curvature, 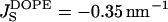(Kozlov et al., 1994; Leikin et al., 1996), we find for the saddle splay modulus of DOPE a range of

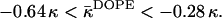(24)

DISCUSSION

Motivated by the recent discovery of a stalk phase in dehydrated lipid systems (Yang et al., 2003; Yang and Huang, 2002, 2003), we have addressed theoretically the conditions of spontaneous formation of fusion stalks resulting in transformation of a lamellar phase into stalk phase. The energy of stalk formation has three major contributions: 1), the elastic energy accounting for the splay, saddle splay and tilt deformations of the membrane monolayers; 2), hydration energy of interaction between the stalk wings, and the adjacent membranes in the lamellar phase; and 3), the reduction in the hydration energy of the system, with the reduction due to the stalk formation of the membrane area exposed to the hydration repulsion between the apposing monolayers.

The effects of the hydration repulsion have been considered previously within the context of contribution to the energy barrier of establishing a local membrane contact and rupture of the contacting monolayers preceding their merger (Kuzmin et al., 2001; Leikin et al., 1987). In the present work we analyze the situation where powerful forces such as osmotic ones bring the membranes into a close and extended contact. The hydration energy, accumulated due to the work of these forces, turns out to be a factor driving rather than preventing stalk formation. According to the results of the present analysis, spontaneous stalk formation is largely due to the hydration effects.

Previous models of stalk formation accounted for the elastic energy of bending (Kozlov and Markin, 1983; Kuzmin et al., 2001; Leikin et al., 1987; Markin and Albanesi, 2002; Markin et al., 1984; Siegel, 1993, 1999), splay (Kozlovsky et al., 2002; Kozlovsky and Kozlov, 2002), and tilt (Kuzmin et al., 2001; Kozlovsky et al., 2002; Kozlovsky and Kozlov, 2002; May, 2002) of membrane monolayers. At the same time, they neglected another elastic contribution resulting from the saddle splay deformation, 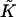(Hamm and Kozlov, 2000), which in the absence of the tilt deformation of the lipid chains becomes the Gaussian curvature of the surface, K. For most membrane processes membrane topology does not change and the energy of the saddle splay deformations remains constant because, according to the Gauss-Bonnet theorem, integral of K and, in a good approximation, of 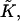over a closed surface is a topological invariant. However, as a result of stalk formation the membrane monolayers undergo a topological rearrangement changing the saddle splay energy. Therefore, the energy of stalk formation depends explicitly on the saddle splay modulus, 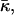and this dependence may be considerable provided that 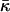has values comparable with the bending constant κ. In the present work we investigate for the first time the effect of the saddle splay modulus on the stalk energy.

Using Eq. 24, we find that the 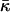values of the lipids exhibiting the equilibrium stalk formation have to be negative in agreement with the previous estimations based on the lateral stress profile within the lipid monolayer (Templer et al., 1998) and the numerical mean field calculations (Szleifer et al., 1990). The obtained absolute values of the splay modulus of DOPC and DOPE (Eqs. 20 and 24) are also in qualitative agreement with the calculated values, which vary for a monolayer between 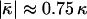(Templer et al., 1998) to 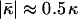and less.

Note that the presented estimations of 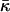(Eqs. 20 and 24), as well as all other quantitative results, have a limited accuracy because of the intrinsic limitations of the elastic stalk model (Kozlovsky and Kozlov, 2002) and an approximate knowledge of the parameters such as the splay (bending) modulus, κ (Rand, 2003), and the distance, δ, between the membrane midsurface and the monolayer neutral plane (Kozlov et al., 1994; Kozlov and Winterhalter, 1991a,b; Leikin et al., 1996). The value of δ = 1.3 nm we used in the computations above is based on the x-ray investigation of DOPC lamellar phases interpreted by the Luzzati method (Rand, 2003; Rand and Fuller, 1994). The quantitative results of the latter may differ by ∼10% from predictions of other methods (Nagle and Tristram-Nagle, 2000a,b).

Summarizing, our model shows that formation of equilibrium stalk observed experimentally can be explained within a reasonable range of parameters by interplay between the hydration and elastic energies, the latter including a considerable contribution of the saddle splay energy.

Possible additional effects of the lipid sample dehydration

We have analyzed the direct effect of dehydration of lipid sample on stalk formation. There may be additional indirect effects related to partial dehydration of the lipid headgroups such as that of DOPC. Some of the water molecules associated with the choline group disassociate upon dehydration and thus decrease the effective size of the headgroup (Cevc and Marsh, 1987). The result is that the repulsion between headgroups is expected to decrease. The consequences of this effect can be analyzed qualitatively by considering a schematic lateral stress profile of DOPC (Fig. 6). Due to the reduced repulsion between the heads, the lateral stress at the head region of a dehydrated DOPC is expected to be less repulsive, as represented schematically by the dashed line (Fig. 6). The effect on the elastic constants is that the spontaneous curvature, J_s, will decrease (become more negative), whereas the saddle splay modulus, 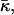will increase (will be less negative; see e.g., Ben-Shaul, 1995; Helfrich, 1990).

FIGURE 6.

Lateral stress profile of a monolayer, σ_L(z). The solid line represents schematically the stress profile for DOPC. The dashed line at the head region represents the effect of either dehydrating the PC head or of replacing it by a PE head.

Both effects, the decrease of J_s and increase of 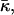will reduce the effective parameter β (Eq. 15) of DOPC, decreasing the stalk elastic energy (Eq. 16), thereby promoting stalk formation.

Similar reasoning helps to find a relationship between the effective parameter of DOPE and that of DOPC. Indeed, hydration of the DOPE polar head is smaller than that of DOPC (Rand and Parsegian, 1989). Therefore, 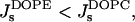and 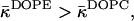resulting in β^DOPE < β^DOPC. This confirms that DOPE has to promote stalk formation as compared to DOPC.

The possible dependence of the monolayer spontaneous curvature, J_s, and saddle splay modulus, 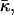on the hydration may require correction of our estimation of 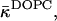Eq. 20. Indeed, this estimation is based on the value of the critical parameter β*^DOPC, which determines the lamellar-stalk phase transition of this lipid in a partially dehydrated state corresponding to the relative humidity ζ = 45%. Hence, to be more accurate, we had to insert into Eq. 20 the unknown value of J_s corresponding to the low humidity rather than the measured value of the fully hydrated state. The resulting value for 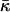also corresponds to ζ = 45% rather than to full hydration. Taking into account this reasoning and the expected dependences of J_s and 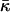on hydration, the estimation given by Eq. 20 represents the upper bound for the saddle splay modulus at full hydration whereas the real value may be more negative.

The effect of dehydration on monolayer elastic constants explains the difference between the estimated range for 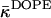(inequality expression Eq. 24), and the considerably more negative value of the Gaussian modulus measured recently for DOPE-Me at full hydration and high temperature of ∼55°C (Siegel and Kozlov, 2004). There is also the fact that 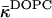at low hydration (Eq. 20) is estimated to be less negative than 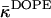(Eq. 24), which must be a consequence of the influence of hydration on this elastic constant.

Possibility of stalk phase formation in fully hydrated state

The stalk phase was observed only in partially dehydrated systems (Yang and Huang 2002; Yang and Huang, 2003). The question arises whether a stalk phase could occur also at full hydration. To analyze this question we compare the free energy of lamellar L_α, stalk, and inverse hexagonal H_II phases. The difference in the average free energy per lipid between the inverse hexagonal H_II phase and the lamellar L_α phase, denoted by f_HII, is (Hamm and Kozlov 1998)

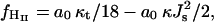(25)

where a₀ is the area per lipid in the membrane plane. The energy of stalk formation from the lamellar phase in a fully hydrated system is given by F_s (Eq. 14). The stalk phase forms if it is more favorable energetically than both the lamellar and the H_II phase: f_HII > 0 and F_s < 0. According to Eqs. 14 and 25, the two conditions are satisfied if the elastic constants of the lipid monolayer fulfill the conditions

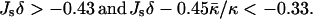(26)

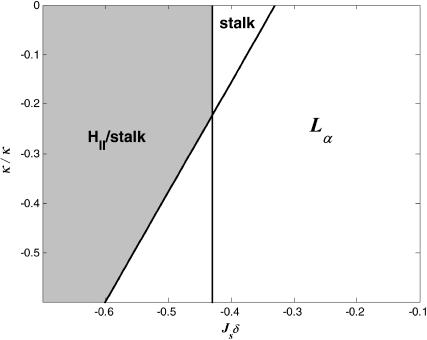
Inequality expressions in Eq. 26 determine the phase diagram at full hydration expressed in terms of the spontaneous curvature, J_s, and the saddle splay modulus, 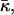and is represented in Fig. 7. Elaboration of the shaded region at the left-hand side of the phase diagram, which includes the phase boundary between the H_II and the stalk phases, is out of the scope of the present model. According to Fig. 7, it seems reasonable that some lipid, or maybe some lipid mixture, has the appropriate elastic constants to form a stalk phase at full hydration. Importantly, the phase diagram (Fig. 7) does not account for a possible formation of other nonlamellar phases, such as the cubic phase, which may form within the same parameter range.

FIGURE 7.

Phase diagram of fully hydrated lipids as a function of the dimensionless forms of the spontaneous curvature, J_sδ, and the saddle splay modulus,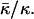

CONCLUSIONS

Our analysis indicates the importance of hydration forces for stalk formation, especially for membranes composed of lipids with PC headgroups. Stalk formation induced by hydration forces may be a general fusion mechanism in situations in which membranes are brought into close contact by specialized machinery. Biological membrane fusion is mediated by specialized fusion proteins, which are thought to produce two actions: to bring membranes into close contact and then to induce membrane merger (McNew et al., 2000; Skehel and Wiley, 2000). The present model proposes that establishment of the intermembrane contact can drive by itself at least a part of the membrane merger—hemifusion. To fulfill this mechanism, the protein machinery should be powerful enough to overcome the hydration repulsion and bring the membranes at least locally to a distance as small as 1 nm or even less. Further evolution of the fusion intermediates into a fusion pore requires, probably, additional action of the protein machinery (McNew et al., 2000) such as bending of the membrane out of its plane (Kozlov and Chernomordik, 2002).

APPENDIX A: EXPRESSIONS FOR THE SPLAY AND SADDLE SPLAY OF THE LIPID CHAINS OF AN AXISYMMETRIC MONOLAYER

The expression for the splay in an axisymmetric monolayer was already derived in Kozlovsky et al. (2002). Here, we also compute the expression for the saddle splay deformation. To derive these expressions, we first define the vectors determining the monolayer deformation. The shape of the monolayer is determined by the orientation of the normal vector at each point of the neutral surface. To characterize the average orientation of hydrocarbon chains, we use a unit vector, 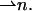The chain orientation, 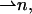can vary along the dividing surface, describing a changing orientation of the chains. Tilt is described by deviation of the chain director, 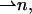from the surface normal, 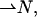according to Hamm and Kozlov (2000),

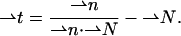(A1)

Consider a monolayer with radial symmetry. We will describe its structure using the cylindrical coordinates {r, θ, z} and the corresponding unit vectors 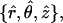where the radial distance, r, is measured from the symmetry axis. The shape of the monolayer surface is given by the tangential angle ϕ(r) of the surface profile. The normal to the surface is

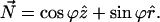(A2)

Two orthonormal tangent vectors to the monolayer surface are

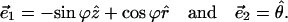(A3)

The arc lengths in the direction of each tangent vector are

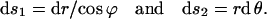(A4)

The tilt vector in an axisymmetric monolayer is given by

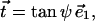(A5)

where ψ(r) is the tilt angle. The surface normal, 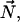and the tilt vector, 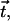determine the chain orientation to be

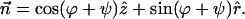(A6)

The chain orientation tensor is (note that )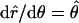

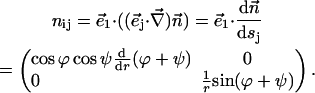(A7)

The splay of the lipid chains is given by the trace of the tensor, 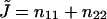(Kozlovsky and Kozlov, 2002), whereas the saddle splay is given by its determinant, 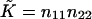(since the tensor is diagonal; (Hamm and Kozlov, 2000). The splay of the hydrocarbon chains can also be expressed as

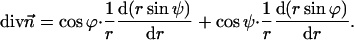(A8)

APPENDIX B: NUMERIC METHOD FOR MINIMIZING THE ENERGY OF A LIPID BILAYER

Accounting for the expressions derived in Appendix A, the energy density per unit area of the neutral surface of an axial symmetric monolayer is given by

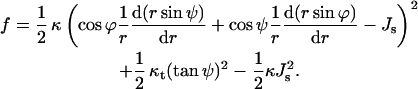(B1)

The tangential angle, ϕ, and the radial distance, r, of the monolayer neutral surface are expressed through the corresponding characteristics of the bilayer midsurface, ϕ_m and r_m, and the distance between the neutral surface of a monolayer and the bilayer midsurface thickness, δ (referred to as the monolayer thickness), by

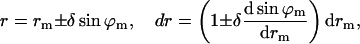(B2)

and

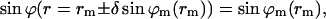(B3)

where the plus and minus signs correspond to the proximal and distal monolayers, respectively. The total energy is the integral of the energy density over the surfaces of the two monolayers,

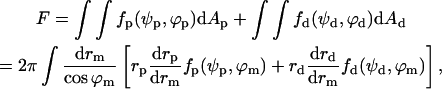(B4)

where the subscripts p and d denote the proximal and distal monolayers, respectively, and the radial distances r_p and r_d are related to r_m through Eq. B2. The energy can be written formally as an integral of a Lagrangian density, 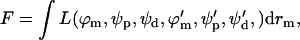where the prime denotes a derivative with respect to r_m. The usual mathematical method to minimize the energy is to solve the corresponding Euler-Lagrange differential equations. However, these equations arising in our case turn out to be nonlinear and too complex to be solved by direct numeric integration. Therefore, we use a procedure consisting of two elements (Kozlovsky and Kozlov, 2002):

1. The nonlinear Lagrangian density is approximated by its Taylor expansion up to a quadratic order, which results in linear equations. Exact solution is then obtained by iterations.

2. The minimization of the quadratic Lagrangian is performed by the method of finite elements (Prenter, 1975) rather than by solving the Euler-Lagrange equations.

The rest of this Appendix contains a detailed account of the method.

Linearization of the problem

The Lagrangian is a functional of three functions of r_m: ϕ_m, ψ_p, and ψ_d. To simplify the notation, we denote x = r_m. To simplify the mathematical expressions, we use a new set of functions, denoted by y_α(x), α = 1,2,3, and defined as

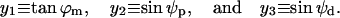(B5)

Using the notation 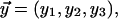the energy is formally written as

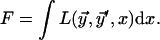(B6)

The method by which we minimize the energy has three steps:

1. There is an initial solution which satisfies the boundary conditions,

2. The solution is improved by a small correction, which solves the linear Euler-Lagrange equations.

3. The calculation is iterated with a better initial solution, 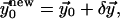until the correction is as small as desired, 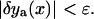To obtain linear Euler-Lagrange equations, the Taylor expansion of the Lagrangian density is derived up to a quadratic order (using the summation convention),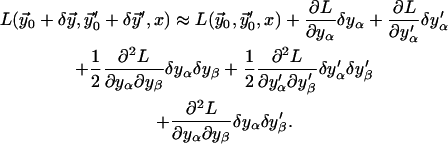

   (B7)

The expansion was calculated using MAPLE software (Maplesoft, Waterloo, ON, Canada).

Minimization of the quadratic Lagrangian by the finite-element method

The Euler-Lagrange method to minimize the Lagrangian produces a set of differential equations that forms a boundary value problem. The solution of a boundary value problem by numeric integration of the differential equations is problematic, and methods that minimize the integral directly are preferred. We used the method of finite elements (Prenter, 1975). The method has two components:

1. Cubic splines are constructed, which form a vector basis of a linear vector space of functions. The functions 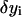are approximated as a linear combination of these base functions.

2. The quadratic Lagrangian becomes a quadratic expression of the linear coefficients determining

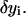
Energy minimization produces a system of linear equations for the coefficients.

Cubic splines interpolation

Spline interpolation represents a smooth function as a sum of polynomials, each defined over a different interval of the argument. It is a general method useful for data interpolation, computer graphics, and the finite-element method. The cubic B-splines, discussed here, are appropriate for the latter.

Consider the interval x₀ ≤ x ≤ x_F. The interval is divided into k subintervals,

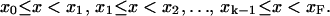(B8)

The partition is called the knots division. There are k + 3 cubic B-splines defined over a knot division with k subintervals. A cubic B-spline, B_i(x), is a compact function, defined over four consecutive subintervals, x_i−2 ≤ x < x_i+2 (the B-splines at the ends of the interval require extension of the partition outside of the interval). It is a different cubic polynomial in each subinterval,

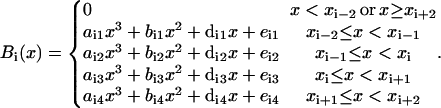(B9)

The coefficients are uniquely chosen, up to an overall constant, by the requirement that B_i(x) will be twice differentiable, B_i(x) ∈ C². The B-splines are used here to solve a boundary value problem. It is therefore useful to define a modified set of B-splines that satisfy the boundary conditions B_i(x₀) = B_i(x_F) = 0. Such set contains k + 1 B-splines. The cubic B-splines span a function vector space of twice differentiable functions. That is, a function, y(x), can be approximated as a linear combination of the cubic B-splines,

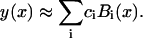(B10)

The approximation is improved as the number of subintervals increases.

Finite-element method

The finite-element method represents the functions and their derivatives by their cubic spline approximation,

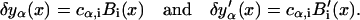(B11)

Substituting these expressions in the quadratic energy integral, Eqs. B6 and B7, the energy becomes a quadratic expression of the coefficients c_α,i,

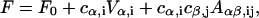(B12)

which we define as

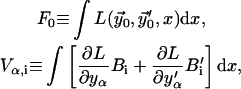(B13)

and

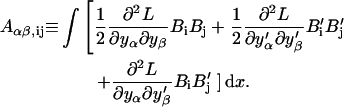(B14)

All the integrals can be performed as they depend on the known functions 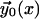and B_i(x). Energy minimization is obtained by the usual condition

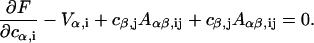(B15)

The system of linear equations is easily solved by matrix methods. In vector notation, it reads

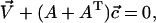(B16)

whose solution is

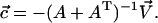(B17)

All calculations were performed by MATLAB software which has a special package for the cubic B-splines. The integrals were performed by MATLAB's usual method of handling functions. The functions are discretized and represented as vectors. An integral is, thus, the sum of the vector's components.

Height constraint

The shape of the midsurface was represented by its slope, y₁ = tan ϕ_m. The reason is that the height difference between the endpoints of the surface, denoted by H, is a linear function of ≈y₁,

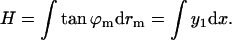(B18)

Changes in the height, ΔH, are a linear function of the cubic spline coefficients,

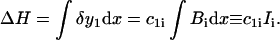(B19)

A constant height, ΔH = 0, could be maintained by the method of Lagrange multiplier. The method defines a new energy functional to be minimized,

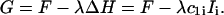(B20)

The Lagrange multiplier λ (not to be confused with the hydration force parameter) is another unknown, treated on the same level as the coefficients c_α,i. Thus, constraining the height is achieved by minimal computational effort.