Enforced Detachment of Red Blood Cells Adhering to Surfaces: Statics and Dynamics

Abstract

We investigated the mechanical strength of adhesion and the dynamics of unbinding of red blood cells to solid surfaces. Two different situations were tested: 1), native red blood cells nonspecifically adhered to glass surfaces coated with positively charged polymers and 2), biotinylated red blood cells specifically adhered to glass surfaces decorated with streptavidin, which has a high binding affinity for biotin. We used micropipette manipulation for forming and subsequently breaking the adhesive contact through a stepwise micromechanical procedure. Analysis of cell deformations provided the relation between force and contact radius, which was found to be in good agreement with theoretical predictions. We further demonstrated that the separation energy could be precisely derived from the measure of rupture forces and the cell shape. Finally, the dynamics of detachment was analyzed as a function of the applied force and the initial size of the adhesive patch. Our experiments were supported by original theoretical predictions, which allowed us to correlate the measured separation times with the molecular parameters (e.g., activation barrier, receptor-ligand characteristic length) derived from force measurements at the single bond level.

INTRODUCTION

Mechanical attachment between cells represents an essential stage in various biological processes, such as cell recognition, immune response, tissue integrity, embryonic growth, and wound healing (Alberts et al., 1989). In general, cell adhesion is primarily mediated by specialized transmembrane proteins called cell adhesion molecules, which involve specific interactions and allow cells that express some ligands to adhere only to other cells that express the appropriate receptors. The initiation of contacts between cells often occurs in situations where external forces (e.g., blood stream) are likely to disrupt the contact and inhibit the formation of stable junctions or cell aggregates. In consequence, beside their binding affinity, the resistance of these ligand-receptor linkages to external forces is an important parameter to measure to gain insight into the fundamental mechanisms of cell adhesion.

With the advent of ultrasensitive force devices such as the atomic force microscope (Florin et al., 1994), biomembrane force probe (Evans et al., 1995), microcantilever device (Tees et al., 2001a), and optical tweezer (Stout, 2001), the strength of single bonds has already been extensively probed experimentally and studied theoretically (Evans and Ritchie, 1997; Strunz et al., 2000; Tees et al., 2001b; Bartolo et al., 2002; Hummer and Szabo, 2003). In particular, it was clearly shown that rupture forces strongly depend upon the rate of force application (Merkel et al., 1999). Yet, at the cellular scale, after formation of the first bond, the stability of adhesive contacts between cells or between cell and template is mainly governed by the capability of cell receptors to be recruited into the contact area and by the collective kinetic and mechanical properties of multiple receptor-ligand bonds. Concomitantly with some biological experiments which show that adhesion forces correlate with contact size (Riveline et al., 2001), the role of force at clusters of adhesion molecules has recently attracted considerable theoretical interest (Seifert, 2000; Evans, 2001a; Boulbitch, 2003; Erdmann and Schwarz, 2004). To date, however, only a handful of experiments designed to provide quantitative measurements on the mechanics of cell adhesion through multiple bonds exist in the literature. As demonstrated more than a decade ago by Evans et al. (1991b) for cell adhesion, and even earlier by Griffith (1921) for polymer adhesion, the intrinsic parameter to probe the strength of adhesion between meso- or macroscopic areas is the separation energy or the fracture energy. The detachment force is not an intrinsic feature of the interaction but depends upon the geometry of the objects in contact. In consequence, a straightforward way to explore the strength of adhesion mediated by a collection of receptor-ligand pairs is to adapt to biological systems the Johnson/Kendall/Roberts, or JKR, method (Johnson et al., 1971), which is well known in the polymer mechanics community. By simply measuring the contact area between functionalized elastic agarose beads and glass slides decorated with the related receptor, Moy et al. (1999) were able to derive free energies associated with the separation of the two bioactive surfaces. This cell-free thermodynamic approach allows a precise measure of the binding affinity of receptor-ligand complexes, but excludes any possibility of ligand mobility and recruitment to the adhesion zone. More recently, Prechtel et al. (2002) proposed a method based on micropipette manipulation to study the dissociation of adhesive contacts between living cells and ligand-decorated vesicles under a linear ramp of force. Yield forces at the rim (which are dimensionally equivalent to energy densities) were found to scale as a power of the loading rate. Although very attractive because of its direct biological relevance, this technique does not always ensure rupture of specific bonds instead of lipids uprooting. Moreover, physiological loading of adhesion patches is usually more or less constant on the timescale of cluster lifetime.

Here, we report on a novel micromechanical approach, which allows us to probe the strength of membrane adhesion over large contact areas and, for the first time, to investigate the detailed dynamics of separation during forced detachment. Our experiments are supported by theoretical predictions recently reported (Brochard-Wyart and de Gennes, 2003) and refined in this article. Both specific adhesion (mediated by the streptavidin-biotin pair) and nonspecific (electrostatic) adhesion were studied and compared. In particular, we show that the drastic difference between the dynamics of detachment in both situations can be rationalized by considering the nature of the underlying dissipative processes: viscous flow versus tearout of specific bonds. The experimental technique is based on a dual-micropipette arrangement, which permits manipulation of individual cells. Red blood cells served as force transducer as well as model cells for adhesion to functionalized glass surfaces. Although it might seem conceptually similar to some previous works (Evans et al., 1991b; Prechtel et al., 2002), our procedure was specifically designed 1), to provide direct measurements of the separation energies from force experiments and 2), to analyze quantitatively the dynamics of unbinding from a minimum number of microscopic parameters, which are related to the energy landscape of single receptor-ligand complexes provided by single molecule spectroscopy experiments.

MATERIALS AND METHODS

Red blood cells

Fresh red blood cells were obtained from donors and washed three times with phosphate-buffered-saline (PBS) 300 mOsm, to discard all leukocytes and plasma proteins. In one series of experiments involving nonspecific adhesion of erythrocytes to positively charged surfaces, we used these native red blood cells, which were osmotically swollen in phophate-buffered saline (PBS), 150 mOsm. To avoid crenation, polyethylene-glycol, PEG, M_w = 3400 mol/g (Sigma, L'Isle d'Abeau Chesnes, France), was added to the suspension at a final concentration of 1 mg/ml. In contrast with bovine serum albumin (BSA), which usually serves as anti-crenation agent, PEG is equally efficient but does not adsorb to the positively charged surfaces. In another series of experiments involving specific adhesion of erythrocytes via biotin-streptavidin interactions, we labeled the surface of erythrocytes with biotin following a previously described protocol (Merkel et al., 1999; Perret et al., 2002). Briefly, the cells were first washed three times in 0.1 M carbonate-bicarbonate buffer (pH 8.5). Then, biotinylation was performed by incubation in a 0.5 mM NHS-PEG³⁴⁰⁰-biotin (Nektar Therapeutics, San Carlos, CA) solution made from carbonate-bicarbonate buffer for 20 min. After three washes with PBS 300 mOsm, the biotinylated cells were stored at 4°C in PBS 150 mOsm + BSA 0.5% (to avoid crenation and inhibit any residual nonspecific adhesion). As estimated in a previous work (Cuvelier et al., 2003), the resulting density of biotin groups at the surface of erythrocytes was ∼5 × 10¹⁵ m⁻².

Test surfaces

As test surfaces, we selected glass beads of ∼30-μm diameter (Polysciences Europe, Eppelheim, Germany). Beads were first cleaned in a piranha solution (H₂0₂/H₂SO₄: 30/70) and rinsed extensively with ultrapure water. For nonspecific adhesion assays, the beads were incubated in a solution of polyethyleneimine (PEI, Research Biochemicals International, Natick, MA), at 0.1% w/w in pure water for 30 min and washed with PBS 150 mOsm before use. For specific adhesion assays, streptavidin-coated beads were prepared by adsorption of biotin-labeled casein, followed by incubation in a solution of streptavidin (Jackson ImmunoResearch Laboratories, West Grove, PA) at 1 mg/ml in PBS. To do so, β-casein (Sigma) was first tagged with EZlink-LC-biotin (Perbio Science, Brebières, France) following a standard procedure (Hermanson et al., 1992). By fluorescence intensity measurements using Cy3-Extravidin (Sigma), we found that that the surface density of available biotin groups was ∼3 × 10¹⁴ m⁻² (D. Cuvelier and P. Nassoy, unpublished results).

Micromechanical procedure

Experimental design

Conceptually, a simple procedure to probe the strength of an adhesive contact between a cell and a surface consists in maneuvering individual cells with a micropipette to form controlled contacts with the surface of interest. After assembling, the cell and the surface are separated by progressively increasing the amplitude of the pipette backsteps, as sketched in Fig. 1. We thus expect that rupture occur at a characteristic threshold force related to the separation energy. The advantage of using pipettes to manipulate the cells is twofold. First, the suction pressure can be varied to tune the membrane tension of the cell (according to Laplace's law). Intuitively, guided by the Young-Dupré equation, which relates the separation energy that we aim to measure, W, to the membrane tension, γ, we may anticipate that γ has to be of the same order of magnitude as W or larger. Second, the axial symmetric geometry imposed by the experimental design allows us to derive a relation between the deformation of the cell and the force applied onto the contact zone, as described in detail by Simson et al. (1998). In other words, the cell serves both as a sticky surface and a force transducer. Furthermore, at a given force, we may investigate the dynamics of unbinding by monitoring the contact radius of the adhesion patch as a function of time by videomicroscopy. We selected red blood cells as adhesive cells for two reasons. First, their mechanical properties are well-known (Mohandas and Evans, 1994) and they are easy to handle. Second, once they are slightly aspirated in a pipette, their surface is smooth, in contrast with most nucleate cells, which present highly corrugated surfaces and complex viscoelastic properties. The actual contact area of swollen red blood cells adhering to flat surfaces can thus be reliably measured by optical microscopy.

FIGURE 1.

Schematic of experimental design. (a) A red blood cell is aspirated in a micropipette (suction pressure ΔP) and brought in contact with a hard surface. (Top) The contour for cell adhesion at rest (f = 0) is a truncated sphere. The equilibrium contact angle, θ_e, is given by 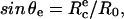where 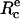is the equilibrium contact radius and R₀ is the radius of the erythrocyte at the apex. (Middle) For a given instantaneous displacement δ of the pipette, the cell is stretched and the adhesion zone is loaded with a mechanical force f(δ), which can be computed from the measure of the membrane tension, γ, the contact radius, R_c, and the maximal radius of the deformed cell, R. The shape of the cell is “onduloidal” and characterized by a contact angle, θ. (Bottom) If the force exceeds a threshold value, f_c, corresponding to a displacement δ_c, the contact is broken, and the cell recovers its spherical shape. (b) Typical sequence of pipette movements. Each cycle consists in a step (forward for compression and backward for extension) of increasing amplitude. At the end of each displacement, the cell is brought back to rest position. This sequence is pursued until failure occurs.

Micromanipulation and test procedure

A schematic of the complete instrumental assembly is shown in Fig. 2.

FIGURE 2.

Complete instrumental apparatus assembled around a bright-field inverted microscope. Light from mercury arc lamp L travels through condenser C and illuminates the sample. Objective O collects the images which can be captured either by fast-rate (100 fps) digital camera dCCD and stored by computer A1 or by analogic camera aCCD (25 fps), visualized on control monitor M and recorded with VCR after image processing IP. Simultaneously, the arbitrary waveform generator AWG controlled by computer A2 via GPIB interface provides the input signal to high-voltage amplifier Amp which drives piezo element P. Piezo translator P is mounted on three-axis motorized micromanipulator μM2 and sets the cell-holding pipette displacement. The bead-holding pipette is connected to mechanical micromanipulator μM1. Both μM2 and μM1 are mounted on the stage of the microscope.

Sample chambers were made of two cleaned glass coverslips glued with vacuum grease and sealed with nail polish to an aluminum support (1-mm thick). The chamber was first filled with a solution of β-casein at 1 mg/ml in PBS to avoid any strong adhesion of red blood cells to glass. After rinsing, the chamber was filled with buffer (PBS 150 mOsm + PEG³⁴⁰⁰ at 0.2 mg/ml). Native (or biotinylated) red blood cells and PEI (or streptavidin)-coated beads were injected and dispersed in the chamber. Then, the chamber was placed on the stage of an inverted microscope (Axiovert 200, Zeiss, Göttingen, Germany). The microscope was equipped with a 100× Plan-Achromat immersion oil objective (1.4 NA), a 0.8 air INA condenser, and a 200-W mercury arc lamp (Oriel Instruments, Stratford, CT). The transmission bright-field images were either collected by an analogic CCD camera (XC-ST70CE, SONY) and recorded at 25 frames/s with a VCR (SVO-95000MDP, SONY) after contrast enhancement (Argus image processor, Hamamatsu, Shizuoka, Japan) or captured by a digital monochrome CCD camera cooled to −30°C (Sensicam, PCO, Kelheim, Germany) at video rates upwards of 100 frames per second, using a custom-modified version of the commercial software (SensiControl4.03).

Manipulation and alignment of beads and erythrocytes were performed with a dual-micropipette arrangement, as shown in the videomicrograph, Fig. 3. To do so, two manipulators were mounted on each side of the microscope stage. On the bead side, we used a mechanical three-axis translator (M-461, Newport, Irvine, CA). On the cell side, the same three-axis translator was motorized with two DC actuators (MotorMike 25-mm scanning range, Oriel Instruments, Stratford, CT) in the x,y plane of observation and controlled with a joystick (Model 18000, Oriel Instruments, Stratford, CT). A linear piezoelectric translator (LISA, P-753-21C, 25-μm scanning range, Physik Instrumente, Karlsruhe, Germany) was placed in series with the coarse x axis for fine and hysteresis-free displacement in unbinding experiments. Control of the piezo was performed through an arbitrary waveform generator (TGA1241, Thurlby Thandar Instruments, Huntingdon, UK) which was programmed via GPIB interface in a LabView (National Instruments, Austin, TX) environment.

FIGURE 3.

(a) Videomicrograph of the dual-micropipette arrangement. The red blood cell is aspirated in the left pipette. The hard test-surface is a large glass bead, which is maneuvered into position with the right pipette. Scale bar is 5 μm. (b) Nonspecific adhesion experiments involve a native swollen red blood cell and a glass bead coated with polyethyleneimine (PEI). The glycocalix (glycolipids and glycoproteins) of the erythrocyte is negatively charged, whereas PEI is a positively charged polymer adsorbed to glass. (c) Specific adhesion experiments involves a biotinylated swollen red blood cell and a streptavidin-coated glass surface. Transmembrane proteins of the erythrocyte are tagged with biotin through a flexible PEG spacer. Immobilization of streptavidin on the bead surface is achieved by first adsorbing biotinylated-casein to glass.

The micropipette aspiration technique used to hold cells and beads was described elsewhere (Needham and Zhelev, 1996). Briefly, borosilicate capillaries (0.7/1.0-mm inner/outer diameter, Kimble, Vineland, NJ) were first pulled into needles with a horizontal laser puller (P-2000, Sutter Instruments, Novato, CA), then cut open and microforged (DMF1000, World Precision Instruments, Stevenage, UK) at desired inside diameters (1.2–1.5 μm for red blood cells and 5–8 μm for beads). The micropipettes were then filled with PBS 150 mOsm + BSA 0.1% w/w and attached to the chucks on the manipulators. The suction pressure in the cell-holding pipette was controlled by adjusting the height of a water-filled reservoir connected to the back of the pipette. A pressure transducer (DP103, Validyne Engineering, Northridge, CA) was used in-line to measure the applied pressure. Typical pressures were in the range of 200–2000 Pa. Membrane tension γ was computed from the formula 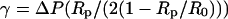(Waugh and Evans, 1979), where ΔP is the applied suction pressure, R_p is the inner radius of the pipette, and R₀ is the radius of the portion of the red blood cell outside of the pipette. Typical values for γ were thus in the range of 0.1–1 mN/m.

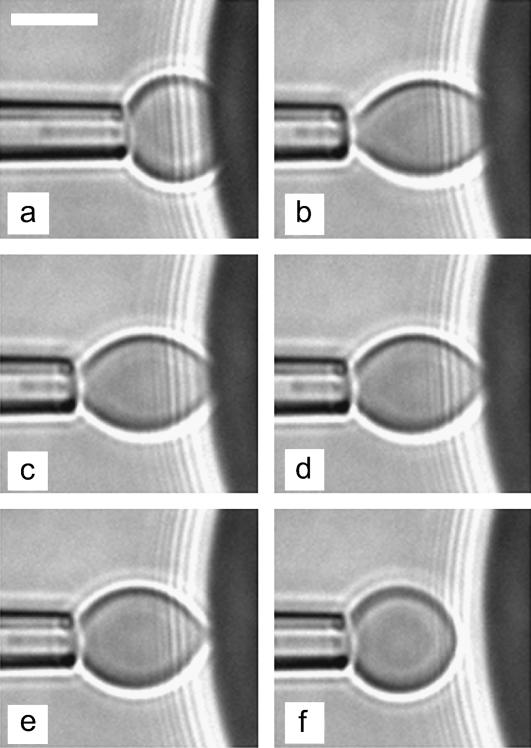
Before the beginning of any experiment, mineral oil was spread at both open sides of the chamber to prevent evaporation. Then, the cell- and bead-holding pipettes were carefully aligned to get the focal plane and the plane of cell-bead contact to coincide. A typical sequence, which summarizes the different possible configurations encountered in our experiments, is displayed in the videomicrographs, Fig. 4. The red blood cell was first brought manually in contact with the surface of the bead. In the absence of external force, the portion of the adhering cell outside of the pipette has the shape of a truncated sphere, with a radius at the apex, R₀ = 3.1 μm. The radius of the unstressed contact area, 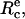is also related to the equilibrium contact angle, θ_e, by 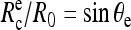(Fig. 4 a and Fig. 1). When the cell is extended (corresponding to positive forces), cell and contact radii, R and R_c, decrease (Fig. 4 b). Eventually, when unbinding occurs, R_c vanishes to zero and the red blood cell recovers its initial spherical shape (R = R₀) (Fig. 4 c).

FIGURE 4.

Videomicrograph sequence of the stepwise separation procedure. (a) Assembly: Adhesive unstressed contact between the pressurized cell and the rigid surfaces. (b) Stretching: The cell-holding pipette is moved back to apply force on the contact zone. The contact radius is decreased. (c) Detachment: The cell was brought back to the rest position (a) and the pipette displacement was increased. The cell is shown to be separated from the test-surface. Scale bar is 5 μm.

Practically for each erythrocyte/bead pair that we investigated, the procedure was the following. First, the piezo translation was carefully adjusted to find the unstressed state of the adhering cell (truncated sphere), considered hereafter as the initial state. Then, the pipette connected to the piezo actuator was moved step by step. At the end of each step, the pipette was brought back to the initial state for 30 s to allow the adhesion patch to reach its equilibrium size. In the next cycle, the amplitude of the step was increased by typically 0.2 μm. For static measurements of rupture forces, the duration of force application was fixed at 1 s. To study the dynamics of detachment, we increased the duration of force steps up to 150 s. In consequence, the temporal window of accessible separation times was in the range 10⁻²–150 s. Although both compression (corresponding to negative forces) and extension were studied, we mainly focused on unbinding events corresponding most often to large extensions.

Analysis

At each cycle of the micromechanical test procedure described above, we measured the three main parameters that characterize the shape of the cell, namely R, R_c, and δ, the deformation of the cell relative to the initial equilibrium state. This analysis procedure was automated and performed by binarizing the digitized images. Knowledge of the erythrocyte contour permits a direct measure of the applied force corresponding to the imposed compression or extension. Evans et al. (1995) have shown that a swollen erythrocyte acts as a soft spring and can be used to measure minute forces in single molecule experiments. For small deformations (<∼R₀/10 ≈ 0.3–0.4 μm), the stiffness of the transducer, k_f, is proportional to the membrane tension and weakly dependent (through logarithmic corrections) on the radius of the pipette, R_p, and on the contact radius between the bead and the cell, R_c, as

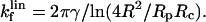(1)

For larger deformations, the mechanical analysis is more complicated, and the spring constant of the capsule must be evaluated by numerical calculation. This detailed analysis has first been reported by Evans et al. (1991a), then refined and experimentally validated by Simson et al. (1998).

Our force calculation is thus based on the numerical methods provided in the latter reference. The main difference lies, however, in the fact that R_c was kept constant during the stretching in Simson et al. (1998), whereas, in our case, R_c varied while the angle θ_e at the contact line was kept constant. At a given deformation δ, the resulting force is therefore a function of δ, R, and R_c (for a same pipette radius, R_p). For the sake of simplicity, instead of computing the force for each (δ, R, R_c) combination, we searched for an empirical analytical f(δ) relation. As seen in the plot, Fig. 5, the numerical solution for the normalized force (symbols) can be well fitted by

(2)

As intuitively expected, we observe that the capsule softens at large δ and small R_c values. The first term in Eq. 2 yields the slope at small elongation, whereas the second term gives the deviation from linearity at large deformation. By comparison with numerical solutions, we checked that the second term could be reasonably chosen to be independent of R_c and R and that the error on the estimated forces due to this empirical approximation was <4%.

FIGURE 5.

Force extension relation for a pressurized swollen red blood cell. The data points correspond to the numerical solution, as derived in Simson et al. (1998) for R_c = 0.5 μm. The lines are empirical fits using Eq. 2 for R_c = 0.5 μm (solid), 0.25 μm (dot), 1 μm (dash), and 1.5 μm (dash-dot).

THEORETICAL FRAMEWORK

Brochard-Wyart and de Gennes (2003) recently proposed a theoretical description for the unbinding of adhesive vesicles or cells. In the present section, we will recall the key features of their approach. In addition to their original calculations, we will provide the main findings without assuming that W ≪ γ. Finally, we shall introduce new theoretical predictions for the dynamics of unbinding when adhesion is mediated by specific interactions.

Unstressed contact (f = 0)

At rest, in the absence of external force, the contact angle of the aspirated cell with the surface, θ_e, is given by sin θ_e = 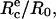and the separation energy, W, is simply given by the Young-Dupré balance of capillary forces as

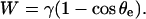(3)

Stressed contact (f ≠ 0): contact radius, R_c, versus force, f

The external force, f, acting on the pipette causes the stretching of the red blood cell. The cell shape, imposed by capillarity, is a surface of uniform curvature, with a contact angle on the adhesive plate imposed by the Young equation (θ = θ_e). Expressing the balance of forces at the entrance of the pipette, at the apex, and at the contact line with the surface readily gives

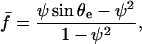(4)

with ψ = R_c/R the normalized radius of contact and 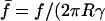) the force scaled by membrane tension.

The relation has a maximum. Only the branch of decreasing force with increasing ψ has a physical meaning. At the maximum located at ψ = (1 − cos θ_e)/sin θ_e, rupture of the adhesive contact arises abruptly. The normalized rupture force is then

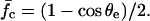(5)

Finally, from Eq. 3, we find

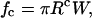(6)

where R^c is the equatorial radius of the cell upon application of the critical force that leads to rupture.

Note that Eq. 6, which relates the rupture force to the separation energy, is coincidentally reminiscent of the Derjaguin approximation (Israelachvili, 1985).

Stressed contact (f > f_c): dynamics of unbinding

Here, the cell is stretched with a constant force f, sufficient to cause complete unbinding. The adhesion patch thus shrinks to zero. We are interested in determining the law ψ(t). We note θ(t), the contact angle between the cell and the surface. By neglecting the second-order term in ψ in Eq. 4 (with θ_e replaced by θ(t)), we may remark that this angle equals ψ plus a force-dependent term.

Case of nonspecific interactions

By analogy with wetting processes of surfaces by liquid droplets, the balance of forces is obtained by writing that the noncompensated Young force is opposed to a viscous force near the contact line (de Gennes, 1985), as

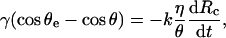(7)

with η the viscosity of the buffer solution and k a numerical constant (of order of 10).

Eq. 7 can be solved providing that several assumptions are fulfilled: 1), θ(t) is not too large (typically <70° so that cos θ can be expanded with an error <10%); 2), ψ ≪ 1, meaning that we focus on the late stages of the adhesion patch shrinkage; and 3), f > f_c. This condition both implies that Eq. 4, which is valid at rest and under force (with θ_e replaced by θ) can be approximated by 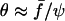and that θ_e ≪ θ(t). Finally, one obtains the law of decay for ψ,

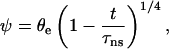(8)

and the separation time, τ_ns, is given by

(9)

with V* = γ/2kη.

Case of specific interactions

Although this situation has already been discussed in Brochard-Wyart and de Gennes (2003), we shall describe it hereafter in more details and introduce some refinements.

The dissipation is now dominated by the tearout of the bonds at the periphery of the contact. As shown by Evans (2001a), the pullout force, ϕ, for individual bonds depends upon the velocity of extraction, V_z,

(10)

with where B is an activation energy, V₀ is a typical thermal velocity (∼10 m s⁻¹), and a_b is the maximal bound length beyond which the complex dissociates.

We assume that the profile of the adhering cell is entirely ruled by capillarity and characterized by a wedge of angle θ at the contact line (see sketch in Fig. 1). As shown below, the flexibility of the linker between the receptor molecules and the surface plays a crucial role in the unbinding dynamics.

Rigid bonds: the adhesion molecules are rigidly bound to the surfaces. As the contact recedes at velocity V = −Ṙ_c, the vertical tearout velocity is V_z = V · dz_b/dx, with z_b the microscopic displacement of the formed bond. We write that the dissipation per unit length of the detached adhesion molecules near the contact line is

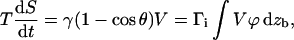(11)

where Γ_i is the surface density of bonds inside the contact zone.

By defining as the maximal elongation of bonds before rupture, we readily obtain, in the limit of small θ,

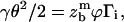(12)

which can be rewritten as

(13)

where 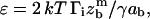which basically compares the separation energy (or, equivalently, the osmotic pressure of the adhesion molecules) to the surface tension. Note that we have identified the vertical velocity of extraction, V_z, to the receding velocity, V, which results in negligible logarithmic corrections.

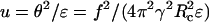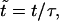To solve Eq. 13, we set and with 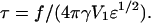Eq. 13 becomes

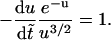(14)

Eq. 14 can be analytically solved in two situations depending on the value of u relative to 1. For rigid bonds, and 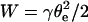of the order of Γ_i kT (for mobile receptors) or Γ_i U ∼ 20 Γ_i kT (for immobile receptors) (Brochard-Wyart and de Gennes, 2002), we find that 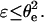Consequently, since θ(t) > θ_e during the unbinding process, it comes out that u > 1 is the case of physical relevance.

The solution (u ≫ 1) is then: 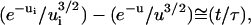and the separation time is given by

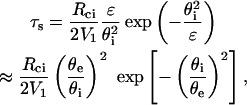(15)

where θ_i is the initial value of θ after force application.

The separation time is thus found to decay exponentially as the square of 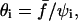with ψ_i being the initial normalized contact radius.

Flexible bonds: the adhesion molecules are connected to the cell surface via flexible spacers. Fig. 6 shows a cartoon that summarizes the notations used in this paragraph.

FIGURE 6.

Sketch of the streptavidin-biotin linkage mediated by a flexible polymer spacer between the red blood cell and the bead surfaces. The notations used in the text are ϕ, the force per binder; κ_s, the stiffness of the spacer; z_s, its length; and z_b, the molecular length of the specific bond.

The force ϕ is both used to dissociate the chemical bond (as defined in Eq. 10) and to elongate the polymer spacer. In the limit of linear response, the stretching length, z_s, is proportional to the force ϕ = κ_sz_s, with κ_s the spring constant of the spacer. The net result is an increase of the viscous loss, because the work of the force per binder is now Eq. 11 is then modified as

(16)

Similarly to the previous approach applied to rigid bonds, we have identified the vertical velocity, V_z, to the receding velocity, V, which results in negligible logarithmic corrections.

Eq. 16 becomes

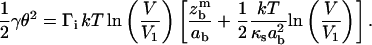(17)

The second term in the square brackets is much larger than unity for flexible spacers as soon as 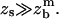Finally, Eq. 17 can be reduced to

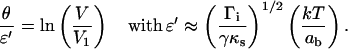(18)

For a flexible polymer, in the limit of small extensions (entropic regime), the spring rigidity is given by 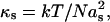with N the total number of monomers and a_s the length of one monomer. Therefore,

To solve Eq. 18, we set and 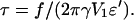Now, the parameter u compares the applied force to a parameter that depends upon the surface tension of the cell, the surface density of adhesion molecules, and their flexibility. Two cases can be considered.

If u ≪ 1, which is achieved for long spacers and/or high binding energy, the solution is 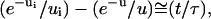and the separation time is then given by

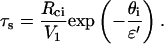(19)

If u ≫ 1, which corresponds to low binding energy and/or semilong flexible spacers, the solution is and the separation time is then given by

(20)

Concluding remarks. Two remarks are worth being made at this stage.

1. Including the elastic energy stored by the polymer spacer into the energy balance significantly affects the dynamics of unbinding, since the shrinking velocity of the adhesion patch scales as e^θ instead of 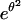in the absence of spacer.

2. In all cases, the prefactor yields the characteristic velocity V₁, with an additional correction depending upon the actual value of the parameter u. Therefore, the measure of the time required for cell-surface separation is expected to directly yield the energy barrier of the molecular receptor-ligand bond (see definition of V₁).

RESULTS

Most of the separation experiments reported hereafter were performed on biotinylated red blood cells in contact with streptavidin-coated surfaces. As shown in the videomicrographs, Fig. 4, these cells initially adhered to the beads with large contact areas. In marked contrast, native red blood cells exhibited insignificant adhesion (i.e., separation forces below 30 pN) when brought in contact with streptavidin surfaces. Hence, these control observations suggest that adhesion between biotinylated erythrocytes and streptavidin beads solely involves the formation of specific bonds. In these conditions, we investigated successively the statics and the dynamics of enforced rupture when adhesion was mediated by biotin-streptavidin interactions. At the end of each section, comparison was done with the unbinding process of erythrocytes adhering via nonspecific interactions onto PEI-coated surfaces.

Statics of unbinding

Force dependence of the contact radius

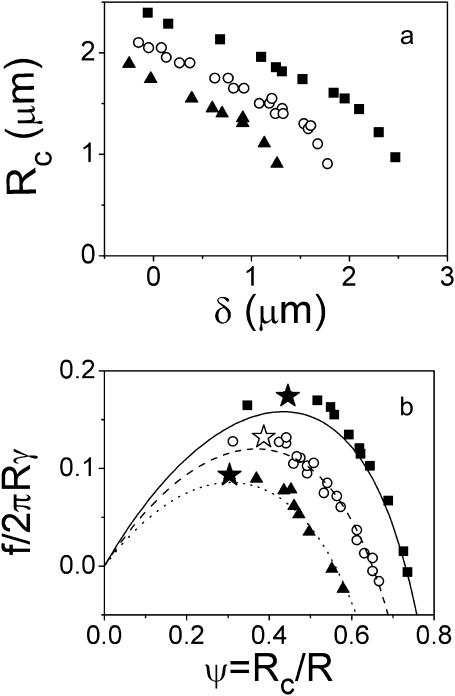
Nearly 30 separation tests were performed and analyzed. Each test corresponded to a different biotinylated red blood cell and a different streptavidin bead. We always kept the procedure identical (as described above), meaning that the pipette holding the blood cell was incrementally pushed toward the surface and retracted from the surface, starting from the rest position. The only variable parameter was the tension of the cell membrane, which was tuned by controlling the aspiration pressure.

At each pipette displacement, δ, we recorded both the maximal radius of the cell (measured at the apex), R, and the contact radius, R_c. In Fig. 7 a, we plotted R_c versus δ for three typical individual tests with three different membrane tensions. As shown, the contact radius reduction did not depend qualitatively on the membrane tension. In all cases, an initial slow and approximately linear decrease of R_c was followed by a sudden drop leading to an abrupt breakage of the contact for values of R_c close to 1 μm. The influence of membrane tension could, however, be observed in the initial contact radius and in the maximal extension required for rupture. The lower the γ, the more the cell spreads onto the surface, and consequently, the higher the contact angle, θ_e, or equivalently the equilibrium contact radius. Also, as intuitively expected, soft cells required further deformation to separate from the surface than stiff cells for identical adhesion energies.

FIGURE 7.

(a) Measurements of contact radii as a function of extension (negative extension corresponds to cell compression) for different membrane tensions of the biotinylated erythrocytes: γ = 0.22 mN /m (▪), 0.35 m N/m (○), and 0.48 mN/m (▴). (b) Force versus contact radius in dimensionless units. Contact radius is normalized by the radius of the stretched cell body measured at the apex, R. Force is scaled by the membrane tension times 2πR. Points represent the experimental data for different values of γ (same as in a). Failure of the adhesive contact is indicated (H, J). The points observed at lower ψ are related to tether extrusion. The lines are calculated from Eq. 4 by setting θ_e equal to the measured contact angle at zero force.

Knowing the deformation δ of the cell and using Eq. 2, we could convert these raw data into force-contact radius data. More precisely, as displayed in Fig. 7 b, we plotted the normalized force 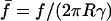as a function of the normalized contact radius ψ = R_c/R for three different values of γ. The lines are the theoretical predictions provided by Eq. 4. Please note that these lines are not fits, since there is no adjustable parameter. θ_e was fixed and derived from the measured contact radius at zero force. In all cases, excellent agreement between experimental results and calculated curves was found. As recalled in the theoretical section, the 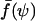relationship presents a maximum, which yields a straightforward estimate of the rupture force. In Fig. 7 b, the actual separation between cell and bead is indicated by a star symbol, which indeed matched with the maximum of the calculated curve. Quite important to notice, rupture did not necessarily coincide with the lower accessible value of ψ. In many cases, when small values of R_c were reached, a tether was pulled out of the cell, meaning that the physical linkage between cell and bead was not completely destroyed. Such a tethering process has already been studied in detail both experimentally and theoretically (Hochmuth and Evans, 1982a; Hochmuth et al., 1982b; Waugh et al., 2001; Hochmuth and Marcus, 2002), and was shown to be accompanied with a relaxation of the extended cell to a spherical shape connected to a thin cylindrical tube. From our viewpoint, the signature of tether formation therefore lies in the reduction of the apparent normalized force, since the apex radius suddenly increases to its initial maximal value R₀. Several other points can be made concerning the plots in Fig. 7 b. As mentioned above, low-tension cells are characterized by larger values (or equivalently larger equilibrium contact angles) than high-tension cells. Further, although the overall behavior remains identical regardless of the membrane tension, the maximal normalized force is seen to increase with decreasing γ, which is also consistent with Eq. 5.

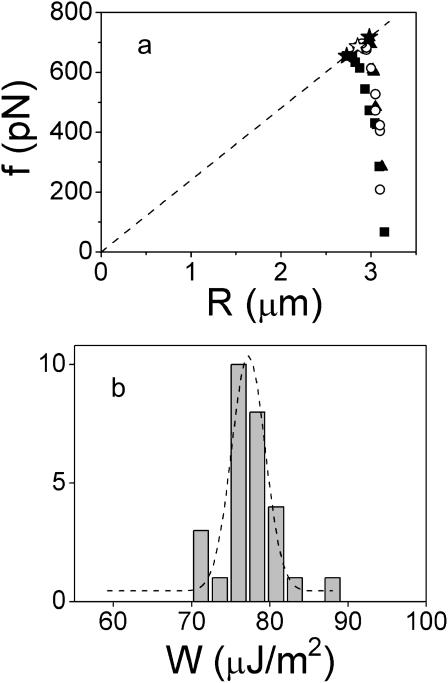
Determination of the separation energy

We have shown that detachment of biotinylated blood cells from streptavidin-coated beads and measurement of rupture forces could be achieved for a large range of membrane tensions, from ∼0.1 to 1 mN/m. As described above in Fig. 7 a, the minimal contact radius before separation was roughly identical for both floppy and tense cells but weakly aspirated cells required larger deformations. This latter effect is quantitatively analyzed in Fig. 8 a, which displays the measured force f as a function of the apex radius R for three different membrane tensions. The data points corresponding to rupture are tagged with star symbols. Even though the variation in cell radii is limited in a small range (from ∼2.7 to 3.2 μm), we may observe that both the rupture force and the cell radius increase with the membrane tension. More important, according to Eq. 6, the ratio f/R^c is expected to be proportional to the separation energy W. As seen in Fig. 8 a, the data points corresponding to contact rupture are reasonably well aligned along a straight segment which is imposed to intercept the origin. From Eq. 6, W can be derived from the slope of this line, and was found to be 76 μJ/m². To further confirm the validity of Eq. 6, we analyzed all our separation tests, i.e., 28 cell-bead separation events, which were investigated at seven different membrane tensions. The histogram in Fig. 8 b cumulates the obtained values for W, which were found to be all grouped at ∼W = 77 ± 4 μJ/m². Although hidden in these reduced data, the tails of the distribution mainly arose from experiments performed on cells that were either very floppy (γ ≈ 0.1 mN/m) or very stiff (γ ≥ 0.8 mN/m). Weakly aspirated cells led to extreme deformations, for which force calculation became less accurate. In contrast, for tense cells, which underwent minor deformations, the uncertainty on force calculation was due to the poor precision in the measurement of cell size reduction.

FIGURE 8.

(a) Force versus cell radius for different membrane tensions of the biotinylated erythrocytes: γ = 0.22 mN/m (▪), 0.35 m N/m (○), and 0.48 mN/m (▴). Failure of the adhesive contact is indicated (H, J). The dashed line is a fit of the three rupture points using Eq. 6. The inset is a magnification of the previous plot at the rupture points. (b) Separation energy derived from 28 detachment experiments performed on biotinylated red blood cells adhering to streptavidin-coated beads. The dashed line is a Gaussian fit.

Locus of failure

A concern that is often raised when dealing with separation experiments on cells is about the locus of failure for molecular bonds. In other words, does the separation energy that we measured above reflect the unbinding of streptavidin-biotin bonds or the extraction of proteins from the cell membrane? To address this problem, we first need to look carefully at the “chemistry” of bead and cell surfaces. On the bead side, streptavidin was immobilized on a layer of adsorbed biotinylated casein. De-adsorption of casein under force cannot be ruled out, although this type of coating is very common in single molecule force experiments (Florin et al., 1994; Ramsden, 1998; Zocchi, 2001). On the cell side, the biotinylation protocol is very classical and consists in tagging with biotin all surface proteins that carry amino groups (e.g., lysine residues). Since the streptavidin-biotin bond is known to sustain high forces under fast loading rates (Merkel et al., 1999), we could not exclude the possibility that cell-bead separation involved uprooting of biotinylated transmembrane proteins instead of dissociation of streptavidin-biotin bonds. This question was also motivated by some separation tests that we performed with the same red blood cell on different streptavidin beads (data not shown): after the first separation, the adhesion energy was observed to drastically decrease in the next cycles, indicating that either streptavidin molecules were transferred to the cell surface or the density of biotinylated proteins was reduced by extraction. To identify the predominant molecular mechanism during separation, we performed additional fluorescence experiments. Beads were coated with Cy3-extravidin, a fluorescent analog of streptavidin. When cell-bead pairs were separated, a weak fluorescent footprint was left on the cell, whereas no apparent “dark” footprint was observed on the bead. We were not able to measure quantitatively the fluorescence intensity. In consequence, even though we still cannot rule out the possibility that a fraction of proteins was uprooted during detachment, this fluorescence experiment suggests that separation is not related to desorption of casein but involves instead the rupture of molecular biotin-streptavidin linkages. Analysis of the dynamics of unbinding in the next section will provide another piece of evidence that contact failure mainly reflects rupture of these specific interactions.

Case of nonspecific adhesion

Native erythrocytes are also known to strongly adhere onto positively charged surfaces (Hategan et al., 2003) via electrostatic interactions through their negatively charged glycocalix. To assess the sensitivity of our approach and the relevance of the measured separation energies, we attempted to apply the above described micromechanical procedure to red blood cells adhering to PEI surfaces. PEI is a highly charged cationic branched polymer that readily adsorbs to clean glass.

Fig. 9 shows three typical experiments that were performed successively on three different cell-bead pairs. We may estimate that the time interval between each separation test is of the order of 30 min. As observed, all erythrocyte-bead pairs exhibited very different behaviors. The first cell was aspirated with the maximal hydrostatic pressure that we could reach with our experimental setup (20 cm H₂O), corresponding to a membrane tension of ∼1 mN/m. Yet, when gentle contact was established with the bead surface, this suction pressure was not sufficient to keep the cell in the pipette (Fig. 9, a and b). The free blood cell then fully spread onto the bead surface, and its equilibrium shape of the cell was a spherical cap characterized by high contact angle. Such an avidity for the surface means that W ≫ γ ∼ 1000 μJ/m². 30 min later, this phenomenon was no longer observed. Full separation experiments could be performed. In the case of the second cell-bead pair that we investigated (Fig. 9 c), the erythrocyte was also highly aspirated (γ = 0.8 mN/m) and forces required for detachment were >2 nN, corresponding to a value for W of 240 μJ/m² (Fig. 9 d). For the third cell-bead pair that we examined (Fig. 9 e), the cell membrane tension could be as low as 0.16 mN/m and W was found to be equal to 55 μJ/m² (Fig. 9 f). Further tests led to nonmeasurable detachment forces, suggesting that W ≪ 10 μJ/m². In brief, this series of successive experiments clearly demonstrates that the adhesion energy measured upon separation of erythrocytes from PEI surfaces is vanishing in time. An obvious explanation is that traces of proteins (from the blood cell suspension or from the casein-coating layer of the chamber) progressively adsorb on the high-affinity surface of the beads and thus passivate it against adhesion of red blood cell. This was confirmed by the following control experiment: injection of 1 μl of casein in PBS (at 0.1 mg/ml) in the chamber completely inhibited any adhesion between blood cells and PEI beads.

FIGURE 9.

Separation tests between native red blood cells and PEI-coated beads. (a and b) Videomicrographs taken <30 min after bead injection into the chamber. Although highly aspirated (γ = 1 mN/m), the cell could not be maintained in the pipette upon adhesion. (c) Videomicrograph taken during a separation sequence for a second cell-bead pair 60 min after preparation of the chamber. Membrane tension of the erythrocyte was 0.8 mN/m (d) Force versus cell radius plot providing the separation energy (dashed line, see Fig. 7) for this second cell-bead pair. (e) Videomicrograph taken during a separation sequence for a third cell-bead pair 90 min after preparation of the chamber. Membrane tension of the erythrocyte was 0.16 mN/m (f) Force versus cell radius plot providing the separation energy (dashed line, see Fig. 7) for this third cell-bead pair. Scale bar is 5 μm.

Dynamics of unbinding

In the previous section, red blood cells were stretched for 1-s periods. The criterion for rupture was that the adhesive contact was destroyed within <1 s. Otherwise, cells were further stretched until detachment occurred. To supplement dynamic information to the detachment process, we monitored the time of separation upon application of a force close to the previously reported static threshold force. As shown hereafter, when force was significantly larger than f_c, detachment usually occurred within <1 s. However, for f ∼ f_c, separation times could be much longer.

Case of specific adhesion

Fig. 10 displays a sequence of six videomicrographs taken during detachment of a biotinylated red blood cell from the surface of a streptavidin bead. In this particular case, rupture was completed within 11.5 s. These images also show that failure seems to process in two distinct phases. During the first phase (∼8 s here), we frequently observed a minor reduction of the contact radius. Then, the adhesive contact underwent a catastrophe-like diminution until separation.

FIGURE 10.

Sequence of videomicrographs during unbinding of a biotinylated red blood cell from a streptavidin-coated surface: (a) unstressed contact; and (b) application of the force: t = 0; (c) t = 8 s; (d) t = 10 s; (e) t = 11 s; and (f) separation, t = 11.5 s. Scale bar is 5 μm.

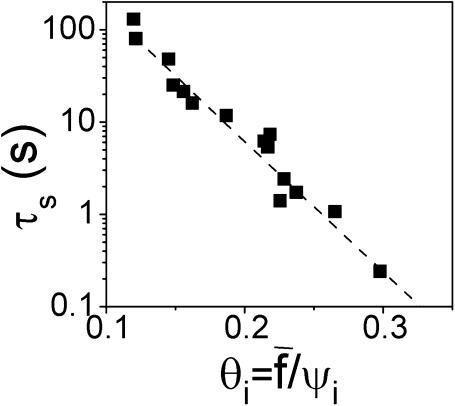
To reach a quantitative level of description for the relationship between separation times and applied forces, we performed a systematic study on nearly 20 cell-bead pairs. Forces ranged from ∼450 pN to 900 pN. Membrane tension of the cells was also varied between 0.15 and 0.8 mN/m. This allowed us to explore “initial” contact radii ranging from 0.9 to 2.1 μm (time zero was taken right after force application). Please note that all the experiments were carried out at constant pipette displacement. Since the contact radius was seen to vary in the timecourse of the experiment, the applied force was not strictly constant according to Eq. 2. However, we checked that the resulting force decrease only became significant (>10%) at the very end of the tearing process, when a tether was about to be extruded (Fig. 10 e). For simplicity, we therefore considered that the applied force was maintained constant during the whole separation process. As predicted from the theoretical calculations (see above), the relevant parameter, which is expected to account for detachment times, is the force scaled by the initial contact radius, or, more precisely, the dimensionless parameter 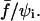Fig. 11 shows the recorded separation times, τ_s, versus 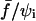in a semilog plot. The most striking feature is that τ_s is observed to span three orders of magnitude. As intuitively expected, unbinding required longer times for low forces and/or large initial contact radii.

FIGURE 11.

Semilog plot of the separation time versus dimensionless parameter 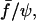which represents the normalized force scaled by the normalized contact radius (see text for details). The dashed line was fitted to with τ₀, α, and q as variable parameters.

The dashed line in Fig. 11 is a fit using the formula with τ₀, α, and q as variable parameters. We obtain a scaling law of ln(τ_s) as 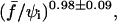which is in excellent agreement with the theoretical predictions for adhesion molecules connected to the surfaces through flexible spacers (Eqs. 19 and 20). The fit also yields α ≈ 0.03. This parameter has to be identified with ɛ′, which was defined in the theoretical section by 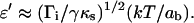In an attempt to estimate ɛ′, we took a_b = 1 nm as a molecular length characterizing the binding pocket of a streptavidin molecule, γ = 0.5 mN/m as an average value for membrane tensions, and Γ_i ≈ 10¹⁴ m⁻² for the density of streptavidin molecules at the bead surface (as estimated in a previous work; Cuvelier et al., 2003) and κ = 1 pN/nm. Providing these values, we obtain ɛ′ = 0.05, which is not too far from the measured value. Furthermore, since the measured values of are in the 0.1–0.3 range, this means that the parameter u defined by u =θ_i/ɛ is >1. Referring back to Theoretical Framework, above, Eq. 20 should be appropriate to fit the τ_s–θ_i curve. The time constant derived from the fit, which was found to be τ₀ ≈ 4800 ± 200 s, can thus be expressed as τ₀ = R_ciɛ′/θ_iV₁. By taking typical values for R_ci ≈ 0.5 μm and θ_i ≈ 0.15, we find V₁ ≈ 1.5 × 10⁻⁷ m s⁻¹. Let us recall that the velocity V₁ is a thermal velocity V₀ (of order 10 m s⁻¹) weighted by a Boltzmann factor, exp(−B/kT), where B is the barrier energy traversed along the unbinding pathway of the specific bond of interest. The derived value for V₁ yields B ≈ 20 kT, which is in good agreement with the energy of the inner barrier of the streptavidin-biotin bond, B = 22 kT, as derived by dynamic force spectroscopy (Merkel et al., 1999).

Case of nonspecific adhesion

For comparison, the dynamics of unbinding of native red blood cells adhering to PEI beads was investigated following the same approach. As stated before, the “adhesiveness” of the PEI beads was shown to slowly decrease in time. This was attributed to the adsorption of proteins to the surface. Consequently, the threshold force, f_c, above which contact is broken, was also varying during the timecourse of the experiment. Fig. 12 shows the temporal evolution of R_c for two cycles, which were extracted from a typical separation sequence. In Fig. 12 a, an extension force of 1150 pN was applied to the red blood cell. We monitored the contact radius over a period of 70 s. The videomicrograph is a snapshot taken at t = 3 s. Within the extension period, no rupture was observed. More important, R_c remained constant within errors. In Fig. 12 b, the blood cell was further stretched by pipette retraction corresponding to a force of 1400 pN. This force led to detachment, meaning that the actual value for f_c in this experiment was between 1150 and 1400 pN. Here, R_c was monitored with a time resolution of 10 ms (video rate of 97 frames/s). We observed that complete separation of the cell-bead pair was achieved within <1 frame.

FIGURE 12.

Contact radius versus time in separation experiments involving nonspecific adhesion between native cells and PEI-coated beads. The arrows indicate the instant at which force is applied. The insets are snapshots which show the shape of the cell in the two time intervals separated by a dashed line. (a) f = 1150 pN < f_c, no separation over 70 s; (b) f = 1400 pN > f_c, separation within <10 ms.

In all the other cell-bead pairs that we investigated, the scenario was similar: we were never able to observe progressive detachment of the cell, indicating that the characteristic separation time was always <10 ms.

In Theoretical Framework, above, we had provided the expression of the separation time in the case of nonspecific adhesion. According to Eq. 9 and by taking 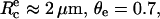V* = γ/2kη ≈ 2 × 10⁻² m s⁻¹, and f_c/f ≈ 0.8, one would obtain τ_ns ≈ 40 μs. This calculated value is therefore consistent with the upper limit derived experimentally.

DISCUSSION

In this work, we have studied some features of the unbinding mechanics of red blood cells adhering to surfaces.

Our experimental procedure is similar in spirit to the pioneer work performed by Evans and co-workers during the last two decades. In his first approach, Evans proposed a method to measure the interfacial free energy for the adhesion of red blood cells by monitoring the reduction of the aspirated tongue in the pipette upon adhesion (Evans, 1980). Separation force measurements between flaccid discocytes and rigid spherocytes were introduced later (Evans, 1985a,b). The mechanical analysis was developed for the cases of both continuum and discrete cross-bridges and was aimed to account for the minimum tension required to separate the adherent membranes. A further refinement was then proposed in a trilogy (Evans et al., 1991a,b; Berk and Evans, 1991), where detachment between agglutinin-bonded erythrocytes was investigated for either large contact areas or point attachments. In particular, it was recognized for the first time that rupture of contacts was a stochastic function of the magnitude and duration of the pulling force. In the case of large contact areas, the experimental procedure, which was based on a detailed analysis of the complex capsule geometry, consisted in aspirating the whole cell in a large pipette until reaching a critical membrane tension to trigger failure. The density of formed cross-bridges was shown to increase with separation.

The main differences in our approach are fourfold:

1. Separation tests were performed at constant membrane tension.

2. Analysis of the geometry of the deformed cell and extension-force conversion was simplified by the fact that red blood cells were osmotically swollen and only partially aspirated in a small pipette.

3. Molecular cross-bridges were chosen to be streptavidin-biotin bonds, which have been extensively studied at the single molecule scale (Merkel et al., 1999; Yuan et al., 2000; Lo et al., 2001).

4. Pulling was performed stepwise, in contrast with linear loadings (at finite speeds), which are commonly used.

More recently, following the advent of sensitive techniques developed to probe individual bonds (Evans et al., 2001b; Litvinov et al., 2002; Li et al., 2003), different groups proposed theoretical approaches to address the problem of collective rupture of adhesive contacts. Erdmann and Schwarz (2004) performed detailed simulations on the rupture forces for a given number of bonds under loading although permitting rebinding. Garrivier et al. (2002) analyzed the kinetics of contact line motion for Dictyostelium discoideum cells submitted to hydrodynamic shears. Smith et al. (2003) mainly focused on the conceptual problem of a free vesicle pulled vertically and succeeded in determining the shape of the vesicle as a function of its reduced volume and the adhesion energy. Finally, Boulbitch (2003) calculated the loading rate dependence of unbinding force between a membrane and a rigid surface starting from a microscopic description of the interface. In comparison, the theoretical approach first proposed by Brochard-Wyart and de Gennes (2003) and further developed in this article is founded on macroscopic parameters (contact angle, contact radius, cell radius). The only molecular parameters that really come into play are the activation barrier, B, and the length of the flexible polymer spacer. Please note that, from the definition of ɛ or ɛ′, the results (Eqs. 15, 19, and 20) are weakly sensitive to the two molecular lengths of the specific bond defined above, and a_b.

In this framework, we could measure the threshold force, which has to be overcome for the cell-bead separation to occur, by simply controlling stepwise pipette displacements and monitoring the cell shape. This critical force f_c was shown to be finely dependent on the cell membrane tension. In agreement with recent theoretical predictions (Brochard-Wyart and de Gennes, 2003) we have experimentally demonstrated that the separation energy density could be derived from f_c and the maximal radius of the elongated cell. Our approach has been shown to equally apply to specific and nonspecific adhesion.

Specific adhesion was mediated by the well-known streptavidin-biotin interaction and we could reliably derive a well-defined separation energy. Under the chosen experimental conditions, we found W = 77 μJ/m². It is worth comparing the separation energy with the adhesion energy measured upon contact formation by the Young-Dupré relation (Eq. 3). We have seen that the equilibrium contact angle was increasing when the membrane tension was decreasing. Collecting all the cases that we investigated, we found an adhesion energy, W_a, of order of 80 μJ/m², meaning that adhesion is ideal. This finding is consistent with the description proposed by Evans (1993): 1), when adhesion is strong, i.e., when membrane tension is dominant, the work to form a contact is expected to be equal to the work require to disrupt it; and 2), when adhesion is weak, i.e., when bending rigidity becomes predominant, the identity between adhesion and separation energies breaks down. Besides, the obtained value for the separation/adhesion energy is also in good agreement with the value of 160 μJ/m² reported by Moy et al. (1999) and derived from static JKR experiments.

In contrast, nonspecific adhesion mediated by electrostatic interactions between positively charged surfaces and native red blood cells was shown to be vanishing in time due to progressive passivation by traces of proteins in the buffer solution.

Our data also yield the first quantitative measurements for the unbinding dynamics of cells loaded by an external step force. In the case of specific adhesion, we observed that detachment times were extremely sensitive to the applied force and could span several orders of magnitude for limited variations of pulling force and initial contact radius upon loading. Separation times were experimentally found to decay as 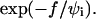To interpret these results we have developed theoretical calculations, which are based on principles first proposed by E. Evans for single bond rupture (Evans and Ritchie, 1997). Our experimental data could be adequately described by the theoretical predictions providing that cell-substrate separation is assumed to be mainly governed by the tearout of adhesion molecules linked to the cell surface through flexible spacers. We are aware that our model may require further refinements, since the applied force is always supposed to be constant, although it is obviously decreasing during detachment. This complication is, however, expected to play a significant role only in the very late stages of detachment, where R_c (and hence the spring constant of the red blood cell) undergoes a drastic decrease. Quite important also, estimates of the prefactors yield two key parameters, namely the surface density of receptor-ligand bonds inside the adhesion patch, Γ_i (through the dimensionless parameter ɛ′) and the energy barrier, B. The obtained value for Γ_i was in good agreement with the one derived from a previous work, in which the dynamics of contact formation of vesicles onto the same surfaces was quantitatively interpreted (D. Cuvelier and P. Nassoy, unpublished results). The activation energy deduced from the fits was found to be of the order of 20 kT, whereas B was estimated to be 22 kT in single molecule experiments (Merkel et al., 1999). This finding together with control fluorescence experiments that exhibited transfer of streptavidin from the bead surface to the cell surface strongly suggest that molecular failure is predominantly located at the streptavidin-biotin linkage. These two pieces of evidence are, however, not definitive, since 1), we were not able to quantify the fluorescence transfer and 2), no data is available concerning the energy barrier for uprooting of integral proteins from the membrane of erythrocytes.

In marked contrast, for nonspecific adhesion of native red blood cells to positively charged surfaces, contact was always observed to break abruptly, within <1 video frame, i.e., 10 ms. Although the theoretical model (Brochard-Wyart and de Gennes, 2003) had predicted very rapid detachment, in the 10–100-μs range, it is worth discussing further the origin of these different dynamic behaviors. As described in Theoretical Framework, above, the unbinding dynamics is governed by hydrodynamic friction near the contact line in the case of nonspecific adhesion. Hence, the characteristic velocity for detachment is 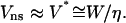On the other hand, when specific bonds are involved, rupture is thermally activated, and the corresponding characteristic velocity is given by In principle, one could expect a combination of both viscous dissipation and tearout. However, for W of order of 1 mJ/m² and B ∼ 20 kT, as measured in our experiments, timescales are clearly separated: the rupture of specific bonds is the limiting process, since it is at least eight orders-of-magnitude slower. Viscous dissipation can become dominant only if the separation energy is considerably reduced or if B drops to ∼4–5 kT. Examination of the values reported in the literature for the activation energies of cell adhesion molecules (antigen-antibody; Schwesinger et al., 2000; Kulin et al., 2002), integrin-fibronectin (Lee and Marchant, 2001; Litvinov et al., 2002; Li et al., 2003), cadherins (Sivasankar et al., 2001), and selectins-carbohydrates (Evans et al., 2001b) reveals that B is typically >10 kT, which means that the dynamics of cell detachment is mostly controlled by the tearout process of specific bonds under load.

CONCLUSION

In summary, our experiments supported by new theoretical predictions present an in-depth analysis of the mechanics of cell-surface detachment from both a static and dynamic viewpoint. Two main findings came out of this work. First, we have experimentally validated the fact that the relevant lengthscale required to derive the density of separation energy from rupture force measurements is the size of the stretched cell before detachment, and not the size of the cell-substrate contact, as it could be intuitively believed. Second, the results on the dynamics of unbinding also shed some light on understanding the forced rupture of specific bonds between cell adhesion molecules at a cellular scale. We have shown that nonspecific cell-substrate detachment is dynamically governed by the viscous dissipation around the contact line, whereas the rate of specific detachment is limited by the tearout process of adhesion molecules located in the belt of the adhesive patch. From our viewpoint, the most interesting aspect of these experimental results and theoretical predictions is that they permit to bridge the gap between a molecular description of bond rupture as yielded by single molecule force spectroscopy and a continuum description of contact failure. Moreover, we have demonstrated that the dynamics of specific detachment involved not only the extraction force ϕ(V) of individual bonds, but also the deformation of the bonds at rupture. This deformation length is the sum of the bond-breaking length and the elongation of the flexible spacers connected to the cell membrane. Although our study was restricted to red blood cells decorated with customized adhesion molecules, we may anticipate that similar effects may be an important contributor in adhesion of eukaryotic cells. Most of the cell adhesion molecules are indeed connected to the cytoskeleton, which may behave as a deformable spacer.

In view of a possible application of the method developed here to other types of cells, refinements to the model need to be made to incorporate the higher complexity of eukaryotic cells. First, the main difficulty will consist in determining a force-extension relation, since living cells may exhibit significant viscoelastic properties due to cytoskeletal reorganization upon external force (Thoumine and Ott, 1997). Also, as suggested by Erdmann and Schwarz (2004), the possibility of rebinding and the influence of the presence of clusters of bonds encountered in focal adhesion patterns (Koo et al., 2002) could be addressed. Experiments on other model systems of artificial cells (gel balls, vesicles filled with gel, etc.) are underway to investigate the passive viscoelastic contribution of the cytoskeleton.