Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Oct 1;87(6):3633–3641. doi: 10.1529/biophysj.104.046243

Probing the Kinetics of Single Molecule Protein Folding

Vitor B P Leite *, José N Onuchic †, George Stell ‡, Jin Wang ‡,§
PMCID: PMC1304877  PMID: 15465871

Abstract

We propose an approach to integrate the theory, simulations, and experiments in protein-folding kinetics. This is realized by measuring the mean and high-order moments of the first-passage time and its associated distribution. The full kinetics is revealed in the current theoretical framework through these measurements. In the experiments, information about the statistical properties of first-passage times can be obtained from the kinetic folding trajectories of single molecule experiments (for example, fluorescence). Theoretical/simulation and experimental approaches can be directly related. We study in particular the temperature-varying kinetics to probe the underlying structure of the folding energy landscape. At high temperatures, exponential kinetics is observed; there are multiple parallel kinetic paths leading to the native state. At intermediate temperatures, nonexponential kinetics appears, revealing the nature of the distribution of local traps on the landscape and, as a result, discrete kinetic paths emerge. At very low temperatures, exponential kinetics is again observed; the dynamics on the underlying landscape is dominated by a single barrier. The ratio between first-passage-time moments is proposed to be a good variable to quantitatively probe these kinetic changes. The temperature-dependent kinetics is consistent with the strange kinetics found in folding dynamics experiments. The potential applications of the current results to single-molecule protein folding are discussed.

INTRODUCTION

Protein folding is a central issue of modern science. It is fundamental for understanding biological structure and function, and it is also connected to many technological applications such as drug design. The crucial question regarding the folding mechanism is how the many possible conformational degrees of freedom converge to the unique native basin. Looking at details of the microscopic kinetics and figuring out the dominant pathways are important, but this approach is sometimes misleading and misses the global picture (Levinthal,1969; Baldwin, 1995; Laurents et al., 1988). The possibility that multiple paths leading to folding may exist has led to an alternative statistical approach to this problem (Bryngelson et al., 1995; Wolynes et al., 1995; Chan and Dill, 1994; Abkevich et al., 1994; Wang et al, 1996).

The resulting energy-landscape theory looks at a coarse-grained-level picture of folding and tries to uncover the general principles governing its mechanisms. In general, the energy landscape is rough due to the many different possible competing interactions among the amino acid residues. On the other hand, the landscape of real proteins has evolved toward a funnel, shaped with a gradient leading toward the native folded basin. There are in general many possible paths leading to folding. A small number of discrete pathways emerge only when the landscape becomes rough and local traps become significant (Wang et al., 1996). The predictions of the funneled-landscape picture of folding have been confirmed and verified by many lattice and off-lattice simulations (Chan and Dill, 1994; Abkevich et al., 1994; Klimov and Thirumalai, 1998; Socci and Onuchic, 1994, 1995; Chahine et al., 2002; Kaya and Chan, 2000, 2002, 2003a,b,c; Boczko and Brooks, 1995). They are also in good qualitative and quantitative agreement with protein-folding thermodynamic and kinetic experiments (Itzhaki et al., 1995; Huang and Oas, 1995; Eaton et al., 1997, 2000; Garcia-Mira et al., 2002; Sabelko et al., 1999; Nguyen et al., 2003, Kuhlman et al., 1998).

The landscape theory of folding defines a temperature where the native protein structure becomes stable, Tf. It also defines a glassy temperature, Tg, where the landscape becomes rough compared with the bias toward a native folded state, and trapping into local minimum occurs. The ratio Tf/Tg defines how good a folder a protein is, i.e., the energy gap should be larger than the underlying roughness of the landscape (Goldstein et al., 1992; Chan and Dill, 1994; Chan et al., 2004; Abkevich et al., 1994; Klimov and Thirumalai, 1998). The cooperativity in the physical interactions can influence the ratio of Tf/Tg significantly (Chan et al., 2004).

There have been theoretical studies on average measurable variables of the folding kinetics (mean first-passage times, MFPT, or average rates) (Bryngelson and Wolynes, 1989; Saven et al., 1994; Wang et al., 1996; Shakhnovich et al., 1989; Gutin et al., 1996; Seno et al., 1998; Cieplak et al., 1999; Klimov and Thirumalai, 1998; Socci et al., 1996). Although the average-value description of the kinetics is important, it can sometimes miss important features of folding dynamics that are crucial for uncovering the fundamental mechanisms. For different sequence compositions or external conditions (physical properties, temperatures, and solvent conditions) the progress of folding can probe different parts of the energy landscape and detect different local barriers. Therefore many possible timescales may coexist, and the kinetics can become nonexponential or multiexponential. In bulk measurements, it is often difficult to distinguish whether the observed nonexponential kinetics is intrinsic or due to the inhomogeneous distribution of single exponential processes. With recent technological advances, however, single-molecule detections have become possible (Moerner, 1996; Lu et al., 1998; Deniz et al., 2000). Single molecules are sensitive probes to the local environments and therefore an ideal tool to understand the structures of the energy landscape of the proteins (Wang and Wolynes, 1995, 1999; Onuchic et al., 1999; Wang, 2003a,b; Schenter et al., 1999). Lately, a number of remarkable initial single-molecule folding experiments have been undertaken (Zhuang et al., 2000, 2002; Jia et al., 1999; Deniz et al., 2000; Schuler et al., 2002; Lipman et al., 2003) but their interpretation is nontrivial. Statistical fluctuations are intrinsic to single molecules, since they are not weighted down by the number of the molecules as they are in the bulk, and they can be directly measured. Single-molecule data are essentially sequences of on-and-off spikes as a function of time. Therefore, to determine whether they are associated with exponential decay is a challenging task.

In this article, we investigate the kinetics of folding based on the moments or fluctuations of the FPTs of folding and dynamic collapse, with respect to temperature and physical properties such as hydrophobicity. From these studies, we are able to determine the way in which the exponential or nonexponential nature of the folding kinetics will emerge as a function of these conditions. Furthermore, we obtain information about the dependence of the distribution of folding times upon various conditions. This gives the full dynamic picture of the folding instead of just the MFPT. The lattice simulation presented is able to establish a link among the energy-landscape theory of protein folding, simulations, and single-molecule folding experiments (Wang and Wolynes, 1995, 1999; Onuchic et al., 1999; Berezhkovskii et al., 1999; Wang, 2003a,b; Lee et al., 2003; Zhou et al., 2003; Gopich et al., 2003a,b; Zhuang et al., 2000, 2002; Jia et al., 1999; Deniz et al., 2000; Schuler et al., 2002; Lipman et al., 2003).

MODEL AND METHODS

The model used for the kinetic simulations has been extensively employed in previous studies (Abkevich et al., 1994; Socci and Onuchic, 1994, 1995). The protein is modeled by a 27-length polymer chain (27-mer) on a three-dimensional cubic lattice. The 27-mer lattice is a renormalized (or reduced) description of small globular proteins. We use a Monte Carlo algorithm with standard polymer local moves—i.e., end, corner flip, and 90° crankshaft (Socci and Onuchic, 1994, 1995). The energy for the heteropolymer is given by

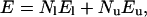graphic file with name M1.gif (1)

where El is the nonbonded contact energy between monomers of the same type and Eu is the energy between monomers of different types. Nl is the number of contacts between monomers of similar type, and Nu is the number of contacts between monomers of dissimilar types. There are only two types of monomers with a hydrophobic or hydrophilic nature. Two limits of the parameters are tested (Chahine et al., 2002):

  1. High hydrophobicity (El = −3 and Eu = −1 in arbitrary units, chosen so that typical temperatures are of order one), where biasing toward the folded state is strong ((El + Eu)/2 = −2) and the roughness of the landscape is weak (the variance or dispersion is small between native and nonnative contact energies (Eu–El) = 2).

  2. Low hydrophobicity (El = −3 and Eu = + 3), where the biasing toward the folded state is weak ((El + Eu)/2 = 0) and the roughness of the landscape is strong (the variance or dispersion is large between native and nonnative contact energies (Eu–El) = 6).

We use the previously-designed sequence ABABBBBBABBABABAAABBAAAAAAB (Shakhnovich and Gutin, 1993). In this study only one good folding sequence is used. Effects of sequence variations are not analyzed. Monte Carlo sampling with a local move set is used to determine the density of states and to define the kinetics of the model (Abkevich et al., 1994; Socci and Onuchic, 1994, 1995; Chahine et al., 2002). The density of states is determined as a function of energy E, number of native nonbonded contacts Q, and the total number of nonbonded contacts Z. Within the microcanonical ensemble, the free energy of the system can be obtained, and the complete thermodynamics can be determined. Four phases are typically found—i.e., the noncompact unfolded states (so-called random-coil states); compact unfolded states; trapping states; and the native state. The transition temperatures Tf (folding) and Tg (local trapping) are determined.

We can measure the MFPT to reach the native state for the designed sequence starting from random-coil configurations. By repeating the dynamic Monte Carlo simulations with different initial conditions, one can obtain information about the statistical distributions of these folding times and therefore determine the high-order moments of the FPT. The moments of first-passage time (τ) of events for folding and collapse are generally given by

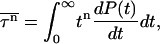graphic file with name M2.gif (2)

where P(t) is the fraction of unfolded (or uncollapsed) proteins. When the system is above the kinetic minimum temperature (specified in detail in the next section), P(t) exhibits exponential behavior, so 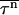Inline graphic is simply given by

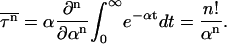graphic file with name M4.gif (3)

The ratio of the nth moment and the mean to the nth power,

graphic file with name M5.gif (4)

can be easily computed in the simulations, and in the high-temperature limit (above the transition temperatures) Rn = n!. This implies a Poisson distribution, and therefore a single-exponential process. The ratio Rn/n! becomes a measure of the deviation from the single-exponential process. As shown below, when the temperature drops, deviations of Rn/n! from 1 are observed and one can infer the effects of fluctuations on an FPT. The n-order moment ratio first rises as the temperature drops, then at an even lower temperature, it returns to single-exponential kinetics.

RESULTS

Exponential and nonexponential behavior

Consistent with previous studies (Socci and Onuchic, 1995; Kaya and Chan, 2000, 2002; 2003c), the mean first-passage time (MFPT) as a function of temperature has a U-shaped dependence, with higher values on both the high and low temperature ranges and a kinetic minimum near the folding temperature. We found that above this temperature, the distribution of first-passage times (FPT) is nearly Poissonian, indicating single-exponential kinetics. At the high temperatures, due to the large thermo motions, the different kinetic paths sense roughly similar barriers since the local details are smeared or washed out by the thermo motions. Only the dominant barriers matter. So there are multiple parallel paths, all experiencing similar barriers, resulting in single-exponential kinetics. On the other hand, when the temperature drops below the temperature of the kinetic minimum, the distribution of FPT deviates from Poissonian significantly, indicating nonexponential kinetics and multiple traps. In certain temperature regimes, the distribution at long times approaches a power law. This indicates that the fluctuation in FPT is significant and deviates from the mean. In other words, the FPT is non-self-averaging and the distribution has fatty tails. This indicates the existence of intermittence, where rare events can give a significant contribution to the folding event. Due to the ruggedness of the underlying energy landscape at low temperatures, specific discrete paths are themselves different from each other and give distinct contributions to the kinetics. The full distribution of FPT, not only its mean, is needed to characterize the whole system dynamics. At even lower temperatures, the kinetics is back to Poissonian, indicating exponential kinetics and the domination of a single trap. By increasing (or decreasing) hydrophobicity, the distribution deviates less (or more) from Poissonian in the same temperature range.

Folding

The results for the folding FPT moments (second, third, and fourth moments) and their ratios as well as their derivatives with respect to temperature are shown in Fig. 1 (low hydrophobicity) and Fig. 2 (high hydrophobicity). For our sequence, at low hydrophobicity, Tg = 1.2 and Tf = 1.6 (Socci and Onuchic, 1994, 1995). The kinetic minimum of folding 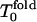Inline graphic is near 1.8. For T > Inline graphic Rn = n!; for Inline graphic Rn/n! > 1; and Rn increases significantly. 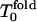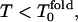For high hydrophobicity, Tg = 1.0 and Tf = 1.3, the kinetic minimum Inline graphic is near 1.5, and one can see a similar behavior: for Inline graphic Rn = n! and for Inline graphic Rn/n! > 1, but Rn does not increase as quickly as for low hydrophobicity.

FIGURE 1.

FIGURE 1

Open in a new tab

Ratios of moments of folding events (a) and their derivatives (b) at low hydrophobicity (LH) as function of temperature. The kinetic minimum, at which the Rn/n! start to increase, is at Inline graphic The numbers 2, 3, and 4 refer to R2, R3, and R4, respectively. The smaller plot shows the detail of R2.

FIGURE 2.

FIGURE 2

Open in a new tab

Ratios of moments of folding events (a) and its derivatives (b) at high hydrophobicity (HH) as function of temperature. The kinetic minimum, at which the Rn/n! start to increase, is at 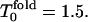Inline graphic The same notation as in Fig. 1 is used.

It is worthwhile to point out that for each of the two models studied, the fastest folding occurs at a model temperature higher than the folding temperature Tf. As pointed out recently by Chan et al. (2004), this model behavior is not similar to that of many real proteins. It corresponds to a situation in which folding rate would decrease when native stability is increased from the transition midpoint. The underlying reason for this critical shortcoming is because the two-letter models studied here are not sufficiently cooperative, with Tf/Tg too small to mimic that of real apparent two-state proteins. Although the simulation results presented are useful, these limitations of the model might have significant impact on their relationship with experiments. The cooperativity can play an important role here in solving this discrepancy.

The simulations are in agreement with analytical calculations as well as detailed models (Lee et al., 2003; Zhou et al., 2003) and with other ways of calculating 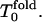Inline graphic This indicates that the ratios of moments or the fluctuations in first-passage times are efficient and sensitive ways to identify the kinetic transition temperatures and the effect of fluctuations. In Figs. 1 and 2 one can see that the derivative of Rn/n! provides an effective parameter for locating Inline graphic As we can see, the sensitivity on the kinetic fluctuations increases rapidly as the order of the moments increases. Although high-order moments will be better indicators than low-order moments, the data requirement is much greater. In principle, there should be a balance in extracting the useful information from the trajectories in the simulations and experiments.

Note that the ratios of the moments will become important at the single-molecule level. In the bulk experiments, the high-order moments are significantly suppressed by the large number of molecules in the sample (on the order of 108 molecules). Furthermore, it is often hard to distinguish the intrinsic dynamics from the observed nonexponential kinetics, since the same data could result from either inhomogeneous distributions of the different protein molecules with exponential kinetics or homogeneous distribution of the intrinsic underlying nonexponential kinetics.

Collapse

Using methods similar to those for the folding simulations, all simulations were repeated to determine the collapse times. For this study, the collapse time is taken to be at the point when the final state for the collapse is achieved—i.e., when the system reaches the nonbonded contacts Z = 25—instead of at the native configuration for the folded state. In the results below we have the same sequence in the same two limits we had before. Now the deviations on Rn are expected to appear when the system reaches the kinetic minimum for collapse Inline graphic For favorable collapsed states, starting with random-coil conformations, the uncollapsed fraction decays exponentially. However if the glassy trapping regime is reached, the dynamics becomes slow and one observes slow trajectories and nonexponential decays.

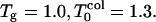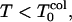For low hydrophobicity, Tg = 1.2, Inline graphic; and for high hydrophobicity, Inline graphic The simulation results of Rn/n! and their corresponding derivatives with respect to temperature as a function of temperature are shown in Figs. 3 and 4. Roughly for Inline graphic Rn/n! = 1, and for Inline graphic Rn/n! > 1. Note that Rn starts to increase above Tg (at T = 1.6 for low hydrophobicity, and at T = 1.3 for high hydrophobicity), a possible indication of kinetic glassy transition temperature TA postulated in the theories of the short-range random first-order phase transitions in glasses (Kirkpatrick et al., 1989). This is an indication that deviation in Rn is a sensitive probe of the dynamics of collapse events (see Figs. 3 b and 4 b for the derivative part).

FIGURE 3.

FIGURE 3

Open in a new tab

Ratios of moments of collapse events (a) and its derivatives (b) at low hydrophobicity (LH) as function of temperature. The numbers 2, 3, and 4 refer to R2, R3, and R4, respectively. The kinetic minimum, at which the Rn/n! start to increase, is at Inline graphic

FIGURE 4.

FIGURE 4

Open in a new tab

Ratios of moments of collapse events (a) and its derivatives (b) at high hydrophobicity (HH) as function of temperature. The kinetic minimum, at which the Rn/n! start to increase, is at Inline graphic The same notation of numbers as in Fig. 3 is used.

The increase in Rn below the transition temperatures is hard to quantify. For folding, the increase is more pronounced at low hydrophobicity. For collapse, the behavior is similar at high and low hydrophobicity. The increase in Rn may be related to the relative depth of local traps and the bias toward the native/collapse state, which yields to large fluctuations in the FPT events.

Very low temperature results

The above results on kinetics and fluctuations on folding are valid for temperatures between the folding and the glassy trapping temperatures. At even lower temperature (see Fig. 5), in the case of collapse in the low hydrophobicity limit, Rn drops. At temperature 0.7 we obtain 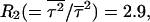Inline graphic which is quite close to 2! (the high temperature limit of Poisson single-exponential kinetics). The exact numbers are hard to obtain, because at low temperatures a significant percentage of runs do not reach the collapsed state (they reach the Monte Carlo step simulation limit first, 1.0 × 109). Still, the results suggest that the ratios at very low temperature behave much as they do in the high temperature limit, as predicted in analytical calculation (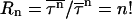Inline graphic) (Wang, 2004a). Due to the finite size of our systems, kinetics is now controlled by a single barrier.

FIGURE 5.

FIGURE 5

Open in a new tab

Ratios of moments of collapse events at low hydrophobicity (LH) including very low temperatures.

It is worthwhile to point out that the temperature in the present models cannot be directly identified with the experimental temperature, because the model interactions are temperature-independent, whereas real effective intraprotein interactions are temperature-dependent (Chan et al., 2004).

In Fig. 6, all kinetic regimes are shown through a plot of the survival population of uncollapsed runs as a function of time. At high temperature (T = 2.0), the system follows an exponential decay. In this regime, multiple diffusive pathways for collapse are available and they are roughly equivalent, yielding a single-exponential characteristic time. At temperatures around the relevant transition temperatures (T = Tg = 1.0), fluctuations in τ are at their highest, diffusive paths are not equivalent, and the system exhibits intermittence. One can clearly see that a single exponential does not fit the survival probability. Even a fit to a stretched exponential is not sufficient and the system shows a power-law behavior over three decades at times longer than MFPT. At very low temperature (T = 0.7), a single path dominates the process. All three regimes are in agreement with the theoretical predictions (Wang, 2004a).

FIGURE 6.

FIGURE 6

Open in a new tab

Survival probability for collapse (uncollapsed fraction) for the low hydrophobicity case, as in Fig. 5. It shows three different regimes: (○) high temperature, T = 2.0; (□) at transition temperature T = Tg = 1.0; and (▵) very low temperature, T = 0.7. The lines are the exponential fits for each temperature. At high and very low temperature the fits appropriately describe the data (continuum lines). At the transition temperature one can clearly see the nonexponential behavior (compare with the dashed line). In the long-time limit between t = 106 and 109, the survival probability is nearly a straight line in the log-log plot implying a power law dependence on time.

One can observe two transition temperatures. The high transition temperature corresponds to a transition where the kinetics exhibits changes from the high-temperature exponential to a nonexponential behavior. The low transition temperature (even lower than the glass or trapping transition temperature) corresponds to the changes in kinetics from higher temperature nonexponential to lower temperature Poisson-exponential.

This kind of kinetic behavior in the fluctuation of the kinetic folding times can be understood physically as follows: At very high temperature, due to the large thermal motion and kinetic energy, the folding has multiple parallel trajectories that cause an average barrier, and therefore the process is a single-exponential one. When the temperature is reduced, the folding event encounters different barriers, and the kinetics becomes multiexponential. When the temperature becomes even lower (below the glassy trapping temperature), the system has only limited states to explore (the others are frozen), and the kinetics is controlled by escapes from a single dominant deep trap. Thus the process becomes a single-exponential one again.

DISCUSSIONS AND CONCLUSIONS

We have studied the fluctuations of protein folding kinetics by examining the ratios of the moments of the first-passage times. This approach can be used to probe the underlying energy landscape structure by kinetics over a broad temperature range. Gruebele's group (Sabelko et al., 1999; Nguyen et al., 2003) observed a “strange” kinetic behavior in which kinetics varies from single-exponential to nonexponential transitions as the temperature decreases. This corresponds to the previous investigation (Kaya and Chan, 2002, 2003c) and our current model prediction in the relatively high temperature regime (the physiological temperature regime), where a change from single-exponential to nonexponential kinetic behavior is observed. Indeed, previous (Kaya and Chan, 2002, 2003c) and current investigations provide evidence that these kinetic features are robust across several different models. This temperature-dependence of the protein dynamics can also be probed in ligand binding experiments. Frauenfelder et al. (1988, 1991) have observed this behavior for the binding kinetics of CO to myoglobin. Sadqi et al. (2003) observed a dynamical slowdown of the hydrophobic collapse upon temperature change. They also observed that, at higher temperatures, as the protein becomes increasingly compact due to a stronger hydrophobic force, there is a slowdown of the dynamics of collapse. This dynamic hydrophobic effect is a high-temperature analog of the dynamic glass transition predicted by theory. In our collapse studies, we also see a similar complex behavior of the kinetics when the temperature changes. To study the role of hydrophobic collapse in folding and its link with the experiments (Sadqi et al., 2003), we plot the evolution of survival probability or the fraction of uncollapse in time. In Fig. 7, we show, under the condition of high hydrophobicity, that the kinetics (the rate) derived from the survival probability at the optimal temperature (T ∼ 1.5) is the fastest (measured by the slope of the curve). The kinetics becomes slower when the temperature either increases or decreases beyond the optimal temperature. This is consistent with kinetic slowdown at higher temperatures observed by Sadqi et al. (2003) in the folding experiments (Kaya and Chan, 2000, 2002, 2003c). We also see similar behavior in the low hydrophobicity case in Fig. 8, except that the optimal temperature is at 2.0. In general, the average kinetics is slower in the low hydrophobicity case than in the high hydrophobicity case, because of the weaker hydrophobic driving force.

FIGURE 7.

FIGURE 7

Open in a new tab

Uncollapsed fraction versus time (Monte Carlo steps) for high hydrophobicity case.

FIGURE 8.

FIGURE 8

Open in a new tab

Uncollapsed fraction versus time (Monte Carlo steps) for low hydrophobicity case.

The high-to-low temperature transition from single-exponential to nonexponential kinetics has been also observed in single-molecule experiments. In the work of Xie's group (Yang and Xie, 2002a,b; Yang et al., 2003), reaction dynamics also experiences nonexponential kinetic behavior and the distribution of kinetics follows an approximate power law. The theoretical framework presented here provides a microscopic foundation to interpret these experiments. Other single-molecule experiments also show similar behavior (Zhuang et al., 2000, 2002; Jia et al., 1999; Schuler et al., 2002; Lipman et al., 2003). In future studies, it will be important to explore these kinetic fluctuations upon changing experimental conditions such as temperature and denaturant solvents (which would be equivalent to changing the hydrophobic contents of the system modeled with low and high hydrophobicity in this study).

One of the advantages of this approach is that it provides a link among theory, simulations, and experiments. In the theoretical approach, the first-passage time and its statistical properties can be easily obtained from the simulations following the procedures outlined in this article. In the experiments, information about FPT properties can be obtained from the kinetic folding trajectories (for example, fluorescence). This will stimulate the current round, and the next, of single-molecule experiments and even more detailed simulations, for study of the full range of kinetic behavior.

More simulations at the microscopic level, which will provide the detailed mechanistic features, are also necessary. The only limiting step is that the statistics of the kinetics requires long-time trajectories. Therefore some intermediate coarse-grained description, for example at the residue-residue level, may be needed to supplement the fully atomistic studies.

This approach proposed for the folding kinetics is quite general. It is not necessarily limited to folding studies. In fact, it is a framework that can be generalized and extended to other systems such as RNA folding, biomolecule binding, viscous liquids, and glassy materials. In fact, such kinetic investigations have already been carried out using an energy landscape framework for viscous liquids and glassy materials (Kirkpatrick et al., 1989; Xia and Wolynes, 2001) and binding of biomolecules (Wang et al., 2004b).

Acknowledgments

J.W. thanks Prof. Peter Wolynes for helpful discussions. V.B.P.L. also thanks J.N.O. and the Center for Theoretical Biological Physics, where part of the work was performed.

Work at the University of California at San Diego was supported by National Science Foundation grants (INT-0000419 and MCB-0084797). G.S. was supported by the Division of Chemical Sciences, Office of the Basic Energy Sciences, Office of Energy Research, U.S. Department of Energy. V.B.P.L. was supported by Fundacão de Amparo à Pesquisa do Estado de São Paulo (Brazil) and a grant from the Conselho Nacional de Desenvolvimento Cientificoe Technológico-National Science Foundation International Program (INT-0000419).

References

  1. Abkevich, V. I., A. M. Gutin, and E. I. Shakhnovich. 1994. Free energy landscape for protein folding kinetics: intermediates, traps, and multiple pathways in theory and lattice model simulations. J. Chem. Phys. 101:6052–6062. [Google Scholar]
  2. Baldwin, R. L. 1995. The nature of protein-folding pathways—the classical versus the new view. J. Biomol. NMR. 5:103–109. [DOI] [PubMed] [Google Scholar]
  3. Berezhkovskii, A. M., A. Szabo, and G. H. Weiss. 1999. Theory of single-molecule fluorescence spectroscopy of two-state systems. Chem. Phys. 110:9145–9150. [Google Scholar]
  4. Boczko, E. M., and C. L. Brooks. 1995. First-principles calculation of the folding free-energy of a 3-helix bundle protein. Science. 269:393–396. [DOI] [PubMed] [Google Scholar]
  5. Bryngelson, J. D., J. O. Onuchic, N. D. Socci, and P. G. Wolynes. 1995. Funnels, pathways, and the energy landscape of protein folding—a synthesis. Proteins Struct. Funct. Genet. 21:167–195. [DOI] [PubMed] [Google Scholar]
  6. Bryngelson, J. D., and P. G. Wolynes. 1989. Intermediates and barrier crossing in a random energy model (with applications to protein folding). J. Phys. Chem. 93:6902–6915. [Google Scholar]
  7. Chahine, J., H. Nymeyer, V. B. P. Leite, N. D. Socci, and J. N. Onuchic. 2002. Specific and nonspecific collapse in protein folding funnels. Phys. Rev. Lett. 88:168101. [DOI] [PubMed] [Google Scholar]
  8. Chan, H. S., and K. A. Dill. 1994. Transition states and folding dynamics of proteins and heteropolymers. J. Chem. Phys. 100:9238–9257. [Google Scholar]
  9. Chan, H. S., S. Shimizu, and H. Kaya. 2004. Cooperativity principles in protein folding. Methods Enzymol. 380:350–379. [DOI] [PubMed] [Google Scholar]
  10. Cieplak, M., T. X. Hoang, and M. S. Li. 1999. Scaling of folding properties in simple models of proteins. Phys. Rev. Lett. 83:1684–1687. [Google Scholar]
  11. Deniz, A. A., T. A. Laurence, G. S. Beligere, M. Dahan, A. B. Martin, D. S. Chemla, P. E. Dawson, P. G. Schultz, and S. Weiss. 2000. Single-molecule protein folding: diffusion fluorescence resonance energy transfer studies of the denaturation of chymotrypsin inhibitor 2. Proc. Natl. Acad. Sci. USA. 97:5179–5184. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Eaton, W. A., V. Muñoz, P. A. Thompson, C.-K. Chan, and J. Hofrichter. 1997. Submillisecond kinetics of protein folding. Curr. Opin. Struct. Biol. 7:10–14. [DOI] [PubMed] [Google Scholar]
  13. Eaton, W. A., V. Muñoz, S. J. Hagen, G. S. Jas, L. J. Lapidus, E. R. Henry, and J. Hofrichter. 2000. Fast kinetics and mechanisms in protein folding. Annu. Rev. Biophys. Biomol. Struct. 29:327–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Frauenfelder, H., F. Parak, and R. D. Young. 1988. Conformational substrates in proteins. Annu. Rev. Biophys. Biophys. Chem. 17:451–479. [DOI] [PubMed] [Google Scholar]
  15. Frauenfelder, H., S. G. Sligar, and P. G. Wolynes. 1991. The energy landscapes and motions of proteins. Science. 254:1598–1603. [DOI] [PubMed] [Google Scholar]
  16. Garcia-Mira, M. M., M. Sadqi, N. Fischer, J. M. Sanchez-Ruiz, and V. Muñoz. 2002. Experimental identification of downhill protein folding. Science. 298:2191–2195. [DOI] [PubMed] [Google Scholar]
  17. Goldstein, R. A., Z. A. Luthey-Schulten, and P. G. Wolynes. 1992. Optimal protein-folding codes from spin-glass theory. Proc. Natl. Acad. Sci. USA. 89:4918–4922. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gopich, I., G. Hummer, and A. Szabo. 2003a. Theory and single molecule experiments. ACS Abst. Phys. 226:112–112. [Google Scholar]
  19. Gopich, I. G., and A. Szabo. 2003b. Statistics of transitions in single molecule kinetics. J. Chem. Phys. 118:454–455. [Google Scholar]
  20. Gutin, A. M., V. I. Abkevich, and E. I. Shakhnovich. 1996. Chain length scaling of protein folding time. Phys. Rev. Lett. 77:5433–5436. [DOI] [PubMed] [Google Scholar]
  21. Huang, G. S., and T. G. Oas. 1995. Submillisecond folding of monomeric λ-repressor. Proc. Natl. Acad. Sci. USA. 92:6878–6882. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Itzhaki, L. S., D. E. Otzen, and A. R. Fersht. 1995. The structure of the transition state for folding of chymotrypsin inhibitor-2 analyzed by protein engineering methods—evidence for a nucleation-condensation mechanism for protein folding. J. Mol. Biol. 254:260–288. [DOI] [PubMed] [Google Scholar]
  23. Jia, Y. W., D. S. Talaga, W. L. Lau, H. S. M. Lu, W. F. DeGrado, and R. M. Hochstrasser. 1999. Folding dynamics of single GCN-4 peptides by fluorescence resonant energy transfer confocal microscopy. Chem. Phys. 247:69–83. [Google Scholar]
  24. Kaya, H., and H. S. Chan. 2000. Energetic components of cooperative protein folding. Phys. Rev. Lett. 85:4823–4826. [DOI] [PubMed] [Google Scholar]
  25. Kaya, H., and H. S. Chan. 2002. Towards a consistent modeling of protein thermodynamic and kinetic cooperativity: how applicable is the transition state picture to folding and unfolding? J. Mol. Biol. 315:899–909. [DOI] [PubMed] [Google Scholar]
  26. Kaya, H., and H. S. Chan. 2003a. Contact order dependent protein folding rates: kinetic consequences of a cooperative interplay between favorable nonlocal interactions and local conformational preferences. Proteins. 52:524–533. [DOI] [PubMed] [Google Scholar]
  27. Kaya, H., and H. S. Chan. 2003b. Solvation effects and driving forces for protein thermodynamic and kinetic cooperativity: how adequate is native-centric topological modeling? J. Mol. Biol. 326:911–931. [DOI] [PubMed] [Google Scholar]
  28. Kaya, H., and H. S. Chan. 2003c. Origins of chevron rollovers in non-two-state protein folding kinetics. Phys. Rev.Lett. 90:258104. [DOI] [PubMed] [Google Scholar]
  29. Kirkpatrick, T. R., D. Thirumalai, and P. G. Wolynes. 1989. Scaling concepts for the dynamics of viscous liquids near an ideal glassy state. Phys. Rev. A. 40:1045–1054. [DOI] [PubMed] [Google Scholar]
  30. Klimov, D. K., and D. Thirumalai. 1998. Linking rates of folding in lattice models of proteins with underlying thermodynamic characteristics. J. Chem. Phys. 109:4119–4125. [Google Scholar]
  31. Kuhlman, B., D. L. Luisi, P. A. Evans, and D. P. Raleigh. 1998. Global analysis of the effects of temperature and denaturant on the folding and unfolding kinetics of the N-terminal domain of the protein L91. J. Mol. Biol. 284:1661–1670. [DOI] [PubMed] [Google Scholar]
  32. Laurents, D. V., and R. L. Baldwin. 1998. Protein folding: matching theory and experiment. Biophys. J. 75:428–434. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Lee, C. L., C. T. Lin, G. Stell, and J. Wang. 2003. Diffusion dynamics, moments, and distribution of first-passage time on the protein-folding energy landscape, with applications to single molecules. Phys. Rev. E. 67:041905. [DOI] [PubMed] [Google Scholar]
  34. Levinthal, C. 1969. Proceedings in Mossbauer Spectroscopy in Biological Systems. P. Debrunner, J. Tsubris, and E. Munck, editors. University of Illinois Press, Urbana, IL. 22.
  35. Lipman, E. A., B. Schuler, O. Bakajin, and W. A. Eaton. 2003. Single-molecule measurement of protein folding kinetics. Science. 301:1233–1235. [DOI] [PubMed] [Google Scholar]
  36. Lu, H. P., L. Y. Xun, and X. S. Xie. 1998. Single-molecule enzymatic dynamics. Science. 282:1877–1882. [DOI] [PubMed] [Google Scholar]
  37. Moerner, W. E. 1996. High-resolution optical spectroscopy of single molecules in solids. Acc. Chem. Res. 29:563–571. [Google Scholar]
  38. Nguyen, H., M. Jäger, A. Moretto, M. Gruebele, and J. W. Kelly. 2003. Tuning the free-energy landscape of a WW domain by temperature, mutation, and truncation. Proc. Natl. Acad. Sci. USA. 100:3948–3953. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Onuchic, J. N., J. Wang, and P. G. Wolynes. 1999. Analyzing single molecule trajectories on complex energy landscapes using replica correlation functions. Chem. Phys. 247:175–184. [Google Scholar]
  40. Sabelko, J., J. Ervin, and M. Gruebele. 1999. Stretching lattice models of protein folding. Proc. Natl. Acad. Sci. USA. 96:6031–6036. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Sadqi, M., L. J. Lapidus, and V. Munoz. 2003. How fast is protein hydrophobic collapse? Proc. Natl. Acad. Sci. USA. 100:12117–12122. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Saven, J. G., J. Wang, and P. G. Wolynes. 1994. Kinetics of protein folding: the dynamics of globally connected rough energy landscapes with biases. J. Chem. Phys. 101:11037–11043. [Google Scholar]
  43. Schenter, G. K., H. P. Lu, and X. S. Xie. 1999. Statistical analyses and theoretical models of single-molecule enzymatic dynamics. J. Phys. Chem. A. 103:10477–10488. [Google Scholar]
  44. Schuler, B., E. A. Lipman, and W. A. Eaton. 2002. Probing the free-energy surface for protein folding with single-molecule fluorescence spectroscopy. Nature. 419:743–747. [DOI] [PubMed] [Google Scholar]
  45. Seno, F., C. Micheletti, A. Maritan, and J. R. Banavar. 1998. Variational approach to protein design and extraction of interaction potentials. Phys. Rev. Lett. 81:2172–2175. [Google Scholar]
  46. Shakhnovich, E. I., and A. M. Gutin. 1993. Engineering of stable and fast-folding sequences of model proteins. Proc. Natl. Acad. Sci. USA. 90:7195–7199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Shakhnovich, E. I., and A. M. Gutin. 1989. Relaxation to equilibrium in the random energy model. Europhys. Lett. 9:569–572. [Google Scholar]
  48. Socci, N. D., and J. N. Onuchic. 1994. Folding kinetics of protein-like heteropolymers. J. Chem. Phys. 101:1519–1528. [Google Scholar]
  49. Socci, N. D., and J. N. Onuchic. 1995. Kinetic and thermodynamic analysis of protein-like heteropolymers: Monte Carlo histogram technique. J. Chem. Phys. 103:4732–4744. [Google Scholar]
  50. Socci, N. D., J. N. Onuchic, and P. G. Wolynes. 1996. Diffusive dynamics of the reaction coordinate for protein folding funnels. J. Chem. Phys. 104:5860–5868. [Google Scholar]
  51. Wang, J. 2003a. Energy landscape theory, funnels, specificity, and optimal criterion of biomolecular binding. Phys. Rev. Lett. 90:188101-1–188101-4. [DOI] [PubMed] [Google Scholar]
  52. Wang, J. 2003b. Statistics, pathways and dynamics of single molecule protein folding. J. Chem. Phys. 118:952–958. [Google Scholar]
  53. Wang, J., and P. G. Wolynes. 1995. Intermittency of single molecule reaction dynamics in fluctuating environments. Phys. Rev. Lett. 74:4317–4320. [DOI] [PubMed] [Google Scholar]
  54. Wang, J., J. G. Saven, and P. G. Wolynes. 1996. Kinetics in a globally connected, correlated random energy model. J. Chem. Phys. 105:11276–11284. [Google Scholar]
  55. Wang, J., and P. G. Wolynes. 1999. Intermittency of activated events in single molecules: the reaction diffusion description. J. Chem. Phys. 110:4812–4819. [Google Scholar]
  56. Wang, J. 2004a. The complex kinetics of protein folding in wide temperature ranges. Biophys. J. 87:2164–2171. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Wang, J., W. M. Huang, H. Y. Lu, and E. K. Wang. 2004b. Downhill kinetics of biomolecular interface binding: global connected scenario. Biophys. J. 87:2187–2194. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Wolynes, P. G., J. N. Onuchic, and D. Thirumalai. 1995. Navigating the folding routes. Science. 267:1619–1620. [DOI] [PubMed] [Google Scholar]
  59. Xia, X., and P. G. Wolynes. 2001. Microscopic theory of heterogeneity and nonexponential relaxations in supercooled liquids. Phys. Rev. Lett. 86:5526–5529. [DOI] [PubMed] [Google Scholar]
  60. Yang, H., and X. S. Xie. 2002a. Statistical approaches for probing single-molecule dynamics photon-by-photon. Chem. Phys. 284:423–437. [Google Scholar]
  61. Yang, H., and X. S. Xie. 2002b. Probing single-molecule dynamics photon by photon. J. Chem. Phys. 117:10965–10979. [Google Scholar]
  62. Yang, H., G. B. Luo, P. Karnchanaphanurach, T. M. Louie, I. Rech, S. Cova, L. Xun, and X. S. Xie. 2003. Protein conformational dynamics probed by single-molecule electron transfer. Science. 302:262–266. [DOI] [PubMed] [Google Scholar]
  63. Zhou, Y., C. Zhang, G. Stell, and J. Wang. 2003. Temperature dependence of the distribution of the first-passage time: results from discontinuous molecular dynamics simulations of an all-atom model of the second-hairpin fragment of protein G. J. Am. Chem. Soc. 125:6300–6305. [DOI] [PubMed] [Google Scholar]
  64. Zhuang, X. W., L. E. Bartley, H. P. Babcock, R. Russell, T. Ha, D. Herschlag, and S. Chu. 2000. A single-molecule study of RNA catalysis and folding. Science. 288:2048–2051. [DOI] [PubMed] [Google Scholar]
  65. Zhuang, X. W., H. Kim, M. J. B. Pereira, H. P. Babcock, N. G. Walter, and S. Chu. 2002. Correlating structural dynamics and function in single ribozyme molecules. Science. 296:1473–1476. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES