Origin of Mechanical Strength of Bovine Carbonic Anhydrase Studied by Molecular Dynamics Simulation

Abstract

The forced unfolding process of bovine carbonic anhydrase II (BCA II) was examined at the atomic level by the molecular dynamics (MD) simulation. By force spectroscopy, experimentally obtained force-extension curves (F-E curves) showed a prominent force peak after 50 nm extension. F-E curves obtained from our simulation had three force peaks appearing after extensions of 10–17 nm, 40 nm, and 53 nm, each signifying a brittle fracture of a specific local structure. Upon undergoing the final fracture at 53 nm of extension, the entire molecule became a single flexible chain and was further extended to its full theoretical length, almost as a random coil. This feature of the 53-nm peak strongly suggested its close correspondence to the experimentally observed force peak at ∼60-nm extension. The 53-nm peak in the molecular dynamics simulation corresponded to the unfolding process of the β-sheeted core that includes zinc-coordinating histidine residues. These results suggest that the structural change occurring at 50–60 nm in atomic force microscopy experiments corresponded to the destruction of the zinc coordination site.

INTRODUCTION

Carbonic anhydrase catalyzes reversible hydration and dehydration of carbon dioxide 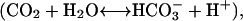the fundamental process in the transport of carbon dioxide in animals, plants, and bacteria. It has long been known that human carbonic anhydrase I and II (HCA I and II) have a unique folding pattern known as the “knot topology” in the C-terminal region (Håkansson et al., 1992), which has also recently been confirmed for bovine enzyme II (BCA II) (Fig. 1 a, Saito et al., 2004). Fig. 1 a shows a “ribbon” representation of the 3-D structure of BCA II obtained from x-ray crystallography (1v9e). The molecule consists of a single polypeptide chain with 259 amino acid residues giving a molecular weight of ∼29,000. It has a structure very similar to that of HCA II (Håkansson et al., 1992), with a central β-sheet consisting of 13 β-strands (Fig. 1 a, thick arrows in different colors) and seven α-helices surrounding the β-sheets (Fig. 1 a, thick helical ribbons in different colors). The overall structure of the molecule is roughly spherical (Fig. 1 b), with a cone-shaped cavity forming the catalytically active site (active-site cavity) with a Zn²⁺ ion as the reaction center. The topological combination for seven α-helices and 13 β-strands in the molecule is shown in Fig. 1 c, where the thick arrows and cylinders of different colors represent β-strands (S0 to S12) and α-helices (H1 to H7), respectively. Three zinc-coordinating histidine residues, His 93, His 95 (in S5), and His 118 (in S6), are placed in the middle of the β-sheet. The aromatic rings of Phe 65 and Tyr 69 in S3, and of Tyr 87, Phe 92, Phe 94, and Trp 96 in S5 form a large hydrophobic cluster lining the back surface of S3 to S5 against the zinc-coordinating frontal side. In contrast, those of Phe 145 in S7, Tyr 192 and Trp 190 in S9, and Trp 207 in S10 form the hydrophobic bottom of the active-site cavity on the frontal side of the central β-sheet. The C-terminal S12 is intercrossed with S0 to form a knot structure (Fig. 1 a, black arrow), which was also observed for HCA II (Håkansson et al., 1992).

FIGURE 1.

(a) The 3-D structure of bovine carbonic anhydrase II (BCAII) obtained from x-ray crystallography. Thick arrows in different colors represent β-strands. The catalytically active site consists of a cone-shaped cavity having a Zn²⁺ ion (red sphere) as a reaction center of the reversible hydration of carbon dioxide. Three histidine residues (stick model) are located in the middle of the β-sheet, and their nitrogen atoms form coordination bonds with the zinc ion. The arrow in black shows the “knot” structure in the C-terminal region. Figure created using MolScript (Kraulis, 1991) and Raster3D (Merritt and Bacon, 1997). (b) A simplified model of the 3-D structure of BCAQ253C. (c) The topological combination for the eleven β-strands and the six α-helices in the molecule. The thick arrows in different colors represent the β-strands (S0 to S12), and the cylinders represent the α-helices (H1–H7). Three histidine residues which form coordination bonds to a zinc ion are shown as the same number of white pentagons with residue numbers. His-93 is located in S5, and His-95 and His-118 are located in S6. (d) The order of unfolding of the BCAQ253C observed in our SMD simulation.

Carlsson and colleagues showed the correlation between the formation of the knot structure and the correct folding of the enzyme, leading to the formation of a catalytically active site (Carlsson et al., 1974). They also showed the stability of β-sheet including the active site in the presence of a denaturant (Anderson et al., 2001). The hydrophobic cluster located on the back of the zinc coordination site described above was found to have a crucial role in the stability of the molecule (Hunt et al., 1999). The correlation between the mechanical rigidity of proteins and their catalytic activity was discussed by Vanselow (2002), who emphasized that an adequate local rigidity was essential for an enzyme to function as a catalyst.

Wang and Ikai (1999) have shown that due to the presence of the knot structure mechanical unfolding of BCA II was almost impossible under a tensile force of ∼2 nN, which is strong enough to break a single covalent bond in their system. Alam et al. then showed a positive correlation between the presence of a knot structure and the mechanical stability of BCA II to a tensile force using atomic force microscopy (AFM) (Alam et al., 2002). In their experiment, to avoid knot tightening, BCA II was stretched from the N-terminus and the 253rd residue which is close to the C-terminus but not included in the knot structure. To covalently link the two residues of the protein to the AFM probe and substrate, they constructed a mutant protein, where one cysteine residue was added to the N-terminus and the other replaced Gln at the 253rd (BCAQ253C). It turned out that the mutant protein was composed of two conformational isomers, Types I and II. Type I was enzymatically active, having a zinc ion at the active site, and a crystal structure very similar to the wild-type protein, including the knot structure. Type II was enzymatically inactive, with no indication of the presence of Zn²⁺, though it had similar spectroscopic (circular dichroism and fluorescence) properties to those of Type I. The C-terminal peptide bonds of Type II were available for digestion by the enzyme, carboxypeptidase Y, whereas those of Type I were not, indicating that Type II did not have a completed knot structure. From its force-extension curves (F-E curves, Fig. 2 a), Type I was found to be more resistant to tensile forces than Type II. This result suggests that there is a correlation between knot formation and the mechanical stability of an enzyme.

FIGURE 2.

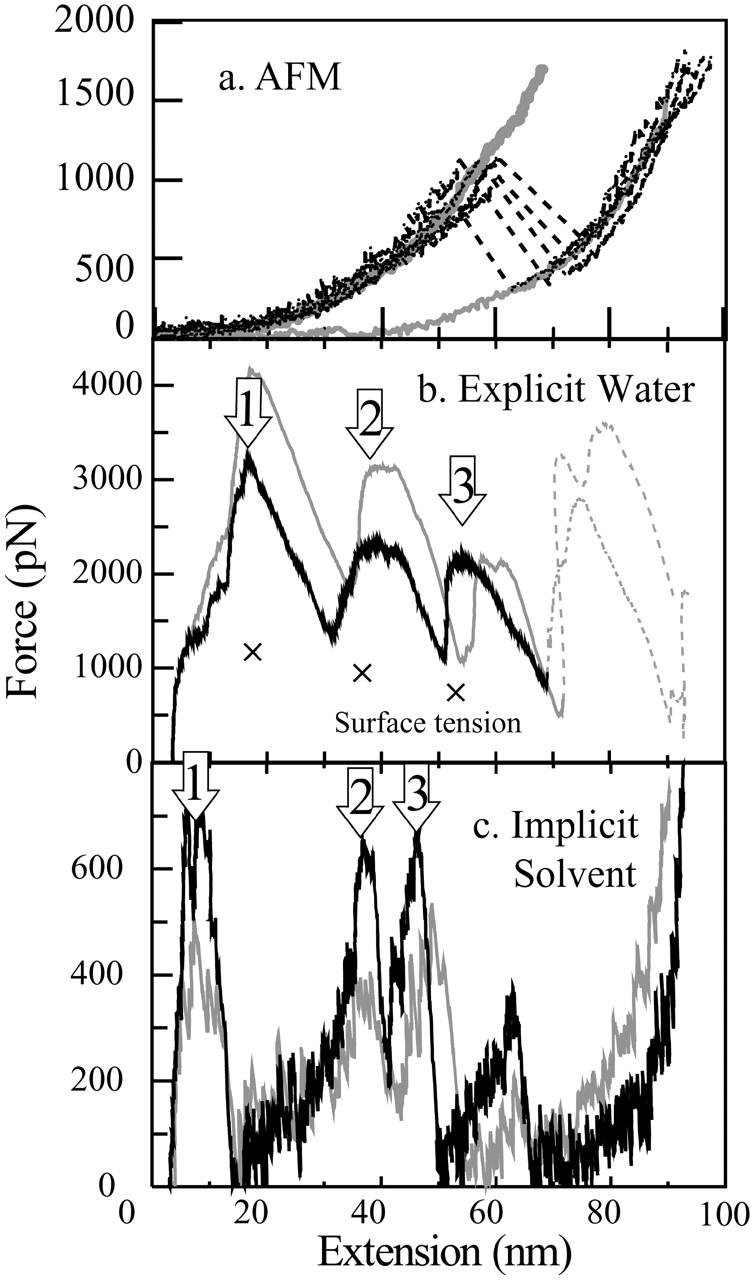
Tensile force applied to the BCAQ253C commonly shows a peak at 50- to 60-nm extension. (a) Force-extension curves of BCAQ253C measured by AFM. The thick gray curve represents the averaged F-E curve of Type I, and the thin gray curve represents that of Type II. The broken lines represent the breakdown of the semihard structure of Type I. (b) F-E curves obtained from the explicit water simulation. .(c) Implicit solvent simulation. The conditions of stretching simulation are as follows: the spring constant is 0.42 N/m (1 k_BT/Ų), and the velocities of the moving springs are 0.5 Å/ps (black curves) and 1 Å/ps (gray curves). The crosses represent the estimated additive force due to the surface tension of the water surrounding the protein molecules. The arrows numbered 1, 2, and 3 represent the three peaks at extensions of 10–17 nm, 40 nm, and 49–53 nm, respectively.

Interestingly, Alam et al. also reported that the F-E curves of the Type I conformer occasionally showed a sudden transition to that of Type II after an extension of 50–60 nm. This result suggested that the Type I conformer experiences a brittle fracture to Type II (broken lines in Fig. 2 a) and that the transition corresponded to a breakdown in the hard core structure that is present in the Type I conformer but not in the Type II. Since it is not possible at this stage, and most probably for sometime in the near future, to directly observe the detailed conformational changes taking place during a stretching experiment of a protein, we postulated that a molecular dynamics (MD) simulation of the stretching process would be an important contribution to the interpretation of experimental observations, by enabling a recreation of the structural changes taking place at the atomic level.

The first computational study of bond breakage by force was reported by Grubmüller et al. (1996); they simulated forced dissociation of the streptavidin-biotin complex by applying an external force through a virtual harmonic spring. The method was later applied to the forced unfolding of protein molecules and given the name of steered molecular dynamics (SMD) simulation by Schulten's group. Stretching experiments on titin (Rief et al., 1997; Kellermayer et al., 1997; Tskhovrebova et al., 1997) motivated a series of SMD simulations on the unfolding/refolding pathway of titin imunnogloblin-like domains (Ig-domains) (Lu et al., 1998; Lu and Schulten, 2000; Gao et al., 2001, 2002). The force-extension profile of titin unfolding obtained by AFM experiments was characterized by a series of equally spaced force peaks having a characteristic saw-tooth pattern that was attributed to the unfolding/refolding of individual globular domains (Lu et al., 1998; Marszalek, et al., 1999). An SMD simulation of the titin Ig-domain (I27) based on an explicit solvent model revealed that the individual force peaks observed in AFM experiments corresponded to cooperative rupture events of interstrand hydrogen bonds. Moreover, the scenarios of unfolding provided by SMD simulations using explicit solvent models revealed the key roles played by water molecules. Simulations based on implicit solvent models carried out by Paci and Karplus (2000) reproduced the characteristic unfolding pattern in the F-E curve with peak positions, in agreement with the results of AFM experiments but with smaller force peaks. Brockwell et al. (2003) examined the influence of the pulling geometry on the unfolding force of all-β protein, E2lip3, using an AFM experiment and MD simulations. They showed a higher resistance of molecules pulled at two β-strands parallel to each other than of those pulled antiparallel, which fits with the theoretical prediction by Rohs et al. (1999).

To interpret the results of AFM experiments on BCAQ253C molecules at the atomic level, conformational changes of the protein during the mechanical unfolding process must be elucidated. We performed a MD simulation to visualize possible processes in the forced unfolding of BCAQ253C Type I. In this simulation, we observed the transformation from Type I to Type II at an extension of 50–60 nm, in close agreement with experimental observations. From the simulation results, we attempted to delineate the atomic level mechanisms responsible for the appearance of force peaks in the F-E curves observed in AFM experiments. We discovered a key structure that makes Type I conformers resistant to tensile forces before the transition, and discuss the structural differences between Type I and II conformers. Although the pulling speed in the MD simulations is 8–9 orders of magnitude higher than that of the AFM experiment, and although the process was a nonequilibrium one, a major feature is reproduced by our MD simulation.

MATERIALS AND METHODS

The x-ray crystal structure of BCAQ253C Type I determined by Saito et al. (2004) was used as the initial protein structure in the system. The number of atoms of the molecule is 4048, including a zinc ion. Although β-strands are named after the order of the topological arrangement in the β-sheet in x-ray crystallography, we named them after the order from the N-terminal to the C-terminal for convenience in explaining the unfolding process. The β-strands S0, S1, S2, S3, S4, S5, S6, SS7, S8, S9, S10, S11, and S12 correspond to βJ, βb, βB, βC, βc, βD, βE, βF, βA, βH, βG, βe, and βI, respectively, in Saito's BCA II (wild-type) data (Saito et al., 2004). S0, which is from 38Q to 39V, is located next to S12, but since it is very short and forms only one hydrogen bond with S12, it is not represented with an arrow in Fig. 1 a.

We applied the SMD simulation method (Lu et al., 1998) to stretch a BCAQ253C molecule and observed the appearance of three major force peaks from the beginning to the end of the molecule stretching. To test the reproducibility of the appearance of major force peaks in the calculated F-E curves, stretching simulations were carried out in two types of solvation conditions: “explicit water” and “implicit solvent” systems. In the explicit water system, one protein molecule was solvated with 14850 TIP3P water molecules in a spherical overall shape. The total number of atoms in the explicit water system was 48,599, including one chloride ion neutralizing the net charge of the system. Before the spherical water simulations discussed in this article, we had carried out a simulation in a periodic boundary condition until the extension length of the protein reached 50 nm, and obtained a similar result to that of this simulation (data not shown). Beyond an extension of 50 nm, the unit cell which was initially cubic was elongated until it became a thin rectangular rod; as a result, the distance between the protein and those in neighboring unit cells became too short to avoid protein-protein interactions. For this reason, we did not continue the periodic boundary condition simulation beyond 50-nm extension. In the implicit solvent system, water was treated as a dielectric continuum based on the generalized Born (GB) model. In the GB model, the electrostatic interaction potential is approximated by an interpolation formula that reduces to a finite level at a short distance, and by a Debye Hückel screened Coulomb interaction at long distances. In addition to the electrostatic interactions based on the GB model, the surface energy of the system was calculated by assuming that it was proportional to the solvent accessible surface area (GB/SA; Tsui and Case, 2001; Weizer et al., 1999). A Sander module of AMBER 7 (Case et al., 2002, for the implicit solvent simulation) and a Sander_classic module of Amber 6 (Case et al., 1999, for the explicit water simulation) were used with the modifications required for SMD simulations (Lu et al., 1998). A virtual spring with a specific spring constant but without length or weight was connected to the Cα atom of the N-terminus of the protein (explicit water system), or two springs were connected to the Cα atoms of the N-terminus and cysteine 253 of the protein (implicit solvent system).

Mathematically, a term for the restoring force as described in Eq. 1 is added to the term of the force in the equation of motion of the Cα atoms of the N-terminus:

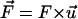(1)

and

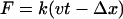(2)

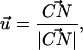(3)

where, k, v, t, Δx, and 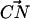are the spring constant of the virtual spring, the translational velocity of the spring, the simulation time, the deflection of the spring, and the vector between the Cα atoms of the N-terminus and cysteine 253, respectively. In the implicit solvent simulation, in addition to the force applied to the N-terminus, a force is applied in the opposite direction at cysteine 253 of the protein. The tensile force applied to the molecule corresponded to F in Eq. 1.

The temperature of the system was set to 300 K by Berendsen's velocity scaling algorithm where a focused system is coupled to an external bath (Berendsen et al., 1984). The time step for the integration of the equation of motion in the simulation was set to 1 fs. All of the bond oscillations involving hydrogen atoms were calculated without using the SHAKE algorithm. The Amber 99 force field was used as the source of interaction parameters for the bonded and nonbonded atom pairs, including a zinc ion (Wang et al., 2000; Cornell et al., 1995). Although in an actual BCA II molecule the zinc ion forms coordination bonds with the nitrogen atoms of the three coordinating histidine residues, we did not introduce coordination bonds into our calculation, since they were not included in the Amber 99 force field. Only nonbonded interactions between the zinc ion and the nitrogens of the histidines, i.e., van der Waals and electrostatic interactions, were included in the calculation. We also thought it was best not to introduce coordination bonds to avoid any possible inconsistency with the total molecular system parameters of Amber. As described later, even neglecting coordination bonds, we could show the bonding of zinc ions from 0 to 50–60 nm extension. In the explicit water system, all of the electrostatic interactions were calculated without cutoffs whereas the van der Waals interactions were cut off at 15 Å. In the implicit solvent system, the electrostatic interactions were cut off at 500 Å. All the calculations were done using a PC cluster system consisting of four PCs with a clock frequency of 1 GHz. Each PC contained four MD-engine II PC accelerator boards (Fuji Xerox, Tokyo, Japan). Each accelerator board was a special-purpose computer with four parallel CPUs dedicated to the calculation of interaction forces between atoms. The system contained 64 CPUs in total concurrently calculating interatomic interactions, resulting in a 64 Gflops performance. Before the protein molecule was stretched, both the explicit and implicit solvent systems were equilibrated for 240 ps: harmonic restraint of the protein molecule for the first 134 ps, then equilibration of the system without the restraint for 106 ps. The backbone root mean-square deviation between the final equilibrated structures and the 3-D structure obtained from x-ray crystallography was ∼0.8 and 1.5 Å in explicit and implicit solvent simulation, respectively (Supplemental Material).

Protein stretching simulation was carried out under conditions closely reproducing those of actual AFM experiments in both the explicit water and implicit solvent simulations. In both simulations, the BCA molecule was unfolded by pulling the molecule from the N-terminus and Cys253 in opposite directions to avoid knot tightening as described above. In the explicit water system, the α-carbon of the N-terminal residue was connected to the spring while the coordinates of the α-carbon of Cys253 were kept fixed. In the implicit solvent simulation, both the N-terminus and Cys253 were connected to the springs. In all of the simulations, since unfolding from the C-terminal side was blocked by the knot structure, the N-terminal side was unfolded first. In the explicit solvent system, the main body of the water molecules was not translated before the unfolding of the knot structure, because the globular structure of the protein, including the knot structure, is left in the C-terminus. By selecting the N-terminal side for pulling, we could reduce the number of translating water molecules; namely, we could reduce the additional force required for the translation of water molecules. The spring constant of the virtual spring was set to 0.42 N/m (we chose a setting seven times higher than that of the AFM cantilever used in the experiment to reduce the simulation time to reaching peak force), and the velocity of the spring movement was set to two different values of 0.5 Å/ps (50 m/s) and 1.0 Å/ps in both the explicit water and implicit solvent systems.

In the explicit water system, due to the influence of water surface tension, the force applied by the virtual spring to the system changed the shape of the water sphere as well as the protein conformation. The net tensile force required for the unfolding of a BCA molecule could not be determined uniquely due to the difficulty in estimating the magnitude of the force required to change the water droplet. In the implicit solvent system, there were no such spurious surface energy contributions, but the interatomic interactions between water molecules and the protein molecule could not be calculated. Therefore, the two systems are complementary to each other.

RESULTS

Occurrence of three peaks as mechanical unfolding proceeds

In all of the four simulations at the two pulling speeds of 0.5 or 1.0 Å/ps and under two different solvating conditions, the BCA molecule was fully unfolded within 3 ns. In Fig. 2, the tensile force applied by the virtual spring is plotted as a function of the extension length of the protein molecule (F-E curve). The extension length was defined as the distance between the Cα of the N-terminal residue and that of Cys-253. All the F-E curves obtained under the four simulation conditions showed three pronounced force peaks, labeled 1, 2, and 3 at extensions of, respectively, ∼10–17 nm (to be called the 10–17 nm peak), 38–40 nm (to be called the 40-nm peak), and 49–53 nm (to be called the 49–53 nm peak), with a small additional peak at 65 nm (implicit solvent) (Fig. 2 b, explicit water system; Fig. 2 c, implicit solvent system). The chain extension and the value at each force peak are presented in Table 1. The 49–53 nm peak was observed at a similar position to that of the experimentally observed force peak of 50–60 nm (Fig. 2 a). Besides the positional similarity, it is most significant that, in both the simulation and experiment, the F-E curve after the peak dropped precipitously to a very low force value and any extension of the protein thereafter was characterized by high compliance (Fig. 2, a and c).

TABLE 1.

Chain extension and value of force at each peak

	First peak		Second peak		Third peak
	Extension (nm)	Force (pN)	Extension	Force	Extension	Force
Explicit Solvent
0.5 Å/ps	17	3200 (1800)	39	2300 (1200)	53	2200 (1400)
1 Å/ps	17	4000 (2600)	39	3000 (1900)	53	2200 (1400)
Implicit Solvent
0.5 Å/ps	10	650	38	600	49	600
1 Å/ps	10	500	38	370	49	500

The height of these force peaks in the explicit solvent simulation at 0.5 Å/ps pulling speed was lower than that at 1.0 Å/ps. This is consistent with the theory of weak bond rupture (Evans and Ritchie, 1997) and with other experimental results using the titin Ig domain (Rief et al., 1997).

In the implicit solvent simulations, the force peak in the simulation at 0.5 Å/ps was higher than that at 1.0 Å/ps. This result is inconsistent with the theoretical prediction described above. The reason for this discrepancy has not yet been identified, but one reason might be insufficient dissipation of energy that is accumulated by the external force and then discharged at bond rupture, due to the absence of collisions between the protein and water molecules in the implicit solvent simulations. However, the results obtained in these simulations are used as a reference for the explicit one, since the extension length at the 40-nm and 50-nm peaks was in agreement with that in the experiment and the configuration of the protein at each peak position was reproducible in all the simulations, as discussed later.

The difference in the peak position between 10 nm in implicit and 17 nm in explicit solvent simulations is attributed to the difference between stretching from both sides and stretching from the N-terminal side. When the molecule was stretched from the N-terminal side and fixed at the C-terminal side, the N-terminal side elongated until the unfolding point reached S2, which required a high tensile force to be unfolded, as described later. Then the C-terminal side was pulled out of the knot structure, and produced the 17 nm peak. When the molecule was stretched from both sides, the C-terminal side moved first, and pulled out from the knot structure with frictional interaction before the unfolding of the C-terminal side stopped at S2 (10 nm peak). The difference in the peak position between 49 nm in the implicit and 53 nm in the explicit solvent simulations was attributed to the difference of the distortion that occurred within the β-sheet, which includes sliding of β-strands along each other, as described later.

The F-E curve of the AFM experiment did not show a peak at 10–17 nm in extension, in contrast to that of the simulations. The reason for the absence of the peak in the experimental data was thought to be due to the deformation of the knot structure due to the perturbation by the AFM tip, since the residue (Cys-253) connected to the probe is close to the knot structure. Actually, at a short extension, it was probably difficult to distinguish a real force peak from the adsorption described above.

Although the 40-nm peak did not appear in the experimental results shown in Fig. 2 a, the possible existence of a corresponding peak is supported by two types of AFM experiments (Afrin et al., 2004; H. Arakawa, M. T. Alam, and A. Ikai, unpublished), as described in the Discussion section. Both experiments suggested a multiple-step rupture event occurring in the extension range of 40–60 nm for the core structure of a protein.

Atomic picture of the unfolding sequence

When the BCA molecule was pulled by the tensile force in our SMD simulation, it was unfolded from the N-terminal side in the order of H2-H3-S1-S2-S3-S4-S5-S6-H4-S7, and from the C-terminal side, in the order of S12-H7-S11-S10-S9, as shown in Fig. 1 d. The sequence of unfolding and the molecular configuration at each force peak were identical in the four simulations. As discussed later, localized resistance against the tensile force appeared in the form of two force peaks (40-nm and 53-nm), where the backbone H-bond array connecting the core β-strands and the hydrophobic contacts between β-strands were broken. Fig. 3 shows snapshots of a simulated process of the unfolding of a molecule as a function of the pulling time, as observed in the explicit water system. Unfolding started from the N- and C-terminal regions, accompanied by a small force. The force then rose rapidly as extension increased up to 17 nm (Fig. 2 b). The unfolding process was slowed down during the unraveling of the knot structure in the C-terminal region where the C-terminal segment of residues 256–259 was pulled out from under the N-terminal segment of residues 38–41 (including S0) with the tensile force of 3200 pN (black curve in Fig. 2 b, Table 1) resulting in the first large force peak. After the C-terminal was pulled out of the knot structure, tensile force fell to a minimum of 1360 pN. Next, S12 in the C-terminal side was unfolded, followed by the sequential unfolding of H2 and H3 in the N-terminal side, and that of H7 in the C-terminal side. Although the unfolding in the C-terminal side paused at the S11 β-strand, unfolding in the N-terminal side proceeded from S1 to S2. When S2 began to be unfolded (Fig. 3 c), the force went up to 2300 pN at an extension of 40 nm (40-nm peak, Fig. 2 b, Table 1). After the 40-nm peak was reached, S2 was separated from S3 and S8, whereas in the C-terminal side, S11 was pulled apart from S7, but the unfolding process came to a pause at S10 again. Since S8 is located at the end of the β-sheet, S8 was also separated from the β-sheet simultaneously with the separation of S2. Immediately after S2 was unfolded, S3 and S4 were pulled apart from the hydrophobic core, whereas the tensile force went down from the second peak to the second bottom of 1140 pN at an extension of 50 nm (Fig. 2 b). Next, as S5 began to be pulled out from the β-sheet core (Fig. 3 d), the third force peak, with a maximum of 2200 pN, was formed at 53-nm extension (53-nm peak, Fig. 2 b, Table 1, Fig. 3 d). Since His-93 and His-95 are in S5 , whereas His-118 is in S6, the unfolding of S5 from S6 induced dissociation of the zinc ion from the three histidines (a red sphere in Fig. 3 d). After the S5 β-strand was unfolded (Fig. 3 e), the tensile force went down from 2200 pN to 1000 pN (Fig. 2 b). Even at the 53-nm peak, S10 was not pulled apart from the S7 of the hydrophobic core in the C-terminal side. Next, S6, H4, and then S7 were sequentially unfolded in the N-terminal side. The entire hydrophobic core was completely disrupted in this process. H5 and H6 were then unfolded, and finally S9 and S10 were separated from each other. At an extension of 65 nm, in the explicit water simulation, an extraordinarily large force peak appeared (gray broken lines in Fig. 2 b), whereas the peak at 65 nm extension in the implicit solvent simulation was small (Fig. 2 c). At this extension, the longitudinal sliding of S10 along S7 in opposite directions was also taking place. Such sliding is sometimes referred to as shearing separation. The required force might have been amplified in the explicit water simulation because the thickness of the water layer surrounding the extended protein molecule became so thin that parts of the molecule became extruded from the surrounding water. Under low hydration conditions, proteins tend to fold more compactly than under full hydration conditions (Steinbach and Brooks, 1993), so that an extra tensile force would be required to stretch the protein molecule. For this reason, peak heights at extensions longer than 65 nm are not reliable. Finally, in both the explicit and implicit solvent simulations, the protein molecule was stretched until the extension of the molecule became ∼90 nm, 96% of 94 nm, which is the length from the 1st to the 253rd residue of the molecule at full extension by taking the length of one amino acid residue as 3.7 Å.

FIGURE 3.

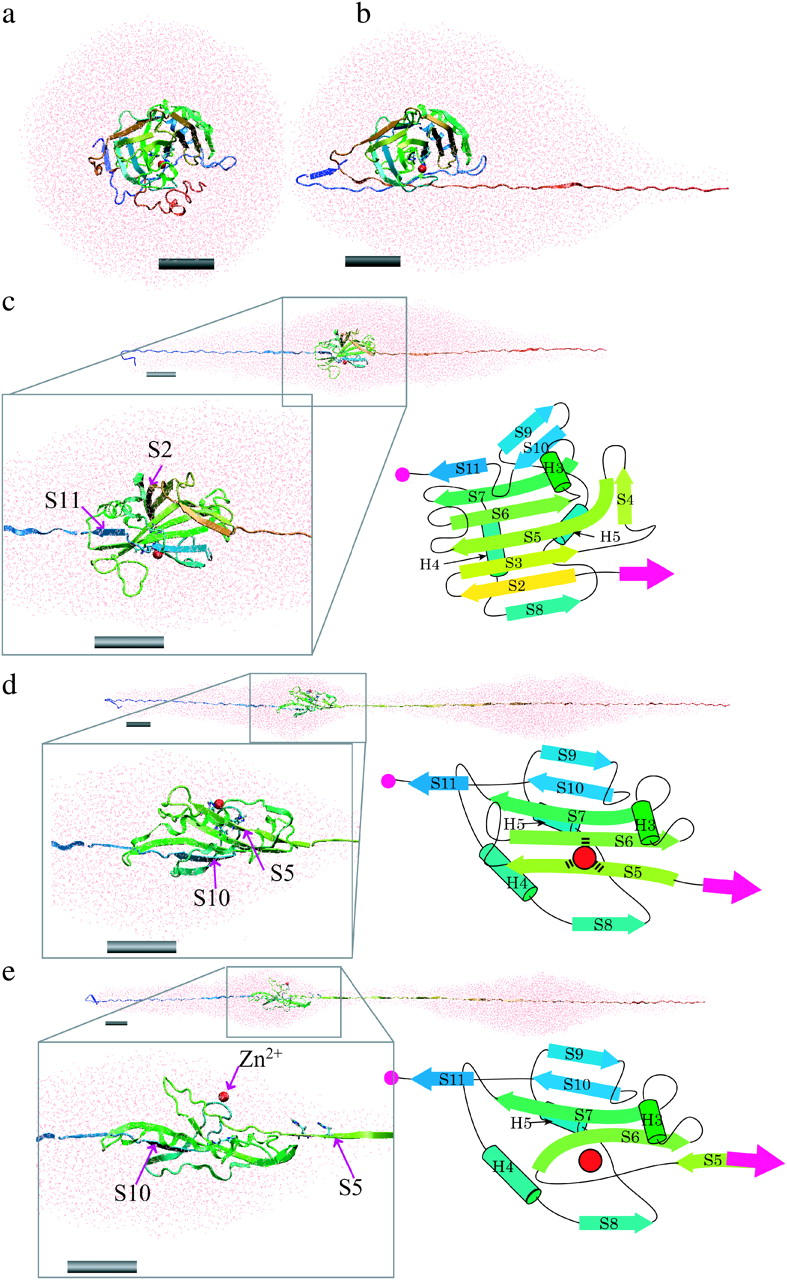
Snapshots showing the structural changes in the protein and surrounding water unfolding as a function of simulation time in the explicit water simulation with a pulling speed of 0.5 Å/ps. (a) The initial structure of the system where the BCAQ253C molecule is soaked in the water droplet. (b) Protein and surrounding water at the 17-nm peak. The unfolding from the C-terminus reached the knot structure, and then the speed of unfolding became slow. (c) At the 40-nm peak. The unfolding of the C-terminal portion pauses at S11, whereas in the N-terminal side, S2 is unfolded. The box in the black line is a magnified view of the remaining β-sheet core containing S2 (yellow arrow) to S11 (blue arrow). A topological diagram of the remaining core is shown in the right of the box. (d) At a 53-nm peak, S5 and S10 pull against each other. The box in the black line is a magnified view of the remaining β-sheet core containing S5 (right green arrow) to S11 (blue arrow). (e) After the 53-nm peak. After the S5 β-strand is pulled apart from the β-sheet, the zinc ion (red sphere) is dissociated from the coordinating histidines. Each gray cylinder represents a scale bar of 2 nm. Figures created by VMD (Humphrey et al., 1996).

Bonding of the zinc ion from 0 to 53 nm extension

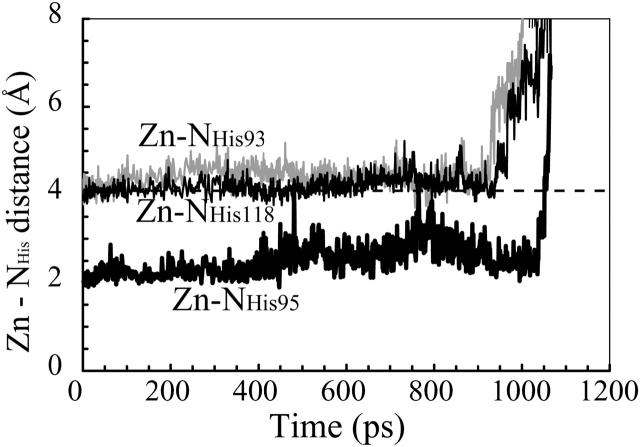
In the explicit water simulation described above, the zinc ion in the active site (the red sphere in Fig. 4 a) was dissociated from the three coordinating histidines upon separation of His-93 and His-95 in S5 from His-118 in S6, as caused by the unfolding of S5 and S6 at an extension of 53 nm. In other words, the zinc ion remained bonded to the three histidines until S5 was pulled away from S6 (Fig. 4 b). Here, the zinc ion was regarded to be bonded to the histidine nitrogen atoms as long as the ion was located within 4 Å of at least one of the three nitrogen atoms. This threshold distance for bonding was chosen according to the definition given by Creighton (1993). The distances between the zinc ion and the nitrogens of His-93 and His-118 were ∼4 Å from the start of unfolding up to 930 ps (51 nm in extension) in elapsed time (Fig. 5, gray line and black line, respectively). Then the distance increased to >4 Å when S5 started to be pulled away from S6 at its N-terminal edge (Fig. 4 a). The distance between the zinc and the nitrogen of His-95 was ∼2.5 Å up to 1034 ps (53 nm in extension) (Fig. 5, thick black line). Then S5 was pulled apart from S6 at 1002 ps within the following 44 ps (Fig. 4 b), resulting in a sudden increase in the Zn–H95 distance beyond 4.0 Å at 1051 ps (Fig. 5), indicating dissociation of the zinc ion from all three histidines at this time (Fig. 4 b). In this process, the tensile force increased from 100 pN to 2100 pN.

FIGURE 4.

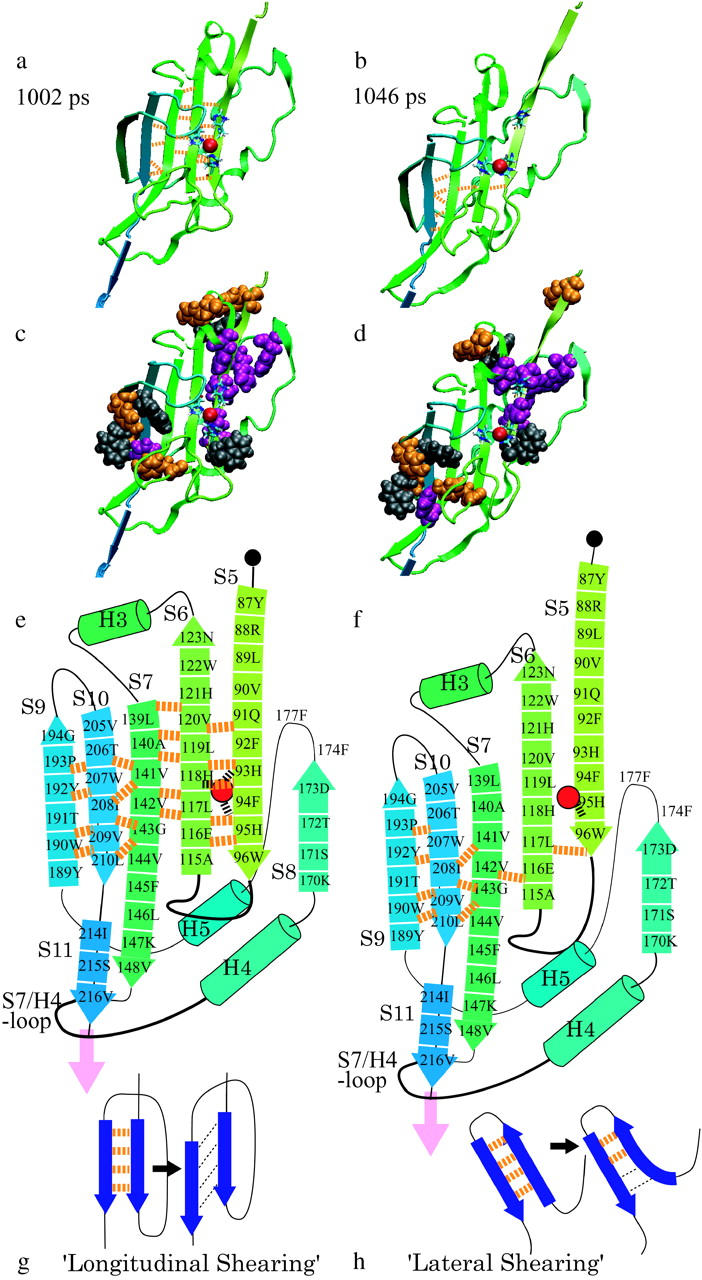
The zinc ion is dissociated from the three histidines at the 53 nm peak in the explicit water simulation. (a) 1002 ps. The zinc ion (red sphere) remains bonded to the three histidines until S5 is pulled apart from the β-sheet. (b) 1046 ps. S5 slides along S6, and the zinc dissociated from His-93 and His-118. (c) Van der Waals models of aromatic residues overlaid on the image a. Tyrosine (orange, residues 87, 126, 192, and 190), tryptophan (gray, residues 96, 122, 190, and 207), and phenylalanine (purple, residues 92, 94, 129 (H4), 145, 174, and 177) are shown. (d) Van der Waals model of the same aromatic residues as in c, overlaid onto the image b. (e and f) Schematic diagrams of a and b, respectively. The broken lines in orange represent the H-bonds. (g and h) Schematic diagram of the longitudinal shearing and lateral shearing (Rohs et al., 1999).

FIGURE 5.

The zinc ion remains bonded to the three histidines until S5 is pulled apart from the β-sheet core by the tensile force at ∼1 ns. The distance between the zinc ion and the three coordinating histidines of His-93 (gray line), His-95 (thick black line), and His-118 (black line) are shown as functions of simulation time. The zinc ion is retained as close as 4 Å to the nitrogens of His-93 and His-118 until 930 ps, and then is dissociated. It was also retained as close as 2.5 Å to the nitrogen of His-95 until 1034 ps, and then was dissociated.

In a real BCA molecule, the zinc ion forms coordination bonds to the three histidines, and if we could incorporate the contribution of the coordination bond in the energy calculation, the force value at the 53-nm peak would be expected to be much higher. A higher rupture force would cause further sliding of β-strands against each other, resulting in a shift of the third peak to a longer extension. Although not conclusive, we predict that the zinc ion remains bonded to the coordinating histidines up to the last force peak in the actual AFM experiments. In the F-E curves of the AFM experiment, a force peak due to the transition from the Type I to Type II conformer was observed at an extension of 50–60 nm. It has also been proven that Type I has a zinc ion but Type II lacks it.

The F-E curves of Type I without a break at ∼60 nm (green curve in Fig. 2 a) might correspond to cases where the coordination bond of zinc ion to S5 and S6 persisted so that those β-strands were not unfolded by the tensile force available in the AFM experiments. The strength of the coordination bond being comparable to that of a covalent bond, it is reasonable that a covalent bond was often broken before the coordination bond.

Mechanical origins of the observed force peaks—role of H-bonds bridging β-strands that are resistant to “longitudinal shearing”

The SMD simulation of the BCA produced three peaks in the F-E curves and, as described above, the first peak was related to the unknotting of the C-terminal topology. In the cases of the 40-nm and 53-nm peaks, as described in the following section, the main mechanical resistance to external forces arose mainly from the interstrand H-bonds, the hydrophobic contact between specific pairs of β-strands, and the frictional interaction between S11 and the loop between S7 and H5 (called here the S7/H5-loop). The cooperative breakdown of these local structures was observed to contribute to a sudden decrease in the tensile force, or, equally, a sudden release of a strain energy related to the macroscopically defined “brittle fracture” in fracture mechanics (Suresh, 1998).

To understand the process, we first turn our attention to the 53-nm peak. Fig. 4 shows a sequence of changes in the structure of the protein molecule taking place between 51.7 nm and 53.7 nm extension, based on the result of the explicit solvent simulation with a pulling speed of 0.5 Å/ps. At 1002 ps, S5 and S6 are bridged by four backbone hydrogen bonds (H-bonds, orange broken lines in Fig. 4 a). As the tensile force was increased further, all of the H-bonds were completely broken within the next 44 ps (Table 2).

TABLE 2.

Identification of the interstrand H-bonds broken at each force peak

Force peak	Inter-strand H–bonds broken at N-terminal side	Inter-strand H–bonds broken at C-terminal side
40-nm peak	S2-S3*, S2-S8	S7-S11
53-nm peak	S5-S6

^*S2-S3 denotes H-bonds between S2 and S3.

When the extension reached 53 nm, S5 and S10 were pulled against each other. Eight β-strands from S1 to S4 and from S11 to S8 in the original β-sheet core were already unraveled and stretched taut. What remained at this extension of the original β-sheet core were S5, S6, S7, and S10 (see Fig. 1 b). In the central β-sheet, laterally adjacent pairs of β-strands were connected in a mutually antiparallel arrangement with interstrand H-bonds, except for the S7-S10 and S7-S11 pairs which were mutually parallel due to the irregularity of the strand ordering. Since S5 and S10 were parallel to each other, they were pulled by the force so that S5 slid along S10, with S6 and S7 between them. Namely, in the N-terminal side, the tensile force pulls up the arrowed tail of S5, whereas in the C-terminal side, the tensile force pulls down the arrowed head of S10 in Fig. 4 e. Since the tensile force is parallel to the direction of S5 and also to that of S10, the force has to break almost all of the H-bonds bridging S5 and S6 simultaneously to unravel S5, or those bridging S7 and S10 to unravel S10. As shown in Fig. 4 e, when S5 and S10 were pulled apart, all of the backbone H-bonds bridging S5 and S6 had to be broken simultaneously, presumably requiring a high tensile force, a situation similar to the longitudinal shearing of two parallel β-strands as described by Rohs et al. (1999) in relation to the mechanics of β-sheet unraveling (Fig. 4 g). In our case, strands S6 and S7 are inserted between S5 and S10. Then, due to the angular deviation between the overall pulling direction and the orientation of S5, there is a possibility that unzipping starts from the N-terminal edge of S5. However, since the angle between the pulling direction vector and the vector from 86T to 96W (orientation of S5) was as small as 20° when S5 started to be unfolded, longitudinal shearing, rather than unzipping, was likely to be a dominant factor for the unfolding of S5.

After S5 was pulled apart from S6, the remaining core consisted of S6, S7, and S10, where the tensile force acted on the peripheral S6 and S10. Since S6 and S10 were antiparallel to each other, the vector between the two points of the force application was perpendicular to the strands, and consequently S7 was unzipped from the edge of S6. Unzipping of H-bonds between antiparallel β-strands (S6 and S10) needs a lower force than for the cooperative breaking of H-bonds between parallel β-strands. This configuration is very similar to that shown in Fig. 4 h, where the H-bonds between two antiparallel β-strands are expected to be unzipped when the two β-strands are pulled apart. This is called “lateral shearing” in contrast to longitudinal shearing by Rohs et al. (1999).

We must next consider the contribution of hydrophobic interactions to the mechanical resistance to the tensile force. In the C-terminal side of the β-sheet, two tryptophan residues (190W in S9 and 207W in S10, colored gray in the space-filling models in Fig. 4 c), two tyrosine residues (189Y and 192Y in S9, orange in Fig. 4, c and d), and one phenylalanine residue (145F in S7, purple in Fig. 4 c) are located near S10. In addition to the two aromatic residues mentioned above (145F and 207W), eleven aliphatic hydrophobic residues (139L, 140A, 141V, 142V, 144V, 146L, and 148V on S7; 205V, 208I, 209V, and 210L in S10) are clustered in S7 and S10. In the N-terminal side of the remaining β-sheet core, one tyrosine residue (87Y, orange in Fig. 4, c and d), two tryptophan residues (96W and 122W, gray in Fig. 4 c), and two phenylalanine residues (92F and 94F, purple in Fig. 4 c) are located in S5 and S6. In addition to the four aromatic residues just mentioned, five hydrophobic residues (58M, 59V, 67V, 89L, and 90V) are located in S5 and S6. As a result of such tight packing of hydrophobic residues, the solvent accessible surface areas (SASAs) of S5, S6, S7, and S10 were small before the 53-nm peak (Fig. 6 a). For this reason, the H-bonds arrayed between S5 and S6 and S7 and S10 were protected from water molecules penetrating between these β-strands. As shown in Fig. 6, there are few water molecules distributed within 8 Å of the oxygen and hydrogen atoms of the backbones of S5 and S6 (Fig. 6, b and c) and those of S7 and S10 (Fig. 6, d and e). Therefore, the H-bonds between S5 and S6 and S7 and S10 were not likely to be broken unless a large tensile force was applied to create cavities between S5 and S6. When such cavities were formed, the H-bonds bridging S5 and S6 began to be broken, and the SASA of S5 jumped up to a level close to its maximum value. Given that the linear dependence of Gibbs free energy on SASA is ∼5 cal/mol·Å² (for alkane; Sitkoff et al., 1994), this jump corresponded to Gibbs free energy difference of 15 kcal/mol. The SASA of S6 and S7 gradually increased during the 53-nm peak, and then showed small jumps after the 53-nm peak. SASA of S10 was small before 70 nm extension, and then jumped at this extension. Increases of SASA of S6, S7, and S10 corresponded to Gibbs free energy differences of 12, 9, and 8 kcal/mol, respectively. Although it is difficult to describe quantitatively, the correlation between the 53-nm force peak and the increase of the SASA of the β-strands including the hydrophobic cluster suggests a contribution of the hydrophobic interaction to the stability of the β-sheet.

FIGURE 6.

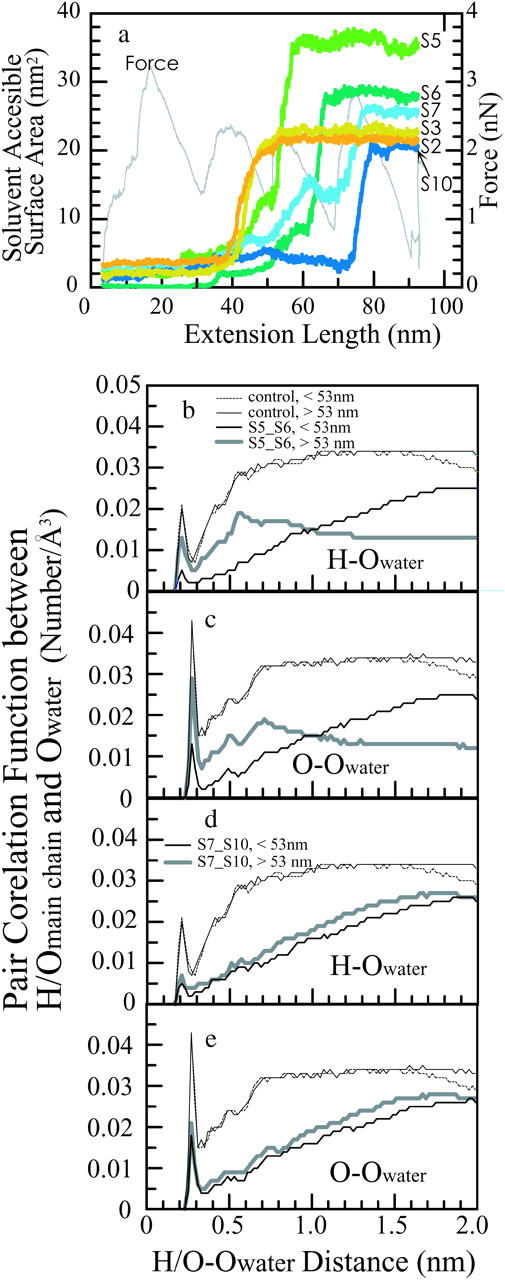
(a) Solvent-accessible surface areas of β-strands S2 (orange curve), S3 (ocher), S5 (lime green), S6 (green), S7 (cobalt), and S10 (indigo) as functions of the simulation time. (b and c) Pair correlation functions between the oxygen atoms of water and the backbone hydrogen atoms (b) or oxygen atoms (c) in S5 and S6. (d and e) Pair correlation functions between oxygen of water and the backbone hydrogen (d) and oxygen (e) in S7 and S10. The thick gray lines represent the pair correlation function before the 53-nm peak, and the thin black line represents that after the 53-nm peak. The thin dotted lines represent the pair correlation functions between the oxygen atoms of water and the backbone hydrogen atoms or oxygen atoms of residues 40–50, which were already stretched taut before the 53-nm peak.

We also conducted an implicit solvent simulation to test the reproducibility of the appearance of peaks in the F-E curve. Although in this model, the zinc ion was not stably bonded to the coordinating histidines even after 200 ps of equilibration time before the BCAQ253C was stretched, we conducted a stretching simulation. We expected that BCAQ253C maintained a Type I conformation without the zinc ion because the 3-D structure of HCA II (77% sequence homology with BCA) without the zinc (Håkansson et al., 1992) is very similar to that of the HCA with a zinc ion. Moreover, apobovine carbonic anhydrase has been used extensively as the starting material for metal substitution experiments (Hunt et al., 1977; Pocker et al., 1977; Calhoun et al., 1985).

We found that the F-E curve obtained from the simulation in the implicit solvent system had a sharp peak at an extension of 49 nm (Fig. 2 c), in agreement with the AFM experiment (Fig. 2 a), and with the result of the simulation in the explicit water system (Fig. 2 b). In the implicit solvent system, as in the explicit water simulation, S5 and S10 were pulled apart from each other at this extension, as shown in Fig. 7. We found that, as in the explicit solvent simulation, the following events occurred: 1), sliding of S5 along S6 with simultaneous rupture of the H-bond array followed by unzipping of S6 from S7; 2), a sudden increase in the SASA of S5 exposing many aromatic or hydrophobic residues (Fig. 7, a and c); and 3), frictional resistance between three residues (K211, E212, and P213 located between S10 and S11) and the S7/H5-loop. In addition, S9, which forms the H-bond patch with S10, collided with the S7/H5-loop. Therefore, the protein molecule resisted the tensile force up to 500 pN before it was unfolded for the same reason as in the explicit water simulation (Fig. 2 c, arrow labeled 3). From the results of both types of simulations, we concluded that the main contribution to the mechanical strength of the BCA molecule was the combined effect of the three structural features described above.

FIGURE 7.

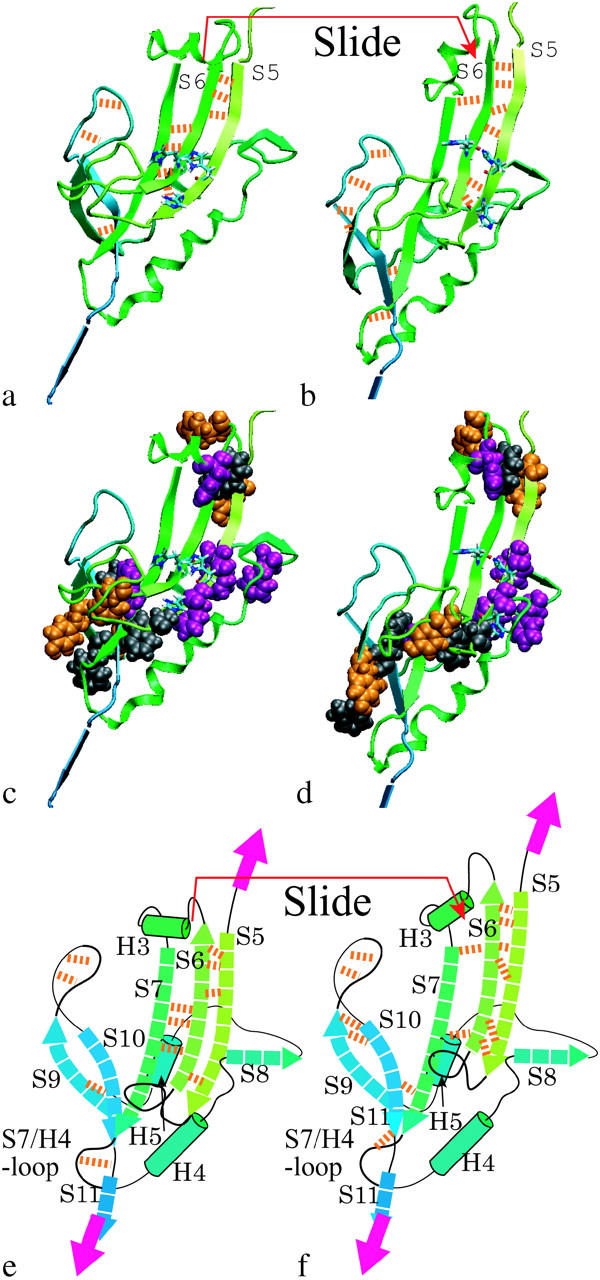
The S5 and S10 β-strands, which are parallel to each other, are pulled against each other at the 49-nm peak. The snapshots are taken from the results of the implicit solvent simulation with a pulling speed of 1.0 Å/ps. (a) 460 ps: four hydrogen bonds (H-bonds) were formed between S5 and S6 (orange broken lines), and three H-bonds were formed between S6 and S7. (b) 470 ps: S6 slides along S7. (c and d) Van der Waals models of the aromatic residues in images a and b, respectively. (e and f) Schematic diagrams of a and b, respectively.

The 40-nm force peak can also be explained as the combined effect of the resistance of H-bonds against longitudinal shearing and the hydrophobic contact. Fig. 8 shows the sequence of structural changes in the protein molecule from 743 ps to 777 ps at a pulling speed of 0.5 Å/ps. S2 formed three H-bonds with S8 on the right and six H-bonds with S3 on the left (orange broken lines, Fig. 8 a) at 743 ps. At an extension of 40 nm, these H-bonds were first broken temporarily and then reformed again. They were completely broken between 743 ps and 777 ps (Fig. 8 b, Table 2). Since S2 and S11 were arranged in parallel with each other, pulling S2 from the β-sheet induced longitudinal shearing, which requires a high tensile force. After S2 is simultaneously pulled apart from S3 and S8, S3 was pulled apart from S4. Since S3 and S11 were antiparallel, the four H-bonds between S3 and S4 were broken successively with a low force in the fashion of lateral shearing. These processes cause the second force peak at this extension.

FIGURE 8.

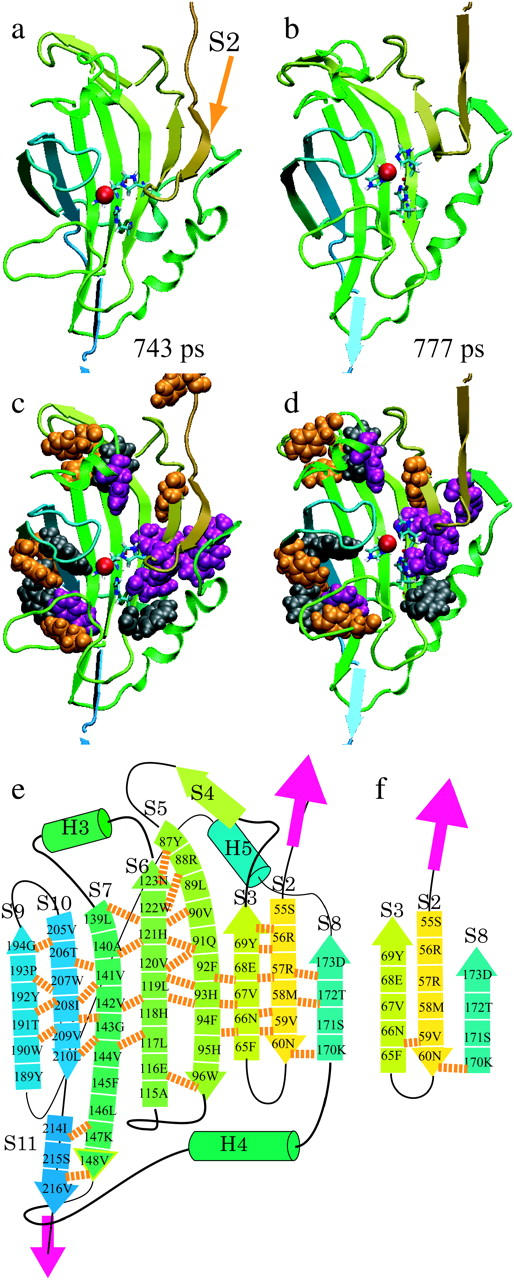
S2 and S10, which are parallel to each other, are pulled apart from each other at the 40-nm peak. The snapshots are taken from the results of the explicit water simulation with a pulling speed of 0.5 Å/ps. (a) 743 ps: S2 forms three H-bonds with S8 on the right, and five H-bonds with S3 on the left (orange broken lines). (b) 777 ps: those H-bonds are completely broken within 34 ps. (c and d) Van der Waals models of aromatic residues in images a and b, respectively. (e and f) Schematic diagrams of a and b, respectively.

In addition, hydrophobic interactions were likely contributing to the mechanical strength of the protein, as in the case of the 53-nm peak. An aromatic cluster consisting of three phenylalanine residues (65F in S3, 174F and 177F between S8 and H6; Fig. 8, c and d, and purple in Fig. 7) and one tyrosine residue (69Y in S3) and the α-helix H5 surrounding S2 prevented water molecules from approaching the H-bonds. The SASAs of S2 and S3 were small before the 40-nm peak, and then jumped up to a level close to the maximum at a 40-nm force peak (Fig. 6 a, orange and ocher curve). This also suggests that the hydrophobic contact contributes to the mechanical strength of the protein, as in the 53-nm peak. Thus, a group of H-bonds bridging S2 and S3 withstand a relatively high threshold of tensile force, and when the threshold is overcome, they break simultaneously within a very short time. Such a process would be recorded as a force peak in the F-E curve.

DISCUSSION

Using SMD simulations, we reproduced the major mechanical fracture patterns of BCA II observed in AFM experiments. In each simulation, the tensile force applied to the BCAQ253C showed three peaks in the F-E curves at extensions of 10–17, 40, and 49–53 nm.

Although the peak at 40 nm extension was not observed in the experiment of Alam et al. (2002), our preliminary data using the force-clamp method developed by Oberhauser et al. (2001) indicated multiple fracture patterns (H. Arakawa, M. T. Alam, and A. Ikai, unpublished). In another AFM experiment where the BCA molecule is stretched under a mildly denaturing condition, the F-E curve showed two intermediate peaks at extensions of ∼40 nm and∼50 nm (Afrin et al., 2004). Such independently obtained AFM data support the two-step or multiple-step rupture mechanism of the β-sheet core suggested from our SMD simulation.

In the explicit solvent simulation, the peak force at ∼53 nm in extension was ∼1300 pN after the subtraction of the surface tension of the water surrounding the protein. From theoretical predictions in relation to the bond rupture force, the strength of the rupture force is proportional to the log (loading rate)

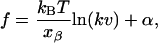(4)

where f is the strength of the bond rupture force, k is the transducer stiffness or the spring constant of the cantilever, v is the pulling speed of the spring, x_β is the distance between a position of potential minimum and a position of potential barrier along a reaction path, k_B is the Boltzmann constant, T is the temperature, and α is a constant (Evans and Ritchie, 1997). From the above formula, in a case where x_β is large, the velocity dependence of the peak force is small. In the case of the titin Ig-domain, x_β has been found to be ∼0.3 nm in length according to Rief et al. (1997). Although the velocity dependence of rupture force of BCAQ253C has not been measured, the x_β can be estimated as follows. The extension of the molecule is elongated by 0.8 nm (length corresponding to two amino acid residues) due to the sliding of S5 along S6 during the 53-nm peak. The elongation was the difference between the chain extension of the protein at the start of sliding of S5 along S6 (Fig. 3 a) and that at the end of sliding when the unzipping between S6 and S7 started instead of the sliding of S5 (Fig. 3 b). During this period, work done by the tensile force is accumulated within the molecule. From this atomic scale picture, x_β can be estimated to be ∼0.8 nm. From the value of x_β, we can calculate the loading-rate dependency of BCA as 5 pN/1 ln unit. Since the loading rate in our simulation is 9 orders of magnitude larger than in the AFM experiment, the increase in the peak force is 105 pN. Furthermore, the strength of the single coordination bond between a zinc and histidine (H118) is ∼20 kcal/mol (Saito et al., 2004). The reaction length is 0.8 nm and the force required to rupture the coordination bond is roughly estimated as 170 pN (energy/length). Subtracting 105 pN and adding 170 pN to 1400 pN (53-nm peak force for an explicit solvent with a pulling speed of 0.5 Å/ps, Table 1), we obtain a value of ∼1500 pN, which is close to the value of the peak force of 1200 pN for the AFM experiment. Though this is a very rough estimation, we believe that the major feature of the BCA molecule observed in the AFM experiment was reproduced in our simulations, because the correction factors are smaller than the observed peak force.

We next noticed that the peak heights in the explicit water case were higher than those in the implicit solvent case. This discrepancy was undoubtedly due partly to the additional force required to elongate the water droplet around the protein molecule. Explicit water simulations by other researchers also show similar saw-tooth patterns in the F-E curves (Lu et al., 1998; Lu and Schulten, 2000). In general, therefore, it is safe to assume that the deformation of water droplets does not overwhelm the force spectroscopy of unraveling of the protein molecule. We attempted to obtain a rough estimate of the surface tension of a water droplet. According to Zakharov et al. (1997), the surface tension of a water droplet was from 48 to 54 mN/m as the radius of the water droplet was increased from 7.7 to 15.4 Å, in contrast to that of bulk water of 72 mN/m. We set the surface tension of the water droplet in our simulation to be ∼55 mN/m (radius 50 Å at initial system). Assuming that the maximum value of the additional force due to the surface tension is equal to γ multiplied by the circumference of the maximum cross section perpendicular to the direction of the force, it was ∼1420 pN at the 17-nm peak (radius ∼41 Å), 1140 pN at the 40-nm peak (radius ∼33 Å), and 800 pN at the 53-nm peak (radius ∼23 Å) (Fig. 2 b, plotted by “×”). After subtracting these values from the peak values of force, we obtained ∼1800 pN at the 17-nm peak, ∼1200 pN at the 40-nm peak, and ∼1400 pN at the 53-nm peak (Table 1, values in parentheses) as the forces required to unfold the corresponding local structures.

The resistance of a β-sheet against shearing deformation has been discussed by Brockwell et al. (2003), and we confirmed it in this work. In addition to this effect, we found that hydrophobic interactions contributed significantly to the mechanical resistance of BCA II against pulling. What determined the peak position in our simulations was found to be the stable hydrophobic interactions between S7 and S10, and the steric hindrance between S9, S11, and the S7/H5-loop.

The equilibrium denaturation experiment of HCA revealed that the β-sheet including S3, S5, S6, S7, and S10 remains in a compactly folded state up to a denaturant concentration of 3 M (Hammarström et al., 1997). Furthermore, CA in a molten globule state was found to have the ability to bind zinc, showing that the zinc binding site including S5 and S6 forms a native structure even with other parts of the protein in a denatured state (for BCA, Anderson et al., 2001; for HCA, Hunt et al., 1977). These experimental results support that the thermodynamically stable local structure, composed of S3, S5, S6, S7, and S10 is also mechanically resistant against forced unfolding by a tensile force. This agreement suggests a correlation between equilibrium stability and mechanical stability of BCA II, although reaction pathways between a folded and an unfolded state might be different from each other.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.