Abstract
We magnetically imaged the magnetic action field and optically imaged the transmembrane potentials generated by planar wavefronts on the surface of the left ventricular wall of Langendorff-perfused isolated rabbit hearts. The magnetic action field images were used to produce a time series of two-dimensional action current maps. Overlaying epifluorescent images allowed us to identify a net current along the wavefront and perpendicular to gradients in the transmembrane potential. This is in contrast to a traditional uniform double-layer model where the net current flows along the gradient in the transmembrane potential. Our findings are supported by numerical simulations that treat cardiac tissue as a bidomain with unequal anisotropies in the intra- and extracellular spaces. Our measurements reveal the anisotropic bidomain nature of cardiac tissue during plane wave propagation. These bidomain effects play an important role in the generation of the whole-heart magnetocardiogram and cannot be ignored.
INTRODUCTION
Early electrocardiographers approximated the distribution of current generators in the heart as a single equivalent current dipole located at a fixed position in the heart whose strength and orientation change during the heartbeat. Frank (1953) replaced this eccentric dipole, and represented the sources of the activation wavefront as a uniform layer of dipoles oriented normal to the surface of the layer. In this “uniform double-layer model,” the potential at any field point is proportional to the total solid angle subtended by the double-layer rim. Later, Wikswo et al. (1979) showed that the magnetic field is given by a particular line integral over the rim of the double layer. Since the double-layer rim determines both the electrical and the magnetic signals, one can argue that the two signals contain the same information, albeit with different geometrical weighting.
These early models give adequate results provided that the field measurement site is far from the sources. Corbin and Scher (1977) performed extracellular potential recordings on the epicardial surface showing results inconsistent with the uniform double-layer model. They argued that tissue anisotropy must be the source of the inconsistencies, and proposed a different model where the dipoles were oriented only in a direction parallel to the long axis of the cardiac fibers. They showed that their model predicted waveforms similar to what they observed in vivo.
Subsequent studies of the effects of tissue anisotropy on extracellular potentials challenged the uniform double-layer models and contributed to the development of the bidomain model (Tung, 1978; Spach et al., 1979; Plonsey and Rudy, 1980; Colli-Franzone et al., 1982; Geselowitz et al., 1982). This model was later expanded and improved by Plonsey and Barr (Barr and Plonsey, 1984; Plonsey and Barr, 1984), Roth and Wikswo (1986, 1994), Sepulveda and Wikswo (1987), Henriquez and Plonsey (1990), and others.
The bidomain model is established as a macroscopic model describing cardiac tissue. It is the first mathematical model successfully describing cardiac tissue while accounting for the fiber orientation and the doubly anisotropic nature of the intra- and extracellular spaces. In the bidomain model, syncytial cardiac tissue is represented by a three-dimensional electrical cable with distinct intracellular and extracellular spaces separated by a cell membrane. The nonlinear properties of the membrane are generally incorporated into the model. For cardiac tissue architecture, the electrical conductivities of the intracellular and extracellular spaces are anisotropic, with differing anisotropy ratios in the two spaces. Although there are various experimental verifications of the bidomain nature of cardiac tissue during stimulation and the onset of propagation, there is little evidence for the need to describe a planar wavefront with a bidomain approach. (Wikswo, 1995).
Our group has developed sophisticated instrumentation dedicated to imaging the magnetic field associated with electrical currents flowing in the cardiac bidomain, i.e., the magnetic action field (MAF). Because the magnetic field is exquisitely sensitive to anisotropy ratios in the bidomain model, this technique is ideally suited for testing the accuracy of models and elucidating the effects of anisotropy, including fiber rotation, in the spread of stimulus and action currents. The question of relative information content between the whole-heart electrocardiogram and magnetocardiogram is not yet resolved (Wikswo and Barach, 1982). A quantitative comparison of images of the transmembrane potential (Vm) and magnetic measurements of currents at the tissue-level will provide key insights on the role of the bidomain in the generation of the magnetocardiogram.
MATERIALS AND METHODS
All experiments were conducted in accordance with National Institutes of Health regulations for the ethical use of animals in research and were approved in advance by the Vanderbilt Institutional Animal Care and Use Committee.
New Zealand white rabbits (n = 4) weighing 3–4 kg were first preanesthetized with intramuscular ketamine (50 mg/kg). The animals were then injected with 2000 units of heparin and anesthetized with sodium pentobarbital (50 mg/kg). The hearts were rapidly excised, mounted on a Langendorff perfusion system and perfused with a modified HEPES solution (130 mM NaCl, 5 mM KCl, 5mM HEPES, 10 mM glucose, 20 mM C2H3O2Na, 1 mM MgCl2, 1 mM CaCl2) adjusted to a pH of 7.40±0.05 with 1 M NaOH. The perfusate was saturated with 100% O2 gas and warmed to 36°C during the duration of the experiments.
To create an essentially two-dimensional myocardium for two of the hearts presented in this article, we cryoablated the endocardial and intramural layers of the left ventricle (LV) tissue by freezing with liquid nitrogen (−196°C) using procedures that have been extensively described and validated previously (Schalij et al., 1992). A cryogenic probe was inserted through the atrioventricular valve into the left ventricular cavity. While the entire heart was submerged in an oxygenated perfusate bath to prevent freezing of the epicardium, the cryoprobe was cooled with liquid nitrogen. After the first minute of cryoablation, perfusion was interrupted and the inside of the heart was frozen for an additional 5 min. After this period, perfusion was restored and the cryoprobe was removed. Cryoablation resulted in a viable epicardial layer ∼1 mm thick. The electrophysiological properties of the epicardial layer, such as conduction velocity and refractory periods, were not affected by this procedure.
At the end of the experiment, the cryoablated hearts were stained with 2,3,5-triphenyltetrazolium chloride (“tetrazolium red,” Sigma, St Louis, MO) then sliced into 1–2 mm sections to evaluate the effects of the endocardial cryoablation. Dehydrogenase enzymes react with the tetrazolium salts to form a bright red formazan pigment. No staining occurs in dead tissue lacking dehydrogenase activity. This staining technique has been evaluated by Fishbein et al. (1981) and has been shown to correlate well with signs of myocardial necrosis.
During the experiments, the isolated Langendorff-perfused heart was mounted in an acrylic dish containing a temperature-controlled perfusate bath and held in place by a Teflon post inserted into the LV. The dish containing the bath and the heart was mounted on a pedestal which can be moved between the optical and the magnetic measuring systems. The electromechanical uncoupling agent 2,3- butanedione monoxime (BDM, Sigma, St Louis, MO; also known as diacetyl monoxime) (Gwathmey et al., 1991; Lin et al., 1997) was added to the perfusate solution at a concentration of 15 mM to block muscle contraction and hence lessen motion artifacts in the data.
Planar wavefronts were induced on the left ventricle via a line of three bipolar coaxial electrodes placed outside of the imaging area. The use of bipolar electrodes reduced artifacts in the recordings of the MAF caused by the stimulation pulse. The electrodes were constructed from 250 μm diameter silver wire inside of 1.5 mm diameter brass tubing. The electrodes were spaced ∼3 mm apart. The electrical stimuli were provided by a computer-controlled current source (Bloom Associates, Narberth, PA). The heart was paced at a 300 ms cycle length with 2 ms electrical stimuli at an amplitude ∼1.5× the diastolic stimulation threshold.
To provide spatial registration of the fluorescent and magnetic images, two thin wires were placed across the heart so that they intersected at a right angle in one corner of the imaging area. The wires and a scale were imaged optically. The wires were imaged magnetically by passing a small current through each wire individually and recording the magnetic field as a function of position. The zero-crossing of the magnetic field provides the location of the wire relative to the magnetic image. The reference wire can also be located in the optical image. With this technique, the two sets of images can be aligned with an accuracy of ∼0.5 mm, the spatial resolution of our MAF recordings.
Optical imaging and data analysis
The optical imaging system used to record the transmembrane potential is as previously described by Lin et al. (1999). The heart was stained with 200 μl of the voltage-sensitive dye di-4-ANEPPS (Molecular Probes, Eugene, OR) stock solution (0.5 mg/mL dimethyl sulfoxide, ∼1 mM). The fluorescence was excited by a diode-pumped, solid-state laser at a wavelength of 532 nm (Verdi, Coherent, Santa Clara, CA). Laser light was delivered to the heart through optical fiber bundles. The emitted fluorescence was imaged with a high-speed CCD camera (Model CA D1-0128T, Dalsa Inc, Waterloo, ON, Canada) using a 607-nm cutoff filter (#25 Red, Tiffen, Hauppauge, NY). The faceplate of the camera was cooled to 15°C via a circulating refrigerated solution. The data were acquired at 2-ms intervals with 12-bit resolution from 128 × 128 sites simultaneously over an area of ∼15 × 15 mm. The digitized pixel intensity from the digital camera was transferred to a PCI bus-master frame grabber board (IC-PCI, Imaging Technology Inc., Bedford, MA) mounted in an IBM-compatible personal computer (Dell Precision Workstation 610, Dell Computer Corp., TX). We placed an LED in the field of view of the imaging camera and fired it with each stimulation pulse. This allowed us to determine the falling edge of the stimulus pulse with an accuracy of 2 ms, given by the frame rate of the CCD camera. Recording the duration of the simulation pulse optically allowed us to synchronize the timing between the optical and magnetic data.
The normalized transmembrane potential distribution of a site on the tissue, ΔV/Vmax, is the ratio −ΔF/Fmax, where Fmax is the fluorescence intensity obtained from the resting tissue and ΔF the variation of fluorescence intensity when the recording site of tissue is excited (Lin et al., 1997). The minus sign represents a decrease in fluorescent intensity with a more positive transmembrane potential. The optical data presented in this article have been filtered by applying a rotationally symmetric Gaussian lowpass filter of 0.6 mm size with a standard deviation of 0.25 mm two times, which allowed us to more accurately calculate the gradient in the transmembrane potential maps. The timing of the stimulation pulses was determined before applying this filter.
To determine cardiac fiber orientation, we recorded the response to a single unipolar electrode placed in the center of the imaging area.
Magnetic imaging and data analysis
The magnetic field perpendicular to the imaging plane (Bz) associated with the action currents resulting from plane wave propagation was recorded using the ultrahigh resolution, low-temperature scanning Superconducting Quantum Interference Device (SQUID) microscope developed by Baudenbacher et al. (2002). In this instrument, a superconducting pickup coil is directly coupled to the flux transformer of the SQUID sensor. The pickup loop used in these experiments was constructed from 20 turns of 25 μm diameter Nb wire wound in two layers onto a sapphire bobbin with a tip diameter of 500 μm. The sapphire bobbin is located in the vacuum space of a cryostat and is thermally anchored to a liquid helium reservoir (−268.9°C). The pickup coil is separated from the room temperature sample by a 25-μm thick sapphire window. With this input configuration, the magnetic field sensitivity of the system is 330 fT/Hz1/2. Fig. 1 depicts schematically the experimental setup, including details of the SQUID microscope Dewar. The SQUID microscope is housed in a three-layer μ-metal magnetically shielded room (Vacuumschmelze, Hanau).
FIGURE 1.
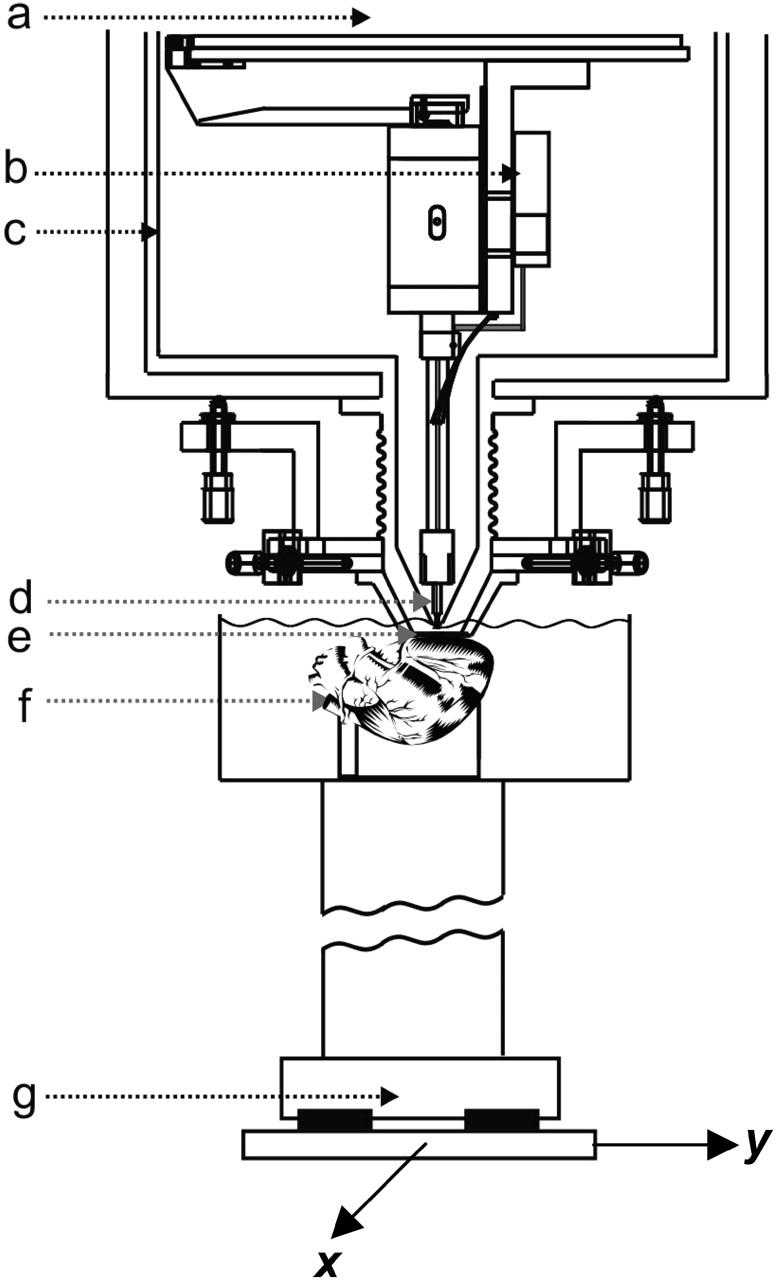
Diagram of the scanning SQUID microscope system showing: (a) liquid helium reservoir; (b) niobium can enclosing a low-Tc SQUID sensor; (c) 77 K radiation shield; (d) superconducting pickup coil; (e) 25 μm think sapphire window; (f) Langendorff-perfused isolated rabbit heart in 36°C bath; and (g) x-y scanning stage.
After the optical imaging, we quickly moved the dish containing the heart from the optical imaging system to the SQUID microscope scanning stage. We brought the heart into light contact with the sapphire window in the tail of the cryostat, reducing the distance between the heart and the pickup coil to ∼100μm. The SQUID is operated in a flux-locked loop with commercial electronics operating at a bandwidth of 1 kHz (Quantum Design DC-5000 controller) and the output voltage is digitized with a PCI-MIO card (National Instruments) with 16-bit resolution at a sampling rate of 5 kHz. The data acquisition is triggered by the stimulation pulse, and a computer-controlled xy-raster scan in 0.5 mm steps recorded the MAF as a function of position over the same area of the LV as was imaged in the optical system. The MAFs were combined using the stimulus pulse for synchronization to produce a time series of two-dimensional magnetic field maps. The time interval between successive field maps is 1 ms, given by the bandwidth of the flux-locked loop electronics. Since the data acquisition is triggered on the rising edge of the 5-ms stimulation pulse, we can determine the termination of the stimulus with an accuracy of 1 ms, which allows us to synchronize the magnetic data and the optical data to an accuracy of 2 ms. The magnetic data presented in this article have been spatially filtered with a rotationally symmetric Gaussian lowpass filter of 2.5 mm size with a standard deviation of 0.5 mm to enhance the display of the data. The oversampled magnetic data at 5 kHz were reduced to the 1 kHz bandwidth of the SQUID electronics by taking the mean over five data points.
The distribution of currents over the imaged area of the LV was calculated from the magnetic images. Using an algorithm described by Roth et al. (1988, 1989), which assumes a two-dimensional current distribution, we solved the inverse problem using the mathematical techniques of Fourier transforms and spatial filtering.
RESULTS
We estimated the direction of the cardiac fibers by imaging the wavefront propagation from a single point stimulus placed in the center of the imaging area. The difference between two successive fluorescence measurements, which indicates the position of the wavefront, is shown in Fig. 2. The anisotropy in the conduction velocity along and transverse to the fiber direction results in an elliptical wavefront. The direction of the axis of cardiac fibers was estimated as the direction of fast propagation of the wavefront, or the direction of the long axis of the ellipse, and is indicated by the arrow in Fig. 2. Furthermore, we have visually inspected high resolution optical images to confirm that the fiber orientation corresponds to the fast propagation direction as estimated from the point stimulus data.
FIGURE 2.
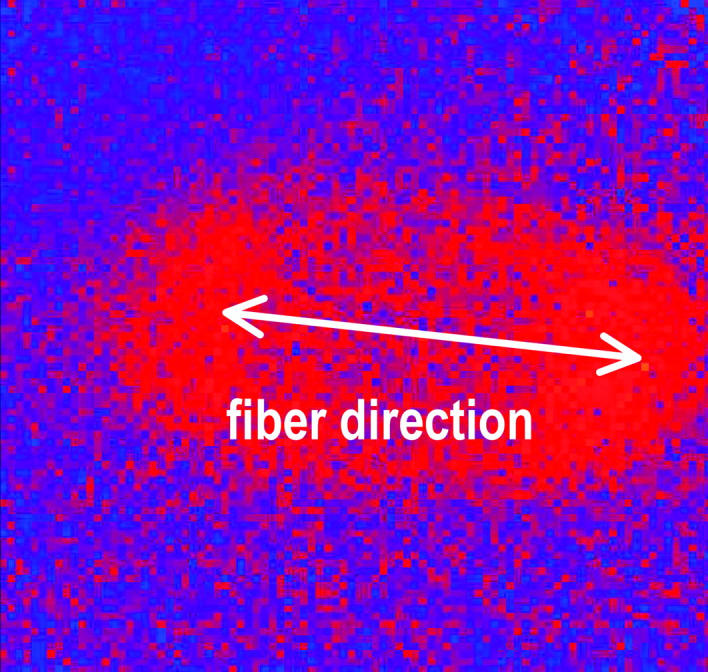
Elliptical wavefront expanding from a point stimulus placed in the center of the imaging area obtained from the difference between two successive fluorescent images. The direction of fast propagation indicates the cardiac fiber orientation.
The progression of a planar excitation wavefront initiated by the row of bipolar electrodes is shown in Fig. 3 for both the optical (right) and magnetic (left) recordings. The wavefront can be defined as the leading edge of the action potential and identified as the border between areas of opposite polarity in the magnetic data. The wavefront is observed to move across the imaging area from the top left corner to the bottom right corner and at an angle of ∼45° relative to the cardiac fiber direction. The time elapsed after the stimulation pulse is indicated on the right.
FIGURE 3.
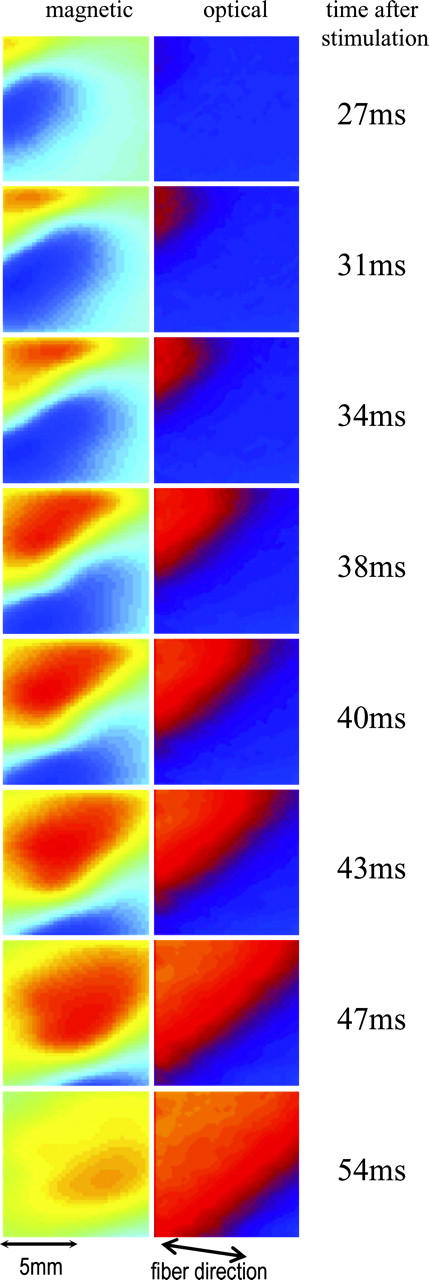
Magnetic (left) and optical (right) images of the progression of a planar excitation wavefront across the imaging area. The wavefront moves diagonally from the top left corner of the imaging area at ∼45° to the fiber orientation. The time elapsed after stimulation is indicated to the right of the frames.
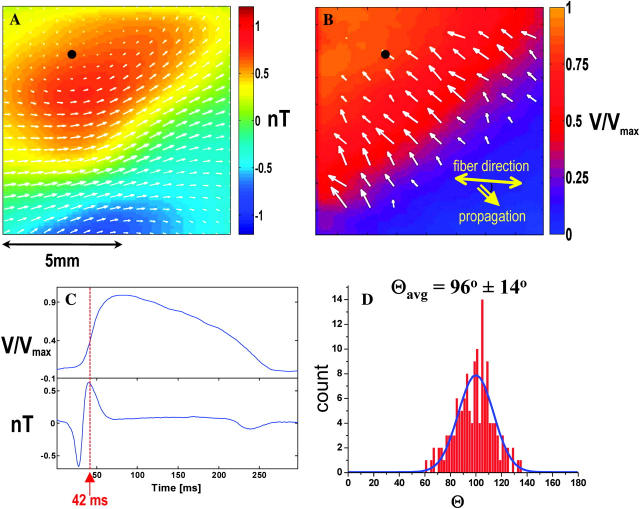
A single time frame from this set, recorded 42 ms after initiation of the wavefront, is shown in more detail in Fig. 4, A and B. For a single (x,y) point indicated by the black dots in Fig. 4, A and B, the transmembrane potential and magnetic waveforms are plotted for a 300 ms interval in Fig. 4 C.
FIGURE 4.
(A) Magnetic image of plane wavefront propagating at an angle of 45° to the fiber direction with arrows indicating the magnitude and direction of the net current. (B) Corresponding optical data with arrows indicating ∇Vm . (C) Time traces from the optical data (top) and the magnetic data (bottom) taken at the points indicated by the black dots in (a) and (b). (D) Angle between net current and ∇Vm.
Assuming a two-dimensional current flow, we calculated the net current distribution over the imaging area from each frame of the magnetic data as described in Roth et al. (1988). This current is superimposed on the magnetic data frame (Fig. 4 A) as arrows indicating the relative magnitude and direction of the currents. The arrows superimposed on the optical data in Fig. 4 B indicate the transmembrane potential gradient, ∇Vm, over a region in the immediate vicinity of the wavefront as calculated from the Vm data. The angle between the net current vector and ∇Vm was calculated for all data points indicated by the arrows in this region. Fig. 4 D shows the distribution of the calculated angles over this area. The data points outside the region were not included in this analysis since ∇Vm is dominated by noise which would lead to ill defined angles. We found the average angle between the net current and ∇Vm to be Θavg = 96 ± 14°. The solid blue line is a Gaussian fit to the data for comparison.
Table 1 lists the results for Θavg for all (n = 4) hearts. For all hearts studied, the magnitude of the magnetic field was between 0.5 nT and 1.5 nT. Our values are the same order of magnitude as those predicted by numerical simulation (Barach and Wikswo, 1994; Roth and Woods, 1999; Murdick and Roth, 2004).
TABLE 1.
Average angle between the gradient in the transmembrane potential and the net action current for each of the n = 4 hearts
| Data set | Preparation | Θavg |
|---|---|---|
| 1 | Frozen endocardium | 96 ± 14° |
| 2 | Frozen endocardium | 89 ± 12° |
| 3 | Whole heart | 90 ± 14° |
| 4 | Whole heart | 96 ± 15° |
DISCUSSION
The bidomain model has been used to predict current distributions associated with propagating wavefronts in cardiac tissue. Using an anisotropic two-dimensional bidomain model, Barach observed that, in a cardiac slice, an expanding elliptical depolarization wavefront has associated with it a total action current density having large curl of one sign leading the wavefront and large curl of the opposite sign after the wavefront (Barach, 1993). Barach and Wikswo expanded this simulation (1994) and calculated the magnetic field distributions, Bz, produced by propagating action currents originating from a point stimulus. The existence of this magnetic field associated with a net action current is a significant signature of the cardiac anisotropic bidomain model with differing intracellular and extracellular anisotropies.
More recently, planar wavefronts in a uniform sheet of cardiac tissue and their associated fields have been predicted numerically using the bidomain model (Roth and Woods, 1999; Weber dos Santos et al., 2002). The authors found that the unequal anisotropy ratios in the intracellular and extracellular spaces leads to a net current density perpendicular to the direction of wavefront propagation and orthogonal to the gradient in the transmembrane potential for plane wavefronts propagating at 45° relative to the fiber direction. This numerical finding is in contrast to traditional models where the MAF was thought to arise from current dipoles aligned along the gradient in transmembrane potential. (Corbin and Scher, 1977; Wikswo, 1983, 1990).
Our experimental examination of these predictions demonstrates that we can indeed magnetically detect a net current parallel to the leading edge of the depolarization wavefront and perpendicular to transmembrane potential gradients as displayed in Fig. 4, A and B, and summarized in Table 1.
Our data indicate no significant difference between cyroablated and whole heart preparation. Kinsley examined sections from different depths of the rabbit left ventricular wall and found that fiber orientation rotated counterclockwise with increasing depth relative to the epicardial surface. In the first 300 μm of depth, the rotation was only ∼6°; however, rotations as large as 75° relative to the epicardium were found near the endocardium (Knisley, 1995). A similar architecture was observed in other types of hearts (Streeter et al., 1969).
Using histological data, Knisley (1995) estimated that the in-plane fiber orientation deviates ± 14° relative to the mean fiber orientation in sections 0.1 – 0.2 mm below the anterior epicardial surface of the left ventricle. The mean fiber orientation was also determined, similar to our experiments, from the fast propagation direction via epifluorescence imaging. The angles are in good agreement with the histological data. The error in estimating the mean fiber orientation using this method was ±12°. We expect a comparable error in our data.
Knisley estimated that the thickness of tissue contributing to the fluorescence signal was ≈300 μm (Knisley, 1995). We modeled the magnetic field generated by a sheet of current as a superposition of a stack of current-carrying thin wires to evaluate the contribution of current at different depths. The magnetic field was normalized to the surface, which allowed us to estimate the contributions of various thicknesses to the total magnetic field. We found that 80% of the magnetic signal comes from approximately the first 500 μm of thickness. Therefore, we do not expect a large difference between our whole heart and cyroablated preparations.
In recent studies, Murdick and Roth (2004) and Weber dos Santos and Dickstein (2003) discussed the presence of a conducting bath surrounding the cardiac tissue. Murdick and Roth concluded that the magnetic field can be viewed as arising from the superposition of two current sources: the traditional dipole model to describe the volume conductor and a line of current parallel to the wavefront to describe the cardiac bidomain. They find that the bath has significant contribution to the total magnetic field for certain angles, especially for a wavefront propagating along the fiber direction where a pure bidomain would produce a zero magnetic field. However, at an angle of 45° the presence of a bath has little effect on the magnetic field component perpendicular to the surface. In our experiments, the left ventricle is pressed against the insulating sapphire window of the Dewar tail, displacing most of the perfusate bath over the tissue surface. Based on the theoretical predictions and our experimental setup we do not expect the bath to play a significant role in our observations.
In summary, we found that net action currents associated with planar wave propagation in cardiac tissue flow along the wavefront and perpendicular to gradients in the transmembrane potential. This is in contrast to a traditional double-layer model where the net current flows along the gradient in the transmembrane potential. Our findings are supported by numerical simulations treating cardiac tissue as a bidomain with unequal anisotropies in the intra- and extracellular spaces. Therefore, the anisotropic bidomain nature of cardiac tissue plays an important role in the generation of the magnetocardiogram and can not be ignored.
Limitations of the experiment and future studies
Of particular interest would be a plane wavefront traveling perpendicular to the fiber direction since numerical simulations predict a zero z component of the magnetic field (Murdick and Roth, 2004). However, this condition is difficult to realize experimentally. Ideally, we would like to measure the MAF as a function of angle at one position with a more sophisticated stimulation protocol, such as a phased-array electrode system that can produce a planar epicardial wavefront moving in an arbitrary direction. (Abbas et al., 1997) In this way, the direction of the planar wavefront propagation can be changed whereas all other conditions remain constant.
Currently, we measure the magnetic and transmembrane potentials in two different systems successively. This requires careful spatial and time registration to compare the two images. Simultaneous measurements of the magnetic field maps, extracellular potentials, and fluorescence signals would lead to much more precise comparison between the measurements and valuable data for a comparison between model predictions and experimental observations. This could be accomplished by incorporating thin film electrodes on the Dewar window and optrodes, bundles of thin optical fibers as developed by Hooks et al. (2001) and Byars et al. (2003), directly into the SQUID microscope system. Detailed histological studies and a more detailed bidomain model as propagated by Pullan et al. (2001) would finally be necessary to make model predictions such as conductivity ratios, the role of the fiber orientation, and to clarify the limitations of the bidomain model.
Acknowledgments
We thank Andre Kleber for his comments on this manuscript.
This work was supported by the National Institutes of Health (R01-HL58241-05, T32 HL07411 and F32 HL073612-01) and the Vanderbilt Institute for Integrative Biosystems Research and Education (VIIBRE).
References
- Abbas, R. A., S.-F. Lin, and J. P. Wikswo, Jr. 1997. A phased-array stimulator for studying anisotropic propagation, planar wavefront collisions, and the effects of wavefront curvature on conduction velocity. Pacing Clin. Electrophysiol. 20:II-1102. [Google Scholar]
- Barach, J. P. 1993. A simulation of cardiac action currents having curl. IEEE Trans. Biomed. Eng. 40:49–58. [DOI] [PubMed] [Google Scholar]
- Barach, J. P., and J. P. Wikswo, Jr. 1994. Magnetic fields from simulated cardiac action currents. IEEE Trans. Biomed. Eng. 41:969–974. [DOI] [PubMed] [Google Scholar]
- Barr, R. C., and R. Plonsey. 1984. Propagation of excitation in idealized anisotropic two-dimensional tissue. Biophys. J. 45:1191–1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baudenbacher, F., N. T. Peters, and J. P. Wikswo, Jr. 2002. High resolution low-temperature superconductivity superconducting quantum interference device microscope for imaging magnetic fields of samples at room temperatures. Rev. Sci. Instrum. 73:1247–1254. [Google Scholar]
- Byars, J. L., W. M. Smith, R. E. Ideker, and V. G. Fast. 2003. Development of an optrode for intramural multicite optical recordings of vm in the heart. J. Cardiovasc. Electrophysiol. 14:1196–1202. [DOI] [PubMed] [Google Scholar]
- Colli-Franzone, P., L. Guerri, C. Viganotti, E. Macchi, S. Baruffi, S. Spaggiari, and B. Taccardi. 1982. Potential fields generated by oblique dipole layers modeling excitation wavefronts in the anisotropic myocardium. Circ. Res. 51:330–346. [DOI] [PubMed] [Google Scholar]
- Corbin II, L. V., and A. M. Scher. 1977. The canine heart as an electrocardiographic generator. Dependence on cardiac cell orientation. Circ. Res. 41:58–67. [DOI] [PubMed] [Google Scholar]
- Fishbein, M. C., S. Meerbaum, J. Rit, U. Lando, K. Kanmatsuse, J. C. Mercier, E. Corday, and W. Ganz. 1981. Early phase acute myocardial infarct size quantification: validation of the triphenyl tetrazolium chloride tissue enzyme staining technique. Am. Heart J. 101:593–600. [DOI] [PubMed] [Google Scholar]
- Frank, E. 1953. A comparative analysis of the eccentric double-layer representation of the human heart. Am. Heart J. 46:364–378. [DOI] [PubMed] [Google Scholar]
- Geselowitz, D. B., R. C. Barr, M. S. Spach, and W. T. Miller III. 1982. The impact of adjacent isotropic fluids on electrograms from anisotropic cardiac muscle. Circ. Res. 51:602–613. [DOI] [PubMed] [Google Scholar]
- Gwathmey, J. K., R. J. Hajjar, and R. J. Solaro. 1991. Contractile deactivation and uncoupling of crossbridges. Effects of 2,3- butanedione monoxime on mammalian myocardium. Circ. Res. 69:1280–1292. [DOI] [PubMed] [Google Scholar]
- Henriquez, C. S., and R. Plonsey. 1990. Simulation of propagation along a cylindrical bundle of cardiac tissue i: mathematical formulation. IEEE Trans. Biomed. Eng. 37:850–860. [DOI] [PubMed] [Google Scholar]
- Hooks, D. A., I. J. LeGrice, J. D. Harvey, and B. H. Smaill. 2001. Intramural multisite recording of transmembrane potential in the heart. Biophys. J. 81:2671–2680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knisley, S. B. 1995. Transmembrane voltage changes during unipolar stimulation of rabbit ventricle. Circ. Res. 77:1229–1239. [DOI] [PubMed] [Google Scholar]
- Lin, S.-F., R. A. Abbas, and J. P. Wikswo, Jr. 1997. High-resolution high-speed synchronous epifluorescence imaging of cardiac activation. Rev. Sci. Instrum. 68:213–217. [Google Scholar]
- Lin, S.-F., B. J. Roth, and J. P. Wikswo, Jr. 1999. Quatrefoil reentry in myocardium: An optical imaging study of the induction mechanism. J. Cardiovasc. Electrophysiol. 10:574–586. [DOI] [PubMed] [Google Scholar]
- Murdick, R. A., and B. J. Roth. 2004. A comparative model of two mechanisms from which a magnetic field arises in the heart. J. Appl. Phys. 95:5116–5122. [Google Scholar]
- Plonsey, R., and R. C. Barr. 1984. Current flow patterns in two-dimensional anisotropic bisyncytia with normal and extreme conductivities. Biophys. J. 45:557–571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plonsey, R., and Y. Rudy. 1980. Electrocardiogram sources in a 2-dimensional anisotropic activation model. Med. Biol. Eng. Comput. 18:87–94. [DOI] [PubMed] [Google Scholar]
- Pullan, A., D. Paterson, and F. Greensite. 2001. Non-invasive imaging of cardiac electrophysiology. Phil. Trans. R. Soc. Lond. A. 359:1277–1286. [Google Scholar]
- Roth, B. J., N. G. Sepulveda, and J. P. Wikswo, Jr. 1989. Using a magnetometer to image a two-dimensional current distribution. J. Appl. Phys. 65:361–372. [Google Scholar]
- Roth, B. J., S. Tan, and J. P. Wikswo, Jr. 1988. Two-dimensional inverse problems in biomagnetism. Phys. Med. Biol. 33:62. [Google Scholar]
- Roth, B. J., and J. P. Wikswo, Jr. 1986. A bidomain model for the extracellular potential and magnetic field of cardiac tissue. IEEE Trans. Biomed. Eng. BME-33:467–469. [DOI] [PubMed] [Google Scholar]
- Roth, B. J., and J. P. Wikswo, Jr. 1994. Electrical stimulation of cardiac tissue: a bidomain model with active membrane properties. IEEE Trans. Biomed. Eng. 41:232–240. [DOI] [PubMed] [Google Scholar]
- Roth, B. J., and M. C. Woods. 1999. The magnetic field associated with a plane wave front propagating through cardiac tissue. IEEE Trans. Biomed. Eng. 46:1288–1292. [DOI] [PubMed] [Google Scholar]
- Schalij, M. J., W. J. E. P. Lammers, P. L. Rensma, and M. A. Allessie. 1992. Anisotropic conduction and reentry in perfused epicardium of rabbit left-ventricle. Am. J. Physiol. 263:H1466–H1478. [DOI] [PubMed] [Google Scholar]
- Sepulveda, N. G., and J. P. Wikswo, Jr. 1987. Electric and magnetic fields from two-dimensional anisotropic bisyncytia. Biophys. J. 51:557–568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spach, M. S., W. T. Miller III, E. Miller-Jones, and R. B. Warren. 1979. Extracellular potentials related to intracellular action potentials during impulse conduction in anisotropic canine cardiac muscle. Circ. Res. 45:188–204. [DOI] [PubMed] [Google Scholar]
- Streeter, D. D., H. M. Spotnitz, D. P. Patel, J. Ross, and E. H. Sonnenblick. 1969. Fiber orientation in the canine left ventricle during diastole and systole. Circ. Res. 24:339–347. [DOI] [PubMed] [Google Scholar]
- Tung, L. 1978. A Bidomain Model for Describing Ischemic Myocardial D.C. Potentials. Massachusettes Institute of Technology, Cambridge, MA.
- Weber dos Santos, R., and F. Dickstein. 2003. On the influence of a volume conductor on the orientation of currents in a thin cardiac tissue. Lecture Notes in Computer Science. 2674:111–121. [Google Scholar]
- Weber dos Santos, R., F. Dickstein, and D. Marchesin. 2002. Transversal versus Longitudinal Current Propagation on a Cardiac Tissue and its Relation to MCG. Biomed. Tech. (Berl.). 47:249–252. [DOI] [PubMed] [Google Scholar]
- Wikswo, J. P., Jr. 1983. Theoretical aspects of the EEG-MEG relationship. In Biomagnetism: An Interdisciplinary Approach. S. J. Williamson, G. -L. Romani, L. Kaufman, and I. Modena, editors. Plenum Publishing, New York. 311–326.
- Wikswo, J. P., Jr. 1990. Biomagnetic sources and their models. In Advances in Biomagnetism. S.J. Williamson, editor. Plenum Press, New York. 1–18.
- Wikswo, J. P., Jr. 1995. Tissue anisotropy, the cardiac bidomain, and the virtual cathode effect. In Cardiac Electrophysiology, From Cell to Bedside. D. P. Zipes and J. Jalife, editors. W. B. Sanders, Philadelphia. 348–361.
- Wikswo, J. P., Jr., and J. P. Barach. 1982. Possible sources of new information in the magnetocardiogram. J. Theor. Biol. 95:721–729. [DOI] [PubMed] [Google Scholar]
- Wikswo, J. P., Jr., J. A. V. Malmivuo, W. H. Barry, M. C. Leifer, and W. M. Fairbank. 1979. The theory and application of magnetocardiography. In Advances in Cardiovascular Physics, Vol. 2. D. N. Ghista, V. E. Vollenhoven, and W. Yang, editors. Karger, Basel, Switzerland. 1–67.