Protein Folding in High-Dimensional Spaces: Hypergutters and the Role of Nonnative Interactions

Abstract

We explore the consequences of very high dimensionality in the dynamical landscape of protein folding. Consideration of both typical range of stabilizing interactions, and folding rates themselves, leads to a model of the energy hypersurface that is characterized by the structure of diffusive “hypergutters” as well as the familiar “funnels”. Several general predictions result: 1), intermediate subspaces of configurations will always be visited; 2), specific but nonnative interactions may be important in stabilizing these low-dimensional diffusive searches on the folding pathway, as well as native interactions; 3), sequential barriers will commonly be found, even in “two-state” proteins; 4), very early times will show characteristic departures from single-exponential kinetics; and 5), contributions of nonnative interactions to Φ-values and “Chevron plots” are calculable, and may be significant. The example of a three-helix bundle is treated in more detail as an illustration. The model also shows that high-dimensional structures provide conceptual relations between different models of protein folding. It suggests that kinetic strategies for fast folding may be encoded rather generally in nonnative as well as in native interactions. The predictions are related to very recent findings in experiment and simulation.

INTRODUCTION

The current conceptual map of protein-folding kinetics is dominated by the coexistence of several apparently distinct approaches. They may be categorized loosely into “energy landscape” (Bryngelson et al., 1995; Onuchic et al., 1995), “diffusion-collision” (Karplus and Weaver, 1976, 1994), “nucleation-condensation” (Fersht, 1999), and “topomer search” (Makarov and Plaxco, 2003) models. Each of these has its own way of visualizing how the collapse of a random coil to a native globule can ever be accomplished in observable time scales, a problem pointed out long ago (Levinthal, 1969). Each has advantages and drawbacks, but it is not clear whether each applies to a restricted subset of real cases, or whether all might have something to say about the folding of any one protein.

The “folding-funnel” picture of the energy landscape has the advantage of visualizing both guided folding and the emergence of on-pathway and off-pathway intermediate states (Dinner et al., 2000). Yet it is hard to escape from the deceptive simplicity of low-dimensional projections of folding funnels that appear necessarily in all graphical portrayals of it. In practice, of course, the dimensionality of the folding space is enormous. Even small (∼100 residue) proteins have a configurational space dimensionality of several hundred (think of the bond angles along the polypeptide main chain alone). In such high-dimensional spaces, qualitatively new features may arise, such as energetically-flat domains that nonetheless are extremely difficult to escape from and so behave as kinetic traps. A second feature is the potential for high cooperativity of structure in several simultaneous dimensions. This corresponds to the existence of narrow gullies in the hypersurface that are hard to find. In more biochemical language these structures might be exemplified by cooperative secondary structure formation alongside native or near-native distant contacts in α-helix bundle proteins (Myers and Oas, 2001), or simultaneous folding and anion binding (Henkels et al., 2001).

The “diffusion-collision” approach, on the other hand, is supported by strong experimental evidence that folding rates are controlled by the rate of diffusion of pieces of the open coil in their search for favorable contacts, rather than a driven collapse along some continuous energy surface (Jacob et al., 1999; Plaxco and Baker, 1998; Goldberg and Baldwin, 1995). Preformed units of secondary structure diffuse hydrodynamically and merge. Larger proteins may do this in an increasingly hierarchical way. The importance of diffusive searches is unsurprising, since under biological conditions, all candidates for energetic interactions, including electrostatics, are locally screened to a few angstroms: much smaller than the dimensions over which sections of protein must move to find their native configurations. Put another way, the vast majority of the space covered by the energy landscape must actually be flat (on a scale of k_BT) rather than funneled. Simple versions of these models have indeed been able to account rather well for folding rates as a function of secondary structure formation (Myers and Oas, 1999, 2001). However, it is not clear how applicable this approach is to cases in which secondary structure forms within a collapsed globule or cooperatively with it.

An attempt to articulate a range of scenarios in which partial ordering of secondary and tertiary structures mutually enhance a favorable folding pathway has been presented under the label of “nucleation-condensation” (Dagett and Fersht, 2003). Originally conceived as a kinetic theory in which a nucleus of native structure corresponds to the transition-state for folding, the picture now also encompasses the hierarchical folding routes of the diffusion-collision model.

A challenge faced by all these models is that the most successful search for inherent features of tertiary structure that correlate with folding rates has found that the topological measure of “contact order” is far more closely related than, for example, molecular weight itself in the case of “two-state” folders (Plaxco et al., 2000). Rationalization of this observation has given rise to a third view of the critical pathway of protein folding, the “topomer search” model (Plaxco and Gross, 2001). The rate determining step is not the rapid formation of local secondary structure, nor the diffusion of subdomains per se, but the organization of large pieces of secondary structure into the same topological configuration as the native state, which thereafter is able to form rapidly. This suggests a partition of the folding space into “rapid” dimensions representing the local formation of secondary structure, and “slow” dimensions representing the topomer search. However, a quantitative relation between the topomer search space and contact order is still unclear, since no native contacts are actually required to form at a purely topologically-defined transition state at all (although many are to be expected from the partial ordering at the secondary level at least). Furthermore, information on the effect on folding rate of replacing specific residues via mutation or “Φ-value” analysis (Fersht, 2000) needs to be taken together with correlations of contact order.

These approaches have one important aspect in common: they all effectively reduce the dimensionality of the search-space by assumption, rather than by derivation. This is both natural and necessary, since data from kinetic experiments do just the same, but there is a danger in overlooking aspects of folding that rely essentially on the presence of many degrees of freedom. Our aim in this work is to take a fresh look at the issue, embracing many simplifications but on this occasion not that of a low dimension of configurational search space. We find in the next section that quite general conclusions may be drawn about the topology of this search space if the dimensionality is kept high. These in turn suggest strategies for protein folding that go beyond those available to native-interactions alone. We work out on example in more detail in the case of three-helix proteins. The approach will additionally help us to see how the existing apparently-distinct paradigms for protein folding are related, and suggest places to look for the information content of the “kinetic code” within proteins that encodes the folding search path, as distinct from the native structure itself.

HIGH-DIMENSIONAL DIFFUSIVE SUBSPACES AND SEARCHES

We start with a very simple and abstract model for protein folding, but one that explicitly retains a very large number of degrees of freedom. The total search space is modeled as the interior of a hypersphere of dimension d and radius R, and the native (target) state as a small sphere of radius R_N at the origin of the space. The entire configuration of the protein corresponds to a single-point particle executing a random walk in the hypersphere. The ratio of R to R_N describes the typical localization on folding in the values of a degree of motional freedom. If the degree of freedom is spatial the appropriate scales are the radius of gyration of a denatured protein, and the size of the fluctuation region of a monomer within the native state. If it is angular, then they are the angle of libration of a bond fluctuating in one local minimum as a fraction of 2π. In either case the appropriate order of magnitude estimate is for single-domain proteins. Bicout and Szabo (2000) introduced this very general framework for discussing flat and funneled landscapes, but then restricted themselves to three-dimensional spaces, a simplification that we shall try to avoid. To explore the timescales of the search for the target space (on which the diffuser will “stick”) we write down the time-dependent diffusion equation for a particle, restricting ourselves to the case of a flat potential at first. The most convenient function to use is the probability density, P(r,t), that the system is a radial distance r from the center of the hypersphere at time t, which obeys

(1)

supplemented by the absorbing boundary condition P(R_N, t) = 0, signifying the stability of the native state. The timescale for the search steps is set by the effective diffusion constant D. The mean passage time from the unfolded ensemble to the native state can be calculated by introducing a uniform current J of diffusers (representing a population of folding proteins) on the boundary of the hypersphere at r = R, as the other boundary condition, and finding the consequent steady state solution to Eq. 1. The mean time to pass from R to R_N over the ensemble of systems is then just the total number of diffusers at steady state normalized by the current, leading to

(2)

This expression indicates how very much qualitatively longer the mean search time is in high dimensions (d > 2), than the low-dimensional estimation of the characteristic time 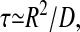which replaces Eq. 2 in d = 1, and 2. This fundamental time is scaled up by the denatured system size (measured in units of the target size R_N) to the power of the number of effective dimensions >2. An analysis of the eigenmode structure of the problem indicates why this is so: for large d, nearly all the diffusers exist in the lowest eigenfunction of the diffusion operator; that eigenfunction is in turn localized to the exponentially large surface of the hyperspherical search space. Another consequence of this rather general structure is that single-exponential kinetics are also a general property of such high-d search spaces.

The central result of Eq. 2 depends on two key physical assumptions: 1), the dimensionality of the space is of realistic values for protein folding—of the order of a hundred or more; and 2), the stability of the folded state is governed by completely cooperative local interactions in the native state only. With these assumptions alone, the model of high-dimensional diffusion we have described is inevitable, and the timescales unreasonably long. The exponentially large search times arise transparently from the factor in Eq. 2. This is of course a restatement of Levinthal's paradox (Levinthal, 1969; Karplus, 1997), but a helpful one, in that the two necessary assumptions for the paradox to arise are clearly seen. The first just gives the large dimensionality of hypersphere, the second the flat diffusive landscape.

Put this way, there are two ways of circumventing the problem. One may drop the assumption of local forces and allow the protein to “fall” toward the single native state down a “funnel” created by forces whose range permeate the entire volume. In this case, the “funneled landscape” appears in the spatial coordinates themselves. As we have remarked above, however, candidates for such long range forces do not present themselves. Without recourse to a continuous potential surface created by long-range forces, there is only one other possibility: all diffusive searches take place in low dimensional subspaces of the full configurational space. In this case the “funnel” only appears in highly projected coordinates that follow successive reductions in the dimension of the search space.

To see how this works, we suppose at first that the d ∼ O(10²) dimensions of the full folding space are now arranged sequentially so that diffusive searches in one dimension at a time allow the protein to find “gateways” into the next subspace (we will see how this may arise naturally in a physical way below). For simplicity we assume that the kinetics of each diffusive search is single exponential with characteristic time τ. Since the diffusion is always maintained in some low-dimensional subspace of the full folding space, τ ∼ R²/D for each subspace, so that rather than the exponentially larger This clearly reduces the folding time enormously, signifying that only a tiny fraction of possible states is visited in the search (Dinner et al., 2000). Note that there is no “freezing” of other degrees of freedom required whereas those currently active for the search are operating—they are simply making typically ineffective explorations of a much larger subspace.

How has such a remarkable reduction in folding time been achieved without the use of a spatially “funneled” energy landscape? Of course energetic interactions have been implied, but these have not been of the spatially-extended type. Instead they have served just to keep the diffusive search within the smaller (d − 1) or (d − 2) dimensional space, once the first subdimensional search is over, then within a (d − 3) or (d − 4) dimensional space after the subsequent successful “adsorption” into the still-smaller subspace, and so on. So, when the high-dimensionality of the search space is retained, the energy landscape looks less like a funnel, and more like a series of high-dimensional gutters (Fig. 1). The diffusing particle (representing of course the random search of the protein through its available conformations) does not have to search simultaneously through both the dimensions of the figure. Instead, it exploits the lower energy state of the entire (d − n − 1)^th dimensional subspace to reach it via a one-dimensional diffusion in the (d − n)^th dimension, which it performs first. Partitioning the configurational space in this way, and by providing an attractive “gutter”, relying on local forces alone, to connect one diffusive subspace to the next, creates the advantageous funnel landscape when the high-dimensional structure is projected into a one- or two-dimensional space. Then the many discrete steps of potential energy that arise from the sequence of “hypergutters” appear artificially close, and serve to create a funnel-like projected energy landscape. The disadvantage of the projection is that the subtle origin of the directed search is obscured. In detail the folding energy landscape will look more like a series of low-dimensional terraces (inset to Fig. 1) nested within the full high-dimensional search space.

FIGURE 1.

Part of the d-dimensional folding space containing a diffusive hypergutter projected onto two dimensions. The diffusing particle (representing the random search of the protein through its available conformations) does not have to search simultaneously through both the dimensions of the figure. Instead, it exploits the lower energy state of the entire diffusive subspace of the (d − n − 1)^th subspace to reach it via a one-dimensional diffusion in the (d − n)^th dimension.

How big do the attractive potentials creating the gutters need to be, and what physical interactions might be enlisted to provide them? Their scale is familiar: these potential steps are just the energies required to counterbalance the entropy-loss associated with reduction of the configuration space by one dimension, or degree of freedom. The associated translational space reduces from the order of R to the order of R_N on restriction to the gutter subspace. Completely reversible folding along the route connecting the gutters is produced by rendering the free energy change on entering the gutter zero. This is in turn the case if the binding energies to the gutters are of the order of the entropic free energy gain on making such a restriction to a degree of freedom:

(3)

To quantify ΔU_gutter therefore needs just an estimate of the order of magnitude of the ratio the dimensionless ratio of the sizes of space enjoyed by a degree of freedom in and out of a restricting gutter. As discussed above, a realistic order or magnitude estimate is giving a value for ΔU_gutter of the order of a few (2–4) k_BT (or of order 4–8 kJmol⁻¹) for realistic proteins. Of course one natural candidate for these stabilizing interactions is simply native attractions formed and retained during the folding search. In the limit of zero cooperativity, any native interaction may form at any point, so reducing the dimensionality of subsequent searches. This is the way that classic “Go-like” interactions overcome the Levinthal paradox, and in our high-dimensional search picture corresponds to entire coordinate planes carrying the native stabilizing energy of the corresponding degree of freedom. However, the energy scale of a few k_BT allows other interpretation: we note that the relatively weak, nonnative-like interactions between residues are also candidates for these gutter-stabilizing interactions, and that it is not necessary to invoke the strength of native contacts during the diffusive search. This is especially useful in early stages of folding, when there is no guarantee that significant native interactions will form. Also, the experimental evidence of strong “cooperativity” (Flanagan et al., 1992) implies that native interactions may not in every case create the successive dimensional reduction without the simultaneous presence of many other native interactions. Of course we do not assume that the energy-entropy balance is exact at each step—indeed it is the mismatches in this picture that give rise to roughness in the landscape, but matching within a few k_BT is necessary in most dimensional reductions to avoid unrealistically long folding times.

Furthermore, the evolutionary tailoring of nonnative interactions provides additional “design-space” within which a pathway to the folded state may be coded, but without compromising the stability of the final, native state. For proteins containing N residues, there are of order N² nonnative interactions that may be encountered during a diffusive search, but only of order N interactions that define the native state. This algebraically much larger design-space for the search pathway corresponds to the more numerous set of planes that carry stabilizing interactions in a high-dimensional space than the set of coordinate planes alone (these, we recall, correspond to the use of native interactions alone). A second consequence of this high-dimensional viewpoint is therefore that in some cases it might be fruitful to look for tuned but nonnative, interactions between sections of partially structured chain that stabilize intermediate search spaces. These may or may not be identified as intermediate states, depending on their occupancy lifetime. We need to articulate carefully what is meant in this context by “nonnative”, for this term is sometimes used to refer to indiscriminate interactions. In that sense, the role of nonnative interactions in determining the type and rate of folding pathways is not a new idea (Zhou and Karplus, 1999). But such previous studies have not introduced any specificity, or evolutionary refinement, into the nonnative interactions, and find, significantly, that increasing the strength of such indiscriminate interactions actually slows folding. Our suggestion is that a discriminating design of key nonnative interactions may significantly speed the search for the native state. It is also likely that a significant proportion of such tailored nonnative interactions that we envisage guiding the search will be increasingly near-native as the search proceeds. This will be the more likely as secondary structure forms, as we shall see by the example of a three-helix bundle below.

Gutter-like landscapes have appeared in the literature, and are sometimes apparent even in the two-dimensional representations of projected folding surfaces. Karplus and Weaver (1994), for example, shows a fast folding route of hen lysozyme in which the early formation of β-sheet structure permits the final approach to the native state to proceed in a subspace of reduced dimension. In this case the gutter-like structure survives a projection onto just two dimensions of folding space. In this case the mutual diffusion of the helical and β-sheet portions of the protein is the dynamical process responsible for the gutter-like feature on the reduced folding surface. This example serves also to indicate an important qualification—some dimensions clearly do possess funnel-like landscapes even without a projection onto low-dimensional spaces. Those involved with the formation of a local α-helix or β-turn structures, for example, create subspaces that have real funnel-like features, directed toward the point in the subspace representing the formation of the complete local secondary structure. However, higher-dimensional hypergutters must already have been visited at higher levels in the regions of locally α- and β-secondary structure. We now take a much simpler fold as an example.

AN EXAMPLE: THREE-HELIX PROTEINS

A clean example of a “hypergutter” structure is furnished by the well-studied triple-helix proteins such as the β-domain of staphylococcal protein A (BdpA) (Myers and Oas, 2001) (and see Fig. 2). In this case, the division of the folding landscape is clearly suggested by the formation of the helices (fast “funneled” or “zipper” dimensions; Fiebig and Dill, 1993), and by the diffusive search of the helical domains for their native juxtaposition. Note that we do not require the helix formation to be complete before the diffusive search begins—indeed the formation of native or nonspecific contacts and secondary structure stability will in general be highly cooperative (Fersht, 2000). All that is required is that the zipper dimensions are explored at much faster timescales than the diffusive dimensions. A very simple model has been successful in describing the kinetics of this protein (Myers and Oas, 2001), using the physical abstraction normal to “diffusion-collision” models of the real protein as spherical domains executing a spatial search. Such models have recently been extended to a family of three-helix bundle proteins (Islam et al., 2002). However, in the light of our expectation that fast-folding proteins find their native state via a sequence of stabilized subspaces, the diffusive degrees of freedom of a three-helix bundle might be more accurately represented by angular coordinates defined at the two turns connecting the three helical sections. In fact the diffusive space of internal angles thus defined is exactly three dimensional: between helix 1 and 2 only one angle needs be specified, whereas between helices 2 and 3 we need two more. In addition there are two azimuthal angular degrees of freedom corresponding to the relative twist of helices 1 and 3 relative to helix 2. These torsional degrees of freedom arise as a consequence of the disorder in the loops connecting the helices. The overall space, therefore, reduces to a product space of total dimension 5. So even relatively coarse-grained models of protein dynamics in which the secondary structure is effectively frozen can lead to high dimensional spaces of nontrivial topology. This construction is illustrated as in Fig. 2. The three angular diffusive degrees of freedom are labeled X_i with i = 1, 2, 3. At each point of the periodic three-dimensional space of these coordinates is a torus formed by the two torsional angles φ₁ and φ₂. Since the diffusive coordinates are angles, they exhibit periodicity, and the search space is itself a periodic three-dimensional lattice. In practice the continuously varying angular coordinate may model a more discrete set of more or less favorable packings (Chothia et al., 1981), but the coarse-grained structure of the search space will be the same. In the figure, we illustrate periodicity in the dimension X₂ only. The region of configuration space in which the first two helices are both in contact with the third is shaded, and the native state is represented by the periodic lattice of small spheres. If the shaded “helical contact” region is enhanced by a weak attraction between the hydrophobic sides of helices 1 and 3 (this state becomes a “gutter” for diffusion in the X₂ coordinate), then the search for the native state will typically proceed by diffusion in the three-dimensional manifold of (X₂, φ₁, φ₂) (without contact between helices), followed by diffusion in the two-dimensional manifold of X₁ and X₃ (now with helices 1 and 3 in contact in a way that also stabilizes their relative rotation). As calculated in the last section, the nonnative binding potential of the third helix to the gutter submanifold needs to be of the order of 3k_BT. Providing that the gutter is as attractive as this, then the predicted mean search time (including prefactors and a weak logarithmic term) for the native state is

(4)

rather than the much longer time for the full five-dimensional search without the gutter subspace of

(5)

Examples of experimental evidence for staged diffusive searches in simple proteins has also been observed in the case of cytochrome C, lysozyme (Bai, 2000), and in the B1 domain of protein G (Park et al., 1999).

FIGURE 2.

Three-helix bundle (BdpA on the left) is coarse-grained to a system of three rods. The three angles constituting the diffusive subspaces are labeled X_i for i = 1, 2, 3. The folding space then looks like the periodic cubic lattice on the right (only the X₂ direction is shown periodic, for clarity) with a two-dimensional torus at each point, defined by the two azimuthal angles of rotation of the helices. The attractive gutter is the two-dimensional space spanned by X₁ and X₃ once X₂-diffusion has brought the third helix into contact with the other two. But for small angles X₂, there is a large topological barrier between the “correct” and “incorrect” sides of attachment of the third helix onto the bundle formed by the other two, and identical with the rapid diffusional subspace of X₁ and X₃.

The three-helix example illustrates our general conclusion that searches within diffusional subspaces in protein folding may be accelerated by local, but not necessarily native, interactions between sections of partially structured chain. In the context of the three-helix protein, the necessary nonspecific interactions are those that keep the first and third helices in contact. These include, but are not restricted to, native and near-native hydrophobic side-chain interactions. The consequent mutual but general attraction of the helices for each other permits the final diffusive search for the native state to take place in a two-dimensional space, rather than the full five-dimensional search configuration space of all the diffusive degrees of freedom available to the protein once the secondary structure has formed. Remarkably, just this conclusion was reached recently by experiments on the helical immunity protein Im7 (Capaldi et al., 2002), in which an on-pathway intermediate state was shown by careful mutation studies to be stabilized by nonnative interactions between two of the helices. An additional example of tuned nonnative interactions guiding a folding pathway occurs in the rather larger Phage 22 Tailspike protein (Robinson and King, 1997), where a nonnative disulphide bond controls the folding search. We remark that in both these cases, the stabilized hypergutter provides an arena in which “diffusion-collision” calculations can operate within a molten globule, so constituting a significant generalization of that model to nonspatial degrees of freedom (Zhou and Karplus, 1999).

CONSEQUENCES OF HIGH-DIMENSIONAL SEARCHES

We have identified two general predictions of this high-dimensional view of folding: 1), the sequential diffusive exploration of low-dimensional subspaces favored by fast folding; and 2), the suggestive stabilization of these subspaces by discriminate but nonnative (or near-native) interactions, without recourse to long-range guiding forces. But it has other things to say concerning common experimental measures of even the deceptively simple “two-state” folders. We derive here three further consequences: 3), early-time structure in kinetics; 4), nonnative contributions to Φ-values; and 5), denaturant dependence and the interpretation of “Chevron plot” behavior.

Relaxation functions in folding kinetics

We first take a very simple case: if the nonnative gutter-stabilizing interactions are perfectly balanced with the entropy changes at each stage of the dimension reduction, then the free-energy profile is itself flat, and the d diffusive dimensions form an effective one-dimensional path along which the folding takes place. This is not, of course, to suggest that the path is unique, since: 1), a large fraction of each subdimension may be explored; 2), the path is at each stage reversible; 3), degrees of freedom inessential to the current dimensional reduction are not “frozen” but are freely exploring their configurations; and 4), the nondiffusive “zipper” dimensions describing the local folding of secondary structure are perpetually exploring their own configurational space rapidly and cooperatively with the slow dimensions. Nonetheless, casting the high-dimensional problem into this form shows that a naïve “reaction coordinate” picture can actually emerge from the concatenation of the sequentially-stabilized hypergutters.

An effective one-dimensional coordinate, X, arises from such concatenation of the gutter dimensions of a very high dimensional space, whose initial condition (for a quenching experiment) will favor the high entropy of the early dimensions: every initial state is completely disordered, and the resulting one-dimensional diffusion equation will be supplemented by the approximate initial condition If the native state is represents by a sink for diffusers at X = 1, it is straightforward to calculate the fraction of unfolded proteins after a quench as

(6)

which we plot as a solid line in Fig. 3. For most of its trajectory, this function mimics a single exponential, but with an effective delay from the moment of quench. This arises from the time it takes for the higher subspaces to be filled—at first the native configuration is “screened” by virtue of being buried in a cloud of states of low entropy. The apparent delay would be noticed only in experiments able to capture the very fastest kinetics after a quench.

FIGURE 3.

Log-linear plot of two relaxation functions. Dashed is the single exponential. Solid curve is the decay of an effective one-dimensional folding path created from a high dimensional landscape with flat free energy.

Φ-Values: nonnative contributions

As a second general prediction, and as an example of the specific calculations possible with the model, we examine the important question of Φ-value analysis and its interpretation. When the mutation of a residue gives rise to a value of Φ close to 1, it means that the change in folding rate arising from the mutation is consistent with comparable changes in the transition state and native state energies. This is usually interpreted to mean that the residue in question enjoys the majority of its native contacts at the transition state (Fersht, 2000). However, this model suggests another physical source of positive values for Φ, since it identifies nonnative interactions as potentially crucial in establishing folding rates. For if a residue contributes via nonnative interactions to the stable hypergutter that concludes the dominant (longest) diffusive search, then mutations to that residue will affect the folding rate, even though it does not necessarily possess any native contacts at the transition state. In the hypergutter model, the “transition state” is, by definition, the subspace after that which takes the longest time to search—the rate-determining step.

To make this more precise, we return to the case of the three-helix bundle and calculate the dependence of the total folding rate on the nonnative potential that stabilizes the two-dimensional “gutter” of the final search. Defining a “fugacity” Δ = σ³e^ɛ/kT, where ɛ is the stabilizing energy of the two-dimensional gutter and 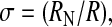the measure of the relative sizes of the two spaces, we expect that as Δ is increased (by increasing ɛ) we take the system from the slower five-dimensional search to the accelerated “3 + 2” dimensional search. By adding the currents of diffusers that find the native state from the 3 + 2- and five-dimensional spaces separately, we find an approximate crossover formula for the folding rate k_f (ignoring weak logarithmic factors):

(7)

where and the slow rate The expression (Eq. 7) also contains, by implication, a prediction of the contribution of the nonnative interactions to the Φ-values of the residues that contribute to it. For, a mutation of any residue will change its contribution to the gutter potential, so

(8)

where n_g is the number of residues that share the burden of providing the nonnative gutter potential ɛ. We have also assumed in the derivation of Eq. 8 that ɛ is also the scale of a single residue's contribution to the stability of the native state—but other reasonable assumptions will only introduce an order-1 prefactor. The functional dependence of Φ_g on the fugacity Δ is actually a rather weakly varying function once the gutter is large enough to produce a reasonable fraction of the maximum acceleration of the folding rate, and tends to a maximum value of 1/n_g (in the limit of high stabilization of the gutter) when see Fig. 4, which shows how both folding rate and Φ_g depend on the gutter potential). This nonnative contribution to Φ will naturally be weak in the two limits of vanishing gutter-potential (when all searches are high-dimensional) and very high gutter potential (when they are always low-dimensional).

FIGURE 4.

Predictions of the folding rate (solid line) relative to the rate of the optimal 2 + 3-dimensional search path, and sum of nonnatively generated Φ-values from residues contributing to a two-dimensional diffusive hypergutter in a three-helix bundle (dashed line). The ordinate is the “fugacity” measure of the attractive potential Δ = σ³e^ɛkT. The value assumed for the spatial reduction σ, is 0.1. The inset contains the expected magnitude of increase in Φ-values with residue index (dashed lines) in a three-helix protein with a two-dimensional kinetic intermediate gutter (e.g., Im7), relative to one without (e.g., Im9). We expect the modifications to be concentrated onto helices 1 and 4, whose mutual contacts stabilize the two-dimensional search space. The solid and dashed bars indicate the experimental results from individual mutations within the helix regions reported in Friel et al. (2003).

Again, a rather general result emerges that may be compared with rate measurements on selectively-mutated systems. For the three-helix bundles, contributions to the stabilizing potential that encourage the terminal helices to diffuse in contact with each other will arise typically from one residue per helical turn, so that n_g ≲ 10 (by counting ∼2 residues per turn on the contact face of a five-turn helix). Since the total predicted nonnative contribution to Φ is of order 1 (from the dimensionless function of Eq. 8 plotted in Fig. 4), this means in turn that mutating these residues might generally give nonnative contributions to their apparent individual Φ-values of order 0.1. The inset to Fig. 4 displays the expected pattern of such enhanced Φ-values against residue index. Remarkably, this is precisely what is seen, again in very recent experiments, on the immunity family of helical proteins Im7 and Im9: the member of the family with an on-pathway intermediate (Im7) (Capaldi et al., 2002) also exhibits increased Φ-values in the appropriate region of the helices 1, 2, and 4 (helix 3 only forms cooperatively with the native state) by just this amount, relative to the protein without the intermediate, Im9 (Friel et al., 2003). Some of the recorded nominal Φ-values exceed unity, which in this and other cases might be a signal that nonnative contributions are serving to enhance them above the native contribution alone. Experimental results are indicated by the solid and dashed bars in the inset.

The magnitude of incremental contributions to Φ from the gutter potentials is restricted to these low values only in very simple topologies such as the three-helix bundle. When key stabilizing interactions succeed in reducing the dimensionality of the search space more drastically, much higher values can result (from differentiation of the higher-dimensional analogs of Eq. 7). In more complex spaces of mutual diffusion of helices and β-turns, values >1 are not unexpected. This approach suggests a natural interpretation of Φ-values >1, such as recorded in acylphosphatase (Chiti et al., 1999), but which do not bear an interpretation in terms of native structure (Fersht, 1999).

The interpretation of nonclassical Φ-values outlined here is closely-related to a recent suggestion arising from some simple lattice Go-type simulations (Ozkan et al., 2001). The simulation also found that kinetic properties are more closely connected with Φ than local “degree of nativeness”. It shares with the present treatment the essential departure from a one-dimensional projection of a transition state, and an identification of the number of permissible pathways, or transition entropy, in controlling the rate of folding.

There are, of course, many caveats attached to such a general calculation. Clearly this coarse-grained level of model cannot pick up specific and discontinuously large shifts of the transition state, which in small proteins will often dominate particular cases. Nor does it anticipate specifically evolved favorable departures from the random imbalances of entropy and energy assumed here, which certainly arise and roughen the landscape, nor does it account for specific behavior from hydration shells. Nonetheless, it underlines the importance for overall folding rates of free-energy structures along a folding pathway, in which successive fluctuations in entropy and energy create a sequence of intermediate states. This type of structure has been investigated theoretically (Wagner and Kiefhaber, 1999), and evidence for its rather general emergence has arisen experimentally very recently (Pappenberger et al., 2000; Sanchez and Kiefhaber, 2003).

Effect of denaturant and Chevron plots

As central a tool to the experimental elucidation of folding kinetics as the protein engineering extraction of Φ-values is the tracking of folding rate with denaturant concentration. As in the case of the Φ-value analysis, this experiment is also usually interpreted as giving information about the transition state (Oliveberg et al., 1995). For example, curvature in the “Chevron plot” that results from a plot of log k_f with [denaturant] is taken to indicate a change of transition state (and by implication the existence of an intermediate). But, as we saw in the last section, some residues may provide dimensional reduction that significantly affects the overall rate via their nonnative interactions, without affecting the transition state itself. In consequence there are contributions to measured Φ-values that arise from this “preexponential” effect. In the same way, if denaturant concentration affects the stability of the low-dimensional search spaces, or gutters, that are principally responsible for controlling the folding rate, then these experiments will also carry signatures of the search-structure.

To make this quantitative, we again examine the consequences of the coarse-grained model for a three-helix bundle that has a two-dimensional subspace stabilized by delocalized hydrophobic interactions along the joining faces of helices 1 and 3. If we assume that the stabilizing energy of the gutter depends on the concentration of denaturant c_d, then the slope of a Chevron plot follows from the folding rate Eq. 7 and

(9)

The first term of Eq. 9 describes the (constant) slope arising from the shift in energy of the transition state, but the second arises from the additional shift to the rate that arises from the shift between five-dimensional and 3 + 2-dimensional searches caused by denaturant. Note that this term has precisely the same form at this level as the nonnative contribution to Φ, whose functional form is given in Fig. 4. Adding denaturant will generally destabilize the gutter, so this term will operate for proteins that in aqueous solution employ the faster 3 + 2-dimensional route (large Δ limit in Fig. 4). As denaturant is increased, Δ will decrease and the maximum in 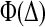will be approached. This will in turn decrease the folding rate beyond the contribution of the first term alone, producing a “rollover” form to the Chevron plot.

An example is given in Fig. 5, in which we assume that the transition state energy depends on denaturant concentration in the same way as the gutter energy, for the sake of illustration. Other assumptions will change the relative size of the rollover effect, but not remove its qualitative presence.

FIGURE 5.

Predictions of the course-grained three-helix bundle model for a “Chevron plot” of ln k_f with the gutter stabilisation energy ɛ (this is plotted as −ɛ since this will be proportional to the usual denaturant concentration). We have taken the dependence of the transition state energy and the gutter energy to be equal: other assumptions will change the relative sizes of initial and final slopes.

RELATIONSHIP TO OTHER MODELS

We stress that the search-space picture explored above is not incompatible with the frameworks or results of the other models discussed in the introduction, but rather serves to show how the apparently alternative models are related, and how high-dimensional features are implicit in all of them. Each emerges from the high-dimensional hypergutter picture when a different projection into a low-dimensional space is applied.

When the flat, diffusional degrees of freedom are projected away onto a reaction coordinate pair, such as R_g and φ_native, then a folding funnel appears, and does so without the presence of any long-range forces. The difference is that, on close examination, the funnel is discrete, or terraced, rather than continuous. Furthermore, it appears when the interactions generating coil-collapse are projected along an ordinate of sequential subspaces, rather than along a spatial coordinate. But when there are many sequential subspaces, an apparently continuous folding funnel appears with all of the features of intermediate states, multiple pathways, etc., ascribed to it (Bryngelson et al., 1995; Dinner et al., 2000) arising in a natural way. Another example of this projection is found in the master-equation approach (Zwanzig, 1995), in which the smoothly funneled high-dimensional energy landscape implies some shaping of the nonnative contacts of the underlying model.

When the projection is orthogonal to one of the later diffusional subspaces, on the other hand, then the same system will appear to map onto a diffusion-collision model. In this case the projection concentrates on the diffusive degrees of freedom one by one, rather than projecting them away into a funnel. The advantage of the hypergutter approach, however, is that it identifies diffusive subspaces in cases where the standard diffusion-collision model does not. The case of diffusion in mutual angular space of helical bundles discussed above is an example, since this occurs within a globule, rather than in the collisional formation of a globule. It also recognizes intermediate cases in which diffusional searches occur simultaneously in high- and low-dimensional spaces, such as a partially-stabilized two-dimensional gutter in the three-helix case, and provides a structure for introducing tailored, rather than indiscriminate, nonnative interactions. The interesting and unexpected prediction of nonnative and positive Φ-values emerges in just this case.

The hypergutter picture is also related to the topomer search model. This is because the rate-determining diffusive searches will in general be completed only when a topological, as well as a spatial, constraint in the final native state is satisfied for the first time. These naturally belong to the levels of coarse-graining at which we treated the helix bundles above.

DISCUSSION AND CONCLUSIONS

We have discussed a conceptual approach to the protein landscape problem that attempts to remain faithful to the high dimensionality of the system. Rather than invoking a continuous energy landscape with long-range forces giving rise to a spatially funneled landscape, we use rather general considerations to point to a high-dimensional structure of “hypergutters”. These structures describe the search for the native state as a sequence of relatively low-dimensional diffusive subspaces. Only spatially-local interactions are required to direct the folding toward the native state in reasonable times. The stabilizing interactions themselves may be either native or nonnative, in the latter case suggesting cases of tailored nonnative interactions. The funneled landscapes then arise through projecting the typically terraced hypergutter structure onto lower dimensional representations. This procedure also suggests a helpful way of conceptualizing links between the apparently divergent views of the folding funnel, collision-diffusion, nucleation-condensation and topomer search models. The rate-determining “gutter” dimensions lie orthogonal to other “zipper” dimensions describing the local formation of secondary structure, that are characterized by a continuous folding funnel.

Looked at another way, our structure is a more detailed examination of the sort of dynamic processes that must be occurring within the “molten globule” phase of protein folding. The formation of the globule itself from the denatured state corresponds in this picture to the first hypergutter in a series. It is clearer in experiment than the subsequent dimensional reductions because it is the only one that makes significant changes to the radius of gyration of the protein.

The high-dimensional search framework is also helpful in understanding how the order in which dimensional reduction takes place is correlated with the tailored interactions that stabilize the searches. In the triple-helix example that we looked at in detail, the nonnative hydrophobic strips that accelerate the final two-dimensional search are “activated” only when the helices themselves form, at least partially (by the formation of some native interactions) and when their axial rotational degrees of freedom align. So the rapid, and dominant, search path coded in the interactions follows the order: helix (partial) formation—three-dimensional search (helix 1 and 3 out of contact)—two-dimensional search (helix 1 and 3 in contact). Other patterns of native and nonnative cooperativity could favor other orderings. For example, a nonnative attraction beween the helices irrespective of their axial orientation would favor a two-dimensional search out of contact before a three-dimensional search in contact as the structure of the five-dimensional search space. Similar structures of search ordering would arise in other systems.

We might note that a pattern of dimensional reduction by nonspecific binding in diffusive searches is a common motif in biology, appearing for example in the search of DNA-binding repressors for their operons (Winter et al., 1981). In this case, the slow search for a specific binding site in d = 3 is substituted for a much more rapid diffusive search in d = 1 (along the DNA) by nonspecific binding of the repressor proteins. In this process too, there is strong evidence that the nonspecific interactions are themselves subtly coded to further speed the search for the binding target.

Several general predictions follow. The first is that special tuning of nonnative interactions may contribute significantly to rapid folding; they stabilize the hypergutter-potentials that keep diffusive search dimensions under control. In the case of helical proteins, candidates for the structure of the gutters are nonspecific contacts of the helices, and the angular, rather than translational, degrees of freedom describing their mutual configurations. In proteins with more complex suctures, other candidates suggest themselves, such as the orientation of helices with respect to β-sheets with which they are in contact in α/β proteins, and the relative orientations of β-turns and partially-folded β-sheets in all-β elements. Very recently, the role of nonnative interactions in stabilizing an on-pathway intermediate, together with a diffusion-collision kinetic route, has been experimentally verified in the case of the immunity protein Im7 (Capaldi et al., 2002). This precisely exemplifies the general mechanism we have suggested, with the additional feature that one of the hypergutters has become so stabilized (and therefore so populated) that it attracts the label of “intermediate state”. Other examples of nonnatively stabilized folding pathways are emerging in both experiments (Robinson and King, 1997) and simulations (Paci et al., 2002b). Perhaps the most remarkable example is the determination by fast kinetic experiments that β -lactoglobulin employs a transient helical motif that is entirely nonnative (Park et al., 1999). By stabilizing a β-turn that otherwise relies on highly nonlocal, and late-forming, structure for its stability, this temporary helix reduces the dimension of the search space for the nonlocal contacts.

Of course, it is not impossible to achieve the dimensional reduction we have outlined by using fully native, rather than nonnative interactions. Such proteins would present a highly bimodal distribution of Φ-values, clustering closely to 0 and 1. A candidate would be acylphosphatase (Paci et al., 2002a) in which the “transition state” strongly constraints the environment of just three residues and the immediate neighbors. In the hypergutter picture, the nine-dimensional search space of these critical regions separately is reduced to three sequential three-dimensional searches by the long lifetimes of the native regions when the remainder of the protein is disordered. One possible advantage of using broadly distributed nonnative interactions, rather than a few local native ones, to stabilize hypergutters, is that the intermediate states are thereby more tightly confined. This in turn may assist in suppressing the pathway to aggregated states, or amyloid formation (Dobson, 2002). This suggestion has recently been made from observations of competing folding pathways in a β -sandwich protein.

As both the sensitivity and time-resolution of kinetic experiments increases, finer details of the intermediate diffusional subspaces in this and other proteins should become equally transparent. Another recent, theoretical, contribution has pointed out that fine-structure of a few k_BT within the transition state on a reaction pathway can accelerate folding (Wagner and Kiefhaber, 1999). As an example of the type of fine-structure predicted, the model contains a natural explanation of the curvature seen in plots of the denaturant dependence of folding rates.

Features of the time-dependent folding curves as functions of temperature or denaturant also follow from the model, including the possibility of an apparent delay before single exponential kinetics set in. It is also possible that “kinetic traps” arise not just from low-energy intermediate states, but from intermediate diffusive subspaces of higher dimension than two, for which the control of dimensionality has been incomplete. This is significant for the topomer search model: we might expect to find departures from the folding time/contact order correlation when, despite sharing the same topology of fold, one protein in a pair has an important diffusional subspace stabilized whereas the other does not. Alternatively, our picture suggests ways of increasing folding times greatly by selective mutations that retain topology and stability of the native state, but destabilize one or more of the on-pathway diffusional subspaces so that intermediate searches are required in d > 3.

The model provides an alternative interpretation of the results of protein engineering analysis, and implies that not all contributions to measured Φ-values at the transition state may arise from native-like interactions. It suggests interpretations for Φ-values of order 0.1–0.2, but also indicates that contributions to larger values (including the nonclassical range Φ > 1) may arise from nonnative interactions with that residue that serve to restrict the folding space. More detailed predictions of nonnative contributions to Φ for the family of bacterial immunity proteins and their mutants are in accord with very recent experiments. Careful double mutant studies would be required to identify such nonnative contributions unequivocally.

Finally this approach suggests that the “kinetic code” that informs the search for the native state may be found in evolved selection of some of the nonnative interactions. The large number of these, of order N times greater than the number of native interactions, make them a likely candidate for information storage, as well as their natural propensity for kinetic control.

The framework and specific examples discussed here suggest useful coarse-grained models of other families of proteins that may be simulated very efficiently, or even approached analytically, as we have done with the three-helix bundles. Strong experimental evidence is currently emerging that supports all of the main predictions of the approach; other experimental tests of the more surprising conclusions are awaited.