Intermediates can accelerate protein folding

Abstract

The effect of intermediates on the rate of protein folding is explored by applying Kramers’ theory of diffusive barrier crossing in the high friction limit. Intermediates are represented as local minima in the transition barrier. We observe that very large or very small additional barriers created by the intermediates slow down the folding process. The rate of folding markedly increases, however, when the additional barriers become >1 k_BT but leave the overall barrier height unchanged. This rate-enhancing effect is caused by a favorable entropic contribution to the free energy of activation, and it increases with the number of intermediates up to a limiting value. From these calculations, we conclude that optimized transition barriers should contain partially folded high energy intermediates.

Various models have been proposed to describe the mechanism of protein folding. The experimental observation of transiently populated, partially folded intermediates in many proteins gave rise to the framework model, which assumes that the native structure is formed in a hierarchical way on a linear pathway involving several consecutive transition states (1, 2). In this model, partially folded intermediates are essential for protein folding by directing the chain to the native state. In theoretical approaches, the folding process is conceived as a movement of molecules on a rough, funnel-like energy landscape starting from the ensemble of unfolded conformations and leading to the native state (3–5). In these models, transiently populated intermediates often represent misfolded structures trapped in local energy minima.

Based on these opposing views, the study of the role of protein folding intermediates has been of major interest in theoretical and experimental work. Recent experimental results provided evidence for the presence of metastable, high energy states located in the transition barrier between the native state and the ensemble of unfolded molecules. Native state hydrogen exchange studies revealed partially unfolded states in cytochrome c (6) and RNase H (7), which are higher in energy than the native protein. Although these intermediates were identified as fluctuations from the native structure under equilibrium conditions, it was postulated that they might represent intermediates on linear folding pathways (6). Local energy minima in the transition barrier also were observed in unfolding reactions of fast-folding proteins that reach the native state without transient population of partially folded intermediates. For the dimeric arc repressor (8) and staphylococcal nuclease (9), a nonlinearity in the denaturant dependence of the free energy of activation for the unfolding reaction (ΔG_u^0‡) was interpreted as evidence for two distinct transition states on a sequential pathway. A similar observation was made for the formation of a helical intermediate in lysozyme folding, which proceeds through a reactive high energy intermediate (10). For chymotrypsin inhibitor 2, a pronounced curvatures in the denaturant dependence of ΔG_u^0‡ was also interpreted as evidence for the presence of high energy intermediates in the transition barrier (11).

The observation of metastable high energy intermediates suggests that the transition barrier between the ensemble of unfolded states and the native protein is broad, including well defined local minima. This is in agreement with recent lattice model simulations in which the observed intermediates were interpreted as “molten globules” (12). Other theoretical models using the capillarity approximation of protein folding also suggest high energy intermediates in the fine structure of folding funnels (13, 14). To investigate the kinetic consequences of partially folded states located on a reaction pathway, we applied Kramers’ theory for diffusion across a potential barrier in the high friction limit (15). The reaction is described by a Brownian motion of a particle in a potential force field. The rate of barrier crossing is calculated via the mean first passage time required to move from the initial well to the bottom of the final well. In this paper, we focus on the question of how the rate of the reaction changes when placing intermediates into the transition barrier. The calculations provided the surprising result that the reaction rate can increase compared to the rate of a single barrier transition without altering the height of the barrier. The acceleration depends on the energy level of the intermediate relative to the energy level of the initial state and on the number of intermediates. These results can be attributed to a favorable effect of the intermediates on the entropy of activation and show that optimized folding landscapes should contain high energy intermediates.

METHODS

We investigated the effect of local minima in an energy barrier on the dynamics of a chemical reaction that was simulated by a Brownian motion of a particle in a potential force field. The dynamics of the barrier crossing process were studied by using the Langevin equation (16)

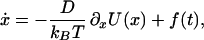1

where x and U(x) denote the reaction coordinate [e.g., number of native contacts or transition coordinate (17)] and the potential of the force field, respectively. D represents the diffusion coefficient, k_B is the Boltzmann constant, and T is the temperature. The thermal motion is represented by the fluctuating force f(t), which is assumed to be a Gaussian white noise with zero mean, 〈f(t)〉 = 0 and uncorrelated amplitudes at different time points, 〈f(t)f(s)〉 = 2Dδ(t − s). In the high friction limit appropriate for protein folding simulations (18), the probability density ρ(x; t) to find the particle at position x after time t is expressed by the Smoluchowsky equation (19):

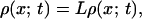2

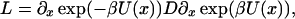3

where L represents the Fokker-Planck (FP) operator and β is 1/k_BT. The mean first passage time (MFPT) t(x) denotes the average time required to cross the barrier starting from any position x of a set of initial states to the final state at x_S. The MFPT is defined by the adjoint FP operator L:

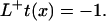4

Solving the equation for t(x) gives

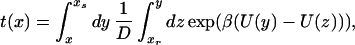5

where x_r and x_S denote the reflecting boundary with ∂_xt(x_r) = 0 and the absorbing boundary with t(x_S) = 0, respectively. In our calculations, the MFPT is independent of the reflecting boundary. The time scale of the reaction is given by the MFPT, which is inversely proportional to the rate of escape k from the initial well at x = −x₀ to the bottom of the final well at x = x_s:

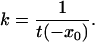6

To determine the folding rates for different scenarios, we computed the mean first passage time for various potentials V(x). All calculations are performed under the constraints that energies are given in k_BT and that the potentials are scaled by a characteristic length of the system, σ₁ and transformed, so that the minimum of the initial well and the final well are at −x₀ = −1 and x₀ = 1, respectively. In this representation, D/2σ is given in 1/s, which was used to normalize the time. The reflecting barrier was located at x_r = −2, and the absorbing barrier was set at x_s = 1. We started the calculation by placing the particle at the position x on the reaction coordinate and calculated the MFPT for arriving at the final state x_S = 1.

For barrier heights ΔU > 3 k_BT, the rate of escape, k, can be approximated by an Arrhenius type of equation (15):

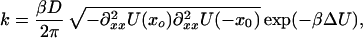7

where x_b and x₀ denote the locations of the top and the bottom of the barrier, respectively. The curvature of the potential at position x is denoted by ∂_xx²U(x).

RESULTS

Effect of a Single Intermediate on the MFPT.

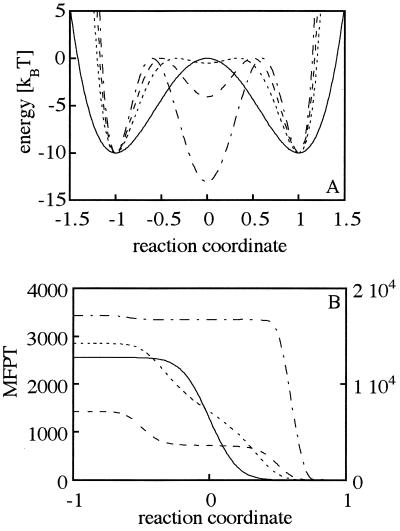
The symmetric double well potential U(x) = ΔU*(x⁴ − 2x²) with minima at x = −1 and x = 1 served as reference (Fig. 1A) where ΔU denotes the barrier height at x = 0. Using a value of ΔU = 10 k_BT to calculate the rate of barrier crossing for the simple two-state process (Eq. 5) yields a mean first passage time of 2,550. The applied barrier height of 10 k_BT corresponds to calculated effective activation energies based on lattice simulations (20). It is also similar to experimentally determined activation enthalpies, which were shown to be ≈15 k_BT (21).

Figure 1.

Effect of a single intermediate on the MFPT of barrier crossing. (A) The potential V = 10x⁴ − 20x² (———) represents the single barrier crossing with a barrier height of ΔU = 10 k_BT. An intermediate at x = 0 is simulated by an x⁶ potential. The first barrier height is kept constant at ΔU₁ = 10 k_BT whereas the second barrier, ΔU₂, is varied. The three representative potentials are given by V1 = 28.4x⁶ − 47.4x⁴ + 9.4x² − 0.5 (ΔU₂ = 0.5 k_BT; ·····), V2 = 47.4x⁶ − 88.8x⁴ + 35.5x² − 4.0 (ΔU₂ = 4.0 k_BT; – – –), and V3 = 76.2x⁶ − 155.6x⁴ + 82.3x² − 13.0 (ΔU₂ = 13.0 k_BT; – · – · –). The reaction coordinate x was normalized and shifted so that the initial and the final state are located at x = −1 and x = 1, respectively. The reflecting boundary is at x_r = −2 whereas the absorbing boundary is at x_s = 1. The MFPT is given in units of the inverse of the diffusion coefficient, which was normalized by the length scale of the system. (B) MFPT for the potentials V, V1, V2, and V3 in dependence of the starting point of the simulation. The lines represent the same scenarios as in A. The values on the left ordinate are valid for potentials V1, V2, and V3. The right ordinate is valid for V3. The MFPTs for starting at x = −1 for the potentials V, V1, V2, and V3 are 2,550, 2,800, 1,480, and 17,000, respectively.

We assumed that an intermediate is represented by an additional well in the potential represented by the polynomial V(x) = ax⁶ − bx⁴ + cx² + d, shown in Fig. 1A. In all calculations, the first barrier height was kept at ΔU₁ = 10 k_BT whereas the relative height of the second barrier was varied by varying the energy level of the intermediate. The reflecting boundary and the absorbing boundary were set to x_r = −2 and x_s = 1, respectively. Fig. 1B shows the MFPT dependence on the starting point x on the reaction coordinate for the three different scenarios. The first case displays a broad barrier with only a minor minimum at x = 0 (ΔU₂ = 0.5 k_BT). It can be regarded as a rough energy barrier for a two-state process for which a mean first passage time larger than that of a double well potential is to be expected (22). Our calculations are in accordance with this result, showing an increase in the MFPT from 2,550 to 2,800 when starting in the initial well. We next simulated a second barrier with ΔU₂ > 3 k_BT. For the case of ΔU₂ = 4 k_BT, we surprisingly observed a decrease in the MFPT to 1,480 for the transition from the initial well to the final well. In the third scenario, the second barrier becomes larger than the first barrier (ΔU₂ = 13 k_BT), which leads to a drastic increase in the MFPT to 17,000 for the overall barrier crossing. Comparing the results for the different scenarios reveals that the broadening of the transition barrier as it occurs for ΔU₂ = 0.5 k_BT is reflected in a reduction of the slope of the MFPT versus the starting point on the reaction coordinate and therefore in an increase of the thermal length scale of the transition (Fig. 1B). In contrast, when a defined local minimum in the transition region exists, the reaction proceeds stepwise, exemplified by the plateau region around the location of the intermediate. When the second barrier exceeds the first barrier, the reaction is drastically slowed down so that the first barrier crossing can almost be neglected.

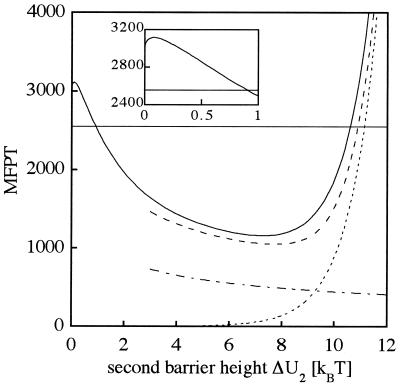
Fig. 2 presents the effect of the second barrier height (ΔU₂) on the MFPT for the overall barrier crossing starting in the initial well at x = −1 and ending in the final well at x = 1. The obtained curve can be divided into three different regions. For low barrier heights (ΔU₂ ≤ 10⁻² k_BT), we observe an increase of the MFPT with increasing barrier height from 2,550 to a maximum of 3,115 (Fig. 2 Inset). It corresponds to the decrease of the diffusion constant for a particle moving in a rough potential compared to that of a smooth potential (22). In the second region (10⁻² k_BT ≤ ΔU₂ ≤ 7.3 k_BT), the MFPT decreases. For ΔU₂ ≥ 1 k_BT, it decays even below the MFPT for a single barrier (2,550) and exhibits a minimum at ΔU₂ = 7.3 k_BT with a value of 1,150. In the third regime (ΔU₂ ≥ 7.3 k_BT), the MFPT increases again because of dominance of the second barrier. The minimum value of the MFPT is effected very little by a change in the overall barrier height. For ΔU₁ = 20 k_BT, the minimum is located at 16.6 k_BT. Accordingly, the maximum effect is observed when the intermediate is 3.4 k_BT, less stable than the initial state compared to an energy difference of 2.7 k_BT for a barrier height ΔU₁ = 10 k_BT. Because the particle is absorbed in the final well, the depth of the latter cannot be essential for the MFPT. This was fully confirmed by our calculations observing only a minor change in the MFPT while lowering the energy level of the final state to a value 30 k_BT below the energy level of the initial well.

Figure 2.

MFPT in dependence of the second barrier height, ΔU₂, calculated by using the Kramers’ ansatz (———), and approximation of the barrier transitions by rate constants. For transitions from the initial state to the intermediate across ΔU₁, the rate is denoted by k₁ whereas the escape rate from the intermediate in the forward and the backward direction is given by k₂. The inverses of the rate constants 1/k₁ (– · – · –) and 1/k₂ (·····) are shown as well as the inverses of the eigenvalues of the overall system 1/λ₁ (– – – –). As a reference, the MFPT of a single barrier crossing is also shown as a horizontal line at MFPT = 2,550. The inset zooms on the second barrier height, ΔU₂, within 1 k_BT. The boundary conditions and the units are described in Fig. 1.

In order to corroborate our results, we used classical reaction rate equations to calculate the rate constants of the system. It implies that both barriers must be >3 k_BT, and it allows the simplification of our model system to a two-stage process. For the triple well potential (Fig. 1A), the transitions across ΔU₁ and ΔU₂ from the initial state to the intermediate and from the final state to the intermediate are k₁ and k₃, respectively. The escape rates from the intermediate state in the forward and backward directions are equal and denoted by k₂.

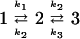This leads to a linear differential equation system for the state probabilities:

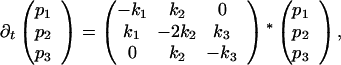8

where p_i(i = 1, 2, 3) denotes the probabilities of the initial state (1), the intermediate (2), and the final state (3). Using the approximation above (Eq. 7), we obtain for the rate constants

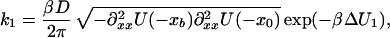9a

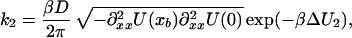9b

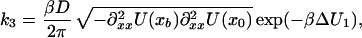9c

where ±x₀ and ±x_b denote the locations of the wells and the barriers, respectively. The dynamics of the reaction is now given by the eigenvalues λ_1,2 of the rate matrix:

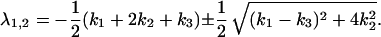10

We consider two different limits for the eigenvalues:

• (i) If ΔU₁ = 10 k_BT and ΔU₂ is small, k₂ becomes much larger than k₁ and k₃ and the eigenvalues reads λ₁ = −(k₁ + k₃)/2 and λ₂ = −(k₁ + 4k₂ + k₃)/2; and

• (ii) by increasing ΔU₂ and therefore decreasing k₂ so that k₂ ≪ k₁ and k₂ ≪ k₃, Eq. 10 yields λ₁ = −(k₂ + k₃) and λ₂ = −(k₁ + k₂).

In the first case, λ₁ is independent of k₂, reflecting the fact that the intermediate can react quickly to either side. Although the escape rate from the intermediate, k₂, is not explicitly in the equation, it is contained in the curvature of U(x), which depends on the energy level of the intermediate. The prefactor 1/2 is required because the transitions k₁ and k₃ are only half way on the reaction coordinate compared to a single barrier crossing. The larger eigenvalue is given by the escape process from the intermediate λ₂ ≈ −2k₂. If, in the second case, the free energy level of the intermediate drops below that of the initial and the final state, the kinetics is given by the transition rates from the initial state to the intermediate, λ₂ ≈ −k₁, and from the final state to the intermediate, λ₁ ≈ −k₃.

In order to compare the Kramers ansatz to the formulation in terms of rate equations, we neglect the backflow of molecules by setting k₃ = 0. The MFPT corresponds either to the lower eigenvalue of the transition matrix,

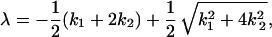11

or it can be determined by using the transition matrix as FP operator L in Eq. 4, yielding

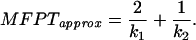12

The two approximations differ slightly in the region in which ΔU₂ reaches its minimum. The influence of ΔU₂ on 1/k₁ and 1/k₂ is shown in Fig. 2. The comparison between MFPT and −1/λ reveals that the system is rather well represented by the simplified model. The behavior of the system in the first regime of ΔU₂ cannot be explained by the simplified model because a prerequisite of the approximation is that the energy barriers are >3 k_BT. Fig. 2 shows the decrease of the MFPT in the second region corresponds to the decrease of 1/k₁ in the simplified model whereas the rise of the MFPT for large values of the second barrier ΔU₂ is caused by the increase in 1/k₂. The relative contribution of the amplitude of the fast phase for the appearance of molecules in the final state is given by λ₁/(λ₁ + λ₂). The results show that the amplitude of the faster reaction becomes significant (>1 %) for ΔU₂ > 6 k_BT. Including the back reaction from the final state to the intermediate in the calculation for the MFPT, the rate-enhancing effect of the intermediate remains conserved. There are observed differences: first, the apparent rate is doubled because it becomes the sum of the forward and the backward rate constants, and, second, there is no decrease of the apparent rate for values of the second barrier height larger than the first one because the system is allowed to accumulate in the intermediate state.

The results obtained with the approximated system were entirely confirmed by computing the spectrum of the FP operator for the triple-well potential. The method we applied uses Hermite polynomials as basis functions and was already extensively studied by Drozdov and Talkner (23). This approach is not confined to barrier heights >3 k_BT as in the approximation above so that two different regimes of the lowest eigenvalue can be identified. First, the inverse of the rate increases because of the roughening of the potential, and, second, it decreases because of the effect of the intermediate. Again, the third regime is not present because the second barrier crossing is not mandatory any more, which results in an accumulation of the molecules in the intermediate state.

Because the first barrier height ΔU₁ is kept constant through all simulations, the decrease of 1/k₁ can be attributed to a change in the preexponential factor in Eq. 9a, which is mainly determined by the curvature of the potential at the bottom of the initial well and the curvature at the top of the first barrier. The curvature of the energy profile increases by lowering the energy level of the intermediate, and, therefore, this preexponential factor increases, too. While approaching the turning point at ΔU₂ = 7.3 k_BT, the rate constant k₂ starts to decrease and dominates 1/λ₁ for ΔU₂ > 7.3 k_BT because of the increase of the second barrier height. This behavior is expected because the second barrier height appears in the exponent of Eq. 9b. A comparison between the Arrhenius equation (Eq. 9b; k = A exp(−ΔE/k_BT) and the Eyring equation (k = p* exp(−ΔG⁺/RT)) (24) for the same barrier crossing reveals that the entropy of the reaction is essentially given by the logarithm of the two preexponential factors, reduced by a term originating from the transmission coefficient, κ, in the prefactor of the Eyring equation

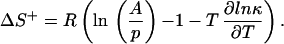13

The difference of the entropy contribution between a transition across the first barrier of a triple-well potential ΔS₁⁺ and the transition to the top of a single barrier ΔS₂⁺ reads

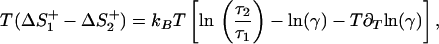14

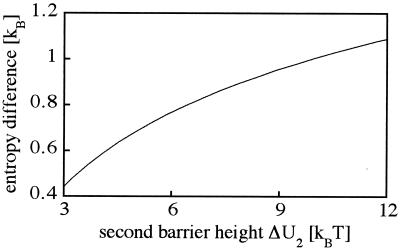
where τ₁ and τ₂ denote the MFPT from the initial state to x = 0 for a potential with and without intermediate, respectively, and γ represents the ratio of the corresponding transmission coefficients, γ = κ₁/κ₂. As shown in Fig. 3, placing an intermediate into a barrier raises the entropy of the first barrier crossing reaction and thus increases the rate constant.

Figure 3.

Increase of the entropy across the first barrier of the double barrier transition relative to the entropy of a half way single barrier crossing. The data were calculated by using Eq. 13.

Effect of Multiple Intermediates on the MFPT.

From the above considerations, the question arises whether the acceleration continues to increase with increasing number of intermediates. In order to simulate multiple intermediates, we used a cosine function with the intrinsic property of equal transition rates between intermediates. For the initial and the final state, x⁴ potentials were singled out, and the positions where the potentials are glued, x = ±(1 − x_B), were determined by equating the curvature of the two functions, which yields for x_B:

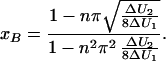15

Then, the potential reads:

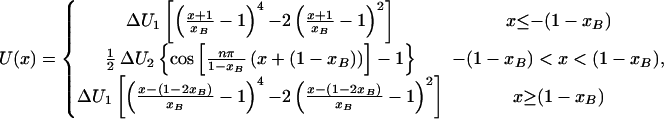16

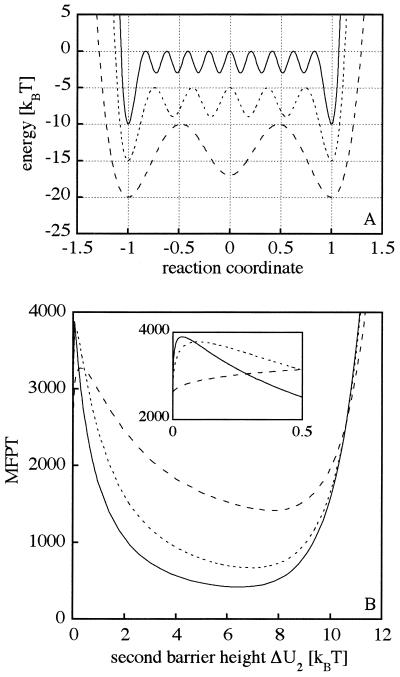
where n denotes the number of intermediates. The potentials for various numbers of intermediates are shown in Fig. 4A. Note the similarity between the MFPT for a single intermediate using a polynomial potential (Fig. 2) and a potential described by Eq. 16 (Fig. 4B). The comparison shows that the characteristic feature of a minimum at ∼7 k_BT is well conserved. Increasing the number of intermediates decreases the minimum MFPT and shifts the minimum to lower values of the second barrier height (Fig. 4B).

Figure 4.

Effect of multiple intermediates on the MFPT. Three examples for 1 (– – – –), 4 (·····), and 8 (———) intermediates are shown in A with energy barriers of ΔU₁ = 10 k_BT and ΔU₂ = 3 k_BT, 4 k_BT, and 7 k_BT, respectively. (B) MFPT calculations depending on the second barrier height, ΔU₂, for the potentials shown in A. The inset zooms on the second barrier height, ΔU₂, within 0.5 k_BT. The boundary conditions and the units are described in Fig. 1.

In terms of rate equations, the linear differential equation system (Eq. 8) for multiple intermediates extends to the form:

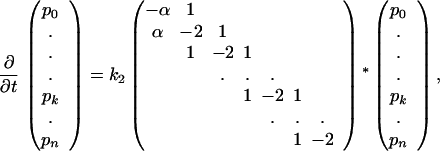17

with α = 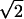exp(−(ΔU₁ − ΔU₂)) = k₁/k₂, and p₀ denotes the probability to find the particle in the initial state where p_i (i = 1 … n) are the state probabilities of the intermediates. Including the final state, the system has n + 2 states in total. Again, the backflow of molecules from the final state to the last intermediate was omitted. In order to trace the question of whether the rate can be increased to infinity with increasing number of intermediates or if there is a limit for the rate, we calculated the eigenvalues of the matrix of Eq. 17, which will be denoted by M. The lowest eigenvalue of M × k₂ determines the kinetics. It can be readily shown by using Eqs. 9b and 16 that k₂ increases proportionally to n². If a limit exists, the lowest eigenvalue of M must be proportional to 1/n². First, we transpose M, which leads to the following eigenvalue problem:

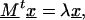18

where λ represents the eigenvalues, and x represents the corresponding eigenvectors. We use the following ansatz for the kth component of the eigenvector:

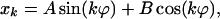19

where A, B, and ϕ are constants to be determined. The ansatz provides N equations for the components of the eigenvector. Eqs. 1 to n − 1 are fulfilled if

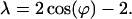20

The first and the last equation yield a homogeneous linear system for the constants A and B:

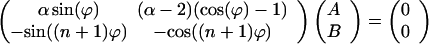21

From the determinant, an equation for the ϕs that are related to the eigenvalues by Eq. 20 can be derived (α ≠ 0)

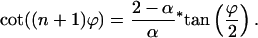22

The lowest ϕ-value, ϕ_min, lies in the interval (0, π/(n + 1)) so that, for large n, tan(ϕ/2) can be approximated by ϕ/2, and the right hand side of Eq. 22 tends to zero in this limit, yielding

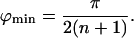23

By expanding cos(ϕ) in Eq. 20 in a Taylor series, the lowest eigenvalue of M is approximated by

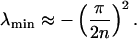24

The result shows that the lowest eigenvalue of the matrix M is proportional to 1/n². As mentioned above, it must be multiplied by k₂ to obtain the apparent rate constant. Because k₂ is proportional to n², the two factors cancel, which proves that the rate enhancing effect becomes limited for large numbers of intermediates.

As shown for a single intermediate, the boundary between a mono- and a biexponential decay is ≈6 k_BT. This threshold is expected to decrease when adding further intermediates into the transition region. Applying the approximation of higher moments of the MFPT, the decay of the initial state can be described by multiexponential kinetics (19). The threshold between single and double exponential kinetics was estimated by the condition that the relative amplitude of the slow phase is <99%. By using the first two moments, the boundary decreases to ≈5 k_BT for eight intermediates.

DISCUSSION

Effect of Intermediates on the Kinetics of Barrier Crossing.

We simulated the process of protein folding in the presence of intermediates with different energy levels by using Kramers’ theory. The results for different scenarios were compared with classical reaction rate theory and with the eigenfunction method of the FP operator by using Hermite polynomials. All methods gave identical results and showed that intermediates can have different effects on the rate of protein folding depending on their energy level (Figs. 1 and 2). If an intermediate has a similar energy as the transition state (ΔU₂ < 10⁻² k_BT), the transition region becomes broader, and the potential becomes rougher. In this scenario, the rate constant decreases, which was already pointed out by Zwanzig (22). By increasing the roughness of the potential, i.e. by stabilizing the intermediate, the rate constant increases with decreasing energy level of the intermediate. Above ΔU₂ = 1 k_BT, the reaction surprisingly becomes even faster than for a single barrier transition with the same maximum barrier height. For a single intermediate, this effect can maximally lead to doubling the rate constant (Fig. 2). The observed rate-enhancement is, however, more pronounced when furnishing the barrier with multiple intermediates (Fig. 4). With 16 intermediates, we obtained a 10-fold increase of the rate constant. Representing the system in terms of rate equations, we were able to show that the rate-enhancing effect runs into saturation for large numbers of intermediates. When the intermediates become too stable, the rate constant decreases again because of the prevailing effect of the increase of the additional barriers (Figs. 1 and 2). The reaction becomes slower than for a single barrier crossing when the energy of intermediates drops below the level of the initial state.

The rate-enhancing effect of intermediates is attributable to a broadening of the transition region in combination with the appearance of defined local minima in the transition barrier. This statement is strengthened by considering the conformational entropy of the forward reaction by using the stationary probability density ρ(x) to find a molecule in the interval [x, x + dx] on the reaction coordinate:

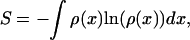25

whereby the stationarity is achieved by reinjecting the absorbed molecule in the final state to the initial state. Again, three different regimes are recognized. If an intermediate mainly increases the broadness of the barrier, the initial state becomes more localized (the variance of the Gaussian distribution decreases), which corresponds to an increase of the order of the system and therefore results in a decrease in entropy. While lowering the energy level of the intermediate, the probability density is smeared out along the reaction coordinate, leading to an increase of entropy and, therefore, to an increase of the rate constant. When the intermediate is too stable, the wells for the initial state and for the intermediates become very narrow and thus localize the molecules in these minima leading again to a decrease in entropy.

Implications for Protein Folding.

Theoretical models suggested that folding proceeds on a funnel-like energy landscape and that experimentally observable transiently accumulating partially folded states often represent intermediates trapped in local energy minima. It was suggested that the direct folding process may occur through metastable high energy intermediates (14) and that the rate-limiting step for the folding process is mainly represented by an entropic barrier (5), which is in contrast to experimental observations on the energetics of the transition state. Experimentally observed barriers for protein folding contain both enthalpic and entropic contributions at room temperature. Comparison of the barriers of several small fast folding proteins showed that the enthalpy of activation is about 10 kcal/mol for all proteins when the folding reactions are compared at identical protein stability (21). The origin of these barriers is unclear but a strong temperature dependence of the activation parameters and an observed enthalpy/entropy compensation suggests major contributions from protein/solvent interactions (25).

Our results on the effect of rugged transition barriers on the rate of kinetic processes suggest that the enthalpic barriers encountered in protein folding are most efficiently crossed when well defined local minima exist in the transition region. It seems very likely that the high energy intermediates detected by native-state hydrogen exchange and by nonlinearity in the denaturant-dependence of ΔG_u^0‡ of many two-state folders represent such local minima in the transition region and thus are evidence for an optimized transition barrier in a protein-folding reaction. The role of these intermediates might be both to direct the ensemble of unfolded states on a small number of well defined pathways and to increase the rate of folding by efficiently crossing the energy barriers caused by a favorable entropic effect. One should keep in mind that our model assumes a well defined saddle region between the ensemble of unfolded states and the native state. A quantitative extension to more complex energy surfaces will be a difficult task.

The presented results raise the question of a useful definition for the transition state of protein folding reactions. It was suggested that the transition state should be defined as the ensemble of conformations with the probability P = 0.5 to go to the native state (17). In our model with local minima in the transition barrier, which is in agreement with many experimental and theoretical observations, this state would be represented by a local minimum for an odd number of intermediates rather than by the top of the barrier (Fig. 1B). Because our results show that the folding rates are strongly influenced by the shape of the transition barriers, it is necessary to characterize the properties of transition state regions rather than thinking in terms of a well defined transition state.

Because we made no assumption on the nature of the energy barrier and merely assumed that the barrier crossing has to take place in the high friction limit of Kramers’ theory, the results are applicable to all kinetic processes in solution that encounter energetic barriers. A similar effect of metastable intermediates on rate constants has been discussed qualitatively by Knowles and coworkers for enzyme catalysis (26). Our calculations show that enzymes could facilitates barrier crossing by creating local minima in the barrier region on binding to the substrate and thus accelerate the reaction without changing the height of the energy barriers.

ABBREVIATIONS

FP

Fokker-Planck

MFPT

mean first passage time