The Elementary Mass Action Rate Constants of P-gp Transport for a Confluent Monolayer of MDCKII-hMDR1 Cells

Abstract

The human multi-drug resistance membrane transporter, P-glycoprotein, or P-gp, has been extensively studied due to its importance to human health and disease. Thus far, the kinetic analysis of P-gp transport has been limited to steady-state Michaelis-Menten approaches or to compartmental models, neither of which can prove molecular mechanisms. Determination of the elementary kinetic rate constants of transport will be essential to understanding how P-gp works. The experimental system we use is a confluent monolayer of MDCKII-hMDR1 cells that overexpress P-gp. It is a physiologically relevant model system, and transport is measured without biochemical manipulations of P-gp. The Michaelis-Menten mass action reaction is used to model P-gp transport. Without imposing the steady-state assumptions, this reaction depends upon several parameters that must be simultaneously fitted. An exhaustive fitting of transport data to find all possible parameter vectors that best fit the data was accomplished with a reasonable computation time using a hierarchical algorithm. For three P-gp substrates (amprenavir, loperamide, and quinidine), we have successfully fitted the elementary rate constants, i.e., drug association to P-gp from the apical membrane inner monolayer, drug dissociation back into the apical membrane inner monolayer, and drug efflux from P-gp into the apical chamber, as well as the density of efflux active P-gp. All three drugs had overlapping ranges for the efflux active P-gp, which was a benchmark for the validity of the fitting process. One novel finding was that the association to P-gp appears to be rate-limited solely by drug lateral diffusion within the inner monolayer of the plasma membrane for all three drugs. This would be expected if P-gp structure were open to the lipids of the apical membrane inner monolayer, as has been suggested by recent structural studies. The fitted kinetic parameters show how P-gp efflux of a wide range of xenobiotics has been maximized.

INTRODUCTION

Multi-drug resistance transporters are clinically important because of their ability to render cells resistant to many chemotherapeutic agents, such as anticancer drugs and antibiotics (Borst and Elferink, 2002; Gottesman, 2002; Poelarends et al., 2002; Ambudkar et al., 2003). In addition, it has become increasingly clear over the past decade that some mammalian multi-drug resistance transporters also play an important role in the absorption, distribution, and elimination of drugs and xenobiotics, and may be responsible for clinically important drug-drug interactions (Lown et al., 1997; Schinkel, 1998; Goh et al., 2002). Binding and transport of substrates by P-gp (the P-glycoprotein product of the human MDR1 gene) has been intensely studied, providing important insights into the structure and function of the protein (Gottesmann and Pastan, 1993; Senior et al., 1995; Ambudkar et al., 1999, 2003; Loo and Clarke, 1999; Hrycyna, 2001; Borst and Elferink, 2002; Schmitt and Tampe, 2002; Seelig and Gatlik-Landwojtowicz, 2004). The catalytic cycle of P-gp and its conformational changes have been studied using purified P-gp remixed with lipids or reconstituted proteoliposomes (Sharom et al., 1993; al-Shawi et al., 2003; Loo et al., 2003; Urbatsch et al., 2003). There is a dose-dependent response between ATPase activity and transport activity in cells (Ambudkar et al., 1997) and reconstituted P-gp proteoliposomes (Sharom et al., 1993; Omote and al-Shawi, 2002).

Any model of the P-gp catalytic cycle must be tested against a rigorous kinetic analysis of transport activity for P-gp expressed in a physiologically relevant cell system and, eventually, in vivo. To date, kinetics analyses of P-gp transport have been limited to steady-state Michaelis-Menten approaches (Stein, 1997; Ho et al., 1995; Doppenschmitt et al., 1999; Kuh et al., 2000; al-Shawi et al., 2003; or compartmental analyses (Demant et al., 1990; Ashida et al., 1998; Ito et al., 1999), neither of which can prove transport mechanism.

Our experimental system was the confluent monolayer of MDCKII-hMDR1 cells that overexpress P-gp (Evers et al., 2000; Tang et al., 2002a,b; Tran et al., 2004). This system was chosen because it is a physiologically relevant model for P-gp in tissue, and it involves no biochemical manipulations to measure transport. Substrate can be added to either face of the polarized cell monolayer, apical or basolateral, and transport to the other chamber is monitored. A potent P-gp inhibitor was used to independently measure passive permeability through the cell monolayer. The P-gp substrates used were amprenavir, an HIV protease inhibitor; quinidine, a Na⁺ channel blocker; and loperamide, an antidiarrheal drug. These drugs were chosen because they are good P-gp substrates and show different mass balance problems (Tran et al., 2004). Furthermore, amprenavir shows no evidence for transport saturation (Polli et al., 2001; Bentz et al., unpublished data), rendering the standard Michaelis-Menten analysis of P-gp transport useless. So amprenavir provided a challenging test case.

A minimal comprehensive mass action model for P-gp transport through a confluent cell monolayer must include the known kinetic barriers to transport. This means that several parameters must be fitted simultaneously, and each has a wide range of potential values. This generates a very large ensemble of initial parameter guesses to be fitted against data. Thus, a hierarchical algorithm for fitting was required to get fits in a reasonable time. This computationally intensive approach is the only way to analyze the kinetics of a system with three or more important elementary parameters. We have applied this approach successfully to the kinetics of membrane fusion (Bentz, 2000; Mittal and Bentz, 2001; Mittal et al., 2002; Bentz and Mittal., 2003). Nevertheless, the first hypothesis of this study was that the data from the experimental system would be consistent enough and the kinetic analysis robust enough that a small compact set of parameter values yielding best fits could be found at all.

The mass action model for P-gp transport is precisely the same as used by all prior studies, i.e., the Michaelis-Menten reaction. Our analysis is more complex because we fit all of the parameters of this reaction. Past work has just used the Michaelis-Menten (or Eadie-Hofstee or Wolf-Hanes) steady-state equations to fit the data. For some data, e.g., the ATPase activity of P-gp, the steady-state equations appear to work well enough. The ATPase of P-gp is in the water, like a soluble enzyme. For other data, e.g., transport through a confluent monolayer of cells, we have found that these equations yield very inaccurate predictions for the elementary parameters (Bentz et al., unpublished data). This is why we focus only on the elementary parameters here.

There is a tendency to view a more complicated analysis of a well-known problem as a way of curve fitting, with enough parameters to make the fit look better. However, aside from the rate constants of the Michaelis-Menten reaction and the density of efflux active P-gp, every other parameter we introduce was fitted to independent data with the minimum flexibility possible. The rate constants of the Michaelis-Menten reaction and the density of efflux active P-gp had to be fitted simultaneously, just as would be the case for a soluble enzyme when the active enzyme concentration is not known. To impose the steady-state equations onto such data would be a choice based upon assumptions. A rigorous fitting is always better and is now possible.

Our findings suggest new hypotheses and, at the same time, support the simplest picture for a transporter whose job is to remove a wide range of amphipathic xenobiotic compounds from epithelial cells as rapidly as possible. First, it seems clear that the primary selective pressure on P-gp function was to maintain a wide substrate range, which means that the binding constants for nearly all substrates should be weak. This is what we found for all three drugs. In fact, were it not for the substantial partition coefficients of these drugs into lipid bilayers, their membrane concentrations would be too low to show significant efflux. Second, for P-gp to acquire the substrate rapidly, the on-rate to P-gp from the inner apical monolayer should be fast. All three drugs had very large association rate constants, suggesting that lateral diffusion of the drug through the lipid bilayer was the sole rate-limiting step. Third, the P-gp efflux rate constants for quinidine and loperamide were about the same as the currently known maximal rate of ATP hydrolysis by P-gp, whereas that for amprenavir was substantially larger. We also note that the combination of weak binding to P-gp and ATP hydrolysis-limited efflux requires that efflux of a substrate into the apical chamber occurs only after many tens of thousands or even millions of substrate molecules have visited the binding site and returned to the inner apical monolayer.

The fitted value of the density of efflux active P-gp, was substantially smaller than values measured by quantitative Western blots in similar, but not identical, cell lines. We believe the reason is not due to misfolded P-gp or substantial intracellular sequestration, but rather due to the architecture of the microvilli of the apical membranes of these cells. We speculate that efflux into the apical chamber happens only from the P-gp at the tips of the microvilli. Drug exiting from P-gp at the base of a microvillus would undergo a long random walk, involving many encounters with the same or a nearby microvillus and the P-gp therein. The quantitative Western blot gives whole cell P-gp estimates, whereas our kinetic analysis estimates only the amount of P-gp that actually succeeds in effluxing the drug directly into the apical chamber. This hypothesis is being studied currently.

MATERIALS AND METHODS

Materials

Amprenavir and GF120918 were from GlaxoSmithKline, USA (Research Triangle Park, North Carolina). Loperamide was from Sigma-Aldrich (St. Louis, MO) and quinidine from Fisher Scientific (Hampton, NH). ³H-Loperamide (10 Ci/mmole) and ³H-amprenavir (21 Ci/mmole) were custom-synthesized by Amersham Pharmacia Biotech (Little Chalfont, England). ³H-Quinidine (20 Ci/mmole) was from ICN Biomedical (Costa Mesa, CA). Dimethylsulfoxide was from Sigma-Aldrich. Dulbecco's modified Eagle's medium (DMEM) was from MediaTech, VWR (Herndon, VA). Transport medium (DMEM with 25 mM HEPES buffer, high glucose, l-glutamine, pyridoxine hydrochloride, without sodium pyruvate, and without phenol red) was from Gibco (Carlsbad, CA). Cholesterol and porcine brain lipids were from Avanti Polar Lipids (Alabaster, AL). Transwell 12-well plates with polycarbonate inserts were obtained from Costar, (Acton, MA). Ultima Gold scintillation cocktail was from PerkinElmer Life Sciences (Boston, MA).

Cell line and culture conditions

The Madin-Darby canine kidney cell line, which overexpresses human MDR1 (MDCKII-hMDR1), was purchased from the Netherlands Cancer Institute (Amsterdam, The Netherlands). Cells were split twice a week and maintained in culture medium (DMEM supplemented with 10% fetal bovine serum, 50 units/ml penicillin and 50 μg/ml streptomycin). Cells were kept at 37°C in 5% CO₂.

Transport assays

Cells were seeded in 12 well plates at a density of 200,000 cells per insert and grown for 4 days in culture medium. Preliminary results using higher and lower plating densities suggested that this density was optimal with respect to obtaining transport stable confluent monolayers at 4 days. After many preliminary experiments, the data presented here for amprenavir were taken from cell passages No. 32 and No. 33 (50–90 μM), No. 34 (100 μM) and No. 36 (1 and 10 μM). For quinidine, No. 36 and No. 37 were used, and for loperamide, No. 39 and No. 40 were used. Cells were given fresh media 1 day after seeding.

Before the experiment, culture medium was removed and cells were preincubated for 30 min with either transport medium alone (see above) or transport medium supplemented with 2 μM GF120918 to inhibit P-gp. Transport of a range of concentrations of amprenavir, loperamide, and quinidine across the confluent monolayer of cells was measured in both directions, i.e., apical to basolateral (A > B) and basolateral to apical (B > A) in the presence and absence of GF120918. For incubations in the presence of GF120918, the inhibitor was added to both chambers; 0.5 μCi/ml of ³H-amprenavir, ³H-quinidine, or ³H-loperamide was added to each respective drug concentration to allow quantification of transport from donor to receiver chambers by liquid scintillation counting. In addition, ¹⁴C-mannitol (0.75 μCi/ml) was added to monitor cell monolayer integrity. At the indicated time points, 25 μL samples were taken from both donor and receiver chambers, mixed with 10 ml of Ultima Gold scintillation cocktail and counted using a Hewlett Packard Liquid Scintillation Counter. The first time point taken was after 6 min, and we used these data at the starting point for fitting. This eliminated the need to correct for some drug binding to the Costar Transwell apparatus and other initial transient effects (Tran et al., 2004). All simulations accounted for the 25 μL aliquots, since loss of volume was not negligible, especially in the apical chamber (Tran et al., 2004).

Cell stability and substrate metabolism

Tran et al. (2004) showed that the stability of the cell monolayer and plasma membrane with respect to passive and active transport was not affected by the prolonged exposure times to amprenavir for at least 6 h. It was also shown that metabolism or decomposition of substrates was insignificant for all drugs on this timescale using Radio HPLC (Agilent Technologies, Palo Alto, CA).

Liposome preparation

Three liposome preparations were used to roughly mimic the lipid compositions of the relevant monolayers of the plasma membrane (Hill and Zeidel, 2000), while not exceeding ternary mixtures:

1. The apical membrane outer monolayer mimic was a (1:1:1) mixture of phosphotidylcholine/sphingomyelin/cholesterol, denoted PC/SM/chol.

2. The basolateral membrane outer monolayer mimic was a (2:1) mixture of phosphotidylcholine/cholesterol, denoted PC/chol.

3. The plasma membrane monolayer, facing the cytosol, mimic was a (1:1:1) mixture of phosphotidylserine/phosphatidylethanolamine/cholesterol, denoted PS/PE/chol.

Lipid mixtures were dried into thin lipid films in round bottom flasks (Buchi Rotavapor R-200, Brinkmann Instruments, Herisau, Switzerland), and freeze-dried overnight on a Flexi-Dry MP freeze-dryer (Kinetics, Union City, CA). Lipid films were suspended in phosphate buffered saline pH 7.4 (Gibco), freeze-thawed in methanol over dry ice for 20 cycles and heated to 35–40°C, and stored at 4°C overnight. Extrusion was done with a Lipex thermal extruder (Northern Lipids, Vancouver, Canada) through two 0.08 μm Nucleopore membranes for at least seven cycles at room temperature. For the PC/SM/chol liposomes, the first three cycles were run at 65°C. Sizes of liposomes were measured by a NICOMP 380-Submicron Particle Sizer (NICOMP, Santa Barbara, CA). The average diameters for all compositions were 100 ± 30 nm. The amount of lipid recovered after extrusion was determined by the absorbance reading of rhodamine-PE, added to each lipid mixture at 0.1 mol %. Lipid recovery as measured by rhodamine-PE was 80–82%.

Equilibrium binding study

Binding of drugs to liposomes was determined by equilibrium dialysis using a 20-cell equilibrium dialyzer (Spectrum, Fort Lauderdale, FL) and the Spectra/Por 4 membrane (Spectrum), which has a 12–14 kD molecular mass cutoff. The partitioning of 10 μM of each drug (amprenavir, loperamide, and quinidine) into 10 mM liposomes was examined. Each half of the Teflon cells received equimolar concentrations of the cold drug. The half cell with liposomes received an additional 0.25 μCi/ml of radiolabeled drug. The cells were allowed to equilibrate in a 37°C water bath, and samples were taken from both half cells at 8 h. Preliminary studies showed that partitioning was independent of drug concentration (for the ranges used in this work), lipid concentration (5–10 mM) and time after 6 h. At the indicated time points, 25 μL samples were removed from the donor and receiver chambers, mixed with 10 ml of Ultima Gold scintillation cocktail and analyzed by a Packard TriCarb 3100-RT liquid scintillation counter.

Partition coefficients were calculated as K = Cm/Cw, where Cw was the mol of drug per liter of aqueous buffer and Cm was the mol of drug per liter of lipid using the average specific volume of 1.6 μL/μmol of total lipid (Chen and Rand, 1997). The equilibrium partition coefficients measured are shown (see Table 2). The molecular basis for differences is under investigation. However, they do show that for association time constants of seconds, the time constants for release from the liposomes is on the order of minutes, roughly validating our assumption of the partition equilibrium over the hourly time course of transport.

TABLE 2.

Drug equilibrium partition coefficients (v/v) with LUV

	PC/SM/chol (1:1:1)	PC/chol (2:1)	PS/PE/chol (1:1:1)
Quinidine	68 ± 7	112 ± 9	717 ± 28
Amprenavir	148 ± 12	205 ± 22	228 ± 17
Loperamide	671 ± 23	1045 ± 122	3138 ± 624

Extruded 0.1 μm LUV of the prescribed lipid composition at 10 mM total lipid concentration was incubated with drug at 10 μM concentration for 6 h. Partition coefficients (mol drug per liter of LUV bilayer/mol drug per liter buffer) were calculated as described in Materials and Methods. Preliminary studies established that equilibrium was reached under these conditions. Mean ± SD of four replicates for each drug are shown.

Numerical integrations

We used the stiffest integrator in MATLAB, ode23s (The MathWorks, Natick, MA). Other MATLAB integrators, although faster, were not accurate enough at the later times of simulations. The time required for the MATLAB subroutine fminsearch to find a local minimum depends on the tolerances of numerical integration and minimization. Empirically, for our data, we have found that setting the relative and absolute tolerances in fminsearch to 10⁻⁶ was an adequate compromise between speed and accuracy. The coefficient of variation, CV, is used to quantify the goodness of fit. CV is defined as the root mean-square error between the data points for a given drug concentration and the simulation generated by MATLAB, divided by the initial substrate concentration in the donor chamber for that data set, to normalize over all the drug concentrations. Termination of fminsearch occurs when the routine detects a local minimum in CV. This gives a vector of best-fitted parameters from the initial guess. That is, the grid of initial guesses generates a set of “best fits”, one for each initial guess. As always, some “best fits” are better than others (Bentz, 2000; Mittal and Bentz, 2001).

KINETIC MODEL OF TRANSPORT ACROSS A CONFLUENT CELL MONOLAYER

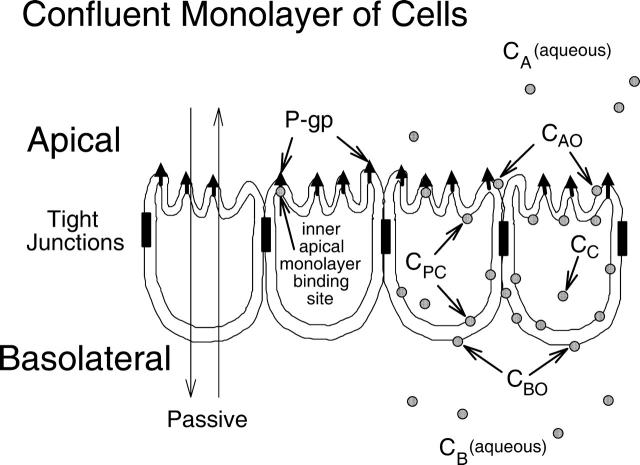
MDCKII-hMDR1 cells polarize with the basolateral membrane attached to the polycarbonate filters (Butor and Davoust, 1992; Tran et al., 2004). Fig. 1 is a cartoon of a confluent cell monolayer, with P-gp (upward arrows) expressed on the apical surface. The apical and basolateral chambers are kept separate by the tight junctions. Van Meer and Simons (1986) showed that the tight junctions of the MDCK cell monolayer kept the apical membrane outer monolayer lipids separate from the outer basolateral membrane monolayer lipids while there was significant lateral diffusion throughout the inner plasma membrane, i.e., between the apical and basolateral sides. Our results quantitatively confirm their results.

FIGURE 1.

Model of a confluent cell monolayer, with the apical membrane on top and the basolateral membrane on the bottom, where it binds to the polycarbonate insert. Passive permeability occurs in both directions. P-gp expressed on the apical membrane transports drug from the inner apical membrane monolayer into the apical chamber. There are two kinetic barriers to transport (see Fig. 3 and accompanying text) flip-flop across the basolateral and apical membranes, with P-gp catalyzing the latter step. The concentration of drug in the apical and basolateral chambers, C_A and C_B, are measured, while the concentration of drug in the inner plasma membrane, C_PC, and the cytosol, C_C, are predicted as part of the data-fitting process.

Active transport by P-gp occurs vectorially, with substrate binding to a site on P-gp within the apical membrane inner monolayer and with efflux into the apical chamber (Sharom et al., 2001; Borst and Elferink, 2002; al-Shawi et al., 2003). We can measure the concentration of substrate in the apical chamber, denoted C_A, and the basolateral chamber, denoted C_B. However, the concentration of substrate in the inner plasma membrane in contact with the P-gp binding site, denoted C_PC, cannot (yet) be measured rigorously in real time. Furthermore, C_PC is related to the drug concentrations in the aqueous cytosol, C_C, and in the basolateral and the apical membrane outer monolayers, i.e., C_BO and C_AO, respectively. All these concentrations are variables of the mass action model and fitted according to the measured values of C_B and C_A over time.

Our aim is to construct a kinetic model for the overall transport process, which contains the minimum number of essential steps to adequately characterize the whole process at a molecular level. The novelty of this model lies primarily in having P-gp as an explicit chemical species, rather than embedded within the Vmax of the Michaelis-Menten analysis or represented by a “rate constant” between compartments. This makes the surface density of efflux active P-gp an explicit variable of the model, to be fitted exhaustively along with the elementary rate constants. Since the fitted range for the surface density of efflux active P-gp should be the same for all drugs, we have a concrete benchmark for the validity of the mass action model and the fitting algorithm.

Another novel element of our analysis was the method for extracting the transport due to P-gp from the total transport, i.e., passive permeability plus active transport. We explicitly fit passive permeability coefficients when P-gp is fully inhibited and then use those rate constants in the fitting of the total transport, when P-gp is active. All prior work has simply subtracted the passive transport data curve from the total transport data curve, and defined this difference as that due to P-gp active transport alone. This would be correct only if transport were irreversible, which is certainly not the case for our experimental system. For example, when there is active transport and the basolateral chamber is the donor, then at any time there is a greater concentration of substrate in the apical chamber than with passive permeation alone. Therefore, there is greater backflow back to the basolateral chamber. The subtraction of passive data from total data underestimates the P-gp transport because backflow is ignored.

Because of these novel approaches in both passive and active kinetics, a fairly detailed description is needed here. First the passive transport model will be constructed, followed by the active transport model. The bottom line for the analysis of passive permeability is to accurately remove this transport from the total transport, so that P-gp mediated transport is accurately estimated. To keep the terminology straight, a glossary is included in the Appendix.

The passive permeation kinetic model

In Tran et al. (2004), we derived an exact solution for the passive permeation across a single permeation barrier, and used this equation to fit the passive permeability coefficient for drugs across the confluent MDCKII-hMDR1 cell monolayer in the presence of the P-gp inhibitor. That is, we measured the overall passive permeability coefficient for permeation from the basolateral chamber to the apical chamber, denoted P_BA, and for the opposite direction, denoted P_AB. We included the possibility of substrate loss by a first order process, e.g., binding to receptors, the experimental apparatus, hydrolysis and/or metabolism. Although the cell monolayer clearly has at least two permeation barriers, the apical and basolateral membranes, the characterization as through a single barrier is adequate for most applications, since intracellular concentrations are not measured. Here we must expand the treatment of passive permeability to include explicitly the apical and basolateral membranes, since P-gp picks up drug from the apical membrane inner monolayer (Sharom et al., 2001; al-Shawi et al., 2003).

Our major assumption was that the substrate concentration in an aqueous compartment is at equilibrium with the lipid monolayer facing the compartment, i.e., we can use a partition coefficient to relate the two concentrations. This is a reasonable assumption for this system, where transport occurs on an hourly timescale. For example, Abreu et al. (2003) have shown that the fluorophor Rhodamine Green-tetradecylamide associates with lipid bilayers within a few seconds. The assumption of partition equilibrium reduces the number of equations to be fitted by about a factor of two. This assumption also means that drug recycling is maximal, since drug effluxed into the apical chamber is immediately equilibrated with the outer apical monolayer.

Equilibrium dialysis binding of drugs to intact cells cannot estimate these individual cell membrane monolayer partition coefficients very well because these drugs are all permeable enough to bind throughout the cell within an hour. Therefore, we used 0.1 μm extruded unilamellar liposomes (LUV) whose lipid compositions mimic, in a very simple way, the lipid compositions of the respective membrane monolayers. For example, we use the partition coefficient for the LUV composed of sphingomyelin/phosphatidylcholine/cholesterol (SM/PC/chol, 1:1:1) to relate the concentration of substrate in the apical chamber, C_A, which we can measure, to the concentration in the apical membrane outer monolayer, C_AO, which we can't measure. We use PC/chol (2:1) as a mimic for the outer basolateral monolayer and phosphatidylethanolamine/phosphatidylserine/chol (PE/PS/chol, 1:1:1) as a mimic for the inner plasma monolayer, i.e.,

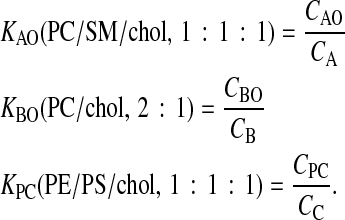(1)

K_BO, K_AO, and K_PC denote the respective partition coefficients, while the LUV lipid compositions used are given in parentheses. Obviously, cell membranes have much more complex compositions (Hill and Zeidel, 2000), but we did not want to exceed ternary mixtures or use exotic lipids.

The moles of drug in contact with the basolateral side of the B > C kinetic barrier are V_BC_B + V_BOC_BO, due to the assumption of partition equilibrium. The standard permeability equation to predict the passive transport across the basolateral membrane is

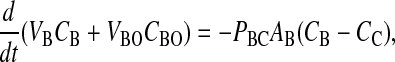or

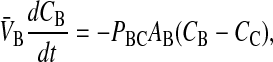where

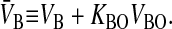(2)

V̄_B is simply the whole basolateral volume accessible to the substrate, since K_BOV_BO is the aqueous equivalent volume of the lipid in the basolateral side. A_B denotes the area of the basolateral outer membrane monolayer capable of permeation. Note that P_BCA_B/V̄_B has the units of a first-order rate constant, s⁻¹.

We assume that the passive permeability coefficient is symmetric across the basolateral membrane into the cytosol, i.e., P_BC = P_CB. It is also the case that substrates can permeate through cell monolayers between the cells, through the tight junctions, which is called paracellular permeation (Ho et al., 2000). Measured passive permeability coefficients contain both terms, and perhaps others. For all our experiments, radiolabeled C¹⁴-mannitol was used to estimate paracellular permeability coefficients, which were <3% of the passive permeability coefficients measured for amprenavir, quinidine, and loperamide (Tran et al., 2004).

Following the same logic as for Eq. 2, the other mass action equations for passive permeability are written as

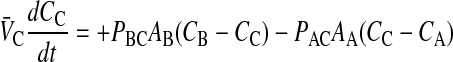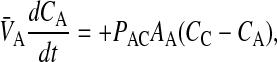where

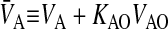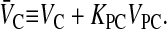(3)

As with the basolateral membrane, we assume that passive permeability across the apical membrane to the cytosol is symmetric, i.e., P_AC = P_CA. However, the permeability coefficient across the apical membrane, P_AC, need not equal P_BC. We cannot measure these permeability coefficients directly in the cell monolayer, but we will account for their effect on total transport as shown below.

When V_DC_D(0) is the total mols of drug initially added to the donor side, whether basolateral or apical chamber, then mass balance equations require at all times that

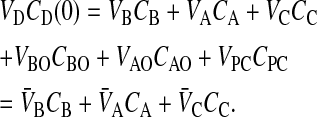(4)

The passive mass action equations, Eqs. 2 and 3, satisfy mass balance trivially.

In Tran et al. (2004), we showed that loss of substrate, defined as drug leaving the donor chamber and not arriving in the receiver chamber in a timely fashion, could be accounted for simply and quantitatively if loss were first order, at least between the experimental time points. Of the three drugs tested, only loperamide showed loss. The loss was not due to metabolism or degradation/hydrolysis (Tran et al., 2004), but rather due to binding to cells or the experimental apparatus. Most importantly, the loperamide loss was first order. The point of this correction was not to discover the mechanism of loss, but rather to calculate the correct passive permeability coefficients when mass balance is a problem. We can add the substrate loss term, using k_v to denote the first order rate constant of loss:

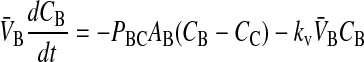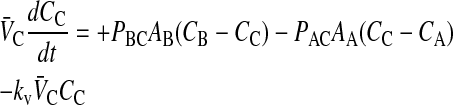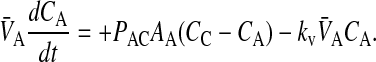(5)

Whether drug loss occurs in the aqueous phase and/or in membranes is irrelevant, due to the equilibrium partition assumption.

When loss is first order, we can independently fit the value of the loss rate constant using the average drug concentration over the entire system, including cell plasma membranes. This is defined by

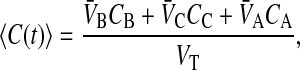where

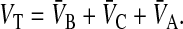(6)

V_T is the effective whole system volume, including partitioning into the cell membranes.

We can now show that the average concentration depends only upon the drug loss rate constant, i.e.,

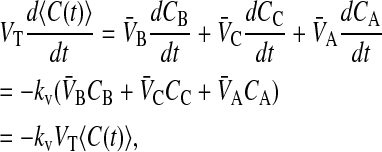(7)

using Eqs. 5 and 6. The solution to Eq. 7 is

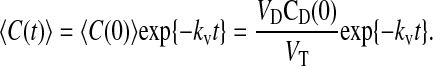(8)

Thus, we can also measure total loss of substrate and correct the estimation of passive permeability coefficients for that loss, as done in Tran et al. (2004).

Finally, we need to consider the issue of estimating membrane areas and the fitting of permeability coefficients. In the passive permeation experiment, we fit the product of the permeability coefficient and the area of membrane access. In the preceding equations, A_A and A_B denoted the area of the apical and basolateral membranes capable of permeation. The question is: what area do we use? A morphometric electron microscopy study has suggested that the total basolateral and apical membranes of MDCKII cells grown on polycarbonate filters, as we use here, have roughly the same area, and that this area is ∼8 times the cross-sectional area of the cell (Butor and Davoust, 1992). However, the actual membrane area of access for permeation is unknown, e.g., due to apical membrane invaginations and basolateral membrane tight binding to the filter support.

It is customary to use the area of the insert onto which the cells grow as the reference for accessible area, i.e., the accessible area would be some multiple of this cross-sectional area. We have assumed that both membranes had areas of access two times that of the cross-sectional area of the insert, i.e., like spheres attached at their equators by the tight junctions. The reason for this choice was simply to align the reported values of the permeability coefficients. Typically, permeability coefficients are fitted assuming a single barrier equation, as was done in Tran et al. (2004). The same data fitted by a single static barrier model of area A or by a two barrier model, each barrier with an area of 2A, will yield the same value for the passive permeability coefficient. Since the bottom line of the passive permeation kinetic analysis is to subtract its contribution to the total transport, this approach is accurate and avoids the confusion of having the same specific permeability represented by two different numbers. Once the issue of membrane access area is resolved, which will not be simple, corrected passive permeability coefficients can be easily predicted from our fitted values. This choice has no effect on the fitting of the active transport parameters.

The second choice we made was how to estimate the values of P_BC and P_AC, given that we could not make intracellular measurements. We fit overall P_BA and P_AB coefficients using the one barrier model (Tran et al., 2004), i.e., the average value across both cell membranes in the B > A or A > B directions, respectively. Depending upon drug, Tran et al. (2004) found that P_BA and P_AB did not have to be time independent or equal. The overall passive permeability barrier of the cells depended upon which side was the donor. To correct the total transport for the contribution by the passive transport, which is the goal in the first place, we have chosen to set P_BC = P_BA and P_AC = P_AB. This allows the donor face to dominate the estimated permeation of drug into the cell, as found in Tran et al. (2004). If the passive permeability coefficients were not constant in time, which was the case for quinidine and loperamide, then we best fit the values for each time interval measured and used an “appropriate” value for each time interval for fitting the active transport parameters, as explained in detail below.

The active transport kinetic model

P-gp is generally assumed to follow the standard Michaelis-Menten reaction (Stein, 1997; Ho et al., 2000; Ambudkar et al., 2003). This reaction takes place within the apical membrane inner monolayer:

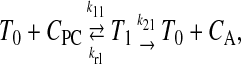(9)

where T₀ is the empty transporter, C_PC the substrate in the apical membrane inner monolayer, T₁ is the transporter bound by substrate, and C_A the substrate after efflux into the apical chamber.

The nomenclature used here, e.g., k₂₁, is read as the second reaction for site 1. The first reaction is association to P-gp and the second reaction is efflux into the apical chamber. This nomenclature was developed to allow for the possibility of two substrate binding sites, such as has been suggested by equilibrium dialysis binding for P-gp (Martin et al., 2000) and for the bacterial multi-drug resistance transporter LmrA in Lactococcus lacti (van Veen et al., 1998). More sophisticated models, including explicit ATP hydrolysis steps, have been proposed (Senior et al., 1995; van Veen et al., 2000; al-Shawi et al., 2003), based upon equilibrium dialysis binding studies, ATP hydrolysis, and/or Michaelis-Menten steady-state kinetic analysis. We shall see for P-gp that the rate constant of association, k₁₁, is so large that whether there is one site or two roughly identical sites, both sites would be filled or empty. Functionally, this means that the number of sites is not kinetically relevant for single substrate measurements. Future experiments examining substrate competition can test the number of binding sites directly. Because of the plan to examine competition, we have retained this notation. In addition, functional two-site kinetics may apply to other multi-drug resistance transporters.

When we append the active transport mass action reaction to the passive permeability kinetics, we obtain the comprehensive kinetic equations for P-gp mediated transport:

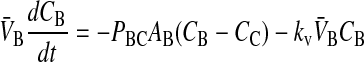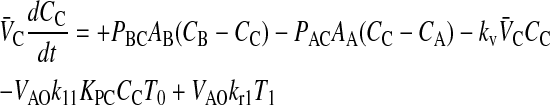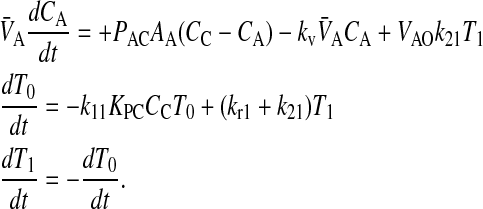(10)

Since we assume that the transporter captures the drug from the apical membrane inner monolayer, the relevant volume is V_AO and the relevant partition coefficient is K_PC. It might appear that the volume for the receptor is 2V_AO, since the transporter crosses the membrane, but its active site is thought to be restricted to the apical membrane inner monolayer (Sharom et al., 2001; al-Shawi et al., 2003), which technically has the volume of V_AO. With respect to fitting parameters, the difference is not significant.

There are several parameters here, but all are important and necessary to obtain realistic estimates for the three elementary rate constants (k₁₁, k_r1, k₂₁) and the density of efflux active P-gp in the apical membrane, denoted T(0). Again, passive permeability coefficients and rate constants for loss are fitted in a separate experiment using the potent P-gp inhibitor GF120918. Partition coefficients are estimated using liposomes whose compositions roughly mimic the cell membrane monolayers.

We can now complete the description of correcting the total transport curve for the effects of passive permeability and loss of drug. Tran et al. (2004) showed for amprenavir that the fitted passive permeability coefficients, P_AB and P_BA, change up to the first half hour and then stabilize. There was no significant loss of amprenavir, but the calculated values for k_v were noisy for the first hour. The other drugs showed different transients for P_AB, P_BA, and k_v. Since the purpose of these fittings was to remove the passive permeability from the total transport, we needed to take these transients into account.

We assume that the passive permeability is the same whether or not P-gp is inhibited by GF120918, so the P_AB and P_BA values are taken in the presence of GF120918. It is nearly impossible to test this assumption, but it is reasonable. During active transport, the true system average drug concentration would have to include the term for T₁, since that is drug-bound to P-gp. When that is done in Eq. 6, then Eq. 7 would contain dT₁/dt and the sum gives the same answer as Eq. 8. Thus, we can estimate the k_v when P-gp is active using Eq. 8. For loperamide, this makes a difference, since Tran et al. (2004) showed that loperamide loss was substantially greater in the presence of GF120918. The reason for this is not known yet.

To incorporate the transients of passive permeability coefficients and k_v values requires a choice. One extreme would be to use all of the individual measurements for P_AB, P_BA, and k_v for each time interval. This would be correct if the passive permeability transients measured in the presence of the P-gp inhibitor GF120918 were exactly the same as in its absence, where we measure total transport. This seems unlikely and we did not want to be fitting the noise of the experiment. The other extreme would be to use the time average of all of the individual measurements for P_AB, P_BA, and k_v. This would largely ignore the transients.

Our approach was to use the individual values until they roughly stabilized and then use the time average from that point on for fitting the remaining time intervals. However, we did not want to make the decision for the stabilization times for each data set, since that would introduce an additional fitting decision. So we used the times found in Tran et al. (2004). For both amprenavir and quinidine, we used individual values for k_v up to 1 h, and the average k_v from all points after 1 h. For the passive permeability coefficients, amprenavir was stable at half an hour, whereas quinidine showed changes for 3 h. For loperamide, both passive permeability coefficients and drug loss coefficients changed for the first 3 h before stabilization.

ALGORITHM FOR HIERARCHICAL EXHAUSTIVE DATA FITTING

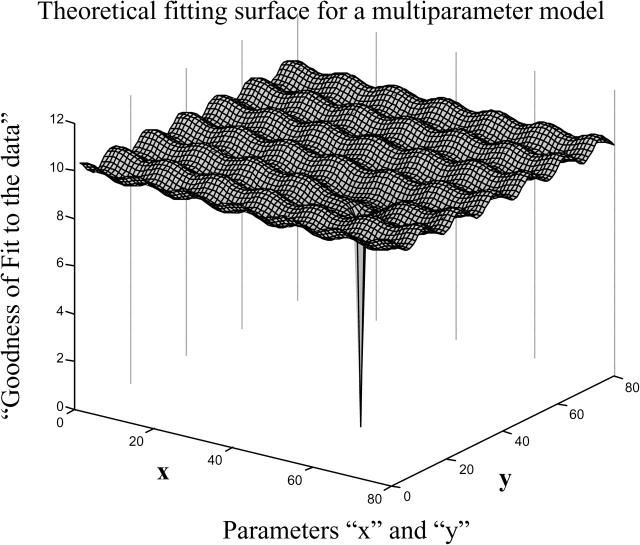
We now use the fitted passive permeability parameters to find all active transport parameter vectors (T(0), k₁₁, k_r1, k₂₁) that will best fit all of the data for total transport. We start by creating a grid of initial vectors of parameter values that spans all possible values for each of the four active transport parameters. The problem of searching a large multi-variable parameter space for kinetic best fits is there are likely to be very many peaks and valleys in the CV surface, just like the protein folding problem (Chan and Dill, 1998). Search routines like fminsearch stop in the first valley encountered. To illustrate this fitting surface, we use a cartoon with two parameters and the oversimplified fitting surface in Fig. 2, since the true fitting surface for our problem depends upon four parameters and cannot be clearly visualized. The initial parameter vector grid we set up can be represented by the grid on the fitting surface, as projected up from the kinetic parameter (X, Y) plane. For each initial vector, MATLAB numerically integrates the kinetic equations, Eq. 10, computes the CV between the data and the simulation, and then the MATLAB function fminsearch adjusts the parameters until a best local fit to the data is obtained. MATLAB's fminsearch stops when a local minimum in CV is reached within the tolerances of the Nelder-Mead simplex (direct search) method on which this minimization routine is based. The consensus answer we seek will be the cluster of fit vectors that are best fits for all drug concentrations used.

FIGURE 2.

The general problem of exhaustive multi-parameter fitting is illustrated by a simple theoretical fitting surface over just two fitting parameters, because our model has four fitting parameters and cannot be clearly visualized. Because the fitting surface can have many local minima, a very wide initial net of initial conditions must be cast to assure that the global best fits are not missed. The real shape of this surface depends upon the model and the data.

To find the best fit, i.e., the “deepest valley”, the initial grid point must be within the “foothills” of the valley with the deepest well, shown by the deep spike in Fig. 2, which is why an exhaustive search of the entire parameter space is necessary. Furthermore, and just as importantly, the exhaustive search will also determine whether there is more than one “deepest” valley, i.e., two or more widely separately sets of parameters that fit the data equally well. A rule of thumb appears to be that if the model is appropriate, i.e., realistic but not overspecified, then as the fitting hierarchy proceeds, the parameter space volume that fits the data best will decrease until a small compact space is found. We call this box the consensus fits, wherein any vector within the consensus space will fit the data for all of the different substrate concentrations equally well. Achieving smaller volumes than we reach should be possible, but the computation time would be much longer. We are studying this problem.

Initial parameter grid

For the rate constants, we begin with plausible ranges, but these parameters are unconstrained, so that fminsearch in MATLAB can move out of the initial range if there is a local minimum for the CV out there. The rate constants are only constrained to be positive.

The initial range for the association rate constant, k₁₁, was 10⁶–10¹² M⁻¹s⁻¹, the upper bound probably being above the lipid lateral diffusion control (Keizer, 1987; Molski et al., 1996; Hinterdorfer et al., 1997). The initial range for the efflux rate constant, k₂₁, was 1–10⁴(s⁻¹), which contains the range of currently known ATP hydrolysis rate constants (Urbatsch et al., 2003; Loo and Clarke, 2000). The initial range for the dissociation rate constant, k_r1, was actually fixed by the substrate binding to P-gp, given by the binding constant K_B = k₁₁/k_r1, which will start in the typical range of 10²–10⁶ M⁻¹ . Again, these are just starting ranges and the fitting was not constrained to remain within these ranges.

The amount of P-gp per cell has been estimated for other cell lines using quantitative Western blots (Ambudkar et al., 1997), but not for the cells we use. Since the expression levels of P-gp depends upon many factors, including some that are unknown at this time, we believe that it is important not to fix this parameter. We refer to T(0) as the density for efflux active P-gp. The terminology used is not meant to imply that other P-gp in the cell are misfolded or sequestered within the cell, but our kinetic analysis only measures those P-gp that efflux drug directly into the apical chamber. We will refine this idea below.

On the other hand, the surface density for any membrane protein has physical constraints. It must be less than the surface density of proteins known to closely pack on the membrane surface, e.g., influenza hemagglutinin (HA) on a viral surface, which is a homotrimer with three transmembrane domains and densely covers the viral surface. In comparison, P-gp has 12 transmembrane domains, which clearly constrains P-gp to a smaller surface density than influenza HA. For computational convenience, T(0) was expressed in mols P-gp/L(apical membrane inner monolayer), but this can be converted to P-gp/μm² (of apical membrane) simply by multiplying by 1.2 × 10⁶, which assumes a 2 nm thick acyl chain region in the apical membrane inner monolayer. For example, the surface density of influenza HA on the virion is ∼16,000/μm² (Mittal et al., 2002), which would mean that T(0) < 16,000/1.2 × 10⁶ M = 0.013 M. We have chosen a minimum surface density for P-gp of four orders of magnitude smaller, which amounts to ∼1 P-gp/μm², which is very conservative. Thus, the range for T(0) has been fixed as 10⁻² M > T(0) > 10⁻⁶ M. It will turn out that the surface density of efflux active P-gp in these cells was smaller than the estimates of P-gp densities obtained from other cell lines using Western blots. In the Discussion, we will suggest why this might be a perfectly consistent result.

These generous ranges are necessary to make sure that all possible parameter vectors that can fit the data are discovered. The problem then becomes that the ranges are so large that the initial search space is huge and cannot be covered in a brute force way, i.e., starting at one end and going to the other end in some linear fashion. Each of the parameters has a theoretical range of at least four orders of magnitude. On a unitary log scale, each parameter generates nine values per decade, i.e., 1–9, with four decades per parameter, yielding (9 × 4)⁴ = 1.7 × 10⁶ initial vectors. Each initial vector was the starting point for a local best fit, which requires at least 5 min on a 2.4 GHz PC. Brute force would require more than 15 years of computation per drug concentration. So we must build a fitting algorithm.

The hierarchical fitting algorithm

Previous experience in fitting kinetic equations for liposome aggregation and fusion (Bentz and Nir, 1981; Bentz et al., 1983), showed that the fitted ranges for the “forward” parameters were not likely to be very sensitive to the reverse reaction. Since those differential equations were similar to the mass action kinetic equations for the Michaelis-Menten reaction, we took that as the first step of the fitting algorithm. That is, as a start, the “forward” B > A data could be fitted using only the “forward” parameters T(0), k₁₁, and k₂₁, with k_r1 fixed at zero. This reduces the first search to three parameters instead of four, which saves a lot of time since fitting time increases roughly by the power of the number of parameters being fitted. Once the forward parameters were fitted to reduce their ranges, then the “reverse” A > B data could be fitted using k_r1 and the reduced range of values found for T(0), k₁₁, and k₂₁. Of course, if this assumption were wrong, the fit to the A > B data would find very different parameter ranges for T(0), k₁₁, and k₂₁. We shall see that this approach works very well and reduces the numbers of initial grid vectors from more than a million to only a few thousand, requiring <2 weeks of computation per drug concentration. The algorithm also produced an interesting artifact, which we will discuss and discard below.

“Model data” as a control

An extremely important control for fitting several parameters to a kinetic model is to simulate “model data” and subject that “model data” to the same analysis as the real data. “Model data”, for the Michaelis-Menten mass action model we have used, was simulated using a parameter vector from the “center of the box” of the consensus vectors for the amprenavir data, as obtained at the end of our data-fitting process. If the transport of amprenavir by P-gp is modeled adequately by the one-binding site Michaelis-Menten reaction, then subjecting the “model data” to the same fitting algorithm must yield the same basic results as observed for the amprenavir data.

RESULTS

The passive and active transport of 90 μM amprenavir across the MDCKII-MDR1 cell monolayers is shown in Fig. 3. The passive permeability was determined in the presence of 2 μM GF120918, a potent inhibitor of P-gp (Hyafil et al., 1993; Polli et al., 2001; Tran et al., 2004), shown by solid symbols. The nmol transported is symmetric over time, i.e., the same for B > A and A > B, which would be expected for a static passive barrier. That was not the case for quinidine and loperamide (Tran et al., 2004). The open symbols show the total transport, when P-gp is active (i.e., without GF120918), with triangles showing the P-gp mediated activation of transport in the B > A direction and the inhibition of transport in the A > B direction. For amprenavir, the passive permeability coefficients were symmetric and constant in time after ∼15 min, i.e., P_BA = P_AB ≈ 200 nm/s. Amprenavir had no significant loss of substrate, i.e., k_v < 1 × 10⁻⁶ s⁻¹.

FIGURE 3.

Passive and active transport of amprenavir across the monolayer of confluent MDCK cells is shown by nmol in the receiver chamber over 6 h when the donor side begins with 90 μM amprenavir. The solid symbols show passive permeability across the cell monolayer when the basolateral chamber was the donor side B > A (♦) and when the apical side was the donor A > B (•). The active transport by P-gp was completely inhibited by preincubation with 2 μM GF120918 added to both chambers. The open symbols show the effect of P-gp on transport of amprenavir across the cell monolayer, which occurs in the absence of GF120918. The fact that the activation of transport in the B > A direction (⋄) over the passive transport by P-gp, indicated by the up arrow, is greater than the inhibition in the A > B direction (O), indicated by the down arrow, proves that there are only two kinetic barriers to transport, as explained in the text.

Above, we have claimed there are only two kinetic barriers for transport of the drugs studied here, i.e., the basolateral and apical membranes. This means that a third kinetic barrier between the apical and basolateral chambers, e.g., through the cytosol, is kinetically irrelevant for these drugs. We can now prove this assertion.

Relative to passive permeability, the activation of B > A transport by P-gp, i.e., from the basolateral chamber to the apical chamber, illustrated in Fig. 3 by the length of the arrow aimed up, was always greater than the inhibition of A > B transport by P-gp, i.e., from the apical chamber to the basolateral chamber, illustrated by the length of the arrow aimed down. Remarkably, this simple test is diagnostic for there being only two barriers to active transport. If there were an additional kinetic barrier between the basolateral membrane inner monolayer and the apical membrane inner monolayer, e.g., substrates following a path through the cytosol, then the predicted shape of Fig. 3 would be just the opposite. The activation arrow would be shorter than the inhibition arrow (simulations not shown). The reason for this is that the additional barrier slows access of substrate to P-gp from the basolateral side, reducing activation, whereas transport from the apical side is hardly affected, since drug escape from P-gp into the apical membrane is rate limiting anyway. Other drugs have shown this “two-barrier” shape (Troutman and Thakker, 2003). Of course, this diagnostic can identify substrates for which there is a third barrier.

Thus, it appears that the nearly all of B > A transport of amprenavir, as well as loperamide and quinidine, follows the path of binding to outer basolateral monolayer, flip-flopping across the bilayer, and then rapid lateral diffusion within the lipids to the apical membrane inner monolayer, where it binds to P-gp, in a highly reversible way, and is effluxed out into the apical chamber. A > B transport is simply the opposite.

Passive and active transport data were collected for 100, 80, 70, 60, 50, 10, and 1 μM amprenavir, just as was done for 90 μM amprenavir in Fig. 3. We did not use the data from 1 and 10 μM amprenavir for fitting parameters and they became a tester data set at the end. The first fitting step is a coarse fitting the B > A data using only the “forward” parameters, with k_r1 = 0. We set up a grid of initial vectors covering a four-order of magnitude range for each parameter. The grid and tolerance is shown in Run I of Table 1. All possible combinations of the three parameters were used as initial vectors, 729 in all.

TABLE 1.

Hierarchical fitting ranges, tolerances, and outcomes

	Data fitted*	Integration tolerance†	Points per decade‡	Initial range for each parameter
Run				T(0) (M)	k11 (M−1s−1)	k21 (s−1)	KB (M−1)
I Forward coarse	B > A	10−8	2 (1 and 3)	10−6–10−2	107–1011	10°–104	kr1 ≡ 0§
II Forward fine	B > A	10−9	3 (1, 2, and 5)	Same as Run I	Same as Run I	Fixed by fit of k21T(0) from Run I	kr1 ≡ 0§
III Forward last	B > A	10−10	9 (1, 2,…, and 9)	3 × 10−6–4 × 10−4	108–1010	Fixed by fit of k21T(0) from Run I	kr1 ≡ 0§
IV Reverse low	A > B	10−7	2 (1 and 3)	3 × 10−5–3 × 10−4	108–1010	Fixed by fit of k21T(0) from Run I	102–106
V Reverse last	A > B	10−8	9 (1, 2,…, and 9)	4 × 10−5–4 × 10−4	109–1010	Fixed by fit of k21T(0) from Run I	Fixed by outcome of Run IV

^*Transport data direction. B > A means basolateral donor and apical receiver. A > B means apical donor and basolateral receiver.

^†Tolerance setting in MATLAB for numerical integration in ode23s for both relative error and absolute error. Settings lower than 1 × 10⁻¹⁰ did not converge in a reasonable time, i.e., >1 h per fit. Tolerance for the fminsearch routine, which determines when the fit is “close enough”, was always set to 10⁻⁶ for both TolX and TolFun tolerances.

^‡Numbers in parentheses are those chosen within each decade tested. For example, in Run II for the decade of 10⁻³ for T(0), the initial points were 1 × 10⁻³, 2 × 10⁻³, and 5 × 10⁻³.

^§All B > A data were fitted assuming irreversible binding of drug to P-gp, i.e., k_r1 ≡ 0. The A > B data were used to fit K_B, and refit k₁₁ and T(0) to affirm the validity of separating the fits.

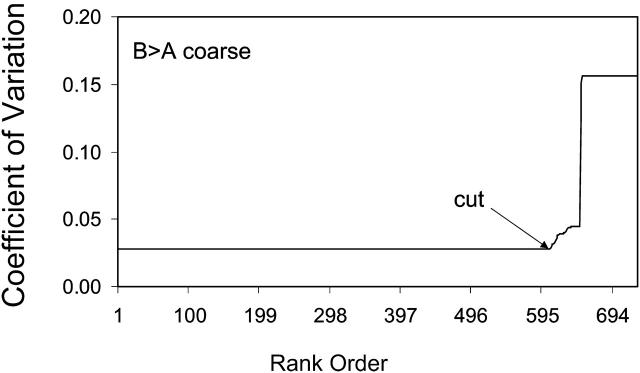
Separate fitting runs were carried out for each substrate concentration. Then, for each concentration, the fitted parameters for each of the 729 fits were sorted by the coefficient of variation. As an example, Fig. 4 shows the CV as a function of CV rank order for 90 μM amprenavir, which is the substrate concentration we will follow through the analysis; ∼609 of the fits had the same CV ∼ 0.03, which gives a very good fit visually. The larger rank orders had progressively worse fits. Thus, we discarded those fits with CV > 0.03.

FIGURE 4.

Coefficients of variation between the data, CV, and the 729 Run I fits to the 90 μM amprenavir data are plotted in a rank order, from best, CV ∼ 0.03, to worst, where CV > 0.4. Fits with a CV < 0.05 are visually very good. The rank-ordered first 609 fits essentially give the same curve, but from a wide range of parameters. Subsequent rank-ordered fits tracked increasingly worse fits, because MATLAB fminssearch was stuck in a local minimum. Fits to the right of the cut were discarded.

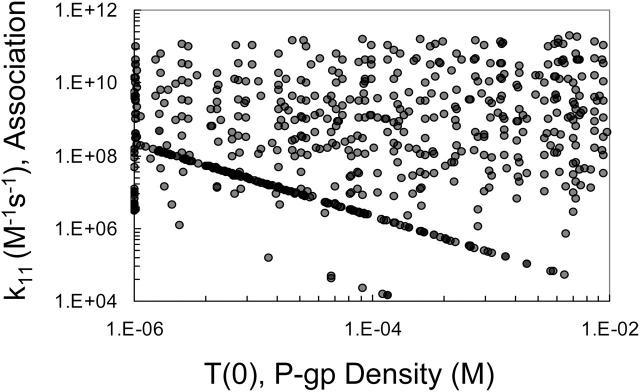
We will now look at the remaining fitted parameters to see if good fits to the data, for 90 μM amprenavir in the example being followed, reduce the fitting volume or show any correlations that would reduce the number of parameters to be fitted. Fig. 5 shows the plot of the fitted values for P-gp density, T(0), and the association rate constant, k₁₁. Fits are found over the entire input range, showing that there has been no reduction in the fitting volume. For some amprenavir concentrations, including 90 μM, a few correlated points were observed forming a straight line with the negative slope of almost exactly −1. These points are an artifact of the fitting algorithm applied to the Michaelis-Menten mass action reaction, which we will address in detail below with the last forward fit, i.e., Run III.

FIGURE 5.

Fitted pairs of the association rate constant, k₁₁, and P-gp density, T(0), for 90 μM amprenavir remaining after the cut in Fig. 4 are graphed here. The range of the parameters has not been reduced in the fitting and they are uncorrelated, except for a small trend line at the bottom, which is examined in Fig. 8.

Fig. 6 shows the plot of the fitted values for P-gp density, T(0), and the efflux rate constant, k₂₁. Although it is clear that there has been no reduction in the fitting volume, the more startling point was that fitted values for these two parameters are essentially perfectly correlated. Each fitted value of T(0) defines the fitted value of k₂₁ ≈ 0.01/T(0) s⁻¹. Thus, these two parameters need not be independently fitted. This is shown as the outcome of Run I in Table 1.

FIGURE 6.

Fitted pairs of the efflux rate constant, k₂₁, and the P-gp density, T(0), for 90 μM amprenavir remaining after the cut in Fig. 4 are graphed here. The possible range of these parameters has not been reduced in the fitting, but there is essentially complete correlation. Thus, for 90 μM amprenavir, the product of k₂₁T(0) ∼ 0.01 M/s.

Why would these two parameters be correlated? Obviously, in terms of the classical Michaelis-Menten analysis, k₂₁T(0) is “Vmax”. The correlation implies that the fit to the whole time course for a single substrate concentration contains an extrapolation to the k₂₁T(0) anticipated at high substrate concentrations.

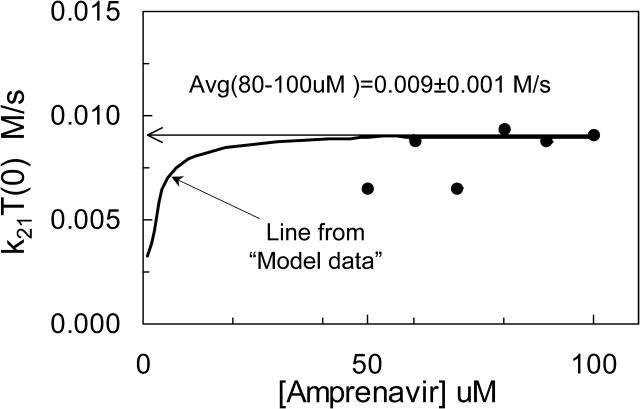
To show that this correlation is not an artifact of the fitting algorithm, we tested it with the “model data”. We generated computer-simulated data using a parameter vector within the set of best fits for amprenavir, as defined in Table 4 below. These “model data” represent perfect data for the case that P-gp is a single site Michaelis-Menten type transporter and there is no experimental error. We note here that the “model data” for P-gp with one or two binding sites were the same, assuming both sites had to be filled for one drug molecule to be effluxed. This is because association was so rapid (simulations not shown). The “model data” for all drug concentrations were then fitted with the algorithm being followed here. For each concentration of substrate, the fitting gave a constant value for k₂₁T(0), which is shown as the solid hyperbolic line in Fig. 7. Interestingly, the small substrate concentrations predict a k₂₁T(0) product that is smaller than the value of k₂₁T(0) used to simulate the data in the first place, i.e., 9 × 10⁻³ M/s. However, as the substrate concentration increased, the predicted k₂₁T(0) becomes equal to the correct value. Thus, even with model data, the correct k₂₁T0 value is obtained only when the substrate concentration is large enough. This fit was the outcome of Run I in Table 1.

TABLE 4.

“Center-of-the-box” parameter values for all simulations

Drug	Active P-gp density T(0) (μM)*	Association to P-gp k11 (M−1s−1)†	Binding constant KB (M−1)‡	Efflux to apical chamber k21(s−1)§	Dissociation to bilayer kr1 (s−1)¶
AMP	50	3 × 109	1300	180	2 × 106
QND	50	3 × 109	6000	16	5 × 105
LPM	50	3 × 109	150	4	2 × 107

^*Simple center-of-the-box value from the consensus range for the three drugs for the concentration of efflux active P-gp in the apical membrane inner monolayer was about T(0) = 5 × 10⁻⁵ M, which will be used for all three drugs.

^†Simple center-of-the-box value from the consensus range for the three drugs was k₁₁ = 3 × 10⁹ M⁻¹s⁻¹, which will be used for all three drugs.

^‡Binding constants were taken as the average value from Table 3, using the high concentration values for loperamide, since that should be due to P-gp.

^§Efflux rate constant k₂₁, from P-gp into the apical chamber, was calculated by the ratio of the fitted k₂₁T(0) for each drug and the center-of-the-box value of T(0) = 5 × 10⁻⁵ M.

^¶Dissociation rate constant k_r1 was calculated by the ratio of the fitted K_B = k₁₁/k_r1 for each drug and the center-of-the-box value of k₁₁ = 3 × 10⁹ M⁻¹s⁻¹.

FIGURE 7.

Fitted values of k₂₁T(0) for 50–100 μM amprenavir, (•), and predicted from simulated “model data” (solid line). Model data were simulated for the Michaelis-Menten reaction model for P-gp, without experimental error, using the parameters given in Table 4 for amprenavir. At each concentration, a predicted k₂₁T(0) is found, just like in Fig. 6. The solid hyperbolic line is the predicted k₂₁T(0) for all the model data. At high substrate concentrations, the k₂₁T(0) used to simulate the model data was recovered. However, at low concentrations, the predicted k₂₁T(0) was smaller than the correct value. The k₂₁T(0) values predicted for each concentration of the amprenavir data are shown by solid circles. For each concentration, the best 300 fits gave the same value for k₂₁T(0), i.e., the standard deviation for each point is much smaller than the size of the symbols. The average of the higher amprenavir concentrations was roughly k₂₁T(0) = 0.009 M/s, which is the value shown in Tables 2 and 4 as k₂₁T(0) = 180 (1/s) × 50 (μM) = 0.009 M/s. Thus, for all subsequent fittings for amprenavir, for each value of T(0) tested, we fixed the value of k₂₁= (0.009 M/s)/T(0).

Fig. 7 also shows the k₂₁T(0) values fitted from the different amprenavir concentrations as diamond symbols. We take the average of the highest three concentrations, which is ∼k₂₁T(0) = 9 × 10⁻³ M/s, which was the value used to simulate the “model data”. In terms of final fitted values, whether we take k₂₁T(0) = 0.012, 0.009, or 0.006 M/s will be insignificant, since we are aiming for the final parameter ranges to be within an order of magnitude box. It is important to note here that we use the same average value for k₂₁T(0) = 9 × 10⁻³ M/s for all subsequent fits, rather than the individual values shown in Fig.7.

The second or fine fitting comes next. As explained in the Fitting Algorithm section, this is a two-parameter fit to the B > A data using T(0) and k₁₁, with the parameter range of the first, or coarse fit, but with a finer grid. Also, k_r1 = 0 and k₂₁ = 0.009/T(0) s⁻¹. A higher stringency is used with ode23s; relative and absolute tolerances were set at 10⁻⁹. The grid and tolerance is shown in Run II of Table 1. All possible combinations of the two parameters were used as initial vectors, 13² = 169 in all. For economy, these fits are not shown. The parameter ranges were reduced to 3 × 10⁻⁶ < T(0) < 3 × 10⁻⁴ and 10⁸ < k₁₁ < 10¹⁰, as shown as the initial range of Run III in Table 1.

This brings us to the final forward fit, with the most stringent tolerances on ode23s, relative and absolute at 10⁻¹⁰, and a unitary grid, i.e., 1, 2, …, 9, 10, 20, …. We use the consensus box of the fine fit, but the exact boundaries are not that crucial since this is an open fit, i.e., fminsearch can find fits outside of the initial box. The grid and tolerance is shown in Run III of Table 1. All possible combinations of the two parameters were used as initial vectors, 18 × 19 = 342 in all.

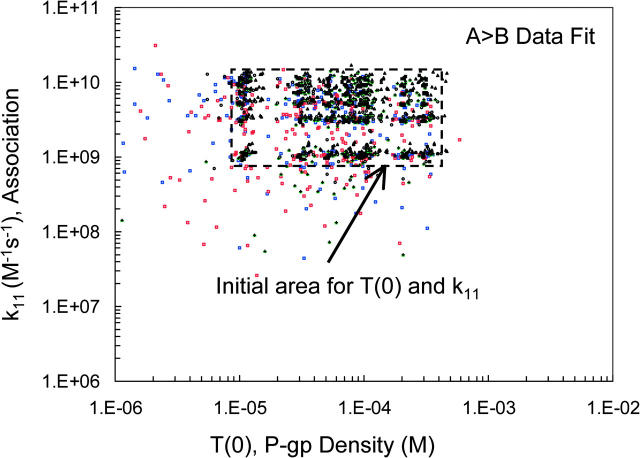
Fig. 8 A shows the outcome of this fitting in terms of the graph T(0) and k₁₁ from the best fits for all fitted amprenavir concentrations, which are color coded, as shown in the legend. The initial grid for T(0) and k₁₁ is shown by the box with a dashed line border. This plot shows that some fits ended far away from the initial grid. With the smallest grid and the highest stringency on the numerical integrations, many possible fits still show up. We can reject the fits that lay against the constraints on T(0) as being unphysical, as explained above. Within the box labeled consensus fits, we find the fit vectors for all amprenavir concentrations, which is what we will use to complete the fitting process using the A > B data.

FIGURE 8.

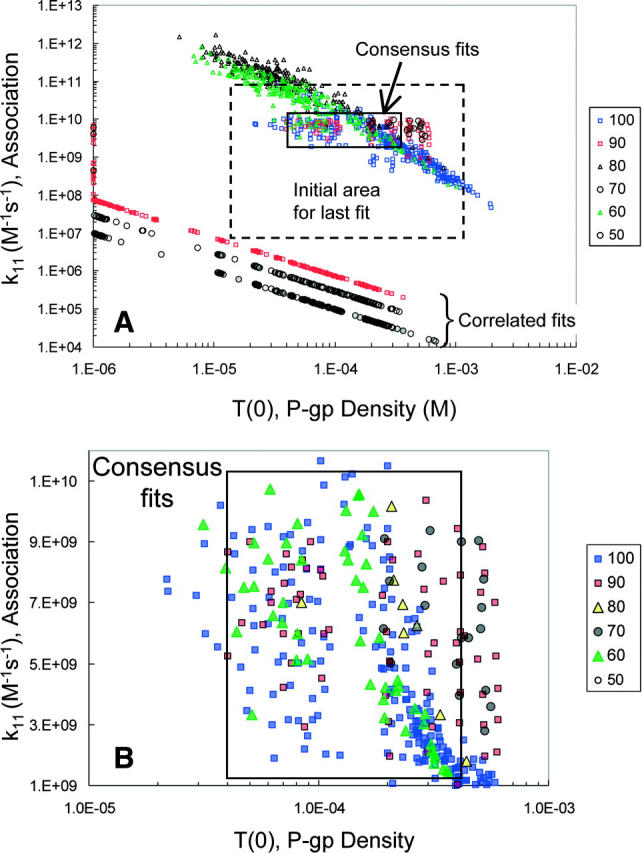
Final forward fits for the amprenavir data. Panel A shows all pairs of T(0) and k₁₁ that best fit the final fitting of the forward B > A amprenavir data, Run III. The initial grid for T(0) and k₁₁ is the box with a dashed line border. The amprenavir concentrations are color coded, as shown by the legend. The box labeled “consensus fits” contains pairs from all amprenavir concentrations, except 50 μM, which had only correlated fits. Thus, any pair within the box gives essentially the same best fit to all amprenavir concentrations. There is also a series of fits labeled “correlated fits”, the straight lines at the bottom. These fits are different for each amprenavir concentration and show no reduction in volume. As explained in the text, these fits are artifacts from applying the fitting algorithm to the mass action kinetics of the Michaelis-Menten reaction. These fits may be discarded. Panel B is a blowup of the consensus fits, showing the distribution of fitted pairs. We shall see in Fig. 11 below that using parameter values in the center of this box gives good fits to all amprenavir concentrations, despite the fact that 1, 10, and 50 μM amprenavir yielded only correlated fits (data not shown).

Before proceeding, though, we need to explain the distinct sets of fits at the bottom of the graph of Fig. 8 A, which we have labeled the correlated fits, one of which was seen even in the coarse fits shown in Fig. 5. For most of the amprenavir concentrations, there was a distinct line of correlated fits with a slope of ∼−1, i.e., for the points on this line k₁₁T(0) = constant. The MATLAB search function fminsearch has found a good fit for the data for some (T(0), k₁₁) pair and that the same curve can be retraced using a slightly larger T(0) and slightly smaller k₁₁, and vice versa, over the entire fitting range.

What is the origin of the correlated fits, and why are their predicted k₁₁ values so much smaller than those for the consensus fits? To answer this question, we continued to use the “model data”, introduced at Fig. 7 for amprenavir. Even though the model data were without error, the exact values used in the simulation were not uniquely found; rather there was a box of consensus fits that contained the “right answer” (data not shown). More remarkably, a series of correlated fits were found as well, orders of magnitude below the consensus fits and the values of k₁₁ used to simulate the model data, just like in Fig. 8 A. The only difference was that all of the correlated fits for the “model data” lay on the same straight line of slope −1, regardless of drug concentration. This suggests that the offset y-intercepts seen in Fig. 8 A for amprenavir were simply due to experimental error.

In Bentz and Nir (1981) and Bentz et al. (1983), we fitted the aggregation and fusion kinetics of liposomes, which follow similar differential equations, but found no “correlated fits”. Because of this, we suspected that the differential equations of the Michaelis-Menten reaction generated this fitting artifact. We have done detailed mathematical analysis of classical Michaelis-Menten kinetics, i.e., as a solution enzyme, and found correlated fits when “k_cat”, which is k₂₁ here, was fixed by the ratio of Vmax/total enzyme concentration, and substrate binding was defined to be irreversible, i.e., the same protocol used to fit the P-gp transport data. When the best fits for the fitted substrate-enzyme rate constant and the total enzyme concentration were plotted like Fig. 8 A, the slope was always −1 and the y intercept depended only on a ratio of all the true total enzyme concentration and the true rate constants (J. Bentz, unpublished data). So, in addition to the consensus fits, our fitting algorithm generated these correlated fits as an artifact. This analysis is beyond the scope of this article and will be published separately.

In any case, it is clear that these correlated fits are not realistic solutions to the data and can be discarded, which is good since they show no reduction in the parameter ranges. These outcomes are shown in Run III of Table 1. Below, we will see that when the A > B data are fitted using k_r1, k₁₁, and T(0), no correlated fits are found.

Fig. 8 B shows a blowup of the consensus fits in Fig. 8 A. Within the box of 40 μM < T(0) < 400 μM and 1 × 10⁹ M⁻¹s⁻¹ < k₁₁ < 1 × 10¹⁰ M⁻¹s⁻¹, the best fits for all concentrations are found, except 50 μM amprenavir, which had only correlated fits. Both 1 and 10 μM amprenavir had only correlated fits, i.e., correlated fits are more prevalent at low substrate concentrations. Below, we will see that a parameter vector chosen from the “center” of the consensus box gives excellent fits to all amprenavir concentrations, even the low concentrations.

This completes the fitting of the B > A data. Now it is time to test the assumption that the fitted values of the forward parameters using the B > A data, with k_r1 = 0, will not change much upon fitting the A > B data with k_r1, T(0), and k₁₁. We will search over the binding constant K_B, since k_r1 = k₁₁/K_B. The grid and tolerance is shown in Run IV of Table 1. All possible combinations of the three parameters were used as initial vectors, i.e., 5 × 6 × 10 = 300 initial points in all. Empirically, we have found that the relative and absolute tolerances on ode23s must be >10⁻⁸ to achieve reasonable fitting speeds. This is likely due to the low amplitudes of change for the A > B transport curves. These tolerances are sufficient to give excellent reliability in the numerical integrations.

Fig. 9 shows the outcome of this fitting of the A > B data in terms of the graph T(0) and k₁₁ from the best 300 fits for each of the amprenavir concentrations, color coded by the legend as in Fig. 8. The initial grid for T(0) and k₁₁ is shown as a box with a dashed line border. The crucial point is that very few of the final fitted (T(0), k₁₁) points moved out of the box of initial grid points, i.e., changes in T(0) or k₁₁ did not strongly affect the fit. Fitting the A > B data comes almost entirely from K_B, or equivalently k_r1. The fitted range was 250 < K_B < 15,000 M⁻¹. This outcome is shown in Run IV of Table 1.

FIGURE 9.

Final reverse fits, A > B, for the amprenavir data, Run V. The 300 best-fitting pairs of T(0) and k₁₁ are shown. The initial grid for T(0) and k₁₁ is shown as a box with a dashed line border. The amprenavir concentrations are color coded as in Fig. 8. The initial pairs of (T(0), k₁₁) were uniformly distributed within the dashed line box, showing that fits for these forward parameters to the A > B data did not change significantly, and no correlated fits were found. This proves that our separation of the forward and reverse fits did not affect the final fitted ranges for the forward parameters.

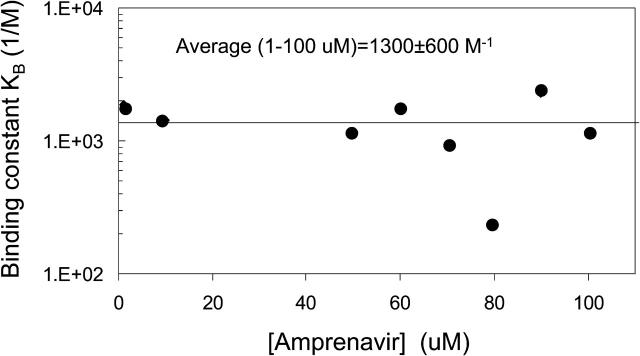
With this assumption satisfied, we refit the A > B data with the unitary grid for K_B. The fits for T(0) and K_B are shown in Fig. 10. The average estimate for 1–100 μM amprenavir was K_B = 1300 ± 600 M⁻¹. It is also interesting that the estimated binding constants did not depend upon amprenavir concentration, unlike the fitting of k₂₁T(0). We note that no correlated fits were found here, as expected, since they were an artifact of imposing irreversible association in the forward fits. All of the fitted parameter ranges for amprenavir are shown (see Table 3).

FIGURE 10.

Best-fit values for K_B as a function of amprenavir concentration. The error bars are the standard deviation over the calculated K_B for the best 300 fits, i.e., each concentration has a very tight fit for its predicted K_B. The overall average for all amprenavir concentrations was K_B = 1300 ± 600 M⁻¹.

TABLE 3.

Parameter estimates from exhaustive fitting

Drug	“Vmax” k21T(0) (M/s)*	Active P-gp density T(0) (per μm2)†	Association to P-gp k11 (M−1s−1)‡	Binding constant KB (M−1)§ “KD,Aq”	Efflux to apical chamber k21 (s−1)¶	Dissociation to bilayer kr1 (s−1)‖
AMP (n = 8)	9 × 10−3	32–320	2 × 109–2 × 1010	(1.3 ± 0.6) × 103 “3 μM”	20–200	>1 × 10+6
QND (n = 6)	8 × 10−4 (No fit for 1 μM)	8–80	2 × 108–1010	(6 ± 3) × 103 “0.2 μM”	8–80	>2 × 10+4
LPM (n = 6)	2 × 10−4 [LPM] = 3–20 μM (No fit for 0.3 μM)	8–80	108–1010	100–200 [LPM] ≥ 10 μM “2 μM”	2–20 [LPM] ≥ 10 μM	>5 × 10+5
				1000–3000 [LPM ]≤ 1 μM “0.2 μM”		>3 × 10+4

^*For amprenavir, the average value for 60–100 μM was k₂₁T(0) = 9 × 10⁻³ M/s, as shown in Fig.7. For quinidine, the asymptote for 0.3–20 μM was k₂₁T(0) ∼ 8 × 10⁻⁴ M/s. At 1 μM quinidine, no stable value for k₂₁T(0) was found. At 30 μM quinidine, the value was much smaller, due to the very small contribution of P-gp to overall transport because of saturation binding. For loperamide, the asymptote for 3–20 μM was roughly k₂₁T(0) ∼ 2 × 10⁻⁴ M/s. A value as large as k₂₁T(0) = 3 × 10⁻⁴ M/s was possible, but subsequent fits were not significantly sensitive to this choice. At 0.3 μM, there was no convergence to a single k₂₁T(0) value. At 30 μM, the value was smaller, likely due to the very small contribution of P-gp to overall transport, as was the case for quinidine. The k₂₁T(0) values shown were fixed by at least the first 250 best fits, which all have the same CV, i.e., these are robust fits at each concentration.

^†Efflux-active concentration of P-gp in the inner apical monolayer was bounded by T(0) = (4–40) × 10⁻⁵M for amprenavir, Fig. 9. For quinidine and loperamide, slightly lower ranges were found, (1–10) × 10⁻⁵M (data not shown), but there is substantial overlap. These units have been converted to a more typical form, assuming a 2 nm lipid monolayer thickness for the acyl chain region. T(0) (Pgp/μm²) = 0.8 × T(0) (μM, inner apical monolayer). The ratio of apical membrane to the insert cross-section area is irrelevant, since it cancels out in this calculation.

^‡Range for k₁₁ found in the final forward fit. As shown for amprenavir in Fig. 8, the range was k₁₁ = (1–10) × 10⁹ M⁻¹s⁻¹. For quinidine and loperamide, the range was broader, k₁₁ = (0.2–10) × 10⁹ M⁻¹s⁻¹ (data not shown).

^§Binding constant between P-gp and the inner apical monolayer shown is the average of the best fits (>160 for each drug concentration) as shown in Fig. 10 for amprenavir. For quinidine, the value for 30 μM was omitted due to active transport saturation, as noted above for k₂₁T(0). For loperamide, there were two ranges of binding constants. At 10 and 20 μM, the binding constant to P-gp was in the range of 100–200 M⁻¹. The fit at 30 μM was not used due to active transport saturation. At 0.3 and 1 μM, the binding constant was in the range of 1000–3000 M⁻¹. For 3 μM loperamide, the binding constant was an intermediate value of ∼600 M⁻¹. Since all A > B flux was fitted to a single binding constant, a better deconvolution of this parameter is not yet possible. Below each binding constant, we show in parentheses the appropriate dissociation constant for each drug relative to the aqueous phase, calculated as K_D,Aq = 1/(K_B × drug partition coefficient{PS/PE/chol}), the liposome mimic for the inner apical monolayer. These aqueous dissociation constants are given only to a single significant digit, and no error bars were calculated. These are intrinsic dissociation constants and are not the same as those derived from a steady-state Michaelis-Menten analyses.

^¶Estimate for the efflux rate constant k₂₁, from P-gp into the apical chamber, given by the ratio of the fitted k₂₁T(0) for each drug and the center-of-the-box value of T(0) = 5 × 10⁻⁵ M. See text and second footnote (^†) above.

^‖Estimate for the dissociation rate constant k_r1, given by the ratio of the center-of-the-box value of k₁₁ = 3 × 10⁹ M⁻¹s⁻¹ and the fitted K_B = k₁₁/k_r1 for each drug. See text and third footnote (^‡) above.

For convenience, we note that the dissociation constant for amprenavir measured from the aqueous phase, which is the typical expression used, would be K_D,Aq = 1/(K_B × the partition coefficient to the PS/PE/chol LUV) = 1/(1300 × 228) = 3.4 μM. This value is listed below the K_B value in Table 3 as 3 μM, since it is not more accurate than one significant digit. We have found that K_D,Aq is not the same as the steady-state Km, which would be fitted from a standard steady-state analysis (J. Bentz, unpublished), but that work is beyond the scope of this article and will be published separately.

To prove the generality of this analysis, we have also examined two other P-gp substrates: quinidine, which is a Na⁺ channel blocker, and loperamide, which is an antidiarrheal drug. These drugs were chosen because they are good substrates for P-gp and are of pharmaceutical significance (Tran et al., 2004). After preliminary studies, we used 0.3, 1, 3, 10, 20, and 30 μM quinidine and loperamide, since these two drugs have nearly identical concentration dependencies with respect to overall transport. We followed the same fitting algorithm as used with amprenavir and, overall, the fits followed the same basic pattern as for amprenavir. We show the fitted parameters for quinidine and loperamide in Table 3.

We are now in a position to see how the fits to the data look when consensus values, over the three drugs, for the parameters are used. We chose a single vector from the “center” of the parameter consensus box to simulate the curves for all of the drugs. These consensus values are shown in Table 4. Many parameters were specific to the drug. However, for all drugs, k₁₁ was set to 3 × 10⁹ M⁻¹s⁻¹ and the density of efflux active P-gp was set to 50 μM (in the apical membrane inner monolayer), i.e., 40 P-gp/μm². This assumes that these three drugs encounter P-gp identically, which would be the simplest and least flexible case. These overall consensus values for k₁₁ and T(0) for all three drugs are not in the “center of the box” for amprenavir shown in Fig. 8 B, due to the fitted ranges of quinidine and loperamide. However, any values within that consensus box for amprenavir will fit all of the data equally well, as we will now see.

Fig. 11 A shows the comparison of the simulation and the data for 100 μM amprenavir. There are four data sets per amprenavir concentration, which were fitted simultaneously, shown by symbols with standard deviations from triplicate runs, from top to bottom over 6 h:

1. A:B > A, denoting amprenavir arriving in the apical compartment when the basolateral chamber is the donor.

2. A:A > B, denoting amprenavir remaining in the apical compartment when the apical chamber is the donor.

3. B:B > A, denoting amprenavir remaining in the basolateral compartment when the basolateral chamber is the donor.

4. B:A > B, denoting amprenavir arriving in the basolateral compartment when the apical chamber is the donor.

FIGURE 11.

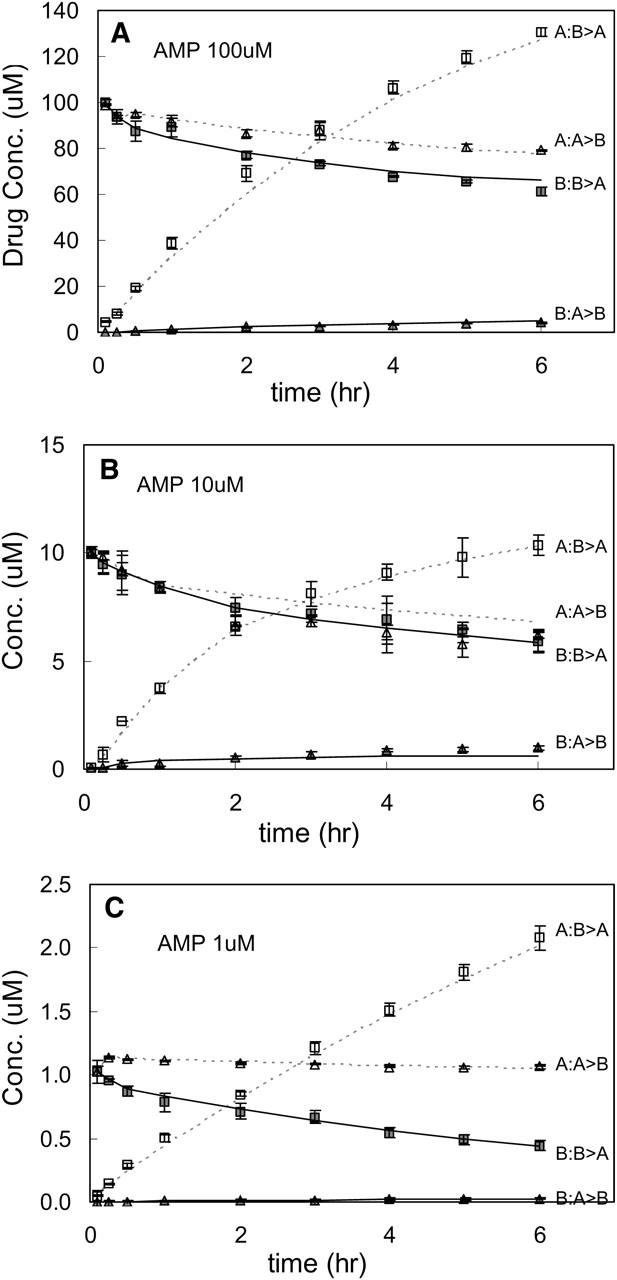
Amprenavir data and the fits data and the fits (using the single-parameter vector in Table 4) are shown. Panel A shows the fit for all four data sets from 100 μM amprenavir. The B:B > A curve denotes the concentration of drug in the basolateral chamber when the donor chamber was the basolateral chamber, i.e., transport runs B > A. A:B > A would be the concentration in the apical chamber when the basolateral chamber is the donor. All B > A data are shown by squares: solid when the basolateral chamber was sampled, i.e., B:B > A, and open when the apical chamber was sampled, i.e., A:B > A. All A > B data are shown by triangles: solid when the basolateral chamber was sampled, i.e., B/A > B, and open when the apical chamber was sampled, i.e., A:A > B. The fits for the basolateral data are shown by the solid line, i.e., both B:B > A and B:A > B. The fits when the apical chamber is sampled are shown by the dotted line, i.e., both A:B > A and A:A > B. This format is also used for Figs. 12 and 13. Data shown were the average of triplicates, with standard deviation error bars. Panel B shows the data and fits for 10 μM amprenavir. Panel C shows the data and fits for 1 μM amprenavir. Note that 10 and 1 μM data sets were not used for fitting parameters. Similar quality fits for 90, 80, 70, 60, and 50 uM amprenavir are not shown.

All four data sets were fitted by the hierarchical analysis, so all of the fits have equal weight. Clearly, all fits are quite good over the entire 6 h time course. Representative fits for other concentrations of amprenavir are shown, 10 μM in Fig. 11 B, and 1μM in Fig. 11 C, neither of which were part of the data set used to fit the parameters, so they are a small tester set.

If there is any systematic deviation in the fits, it is in some of the A:B > A curves. For some cases, there was a slight underestimate at the early time points and/or a slight overestimate at the long time points. We could have made the fits look even better, if for each drug concentration we had used its individual fitted value of k₂₁T(0), Fig. 7, and its fitted value of K_B, Fig. 10. That could have been justified on the grounds that the cell monolayers are certainly not physically identical from plate to plate and day to day. However, that is the kind of curve fitting we avoid. If there is an underlying cause, e.g., multiple binding sites on P-gp or a second transporter, as we will discuss below for the drug loperamide, it is too slight to be further analyzed for amprenavir.

We now turn to the fits for the second drug, quinidine. In general, the fitting results for quinidine follow the same pattern as we saw for amprenavir. For economy, we show only three final fits for quinidine—10 μM in Fig. 12 A, 1 μM in Fig. 12 B, and 0.3 μM in Fig. 12 C—in the same format as Fig. 11 for amprenavir. The fits for 20 and 30 μM quinidine were of the same quality as 10 μM. The fit for 1 μM quinidine shows a small underestimate of the fitted curve; the fit for 3 μM quinidine was similar. However, the good fit for 0.3 μM quinidine A:B > A curve shows that the underestimate for the 1 μM data is just random error and would not have been noticed without the predicted curves.

FIGURE 12.

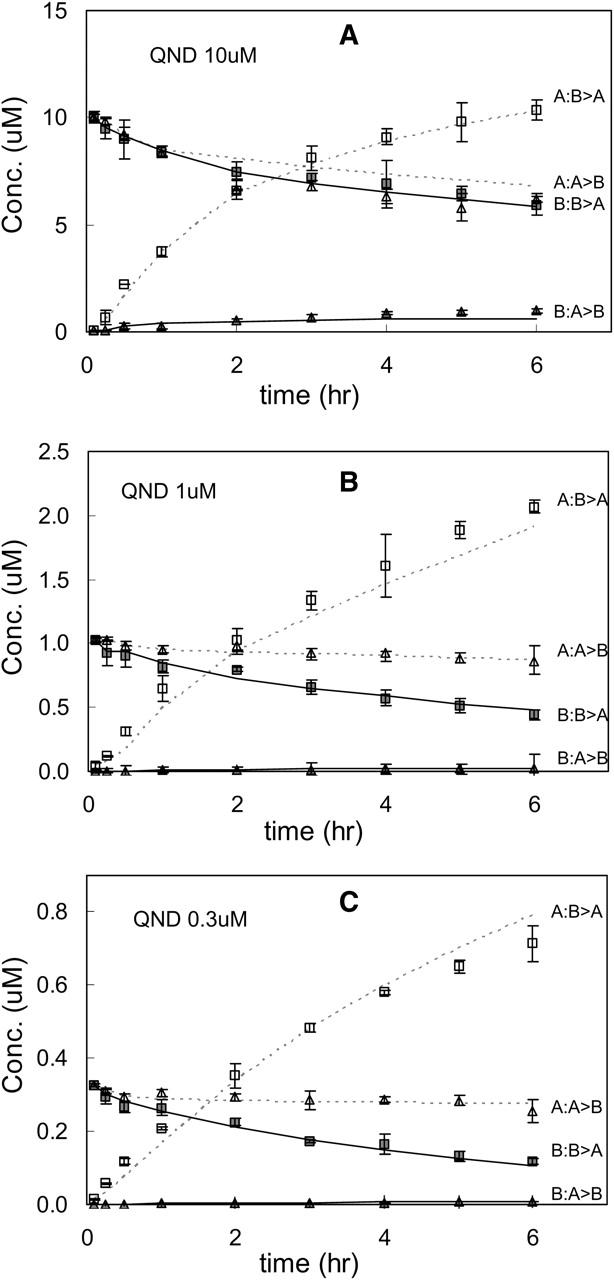
Quinidine data and the fits (using the single-parameter vector in Table 4) are shown with the same format as Fig. 11. Panel A shows the fits for 10 μM quinidine, panel B for 1 μM quinidine, and panel C for 0.3 μM quinidine. Other quinidine concentrations—1, 2, 5, and 20 μM—showed essentially the same quality fits (data not shown).

This is an important point. Before the analysis and the plotting of the fits, all of the data looked fine. Here, for 1 μM quinidine, because of the predicted curve for the A:B > A data, we can see some systematic deviation. We have done these experiments many times, and it is typical for amprenavir and quinidine for one or two concentrations out of 6–9 total concentration tested to show a small deviation, like 1 μM quinidine. But it was never the same concentration each time. The confluent cell monolayers are not identical, and to just repeat the 1 μM quinidine case until it looked better misses one of our most important points. We want to fit the average value of the parameters on the average day. In any case, like amprenavir, if there is any systematic deviation in the quinidine curves, it is too slight to be analyzed further.

The third drug was loperamide. For economy and to compare with quinidine and amprenavir, we show only three final fits for loperamide: 10 μM in Fig. 13 A, 1 μM in Fig. 13 B, and 0.3 μM in Fig. 13 C.

FIGURE 13.

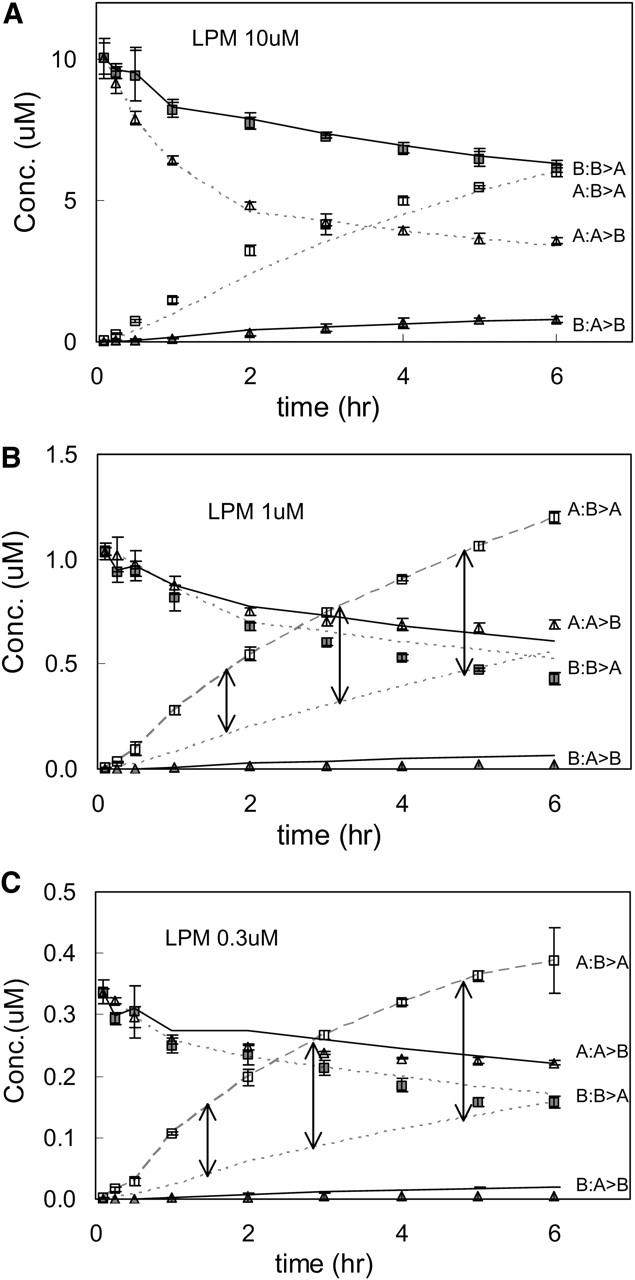
Loperamide data and the fits (using the single-parameter vector in Table 4) are shown with the same format as Fig. 11. Panel A shows the fits for 10 μM loperamide, panel B for 1 μM loperamide, and panel C for 0.3 μM loperamide. In panels B and C, the A/B > A data are connected by a dashed line to guide the eye, and the fit is shown by the lower dotted lines. The vertical arrows connect these two curves to show the extent of the model's underestimate of these data. See text for a discussion of possible explanations; 3 and 20 μM loperamide showed essentially the same quality fits as 10 μM (data not shown).

In Fig. 13 A, the fit to 10 μM loperamide is good enough, although the A:B > A data are slightly underestimated. Fits for 20 and 30 μM loperamide were similar. In Fig. 13 B, the fit for 1 μM loperamide underestimates the A:B > A data substantially. The B:A > B data are substantially underestimated, because the loperamide binding constant was fixed at the “high” concentration value shown in Table 3. The deviations were less for 3 μM loperamide, but worse for 0.3 μM loperamide, Fig. 13 C. Clearly, some other transport process is occurring for loperamide. The slight deviations for the amprenavir and quinidine fits are very different from this across the time range underestimate for the low loperamide concentrations. This is not a failure of the model or the fitting process, but rather it shows the sensitivity of the kinetic analysis as an analytical tool. The nature of this additional transport process will be discussed in detail below

DISCUSSION

The clinical and biological relevance of P-gp is clear; the question is how to elucidate the mechanism of action of this complex membrane transporter. Mechanistic models for P-gp activity, and similar multi-drug transporters, have been proposed based upon ATPase activity, Michaelis-Menten steady-state analyses, and equilibrium binding studies of purified/lipidated reconstitutions of P-gp and/or of plasma membrane vesicles (Senior et al., 1995; van Veen et al., 2000; Qu et al., 2003; al-Shawi et al., 2003; Loo et al., 2003; Urbatsch et al., 2003). The confluent monolayer system that we use is a better physiological model system of in vivo P-gp activity, but it is more difficult to use. It requires a more sophisticated kinetic analysis to extract the elementary rate constants and the surface density of efflux active P-gp. The confluent monolayer of cells does not readily permit transport/ATP hydrolysis stoichiometric studies. Nevertheless, we believe that resolution of differences in parameter estimates between the different expression systems will be required to elucidate the in vivo activity of P-gp.

Our kinetic analysis was the unavoidable consequence of not imposing the steady-state Michaelis-Menten equations onto the data. P-gp active transport has (at least) four kinetically important parameters, which become convolved into the Vmax and Km of the Michaelis-Menten equation. We felt that this convolution would hinder the resolution of P-gp mechanism. This meant we had to simultaneously fit the four most important kinetic parameters of P-gp transport.

Our kinetic data cannot address the question of multiple substrate binding to P-gp, since the association and dissociation kinetics for all drugs tested were so rapid that any number of postulated binding sites on P-gp would be empty or filled together. The predicted transport kinetics are essentially identical (simulations not shown). Future work involving substrate competition can address these issues directly.

The two main questions we could address were: 1), would the physiologically relevant polarized monolayer of MDCKII-hMDR1 cells yield adequately precise data for a rigorous analysis, and 2), was the simplest Michaelis-Menten one-site mass action reaction adequate to fit the data generated? The answer was yes, for both questions.

Simultaneous fitting of all parameters to all data was attempted, but was too slow, i.e., after weeks only a small part of the search space was covered. A much more sophisticated search program would be needed. However, the algorithm we constructed worked. A complete fit for one drug concentration required ∼7–9 days on a 2.8 GHz PC. The keys to the success of the fitting algorithm used here were:

1. The validity of the assumption that the data could be fitted in two stages. First, the B > A forward data could be used to yield good fits for the surface density of efflux active P-gp, T(0), and the forward rate constants, k₁₁ and k₂₁, even though k_r1 was fixed at zero for these fits to reduce computation time. Second, the A > B reverse data would be fitted essentially only by the dissociation rate constant k_r1, since the forward rate constants only weakly affect the A > B fits. The correlated fits were unexpected, but now it is known that they are artifacts for this fitting algorithm used on the Michaelis-Menten mass action reaction and can be discarded.

2. The unexpected, but understandable, finding that the best fits to the B > A forward data had the product of k₂₁T(0) = constant, like Vmax in the Michaelis-Menten analysis, even though no steady-state assumption had been imposed. This allowed us to reduce the dimensions of the more refined forward fits to only T(0) and k₁₁, thereby markedly accelerating the last fitting of the “forward” parameters.

The final fitted parameter ranges for all three drugs are shown in Table 3. Clearly, the benchmark column was the predicted surface density of efflux active P-gp on the apical membrane. The independent analyses of each of the three drugs yielded overlapping ranges. This overlap would not occur if the model had “excess” parameters. There are just too many different ways for different ranges to have been chosen. Of course, the overlap does not prove that the fitted values are accurate. There could be an unknown systematic error that shifts the range from the “true” value. However, the analysis of the model data, generated by simulations, found the correct value of T(0), once the correlated fits were discarded. This shows that the analysis, per se, was not introducing any systematic error. There was no significantly different outcome between the analysis of the model data and that of the drug transport data. If there is a systematic error, then it appears to be relatively minor.

So how do these fitted values for T(0) compare with estimates for the amount of P-gp per cell made by quantitative Western analysis? This has not been done with this cell line, but has been done with similar cell lines (Ambudkar et al., 1997; Ito et al., 1999). As stated above, since the expression levels of P-gp depend upon many factors, not all of which are necessarily known, we treated it as a fitted parameter. However, it appears that the fitted value range for the surface density of efflux active P-gp is at least 10 times smaller than the total P-gp estimated in Ambudkar et al. (1997) for a similar cell line. Because of the differences in cell systems, this quantitative difference could be argued several ways, but we speculate that both estimates are probably essentially correct.

So, how can more than 90% of P-gp in the confluent monolayer not be efflux active? It is believed that most expressed P-gp is in the plasma membrane, not sequestered inside the cell, and we have no reason to believe that a large fraction of the P-gp is misfolded. This is where the appreciation of the interplay between the essential transport parameters of P-gp and the details of the expression system becomes important. By definition in the kinetic model, the P-gp that are efflux active are those that send their drug directly into the apical chamber, where it equilibrates “instantly”, according to the partition coefficients, between the sampling volume of the apical chamber and the outer apical monolayer.

Fig. 14 shows our hypothesis about why only the P-gp at the tips of the microvilli will be efflux active. The microvilli on the apical membrane of MDCK II cells are columns longer than the aqueous space between them (Butor and Davoust, 1992). The random walk of drug released from P-gp at the base of a microvillus will almost certainly encounter the same or a neighboring microvillus rather than release into the apical chamber. Flip-flop would put the drug in the inner apical monolayer, where the cycle would be repeated. Only those drug molecules that are released from P-gp at the tip of the microvillus would have a reasonable probability of escaping directly into the apical chamber. As an illustration only, a cartoon path is indicated in the figure. Interestingly, the surface area of a microvillus tip is ∼10% of the total microvillus surface area, crudely estimated from the micrographs of Butor and Davoust (1992). Quantitative studies of this hypothesis are ongoing.

FIGURE 14.

Blowup of the model of an apical membrane showing microvilli, roughly to scale. The figure qualitatively illustrates that the random-walk pathway of drug released at the base of a microvillus will be tortuous, involving many subsequent interactions with the same or a neighboring microvillus and the P-gp they contain. Only the P-gp at the tips of the microvilli can efflux the drug directly into the apical chamber where it can be measured. The hypothesis is that the efflux-active P-gp would be at the top of the microvillus.

A very interesting corollary to this hypothesis is that the cell could substantially alter its P-gp transport by fairly subtle changes in the protein spindles that create the microvilli. Almost any change in dimension would have an effect on the density of efflux active P-gp.

The estimated ranges for the association rate constants, k₁₁, were the same for all three drugs and were very large. This suggests that association is rate-limited by lateral diffusion through the inner monolayer of the plasma membrane. This also suggests that the drug binding site in P-gp is essentially open to the apical membrane inner monolayer. Studies have suggested that the binding site involves the inner apical portions of the transmembrane domain helices 4–6 and 10–12 (Loo and Clarke, 1999; Loo et al., 2003). If the other six transmembrane domain helices were surrounding and blocking those comprising the binding site, then such rapid ingress would not be expected.

No atomic level crystal structure for P-gp has been published to date. The best guesses about its structure in the membrane come from mutational and cross-linking studies on P-gp (Gottesmann and Pastan, 1993; Loo and Clarke, 1999, 2000, 2001; Stenham et al., 2003), electron diffraction of two-dimensional crystals (Rosenberg et al., 1997, 2001, 2003, 2004), and the crystal structures of the bacterial homologs MsbA and BtuCD (Chang and Roth, 2001; Locher et al., 2002; Chang, 2003). Remarkably, all nucleotide bound structural models or homologs show open access to the center of P-gp from the apical membrane inner monolayer. Thus, there appears to be an agreement between the very large kinetic association rate constants we have measured and the predicted openness of the structure of P-gp within the plasma membrane.

We allowed our fitting program to seek rate constants without constraints, which led to some very large fitted values for k₁₁. The maximum value for the association rate constant is not known. The classical Smoluchowski solution for diffusion controlled on-rate constant in three dimensions does not work in two dimensions, making a maximal value dependent upon two-particle correlation functions (Keizer, 1987; Molski et al., 1996; Hinterdorfer et al., 1997). However, assuming that the lateral diffusion coefficients of these drugs in bilayers are similar to that of ibuprofen (Gaede and Gawrisch, 2003), we can use the simplified approximate solutions to the two-dimensional diffusion equation to estimate that the upper bound for k₁₁. We found that it should be of the order of 10⁹–10¹⁰ M⁻¹s⁻¹ (Keizer, 1987; Hinterdorfer et al., 1997). Thus, the lower range of the estimates for k₁₁ appears to be the right answer. Better estimates for the upper bound for k₁₁ are being pursued by more rigorous calculations.

The estimated efflux rate constants, k₂₁, were also very fast. Although it is believed that ATP binding, per se, provides the energy for transport (Rosenberg et al., 2001), ATP hydrolysis is required for the efflux cycle to be completed (Urbatsch et al., 2003). To date, the maximal ATP hydrolysis rates found for detergent solubilized and lipid reconstituted P-gp are on the order of 10–20 s⁻¹ (Urbatsch et al., 2003; Loo and Clarke, 2000). The estimated efflux rate constant, k₂₁, for quinidine and loperamide are at or just below the limit of these published ATP hydrolysis rates for other drugs.

For amprenavir, the estimated efflux rate constant exceeds these ranges by more than 10-fold. This difference is not due to the fitting process. A simple calculation based solely on the nmol of drug transported per well shows that the efflux rate constant for amprenavir must exceed that of quinidine by 10-fold or more. As an example, we use the 1-h time point to compare the B > A transport with 20 μM quinidine, where P-gp transport is nearly saturated, with 100 μM amprenavir, where P-gp transport shows no signs of saturation (data not shown). These data are like that shown in Fig. 3. Subtracting the nmol transported without inhibitor (17.3 for amprenavir and 3.3 for quinidine) from the nmol transported with inhibitor (8.2 for amprenavir and 2.0 for quinidine) yields the transport due to P-gp (ignoring the backflow), i.e., 9.1 nmol for amprenavir and 1.3 nmol for quinidine. Thus, per hour per well, ∼9.1/1.3 = 7 times more amprenavir is transported than quinidine. Since P-gp is not saturated in 100 μM amprenavir, a >10-fold higher efflux rate constant for amprenavir over quinidine is clearly required, even by this crude calculation. The same comparison between 20 μM quinidine and 20 μM loperamide, both of which show close to saturation for P-gp, yields >0.3/1.3 ∼ 0.23 times less loperamide transported per well than quinidine. This is essentially the same ratio shown by the efflux rate constants in Table 3. Choosing other times or concentrations gives comparable results.

The relationship between P-gp transport and its ATPase activity remains quantitatively unclear. ATP hydrolysis has always been measured in reconstituted systems and, recently, Modok et al. (2004) showed that lipid composition matters. This is a new variable for P-gp ATPase activity. We work with P-gp in the asymmetric apical membrane of a living cell. In addition, there is coupling between ATPase activity and drug binding (al-Shawi et al., 2003; Omote et al., 2004). It seems reasonable to suggest that the maximal ATPase activity of P-gp has not yet been measured. The ATPase activity caused by these drugs will be examined, as a function of reconstitution conditions to more clearly mimic the intact membrane. This is one focus of our work on comparing different P-gp expression systems: to learn from their differences.

Weak substrate binding and rapid efflux had been speculated as an important element in P-gp broad substrate specificity and its primary job of not allowing xenobiotics into the cell cytoplasm (Seelig and Landwojtowicz, 2000; al-Shawi et al., 2003; Seelig and Gatlik-Landwojtowicz, 2004). Our predicted binding constants confirm the speculation. Interestingly, although loperamide and quinidine show P-gp transport in the same aqueous concentration range, this appears to be due to loperamide's larger partition coefficient for all the LUV compositions (Table 2), since it has the weakest binding constant to P-gp of the three drugs we tested. Although our partition coefficients are based upon model lipid compositions, they are likely to be reasonable in a relative sense and perhaps in an absolute sense. So P-gp “specificity” is due to the independent contributions of partition coefficient and specific binding to P-gp.

Our kinetic analysis has provided a means to estimate the free energies of P-gp interaction with these drugs. When we choose amprenavir as a norm, then estimates for differences in free energy of binding, roughly given by ΔΔG = RTln{K_B(Drug)/K_B(AMP)}, is about (2.6 kJ/mol) × ln{6000/1300) ≈ 3.9 kJ/mol for quinidine and (2.6 KJ/mol) × ln{150/1300) ≈ −5.5 kJ/mol for loperamide at 37°C. If we assume that H-bonds range from 5–10 kJ/mol (Seelig. and Gatlik-Landwojtowicz, 2004), then there appears to be <1 H-bond difference for all three drugs at the binding site. Of course, hydrophobic interactions could also be the cause of the difference. On the other hand, for the efflux rate constant, k₂₁, the rough values for transition state free energies, given by ΔΔG^‡ = RTln{k₂₁T(0)(Drug)/k₂₁T(0) (AMP)}, is about (2.6 kJ/mol) × ln{0.0008/0.009) ≈ −6.3 kJ/mol for quinidine and (2.6 kJ/mol) × ln{0.0002/0.009) ≈ −9.9 kJ/mol for loperamide, at 37°C. This assumes that the density of efflux active P-gp is the same. Thus, relative to amprenavir, this suggests that efflux could involve breaking one more hydrogen bond for quinidine and 1–2 H-bonds more for loperamide. Other weak interactions are certainly possible. Whatever the case, our data suggest that the binding and the efflux sites are not identical, as has been proposed from equilibrium binding studies (Martin et al., 2000), but neither binds these drugs particularly strongly.

This leads us to the last fitted parameter, the dissociation rate constant k_r1. Often, reverse rate constants are measured by preloading a system with substrate, then diluting the sample or competing the bound substrate off. Fitting the release of substrate to a log plot, appropriate for first-order release, gives an estimate for the dissociation rate constant. This is straightforward when used with molecules in solution. However, with membrane systems, which have bilayers and internal compartments, there is reason to believe that the safest way to measure a reverse rate constant, like k_r1, is as part of the process of fitting all the rate constants (Bentz and Nir, 1981; Bentz et al., 1983). This reduces the possibility of barriers, other than the expected one, being responsible for the release of the substrate. However, measuring all rate constants as part of the same experimental design is rarely done in macroscopic systems, as we have done here, simply because it is so hard to obtain unambiguous answers (Bentz et al., 1983). The Michaelis-Menten steady-state analysis used for enzymes and membrane transport (Stein, 1997) irretrievably subsumes the reverse rate constant into the Km.

In part, the confluent cell monolayer system was competent to allow fitting of the dissociation rate constant k_r1 because the forward association rate constant was so fast. This caused the fitting of the forward B > A data to be rather insensitive to the value of the dissociation rate constant k_r1. From computer simulation, it was clear that given the large forward rate constants, the fact that there was any A > B transport in the face of active P-gp could only mean that binding of the drugs to P-gp was weak.

Dissociation rate constants have been reported for the P-gp substrates vinblastine and XR9576, using cell membrane vesicles preloaded with these drugs (Martin et al., 2000). The aqueous K_D values reported for these drugs were 10 and 3 nM, respectively. From the K_D,Aq values shown in Table 3, it is clear that they bind much more strongly than the drugs used here, from 20 times (vinblastine versus quinidine) to 1000 times (XR9576 versus amprenavir). However, the reported rate constant for substrate release from these vesicles into the medium are >6 orders of magnitude smaller than what we found for k_r1 for these drugs. This difference cannot be explained by the difference in binding constants. The barriers cannot be the same, but a direct comparison will be needed to resolve this problem.

We can estimate the average number of drug molecules that visit the binding site before one of them is effluxed using the ratio of the dissociation rate constant and the efflux rate constant, k_r1/k₂₁. From Table 4, we find that for each amprenavir effluxed into the apical chamber, ∼10,000 amprenavir molecules bind to P-gp and escape back to the apical membrane inner monolayer. The ratio for quinidine is ∼1:30,000 and for loperamide is ∼1:5,000,000. This picture of the process is quite different from that derived from equilibrium binding studies, which typically show a substrate binding to P-gp, then moving to the efflux site and then being effluxed. The rate constants predict that the vestibule of P-gp is quite busy, with substrate molecules binding briefly and then diffusing out, with only the occasional bound substrate being effluxed.

We now turn to the deviation from predictions found at low concentrations of loperamide. The higher concentrations of loperamide, ≥10 μM, fit the data well, just like amprenavir and quinidine, suggesting that at the higher concentrations, the active transport was due to P-gp, since that is the overexpressed transporter. At low concentrations of loperamide, at and below 3 μM, the A:B > A data were significantly larger than the predicted values. Part of the deviation was due to using the binding constant for the larger loperamide concentrations, Table 4, but in addition we do not have an estimate for the appropriate k₂₁T(0) for the low loperamide concentrations. Further studies will be required to fully understand the cause of the deviation. However, since the passive transport was symmetric (Tran et al., 2004), showing that the extra transport was inhibited by GF120918, the deviation appears to be due to a transporter inhibited by GF120918.

If this is the case, then the likely choice is the endogenous canine MDR transporter, since the parent MDCKII cell line to the cell line we use here has MDR-like transport activity, including inhibition by GF120918 (Evers et al., 2000; Tang et al., 2002a,b). The fact that the endogenous transporter appears only at low loperamide concentrations suggests that it has a higher affinity for loperamide than P-gp. In Table 3, we show that the loperamide binding constant to P-gp at high concentrations was 100–200 M⁻¹, whereas at the lower concentrations it was an order of magnitude larger. The endogenous transporter would be predicted to have a much lower expression level than P-gp, both because P-gp is overexpressed and because the model to fit the data at higher loperamide concentrations. If this is correct, the endogenous transporter would have an affinity for quinidine that is equal to or less than P-gp, since that data were well-fitted down to 0.3 μM quinidine.

Although this explanation makes sense, what are the alternatives? If the excess transport observed at low loperamide concentration were attributed to the proposed second site on P-gp (Martin et al., 2000), then the binding of loperamide to the second site at higher concentrations must inhibit transport. The model underestimates transport as the loperamide concentration decreases. If this were correct, then quinidine and loperamide must have qualitatively different interactions with P-gp, since the model fits the quinidine data from 0.3 to 30 μM. Although this is also a hypothesis, it requires that P-gp loses transport activity as the concentrations of the xenobiotic goes up, which is counterintuitive at this time. We are studying this question to determine which hypothesis works better.

In principle, another hypothesis would be that the partition coefficients for loperamide increase at low concentrations, which would increase transport. The LUV showed no concentration dependence for the partition coefficient, but cell monolayers could change, theoretically. However, by simulations, we found that 10-fold changes in any or all partition coefficients could increase loperamide transport by only 30%, whereas the underestimate in Fig. 13 C is over 100%. So this hypothesis cannot readily explain the deviation.

Actually, this deviation illuminates the power of the model as an analytical tool. It showed where the transport is augmented by something outside of the model used, e.g., an additional transporter or an additional binding site on P-gp. It is useful to note here that the appearance of a second transporter does not affect the fitted parameters in Table 3. That is, there is no reason to put a second transporter into the kinetic model and reanalyze all of the amprenavir and quinidine data, because only one transporter was needed to fit those data. No parameter estimates would change. The kinetic analysis cannot identify the transporter for amprenavir or quinidine, but it is commonly believed that it is P-gp. For the loperamide data, we already know how a model with two transporters would fit. It would give the parameters listed in Table 3 for [LPM] > 10 μM for high concentrations and the parameters for [LPM] < 3 μM for low concentrations. The values for those parameters would not change significantly. We are pursuing this question in the context of competition by two different drugs.

In conclusion, the single site mass action Michaelis-Menten reaction for P-gp was exhaustively fitted to transport data from polarized cell monolayers of MDCKII-hMDR1 cells. The results show that this reaction is adequate to explain the data, although the fits do not rule out multiple sites. We have shown for three drugs that there are only two kinetic barriers to passive transport across the polarized cell monolayers, i.e., the basolateral and the apical plasma membranes. This implies that although there is certainly transport through the cytosol, it is a minor kinetic pathway. The fitted elementary rate constants provide a deeper description of the function of P-gp than steady-state or compartmental analysis, since the interaction of the drug with the protein is the focus. The finding that the most physiologically relevant expression system for P-gp, the confluent cell monolayer that requires hours to reach steady state without loss of function (Tran et al., 2004), allows the measurement of very fast rate constants of association and dissociation. This is due to the fact that the amount of efflux-active P-gp expressed per entire 1.13 cm² cell monolayer is extremely small, ≤0.5 pmol. Reconstituted systems typically have such high concentrations of protein that the on and off rates of binding would be too fast to measure reliably. Functional analysis of mutations can now be attributed to the proper rate constant, developing much more rigorous structure/function relationship for P-gp.

APPENDIX: GLOSSARY

Units for all concentrations are molar, either in the aqueous media or the lipid bilayer; all volumes are liters; all times are seconds; and all partition coefficients are v(lipid)/v(aqueous), unless otherwise specified.

• C_B, concentration of drug in basolateral chamber.

• C_C, concentration of drug in cytosol.

• C_PC, concentration of drug in cytosolic side of plasma membrane, mols per liter of inner monolayer.

• C_A, concentration of drug in apical chamber.

• K_PC, equilibrium partition coefficient to the plasma cytosolic monolayer.

• K_BO, equilibrium partition coefficient to the basolateral membrane outer monolayer.

• K_AO, equilibrium partition coefficient to the apical membrane outer monolayer.

• k_v, first order rate constant for drug loss from aqueous chambers (s⁻¹).

• P_BCA_B, permeability coefficient across the basolateral membrane times its area (L/s).

• P_ACA_A, permeability coefficient across the apical membrane times its area (L/s).

• T(0), total concentration of transporter in apical membrane inner monolayer.

• T₀, concentration of transporter with no bound drug.

• T₁, concentration of transporter with one bound drug molecule.

• V_B, volume of Costar Transwell basolateral chamber (1.5 mL).

• V_A, volume of Costar Transwell apical chamber (0.5 mL).

• V_C, volume of entire cell monolayer cytosol (∼1 μL).

• V_AO, volume of entire cell monolayer outer apical membrane facing the Costar apical chamber (0.5 nL used here, but perhaps as much as 2 nL due to microvilli).