Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Oct 22;88(1):76–84. doi: 10.1529/biophysj.104.049239

Monte Carlo Simulation for Single RNA Unfolding by Force

Fei Liu *, Zhong-can Ou-Yang *,†
PMCID: PMC1305054  PMID: 15501942

Abstract

Using polymer elastic theory and known RNA free energies, we construct a Monte Carlo algorithm to simulate the single RNA folding and unfolding by mechanical force on the secondary structure level. For the constant force ensemble, we simulate the force-extension curves of the P5ab, P5abcΔA, and P5abc molecules in equilibrium. For the constant extension ensemble, we focus on the mechanical behaviors of the RNA P5ab molecule, which include the unfolding force dependence on the pulling speed, the force-hysteresis phenomenon, and the coincidence of stretching-relaxing force-curves in thermal equilibrium. We particularly simulate the time traces of the end-to-end distance of the P5ab under the constant force in equilibrium, which also have been recorded in the recent experiment. The reaction rate constants for the folding and unfolding are calculated. Our results show that the agreement between the simulation and the experimental measurements is satisfactory.

INTRODUCTION

Ribonucleic Acid (RNA) is now known to be involved in many biological processes, such as carriers of genetic information (messenger RNAs), simple adapters of amino acids (transfer RNAs), and enzymes catalyzing the reactions in protein synthesis, cleavage, and synthesis of phosphodiester bonds (Cech, 1987, 1993). In particular, recent discoveries indicated that a class of RNA called small RNA operates many of cell's control (for a report, see Couzin, 2002). These diverse and specific biological functions of RNA are guided by their unique three-dimensional folding. Therefore, prediction or measurements of RNA folding and folding dynamics becomes one of central problems in biological studies.

In addition to standard experimental methods, such as x-ray crystallograph and NMR spectroscopy, single-molecule manipulation technique developed in the past decade provides a fresh and promising way in resolving the RNA folding problem (Essevaz-Roulet et al., 1997; Rief et al., 1999; Liphardt et al., 2001, 2002; Harlepp et al., 2003; Onoa et al., 2003). As a concrete example, an optical tweezer setup, which is also the experiment we consider in this work is sketched in Fig. 1 (Smith et al., 1996; Wang et al., 1997): a single RNA molecule is attached between two beads with RNA:DNA hybrid handle; one bead is held by a pipette, and the other is in a laser light trap. (In practice, the RNA is attached between the two beads with two RNA:DNA hybrid handles. To simplify simulation method, only one handle is considered. It should not change following discussions.) By moving the position of the pipette, the distance between the two beads and the force acting on the bead in the light trap can be measured with high resolution. This sophisticated setup has shown its abilities in recording the time-traces of the end-to-end distance of a small 22-basepair RNA hairpin (Liphardt et al., 2001), and resolving complicated unfolding pathways of 1540-base long 16S ribosomal RNA (Harlepp et al., 2003).

FIGURE 1.

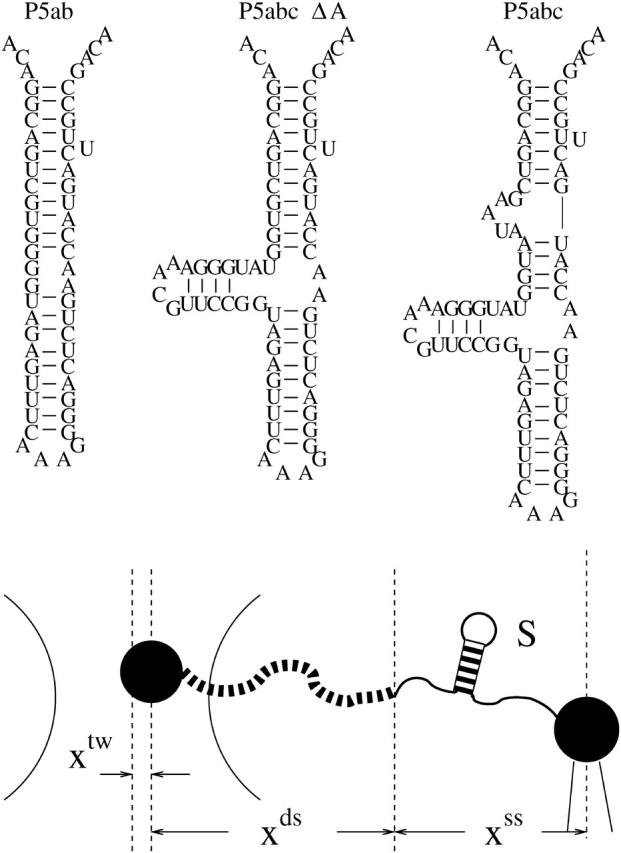
FIGURE 1

Open in a new tab

Sketch of an optical tweezer setup and the RNA molecules studied in the work. We denote the region between the two arcs as the optical trap. RNA molecules are attached between the two beads (larger black points) with a RNA:DNA hybrid handle (black dash curves). In theoretical model, the effect of the two beads has been neglected. The total extension x = xtw + xds + xss is externally controlled, whereas the individual extensions, xtw, the position of the bead with respect to the center of the optical trap; xds, the end-to-end distance of the double-stranded DNA (dsDNA) handles; and xss, the end-to-end distance of the single RNA are freely fluctuated. The RNA native structures for the three small RNA sequences, P5ab, P5abcΔA, and P5abc are folded by Vienna Package 1.4.

On the theoretical side, although complete three-dimensional RNA folding prediction so far seems enormously difficult (Tinoco and Bustanmante, 1999), RNA structural prediction from a physical point of view has made great progress on the level of secondary structure (Zuker and Stiegler, 1981; McCaskill, 1993; Hofacker et al., 1994). The advent of the single-molecule experiments addresses a challenging issue for theorists: whether or how can we apply the known secondary structural RNA knowledge to explain or predict the phenomena observed in the single-molecule experiments? Under force stretching or twisting, the elastic properties which were cared little about or even neglected before now must be seriously taken into account. As an attempt, in this work we construct a Monte Carlo simulation method, which can uniformly investigate the RNA thermodynamical and kinetic unfolding behaviors. Compared to the enormous simulation works about force unfolding proteins, the simulations for RNAs are few (Harlepp et al., 2003; Liu and Ou-Yang, 2004). The work here should fill this gap. In addition, our simulation can build a connection between the analytical studies of force unfolding RNA and the real experiments.

The organization of this work is as follows. In the next section, we simply review a stochastic RNA folding algorithm which was developed by Flamm et al. (2000). Then we show how the algorithm can be extended to the force stretching case by applying a polymer elastic theory. According to different experimental setups, two ensembles—the constant force and constant extension ensembles—are considered, respectively. To demonstrate the correctness of our method, we simulate the experiment carried out by Liphardt et al. (2001) in Results section. We study the force-extension curves of three RNA molecules in equilibrium in the constant force ensemble and the mechanical behaviors of P5ab molecule in the constant extension ensemble in detail. The behaviors include the pulling speed dependence of unfolding force, the force-hysteresis phenomenon, and the coincidence of stretching-relaxing force curves in thermal equilibrium. Because the molecule's extension jumps between two values around unfolding force, in the following part, we particularly study the kinetics of the P5ab under the constant force. The main reason for choosing the P5ab for study is that its equilibrium and kinetic properties have been explored by experimenters in great detail, which provide us a good opportunity for testing the accuracy of our simulation. On the other hand, the structure of the P5ab is simpler but has an intriguing two-state folding and unfolding behavior with or without mechanical force. It is an ideal system for further theoretical analysis, e.g., application of the Jarzynski equality (Ritort et al., 2002), the microscopic theory of folding and unfolding kinetics (Hummer and Szabo, 2003; Hyeon and Thirumalai, 2003), etc. In the final section, we compare our method with two previous theoretical models and point out possible extensions of this algorithm.

MODEL

RNA folding conformational space without force

A RNA sequence is denoted by a nucleotides string l = (x1, x2, … , xn), xi ∈ {A, U, C, G}; the bases x1 and xn are the nucleotides at 5′ and 3′ end of the sequence, respectively. A secondary structure S of a RNA sequence is a list of basepairs [xi, xj] that must satisfy two conditions: every base forms a pair with at most one other base, and if any two basepairs [xi, xj] and [xk, xl] are in the list, then i < k < j implies i < l < j. All structures of the sequence l comprise a set, S(l) = {S0, S1, … , Sm, 0}, here 0 denotes the completely open chain conformation.

To describe the folding or unfolding process as a time-ordered series of the structures in the set S(l), a relation M which specifies whether two structures are accessible from each other by an elementary “move” must be reasonably defined. The definition is identical to specifying a metric in the set S(l). Any secondary structure formation or dissolving hence can be described by a succession of elementary steps chosen according to some distributions from a pool of acceptable moves in the conformational space C(l) = {S(l), M}. In the absence of mechanical force, two kinds of move sets have been proposed in modeling secondary structural RNA folding: one is the formation or decay of a single helix (Mironov and Lebedev, 1993; Gultyaev et al., 1995; Breton et al., 1997), and the other is the removal or insertion of single basepairs per time step (Flamm et al., 2000). We make use of the latter, for it is the simplest move set on the level of secondary structure. Moreover, we mainly focus on smaller RNA in present work. The formation or removal of a helix may cause larger structural changes, whereas its physical relevance of RNA folding or unfolding seems debatable.

RNA unfolding move set and energy model with mechanical force

According to the difference of the external controlled parameters, the RNA unfolding experiments can be carried out under constant extension and constant force, i.e., the constant extension and the constant force ensembles (Liphardt et al., 2001). The move set and the system energies mentioned above must be extended correspondingly.

We first consider the constant extension ensemble. Fig. 1 is the sketch of an optical tweezer setup for this ensemble. Two simplifications have been made in our model. We suppose that changes of the extensions of RNA and the handle proceed along one direction. Physical effects of the beads are neglected. Consequently, any state of the system can be specified with three independent quantities, the position of the bead with respect to the center of the optical trap, xtw, the end-to-end distance of the handle, xds, and the RNA secondary structure S, i.e., the system in i-state 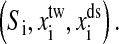Inline graphic Here we do not include xss, the extension of the RNA for the sum of individual extensions satisfies constraint condition, x = xtw + xds + xss, where x is the distance between the centers of the light trap and the bead held by the pipette, and it also is the external controlled parameter in the constant extension ensemble. The move set for this system is extended as follow,

graphic file with name M2.gif (1)

The first kind of the moves is the removal or insertion of single basepairs while keeping the extensions xtw and xds. The other two kinds are to respectively move the positions of the bead in the light trap and the end of the handle which connects RNA with a small displacement δ, whereas the secondary structure is fixed. Therefore, unfolding the single RNA for the constant extension ensemble proceeds in an extended conformational space C(l) × Rtw × Rds, where Rtw = (0, +∞) and Rds = (0, lds), and lds is the contour length of the dsDNA handle. Given the system state i, we can write its whole energy as

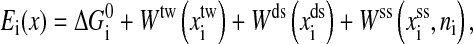graphic file with name M3.gif (2)

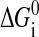where Inline graphic is the free energy obtained from folding the RNA sequence into the secondary structure Si, and the elastic energies of the optical trap, the handle, and the single-stranded part of the RNA are

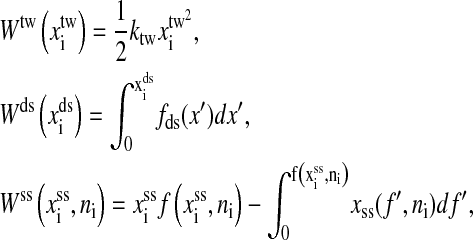graphic file with name M5.gif (3)

respectively. In the expression Wds, fds(x′) is the average force of the handle at given extension x′,

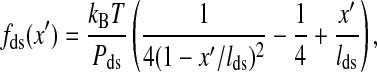graphic file with name M6.gif (4)

where Pds is the persistence length, respectively. In the expression Wss, xss(f′, ni) is the average extension of the single stranded part of the RNA whose bases (exterior bases) is ni at given force f′,

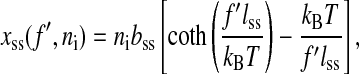graphic file with name M7.gif (5)

where bss and lss are the monomer distance and the Kuhn length of the single-stranded RNA, respectively (Bustamante et al., 1994; Smith et al., 1996). Note that 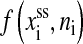Inline graphic is the inverse function of xss(f′, ni). Similar elastic energies have been used in dsDNA unzipping problem (Bockelmann et al., 1998).

In the real experiments, constant force can be imposed on RNA molecules with feedback-stabilized optical tweezers capable of maintaining a preset force by moving the beads closer or further apart. Including the feedback mechanism in theoretical study is not essential now. A possible move set for the constant force ensemble is the same with the set for the constant extension ensemble. The system energies in state i contain the free energy of the secondary structure Si and the work 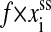Inline graphic done on the single RNA by the constant force f. (Because the handle only transfers constant force to the RNA molecule, its contribution has been viewed as one part of the feedback mechanism.) However, this naive extension is unreasonable for the elastic characteristics of the single RNA cannot be correctly taken into account in this way. A strict Monte Carlo method in studying chain molecules under a constant force should contain complicated conformational transitions (Zhang et al., 2001). To avoid complicated conformational description, in this work, we propose an energy expression on the coarse-grain level for the given secondary structure Si under constant force f,

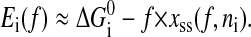graphic file with name M10.gif (6)

Here we replace the extension 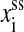Inline graphic with average extension xss(f, ni). The physics underlying the formula is that the maximum probable conformations are the most important for the work. Apparently, xss(f, ni) contains the elastic characteristics of the RNA. As the formula is also used in kinetic studies, additional requirement of the formula is that, under mechanical force the conformational relaxation process of the single-stranded part of the RNA is faster than the slowest process of the secondary structural arrangement. In contrast to the constant extension ensemble, the RNA secondary structure S can completely specify any state of the constant force ensemble. Therefore, the move set for this ensemble is the same with the set for RNA folding without force, i.e., its unfolding space is C(l).

Continuous time Monte Carlo algorithm

Given the move sets and the unfolding conformational spaces, the RNA unfolding for the two ensembles can be modeled as a Markov process in their respective spaces. After conventional stochastic kinetics of chemical reactions, these processes are described as the master equation,

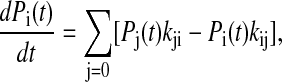graphic file with name M12.gif (7)

where Pi(t) is the probability of the system being i-state at time t, and kij is the transition probability from i-state to j-state. The nonzero transition probabilities satisfy the detailed balance condition,

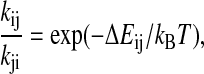graphic file with name M13.gif (8)

where kB is Boltzmann constant, ΔEij = Ej − Ei. For the rates kij we assume a symmetric rule (Kawasaki, 1966; Flamm et al., 2000)

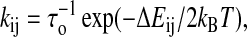graphic file with name M14.gif (9)

where τo is used to scale time axis of the unfolding process; its value will be determined by the kinetic experimental data. Other rules for the transition probabilities such as Metropolis rule can be chosen. Although different rules do not change the equilibrium and kinetic results, computer simulations show that the symmetric rule is more efficient than the others.

The form of the master equation looks relatively simple, however it is mathematically intractable to solve analytically for simple “reaction” system such as RNA P5ab. Previous work has demonstrated that a continuous time Monte Carlo simulation is an excellent approach toward the stochastic process described by Eq. 7 (Bortz et al., 1975; Gillespie, 1976; Flamm et al., 2000). As a variant of the standard Monte Carlo method, the continuous time Monte Carlo method is very efficient and fast because of lacking of waiting times due to rejection. Here we are not ready to present detailed knowledge about this method (Newman and Barkema, 1999). We just point our why this method is important in RNA folding studies. One is that the energy landscape of RNA folding is supposed to be rugged with a lot of deep local minima, and the other is that the method provides an inner clock to measure time.

Parameters and measurement

We simulate the single RNA folding and unfolding under mechanical force at the experimental temperature T = 298K. The elastic parameters used are: Pds = 53 nm, lds = 320 nm, bss = 0.56 nm, lss = 1.5 nm, and ktw = 0.2 pN/nm. We use the single-stranded DNA parameters for the single stranded part of RNA because they have similar chemical structure. The displacement δ = 0.1 nm. The free energy parameters for the RNA secondary structures are from the Vienna package 1.4 (Hofacker, 2003) in standard salt concentrations [Na+] = 1 M and [Mg2+] = 0 M. (To account for the different ionic conditions between the experiment ([Na+] = 250 mM and [Mg2+] = 10 mM or EDTA) and standard conditions, two simple salt corrections have been suggested in Refs. (Cocco et al., 2003; Gerland et al., 2003). But our calculation (see discussion) shows that such corrections might not be correct. In this work we instead use the free energy parameters at standard condition.) In addition to the standard Watson-Crick basepairs (AU and CG), GU basepair is allowed in our simulation. Formation of isolated basepairs is forbidden because of their instability. In the constant extension ensembles, the force fi acting on the RNA molecule at i-state is calculated by 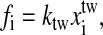Inline graphic and the bead-to-bead distance 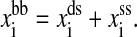Inline graphic In the constant force ensemble, the extension of the molecule is xss(f, ni) if the secondary structure in this step is Si at a given force f.

RESULTS

Force-extension curves in equilibrium and nonequilibrium

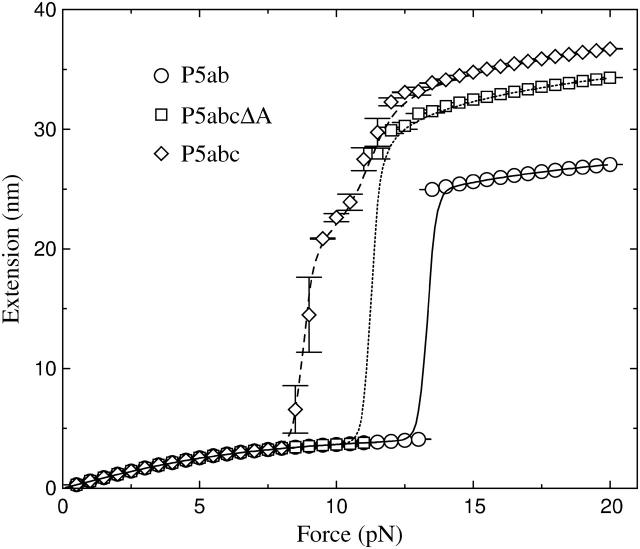
To test the accuracy of our method, we simulate extension-force curves of RNA molecules in the two ensembles. In contrast to the constant extension ensemble, more theoretical works were concerned about the constant force ensemble (Lubensky and Nelson, 2002, and references therein). For this ensemble, we study three small RNAs—P5ab, P5abcΔA, and P5abc in equilibrium (see Fig. 2). These molecules represent major structural units of larger RNA assemblies: the native state of the P5abcΔA is similar with the hairpin P5ab except for an additional helix and thus is a three-helix junction, and the P5abc is comparatively complicated and contains an A-rich bulge (see Fig. 1). When these molecules are stretched by small force, their extensions increase monotonically. However, when the force increases to ∼13.3 pN, the extension of the P5ab is interrupted by an ∼20-nm jump. Similar to the P5ab, the extension of the P5abcΔA also has a sharp jump at the force ∼11.3 pN. These curves show that the mechanical unfolding transitions for the P5ab and the P5abcΔA are all or none. As the two molecules are almost the same, and the free energy of the latter is lower than the energy of the P5ab, we conclude that the presence of the additional helix in the P5abcΔA destabilizes the molecular structure. Compared to simple all or none behaviors of the two molecules, the extension-force curve of the P5abc provides more features: the extension has a large jump (∼17 nm) around the force 8.0 pN, and an inflection is followed and the extension increases gradually to full length. The smaller unfolding force of the P5abc shows that the presence of th e A-rich bulge makes the molecule unstable. Because the jump is ∼2/3; of the full extension, the transition represents unfolding of the P5a helix and parts of the three-helix junction. All results obtained above are considerably consistent with the experimental measurements (Liphardt et al., 2001).

FIGURE 2.

FIGURE 2

Open in a new tab

Extension-force curves for the P5ab, P5abcΔA, and P5abc molecules in the constant force ensemble. The foldings and unfoldings for the P5ab and P5abcΔA under the constant force are all or none around the transitions 13.3 pN and 11.3 pN, respectively, whereas the extension-force curve for the P5abc has an intermediate between 8.0 and 11.0 pN. The symbols are the results from the Monte Carlo simulation, and the lines are obtained from exact numerical calculation.

For the constant extension ensemble, we focus on the mechanical behaviors of the P5ab, whose equilibrium characteristics also have been studied in the previous theoretical work (Gerland et al., 2003). At the beginning of simulation t = 0, the system will be run ∼107 τ0 under a preset whole extension x0 to ensure that it is in equilibrium. We then continually stretch the molecule by increasing the whole extension δx = 2 nm after a dwell time δt (in unit τo), or at the time t = n δt, the whole extension is xn = x0 + n δx, n = 0, 1, ⋯. When the extension reaches a maximum value xe, where the molecule is unfolded completely, the molecule will continually relax by decreasing its extension δx after δt till the origin extension x0 is reached. We periodically perform the stretching-relaxing cycles. Average physical quantities 〈A〉 at xn observed between the times (n)δt and (n + 1)δt, such as the average force f and the average extension xbb can be obtained by a time-average 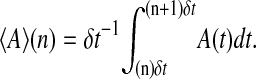Inline graphic This simulation schedule is efficient, for the system will reach equilibrium state faster than the simulation beginning at the same initial condition at different whole extensions. In addition, whether the system reaches equilibrium state can be simply determined by the coincidence of the stretching and relaxing curves. In the real experiment the same method was used to indicate thermal equilibrium (Liphardt et al., 2001).

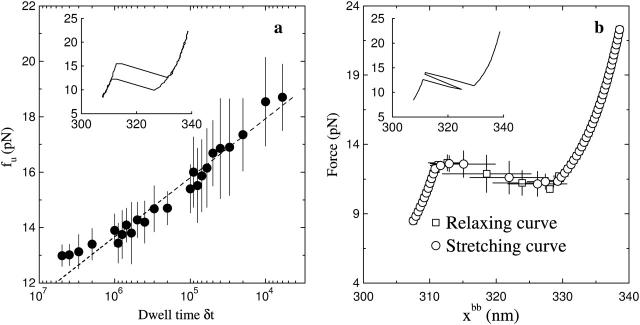
We simulate the stretching-relaxing curves of the hairpin P5ab; the results are shown in Fig. 3. When the dwell time is short, the stretching-relaxing extension-force curves are incoincident; see the inset in Fig. 3 a, where δt = 105. It indicates that the loading rate of force is faster than the slowest relaxing process of the P5ab, or the presence of force-hysteresis phenomenon. The average unfolding force fu as function of the dwell time is calculated. We find that fu is a linear function of the logarithm of the dwell time (between 106 and 104). As predicted by Evans and Ritchie (1997), for the intermediate pulling speed the fu linearly grows with the logarithm of the force loading rate γ = ktwv, fu ∼ ln(γ). In our case, the pulling speed is v ≈ δx/δt. Hence fu ∼ − ln(δt). When the dwell time is longer (here ∼106), or the pulling speed is sufficiently slow, however, the linear relation is no longer satisfied. At this loading rate, the average stretching-relaxing curve is coincident, or the system is thermodynamical equilibrium. We find that the force-extension curve is interrupted at 13.0 pN by an ∼20-nm plateau (see Fig. 3 b). In the several stretching curves the extensions of the P5ab around the unfolding force jump from the folded to unfolded state and then turn back, though the whole extension increases after a longer dwell time (see the inset in Fig. 3 b). The quantitative and qualitative results of the simulation for the P5ab agree with the experiment quite well (Liphardt et al., 2001).

FIGURE 3.

FIGURE 3

Open in a new tab

Extension-force curves for P5ab molecule in the constant extension ensemble. (a) The average unfolding force fu as a function of the dwell time; here δx = 2 nm. The dash line is the fitting function of fu with respect to the logarithm of δt. (Inset) force hysteresis phenomenon at δt = 105 (in unit τ0). (b) The average stretching-relaxing force-extension curves in thermal equilibrium, where the dwell time 5 × 106. (Inset) a force-extension trace showing hopping.

Kinetics of folding and unfolding at constant force

Compared to the general thermodynamics of RNA under force in equilibrium, single-molecule methods are more interesting in kinetic folding and unfolding studies. With the single molecule experiments we can follow the actual folding or unfolding trajectories of single molecules on high resolution even when they occur in equilibrium state, which will shed light on the difficult kinetic folding problem. We mentioned above that the extension of the P5ab in the constant extension ensemble may hop back and forth between two states. To investigate this bistability, Liphardt et al. (2001) imposed a constant force on the P5ab and P5abcΔA. They found that, when the force was held constant at the transition within ∼1 pN, the P5ab and P5abΔA switched back and forth with time from the folded hairpin (hp) to the unfolded single strand (ss). A two-state kinetics was proposed to explain the intriguing phenomenon. 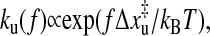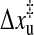The rate constants for unfolding reaction can be fit to an Arrhenius-like expression of the form Inline graphic where Inline graphic is the thermally averaged distance between the hairpin state and the transition state along the direction of force. A similar expression also holds for the folding rate kf(f). Apparently, this description can not clarify the physics underlying the folding and unfolding reactions.

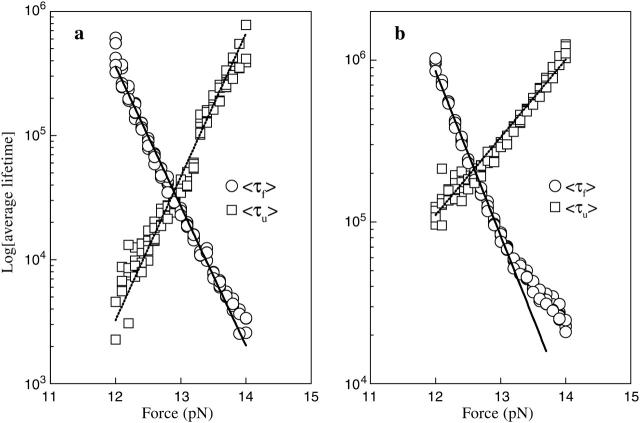
Because our simulation is based on the microscopic interactions, we are interested in whether the similar time traces can be obtained by simulation. The question is relevant to the correctness of the move set we designed. Same with the experiment, we record the extension-time traces of the RNA molecules at different constant forces in equilibrium. For example, one extension-time traces for the P5ab is shown in Fig. 4 a. The extension of the molecule jumps between two values, ∼5 nm and ∼22 nm around the transition force. Because the jumps are extremely rapid with respect to the lifetimes of the molecule in the two states, we simply classify the states whose extensions are larger than 15 nm as the single stranded states, and the others as the hairpin states. In addition, there are significant fluctuations about the two states. Around the transition the frequencies of the different lifetimes at the single stranded state and the hairpin state can be obtained by a long time simulation (to get enough data, the simulation time is 109τ0 after equilibrium). Fig. 4 c shows the frequency distributions of a typical simulation at a force 12.90 pN. These distributions can be fit to an exponential function ∝ exp(− t/〈τi〉) very well, where 〈τi〉, i = u, f denote the force-dependent average lifetimes at the two states, respectively. For example, the average lifetimes in this simulation are 〈τu〉 ≈ 3.4 × 104τo and 〈τf〉 ≈ 3.1 × 104τo. We calculate all average lifetimes near the transition force of the P5ab, and their corresponding values with different forces are shown in Fig. 5 a. We find that the logarithms of the lifetimes for the two states are strikingly consistent with linear functions of the forces. Because the reaction rate constants are the inverse of the average lifetimes, we fit τo by making 〈τu〉(f*) = 〈τf〉(f*) equal to the experimental value 1/k*, where k* ≡ ku = kf, and had 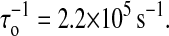Inline graphic Using the same method, the reaction rate constants for the P5abcΔA also are calculated. A comparison of the simulation results and the experimental data is listed in Table 1. Because our simulation does not need additional fitting parameters, the striking consistence of our results with the experiment assures us that the RNA folding and unfolding model proposed here has grabbed the main physics.

FIGURE 4.

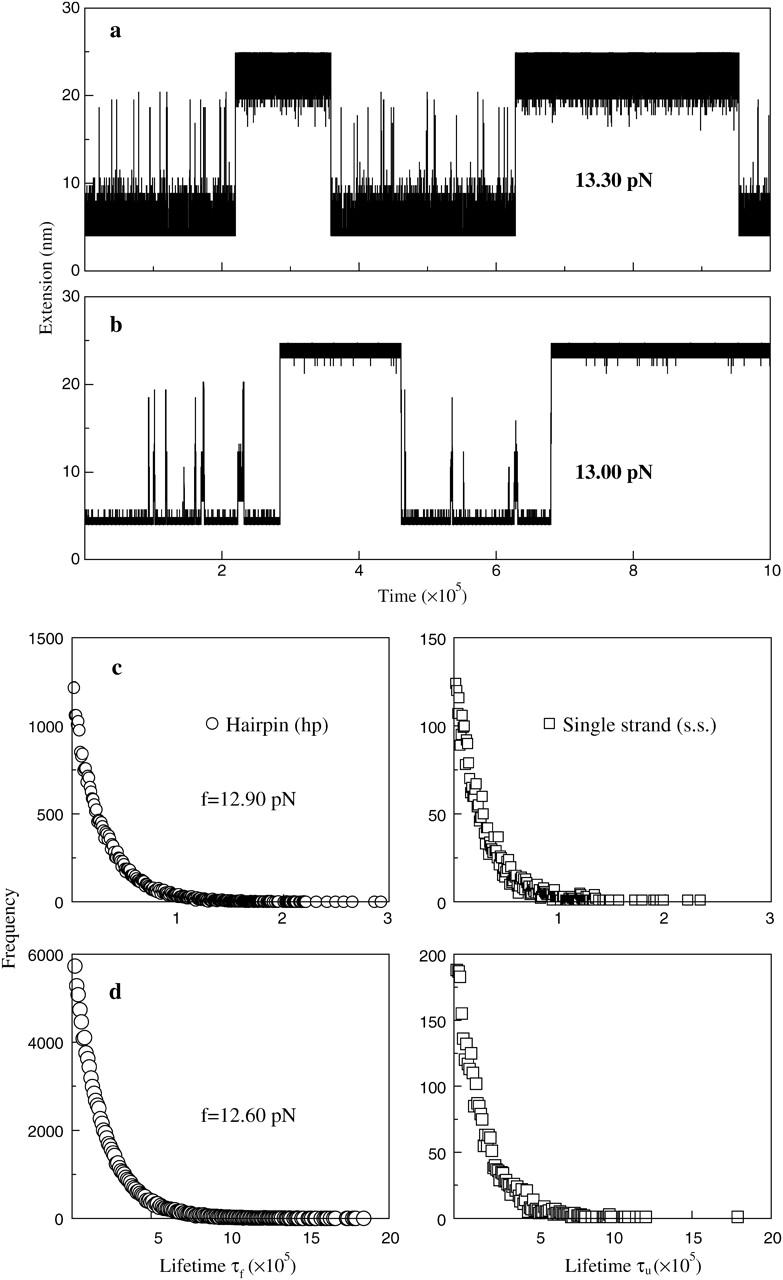
FIGURE 4

Open in a new tab

Extension versus time traces of the P5ab molecule at constant forces in equilibrium: (a) the dynamics proposed by us and (b) the fork dynamics proposed by Cocco et al. (2003). The frequency distributions of the lifetimes of the single strand and hairpin states: (c) the dynamics proposed by us and (d) the fork dynamics. The average lifetimes of the two states in simulations can be obtained by fitting to exponential functions.

FIGURE 5.

FIGURE 5

Open in a new tab

Log of the average lifetimes of the single stranded and hairpin states for the P5ab molecule at different forces around the transitions: (a) dynamics proposed in this work; (b) fork dynamics. The time is in unit τo, which can be obtained by fitting with experimental data. Note the slopes of ln 〈τf〉 and ln 〈τu〉 are independent of the value τo.

TABLE 1.

Molecule 〈Δx〉(nm) f* (pN) ln kf(f)(s−1) ln ku(f)(s−1)
P5ab,Mg+2 19 ± 2 14.5 ± 1 41 ± 1.9 − (2.8 ± 0.1)f −39 ± 2.3 + (2.9 ± 0.2)f
P5ab, by Cocco et al. (2003) 15.1 27.5 − 2.74f −42.9 + 1.93f
P5ab, EDTA 18 ± 2 13.3 ± 1 37 ± 4.0 − (2.7 ± 0.3)f −32 ± 4.8 + (2.6 ± 0.4)f
P5ab, by us 20.0 12.9 ± 0.5 36.1 ± 1.4 − (2.7 ± 0.1)f −31.5 ± 0.7 + (2.6 ± 0.1)f
P5ab, fork dynamics 20.0 12.6 ± 0.3 16.8 ± 0.2 − (1.1 ± 0.0)f −26.7 ± 0.2 + (2.3 ± 0.0)f
P5abcΔA, Mg+2 22 ± 4 12.7 ± 0.3 58 ± 7.5 − (4.2 ± 0.5)f −39 ± 9.3 + (2.7 ± 0.7)f
P5abcΔA, by Cocco et al. (2003) 12.9 9.4 − 2.05f −43.8 + 2.06f
P5abcΔA, EDTA 23 ± 2 11.4 ± 0.5 31 ± 6.0 − (2.6 ± 0.5)f −31 ± 11 + (2.5 ± 0.3)f
P5abcΔA, by us 25.0 11.3 ± 0.6 36.2 ± 1.8 − (3.4 ± 0.2)f −27.8 ± 0.8 + (2.3 ± 0.1)f
Open in a new tab

Simulation results for the P5ab and P5abcΔA compared to the experimental data from Liphardt et al. (2001) (in bold). Cocco et al. (2003) have studied the rate constants of folding and unfolding in the presence of Mg+2. However, they did not give any results in the absence of the ion about which we concern here. We list their results as a comparison. Note in our model the τo value of the P5ab is the same with the value of the P5abcΔA, but it does not equal to the τo in the fork dynamics.

DISCUSSION AND CONCLUSION

It is noteworthy to compare our method with two recent theoretical works. One is the direct numerical method proposed by Gerland et al. (2003). Their method was an extension of the partition function method in predicting secondary structure; the partition function over all secondary structures were calculated by dynamic programming (McCaskill, 1993). The simulation for the constant extension ensemble in equilibrium in a sense can be viewed as a Monte Carlo implement of the integral equation (Eq. 4) in their work. The numerical method therefore provided a good test for our simulation. But compared to their method, our simulation is more important in study of nonequilibrium phenomena, such as the extension jumps, stretching-relaxing hysteresis, and the time traces of the extension of the molecules, which are beyond the scope of thermodynamic equilibrium.

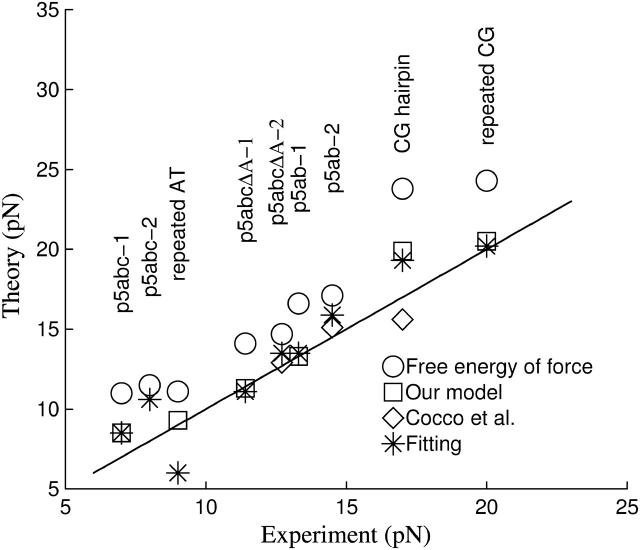
The other interesting work was given by Cocco et al. (2003). They proposed a simple dynamical model to explain the slow folding and unfolding kinetics of the small RNA molecules under constant force. There are several differences with our method. First is the expression of the work done by force. They suggested that its formula is the free energy of force, 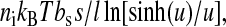Inline graphic where u = lssf / kBT. Our simulations, however, show that it cannot solve the unfolding forces which are consistent with the experimental measurements even if an ionic correction is applied. To precisely calculate the unfolding forces due to the different works, we develop a numerical method which can exactly calculate RNA unfolding in equilibrium by constant force (Liu and Ou-Yang, in preparation). This method is based on the same idea proposed by Gerland et al. (2003). We are not ready to present it here, but only show the relevant results. We calculate unfolding behaviors of six different RNA sequences in different experimental conditions with the works proposed by Cocco et al. (2003) and us, respectively (the sequences and the conditions are listed in the caption of Fig. 6). Three extension-force curves for the P5ab, P5abcΔA, and P5abc molecules using the work proposed by us are shown in Fig. 2, and the unfolding forces of them and their respective experimental measurements are shown in Fig. 6. We can get the following conclusions from the calculation. First our simulation is successful for the agreement of the two different methods is striking. Second, precision of the work formula we proposed is satisfactory. Using the previous work formula, the discrepancies between the theoretical predictions and experimental measurements cannot be eliminated even if a reasonable ionic correction is introduced. Of course, we cannot exclude a possibility that the free energy parameters of RNA are not precise enough in the force stretching cases.

FIGURE 6.

FIGURE 6

Open in a new tab

Unfolding forces solved by the exact numerical method for six sequences in the different experimental conditions. Temperature T = 298K and [Na+] = 0.25M: P5ab-1, P5abcΔA-1 and P5abc-1. Temperature T = 298K, [Na+] = 0.25M and [Mg2+] = 0.01M: P5ab-2, P5abcΔA-2, and P5abc-2. Temperature T = 293K and [Na+] = 0.15M: repeated AT and CG sequences (Rief et al., 1999). Temperature T = 298 and [Na+] = 0.15M: CG hairpin (Bustamante et al., 2000). The symbols represent: unfolding forces calculated by the free energy of force with ionic correction −0.193kBT ln([Na+] + 3.3[Mg2+]1/2) on RNA free energy (○), unfolding forces using our work formula without ionic correction (□), theoretical values predicted by Cocco et al. (2003) (⋄), and unfolding forces calculated by the free energy of force with best fitting ionic correction, −0.800kBT ln([Na+] + 3.3[Mg2+]1/2) (*).

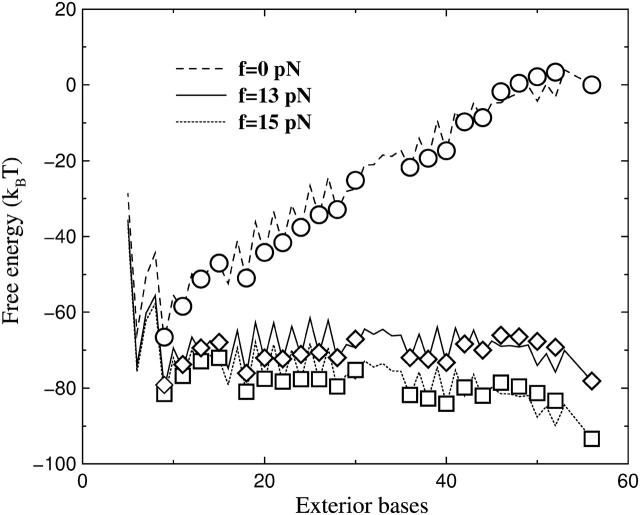
Then is the choice of the move set. Cocco et al. (2003) restricted the formation or removal basepair just proceeding in the “fork” location (fork dynamics). Their consideration was that pairing of the two distant bases is inhibited by a kinetic barrier. The folding and unfolding rate constants solved by their numerical method also agreed with the experiment; see Table 1. We simulate the fork dynamics for P5ab molecule to quantitatively understand the differences between their move set and ours. The results are shown in Fig. 4, b and d, and Fig. 5 b. We find that the fluctuations of the fork dynamics at the hairpin state and the single stranded state are smaller. Although in the fork dynamics the logarithms of the lifetimes for the two states are also consistent with linear functions of the forces (see Table 1), the value of τo in the dynamics is one order of magnitude smaller than the value in our model, i.e., 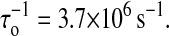Inline graphic Why do the two move sets result in distinct folding and unfolding dynamics? We give a qualitative interpretation. In our dynamic model, because the bases can freely form pairs with other bases, the energy landscape should be very rugged compared to the landscape of the fork dynamic model; whereas the ruggedness is responsible for the larger extensional fluctuations and slower diffusion rate or smaller 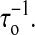Inline graphic As a proof, we show their free energy landscapes in Fig. 7. Recent theoretical analysis also supports our explanation (Hyeon and Thirumalai, 2003). Therefore, the fork dynamics loses the important physics in RNA folding and unfolding. Finally the fork dynamics must preset the RNA native structure. It is only available for unzipping simpler RNA hairpins. Their dynamics is not suitable for studying general RNA unfolding by force. On the contrary, because our model is based on a general RNA folding algorithm, and the kinetic inhibition effects are naturally taken into account by the entropy term in RNA free energy (McCaskill, 1993), we do not need to preset a molecular native state.

FIGURE 7.

FIGURE 7

Open in a new tab

Free energy landscapes of the two dynamics for the exterior bases of the P5ab. Here three typical forces are chosen. The symbols are from the fork dynamics, and the lines are calculated by the exact numerical method. We find that the landscapes for the fork dynamics are smoother.

Several improvements can be added in the algorithm, e.g., adding the effects of Mg+2, or uniforming the two different ensembles into one by including force feedback mechanism. But how to extend of our method to include complicated tertiary interactions should be the main task in following theoretical studies (Liphardt et al., 2001; Onoa et al., 2003). Recent works have shown that the inclusion of pseudoknots is possible (Rivas and Eddy, 1999; Isambert and Siggia, 2000).

Acknowledgments

We thank Dr. Flamm for providing us his computer program KINFOLD. It is also a pleasure to acknowledge Professor H.-W. Peng and J.-X. Liu for many helpful discussions in this work.

References

  1. Bockelmann, U., B. Essevaz-Roulet, and F. Heslot. 1998. DNA strand separation studied by single molecule force measurements. Phys. Rev. E. 58:2386–2394. [Google Scholar]
  2. Bortz, A. B., M. H. Kalos, and J. L. Lebowitz. 1975. A new algorithm for Monte Carlo simulation of Ising spin systems. J. Comput. Phys. 17:10–18. [Google Scholar]
  3. Breton, N., C. Jacob, and P. Daegelen. 1997. Prediction of sequentially optimal RNA secondary structures. J. Biomol. Struct. Dyn. 14:727–740. [DOI] [PubMed] [Google Scholar]
  4. Bustamante, C., J. F. Marko, E. D. Siggia, and S. B. Smith. 1994. Entropic elasticity of lambda-phage DNA. Science. 265:1599–1600. [DOI] [PubMed] [Google Scholar]
  5. Bustamante, C., S. B. Smith, J. Liphardt, and D. Smith. 2000. Single-molecule studies of DNA mechanics. Curr. Opin. Struct. Biol. 10:279–285. [DOI] [PubMed] [Google Scholar]
  6. Cech, T. R. 1987. The chemistry of self-splicing RNA and RNA enzymes. Science. 236:1532–1539. [DOI] [PubMed] [Google Scholar]
  7. Cech, T. R. 1993. Strucuture and mechanism of the large catalytic RNAs: group I and group II introns and ribonuclease P. In The RNA World. R. F. Gesteland and J. F. Atkins, editors. Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY. 239–269.
  8. Cocco, S., J. F. Marko, and R. Monasson. 2003. Slow nucleic acid unzipping kinetics from sequence-defined barriers. Eur. Phys. J. E. Soft Matter. 10:153–161. [DOI] [PubMed] [Google Scholar]
  9. Couzin, J. 2002. Small RNAs make big splash. Science. 298:2296–2297. [DOI] [PubMed] [Google Scholar]
  10. Evans, E., and K. Ritchie. 1997. Dynamic strength of molecular adhesion bonds. Biophys. J. 72:1541–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Essevaz-Roulet, B., U. Bockelmann, and F. Heslot. 1997. Mechanical separation of the complementary strands of DNA. Proc. Natl. Acad. Sci. USA. 94:11935–11940. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Flamm, C., W. Fontana, I. Hofacker, and P. Schuster. 2000. RNA folding at elementary step resolution. RNA. 6:325–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gerland, U., R. Bundschuh, and T. Hwa. 2003. Mechanically probing the folding pathway of single RNA molecules. Biophys. J. 84:2831–2840. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gillespie, D. T. 1976. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comp. Phys. 22:403–434. [Google Scholar]
  15. Gultyaev, A. P., F. H. D. van Batenburg, and C. W. A. Pleij. 1995. The computer simulation of RNA folding pathways using a genetic algorithm. J. Mol. Biol. 250:37–51. [DOI] [PubMed] [Google Scholar]
  16. Harlepp, S., T. M. Marchal, J. Robert, J.-F. Leger, A. Xayaphoummine, H. Isambert, and D. Chatenay. 2003. Probing complex RNA structures by mechanical force. Eur. Phys. J. E. Soft Matter. 12:605–613. [DOI] [PubMed] [Google Scholar]
  17. Hofacker, I. L. 2003. The Vienna RNA secondary structure server. Nucleic Acids Res. 31:3429–3431. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hofacker, I. L., W. Fontana, P. F. Stadler, S. Bonhoeffer, M. Takcer, and P. Schuster. 1994. Fast folding and comparison of RNA secondary structures. Monatsh. Chemie. 107:2903–2912. [Google Scholar]
  19. Hummer, G., and A. Szabo. 2003. Kinetics from nonequilibrium single-molecule pulling experiments. Biophys. J. 85:5–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hyeon, C.-H., and D. Thirumalai. 2003. Can energy landscape roughness of proteins and RNA be measured by using mechanical unfolding experiments. Proc. Natl. Acad. Sci. USA. 100:10249–10253. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Isambert, H., and E. D. Siggia. 2000. Modeling RNA folding paths with pseudoknots: application to hepatitis delta virus ribozyme. Proc. Natl. Acad. Sci. USA. 97:6515–6520. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kawasaki, K. 1966. Diffusion constants near the critical point for time-dependent Ising models. Phys. Rev. 145:224–230. [Google Scholar]
  23. Liphardt, J., B. S. Dumont, S. B. Smith, I. Tinoco, and C. Bustamante. 2002. Equilibrium information from nonequilibrium measurements in an experimental test of Jarzynski's equality. Science. 296:1832–1835. [DOI] [PubMed] [Google Scholar]
  24. Liphardt, J., B. Onoa, S. B. Smith, I. Tinoco, and C. Bustamante. 2001. Reversible unfolding of single RNA molecules by mechanical force. Science. 292:733–737. [DOI] [PubMed] [Google Scholar]
  25. Liu, F., and Z.-c. Ou-Yang. 2004. Unfolding single RNA molecules by mechanical force: a stochastic kinetic method. Phys. Rev. E. 70:040901–040904. [DOI] [PubMed] [Google Scholar]
  26. Lubensky, D. K., and D. R. Nelson. 2002. Single molecule statistics and the polynucleotide unzipping transition. Phys. Rev. E. 65:031917. [DOI] [PubMed] [Google Scholar]
  27. McCaskill, J. S. 1993. The equilibrium partition function and base pair binding probabilities for RNA secondary structure. Biopolymers. 29:1105–1119. [DOI] [PubMed] [Google Scholar]
  28. Mironov, A., and V. F. Lebedev. 1993. A kinetic model of RNA folding. Biosystems. 30:49–56. [DOI] [PubMed] [Google Scholar]
  29. Newman, M. E. J., and G. T. Barkema. 1999. Monte Carlo Methods in Statistical Physics. Clarendon Press, Oxford.
  30. Onoa, B., S. Dumont, J. Liphardt, S. B. Smith, I. Tinoco, and C. Bustamante. 2003. Identifying kinetic barriers to mechanical unfolding of the T. thermophila ribozyme. Science. 299:1892–1895. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Rief, M., H. Clausen-Schaumann, and H. E. Gaub. 1999. Sequence-dependent mechanics of single DNA molecules. Nat. Struct. Biol. 6:346–349. [DOI] [PubMed] [Google Scholar]
  32. Ritort, F., C. Bustamante, and I. Tinoco, Jr. 2002. A two-state kinetic model for the unfolding of single molecules by mechanical force. Proc. Natl. Acad. Sci. USA. 99:13544–13548. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Rivas, E., and S. R. Eddy. 1999. A dynamic programming algorithm for RNA structure prediction including pseudoknots. J. Mol. Biol. 285:2053–2068. [DOI] [PubMed] [Google Scholar]
  34. Smith, S. B., Y. Cui, and C. Bustamante. 1996. Overstretching B-DNA: the elastic response of individual double-stranded and single-stranded DNA molecules. Science. 271:795–799. [DOI] [PubMed] [Google Scholar]
  35. Tinoco Jr., I., and C. Bustanmante. 1999. How RNA folds. J. Mol. Biol. 293:271–281. [DOI] [PubMed] [Google Scholar]
  36. Wang, M. D., H. Yin, R. Landick, J. Gelles, and S. M. Block. 1997. Stretching DNA with optical tweezers. Biophys. J. 72:1335–1346. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Zhang, Y., H. Zhou, and Z.-C. Ou-Yang. 2001. Stretching single-stranded DNA: interplay of electrostatic, base-pairing, and base-pair stacking interactions. Biophys. J. 81:1133–1143. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Zuker, M., and P. Stiegler. 1981. Optimal computer folding of larger RNA sequences using thermodynamics and auxiliary information. Nucleic Acids Res. 9:133–148. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES