Line Tension and Interaction Energies of Membrane Rafts Calculated from Lipid Splay and Tilt

Abstract

Membrane domains known as rafts are rich in cholesterol and sphingolipids, and are thought to be thicker than the surrounding membrane. If so, monolayers should elastically deform so as to avoid exposure of hydrophobic surfaces to water at the raft boundary. We calculated the energy of splay and tilt deformations necessary to avoid such hydrophobic exposure. The derived value of energy per unit length, the line tension γ, depends on the elastic moduli of the raft and the surrounding membrane; it increases quadratically with the initial difference in thickness between the raft and surround; and it is reduced by differences, either positive or negative, in spontaneous curvature between the two. For zero spontaneous curvature, γ is ∼1 pN for a monolayer height mismatch of ∼0.3 nm, in agreement with experimental measurement. Our model reveals conditions that could prevent rafts from forming, and a mechanism that can cause rafts to remain small. Prevention of raft formation is based on our finding that the calculated line tension is negative if the difference in spontaneous curvature for a raft and the surround is sufficiently large: rafts cannot form if γ < 0 unless molecular interactions (ignored in the model) are strong enough to make the total line tension positive. Control of size is based on our finding that the height profile from raft to surround does not decrease monotonically, but rather exhibits a damped, oscillatory behavior. As an important consequence, the calculated energy of interaction between rafts also oscillates as it decreases with distance of separation, creating energy barriers between closely apposed rafts. The height of the primary barrier is a complex function of the spontaneous curvatures of the raft and the surround. This barrier can kinetically stabilize the rafts against merger. Our physical theory thus quantifies conditions that allow rafts to form, and further, defines the parameters that control raft merger.

INTRODUCTION

Microdomains of cell membranes that are rich in cholesterol and sphingolipids are known as “rafts” (Anderson and Jacobson, 2002; Simons and Ikonen, 1997; Simons and Vaz, 2004). Rafts are receiving increasing attention because they contain and concentrate important proteins that must interact with each other to carry out cellular function, such as signal transduction (Harder, 2004). Cellular rafts are small, making it difficult to unambiguously study their properties (Edidin, 2001; Pralle et al., 2000; Prior et al., 2003; Sharma et al., 2004). In lipid bilayer membranes, however, large domains form that are rich in cholesterol and sphingolipids (Baumgart et al., 2003; Crane and Tamm, 2004; Dietrich et al., 2001; Feigenson and Buboltz, 2001; Samsonov et al., 2001; Veatch and Keller, 2002; Veatch et al., 2004). The large size of these domains facilitates their study. Bilayer rafts are circular and rapidly resume this shape after an external perturbation, showing that a line tension (an energy per unit length of boundary) exists at the boundary of the raft. If many small rafts were to merge into a large one, the total length of raft boundary would be reduced, as would the boundary's energy. Opposing this reduction in energy is the decreased entropy that would result if many rafts were to become one. Because of the competition between smaller boundary energies and unfavorable entropy with raft merger, the raft area will be distributed over smaller raft sizes for smaller line tension. Because line tension controls the size distribution of rafts, it is important to develop a theory that can explain and predict line tension on the basis of the physical properties of the membrane.

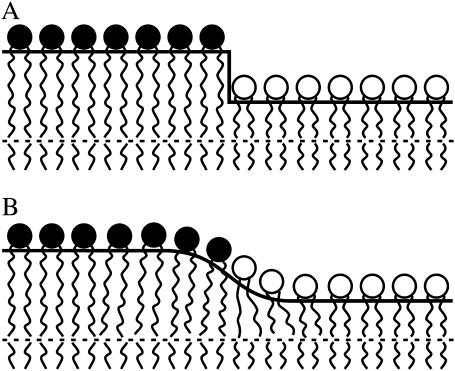
Rafts are thicker than the membrane surrounding them (the “surround”) in lipid bilayer systems, as shown by both atomic force microscopy (Lawrence et al., 2003; Yuan et al., 2002) and x-ray diffraction (Gandhavadi et al., 2002). If the orientation and length of the lipids are the same as they are at some distance from the boundary, an abrupt “step-like” change in thickness would exist at the raft boundary, and this would create a significant hydrophobic surface exposed to water (Fig. 1 A). For a hydrocarbon-water surface tension of 50 erg/cm², creating a step change in bilayer thickness of 0.5–1 nm would require ∼5–10 kT/nm (kT ≈ 4 × 10⁻¹⁴ erg). This energy per unit length is equal to a line tension of 20–40 pN. This value is unrealistically high and almost two orders of magnitude greater than an experimentally determined value (Baumgart et al., 2003). If lipids were to deform at the boundary so as to prevent the creation of hydrophobic surfaces by protruding rafts, the line tension would be reduced. Elastic deformations near the boundary of the monolayers should thus smooth out the interface and minimize the sum of the elastic and hydrophobic energy of the interface (Fig. 1 B). The lengths of the membrane spanning domains of membrane proteins are generally different from the thickness of the surrounding lipid bilayer; this is known as “hydrophobic mismatch”. The lipid deformations necessary to compensate for this mismatch have been considered (Fattal and Ben-Shaul, 1993; Harroun et al., 1999; Lundbaek and Andersen, 1999). For proteins, only the surround can deform in response to the mismatch, whereas for rafts, both raft and surround will deform.

FIGURE 1.

A schematic representation of the raft boundary. The raft, on the left, is thicker than the surround on the right. (A) A step in monolayer thickness creates a large hydrophobic surface. (B) Monolayer deformation at the raft boundary alleviates any creation of hydrophobic surfaces exposed to water.

Three fundamental lipid monolayer deformations in continuum elasticity theory are splay (a generalization of bending), tilt, and area compression. The physics and equations of these deformations were first described in classical articles (Frank, 1958; Helfrich, 1973) and are now employed to calculate a variety of physical membrane phenomena (Fournier, 1999; Hamm and Kozlov, 1998, 2000; MacKintosh and Lubensky, 1991; May, 2002; May and Ben-Shaul, 1999; Nielsen et al., 1998). The three modes of deformation—splay, tilt, and area stretching—could be considered together, but this would lead to unwieldy equations, necessitating that physical intuition be sought by considering two deformations at a time. We previously combined the deformations of tilt and area compression, allowing the hydrophobic mismatch to be completely compensated by the deformations; we calculated the line tension of such rafts (Akimov et al., 2004). But the energy to deform a monoloyer by area compression is significantly greater than that needed to deform by splay and tilt. This is readily seen by using the elastic moduli to compare the energy/area necessary for each deformation: for compression the modulus is E_a ∼ 120 erg/cm² (Rawicz et al., 2000), for splay 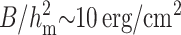for a monolayer thickness h_m ∼ 2 nm (Niggemann et al., 1995; Rawicz et al., 2000), and for tilt the modulus is K ∼ 40 erg/cm² (Hamm and Kozlov, 1998, 2000; May, 2002). Area compression is even greater for cholesterol enriched membranes, which have severalfold higher compression moduli (Evans and Needham, 1987; Meleard et al., 1997; Needham et al., 1988; Needham and Nunn, 1990). Thus, lipids should deform at the boundary of a raft through splay and tilt, with little contribution from area compression. Also, it is well known that spontaneous curvature is a critical determinant of splay, and in turn splay is a controlling membrane deformation of several membrane processes, such as membrane fusion (Kozlovsky and Kozlov, 2002; Kuzmin et al., 2001; Markin and Albanesi, 2002). Splay and spontaneous curvature should thus be explicitly considered to properly describe the physics of line tension. In this article, we systematically utilize the deformations of splay and tilt to calculate line tension according to the theory of continuous elastic membranes.

Statement of the problem

The model

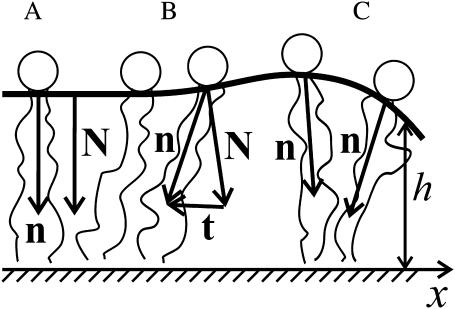
We consider a bilayer for which mirror symmetry is maintained with respect to the midplane between monolayers. For mirror symmetry, phase separation of lipids occurs at the same transbilayer location for both monolayers so that the raft and the surround, each separately, consist of identical monolayers; the midplane is always flat. This allows us to consider the deformations of only a single monolayer of the bilayer. To describe the boundary of a raft, we introduce a Cartesian coordinate system in which the plane z = 0 is located at the midplane of the bilayer; the x axis is perpendicular to the raft boundary, which is located at x = 0. We approximate the boundary of the raft as a straight line. We thus introduce an infinite monolayer that consists of two semiinfinite stretches: each stretch (raft on the left, surround on the right) has a different equilibrium thickness; they meet at x = 0. The geometry and mechanical deformations of a single monolayer are treated by introducing a dividing surface. We choose the neutral surface as our dividing surface; this is defined as the surface for which the deformations of monolayer stretching (or compression) and bending are energetically uncoupled from each other (Ben-Shaul et al., 1996; Kozlov et al., 1994; Leikin et al., 1996). Experiment and theoretical analysis show that this surface is located along the interface between the polar headgroups and the hydrocarbon tails (Kozlov et al., 1994; Leikin et al., 1996). The neutral surface is described by a unit vector—the normal N, which is perpendicular to the surface—and by its distance h from the bilayer midplane (Fig. 2). We define h as the monolayer thickness. We show in Appendix 1 that hydrophobic exposure to water must be completely eliminated at the raft boundary; the raft and the surround thus have the same thickness at x = 0 and the neutral surface is continuous. We assign at every point on the surface a unit vector director, n, that indicates the average direction of the asymmetric lipid molecule at that location (Fig. 2). Our approximation that the raft boundary is a straight line is strictly valid if the radius of the raft is much greater than the characteristic length over which the deformations decay. Because the system is invariant along the raft boundary, our system is essentially one-dimensional, and all deformations vary along an axis perpendicular to the raft boundary. We assume that a monolayer is volumetrically and laterally incompressible. Lipids must be transferred from the interior of the raft and/or surround if the length of the boundary is to increase. We calculate the work required to create the additional boundary that smoothly connects the raft and surround as the energy necessary to elastically deform it. We refer to our calculated elastic energy of deformation per unit length of interface as “line tension”.

FIGURE 2.

An illustration of tilt and splay. (A) In the unperturbed flat monolayer, the normal N and director n are parallel. (B) Lipid tilt is illustrated. The tilt vector is parallel to the neutral surface. Tilt does not alter monolayer thickness. (C) Splay is illustrated. In splay, adjacent directors are not parallel to each other and monolayer thickness changes. The direction of the x axis is indicated.

The deformations of splay and tilt

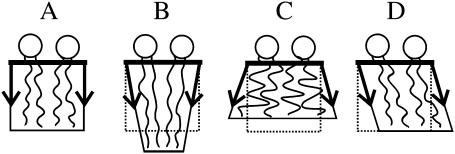
Any arbitrary small perturbation of the monolayer from the flat state (Figs. 2 A and 3 A) can be described by a combination of three independent deformations: tilt, splay, and area compression. In tilt, the director deviates from the normal to the neutral surface (Figs. 2 B and 3 D). Quantitatively, the tilt vector is defined by t = n/(n·N) − N (Hamm and Kozlov, 2000; MacKintosh and Lubensky, 1991). Tilt is completely described by the local director and the normal. t is perpendicular to N (t·N = 0) and parallel to the neutral surface. The magnitude of t is tanθ, where θ is the angle between N and n. For small perturbations, t = n − N. When lipids tilt, the area per lipid remains constant and the acyl chains elongate as they incline, so as to maintain lipid volume. Tilt, therefore, does not alter monolayer thickness (Fig. 3 D). In splay, adjacent directors are no longer parallel to each other but always lie in a single plane. This plane, however, can change with splay (Figs. 2 C and 3, B and C). Splay is quantitatively the first derivative of the director along the neutral surface (i.e., div n). Defining the geometric curvature, J, of the neutral surface by J ≡ −div N yields, for small deformations, the relation div n = −J + div t. This shows that for small deformations, splay is a combination of monolayer bending (div N) and nonuniform tilt (div t). In this article, we use equations that apply to small deformations.

FIGURE 3.

Monolayer deformations. (A) Undisturbed monolayer, (B) negative splay, (C) positive splay, and (D) tilt. The sketch illustrates why splay changes the monolayer thickness (B and C) whereas tilt (D) does not. The volume per lipid is not altered by any of the deformations.

By definition, the direction of N points from headgroup toward the hydrocarbon core (Fig. 2) and thus positive curvature corresponds to negative divergence of N. Because the directors are not parallel to each other in splay, splay alters monolayer thickness. We illustrate by considering the acyl chains of a lipid (Fig. 3). To conserve volume, the chains must elongate if they incline toward each other (Fig. 3 B) and must shorten if they incline away from each other (Fig. 3 C). Negative splay thus increases (Fig. 3 B) and positive splay decreases (Fig. 3 C) the monolayer thickness. In area compression (expansion), the area per lipid molecule changes; the thickness changes accordingly because of volume incompressibility. The characteristic energy of monolayer area compression (elastic modulus E_a ∼ 120 erg/cm²) (Rawicz et al., 2000) is considerably larger than those of splay (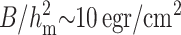) and tilt (K ∼ 40 erg/cm²) (Hamm and Kozlov, 1998, 2000; May, 2002), and the difference becomes greater at higher cholesterol concentrations. This is the reason we assume that the neutral surface is not laterally compressible (or stretchable). We describe all deformations by a combination of tilt and splay. (On first principles, there is a fourth deformation, twist, in which the directors do not remain in the same plane. It is quantitatively proportional to n·curl n. For an isotropic, homogeneous raft and surround with a laterally invariant straight boundary, it is readily shown that curl n = 0, and thus we do not consider twist.)

The free elastic energy of a monolayer

Monolayers are planar (with zero geometric curvature) within the interior of both the raft and the surround, and hence all directors are parallel to each other and perpendicular to the neutral surface. For small perturbations, the elastic energy of a deformed monolayer is a quadratic function of the deformations of splay and tilt. t, N, and n are characterized by their projections, t = t_x, N = N_x, and n = n_x, onto the x axis. In the initial flat state, these three projections are zero everywhere. For small deviations from a flat monolayer, div n = dn/dx, and the free energy per unit area is given by

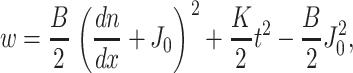(1)

where B is the splay elastic modulus (i.e., the bending modulus), K is the tilt modulus, and J₀ is the spontaneous curvature of the monolayer. Equation 1 is a one-dimensional version of that derived by Hamm and Kozlov (1998, 2000). The first term is the energy of splay and the second term is the energy of tilt. The “+” sign between dn/dx and J₀ is consistent with the standard sign convention that at equilibrium, a monolayer having positive spontaneous splay (or curvature; e.g., a lysolipid) bends toward the hydrocarbon core. A monolayer of nonzero spontaneous curvature is stressed within a flat bilayer and hence stores elastic energy relative to the unstressed monolayer. The work necessary to bend a monolayer from its spontaneous curvature to the flat reference state is subtracted in the third term.

The total elastic energy of the system is the integral of the energy density, w, over the area of the neutral surface. Because w does not depend on y, the free energy of the monolayer W per unit length of boundary is

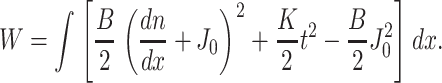(2)

The lateral and volumetric incompressibility assumptions can be written as

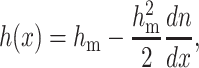(3)

where h_m is the thickness of the flat monolayer. Equation 3 provides the quantitative relation between splay and the change in monolayer thickness.

Solution of the problem

Elastic free energy of a monolayer with fixed boundary conditions

We determined the deformations at the raft boundary and their energies by minimizing the energy in Eq. 2 with respect to n(x) and t(x). The minimization was subject to the constraint of Eq. 3, to the boundary condition that at x = 0 the thickness and directors are the same for the raft and surround stretches of the monolayer, and to the boundary condition that the two stretches are unperturbed at x = ±∞. We denote whether a parameter (e.g., elastic moduli, spontaneous curvature, equilibrium thickness) is associated with a raft or a surrounding monolayer by utilizing the subscript r for the raft and s for the surround.

We illustrate our method of calculation by considering a surround stretch (a semiinfinite monolayer, x > 0) of equilibrium thickness h_s. After deformation, the thickness of this stretch of monolayer is h(x). We utilize the deviation of the neutral surface from its flat, undisturbed state by defining

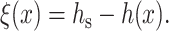(4)

Replacing h_m by h_s, Eq. 3 acquires the form

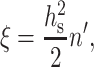(5)

where 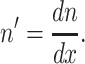Using Eqs. 4 and 5, we may rewrite t in terms of n as:

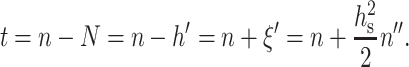(6)

This yields the elastic free energy of a semiinfinite monolayer as

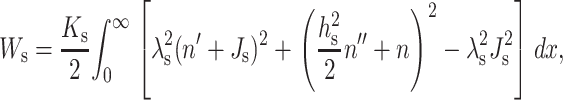(7)

where 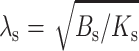is an elastic length constant. Equation 7 can be expanded to yield

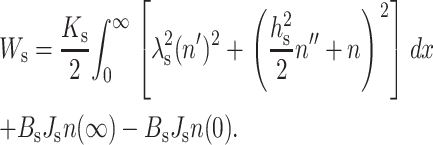(8)

We minimized W_s with respect to n(x), yielding the fourth-order differential equation

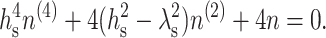(9)

Because only the integral appearing in Eq. 8 depends on n(x) and it is independent of J_s, Eq. 9 is independent of J_s. Four boundary conditions must be specified. Two of them follow from the requirement that the monolayer far from the boundary is undisturbed. Because the director is constant and perpendicular to the plane z = 0 far from the boundary, its projection on the x axis is zero, yielding

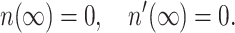(10)

For the last two boundary conditions, the most general expression is obtained by setting the values of the monolayer thickness and directors at x = 0:

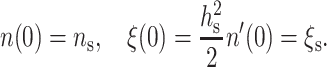(11)

The solution of Eq. 9, subject to the boundary conditions of Eqs. 10 and 11, is

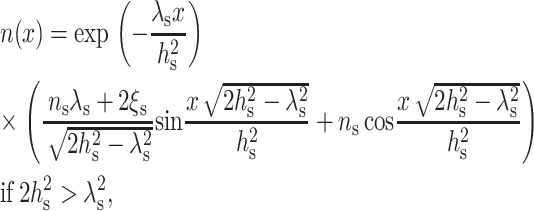(12)

or

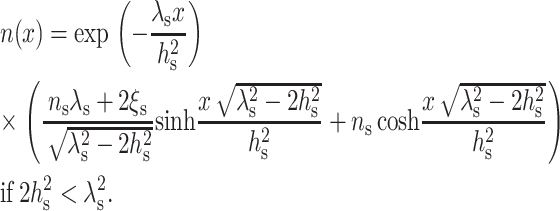(13)

As seen from either Eq. 12 or Eq. 13, the decay length of the deformation is 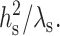Substituting either Eq. 12 or Eq. 13 into Eq. 7 yields the minimum elastic free energy of the deformed monolayer as

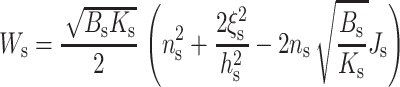(14)

Either Eq. 12 or 13 is physically appropriate, depending on the sign of 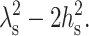Using the standard values for the bending modulus B_s = 4 × 10⁻¹³ erg = 10 kT and the tilt modulus K_s = 40 erg/cm² = 10 kT/nm², yields 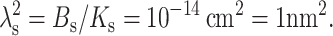Because 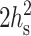is ∼5–10 nm² > 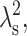Eq. 12 is the physically valid solution for n(x), and thus we use it in all calculations that follow.

Line tension

We join the raft stretch of equilibrium thickness h_r and the surround stretch of equilibrium thickness h_s, side by side, into one monolayer, and match their thickness and directors at the boundary (x = 0). The monolayer thickness is matched via ξ from the physical necessity (see Appendix 1) that the system must deform at the raft boundary so that the lipids do not expose hydrophobic surfaces to water. We thus set the raft and surround thickness equal at the raft boundary, and make the monolayer thickness h(x) a continuous function along the entire neutral surface. The value of n for the two monolayers is matched at the boundary (x = 0) via continuity. The matching conditions are

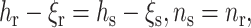(15)

at the boundary (x = 0), where n_r and n_s are the projections of the directors onto the x axis and ξ_r and ξ_s (Eq. 4) are the deviations of the deformed neutral surface from the unperturbed, flat one; Eq. 15 is equivalent to h_r − h_s = ξ_r − ξ_s = δ, where δ is the hydrophobic mismatch. Making the replacements of n_s → −n_r, ξ_s → ξ_r, B_s → B_r, K_s → K_r, J_s → J_r, and h_s → h_r in Eq. 14, we obtain that the total elastic free energy is

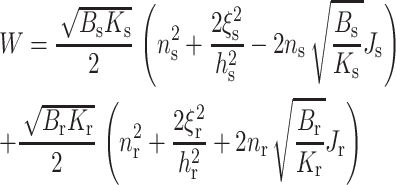(16)

Because lipids in a raft are more ordered and the raft firmer than the surrounding monolayer (Ipsen et al., 1987; Veatch et al., 2004; Vist and Davis, 1990), we differentiate between the elastic moduli of the raft and surrounding bilayer. The signs within the parentheses of Eq. 16 correspond to a raft on the left (x < 0) and a surround on the right (x > 0). Minimization of Eq. 16, subject to the boundary values of n and ξ, yields the line tension

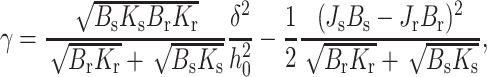(17)

where h₀ = (h_r + h_s)/2. The first term of Eq. 17 shows that line tension increases quadratically with increased height mismatch δ. The second term depends on the spontaneous curvatures. Because the second term is positive and subtracted from the first term, nonzero spontaneous curvature, for either the raft or the surround, will reduce line tension. It is notable that γ depends quadratically on both hydrophobic height mismatch (δ) and spontaneous curvature difference (ΔJ = J_s − J_r), independently of each other. Physically, one might expect a cross-term (δΔJ) to contribute to the energy of the boundary because the smooth curving boundary creates, both within the raft and within the surround, splay deformations that depend linearly on δ. The energy of these deformations would contribute terms ∼δJ_s and ∼δJ_r to the total energy of the boundary. However, as we now show, the monolayer thickness does not change monotonically over the interface, but rather, the thickness oscillates. Because monolayer thickness and splay are related (by Eq. 3), the sign of the splay changes along the boundary region of the monolayer and, as it does so, the contribution of the cross-term to energy also changes sign. In fact, for our semiinfinite raft and surround monolayers, calculation shows that the energies in regions of positive and negative splay precisely cancel each other out, leading to the absence of a cross-term in the final expression of line tension, as given by Eq. 17.

Monolayer shape

We analytically obtained the shape of the neutral surface in the transition zone of the raft boundary by determining the boundary values of each director, n, and height deviation, ξ, that minimize the elastic free energy (Eq. 16). These values are

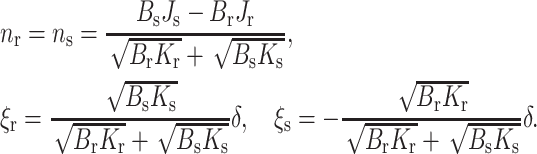(18)

Substituting Eq. 18 into Eq. 12 and using the definition of ξ (Eq. 4), we obtain the equilibrium profile of the neutral surface for the monolayer of the surround (x > 0) as

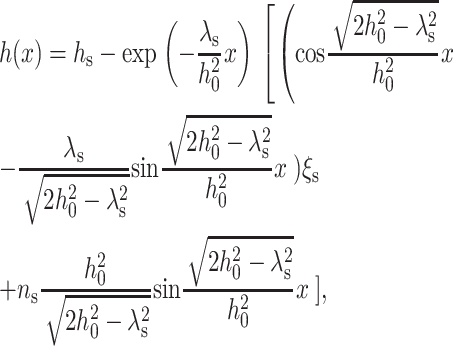(19)

where 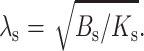The profile of the neutral surface within the raft monolayer (for x < 0) is

(20)

where 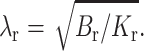Thus the monolayer thickness varies nonmonotonically over the interface.

Interaction of two parallel straight boundaries

When two rafts come into proximity, their boundaries interact. We approximate the apposed boundaries as two parallel, straight lines that are separated by a strip of surround of width L = 2d. We place the origin of the coordinate system in the middle of the strip, locating the boundaries of the two rafts at x = ±d. We assign the equilibrium thickness h_r to each of the rafts and the equilibrium thickness h_s to the intervening surround. We determine the interaction energy by first calculating the energy of the finite strip of surround between rafts subject to general boundary conditions. We add to this the energy of the semiinfinite rafts (Eq. 14), also subject to arbitrary boundary conditions. We then match the boundary values of n and h for the rafts and surround at x = ±d and then minimize the total energy. The analytical expression for the energy of interaction, derived through symbolic manipulation software (Maple 7, Ontario, CA), is extremely long and not particularly helpful. We therefore illustrate in Results the salient features of the interaction energies graphically.

RESULTS

Values of the elastic moduli for the raft and the surround

Line tensions and director fields depend on the elastic moduli and the spontaneous curvatures of the raft and the surround. The presence of a high concentration of cholesterol increases the moduli of stretching a bilayer three- to fivefold (Evans and Rawicz, 1990; Needham et al., 1988; Needham and Nunn, 1990) and increases the bending modulus two- to threefold (Evans and Rawicz, 1990). In contrast, for lipids in the H_II phase, high cholesterol increases the bending modulus by only 30–50% (Chen and Rand, 1997). It is thus not entirely clear whether the bending modulus of the raft is the same or much larger than that of the surround. Because of this, we consider the behavior of line tension for a firm (B_r > B_s = 10 kT) and a flexible (B_r = B_s = 10 kT) raft. The effect of cholesterol on tilt modulus has not yet been addressed by experiment. The tilt modulus K may be less sensitive to cholesterol content than the other moduli. Theoretical estimations indicate that tilt modulus is roughly equal to the surface tension, σ ∼ 40 dyn/cm (Rawicz et al., 2000), between the monolayer hydrocarbon core (at the neutral surface) and water (Cohen and Melikyan, 2004; Hamm and Kozlov, 1998; Kuzmin et al., 2001; May, 2002). Cholesterol probably does not affect σ to a great extent. However, as the effect of cholesterol on the tilt modulus is not known, we consider the case of a firm raft for tilt modulus greater (K_r > K_s = 10 kT/nm²) or the same (K_r = K_s = 10 kT/nm²) as that of the surround.

Line tension depends on spontaneous curvature

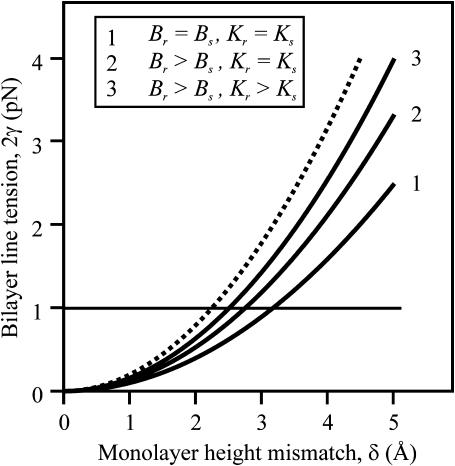
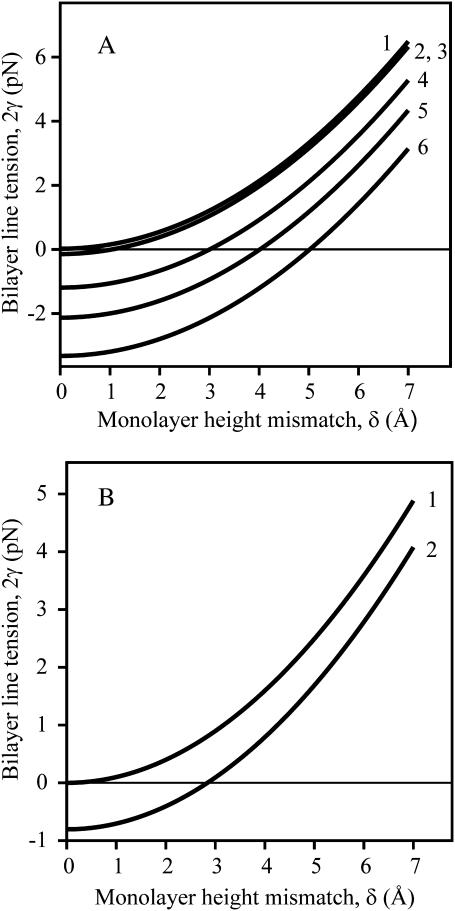
The dependence of line tension, γ, on height mismatch, δ, is shown (Fig. 4) in the case of J_r = J_s = 0, for a flexible raft having the same tilt moduli as the surround (curve 1), and a firm raft with the same (curve 2) and larger tilt moduli (curve 3) than the surround. Line tension is also shown for a perfectly firm raft, one with infinitely large bending and tilt moduli (dotted curve). As the elastic moduli become greater, so does γ. The line tension between rafts and liquid-disordered domains has been estimated as ∼1 pN = 0.25 kT/nm (horizontal line in Fig. 4) by analyzing the shape of budding of liquid-ordered sphingomyelin/cholesterol regions in giant unilamellar vesicles (Baumgart et al., 2003). This line tension corresponds to a monolayer thickness mismatch of ∼2–4 Å if spontaneous curvature is zero everywhere; the mismatch is larger for nonzero spontaneous curvatures.

FIGURE 4.

Dependence of bilayer line tension, 2γ, on equilibrium thickness mismatch δ for J_r = J_s = 0. Curve 1 is a flexible raft for K_r = 10 kT/nm², curve 2 is a firm raft for K_r = 10 kT/nm², and curve 3 is a firm raft for K_r = 40 kT/nm². The dotted curve is drawn for a perfectly firm raft (B_r → ∞ and K_r → ∞). For this and all subsequent figures, h₀ = 20 Å.

The influence of monolayer spontaneous curvature on γ is illustrated in Fig. 5. For a firm raft (Fig. 5 A), line tension is greatest if J_r = 0 (curves 1–3). Here, J_s has almost no effect on γ: The three curves almost lie on top of each other: the curves for J_s = ±0.1 nm⁻¹ (curves 2 and 3) are identical and the line tension is only slightly greater for J_s = 0 (curve 1).

FIGURE 5.

Dependence of bilayer line tension, 2γ, on equilibrium thickness mismatch δ for nonzero-spontaneous curvature. (A) A firm raft. J_r = 0 for curves 1, 2, and 3; J_s = 0 (curve 1), J_s = −0.1 nm⁻¹ (curve 2), J_s = +0.1 nm⁻¹ (curve 3). J_r = 0.1 nm⁻¹ for curves 4, 5, and 6; J_s = 0.1 nm⁻¹ (curve 4), J_s = 0 (curve 5), J_s = −0.1 nm⁻¹ (curve 6). Elastic moduli for the raft are B_r = 40 kT and K_r = 10 kT/nm², δ = 5 Å; all other parameters are as in Fig. 4. (B) A flexible raft. J_r = 0, J_s = 0 for curve 1; J_s–J_r = ±0.2 nm⁻¹ for curve 2. The elastic moduli are B_s = B_r = 10 kT and K_s = K_r = 10 kT/nm².

For J_r ≠ 0 (curves 4, 5, and 6) however, the situation is different and a potentially profound effect that may be of great biological significance appears. When J_r ≠ 0 (J_r = 0.1 nm⁻¹ for the illustrated curves), γ is negative for sufficiently small (but hardly vanishing) δ. Rafts would be unstable if γ < 0, and thus, under such conditions, would not form in the first place. Whenever our model yields γ < 0, rafts will not form unless molecular interactions, not incorporated in our model, were sufficiently strong so as to make the total line tension positive. In the case of J_r ≠ 0, the spontaneous curvature of the surround affects γ. Line tension is greatest when J_s and J_r have the same sign (curve 4), and is smallest for J_s and J_r of opposite sign (curve 6); line tension is intermediate for J_s = 0 (curve 5).

For a flexible raft (Fig. 5 B), γ depends on (J_r − J_s)² (see Eq. 17). As a consequence γ is the same for J_r = 0 and J_s = ±0.2 nm⁻¹ as it is for J_r = ±0.2 nm⁻¹ and J_s = 0 (curve 2). For small δ, γ < 0. As is the case for a firm raft, γ for a flexible raft is never negative for J_r = J_s = 0 (curve 1). Because variables such as spontaneous curvature and height mismatch depend on lipid composition, we expect that experimentally determined values of γ will vary greatly with membranes of differing lipids.

The critical spontaneous curvature of rafts

Consider the critical spontaneous curvature, J*, that yields γ = 0. For an extremely firm raft, B_r ≫ B_s, Eq. 17 can be written in the form

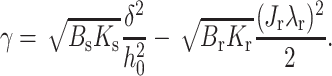(21)

Equation 21 explicitly shows that γ of an extremely firm raft depends on the elastic moduli of the surrounding monolayer but is independent of J_s. For a raft that is not as firm (e.g., B_r = 4B_s), Eq. 21 is still valid for large γ, but the entire Eq. 17 must be used in the vicinity of γ = 0. (An additional term ∼J_rJ_s now appears.) For these moderately firm rafts, γ depends on J_s if J_r ≠ 0, as can be seen from Fig. 5 A. For extremely firm rafts, Eq. 21 shows that if

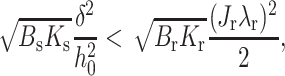(22)

γ becomes negative. Experimentally, if a raft is to form for contributions from interactions not captured by a continuum elastic model must be great enough to generate a positive total line tension. We estimate J* for the typical values of B_s = 10 kT, K_s = 10 kT/nm², h₀ = 2 nm, B_r ∼ 4B_s = 40 kT, and δ = 0.5 nm. Because γ varies with the square root of the elastic moduli, the uncertainty in the ratio between the tilt moduli, K_r and K_s, does not seriously impede a meaningful estimation

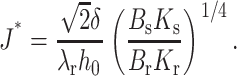(23)

This yields J* ∼ 1/5 nm⁻¹ for K_r = 4K_s, and J* ∼ 1/8 nm⁻¹ for K_r = K_s. By comparison, the spontaneous curvature of cholesterol is ∼−1/2.5 nm⁻¹, lysophosphatidylcholine is ∼1/3.8 nm⁻¹, and dioleoylphosphatidylethanolamine is ∼−1/2.8 nm⁻¹ (Fuller and Rand, 2001). Thus, differences in spontaneous curvature of cholesterol/sphingolipid rafts and surrounds may be larger than J* for plasma membrane lipid compositions. Therefore, from the perspective of membrane mechanics, raft size, and/or shape in a region of a plasma membrane should depend not only on cholesterol and sphingolipid content, but on compositions of the other lipids in the region as well.

For a flexible raft, the line tension can be written as

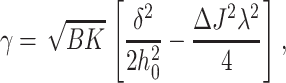(24)

where ΔJ = J_s − J_r. If ΔJ ≠ 0, γ can become < 0. The critical difference in spontaneous curvature for the flexible raft, ΔJ*, is

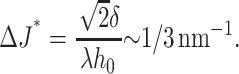(25)

As a practical matter, to achieve this large a difference, the spontaneous curvatures of the raft and surround would have to have opposite signs. We therefore suggest that a flexible raft is more likely to be stable than a firm raft.

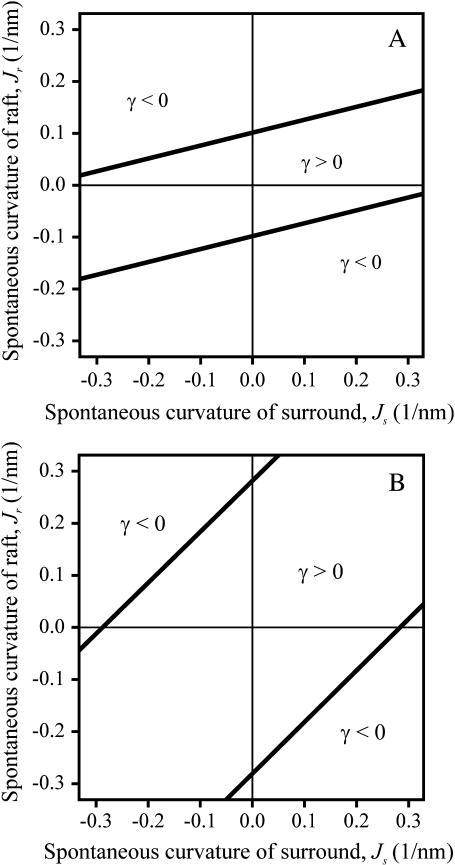
The values of J_s and J_r for which γ > 0 and γ < 0 are readily illustrated for a firm (Fig. 6 A) and flexible raft (Fig. 6 B). The straight lines (γ = 0) separate regions of positive and negative line tension. Their slope is B_s/B_r. For an extremely firm raft (B_r ≫ B_s), the lines become horizontal and γ becomes independent of J_s (see Eq. 21). Based on elastic contributions alone, rafts can form only for values of J_r and J_s that yield γ > 0, the region between the lines. The J_r intercepts are 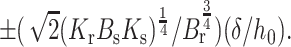Clearly, the smaller the height mismatch, δ, and the more firm the raft, the narrower is the range of spontaneous curvatures, J_r and J_s, for which γ > 0. Because biological rafts contain protein, they may be firmer than lipid bilayer rafts. In general J_r ≠ J_s, and thus in the absence of height mismatch, the elastic nature of monolayers will reduce the total line tension that results from all molecular interactions. The reduction may be large enough to prevent rafts from forming.

FIGURE 6.

Phase diagram for stability of the raft as a function of the spontaneous curvature of raft, J_r, and surround, J_s. A raft is stable only in the region γ > 0. (A) Firm raft. B_r = 4B_s = 40 kT, K_r = K_s = 10 kT/nm². (B) Flexible raft. B_r = B_s = 10 kT and K_r = K_s = 10 kT/nm². For both panels A and B, δ = 4 Å.

Monolayer shape varies as a damped sinusoid in the transition zone

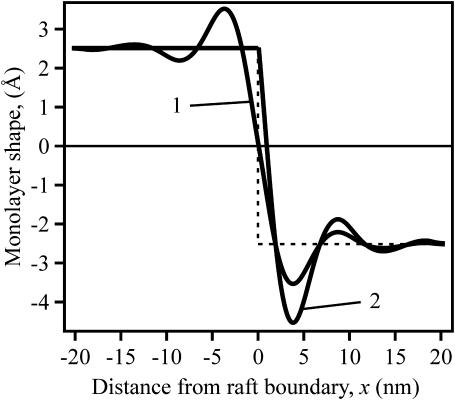
An inspection of the equilibrium shape of the neutral surface (Fig. 7) shows that height does not monotonically decrease as the thick raft meets the thinner surround, but rather the height oscillates as it decreases. Equations 19 and 20 show that there are two characteristic lengths. One, 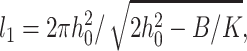determines the wavelength of the oscillation and the other, 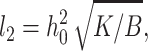determines the decay length of the monolayer deformations at the raft boundary. For a flexible raft (Fig. 7, curve 1), the oscillations occur both within the raft and the surround region. For increasingly firm rafts, oscillations are attenuated within the raft and accentuated within the surround. For an absolutely firm raft (curve 2), height cannot vary within the raft and as a consequence, height variation maximizes within the surround. An inspection of Eq. 3 for h(x) and Eq. 11 for the boundary conditions at x = 0 shows that h(x) is continuous across the boundary, but that its derivative dh/dx is generally discontinuous. Curve 1 is smooth at the boundary, without a discontinuity in slope at the boundary, because the elastic moduli of the flexible raft and surround are the same. In contrast, the elastic properties are quite different for the surround and a perfectly firm raft, and here the discontinuity in dh/dx is large and visually obvious (Fig. 7, curve 2).

FIGURE 7.

The profile of the neutral surface near the raft boundary. The monolayer shape is plotted as h(x) − (h_r + h_s)/2. The numerical values thus provide, in Å, the deviation of monolayer height from the average thickness of the raft and surround. The dotted line indicates the underformed, step-like raft boundary. For the flexible raft (curve 1), B_r = B_s = 10 kT and K_r = K_s = 10 kT/nm². For the perfectly firm raft (curve 2), B_r → ∞ and K_r → ∞. In both cases, δ = 5 Å.

Interaction between rafts

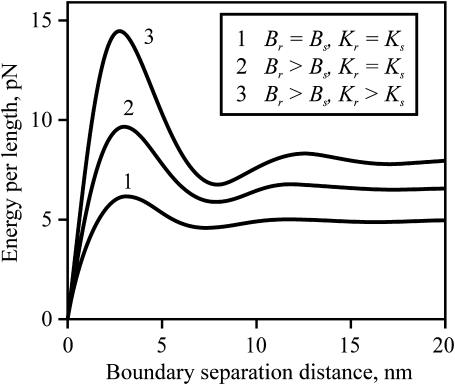
For two rafts to come into contact, they must overcome an energy barrier. For either two flexible rafts (Fig. 8, curve 1) or two firm rafts (Fig. 8, curves 2 and 3), an energy barrier is located at a separation distance of ∼2–4 nm between boundaries if spontaneous curvature is zero everywhere. The energy barrier between rafts is more sensitive to the elastic moduli of the rafts than is the energy required to deform the boundary of an isolated raft. For example, the ratio of the barriers for a firm raft (Fig. 8, curve 3) compared to a flexible raft (curve 1) is ∼2.5, but the ratio of energies at infinite separation (the line tension) is only ∼1.5.

FIGURE 8.

The energy barrier between interacting rafts for zero spontaneous curvature everywhere. The total energy per unit length of two straight parallel raft boundaries as a function of their separation distance, L, is plotted. The line tension of an isolated raft is the energy at large separation, divided by two. The interaction energy at any separation distance is the deviation of that energy from the energy at large separation. The curve number is rank ordered with increasing raft firmness: B_r = B_s = 10 kT and K_r = K_s = 10 kT/nm² (curve 1), B_r = 4B_s = 40 kT and K_r = K_s = 10 kT/nm² (curve 2), and B_r = 4B_s = 40 kT and K_r = 4K_s = 40 kT/nm² (curve 3). δ = 5 Å.

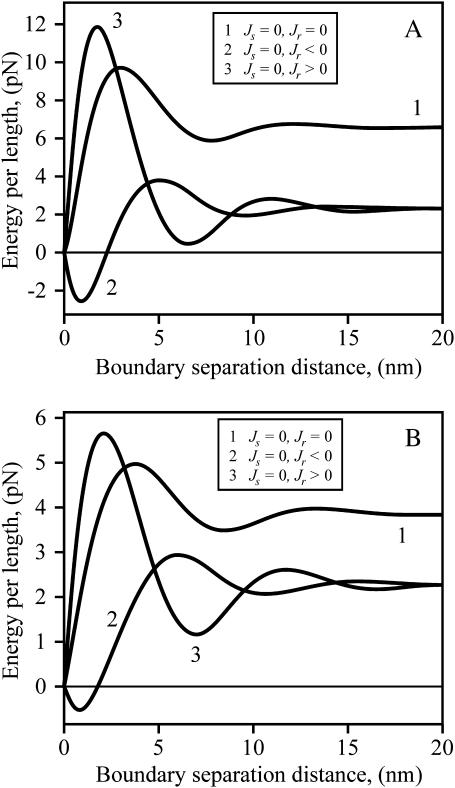
To consider the influence of spontaneous curvature on the raft interaction, we first vary J_r for a firm (Fig. 9 A) and flexible (Fig. 9 B) raft, while maintaining J_s = 0. For both firm and flexible rafts, the barrier is higher and shifted to a slightly smaller separation distance for J_r > 0 compared to J_r = 0. Just the opposite is the case for J_r < 0: its barrier is lower and shifted to a somewhat larger separation distance than for J_r = 0. That is, the energy barrier depends on the sign of J_r. This is in distinct contrast to the line tension of an isolated raft: γ depends only on the magnitude of J_r, and is independent of sign (e.g., see Eq. 17 and note that at large separation, curves 2 and 3 overlap).

FIGURE 9.

The energy barrier between rafts for J_s = 0 and varied J_r. The total energy per unit length of two straight parallel raft boundaries as a function of their separation distance, L, is plotted. (A) Firm rafts (B_r = 4B_s = 40 kT, K_r = K_s = 10 kT/nm²). J_r = 0 (curve 1), J_r = −0.1 nm⁻¹ (curve 2), and J_r = +0.1 nm⁻¹ (curve 3). (B) Flexible rafts (B_r = B_s = 10 kT, K_r = K_s = 10 kT/nm²). J_r = 0 (curve 1), J_r = −0.2 nm⁻¹ (curve 2), and J_r = +0.2 nm⁻¹ (curve 3). For panels A and B, δ = 5 Å.

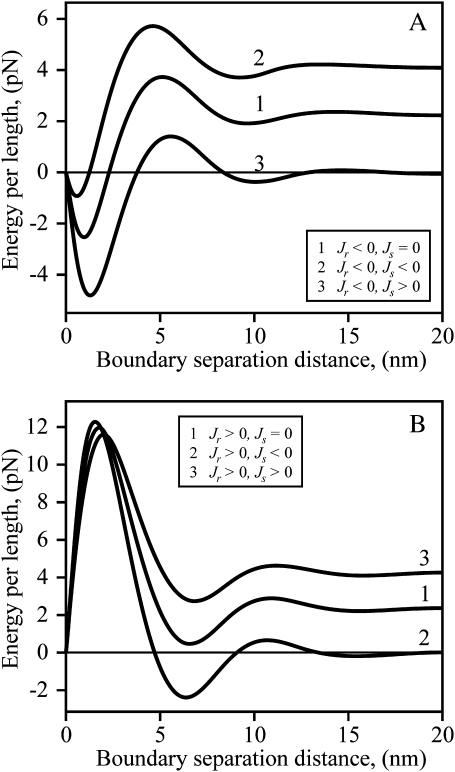
The consequences of varying the spontaneous curvature J_s of the intervening strip of surround between two firm rafts depend on the sign of J_r. For J_r < 0 (Fig. 10 A), as J_s is varied from positive (curve 3) through zero (curve 1) and to negative values (curve 2), the total energy increases to an extent that is almost independent of separation distance. As a consequence, the barrier height of interaction is relatively insensitive to J_s. In contrast, for J_r > 0 (Fig. 10 B), the barrier heights decrease as J_s is switched from negative to positive values. The magnitude of the peak of the barrier of total energy does not significantly vary with J_s, but the energy minimum near the barrier as well as the line tension of the isolated rafts increase with more positive J_s. The same qualitative features pertain to a flexible raft (not shown). We have seen that line tension depends on the parameters of the raft and the surround in fairly straightforward ways. The interactions between rafts depend on these same parameters, but in much more complex manners.

FIGURE 10.

The dependence of energy barriers between rafts on J_s for positive and negative J_r. The total energy per unit length for two straight parallel boundaries of firm rafts is plotted. (A) J_r = −0.1 nm⁻¹ < 0. Curves are drawn for different spontaneous curvature of the strip of surround that separates the rafts. J_s = 0, curve 1; J_s = −0.1 nm⁻¹, curve 2; J_s = +0.1 nm⁻¹, curve 3. B_r = 4B_s = 40 kT, K_r = K_s = 10 kT/nm², δ = 5 Å. (B) J_r = +0.1 nm⁻¹ > 0. J_s = 0, curve 1; J_s = −0.1 nm⁻¹, curve 2; J_s = +0.1 nm⁻¹, curve 3. B_r = 4B_s = 40 kT, K_r = K_s = 10 kT/nm², δ = 5 Å. The differences in energies in Figs. 8, 9, and 10 illustrate the complex dependence of interactions on J_r and J_s.

The repulsive interaction between rafts (the cause of the barrier) can kinetically stabilize rafts against merger. (This is analogous to the well-known stabilization of colloidal particles through repulsion of their electrical double layers as described by the Deryaguin-Landau-Verwey-Overbeck theory; Hunter, 2001) Consider an ensemble of identical rafts of radius R that undergo Brownian motion. How large an energy barrier would be required to prevent contact that would lead to merger? Letting x₀ = the mol fraction of molecules that form rafts and D = the diffusion coefficient of a raft, we obtain that x₀/R² is the concentration of rafts and 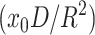is roughly the number of collisions a single raft will make with others per unit time. The frequency of collisions, ν, leading to merger is

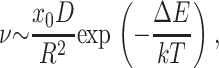(26)

where ΔE is the repulsive barrier that must be overcome for raft merger. For raft radius R ≫ λ (the characteristic length of monolayer deformation λ ∼ 2–4 nm), we can use a two-dimensional analog of the classical Deryaguin approximation for calculating short-range interactions between surfaces (described in Hunter, 2001). We replace the circular raft boundaries by two straight boundaries of effective length 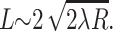The barrier height ΔE that the two rafts have to surmount to merge is ∼ΔWL, where ΔW is the interaction barrier height per unit length of boundary. For R ∼ 10 nm, D ∼ 10⁻⁸ cm²/s (diffusion coefficients only vary as log(R) in two dimensions; Saffman and Delbruck, 1975), λ ∼ 3 nm, x₀ ∼ 0.5, ΔW ∼ 2–10 pN (0.5–2.5 kT/nm) we find that 1/ν = τ ∼ 0.1 s for ΔW = 2 pN and τ ∼ 10¹⁰ s for ΔW = 10 pN. Figs. 8–10 illustrated that barrier heights are altered in complex manners by parameters of the raft and surround. Because relatively small changes in barrier heights can so dramatically alter the characteristic times of raft merger, and these times can be extraordinarily large, it may be that rafts never overcome the barrier, in which case repulsion would kinetically stabilize small rafts against merger. They could still merge, however, if boundary undulations reduced the kinetic barrier.

DISCUSSION

We found that when the monolayers can deform at the raft boundary by splay and tilt, important physical phenomena emerge that are not possible if only area compression/stretch and tilt are permissible (Akimov et al., 2004). First, the calculated line tension is smaller and is in better accord with an experimentally determined value (Baumgart et al., 2003). Second, the thickness profile of the raft does not monotonically decrease at the raft boundary to meet the thinner surround (as previously calculated), but rather the thickness varies as a damped sinusoid in the transition zone between the raft and the surround. Third, this sinusoidal variation in monolayer thickness results in energy barriers between rafts that can kinetically stabilize them against merger. Fourth, nonzero spontaneous curvatures of either the raft or the surround lower the raft line tension. The contribution of hydrophobic mismatch to γ will be negative if the difference in spontaneous curvature between the raft and surround is sufficiently large.

Approximations of the model

A difference in raft and surround thickness would expose a hydrophobic surface to water in a step-like fashion if lipids did not readjust so as to minimize the energy of the system. In addition to the elastic deformations we have considered, the energy of this readjustment is determined by mixing of lipids at the raft boundary; this mixing is controlled by lipid-lipid interactions and standard entropies of mixing. If lipids could only reside at discrete sites, lipid mixing would disperse the single step of hydrophobic exposure into a “staircase” of exposure; the extent of hydrophobic exposure would be the same for the single step as for the staircase. Averaging lipid location over position and time yields a continuous neutral surface that smoothly joins the thick raft and thin surround. The extent of hydrophobic exposure is not altered by going from the discrete to the continuous limit: the area per lipid along the continuous, curved neutral surface in the transition zone is greater than the area per lipid along the flat midplane between monolayers; the projection of the neutral surface onto the perpendicular to the midplane is the amount of hydrophobic exposure. In other words, lipid mixing cannot eliminate hydrophobic exposure; elastic deformations are required to do so. We have found that for a height mismatch of 0.5 nm, elastic deformations reduce the energy at the boundary from 5 kT/nm (the energy for exposing the hydrophobic surfaces to water) to 0.25 kT/nm. Energies of hydrophobic exposure to water are so large that whatever processes most effectively eliminate exposure should be of greatest consequence. That is, if the hydrophobic height mismatch were sufficiently large, the elastic deformations will dominate the energy of the interface, and any contributions to line tension from lipid-lipid interactions and lipid mixing would be unimportant. Our model should be a good approximation to reality in this case. Where height mismatch is negligible, our model cannot be applied. But even when hydrophobic mismatch does not dominate, our calculations show that differences in spontaneous curvatures between a raft and a surround will always reduce line tension, an effect that was previously unappreciated.

We treated the raft boundary as a straight edge. Whenever the radius of a circular raft is much larger than all characteristic lengths in the system, the approximation is valid. The two characteristic lengths in the system are the oscillation wavelength 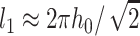and the elastic length 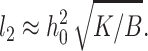Because l₁ ∼ 10 nm and l₂ ∼ 2–4 nm, our calculated values for γ should be applicable for rafts with diameters ≥∼50 nm, diameters consistent with many experimental measures of rafts in cell plasma membranes, although a wide range of sizes are reported (Anderson and Jacobson, 2002). The deformations at the raft boundary decay over a length of ∼3–6 lipid molecules on both sides of the interface and the oscillations in raft interactions occur over a distance that corresponds to a span of ∼12 lipid molecules.

Our model assumes mirror symmetry of two monolayers with respect to the midplane of the bilayer. In order for symmetry to be true, rafts would have to span both monolayers and not be able to occur independently within separate monolayers. In other words, the coupling between rafts within the two monolayers of a bilayer must be tight. Experimentally, such tight coupling is observed (Samsonov et al., 2001), although the physical reasons for this coupling are not yet known.

We have also assumed that the neutral surface is nonstretchable. The area compression/stretching modulus of a monolayer is ∼120 erg/cm² = 30 kT/nm² (Rawicz et al., 2000). This is only three times greater than K, but six times greater than 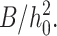As the cholesterol content of monolayers increases, the compression and bending moduli probably increase by a greater factor than does the tilt modulus. The small amount of stretching that does occur at the neutral surface should be of little consequence and would not significantly affect our results. When a bilayer membrane surrounds a hydrophobically mismatched inclusion (i.e., an incorporated protein), it will adjust to the mismatch by bending and tilt deformations, with little area stretching/compression. To quantitatively illustrate the consequences, we compare the energy of bilayer deformation for incorporation of a right cylindrical inclusion, which has been calculated assuming area stretching and bending (Nielsen et al., 1998). We divided this calculated energy by the circumference of the inclusion to estimate line tension, and applied our boundary condition for a perfectly firm raft to a nondeformable inclusion. This yields a line tension approximately three to four times greater than we calculated for bending and tilt deformations (calculations not shown). Bending and tilt deformations are the energetically favored deformations.

The occurrence of rafts depends on composition of lipids other than cholesterol and sphingolipids

In an actual membrane, rafts will exist and be stable only if the line tension is >0. Our calculations show that when height mismatch is the dominant determinant of line tension, line tension will be >0 for only limited ranges of J_r and J_s. As part of cellular function, lipid composition (other than just cholesterol and sphingolipids) may be altered in regions of plasma membrane; this could cause rafts to appear or disappear. In a recent report, it was concluded that rafts contain only a few protein molecules, in which case the rafts would be exceedingly small (Sharma et al., 2004). Our model shows that changes in J_r and J_s can dramatically alter values of γ, which in turn would greatly alter raft size. Because the values of J_r and J_s may vary according to cell type and culturing conditions, particular measures of raft size may not reflect general cell biological principles.

The cause of oscillations across the boundary

The nonmonotonic monolayer shape of the raft boundary results from the assumption of volumetric incompressibility and the deformation of splay. This can be appreciated from Eq. 3 which gives h(x) in the case of volumetric incompressibility. In the absence of tilt (n = N), we obtain from Eq. 3 that

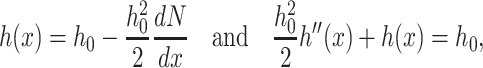(27)

because N = h′(x). Differential Eq. 27 is that of a harmonic oscillator for h(x) in the x-direction, showing that h varies sinusoidally with x. It is the deformation of splay (bending) alone that imposes the oscillatory height profile. In the absence of tilt, splay would cause the boundary to oscillate indefinitely in space with amplitude ∼δ, the height mismatch. But because lipids can tilt, splay energy is converted to tilt energy. It is the deformation of tilt that causes the oscillations to decay over the transition zone of the raft boundary. From Fig. 7 (curve 1), it is seen that the height of the primary oscillation is ∼δ, precisely as expected according to our physical explanation.

Oscillations across the boundary determine the energy of raft interactions

The energy of the system is completely determined by the director field, as given by Eq. 7. Because the superposition of director fields determines the interaction energies, the shape of the interaction profile between rafts is determined by the shape of the raft boundary (i.e., the director field over the boundary). For a monolayer that deforms at a raft boundary by stretch and tilt, the height mismatch decays monotonically and therefore the interactions between rafts also change monotonically with distance of separation. Because the deformation energy is greater for two separate rafts than for one merged raft, the rafts attract each other at all separation distances (Akimov et al., 2004). In the more realistic case of deformation by bending and tilt, the shape of the neutral surface of the raft boundary oscillates and hence the interaction between rafts also oscillates, as a function of separation. Consequently, a series of energy barriers must be overcome for rafts to come into contact. The energy barriers occur because, at the boundaries of the two rafts, the projection of the directors onto the x axis are pointed in opposite directions. As the rafts come closer together, the deformations overlap and energy must be expended to reorient the directors. For a flexible raft, the deformations are comparable to those of the flexible surround. But for a firm raft, the deformations are more confined to the flexible surround. The firmer the raft, the greater is the energy barrier. Small rafts in cell membranes contain proteins, and these rafts may be sufficiently firm to kinetically stabilize them against merger.

Models that account for hydrophobic mismatch between proteins and the surrounding bilayer also exhibit oscillations at the protein boundary and energy barriers that oppose the approach of these proteins. Mean-field calculations do not capture these oscillations (Marcelja, 1976), but Monte-Carlo calculations for lipid membranes with protein inclusions do reveal a repulsive barrier at an intermediate separation (Lague et al., 1998; Sintes and Baumgartner, 1997). Elastic continuum models, similar to ours, that allow bending to compensate for hydrophobic mismatch between protein and bilayer lead to nonmonotonic interactions between proteins. These include models that consider stretch/compression and bending (Dan and Safran, 1998; Sens and Safran, 2000), compression/stretching, tilt, and bending (Fournier, 1999; May and Ben-Shaul, 1999), and a “director model” (Bohinc et al., 2003; May, 2002; May and Ben-Shaul, 2000). A nonmonotonic perturbation profile of a membrane near a cylindrical protein, without hydrophobic mismatch, has also been predicted for a model that allows compression/stretching and bending (Dan and Safran, 1998). A recent elastic deformation model that includes bending also predicts an oscillatory interaction between fusion peptides that are inserted obliquely into a single monolayer of a bilayer (Kozlovsky et al., 2004).

The larger the radius, R, of the raft the greater is the waiting time for raft merger. The estimates for waiting times are not quantitatively reliable because they depend exponentially on imprecisely known quantities. But it is highly unlikely that large rafts, on the order of microns, can merge through a mechanism of boundary contact without distortion. We suggest that local contacts created by short wavelength fluctuations in the boundary are responsible for mergers: for a fluctuating boundary, the local radii are much smaller than the radius of the raft and thus waiting times of merger should be greatly reduced.

A physical intuition for the energy required to create a raft boundary

Now that a rigorous formal derivation of line tension has been achieved, one can more easily approach the problem with an intuitive physical insight that permits quantitative calculation. For example, the quantitative relation between line tension of a flexible and a perfectly firm raft, for J_r = J_s = 0, is easily understood. If the raft and the surround have the same elastic moduli, they cover the height mismatch, δ, to the same extent. For a perfectly firm raft, the surround alone must deform to entirely cover the mismatch. As a consequence, the height of the deformation of the surround increases by a factor of two. Because energy density is a quadratic function of deformation, the work expended to cover the mismatch increases fourfold compared to the case of a flexible raft. But the area of deformation is reduced by a factor of two. Thus the energy of deformation (i.e., the line tension) is twofold greater for the perfectly firm raft (Fig. 4, dotted curve) than for the flexible raft (curve 1), and this is true for any value of δ.

Consider the creation of a firm raft with a boundary of some height mismatch. We start from a monolayer formed of a flat raft and a flat surround, each in isolation. The raft and surround are brought into contact, creating a “step-like” boundary. Although this exposes a portion of the hydrophobic core of the thicker raft monolayer to water, elastic deformations completely eliminate this exposure. Therefore, the work required to expose a hydrophobic surface to water is excluded from our calculation for free energy. The monolayer is free to deform over the transition zone, length 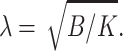The monolayer thickness can be changed only by splay, a combination of bending and nonuniform tilt. Because the flexible surround has smaller elastic moduli than the firm raft, it is the surround that will deform to eliminate the height mismatch. The work necessary for the required splay is ∼λ_sB_s(dn/dx)² where dn/dx ∼ δ/(h₀λ_s) yielding an energy 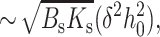the first term of Eq. 21. But the firm raft does not remain flat in the transition zone. Rather than deforming to eliminate the height mismatch, in the transition zone the firm raft deforms spontaneously from its initial zero geometric curvature to its spontaneous curvature J_r. This lowering of energy is given by the energy of splay 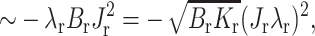the second term of Eq. 21. Independent of the relative elastic moduli of raft and surround, nonzero spontaneous curvature, of either raft or surround, lowers line tension (Eq. 17). This occurs because a monolayer is stressed when flat and at the boundary it gains an additional degree of freedom. The monolayer deforms at the boundary, relieving stresses, and line tension is reduced.

APPENDIX 1

Our assumption that deformations must completely eliminate the exposure of hydrophobic surfaces to water at the raft boundary is, in actuality, a physical necessity. Consider the consequences if the thickness of the hydrophobic mismatch after deformation, Δ, were not zero. If Δ ≠ 0, the elastic energy density to deform the monolayers at the raft boundary (in a quadratic approximation and for zero spontaneous curvature) is

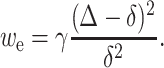(A1)

Equation A1 satisfies the limiting cases in which the hydrophobic mismatch is completely eliminated (Δ = 0, w_e(0) = γ) or not compensated at all (Δ = δ, w_e(δ) = 0). If mismatch was incomplete, the energy of the hydrophobic region of the boundary still exposed to water would have to be added to w_e to obtain the total energy of the boundary. The hydrophobic energy is σ|Δ| where σ is the surface tension of the oil/water interface. So

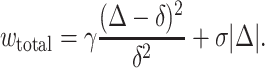(A2)

The minimum of w_total is located at

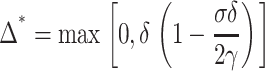(A3)

For δ = 5 Å monolayer line tension γ = 1–2 pN (Fig. 4) we obtain that Δ* = 0. In other words, the hydrophobic exposure at raft boundary is completely eliminated.