Theory of Optical Spectra of Photosystem II Reaction Centers: Location of the Triplet State and the Identity of the Primary Electron Donor

Abstract

Based on the structural analysis of photosystem II of Thermosynechococcus elongatus, a detailed calculation of optical properties of reaction-center (D1–D2) complexes is presented applying a theory developed previously. The calculations of absorption, linear dichroism, circular dichroism, fluorescence spectra, all at 6 K, and the temperature-dependence of the absorption spectrum are used to extract the local optical transition energies of the reaction-center pigments, the so-called site energies, from experimental data. The site energies are verified by calculations and comparison with seven additional independent experiments. Exciton relaxation and primary electron transfer in the reaction center are studied using the site energies. The calculations are used to interpret transient optical data. Evidence is provided for the accessory chlorophyll of the D1-branch as being the primary electron donor and the location of the triplet state at low temperatures.

INTRODUCTION

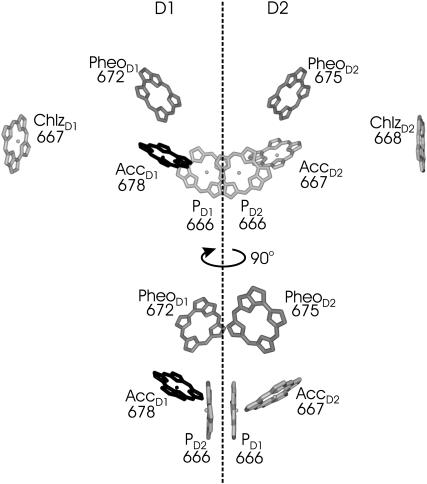
It is a challenging task to understand how excitation energy and electron transfer reactions are triggered in photosystem II (PS-II). The recent progress in structural analysis of PS-II at 3.5 Å resolution (Ferreira et al., 2004) and at 3.2 Å resolution (Biesiadka et al., 2004) revealed the orientations of optical transition dipole moments of the reaction-center (RC) pigments that are bound in the D1–D2 subunits. The orientations and the number of chlorophylls in the antenna subunits CP43 and CP47 are less well defined. Critical parameters for the modeling of excitation energy transfer are the optical transition energies of the pigments in their local protein environments. Those so-called site energies of the pigments can be obtained from the fit of optical spectra. We present results for the D1–D2 reaction-center complex that contains six chlorophylls and two pheophytins as shown in Fig. 1. The six pigments in the center, i.e., the two special-pair pigments P_D1 and P_D2, the two accessory chlorophylls Acc_D1 and Acc_D2, and the two pheophytins Pheo_D1 and Pheo_D2, will be denoted as core pigments in the following.

FIGURE 1.

Arrangement of pigments in the PS-II RC. Numbers are the wavelengths in nanometers corresponding to the site energies of the pigments, determined as described in the text. The lower section of the figure contains an additional view on the six core pigments, obtained after a 90° rotation.

Another difference of the new structural data (Ferreira et al., 2004; Biesiadka et al., 2004) with respect to the earlier data with lower resolution (Zouni et al., 2001) is that the distance between the central special-pair chlorophylls P_D1 and P_D2 is smaller than originally found (Zouni et al., 2001) and this smaller distance leads to a coupling that is larger by a factor of 2–3 than the coupling between any other two pigments in the RC, whereas the previous data gave similar couplings (Renger and Marcus, 2002b). As a result, the multimer model (Durrant et al., 1995; Renger and Marcus, 2002b; Barter et al., 2003) that assumes equal site energies for the pigments has to be reevaluated, and different site energies have to be assumed to describe the spectra. In particular, the assignment of optical transition dipoles in the new data (Ferreira et al., 2004; Biesiadka et al., 2004) allows for a more quantitative description of optical experiments.

As in the bacterial reaction center (bRC), electron transfer in PS-II is known (Shkuropatov et al., 1997, 1999) to proceed only along one of the two branches, which are related by a pseudo-twofold rotation symmetry. However, an important difference between these two types of RCs is that only the PS-II RC can create a high enough redox potential for the splitting of water and the evolution of oxygen that forms the basis for life. Neither the reasons nor the consequences of the high redox potential of PS-II RC are well understood. One reason for the higher redox potential is likely to be the somewhat smaller overlap of the two special-pair chlorophyll wave-functions that leads to a more localized cation state in PS-II than in bRC.

A consequence of the high redox potential is that the PS-II RC cannot use carotenoids for photoprotection, i.e., the quenching of chlorophyll triplet states, because the carotenoids would be oxidized if they were in close-enough proximity to the RC chlorophylls for Dexter-type triplet transfer. An alternative quenching mechanism for the triplet states concerns the quenching by the singly reduced quinone Q_A (van Mieghem et al., 1995; Noguchi, 2002). This quenching is more efficient in PS-II than in bRC, because in the latter the triplet state is localized at the special-pair, whereas in the former it is likely to be localized at the accessory chlorophyll of the D1-branch (van Mieghem et al., 1991), Acc_D1, which is closer to Q_A. The calculations presented here confirm the localization of the triplet state at Acc_D1.

Due to the large excitonic coupling between the two special-pair bacteriochlorophylls in bRC, the excitation energy relaxes to the low-energy special-pair band and electron transfer starts from the special-pair. In addition, it was found (van Brederode et al., 1997, 1999b) that direct excitation of the accessory bacteriochlorophyll can lead to primary charge separation from there. The latter observation triggered a discussion on the primary donor in PS-II (van Brederode et al., 1999a; Dekker and van Grondelle, 2000; Prokhorenko and Holzwarth, 2000; Diner et al., 2001; Diner and Rappaport, 2002; Barter et al., 2003), since in PS-II the excitonic coupling in the special-pair is much weaker than in the bRC and, therefore, the lowest excited state in the PS-II RC is not necessarily localized at the special-pair. In fact, fluorescence line-narrowing spectra at 5 K (Peterman et al., 1998) contain signatures of a carbonyl stretch vibration at 1669 cm⁻¹ which was assigned by static and time-resolved infrared spectroscopy to Acc_D1 (Noguchi et al., 1993, 1998, 2001). In the light of the latter finding and the structural similarity between the two types of RCs, it may be expected that the detour of electron transfer starting at the accessory bacteriochlorophyll in bRC becomes the main primary electron transfer event in PS-II. The present calculations support this idea.

An interesting prediction of a previous multimer model (Merry et al., 1996) is the existence of two low energy exciton states, which are localized on the two different branches of the RC. This model was used to explain the relatively slow relaxation times that were measured in transient anisotropy experiments (Merry et al., 1996) at room temperature. Consistent with this idea, the decrease of the quantum yield of fluorescence between 4 K and 70 K (Groot et al., 1994) was explained by assuming that trap states localized on the electron transfer inactive branch are responsible for fluorescence and that those states are thermally activated and quenched by charge transfer upon raising the temperature (Groot et al., 1994). The present calculations do not support the latter idea. Instead, they are consistent with the suggestion (Peterman et al., 1998) that a certain fraction of the RCs is unable to perform charge separation, and fluoresces. With respect to the anisotropy decay (Merry et al., 1996), the calculations suggest that it is due to excitation energy transfer between Pheo_D2 and Acc_D1.

METHODS

Theory of optical spectra

A theory of linear optical spectra is used that was recently developed by one of us (Renger and Marcus, 2002a). The theory takes into account an exciton relaxation-induced lifetime broadening and vibrational sidebands that are due to the coupling of optical transitions to vibrational degrees of freedom described by a spectral density. A representation in terms of partly delocalized excited states (exciton states) of the complex is used. The exciton coefficients 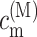and energies ɛ_M are obtained by a diagonalization procedure from the excitonic (Coulomb) couplings between localized excited states and the site energies of the pigments, as usual (e.g., Renger et al., 2001). The excitonic couplings obtained from the structural data (Biesiadka et al., 2004) within the transition monopole method (Chang, 1977) are shown in Table 1. We note that applying a simple point-dipole approximation results in a 50-cm⁻¹ larger special-pair coupling, whereas for the remaining couplings the point-dipole and transition monopole approximations give very similar values. Linear optical spectra are characterized by the lineshape function D_M(ω) of the transition between the ground state and the M^th exciton state,

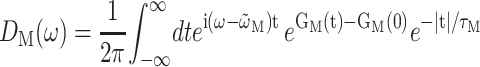(1)

(Renger and Marcus, 2002a), where 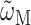is the transition frequency that takes into account reorganization effects due to the exciton-vibrational coupling

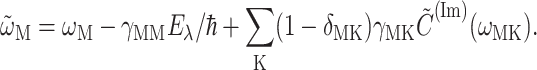(2)

Here, 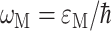is the vertical transition energy at the minimum position of the ground state potential energy surface, E_λ is the reorganization energy,

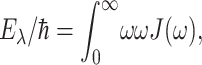(3)

and is the imaginary part of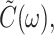

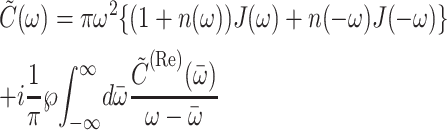(4)

(Renger and May, 2000), where 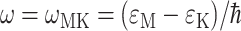and 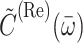is the first part on the right-hand side of Eq. 4 with 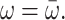The γ_MK in Eq. 2 is an exciton-vibrational coupling constant that depends on the eigen-coefficients 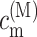of exciton states and on the correlation radius of protein vibrations R_c (Renger et al., 2001),

(5)

A value of R_c = 5 Å is used in the present calculations that was determined from time-resolved pump-probe spectra (Renger and Marcus, 2002b). (The frequency domain spectra studied here do not depend critically on the value of R_c.) The time-dependent function G_M(t) in Eq. 1 is

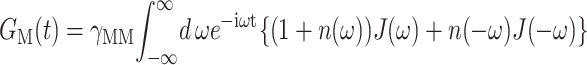(6)

(Renger and Marcus, 2002a), and the reciprocal of the dephasing time τ_M in Eq. 1 is

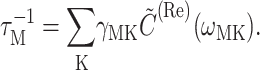(7)

The temperature-dependence of the optical lineshape function D_M(ω) is given by the mean number of vibrational quanta excited at a given temperature n(ω) = (e^ℏω/kT − 1)⁻¹ entering Eq. 1 via Eqs. 4 and 6. The spectral density J(ω) in Eqs. 4 and 6 was extracted (Renger and Marcus, 2002a) from the 1.6-K fluorescence line-narrowing spectra of B777-complexes, measured by Creemers et al. (1999), as

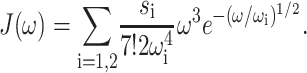(8)

The numerical coefficient in Eq. 8 was chosen so that 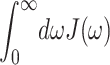equals the Huang-Rhys factor, s₁ + s₂. The extracted parameters are s₁ = 0.8, s₂ = 0.5, ℏω₁ = 0.069 meV, and ℏω₂ = 0.24 meV. The maxima of the two contributions in Eq. 8 occur at frequencies 36 ω_i, i.e., at 20 and 70 cm⁻¹. In the present calculation for PSII complexes we used the same functional form as in Eq. 8 but, as determined from the temperature-dependence of absorption spectra discussed below, rescaled the Huang-Rhys factor S = s₁ + s₂ by a factor of 0.5; i.e., we set s₁ = 0.4, s₂ = 0.25.

TABLE 1.

Calculated couplings in transition monopole approximation, obtained using the transition monopoles of Chang (1977), in units of cm⁻¹ and the 3.2 Å resolution structural data of Biesiadka et al. (2004) (file 1W5C.pdb in the Brookhaven Protein Data Bank)

	PD2	AccD1	AccD2	PheoD1	PheoD2	ChlzD1	ChlzD2
PD1	158	−29	−58	−3	11	1	1
PD2		−59	−27	14	−5	1	1
AccD1			8	55	−3	3	0
AccD2				3	66	0	2
PheoD1					2	−3	0
PheoD2						0	−4
ChlzD1							0

The following effective dipole strengths have been assumed: 4.0 D for Chls and 3.1 for Pheos.

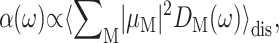The lineshape function D_M(ω) enters the expression for circular dichroism linear absorption and linear dichroism 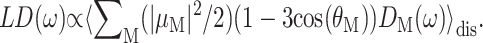The above expressions use the rotational strength r_M, the square of the transition dipole moment of the Mth exciton state 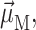and the angle θ_M of 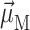with the normal of the membrane. The 〈…〉_dis is an average over static disorder in site energies. A Gaussian distribution function of width (full width at half-maximum), Δ_dis, is assumed for the site energies, and the disorder average is performed numerically by a Monte Carlo method. The fluorescence signal is obtained as described in detail elsewhere (Renger and Marcus, 2002a).

In the calculation of triplet-minus-singlet (T-S) spectra, the triplet absorption spectrum of the complex is calculated by neglecting the oscillator strength and excitonic couplings of the pigment, where the triplet state is localized. For the absorption spectra that involve a reduced (oxidized) pigment, in addition to neglecting the oscillator strength and excitonic couplings of that pigment, electrochromic shifts in site energies of the remaining pigments are taken into account in the following way. For the reduced (oxidized) pigment a negative (positive) elementary charge is evenly distributed over the atoms of the π-system of this pigment and the electrochromic transition energy shift ΔE of another pigment in the ground state is calculated as the interaction energy of the atomic partial charges δq_i of the reduced (oxidized) pigment and the vector of the pigment in the ground state. The vector 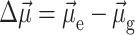denotes the change in permanent dipole moments of the excited and ground states, which is known (Krawczyk, 1991) for chlorophylls to be oriented approximately in the direction of N_B → N_D and to have a magnitude of ∼1 D. The electrochromic shift is given as 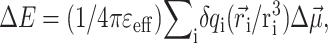where ε_eff is an effective dielectric constant and 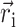is a vector between the centers of the pigment in the ground state and the reduced (oxidized) pigment.

Extraction of site energies

A genetic algorithm is used to obtain the site energies of the six chlorophylls (Chls) and two pheophytins (Pheos) in D1–D2 complexes. The genetic algorithm works as follows:

1. A random set of site energies is generated N_s times.

2. From a simultaneous calculation of absorption, linear dichroism, circular dichroism and fluorescence spectra, and comparison with experimental data, a ranking of the N_s sets of site energies is obtained.

3. Two different types of genetic operations are performed to optimize the site energies, point mutations, and crossing over. For point mutation, one or two randomly chosen site energies of randomly selected pigments are varied in a random way within a certain limit. In the crossing-over operation, two sets of site energies with intermediate ranking are selected. A pigment number i_p is randomly chosen and serves as a border for crossing-over of site energies: The site energies of all pigments i with i < i_p of the first set are exchanged with the respective site energies of the second set. The number of crossing-over operations is ∼10% of N_s.

4. From the modified sets of site energies new spectra are calculated and a new ranking is obtained. The two best sets from the previous ranking are included in the present one.

5. Points 3–4 are repeated until the genetic operations no longer lead to changes in the first place of the ranking for a certain number (≈100) of cycles.

Theory of excitation energy transfer

For the description of excitation energy transfer among the six core pigments an harmonic oscillator version (Renger and Marcus, 2003) of the modified Redfield theory is used, which was originally derived for Brownian oscillators (Zhang et al., 1998a). The rate constant for exciton relaxation between delocalized exciton states M and N, which includes the diagonal part of the exciton-vibrational coupling nonperturbatively, reads

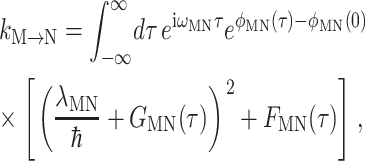(9)

(Renger and Marcus, 2003), where the λ_MN and the time-dependent functions φ_MN(τ), G_MN(τ), and F_MN(τ) are related to the exciton coefficients and the spectral density as shown in the Appendix.

For the description of exciton transfer between the localized excited states of the two peripheral chlorophylls (Chlz) and the six core pigments a modified Förster theory is used (Fetisova et al., 1996; Sumi, 1999). The rate constant k_n→M for transfer between the localized excited state n of a Chlz and a delocalized state M of the six core pigments is then calculated from

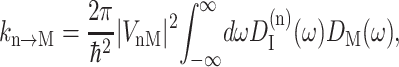(10)

where the lineshape function D_M(ω) of exciton state absorption is given in Eq. 1 and the fluorescence lineshape function of the localized donor state 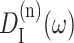is

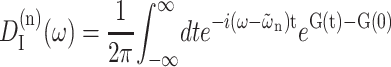(11)

(Lax, 1952; May and Kühn, 2000), with G(t) = G_M(t)/γ_MM, using Eq. 6, and the 0 → 0 transition energy 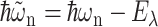that follows from the site energy ℏω_n of pigment n and the reorganization energy E_λ in Eq. 3. The excitonic coupling between local state n and extended state M, V_nM, in Eq. 10 is expressed in terms of local couplings V_nm and exciton coefficient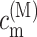s as 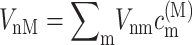(Fetisova et al., 1996).

Disorder-averaged lifetimes and pigment contributions

The probability P_ω(τ₁,τ₂) that an exciton state with energy ℏω has a lifetime τ that obeys τ₁ < τ < τ₂ is given as

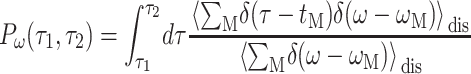(12)

(Renger and Marcus, 2002b), where 〈…〉_dis denotes an average over disorder in site energies and t_M is the lifetime of exciton state M, obtained from the inverse of 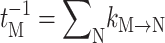, using Eq. 9 for the 6 core pigments. For the two Chlz localized excited states are assumed and the sale constant in Eq. 10 is used, instead.

The density of exciton state M is calculated from

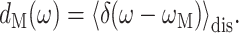(13)

To learn about the contributions of a pigment, say m, to the different exciton states we define the exciton states pigment distribution as

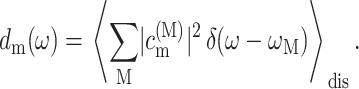(14)

Calculation of primary electron transfer

In the calculation of electron transfer it is assumed that at an initial time zero the overall population of exciton states of the six core pigments is unity and that there is a thermal population of exciton states before electron transfer. The decay rate constant k_et due to electron transfer then is

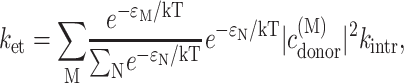(15)

where ɛ_M is the energy of exciton state M, 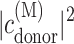is the probability of the primary electron donor pigment to be excited in exciton state M, and k_intr is the intrinsic rate constant for electron transfer between the primary donor and its neighbor. The decay of exciton population is then obtained as where 〈…〉_dis denotes an average over disorder in site energies. The intrinsic rate constant k_intr is assumed to be independent on disorder.

RESULTS

Extraction of the parameters

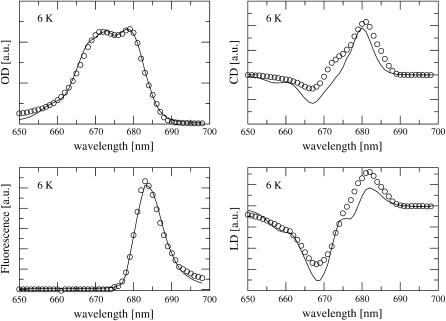
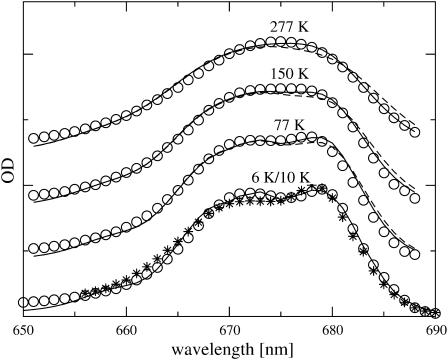
The site energies and the inhomogeneous width were determined from a simultaneous fit of the linear absorption, circular dichroism, linear dichroism, and fluorescence spectra, all at 6 K, measured by Germano et al. (2000, 2001). Fig. 2 compares the experimental data with calculated spectra which were obtained using the mean site energies shown in Fig. 1, and an inhomogeneous width (full width at half-maximum) of 180 cm⁻¹ for all site energies. A Huang-Rhys factor S = 0.65 was determined from the fit of the spectra in Fig. 2 and in addition from the fit of the temperature-dependence of linear absorption, measured by Germano et al. (2001) at 6 K and by Konermann and Holzwarth (1996) at 10 K, 77 K, 150 K, and 277 K, shown in Fig. 3. The quality of the fit could be somewhat improved by assuming a temperature-dependence of the site energy of Acc_D1, shifting from 678 nm at 6 K to 675 nm at 277 K. This result is supported by calculations of T-S spectra, discussed below.

FIGURE 2.

Absorption (OD), circular dichroism (CD), and fluorescence and linear dichroism (LD) spectra of D1–D2 complexes at 6 K. Solid lines show calculations obtained for the optimized site energies given in Fig. 1. Circles are the experimental data (Germano et al., 2001, 2000).

FIGURE 3.

Temperature-dependence of absorption spectra of D1–D2 complexes. Asterisks correspond to the experimental data by Germano et al. (2001) at 6 K, circles show the experiments by Konermann and Holzwarth (1996) at 10 K, 77 K, 150 K, and 277 K, solid lines are the spectra calculated taking into account a temperature-dependence of the site energy of Acc_D1 (678 nm at 6K/10K, 677.5 nm at 77 K, 677 nm at 150 K, and 675 nm at 277 K), and dashed lines are calculations with constant site energy of Acc_D1 (678 nm). The spectra at different temperatures have been shifted vertically by adding a constant for better visibility.

Calculation of independent spectra

In the following the parameters extracted from the fit of optical spectra in Figs. 2 and 3 are used to calculate independent spectra and to compare them with experiments.

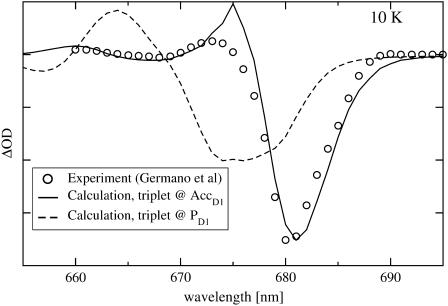
In Fig. 4 the 10 K T-S spectra obtained when the triplet is assumed to be located either on P_D1 or on Acc_D1 are compared with experimental data (Germano et al., 2001). It is clearly seen that locating the triplet at Acc_D1 gives excellent agreement with experimental data, whereas a triplet location at P_D1 cannot explain the experiment.

FIGURE 4.

10-K triplet-minus-singlet (T-S) spectrum. Circles are experimental values by Germano et al. (2001), solid line is calculation assuming triplet localized at Acc_D1, and dashed line assuming triplet localization at P_D1.

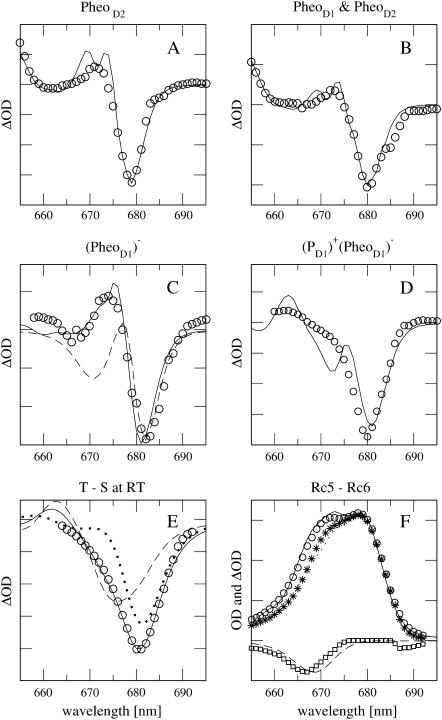
Recently, Germano et al. (2001, 2000) replaced the pheophytin of the D2-branch (Pheo_D2) by a chemically modified pheophytin and measured linear absorption, circular, and linear dichroism of the modified D1–D2 complexes at 6 K. The modified pheophytin absorbs in solution 13 nm to the blue of the native pheophytin. Since this shift can be expected to be different in a protein environment it was treated as a parameter in the calculation of the spectra. All of the spectra of the modified D1–D2 complexes can be well described within the present model, assuming a 23-nm blue-shift of the site energy of the modified pheophytin. In Fig. 5 A the absorption difference between modified and native D1–D2 complexes is compared with experimental data (Germano et al., 2001). Excellent agreement is obtained for the main bleaching occurring in theory and experiment at 679 nm.

FIGURE 5.

(A) 5-K absorption difference spectrum with modified Pheo_D2. Solid line is calculation; circles are experimental values (Germano et al., 2001). (B) 5-K absorption difference spectrum with modified Pheo_D1 and Pheo_D2. Solid line is calculation; circles are experimental values (Germano et al., 2001). (C) 77-K absorption difference spectrum with reduced Pheo_D1. Solid line is calculation, circles are experimental values (Vacha et al., 2002), and dashed line shows calculation without electrochromic shifts. (D) Calculation (solid line) of 10-K absorption difference spectrum with reduced Pheo_D1 and oxidized P_D1, comparison with experimental data (van Kan et al., 1990). (E) 277-K T-S spectrum, circles are experimental values (Durrant et al., 1990), dotted line shows calculation for triplet localized at Acc_D1, dashed line for triplet localized at P_D1, and solid line for a mixture of both according to a thermal population of triplet states (for details, see text). (F) 77-K absorption and difference spectra of RC-6 and RC-5 preparations (for explanation, see text). Solid (RC-6) and dotted (RC-5) lines are calculations, triangles, and circles are experimental values (Vacha et al., 1995); dashed line and squares are theoretical and experimental difference spectra, RC-5−RC-6.

In Fig. 5 B, the absorption difference calculated for the case that both pheophytins were exchanged is compared to experimental data by Germano et al. (2001, 2000).

In Fig. 5 C, the absorption difference for reduced pheophytin of the D1-branch (Pheo_D1) is compared with experimental data by Vacha et al. (2002). Without including electrochromic shifts of site energies, the dashed line in Fig. 5 C is obtained, which can describe the experimental main bleaching at ∼680 nm but does not contain the positive band at 675 nm in the experiment. Inclusion of electrochromic shifts of site energies, using an effective dielectric constant ε_eff = 1.5, gives agreement between calculated and experimental spectra.

In Fig. 5 D the absorption difference for reduced Pheo_D1 and oxidized P_D1 at 10 K (assuming ε_eff = 1.5 as before) is compared with experimental data by van Kan et al. (1990). The theory predicts a main bleaching ∼680 nm, as observed in the experiments. The high energy shoulder ∼670 nm in the experimental bleaching appears as a separate peak in the theory.

In Fig. 5 E, calculated T-S spectra at 277 K are compared with experimental data by Durrant et al. (1990). The agreement between theory and experiment can be improved by assuming a thermal distribution of the triplet state between Acc_D1 and P_D1 according to an energy difference of 10 meV between the two triplet states, 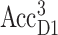and 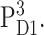The temperature-dependence of the site energy of Acc_D1 determined in Fig. 3 was taken into account and was crucial for the agreement between theory and experiment. (Neglecting this temperature-dependent shift results in a 2-nm red-shift of the main bleaching.)

In Fig. 5 F, calculated absorption spectra of complexes that lack one of the Chlz (RC-5) are compared with data measured by Vacha et al. (1995). In both cases, assuming that either Chlz_D1 or Chlz_D2 is absent, good agreement is obtained between experiment and theory. In the experimental absorption difference spectrum between RC-5 and the complex with six chlorophylls (RC-6, Fig. 1), in addition to the main bleaching at 667 nm, a small additional bleaching is observed between 685 and 690 nm that is not obtained in the calculations.

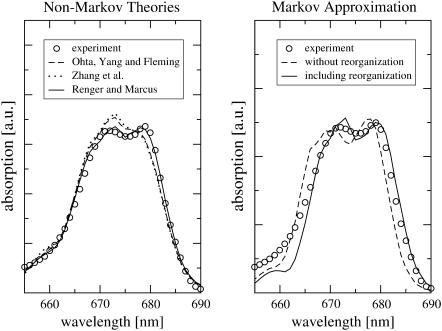
Comparison of different theories

The present theory of linear optical spectra (Renger and Marcus, 2002a) contains other theories (Ohta et al., 2001; Zhang et al., 1998b) as limiting cases. If the reorganization effects due to the off-diagonal part of the exciton-vibrational coupling that shift the exciton energy in Eq. 2 (the last term in this equation) are neglected, an earlier theory by Ohta et al. (2001) is obtained. If, in addition, the dephasing due to exciton relaxation is neglected, by setting 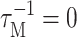in Eq. 1 an earlier lineshape function of Zhang et al. (1998b) is recovered. All these theories contain the diagonal part of the exciton-vibrational coupling nonperturbatively and are capable of describing vibrational sidebands in the spectra.

The different theories are compared in Fig. 6 (left), where the 6-K absorption spectra calculated, using the parameters determined above, are shown together with experimental data (Germano et al., 2001). For the present system the neglect of reorganization effects due to the off-diagonal part of the exciton-vibrational coupling leads to a shift and change of intensity of the two main bands, whereas the exciton relaxation-induced dephasing only gives minor corrections.

FIGURE 6.

Comparison of different theories of linear absorption (explanation is given in the text).

If a Markov approximation is applied, the lineshape function becomes 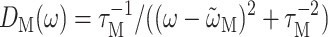(e.g., Renger and Marcus, 2002a) and the solid line in Fig. 6 (right) is obtained. The neglect of vibrational sidebands leads to the discrepancy between theory and experiment on the high-energy side of the spectrum. If, in addition, the reorganization effects are neglected by setting 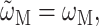an overall blue-shift of the spectrum results and the relative intensities of the two main bands change (Fig. 6, right, dashed line).

Delocalization of excited states and excitation energy transfer

The densities of exciton states d_M(ω), in Eq. 13, of the six core pigments are compared in Fig. 7 with the exciton states distribution of the six core pigments d_m(ω), Eq. 14. The two lowest exciton states M = 1 and 2 are dominated by contributions from Acc_D1 and Pheo_D2, respectively, as seen in Fig. 7 (top). The special-pair pigments P_D1 and P_D2 contribute in equal parts to exciton states M = 3 and M = 6. The fourth and fifth exciton states are dominated by Pheo_D1 and Acc_D2, respectively.

FIGURE 7.

Density of exciton states d_M(ω) and exciton states pigment distributions d_m(ω) of the six core pigments.

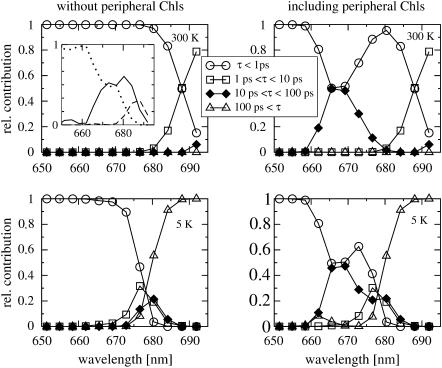
In Fig. 8 (top left), the exciton lifetimes for the six core pigments calculated at 6 K are shown. Except for the red part of the spectrum, where lifetimes between 1 and 10 ps are found, ultrafast subpicosecond exciton-state lifetimes are obtained. The inset shows the distribution of subpicosecond lifetimes. For wavelengths shorter than 670 nm, sub-100-fs lifetimes dominate (dotted line); between 670 and 680 nm, there are strong 100–500 fs components (besides the sub-100-fs lifetimes), and between 680 and 685 nm, the subpicosecond lifetimes are in the range of 500 fs to 1 ps. At low temperatures, shown for the core pigments in Fig. 8 (bottom left), subpicosecond relaxation times dominate in the blue part of the spectrum and picosecond lifetimes are obtained between 675 and 685 nm. In Fig. 8 (right), the lifetimes are shown that are obtained including Chlz_D1 and Chlz_D2. In this case, at both temperatures, additional lifetimes in the range between 10 ps and 100 ps are found ∼670 nm, where Chlz_D1 and Chlz_D2 absorb. Electron transfer was not included for simplicity but will be investigated below.

FIGURE 8.

Calculation of disorder averaged exciton lifetimes at 6 K (top) and at room temperature (bottom). (Left) For the six core pigments; (right) including also the two peripheral chlorophylls Chlz_D1, Chlz_D2. Inset (top left) shows subpicosecond lifetimes: τ < 100 fs (dotted line), 100 fs < τ < 500 fs (solid line), and 500 fs < τ < 1 ps (dashed line).

Calculation of primary electron transfer

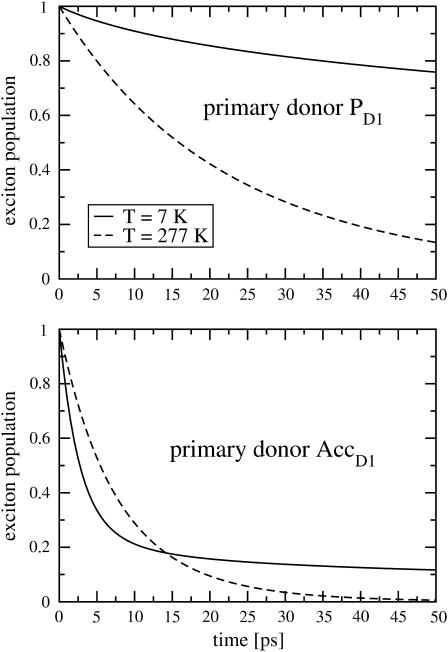
In Fig. 9 the decay of exciton population due to electron transfer is calculated for different temperatures, and assuming that the primary electron donor is either P_D1 (top) or Acc_D1 (bottom). The decay rates obtained at room temperature are in the same order of magnitude for the two cases considered. When the temperature is lowered to 7 K the decay rate increases if Acc_D1 is assumed to be the primary donor and the rate decreases drastically when P_D1 is the primary donor. At low temperature the decay becomes multiexponential. In the calculations a temperature-independent intrinsic charge separation rate constant k_intr = (2 ps)⁻¹ was assumed.

FIGURE 9.

Calculation of exciton population decay at 7 K (solid lines) and at room temperature (dashed lines) due to primary electron transfer. (Top) Assuming primary donor is P_D1; (bottom) assuming primary donor is cc_D1.

DISCUSSION

Character of excited states

The largest site energies are obtained for P_D1 and P_D2 and the lowest one for Acc_D1. As a consequence of this difference in site energies that is larger than the coupling in the special-pair, the lowest exciton state is not dominated by the special-pair as in bRC but by Acc_D1 ( Fig. 7, top). This result is in agreement with fluorescence line-narrowing (Peterman et al., 1998) and infrared spectroscopic studies (Noguchi et al., 2001), discussed in the Introduction. Similarly, because of its second lowest site energy, Pheo_D2 dominates the second lowest exciton state.

The strong coupling between P_D1 and P_D2 gives rise to two exciton states at 675 and 660 nm which are delocalized over the two pigments, as seen in Fig. 7 (center). In this respect the P_D1/P_D2 dimer is still a special-pair as its counterpart in bRC. The high-energy exciton state of the special-pair carries only very little oscillator strength, as can be judged from the absorption spectrum in Fig. 2 (top left).

Although the remaining exciton states are dominated by single pigments, there is still delocalization as it becomes obvious in Fig. 7 by the additional peaks in the exciton states pigment distributions d_m(ω). For example from the 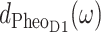in Fig. 7 (bottom), it is seen that Pheo_D1 contributes mainly to an exciton state at 672 nm (M = 4) but that it also participates in the lowest exciton state (M = 1). Overall, the delocalization of excited states of the core pigments in the present model is lower than in the previous multimer model of equal site energies (Durrant et al., 1995; Renger and Marcus, 2002b) and larger than in a model that assumes delocalization only in the special-pair (Konermann and Holzwarth, 1996). We note that the new quantity, the exciton states pigment distribution d_m(ω) in Eq. 14 is a simple and intuitive way to illustrate the delocalization of excited states in the presence of disorder.

The excited states of the peripheral chlorophylls are localized and carry the oscillator strength of monomeric chlorophyll. The stronger coupling between the six core pigments redistributes their oscillator strength to the red side of the spectrum, as found earlier (Durrant et al., 1995; Renger and Marcus, 2002b). Therefore, there is a large contribution from Chlz in the blue part of the absorption spectrum of D1–D2 RC-complexes.

The temperature-dependence of the site energy of Acc_D1 inferred from the calculation of the temperature-dependence of absorption and T-S spectra may be due to a partial charge transfer character of the excited state of Acc_D1. In bacterial reaction centers a 30-nm blue-shift of the low-energy absorption band is observed (Huber et al., 1998) between 15 K and room temperature. This shift was explained recently (Renger, 2004) by a dynamic localization of a mixed excited/charge transfer state.

From unconventional Stark spectra measured by Frese et al. (2003), such a charge transfer character of a state in the red side of the spectrum was suggested. Further support for this view is obtained from calculation of absorption difference spectra of PS-II core complexes (data will be presented in a forthcoming publication). In those calculations the same site energies as in D1–D2 complexes can be assumed except for Acc_D1 which has a 3-nm red-shifted site energy in PS-II core complexes. Since charge transfer interactions depend on wavefunction overlaps of different pigments, small conformational changes of the protein, as they may occur in different preparations, can have a visible effect on the optical spectra. The small negative bleaching between 685 nm and 690 nm in the experimental difference spectrum of the preparations with five and six chlorophylls (Fig. 5 F) might have the same origin. Alternatively, it was suggested by Konermann and Holzwarth (1996) that an additional non-stoichiometrically bound chlorophyll absorbs at this wavelength.

Besides the site energies, an important parameter determined from the temperature-dependence of the absorption spectrum in Fig. 3 is the Huang-Rhys factor S = 0.65. This value is in agreement with the S = 0.7 determined from hole-burning studies (Groot et al., 1996) for the lowest state and the S = 0.7 determined for Pheo_D1 (Tang et al., 1990) and the S < 1 determined for higher energy exciton states (Jankowiak et al., 1989). Larger S-values (S = 1.6−1.9) for a low-energy exciton state have been obtained from fluorescence line-narrowing (Peterman et al., 1998) and site-selective T-S absorption spectra (Jankowiak et al., 1989; Kwa et al., 1994).

In our calculations, for simplicity, the same S-factor was assumed for all pigments. A more detailed description should include the mixing with charge transfer states and will lead to a larger S-factor of the states with partial charge transfer character (Renger, 2004).

Verification of site energies

The difference spectra in Figs. 4 and 5 A, B, and E, that involve the two low-energy pigments, Acc_D1 and Pheo_D2, show a negative bleaching at ∼680 nm. The difference between the site energies of these pigments and the position of the main bleaching at 680 nm is due to the excitonic coupling between the core pigments. The latter is also responsible for the positive peak occurring between 670 nm and 678 nm in the 10 K T-S spectrum and in the difference spectra with modified pheophytins.

In the case of reduced Pheo_D1 in Fig. 5, C and D, there is a mixture of excitonic and electrochromic effects that explains why a bleaching at 681 nm is found, although the site energy of Pheo_D1 is at 672 nm. By reducing Pheo_D1 the change in excitonic coupling to Acc_D1 leads to a blue-shift of the low-energy exciton band, which is dominated by Acc_D1, causing the main bleaching at 681 nm in the difference spectrum. We note that the contribution of Pheo_D1 in the lowest exciton state (and hence its excitonic coupling with Acc_D1) is seen also in Fig. 7 (bottom). The bleaching of an exciton state at 671 nm, which is dominated by Pheo_D1, is compensated by electrochromic effects in the difference spectrum with reduced Pheo_D1 in Fig. 5 C. In the spectrum with reduced Pheo_D1 and oxidized P_D1 in Fig. 5 D this bleaching appears in the theoretical spectrum as a separate peak and in the experimental spectrum as a shoulder. The value of ε_eff = 1.5 used in the calculation of electrochromic shifts in site energies is smaller than the ε_eff = 4.5−4.7 for the electron transfer active L-branch of bRC but similar to the ε_eff = 1.5−1.6 for the electron transfer-inactive M-branch of bRC reported by Steffen et al. (1994).

The localization of the triplet at Acc_D1 at low temperatures in Fig. 4 agrees with an earlier prediction of van Mieghem et al. (1991), who inferred from EPR measurements that the triplet is localized on a pigment with a chlorin plane that is tilted by 30° with respect to the membrane. The verification and specification of this earlier proposal (van Mieghem et al., 1991) by calculations that are based on parameters extracted from independent experiments is a main result of the present article. The calculations in Fig. 4 prove both the site energy of Acc_D1 and the localization of the triplet state at this pigment, at low temperatures.

The thermally activated hopping of the triplet between Acc_D1 and P_D1 at higher temperatures in Fig. 5 F is in agreement with FTIR measurements (Noguchi et al., 1993), EPR measurements (Kamlowski et al., 1996), and T-S spectra on mutants (Diner et al., 2001). For the energy difference of the two triplet states, 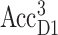and 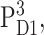values of 8 meV (Noguchi et al., 1993) and 13 meV (Kamlowski et al., 1996) were inferred from the temperature-dependence of the spectra. The present value of 10 meV is in between those two earlier values. The contribution due to the triplet state at P_D1, provides evidence for the site energy of the special-pair pigments P_D1 and P_D2, which give rise to an exciton state ∼675 nm (compare to Fig. 7) that is bleached upon triplet formation at P_D1 and leads to the high energy shoulder in the spectrum in Fig. 5 E. Additional support for this assignment is obtained from difference spectra of PS-II core complexes with oxidized P_D1 (data will be presented in a future publication).

The experimental and calculated difference spectra, RC-5−RC-6 in Fig. 5 F, show a main bleaching ∼667 nm, which agrees with the site energies assigned for the two Chlz. Since the excited states of the Chlz are localized, the bleaching occurs at the position of their site energy. There is support for the present assignment of nearly equal site energies for the two Chlz from time-dependent measurements as will be discussed in detail later.

Finally, we note that there is one experiment (Jankowiak et al., 1999) where Pheo_D2 was reported to be reduced and a main bleaching in the difference spectrum was measured at 668 nm, which cannot be described by the present set of parameters. The interpretation (Jankowiak et al., 1999) of the 668-nm bleach as site energy of Pheo_D2 is in contrast with the present assignment of 675 nm, which can explain the exchange experiments by Germano et al. (2001, 2000), which show a main bleaching at 680 nm as shown in Fig. 5 A and discussed above. Based on their interpretation of the 668-nm bleach, it was suggested (Jankowiak et al., 1999) that Pheo_D2 is effectively decoupled from the other reaction-center pigments. On the basis of the recent structural data (Biesiadka et al., 2004; Ferreira et al., 2004), neither the excitonic couplings nor the present determination of site energies, support this so-called pentamer model (Jankowiak et al., 1999).

Functional implications

Using the parameters determined and verified from optical spectra, excitation energy transfer was calculated in Fig. 8. Fig. 8 (left) shows that exciton relaxation among the six core pigments occurs on a subpicosecond timescale in agreement with pump-probe experiments (Durrant et al., 1992). The increase of lifetimes with decreasing energy (increasing wavelength) is due to a decrease in the number of downhill relaxation channels. This effect is stronger at low temperatures, because the contribution of uphill channels is less at low temperatures than at room temperature, due to the detailed balance for up- and downhill rate constants.

In Fig. 8 (right), it is seen that Chlz_D1 and Chlz_D2 transfer their excitation energy on a 10–100 ps timescale to the core pigments. The latter result is in agreement with pump-probe experiments by Vacha et al. (1995), who find a 50% decrease of a slow component ∼670 nm when they compare the kinetics in RC-5 and RC-6 preparations after 665-nm excitation. It is likely that the remaining 50% of the slow component in RC-5 preparations is due to the second Chlz and, therefore, that both Chlz absorb ∼670 nm, in agreement with the present and our earlier (Renger and Marcus, 2002b) calculations.

The lifetimes in the 100-fs to 1-ps range obtained at room temperature at low energies ∼680 nm (Fig. 8, top left, inset) agree with relaxation times found in transient anisotropy measurements (Merry et al., 1996) at room temperature. From the anisotropy studies (Merry et al., 1996) an angle of 70 ± 10° was obtained for the two low energy exciton states that are responsible for the decay of the anisotropy. As shown in Fig. 7 (top), the two lowest exciton states in the present model are dominated by Acc_D1 and Pheo_D2. The angle between their optical transition dipole moments is 68°. We conclude that the experimental anisotropy decay reflects excitation energy transfer between Acc_D1 and Pheo_D2. The calculations in Fig. 8 (bottom left) predict that the anisotropy decay should slow down at low temperatures.

In the calculation of primary electron transfer in Fig. 9 assuming a constant intrinsic rate constant k_intr, a very different temperature-dependence of the primary electron transfer is found when the primary donor is assigned either to Acc_D1 or to P_D1. The first case is associated with an acceleration of electron transfer, because at low temperatures only the lowest exciton state is populated and this state is dominated by Acc_D1. Because of the minor contribution of P_D1 in the lowest exciton state (as seen in Fig. 7, middle), electron transfer slows down considerably with decreasing temperature if P_D1 is assumed to be the primary donor. There are contrasting experimental evidences concerning either an increase (Groot et al., 1997) or a decrease (Greenfield et al., 1997, 1999) of the primary electron transfer rate with temperature.

A rather direct way of detecting primary charge transfer was chosen by Greenfield et al. (1997, 1999), who detected the time-dependent rise of the pheophytin anion band and simultaneously the bleach of the Q_x band of pheophytin. In their studies (Greenfield et al., 1997, 1999) the fast phase of electron transfer was found to increase between (8 ps)⁻¹ at 277 K and (5 ps)⁻¹ at 7 K. This increase of the rate is in agreement with the present calculations, if the primary electron donor is identified as Acc_D1. If P_D1 is the donor the calculated decrease of the rate with decreasing temperature is much more dramatic than in the alternative set of experimental data (Groot et al., 1997). Based on the above results, we infer that Acc_D1 is likely to be the primary donor in PS-II.

We note that the multiexponential decay that is calculated for low temperatures is due to the disorder that can give rise to a lowest energy exciton state that is localized on a pigment different from the primary donor, an effect discussed earlier by Prokhorenko and Holzwarth (2000). However, this effect disappears at higher temperatures when more states than the lowest exciton state contribute, although multiexponential decay is also measured at room temperature (Greenfield et al., 1997). We, therefore, conclude that additional sources for dispersive kinetics are present in the experiment, as, for example, a distribution of intrinsic charge transfer rate constants.

This point is related to the question: Which is the fluorescent state in D1–D2-complexes at low temperatures? In the calculation of fluorescence in Fig. 2 we implicitly assumed that there exists a certain fraction of complexes which are not capable of performing charge transfer and fluoresce but have an identical excitonic structure to those complexes that transfer electrons. In the following, the internal consistency of this assumption is discussed.

In electron transfer-active complexes, the quantum yield of the fluorescence is limited by the competition of fluorescence and charge transfer, both occurring from an equilibrated excited state manifold. The relative yield 〈k_flu/(k_flu + k_cs)〉_dis, calculated from the present parameters, the k_et in Eq. 15 and a k_flu = (4 ns)⁻¹ (Groot et al., 1996), varies between 0.02 at 4 K and 0.008 at 60 K. These values have to be compared with the ratio η_D1D2/η_Chl of fluorescence quantum yields of D1–D2-complexes and of chlorophyll a in solution, that varies between 0.07/0.3 = 0.23 at 4 K and 0.06/0.3 = 0.20 at 60 K (Groot et al., 1994). The one-order-of-magnitude difference between the calculated and measured yields shows that, in the present model, the trap fluorescence is too weak to explain the experiment. However, part of the decrease of the experimental yield with increasing temperature might be due to decreasing trap fluorescence.

The spectrum, obtained for the trap fluorescence by weighting the homogeneous fluorescence of every complex by the factor k_flu/(k_flu + k_cs) and averaging over disorder, is similar in shape to the fluorescence spectrum calculated in Fig. 2 but red-shifted by 2–3 nm. In addition, in the present model, the trap fluorescence is dominated by Pheo_D2. However, site selection experiments show that the fluorescence at low temperatures is mainly due to chlorophyll and not due to pheophytin (Kwa et al., 1994; Peterman et al., 1998; Konermann et al., 1997). In summary, the present model is consistent with a fluorescence occurring from an exciton state with the main contributions from Acc_D1 and disagrees with a model that assumes major contributions to the fluorescence from trap states. It is inferred, therefore, that Acc_D1 plays a double role; it acts as the primary electron donor in one fraction and fluoresces in another fraction of complexes in the sample.

What could be the functional relevance of Acc_D1 be to the location of the triplet state and the primary electron donor? As discussed in the Introduction, it was suggested (van Mieghem et al., 1995; Noguchi, 2002) that triplets at Acc_D1 can be efficiently quenched by singly reduced Q_A. Since these triplet states that are formed by charge recombination can react with triplet oxygen to form the physiologically dangerous singlet oxygen, the proposed quenching mechanism (Noguchi, 2002), and thereby the location of the triplet state, are of importance for protecting the photosystem under light stress.

If Acc_D1 is the primary electron donor, electron transfer is favored energetically only along one branch for the following reasons: The neighboring P_D1 has the lowest oxidation potential since the cation is known to be stabilized there, and so in a simple picture it has the highest HOMO level of the core pigments. Therefore, it is likely that the highest LUMO level also belongs to P_D1 and, hence, P_D1 could transfer an excited electron energetically downhill along both branches. For the same reasons, the Acc_D1 can transfer the electron downhill only to the Pheo_D1. The unidirectionality of electron transfer in PS-II might have the advantage to limit the photophysical damage to one branch.

CONCLUSIONS

In this work a description of 11 independent experiments of D1−D2 reaction-center complexes is obtained using a consistent set of parameters. The site energies, obtained from a genetic algorithm, are almost symmetric in the two branches, except for that of Acc_D1, the latter being lower by ∼30 meV than the one of its D2-counterpart Acc_D2. Moreover, Acc_D1 has the lowest site energy of all reaction-center pigments and dominates the lowest exciton state in PS-II RC.

From the calculations of T-S spectra at different temperatures strong evidence is obtained for the stabilization of the triplet state at Acc_D1 at low temperatures and a thermal distribution between P_D1 and Acc_D1 at higher temperatures. An energy difference of 10 meV is obtained for the two triplet states, 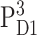and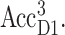

Using a simple model for primary electron transfer a measured temperature-dependence of the fast phase can only be explained if Acc_D1 is assumed to be the primary electron donor in PSII. An intrinsic electron transfer rate constant of (2 ps)⁻¹ is inferred from the calculations.

Exciton relaxation was studied using the parameters (site energies, width of inhomogeneous distribution function for the site energies, and the spectral density) determined and verified from the spectra. Subpicosecond relaxation kinetics is found for the six core pigments. The two Chlz transfer their excitation energy on a 10–100-ps timescale to the core pigments.

Besides being the location of the triplet and the primary electron donor, Acc_D1 shows other unique properties: Its site energy depends on temperature and varies in different preparations. An interpretation of these unusual properties is suggested that is based on a partial charge transfer character of the excited state of Acc_D1.

APPENDIX: HARMONIC OSCILLATOR-MODIFIED REDFIELD THEORY FUNCTIONS

The functions in Eq. 9 are

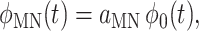(16)

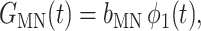(17)

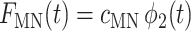(18)

(Renger and Marcus, 2003), and are related to the spectral density in Eq. 8 via the function φ_n(t),

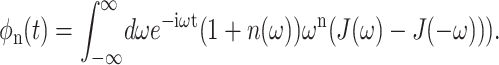(19)

The time-independent part in the integrand in Eq. 9, λ_MN, is

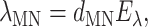(20)

using the reorganization energy E_λ in Eq. 3. The coefficients a_MN, b_MN, c_MN, and d_MN in the above equations are given by the exciton coefficients and the correlation radius of protein vibrations as

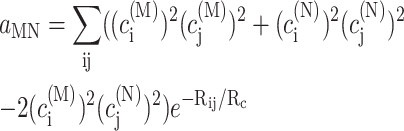(21)

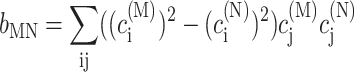(22)

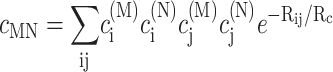(23)

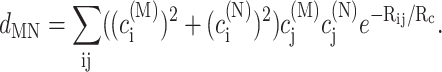(24)

In the limit of localized vibrations (R_c → 0) our earlier result (Renger and Marcus, 2003) is recovered, i.e.,

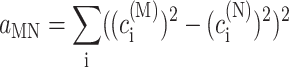(25)

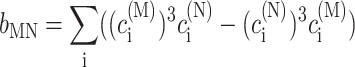(26)

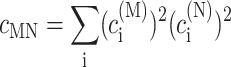(27)

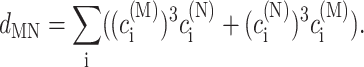(28)