Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Dec 30;88(3):1659–1665. doi: 10.1529/biophysj.104.053850

Tetrameric Mouse Acetylcholinesterase: Continuum Diffusion Rate Calculations by Solving the Steady-State Smoluchowski Equation Using Finite Element Methods

Deqiang Zhang *,†, Jason Suen †, Yongjie Zhang , Yuhua Song **, Zoran Radic ‡, Palmer Taylor ‡, Michael J Holst §, Chandrajit Bajaj ¶,‖, Nathan A Baker **, J Andrew McCammon *,†,‡
PMCID: PMC1305222  PMID: 15626705

Abstract

The tetramer is the most important form for acetylcholinesterase in physiological conditions, i.e., in the neuromuscular junction and the nervous system. It is important to study the diffusion of acetylcholine to the active sites of the tetrameric enzyme to understand the overall signal transduction process in these cellular components. Crystallographic studies revealed two different forms of tetramers, suggesting a flexible tetramer model for acetylcholinesterase. Using a recently developed finite element solver for the steady-state Smoluchowski equation, we have calculated the reaction rate for three mouse acetylcholinesterase tetramers using these two crystal structures and an intermediate structure as templates. Our results show that the reaction rates differ for different individual active sites in the compact tetramer crystal structure, and the rates are similar for different individual active sites in the other crystal structure and the intermediate structure. In the limit of zero salt, the reaction rates per active site for the tetramers are the same as that for the monomer, whereas at higher ionic strength, the rates per active site for the tetramers are ∼67%–75% of the rate for the monomer. By analyzing the effect of electrostatic forces on ACh diffusion, we find that electrostatic forces play an even more important role for the tetramers than for the monomer. This study also shows that the finite element solver is well suited for solving the diffusion problem within complicated geometries.

INTRODUCTION

Acetylcholinesterase (AChE, E.C. 3.1.1.7) terminates neurotransmission at the neuromuscular junction and other cholinergic synapses by rapidly hydrolyzing the neurotransmitter acetylcholine (ACh; Massoulie et al., 1993; Taylor and Radic, 1994). In physiological conditions, AChE exists in forms of various tetramers depending on its tissue distribution (Massoulie et al., 1993). The association of the monomers may affect the catalytic activity of the enzyme (Taylor and Radic, 1994). Although AChE has many variants from alternative splicing of a single gene in some species, the tetrameric subtype T is the only form expressed in the adult nervous system and muscles in mammals (Massoulie, 2002). The tetramerization of AChE is determined by a small C-terminal domain called the “t peptide”. It is necessary for the amphiphilic character of AChE and the formation of tetramers, as AChE only forms nonamphiphilic monomers if the t peptide is deleted (Duval et al., 1992). Four t peptides can assemble into tetramers with their anchoring proteins ColQ and PRiMA, and these heteromeric associations represent the physiological functional species in muscles and brains (Feng et al., 1999; Perrier et al., 2002).

Crystallographic studies have revealed two distinct tetrameric forms of AChE, and they are both in the form of a dimer of two canonical homodimers assembled through four-helix bundles. The two tetramers can be described as (Bourne et al., 1999a; refer to Fig. 2, a and b) 1), a loose, pseudosquare planar tetramer with antiparallel alignment of the two four-helix bundles and a large space in the center where the t peptide sequences may be buried (PDB: 1C2B); and 2), a compact, square nonplanar tetramer with parallel arrangement of the four-helix bundles that may expose all the four t peptide sequences on a single side (PDB: 1C2O). The electron density for the t peptides was observed, but could not be resolved at the crystallographic resolution (4.2 Å and 4.5 Å). Another crystal structure (PDB: 1EEA; Raves et al., 1998) of tetrameric AChE is essentially the same as 1C2B. A third form (PDB: 1MAA; Bourne et al., 1999b) is a tetramer with a compact, pseudosquare planar shape from soluble mouse AChE (mAChE), which lacks the sequence of the amphiphilic C-terminal t residues, hence the four-helix bundles can come into direct contact at the interface.

FIGURE 2.

FIGURE 2

Open in a new tab

Electrostatic potential mapped onto the solvent accessible molecular surface for AChE tetramers (a) 1C2O, (b) 1C2B, and (c) INT. Blue represents positive potential value, and red represents negative potential value.

Both models (1C2O and 1C2B) are consistent with the tetrameric arrangements of AChE observed in situ (Ridger et al., 1973) and some of the features in earlier models (Blong et al., 1997; Giles, 1997; Lee and Taylor, 1982; Taylor and Radic, 1994). Although various intersubunit disulfide bonds are involved in the tetramerization, they are not necessary in the formation of the tetramer and may contribute to the stability of the association instead (Simon et al., 1998). A flexible tetramer model has been proposed to account for the two distinct forms of AchE (Bourne et al., 1999a). In changing from one structure to the other, the tetramer needs to undergo a significant conformational transition (Bourne et al., 1999a). Most recently the complex of the proline rich attachment domain of ColQ and the tryptophan amphiphilic tetramerization (WAT) sequence of AChE has been crystallized (Dvir et al., 2004). The crystal structure reveals a novel supercoil structure in which four parallel WAT chains form a left-handed superhelix around an antiparallel left-handed proline rich attachment domain helix resembling polyproline II (Dvir et al., 2004). This structure certainly will help our understanding of the tetramerization of AChE; however, the coordinates of the structure were not yet released in the protein data bank at the time of this study. Qualitatively, it appears that the structure proposed by Dvir et al. has the active sites exposed on alternate sides of the mean plane of the tetramer, somewhat similar to 1C2B.

Since the tetramer is the major form of AChE in cholinergic synapses, it is important to know whether the tetrameric association changes the diffusion rate of ACh to these enzymes. The diffusion of ACh to AChE is governed by the Smoluchowski equation. Using a recently developed steady-state Smoluchowski equation solver (SMOL) that employs finite element methods (Song et al., 2004a,b), we have calculated the diffusion-controlled reaction rates of ACh for three different tetrameric forms of mAChE using 1C2O, 1C2B, and an intermediate structure as templates at various ionic strength conditions. As shown previously (Song et al., 2004a,b), this procedure requires far less computer time than Brownian Dynamics simulation and is therefore preferred for very simple ligands. Our results show that in the limit of zero salt, there is very little difference in reaction rates per active site between all three tetrameric forms and AChE monomer. However, at higher ionic strength, the reaction rates per active site for the tetramers are lower than AChE monomer. By analyzing the effect of electrostatic forces on ACh diffusion, we find that electrostatic forces play an even more important role for the tetramers than for the monomer.

METHODS AND MODELING DETAILS

Structure preparation

In choosing a reliable structure of the tetrameric AChE, the two crystal structures of AChE from Electrophorus electricus (EeAChE; PDB entry: 1C2B and 1C2O; Bourne et al., 1999a) were downloaded from the Protein Data Bank (http://www.rcsb.org/pdb). Using these two low-resolution structures as templates, we fit the mAChE monomer previously used in diffusion simulations (Song et al., 2004a,b; Tara et al., 1998; Zhou et al., 1998a) to form tetrameric models of mAChE. The monomeric mAChE structure was based on the crystal structure of mAChE-fasciculin2 complex (PDB: 1MAH; Bourne et al., 1995), and perturbed by molecular dynamics with an ACh-like ligand in the active site gorge to produce gorge conformations with larger width (Tara et al., 1998). This has been shown to be necessary to reproduce the correct diffusion simulations with a fixed biomolecular structure, to reflect the conformational gating dynamics of the enzyme (Baker and McCammon, 1999; Song et al., 2004a,b; Zhou et al., 1998a,b). In addition to the crystal structures, an intermediate structure (INT) was generated by morphing the two crystal structures using the morph script in visual molecular dynamics (Humphrey et al., 1996). The diffusing ligand ACh was modeled as a sphere with an exclusion radius of 2.0 Å and a diffusion constant of 7.8 × 104 Å2/μs.

Solving the steady-state Smoluchowski equation by finite element methods

The Smoluchowski equation describes the diffusing dynamics of particles in a potential field under the overdamped relaxation condition (Smoluchowski, 1917). For a steady-state diffusion process, it has the form of

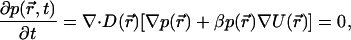graphic file with name M1.gif (1)

where p(r) or p(r, t) is the distribution probability of the diffusing particle at position r at time t, D(r) is the diffusion tensor, β = 1/kT (k is the Boltzmann constant and T is the absolute temperature), and U(r) represents the scalar potential field.

The steady-state Smoluchowski equation (SSSE) is a partial differential equation. The analytical solution can be obtained only for simple geometries and potential fields. For a system with boundaries as complex as a biomolecule, numerical methods must be used to solve a partial differential equation such as the SSSE. A number of such methods have been developed over the last 30 years or so, which includes finite difference, finite volume, finite element, etc. (Quarteroni and Valli, 1994). Recently a Smoluchowski equation solver based on finite element methods has been developed for solving SSSE with complex geometries (Song et al., 2004a,b). SMOL uses the finite element software package FEtk (Holst, 2001; http://www.fetk.org/) for finite element geometric routines, multilevel solvers, and residual-based error estimations. For more details about the solver, see references (Song et al., 2004a,b).

To get a unique solution for a partial differential equation, boundary conditions need to be defined. For the current problem, the following boundary conditions are defined:

graphic file with name M2.gif (2)
graphic file with name M3.gif (3)
graphic file with name M4.gif (4)

where pbulk is the bulk concentration, Γb is the outer boundary for the problem (40 times the radius of the biomolecule), Γa is the reactive boundary for the active site in the biomolecule, and Γr is the nonreactive surface for the biomolecule. The flux operator J(p;r) is defined as

graphic file with name M5.gif (5)

The diffusion-controlled reaction rate constant k is given by integration of the flux over the reactive boundary:

graphic file with name M6.gif (6)

The reactive boundary for the tetramer is simply the sum of four individual active sites. Hence, the reaction rate for each individual active site can be calculated by using the corresponding reactive boundary for the active site in Eq. 6. The molecular surface-based reactive boundary definition is used in this study, as it has been shown to best reproduce the experimental rate measurements (Song et al., 2004a). The placement of the reactive surface is the same as the one used in the previous studies of monomeric mAChE (Song et al., 2004a,b; Tara et al., 1998).

Adaptive finite element mesh generation for mAChE tetramer

The quality of the finite element mesh is critical to the well-posedness of the discretization of the SSSE. The Levelset Boundary Interior Exterior-Mesher software (http://www.ices.utexas.edu/CCV/software/) is used to generate and refine the tetrahedral meshes from the inflated van der Waals-based accessibility data for the mAChE tetramers. Initially the Levelset Boundary Interior Exterior method (Zhang et al., 2003, 2004) is used to generate adaptive tetrahedral meshes for the volume between the molecular surface and a small outer sphere. This gives very fine triangular elements near the active site gorge, but coarser elements everywhere else. The mesh is then extended to the entire diffusion domain with spatial adaptivity in that the mesh element size increases with increasing distance from the biomolecule. Quality improvement is normally needed to get a good tetrahedral mesh as judged by the Joe-Liu parameter, edge-ratio, etc. The number of tetrahedral elements varies from 50,000 to 70,000 for different tetramer geometries. Fig. 1 shows the meshes generated for (a) 1C2O, (b) 1C2B, (c) INT, and (d) the gorge.

FIGURE 1.

FIGURE 1

Open in a new tab

Surface meshes generated from the tetrahedral meshes for AChE tetramers (a) 1C2O, (b) 1C2B, and (c) INT used in the finite element solution of the Smoluchowski equation. The locations of the gorges are highlighted with square boxes. Solid square boxes indicate the gorge openings toward the view direction, whereas dashed square boxes indicate gorge openings opposite to the view direction. A close-up of one of the gorges is also shown in d. The resolution of the gorge is higher than other parts of the molecular surface.

Calculation of potential of mean force

APBS 0.3.1 (http://agave.wustl.edu/apbs/; Baker et al., 2001) is used to calculate the potential of mean force, which is the potential field U(r) in Eqs. 1 and 5, for each form of the tetrameric mAChE. The potential of mean force corresponds to the electrostatic potential obtained by solving the Poisson-Boltzmann equation. Nonpolar forces are neglected in this study. The CHARMM22 force field is used to assign the partial changes and radii of the atoms in the mAChE tetramers. The dielectric constant is set as 4.0 for the protein and 78.0 for the solvent. The solvent probe radius is set as 1.4 Å, and the ion exclusion layer is set as 2.0 Å. The ionic strength is varied from 0 to 0.67 M to get the reaction rate at different ionic strengths.

To allow the potential to approach zero at the outer boundary, a large space of 40 times the radius of the biomolecule is required. A series of nested potential grids with increasing grid spacing is constructed. The dimensions of the finest grid are given by the psize.py utility in the APBS software package, and the coarsest grid dimensions are set to cover the whole problem domain plus two grid spacings (to allow gradient calculation) in each dimension. The setup for the rest of the grid hierarchy is calculated using a geometric sequence for grid spacing. For structure 1C2O, the finest grid has dimensions of 153.88 Å × 135.356 Å × 137.034 Å with 353 grid points in each direction. This corresponds to a 0.437 Å × 0.385 Å × 0.389 Å grid spacing setup. The coarsest grid has dimensions of 7700 Å × 6800 Å × 6900 Å with 225 grid points in each direction. The corresponding grid spacing settings are 34.375 Å × 30.357 Å × 30.804 Å.

RESULTS AND DISCUSSION

Fig. 2 shows the electrostatic potential calculated by APBS mapped onto the solvent accessible surface for all three tetrameric mAChE structures. Here the probe radius was set to 2.0 Å, which is approximately the size of the diffusing particle ACh. The ionic strength is 0.15 M. The most apparent feature of the pictures is that the peripheral site of every gorge has significant negative electrostatic potential (see Fig. 1 for locations of the gorges). It seems that the electrostatic potential is more negative for the compact tetramer 1C2O compared with either the loose tetramer 1C2B or the intermediate structure INT. Since the electrostatic force plays an important role in guiding the diffusing ACh to the active site of AChE, it is natural to ask whether the electrostatic potential enhancement in tetramerization will lead to faster diffusion/reaction.

Using the recently developed SMOL software(Song et al., 2004a,b) based on the finite element toolkit FEtk (Holst, 2001; http://www.fetk.org/), the diffusion-controlled reaction rates for two crystal structures (1C2O and 1C2B) and an INT of mAChE are calculated by solving the SSSE. Fig. 3 shows the reaction rates for each subunit (a, b, and c) and for the tetramer (d) plotted versus the ionic strength for 1C2O (a), 1C2B (b), and INT (c). For comparison purposes, the experimental reaction rate previously measured for soluble mAChE monomer is also plotted. Note that the rates presented here refer to per active site or subunit of AChE.

FIGURE 3.

FIGURE 3

Open in a new tab

Reaction rates calculated by SMOL plotted versus ionic strength for individual active sites (AS1-4) of AChE tetramers (a) 1C2O, (b) 1C2B, and (c) INT, and all active sites of all three structures in d. As a comparison, the rates for AChE monomer (Radic et al., 1997; Tara et al., 1998) are also plotted.

Fig. 3 shows that the reaction rate per active site is comparable to or even higher than that of the monomer in the limit of zero salt for all of the tetramers. However, the reaction rates per active site are generally lower than that of the monomer at high ionic strengths.

For structure 1C2O, the entrances to two of the four gorges are partially blocked by another subunit in the complementary dimer, whereas the other two gorges are completely accessible from outside. As a result, the four active sites in 1C2O can be classified into two groups in Fig. 3 a: one group includes the two open gorges, and another group includes the two partially blocked gorges. At 0.15 M ionic strength, the former group has a reaction rate of ∼85% of the monomer rate, and the latter has a reaction rate of ∼50% of the monomer. At higher ionic strength, the rate of the open gorges approaches the monomer rate, whereas the rate of the partially blocked gorges remains at 50% of the monomer rate. Interestingly, in the limit of zero salt all four gorges have approximately the same reaction rate as the monomer. The implications will be discussed shortly.

In the case of structure 1C2B, all four gorges are accessible and have a tetrahedral arrangement. The reaction rates are all similar to the open gorge groups in 1C2O, although slight differences can be seen (Fig. 3 b). The rates for the intermediate structure INT are close to those of 1C2B as judged by the similarity of the four active sites (Fig. 3 c). Fig. 3 d compares the average reaction rates of the active sites of the three tetramers along with 50%, 75%, and 100% of the monomer rate. In the limit of zero salt, all three tetramers have an average reaction rate per active site equal to 100% of the monomer rate. At ionic strength near 0.05 M, the tetramer rates are only 50% of the monomer. At higher ionic strengths, the tetramer rates again increase, with 1C2O approaching 67% of the monomer rate, and 1C2B and INT approaching ∼75% of the monomer rate.

To understand the physical origin of the reduced rates per active site in the tetramers relative to the monomer, additional calculations were performed for the 1C2O tetramer with only one site active and with reflective boundary conditions at the other three sites. When one of the more exposed sites (AS1) was active, the rate at 0.15 M ionic strength was found to be 1.94 × 1011 mol−1min−1, i.e., nearly equal to the corresponding monomer rate. When one of the more occluded sites (AS2) was active, the rate at 0.15 M ionic strength was found to be 1.15 × 1011 mol−1min−1; this is nearly 40% higher than in the fully active 1C2O tetramer, but only about half of the rate of the corresponding monomer. We conclude that the rate reductions result from competition among the active sites (“sink-sink” interactions), with an additional steric contribution in the case of the occluded active sites.

By comparing the structure of 1C2O, 1C2B, INT, and the monomer, it seems that the accessibility of the substrate to the peripheral site is different between the tetramer and monomer, consistent with experimental findings (Saxena et al., 2003). Because the overall reaction rate is dictated by both the geometry and the electrostatic potential of the biomolecule, it is necessary to consider the case without the electrostatic potential in the diffusion by setting the charge of the diffusing particle to zero. Table 1 lists the reaction rates for a neutral diffusing particle such as TFK0. It is seen here that the free diffusion rate without the electrostatic force guidance for most active sites in the tetramers is only 65% of that for mAChE monomer. For active sites 2 and 4 in 1C2O, the rate is even lower, ∼30% of that for mAChE monomer. Overall, mAChE tetramers react with neutral ligand much slower than the monomer. This is again consistent with the conclusion that the accessibility to the peripheral site is affected by the association of monomers into tetramers (Saxena et al., 2003). However, the reaction rate for charged ligand is comparable to that of the monomer, indicating the strong enhancement of the reaction rate by electrostatic force.

TABLE 1.

Reaction rates (in 1010 mol−1min−1) of a neutral ACh-like ligand for different AChE tetramers calculated by SMOL

Tetramer AS1 AS2 AS3 AS4 All-AS
1C2O 8.06 3.27 7.97 3.52 5.70
1C2B 6.99 6.59 7.56 7.55 7.17
INT 7.80 6.94 7.01 6.81 7.14
Open in a new tab

The rates are listed for each individual active site (AS1-4) and the average for all active sites (All-AS). The rate of a neutral ACh-like ligand for AChE monomer is calculated to be 9.27 × 1010 mol−1min−1.

To evaluate the rate enhancement by electrostatic force, we define an electrostatic guidance factor (EGF) as

graphic file with name M7.gif (7)

where q is the charge carried by the diffusing particle or ligand. Fig. 4 shows the EGF plotted as a function of ionic strength for each individual active site of all three tetramer structures and for all four active sites overall.

FIGURE 4.

FIGURE 4

Open in a new tab

EGF as defined in Eq. 7 plotted as a function of ionic strength for individual active sites (AS1-4) of AChE tetramers (a) 1C2O, (b) 1C2B, and (c) INT, and (d) for all active sites of the three structures. The EGF for AChE monomer is also plotted as a comparison.

It is evident from Fig. 4 that the electrostatic force plays a bigger role for the tetramers than the monomer. Especially in the limit of zero salt, the EGF for the tetramers is three or more times more effective than the monomer, with the EGF of active sites 2 and 4 (the two partially blocked gorges) approaching 6 times of that of the monomer. At higher ionic strengths, the EGF for the tetramers is approximately twice that for the monomer.

CONCLUSIONS

We have calculated the reaction rates of ACh for three different AChE tetramers by solving the SSSE using finite element methods. The reaction rates differ for different active sites in the compact tetramer crystal structure, and the rates are similar for different active sites in the other crystal structure and the intermediate structure. In the limit of zero salt, the overall reaction rates per active site for the tetramers are the same as that for the monomer, whereas at higher ionic strength, the rates per active site for the tetramers are ∼67%–75% of the rate for the monomer. Although the overall reaction rates for the tetramers are lower than the monomer at higher ionic strengths, we have observed significant rate enhancement by electrostatic force in the tetramers. The reaction rate of a neutral ligand for the tetramers is much lower than that for the monomer AChE, because the accessibility to the peripheral site is affected due to the formation of tetramer from four monomers.

The biological significance of these results seems to be as follows. Although the rate per active site in the tetramer is ∼2/3 that of the monomer, the net rate for the tetramer is 2–3 times greater than that of a monomer, insuring rapid clearance of ACh from the synapse. Electrostatic steering of ACh to the catalytic sites is critical to this high level of activity, and helps to offset the competition among the active sites of the tetramer.

Acknowledgments

This work was in part supported by the National Institutes of Health, the National Science Foundation (NSF), the Howard Hughes Medical Institute, the NSF Center for Theoretical Biological Physics, the National Biomedical Computing Resource, the W. M. Keck Foundation, and Accelrys. The work at the University of Texas was supported in part by NSF grants ACI-9982297, 0220037, and CCR-9988357 and a subcontract from the University of California at San Diego as part of the NSF-National Partnership for Advanced Computational Infrastructure. N.A.B. is an Alfred P. Sloan Research Fellow.

References

  1. Baker, N. A., and J. A. McCammon. 1999. Non-Boltzmann rate distributions in stochastically gated reactions. J. Phys. Chem. B. 103:615–617. [Google Scholar]
  2. Baker, N. A., D. Sept, S. Joseph, M. J. Holst, and J. A. McCammon. 2001. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc. Natl. Acad. Sci. USA. 98:10037–10041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Blong, R. M., E. Bedows, and O. Lockridge. 1997. Tetramerization domain of human butyrylcholinesterase is at the C-terminus. Biochem. J. 327:747–757. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bourne, Y., J. Grassi, P. E. Bougis, and P. Marchot. 1999a. Conformational flexibility of the acetylcholinesterase tetramer suggested by X-ray crystallography. J. Biol. Chem. 274:30370–30376. [DOI] [PubMed] [Google Scholar]
  5. Bourne, Y., P. Taylor, P. E. Bougis, and P. Marchot. 1999b. Crystal structure of mouse acetylcholinesterase: a peripheral site-occluding loop in a tetrameric assembly. J. Biol. Chem. 274:2963–2970. [DOI] [PubMed] [Google Scholar]
  6. Bourne, Y., P. Taylor, and P. Marchot. 1995. Acetylcholinesterase inhibition by fasciculin: crystal structure of the complex. Cell. 83:503–512. [DOI] [PubMed] [Google Scholar]
  7. Duval, N., J. Massoulie, and S. Bon. 1992. H and T subunits of acetylcholinesterase from Torpedo, expressed in COS cells, generate all types of globular forms. J. Cell Biol. 118:641–653. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Dvir, H., M. Harel, S. Bon, W.-Q. Liu, M. Vidal, C. Garbay, J. L. Sussman, J. Massoulie, and I. Silman. 2004. The synaptic acetylcholinesterase tetramer assembles around a polyproline II helix. EMBO J. 23:4394–4405. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Feng, G. P., E. Krejci, J. Molgo, J. M. Cunningham, J. Massoulie, and J. R. Sanes. 1999. Genetic analysis of collagen Q: roles in acetylcholinesterase and butyrylcholinesterase assembly and in synaptic structure and function. J. Cell Biol. 144:1349–1360. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Giles, K. 1997. Interactions underlying subunit association in cholinesterases. Protein Eng. 10:677–685. [DOI] [PubMed] [Google Scholar]
  11. Holst, M. J. 2001. Adaptive numerical treatment of elliptic systems on manifolds. Adv. Comput. Math. 15:139–191. [Google Scholar]
  12. Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD: visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
  13. Lee, S. L., and P. Taylor. 1982. Structural characterization of the asymmetric species of acetylcholinesterase from Torpedo: 2. Component peptides obtained by selective proteolysis and disulfide bond reduction. J. Biol. Chem. 257:2292–2301. [PubMed] [Google Scholar]
  14. Massoulie, J. 2002. The origin of the molecular diversity and functional anchoring of cholinesterases. Neurosignals. 11:130–143. [DOI] [PubMed] [Google Scholar]
  15. Massoulie, J., L. Pezzementi, S. Bon, E. Krejci, and F. M. Vallette. 1993. Molecular and cellular biology of cholinesterases. Prog. Neurobiol. 41:31–91. [DOI] [PubMed] [Google Scholar]
  16. Perrier, A. L., J. Massoulie, and E. Krejci. 2002. PRiMA: the membrane anchor of acetylcholinesterase in the brain. Neuron. 33:275–285. [DOI] [PubMed] [Google Scholar]
  17. Quarteroni, A., and A. Valli. 1994. Numerical Approximation of Partial Differential Equations. Springer-Verlag, Berlin.
  18. Radic, Z., P. D. Kirchhoff, D. M. Quinn, J. A. McCammon, and P. Taylor. 1997. Electrostatic influence on the kinetics of ligand binding to acetylcholinesterase—Distinctions between active center ligands and fasciculin. J. Biol. Chem. 272:23265–23277. [DOI] [PubMed] [Google Scholar]
  19. Raves, M. L., K. Giles, J. D. Schrag, M. F. Schmid, G. N. Phillips Jr., W. Chiu, A. J. Howard, I. Silman, and J. L. Sussman. 1998. Quaternary structure of tetrameric acetylcholinesterase. In Structure and Function of Cholinesterases and Related Proteins. B. P. Doctor, P. Taylor, D. M. Quinn, R. L. Rotundo, and M. K. Gentry, editors. Plenum Publishing, New York. 351–356.
  20. Ridger, F., S. Bon, J. Massoulie, and J. Cartaud. 1973. Observation par microscopie électronique des formes allongées et globulaires de acétylcholinestérase de Gymnote (Electrophorus electricus). Europ. J. Biochem. 34:539–547. [DOI] [PubMed] [Google Scholar]
  21. Saxena, A., R. S. Hur, C. Y. Luo, and B. P. Doctor. 2003. Natural monomeric form of fetal bovine serum acetylcholinesterase lacks the C-terminal tetramerization domain. Biochemistry. 42:15292–15299. [DOI] [PubMed] [Google Scholar]
  22. Simon, S., E. Krejci, and J. Massoulie. 1998. A four-to-one association between peptide motifs: four C-terminal domains from cholinesterase assemble with one proline-rich attachment domain (PRAD) in the secretory pathway. EMBO J. 17:6178–6187. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Smoluchowski, M. V. 1917. Versuch einer mathematischen Theorie der koagulationskinetik kolloider Lonsungen. Z. Phys. Chem. 92:129–168. [Google Scholar]
  24. Song, Y. H., Y. J. Zhang, C. L. Bajaj, and N. A. Baker. 2004a. Continuum diffusion reaction rate calculations of wildtype and mutant acetylcholinesterase: adaptive finite element analysis. Biophys. J. 87:1558–1566. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Song, Y. H., Y. J. Zhang, T. Y. Shen, C. L. Bajaj, A. McCammon, and N. A. Baker. 2004b. Finite element solution of the steady-state Smoluchowski equation for rate constant calculations. Biophys. J. 86:2017–2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Tara, S., A. H. Elcock, P. D. Kirchhoff, J. M. Briggs, Z. Radic, P. Taylor, and J. A. McCammon. 1998. Rapid binding of a cationic active site inhibitor to wild type and mutant mouse acetylcholinesterase: Brownian dynamics simulation including diffusion in the active site gorge. Biopolymers. 46:465–474. [DOI] [PubMed] [Google Scholar]
  27. Taylor, P., and Z. Radic. 1994. The cholinesterases: from genes to proteins. Annu. Rev. Pharmacol. Toxicol. 34:281–320. [DOI] [PubMed] [Google Scholar]
  28. Zhang, Y. J., C. L. Bajaj, and B. S. Sohn. 2003. Adaptive and quality 3-D meshing from imaging data. In Proc. 8th ACM Symposium on Solid Modeling and Applications. ACM Press, Seattle, WA. 286–291.
  29. Zhang, Y. J., C. L. Bajaj, and B. S. Sohn. 2004. 3D finite element meshing from imaging data. CMAME, special issue on Unstructured Mesh Generation. In press. [DOI] [PMC free article] [PubMed]
  30. Zhou, H. X., J. M. Briggs, S. Tara, and J. A. McCammon. 1998a. Correlation between rate of enzyme-substrate diffusional encounter and average Boltzmann factor around active site. Biopolymers. 45:355–360. [DOI] [PubMed] [Google Scholar]
  31. Zhou, H. X., S. T. Wlodek, and J. A. McCammon. 1998b. Conformation gating as a mechanism for enzyme specificity. Proc. Natl. Acad. Sci. USA. 95:9280–9283. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES