Red Blood Cell Membrane Fluctuations and Shape Controlled by ATP-Induced Cytoskeletal Defects

Abstract

We show theoretically how adenosine 5′-triphosphate (ATP)-induced dynamic dissociations of spectrin filaments (from each other and from the membrane) in the cytoskeleton network of red blood cells (RBC) can explain in a unified manner both the measured fluctuation amplitude as well as the observed shape transformations as a function of intracellular ATP concentration. Static defects can be induced by external stresses such as those present when RBCs pass through small capillaries. We suggest that the partially freed actin at these defect sites may explain the activation of the CFTR membrane-bound protein and the subsequent release of ATP by RBCs subjected to deformations. Our theoretical predictions can be tested by experiments that measure the correlation between variations in the binding of actin to spectrin, the activity of CFTR, and the amount of ATP released.

INTRODUCTION

It is well established that both the amplitude of membrane fluctuations and overall red blood cell (RBC) shape are influenced by metabolic activity controlled by the intracellular concentration of adenosine 5′-triphosphate (ATP). RBC fluctuations were investigated in a series of experiments (Tuvia et al., 1998; Levin and Korenstein, 1991), indicating that this activity is related to a cytoskeleton component, since the fluctuations of RBC shells (cells where the lipid membrane is removed) behave similarly to intact cells. Various chemical and physical changes that interfere with the cytoskeleton-bilayer coupling were shown to reduce or even eliminate the ATP-induced membrane fluctuations (Tuvia et al., 1998; Levin and Korenstein, 1991). The effect of ATP on RBC membrane fluctuations can be treated theoretically, in terms of an enhanced effective temperature that then enters the usual equilibrium thermodynamic description. The physical origin of this effect and the reason behind the success of the effective temperature model is not yet known. The phenomenon of shape changes of RBC in response to changes in ATP levels is also well documented (Wong, 1999; Lim et al., 2002); here again, the reason for the dependence on ATP is not known (Hoffman, 2001, 2004; Nakao, 2002).

In this article, we show that cytoskeletal defects induced by ATP can account for both the enhanced membrane fluctuations as well as the overall cellular shape changes. By focusing on ATP-induced spectrin-actin dissociations (Sackmann, 1994), we predict the magnitude of the effective temperature and its dependence on ATP concentration, in agreement with published experiment data. These transient dissociations modify the cytoskeleton shear modulus and the effective surface tension of the membrane, which in turn changes the relative area difference between the two leaflets of the lipid bilayer. This can change the shape of the RBC from the normal discocyte to the abnormal echinocyte at low levels of ATP. We also suggest that deformation-induced defects can activate the membrane-bound cystic fibrosis transmembrane conductance regulator CFTR, leading to the release of ATP into the extracellular environment.

We now briefly review the structure of the RBC membrane: The surface of the RBC is a composite material containing an outer lipid bilayer, and an inner, two-dimensional cytoskeleton network (Bennett, 1989) attached in a sparse manner to the lipid bilayer (Gov et al., 2003; Gov and Safran, 2004). The links of the network consist of flexible spectrin molecules (R ∼ 80–100 nm), cross-linked at the network nodes by a complex containing a short (∼30 nm) actin filament, band-4.1, and other proteins (Bennett, 1989; Takakuwa, 2001).

The spectrin cytoskeleton of the RBC is slightly stretched and under tension, even in the un-deformed state of RBC (Zeman et al., 1990; Petrov et al., 1979; Fournier et al., 2004). This is because the spectrin filaments are attached to the bilayer and are therefore constrained from accessing all possible network configurations. This tension is balanced by the curvature energy of the bilayer, which consequentially develops small amplitude undulations with a wavelength of the order of the spectrin filament length (Zeman et al., 1990), and a typical height of ∼15 nm (Fig. 1). Equating the stretching force of the spectrin (modeled by a spring with spring constant μ and equilibrium length R₀) with the force of curving the membrane (related to its bending modulus, κ), we find

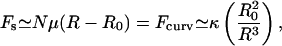(1)

where R ∼80–100 nm is the average equilibrium length of the spectrin filaments, R₀ ∼70 nm is an estimate of the radius of gyration the free spectrin filament in solution, and 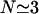is the number of spectrin filaments per network unit cell (Fig. 1), which is equal to 3 for a defect-free, triangular network. Solving this equality, using R₀ ∼70 nm, J ∼10 k_BT (Zilker et al., 1987), and μ ∼6 × 10⁻⁶ J/m² (Discher et al., 1994; Heinrich et al., 2001; Engelhardt et al., 1984), we find that the average spectrin molecule is stretched by ∼20%: 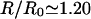(Fig. 1).

FIGURE 1.

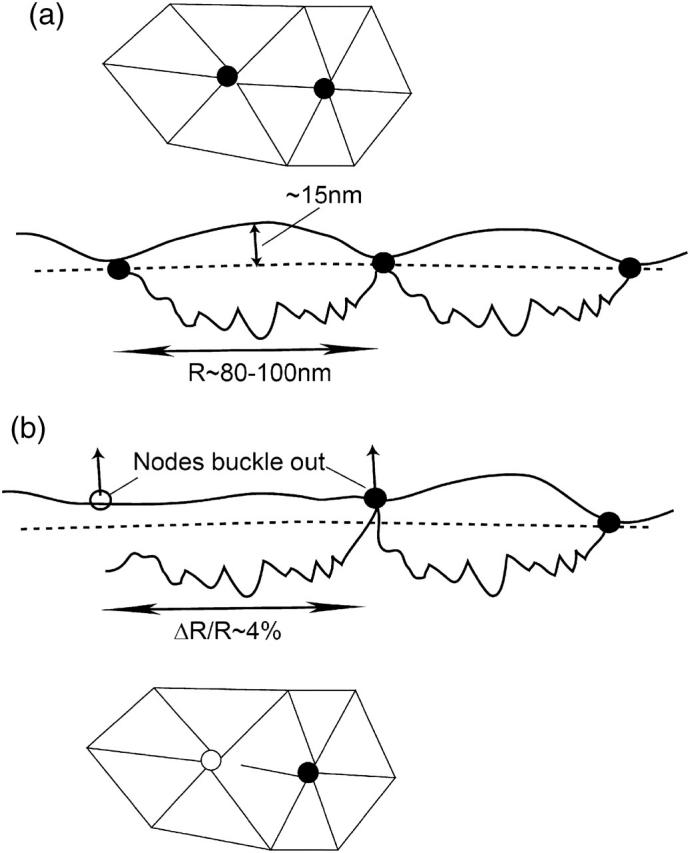
(a) Overview of the (almost) regular triangular network of the RBC cytoskeleton. Below we sketch a sideways view of the equilibrium height profile of the RBC membrane: the stretched spectrin filaments (bold jagged lines) are balanced by static height fluctuations of the bilayer. (b) A sketch of an ATP-induced dissociation of a spectrin filament, resulting in two buckled fivefold nodes.

In actual RBC, the overall symmetry of the spectrin network is hexagonal (Sackmann,1995). Nevertheless, transient and local defects in this network can occur, activated by either thermal or chemical (ATP) energy. The simplest kind of defect is the dissociation of one end of a spectrin filament from one of the network nodes, where short actin filaments serve as cross-linkers. The association energy between the spectrin and the actin linker (provided that additional proteins, such as protein-4.1, are present) is E_5,0 ∼ 5 kCal/mol ∼ 7 k_BT (Bennett, 1989), making spontaneous thermal dissociations highly unlikely. However, the consumption of ATP can promote spectrin-actin dissociation by phosphorylation of the protein-4.1 (Nakao, 2002; Sackmann, 1994; Bennett, 1989; Ling et al., 1988; Manno et al., 1995; Pestonjamasp and Mehta, 1995) (with the involvement of various membrane-bound kinases). The ATP-driven dissociation process is the focus of our work.

Larger-scale, topological defects, whereby the connectivity of the hexagonal network is modified, are more difficult to create. In these cases the hexagonal symmetry is broken by random defects, with nodes that have either five or seven attached spectrins (Fig. 1). These defects are likely to be induced by a combination of thermal and chemical (ATP) energy. The creation and motion of these defects allows the network to constantly rearrange, in response to external deformations.

We now summarize the main results: We begin by analyzing, in detail, the effects that changes to the cytoskeleton induce on the observed height fluctuations of the membrane in Analysis of the Static Fluctuation Spectrum. We show that as a function of the ATP concentration, a renormalization of both the elastic properties and the effective temperature gives a consistent description of the experimental data. In ATP-Driven Membrane Fluctuations we introduce our model of ATP-induced, transient cytoskeleton dissociations, and show how this mechanism can account for the ATP contribution to the observed height fluctuations of the RBC membrane. The effect of the ATP concentration on the overall elasticity of the cytoskeleton is described in ATP-Driven Steady-State RBC Shape. In particular, we are able to quantitatively relate the ATP concentration to the discocyte-echinocyte shape transition. Topological defects in the cytoskeleton and their role in RBC deformation and ATP-release are discussed in Deformed RBC: Topological Defects, and CFTR Activation and ATP Release, respectively.

ANALYSIS OF THE STATIC FLUCTUATION SPECTRUM

We analyze in this section the experimental measurements of the static fluctuations in RBC, that is, the height fluctuations as a function of the wavevector q (Zilker et al., 1987). We have previously analyzed this data for normal RBC (Gov et al., 2003) in terms of equilibrium thermodynamics, which we shall extend here to include ATP-driven fluctuations as well as for the stomatocyte and echinocyte cells. This analysis is complicated by the mixing of the thermal and nonthermal contributions to the fluctuation amplitude. In the absence of ATP, such as in depleted cells or washed ghosts (Tuvia et al., 1998; Levin and Korenstein, 1991), the root-mean square (RMS) amplitude of the fluctuations is 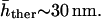This is therefore a measure of the amplitude of the thermal fluctuations alone. When ATP is added, the fluctuation amplitude rises and saturates at physiological concentrations, giving 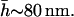In our previous phenomenological model (Gov et al., 2003), we have shown that a consistent description of both the static and dynamic data is possible if we treat the ATP effect as introducing a higher effective temperature T_eff/T ∼ 3.

We have previously proposed a phenomenological model to describe the fluctuation spectra of the RBC (Gov et al., 2003). This model describes a soft cytoskeleton shell, which is sparsely attached to the bilayer. The average bilayer-shell distance is related to the observed amplitude of thermal fluctuations, and depends on the undulations of both the bilayer and spectrin filaments (Fig. 1). The spectrin filaments form a connected quasi-two-dimensional shell that has a three-dimensional thickness of d ∼ 30 nm, due to the conformations of the soft filaments out of the plane of the shell. This can be modeled by a restoring force on the bilayer, which we account for via an harmonic potential. The force acts at all bilayer-spectrin distances due to the relatively delocalized and soft nature of the spectrin network. Additionally, the sparse attachment points of the membrane to this potential induce an effective surface tension in the bilayer (Gov and Safran, 2004). The resulting free energy is therefore given by

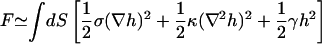(2)

(Gov et al., 2003), where σ is the effective surface tension and γ describes the confining harmonic potential. The spectrin filaments behave as entropic springs, where they can have random conformations in the half-space beneath the lipid bilayer, since they are not strongly adsorbed to the bilayer, except at their ends (Everaers et al., 1996). This would predict a fluctuation amplitude given by

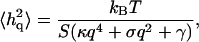(3)

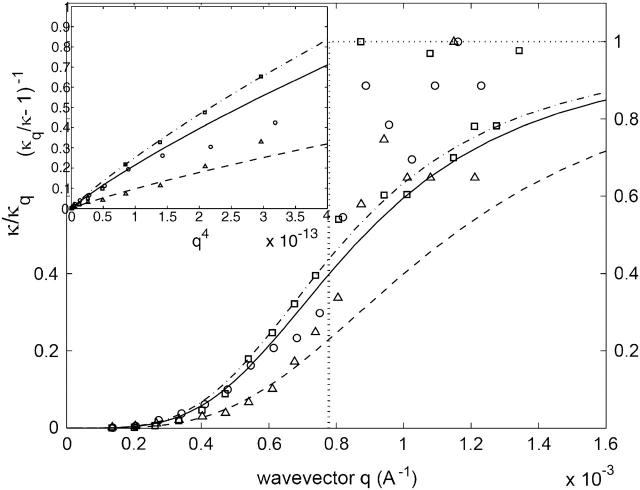
where 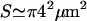is the observed surface area of the cell and the bare bending modulus is κ ∼ 2 × 10⁻²⁰ J. We can use this to define a renormalized effective bending modulus, κ_q (see Fig. 3),

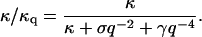(4)

FIGURE 3.

Calculated normalized effective bending modulus κ_q (Eq. 4) compared with the experimental data (Zilker et al., 1987): normal cells, circles (solid line), stomatocytes, squares (dashed-dot line), and echinocytes, triangles (dashed line). The vertical dotted line shows the crossover wavevector q₀. Inset shows the same data in the limit of small q-values, to determine the ratio γ/κ.

The simplest description of the membrane neglects the thickness of the cytoskeleton and the sparse attachments to the bilayer, and treats a bilayer that is completely attached to a two-dimensional (i.e., zero-thickness) cytoskeleton (Strey et al., 1995; Peterson, 1992). In this case, the membrane has, at all lengthscales, the bare bending modulus of the bilayer and the shear modulus of the cytoskeleton. This model would predict very small fluctuations due to the large shear restoring force. However, this model is ruled out by the observed distribution of the fluctuation amplitude among different shape modes and over the RBC surface (Strey et al., 1995; Peterson, 1992). We therefore must take into account the relatively weak coupling between the bilayer and cytoskeleton, due to the sparse connections and the soft nature of the cytoskeleton shell.

The elastic properties of the combined bilayer-cytoskeleton membrane are bounded by the two limits:

1. The cytoskeleton does not form a shell unless it is adsorbed onto the lipid bilayer. In this case the spectrin network forms an array of polymers that are grafted to the bilayer (Laradji, 2002; Hiergeist and Lipowsky, 1996). The bending modulus κ of the bare lipid bilayer is then renormalized (typically enhanced by a factor of 1.5–2.5) and an effective surface tension appears.

2. On the other hand, if the cytoskeleton does form a rigid shell on its own, the bilayer assumes its bare bending modulus; however, the rigid shell of the cytoskeleton constrains the thermal fluctuations of the bilayer to be smaller in amplitude than the distance to the rigid shell. The actual RBC cytoskeleton is somewhere in between these two limiting cases. In the absence of the bilayer, it does form a rigid shell, but only as a metastable structure, that survives for ∼20 min (Tuvia et al., 1998; Levin and Korenstein, 1991).

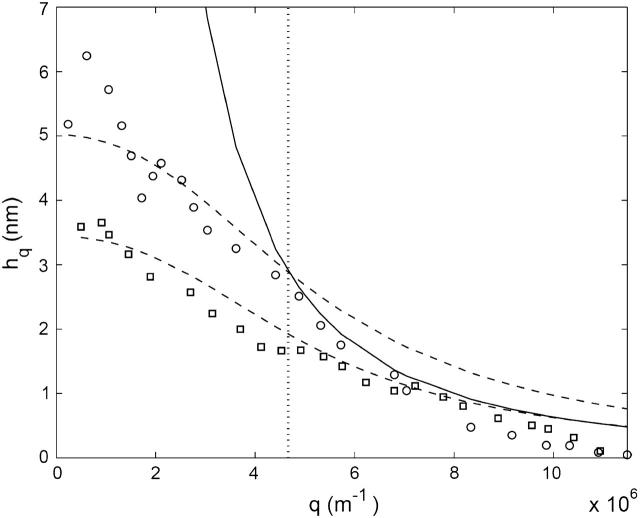
We now analyze the static fluctuation spectrum, that is, the height fluctuations as a function of the wavevector q (Zilker et al., 1987). In the limit of short wavelengths (large q) we find that the data for the mean-square amplitude is reasonably described by the expression (Fig. 2)

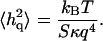(5)

At the largest wavevectors the observations are noisy due to experimental limitations. We view this value of κ as indicative of the bare value of the bilayer, since in this limit, the bilayer is largely free of the sparse cytoskeleton connections. The amplitude of fluctuations is also small compared with the average bilayer-cytoskeleton distance of d ∼ 30 nm, so that interaction between the two is small.

FIGURE 2.

Amplitude of height fluctuations as a function of wavevector q. The calculation for small q-values (Eq. 3) is shown by dashed lines, and for large q-values (Eq. 5) by the solid line. The experimental data (Zilker et al., 1987): normal cells, circles; stomatocyte, squares. The vertical dotted line shows the crossover wavevector q₀.

In the other limit of small wavevectors, we find that the amplitude saturates. To find the value of the parameters γ and σ we plot the renormalized effective bending modulus κ_q (Eq. 4, Fig. 3). Using this plot we find the ratio γ/κ. Fitting the data, we get the following values for the small q range: γ ∼ 1 − 8 × 10⁷ J/m⁴ and σ ∼ 5 − 12 × 10⁻⁷ J/m², where the variability represents the natural spread of values among different cells. Using these values to fit the experimental data for the absolute static fluctuation amplitude (Eq. 3, Fig. 2), we find that it is enhanced by a factor of ∼3, which we attribute to an increased effective temperature T_eff/T ∼ 3 due to the ATP-driven height fluctuations. Note that exactly the same enhancement factor explains the measurements of the dynamic fluctuation amplitude in ATP-depleted and ATP-containing RBC ghosts in very different experiments (Tuvia et al., 1998; Levin and Korenstein, 1991; see also Fig. 4, this article), showing the overall consistency of our description.

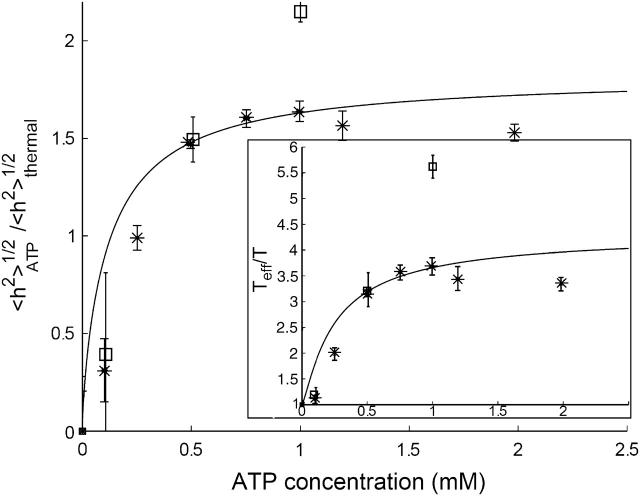
FIGURE 4.

Calculated ATP-induced RMS height fluctuations 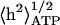as a function of the ATP concentration, using (Eq. 13) (solid line), compared with the experimental data (asterisks, ghost; squares, shell) (Tuvia et al., 1998). Both are normalized by the thermal contribution. In the inset we plot the calculated and measured effective temperature T_eff/T.

The wavevector, below which the cell displays an enhanced effective temperature as well as a relatively large effective surface tension (Gov et al., 2003; Fournier et al., 2004), is given by q₀ = (γ/κ)^1/4 ∼ 200 nm. It is satisfying that both effects set in at the same wavevector, since both stem from the forces that the cytoskeleton applies to the bilayer: the tension arises from the localized coupling sites (Gov and Safran, 2004), whereas the effective temperature arises (possibly) from ATP-induced kicks due to rearrangements in the cytoskeleton. A similar model of an effective temperature that depends on lengthscales was recently calculated for actin gels driven by myosin motors (Liverpool, 2003).

For comparison, we use the data for the stomatocyte cell (Zilker et al., 1987) (Figs. 2 and 3). These cells are known to have a weakened cytoskeleton and a much expanded bilayer (Lim et al., 2002) (see also ATP-Driven Steady-State RBC Shape, below). The first effect is taken into account by a reduction of the surface tension σ and γ by ∼15%, since both are linearly dependent on the shear modulus of the cytoskeleton μ (Gov and Safran, 2004), which is reduced by this amount (see ATP-Driven Steady-State RBC Shape). The weaker cytoskeleton allows the bilayer to have a shape transition into a stomatocyte, which is characterized by a stretched-out bilayer (Lim et al., 2002). In this case, ATP-induced defects in the cytoskeleton do not translate into normal motion of the bilayer, and the effective temperature is therefore found to be T_eff/T ∼ 1.2.

The data for the echinocyte cell (Zilker et al., 1987) (Fig. 3) fits with our expectation of increased surface tension and harmonic potential parameters by a factor of ∼2.2, compared to the values for the normal RBC (see ATP-Driven Steady-State RBC Shape). We also expect the effective temperature to be essentially given by its bare, thermal value, since ATP activity is absent in the cytoskeleton of the echinocyte (see ATP-Driven Steady-State RBC Shape). Indeed, measurements of the effective absolute fluctuation amplitude are found to be ∼3.8 times smaller than for the normal RBC.

The model described above, whereby the effect of the ATP activity is taken into account as a modification of the elastic moduli and the effective temperature, will be justified in the remainder of this article. In addition, further predictions of this model for other RBC properties will be discussed. In the next section, we relate ATP activity to local defects in the cytoskeleton (Fig. 1). These local spectrin-actin dissociations may result in a normal motion of the membrane. A locally weakened cytoskeleton was indeed observed to produce normal deformations of the membrane on the lengthscale of single network filaments (Reinhart and Chien, 1987). Such local buckling and dissociation of the cytoskeleton allow the bilayer to have normal motion larger than the bilayer-cytoskeleton separation d (Fig. 1).

We note that our analysis of the dynamic fluctuation data (Gov et al., 2003) is consistent with an effective value of the average bilayer-cytoskeleton distance d, which is determined by the soft potential strength, γ, deduced from our analysis of the static fluctuation data. The slow water flow appropriate to the measurements of the low frequencies of dynamic bilayer fluctuations is such that the cytoskeleton is nearly impermeable. This is because on the slow timescale of the water flow, the spectrin network fluctuates and effectively covers the entire two-dimensional plane. The transient, ATP-induced defects are much faster than these slow flows, so that the water is bounded on one side by the bilayer and on the other side by the spectrin network (Gov et al., 2003) which, on average, is at a distance d from the bilayer. Since the restoring force is constant, the ATP activity is best taken into account through an increased effective temperature, i.e., increased agitation force.

ATP-DRIVEN MEMBRANE FLUCTUATIONS

The consumption of ATP is known to induce large membrane fluctuations (Gov et al., 2003; Tuvia et al., 1998; Levin and Korenstein, 1991). Since the hydrolysis of ATP releases ΔE_atp ∼ 13 k_BT, it provides more than enough energy to dissociate the spectrin from the actin at the nodes of the network; that energy cost is only ΔE_sa ∼ 7 k_BT. The rate of energy transfer by this mechanism into shape fluctuations of the membrane is limited by the following quantities: the elastic energy released in the membrane, the concentration of ATP, and the time it takes for the membrane to dissipate this energy and reattach to the cytoskeleton. The ATP-induced dissociations of spectrin are transient, because the dissociated spectrin can re-associate with the actin filament.

The adsorption of ATP to the phosphorylation sites at the spectrin-actin junctions can be described by the equilibrium occupation probability; this assumes that the ATP in the cytoplasm can be treated as a reservoir with concentration n_ATP. Standard thermodynamics (Callen, 1985) gives

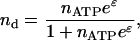(6)

where ɛ (in units of k_BT) is the energy to preferentially adsorb at the spectrin-actin sites as opposed to anywhere else on the membrane surface, and is given by the balance

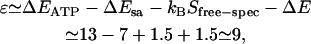(7)

where S_free-spec is the entropy change due to the release of the spectrin filament. The last term in Eq. 7 represents the mechanical energy released by the spectrin dissociation, which is estimated as due to the large adsorption energy, the ATP occupation of the spectrin-actin sites is saturated at a relatively low ATP concentration, in agreement with experimental data (see Fig. 4).

Next we calculate the height fluctuation of a single network unit-cell (Fig. 1) due to the ATP-induced spectrin dissociation. Each spectrin filament that is dissociated from the actin linkers reduces the local coordination number, N, in Eq. 1 from 3 to 2. In equilibrium this causes the local membrane length, R, to increase by ∼4%, and changes the local height of the membrane (Fig. 1). On both sides of the dissociated spectrin there are now fivefold nodes that tend to buckle upwards (Seung and Nelson, 1988; Carraro and Nelson, 1993; Lidmar et al., 2003; see also Fig. 1, this article). The bilayer bending modulus resists the cytoskeleton buckling of the fivefold defects, so that the resulting height fluctuation given by balancing the elastic forces is ∼25 nm. The total bilayer area is of course conserved. We therefore find that the ATP-induced spectrin dissociation converts the stored elastic energy of the filament into normal motion of the membrane.

We show below how this energy is added to the thermal energy k_BT that is dissipated by each membrane mode, giving an enhanced effective temperature of the order of the measured factor of T_eff/T ∼ 3 (Gov et al., 2003). Our estimate is valid under the condition that the ATP-induced processes, similar to the thermal motion of the membrane, are spatially incoherent. Note that the use of the effective temperature terminology is a misnomer, since we will show below that the ATP-induced membrane fluctuations have a distinct nonthermal character, such as a dependence on the fluid viscosity. We shall still use this term as an easy way of relating the amplitude of the ATP-induced fluctuations to the amplitude of the thermal component.

We now calculate the local transfer of energy from the ATP to the membrane motion, on the scale of a single network element (Fig. 1). Each unit-cell of the membrane converts the dissociations into local normal motion; the cell motions are independent of each other and of longer wavelength fluctuations. To describe the local dynamics of a single network element (patch), i.e., the spectrin filament and the overlying bilayer, we write the equation of motion for the amplitude h of the membrane fluctuations (in the usual limit of large damping) in one unit cell of the spectrin network as

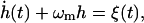(8)

where a² is the area of the membrane contained in one network triangle (the mesh size of the spectrin network: a ∼ 80 nm), η is the viscosity of the surrounding fluid, and ξ(t) is the normalized force, given by ξ(t) = F(t)/(4a²ηk), where k ∼ 1/a and F(t) is the actual force. The first term on the left-hand side of Eq. 8 is the viscous damping of the membrane due to the surrounding fluid, and the second term is the restoring force due to the curvature stiffness of the bilayer. Here, η ∼ 3η_water is a slightly enhanced, effective viscosity due to the cytoskeleton confinement of the membrane fluctuations (Gov et al., 2003; Gov and Safran, 2004).

Note that a full treatment, of the spatial height correlations for all k-modes of the ATP-driven undulations, is beyond the scope of this article. It is not clear, a priori, whether the ATP-induced fluctuations produce a correlation function with a k-dependence that is different from the 1/k⁴ thermal result. For simplicity, we here treat the fluctuations of a single membrane-cytoskeleton patch (unit cell), to calculate the contribution to the overall height fluctuations. The calculated effective temperature will be used for describing the integrated height fluctuations and comparing to the thermal contribution. For a description of the detailed k-dependence it is less useful, although in some cases the active and thermal fluctuations turn out to have the same 1/k⁴ dependence (see summary in Ramaswamy et al., 2000).

The membrane (in one unit cell of the spectrin network) kicked by the dissociation has a characteristic fluctuation frequency of ω_m ≃ κ/4ηa³ ∼ 10³ Hz. This should also include the reassociation time, τ_re, which is the Zimm time (Doi, 1996) that it takes for the detached end of the filament to thermally diffuse back to the attachment site, and reattach. Since the detached spectrin is confined by the bilayer and neighboring spectrin filaments, only a short segment of the spectrin molecule (Lenormand et al., 2003) can actually diffuse freely. This results in τ_re ∼ 10⁻⁷ s, which can therefore be neglected.

Note that this short reassociation time makes it highly unlikely that the spectrin filament will reassociate at a node different from the one it was dissociated from. Furthermore, for the dissociated end of the spectrin filament to connect to a different node, it needs to surmount an energy barrier. This barrier, likely of an order of a few k_BT, is due to the steric repulsion from neighboring filaments, which oppose the large-scale rearrangement of the filaments. The ATP-induced dissociations shown in Fig. 1, therefore, mostly produce a transient fivefold node. More extensive defects, involving five- and sevenfold nodes, can be thermally excited in addition to the ATP-induced dissociation stage. These topological defects involve large-scale rearrangement of the filaments, due to thermal excitation or applied stress. The ATP-induced transient dissociations, therefore, do not directly give rise to changes in the overall topology of the cytoskeleton network, as is further discussed in Deformed RBC: Topological Effects, below.

In Fig. 4 the data from an RBC ghost and shell is shown (Tuvia et al., 1998; Levin and Korenstein, 1991). The natural frequency of the fluctuations of the ghost is that of the intact membrane ω_m. For the exposed cytoskeleton (shell) the dissociated spectrin is no longer confined by the membrane, and the reassociation time for the whole length of the spectrin determines the natural frequency of the cytoskeleton as τ_re ∼10 ms ⇒ ω_m ∼ 10² Hz. At the same time the shell has a lower overall tension in the spectrin filaments, so that the force F due to the ATP-induced disconnections is lower. Together these conflicting trends result in a slightly larger T_eff/T (Eqs. 13 and 16) in the shell compared with the ghost (Fig. 4).

Fourier-transforming Eq. 8 in time, we get

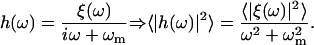(9)

We model the force correlation function as an exponential in time

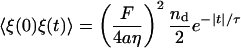(10)

(Liverpool, 2003; Granek, 1999), where n_d is given by Eq. 6 and τ ∼ 1 ms is the estimated average time for the ATP-induced spectrin-actin dissociation. This is the timescale at which spectrin is dissociated from the weakened binding site, due to the ATP (Tuvia et al., 1998, 1992; Levin and Korenstein, 1991; Herscher et al., 1994). The release of a spectrin filament gives a driving force of magnitude of F ≃ μ(R − R₀) ∼ 0.2 pN. Upon Fourier-transforming in time, we get

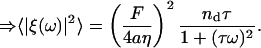(11)

Plugging this into Eq. 9, we find

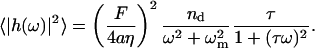(12)

Integrating over all frequencies, we find that the equal time (static) correlation function for height fluctuations is

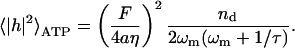(13)

For the RBC case, where ω_m ≤ τ⁻¹ (in normal conditions), we can write

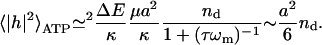(14)

The maximal RMS height fluctuation due to ATP is 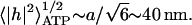Note that the ATP-induced amplitude is proportional to the ratio of the released tension in the cytoskeleton and the curvature modulus of the membrane. At physiological concentrations of ATP (i.e., in normal RBC), our model predicts a finite-amplitude kick due to ATP, which is in agreement with the time-series analysis of the fluctuation signal (Bitler and Korenstein, 2004). This means that the motion on the lengthscale of the cytoskeleton network ( 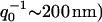is not thermal and does not satisfy the fluctuation-dissipation theorem (Liverpool, 2003). However, at larger scales an effective thermal equilibrium description can be used since nonlinear couplings mix the energy of the discrete motion into membranes modes of larger wavelength. Thus, at lengthscales and timescales that are much longer than the scale at which the ATP-induced motion occurs (q ≪ q₀), the continuum effective-temperature treatment is reasonable.

Assuming that the ATP-induced fluctuations are incoherent with respect to the thermal contribution, we predict an additive contribution to the total mean-square fluctuation amplitude (Main,1984), 〈|h|²〉_total = 〈|h|²〉_ATP + 〈|h|²〉_thermal. In Fig. 4 we compare our calculated ATP-driven height fluctuations (Eq. 13) with the available data (Tuvia et al., 1998; Levin and Korenstein, 1991), in a plot of the measured RMS height, normalized by the thermal contribution (corresponding to zero ATP), 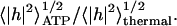For the calculated fluctuations we normalize by the calculated thermal contribution (Gov et al., 2003), 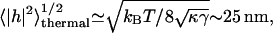where γ ≃ 7.7 × 10⁷ J/m⁴ describes the confining effect of the cytoskeleton. Finally we can define an effective temperature for height fluctuations, by comparing with the thermal contribution T_eff/T = 1 + 〈|h|²〉_ATP/〈|h|²〉_thermal (Fig. 4, inset). The agreement of our model with the data is rather good, except for low ATP concentrations, where there seems to be a threshold behavior in the experiments. This could arise from competing ATP-adsorption sites other than the spectrin-actin nodes, which effectively lower the available ATP concentration.

Note that from Eq. 14 we get that T_eff/T ∝ ΔE, in the limit where T_eff/T ≫ 1. This means that the ATP-induced mechanical energy that is given to the membrane is linearly proportional to the effective thermal energy of the membrane fluctuations. This is similar to a generalized equipartition theorem that was suggested for describing the effective temperature in sheared glassy materials (Berthier and Barrat, 2002).

Our model predicts (Eq. 13) that the effective temperature depends on the viscosity as

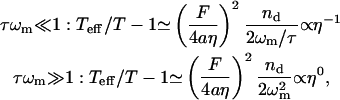(15)

since only the membrane frequency depends on the viscosity, whereas the chemical timescale for the spectrin-actin dissociation, τ, is independent on the viscosity. The first limit pertains to the RBC case, where a 1/η dependence has indeed been measured (Tuvia et al., 1997; Fricke and Sackmann, 1984). It is interesting to note that similar results were observed (Manneville et al., 2001) in the case of membrane fluctuations due to light-activated ion channels. Note that the ATP-driven activity that we propose is not due to molecular motors such as myosin.

We therefore conclude that the ATP-induced membrane height fluctuations induced by spectrin dissociations can quantitatively explain the observations of the concentration and viscosity dependence of this effect (Gov et al., 2003; Tuvia et al., 1998; Levin and Korenstein, 1991).

ATP-DRIVEN STEADY-STATE RBC SHAPE

In addition to enhancing the membrane fluctuations, ATP-induced transient defects of the spectrin network are also important in determining the average shape of RBC (Hoffman, 2001, 2004; Nakao, 2002). The intimate experimental correlation between the amplitude of membrane fluctuations and overall cell shape was demonstrated in Fricke et al. (1986). ATP is clearly important for maintaining the discocyte shape of a free RBC, since it has been observed that depletion of ATP causes a change from the discocyte to the echinocyte shape (Lim et al., 2002). This change of shape suggests that the loss of ATP results in a stiffer cytoskeleton that pulls the bilayer over a smaller cytoskeleton-projected area. The need to accommodate the bilayer area over a smaller projected area results in the appearance of the spicules of the echinocyte shape (Lim et al., 2002). In our model, the physical origin of this effect is simply related to the change in the number of released spectrin filaments, when the number of defects is reduced as ATP is reduced. We estimate this effect by relating it to the pulling force that the cytoskeleton exerts on the bilayer, and predict its dependence on the ATP concentration.

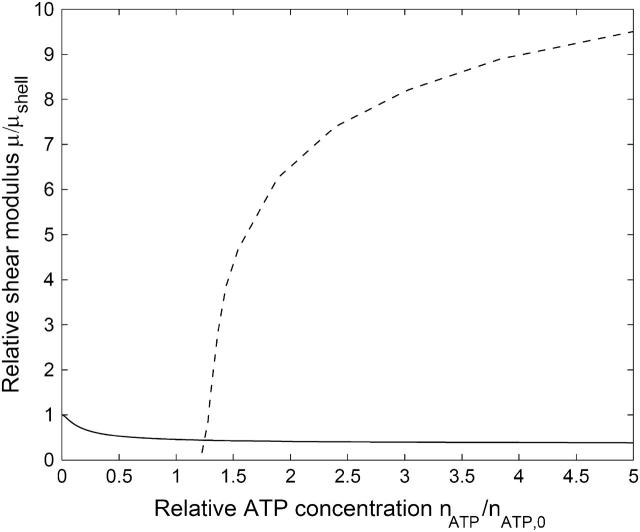
We begin by counting the different numbers of ATP-induced defects in the cytoskeleton. The proportion of dissociated ends of spectrin filaments at any given time, n_dis, is given by the proportion of ATP bound to the activation sites (Eq. 6), times the proportion of the association-reassociation cycle that the spectrin is dissociated: 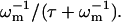We do not know this last ratio very precisely, but since the RBC is normally in the limit of 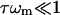(Eq. 16), we expect it to be close to one. Considering that there are two dissociation sites per spectrin filament, the proportion of associated spectrin filaments is given by n_a = (1 – n_dis)², whereas the proportion of filaments that are cut at both ends is 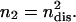In Fig. 5 we plot the dependence of these quantities on ATP concentration, using the ratio ω_m/(τ + ω_m) = 0.8. We also plot the average value of the shear modulus of an intact RBC (at physiological levels of ATP n_{ATP, 0} ∼ 1.5 mM) normalized by the value for a cytoskeleton shell (no ATP) (Lenormand et al., 2003, 2001; Sleep et al., 1999; Hénon et al., 1999). Note that .

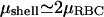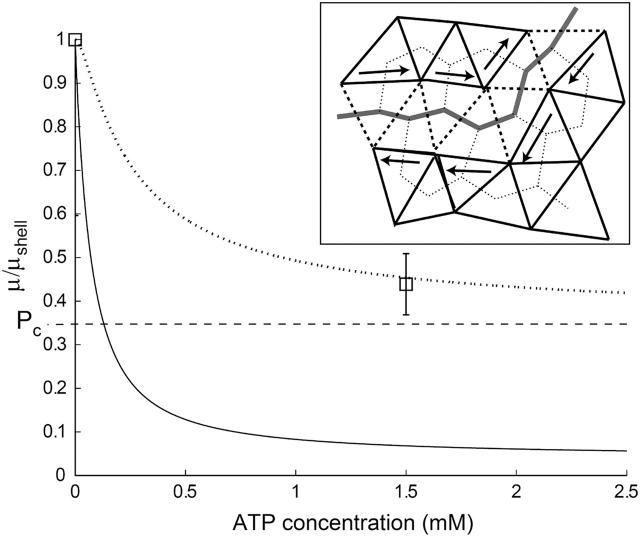
FIGURE 5.

Calculated proportion of doubly-connected (dotted line) and associated (solid line) spectrin filaments, as a function of the ATP concentration, compared with the critical concentration for two-dimensional bond percolation on a triangular lattice (dashed line). Squares mark the measured normalized shear elasticity of a shell (n_ATP ∼ 0) and intact RBC (Lenormand et al., 2003; Sleep et al., 1999). In the inset we show the path of dissociated filaments in both the triangular and complementary honeycomb lattices.

From Fig. 5 we find that the reduction in the shear modulus of the cytoskeleton follows the proportion of filaments that are dissociated at both ends. This can be understood by examining a path of dissociated filaments in the network (Fig. 5, inset). The two parts of the cytoskeleton network on either side of the path can slide freely relative to each other only when the dissociated filaments are cut at both ends. Filaments that are cut at one end only will interfere with each other and produce the usual entropic restoring force. Since the process of ATP-induced dissociations is fast on the timescale of stress measurements (Lenormand et al., 2003, 2001; Sleep et al., 1999; Hénon et al., 1999), we can take the average shear modulus to be proportional to the average number of doubly-connected spectrins, μ ∝ 1 – n₂. For comparison, we also plot the threshold density for bond percolation on a two-dimensional triangular lattice as 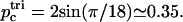This marks the concentration below which there is no connected path of fully connected spectrin filaments across the cell surface. Due to the transient nature of the dissociation process, the static shear modulus does not vanish at the percolation threshold, as it would for static (permanent) dissociations of the filaments. However, the shear response of the cytoskeleton on timescales of the order of ω_m is likely to vanish at the percolation density (Farago and Kantor, 2000; Vernon et al., 2001). The critical percolation density for a connected path of fully connected spectrins corresponds to the critical density for a path that disconnects the lattice in two, and is equivalent to bond percolation on a honeycomb lattice (Fig. 5, inset): 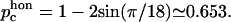The advantage for the RBC to be close to the percolation limit may be that it allows release of shear stress over the entire surface of the membrane by allowing the two parts of the lattice on both sides of the cut to slide with respect to each other.

The effect of the ATP-induced dissociations determines the overall equilibrium shape of free RBC by determining the number of defects in the spectrin cytoskeleton, which, in turn, determines the pulling tension that the cytoskeleton exerts on the bilayer. The increase in the tension δμ acting on the inner leaflet of the bilayer is balanced by a variation in the areas of the two leaflets. This balance can be written as

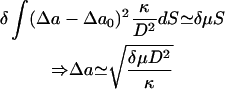(16)

(Lim et al., 2002), where D ∼ 5 nm is the bilayer thickness, Δa is the relative area difference of the two bilayer leaflets, and Δa₀ ∼0 is the value for the discocyte shape (Lim et al., 2002).

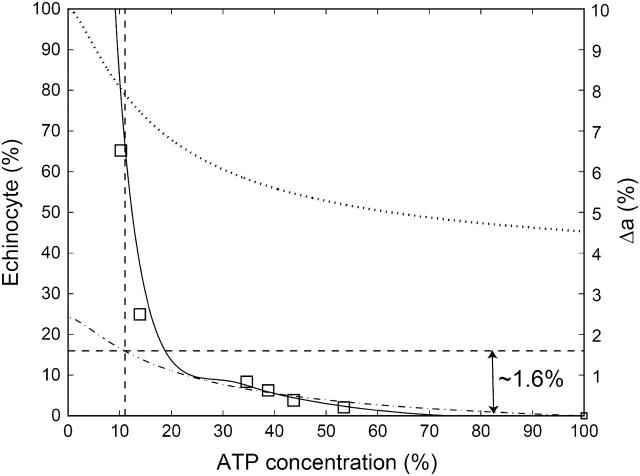
In Fig. 6 we plot both μ and Δa as a function of the ATP concentration, where 100% corresponds to physiological levels of ATP. The calculations of Lim et al. (2002) predict that an increase in the relative area difference of Δa ∼ 1.6% from the discocyte shape induces a shape transition to an echinocyte. We find that the critical ATP concentration at which this transition should therefore occur is ∼10%, which indeed correlates with a sharp increase in the measured probability (Féo and Leblond, 1974) for the echinocyte shape to appear (Fig. 6). We conclude that our model gives a quantitative explanation of the ATP-induced shape transformations of the RBC.

FIGURE 6.

Measured percentage of echinocytes (solid line and squares) (Féo and Leblond, 1974) as a function of the relative ATP concentration, compared with the relative shear modulus of Fig. 3 (dotted line). The calculated change in the relative area difference between the bilayer leaflets Δa (Eq. 16) is shown (dash-dot line). The vertical dashed line shows the critical ATP concentration where a difference of Δa ∼ 1.6% occurs relative to the discocyte value, and signals the discocyte-echinocyte transition (Lim et al., 2002).

The RBC can self-regulate the concentration of ATP through its effect on the cytoskeleton and membrane tension; according to our model, lower ATP levels result in increased tension exerted by the cytoskeleton on the bilayer (Fig. 5), which increases the bilayer permeability to cations (Johnson, 1994). This in turn increases the rate of ion pumping (to restore the correct osmotic level), which results in increased ATP concentration (Ataullakhanov and Vitvitsky, 2002). The equilibrium physiological level is therefore found from the balance of these two opposing trends. We translate the shear stress Σ applied to the cells in the shear flow experiments (Johnson, 1994) to an effective shear modulus which pulls on the bilayer from inside the cell, i.e., applied by the cytoskeleton on the membrane, by 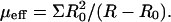Using the (scattered) experimental data, we show in Fig. 7 that the equilibrium concentration is close to the physiological level.

FIGURE 7.

The self-regulation of the ATP levels through the cytoskeleton tension. Calculated reduction in shear modulus due to ATP concentration (solid line) (Fig. 5). Derived dependence of the ATP concentration on the membrane shear stress (dashed line) (Johnson, 1994), through its effect on the membrane ion permeability (Ataullakhanov and Vitvitsky, 2002). The equilibrium concentration is found at the crossing point of the graphs, close to the physiological concentration n_ATP,0 ∼ 1.5 mM.

It is interesting to note that ATP concentration in RBC decreases with increasing age of the individual (Rabini et al., 1997), or near the end of the RBC life-span (Tochner et al., 1975). We predict that, with increasing age, lower ATP concentrations should correspond to a denser cytoskeleton and higher shear modulus. An increase of ∼20% in the elastic modulus was measured in aged RBCs (Fricke and Sackmann, 1984; Sutera et al., 1985), which, according to our model (Fig. 5), corresponds to a decrease of ∼75% in the ATP concentration. Using our model (Fig. 5) we predict that the RBC shear modulus increases by ∼15% over an individual's life of 100 years, when the ATP concentration is reduced by ∼65% (Rabini et al., 1997). Recently, atomic-force microscopy experiments allow direct observation of the changes in the cytoskeleton between young and old RBC (Liu et al., 2003; A. Ostafin, personal communication, 2004), have shown the marked increase in network connectivity as a function of age. Young cells have approximately one-half as many spectrin connections intact, after the cell is ruptured and washed. This is in agreement with our model (Fig. 5), whereby doubly-dissociated filaments are presumably those that are missing.

On the other hand, increased levels of ATP are associated with hereditary stomatocytosis (Ataullakhanov and Vitvitsky, 2002), where a leaky membrane promotes higher metabolic activity of ion pumps and a concurrent rise in ATP levels, by up to a factor of 5. At these ATP levels we predict the number of doubly-connected spectrins and shear strength to decrease by ∼12% compared to the normal discocyte. This calculated reduction in cytoskeleton tension is translated into a change of ∼0.5% in the relative area difference Δa (Eq. 16), which indeed induces the stomatocyte shape transition (Lim et al., 2002). The saturation shown in Fig. 4 breaks down when the ATP levels increase beyond the transition from discocyte to stomatocyte. In this case the bilayer is fully expanded and the ATP-induced spectrin dissociations do not translate into normal bilayer motion, as in the normal cell (Fig. 1). The effective temperature therefore goes down to the bare thermal value in these abnormal cells (see Analysis of the Static Fluctuation Spectrum, above).

In severe spherocytosis the cytoskeleton is effectively destroyed, and there is therefore no tension in the spectrin filaments, which results in much reduced membrane fluctuations (Zilker et al., 1987) and stronger cell-substrate adhesion properties (Wandersee et al., 2004). Note that in these cells, as the ATP content is reduced with age, so does the adhesion strength reduce (Wandersee et al., 2004)—indicating a certain recovery of cytoskeletal strength, in accordance with our model.

Lastly, agents that increase the binding of the spectrin-actin-protein 4.1 complex, such as Ca²⁺ ions (Nakao, 2002; Wallis et al., 1993; Fricke et al., 1986; Vest et al., 2004), are found to induce cytoskeleton shrinkage and increased connectivity (A. Ostafin, personal communication, 2004), which can be reversed by ATP perfusion (Nakao, 2002), as follows from our model. ATP loss from electroporated RBC explains, according to our model, their shape transformation to echinocytes (Schwarz et al., 1999). Addition of vanadate, which was found to inhibit membrane fluctuations (Tuvia et al., 1998; Levin and Korenstein, 1991), was also found to induce the echinocyte shape (Schwarz et al., 1999), as expected from our model. Antibodies for protein-4.1 block its phosphorylation and therefore lead to reduced dissociations and echinocyte shape, whereas spectrin antibodies prevent reassociations of spectrin filaments and stomatocyte shape (Pestonjamasp and Mehta, 1995).

DEFORMED RBC: TOPOLOGICAL DEFECTS

In addition to the transient defects discussed so far, there is likely to be a finite population of nontransient, topological defects. The creation of such defects involves, as a first stage, the dissociation of a spectrin filament, and is thereby related to the ATP-induced dissociations we discussed above. These topological defects will be shown to proliferate when the cell is subject to strong static deformations. These circumstances arise when the RBC is pulled into a thin capillary, stretched by optical tweezers, or flows through a porous filter (Evans, 1983, 1989; Reinhart et al., 1991; Dao et al., 2003; Sprague et al., 1998, 2003). We show that when the deformation of the RBC membrane is large enough, the cytoskeleton buckles and folds through the appearance of long-lived defects. Topology requires that there are 12 fivefold defects in a closed triangulated vesicle (Bowick et al., 2000). We will focus here on the cases when far more numerous defects appear, due to deformations.

The hexagonal cytoskeleton network in the discocyte RBC is relatively flat on the scale of the spectrin filaments (Sackmann, 1995). The simplest topological defect that can be excited in this hexagonal network involves the dissociation of a spectrin filament at both ends, its rotation by 90°, and its reattachment to neighboring nodes (Fig. 8). We assume that it is much less likely to have two spectrin filaments connecting the same nodes due to their steric repulsion. We therefore have defects with quadrupole symmetry, which contains two sevenfold and fivefold pairs (Magnasco, 1994). A line of adjacent defects results in a separation of the quadrupole into two separated pairs of defective dipoles (Fig. 8). Note that since two ends of a spectrin filament must be simultaneously cut for these excitations, it is highly unlikely to occur due to thermal fluctuation. This initial stage of dissociation of the spectrin filament at both ends is therefore dependent on the ATP-induced process we discussed in the previous sections. The ATP-induced dissociations (Fig. 1) will cause doubly-cut spectrin filaments to exist (Fig. 5), but since they reassociate at the same nodes from which they were dissociated, no topological defects arise directly. For the topological defects to be created, the doubly-cut spectrin filament needs to be rotated by a large angle, so that it finds new nodes to reassociate with. This rotation requires thermal or elastic energy, since there is an energy barrier to overcome. This barrier results from the steric repulsion of neighboring filaments, and is likely to be of the order of a few k_BT. This additional energy comes from thermal excitation or an external stress, and results in cytoskeleton dynamics which are much slower than the timescale of ATP-induced membrane fluctuations (Fischer, 2004). Note that the rearrangement of the filaments away from the hexagonal symmetry is limited by the ability of the short actin filaments at the nodes to cross-link only a finite number of spectrin filaments, probably not more than eight per node (Liu et al., 1987). Large-scale deviations from the hexagonal order are therefore mostly limited to five- to sevenfold defects, and no structural instability occurs.

FIGURE 8.

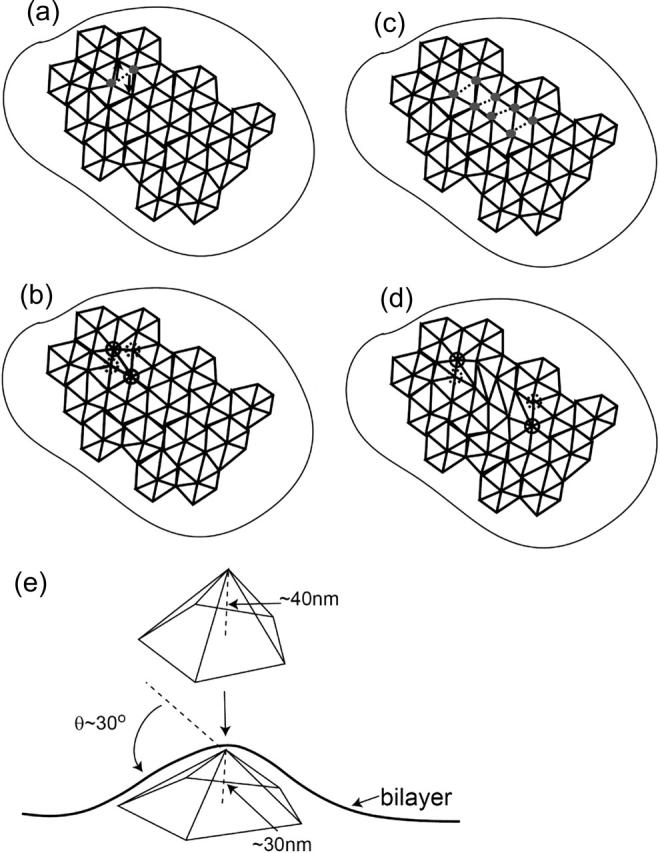
Schematic picture of the simplest quadrupole defect in the spectrin network. The defect arises from the rotation of the dashed filament in a, to produce two pairs of fivefold (dashed rings) and sevenfold defects (solid rings) (b). A linear arrangement of such defects produces two separated dipoles (c and d). (e) The shape of a buckled fivefold defect in the presence of the bilayer.

Such quadrupole defects will cause the cytoskeleton to buckle out of the (local) plane. In the absence of the bilayer, every fivefold defect would form a buckled pyranide with height ∼40 nm. By minimizing both the stretching energy of the spectrin filaments around a single fivefold pyramid shape and the bending of the covering patch of bilayer, this height is reduced to ∼30 nm (Fig. 8). Following the study of such buckling transitions by Seung and Nelson (1988), Carraro and Nelson (1993), and Lidmar et al. (2003), we arrive at the following conclusions: 1), quadrupole defects buckle out of the plane, as does a linear collection of such defects, which then forms a buckled fold-line; and 2), the strain field is highly localized near the core of these composite defects, since there is strong cancellation of the long-range strain field by adjacent five- and sevenfold defects. The lines of defects arrange themselves uniformly (no clustering) over the curved membrane (Bowick et al., 2000).

With this, we estimate the critical radius of the RBC membrane below which the cytoskeleton buckles and forms fold-lines. We consider a simplified model, where we compare the elastic energy of a continuously bent membrane in the shape of a cylinder of radius R, with the energy of a membrane of equal area that is folded by linear fold-lines connected by flat faces (Fig. 9),

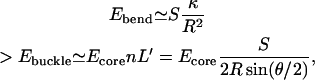(17)

where the conserved membrane area is S = 2πRL, and the effective length when folded is L′ = S/(n2R sin(θ/2)), with 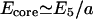where E₅ ∼ 0.7 k_BT is the elastic bending energy of a single fivefold defect (core energy). In this model we assume that the cylindrical bending of the membrane involves mainly curvature energy with very little static shear of the cytoskeleton. If in addition we would include the shear energy, this would only renormalize the prefactor of the bending energy, because the shear term has the same 1/R² dependence as the curvature energy. The turning angle at the fivefold defect (Fig. 8) is θ ≃ 40°, so that we find n = 2π/θ ≃ 5. Plotting these energies in Fig. 9 we find that for radius R < 0.4 μm the membrane prefers to form buckled fold-lines. We emphasize that the above calculation is only semiquantitative. Each fold-line, when it buckles, will have ∼100 defects along its length.

FIGURE 9.

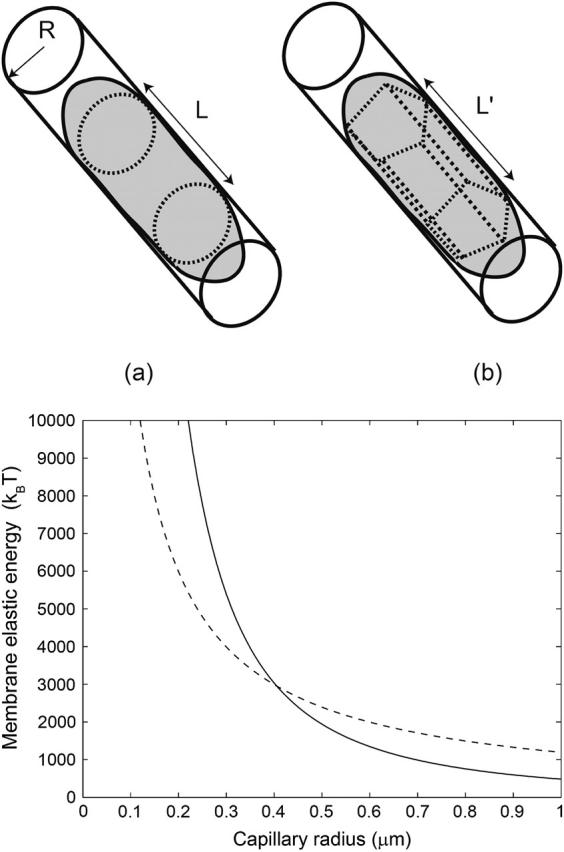
Schematic picture showing the buckling transition of a cylindrical membrane from round (a) to polygonal cross-section (b). The latter has fold-lines along its length. Below that we plot the calculated membrane energies for these geometries, given by Eq. 17, as a function of radius of the capillary. Solid line is for smooth bending (a), whereas the dashed line is for fold-lines (b). For radii less than the critical value of R_c ∼ 0.4 μm, the RBC membrane forms fold-lines.

Deformed RBC show regions where the local curvature is large: R ∼ 0.5 μm (Evans, 1983, 1989; Reinhart et al., 1991; Dao et al., 2003). Note that this is of the order of the radius of the echinocyte spicules (Lim et al., 2002). Numerical calculations using a continuous membrane (i.e., not allowed to buckle) also show the appearance of high-curvature lines in deformed RBCs (Dao et al., 2003). If one does allow for defects, we expect these regions to buckle when the local radius is smaller than the critical radius. Indeed, the continuous membrane calculations (Dao et al., 2003) give a smaller deformation (by ∼10%) compared to the measurement, which might indicate that the RBC cytoskeleton buckles (Dao et al., 2003). Folds with even smaller radii of curvature were measured in cells pushed through porous filters (Reinhart et al., 1991), with the smallest value of ∼85 nm, which is limited by the size of a single unit cell of the cytoskeleton network.

We conclude that network defects that contain fivefold nodes induce a spontaneous local curvature. They are therefore likely to spontaneously appear as fold-lines in the membrane of highly deformed RBCs. This prediction must be experimentally tested. The observed shape memory of the RBC can be related to accumulation of static (or long-lived) defects at regions of higher curvature, such as the rim of the discocyte or the spicules of the echinocyte (Gass et al., 1991; Fischer, 2004). The role of the ATP-driven dynamic dissociations described in the previous sections is important not only for the creation of the topological defects (as described in the beginning of this section), but also to allow these structural defects to move (flow) around on the RBC surface, in response to external forces (fluidlike properties of driven biological networks is seen in many cell types: Fabry et al., 2001).

CFTR ACTIVATION AND ATP RELEASE

We propose that the defects of the spectrin network induced by the deformation of RBC in porous filters (Sprague et al., 1998) play a role in the release of ATP from deformed RBC. Extracellular ATP from RBC is an important factor in the process of vascular dilation (Sprague et al., 2003; Pelleg et al., 2001; Liu et al., 2004).

The defects in the spectrin cytoskeleton partially free some of the bound actin in the network and hence activate the membrane-bound protein CFTR (Chasan et al., 2002), which can then release ATP (Sprague et al., 1998). It has been demonstrated that low concentrations of actin monomers attach to CFTR and activate it (Chasan et al., 2002). These atomic-force microscopy studies of CFTR show a complex with an average diameter of ∼30 nm and suggest that CFTR becomes activated by interaction with monomers or small segments of actin.

We therefore suggest that the release of ATP from a deformed RBC proceeds as follows. The deformation of the RBC causes the appearance of fold-lines in the membrane, which contain numerous fivefold defects in the spectrin network. The surface of the short actin filament at the node of each fivefold defect is therefore partially exposed, and is free to attach to CFTR molecules, which diffuse freely in the cell membrane. This attachment activates the CFTR (Chasan et al., 2002) and releases ATP (Braunstein et al., 2001) (Fig. 10). An experimental test of our model would be a measurement of the amount of ATP released as a function of the total length of fold-lines in the deformed RBC membrane. The length of fold-lines induced by deformations is proportional to the overall length of the cell in the cylindrical pore. Conservation of the membrane area implies that this length is L′ ∝ 1/R, where R is the radius of the pore. This relation between the released ATP and filter pore radius is indeed found experimentally, as shown in Fig. 10.

FIGURE 10.

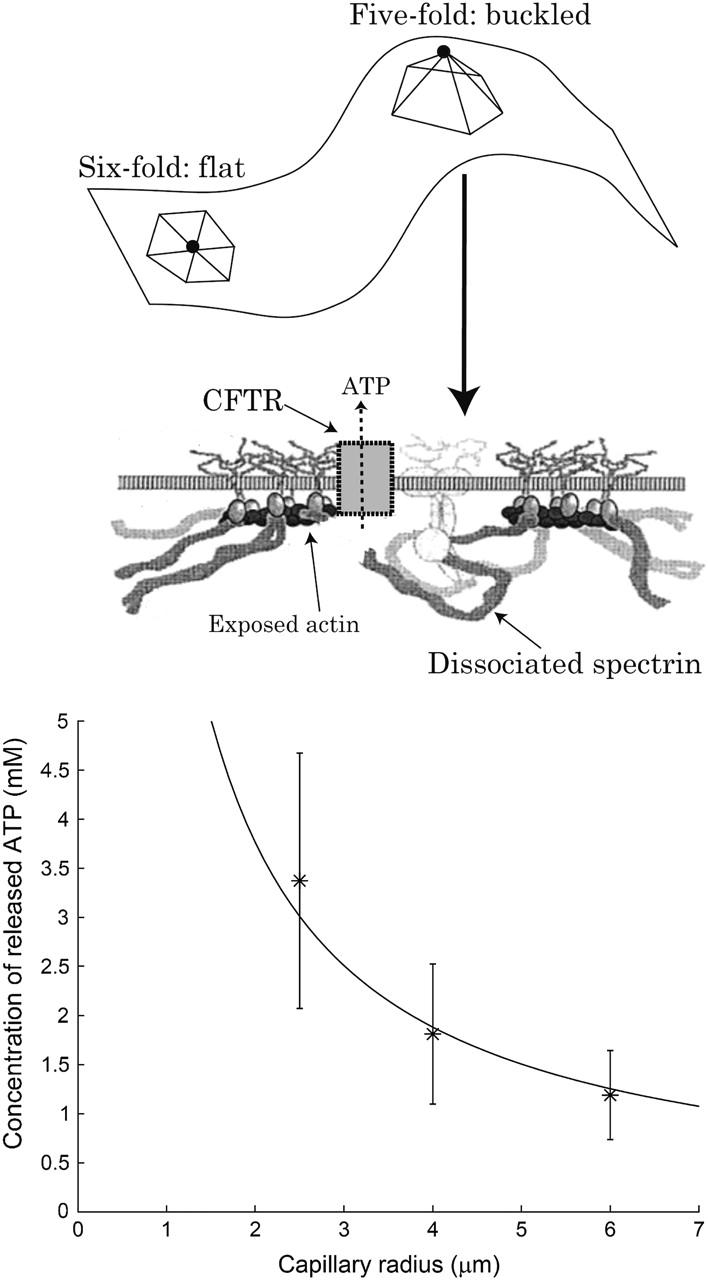
Schematic picture of the relation between cytoskeleton defects and ATP release. In a fivefold defect a single spectrin molecule is detached from the actin node (solid circle). The CFTR molecule can then bind to the freed actin filament, allowing ATP release. Below we plot the measured concentration of ATP released from deformed RBC in capillaries of different radii (asterisks) (Sprague et al., 1998), compared with the predicted 1/R dependence of the length of fold-lines (solid line).

We can compare the deformation-induced ATP current with recent experiments on deformed RBC in polycarbonate filters that have measured the influx of Ca²⁺ ions (Brain et al., 2004). The measured calcium ion flux in this study follows a 1/R² relation, which is different from that of ATP release (Fig. 10). Although both extracellular ATP (Abe et al., 2003) and binding of actin filaments (Furukawa et al., 1997) are known to inhibit calcium ion channels, direct membrane tension is known to increase nonspecific cation permeability. This tension, due to the cylindrical confinement, is indeed proportional to 1/R² (Eq. 17). In this case, therefore, no cytoskeleton defects are directly involved in the stress-induced current.

We predict that ATP is released by the activation of CFTR in deformed RBC, but not by the transient dissociations of spectrin induced by ATP. This is because the reassociation time for the spectrin-actin complex, τ_re ∼ 10⁻⁷ s, is much shorter than the time τ_diff ∼ (30 × 10⁻⁹)²/10⁻¹² ∼ 10⁻³ s for actin and CFTR to diffuse a distance of 30 nm, which is their average separation, with a diffusion constant of ∼10⁻¹² m²/s, typical of membrane proteins in a lipid bilayer (Almeida and Vaz, 1995).

Another possible mechanism for actin-CFTR association, due to membrane deformation, does not rely on network defects. Extreme stretching and unfolding (Law et al., 2003; Discher and Carl, 2001; Lee and Discher, 2001) of spectrin filaments may allow the actin segments to become more accessible to interact with the CFTR molecules. The result would be the activation of CFTR and the release of ATP as proposed above. Stretching of the cytoskeleton is indeed observed (Cho et al., 1999) to reduce the steric interaction of the spectrin filaments and membrane ion channels, increasing their diffusion coefficient in the membrane. Detailed experiments that measure the number of defects and structure of the deformed cytoskeleton may distinguish between this possibility and our model of CFTR activation due to the proliferation of fivefold defects along fold-lines in deformed cells.

Our proposed model can be tested experimentally by various methods, some of which we suggest below (the role of actin association with the activation of an ion exchanger was shown in Kurashima et al., 1999). The role of free actin in the process of ATP release can be probed by strongly attaching the spectrin to the actin, thereby stiffening the cytoskeleton and decreasing the probability of dissociation of the actin-spectrin complexes when the RBC is deformed. We would predict that decreased dissociation would activate fewer CFTR molecules and thus decrease the amount of ATP released. Calmodulin or adducin are substances that may strengthen the actin-spectrin binding (Bennett, 1989). Alternatively, a weakening agent (such as hemin, see Liu et al., 1985) can be added, so that the spectrin becomes more easily dissociated from the actin; we would then predict an increase in the amount of ATP released. Addition of various actin-binding proteins is predicted to inhibit ATP release, since these molecules will bind to the exposed actin and prevent CFTR activation.

A more direct probe of the concentration of exposed actin in deformed RBC can be obtained by adding molecular labels (such as FITC-Phalloidin, TRITC-Phalloidin, etc.) that fluoresce when attached to actin. Another procedure may involve breaking deformed RBCs and exposing them to antibodies that bind to CFTR and actin, to measure whether the two are bound in larger numbers compared with un-deformed RBC.

Recent experiments (Olearczyk et al., 2004) show that spermine NONOate inhibits ATP release from stressed RBCs. This result can be due to the known affinity of spermine to actin, so that it binds to the exposed actin and prevents CFTR activation.

Increased levels of extracellular ATP may be beneficial to Cystic Fibrosis patients (Knowles et al., 1991; Brézillon et al., 1997). It may be worth considering treatment of these patients with a drug that somewhat weakens the RBC cytoskeleton and thereby facilitates spectrin network deformations with the consequent release of actin, activation of CFTR that will lead to more effective regulation of extracellular ATP levels (Abraham et al., 2001). The disadvantage of such an approach may be a resulting anemia, but still prove advantageous overall.

Our proposed mechanism for ATP release in response to mechanical deformations may also explain the observed ATP released from endothelial cells (Bodin and Burnstock, 1998). In these cells ATP is released during the time (∼3–5 min) that their cytoskeleton rearranges in response to variations in the applied shear flow (Bodin and Burnstock, 1998). During the cytoskeletal rearrangement actin is depolymerized and polymerized, so that some of it is freed from the cytoskeleton and can activate CFTR, leading to ATP release. If we model the cells as thin disks of constant thickness and volume, then the applied shear induces a linear elongation, which modifies the surface actin network. The volume of redistributed actin, and ATP released, are therefore predicted to be linear with the shear flow, as is observed (Bodin and Burnstock, 1998). A similar linear relationship was observed under controlled distension (Knight et al., 2002).

CONCLUSION

To conclude, we have put forward a unified model of the effects of ATP on the fluctuations and overall shape of the RBC membrane. Some biological implications of this model are discussed in CFTR Activation and ATP Release, above, and in the Appendix. At this stage, these predictions of the model have to be tested experimentally:

1. Dependence of the effective temperature on the ATP concentration and fluid viscosity.

2. The RBC cytoskeleton is close to the percolation limit.

3. The ATP-dependence of the echinocyte and stomatocyte shape transitions.

4. The age-related changes in the RBC cytoskeleton.

5. Fold-lines in the membrane have a high population of defects.

6. CFTR and exposed actin association are related to the cytoskeleton defects and control the release of ATP.

7. The role of ATP in the invasion of the malaria parasite into the RBC.

Since spectrin-actin based cytoskeletons appear in other cell types, such as nerve and outer-hair cells, our analysis may serve to explain changes in fluctuations over all shape and elastic properties that are driven by ATP.

In light of the above work, it can be asked why does the RBC need to expend energy (in the form of ATP) to soften its cytoskeleton, instead of having an overall softer static spectrin network? We believe that our study also indicates the answer to this question. The RBC uses ATP to increase the amplitude of the membrane fluctuations, since these help the RBC move through narrow capillaries (Tuvia et al., 1998; Levin and Korenstein, 1991). As we showed above, these fluctuations arise from the same process (spectrin dissociations) that causes overall cytoskeleton softening, so that the static (ATP-depleted) cytoskeleton should be stiffer than normal.

This situation highlights the peculiarities of living matter, where the elastic properties are determined by biological energy consumption (usually in the form of ATP). It also shows cellular motion that is ATP-driven but does not involve specific molecular motors.

APPENDIX: MALARIA PARASITE AND RBC

The RBC is the target of the malaria parasite Plasmodium falciparum. A crucial step in the infection is the invasion of the RBC by the parasite, a process which is still poorly understood, and appears to depend strongly on the intracellular ATP concentration (Dluzewski et al., 1992; Gratzer and Dluzewski, 1993). We therefore propose that the ATP-induced dissociations of spectrin-actin filaments may be instrumental in the invasion process of the parasite. Since the dissociations are transient, and the size of the parasite relatively large (diameter of ∼1 μm), it is unlikely that an individual dissociation process allows the parasite to enter the cell. A slower process of membrane transformation occurs at the binding site of the parasite to the outer membrane of the RBC (Gratzer and Dluzewski, 1993), which is facilitated by the intracellular ATP. A region devoid of cytoskeleton forms at the binding site, whereas the removed cytoskeleton proteins form a dense annular ring at the periphery of the cleared patch. The parasite is then able to move into the cell in a process similar to endocytosis. Cytoskeleton-rich knobs form on the surface of the invaded RBC.

We now propose a mechanism whereby the invasion of the RBC is facilitated by our model of ATP-induced spectrin-actin dissociations. At the binding site, the parasite is able to introduce proteins into the RBC membrane, which penetrate the lipid bilayer and interact with the cytoskeleton (Gratzer and Dluzewski, 1993). Among these are various actin-binding proteins (Forero and Wasserman, 2000), such as PfHRP-1 (Gratzer and Dluzewski, 1993), HRPII (Benedetti et al., 2003), and ROPE (Morrissette and Sibley, 2002). When ATP induces spectrin-actin dissociations, these proteins are able to block the reassociation process, by binding to the exposed actin filament (foot-in-the-door mechanism). In particular, the ROPE protein is known to mimic the spectrin protein, and therefore prevent it from reassociation. After some time, the cytoskeleton exposed to these proteins therefore disintegrates, with the dissociated spectrin filaments piling up at the rim, and knobs of actin and bound associated proteins left behind.

After successful invasion the parasite induces a sharp reduction in the intracellular concentration of ATP (Murray and Perkins, 1989). This prevents the cell from invasion by another parasite. Towards the last stage of cell rupture, the parasite induces cation leakage (Ginsburg, 1990), which increases ATP levels (similar to the stomatocyte case discussed at the end of ATP-Driven Steady-State RBC Shape, above), and makes the cytoskeleton softer and susceptible.

If this model is correct, one can then propose the use of various drugs to prevent parasite invasion through blocking the spectrin-actin dissociations. Since this will make all the RBCs in the body stiff and abnormal, it is better to design membrane-bound drugs that prevent spectrin-actin dissociations only when the parasite is attached to the outer membrane.