Probing Electric Fields in Protein Cavities by Using the Vibrational Stark Effect of Carbon Monoxide

Abstract

To determine the magnitude and direction of the internal electric field in the Xe4 cavity of myoglobin mutant L29W-S108L, we have studied the vibrational Stark effect of carbon monoxide (CO) using infrared spectroscopy at cryogenic temperatures. CO was photodissociated from the heme iron and deposited selectively in Xe4. Its infrared spectrum exhibits Stark splitting into two bands associated with CO in opposite orientations. Two different photoproduct states can be distinguished, C′ and C″, with markedly different properties. For C′, characteristic temperature-dependent changes of the area, shift, and width were analyzed, based on a dynamic model in which the CO performs fast librations within a double-well model potential. For the barrier between the wells, a height of ∼1.8 kJ/mol was obtained, in which the CO performs oscillations at an angular frequency of ∼25 cm⁻¹. The magnitude of the electric field in the C′ conformation was determined as 11.1 MV/cm; it is tilted by an angle of 29° to the symmetry axis of the potential. Above 140 K, a protein relaxation leads to a significantly altered photoproduct, C″, with a smaller Stark splitting and a more confining potential (barrier >4 kJ/mol) governing the CO librations.

INTRODUCTION

Electrostatic interactions play an essential role in the overall stabilization of the three-dimensional architecture of individual proteins and multiprotein assemblies. Moreover, specific electric fields at active sites are key determinants of protein reactivity and functional processes. Ligand binding affinities, enzymatic catalysis, ion transport through cell membranes, and protein-protein interactions are all governed to a large extent by electrostatic forces (Honig et al., 1986; Sharp and Honig, 1990; Sitkoff et al., 1994; Nakamura, 1996; de Groot et al., 2003). Calculation of electric fields in the protein interior is nontrivial because of the complicated, heterogeneous environment and the long-range nature of the Coulombic force. Recent years have witnessed enormous activity in the development and application of computational methods to study these interactions (Nakamura, 1996; Norel et al., 2001; Fogolari et al., 2002; Sheinerman and Honig, 2002; Boresch et al., 2003; Fogolari et al., 2003; Werner and Caflisch, 2003; Feig et al., 2004; Nienhaus et al., 2005; Swanson et al., 2004).

Direct measurements of electric fields in proteins are still scarce, however (Varadarajan et al., 1989; Lockhart and Kim, 1992; Antosiewicz et al., 1996; Park et al., 1999; Kriegl et al., 2003). Electrostatic interactions can be determined in various ways, for example, from pK_a shifts of titrating groups (Gilson and Honig, 1987; Yang et al., 1993), chemical shifts in NMR experiments (Park et al., 1991) or shifts in redox potential (Varadarajan et al., 1989). In recent years, spectroscopic approaches have been advanced, especially by Boxer and co-workers, that exploit the sensitivity of a chromophore to an electric field (Stark effect) (Pierce and Boxer, 1995; Bublitz and Boxer, 1997; Andrews and Boxer, 2002; Kriegl et al., 2003; Suydam and Boxer, 2003; Merchant et al., 2003; Nienhaus et al., 2005). For the measurement of local electric fields in proteins, the vibrational Stark effect (VSE) appears particularly attractive (Hush and Reimers, 1995; Reimers et al., 1996). Much work has been carried out using carbon monoxide (CO) as a local field probe, but the method has lately also been extended to nitriles (Andrews and Boxer, 2000, 2002), nitric oxide (NO) (Park et al., 2000; Park and Boxer, 2002) and other bond types such as C–F or C–D (Suydam and Boxer, 2003).

To site-specifically probe electric fields within proteins, one aims to introduce small Stark effect sensors at well-defined positions (Park and Boxer, 2002). For example, CO can be bound to the central iron atom of heme proteins to assess the electric field at the active site (Kushkuley and Stavrov, 1996, 1997). Pronounced shifts in the frequencies of its infrared (IR) stretching bands in a large number of mutant myoglobin (Mb) proteins revealed alterations in the local fields at the heme iron (Franzen, 2002). Free (unbound) CO has recently been employed to measure electric fields in cavities in the protein interior (Kriegl et al., 2003). In Mb, these internal cavities play important roles as transient ligand storage sites in the physiological ligand binding process. At cryogenic temperatures, CO ligands can be trapped selectively in these locations, denoted by B, C, and D in Fig. 1 A. In each location, the CO has a characteristic IR spectrum that reflects the specific interactions of the CO and the local electric field (Nienhaus et al., 2003a,b, 2005).

FIGURE 1.

(A) Essential structural features at the active site of myoglobin mutant L29W. Residues Trp-29 and His-64 of bound-state conformations A_I and A_II are depicted in dark gray and light gray, respectively. Residues lining the Xe4 cavity are shown in dark gray. CO ligands are included in the heme-bound A_I conformation (A), at the primary docking site B and in the Xe4 (C) and Xe1 (D) cavities. (B) Schematic reaction energy surface of mutant L29W-S108L with heme-bound state A and photoproduct states B, C, and D. (C) Orientation of the CO dipole and its confining potential V with respect to the internal electric field E. The Cartesian coordinates {x′, y′, z′} arise from a rotation of the {x, y, z} system by the angle β around the x axis. The E-field and the symmetry axis of the potential V are oriented along the z and z′ axes. The angles θ, ϕ denote the orientation of the CO molecular axis with respect to the potential V, and γ is the angle between the dipole and E. (D) One- and two-dimensional depictions of the potentials used to model the dynamics of the CO molecule in site C′.

Ligands trapped in photoproduct site C, i.e., the Xe4 cavity of Mb mutant L29W-S108L (Fig. 1 A), give rise to a doublet of IR bands, representing opposite orientations of the ligand, with Stark shifts arising from an internal electric field at the docking site (Kriegl et al., 2003). With increasing temperature, pronounced changes of the spectral area and the Stark splitting of the doublet were observed and described quantitatively with a simple dynamic model in a combined classical and quantum-mechanical treatment. The cavity environment was modeled as a static, symmetric, double-humped potential constraining the rotational motion of the CO ligand. Hence, it performs ultrafast, two-dimensional rotational oscillations within each of the two opposite orientations and only rarely performs end-to-end rotations. From the Stark splitting, an electric field component along the symmetry axis of the potential of ∼10 MV/cm was determined. Meanwhile, our dynamic model has been confirmed by femtosecond IR pump-probe measurements of the anisotropy decay (Helbing et al., 2005).

Here we have revisited the analysis of the CO dynamics in the C photoproduct site of Mb mutant L29W-S108L and the determination of the local electric field. Whereas we had previously only considered the band area and Stark splitting as observables, we present here an extended analysis that also includes the widths of the bands. It enables us to determine the absolute magnitude of the electric field and its angle to the symmetry axis of the CO libration, and not only the component along the symmetry axis of CO motion. We have also determined the transition polarizability of the CO molecule by comparing the temperature dependencies of the overall band area and Stark splitting. Moreover, we give evidence that a protein conformational change occurs above 140 K while the CO is in the C photoproduct state. It leads to pronounced changes in the local electric field and the CO dynamics in the cavity.

MATERIAL AND METHODS

Sample preparation

Sperm whale Mb double mutant L29W-S108L was expressed in Escherichia coli, purified as described (Springer and Sligar, 1987), and lyophilized for storage. For the experiments, the protein powder was dissolved at a concentration of ∼15 mM in glycerol/potassium phosphate buffer (pH 8.0) cryosolvent (3:1 by volume), stirred under a ¹³C¹⁸O atmosphere, and reduced with sodium dithionite solution. ¹³C¹⁸O was chosen because the reduced solvent absorption at the lower wavenumber of its stretching vibration, as compared with ¹²C¹⁶O, allowed us to achieve the data quality required for the quantitative analyses presented below. For the experiments, a few microliters of the sample solution were sandwiched between two CaF₂ windows (diameter 25.4 mm) separated by a 75-μm-thick mylar washer.

Fourier transform infrared spectroscopy

The sample was mounted in a copper block on the cold finger of a closed-cycle helium cryostat (SRDK-205AW, Sumitomo, Tokyo, Japan). The sample temperature was adjustable in the range 3–320 K with a digital temperature controller (model 330, Lake Shore Cryotronics, Westerville, OH). Samples were photolyzed with a continuous-wave, frequency-doubled Nd-YAG laser (Forte 530-300, Laser Quantum, Manchester, UK) with ∼300 mW output at 532 nm, yielding a photolysis rate coefficient k_L ≈ 20 s⁻¹. Transmission spectra in the mid-IR (1800–2400 cm⁻¹, 2 cm⁻¹ resolution) were collected with a Fourier transform infrared spectroscopy (FTIR) spectrometer (IFS 66v/S, Bruker, Karlsruhe, Germany). To determine the temperature dependence of the IR bands, spectra were taken continuously, one for every Kelvin, while the sample was heated or cooled at a constant rate of 5 mK/s. Comparison of the results obtained with increasing and decreasing temperature enabled a clear-cut separation between spectral changes from equilibrium processes and those from rebinding.

Data analysis

At each temperature, transmission spectra, I_light(ν) and I_dark(ν), were collected with and without prior illumination. Absorbance spectra were calculated according to A(ν,T) = log[I_dark(ν)/I_light(ν)]; a linear baseline was subtracted. To determine the total band areas (zero^th moments), the absorbance spectra were integrated numerically at each temperature and normalized to the value at the lowest temperature. The IR bands were fitted individually with Gaussians to yield absolute line positions (first moments), ν⁺(T) and ν⁻(T), and variances (second moments), σ², of both bands. We note here that fitting with Gaussians involves an approximation because the line shapes resulting from our theoretical model (vida infra) are asymmetric and thus non-Gaussian. However, fitting with Gaussians is a robust procedure, and we take our ability to closely reproduce the shapes of the spectra as evidence that the errors introduced by this approach are small. Moreover, the theoretical treatment involves a simple model potential that has been introduced heuristically on the basis of the temperature dependence of line positions and widths, as obtained from Gaussian fits. Therefore, an analysis based on the detailed shapes of the bands instead of fitting Gaussian would only be as good as the chosen model potential approximates the real potential.

Obviously, for a doublet of bands that arise from Stark splitting by an internal electric field, the band position at zero electric field cannot be obtained directly from the data. Therefore, the Stark shift was determined from the individual line positions, as described previously (Kriegl et al., 2003),

(1)

This procedure is justified if the two bands of the doublet exhibit equal amounts of shift in opposite directions with temperature.

THEORETICAL BACKGROUND

Vibrational Stark effect

VSE has been studied theoretically for more than three decades (Hush and Williams, 1974); quantitative experimental analyses have become available only in recent years, however (Park et al., 1999; Park and Boxer, 2002). In conventional Stark spectroscopy experiments, samples are exposed to an externally applied electric field, and its effect on the transition is measured (Pierce and Boxer, 1995; Bublitz and Boxer, 1997; Andrews and Boxer, 2002; Suydam and Boxer, 2003). Electric fields already present in the protein interior likewise give rise to a Stark effect. The electric field causes a frequency shift, Δv, and a change in the transition dipole moment, M, of the vibrational absorption transition. Quantitatively, the effect can be described by power expansions in the electric field, E, acting on the vibrational transition,

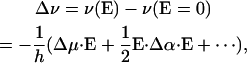(2)

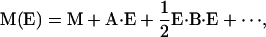(3)

where the Stark parameters appear as coefficients in the expansions. They are denoted Stark tuning rate or difference dipole moment, Δμ, difference polarizability, Δα, and transition polarizibility and hyperpolarizibility tensors, A and B, respectively. Calculations on nitriles and carbonyls (Brewer and Franzen, 2003) and experiments on free CO in frozen 2-methyl tetrahydrofuran (Park and Boxer, 2002) have shown that contributions from the second-order coefficients Δα (Eq. 2) and B (Eq. 3) are negligible for these molecules.

What are the physical origins of the field-dependent changes? For a rigid, harmonic vibrator, an applied electric field cannot cause a dependence of the dipole moment on the vibrational level. Therefore, early theoretical treatments of the effect focused on changes in the molecular geometry (Hush and Williams, 1974). Later on, bond anharmonicity was recognized to give rise to the VSE (Lambert, 1988). Using first-order perturbation theory, contributions from mechanical and electrical anharmonicity can be distinguished (Bishop, 1993). Mechanical anharmonicity derives from changes of the molecular geometry in the different vibrational energy levels due to an anharmonic potential energy surface, whereas changes in the harmonic force constants are responsible for electrical anharmonicity (Park et al., 1999, 2000; Andrews and Boxer, 2000, 2002; Park and Boxer, 2002). Note that the two effects are coupled due to the well-known correlations between bond lengths and force constants (Badger's rule) (Badger, 1934). Recent density functional theory calculations by Brewer and Franzen suggest that, for carbonyls and nitriles, field-induced changes of the molecular geometry are mainly responsible for the VSE (Brewer and Franzen, 2003).

CO dynamics in a protein cavity

By using appropriate illumination procedures, CO can be transferred selectively into the Xe4 cavity, thereby creating photoproduct state C (Fig. 1 A). A schematic of the reaction surface, with bound state A and photoproduct states B, C, and D is depicted in Fig. 1 B. The doublet structure of the CO stretching absorption and the symmetric shifts of both bands with temperature suggest that the two bands result from Stark splitting due to CO residing in this cavity preferentially in two opposite orientations. To describe the CO dynamics, we have introduced a simple, time-independent model potential (Kriegl et al., 2003),

(4)

with two minima at CO orientation angles θ = 0° and 180° (Fig. 1 D, top). The CO performs fast librational dynamics within each minimum, the angle θ increasing with temperature. End-to-end rotations, i.e., transitions between the two minima, occur infrequently by overcoming an energy barrier of height V₀. Motions within a well can be described classically above ∼20 K. Below this temperature, zero-point motions prevent a closer alignment of the CO with the direction of the potential minimum. End-to-end rotations are much slower than CO librations, and we cannot determine the CO flipping rates with our spectroscopic experiments. In Fig. 1 C, the geometric relations are sketched between the electric field E (chosen along the z axis) and the symmetry axis of the potential (chosen along the z′ axis) governing the CO dynamics. The E-field is assumed to maintain an angle β with respect to the direction of the potential minimum (Eq. 4). Consequently, the molecular axis of the CO (which is assumed to coincide with M and Δμ) can be anywhere on a cone at a given angle θ; i.e., at an arbitrary angle ϕ. The angle between the E-field and the CO molecular axis is denoted by γ.

Temperature dependence of CO stretching bands

Band areas

The vibrational absorption spectrum, 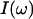, is proportional to the Fourier transform of the time-autocorrelation function of the transition dipole moment, 〈M(0)·M(t)〉 (Gordon, 1965; Lim et al., 1995a),

(5)

The transition dipole vector M(t) of the CO stretching vibration is oriented along the CO axis; its magnitude decays to zero with time due to vibrational dephasing. Orientational motion of the CO will affect the temporal decay of the correlation function and, therefore, the shape of the infrared absorption. The dynamics of the CO transition dipole moment in the potential, Eq. 4, leads to a biphasic decay of 〈M(0)·M(t)〉 (Lim et al., 1995b). An initial, fast decay can be ascribed to essentially ballistic reorientation, which corresponds to a broad component in the spectrum that cannot be resolved from the background. A second, more slowly decaying component of 〈M(0)·M(t)〉 arises from the constraints imposed by the potential; it gives rise to the narrow CO stretching bands observed in the IR spectra.

In previous work (Kriegl et al., 2003), we neglected an electric field effect on the vibrational transition moments, Eq. 3, because similar results from the analyses of the band areas and positions suggested only a small contribution from the transition polarizability to the temperature dependence of the band areas. Still, we noticed that the parameter V₀ from the band area analysis was overall ∼10% smaller than the one from the Stark shifts. On the basis of the precise ¹³C¹⁸O data, we felt encouraged to also examine the small effect by the transition polarizability. Obviously, we can only consider the component A_‖ parallel to the transition dipole axis of the CO molecule and not the entire tensor A, which is exact for a system with rotational symmetry around its transition dipole axis (Andrews and Boxer, 2000).

The area of the narrow, visible component of the spectrum is given by the amplitude of the slowly decaying part of the correlation function,

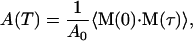(6)

where the time τ is longer than the characteristic time of the fast librations, but shorter than the time for end-to-end rotations of the CO in the cavity. A₀ is an appropriately chosen normalization constant. By plugging the transition moments, Eq. 3, into Eq. 6, and neglecting the term quadratic in E, we obtain

(7)

The angles θ and γ are depicted in Fig. 1 C. The angular brackets in Eq. 7 denote thermal averages; their evaluation is presented in the Appendix) (Eqs. A6, A7, and A12). The band area is finally obtained as

(8)

Here, D(α) denotes Dawson's integral, Eq. A4, and 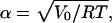with gas constant R and absolute temperature T.

Band shifts

According to Eq. 2, the field-induced frequency shift of the vibrational transition is proportional to the field; its magnitude is given by the Stark tuning rate Δμ, which was earlier shown to be aligned with the transition dipole moment M within the experimental error (Park et al., 1999; Park and Boxer, 2002). Neglecting the term quadratic in E, the frequency shift of the band equals

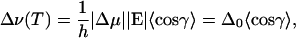(9)

(10)

In Eq. 9, we have introduced Δ₀ = h⁻¹|Δμ||E|, which is the maximum frequency shift that would be obtained from the classical calculation for T → 0 if the transition dipole moment M were oriented perfectly parallel or antiparallel with respect to E. The evaluation of 〈cosγ〉 is shown in Eq. A10 in the Appendix.

The band shifts saturate for T → 0, however, because of quantum-mechanical zero-point vibrations of the CO in the cavity (Kriegl et al., 2003). At very low temperatures, the angle θ is small, so that our potential energy function, Eq. 4, can be replaced by the leading term in its power series expansion,

(11)

corresponding to a two-dimensional harmonic oscillator. Within this approximation, the quantum-mechanical analysis yields the following equation for the limiting average angle due to zero-point vibrations (Kriegl et al., 2003),

(12)

Here, with being Planck's constant divided by 2π, moment of inertia, I, and angular frequency of CO libration, ω. D(b/2) again denotes Dawson's integral, Eq. A4. Equation 12 allows us to determine b and thus the product Iω from comparing the experimentally observed limiting frequency shift with the extrapolation of the classical fit to T = 0. Moreover, V₀ is obtained from the classical fit, and because V₀ = 1/2 I ω² in the limit T → 0, both I and ω can be determined independently, yielding

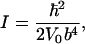(13)

and

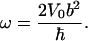(14)

Band widths

Analysis of the Stark splitting reveals only the projection |E| cosβ onto the symmetry axis of the CO dipole. The tilt angle β between the two axes and thus the absolute magnitude of the electric field can be obtained from the temperature dependence of the widths of the IR bands. A number of independent, additive contributions contribute separately to the width: 1), at a nominal resolution of 2 cm⁻¹, our FTIR spectrometer contributes in a substantial, though temperature-independent way; 2), static heterogeneity of CO bands in proteins is a well-studied phenomenon (Hong et al., 1990; Fayer, 2001). Different protein conformations provide environments with differing interactions with the CO. Our line-broadening analysis focuses on the temperature range T < 80 K, where most conformational degrees of freedom are arrested. Therefore, we also take this contribution as temperature independent; 3), vibrational dephasing of the CO stretch is another line-broadening contribution, which is related to both the intrinsic lifetime T₁ of the excited state and the pure dephasing time T₂* describing the adiabatic modulation of the vibrational energy levels by thermal fluctuations of the environment (Tokmakoff and Fayer, 1995). Vibrational echo studies of MbCO have provided the intrinsic lifetime of the stretching vibration of heme-bound CO (Rella et al., 1996a,b; Fayer, 2001). The homogeneous line width due to dephasing was shown to vary only weakly, between 0.3 and 0.4 cm⁻¹ from 5 to 80 K. For photodissociated CO inside a heme protein, dephasing has not yet been measured, but the experiments with heme-bound CO suggest that this contribution is likewise small and only weakly temperature dependent; and 4), CO librations in the cavity cause perpetual changes of the angle between the electric field in the cavity and the CO molecular axis, thus modulating the Stark splitting. This contribution to the heterogeneity of the IR bands is expected to have a pronounced temperature dependence.

We subsume the first three line-broadening mechanisms in a constant term c², so that the overall variance, or second moment, , of the CO stretching band can be written as

(15)

In the framework of our dynamic model, the temperature dependence of 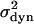is given by

(16)

This expression can be evaluated with Eqs. A6, A7, A13, and A14, yielding

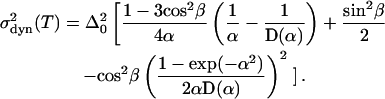(17)

In the classical model, 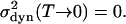Quantum-mechanical zero-point vibrations, however, lead to a finite contribution for T → 0. For a two-dimensional quantum-mechanical harmonic oscillator, the calculation of this component to the line width yields

(18)

with 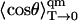given by Eq. 12, and ψ _0,0(θ, ϕ) is the ground-state energy eigenfunction of the two-dimensional harmonic oscillator. Evaluation of Eq. 18 yields

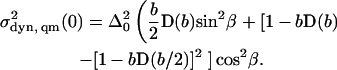(19)

Band shapes

The shapes of the CO stretching bands can be calculated by converting the probability density of finding a CO molecule at an angle γ with respect to the electric field (Fig. 1 C), P(γ), into a probability density in frequency space, P(ν), with P(γ) obtained from Eq. A2 as

(20)

In this expression, the potential V(θ) has been recast into a potential V(γ,ϕ) using the identity cos θ = −sin β sin ϕ sin γ + cos β cos θ; subsequent integration over ϕ yields P(γ). With the parameter Δ₀ as introduced in Eq. 9, the Stark shift, ν, corresponding to a particular angle γ, is given by ν = Δ₀ cos γ, so that

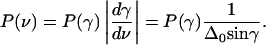(21)

To compare experimental spectra with this expression, we have calculated P(ν) for both infrared bands using the asymmetric potential in Fig. 1 D (bottom). Moreover, P(ν) was convoluted with a Gaussian to account for additional line broadening effects as described in the previous subsection, so that the shape of the spectra is finally given by

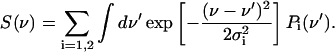(22)

RESULTS AND DISCUSSION

FTIR-TDS spectroscopy

Similar to mutant L29W, the photolysis difference spectrum of the double mutant L29W-S108L shows two bands of heme-bound CO at 3 K, a predominant A_I at ∼1857 (1946) cm⁻¹ and a minority species A_II at ∼1868 (1974) cm⁻¹. The numbers in parentheses refer to the standard ¹²C¹⁶O isotope. These bands have been associated with two discrete active-site conformations (Ostermann et al., 2000; Nienhaus et al., 2003a) (Fig. 1 A). After brief illumination at ∼10 K, CO ligands settle into the primary docking site B. With prolonged illumination at specific temperatures, ligands can be selectively trapped in secondary docking sites, C and D, which correspond to the xenon-binding cavities Xe4 and Xe1 (Nienhaus et al., 2003a,b). Depending on the temperature at which the sample was illuminated, CO ligands in photoproduct site C have two distinctly different stretching spectra. These two photoproduct states have been named C′ and C″, with stretching bands at 2026 and 2038 cm⁻¹ and 2031 and 2036 cm⁻¹ at 3 K, respectively. The appearance of state C″ has been attributed to a partial relaxation of distal residues His-64 and Trp-29 toward the A_II conformation, which occurs above ∼140 K while the CO ligand is still trapped at site C (Nienhaus et al., 2003a).

In Fig. 2, we present data from temperature derivative spectroscopy (TDS) experiments on the C′ and C″ photoproduct states. The sample was illuminated during cooling from 160 to 3 K at 5 mK/s. Subsequently, the laser was switched off, and the temperature was ramped to 180 K at the same rate, while FTIR spectra were collected continuously, one spectrum per Kelvin. FTIR absorbance difference spectra, ΔA(ν, T), were calculated from the transmittance spectra, I(ν, T), at successive temperatures, yielding the spectral changes occurring within 200 s (and 1 K). In Fig. 2, absorbance changes in the bands of heme-bound and photolyzed CO are presented as logarithmically spaced contour plots, with solid/dotted contours marking an absorbance increase/decrease, respectively. The presence of only a small rebinding feature below 40 K in Fig. 2 A indicates that essentially all CO ligands in proteins in the A_I conformation have been transferred to photoproduct states C′ and C″. The observed feature is mainly due to recombination from intermediate state B in the minority conformation A_II. Rebinding from intermediate states C′ and C″ in A_I is seen as two peaks at ∼120 and ∼160 K in Fig. 2 A. The corresponding photoproduct map (Fig. 2 B) shows absorbance changes in the photoproduct bands of A_I and A_II. From comparing panels A and B, it is obvious that there are pronounced spectral changes in the photoproduct bands that do not originate from ligand rebinding.

FIGURE 2.

TDS contour maps of myoglobin mutant L29W-S108L after different illumination protocols. (A, B) Slow cooling under illumination from 160 to 3 K traps ligands in C′ and C″, from where they recombine at 120 and 160 K. (C, D) After slow cooling under illumination from 100 to 80 K and further on to 3 K in the dark, rebinding occurs exclusively from C′. (E, F). After extended illumination (15,000 s) at 160 K and subsequent cooling to 3 K in the dark, ligands rebind exclusively from C″. (Left column) Absorbance changes in the IR bands of heme-bound CO indicate recombination. (Right column) Absorbance changes in the photoproduct bands originate from both CO dynamics and recombination. Contours are spaced logarithmically. Solid/dotted lines represent an absorbance increase/decrease, respectively.

To selectively populate the C′ photoproduct state, the sample was cooled from 100 to 80 K under illumination and further to 3 K in the dark. In the TDS experiment, rebinding occurs in the temperature interval 80–140 K, as can be inferred from the absorbance changes in the bands of heme-bound CO (Fig. 2 C). By contrast, the photoproduct bands change their intensities already from the lowest temperatures on (Fig. 2 D). Illumination for 15,000 s at 160 K and subsequent cooling in the dark traps photodissociated ligands preferentially in photoproduct C″ (Fig. 2, E and F). A small fraction of CO that escapes to the Xe1 cavity (D) does not show up in Fig. 2 F at the chosen contour levels (see below). Again, the bound-state bands show rebinding exclusively at high temperatures (∼170 K), whereas the photoproduct spectra change continuously with temperature.

Intermediate state C′

Electric field determination

Previously, we had restricted ourselves to the analysis of the peak positions of the stretching bands (Kriegl et al., 2003), which yields only the projection of the electric field onto the symmetry axis of the CO potential. Here we determine both the absolute magnitude of E and its tilt angle β to the symmetry axis of the cavity potential by analyzing both band shifts and widths.

In Fig. 3 A, pronounced temperature-dependent changes in area, position, and width are observed for the stretching bands of the CO in the C′ photoproduct site between 10 and 80 K. Fig. 4 B shows the temperature dependence of the band shifts. The plateau from zero-point motions below 20 K is followed by a continuous decrease toward higher temperature. This dependence was fitted with the classical model, Eqs. 9 and 10, between 20 and 75 K, yielding the barrier height V₀ = 1.81 ± 0.06 kJ/mol and Δv(0) = 6.20 ± 0.04 cm⁻¹ (Table 1). With Eq. 23, we compute the magnitude of the field component along the symmetry axis of CO libration,

(23)

yielding |E| cos β = 9.7 MV/cm. Here, we have introduced |Δμ| = 0.038 D for ¹³C¹⁸O, which corresponds to the value |Δμ| = 0.04 D that Boxer and co-workers (Park et al., 1999) reported for the Stark tuning rate of free ¹²C¹⁶O, rescaled by the inverse ratio of the square roots of the reduced masses. From the analysis of the ratio between the experimentally observed Δv(T → 0) and the classical approximation, the parameter b was determined as 0.30 ± 0.02. With V₀ = 1/2 I ω² = 1.81 kJ/mol, we obtain the moment of inertia, I = 2.4 ± 0.5 × 10⁻⁴⁶ kg m², and the angular frequency of the CO oscillations in the potential, ω = 26.6 ± 1.0 cm⁻¹. From rotational spectra in the gas phase, the moment of inertia of ¹³C¹⁸O has been determined as 1.596 × 10⁻⁴⁶ kg m² (Puzzarini et al., 2003). For a two-dimensional rotational oscillator, we would expect twice this value. Our value for I is somewhat smaller, but still in good agreement, considering that it depends on the inverse forth power of b (Eq. 13). With I = 3.192 × 10⁻⁴⁶ kg m², ω = 23.0 ± 0.4 cm⁻¹ (Eq. 14).

FIGURE 3.

FTIR photoproduct spectra of ¹³C¹⁸O in the Xe4 cavity of Mb mutant L29W-S108L. (A) Spectra of intermediate C′ from 10 to 80 K in steps of 10 K. (B) Spectra of intermediate C″ from 10 to 100 K in steps of 15 K. The small band at ∼2023 cm⁻¹ represents photoproduct D, with CO ligands trapped in the Xe1 cavity.

FIGURE 4.

Temperature dependence of the ¹³C¹⁸O stretching bands of intermediate C′. (A) Overall band area A(T), (B) the relative peak shift, Δν(T), and (C) width parameters σ. The width parameters σ are plotted individually for both bands of the C′ doublet (squares, peak at 2038 cm⁻¹; diamonds, peak at 2026 cm⁻¹). Solid lines in panels A–C represent fits according to the model presented in the text. In panel A, the dashed-dotted line is a fit considering only the first term of Eq. 8 giving V₀ = 1.64 kJ/mol, the dotted line is a model calculation with V₀ = 1.81 kJ/mol obtained from the first moment fit. The dashed lines in panels B and C represent model calculations with two local minima in one potential well (see Fig. 1 D, bottom) to model the broadening of the peak at 2026 cm⁻¹. Dotted lines in panel C are model calculations with β = 20, 25, 35, and 40°.

TABLE 1.

Temperature dependence of the stretching bands of ¹³C¹⁸O in photoproduct states C′ and C″: fit parameters of dynamic model

Photoproduct state	C′*	C″
ν(3 K) (cm−1)	2032.10 ± 0.02	2033.6 ± 0.1
Δv(0) (cm−1)	6.20 ± 0.04†	2.79 ± 0.02
V0 (kJ/mol)	1.81 ± 0.06	4.1 ± 0.2 / 8.0 ± 0.4‡
ω (cm−1) (exp.)	26.6 ± 1.0	ND§
ω (cm−1)¶	23.0 ± 0.4	34.6 ± 0.9
I × 1046 (kg·m2)	2.4 ± 0.5	ND
β (°)	29 ± 1	ND
|E| (MV/cm)	11.1	4.4‖
A‖ (cm−1/(MV/cm)−1)	0.038 ± 0.005	ND

^*Data for different CO isotopes have been presented in Kriegl et al. (2003).

^†The errors reflect a 50% increase of χ² upon variation of the parameter, keeping all other parameters fixed.

^‡Analysis of band areas/peak shifts, respectively.

^§ND, not determined.

^¶Calculated with V₀ = 1/2 I ω² and I = 2 × 1.596 × 10⁻⁴⁶ kg m² (Puzzarini et al., 2003).

^‖Field component in the direction of the minimum of the cavity potential.

The CO stretching band at 2038 cm⁻¹ is remarkably narrow at 3 K, but its width increases substantially with temperature (Fig. 4 C, open squares). We performed an analysis of the temperature dependence of the band width on this band. The classical and quantum-mechanical expressions, Eqs. 17 and 19, give only the dynamic broadening. However, the offset c² in Eq. 15 can be determined by simultaneously fitting with both expressions. In the limit T → 0, the line width is determined by Stark effect contributions from zero-point motions plus additional broadening mechanisms subsumed in c²,

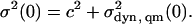(24)

By using b = 0.30 and Δ₀ = Δv(0)/cos β from the classical analysis of the band shifts, the second term in Eq. 24 depends solely on the tilt angle β. Moreover, by using V₀ = 1.81 kJ/mol from the band shift, the classical expression, Eq. 17, also depends only on β. A simultaneous fit of the quantum-mechanical and classical expressions to the experimental data, shown as solid line in Fig. 4 C, yields the tilt angle β = 29 ± 1°. The additional dotted lines, simulated with tilt angles of 20, 25, 35, and 40°, provide clear evidence of the sensitivity of the curves to tilt angle variation. With this result, the absolute magnitude of the electric field inside the Xe4 cavity can be calculated as |E| = 9.7 MV/cm / cos 29° = 11.1 MV/cm.

The peak at 2026 cm⁻¹, representing the opposite orientation of the CO dipole in the Xe4 cavity, is significantly broader. It shows a weaker broadening with temperature, though qualitatively similar to the behavior of the 2038-cm⁻¹ band (Fig. 4 C, open diamonds). Moreover, the widths of the two bands merge at higher temperatures. A larger width suggests increased heterogeneity. Simple static disorder can be excluded as an explanation because this will merely give an additive contribution to the width over the entire temperature range. The observed broadening suggests a more complicated potential in one of the two orientations, which could arise from different interactions of the C and the O atoms with the atoms lining the cavity. We have studied such a scenario by a model potential that has two local minima within one of the two wells, separated by a small barrier (Fig. 1 D, bottom). Two small, two-dimensional subwells of Gaussian shape were introduced in the left potential well at θ = 30°; ϕ = 90 and 270°, respectively. An additional, two-dimensional Gaussian was introduced between the two subwells, creating a barrier of ∼0.3 kJ/mol.

Using V₀ = 1.81 kJ/mol, a classical simulation was performed with this model, in which the averages were calculated by numerical integration. The dashed lines in Fig. 4, B and C, indicate that this simplified model describes the experimental data reasonably well. At lower temperatures, the CO molecules become trapped in either one of the two subminima, which leads to the observed broadening of the band at 2026 cm⁻¹. At higher temperatures, however, the 0.3-kJ/mol barrier between the wells can easily be surmounted, and the line width of the broader line approaches the one of the 2038-cm⁻¹ band.

Temperature dependence of the spectral area

With increasing temperature, the two stretching bands of CO in state C′ markedly lose intensity (Fig. 3 A). Previously, we did not take Stark effects on the transition moments into account (Kriegl et al., 2003). Then, only the first term in Eq. 7 contributes to the spectral area, and the temperature dependence of the area is entirely governed by the square of 〈cosθ〉, whereas the Stark shift depends linearly on 〈cosθ〉. Similar results for the potential parameter V₀ from areas and shifts strongly supported our dynamic model, considering that the two observables are entirely unrelated in the experiment. The 10% smaller V₀ from the areas may result from a small transition polarizability contribution (Eq. 7). Fig. 4 A shows the total band area as a function of temperature; the dashed-dotted line is the best fit with A_‖ = 0, yielding V₀ = 1.64 ± 0.1 kJ/mol. The temperature dependence of the area is extremely sensitive to V₀. A simulation using V₀ = 1.81 kJ/mol, the best-fit value obtained from the Stark shifts (Fig. 4 A, dotted line), deviates markedly from the data. However, by including the transition polarizability term (Eq. 7), the agreement with the data can be significantly improved (Fig. 4 A, solid line). Using the angle β = 29° and E = 11.1 MV/cm from the fit of the band widths, we obtain A_‖/|M| = 0.028 ± 0.004 (MV/cm)⁻¹. This value is similar to the value of A_‖/|M| = 0.03 (MV/cm)⁻¹ reported for HCN by Andrews and Boxer (2000). With the transition dipole moment for free CO in frozen 2-methyl-tetrahydrofuran (Park and Boxer, 2002), |M| ≈ 0.077 D = 1.32 cm⁻¹/(MV/cm)⁻¹, the component of the polarizability tensor parallel to the CO molecular axis is then determined as A_‖ = 0.038 cm⁻¹/(MV/cm)⁻¹. Although the resulting parameters appear realistic, we emphasize that this analysis rests on a small correction, and thus, the systematic error may be significantly larger than the statistical one given above.

Whereas fast librations give rise to a measurable spectral shift and broadening of the stretching bands, end-to-end rotations are not apparent in the C′ spectra because of their much larger characteristic times. Their presence could, in principle, be inferred from the change of the population ratios of the two orientations, N₂₀₂₆/N₂₀₃₈, with temperature, which are usually calculated from band areas. However, slight asymmetries in the potential also lead to somewhat different temperature-dependent changes in the band areas, and thus, the two effects cannot be disentangled cleanly from the data. Therefore, we have refrained from such an analysis here.

Temperature dependence of band shapes

Our dynamic model predicts asymmetric line shapes arising from the Stark shifts of an ensemble of CO molecules with different angles γ with respect to the electric field E, characterized by an orientational distribution P(γ), as given in Eq. 20. Consequently, the analysis of the experimental data with fits of symmetric, Gaussian bands introduces systematic errors, which will only be negligible if the total asymmetry is small. To verify that these approximations do not change our results markedly, we have compared the experimental spectra with spectra simulated according to our dynamic model, using the parameters in Table 1.

In Fig. 5, we have plotted the experimental spectra at 40, 50, 60, and 70 K together with spectra simulated according to Eq. 22. Additional line-broadening mechanisms, taken to be temperature independent, were accounted for by convoluting the bands at 2026 and 2038 cm⁻¹ with Gaussians having width parameters σ = 0.96 and 1.4 cm⁻¹, respectively. For the solid lines, the amplitudes of the bands were scaled individually to match the experimental data. For the open circles, the bands were aligned at 40 K and then scaled for the higher temperatures according to the loss of area as expected from the autocorrelation expression, Eq. 6. The good agreement between the measured spectral shapes and those predicted from our model provides confidence that the approximations inherent in the Gaussian analysis do not introduce significant errors. The deviations between calculated and measured spectra between the two bands may reflect deviations of the potential from the simple model function employed here.

FIGURE 5.

Comparison of measured ¹³C¹⁸O stretch spectra of intermediate C′ at 40, 50, 60, and 70 K with simulations based on Eqs. 21 and 22. Experimental data are shown as squares; the simulations of the band shapes are given as solid lines (individual bands shown as dotted lines). Amplitudes were fitted individually at each temperature. Spheres show simulated bands, with band amplitudes fitted at 40 K and scaled according to the autocorrelation analysis for the higher temperatures.

Intermediate state C″

The TDS contour plots (Fig. 2, E and F) and absorbance spectra (Fig. 3 B) of intermediate C″ reveal temperature-dependent spectral changes of the CO stretching bands that are qualitatively similar to those of the C′ bands (Figs. 2, C and D, and 3 A). The C″ photoproduct bands are located at 2031 and 2036 cm⁻¹ at 3 K, and therefore, the Stark splitting is less than half that of C′. Moreover, as is evident from the spectra in Fig. 3, the overall loss in spectral area is much smaller than the one for C′, and the temperature-dependent frequency shifts are significantly reduced. Within our dynamic model, both observations imply that librational motions of the CO are much more constrained by the potential in the C″ state. This observation is thus in line with our interpretation that the C′ → C″ transition corresponds to a relaxation, in which the protein structure evolves toward the A_II conformation (Nienhaus et al., 2003a). In this process, the indole side chain of Trp-29 shifts and rotates, thus causing a partial collapse of the Xe4 cavity.

Fig. 6 A shows the temperature dependence of the total band area and the individual bands of the C″ doublet. In contrast to the C′ doublet, the two C″ bands behave clearly differently (Fig. 3 B). There is a weak gain in the area of the 2036-cm⁻¹ band between 10 and 60 K, followed by a loss toward higher temperatures. By contrast, the 2031-cm⁻¹ band experiences a gradual loss of area with temperature, and close inspection of the increased slope below ∼60 K suggests that there is a net transfer of population from the low- to the high-frequency band, which overcompensates for the loss due to the enhanced librational motions in the 2036-cm⁻¹ band. The overall area should, however, not be affected by this process. The temperature dependence of the total band area is well described with the classical expression (Eq. 8), neglecting the transition polarizability, A_‖. From a fit of the overall area with Eq. 8 in the temperature range 20 K < T < 120 K, a potential parameter V₀ = 4.1 ± 0.2 kJ/mol is obtained, significantly larger than the one for the C′ state.

FIGURE 6.

Temperature dependence of the ¹³C¹⁸O stretch bands of intermediates C″ and D. Solid lines are simulated curves from fits as explained in the text. (A) Overall and individual band areas, A(T), and (B) the average peak shift, Δν (T), of C″. Also shown are the individual shifts with respect to 2033.63 cm⁻¹, shifted down by 0.2 cm⁻¹ for clarity. (C) Overall band area, A(T), of D.

The smaller overall splitting, together with the much more constraining C″ cavity, as indicated by the large V₀, results in only minute changes in the band positions. Fig. 6 B shows the band shifts with respect to the position at zero field, ν(0), as determined assuming symmetric shifts (Eq. 1). The total shift is only ∼0.1 cm⁻¹, and thus a mere 7% of the change observed for C′. The fit with Eq. 10 in the temperature range 20 K < T < 80 K (Fig. 6 B, solid line) yields V₀ = 8.0 ± 0.4 kJ/mol, which is about twice the value obtained from the overall area. With Δv(0) = 2.79 ± 0.04 cm⁻¹ and Eq. 23, the field component in the direction of the potential minimum, |E| cos β = 4.4 MV/cm.

The pronounced deviations between the V₀ values obtained from the areas and the Stark shifts raises questions about the origin of these discrepancies. The analysis of the individual bands reveals a rather complex behavior of the band shifts with temperature (Fig. 6 B). The individual shifts are calculated with respect to ν(3 K) = 2033.63 cm⁻¹; they were shifted down by 0.2 cm⁻¹ in the figure to not overlap with the averaged data. These data clearly point to additional effects that become apparent at the smaller level of CO librational amplitudes. The 2036-cm⁻¹ band shift even increases with temperature in the lower temperature region. This effect may be connected to the end-to-end rotations observed from the areas in the same temperature range. These transitions may involve spectrally distinct subpopulations of the heterogeneously broadened line and so give rise to an additional shift of the band. This effect is known as kinetic hole burning (Steinbach et al., 1991; Huang et al., 1997; Ormos et al., 1998). Furthermore, in addition to librations, the CO may also perform translational motions, which would modify the electrostatic interactions with neighboring groups and thus cause additional shifts of the CO frequency (Phillips et al., 1999; Franzen, 2002). This could explain the peculiar behavior of the 2031-cm⁻¹ band above ∼70 K. In conclusion, in a strongly confining cavity such as C″, the small librational amplitudes of the CO produce only a weak temperature dependence of the Stark shifts, and therefore, additional, temperature-dependent effects become significant.

The small additional band at ∼2023 cm⁻¹ in Fig. 3 B is associated with CO in photoproduct state D, as implicated by experiments with the additional L104W mutation, in which site D is blocked (data not shown), and consequently, this band is absent. Illumination at higher temperatures leads to substantial enhancement of this band without changing the C″ doublet. Previous studies with other mutants and the ¹²C¹⁶O isotope gave evidence of a rather broad band with unresolved substructure (Nienhaus et al., 2003a), suggesting only small Stark splitting due to a comparatively weak electric field in the Xe1 cavity. Although the band is rather weak, we can still analyze the temperature dependence of the area in a reasonable way, as shown in Fig. 6 C. A fit in the temperature range 20 K < T < 80 K (Fig. 6 C, solid line) yields V₀ = 1.8 ± 0.2 kJ/mol, which is similar to the potential parameter of the C′ state.

CONCLUSION

The CO molecule has been employed as a probe to sense electric fields in the interior of Mb. Within a protein cavity, the CO performs ultrafast librational motions that produce a characteristic temperature dependence of the CO stretching bands (Helbing et al., 2005). By using a combined classical and quantum-mechanical description, we have presented a detailed analysis of the temperature dependence of the infrared spectra of CO in the C′ photoproduct state of Mb mutant L29W-S108L. From the band areas, positions, and widths, the librational amplitudes of CO, the electric field in the cavity, the tilt angle β of the electric field with respect to the symmetry axis of the cavity potential, and the transition polarizability of the CO were determined. The weak confinement of CO in the C′ photoproduct state ensures that the librational dynamics dominates the temperature dependence of the CO stretching bands, enabling a precise evaluation of the parameters. With CO residing in the Xe4 cavity, a second conformation, C″ was observed, which differs from C′ by the size of the Stark splitting and a markedly stronger confinement of the ligand. In C″, the dynamics is severely constrained, as shown by the qualitative analysis, and additional effects produce band shifts that are beyond the framework of our model. The approach presented here, employing CO or possibly other small molecules as subnanoscopic voltage sensors in proteins with internal hydrophobic cavities, may find application in a variety of heme proteins and probably also nonheme proteins in the future.

APPENDIX

Calculation of band areas, Stark splittings, and band widths (Eqs. 8, 9, and 16) require evaluation of and other thermal averages. The former is given by

(A1)

Assuming a Boltzmann distribution for the energies, the angular probability density, P(θ,ϕ), of finding a CO molecule in a particular orientation (Fig. 1 C), is given by

(A2)

with universal gas constant, R, and absolute temperature T. The normalization constant, N(T), can be expressed as

(A3)

with 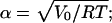D(x) denotes Dawson's integral,

(A4)

In the numerical computation, we use Rybicki's approximation of D(x) (Rybicki, 1989),

(A5)

Using Eqs. A2–A4, evaluation of the integral in Eq. A1 finally yields

(A6)

Analogously, one obtains for the thermal average of the square of cos θ,

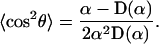(A7)

Thermal averages containing the angle γ between the molecular axis and E can be recast into equations containing the averages A6, A7, and the angle β between the electric field and the cavity potential. The relations between the electric field, E, the transition dipole moment, M, and the orientation of the cavity potential, V(θ), which governs the CO dynamics, are depicted in Fig. 1 C for an arbitrary direction of E with respect to the cavity potential. We have chosen E along the z-direction of our primary coordinate system {x, y, z}. The CO orientation is described by polar angles θ, φ, in the coordinate system {x′, y′, z′}. To introduce a tilt between the two coordinate systems, we chose a rotation around the x-coordinate. The angle γ (Fig. 1 C) can thus be determined by a transformation into the {x′, y′, z′} system according to

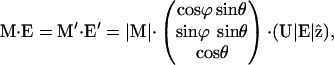(A8)

with the rotation matrix

(A9)

By introducing the angle β between E and the z′ axis, i.e., the direction of the potential energy minimum (Fig. 1 C), this transformation allows us to eliminate the angle γ. Thus, we obtain:

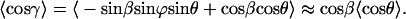(A10)

(A11)

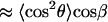(A12)

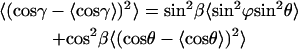(A13)

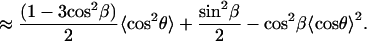(A14)

We note that the approximations introduced here hold only for small angles β. These expressions are further evaluated by substituting for and using Eqs. A6 and A7.