Dual-Color Photon-Counting Histogram

Abstract

We report on the development of dual-color photon-counting histogram (PCH) analysis. Dual-color PCH is an extension of regular PCH and considers the photon counts received in two detection channels instead of one. Because each detection channel records a different color, dual-color PCH distinguishes fluorescent species not only by differences in their brightness, but also according to their color. The additional discrimination by color increases the sensitivity of PCH in resolving a mixture of species considerably. Most dual-color fluorescence fluctuation experiments are performed on fluorophores with overlapping emission spectra. This overlap results in spectral cross talk between the detector channels, which reduces resolvability. Here, we demonstrate that dual-color PCH is able to resolve binary dye mixtures in the presence of cross talk from a single measurement without any additional information about the sample. We discuss the effect of sampling time on the fit parameters of dual-color PCH. Differences between dual-color fluorescence correlation spectroscopy and dual-color PCH will also be addressed. We quantitatively resolve a mixture of the two fluorescent proteins CFP and YFP, which is challenging because of the strong spectral overlap of their emission spectra. Dichroic mirrors are needed to direct the light into the two detection channels. We quantify the influence of these filters on dual-color PCH analysis and determine the optimal transition wavelength of the dichroic mirror for the CFP-YFP pair.

INTRODUCTION

Fluorescence fluctuation spectroscopy (FFS) derives information about physical processes by observing the spontaneous variations of the fluorescence signal within a small observation volume (Magde et al., 1972; Weissman, 1981). Number fluctuations of fluorescent particles within the observation volume are a main source for the fluctuations in the fluorescence signal. Other processes, such as chemical reactions that occur in the observation volume and change the fluorescence of the reacting molecules also contribute to signal fluctuations. Observation volumes of <1 fl are conveniently created by modern techniques, such as confocal and two-photon microscopy (Berland et al., 1995; Denk et al., 1990; Rigler et al., 1993). These small observation volumes allow the routine measurement of samples at the single-molecule level. The high temporal resolution and excellent detection sensitivity make FFS an attractive technique for studying the behavior of biomolecules at physiologically relevant concentrations (Thompson, 1991).

Statistical analysis of the fluorescence fluctuations unlocks information hidden in the stochastic signal. Autocorrelation analysis of the data is used by fluorescence correlation spectroscopy (FCS), which is the most widely used fluorescence fluctuation technique. FCS characterizes transport processes, such as diffusion and flow, determines chemical reaction rates, and monitors the particle concentration in the observation volume (Hess et al., 2002; Schwille, 2001; Thompson et al., 2002).

We originally developed the photon-counting histogram (PCH) technique as an alternative method for analyzing fluctuation experiments (Chen et al., 1999). A similar technique, fluorescence intensity distribution analysis (FIDA), has been introduced as well (Kask et al., 1999). We developed PCH to gain access to information embedded in the amplitude statistics of the detected photon counts, which is largely ignored by FCS. The amplitude statistics preserves information about the molecular brightness of fluorescent particles. Molecular brightness is the average photon count rate of a fluorophore in the observation volume. A bright fluorophore will produce, on average, a more intense burst of photons as it travels through the observation volume than a dim molecule. PCH analyzes the histogram of the received photon counts and resolves mixtures of fluorophores from the characteristic shape of the histogram function. Thus, PCH differentiates species according to their brightness, whereas the autocorrelation function separates species by differences in diffusion time.

A hallmark of biological systems is the assembly of biomolecules to perform complex functions. Resolving a mixture of biological species and characterizing their interactions is important for understanding how biological processes work. FCS resolves multiple species from differences in their molecular weights, which translate into differences in their diffusion coefficients. Unfortunately, FCS lacks sensitivity in separating species with similar molecular weights, such as a monomer-dimer protein mixture (Meseth et al., 1999). PCH overcomes this shortcoming of the autocorrelation approach because it separates species according to their molecular brightness instead of their molecular weight. We previously demonstrated that PCH is capable of resolving mixtures of proteins that carry either one or two fluorescent dyes without any prior knowledge about the system (Müller et al., 2000). In addition, we demonstrated that molecular brightness is a robust parameter for measurements in living cells (Chen et al., 2002). We modified PCH theory to include nonideal detector effects (Hillesheim and Müller, 2003). We used our new theory to measure EGFP and fusion proteins over a wide concentration range and succeeded in observing the oligomerization of nuclear receptors in living cells (Chen et al., 2003).

The lack of sensitivity of conventional FCS in detecting association between biomolecules prompted the development of dual-color FCS (Schwille et al., 1997). Dual-color FCS utilizes two separate detection channels, with each channel recording its own color of light. Suppose you label protein A with a red dye and protein B with a blue dye. Monomeric proteins only generate a burst of photons of a single color, which produces a signal in one of the two channels. The dimeric complex of proteins A and B carries both a red and a blue fluorophore. Whenever the dimeric complex passes through the observation volume, the red and the blue dye generate a burst of light that is recorded simultaneously in both detection channels. Dual-color FCS uses cross-correlation analysis to pick out the simultaneous fluctuations in both detection channels and thereby substantially increases the sensitivity of detecting protein-protein interactions as compared to traditional FCS. The increase of sensitivity and robustness of the cross-correlation approach has been discussed in the literature (Bacia and Schwille, 2003; Medina and Schwille, 2002).

Just as in the case of FCS, adding a second detector channel allows PCH to separate species not only by their brightness, but also according to their color, which should increase the sensitivity of separating mixtures significantly. In fact, two-channel FIDA has been introduced previously and was shown to be significantly more sensitive in separating species than regular FIDA (Kask et al., 2000). Here, we report on the development of dual-color PCH. We describe the theory and test the performance of dual-color PCH experimentally. Spectral cross talk between the detector channels caused by overlapping fluorescence emission spectra presents a challenge for dual-color FCS. In contrast to FCS, dual-color PCH directly resolves binary mixtures in the presence of spectral cross talk by a single measurement. Thus, dual-color PCH provides information not readily accessible by dual-color FCS. We are interested in probing protein interaction in living cells by dual-color PCH. One commonly used pair of fluorescent proteins in dual-color studies is cyan fluorescent protein (CFP) and yellow fluorescent protein (YFP). We will not resolve a tertiary mixture of a heterodimer (AB) and its monomers (A and B) in this article. The presence of energy transfer in the heterodimer and nonideal detector effects, such as afterpulsing, need to be considered for such a study and are currently not included into our theory of dual-color PCH. We will instead demonstrate the resolution of a binary mixture of CFP and YFP in vitro from a single measurement, despite the considerable spectral overlap between these proteins. The choice of optical filters influences the degree of cross talk between the detection channels and therefore the resolvability of the binary mixture. We explicitly discuss the influence of optical filters on the resolvability of the CFP/YFP mixture by dual-color PCH. In addition, we discuss the influence of sampling time on the brightness and number of molecules recovered from dual-color PCH analysis and present a model that approximately describes the effects of sampling time on the fit parameters.

THEORY

Theory of dual-color PCH

The derivation of dual-color PCH theory closely follows the argumentation used in the publication where we first introduced PCH (Chen et al., 1999). We will use the term single-color or single-channel PCH to refer to our original PCH formulation. In addition, we use the terms dual-color and dual-channel PCH interchangeably. Single-color PCH is based on the fact that the histogram of the photon counts is an experimental measure of the probability distribution function (pdf) of the photon counts. In dual-color PCH the fluorescent light is split into two detector channels by a dichroic mirror and a theory that describes the combined photon count statistics of both photon detectors is needed. In other words, we need to construct a bivariate pdf of the detected photon counts.

We start by considering a single particle in a closed volume. Assume that the particle is fixed at position 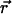within the optical observation volume. The fluorescence intensity detected depends on the spatial location because the light intensity of the excitation varies across the sample volume and the optical collection efficiency depends on apertures such as pinholes. It is useful to define a function that characterizes the spatial dependence of the collected fluorescence intensity. We use the normalized point spread function (psf) to characterize this spatial dependence,

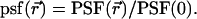(1)

The actual point spread function (PSF) of an instrument will be approximated by model functions. In particular, we use a three-dimensional Gaussian and the squared Gaussian-Lorentzian to approximate the PSF. From now on, we will use the labels A and B to distinguish between the two detection channels. We use the same PSF for both detection channels, because two-photon excitation allows us to coexcite fluorescent dyes with the same laser beam. Let us for the moment consider only channel A. In this case, the theory of single-channel PCH applies. 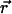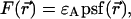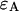The fluorescence intensity of the single fluorophore at position is given by where is the brightness of the fluorophore in channel A. Detectors count photons instead of measuring intensities, and we are interested in the probability of detecting k_A photons in channel A during a sampling time T for a molecule fixed at position 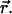This probability is given by a Poisson distribution,

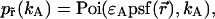(2)

where 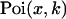is the Poisson function with average x. The Poisson function arises because of the shot noise contribution inherent in photon detection. The molecular brightness ɛ describes the average number of detected photons from a single molecule during the sampling time T, which is a dimensionless number. In the limit of short sampling times, where the diffusion time is much less than the sampling time, we directly calculate the photon count rate by 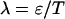. The units of the photon count rate are in photon counts per second and molecule (cpsm). The probability of detecting 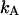photons in detection channel A and 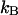photons in detection channel B is given by the joint probability,

(3)

where 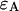and are the brightness values measured in channel A and B, respectively. It is convenient to define 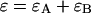and 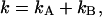which allows us to rewrite the expression of the joint probability using only a single Poisson function together with a prefactor,

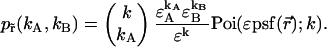(4)

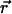In the next step, we let the particle diffuse freely throughout the closed volume. Because the particle can be found with equal probability at any position within the closed volume, we need to average over all space. The probability of finding the particle at position is 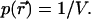The corresponding bivariate pdf of a single diffusing particle is given by

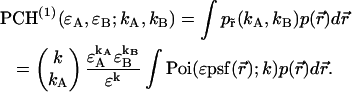(5)

Because the single-channel pdf for a single particle is given by (Chen et al., 1999)

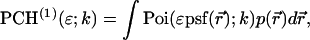(6)

Eq. 5 can be rewritten as

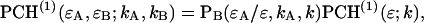(7)

where P_B is the Binomial distribution function,

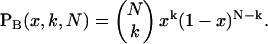(8)

We just demonstrated that the bivariate pdf can be expressed as a univariate pdf times a prefactor.

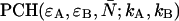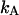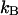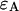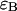As is shown in Appendix A, Eq. 7 can be generalized to the experimentally relevant situation of an open volume. The corresponding dual-channel PCH function describes the probability of detecting and photons in the two detection channels for a single fluorescent species, which depends on three parameters, the molecular brightnesses ( and ) and the average number of particles 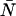in the optical observation volume,

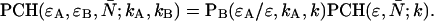(9)

This result is useful, because it allows the computation of dual-channel PCH using the existing algorithms for single-channel PCH. A direct calculation of dual-color PCH requires repeated convolution of single-particle PCH functions, just as is the case for single-channel PCH. Convolution over two dimensions is a time-consuming operation that scales with N⁴, where N represents the linear dimension of the array of photon counts. Equation 9 provides a more efficient algorithm that scales with N², because direct calculation of single-channel PCH functions requires convolutions over one dimension only. To improve the algorithm further we use the fast Fourier transform to calculate single-channel PCH functions as shown in Appendix B.

As is the case with regular PCH, the presence of more than one species is given by successive convolutions of the dual-color PCH function of each species, provided the species are independent from one another. Each species is characterized by three parameters, the brightness values 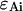and 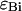in each detection channel and the number of molecules 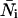of species i. For example, for two independent species the photon count distribution 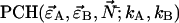is given by

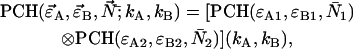(10)

where we use vector notation to organize the parameters of all species ().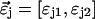

Dual-color PCH and two-dimensional FIDA are very similar, because both methods describe the same mathematical object, the joint probability distribution function of the photon counts in two detection channels. However, the mathematical description used is quite different. FIDA is based on a generating function, which is numerically integrated and Fourier transformed (Kask et al., 2000). PCH, on the other hand, is based on the probability distribution function of a single molecule enclosed in a volume V. We demonstrated that dual-color PCH reduces mathematically to a one-dimensional PCH times a prefactor. This together with the Fourier transformation described in Appendix B provides a very efficient algorithm for calculating the joint probability distribution function of the photon counts in two detection channels.

Resolving binary mixtures with dual-color PCH: basic concept

Dual-color PCH analysis distinguishes between dependent and independent events. To illustrate the concept let us consider the independent molecules A and B. Let's assume for simplicity that molecule A is solely detected by channel A, and molecule B is solely detected by channel B. Both detector channels will register photons simultaneously only when by coincidence both molecules A and B are present in the observation volume of the microscope. On the other hand, if the molecules form a dimer AB, then both channels will simultaneously detect a signal whenever the dimer AB crosses the laser beam. The photon-counting histogram of the dimer reflects a higher probability for observing photons simultaneously in both channels than is the case for independent molecules. This interdependency between the photon counts of each channel is illustrated in Fig. 1, which displays the modeled photon count distributions for two independent particles, A and B, (Fig. 1 A) and for purely dimeric particles, AB, (Fig. 1 B). The two-dimensional PCH surface for the dimer reflects an increased probability to observe high photon counts in both channels and a reduced probability to observe high counts in only one channel. On the other hand, the two-dimensional PCH surface for independent monomers exhibits a lower probability to observe high photon counts in both channels and a higher probability to observe high photon counts in only one of the channels.

FIGURE 1.

Modeled PCH functions for two species, A and B. For simplicity, we assume that particle A is only detected in channel A, and particle B is exclusively detected in channel B. Their brightness values are 14 counts per molecule per sampling time. (A) Photon count distribution for an independent mixture of A and B molecules with particle numbers of 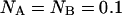each. (B) Photon count distribution for the dimer AB with a particle numbers of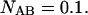

The influence of sampling time T on the photon count rate λ

PCH and FIDA theory assumes that the sampling time T is much less than the diffusion time 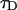of the molecules. In other words, the particle position is well defined during each sampling period T. In this limit, the molecular brightness ɛ(T) is proportional to the sampling time,

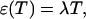(11)

where λ is the photon count rate of a single molecule. Longer sampling times are advantageous, because the signal/noise ratio improves. For sampling times that are on the order of the diffusion time or larger the experimental histograms are still fit within experimental error by conventional PCH theory, but in this regime the theory is not modeling the physical system accurately anymore, and Eq. 11 is no longer valid. The particle diffuses to a different position during the sampling time, and the particle position is not well defined anymore. We refer to this effect as undersampling, because the intensity variations due to the moving particle are obscured by their integration over the sampling time.

An algorithm, called FIMDA (Palo et al., 2000), was introduced to take the influence of sampling time on the brightness into account. FIMDA fits multiple experimental histograms, which differ in their sampling time T, using FIDA to determine ɛ(T). The photon count rate λ and the diffusion time 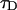are determined by fitting ɛ(T) as a function of the sampling time to a model based on the first two fluorescence intensity moments.

Here we describe a slightly different approach that takes undersampling into account. Instead of fitting multiple histograms with different sampling times, a single experimental histogram with sampling time T is fit to regular PCH. The fit returns the brightness ɛ(T) and the average number of molecules in the optical volume N(T). In addition, we calculate the experimental autocorrelation function from the raw data and get the diffusion time τ_D of the sample from a fit to a simple diffusion model. The molecular brightness ɛ(T) is related to the photon count rate λ by (Müller, 2004),

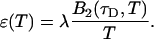(12)

The binning function 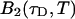describes the influence of the sampling time on the second fluorescence intensity cumulant, and its functional form depends on the shape of the point spread function. For a three-dimensional Gaussian PSF is given by (Müller, 2004),

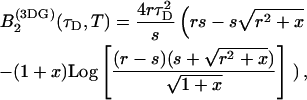(13)

where we introduced the dimensionless sample time, 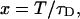and the parameter 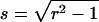. The ratio between the axial and radial beam waste is given by r.

Knowledge of the diffusion time τ_D allows us to calculate the photon count rate λ from the experimentally determined brightness ɛ(T) using Eqs. 12 and 13. The corrected average number of molecules in the observation volume 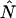is determined from the first moment of the photon counts (Müller, 2004),

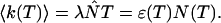(14)

The corrected number of molecules is given by

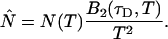(15)

We will refer to 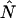as the instantaneous number of molecules in the observation volume.

Equations 12 and 15 allow us to correctly determine the photon count rate per molecule λ and the average number of molecules in the optical volume for arbitrary sampling times. The qualitative influence of sampling time T on the molecular brightness ɛ(T) and the number of molecules N(T) is easy to understand. The molecular brightness ɛ(T) increases less than linear with sampling time T, because sometimes a particle is leaving the observation volume during the sampling time T. The number of molecules N(T) increases with sampling time, because sometimes a particle that was outside of the observation volume at the start of the sampling period diffuses into the volume during the time period T, thus effectively increasing the number of molecules.

Both methods, FIMDA and the one presented here, treat undersampling of the photon count distribution by considering its first two moments. This approach relies on the fact that mathematically the distribution function and all its moments contain equivalent information. We demonstrated experimentally that PCH and cumulant analysis that is based on moments provide the same information. The first two moments uniquely determine the brightness and the number of molecules of a single fluorescent species. Treating undersampling effects of the photon count distribution based on the first two moments is strictly speaking only correct for the case of a single species. For more than one species higher order moments are important to uniquely determine the brightness and number of molecules of each species (Müller, 2004). In other words, FIMDA and the approach presented here are approximations that ignore moments beyond the second order. Theories that take the effect of sampling on higher order moments into account have not been described yet. Thus, the approach we will take is to determine the brightness values 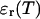of each species from PCH analysis of a histogram sampled with time T. The photon count rate 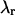of each species is subsequently determined from the recovered brightness value and the diffusion time with Eq. 12. The diffusion time of each species is determined from a fit of the correlation function. This approach relies on the fact that the first two moments are the most important for determining the brightness dependence on sampling time.

The influence of sampling time on two-dimensional photon count distributions has not been investigated yet. We show in Appendix C using bivariate cumulants that the photon count rates, 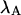and 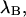in the two detection channels are related to brightness by the same expression valid in the one-dimensional case,

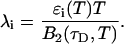(16)

The instantaneous number of molecules 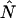for dual-color PCH is also given by the same expression as in the single-channel case,

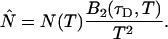(17)

Equations 16 and 17 are exact for a single species and represent an approximation if more than one species is present, just as in the case of single-channel PCH. We analyze a two-dimensional histogram using our dual-color PCH theory, which yields the brightness values 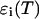and the number of molecules N(T) for each species. The diffusion time 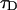of each species is determined from fits of the auto- or cross-correlation function. The photon count rates the corrected number of molecules are subsequently determined from Eqs. 16 and 17.

MATERIAL AND METHODS

Instrumentation

All measurements were performed on a homebuilt two-photon microscope. A mode-locked Ti:sapphire laser (Tsunami, Spectra-Physics, Mountain View, CA) pumped by an intracavity doubled Nd:YVO4 laser (Millennia V, Spectra-Physics) serves as source for two-photon excitation. The laser light passes through a beam expander, enters the modified fluorescence turret of an Axiovert 200 microscope (Zeiss, Thornwood, NY) and is reflected by a dichroic mirror into the microscope objective. A 63× C-Apochromat water immersion objective (N.A. = 1.2) is used to focus the light and to collect the fluorescence (Fig. 2). An excitation wavelength of 780 nm with an average power of 4 mW after the objective was used for the binary dye mixture experiments. Fluorescein was measured with a power of 2 mW after the objective and an excitation wavelength of 902 nm. The CFP-YFP experiments were performed with a 63× Apochromat oil-immersion objective (N.A. = 1.4) at an excitation wavelength of 902 nm and a power of 1.35 mW after the objective. We measured the power of the light passing through the objective in the absence of any immersion liquid. The fluorescence emission was split into two different channels by a second dichroic mirror; a 545-nm dichroic (545DCLP) for the rhodamine 6G and Alexa 488 pair and a 525-nm dichroic (525DCXRU) for the CFP and YFP protein pair (Chroma Technology, Brattleboro, VT). The fluorescence of each channel was detected by an avalanche photodiode (APD) (SPCM-AQ-14, Perkin-Elmer, Dumberry, Québec). The outputs of both APD units are directly connected to a dual-channel data acquisition card (ISS, Champaign, IL), which records the complete sequence of photon counts to computer memory. The data were typically sampled at 20 kHz. Analysis of the data was performed with programs written for IDL (Research Systems, Boulder, CO).

FIGURE 2.

Experimental setup for dual-color PCH experiments. The beam of the Ti:Sapphire laser is reflected by the excitation dichroic mirror, passes through the objective, and excites fluorescence in the focal spot by two-photon absorption. The fluorescence with the emission spectrum 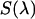is collected by the same objective, passes through the dichroic and another barrier filter. The transmission of these optical elements is characterized by 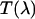. A removable mirror passes the light to a spectrograph that records the fluorescence spectrum, 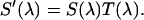Dual-color PCH experiments are performed with the mirror removed. The fluorescence is split by another dichroic mirror into two channels and recorded by APD detectors with detection efficiency

Sample preparation

Alexa 488 (Molecular Probes, Eugene, OR) and rhodamine 6G (Acros Organics Morris Plains, NJ) were dissolved in water with 0.02% (by volume) of NP-40 (Sigma, St. Louis, MO). The small amount of detergent was added to prevent rhodamine 6G from adsorbing to the surface of our sample holder. Dye concentrations were determined by absorption measurements using a molar extinction coefficient of 116,000 M⁻¹cm⁻¹ at 529 nm for rhodamine 6G (in ethanol) and 73,000 M⁻¹cm⁻¹ at 494 nm for Alexa 488 (in water). Fluorescein (Molecular Probes) was dissolved in 50 mM Tris[hydroxymethy]amino-methane (TRIS) (Sigma) at a pH of 8.5, and diluted to a concentration of ∼20 nM.

Plasmids, pRSET A ECFP, and EYFP were a kind gift from Dr. G. Patterson (Cell Biology and Metabolism Branch, National Institutes of Health). His-tagged CFP and YFP were prepared according to Patterson et al. (1997). The stock protein solutions were diluted and measured in phosphate buffered saline (Sigma).

Data analysis

PCH functions are calculated for a Gaussian-Lorentzian PSF. The observation volume is referenced to a three-dimensional Gaussian function with a shape factor of 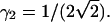A nonlinear least-squares optimization program is used for fitting the experimentally determined dual-color PCH function 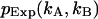to the theoretical function 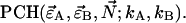The reduced 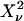of the fit is given by,

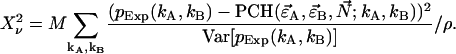(18)

The sum is taken over all elements k_A and k_B with 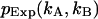greater than zero. The degrees of freedom ρ is determined by r₀−p, where r₀ equals the number of terms in the sum and p is the number of free-fit parameters. M is the number of data points taken and is proportional to the data-acquisition time. The variance of 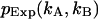is given by 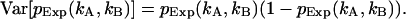The confidence interval of fit parameters was determined either from the covariance matrix or from F-test analysis (Bevington and Robinson, 1992).

Brightness spectra

The fluorescence emission spectrum S(λ) of a fluorophore is modified by the microscope optics. T(λ) characterizes the transmission function of our microscope and includes the optical properties of the objective, two-photon dichroic and other optical filters (Fig. 2). We directly measure the modified emission spectrum, 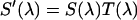, with a spectrograph (USB2000 miniature fiber optic spectrometer, Ocean Optics, Dunedin, FL) mounted on the side port of the microscope. All recorded spectra have been corrected for the instrumental response of the spectrograph. Single-color PCH experiments are performed by replacing the spectrograph with an APD detector. It will be useful for the later discussion to define the term brightness spectrum B(λ),

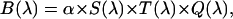(19)

where Q(λ) is the detection efficiency of the detector. The efficiency Q(λ) of the APD was obtained from data provided by the manufacturer. The brightness ɛ, which can be experimentally determined from PCH measurements, specifies the factor α,

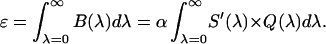(20)

Equations 19 and 20 allow us to construct brightness spectra for fluorophores. The total brightness ɛ measured in a single-color experiment is simply the integral over the complete brightness spectrum.

In a dual-color experiment the fluorescence signal is divided into two detection channels. The optics that splits the signal is characterized by a transmission function for each channel, 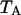and 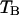. The brightness of each channel is given by,

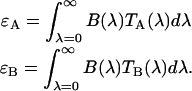(21)

In our case, a dichroic filter is used to separate light into the two detection channels. Because the absorption of the filter is negligible, the combined transmission of both channels is one, 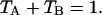In other words, the combined brightness of both detection channels equals the single-color brightness,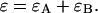

RESULTS

Experimental dual-color PCH: single-species measurements

We performed experiments with a fluorescent dye solution to test our PCH theory on a simple system. Fig. 3 shows the dual-color PCH of an aqueous Alexa 488 solution sampled at 20 μs with a total measurement time of 60 s. A 50/50 beam splitter was used to distribute the fluorescence with approximately equal intensity into each detection channel. A fit of the experimental histogram to a single-species model yields a reduced 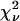of 1.5 and describes the data within experimental uncertainty (Fig. 3). The fit returned brightness parameters of 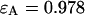and 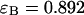for each channel and an average particle number of N = 2.51. The brightness ratio 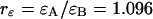is close to one as expected for a 50/50 beam splitter. The intensity ratio 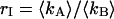of both detector channels provides an independent check of our PCH analysis. The intensity ratio (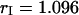) is identical to the brightness ratio 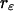, as expected, because the intensity and brightness of each channel are related by 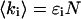(Chen et al., 1999).

FIGURE 3.

Dual-color PCH of Alexa 488. The dye solution was excited at 780 nm. A 50/50 beam splitter was used to direct the fluorescence into the two detection channels. The graph shows the total number of events with 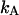photons detected in channel A and 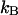photons detected in channel B (solid line). The dashed gray lines represent the best fit of the experimental histogram to a single-species model. The fit resulted in a reduced χ-square of 1.5 and fit parameters of 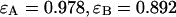, and an average particle number of .

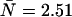Experimental dual-color PCH: dependence of brightness on sampling time T

The purpose of the following experiment is to experimentally verify our theoretical model (Eqs. 16 and 17) that connects the sampling time dependent brightness and number of molecules of dual-color PCH analysis to the photon count rate λ and the instantaneous number of molecules 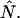Dual-color PCH data were taken with a 50/50 beam splitter on an aqueous fluorescein solution. Photon counts were sampled at 5 μs with a total measurement time of 60 s. The sequence of photon counts for each detection channel was rebinned by software to sampling times of 10 μs, 20 μs, 50 μs, 100 μs, and 200 μs by combining adjacent photon counts before calculating the histogram. Each histogram was fit by dual-color PCH. The recovered brightness and the number of molecules are shown in Fig. 4 as a function of the sampling time T. The autocorrelation function of each channel and the cross-correlation function were calculated from the stored sequence of photon counts in software. A fit of the correlation functions returned a diffusion time of τ_D = 26 μs (data not shown). We calculate the binning function 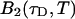and use Eq. 16 to connect the brightness with the photon count rate. The dashed line in Fig. 4 A describes the theoretical brightness 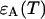in channel A as a function of sampling time T for a photon count rate of 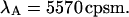The solid line describes the corresponding brightness in channel B based on a photon count rate of Note that the theoretical model matches the experimental brightness values. We also calculated the sampling time dependent number of molecules N(T) with the help of Eq. 17 for an instantaneous number of molecules of . The solid line in Fig. 4 B represents the theoretical model and fits the experimental data.

FIGURE 4.

Sampling time dependence of dual-color PCH parameters. A solution of fluorescein was measured with a 50/50 beam splitter in a two-channel setup. The original data sampled at 5 μs were rebinned in software to sampling times of 10, 20, 50, 100, and 200. The histogram for each sampling time was fit independently by dual-color PCH to a single species. (A) The brightness 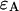in channel A (+) and the brightness 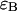in channel B (⋄) are shown as a function of sampling time T. The theoretical model calculated for a diffusion time of 26.3 μm²/s, a beam waist ratio of 6, and a photon count rate of 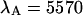cpsm is shown as a dashed line. The same model is calculated using a photon count rate of 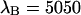cpsm for channel B (solid line). (B) The number of molecules N (□) determined from PCH analysis is graphed as a function of sampling time T. The dashed line represents the theoretical model calculated for a diffusion time of 26.3 μm²/s and an instantaneous number of molecules of .

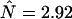Experimental dual-color PCH: binary dye mixture

Dual-color experiments require fluorescent dyes with differences in their emission spectrum. Ideally, the fluorescence emission spectra of both dyes do not overlap. This allows perfect separation of the fluorescent light coming from each fluorophore into different detection channels by optical filters. Unfortunately, the ideal case is rarely achievable in actual experiments. The emission spectrum of organic fluorophores is very broad with a long tail at red wavelengths. Thus, the emission spectra of most fluorescent dye pairs overlap significantly and a clean separation of the optical signal from a mixture of both fluorophores is impossible. This spectral overlap introduces cross talk between the different detection channels, as some light bleeds into one channel, while most of it is detected by the other channel. Spectral cross talk is illustrated in Fig. 5 A, where the emission spectra of the fluorescent dyes Alexa 488 and rhodamine 6G are shown together with the transmission curve of the dichroic mirror used for separating the fluorescence into the two detection channels.

FIGURE 5.

Study of a 55:45% mixture of Alexa 488 and rhodamine 6G with dual-color PCH. (A) Fluorescence emission spectra of Alexa 488 (solid line) and rhodamine 6G (dashed line) are graphed together with the transmission curve (dotted line) of the dichroic filter used to separate both dyes into the two detection channels. The y axis on the right represents transmission. The spectra are normalized to a peak amplitude of one. (B) The reduced χ-square (⋄) of experimental dual-color histograms fit to a single-species model is plotted as a function of the total photon count rate of both detection channels, 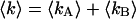. The dashed line represents the expected reduced χ-square based on modeling as explained in the text and represents the degree of misfit of the data by a single-species model. The x axis on the top of the graph shows the number of molecules of Alexa 488 in the observation volume as determined from fits of the data to a two-species model. (C) The brightness parameters of Alexa 488 (⋄) and rhodamine 6G (▵) recovered by individual fits of the dual-color histogram to a two-species model are plotted together with their error bars (±σ) as a function of the total photon count rate 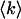. The dashed lines indicate the brightness values recovered by a simultaneous analysis of all experimental data sets to a global two-species model, where the brightness values are the same for each data set. The brightness values of a pure solution of Alexa 488 (×) and of rhodamine 6G (+) were measured independently as a control and are shown for comparison. (D) The number of molecules of Alexa 488 (⋄) and rhodamine 6G (▵) in the observation volume and their error bars (±σ) were determined from fits of the dual-color histogram to a two-species model. The solid lines are fits of the data to a linear function, 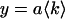. The ratio of their slopes characterizes a 57:43% mixture.

We use dual-color PCH to resolve binary dye mixtures of rhodamine 6G and Alexa 488. We prepared a series of 55:45% mixtures of Alexa 488 and rhodamine 6G from stock solutions and then diluted each to a different absolute concentration. The samples were measured using a dichroic filter centered at 545 nm. For each sample, data were collected for 160 s with a sampling time of 50 μs. Fitting the histogram of each sample to a single-species model produced reduced χ-squares of 20 or higher (Fig. 5 B), clearly indicating that a single species is not sufficient to describe the data. A fit of each data set to a two-species model returned reduced χ-squares between 0.9 and 1.7. The brightness values of species 1 (diamonds) and species 2 (triangles) recovered from the fits are shown in Fig. 5 C for all samples. We choose the total photon count rate of both channels, 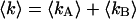, as the x axis of the plot. The brightness values of channels A and B are shown in black and gray, respectively. Note, that the individual brightness values are almost identical for all samples. This is expected because molecular brightness is a molecular property and, therefore, independent of the dye concentration.

We also performed a global analysis of the data, where the brightness values of the two species are linked across all data sets. The brightness values of the global fit 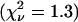are shown as dashed lines. We also measured each of the two dyes separately as a control experiment and determined their brightness values. The values recovered for Alexa 488 (×) match the brightness of the first species (diamonds), and the values recovered for rhodamine 6G (+) match the brightness of the second species (triangles) as shown in Fig. 5 C.

The average number of molecules of each species determined from dual-color PCH analysis is shown in Fig. 5 D in a double-logarithmic plot as a function of the total photon count rate . The solid lines are fits of the data to a linear function of the form, 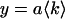, and illustrate that the number of molecules increases linearly with the photon count rate, as expected. We used the slope a of each fit to determine the composition of the sample and arrived at a 57:43% mixture, which is in excellent agreement with the expected value of 55:45%.

The diffusion times of the two dyes as determined from FCS analysis of the correlation function are within experimental error identical. We recovered a diffusion time of τ_D = 30 μs and a beam waste ratio r = 6. This diffusion time results in a value of the binning function B₂ of 1.47. The binning function allows us to calculate the photon count rate from Eq. 16 for data taken with a sampling time of 50 μs. The molecular brightness values determined from global analysis of the binary dye mixture translate into photon count rates of 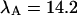kcpsm and 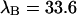kcpsm for Alexa 488 and 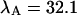kcpsm and 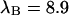kcpsm for rhodamine 6G. The number of molecules N(T) is similarly corrected with the help of Eq. 17. The concentration ratio based on the instantaneous number of molecules is identical to the concentration ratio 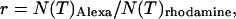because the binning factor 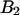of both dyes is identical.

CFP-YFP mixture

One potential application of dual-color PCH is the study of protein interactions in living cells using proteins labeled with fluorescent proteins. The pair of fluorescent proteins most commonly used in such studies is CFP and YFP. They currently present the best compromise in terms of spectral distinction and photostability. Fig. 6 A shows the brightness spectra of CFP and YFP. A dichroic filter centered at 525 nm is used to direct the light into the two detection channels. The spectral overlap of both fluorophores is significant, and resolution of CFP and YFP by color is challenging. Here, we will use dual-color PCH to resolve such a mixture in vitro.

FIGURE 6.

Study of binary mixture of CFP and YFP by dual-color PCH. (A) Brightness spectra of CFP (solid line) and YFP (dashed line) are shown together with the transmission curve (dotted line) of the dichroic filter used to separate both dyes into the two detection channels. The y axis on the right represents transmission. The light and dark shaded gray areas represent the spectral cross-talk components of CFP and YFP, respectively. (B) The molecular brightness values of a solution of CFP (□) alone and of YFP (⋄) alone were determined by PCH analysis and serve as a control. The solid lines mark the molecular brightness values and their standard deviation (±σ) as determined by dual-color PCH analysis of a binary mixture of equal concentrations of CFP and YFP. The sample was remeasured after a dilution by a factor of two and analyzed using a two-species model. The dashed lines show the corresponding molecular brightness values and their standard deviation.

We first measured solutions of CFP and YFP individually as a control experiment. The dual-color histograms of both samples are described within experimental error by a single species (Table 1). The measured brightness values of CFP and YFP are also plotted in Fig. 6 B. Next, we mixed equal concentrations of CFP and YFP to create a binary mixture. We acquired data for 300 s with a sampling time of 50 μs and analyzed the histogram with dual-color PCH. A fit to a single species failed to describe the data 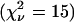. A two-species fit describes the histogram within error . We subsequently diluted the sample by a factor of two and remeasured the sample. Again, a single-species model failed to describe the data 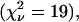whereas a two-species fit returned a reduced χ-square of 0.7. The fit parameters and their uncertainties are compiled in Table 1 and the brightness values are shown in Fig. 6 B. The brightness values recovered for the protein mixture match within experimental error the brightness values obtained for CFP and YFP in the control experiments. Thus, dual-color PCH quantitatively resolved a solution of YFP and CFP. Note that the mixture was resolved without any prior information about the sample by a single measurement. This illustrates the strength of dual-color PCH.

TABLE 1.

Analysis of binary mixtures of CFP and YFP by dual-color PCH

	CFP			YFP
	ɛA	ɛB	N	ɛA	ɛB	N
A	0.0487 ± 0.0027	0.0962 ± 0.0054	3.58 ± 0.23
B				0.110 ± 0.0073	0.0351 ± 0.0024	3.16 ± 0.23
C	0.047 ± 0.018	0.107 ± 0.020	3.3 ± 1.5	0.125 ± 0.017	0.023 ± 0.019	3.4 ± 1.5
D	0.041 ± 0.021	0.100 ± 0.022	1.5 ± 0.8	0.116 ± 0.021	0.024 ± 0.020	1.6 ± 0.8

The table lists the fit parameters and their standard deviation based on dual-color PCH analysis of samples containing CFP and YFP. The number of molecules N and the brightness in each detection channels, ɛ_A and ɛ_B, of each species are shown together with the experimental uncertainty (±σ) as determined from error analysis. Measurements on a CFP (sample A) and YFP (sample B) solution serve as controls. Sample C is a solution of CFP and YFP with equal concentrations. Sample D was prepared by diluting sample C by a factor of two.

Analysis of the autocorrelation function yields a diffusion time of 220 μs for both CFP and YFP. The corresponding binning factor 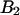of 1.07 results in corrections due to sampling time of <10%. We can safely ignore this correction given the experimental uncertainty of the fit parameters. The photon count rates of CFP and YFP are directly calculated from the brightness in Table 1 using Eq. 11. 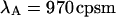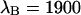We arrive at photon count rates of and cpsm for CFP and 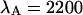cpsm and 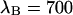cpsm for YFP.

Optimal filters for dual-color PCH

As we have shown, dual-color PCH is capable of resolving CFP and YFP mixtures. But the lower brightness of fluorescent proteins as compared to organic dyes, such as rhodamine, and the large spectral cross talk decreases the sensitivity of resolving species. As a consequence, longer data sampling times are required to achieve a sufficient signal/noise ratio for resolving the mixture. Identifying the best optical filter combination that maximizes the sensitivity of resolving species is of practical importance. To determine the best experimental setup we will consider ideal dichroic filters. The transmission spectrum of our ideal filter is a step function. The filter reflects 100% of the light into channel B below the transition wavelength and transmits 100% of the light into channel A above the transition wavelength.

To identify the best transition wavelength for the optical filter we use the following procedure. The brightness values of CFP and YFP 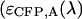, , 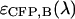, 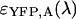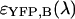) are computed as a function of transition wavelength λ from the corresponding brightness spectra according to Eq. 21. These brightness values of CFP and YFP are used to compute dual-color PCH function p(λ) with an average number of molecules of one for CFP and YFP. These theoretically determined PCH functions p(λ) were fit to a single-species model and the reduced χ-square 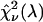of the fit was recorded. A fit of a two-species PCH to a single-species model results in a misfit. The reduced χ-square of the fit 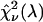characterizes the misfit between the data and a single-species model and provides a measure of our ability to distinguish between single- and two-species system. In other words, the maximum of the χ-square function 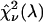shown in Fig. 7 characterizes the optimal transition wavelength of the dichroic filter.

FIGURE 7.

Normalized 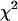as a function of transition wavelength of an ideal dichroic filter. The ideal dichroic has 100% transmission below its transition wavelength and 100% reflection above this wavelength. The brightness values of a CFP and YFP mixture of equal concentrations are calculated from the corresponding brightness spectrum as a function of the transition wavelength of the dichroic filter. Dual-color PCH functions are calculated for each set of parameters and are fit to a single-species model. The χ-square function is used as a merit function to describe the misfit between the data and a single-species model. The optimal transition wavelength corresponds to the maximum of the merit function and occurs at 514 nm. The inset shows the brightness spectra of CFP (gray line) and YFP (black line) together with the transmission curve of the best ideal dichroic filter (dashed line).

We arrive at an optimal transition wavelength of 514 nm (Fig. 7). The dichroic filter used in our experiments has a transition wavelength of ∼525 nm. A look at Fig. 7 shows that we could improve our sensitivity of resolving CFP-YFP mixtures by a factor of two by choosing a transition wavelength centered at 514 nm. Real dichroic filters neither have 100% transmission nor perfectly sharp edges. Does the result change if we consider real instead of ideal dichroic filters? We performed modeling using the measured transmission curve of our filter. The new χ-square curve is virtually identical to the one for the ideal filter and the optimal transition wavelength remains unchanged (data not shown).

The use of a dichroic centered around 514 nm leads to a small brightness value of YFP in the cross-talk channel. Afterpulsing of the photo detector contributes to the photon-counting histogram when the brightness is low (Hillesheim and Müller, 2003). We currently cannot describe these experimental dual-color data, because our theory does not include afterpulsing. We chose a dichroic filter centered at 525 nm as a compromise. The signal statistics are not optimal, but the effect of afterpulsing is negligible under these conditions, which allows us to fit the data using our ideal theoretical model.

We could not directly verify our procedure for optimizing the dichroic filters of the CFP/YFP pair because afterpulsing contributes significantly to the low brightness of YFP in the blue emission channel. We decided to test our method using the Alexa 488/rhodamine 6G pair. A 2:1 mixture of Alexa 488 and rhodamine 6G was prepared from stock solution and measured using a sampling time of 50 μs for a total of 160 s. The sample was measured both with a dichroic filter centered at 525 nm and another one centered at 545 nm. The experimental histograms were fit to a single-species model resulting in χ-square values of 50 and 62 for transition wavelengths of 525 and 545 nm, respectively. We repeated this experiment four times to achieve better sampling and arrived at an average ratio of the experimental χ-squares of 0.83. We determined from the brightness spectra of both dyes the χ-square function 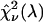for ideal dichroic filters assuming a 2:1 mixture of Alexa 488 and rhodamine 6G. The function 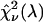has a similar shape as the curve shown in Fig. 7, but with a maximum at a transition wavelength of λ = 536 nm. The transition wavelengths of nm and 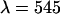nm lead to a ratio of their χ-square values of 0.8, which is in excellent agreement with the experimental ratio of 0.83.

The next question we would like to address is whether we can improve the CFP/YFP experiment by adding optical band-pass filters. Spectral cross talk is undesirable, because it complicates the resolution of species by fluorescence fluctuation spectroscopy. By passing certain wavelength bands, we could reduce the amount of spectral cross talk between the fluorescent dyes. However, at the same time as spectral cross talk is reduced, the brightness in each channel is reduced, because fewer photons arrive at the detector. The molecular brightness is a crucial parameter that determines the signal/noise ratio of single-color PCH studies (Müller et al., 2000). We expect that, similar to single-channel PCH, the molecular brightness plays a crucial role in dual-color PCH studies. Thus, adding optical band-pass filters leads to two competing effects, a reduction in spectral cross talk, which increases the sensitivity for resolving species, and a reduction in molecular brightness, which lowers this sensitivity. To evaluate these effects, we modeled dual-color PCH functions with ideal optical filters using the CFP and YFP brightness spectra. We use an ideal cut-off filter, which transmits 100% below its transition wavelength 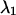and an ideal cut-on filter that transmits 100% above its transition wavelength 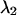. We systematically calculated the brightness of CFP and YFP as a function of the transition wavelengths, with the condition that 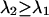. Note that our ideal dichroic study is reproduced by the special case that . We calculated dual-color PCH functions using the brightness parameters and chose for the number of molecules, 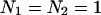. The PCH functions were fit to a single-species model and the reduced χ-square of the misfit was recorded. Fig. 8 shows the contours of the reduced χ-square as a function of the transition wavelengths. We normalized the χ-square by setting its value at 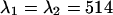nm to one, which corresponds to the optimal dichroic setting. The maximum reduced χ-square value is 1.09 and occurs for 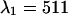nm and 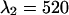nm (see inset in Fig. 8). However, the increase in the reduced χ-square value from 1.0 to 1.09 is very small. Thus, we conclude that band-pass filters will not increase the signal/noise ratio for resolving CFP-YFP mixtures.

FIGURE 8.

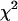as a function of transition wavelength of ideal band-pass filters. We use an ideal cut-off filter with 100% transmission below 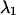and an ideal cut-on filter with 100% transmission above 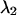. The brightness values of a CFP and YFP mixture of equal concentrations are calculated from the corresponding brightness spectrum for 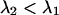. Dual-color PCH functions are calculated for each set of parameters and are fit to a single-species model. The χ-square function characterizes the misfit between the data and a single-species model. We normalized the χ-square function to one at 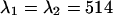nm, which corresponds to the best dichroic transition wavelength (+). The χ-square surface is shown as contour plot with a maximum of 1.09 at 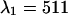nm and 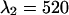nm. The inset shows the brightness spectra of CFP (gray line) and YFP (black line) together with the transmission function of the ideal band-pass filters (dashed lines).

DISCUSSION

PCH analysis of mixtures of Alexa 488 and rhodamine 6G at different dye concentrations demonstrates that molecular brightness is a robust parameter over the concentration range studied (Fig. 5 C). There are limits to dual-color PCH analysis at very low and very high concentrations. At very low concentrations the background of the sample starts to be a contributing factor. The brightness values recovered from PCH analysis will be compromised, if corrections for the background are not taken into account. At high concentrations the photon count rate is sufficiently high that the dead time of the detector plays an important factor (Hillesheim and Müller, 2003). The brightness values recovered from PCH analysis will be incorrect, because dead time changes the photon count statistics, but our theory assumes ideal photon detection. In fact, we have seen an apparent concentration dependence of the molecular brightness for the binary dye mixture for concentrations higher than the ones shown in Fig. 5 C. These apparent changes in the brightness are an artifact due to detector dead time.

Fig. 5 B shows the reduced χ-square values (diamonds) for the binary dye mixture as a function of the average number of molecules of Alexa 488. We calculated dual-color PCH functions using the brightness parameters from the global analysis of the binary dye study and keeping the concentration ratio between the two dyes at a 57:43% ratio. The reduced χ-square of the modeled PCH functions fit to a single-species model is plotted as the dashed line in Fig. 5 B. The experimentally determined reduced χ-square values coincide with the ones based on our modeling. The χ-square curve, which characterizes the severity of the misfit between the data of the binary dye mixture and a single-species model, has a maximum close to 0.1 Alexa 488 molecules in the observation volume. This behavior is qualitatively easy to understand. The probability of two different particles being present in the volume by coincidence decreases rapidly with diminishing concentration. Thus, at low concentrations only single molecules occupy the observation volume. Such conditions allow the best discrimination between different species, because each crossing of a molecule through the observation volume triggers a burst of photons with the spectral characteristics of the particular fluorophore. The detection of these photons in both channels is not confounded by the presence of other fluorescing molecules. At high concentrations many molecules occupy the observation volume simultaneously. The changes in the fluorescence signal due to a molecule entering or leaving the volume are relatively small compared to the signal from the remaining molecules. In other words, fluctuations decrease with increasing concentration, and the χ-square value decreases, because it is becoming harder to resolve species. On the other hand, at very low concentrations the observation volume is vacant most of the time, and no fluorescence signal is recorded during these times. Thus, the total number of single-molecule events, which carry the signal for discriminating species, decreases as the concentration is lowered, which results in a reduction of the χ-square value.

The presence of spectral cross talk has important consequences for fluorescence fluctuation spectroscopy. To make this point more clear let us again consider the simple case of a binary mixture of two dyes. We will specifically address differences between dual-color FCS and dual-color PCH. In many cases, dual-color FCS is not able to separate a binary mixture with spectral overlap using data from a single measurement. This is because six parameters are required to resolve a binary mixture. In the case of FCS, these parameters are the fractional intensity of each dye in each channel and the average particle number of the dyes. The fractional intensities of each channel add up to one, thus introducing two constraints, which reduce the number of unknown parameters to four. If the diffusion coefficients of the two species are approximately the same, then FCS only provides three amplitudes; the autocorrelation fluctuation amplitude of each channel and the cross-correlation amplitude. This information is insufficient to determine the four unknowns and additional control experiments are required to constrain the parameters of the mixture. Therefore, dual-color FCS resolves binary mixtures only if the diffusion times of the two species are well separated. However, the differences in the diffusion coefficient are in many interesting cases insufficient for resolving mixtures.

In contrast to the three amplitudes accessible by dual-color FCS, the dual-color PCH algorithm considers the complete two-dimensional surface of photon counts to identify components. This surface contains information from higher photon count moments that provide additional information not present in FCS. Our experiment with a binary dye mixture of rhodamine and Alexa demonstrates that dual-color PCH resolves species in the presence of cross talk. Fits of the data to a two-species model determine the brightness in each detection channels for both species (Fig. 5 C). To demonstrate the robustness of the technique we measured mixtures at different dye concentrations. The brightness values measured for each dye stay constant because molecular properties are concentration independent (Fig. 5 C).

Dual-color FCS has an advantage over PCH in the absence of cross talk between the channels. A positive fluctuation amplitude of the cross-correlation function clearly indicates the presence of a heterocomplex. Inspection of the dual-color PCH function does not provide such a direct and visual interpretation of the data, but requires a fit to a model to establish the presence of a heterocomplex. However, this advantage disappears with increasing presence of cross talk as discussed above. In addition, dual-color FCS provides information about dynamic processes from the shape of the correlation function, which is ignored by PCH.

To observe the emission of each fluorophore of a mixture, one needs to excite all fluorophores simultaneously. Two-photon excitation has the advantage that it is usually possible to find an excitation wavelength, where all fluorophores are coexcited (Heinze et al., 2000). This is due to the fact that, in contrast to one-photon excitation, the two-photon excitation spectra of many commonly used dyes overlap. For example, the data shown in Fig. 5 were taken with an excitation wavelength of 780 nm, a wavelength that excites both rhodamine 6G and Alexa 488 efficiently.

We describe a model that takes the effects of sampling time on the brightness and the number of molecules of dual-color PCH into account. The data presented in Fig. 4 show good agreement between theory and experiment for the case of a single species. Although this model represents an approximation for the case of more than one species, the experiments with the binary dye mixture demonstrate that the model also works well for two species. Fig. 5 C displays the brightness values for the two-species fits of the dye mixture together with the brightness of each dye determined from a single-species sample. The values recovered from both dye samples are identical to the brightnesses of the binary mixture. In other words, the sampling time affects each brightness value in the binary mixture the same as in the single-species case.

We demonstrated the successful resolution of a binary mixture of CFP and YFP. We also determined the optimal dichroic filter for resolving this mixture, when the number of molecules of CFP and YFP, 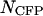and 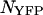, equals one. Note that the optimal transition wavelength depends on the values of 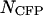and (data not shown). However, there is a simple relationship, which we will state without proof. The optimal dichroic transition wavelength only depends on the concentration ratio of the proteins. Thus, our result applies to all mixtures where CFP and YFP are present at roughly equal concentrations. The procedure we outlined for optimizing the optical filters for the CFP-YFP mixture is applicable to any other pair of fluorophores and provides an objective method for optimizing dual-color PCH experiments of fluorescent dyes with spectral overlap.

We would like to add a word of caution about interpreting brightness values based on PCH analysis. The average number of molecules and the molecular brightness depend on the PSF selected for PCH analysis. We typically chose a Gaussian-Lorentzian or a three-dimensional Gaussian PSF. Both models describe our experimental histograms, although the Gaussian-Lorentzian model provides slightly better fits. A similar situation is encountered in FCS, where both the Gaussian-Lorentzian and the three-dimensional Gaussian model fit experimental correlation functions equally well (Müller et al., 2003). The average number of molecules N is calculated from the fluctuation amplitude where the value of the factor depends on the shape of the PSF (Thompson, 1991). Thus, different choices of the PSF lead to different values for the number of molecules N. The brightness is affected in a similar way by the shape factor 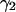. The first two factorial moments 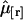of the photon counts are sufficient to relate the brightness values for different PSFs to one another,

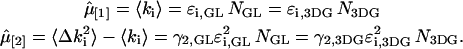(22)

The indices GL and 3DG refer to the Gaussian-Lorentzian and the three-dimensional Gaussian PSF, respectively. The values of 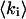and are the mean and the variance of the photon counts in detection channel i and are independent of the shape of the PSF. The above equations determine the relationship of the brightness and the average number of molecules for two different PSFs,

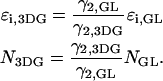(23)

In other words, the PCH parameters for different PSFs are related to one another by the ratio of their shape factors. Neither the Gaussian-Lorentzian nor the three-dimensional Gaussian describe the experimental PSF precisely (Hess and Webb, 2002), but serve as model functions that approximate the experimental PSF. The choice of the PSF is, as long as it describes the data, a matter of convenience. We decided to express all PCH parameters assuming a three-dimensional Gaussian PSF, because most FCS studies use this PSF.

In contrast to two-photon microscopy, the PSF of confocal microscopes is not well reproduced by a Gaussian-Lorentzian or three-dimensional Gaussian function, which leads to deviations between experiment and theory (Hess and Webb, 2002). This problem was recently addressed in the literature where single-channel PCH functions for confocal microscopy were introduced (Perroud et al., 2003). It is straightforward to construct the corresponding dual-color PCH functions because of the relationship between dual-channel and single-channel PCH (Eq. 9).

Let us briefly compare the differences between dual-color PCH and single-color PCH. The brightness ɛ for the single-channel experiment is given by the sum of the brightnesses in each channel, 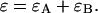We see that CFP and YFP have the same single-channel brightness under our experimental conditions (Table 1). Thus, single-channel PCH cannot distinguish between CFP and YFP because there is no brightness contrast between the fluorophores. This result can also be inferred from Fig. 7. Single-color PCH corresponds to the case where the transition wavelength of the dichroic filter is positioned so that all the light is received exclusively by one of the two channels. The χ-square value goes to zero under this condition as shown in Fig. 7. In other words, a single-species model describes the CFP-YFP mixture perfectly because the brightness of both species is identical. The same argument holds for the Alexa 488 and rhodamine 6G mixture. The single-channel brightnesses of both dyes are approximately the same and the brightness contrast between them is minimal. One way of achieving brightness contrast in single-channel PCH is by adding colored filters that block part of the emission spectrum of one of the dyes. However, this approach reduces the brightness of the fluorophore and, therefore, reduces the signal statistics of the experiment. Dual-color PCH is clearly the superior method for resolving a mixture of fluorophores that are spectrally distinct.

CONCLUSIONS AND SUMMARY

We introduced dual-color PCH theory and experimentally tested the technique. We successfully resolved binary dye mixtures and a solution of fluorescent proteins. An interesting feature of dual-color PCH is that it allows the resolution of dye mixtures in the presence of spectral cross talk from a single measurement. This technique should prove useful for studying protein interactions. We are specifically interested in applying dual-color PCH to detect protein interactions directly in living cells. So far, we demonstrated that single-channel PCH is capable of characterizing homodimer formation in the intercellular environment. Dual-color PCH would allow studying the formation of heteroprotein complexes in cells. However, as noted earlier, energy transfer between the pair of fluorophores of the heterocomplex will change the brightness of both the donor and acceptor. These effects need to be considered for any quantitative analysis of protein interactions by dual-color PCH. In addition, afterpulsing and dead time of the photo detector are contributing factors at low molecular brightness and at high photon count rates. These conditions are typically present in cellular fluorescence fluctuation experiments. The theory presented here assumes an ideal photo detector. We need to extend dual-color PCH theory and quantitatively account for nonideal detector effects as was done previously for single-channel PCH theory. This will be the topic of a forthcoming study.

APPENDIX A

Equation 7 applies to a single diffusing particle. To treat the case of two independent, but identical particles diffusing within an enclosed volume of V, we need to introduce two spatial coordinates and 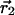to account for both particles. The pdf PCH⁽²⁾ of two identical, freely diffusing particles is now described by

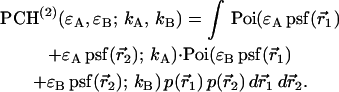(24)

Next, we rewrite Eq. 24 using a single Poisson function,

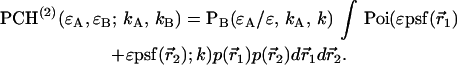(25)

The symbols used are defined in the Theory section of the manuscript. The integral in Eq. 25 is identical to the univariate PCH function for two independent molecules, 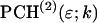(Chen et al., 1999). Thus, the bivariate photon count distribution for two particles is again related to the univariate photon count distribution,

(26)

It is straightforward to generalize this result to the case of N independent molecules diffusing in a closed volume V,

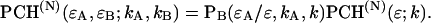(27)

Finally, in the last step we choose an open system instead of a closed system. This allows us to consider a small subvolume, instead of the total sample volume. Although the total sample volume contains an astronomically high, but conserved number of fluorescent molecules, the reference volume is chosen so that the number of particles is countably small. For convenience, we choose the volume of the PSF as our reference volume. Because we are now dealing with an open system, the number of particles is not conserved, but fluctuates. In the case of a small open volume surrounded by a large reservoir, the number fluctuations are Poissonian distributed,

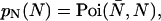(28)

with N being the actual number of particles within the reference volume V₀. The average number of particles 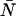is calculated from the particle concentration c by, with as Avogadro's constant. We take the open system into account by averaging over all distribution functions PCH^(N) with weights given by the probability of observing N-particles,

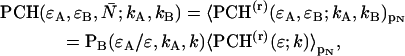(29)

where we used Eq. 27 to arrive at an expression in terms of univariate PCH functions. Because the univariate PCH for an open volume is defined by (Chen et al., 1999),

(30)

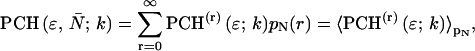we arrive at Eq. 9 by combining Eqs. 29 and 30.

APPENDIX B

Calculation of the r-particle PCH function requires r-successive convolution of the single particle PCH function (Chen et al., 1999),

. (31)

A convolution is transformed into a simple multiplication in Fourier space. Because the fast Fourier transform scales as it is computationally advantageous to compute PCH using the fast Fourier transform algorithm, as compared to convolutions, which scale with We write the Fourier transform ℱ of as

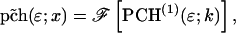(32)

and the Fourier transform of is given by

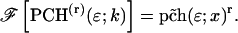(33)

For r = 0 we have the special case 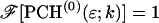. Using Eq. 30 it is straightforward to show that the single-channel PCH function is determined by

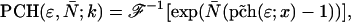(34)

where 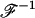denotes the inverse Fourier transform.

APPENDIX C

The two-dimensional probability distribution function of the photon counts contains from a mathematical point of view the same information as its bivariate moments. We specifically will use bivariate cumulants 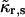, which are related to bivariate moments, but have properties particularly useful for fluctuation spectroscopy. We denote the order of the bivariate cumulant 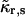by r + s. The bivariate, integrated intensity cumulants up to order two are given by,

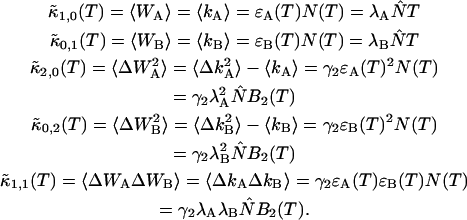(35)

The cumulants up to order two are statistically the most significant and we will ignore higher order moments as was done in the one-dimensional case for determining the effect of binning time on the brightness of a species. Equation 35 expresses the cumulants in terms of ordinary moments of the integrated intensity and moments of the photon counts. In addition, the equation connects the cumulants with the brightness and number of molecules, which depend on the sampling time, and a model that uses the binning function to take undersampling into account. All bivariate cumulants with one of the indices being zero are identical to their corresponding univariate cumulant. We have previously described the relationship between univariate, integrated intensity cumulants, their brightness, and the effects of sampling time T (Müller, 2004). Thus, we only need to discuss the cumulant 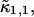which is defined by,

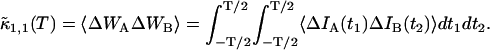(36)

This function is defined as,

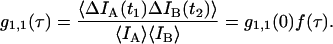(37)

The cross-correlation function only depends on the time difference, 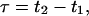because we are assuming a stationary process. The cross-correlation function is given by the product of the cross-correlation amplitude 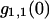and a time-dependent factor 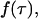which is model dependent. For a three-dimensional Gaussian point spread function 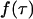is given by,

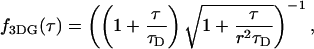(38)

with 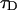as the diffusion time and 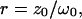the ratio of the axial to the radial beam waist. The fluctuation amplitude for a single diffusing species is given by,

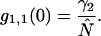(39)

Because 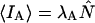and 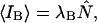we rewrite Eq. 36 with the help of Eqs. 37–39,

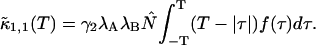(40)

The binning function is defined by (Müller, 2004),

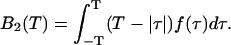(41)

Equations 40 and 41 prove the relationship between the cumulant 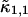and the binning function of Eq. 35. It can be shown that for short sampling times, 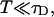the binning function is quadratic with sampling time, 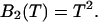The cumulant 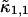reduces in this case to, 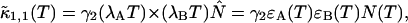where we used the relationship between brightness and photon count rate (Eq. 11). The above equation connects the cumulant 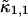with the brightness values in each channel as shown in Eq. 35.

In dual-color PCH each species is uniquely identified by three parameters, the brightness in each channel and the average number of molecules. But there are more than three cumulants in Eq. 35 that describe the brightness in each channel. In other words, the system of equations is overdetermined and its solution requires minimization using a least-squares approach. However, inspection of Eq. 35 reveals that there are exactly two combinations of cumulants that describe the brightness in each channel,

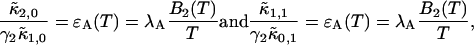(42)

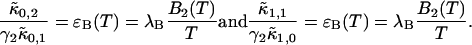(43)

These equations reveal that both solutions lead to exactly the same dependence of the brightness on the sampling time. Therefore, we conclude that the dependence of the brightness on the sampling time is given by Eq. 16. The corrected number of molecules is described by Eq. 17 as can be verified by inserting Eq. 16 into the expressions describing the cumulants of first order.