Abstract
HIV-1 integrase (IN) is an essential enzyme for the viral replication and an interesting target for the design of new pharmaceuticals for multidrug therapy of AIDS. Single and multiple mutations of IN at residues T66, S153, or M154 confer degrees of resistance to several inhibitors that prevent the enzyme from performing its normal strand transfer activity. Four different conformations of IN were chosen from a prior molecular dynamics (MD) simulation on the modeled IN T66I/M154I catalytic core domain as starting points for additional MD studies. The aim of this article is to understand the dynamic features that may play roles in the catalytic activity of the double mutant enzyme in the absence of any inhibitor. Moreover, we want to verify the influence of using different starting points on the MD trajectories and associated dynamical properties. By comparison of the trajectories obtained from these MD simulations we have demonstrated that the starting point does not affect the conformational space explored by this protein and that the time of the simulation is long enough to achieve convergence for this system.
INTRODUCTION
HIV-1 integrase (IN) is one of the three enzymes encoded by the viral genome, in addition to reverse transcriptase and protease. It has the function of catalyzing the integration of the transcribed double-stranded viral DNA into the host chromosome. This process occurs in two sequential reactions (Brown, 1997): in the first step, termed 3′ processing, a water molecule attacks at the 3′ ends of the viral DNA removing a dinucleotide; in the second step, called “strand transfer”, each exposed viral DNA 3′-OH ribose is activated for nucleophilic attack to opposite strands of the host DNA, across a five-basepair stretch, becoming covalently attached to it.
HIV-1 IN is a 32-kDa enzyme comprised of three structurally and functionally distinct domains, all of them required for full catalytic activity (Engelman et al., 1993). The N-terminal domain (residues 1–50) contains a conserved HHCC motif (Johnson et al., 1986), which binds a Zn2+ ion (Burke et al., 1992; Bushman and Craigie, 1991; Haugan et al., 1995; Lee and Han, 1996; Zheng et al., 1996) that promotes the multimerization (Zheng et al., 1996) and enhances the catalytic activity (Lee and Han, 1996; Zheng et al., 1996). The catalytic core domain (residues 50–212) contains the conserved D,D-35-E motif, common to all retroviruses, retrotransposons, and some bacterial transposases (Engelman and Craigie, 1992; Kulkosky et al., 1992; Polard and Chandler, 1995; Rowland and Dyke, 1990). This motif is represented, by the residues Asp-64, Asp-116, and Glu-152 in HIV-1 IN that are crucial for the activity. Finally, the C-terminal domain (residues 212–288) appears to have a nonspecific DNA binding activity (Engelman et al., 1994; Vink et al., 1993; Woerner and Marcus-Sekura, 1993). All of the three isolated domains form homodimers in solution whereas the activity of IN is mediated by a multimeric complex that requires the presence of at least one integrase active site, and the conserved amino acids Asp-64, Asp-116, and Glu-152 (Drelich et al., 1992; Engelman and Craigie, 1992; Kulkosky et al., 1992). Either manganese (in vitro) or magnesium (in vitro and in vivo) is essential as a catalytic cofactor, and furthermore it has been proposed that two of the divalent metal ions are coordinated to the active site residues Asp-64, Asp-116, and Glu-152 (Beese and Steitz, 1991; Ellison and Brown, 1994; Hazuda et al., 1997; Vink et al., 1994; Wolfe et al., 1996).
Structural information is available for all three domains of HIV-1 IN. The solution structures of the isolated N-terminal and C-terminal domains have been determined by NMR (Cai et al., 1997; Eijkelenboom et al., 1997, 1995; Lodi et al., 1995). The catalytic core domain of HIV-1, simian immunodeficiency virus, and Rous sarcoma virus integrases have been determined by x-ray crystallography as a single domain dimer (Bujacz et al., 1995, 1996; Dyda et al., 1994; Goldgur et al., 1998) and together with the N-terminal (Wang et al., 2001) or C-terminal (Chen et al., 2000a,b; Yang et al., 2000) domain. However, there is no complete structural information about the loop region between the residues 140–145, mainly because of its high B-factors that suggest substantial flexibility in this region. The aforementioned loop is located close to the active site and mutations that constrain this loop have demonstrated that its mobility is important for catalytic activity (Greenwald et al., 1999) and that it is involved in stabilization of the substrate during the reaction with the DNA substrate (Esposito and Craigie, 1998; Heuer and Brown, 1997).
HIV-1 IN, being an essential enzyme for the viral replication, has become a very attractive target for antiretroviral therapy after the emergence of HIV-1 strains resistant to reverse transcriptase and protease inhibitors. One of the most promising classes of integrase inhibitors comprises compounds with a diketo acid functionality and the capability of selective inhibition of the strand transfer reaction (Hazuda et al., 2000). Single or multiple mutations in HIV-1 IN at residues T66, S153, or M154 confer degrees of resistance to one or more compounds belonging to this class (Hazuda et al., 2000). Given the unavailability of three-dimensional structures for the mutated enzyme and the lack of information about the reasons why these few mutations close to the active site confer resistance to the inhibitors, we carried out a molecular dynamics (MD) study of the HIV-1 IN T66I/M154I catalytic core domain. Previous MD simulations were carried out on the wild-type HIV-1 IN catalytic core domain as well as with (Barreca et al., 2003; Ni et al., 2001) and without (Lins et al., 2000, 1999; Weber et al., 1998) the inhibitor 5CITEP complexed in the active site. Another MD simulation has been carried out on IN T66I/M154I with the same inhibitor complexed (Barreca et al., 2003) but no conformational study on the double mutant enzyme alone is available. These previous MD studies showed that significant and apparently important conformational interactions occur in the active region and demonstrated the importance of the flexibility of the loop containing residues 138–149. It has been shown that the mobility of this loop in the wild-type IN is constrained due to the presence of the 5CITEP inhibitor within the active site (Barreca et al., 2003).
The aim of this study is to understand if there are significant differences in the dynamical behavior of the mutated enzyme with respect to the previously published (Lins et al., 2000, 1999) wild-type enzyme in terms of flexibility of the protein and orientation of the residues important for the catalytic activity.
Because there is no complete IN structure available, to be able to computationally characterize the whole structure of the protein, it is important to understand whether the starting conformation of an MD simulation may significantly affect the results. This might be particularly important for the highly flexible regions that may play a role in the catalytic activity (Greenwald et al., 1999). To address this issue we have performed four 2-ns MD simulations on the HIV-1 IN catalytic core domain T66I/M154I mutant starting from four different conformations. These conformations were selected from a previously carried out MD simulation (Barreca et al., 2003) by choosing the snapshots that displayed the highest RMSD in the loop containing residues 138–149.
We show that the dynamic behavior of HIV-1 IN T66I/M154I does not display significant differences with respect to the behavior of the wild-type IN described in a previous study (Lins et al., 1999). By using essential dynamics (Daura et al., 1999) and cluster analyses we demonstrate that the starting structure, when it comes from molecular dynamics simulations, does not affect the conformational space sampled by this system and that within the simulation time the system is likely to reach convergence (Smith et al., 2002).
METHODS
Structures
Four snapshots from a prior 1.8-ns MD simulation carried out on HIV-1 IN T66I/M154I (Barreca et al., 2003) have been taken as starting points for the minimization and equilibration protocol. The choice of the snapshots was based on the highest difference in the root-mean-square deviation (RMSD) of the loop region 138–149, one of the most flexible parts of the protein (Barreca et al., 2003; Lins et al., 2000, 1999), and known to play an important role in the catalytic activity (Greenwald et al., 1999).
To select the starting structures, the loop conformations were compared over all of the MD snapshots by superimposition of their backbone atoms. Based on examination of the loop motions, two loop conformations were selected as being representative of the extreme positions of the range of loop motion. Two other conformations were chosen between the two extremes, resulting in a total of four starting structures.
Molecular dynamics simulations
All four conformations of the protein were extracted from a 1.8-ns MD trajectory described elsewhere (Barreca et al., 2003). The protein was solvated in a cubic box (with 7.2-nm edges) of preequilibrated waters. Water molecules that were found to be within 0.26 nm of any atom in the solute were removed. Two negative counterions were placed in the proximity of the regions of the protein surface with the most favorable electrostatic potential calculated using the particle-based method implemented in the GROMACS (van der Spoel et al., 1994) package v3.0.5. The protein and solvent interact via the CHARMM27 force field where all protein atoms are explicitly represented (MacKerell et al., 1998) and water is characterized by the TIP3P model (Jorgensen et al., 1983; Neria et al., 1996). The hydrogen atoms of the protein were placed using the HBUILD routine implemented in CHARMM (Brooks et al., 1983). The SHAKE algorithm (Ryckaert et al., 1977), with a tolerance of 10−7 nm, was applied to constrain all bonds involving hydrogen atoms in all simulations.
The temperature was kept constant by coupling to a heat bath through the Berendsen algorithm (Berendsen et al., 1984). The pressure was adjusted by isotropic position scaling using a Berendsen-like algorithm. To avoid edge effects, periodic boundary conditions were applied to all of the simulations. Atomic coordinates were saved every 0.5 ps for later analysis. A 1.0-nm short-range cutoff was used for all nonbonded interactions and long-range electrostatic interactions were treated by the particle-mesh-Ewald method (Essmann et al., 1995) with a grid size of 7.2 × 7.2 × 7.2 nm.
Before the MD runs were performed, the system was energy minimized by 200 steps of steepest descent keeping the solute (protein, magnesium ion, and chloride ions) fixed, followed by 1000 steps of conjugate gradient with no constraints. The system was heated up to 300 K over a period of 30 ps, with a 2-fs time step and equilibrated for 70 ps with the velocities being reassigned in the system every 0.1 ps. The system was further equilibrated, with a 2-fs time step, for 50 ps at which point the energy of the system achieved complete stability. Production runs were performed at 300 K and carried out under NPT (i.e., constant number of particles, pressure and temperature) conditions for 2 ns with a 2-fs time step.
All MD simulations were performed using the NAMD (Kale et al., 1999) program and analyses of the trajectories were performed using the GROMACS software package (van der Spoel et al., 1994).
Essential dynamics
Essential dynamics (Amadei et al., 1993) is a technique that allows the identification of the correlated motions of a protein during a trajectory generated by an MD simulation. After removal of the rotational motions, a covariance matrix is constructed. The diagonalization of the matrix leads to a set of eigenvectors/eigenvalues. Each eigenvector represents one single direction in a multidimensional space whereas the eigenvalue is the amplitude of the motion along the eigenvector. The Cα displacement along each eigenvector can provide insights into the concerted motions of the protein along each direction along with their amplitude. The projection of the displacements on each eigenvector shows the width of the essential space explored by the system as a function of time. A comparison of the conformational space sampled by different trajectories generated for the same system can be made to gain insight into the amount of essential space explored by the system during the MD simulation. For the purpose of comparing different trajectories, essential dynamics can be performed on a combined trajectory, constructed by concatenating each individual trajectory (van Alten et al., 1995). If the motions are similar, the eigenvectors and the eigenvalues coming from individual trajectories should be similar to the motions observed in the concatenated trajectory (van Alten et al., 1995).
Cluster analysis
Cluster analysis was performed using the GROMOS method (Daura et al., 1999). Structures of the protein were taken from the MD trajectory at 10-ps intervals. The matrix of atom positional root-mean-square deviations between pairs of structures was calculated for the backbone atoms of residues 57–208 (the catalytic core domain) of the protein and of residues 137–150 for the flexible loop considered independently. The criterion of similarity for two structures was the backbone atom positional RMSD ≤ 0.10 nm for the backbone atoms of residues 57–208 of the protein and of residues 137–150 for the flexible loop.
This method, described in detail by Daura et al. (1999), is considered to be an effective tool for judging the convergence of MD simulations, especially if this analysis involves the comparison of multiple trajectories, generated from different starting conformations of the same system (Smith et al., 2002). The convergence of a simulation can be considered achieved when the plot of the number of clusters as a function of time reaches a plateau.
RESULTS AND DISCUSSION
Comparative analysis
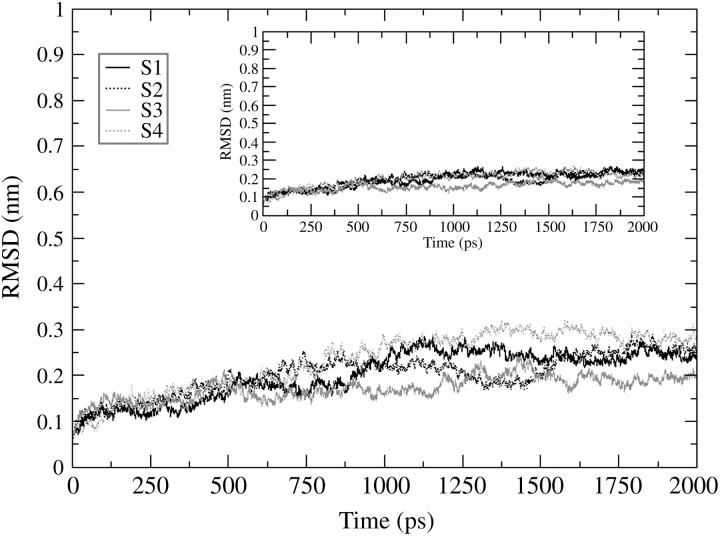
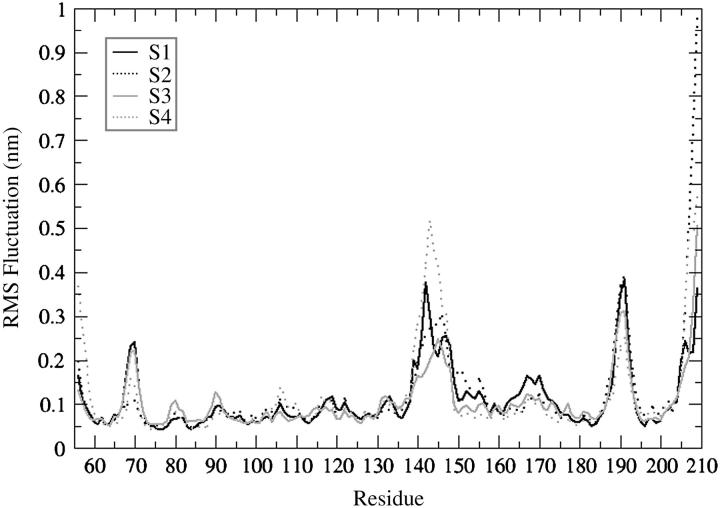
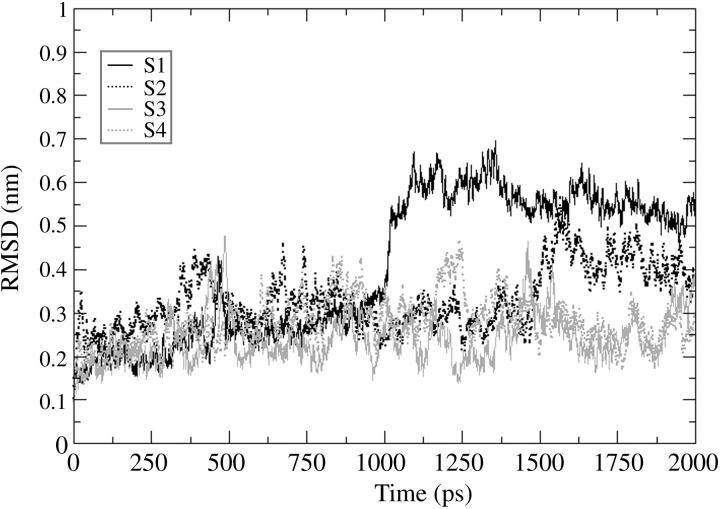
The four 2-ns MD trajectories computed for the HIV-1 integrase double mutant (T66I/M154I) catalytic core domain starting from different conformations have been compared and are designated by S1, S2, S3, and S4, where S1 is the starting conformation chosen from the 1.8-ns MD simulation (Barreca et al., 2003) at 90 ps, S2 from 630 ps, S3 from 1160 ps, and S4 from 1650 ps. Fig. 1 shows the RMSD of the backbone atoms with respect to the equilibrated conformation for each of the 2-ns trajectories (S1, S2, S3, S4), and where rotational and translational motions were removed. Each simulation rapidly achieves stability in the atom positional RMSD with values between 0.2 and 0.3 nm. The values of RMSD increase to ∼0.15 nm after 150 ps maintaining low structural changes for 750 ps. After 1000 ps, the RMSD values undergo larger fluctuations with respect to the first portion of the simulations. The relatively high values and the irregular profile of the plots reflect the structural changes of highly flexible protein regions. From the analysis of the root-mean-square fluctuation (RMSF) per residue (Fig. 2) we can see that there are three loop regions that display a large flexibility. These three regions comprise residues 66–74, 138–149, and 185–195. The simulations that show a wider fluctuation in atom positional root-mean-square deviation in the region between residues 138 and 149 are S1 and S4 (Fig. 2). The difference in the values of fluctuations for the most flexible regions may be explained considering how far the conformations of the starting structures of these regions are from their most favorable configuration (i.e., configurations after the convergence of the simulation). The loop containing residues 138–149 has the highest difference in fluctuations among the four trajectories with respect to the other two loop regions because the criteria for choosing the four starting conformations was based on its highest degree of diversity among the snapshots of the 1.8-ns MD simulation (Barreca et al., 2003). Fig. 3 shows the backbone RMSD of the loop region 138–149 calculated with respect to each equilibrated structure. Simulations S1 and S2 are the ones that show a wider RMSD in their loop regions with respect to the conformation at the beginning of the production phase (i.e., 0 ps). In particular, S1 has a large transition in the loop conformation after 1000 ps of MD simulation (from 0.35 to 0.7 nm), whereas a smaller transition occurs to the S2 loop that increases from 0.35 to 0.45 nm after 1500 ps. The loop shows very similar RMSD with respect to the equilibrated structures (0 ps), for all four structures, with the exception of the transitions mentioned previously that occurred in the case of the S1 and S2 simulations (Fig. 3). The inset in Fig. 1 shows the backbone RMSD of the protein after removing the contribution of the flexible loop comprised of residues 138–149. It is evident that in this case the profile is much more stable than the one displayed for the whole protein. S1, S2, and S4 have an almost perfect overlapping pathway whereas S3 is the simulation with the lowest value of RMSD (Fig. 1, inset). Moreover, the RMSD value for the S3 flexible loop (see Fig. 3) fluctuates around the same average value for the entire simulation. Therefore, the RMSD calculated for the whole protein is extensively influenced by the catalytic loop (residues 138–149).
FIGURE 1.
Root-mean-square deviation (RMSD) of double mutant HIV-1 IN (T66I/M154I) backbone atoms with respect to the equilibrated conformation as a function of time. The inset figure shows the RMSD calculated for the protein backbone atoms after removing the contribution of the catalytic loop (residues 138–149). S1 stands for simulation 1 (black solid line); S2 stands for simulation 2 (black dotted line); S3 stands for simulation 3 (gray solid line); and S4 stands for simulation 4 (gray dotted line).
FIGURE 2.
Backbone atom RMSF per residue for the four trajectories: S1-simulation 1 (black solid line), S2-simulation 2 (black dotted line), S3-simulation 3 (gray solid line), and S4-simulation 4 (gray dotted line).
FIGURE 3.
Root-mean-square deviation of the backbone atoms of the catalytic loop (residues 138–149) as a function of time with respect to the equilibrated conformation (0 ps). S1 stands for simulation 1 (black solid line); S2 stands for simulation 2 (black dotted line); S3 stands for simulation 3 (gray solid line); and S4 stands for simulation 4 (gray dotted line).
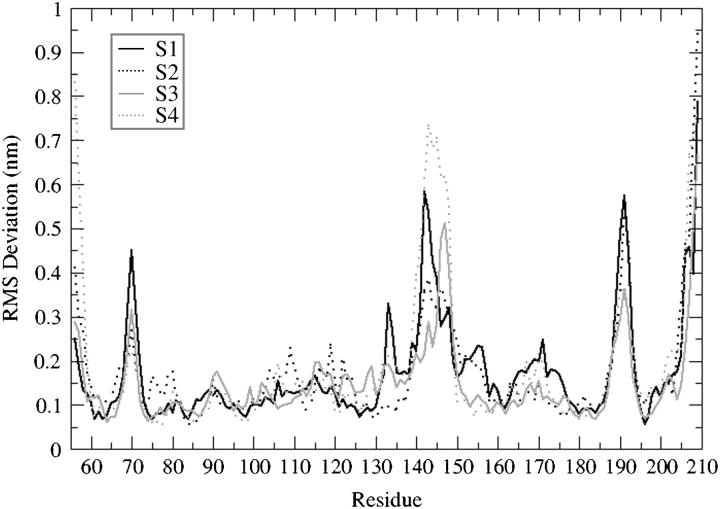
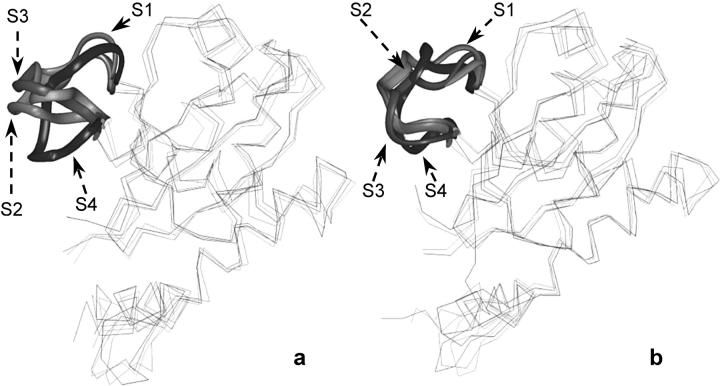
The static regions of the protein overlap very well for all four trajectories (Fig. 2), explaining that the parts of the protein with well-defined secondary structure elements do not show particular differences in their dynamical behavior. Fig. 4 shows the backbone RMSD per residue (with respect to the 0-ps conformation) for the four MD simulations. This is different for loop 138–149, which shows very different deviations among the four equilibrated structures. This is significant because the difference in width of the deviation from their conformation at the beginning of the production run may be in agreement with the tendency of our MD simulations to achieve convergence when starting from different configurations. Comparing the superimposition of the four starting structures of double mutant IN (T66I/M154I) with the superimposition of the four average structures obtained after the 2-ns MD simulations we can see that the flexible loop adopts a similar conformation (Fig. 5), independently of the starting configuration.
FIGURE 4.
Backbone RMSD per residue with respect to the equilibrated conformation (0 ps): S1 (black solid line), S2 (black dotted line), S3 (gray solid line), and S4 (gray dotted line).
FIGURE 5.
(a) Superposition of the four starting snapshots (S1, S2, S3, and S4); (b) average structures calculated for the four trajectories (S1, S2, S3, and S4). The conformations of the loop region comprised of residues 138–149 are displayed as solid ribbon.
Essential dynamics
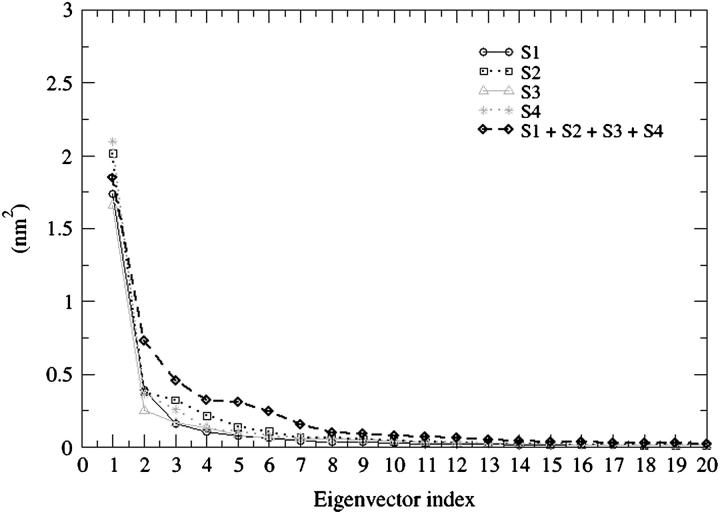
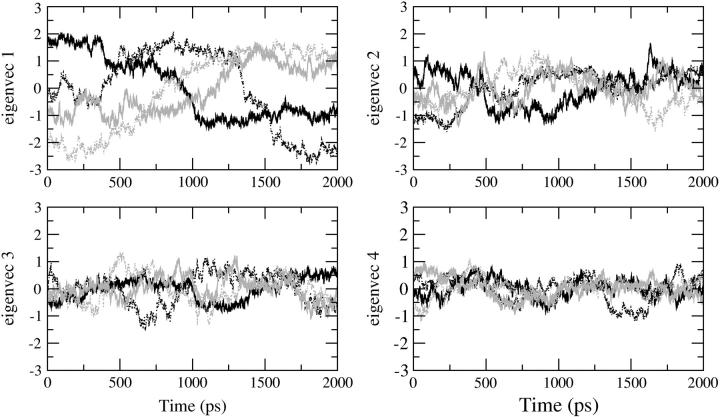
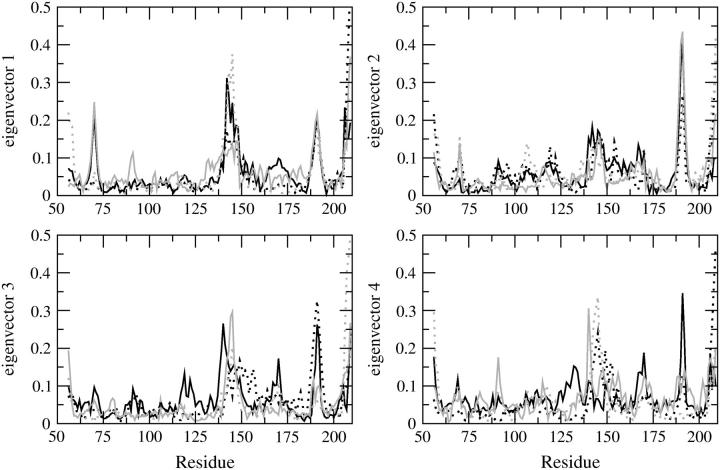
Fig. 6 shows the plot of the eigenvector index against eigenvalues, both derived from the covariance matrix of the α-carbons for the four trajectories and for the concatenated trajectory. The eigenvalue belonging to the first eigenvector is very similar among the four MD simulations as well as for the combined trajectories. If the motions identified for the combined trajectory are similar to those coming from the individual trajectories, the eigenvalues (and eigenvectors) should be similar. The plot indicates that the properties of the motions described by the essential eigenvectors are almost identical. By projecting the trajectory on each of the most important eigenvectors (Fig. 7) the essential space explored by the protein along each direction (eigenvector) is made evident. In this case it is possible to understand the most important eigenvectors for the essential motions of the protein and to compare the essential space explored by the four trajectories. In Fig. 7 the four eigenvectors that define the essential space (i.e., four essential degrees of freedom out of 462) are displayed. The pathway followed by each trajectory for the exploration of the essential space is different because the starting conformations of the MD simulations are different. Nevertheless, the range of conformational space explored along each eigenvector is very similar for all four trajectories. Fig. 8 shows the α-carbon displacement along the four main eigenvectors. The essential motions identified are very similar for all four MD simulations. These motions are also well correlated with the Cα displacement obtained from the concatenated trajectory. The most flexible regions comprise residues 138–149 and 185–195 for all of the first four eigenvectors, indicating that these regions are exploring a wide conformational space because their motions have large amplitude along all of the four most important directions of the essential space.
FIGURE 6.
Eigenvalues derived from the covariance matrices of the four MD simulations: S1 (black solid line, circles); S2 (black dotted line, squares); S3 (gray solid line, triangles); S4 (gray dotted line, stars); concatenated trajectories (black dashed line, diamonds).
FIGURE 7.
Projections of the four simulations (S1, black solid line; S2, black dotted line; S3, gray solid line; S4, gray dotted line) on the four selected eigenvectors.
FIGURE 8.
Residue displacement calculated for each Cα atom along the four selected eigenvectors: S1 (black solid line); S2 (black dotted line); S3 (gray solid line), and S4 (gray dotted line).
Cluster analysis
The cluster analysis probes the dependence of the results on the initial structure used for the simulation (Laboulais et al., 2002). The convergence of different trajectories calculated by MD simulations may be an artifact due to a too-short time of conformational sampling. Because the flexible loop comprising residues 138–149 is of primary importance for catalytic activity (Greenwald et al., 1999), we also performed a cluster analysis on this part of the protein. However, we chose the region from residue 137 to residue 150. By doing so, we attempted to avoid end effects by treating this part of the protein as a 14-residue peptide.
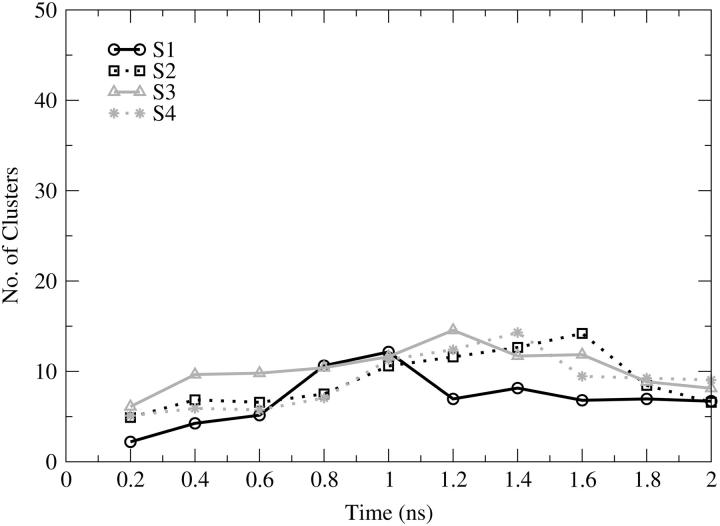
Fig. 9 shows the total number of clusters as a function of cumulative time for the entire protein. This quantity provides information about how much conformational space has been populated in the simulation. All of the simulations show a limited sampling either because of the low temperature or because of the well-defined secondary structure of the system. The total number of clusters identified for the four simulations is very similar; 32 clusters were found for S1, S2, S4, and 37 for S3. From Fig. 9 we can see that there are overlaps in the number of clusters over all of the trajectories. Such an overlap may indicate that the conformational space accessible by the system is similar for all of the MD simulations regardless of the starting conformation; however, this is only true if the conformations in the clusters identified in one simulation are similar to those in the other one. The conformational sampling increases slightly during the first 1.4 ns for S2, S3, and S4 and during the first 1.0 ns for S1. After these times, the number of clusters identified decreases and seems to reach a stable value for the last 0.25 ns. Note that a decrease in the number of clusters is possible because all clusters are redefined at each analysis point (i.e., every 200 ps). For example, conformations that were members of two separate clusters in a prior analysis point may later be merged into one cluster due to nearby sampling, resulting in a reduction in the total number of clusters. It can be seen in the overlay of the four trajectories in Fig. 9 that all of them converge to approximately eight clusters revealing that 2 ns of explicit solvent simulation at 300 K does not allow the protein to access wider conformational sampling.
FIGURE 9.
Number of clusters as a function of cumulative time, calculated for the entire protein. S1 (black solid line, circles); S2 (black dotted line, squares); S3 (gray solid line, triangles); S4 (gray dotted line, stars).
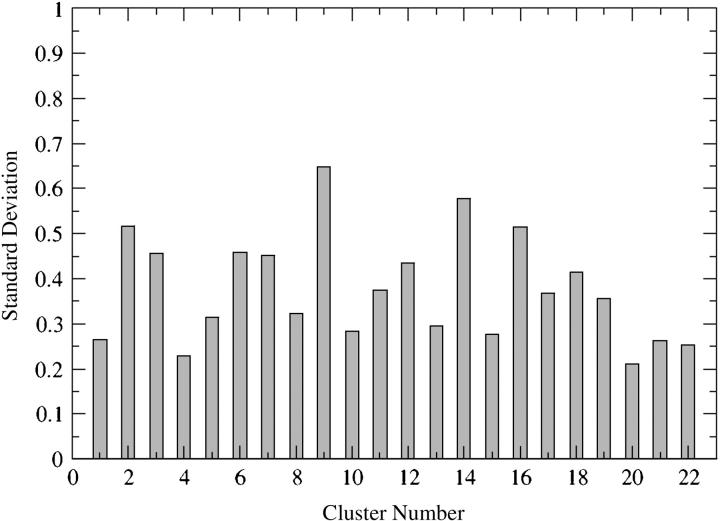
To demonstrate that the conformational space explored by the protein during the four MD simulations is correlated, a comparison of the clusters with a minimum of three member conformations was carried out as follows: the average conformation was calculated for every cluster (22 clusters for each MD simulation contained three or more conformations), and the RMSD was computed with respect to a reference structure (i.e., starting conformation of the MD simulation carried out on the IN double mutant T66I/M154I by Barreca et al., 2003). The values of RMSD were next compared for every cluster and their standard deviations were calculated. Fig. 10 shows the standard deviation values for each of the 22 clusters identified for all of the four MD simulations. The average structures of the majority of the clusters are similar as indicated by the low values of the standard deviation, largely between 0.21 and 0.46. This demonstrates that there is a good correlation among the conformations collected in each cluster obtained by the MD simulations starting from different conformations. Higher standard deviation values for clusters 2, 9, 14, and 16 (Fig. 10), respectively, of 0.52, 0.65, 0.58, and 0.51, are due to only one value of RMSD out of the four used to calculate the standard deviation within each cluster. However, the three remaining values of RMSD are quite similar (note that the RMSD values are calculated between the average conformation of each cluster and a reference structure, in this case the starting conformation of the MD simulation carried out on the IN double mutant T66I/M154I by Barreca et al., 2003).
FIGURE 10.
Comparison of clusters with a minimum of three member conformations for simulations S1, S2, S3, and S4. The RMSD between the average conformation of each cluster and a reference structure (the equilibrated structure of the prior MD simulation carried out on IN T66I/M154I by Barreca et al., 2003) has been calculated; these RMSD values within each single cluster have been compared by calculating their standard deviation.
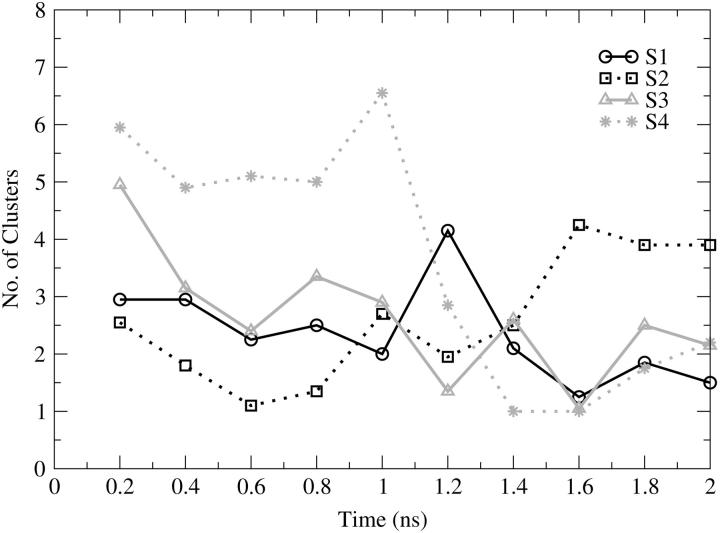
Fig. 11 shows the number of clusters identified for the flexible loop region (between residues 137–150), considered as a 14-residue peptide. Given the relatively high flexibility of the loop it is surprising that the total number of clusters identified is between 8 (S1) and 18 (S4). The higher number of clusters found for the S4 simulation is reasonable given that the flexible loop shows the highest fluctuation during this trajectory (see Fig. 2). The plot shows a disordered conformational sampling for the loop, with no increase throughout all of the MD simulations. Between 1.0 and 1.5 ns there are many overlaps in the explored conformational space, demonstrating that similar conformational sampling takes place for loop 138–149 in all four trajectories. After 1.6 ns, the sampling seems to reach a more stable profile.
FIGURE 11.
Number of clusters as a function of cumulative time, calculated for the catalytic loop (from residue 137 to residue 150). S1 (black solid line, circles), S2 (black dotted line, squares), S3 (gray solid line, triangles), S4 (gray dotted line, stars).
Conformational characteristics of HIV-1 integrase T66I/M154I
We have previously reported the results of MD simulations for the catalytic core domain of HIV-1 integrase wild type (Lins et al., 2000, 1999; Weber et al., 1998) and double mutant T66I/M154I with the inhibitor 5CITEP in complex (Barreca et al., 2003). In this work we have performed four 2-ns MD simulations on the double mutant enzyme but with no inhibitor present.
The dynamic behavior of the double mutant system shows the same general characteristics described for the wild type (Lins et al., 2000, 1999) and for the double mutant with 5CITEP (Barreca et al., 2003). The analysis of flexibility shows that there are three regions of the protein (comprising residues 66–74, 138–149, and 185–195) having higher mobility (Figs. 2 and 8) than the rest of the protein. This result is in perfect agreement with the results obtained on the wild type (Lins et al., 2000, 1999) and on the double mutant complex (Barreca et al., 2003), as well as with the crystallographic data (Bujacz et al., 1995; Dyda et al., 1994). Barreca et al. (2003) proposed that the restraint of the flexibility of this loop caused by the 5CITEP in complex with wild type IN is one of the mechanisms of inhibition. Our results constitute further evidence for this hypothesis because the mobility of the loop is not influenced by the mutations in the absence of inhibitor.
The secondary structure analysis carried out with the DSSP algorithm (Kabsch and Sandler, 1983) shows conservative secondary structural elements (see Supplementary Material), without the extension of the helix α-4 identified by Lins et al. (1999) for the IN wild type. The flexible loop, comprising residues 138–149, shows, as expected, a random coil conformation for the entire length of the simulation.
The active site has three essential residues, namely Asp-64, Asp-116, and Glu-152. A magnesium ion, that works as a cofactor for IN, is bridging the two catalytic residues Asp-64 and Asp-116. We have monitored the relative distances among the three catalytic residues during the simulation and the side-chain dihedral angles (data not shown). They do not undergo significant variations in their relative orientations, showing high stability during the 2-ns production run. We also monitored the dihedral angle variations for the residues that have been identified to be important for the biological activity such as Gln-62, Tyr-143, Gln-148, Asn-155, Lys-156, and Lys-159 (Barreca et al., 2003; Lins et al., 1999). The Gln-62 side chain moves toward residue Asp-116 after ∼750 ps, maintaining the orientation for the remaining 1250 ps. The analysis of the dihedral angles χ1 and χ3 has shown that after 750 ps, dihedral angles changed in such a way as to allow this residue to make hydrogen bonds with the Asp-116 side chain. When the distance between these two residues is not within a hydrogen-bonding distance, a water molecule bridges the two side chains, keeping the Gln-62 orientation stable. This residue is important for the interaction with diketo-enolic compounds, because it is involved in the formation of a cleft occupied by 5CITEP (Barreca et al., 2003). Moreover, Gln-62 has been shown to be important in the formation of a hydrogen-bonding network that causes rigidity of the catalytic loop in the wild-type IN (Barreca et al., 2003). In our simulations the side chain of Gln-62 exhibits a stable distance from D116 (after 750 ps) and Glu-152 (data not shown). On the contrary, the distance between Gln-62 and Gln-148 (one of the catalytic loop residues) is not stable and its value does not allow the formation of the hydrogen bond between Gln-62 and Gln-148, which is considered responsible for the stabilization of the loop in wild-type IN (Barreca et al., 2003).
Other MD simulations carried out on the same system in complex with the Merck inhibitor L-731,988 (Hazuda et al., 2000) have demonstrated that Gln-62 is very important in stabilizing the interaction of the inhibitor with the protein (Brigo et al., 2005).
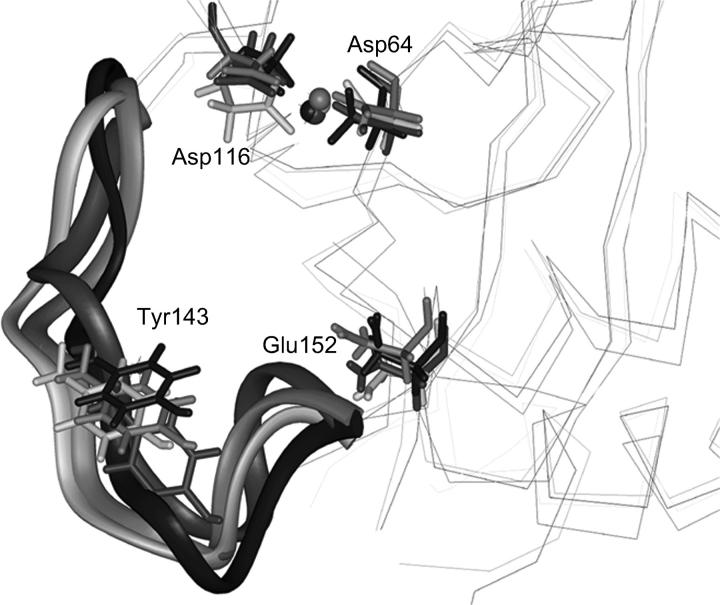
Tyr-143 is a residue in the active site loop, which has been proposed to play an important role in the catalytic activity (Chen et al., 2000a; Esposito and Craigie, 1998; Lins et al., 1999). In our simulations its side chain is always pointing away from the active site (Fig. 12). Only occasionally it has shown to be involved in hydrogen bonds with the side chain of Glu-152 when the conformation of the loop was favorable for this interaction. Given the mobility of the loop, no conservative interaction between this residue and any other protein residue has been found.
FIGURE 12.
Superposition of the average structures obtained from the four trajectories (S1, S2, S3, and S4). Residues Asp-64, Asp-116, Glu-152, and Tyr-143 are represented as sticks. The flexible loop comprised between residues 138 and 149 is represented as ribbon.
CONCLUSIONS
In this study, we have analyzed in detail the dynamic behavior of double mutant HIV-1 IN (T66I/M154I) with no inhibitor, in an effort to understand if differences exist with respect to previously published results for wild-type integrase (Barreca et al., 2003; Lins et al., 1999) and on the double mutant in complex with the 5CITEP inhibitor (Barreca et al., 2003). The analyses have been focused on the catalytic loop consisting of residues 138–149, whose flexibility has been demonstrated to play an important role in the catalytic activity (Greenwald et al., 1999). We found a very high mobility of this region, in agreement with the values of flexibility found for the same region in the wild-type integrase alone (Lins et al., 1999) and of the same double mutant in complex with the inhibitor 5CITEP (Barreca et al., 2003). Double mutant IN (T66I/M154I) showed high flexibility of the catalytic loop in the inhibitor bound state. This protein alone maintains the same flexibility features of the wild type and the same secondary structure elements, implying that the mutations do not lead to major conformational changes but only to the resistance to the inhibitory activity of the diketo-enolic acid compounds (Hazuda et al., 2000). In our simulations, the double mutant integrase behaves like the wild type maintaining its catalytic activity and, presumably, its capability of forming either the active multimeric complex (Engelman et al., 1993) or the protein-substrate interactions. These results constitute further evidence of the importance of the active site loop (138–149) for the catalytic activity of the enzyme, because the comparison of several MD simulations demonstrated different behaviors of this region. The data reported by Barreca et al. (2003) together with the results discussed herein, might indirectly lead to the understanding of the mechanism of inhibition of compounds belonging to the diketo-acid chemical class (Hazuda et al., 2000). Because the only differences in the dynamic behavior of IN revealed by already-published studies as well as by ongoing further comparative MD simulations (Brigo et al., 2005) are related to the catalytic loop flexibility, which is low only in the WT IN in complex with 5CITEP. The preservation of loop flexibility in the DM IN in complex with 5CITEP (Barreca et al., 2003) and with L-731,988 (Brigo et al., 2005) clearly demonstrates that the mutations have as primary effect a slight modification of the binding mode of these diketo acid inhibitors (Barreca et al., 2003; Brigo et al., 2005). This change in the molecular recognition of this class of compounds allows the enzyme to reestablish its catalytic loop flexibility that seems to be an essential condition for the enzyme to carry out its catalytic activity. From the published drug-resistance data (Hazuda et al., 2000) it is evident that a diketo acid inhibitor can still bind within the DM IN active site but with a lower affinity (Brigo et al., 2005). The lower binding affinity of DM IN for diketo acids inhibitors has also a reflection in the molecular recognition of the DNA substrate (Lee and Robinson, 2004). The single mutation M154I is capable of significantly increasing the catalytic activity of the enzyme (Lee and Robinson, 2004) and of conferring some degrees of resistance to the diketo acid inhibitors (Hazuda et al., 2000). On the other hand, the single mutation T66I confers a slightly higher resistance to the diketo acids (Hazuda et al., 2000) but, at the same time, it attenuates the catalytic activity (Lee and Robinson, 2004). The double mutation T66I/M154I described herein decreases the catalytic activity of the enzyme (Lee and Robinson, 2004) but confers an almost threefold increase of inhibitor resistance (Hazuda et al., 2000). These data demonstrate that the pressure given by the inhibitors to the virus induces mutations that lead to a decrease in catalytic activity efficiency. Under the structural point of view, we demonstrated that the overall dynamical behavior of the enzyme is not affected by the double mutation. The real mechanism of resistance seems to depend on the modification of intramolecular hydrogen bonds (Barreca et al., 2003) and on the orientation of active-site residue side chains, such as Gln-62, Tyr-143, Gln-148, Asn-155, Lys-156, and Lys-159 (Brigo et al., 2005; Barreca et al., 2003) that lead to a nonproductive interaction between the enzyme and the diketo acid inhibitor (Brigo et al., 2005; Barreca et al., 2003). The variation in the binding mode of this class of compounds allows the enzyme to reestablish its catalytic loop flexibility. On the other hand, the orientation of the aforementioned side chains is also very important for the catalytic activity of the double mutant IN that results significantly attenuated (Lee and Robinson, 2004).
In this contribution we show that MD simulations carried out on systems with well-defined secondary structure elements lead to perfectly comparable results. The RMSFs per residue are almost identical for the regions with limited flexibility, whereas some differences are shown for the three flexible loops due to the different pathways they took toward convergence. Essential dynamics analyses have shown that the motions along each of the most significant eigenvectors are also similar and that the essential space explored by the system is alike regardless of their different pathways. The cluster analysis demonstrates that the time of simulation we used allows the systems to explore the same conformational space. However, the convergence of MD simulations carried out starting from conformations obtained from methods such as simulated annealing that covers a wider range of free energy should be verified. In this article we wish to point out that molecular dynamics simulations carried out on small proteins without significant conformational disorder (i.e., well-defined secondary structure elements), such as the HIV-1 integrase catalytic domain, starting from different MD simulations snapshots, do not show significant differences either in the conformational sampling or dynamic behavior. Comparison between the trajectories studied herein showed that the similarity of the quantities analyzed provides a reasonable way of demonstrating the reproducibility of MD simulations.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
We express gratitude to National Resource Allocation Committee for a grant of supercomputer time to J.M.B. Additional computing, data storage, and visualization resources were provided by the Institute for Molecular Design and the Texas Learning and Computation Center at the University of Houston. We also express gratitude to Accelrys, Inc. for software licenses provided to the Institute for Molecular Design at the University of Houston. We also thank Dr. Maria Letizia Barreca for valuable discussions.
This project was supported by the National Institutes of Health Program on Structural Biology of AIDS-Related Proteins (GM56553) and the Robert A. Welch Foundation (E-1497).
Alessandro Brigo's present address is The Genetics Company, Wagistrasse 27, 8952 Schlieren, Switzerland (www.the-genetics.com).
Gabriela Iurcu Mustata's present address is Emisphere Technologies, Tarrytown, NY 10591.
Keun Woo Lee's present address is Dept. of Biochemistry, Gyeongsang National University, Gazwa-dong, Jinju, Kyeongnam-do, 660-701, Korea.
References
- Amadei, A., A. B. M. Linssen, and J. H. C. Berendsen. 1993. Essential dynamics of proteins. Proteins. 17:412–425. [DOI] [PubMed] [Google Scholar]
- Barreca, M. L., K. W. Lee, A. Chimirri, and J. M. Briggs. 2003. Molecular dynamics studies of the 1QS4 and double mutant HIV-1 integrase complexed with the 5CITEP inhibitor: mechanism for inhibition and drug resistance. Biophys. J. 84:1450–1463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beese, L. S., and T. A. Steitz. 1991. Structural basis for the 3′-5′ exonuclease activity of Escherichia coli DNA polymerase I: a two metal ion mechanism. EMBO J. 10:25–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, A. Di Nola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
- Brigo, A., K. W. Lee, F. Fogolari, G. Iurcu Mustata, and J. M. Briggs. 2005. Comparative molecular dynamics simulations of HIV-1 integrase and the T66I/M154I mutant: binding modes and drug resistance to a diketo acid inhibitor. Proteins. In press. [DOI] [PubMed]
- Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. A program for macromolecular energy minimization and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- Brown, P. O. 1997. Integration. In Retroviruses. J. M. Coffin, S. H. Hughes, and H. E. Varmus, editors. Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY. 161–203.
- Bujacz, G., M. Jaskolski, J. Alexandratos, A. Wlodawer, G. Merkel, R. A. Katz, and A. M. Skalka. 1995. High-resolution structure of the catalytic domain of avian sarcoma virus integrase. J. Mol. Biol. 253:333–346. [DOI] [PubMed] [Google Scholar]
- Bujacz, G., M. Jaskolski, J. Alexandratos, A. Wlodawer, G. Merkel, R. A. Katz, and A. M. Skalka. 1996. The catalytic domain of avian sarcoma virus integrase: conformation of the active-site residues in the presence of divalent cations. Structure. 4:89–96. [DOI] [PubMed] [Google Scholar]
- Burke, C. J., G. Sanyal, M. W. Bruner, J. A. Ryan, R. L. LaFemina, H. L. Robbins, and A. S. Zeft. 1992. Structural implications of spectroscopic characterization of a putative zinc finger peptide from HIV-1 integrase. J. Biol. Chem. 267:9639–9644. [PubMed] [Google Scholar]
- Bushman, F. D., and R. Craigie. 1991. Activities of human immunodeficiency virus (HIV) integration protein in vitro: specific cleavage and integration of HIV DNA. Proc. Natl. Acad. Sci. USA. 88:1339–1343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai, M., R. Zheng, M. Caffrey, R. Craigie, G. M. Clore, and A. M. Gronenborn. 1997. Solution structure of the N-terminal zinc binding domain of HIV-1 integrase. Nat. Struct. Biol. 4:567–577. [DOI] [PubMed] [Google Scholar]
- Chen, J. C. H., J. Krucinski, L. J. W. Miercke, J. S. Finer-Moore, A. H. Tang, A. D. Leavitt, and R. M. Stroud. 2000a. Crystal structure of the HIV-1 integrase catalytic core and C-terminal domains: a model for viral DNA binding. Proc. Natl. Acad. Sci. USA. 97:8233–8238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, Z., Y. Yan, S. Munshi, Y. Li, J. Zugay-Murphy, B. Xu, M. Witmer, P. Felock, A. Wolfe, V. Sardana, E. A. Emini, D. J. Hazuda, and L. C. Kuo. 2000b. X-ray structure of simian immunodeficiency virus integrase containing the core and C-terminal domain (residues 50–293): an initial glance of the viral DNA binding platform. J. Mol. Biol. 296:521–533. [DOI] [PubMed] [Google Scholar]
- Daura, X., K. Gademann, B. Jaun, D. Seebach, W. F. van Gunsteren, and A. E. Mark. 1999. Peptide folding: when simulation meets experiment. Angew. Chem. Int. Ed. Engl. 38:236–240. [Google Scholar]
- Drelich, M., R. Wilhelm, and J. Mous. 1992. Identification of amino acid residues critical for endonuclease and integration activities of HIV-1 IN protein in vitro. Virology. 188:459–468. [DOI] [PubMed] [Google Scholar]
- Dyda, F., A. B. Hickman, T. M. Jenkins, A. Engelman, R. Craigie, and D. R. Davies. 1994. Crystal structure of the catalytic domain of HIV-1 integrase: similarity to the other polynucleotidyl transferases. Science. 266:1981–1986. [DOI] [PubMed] [Google Scholar]
- Eijkelenboom, A. P., R. A. Lutzke, R. Boelens, R. H. Plasterk, R. Kaptein, and K. Hard. 1995. The DNA-binding domain of HIV-1 integrase has an SH3-like fold. Nat. Struct. Biol. 2:807–810. [DOI] [PubMed] [Google Scholar]
- Eijkelenboom, A. P., F. M. van den Ent, A. Vos, J. F. Doreleijers, K. Hard, T. D. Tullius, R. H. Plasterk, R. Kaptein, and R. Boelens. 1997. The solution structure of the amino-terminal HHCC domain of HIV-2 integrase: a three-helix bundle stabilized by zinc. Curr. Biol. 7:739–746. [DOI] [PubMed] [Google Scholar]
- Ellison, V., and P. O. Brown. 1994. A stable complex between integrase and viral DNA ends mediates human immunodeficiency virus integration in vitro. Proc. Natl. Acad. Sci. USA. 91:7316–7320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engelman, A., F. D. Bushman, and R. Craigie. 1993. Identification of discrete functional domains of HIV-1 integrase and the organization within an active multimeric complex. EMBO J. 12:3269–3275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engelman, A., and R. Craigie. 1992. Identification of conserved amino acid residue critical for human immunodeficiency virus type 1 integrase function in vitro. J. Virol. 66:6361–6369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engelman, A., A. B. Hickman, and R. Craigie. 1994. The core and carboxy-terminal domains of the integrase protein of human immunodeficiency virus type 1 each contribute to nonspecific DNA binding. J. Virol. 68:5911–5917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esposito, D., and R. Craigie. 1998. Sequence specificity of viral end DNA binding by HIV-1 integrase reveals critical regions for protein-DNA interaction. EMBO J. 17:5832–5843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Essmann, U., L. Perera, M. L. Berkowitz, J. Darden, H. Lee, and L. G. Pedersen. 1995. A smooth particle mesh Ewald method. J. Chem. Phys. 103:8577–8593. [Google Scholar]
- Goldgur, Y., F. Dyda, A. B. Hickman, T. M. Jenkins, R. Craigie, and D. R. Davies. 1998. Three new structures of the core domain of HIV-1 integrase: an active site that binds magnesium. Proc. Natl. Acad. Sci. USA. 95:9150–9154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenwald, J., V. Le, S. L. Butler, F. D. Bushman, and S. Choe. 1999. The mobility of an HIV-1 integrase active site loop is correlated with catalytic activity. Biochemistry. 38:8892–8898. [DOI] [PubMed] [Google Scholar]
- Haugan, I. R., B. M. Nilsen, S. Worland, L. Olsen, and D. E. Helland. 1995. Characterization of the DNA-binding activity of HIV-1 integrase using a filter binding essay. Biochem. Biophys. Res. Commun. 217:802–810. [DOI] [PubMed] [Google Scholar]
- Hazuda, D. J., P. J. Felock, J. C. Hastings, B. Pramanik, and A. L. Wolfe. 1997. Differential divalent cation requirements uncouple the assembly and catalytic reactions of human immunodeficiency virus type 1 integrase. J. Virol. 71:7005–7011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hazuda, D. J., P. Felock, M. Witmer, A. Wolfe, K. Stillmock, J. A. Grobler, A. Espeseth, L. Gabryelski, W. Schleif, C. Blau, and M. D. Miller. 2000. Inhibitors of strand transfer that prevent integration and inhibit HIV-1 replication in cells. Science. 287:646–650. [DOI] [PubMed] [Google Scholar]
- Heuer, T. S., and P. O. Brown. 1997. Mapping features of HIV-1 integrase near selected sites on viral and target DNA molecules in an active enzyme-DNA complex by photo-cross-linking. Biochemistry. 36:10655–10665. [DOI] [PubMed] [Google Scholar]
- Johnson, M. S., M. A. McClure, D. F. Feng, J. Gray, and R. F. Doolittle. 1986. Computer analysis of retroviral pol genes: assignment of enzymatic functions to specific sequences and homologies with nonviral enzymes. Proc. Natl. Acad. Sci. USA. 83:7648–7652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen, W. L., J. Chandrasekar, J. Madura, R. Impey, and M. Klein. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
- Kabsch, W., and C. Sander. 1983. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers. 22:2576–2637. [DOI] [PubMed] [Google Scholar]
- Kale, L., R. Skeel, M. Bhandarkar, R. Brunner, A. Gursoy, N. Krawetz, J. Phillips, A. Shinozaki, K. Varadarajan, and K. Schulten. 1999. NAMD2: greater scalability for parallel molecular dynamics. J. Comp. Phys. 151:283–312. [Google Scholar]
- Kulkosky, J., K. S. Jones, R. A. Katz, J. P. Mack, and A. M. Skalka. 1992. Residues critical for retroviral integrative recombination in a region that is highly conserved among retroviral/retrotransposon integrases and bacterial insertion sequence transposases. Mol. Cell. Biol. 12:2331–2338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laboulais, C., M. Ouali, M. Le Bret, and J. Gabarro-Arpa. 2002. Hamming distance geometry of a protein conformational space: application to the clustering of a 4-ns molecular dynamics trajectory of the HIV-1 integrase catalytic core. Proteins. 47:169–179. [DOI] [PubMed] [Google Scholar]
- Lee, S. P., and M. K. Han. 1996. Zinc stimulates Mg2+-dependent 3′-processing activity of human immunodeficiency virus type 1 integrase in vitro. Biochemistry. 35:3837–3844. [DOI] [PubMed] [Google Scholar]
- Lee, D. J., and W. E. Robinson, Jr. 2004. Human immunodeficiency virus type 1 (HIV-1) integrase: resistance to diketo acid integrase inhibitors impairs HIV-1 replication and integration and confers cross-resistance to L-chicoric acid. J. Virol. 78:5835–5874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lins, R. D., A. Adesokan, T. A. Soares, and J. M. Briggs. 2000. Investigations on human immunodeficiency virus type 1 integrase/DNA binding interactions via molecular dynamics and electrostatics calculations. Pharmacol. Ther. 85:123–131. [DOI] [PubMed] [Google Scholar]
- Lins, R. D., J. M. Briggs, T. P. Straatsma, H. A. Carlson, J. Greenwald, S. Choe, and J. A. McCammon. 1999. Molecular dynamics studies on the HIV-1 integrase catalytic core domain. Biophys. J. 76:2999–3011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lodi, P. J., J. A. Ernst, J. Kuszewski, A. B. Hickman, A. Engelman, R. Craigie, G. M. Clore, and A. M. Gronenborn. 1995. Solution structure of the DNA binding domain of HIV-1 integrase. Biochemistry. 34:9826–9833. [DOI] [PubMed] [Google Scholar]
- MacKerell, A. D., D. Bashford, M. Bellot, R. L. Dunbrack, J. D. Evanseck, M. J. Field, et al. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. Ser. B 102:3586–3616. [DOI] [PubMed] [Google Scholar]
- Neria, E., S. Fischer, and M. Karplus. 1996. Simulation of activation free energies in molecular systems. J. Chem. Phys. 105:1902–1921. [Google Scholar]
- Ni, H., C. A. Sotriffer, and J. A. McCammon. 2001. Ordered water ligand mobility in the HIV-1 integrase-5CITEP complex: a molecular dynamics study. J. Med. Chem. 44:3043–3047. [DOI] [PubMed] [Google Scholar]
- Polard, P., and M. Chandler. 1995. Bacterial transposases and retroviral integrases. Mol. Microbiol. 15:13–23. [DOI] [PubMed] [Google Scholar]
- Rowland, S. J., and K. G. Dyke. 1990. Tn552, a novel transposable element from Staphylococcus aureus. Mol. Microbiol. 4:961–975. [DOI] [PubMed] [Google Scholar]
- Ryckaert, J. P., G. Ciccotti, and H. J. C. Berendsen. 1977. Numerical integration of the Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comp. Phys. 23:327–341. [Google Scholar]
- Smith, L. J., X. Daura, and W. F. van Gunsteren. 2002. Assessing equilibration and convergence in biomolecular simulations. Proteins. 48:487–496. [DOI] [PubMed] [Google Scholar]
- van Alten, D. M. F., A. Amadei, A. B. M. Linssen, V. G. H. Eijsink, G. Vriend, and H. J. C. Berendsen. 1995. The essential dynamics of thermolysin: confirmation of the hinge-bending motion and comparison of simulations in vacuum and water. Proteins. 22:45–54. [DOI] [PubMed] [Google Scholar]
- van der Spoel, D., R. van Drunen, and H. J. C. Berendsen. 1994. Groningen Machine for Chemical Simulations. Department of Biophysical Chemistry, BIOSON Research Institute, University of Groningen, Nijenborgh, The Netherlands.
- Vink, C., R. A. Lutzke, and R. H. Plasterk. 1994. Formation of a stable complex between the human immunodeficiency virus integrase protein and viral DNA. Nucleic Acids Res. 22:4103–4110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vink, C., A. A. M. Oude Groeneger, and R. H. A. Plasterk. 1993. Identification of the catalytic and DNA-binding region of the human immunodeficiency virus type I integrase protein. Nucleic Acids Res. 21:1419–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, J., H. Ling, W. Yang, and R. Craigie. 2001. Structure of a two-domain fragment of HIV-1 integrase: implication for domain organization in the intact protein. EMBO J. 20:7333–7343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber, W., H. Demirdjian, R. D. Lins, J. M. Briggs, R. Ferreira, and J. A. McCammon. 1998. Brownian and essential dynamics studies of the HIV-1 integrase catalytic domain. J. Biomol. Struct. Dyn. 16:733–745. [DOI] [PubMed] [Google Scholar]
- Woerner, A. M., and C. J. Marcus-Sekura. 1993. Characterization of a DNA binding domain in the C-terminus of HIV-1 integrase by deletion mutagenesis. Nucleic Acids Res. 21:3507–3511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfe, A. L., P. J. Felock, J. C. Hastings, C. U. Blau, and D. J. Hazuda. 1996. The role of manganese in promoting multimerization and assembly of human immunodeficiency virus type 1 integrase as a catalytically active complex on immobilized long terminal repeat substrates. J. Virol. 70:1424–1432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang, Z. N., T. C. Mueser, F. D. Bushman, and C. C. Hyde. 2000. Crystal structure of an active two-domain derivative of Rous sarcoma virus integrase. J. Mol. Biol. 296:535–548. [DOI] [PubMed] [Google Scholar]
- Zheng, R., T. M. Jenkins, and R. Craigie. 1996. Zinc folds the N-terminal domain of HIV-1 integrase, promotes multimerization, and enhances catalytic activity. Proc. Natl. Acad. Sci. USA. 93:13659–13664. [DOI] [PMC free article] [PubMed] [Google Scholar]