Untangling the wires: A strategy to trace functional interactions in signaling and gene networks

Abstract

Emerging technologies have enabled the acquisition of large genomics and proteomics data sets. However, current methodologies for analysis do not permit interpretation of the data in ways that unravel cellular networking. We propose a quantitative method for determining functional interactions in cellular signaling and gene networks. It can be used to explore cell systems at a mechanistic level or applied within a “modular” framework, which dramatically decreases the number of variables to be assayed. This method is based on a mathematical derivation that demonstrates how the topology and strength of network connections can be retrieved from experimentally measured network responses to successive perturbations of all modules. Importantly, our analysis can reveal functional interactions even when the components of the system are not all known. Under these circumstances, some connections retrieved by the analysis will not be direct but correspond to the interaction routes through unidentified elements. The method is tested and illustrated by using computer-generated responses of a modeled mitogen-activated protein kinase cascade and gene network.

Advances in high-throughput genomics and proteomics analysis facilitate the monitoring of the expression levels of large gene sets and the activity states of signaling proteins in living cells. The explosive growth in the amount of data calls for the development of novel quantitative approaches for analysis. Thus far, our understanding of cellular signaling and gene networks has been almost exclusively qualitative. Recently, both qualitative and mechanistic mathematical modeling have been applied to better understand network molecular organization and kinetics in quantitative terms (1–8). The mechanistic “bottom-up” approach has the advantage of being readily testable against experiments as a computer replica of cellular networks. However, a major disadvantage of a mechanistic modeling is the large number of molecular processes to be considered, complicated by the fact that values for multiple kinetic parameters are unknown. Moreover, a bottom-up approach inevitably misses the interactions and regulatory feedbacks still awaiting discovery.

As an approach to studying cellular networks, we developed a form of “top-down” sensitivity analysis to quantify the input–output relations and molecular interactions in regulatory networks (9). The control of the input signal over the output target was quantified as the ratio of the input-to-output changes at steady state (called the response coefficient in the limit of infinitesimal changes). The signal may be a hormone, growth factor, neurotransmitter, or experimental intervention (e.g., an inhibitor), and the target process may be the phosphorylation state or activity of a protein, mRNA level, or transcription rate. If a full set of molecular interactions is known, the (global) network response to a signal or experimental perturbation can be predicted and expressed in terms of the individual (local) responses by using a “map” of network connections (9). However, when detailed information about molecular mechanisms is lacking, a top-down analysis has advantages, because it can be applied experimentally to any cellular network regardless of its degree of complexity (10, 11).

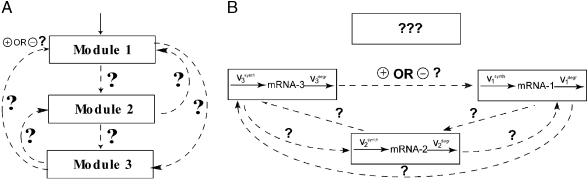
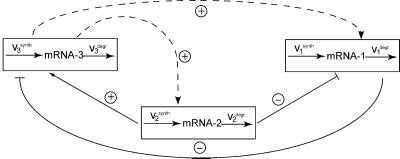
The daunting challenge of understanding the coordinated behavior of numerous molecular interactions can be facilitated by analyzing them within a “modular” framework (12, 13). A complex cellular network can be divided conceptually into reaction groups referred to as functional units or modules. Each module consists of several signaling or gene interactions and performs one or more identifiable tasks. For instance, each of the three tiers of the mitogen-activated protein kinase (MAPK) cascade can be considered as a functional module that involves unphosphorylated, monophosphorylated, and bisphosphorylated forms of a protein kinase and the reactions converting these forms. Modules need not be rigid, and entire MAPK cascades can serve as functional modules in a signaling network that involves growth factor and stress-activated pathways. For gene networks, modules can involve mRNAs of a particular gene or gene cluster with regulatory interaction loops running through metabolic and signaling pathways (14). Modules can be interconnected in multiple ways, many of which may be unknown, even when the network components are identified in genetic and biochemical studies. Fig. 1 illustrates such potential interactions for a three-module cascade and dynamic connections as well as possible unknown components for a gene-expression network.

Figure 1.

A three-module cascade (A) and a gene network (B). The question marks stand for unknown connections and additional network components (e.g., uncharacterized genes), which can influence and in turn be affected by the known components.

One of the fundamental problems in cell biology is to infer and quantify interconnections in complex regulatory networks. The present paper proposes a powerful method for attacking such questions, assuming that knowledge of at least some network components is on hand. Specifically, we develop a methodology capable of unraveling and quantifying unknown molecular or modular connections in signaling and gene networks. We demonstrate how, by making systematic perturbations (using inhibitors, activators, changes in external signals, etc.) and measuring global responses only, one can discover a network “interaction map” that can be expressed in terms of module-to-module connection strengths. Importantly, we select experimental interventions that directly perturb single modules, and we apply as many perturbations as there are modules. We illustrate this approach by applying perturbations to model networks and comparing quantitative reconstructions to known interaction maps.

Methods

Fundamentals of Top-Down Regulatory Analysis of Modular Cellular Networks.

Quantitation of a network interaction map.

We conceptually divide a signaling or gene network into modules (m). The degree of complexity of each module is not restricted, and generally a module involves many cellular components (intermediates) connected by chemical reactions (intramodular interactions). We assume that only a single intermediate, referred to as “communicating,” serves as the module output (this simplifying assumption is relaxed in Appendix 1, which is published as supporting information on the PNAS web site, www.pnas.org). A communicating molecule may be the active form of a kinase, a second messenger, mRNA, or transcription factor influencing other modules. Thus, communicating intermediates form molecular connections between modules, referred to as intermodular interactions.

A top-down regulatory analysis “black-boxes” the molecular organization of network modules, considering only communicating intermediates (the module outputs). We designate by x_i, i = 1, … , m, the activities (concentrations) of communicating intermediates. Following our previous work (9), we quantify intermodular interactions in terms of the fractional changes (Δx_i/x_i) in the activity of communicating intermediate (x_i) of a particular module (i) brought about by a change in the (output) activity (x_j) of another module (j). Output activities of all other modules (x_k, k ≠ i,j) are assumed to remain fixed, whereas the affected module (i) is allowed to relax to its steady state. A mathematical definition requires the changes (Δx/x) to be infinitesimally small, resulting in log-to-log derivatives,

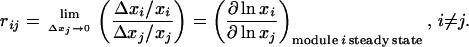1

The coefficient r_ij is referred to as the local response (coefficient), which quantifies the sensitivity of module i to module j. The term “local” indicates that the response results from immediate interactions between two modules when all other network interactions are held constant. A response coefficient r_ij less than 1 means that (small) fractional changes in module j output are attenuated in module i, whereas a response greater than 1 means that these fractional changes are amplified by the factor r_ij. A response coefficient of 0 means that module j has no direct effect on module i, whereas a negative response coefficient means inhibition.

Because each module is assumed to have a single communicating intermediate, all interactions between network modules are quantified by m⋅(m − 1) intermodular response coefficients, r_ij. These “connection” coefficients indicate how the network is “wired” and compose the m × m matrix, r, hereafter referred to as the network interaction map. The ith row of the matrix r quantifies how module i is affected by each network module through immediate interaction, whereas the jth column of r measures how module j directly influences each network module. We assign values of −1 to the diagonal elements (r_ii) of the matrix r, r_ii = −1, i = 1, … , m.

Local and global network responses to perturbations.

Conceptually considering module i “in isolation” from the network, we determine the local response coefficient (r_ipi) of x_i to a perturbation of parameter p_i, intrinsic to module i as follows: r_ipi = (∂lnx_i/∂p_i)_{module i steady state}. When module i is isolated from the network, changes in parameters p_j, influencing other modules (j), have no effect on module i, and therefore the local response of x_i to a perturbation in p_j equals zero. Local responses to perturbations, affecting single modules only, form the diagonal m × m matrix, dgr_p, with diagonal elements r_ipi and all off-diagonal elements equal to zero.

If following a parameter (p_i) perturbation intrinsic to module i an entire network is allowed to relax, this perturbation not only causes changes in those modules directly affected by module i but also propagates further into the network through interactions between other modules. The resulting time-dependent or stationary responses are called “global” responses of the network. We designate by R_jpi the global response coefficient of module j to a perturbation in p_i and by R_p the m × m matrix composed of these coefficients:

2

The difference between the local dgr_p and global R_p responses is that only module i is allowed to reach the steady state to determine r_ipj, whereas an entire network is permitted to relax to its steady state to measure R_ipj.

Models of Signaling and Gene Networks Used to Test and Illustrate the Proposed Approach.

Computer simulation of MAPK cascade responses to specific perturbations.

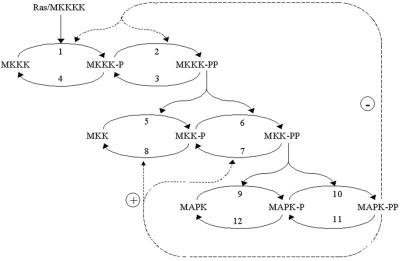
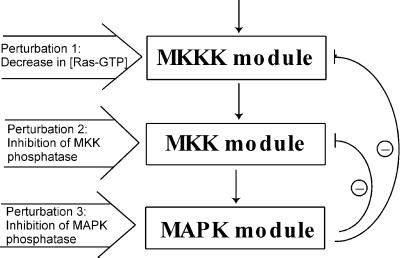
MAPK cascades consist of several levels, where the activated kinase at each level phosphorylates the kinase at the next level down the cascade. The three-tiered MAPK cascade comprises MAPK (the terminal level), MAPK kinase (MKK) and MKK kinase (MKKK) (Fig. 2). MAPKs are activated by MKKs, which phosphorylate them at conserved threonine and tyrosine residues. At one level upstream, MKKs themselves are phosphorylated at serine and threonine residues by MKKKs. The kinases of the first level, MKKKs, are activated by incompletely understood mechanisms, involving interactions with the membrane-bound GTPase Ras (in the case of the MKKK Raf-1) and phosphorylation of Raf-1 at a tyrosine residue by an unknown protein kinase (15). Thus, Ras-GTP and unknown membrane kinase(s) function as the input signal that activates MKKK (Raf-1). At each cascade level, protein phosphatases inactivate the corresponding kinases (Fig. 2). Our computational model of the MAPK cascade resembles models developed previously (16, 17) but includes two negative feedbacks. The first is formed by bisphosphorylated MAPK (MAPK-PP)-mediated inhibition of the MKKK-activating reaction, and the second results from MAPK-PP-induced activation of the MKK phosphatases (18, 19). The kinetic equations, moiety conservation relations, and rate expressions are presented in Table 1, which is published as supporting information on the PNAS web site. We used the model to generate global responses of the cascade communicating intermediates to perturbations, which imitated experimental interventions.

Figure 2.

Kinetic scheme of the MAPK cascade. Feedback effects of MAPK on the rate of MKKK and MKK phosphorylation are shown schematically by dashed lines. MKKKK, MKKK kinase; P and PP, monophosphorylated and bisphosphorylated forms.

Computer simulation of responses of a gene network to specific perturbations.

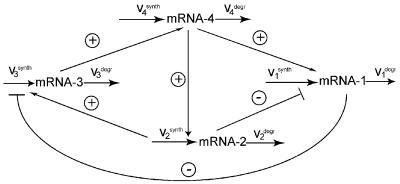
A kinetic scheme of a four-gene network is depicted in Fig. 3. The level of each mRNA species is determined by the rate of transcription and degradation, d[mRNA_i]/dt = v − v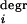. Gene interactions result in nonlinear dependences of transcription rates (v) on other mRNA_j concentrations, which act as communicating intermediates (x_i). The rates are described by the Hill-type equations (1, 3) and presented in Table 2, which is published as supporting information on the PNAS web site. Network responses to perturbations in transcription rates were used to infer functional interactions between genes.

Figure 3.

Kinetic scheme of a four-gene network. Arrows correspond to activation interactions, whereas lines with blunt ends represent inhibitions.

Results

Relation Between the Local and Global Network Responses.

Global responses to perturbations can be measured in experiments with intact cellular systems. However, local responses governed by the network interaction map cannot be captured by using intact cells. To measure the kinetics of local interactions between two modules (proteins) directly, they should be isolated from the network. Sometimes the interaction of interest can be reconstituted “in vitro,” but often only an entire system is accessible experimentally. We are left with the question of how to determine quantitatively the network interaction map if only global responses can be assessed. We demonstrate that by making parameter perturbations to all modules and measuring the global network responses, we can retrieve the unknown interaction map (see Appendix 2, which is published as supporting information on the PNAS web site, for the abstract mathematical derivation).

An experimental intervention to perturb a parameter (p_i) intrinsic to module i can employ a specific inhibitor or activator of a reaction within module i, an antisense mRNA affecting the expression level of a protein, or a plasmid changing the rate of transcription. A parameter change, Δp_i, first causes a local perturbation in x_i, which subsequently propagates through intermodular interactions described by the local response coefficients (r_ij). After the network has relaxed to a new steady state, the resulting global changes in communicating intermediates (x_k) brought about by a perturbation (Δp_i) are related through

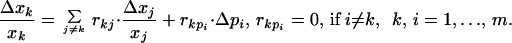3

Dividing both sides of Eq. 3 by Δp_i and using matrix notations, we arrive at

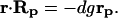4

In intact cells, only the global response matrix, R_p, can be monitored experimentally, whereas neither the network interaction map, r, nor local responses to parameter perturbations, dgr_p, can be measured. We demonstrate how the elements of both matrices, r and dgr_p, can be calculated by using the matrix R_p. After multiplying both sides of Eq. 4 by the inverse matrix R_p⁻¹, we obtain, r = −dgr_p⋅R_p⁻¹. Because all the diagonal elements of the matrix r are equal to −1, the elements of the diagonal matrix, dgr_p, are expressed readily in terms of the diagonal elements of the matrix, R_p⁻¹. Designating by dg(R_p⁻¹) the diagonal matrix with diagonal elements (R_p⁻¹)_ii and all off-diagonal elements equal to zero, we have I = dgr_p⋅dg(R_p⁻¹), where I is the identity matrix. By expressing dgr_p from this equation, we obtain

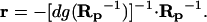5

This final expression gives us the answer: if the (global) responses of a cellular network to perturbations to all modules have been measured, the network interaction map (r) can be retrieved by the inversion of the response matrix (R_p).

Importantly, our method does not require the parameter changes (Δp_i) to be measured or estimated. Instead of response coefficients, one can simply consider the global (Δ_ilnx_j) fractional changes in communicating intermediates (x_j) caused by a parameter change Δp_i. Accordingly, we redefine the global response matrix, R_p, with coefficients R_jpi to be determined by the global fractional changes brought about by a perturbation Δ p_i,

6

Here the derivatives, which were considered in Eq. 2, are substituted by the finite changes (divided by the initial or the mean value). However, the crucial distinction is that according to Eq. 2, the parameter changes (Δp_i) should be known, whereas Eq. 6 merely considers the differences in intermediates x_j after and before perturbation to determine the global response matrix, R_p. Using Eq. 6, one obtains exactly the same relationship (Eq. 5) that expresses the network interaction map in terms of the measured changes in the levels of communicating intermediates without requiring any knowledge about the values of parameter changes. This technique enhances the applicability of the proposed analysis in cases where it is difficult or impossible to quantify the values of parameter perturbations.

Practical Application of the Proposed Methodology.

We now outline three steps of experimental applications for the proposed method.   i.  Conceptually divide the network under consideration into interacting modules and identify communicating intermediates. ii.  Use an inhibitor or other perturbation that affects a single network module only, e.g., module 1, and measure the difference in the steady-state levels of communicating intermediates before [x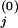] and after [x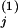] the perturbation. Then, calculate the first column of the matrix R_p by using, e.g., the central fractional differences defined as the finite difference in the activities divided by the mean value,

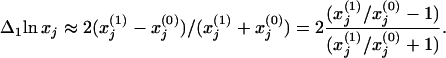7

Repeat for remaining network modules (i = 2, … , m) by using a perturbation directly affecting that module only, and calculate the remaining columns of the matrix R_p (Δ_ilnx₁, … , Δ_ilnx_m)^T. The presentation in terms of the relative values given in Eq. 7 may help where quantitation of the absolute activities is difficult, e.g., when Western blotting is used to quantify the relative amount of a protein or determining the ratio of the fluorescence intensities from gene arrays (14). iii.  Apply Eq. 5 to reveal and quantify the network interaction map in terms of the matrix r of intermodular (local) response coefficients.

Unraveling the MAPK Cascade Interaction Map: An Illustration.

MAPK cascades are widely involved in eukaryotic signal transduction, and these pathways are conserved from yeast to mammals (20). Mammalian cells express at least four different MAPK families including the ERK cascade (which is our primary example) and the c-Jun N-terminal kinase (JNK) and p38 MAPK cascades. In many cell types, MAPK cascades are regulated by multiple feedbacks. For instance, in mammalian cells inhibitory phosphorylation of the GDP/GTP exchange factor, SOS, by ERK provides a mechanism for switching off Ras and, thereby, Raf-1 signaling, creating a negative feedback as shown schematically in Fig. 2 (18). In Xenopus oocytes, two MAPK pathways, the p42 MAPK and JNK cascades, appear to be embedded in positive-feedback loops (21, 22). Some regulatory feedbacks are well documented, but the complete interaction map of the MAPK pathways is unknown. For example, it is not understood yet which interactions form positive feedbacks in the JNK cascade (22). Also, both negative- and positive-feedback interactions may differ in various cell types.

Our method may provide a universal tool to analyze the interaction map of MAPK pathways in various cells. To test and illustrate the method, we retrieve the interaction map from computer-generated responses of a kinetic model of the MAPK cascade to perturbations, which simulate experimental interventions. The first step is to identify modules and communicating intermediates based on biological information. We define three MAPK cascade modules that involve different phosphorylation forms of MKKK, MKK, and MAPK, respectively, and the reactions converting these forms (e.g., module 2 includes MKK, MKK-P, and MKK-PP and reactions 5–8, Fig. 2). The bisphosphorylated forms (such as MKK-PP) play the role of communicating intermediates (x_i) influencing other modules. Importantly, the concentration x_i does not determine the concentration of the remaining forms within a module, because two of the three forms are independent variables within a mechanistic description (17). Our method has the advantage of monitoring only communicating intermediates to untangle and quantify the web of intermodular interactions.

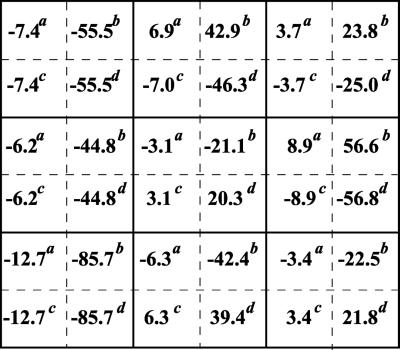
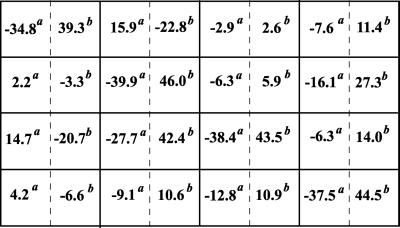
In the second step, we apply three different perturbations, each affecting a single module. As a perturbation to the first module, we inhibited the input signal by decreasing the Ras-GTP concentration. As relevant interventions to module 2, either the maximal activities of the phosphatase, which dephosphorylates MKK-PP and MKK-P, or the kinase that acts on MKK were inhibited. The different perturbations were applied to illustrate that network interactions to be detected with the method would not depend on what particular molecular processes within a module are affected. Module 3 was perturbed by inhibiting either the maximal activity of the MAPK phosphatase or the kinase. After each perturbation, the MAPK cascade was allowed to reach a new steady state, and the global responses of communicating intermediates were calculated according to Eq. 7. Fig. 4 presents the matrices R_p obtained for inhibition values of 10 and 50%. It is convenient to multiply the elements of R_p by 100, which would correspond to changes in x_i expressed as a percentage of the mean. As follows from Eq. 5, this multiplication does not change the resulting interaction map, r. The 10% perturbation brought about (global) fractional changes of communicating intermediates of less than 13%, whereas a 2-fold inhibition (50%) resulted in up to 86% changes. Perturbations of this magnitude are not justified mathematically, but the simulation results show that our method can handle them well.

Figure 4.

Global fractional responses obtained by simulating experimental perturbations to the MAPK cascade. Four global response matrices (R_p⋅100, designated by superscripts a–d) were generated by applying the following 12 parameter perturbations. a or b, 10 or 50% decrease, respectively, in: [Ras-GTP], perturbation to module 1; the catalytic activities of steps 5 and 6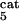 (k and k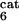; see Table 1, which is published as supporting information on the PNAS web site), module 2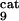; k and k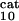, module 3. c or d, 10 or 50% decrease, respectively, in: [Ras-GTP], module 1; the maximal activities of steps 7 and 8 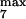(V and V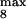; see Table 1), module 2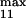; V and V, module 3.

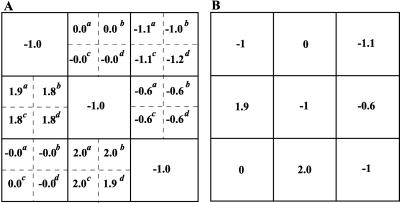
Four different matrices (R_p), displayed in Fig. 4, were substituted into Eq. 5 to retrieve the network interaction map (r). Notably, both different simulated inhibitors and perturbation values, which brought about widely diverse global changes in communicating intermediates (Fig. 4), resulted in four nearly identical “experimental” interaction maps (rounded to the nearest tenth, Fig. 5A). Module 1 was found to affect directly module 2, which in turn affects module 3. Both local interactions appear “ultrasensitive” with response coefficients r₂₁ and r₃₂ ranging from 1.8 to 1.9 and 1.9 to 2.0, respectively, for different perturbations used. The local interactions, r₁₂ and r₃₁, which describe potential effects of modules 2 and 1 on modules 1 and 3, respectively, appear to be zero. Our method unraveled and quantified negative feedbacks from module 3 to modules 1 and 2 (Fig. 6). The response coefficient, r₁₃, ranged from −1.0 to −1.2, and r₂₃ was equal to −0.6 for all perturbations used. It is instructive to compare the network interaction map retrieved from “measured” global responses with the correct map, which was calculated according to Eq. 1 for the model example, where molecular interactions were known. As shown in Fig. 5 A and B, both experimental and theoretical interaction maps appear nearly identical.

Figure 5.

Retrieved “experimental” interaction maps (A) and known “theoretical” interaction map (B). Four experimental local interaction matrices (r) were retrieved from the data shown in Fig. 4. The response coefficients marked by superscripts a–d correspond to perturbations indicated in the legend to Fig. 4.

Figure 6.

Revealed interactions between MAPK cascade modules. Responses of every module to perturbations to each single module were measured, and intermodular connections were discovered and quantified by using Eqs. 8 and 10.

Unraveling the Wiring of a Gene Network.

Our approach can be applied to untangle gene network interactions (wiring) by carrying out specially designed gene microarray experiments. Gene networks are high-level conceptual representations of interactions between genes (14). These interactions proceed through multiple protein products (e.g., transcription factors) and metabolic intermediates, which are not considered explicitly in the analysis, such that the mRNAs themselves act as communicating intermediates. Fig. 3 illustrates this for a four-gene network. Assuming that no preliminary knowledge is available about gene interactions, we performed two series of four different perturbations to the network as required by the method. The transcription rate of each gene was perturbed independently by decreasing the corresponding maximal activity by 30% or by increasing it by 50%. After each perturbation, the gene network relaxed to its new steady state, and mRNA responses were calculated according to Eq. 7. The global response matrices (R_p) obtained for perturbation values equal to either 30 or 50% are shown in Fig. 7.

Figure 7.

Global fractional responses obtained by simulating experimental perturbations to the gene network shown in Fig. 3. Two global response matrices (R_p⋅100, designated by superscripts a and b) were generated by applying the following eight parameter perturbations. a or b, 30% decrease or 50% increase, respectively, in: the maximal activity of the transcription rate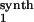 v (V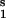; see Table 2, which is published as supporting information on the PNAS web site), perturbation to module 1; V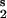, module 2; V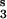, module 3; and V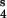, module 4.

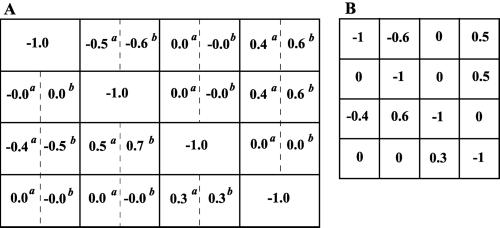
The network interaction map was determined by taking the inverse of R_p and substituting it into Eq. 5. Both simulated perturbations, i.e., inhibition or activation, resulted in nearly identical experimental interaction matrices (rounded to the nearest tenth; Fig. 8A). All the gene interactions shown in Fig. 2 were retrieved successfully (Fig. 8). Importantly, for both examples considered here, inevitable mistakes related to the substitution of the infinitesimal changes by finite ones did not lead to erroneously predicted interactions, e.g., absent in the network but found by the proposed method. Fig. 8 demonstrates that experimentally obtained network wiring and its quantitation nearly coincides with the known (correct) interaction map for this model system. We conclude that the proposed method can be a powerful tool for unraveling interactions in gene networks.

Figure 8.

Retrieved experimental interaction maps (A) and known theoretical interaction map (B). Two experimental local interaction matrices (r) were retrieved from the data shown in Fig. 7. The response coefficients marked by superscript a and b correspond to perturbations indicated in the legend to Fig. 7.

Discussion

Recently, high-throughput technologies have enabled the acquisition of data on the expression of thousands of genes and the functional state of hundreds of proteins. However, there are no methods capable of providing quantitative interpretations of genomics and proteomics data sets in a manner that unravels the wiring of cellular machinery. This paper proposed a powerful quantitative method to unravel interactions in signaling and gene networks. A dynamic connection between two network components is quantified by the extent to which a small change in one component affects the level or activity of the other, provided all remaining interactions are kept unchanged. The resulting quantifier is known as a response coefficient, which is a convenient and unambiguous measure of the sensitivity of a particular component to a local, direct effect by another component. A network component may be a protein, a gene, or a module involving a number of interacting proteins and genes when considered within a modular framework (12, 13). The present paper demonstrates that monitoring of signaling and gene-expression responses to systematic perturbations is sufficient to infer and quantify signal transduction maps and gene connections.

A series of studies was concerned with the determination of complex reaction mechanisms by experimental evaluation of the Jacobian matrix elements from time-series analysis (23, 24). Methods for the deduction of chemical reaction pathways from measurements of species concentrations were pioneered by Ross and coworkers (25, 26). These studies used ranked time-lagged correlation functions among pairs of chemical species coupled with a multidimensional scaling analysis and heuristic algorithms to deduce a diagram describing the interactions between chemical species. The method that we propose here exploits the modular organization of signaling and gene networks and the absence of mass flow between modules (assuming proteins are not significantly sequestered in intermodular interactions). We demonstrated that steady-state measurements of only communicating intermediates (the number of which is much smaller than the number of all independent protein forms) are sufficient to quantify interactions within a modular framework.

Our technique involves a matrix inversion (Eq. 5). This inversion may give rise to numerical errors if the experimentally measured matrix R_p is ill-conditioned. Various preconditioning methods might be used to rescale data, but a singular-value decomposition of R_p can avoid these potential errors by dropping the least meaningful modes. In general, a matrix of lower rank will result, which will constrain the estimates of the local response matrix r (which is the normalized Jacobian matrix, see Appendix 2, which is published as supporting information on the PNAS web site) to a lower dimensional subspace. A similar approach is based on the observation that a vector that quantifies dynamic connections leading to a particular module (i.e., a row of the matrix r) is orthogonal to the linear subspace (H) spanned by vectors composed of measured network responses to perturbations influencing other modules (columns of R_p) (27). If the rank of H decreases because of ill conditioning, additional experiments should be performed by applying different perturbations. Any perturbation directly affecting a single module is appropriate. For instance, in signaling networks one can inhibit or mutate enzymatic activities or change the abundance of a protein operating within a single module. For gene networks, suitable experimental interventions involve the inhibition of a transcription rate or transfection with a plasmid expressing a gene that results in an increase in the mRNA synthesis rate. Applying such perturbations to a model gene network, all gene interactions were unraveled and quantified (Fig. 3). By applying perturbations to the MAPK pathway conceptually partitioned into modules, we detected all existing interactions between modules including the inhibition of module 2 by module 3 (Fig. 6). Mechanistically, this negative feedback occurred as the activation of an enzyme within module 2 (MKK phosphatase) by a communicating intermediate of module 3 (MAPK-PP, Fig. 2). Clearly, the molecular mechanisms cannot be predicted by the method. However, any manifestation of interaction detected by the method can be investigated further mechanistically to advance understanding in molecular terms.

Other biological applications of the method include systems in which some components are unknown or uncharacterized. To illustrate these applications, we revisit the example of a four-gene network, assuming that only three genes (1, 2, and 3) are known (cf. Figs. 1B and 3). If we were unaware of the existence of an additional gene (number 4) or simply assumed that this gene did not interact with the system under study, we would bring about perturbations to only three genes and measure the global responses of only those genes. As a result, we would obtain the global response matrix (R_p) corresponding to the first three rows and columns of the matrices presented in Fig. 7. Taking the inverse of this reduced matrix R_p and substituting into Eq. 5, we obtain the network interaction map shown in Figs. 9 and 10. We can see that the connections between three known genes, which were identified previously by using perturbations to all four genes (Figs. 3 and 8), also were retrieved by using incomplete information. Importantly, new connections were found for the system with only three identified genes. In the four-gene network, gene 3 directly affected neither gene 1 nor gene 2. However, using incomplete information, we found that gene 3 affects both gene 1 and gene 2. This finding reflects interaction paths from gene 3 through gene 4. The results of our previous work (9) imply that the corresponding responses r₁₃ and r₂₃ determined for this three-gene network are equal to the (mathematical) products r₁₄⋅r₄₃ and r₂₄⋅r₄₃, respectively, determined for a four-gene network (cf. Figs. 8 and 10). If it were known that neither the protein product of gene 3 nor proteins interacting with this product could affect gene 1 or 2 directly, this would imply the existence of unidentified gene(s) that perform those interactions. Therefore, the proposed method is able to provide an unbiased analysis to indicate the existence of unknown or uncharacterized components in the system.

Figure 9.

Retrieved wiring for a three-gene network. Because gene 4 was an unknown component, (quasi)direct effects of gene 3 on genes 1 and 2 were revealed.

Figure 10.

Interaction maps retrieved from incomplete data. Two experimental local interaction matrices (r) were retrieved from the global response matrix corresponding to the first three rows and columns of the matrices shown in Fig. 7. The response coefficients marked by superscripts a or b correspond to perturbations indicated in the legend to Fig. 7.

Abbreviations

MAPK

mitogen-activated protein kinase

MKK

MAPK kinase

MKKK

MKK kinase

P

monophosphorylated

PP

bisphosphorylated