Spatiotemporal Image Correlation Spectroscopy (STICS) Theory, Verification, and Application to Protein Velocity Mapping in Living CHO Cells

Abstract

We introduce a new extension of image correlation spectroscopy (ICS) and image cross-correlation spectroscopy (ICCS) that relies on complete analysis of both the temporal and spatial correlation lags for intensity fluctuations from a laser-scanning microscopy image series. This new approach allows measurement of both diffusion coefficients and velocity vectors (magnitude and direction) for fluorescently labeled membrane proteins in living cells through monitoring of the time evolution of the full space-time correlation function. By using filtering in Fourier space to remove frequencies associated with immobile components, we are able to measure the protein transport even in the presence of a large fraction (>90%) of immobile species. We present the background theory, computer simulations, and analysis of measurements on fluorescent microspheres to demonstrate proof of principle, capabilities, and limitations of the method. We demonstrate mapping of flow vectors for mixed samples containing fluorescent microspheres with different emission wavelengths using space time image cross-correlation. We also present results from two-photon laser-scanning microscopy studies of α-actinin/enhanced green fluorescent protein fusion constructs at the basal membrane of living CHO cells. Using space-time image correlation spectroscopy (STICS), we are able to measure protein fluxes with magnitudes of μm/min from retracting lamellar regions and protrusions for adherent cells. We also demonstrate the measurement of correlated directed flows (magnitudes of μm/min) and diffusion of interacting α5 integrin/enhanced cyan fluorescent protein and α-actinin/enhanced yellow fluorescent protein within living CHO cells. The STICS method permits us to generate complete transport maps of proteins within subregions of the basal membrane even if the protein concentration is too high to perform single particle tracking measurements.

INTRODUCTION

Fluorescence fluctuation techniques have been among the most successful methods for quantitative measurements inside living cells. They provide key insights into the dynamics and interactions of intracellular and transmembrane proteins. The original fluorescence correlation spectroscopy (FCS) method is based on temporal autocorrelation analysis of fluorescence intensity fluctuations collected in time from a tiny focal volume defined by the microscope focus of the excitation laser beam within a sample (Elson and Magde, 1974; Magde et al., 1972). The magnitude and time decay of the fluorescence intensity fluctuations contain information on the concentration and dynamics of the fluorescent molecules in the observation volume. Since the introduction of FCS, there have been many improvements in both the technology and computer processing power that have made possible the analysis of increasingly complex systems. For example, the introduction of confocal optics allowed for single molecule detection (Rigler et al., 1993), two-photon fluorescence cross-correlation allows measurement of the dynamics of interacting molecules (Heinze et al., 2000), fluorescence correlations between two adjacent focal volumes have been used to determine velocity magnitude and direction in microstructured channels (Dittrich and Schwille, 2002), and scanning FCS has been utilized to investigate protein-membrane interactions (Ruan et al., 2004).

An imaging analog of FCS, image correlation spectroscopy (ICS), was introduced to examine the distribution and aggregation of cell membrane components (Petersen et al., 1993). ICS involves spatial correlation analysis of fluorescence fluctuations within an image sampled using a laser-scanning microscope (LSM). The image pixels are effectively spatially parallel intensity measurements from many confocal excitation volumes across the surface imaged. The image cross-correlation spectroscopy (ICCS) technique has also been introduced to measure transport properties (Wiseman et al., 2004, 2000) and co-localization of two different labeled molecules (Brown and Petersen, 1998). One of the advantages of the image correlation techniques is that the specific imaging timescales allow for measurements of slow transport properties, even in quasistatic systems, as in the case of transmembrane proteins in cells. A recent extension of the ICS family is intensity subtraction analysis, which uses sequential uniform intensity subtraction from confocal images to extract information about the brightest population in a system containing a distribution of aggregate sizes (Rocheleau et al., 2003).

One important problem in biophysics is characterizing the motion and interactions of membrane proteins, extracellular matrix components, and intracellular messengers involved in the regulation of cell migration at the molecular level. As recent studies have shown, the molecular partners involved in cell migration are numerous and their interactions complex (Lauffenburger and Horwitz, 1996). Cell migration is a dynamic, integrated process that is coordinated both spatially and temporally. Although numerous components are known to interact before, during, and after the formation of focal adhesions, less is known about the exact timing, the number of components, and the transport mechanisms involved in these interactions. New biophysical techniques have begun to reveal important quantitative aspects of the molecular mechanisms concerned. For example, fluorescence speckle microscopy has been used to investigate actin polymerization at the front edge of migrating newt lung epithelial cells (Ponti et al., 2004), and single particle tracking (SPT) has also revealed movements of adhesion proteins in apical cell membranes (Sheetz et al., 1989).

ICS analysis can quantify diffusion coefficients and flow speeds of fluorescently labeled adhesion macromolecules within the plasma membrane of living cells (Wiseman et al., 2000). It relies on correlating the amplitude of fluorescence intensity fluctuations arising from spontaneous variations in molecular number within the illumination volume defined by the focal spot of the LSM. These fluctuations arise as particle clusters move in and out of the volume by diffusion, by flow, or by a combination of both. However, the ICS technique is not currently sensitive to the direction in which flowing fluorescent entities exit the correlation volume; it only follows the temporal correlation of fluctuations irrespective of the spatial direction of entry or exit from the focus. As a consequence, ICS can measure only the magnitude of the velocity, but not its direction.

We introduce a novel technique called space-time image correlation spectroscopy (STICS), which is an extension of temporal ICS. In contrast with ICS, STICS does not separate the spatial fluctuation analysis from the temporal; instead, it relies on a complete calculation of both the temporal and all-spatial correlation lags for intensity fluctuations from an LSM-sampled image series. Monitoring of the two-dimensional average spatial correlations for every time lag yields information on both directed flow and diffusion. Further analysis is needed if a large immobile fraction is present. Fourier-filtering the zero-frequency components in time efficiently removes the immobile population contribution to the spatial correlations. Since fluorescence measurements in crowded biological membranes often involve a labeled macromolecule population undergoing diffusion and/or directed motion in the presence of immobile fluorescent species, STICS is ideal for isolating the fluctuations due the mobile component population.

We have recently reported the first application of STICS for cellular measurements (Wiseman et al., 2004). In this study we present a full systematic treatment of the method to illustrate its capabilities and limitations. We will first present application of STICS for analyzing computer-simulated images and fluorescent microsphere samples to demonstrate the general approach and to determine the detection limits. By using filtering in Fourier space to remove frequencies associated with immobile components, we can detect directional protein transport even in the presence of a large fraction (>90%) of immobile species. We also present results from two-photon laser-scanning microscopy STICS studies of actinin/enhanced green fluorescent protein (EGFP) fusion constructs at the basal membrane of living CHO cells. We illustrate cases of measuring protein diffusion, protein flow in random directions, and net flow within living cells using STICS. We are able to quantify protein fluxes with magnitudes of μm/s from retracting lamellar regions and protrusions for adherent cells plated on fibronectin. We also demonstrate the measurement of correlated directed flows (magnitudes of μm/min) of interacting α5 integrin/enhanced cyan fluorescent protein (ECFP) and α-actinin/enhanced yellow fluorescent protein (EYFP) within living CHO cells using two-color STICS.

MATERIALS AND METHODS

Computer simulations

A simulation program of laser-scanning microscopy of point emitters in a two-dimensional system was written in IDL (RSI, Denver, CO) to test ICS and its STICS derivative. This program allows the user to set a wide variety of experimental system and instrumental collection parameters, including the flow and diffusion characteristic times of several simulated fluorescent particle populations, their densities, the laser beam characteristics, white-noise levels, interacting fractions, image size, pixel size, time step, and number of images. The simulations were run on standard desktop PCs.

Fluorescent microsphere preparations

Fluorescent microspheres with a radius of 0.1 μm were obtained from Molecular Probes (Eugene, OR). The microspheres contained two different fluorophores with the following spectral properties: 505/515 nm and 580/605 nm (absorption/emission). For sample preparation, both types of Fluospheres were diluted by a factor of 5 in doubly distilled water, and drops of the solution were deposited on coverslips. Particle flow was generated by convective currents near the edge of the drop. These samples were imaged using two-photon fluorescence microscopy (details below) to provide images of two independent particle populations with no spectral overlap. Using the image analysis freeware program ImageJ (National Institutes of Health, Bethesda, MD), a separate single-channel image series of fluorescent spheres was then added to both channels of the image series of the independent fluorescent particles in the mixed sample. This effectively created an artificial interacting fraction between the two independent fluorescent sphere populations, as the added signal from this third superimposed image series appeared in both channels. In this way, we were creating pixels with identical intensity in both channels, thus artificially creating a cross-channel signal that mimicked two interacting red and green microspheres. The fraction and the flow direction of this artificial (added) interacting population were systematically varied before applying STICS analysis.

Cell culture

CHO-K1 cells (a mutant cell line that is deficient in expression of the α5 integrin; Schreiner et al., 1991) along with CHO-K1 cells transfected with visible fluorescent protein (VFP) fusions with α-actinin and/or α5 integrin were cultured in minimum essential medium supplemented with 10% fetal bovine serum, and glutamine. For VFP-expressing cells, 0.5 mg/mL neomycin (G418) was also added to the growth media. Cells were maintained in a humidified, 8.5% CO₂ atmosphere at 37°C. Cells were lifted with trypsin and plated on 40-mm diameter No. 1.5 coverslips. The coverslips were precoated with an integrin-activating extracellular matrix protein (2, 5, or 10 μg/mL fibronectin) or with a non-integrin activating matrix (200 μg/mL poly-d-lysine). For imaging, the samples were maintained in CCM1 medium at 37 ± 0.2°C in a Bioptechs FCS2 closed incubation chamber (Bioptechs, Butler, PA), in combination with a Bioptechs objective heater. Nontransfected CHO cells were used as control samples to determine autofluorescence background levels. Cell samples that had been fixed with 4% paraformaldehyde in PBS for 20 min at room temperature were also prepared for each type of cell line studied. The fixed cells were imaged in each experiment to provide a control for any contributions from mechanical vibrations, stage translations, and laser fluctuations.

Two-photon laser-scanning microscopy

Two-photon microscopy of the fluorescent microspheres was conducted using an Olympus Fluoview 300CLSM/IX70 inverted microscope (Olympus, Melville, NY), coupled with a Tsunami (model 3960) pulsed femtosecond Ti:sapphire laser (Spectra Physics, Mountain View, CA) pumped by a Millennia XsJS laser. The microspheres were excited at 800 nm and point detection was achieved with two external photomultiplier tubes (Hamamatsu, Bridgewater, NJ). For imaging our microspheres, a 720 DCSPXR excitation dichroic mirror, a 555-dclp emission beam splitter, and HQ525/50 HQ610/75 emission filters (all from Chroma Technology, Brattleboro, VT) were employed for light detection. All images were collected using a PlanApo Olympus 60× (NA 1.40) oil immersion objective lens. Images were collected with a typical optical zoom setting of 2× corresponding to x and y pixel dimensions of 0.23 μm/pixel. Image time-series of 100 frames with a time delay of 0.45s between frames were collected.

Two-photon imaging of cells was conducted using a Biorad RTS2000MP video-rate-capable two-photon/confocal microscope (Biorad, Hertfordshire, UK), coupled with a MaiTai pulsed femtosecond Ti:sapphire laser (Spectra Physics, Mountain View, CA) tunable over from 780 to 920 nm. The microscope uses a resonant galvanometer mirror to scan horizontally at the NTSC line-scan rate. Point detection is employed using one or two photomultiplier tube(s) with fully open confocal pinholes when imaging. For imaging EGFP in cells, the laser was tuned to a wavelength of 890 nm, and a 560 DCLPXR dichroic mirror and an HQ528/50 emission filter were employed for light detection. For imaging cells expressing both ECFP and EYFP fusion proteins, the laser was tuned to 880 nm, and a D500LP dichroic mirror and HQ485/22 and HQ560/40 emission filters were used for detection and separation of the emitted fluorescence. All filters were from Chroma Technology.

All image time-series were collected using a PlanApo Nikon (Nikon, Tokyo, Japan) 60× oil immersion objective lens (NA 1.40), which was mounted in an inverted configuration. Images having dimensions of 480 (height) × 512 (width) pixels were collected with a typical optical zoom setting of 2× corresponding to x and y pixel dimensions of 0.118 μm/pixel. Image series with time delays of 1, 5, or 10 s between sequential frames and 60, 120, or 150 frames in total were collected from single cells. Individual image frames sampled from the cells were accumulated as averages of 32 video rate scans (i.e., ∼1 s per frame).

Image autocorrelation and cross-correlation analysis

Microscope image time-series volumes were viewed, and image subsections of 16², 32², 64², 128², or 256² pixels in size were selected from regions of the cell and exported for image correlation analysis using a custom Interactive Data Language (IDL 6.0, RSI) program written for the PC. Correlation calculations for each image time-series and nonlinear least-squares fitting of the spatial correlation functions were performed in a Windows environment on a 1.3-GHz processor PC using programs written in IDL. Discrete intensity fluctuation autocorrelation functions were calculated from the image sections as has been previously described (Wiseman et al., 2000). The equations used for the calculation and fitting of the normalized intensity fluctuation autocorrelation and cross-correlation functions (both spatial and temporal) are described below.

THEORY

ICS and ICCS have been introduced in previous contributions (Petersen et al., 1993; Wiseman and Petersen, 1999). We will provide a summary of the basic concepts behind these techniques to introduce the theory necessary for STICS analysis.

Generalized spatiotemporal correlation function

ICS is based on the correlation of fluorescence intensity fluctuations measured from an observation area defined by the diffraction-limited focal spot of the exciting laser beam in a laser-scanning microscope. The intensity fluctuations in fluorescence are recorded in an image series as the laser beam is repeatedly rastered across the sample. Spatial and temporal correlation is then applied to the image time-series.

We define a generalized spatiotemporal intensity fluctuation correlation function which is a function of spatial lag variables ξ and η and of a temporal lag variable τ for detection channels a and b:

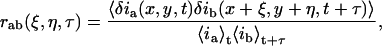(1)

where δi_a(b)(x,y,t) is the intensity fluctuation in channel a(b) at pixel position (x,y) and time t with and 〈…〉 in the denominator represent spatial ensemble averaging over images at time t and t+τ in the time-series, and the numerator is also an ensemble average over all pixel fluctuations in pairs of images separated by a lag-time of τ. White-noise sources contribute to the numerator only at zero lag (temporal and spatial), whereas they will contribute to the average intensities in the denominator. Correction methods dealing with white-noise and background correlation have been reported (Wiseman and Petersen, 1999). The zero-lag amplitude value has not been weighed for all fits in the current work.

Spatial correlation and cross-correlation

ICS has traditionally treated the cases for spatial and temporal correlations separately. The spatial correlation function r_ab(ξ, η, 0) is defined by evaluating Eq. 1 with zero time-lag:

(2)

These functions are typically calculated by Fourier methods and fit to standard Gaussian functions by nonlinear least-squares methods (Petersen et al., 1993; Wiseman and Petersen, 1999). The Gaussian fit function for the spatial correlation of the n^th image is given as a two-dimensional spatial correlation function,

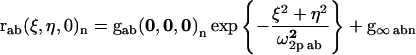(3)

(note that in this fitting equation and those that follow, the fit parameters are highlighted in bold type). Fit parameters are the zero-lag amplitude g_ab(0,0,0)_n, the two-photon correlation radius ω_{2p ab}, which is proportional to the laser-beam horizontal radius, and the offset g_∞abn. For an ideal system of non-interacting particles, the zero-lag amplitude g_ab(0,0,0)_n is inversely proportional to the mean number of independent fluorescent particles in the correlation area defined by the focus of the laser (Petersen et al., 1993). When a = b = 1 or 2, Eq. 2 defines a spatial autocorrelation function for one detection channel, and when a = 1 and b = 2, Eq. 2 defines a spatial cross-correlation function between two detection channels.

Temporal correlation and cross-correlation

The temporal correlation function is given by evaluating the generalized correlation function at zero spatial lags:

(4)

Its decay will essentially depend on the temporal persistence of the average spatial correlation of intensity fluctuations between images in the time-series separated by a lag-time of τ as measured from an ensemble of focal spots (correlation areas) within a sampled image area. The same equality and inequality relationships hold for the a and b subscripts in defining temporal auto- and cross-correlation functions as was outlined above for the spatial case.

Decay models for correlation functions

The rate and shape of the decay of the correlation functions will reflect any dynamic process that contributes fluctuations on the timescale of the measurement. The actual decay models for fluorescence correlation will depend on both the underlying dynamics of the fluctuating process and the geometry of the focal spot (the point-spread function; Thompson, 1991). We consider four separate functional forms that are analytical solutions for the generalized intensity fluctuation correlation function appropriate for specific cases of two-dimensional transport phenomena as measured within a membrane system illuminated by a TEM₀₀ laser beam with Gaussian transverse intensity profile. See below.

Two-dimensional diffusion

(5)

Two-dimensional flow

(6)

Two-dimensional diffusion and flow for a single population

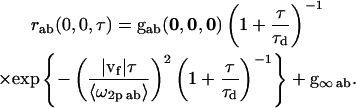(7)

Two-dimensional diffusion and flow for two populations (i = 1, 2)

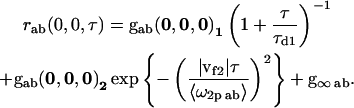(8)

The highlighted fit-parameters are the zero-lag amplitude g_ab(0,0,0), the offset g_∞ab, the characteristic diffusion decay time τ_d, and the mean speed of the particles |v_f|,

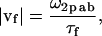(9)

where τ_f is the characteristic flow time. The effective e⁻² correlation radius 〈ω_{2p ab}〉 is calculated by averaging the individual ω_{2p ab} obtained from fitting Eq. 3 for every image in the time-series. The best fit characteristic diffusion time combined with the average correlation radius allows calculation of the diffusion coefficient:

(10)

It is important to distinguish ω_2p, the effective two-photon e⁻² correlation radius, and ω₀, the e⁻² beam radius, because ω_2p is equal to ω₀ divided by the square-root of 2. Note that in Eq. 9, the mean speed |v_f| is directionally blind (a velocity magnitude). ICS is not sensitive to the direction in which the particles escape the correlation area, because the basic analysis does not include non-zero spatial lags with the temporal lags (see Eq. 4).

Space-time image correlation and cross-correlation spectroscopy (STICS)

The object of the current work is to extend ICS and ICCS to obtain flow vectors, or essentially to determine the direction in which the particles are exiting the correlation areas if directed flux is present. To achieve this, one must combine the spatial information imbedded in the two-dimensional spatial correlations with the time-dependent transport measured by the temporal correlation. For this we define a discrete approximation to the full space-time correlation function as

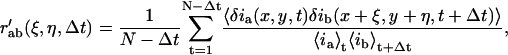(11)

where N is the total number of images in the time-series. The value r′_ab represents the average cross-correlation function for channels a and b, for all pairs of images separated by a lag-time of Δt. This generalized space-time correlation function can be considered as a time-series, where the images are averaged two-dimensional spatial (cross-)correlation functions, and the time variable is actually the lag-time (Δt) between all images pairs for which the correlation was computed.

For an image time-series collected using an LSM, r′_aa(ξ, η, 0) is the average spatial autocorrelation function from each image (Eq. 1 averaged for each image n in the series; see Fig. 1). It will appear as a two-dimensional Gaussian with peak value at (ξ = 0, η = 0). Assuming that the temporal resolution is sufficiently high for intensity fluctuations to be correlated between successive images, r′_aa(ξ, η, 1), r′_aa(ξ, η, 2), … are also going to appear as Gaussian spatially distributed correlations. However, if some particles have moved between frames, the correlation function is going to change depending on the kind of microscopic motion undergone by the particles. The simplest case is to imagine the particles as stationary, then the correlation stays unchanged for Δt = 0 to N and centered at (ξ = 0, η = 0). If we now consider the particles as diffusing, they will tend to exit the correlation area in a symmetric fashion, thus broadening the correlation Gaussian in every direction, analogous to a tracer diffusion experiment. The peak will stay centered at (ξ = 0, η = 0) but its value will decrease hyperbolically (see Eq. 5). Finally if the particles are flowing uniformly, the spatial correlation Gaussian peak is going to maintain its original shape as a function of time, but its peak value will be shifted to lag positions (ξ = −v × Δt,η = −v_y × Δt) where v_x and v_y are the x and y velocities of the particles. This is consistent with the observation that for a flowing population, the temporal autocorrelation function r_aa(0, 0, τ) decays as a Gaussian. The negative signs in the expression for ξ and η arise from the fact that the Gaussian correlation peak moves in a direction opposite to the flow. This analysis is only valid as long as the particles undergoing concerted motion stay within the bounds of the analyzed region. The two-population combined case of a flowing and diffusing population is illustrated in Fig. 1, where the diffusion spatial Gaussian correlation peak (DG) broadens and stays centered at (ξ = 0, η = 0) and the flowing Gaussian correlation peak (FG) shifts in a direction opposite to the flow of the particles (as indicated by the open arrows on the simulated images). In this case the flowing and diffusing populations were equally represented (in terms of density and intensity); however, in the cell system in this study the actively transported subpopulation is usually a small fraction of the total dynamic species population. This effectively makes tracking the flowing Gaussian difficult, as it is hard to resolve near the zero-lags origin due to the diffusing and immobile populations. A solution to this problem is presented in the next section.

FIGURE 1.

Schematic illustration of the algorithm used to compute the discrete approximation to a generalized spatiotemporal correlation function for a simulated system with flow and diffusion. The Gaussian autocorrelation peaks for each image are shown in the left column (Δt = 0), the cross-correlation for a lag-time of 1 time-unit in the middle column (Δt = 1), and for the second longest lag-time of N–1 time-units in the right column (Δt = N−1, where N is the number of frames in the image series). The open arrows on the simulation images represent the direction of the flow. The averaged Gaussian correlation functions r′_aa(ξ, η, Δt) are shown at the bottom for Δt = 0,1 and N–1. The separation of the Gaussian correlation peak due to flow (FG) from the Gaussian correlation peak arising from the diffusing population (DG) is clearly seen.

Immobile population removal

The most general case is a combination of diffusion, flow, and immobile populations. The challenge is to extract the velocity direction by following the flow Gaussian correlation peak, without influence from the correlations of the immobile or slowly diffusing populations (which effectively remain centered at (0, 0) spatial lags). The immobile population contribution to r′_aa(ξ, η, Δt) can be removed by Fourier-filtering in frequency space the DC component for every pixel trace in time before running the space-time correlation analysis. The intensity values in channel a for a given pixel value, say i_a(0, 0, t), contains contributions to the signal of interest from dynamic and immobile component signals and spurious white-noise sources. The signal from dynamic components (flow and diffusion) contribute intensity fluctuations that change as a function of time for a given pixel trace. However, an immobile component only adds a constant intensity offset to the single pixel intensity trace through time, so removing the DC frequency component eliminates this contribution from the correlation analysis. For a given pixel location (x,y), the corrected intensities are given by

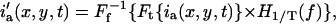(12)

where T is the total acquisition time of the image series, H_1/T(f) is the Heavyside function which is 0 for f < 1/T and 1 for f > 1/T, 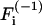denotes the (inverse) Fourier-transform with respect to variable i, and f is the pixel temporal-frequency variable.

RESULTS AND DISCUSSION

Simulations

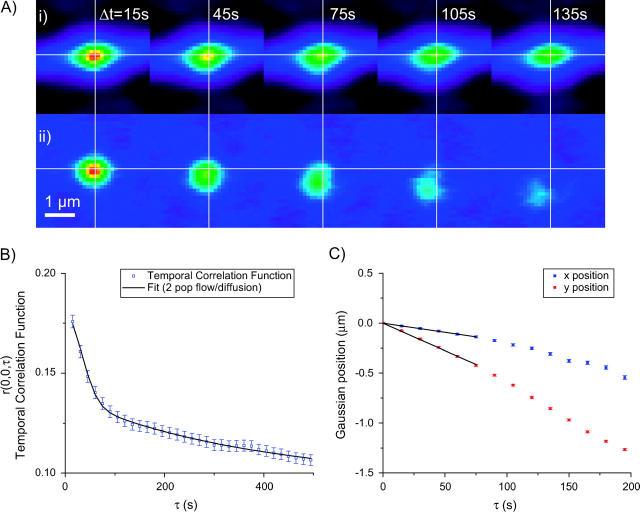
Using our laser-scanning microscopy simulation program (see Materials and Methods) we ran three different sets of simulations for point particles, exhibiting i), pure flow with v_x = −0.12 μm/s and v_y = 0.08 μm/s; ii), pure diffusion with D = 0.01 μm²/s; and iii), a two-population (one flowing, one diffusing) combination with v_x = −0.12 μm/s, v_y = 0.08 μm/s, and D = 0.01 μm²/s. Fig. 2 A shows the results of STICS analyses (without any Fourier-filtering) performed on these simulations. All the populations are set to have the same total number of particles (density of 50 particles/μm²), with equal quantum yields. All simulations are 128 × 128 pixels at a resolution of 0.06 μm/pixels, and 500-frames-long, with a time step of 0.02 s/frame. The beam radius is set at 0.4 μm. The consequences of flow or diffusion on the evolution of the two-dimensional contour plot of the correlation function are evident. As expected in simulation i, the Gaussian flow correlation peak shifts with a direction opposite to the flow, and in simulation ii, the central Gaussian correlation peak broadens due to diffusion. In the combined case of simulation iii, the flow and diffusion the Gaussian peaks are initially superimposed and they separate after the flowing population has moved by more than a correlation radius.

FIGURE 2.

STICS and ICS analysis results for computer-generated simulations. (A) A contour plot of the STICS correlation functions for the case of i), flow (v_x = −0.12 μm/s and v_y = 0.08 μm/s); ii), diffusion (D = 0.01 μm²/s); and iii), two-populations' flow and diffusion (v_x = −0.12 μm/s, v_y = 0.08 μm/s, and D = 0.01 μm²/s). (B) The ICS temporal autocorrelation functions (Eq. 4) and best fits for the same simulations. (C) Plots of the peak position of the STICS Gaussian correlation peaks from A as a function of time. The peak position versus time gives an estimate of the concerted velocity of the particles in case i, of v_x = −0.119 ± 0.002 μm/s and v_y = 0.0792 ± 0.0005 μm/s and in case iii, of v_x = −0.096 ± 0.007 μm/s and v_y = 0.068 ± 0.006 μm/s, respectively. All simulations were 128 × 128 pixels with 500 frames at a density of 50 particles/μm², using 0.02 s/frame, 0.06 μm/pixel, and an e⁻² radius of 0.4 μm.

The temporal-decay of the zero spatial lags center of these contours is r′_aa(0, 0, τ) (where channel a denotes a single collection channel for these simulations); i.e., the temporal autocorrelation function (Eq. 4) This is shown for simulations i–iii (Fig. 2 B). Once again, we can clearly distinguish between the various types of transport. The Gaussian profile of Eq. 6 (squares) is fitted to give a velocity magnitude of 0.152 ± 0.004 μm/s and the fit to the hyperbolic profile of Eq. 5 (triangles) yields a diffusion coefficient of 0.008 ± 0.002 μm²/s via Eq. 10. Notice that the velocity magnitude is close to the input value, but there is no directional information to be gathered from the ICS analysis. The analysis of the combined case (open circles) provides information on the motion of both populations, with a fit (Eq. 9) velocity of 0.144 ± 0.004 μm/s, and a diffusion coefficient of 0.009 ± 0.002 μm²/s.

Performing STICS on simulation i yields peak positions for the two-dimensional correlation Gaussian (Fig. 2 C, squares). Fitting for the x- and y-peak displacements provides an estimate of v_x = −0.119 ± 0.002 μm/s and v_y = 0.0792 ± 0.0005 μm/s. The analysis of the central diffusion peak in simulation ii provides an estimate of the accuracy of our results for these simulations. The x and y velocities should be zero and they are found to be v_x = 0.006 ± 0.01 μm/s and v_y = −0.007 ± 0.006 μm/s (Fig. 2 C, triangles). Moreover, the STICS analysis applied to simulation iii without modification is not accurate, because of the perturbation to the velocity analysis due to the presence of the second Gaussian correlation peak for the diffusing population, which is centered at (ξ = 0, η = 0). In the situation where both flowing and diffusing populations are present, there are two cases where STICS analysis can still be performed accurately (see Fig. 3). First, if the diffusing population is fast compared to the directional flow, then its effects on the flow correlation peaks will be short-lived as the central Gaussian will decay quickly. Second, if the diffusing population is slow, it can be considered as quasi-immobile and its intensity contribution is also going to be mostly eliminated by the Fourier-filtering described previously. To determine the timescales where these problems would arise, we performed simulations where we systematically varied the diffusion coefficient while keeping the velocity of the particles fixed. These simulations showed that the STICS analysis is still valid when the characteristic diffusion time is approximately five times faster or slower than the flow characteristic time (see Fig. 3). In simulation iii (Fig. 2 A), the diffusion is neither fast nor slow compared to the flow, and the time-evolving Gaussian correlation peak can be fit to give v_x = −0.096 ± 0.007 μm/s and v_y = 0.068 ± 0.006 μm/s (Fig. 2 C, circles) after Fourier-filtering. Notice that the x and y velocities are slightly smaller in this combined case than for the flow-only case. This is because the remnants of the diffusing population contribution effectively weight the flowing Gaussian back toward the zero-lags center when we try to fit the position of the Gaussian peak. In such a scenario, if one can assume that the total flow is dominated by the directional flux (as opposed to separate flows in random directions), then one can scale the x and y velocities from STICS analysis according to the total velocity obtained by ICS analysis to get v_x = −0.118 ± 0.008 μm/s and v_y = 0.083 ± 0.007 μm/s. Note that the temporal ICS analysis will be sensitive to all flow processes present, which will all contribute to the decay of the correlation function. For the case of the adhesion protein transport at the membrane in cells that we report in this study, the second scenario of faster diffusion (τ_D < τ_f) was usually observed.

FIGURE 3.

STICS analysis results for computer simulations of two populations, one flowing (v_x = −0.12 μm/s and v_y = 0.08 μm/s) and one diffusing (varying diffusion coefficients). (A) The x velocity as resolved by STICS with and without the immobile population filtering. (B) The y velocity as resolved by STICS with and without the immobile population filtering. On both graphs, each point and error bar represents the average result of 100 simulations with standard deviation. The shaded regions show the set velocities in the simulation with an acceptable error of ±10%. The computer simulations were 128 × 128 pixels with 100 frames at a density of 100 particles/μm², using 0.1 s/frame, 0.06 μm/pixel, and an e⁻² radius of 0.4 μm.

If the flow characteristic time is slow compared to the image acquisition rate, then some analysis artifacts are introduced by the Fourier-filtering, which complicates the case of a slowly flowing population. If the particles do not move more than a correlation radius over the time of acquisition of the entire image-series, then removing the DC offset will spatially anticorrelate the intensities over a short distance in the direction of the flow. In other words, the central Gaussian peak is reduced in width, and accompanied by two diametrically opposed depressions aligned with the flow direction. Nevertheless, these artifacts are of no real consequence in the determination of the flow direction because a Gaussian can still effectively be fit to the correlation functions. Moreover, we can neglect signal fluctuations due to bleaching in flow/diffusion measurements as long as the characteristic times associated with these processes are shorter than the bleaching time (simulation results not shown). This was the case for the cell measurements reported below.

Fluorescent microspheres

Fluorescent microsphere samples containing a mixture of flowing spheres emitting at two different wavelengths (referred to as red and green) were prepared and imaged by two-photon laser-scanning microscopy (see Materials and Methods) to generate an image series of two independent particle populations (referred to as non-interacting). By adding another image series of flowing microspheres to both independent channels in the collected time-series, we could effectively introduce an artificial interacting population. The direction of flow of the interacting population added by image processing was chosen by the user and is thus independent of the direction of flow of the original non-interacting particle populations. A typical image from this image-processed time-series is shown in Fig. 4 A. It has an equal density of red and green microspheres, with ∼40% of each population interacting. Such an image time-series was then analyzed with two-color STICS, yielding directional flow information for the red and green populations, as well as for the interacting fraction. We can recover the flow directions of the non-interacting red and green microsphere populations to within 8° in the presence of the interacting population, as compared with the recovered flow directions of the original image time-series (i.e., analysis performed without the addition of the interacting population). Moreover, we can find the direction of flow of the interacting population to within 5°. Fig. 4 B shows the one-to-one relationship between the recovered velocity magnitudes (in x and y) for the added population as measured by STICS from the image time-series before the addition and the velocity magnitude of the added (interacting) population as measured by STICS in the dual-channel constructed image time-series in the presence of the non-interacting microsphere populations. The data are plotted for several experiments in which the direction of flow of the added interacting population was different in each case. The magnitudes of the velocities measured by STICS analysis on the dual-channel image time-series differ by <10% from the original values (as measured separately before the addition of the artificial interacting population; see Table 1). Note that the density of the added interacting particle population was five times lower than the density of each independent fluorescent particle population.

FIGURE 4.

(A) A composite image of fluorescent microspheres consisting of two different fluorescent particle populations (red and green) and an added interacting particle population (yellow overlap). The composite image was made by adding an independent image of fluorescent spheres (our artificial interacting population) to both detection channel images. For each image time-series constructed, the velocities of the non-interacting populations remained constant whereas the interacting fraction's direction of flow was systematically changed. (B) A plot of the interacting population velocity magnitudes in x and y measured by STICS in the composite image series (i.e., with the added population and the red and green microspheres present) versus the velocity magnitude of the introduced interacting population measured by STICS in its original image series (i.e., without the red and green particles present).

TABLE 1.

STICS-measured parameters for a microsphere-image time-series (see Fig. 3)

	First population velocity (μm/min)		Second population velocity (μm/min)		Added population velocity (μm/min)		Interacting population velocity (μm/min)
Set #	vx	vy	vx	vy	vx	vy	vx	vy
1	0.11 ± 0.04	−1.53 ± 0.05	0.14 ± 0.05	−1.48 ± 0.05	−0.01 ± 0.05	−3.9 ± 0.1	−0.01 ± 0.09	−4.2 ± 0.2
2	0.27 ± 0.05	−1.24 ± 0.04	0.30 ± 0.03	−1.22 ± 0.05	1.39 ± 0.04	0.09 ± 0.04	1.21 ± 0.07	−0.25 ± 0.08
3	0.03 ± 0.01	−1.0 ± 0.1	0.16 ± 0.03	−1.23 ± 0.05	−1.26 ± 0.03	2.27 ± 0.03	−1.08 ± 0.04	2.13 ± 0.04
4	0.03 ± 0.06	−1.08 ± 0.06	0.11 ± 0.09	−0.98 ± 0.04	−1.44 ± 0.03	0.60 ± 0.01	−1.33 ± 0.03	0.52 ± 0.03
5	0.02 ± 0.05	−1.27 ± 0.03	0.03 ± 0.05	−1.20 ± 0.05	−0.31 ± 0.03	−1.05 ± 0.02	−0.22 ± 0.05	−1.02 ± 0.04
6	0.12 ± 0.02	−0.51 ± 0.05	0.17 ± 0.03	−0.63 ± 0.05	0.21 ± 0.02	0.98 ± 0.02	0.19 ± 0.02	1.00 ± 0.02

The column Added population velocity refers to the STICS analysis results before image addition when applied to the single-channel image time-series that is subsequently added to the dual-channel image time-series to create an interacting population. The column Interacting population velocity refers to the two-color STICS analysis results after image addition for the co-localized (interacting) population in the composite image. These values should, in theory, be equal to the values in the column Added population velocity.

The STICS analysis for the single non-interacting populations is influenced by both the fraction that is flowing independently and the movements of the interacting fraction. As long as the overall contribution to the image intensity from the interacting population does not exceed that of the non-interacting population, STICS can detect the differences in flow direction between the populations. In the case where this effect becomes dominant (i.e., equal contribution from interacting and non-interacting species), one can fit two Gaussians in r′_aa(ξ, η, τ) (a = 1 or a = 2) to extract the two flow directions. Conversely, the STICS analysis of the interacting population can also be influenced by the single non-interacting populations if these flow in the same direction and random spatial cross-correlations occur. These effects account for the errors in magnitude and direction of the measured velocities in the constructed image series as compared with the velocities measured from the original image series of the independent microspheres.

Velocity mapping of protein transport in living cells

We measured the phenomena of directed and nondirected transport in living cells expressing adhesion protein EGFP fusion constructs using STICS. We first measured α-actinin/EGFP constructs expressed in CHO-K1 cells plated on fibronectin. The protein α-actinin is a cytoplasmic molecule that binds to the integrins at the membrane and also links the actin cytoskeleton (Lauffenburger and Horwitz, 1996). We have previously determined that α-actinin is more mobile in the peripheral regions of the CHO cells where there is active lamellar extension, retraction, and membrane ruffling when the cells are activated on fibronectin (Wiseman et al., 2004). We focused our measurements on such active peripheral areas (see Fig. 5).

FIGURE 5.

Two-photon LSM images of the basal membrane of CHO cells expressing EGFP-labeled α-actinin. The regions analyzed with ICS and STICS are shown as open squares and the STICS analysis results are shown in Figs. 5–7. (A) A 64² pixel region where the temporal autocorrelation function is best fit to a single-population diffusion model (Eq. 5). (B) A 128² pixel region where the temporal autocorrelation function is best fit to a two-population flow/diffusion model (Eq. 8). (C) A 128² pixel region where the temporal autocorrelation function is best fit to a two-population flow/diffusion model (Eq. 8). All images are 512 × 480 pixels at a resolution of 0.118 μm/pixel, and a total of 180, 360, and 120 frames at a resolution of 5, 5, and 15 s/frame for A–C, respectively.

Fig. 6 shows the ICS and STICS analysis results for a typical 64 × 64 pixel region from the cell periphery (Fig. 5 A). As is evident from Fig. 6 B, the temporal autocorrelation function can be fit very well by Eq. 5, which yields a diffusion coefficient of (9 ± 1) × 10⁻⁴ μm²/s. We show contour plots of the Gaussian correlation peaks for different time lags in Fig. 6 A for i), the unmodified image time-series (without the immobile population removed); and ii), the filtered image time-series (with the immobile population removed). As expected, in both cases the correlation peaks stay centered at zero spatial lags (indicated by the white crosshairs). Fitting for the displacement of the Gaussian yields a very small velocity v_STICS = (1.2 ± 0.8) × 10⁻³ μm/s (from v_x = (−0.9 ± 0.8) × 10⁻³ and v_y = (−0.8 ± 0.7) × 10⁻³ μm/s, see Fig. 6 C), which can be attributed to either a real but very slow concerted flux of the proteins, or to an experimental artifact such as a slow stage drift. These values are on the order of the precision of our measurements, which was assessed by applying the STICS analysis to cells fixed in 4% paraformaldehyde. The corresponding values v_x = (0.4 ± 0.3) × 10⁻³ and v_y = (0.2 ± 0.3) × 10⁻³ μm/s establish our detection limits. These results illustrate a membrane region consisting mainly of protein-diffusing and immobile proteins, and show how the random walk is manifest in both the ICS and STICS analyses.

FIGURE 6.

In vivo ICS and STICS analysis of protein diffusion in a peripheral basal membrane region of a CHO cell (Fig. 5 A) expressing EGFP-labeled α-actinin. (A) Contour plots of space-time correlation functions from STICS analysis (Eq. 11) as a function of lag-time for i) with and ii) without the immobile population contribution present. (B) A plot of the ICS temporal autocorrelation function and best fit to a single-population diffusion model (Eq. 5). The recovered diffusion coefficient was D = (9 ± 1) × 10⁻⁴ μm²/s. (C) Peak tracking plot of the STICS correlation peaks reveals that they stay centered at zero spatial lags, within the precision of our measurement.

The same analyses were applied to a different region from the periphery of another cell (Fig. 5 B) and reveal different protein transport. Fig. 7 shows our results for a 128 × 128 pixel region in which clusters of α-actinin are clearly resolved, and these clusters can be observed to flow in a directed fashion on what appear to be defined linear tracks. However, the ICS (Fig. 7 B) and STICS (Fig. 7, A and C) analyses yield very different values for flow: v_ICS = (13 ± 1) × 10⁻³ μm/s and v_STICS = (1.1 ± 0.7) × 10⁻³ μm/s (from v_x = (−0.67 ± 0.02) × 10⁻³ and v_y = (−0.9 ± 0.8) × 10⁻³ μm/s). The total velocity value for ICS is approximately 10 times higher than the velocity value measured by STICS. This is due to the fact that STICS only measures the net resultant directed component (here the majority, but not all of the clusters, were observed to be traveling to the left and down in the image series), whereas ICS measures an average total flow speed (and a small diffusion coefficient in this case). Hence the combination of ICS and STICS allows us to distinguish between directional flow in one direction (see also Fig. 8), or directional flow in many random directions as was the case here. Visual tracking of the resolved clusters shows that the directions are random, with more moving toward the lower left of the image. In this case, single particle tracking (SPT) analysis will, in principle, provide more information about the range of transport (Saxton and Jacobson, 1997). However, it proved difficult to track the clusters with the fluorescence signal/noise and for the density of expression of EGFP proteins typical for these transfected cells (SPT data not shown).

FIGURE 7.

In vivo ICS and STICS analysis of protein flux in random directions in a peripheral basal membrane region of a CHO cell (Fig. 5 B) expressing EGFP-labeled α-actinin. (A) Contour plots of space-time correlation functions from STICS analysis as a function of time for i) with and ii) without the immobile population contribution present. (B) A plot of the ICS temporal autocorrelation function and best fit to a two-population flow/diffusion model (Eq. 8). The recovered ICS velocity and diffusion were v_ICS = (13 ± 1) × 10⁻³ μm/s and D = (8 ± 1) × 10⁻⁴ μm²/s. (C) Peak tracking plot of the STICS correlation peaks reveals that they stay centered at zero spatial lags, within the precision of our measurement, yielding a very small velocity of v_STICS = (1.1 ± 0.7) × 10⁻³ μm/s.

FIGURE 8.

In vivo ICS and STICS analysis of directed protein flow in a peripheral basal membrane region of a CHO cell (Fig. 5 C) expressing EGFP-labeled α-actinin. (A) Contour plots of space-time correlation functions from STICS analysis as a function of time for i) with and ii) without the immobile population contribution present. (B) A plot of the ICS temporal autocorrelation function and best fit to a two-population flow/diffusion model (Eq. 8). The recovered velocity was v_ICS = (7.7 ± 0.8) × 10⁻³ μm/s and a small diffusion coefficient was measured: D = (6 ± 1) × 10⁻⁵ μm²/s. (C) Peak tracking plot of the STICS correlation peaks (after the immobile population removal) shows a net displacement of the Gaussian center, yielding velocities of v_x = (1.8 ± 0.3) × 10⁻³ and v_y = (5.5 ± 0.2) × 10⁻³ μm/s.

The true advantage of STICS emerges in situations where no bright clusters are clearly resolved (hence SPT would be impossible), but concerted flux of protein can be detected by correlation analysis. Fig. 8 shows analyses results for a 128 × 128 pixel region of a basal membrane of a CHO cell expressing EGFP-labeled α-actinin (Fig. 5 C). Here the ICS analysis again detects flow and diffusion of two separate populations (Fig. 8 B) with v_ICS = (7.7 ± 0.8) × 10⁻³ μm/s and a small diffusion coefficient D = (6 ± 1) × 10⁻⁵ μm²/s. The STICS analysis also detects a directional flow (Fig. 8, A and C) with v_x = (1.8 ± 0.3) × 10⁻³ and v_y = (5.5 ± 0.2) × 10⁻³ μm/s. This example illustrates the importance of removing the immobile population, since the Gaussian correlation peak in Fig. 8 A i) is dominated by immobile protein population spatial correlations and thus stays centered at zero spatial lags. However, after the immobile population removal, one can see the Gaussian peak clearly moving away from the zero lags center toward the bottom left corner in a directed fashion and the residual central peak from the diffusion population (Fig. 8 A ii).

The formation and disassembly of adhesions as lamellar protrusions are extended or retracted must result in some form of transport of adhesion macromolecules into or out of the transient lamellar extension. Fig. 9 shows the heterogeneous spatial distribution of α-actinin in another CHO cell, close to the edge where lamellar protrusions are clearly visible in the lower part of the image. During the course of this 60-frame (300 s) image series, the protrusions retract and adhesion structures disassemble. STICS analysis shows that there is a net flux of proteins directed toward the interior of the cell (Fig. 9, arrows), with the average flow rate of 0.22 ± 0.04 μm/min (see Table 2), in agreement with rates of filamentous actin retrograde flow (Vallotton et al., 2003). ICS analyses on the same regions show greater variations in the total velocity measured (50% spread versus 17% for STICS). However, given the relatively small size of these regions (16² or 32² pixels) it was hard to determine fit parameters to the temporal autocorrelation function with high precision as the signal/noise ratio depends on the number of independent fluctuations sampled (Meyer and Schindler, 1988). STICS is not as sensitive to spatial sampling as ICS because we are simply tracking a Gaussian peak, which is far easier than fitting a noisy temporal autocorrelation curve with a three-parameter hyperbola or Gaussian. Hence the discrepancy between the two analyses is due to the better performance of STICS in this small spatial sampling regime. In the case of ruffling membranes, however, surface height variations are going to lead to intensity variations due to the intensity distribution of the point-spread function and we exclude such regions from analysis. Such variations are detected as changes in the fit radius of the spatial correlation functions (Wiseman et al., 2004). Fluorescent speckle microscopy (FSM) has also been used to investigate filamentous actin flow at the leading edge of migrating cells (Vallotton et al., 2003). Tracking very small amounts of a fluorescent derivative of the monomer that forms the actin filaments allowed the authors to generate retrograde actin flow maps with excellent spatial resolution (1 μm² regions, or ∼8² pixels in our case). The advantage of FSM is that it does not average flow directions because it follows the trajectories of single speckles, hence it can have greater precision in regions where there is flow in several directions. However, FSM requires specialized fluorescent labeling techniques, whereas STICS can be used without special labeling (i.e., standard VFP transfected cells) using standard LSM imaging approaches with approximately the same spatial resolution.

FIGURE 9.

Two-photon STICS velocity map image of EGFP/α-actinin flux in the vicinity of a retracting lamellar extension in a CHO cell plated on fibronectin. The original image-series reveals that the extended lamellar protrusions are retracting. Selecting regions of 16 × 16 or 32 × 32 pixels and performing the STICS analysis reveals a net flow of the α-actinin toward the cell interior (arrows). The spatial scale is shown as a bar and the velocity scale is shown as an arrow. The original image-dimensions are 512 × 480 pixels at 0.118 μm/pixel and a total of 120 images at 5 s/frame.

TABLE 2.

STICS-measured parameters for image regions of a CHO cell (see Fig. 7)

Region	1	2	3	4	5	6	7	8
vx (μm/min)	−0.07 ± 0.04	−0.06 ± 0.01	0.06 ± 0.06	0.01 ± 0.05	0.052 ± 0.006	0.17 ± 0.02	0.24 ± 0.05	0.09 ± 0.04
vy (μm/min)	0.18 ± 0.04	0.14 ± 0.01	0.17 ± 0.02	0.25 ± 0.05	0.25 ± 0.02	0.17 ± 0.02	0.12 ± 0.07	0.22 ± 0.04

Another advantage of the STICS method is that it can be carried out in a cross-correlation scheme, with dual color labeling of different macromolecular species. If the zero time-lag cross-correlation function is non-zero, it means that the proteins are interacting in a common complex (Wiseman et al., 2004). Furthermore, if we monitor the spatial cross-correlation peaks in subsequent time lags, then we can determine if the proteins are flowing or diffusing together. We imaged CHO cells expressing α5 integrin/EYFP and α-actinin/ECFP using two-photon microscopy and dual channel detection, and analyzed the spatiotemporal intensity fluctuations from both channels via two-color spatiotemporal image cross-correlation spectroscopy (STICCS). The two-photon microscopy images have been corrected for an 8% bleedthrough of the ECFP signal into the EYFP detection channel, as had been determined from control measurements on cells expressing just ECFP α-actinin or EYFP α5 integrin alone. We found that α5 integrin and α-actinin are actively transported as a complex in some regions of the cell (see Fig. 10), with an average transport velocity of 0.16 ± 0.03 μm/min. Moreover, non-zero temporal cross-correlation functions were calculated for α5 integrin and α-actinin outside of visible focal adhesions (for example, in region 2 of Fig. 10), meaning that both components that are known to interact in mature adhesions are also present as co-transported microcomplexes throughout the cell as we have reported recently (Wiseman et al., 2004). In this study, however, we have added the directional measurement and obtained vectors via STICCS analysis for the co-localized flowing populations.

FIGURE 10.

Two-photon auto- and cross-correlation STICS velocity map images of ECFP/α-actinin and EGFP/α5 integrin at the basal membrane of a CHO cell on a fibronectin substrate. (A) STICS velocity map for ECFP/α-actinin (channel 1); (B) STICS velocity map for EYFP/α5 integrin (channel 2); and (C) two-color STICCS velocity map of channel 1 with channel 2 showing flow vectors for co-transported ECFP/α-actinin and EGFP/α5 integrin. The spatial scale is shown as a bar and the velocity scale is shown as an arrow. The original image dimensions are 512 × 480 pixels at 0.118 μm/pixel and a total of 120 images at 5 s/frame.

CONCLUSION

We have shown that STICS, along with ICS, are powerful tools for the investigation of protein dynamics and interactions, and that STICS provides a way of measuring full directional velocity vectors in the case of concerted macromolecular flow. The applications are not limited by expression levels in the cell, since this technique does not rely on optically resolving and tracking individual molecules, and they do not require any special labeling approaches. Using STICS with ICS, we can distinguish between diffusion, protein flow in random directions, directed flux in a single direction, or a combination of these transport modes. By employing Fourier-filtering with the STICS analysis, we can effectively perform these measurements even in cell membrane environments where there are significant levels of immobile proteins (>90% immobile fraction, simulation results not shown). Gaining directional information helps in understanding complex phenomena such as adhesion formation and disassembly, membrane protein transport, and transport in polarized cell systems. The application of STICCS to double-label cross-correlation experiments also promises new insights into detecting molecular interactions and co-transport of macromolecules in cells.