Imaging α-Hemolysin with Molecular Dynamics: Ionic Conductance, Osmotic Permeability, and the Electrostatic Potential Map

Abstract

α-Hemolysin of Staphylococcus aureus is a self-assembling toxin that forms a water-filled transmembrane channel upon oligomerization in a lipid membrane. Apart from being one of the best-studied toxins of bacterial origin, α-hemolysin is the principal component in several biotechnological applications, including systems for controlled delivery of small solutes across lipid membranes, stochastic sensors for small solutes, and an alternative to conventional technology for DNA sequencing. Through large-scale molecular dynamics simulations, we studied the permeability of the α-hemolysin/lipid bilayer complex for water and ions. The studied system, composed of ∼300,000 atoms, included one copy of the protein, a patch of a DPPC lipid bilayer, and a 1 M water solution of KCl. Monitoring the fluctuations of the pore structure revealed an asymmetric, on average, cross section of the α-hemolysin stem. Applying external electrostatic fields produced a transmembrane ionic current; repeating simulations at several voltage biases yielded a current/voltage curve of α-hemolysin and a set of electrostatic potential maps. The selectivity of α-hemolysin to Cl⁻ was found to depend on the direction and the magnitude of the applied voltage bias. The results of our simulations are in excellent quantitative agreement with available experimental data. Analyzing trajectories of all water molecule, we computed the α-hemolysin's osmotic permeability for water as well as its electroosmotic effect, and characterized the permeability of its seven side channels. The side channels were found to connect seven His-144 residues surrounding the stem of the protein to the bulk solution; the protonation of these residues was observed to affect the ion conductance, suggesting the seven His-144 to comprise the pH sensor that gates conductance of the α-hemolysin channel.

INTRODUCTION

α-Hemolysin of Staphylococcus aureus is a self-assembling 232.4-kDa toxin that binds in its monomeric form to the plasma membrane of a susceptible cell, where it oligomerizes to form a water-filled transmembrane channel (Bhakdi and Tranum-Jensen, 1991; Gouaux, 1998). Uncontrolled permeation of water, ions, and small organic molecules through the transmembrane pore of α-hemolysin may cause death to the host cell via irreversible osmotic swelling leading to cell wall rupture (lysis), dissipation of membrane potential and ionic gradients, and rapid discharge of vital molecules, such as ATP. This pore-forming property of α-hemolysin has been identified as a major mechanism by which proteinaceous exotoxins can damage cells. Among cells highly susceptible to α-hemolysin are blood cells of several types, including human platelets (Bhakdi et al., 1988) and monocytes (Bhakdi et al., 1989), rabbit erythrocytes (Cooper et al., 1964) and macrophages (McGee et al., 1983), endothelial cells of rabbits (Seeger et al., 1990), pigs (Suttorp et al., 1985), and humans (Grimminger et al., 1997), as well as human keratinocytes (Walev et al., 1993). If applied in sufficient dosage, α-hemolysin is expected to permeate any mammalian cell membrane (Bhakdi and Tranum-Jensen, 1991).

The crystallographic structure of the assembled α-hemolysin revealed a heptametic organization of its protomers (Song et al., 1996). An atomic-detail model of α-hemolysin in its native environment is shown in Fig. 1. The protein has a mushroomlike shape, with a 50-Å β-barrel stem protruding from the cap domain through the lipid bilayer into the cell's interior. The cap of the protein conceals a large vestibule connected to the cell's exterior through a large opening at the top of the cap. The narrowest part of the channel is located at the base of the stem, where the β-barrel pore connects to the vestibule. Seven side channels lead from the vestibule to the cell's exterior, exiting near the membrane surface.

FIGURE 1.

Microscopic model of the α-hemolysin channel in its native environment, a lipid bilayer membrane. The channel is drawn as a molecular surface separating the protein from the membrane and water. The surface is colored according to the type of the exposed residues: red, blue, green, and white correspond to negatively charged, positively charged, polar, and nonpolar side chains, respectively. This surface is cut by the plane normal to the lipid bilayer, passing through the geometrical center of the protein. All but phosphorous atoms of the DPPC lipid bilayer are shown in green; the phosphorus atoms are shown as spheres. Water and ions are not shown. The model comprises 288,678 atoms.

Several properties of α-hemolysin make this membrane channel suitable for various biotechnological applications: assembled α-hemolysin is stable over a wide range of pH and temperature, its transmembrane pore is open at normal conditions (Menestrina, 1986), α-hemolysin can bind to various biological or synthetic lipid bilayers (Korchev et al., 1995), and the binding proceeds spontaneously and does not require specific ionic conditions. The transmembrane pore of α-hemolysin can facilitate controlled delivery of ions and small organic compounds such as sugars or nucleotides across a cell's plasma membrane or through the walls of synthetic lipid vesicles (Bhakdi et al., 1993). Using genetically engineered α-hemolysins, for which assembly and conductance can be triggered or switched on or off by external biochemical or physical stimuli including light, a lipid bilayer can be made permeable for small solutes at will (Bayley, 1995; Russo et al., 1997).

Suspended in a lipid bilayer, an α-hemolysin channel becomes a stochastic sensor when a molecular adaptor is placed inside its genetically reengineered stem, influencing the transmembrane ionic current induced by an applied voltage bias. Reversible binding of analytes to the molecular adaptor transiently reduces the ionic current. The magnitude of the current reduction indicates the type of analyte, whereas the frequency of the current reduction intervals reflects analyte concentration. Such stochastic sensors were demonstrated to simultaneously measure, with a single sensor element, concentrations of several organic analytes (Gu et al., 1999) and solution concentrations of two or more divalent metal ions (Braha et al., 2000). The nanometer size pore of α-hemolysin was used in another type of stochastic sensor to simultaneously determine concentrations of two different proteins (Kasianowicz et al., 2001).

The transmembrane pore of α-hemolysin was found to conduct not only small solutes, but also rather big (tens of kDa) linear macromolecules. Thus, driven by a transmembrane potential, DNA or RNA strands can translocate through the pore of α-hemolysin, producing the ionic current blockades that reflect the chemical structure of individual strands (Kasianowicz et al., 1996). Statistical analysis of many such blockage currents allowed the researchers to discriminate different sequences of RNA (Akenson et al., 1999) and DNA (Meller et al., 2000) homopolymers, as well as the segments of purine and pyrimidine nucleotides within a single RNA molecule (Akenson et al., 1999). A single nucleotide resolution has been demonstrated for individual Watson-Crick basepairs at the termini of single DNA hairpins (Vercoutere et al., 2001; Howorka et al., 2001; Vercoutere et al., 2003; Nakane et al., 2004; Mathé et al., 2004), raising the prospect of creating a nanopore sensor (Li et al., 2001; Heng et al., 2004) capable of reading the nucleotide sequence directly from a DNA or RNA strand.

As illustrated by these examples, permeation of water, ions, and solutes through the transmembrane pore of α-hemolysin is central to both the natural function and biotechnological application of α-hemolysin. Measurements have indicated a high sensitivity of the channel conductance to the atomic level detail of the pore and to the structure of the conducted solutes (Menestrina, 1986; Krasilnikov and Sabirov, 1989; Kasianowicz et al., 1996; Akenson et al., 1999; Gu et al., 1999; Braha et al., 2000). The α-hemolysin channel was found to undergo a dose- and voltage-dependent inactivation in the presence of divalent and trivalent cations (Menestrina, 1986). Its ionic conductance as well as anion-selectivity is sensitive to pH and to the chemical composition of the lipid bilayer (Krasilnikov and Sabirov, 1989; Korchev et al., 1995). Understanding these phenomena is a prerequisite for developing successful antitoxin treatments.

The sensitivity of the ionic current to the atomic details of the pore is best illustrated by the performance of the stochastic sensors that can identify protonation states of individual residues forming the walls of the α-hemolysin pore (Kasianowicz and Bezrukov, 1995) or distinguish different types of individual metal ions (Braha et al., 2000). To further advance applications of the stochastic sensors, a method for relating atomic-scale features of the pore and of the analytes to the ionic currents produced upon applying a transmembrane bias should be developed. In particular, as A, C, G, and T nucleotides differ from each other by only a few atoms, achieving the goal of sequencing DNA will require such capability.

Currently, no instrument exists that can visualize permeation of ions and solutes through transmembrane channels at atomic detail. The permeation process, however, can be investigated at atomic resolution through microscopic simulations (Im and Roux, 2002; Miloshevsky and Jordan, 2004). Theoretical models describing ion conductance through α-hemolysin supplemented early experimental studies of the channel (Menestrina, 1986; Krasilnikov and Sabirov, 1989). After the discovery of the crystallographic structure (Song et al., 1996), quantitative studies relying on the atomic structure became possible (Smart et al., 1998; Misakian and Kasianowicz, 2003; Noskov et al., 2004; Cozmuta et al., 2005). Until recently, only small parts of the α-hemolysin channel could be simulated with all-atom molecular dynamics (MD) methods (Shilov and Kurnikova, 2003).

Advances in computational technology permit one today to use MD simulations as a kind of a computational microscope to obtain dynamic images of biomolecular systems. Channels like α-hemolysin now can be investigated as integral units, i.e., in their native environment, and without losing atomic precision. In this method, a molecular system is approximated by an ensemble of virtual atoms interacting with each other according to a molecular force field (Allen and Tildesley, 1987), which has been developed and calibrated to reproduce quantitatively physical properties of the simulated system. The large scale of the simulations, however, may raise concern about the applicability of the force fields describing interactions between atoms, as these force fields were not tested at the time of their development to reproduce physical properties of biomolecular systems of such size. As the results will show, although our simulations are very large, results are highly accurate and compare favorably with experiments.

In this article, we report, to our knowledge, the first MD study of α-hemolysin in situ, i.e., in a lipid bilayer. Our original motivation for conducting this study was examining the capabilities of MD for predicting conductance of large membrane channels like α-hemolysin, when an external electrostatic potential is applied across the membrane. The wealth of information uncovered by our simulations allowed us to perform a thorough analysis of the α-hemolysin properties in its native environment. Below we examine in detail fluctuations of the α-hemolysin structure, the average occupancy of the transmembrane pore, the osmotic permeability, the current voltage dependence, and the selectivity of the α-hemolysin channel. Furthermore, by altering the protonation state of the histidine residues, we observed changes in ionic conductance that agree with the experimentally observed changes when altering pH of the α-hemolysin environment. Hence, we propose below a mechanism for pH-dependent gating of α-hemolysin conductance and selectivity. Finally, we provide the electrostatic potential maps of α-hemolysin at several transmembrane biases and characterize the permeability of the side channels for water and ions.

METHODS

System setup

Atomic coordinates of α-hemolysin were taken from the Protein Data Bank (entry 7AHL). Coordinates of the atoms that were missing in the crystallographic structure (residues dLys-30, gLys-30, aLys-70, dLys-240, fLys-283, and aArg-66) were reconstructed using the psfgen structure building module of NAMD2 (Kalé et al., 1999). All reconstructed residues are located on the periphery of the α-hemolysin cap, far from the α-hemolysin pore.

There are four groups of histidine residues in the α-hemolysin channel, forming concentric circles around the central pore. At pH 8.0, we expect all of them to be neutral. The CHARMM27 force field provides a choice of two atomic topologies describing neutral histidines: in the HSE state, the shared proton is localized on atom NE2, whereas in the HSD state, the shared proton is localized on atom ND1. Histidines 35 and 48, which are located at the interface of two adjacent protomers, were found to be critical for lysis activity and oligomerization of the toxin (Pederzolli et al., 1991a; Walker and Bayley, 1995). Conformations of their neighboring (in the x-ray structure) residues suggest the HSE state of His-35 and His-48, as it enables the interprotomer hydrogen bonds between His-35 and Ile-95 and Tyr-101, as well as between His-48 and Thr-22 and Asp-24. The formation of these hydrogen bonds was confirmed during the equilibration. Analysis of the x-ray structure does not suggest any particular (neutral) protonation state of His-144 and His-259; therefore, the protonation states of these residues were chosen to be the same as those of His-35 and His-48. In our subsequent MD runs, we found aromatic rings of both His-144 and His-259 residues changing their orientations within several nanoseconds, which led us to believe that the initial choice of the (neutral) protonation state for this residues should not have a dramatic effect on ion conductance (contrary to changing the protonation state from neutral to charged).

The x-ray structure of the α-hemolysin channel contains 818 water molecules, most of which are located in the water-exposed “cap” and “rim” parts of the protein. Additional 313 water molecules were placed inside the internal cavities of the protein using the Dowser program (Zhang and Hermans, 1996). After that, a 3 Å layer of water was created around the entire protein using the Solvate program (Grubmüller et al., 1996), which also populated the transmembrane pore and the seven side channels with water.

The resulting structure was oriented in space to align the symmetry axis of the transmembrane pore with the z axis. A patch of a preequilibrated and solvated DPPC lipid bilayer was oriented parallel to the x, y plane. The protein was embedded into the membrane; the center of mass of α-hemolysin's hydrophobic belt (residues 118–126 and 132–142) was aligned with the center of mass of the lipid bilayer. All lipid molecules that overlapped with the protein stem were removed, along with all water molecules around the stem of the protein that overlapped with the lipid bilayer.

The protein-lipid complex was solvated in a rectangular volume of preequilibrated TIP3P (Jorgensen et al., 1983) water molecules. Corresponding to a solution concentration of 1 M, K⁺ and Cl⁻ ions were added at random positions that located at least 4 Å away from the protein and the membrane, and 3 Å away from each other. The final system (Fig. 1) measured 135 × 137 × 148 ų in size and included 288,678 atoms.

We performed 2000 steps of minimization followed by gradual heating from 0 to 295 K in 3 ps. The system was then equilibrated in the NpT ensemble for 1.3 ns with the backbone of the protein restrained, and for another 3.0 ns without any restraints, keeping the ratio of the unit cell in the x, y plane constant while allowing fluctuations along all axes. The protein structure was monitored during the equilibration. After 1.3 ns of the unrestrained equilibration, the root mean-square deviation of the backbone atoms from the initial structure reached 1.6 Å and remained at this level for the rest of the equilibration.

When merging the protein with the lipid bilayer, the rim of the protein overlapped with the initially flat bilayer, inducing through steric repulsion a complementary depression on the lipid bilayer (Fig. 1). During the minimization and the following equilibration with the backbone of the protein restrained, the lipids adjusted their conformations, minimizing the steric hindrances with the rim of the protein. In accordance with the recent high resolution crystallographic structure (Galdiero and Gouaux, 2004), we found lipid headgroups in the pockets of the rim domain as well as in the rim-stem crevice (Fig. 1). These lipids, however, did not bind tightly to the protein; their conformations were observed to undergo large fluctuations.

During the unrestrained equilibration, we observed a small (up to 10%) asymmetric compression of the transmembrane pore (see also Fig. 5). At the end of the equilibration, the area per lipid reached 62 Ų, which is comparable to the expected value for a DPPC bilayer in a fluid phase, namely, 64 Ų at 50°C (Nagle and Tristram-Nagle, 2000). Although the temperature of equilibration was set below the gel phase transition point, which is ≈41.5°C (Cevc and Marsh, 1987), the lipid bilayer did not undergo the transition to the gel phase during the equilibration (the lipid bilayer was initially in the fluid phase). We noticed, however, that at the end of our more than 20 ns simulations in the NVE ensemble, which followed the initial equilibration (see Results), the DPPC bilayer underwent partial transition into the gel phase: the lipid tails aligned with each other, forming an angle of ≈20° with the normal to the lipid bilayer; the lateral arrangement of the lipids developed a local hexagonal order.

FIGURE 5.

Asymmetry of the transmembrane pore. (Top) The ratio of the inertia moments of water inside the stem part of α-hemolysin, averaged over a 50 ns MD simulation. The inset shows a typical conformation of the transmembrane pore, viewed from the trans side (cf. Fig. 1). The cross section of the stem is an ellipse, on average. The longer axis of the elliptical cross section was observed to align with the boundary of two adjacent protomers. (Bottom) Normalized distribution of the angle that is formed by the major axis of the ellipse and the x axis. The distribution has two maxima, reflecting the two (out of seven) most frequent orientations of the ellipse. The reorientation of the cross section was observed to occur within several ns.

MD methods

All our MD simulations were performed using the program NAMD (Kalé et al., 1999), the CHARMM27 force field (MacKerell et al., 1998), periodic boundary conditions, and particle-mesh Ewald (PME) full electrostatics (Batcho et al., 2001) with a dielectric constant ε₀ = 1. The latter was computed over 96 × 96 × 96 and 128 × 128 × 128 grids. To speed up our calculations, most of our simulations were carried out with the coarser (96 × 96 × 96) PME grid. The only noticeable consequence of that, if compared to the 128 × 128 × 128 grid, was a larger drift of the system center of mass, which was eliminated by aligning the resulting trajectories with the x-ray structure (this procedure is described in more detail in the next section). The temperature was kept at 295 K by applying Langevin forces (Brünger, 1992) to all heavy atoms of the lipid tails; the Langevin damping constant was set to 1 ps⁻¹. The integration time step chosen was 1 fs. The equilibration in the NpT ensemble was performed using the Nosé-Hoover Langevin piston pressure control (Martyna et al., 1994) at 1 bar. Van der Waals energies were calculated using a smooth (10–12 Å) cutoff. Restraints were imposed by harmonic forces; the force constants were set to 1 kcal/(Ų mol). All simulations at a nonzero external electric field were carried out in the NVTH ensemble.

Ionic current

To measure the current/voltage dependence, a uniform electric field, directed normal to the lipid bilayer, was applied to all atoms in the system. The field induced, at the beginning of the simulation, a rearrangement of the ions and water that focused the electric field to the vicinity of the membrane and the protein, abolishing the field gradient in the bulk. The resulting transmembrane voltage bias V depended both on the magnitude of the applied field E and on the extension of the system along the z axis L_z: V = − EL_z (Crozier et al., 2001; Aksimentiev et al., 2004). Note that although the applied electric field is uniform, the resulting total electrostatic potential around the protein is nonuniform, and complies with the local dielectric properties of the protein and the membrane (for an example, see Fig. 2). In real solution, the condition of zero field in the bulk requires concentration of ions of the same charge as the change of the electrodes at the membrane boundary. An opposite layer must be formed on the other side of the same bulk compartment, near the electrode. If an MD simulation is carried out without periodic conditions, the boundary of the simulation cell must fulfill the role of polarizing electrode, attracting ions of the opposite charge. Under periodic conditions, which are deployed in all our simulations, this role is fulfilled by the opposite surface of the membrane in the cells above and below.

FIGURE 2.

Electrostatic potential maps of α-hemolysin. (a) A cut through the averaged (over an 11.2 ns simulation and the sevenfold symmetry of α-hemolysin) electrostatic potential along the z axis. A 0.6 V transmembrane bias was applied in this simulation. The average was taken over the instantaneous potentials computed by solving Poisson's equation; all point charges were approximated by Gaussians of inverse width β = 0.258 Å⁻¹. (b) Same as in a, but β = 0.395 Å⁻¹. (c) Profiles of the electrostatic potentials along the transmembrane pore of α-hemolysin. The red circles and the black squares correspond to β = 0.258 Å⁻¹ and β = 0.395 Å⁻¹, respectively. The black lines indicate fluctuations of the electrostatic profile in time (β = 0.395 Å⁻¹). (d) The electrostatic radii of the channel (see text). The symbols have the same meaning as in c.

To compute ionic currents, coordinates of all atoms were recorded every picosecond. At time t, the instantaneous ionic current is

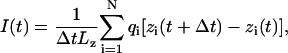(1)

where z_i and q_i are the z coordinate and the charge of atom i, respectively. The sum in Eq. 1 runs over the volume of interest, which in our case was either the entire system or the channel's interior; the K⁺ and Cl⁻ currents were computed by running the sum over the atoms of corresponding type. To avoid a systematic error introduced by the drift of the center of mass of the entire system, before computing the instantaneous currents, all recorded snapshots of the system were aligned with the snapshot taken at the beginning of the simulation, using the position and the orientation of the protein as a reference. To compute an average current at a given bias, instantaneous currents I(t) were first integrated to produce a cumulative current curve; applying a linear regression fit to the cumulative current curve yielded the average current. The choice of Δt in Eq. 1 did not influence the resulting average currents when varied from 1 to 10 ps. The voltage signs will be referred to relative to the bulk of the cis compartment (Fig. 1); a current is defined as positive when cations flow into this compartment.

Electrostatic potential map

To visualize a distribution of the electrostatic potential in our simulations, we recorded internal electrostatic potentials computed by our molecular dynamics engine, NAMD (Kalé et al., 1999). NAMD evaluates long-range electrostatic forces via PME (Batcho et al., 2001). Every point charge is approximated by a spherical Gaussian (Essmann et al., 1995)

(2)

normalized to give the original charge upon integration. The positive parameter β determines the width of the Gaussian. The electrostatic potential is obtained by solving the Poisson equation

(3)

where the sum runs over all atoms. Equation 3 is solved numerically on the grid using fast Fourier transforms; the grid density determines the accuracy of the resulting potential.

To determine the mean electrostatic potential, instantaneous electrostatic potentials φ(r) were averaged over the entire MD trajectory. The resulting potential was averaged over the sevenfold symmetry of α-hemolysin. A cut through such an average, in our case, along the x, z plane, yields an electrostatic potential map; Fig. 2, a and b, show examples of such maps. Both maps originated from the same 11.2 ns simulation, in which we applied a 0.6 V bias. These maps differ by their resolution, reflecting different inverse widths β of Gaussians that approximated the distributions of atomic charges before computing instantaneous potentials φ(r). As might be expected, increasing β increased the resolution of the map but did not alter its shape. Further increase of the resolution decreased the convergences of the time average. The computation of the average electrostatic maps can be carried out with the PME electrostatics module of NAMD (Kalé et al., 1999).

From the three-dimensional potentials, we can extract a mean profile of the electrostatic field along the transmembrane pore of α-hemolysin. To take the average over the volume confined by the pore, this volume was divided into a set of disk-shaped segments. Each segment was assigned a 0.75 Å initial radius, which was then gradually increased in 0.25 Å increments, until the average potential within the newly added volume became by 25 mV greater than the average over the entire segment. The radius R_E(z), at which these iterations terminated, defined the volume inside the pore accessible for positive ions. Outside the channel, R_E was set to 46 Å. For the electrostatic potentials shown in Fig. 2, a and b, the mean electrostatic profiles V_pore(z) and the electrostatic radii R_E(z) are plotted in Fig. 2, c and d, respectively. Changing the resolution of the potentials had a minor effect on V_pore(z) and R_E(z).

For any cross section, we found the electrostatic radius of the pore R_E(z) smaller than the radius of the van der Waals surface approximating the pore walls. Therefore, the profile R_E(z) defines the cation-accessible space inside the pore, which also implies that the pore has a wider cross section for anions. This alone, however, cannot explain the anion selectivity of the α-hemolysin channel, because the magnitude of the applied field was not found to affect the electrostatic radius R_E(z), contrary to the channel's selectivity (see Results).

Determining the osmotic permeability from equilibrium simulations

The method for determining the osmotic permeability for water of a membrane channel has been described in detail and validated elsewhere (Zhu et al., 2004). In brief, a collective coordinate of all water molecules inside the channel, n, is defined as

(4)

where S(t) denotes the set of water molecules in the channel at time t, L is the length of the channel (the latter is assumed to align with the z axis), and dz_i is the displacement of water molecule i in the z direction during dt. Demanding n = 0 at t = 0, n(t) can be uniquely determined by integrating dn. If a water molecule enters or exits the channel within the sampling interval dt, only the portion of its displacement within the channel contributes to the sum.

To obtain a quantitative measure of water diffusion through the channel, all available trajectories n(t) are concatenated into a single one. The resulting trajectory is divided equally into M short pieces such that each subtrajectory n_j(t) (j = 1, …M) has length t_M and is treated as an independent subtrajectory. After shifting each subtrajectory to provide n_j(t)|_{t = 0} = 0, the mean- square displacement (MSD) of n(t) over the t_M interval is

(5)

At equilibrium, n(t) can be described as a one-dimensional unbiased random walk, with a diffusion coefficient D_n that obeys

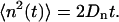(6)

A linear regression fit to the plot of MSD(t_M) versus t_M yields the collective diffusion coefficient D_n of water inside the channel. The osmotic permeability of a channel p_f is related to D_n according to (Zhu et al., 2004)

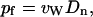(7)

where v_W is the average volume of a single water molecule (18 cm³/mol).

Transport properties of the KCl electrolyte

The outcome of a molecular dynamics simulation depends on the choice of parameters describing the interatomic interactions in the simulated system, i.e., the molecular force field. To estimate a systematic error introduced into our simulations by the imperfections of the CHARMM27 force field, we carried out a set of test simulations to determine the transport properties of the KCl electrolyte.

As a test system, we chose a cube of preequilibrated TIP3P water molecules, with K⁺ and Cl⁻ ions added at random positions, amounting to a desired concentration. Each system was first equilibrated for 1 ns in the NpT ensemble. Subsequently, an external electric field was applied along the z axis to induce electromigration of the ions. The latter simulations were performed in the NVT ensemble; the temperature was controlled by the Langevin thermostat that applied to all nonhydrogen atoms. The damping effect of the Langevin forces on the mobility of the ions was found to be negligible when the Langevin coupling constant was set to 0.2 ps⁻¹ or lower. Coordinates of all atoms were recorded every picosecond; the ionic currents were computed using Eq. 1.

The results of our test simulations are summarized in Fig. 3. The total ionic current I in a 1 M solution of KCl was found to be linearly proportional to the applied electric field E (Fig. 3 a), yielding a bulk conductivity κ of 12.3 S/m, which is close to the measured conductivity of 11.0 S/m. We note, however, that this rather good agreement between experiment and simulation is likely due to the cancellation of the imperfections of the force field, and is not due to an absolute accuracy of the latter, as the TIP3P model of water deployed in our simulations with the CHARMM27 force field does not reproduce quantitatively transport properties of bulk water (Lamoureux et al., 2003; Yeh and Hummer, 2004).

FIGURE 3.

Bulk conductivity of KCl. (a) Ionic current I versus applied electrical field E. Each point derived from a 1 ns simulation. A linear regression fit, shown as a solid line, yielded a bulk conductivity of 12.3 S/m. (b) Conductivity κ of 1 M KCl (squares) and of 0.1 M KCl (diamonds) versus the size of the simulated system L = (L_xL_yL_z)^1/3. The dashed lines indicate the experimental value at 22.5°C, i.e., 11.0 and 1.2 S/m, respectively. The variation of the simulated conductivity with L is <10% at both concentrations. (c) Conductivity κ versus molar concentration c. Kohlrausch's law (Atkins, 1998) ( where Λ₀ = 14.98 mS m²/mol is the limiting molar conductivity of KCl) is plotted as a dashed line; black diamonds show experimentally measured conductivities (Coury, 1999). (d) Molar conductivity Λ_m = κ/c versus molar concentration c. The dashed line and the solid diamonds have the same meaning as in panel c. The simulated molar conductivities deviate from theory and experiment at intermediate concentrations, but converge to experimental values at low and high salt conditions.

Changing the size of the simulated system L did not alter the bulk conductivity of 1 M KCl (Fig. 3 b), indicating that the latter is not affected by the finite size of the simulated system. As might be expected, the conductivity κ of the KCl solution increases with its concentration c (Fig. 3 c); however, the simulated dependence does not comply with Kohlrausch's law (Atkins, 1998). Kohlrausch's law, shown as a dashed line in Fig. 3 d, predicts that the molar conductivity Λ_m decreases as a square root of the electrolyte concentration, whereas the simulated dependence is nonmonotonic. This deviation of the simulated conductance from Kohlrausch's law is not an artifact of the finite size system, because the conductance of KCl at 0.1 M does not depend on the system size (Fig. 3 b). Despite this qualitative discrepancy, the absolute values of the measured and simulated conductivities agree well with each other, in particular, at high and low salt conditions.

The currents resulting from electromigration of Cl⁻ and K⁺ ions at 1 M concentration are given in Table 1. To account for the drift of the center of mass of the simulated system due to a nonzero momentum arising from PME electrostatics and Langevin thermostat, the currents given in Table 1 were computed relative to the motion of the center of mass of all ions. Although these simulations were carried out for periodic boundary conditions, the output coordinates were not wrapped to the same unit cell. The simulated ratio of the currents was found to be independent of the applied electric field and equal to 1.10, which is in agreement with the experimentally measured ratio of the limiting molar conductivities (low salt conditions), 1.04 (Coury, 1999).

TABLE 1.

K⁺ and Cl⁻ currents in a 1 M solution of KCl; the total currents are plotted in Fig. 3 a

Electric field (V/10 nm)	0.082	0.164	0.410	0.819
ICl (nA)	2.93	5.91	14.1	28.7
IK (nA)	2.66	5.35	12.8	26.0
ICl/IK	1.10	1.10	1.10	1.10

RESULTS AND DISCUSSION

We carried out a total of ∼100 ns simulations of the α-hemolysin channel in its native environment. After the system had been assembled (see Methods), external electric fields of different magnitudes were applied to measure the current/voltage dependence. The RMSD of the protein gradually increased with time, but did not exceed 2.8 Å. Large structural fluctuations were observed in the loops of the protein at the trans end of the β-barrel (residues 127–131 that are located in the beginning of the stem). In addition to an initial 4.3-ns equilibration in the NpT ensemble, the system was also equilibrated for 4 ns in the NVT ensemble.

To study the effect of pH on the ion conductance of α-hemolysin, the protonation states of His-144 and His-259 were changed from neutral to protonated; additional ions were introduced to keep the entire system neutral. As these changes were carried out on the already equilibrated structure, we performed only a short, 50 ps, equilibration of the modified structure before applying external electric fields. In the remainder of this study, the system having all histidines neutral will be referred to as a pH 8.0 structure, whereas a pH 4.5 structure will refer to that with His-144 and His-259 protonated. Location of these residues is indicated in Fig. 1. The above pH values should not be taken literally, as they only indicate the protonation states of the histidines.

Structural fluctuations and occupancy of the transmembrane pore

Unlike the previous simulations of α-hemolysin (Shilov and Kurnikova, 2003; Noskov et al., 2004; Cozmuta et al., 2005), in our simulations no artificial forces restrained the conformation of α-hemolysin after completing the initial equilibration. As the design of our systems mimics the natural environment of assembled α-hemolysin, our simulations provided a realistic account of the structural fluctuations occurring in vivo or in vitro, on the timescale of 0.1 μs or less.

Analysis of the structural fluctuations was carried out on all MD trajectories originating from the pH 8.0 structure; the total duration of the analyzed trajectories amounts to ∼50 ns. The application of the external electric field was not observed to influence fluctuations of the α-hemolysin structure described below.

To identify the volume occupied by water inside the transmembrane pore, we divided the interior of the channel into disk-shaped segments centered around the symmetry axis of the channel. Each disk was assigned a 5 Å initial radius, which was then gradually increased in 0.5 Å increments until the ratio of water to nonwater atoms within the shell defined by the subtraction of two consecutive segments dropped below 20%. The channel's profile was sampled every 3 Å. The top and the bottom boundaries of the channel were defined to encompass the entire x-ray structure. We could deploy this method for identifying the boundaries of the α-hemolysin pore, because the density of water falls sharp near the pore walls.

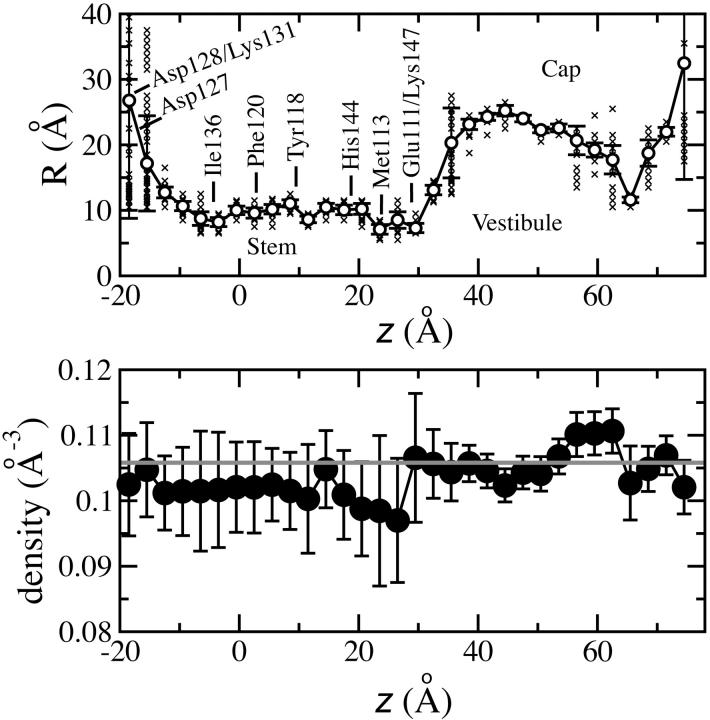
Fig. 4 (top) illustrates the average radial profile of the internal volume of the α-hemolysin channel occupied by water. The average was taken over a 50-ns-long collection of MD trajectories originating from the pH 8.0 structure. The narrowest parts of the pore are located at z = 23.5 Å (Met-113) and z = 29.5 Å (Lys-147 and Glu-111); their average radii are 7.1 ± 0.7 and 7.3 ± 0.7 Å, respectively.

FIGURE 4.

Structural fluctuations and occupancy of the transmembrane pore of α-hemolysin. (Top) The average radial profile of the transmembrane pore (circles). The average was taken over a 50 ns MD trajectory; the averaging method is described in the text. The error bars indicate the standard deviations of the average radii due to structural fluctuations of the pore. The lipid bilayer is centered at z = 0. The small symbols (x) display the distribution of the local radii during the 50 ns simulation. (Bottom) The average atomic density inside the transmembrane pore, defined by the radial profile shown at the top. The error bars indicate the standard deviations of the average. The shaded line shows the average number density of the entire system. The data suggest that water always fully occupies the internal volume of the transmembrane pore.

The error bars in Fig. 4 (top) indicate the standard deviations of the average radii due to structural fluctuations of the pore. Overall, the channel's structure appeared to be rather rigid. The radial boundaries of the channel are diffuse at z = 36 Å, where the seven water-filled side channels connect to the vestibule. Large fluctuations of the radial profile at both ends of the channel are artifacts of our measuring method.

The average occupancy of the channel is shown in Fig. 4 (bottom). The averaged density of all atoms inside the channel (solid circles) is close to the averaged atomic density of the entire system (shaded line). The density of atoms inside the pore fluctuates very little in time, indicating that the transmembrane pore of α-hemolysin is always filled with water, unlike the pore of MscS (Anishkin and Sukharev, 2004; Sotomayor and Schulten, 2004), or a generic hydrophobic nanopore of a similar radius (Beckstein et al., 2001).

Although the radial profile of the channel does not change much in time, the pore continuously undergoes structural fluctuations. A typical conformation of the transmembrane pore is shown in Fig. 5 (top); the stem of the channel has an elliptic cross section, on average. To characterize this asymmetry quantitatively, we computed the principal moments and axes of inertia of the water slab confined within the stem part of the transmembrane pore. The biggest moment of inertia was always oriented along the pore; the ratio of the second to the third moments gave a quantitative measure of the pore asymmetry. A normalized distribution of this ratio is shown in Fig. 5 (top). Visually, the asymmetry of the pore appears greater than is suggested by the ratio of the inertia moments. This is explained by the fact that the ratio of inertia moments measures the average asymmetry of the entire water slab, whereas the snapshot depicts its most asymmetric projection.

Visual examination of the asymmetric conformation of the stem with VMD (Humphrey et al., 1996) revealed that the orientation of the elliptical cross section changes with time. In Fig. 5 (bottom), we plotted a normalized distribution of the angle formed by the major axis of inertia with the x axis. The distribution has two maxima, separated by ≈51 (360/7) degrees, which conforms with the heptameric organization of the channel. When viewed from the trans side, the longer axis of the elliptical cross section aligns with the boundary of two adjacent protomers. Larger distortions were observed to take place at both ends of the stem. Physiological implications of this highly favorable asymmetric conformation require further investigation.

Osmotic permeability for water of the transmembrane pore

Fig. 6 illustrates diffusion of water through the α-hemolysin channel at different simulation conditions. The collective coordinate of all water molecules inside the channel, n(t) (see Methods), is plotted versus time. At first look, neither the sign nor the magnitude of the transmembrane potential has a noticeable deterministic effect on the shape of the trajectories. However, after taking into account the voltage-dependent selectivity of α-hemolysin (see also below), we noticed that the total amount of water permeated through the α-hemolysin pore at a given voltage bias, as shown in Fig. 6, correlates with the total number of ions transported by the electric field from one side of the membrane to the other (see Table 2). The number of water molecules coupled to each transported ion is on average nine, which is in agreement with a previous estimate (Gu et al., 2003). These electroosmotic effects, apparent on the timescale of 10 ns, were not found to influence the collective diffusion of water on the timescale of 100 ps or less, and, therefore, all trajectories were considered as free equilibration for the purpose of computing the osmotic permeability of water.

FIGURE 6.

Computing the osmotic permeability of α-hemolysin for water. The collective coordinate of all water molecules inside the channel, n(t), (Eq. 4) is plotted versus time. n(t) quantifies the net amount of water permeation through the channel. (Inset) Mean-square displacement of n(t) versus time. The calculations were carried out with two sets of boundaries: −15.5 < z < 71.5 (squares) and −3.5 < z < 65.5 (circles) (cf. Fig. 4, top). A linear regression fit to the MSD curves yields the collective diffusion constant of water of 310 ± 10 molecules²/ns, which gives, after taking into account a correction for the low viscosity of TIP3P water, the osmotic permeability for water of 1.9 × 10⁻¹²cm³/s (see text).

TABLE 2.

Ion conductance of α-hemolysin

pH	bias (V)	Itotal (pA)	Ntotal	ICl (pA)	NCl	IK (pA)	NK	Simulation time (ns)
8.0	1.2	1360	44.1	490	15.9	870	28.2	5.23
8.0	0.6	700	48.8	300	19.7	400	28.9	11.22
8.0	0.24	280	20.2	140	11.0	140	9.2	10.56
8.0	0.12	130	6.3	70	3.5	60	2.8	8.92
8.0	0.0	−10	0.0	20	1.4	−30	−1.4	8.30
8.0	−0.12	−110	8.0	−10	1.6	−100	6.4	11.02
8.0	−0.24	−160	11.8	−90	8.2	−70	3.6	12.44
8.0	−1.2	−950	30.0	−580	17.7	−370	12.3	4.96
4.5	1.2	1460	50.3	600	21.5	860	28.8	5.42
4.5	0.6	720	27.8	330	13.0	390	14.8	6.42
4.5	0.24	200	13.6	130	8.8	70	4.8	11.04
4.5	−0.24	−280	17.3	−140	8.3	−140	9.0	10.81
4.5	−0.6	−390	13.5	−330	9.8	−60	3.7	6.00
4.5	−1.2	−520	26.8	−390	19.6	−130	7.2	7.29

The average currents were computed by applying a linear regression fit to the cumulative current curves (cf. Fig. 11). The number of ion permeations was computed by dividing the total charge transported through the channel by the unitary charge (1.6 × 10⁻¹⁹C).

The collective diffusion coefficient, D_n, was determined from n(t) by plotting the MSD versus time, as shown in Fig. 6 (inset). The calculations were carried out with two sets of boundaries: −15.5 < z < 71.5 (squares) and −3.5 < z < 65.5 (circles) (see Fig. 4 (top) for the definition of z). A linear regression fit to both curves yielded the collective diffusion constant of 310 ± 10 molecules²/ns. From Eq. 7, the osmotic permeability of the α-hemolysin channel is found to be 5.6 × 10⁻¹² cm³/s.

Experimentally, the average single-channel permeability of α-hemolysin for water was found to be in the range of 1.3–1.5 × 10⁻¹² cm³/s (Paula et al., 1999), depending on pH of the solution. The factor 3 discrepancy between these results and our simulations originates from the properties of the TIP3P model of water that is known to underestimate the viscosity of water by a factor of 2.87 (Yeh and Hummer, 2004). After scaling down the computed osmotic permeability to account for the low viscosity of TIP3 water, we obtain a permeability of 1.9 × 10⁻¹² cm³/s, which is much closer to the experimental value.

The permeability of the side channels for water and ions

In addition to the main transmembrane pore, the vestibule of the α-hemolysin channel is connected to the bulk at the cis side through a maze of side channels that penetrate the walls of the vestibule at the junctions of two adjacent protomers. A cut through the upper part of a side channel, where it connects to the vestibule, is shown in Fig. 1; ∼5–7 Å away from the vestibule, the side channels turn into several beds, and their boundaries become difficult to visualize. Due to these highly irregular boundaries, we limited our investigation of the permeability of the side channels to qualitative observations.

To investigate if water can permeate through the side channels, we took a random MD trajectory and selected several hundred water molecules that occupied, at the beginning of the simulation, the most narrow part 20 Å < z < 30 Å of the transmembrane pore. We followed the trajectory of each selected molecule, visually identifying those that appeared to permeate through the walls of the protein.

In Fig. 7, we present four such trajectories, sampled every 20 ps. Red, blue, orange, and yellow spheres indicate the positions of the water oxygens; all trajectories started in the interval 20 Å < z < 30 Å inside the transmembrane pore (for clarity, some parts of the trajectories are not shown). As indicated by the red spheres, water can pass from the vestibule of the α-hemolysin channel to the bulk at the cis side directly through the interface of two adjacent protomers. Another water molecule, represented by blue spheres, took initially the same path as the red one, but instead of going directly to the bulk, moved down into the rim-stem crevice. This molecule continued to diffuse within the rim-stem crevice, entering at the end of the trajectory the neighboring side channel, to which the orange trajectory led directly from the vestibule. These observations revealed that the side channels are interconnected through the rim-stem crevice. The yellow trajectory illustrates another water molecule diffusing along the side channel into the rim-stem crevice. At the end of the trajectory, this water molecule hydrated lipid headgroups.

FIGURE 7.

Diffusion of water through side channels of α-hemolysin. Red, blue, orange, and yellow spheres illustrate positions of four water oxygens during a 3 ns simulation. At the beginning of the simulation, these water molecules located in the 20 Å < z < 30 Å portion of the transmembrane pore (cf. Fig. 4, top). For clarity, three protomers are shown in cartoon representation (white, pink, and cyan), whereas the other four are shown as a solvent-excluded surface (green). After entering the side channel from the vestibule, water was found to diffuse either directly to the bulk (red trace) or into the rim-stem crevice (blue, orange, and yellow traces). Water was also observed to diffuse around the stem through the rim-stem crevice, visiting several side channels (blue), and to diffuse directly into the crevice from the bulk (data not shown). See also Fig. 1.

The number of water molecules within the rim-step crevice was not observed to change deterministically in time. Within the ring-shaped volume defined as x² + y² > 15², x² + y² < 35², and 16 < z < 30, we found ∼480 ± 20 water molecules. After ∼11 ns, only one-fifth of these molecules remained within the same volume, indicating that water in the rim-step crevice is mobile.

When assembling the system, ions were not placed in any of the internal cavities of the protein, including the side channels. Within the 50 ns of analyzed MD trajectories, we observed only one Cl⁻ ion entering the side channel from the bulk, permeating all the way to the junction of the side channel with the vestibule. From the vestibule side, both K⁺ and Cl⁻ ions were observed to visit transiently the opening of the side channel, but never completed the permeation. These observations, together with the electrostatic potential maps (discussed below), suggest that the side channels can conduct ions, although the rate of conduction is apparently rather small, ∼1 ion per 50 ns.

The electrostatic potential map

Fig. 8 displays the average electrostatic maps of α-hemolysin at +120 mV (left) and −120 mV (right) transmembrane biases. The corresponding average electrostatic profiles along the symmetry axis of the α-hemolysin pore are shown in Fig. 9. These maps were computed by averaging the instantaneous solutions of the Poisson equation over the entire MD trajectories, sampled every 10 ps (see Methods). The distributions of the electrostatic potential is qualitatively similar to that at a 0.6 V bias (cf. Fig. 2). Away from the lipid membrane and the protein, the potential is uniform. The stem part of the channel confines most of the electrostatic potential gradient that drives the ionic current; the vestibule of the protein is equipotential with the bulk at the cis side. This is in agreement with the previous estimates of the electrostatic potential derived from the binding kinetics of individual oligonucleotides inside the α-hemolysin cap (Howorka and Bayley, 2002).

FIGURE 8.

Electrostatic potential maps of α-hemolysin at +120 mV (left) and at −120 mV (right) transmembrane bias. Each contour plot is a cut through the three-dimensional potential along the x, z plane. The maps were averaged over 9 (left) and 11 (right) ns trajectories. Color coding of the potential values is indicated on the right. All charged atoms contribute to the electrostatic maps shown (see Methods). The average profiles along the symmetry axis of the α-hemolysin pore are plotted in Fig. 9.

FIGURE 9.

Average electrostatic potential along the symmetry axis of the α-hemolysin pore at +120 (circles) and −120 (squares) mV bias. The locations of the maxima in both profiles (indicated by vertical arrows) correlate with that of the average relative ion occupancy of the channel (cf. Fig. 10). Diamonds indicate the electrostatic profile at a zero external bias. Due to its low resolution, the zero bias potential has only a qualitative meaning. Lipids and protein are overlaid geometrically faithfully.

In all electrostatic maps computed, the interior of the lipid bilayer appears positively biased by ∼800 mV relative to the bulk of the solution. This is in agreement with the experimentally measured dipole potential of a DPPC bilayer in a gel phase of 575 mV (Simon and Mcintosh, 1989).

We found that the pockets of water in the rim domain of the protein and in the rim-stem crevice are equipotential with the bulk solution at the cis side. Along the side channels leading from the bulk at the cis side to the vestibule of the protein, the electrostatic barriers are <200 mV, indicating that these channels may be permeable for ions, although their conductivity should be much smaller than that of the transmembrane pore.

The average electrostatic profiles along the symmetry axis of the α-hemolysin pore at ±120 mV are shown in Fig. 9. The drop of the potential across the stem part of the channel is nonuniform, having three local maxima, regardless of the direction of the transmembrane bias. The locations of the maxima correlate with the occupancy of the channel by K⁺ and Cl⁻ ions, as shown in Fig. 10.

FIGURE 10.

Distribution of ions inside the pore of α-hemolysin. (Top) Average normalized densities of K⁺ and Cl⁻ ions. (Inset) The total number of K⁺ and Cl⁻ ions increases during the equilibration. (Bottom) Relative occupancy of the α-hemolysin channel. This plot was obtained by dividing the density of Cl⁻ ions by that of K⁺, and averaging over different simulation conditions (all trajectories originated from the pH 8.0 structure). The error bars indicate the standard deviation of the average over different simulation conditions (see Table 2).

Our method for computing the average electrostatic potential maps takes into account contributions from all charged atoms in the system, including the ions confined inside the channel. The application of an external bias facilitates sampling of the channel's interior by the ions, and, thereby, averaging of the electrostatic potential. Computing, to the same accuracy, the average electrostatic potential without applying an external bias requires longer simulation times. Therefore, the average electrostatic profile at equilibrium, shown in Fig. 9 by diamonds, has a lower resolution than similar profiles computed at ±120 V. As a consequence of the insufficient sampling, the three peaks, apparent in the stem region of the pore at ±120 V, could not be resolved at 0 V. The two main features of the equilibrium potential, i.e., the well at the beginning of the stem and the barrier at the constriction region, coincides with the location of the charged residues in the α-hemolysin structure, Figs. 1 and 4. Due to its low resolution, the electrostatic potential at zero bias has only a qualitative meaning.

The distribution of ions inside the transmembrane pore

To compute the average density of K⁺ and Cl⁻ ions, the volume inside the channel was discretized along the channel axis Fig. 4 (top). The average was taken over all trajectories that originated from the pH 8.0 structure. The resulting density profiles are shown in Fig. 10.

Before computing the average densities, we noticed that the total number of all ions inside the channel depends on the magnitude of the electric field applied in the simulation. This number was found to vary from 50 to 70; higher electric fields were observed to produce higher concentration of ions. The total number of ions can also evolve in time: during the 8.2 ns equilibration, the total number of ions inside the α-hemolysin channel increased from 27 to 53 (Fig. 10, inset). On average, the total amounts of K⁺ and Cl⁻ ions occupying the α-hemolysin pore were comparable.

Fig. 10 (top) illustrates the averaged (over 50 ns) distributions of K⁺ and Cl⁻ ions inside the α-hemolysin channel. Before averaging over all MD trajectories, all instantaneous distributions were normalized to unity. K⁺ ions were observed to accumulate at both ends of the channel. The stem region confines only up to 20% of all ions that are in the channel.

The relative occupancy of the channel is shown in Fig. 10 (bottom). The occupancy was obtained by dividing the density of Cl⁻ ions by that of K⁺, and averaging over different simulation conditions. The resulting relative occupancy has a well-defined profile. In the cap domain, Cl⁻ ions have a slightly higher concentration, which becomes four times the concentration of K⁺ ions at z = 30 Å. In that part of the protein, the stem connects to the vestibule; the inner wall of the vestibule at the bottom is positively charged. At z = 20 Å, the concentration of K⁺ ions is twice the concentration of Cl⁻ ions; at z = 11 Å, the ratio is reversed. Another region with an increased concentration of K⁺ is located near z = 5 Å. This intricate dependence of the relative ion occupancy is rather unexpected, as the inner wall of the stem does not contain any charged residues from z = −18 Å to z = 23 Å (see Fig. 1). The profile of the relative ion occupancy conforms to the average electrostatic potential shown in Figs. 8 and 9.

Overall, the distributions of K⁺ and Cl⁻ ions agree qualitatively with the distributions computed by Brownian dynamics and Poisson-Nernst-Plank electrodiffusion theory (Noskov et al., 2004). We note, however, that, although detailed quantitative comparison of the distributions is not possible, the relative ion occupancies of the stem region of the protein are different. This difference could originate from the protonation states of His-144 which were neutral in our study and protonated in Noskov et al. (2004), as well as from the replacement of the lipid bilayer by a slab of nonstructured dielectric material in the Brownian dynamics/electrodiffusion studies (Noskov et al., 2004).

The current/voltage dependence

To obtain the current/voltage dependence, the system shown in Fig. 1 was simulated at different values of the applied transmembrane bias. To reduce the time required for establishing a stationary voltage gradient at small (±120 mV) biases, we carried out simulations at 1.2 V and −1.2 V first, and then used the final conformations from these simulations to restart simulations at lower transmembrane biases. The lipid bilayer remained impermeable for water and ions for all voltage biases studied; the electrostriction effects were found to be minimal: the average width of the bilayer, measured by the locations of the phosphorous atoms, fluctuated between 39.7 and 40.3 Å when the bias was varied from 0 to 1.2 V.

The resulting cumulative currents are shown in Fig. 11. A linear increase of the cumulative currents with time indicates a stationary current. To eliminate the noise associated with stochastic motion of ions in the bulk, only ions residing inside the channel were taken into account when computing the instantaneous currents with Eq. 1.

FIGURE 11.

Cumulative currents through the transmembrane pore of α-hemolysin, resulting from the application of an external electric field. A linear increase of the cumulative currents with time indicates stationary currents; a linear regression fit to these curves gives the average current. The cumulative currents are shown in the units of the unitary charge (e = 1.6 × 10⁻¹⁹C). The open circles and the solid squares indicate the MD trajectories originating from the pH 8.0 and pH 4.5 structures, respectively.

Due to the timescale limitation of MD (∼10 ns), the smallest ionic current that can be sampled sufficiently with available computer resources is ∼100 pA, which, in the case of α-hemolysin, corresponds to a smallest applied voltage bias of ∼100 mV. The reason is that a statistically meaningful simulation of ionic permeation must include at least several full ion permeations through the channel during the timescale of the MD run. We ran our simulations typically for 5–11 ns and observed tens of full permeations. As the pore of α-hemolysin can accommodate from 50 to 70 ions at 1 M KCl, we computed the number of full permeations by dividing the total charge transported through the channel by the unitary charge (1.6 × 10⁻¹⁹C). Table 2 provides the simulation times and the respective number of ion permeations for each run used to determine the I/V curve.

Applying a linear regression fit to the cumulative current curves shown in Fig. 11 yielded the current/voltage dependence (Fig. 12). The current/voltage dependence is in good agreement with experiment. It is asymmetric, indicating that α-hemolysin partially rectifies the ionic current at negative voltage biases (a negative bias drives positive ions from the vestibule of α-hemolysin across the membrane through the transmembrane pore). This rectification is caused by an asymmetric distribution of charged residues along the transmembrane pore of α-hemolysin (Henrickson et al., 2000; Misakian and Kasianowicz, 2003; Noskov et al., 2004). The absolute values of the ionic currents are also close to experimental values: at 120 mV and 21°C, the simulations predicted an ionic current of 130 ± 10 pA, which, after taking into account an 11% correction for the high bulk conductivity of KCl, is in close agreement with the experimental value of 112 ± 3 pA (Meller and Branton, 2002). The ratio of the ionic currents at ±120 mV, which in our simulation is 1.2, compares well with the measured value of 1.17 (Krasilnikov and Sabirov, 1989). This ratio increases with the absolute value of the applied bias.

FIGURE 12.

Current/voltage characteristics of α-hemolysin computed with MD. The open circles and the solid squares indicate currents computed with the pH 8.0 and the pH 4.5 structures, respectively. The semisolid squares mark the simulations in which one of the loops at the trans end of the channel peeled off, transiently blocking the pore entrance. Each data point is derived from a 288,678-atom simulation of the system shown in Fig. 1. The dashed line indicates the linear fit through the data point at 120 mV and the origin. In accordance with experimental studies (Menestrina, 1986; Krasilnikov and Sabirov, 1989), the I/V curve is sublinear at V < 0 and a 1 M concentration of KCl. The absolute value of the ionic current at 120 mV, and the ratio of the currents at ± 120 mV, are also in good agreement with experiment (Meller and Branton, 2002; Krasilnikov and Sabirov, 1989). See also Fig. 11 and Table 2.

Selectivity

As shown in Fig. 10, K⁺ ions tend to accumulate at both ends of the channel, and, therefore, the ratio of the total number of K⁺ to Cl⁻ ions depends strongly on the definition of the channel's boundaries. Thus, by shrinking the boundaries from 15.5 Å < z < 71.5 Å to 12.5 Å < z < 68.5 Å, we could change this ratio from 1.04 to 0.96. Prompted by this example, rather than looking at the relative occupancy of the channel, we characterized the selectivity of α-hemolysin by computing individual currents of K⁺ and Cl⁻ species, resulting from the application of an external electric field. Table 2 summarizes our results.

First, we noticed that K⁺ and Cl⁻ currents exhibit larger fluctuations than their sum, i.e., the total current. As might be expected, without applying an external electric bias, the total current remained zero over 8.3 ns of equilibration. Nevertheless, the currents resulting from diffusion of K⁺ and Cl⁻ ions were nonzero, amounting to ∼±25pA. From these observations, we estimated the stochastic component (or noise) in the K⁺ and Cl⁻ currents to be at least 25 pA over the timescale of 10 ns.

We found that the simulated selectivity of α-hemolysin depends both on the direction and the amplitude of the applied voltage. At large positive bias, i.e., +1.2 V, the total current is dominated by the flow of K⁺ ions. The preference for K⁺ ions decreased as we lowered the transmembrane bias, and at ±0.24 V the channel is marginally selective to Cl⁻. At −1.2 V, the channel's selectivity to Cl⁻ is apparent. At ±120 mV, the magnitudes of the K⁺ and Cl⁻ currents are comparable to their typical fluctuations, and therefore, these data were not used to draw the conclusions about the channel's selectivity. The directional selectivity of α-hemolysin is not surprising, taking into consideration the asymmetry of its pore and of the distribution of the electrostatic potentials (cf. Figs. 1 and 8). The dependence of α-hemolysin selectivity on the magnitude of the applied bias originates from the reaction of the protein structure to the applied electric field. We observed, for example, residues His-144, Tyr-118, Phe-120, and Ile-136, which are located at the outer surface of the β-barrel, to change their orientations when altering the transmembrane bias from +1.2 to −1.2 V (see also Fig. 14). These results demonstrate that a local adjustment of the protein structure in response to an external electric field, not accompanied by any large structural changes, could be sufficient to gate the selectivity of a membrane channel.

FIGURE 14.

Average profile of the electrostatic potential along the symmetry axis of the α-hemolysin channel. Circles and squares indicate +1.2 and −1.2 V biases, respectively; black and red symbols correspond to the simulations carried out with the pH 8.0 and the pH 4.5 structures, respectively. Lowering the pH was assumed to change the protonation states of seven His-144, altering the average potential in the upper half of the stem (0 < z < 30). These changes parallel the changes in the ionic conductance (Figs. 11 and 12) and ionic selectivity (Table 2).

Conditional selectivity of a membrane channel to the direction of the salt gradient was reported earlier from both experimental (Gu et al., 2000, 2003; Alcaraz et al., 2004) and theoretical (Noskov et al., 2004) studies. In our case, we found that selectivity depends on the direction of the applied electrostatic field. As in the case of the salt gradient, the flow of ions, driven by an electrostatic potential gradient, is nonequilibrium, and, therefore, our observations do not violate the second law of thermodynamics. As will be demonstrated below, changing the protonation state of His-144 increases the selectivity of the α-hemolysin channel for Cl⁻.

To determine the relative permeability of α-hemolysin for K⁺ and Cl⁻ ions at equilibrium, equilibrium trajectories were analyzed using the collective diffusion method deployed earlier to compute the osmotic permeability of α-hemolysin for water (see Methods). The collective coordinates of all K⁺ and Cl⁻ ions inside the channel are plotted versus time in Fig. 13. The corresponding MSDs are shown in the inset of that figure. A linear regression fit to the MDS curves yields a collective diffusion constant of 0.32 ions²/ns for K⁺ and 0.38 ions²/ns for Cl⁻, indicating a marginally higher mobility of Cl⁻ ions at equilibrium. The ratio of the ionic mobilities is close to that simulated in the bulk (Table 1). The values of the collective diffusion constants conform to the magnitude of K⁺ and Cl⁻ current fluctuations, when an external electric field drives the ionic flow. Indeed, using Eq. 6, we estimate that, on average, ∼2.5 K⁺ and Cl⁻ ions diffuse spontaneously through the α-hemolysin pore in 10 ns.

FIGURE 13.

Equilibrium ionic permeability of α-hemolysin. The collective coordinate of all K⁺ and Cl⁻ ions, n, (Eq. 4) is plotted versus time. The inset shows the mean-square displacements of n. A linear regression fit to these data yields the collective diffusion coefficients of K⁺ and Cl⁻ of 0.32 and 0.38 ions²/ns, respectively.

Using the data presented in Table 2, we could estimate the “effective mobility” of K⁺ and Cl⁻ ions inside the α-hemolysin channel. For simplicity, we assumed that mobilities of K⁺ and Cl⁻ ions are equal. Given a definition of the effective mobility μ as a ratio of the average ion velocity v to the applied electric field E, i.e., μ = v/E, the effective mobility is

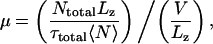(8)

where N_total is the total number of ion permeation computed by dividing the total charge transported through the channel by the unitary charge (1.6 × 10⁻¹⁰C), τ_total is the total simulation time, 〈N〉 = 60 ± 10 is the average number of K⁺ and Cl⁻ ions inside the pore, and L_z = 87 Å is the length of the channel. We found the effective mobility to vary between 0.38 × 10⁻⁸ and 1.0 × 10⁻⁸ m² V⁻¹ s⁻¹, which is ∼7–20 times smaller than the bulk mobility of a K⁺ ion (7.62 × 10⁻⁸ m² V⁻¹ s⁻¹).

Influence of pH on conductance, selectivity and electrostatic potential of α-hemolysin

The pH of the environment is known to influence the ion conductance of α-hemolysin. The most dramatic changes are observed at low salt conditions (Menestrina, 1986; Krasilnikov and Sabirov, 1989; Walker et al., 1992; Korchev et al., 1995). However, even at 1 M KCl, pH has a noticeable effect on the current/voltage curve and ion selectivity. Thus, lowering the pH from 7.5 to 5.0 increases the ionic current by several percents at both positive and negative biases (Gu and Bayley, 2000; Bezrukov, 2000), the I/V curve becomes less rectifying, whereas the anion-selectivity increases almost twice (Menestrina, 1986; Gu et al., 2001). At a given pH, the magnitude of the open-pore current fluctuates in time. The magnitude of the current fluctuations depends on the solution pH, attaining a maximum at pH 6.0 (Bezrukov and Kasianowicz, 1993; Kasianowicz and Bezrukov, 1995). Both the pH-dependent fluctuations and the selectivity of the ionic currents are believed to have the same origin: a group of residues that can change their charges upon protonation, altering the electrostatic potential inside the pore, and, thereby, the ionic current. From the analysis of the current fluctuations, the pKa of these residues was estimated to be 5.5 (Bezrukov and Kasianowicz, 1993; Kasianowicz and Bezrukov, 1995), whereas a fit to the pH dependence of the current rectification ratio gave a pKa of 6.2 (Walker et al., 1992). The inner wall of the transmembrane pore has several residues that can change their protonation states upon altering pH; however, their pKa values (Glu, pKa = 4.1; Asp, pKa = 3.9; Lys, pKa = 10.5) do not match the estimates.

The pKa of a histidine side chain in water is ∼6.1, and, therefore, it can change its protonation state from neutral at pH 8.0 to positively charged (protonated) at pH 4.5. Naturally, histidines were the first residues suspected in the pH gating of the α-hemolysin conductance. The first experiments, however, demonstrated that a chemical modification of histidines with diethylpyrocarbonate before assembly disables binding and oligomerization of the toxin, whereas in the assembled toxin, only a fraction of histidine residues is accessible for chemical modification with this compound from the solution (Pederzolli et al., 1991b). Later, the crystallographic structure (Song et al., 1996) revealed the lack of histidine side chains inside the transmembrane pore of α-hemolysin.

As the group of residues that alter their protonation states upon changing pH remains unidentified (Gu et al., 2001), we propose here to reconsider the role of histidines in the pH-gating and suggest a mechanism explaining the observed changes of the channel conductance.

The sequence of α-hemolysin has four groups of histidine residues (see Fig. 1). His-48 and His-35 are located in the cap domain of the protein, at the interface of two adjacent protomers, where they form hydrogen bonds to residues of the adjacent protomers. Due to their buried conformations, we did not expect them to change their protonation states when lowering the pH from 8.0 to 4.5. Residues His-259 are located in the rim domain of the protein at z ≈ 17 Å, where they interact with the headgroups of the DPPC bilayer. As these residues are exposed to water, changing pH can affect their protonation states, and, therefore, in the pH 4.5 structure these residues were chosen to have charge +1. However, changing the protonation states of His-259 should not influence the conductance and selectivity of α-hemolysin, as these residues are located 42 Å away from the center of the transmembrane pore.

Residues His-144 are located at the outer side of the β-barrel in the rim-step crevice at z = 18 Å (Fig. 1). They were found to be in contact with the buffer solution through a network of water-filled side channels, as well as through interfacial water hydrating the lipid headgroups. The latter was recently demonstrated to be an excellent proton conductor (Serowy et al., 2003). Accordingly, the pH of the cis compartment should be able to readily affect the protonation states of His-144. The rim domain of the protein shields these residues from interacting with larger solutes, like diethylpyrocarbonate (Pederzolli et al., 1991b), or a 450-Da dianionic sulfhydryl reagent (IASD) (Walker and Bayley, 1995). Due to their proximity to the constriction region of the pore, the protonation state of the His-144 side groups can directly affect the ionic conductance and selectivity of α-hemolysin. Although at pH 4.5 a fraction of Asp and Glu residues may become neutral, we did not consider this possibility here, assuming that only His-144 and His-259 change their protonation states upon lowering pH from 8.0 to 4.5. We note, however, that at the present time there is no direct physiological evidence that His-144 and His-259 change their protonation states when lowering pH from 8.0 to 4.5.

To examine if changing the protonation state of His-144 affects the ionic conductance and selectivity of α-hemolysin, electric fields opposite in direction but equal in magnitude were applied to the pH 4.5 structure. These simulations were carried out at ±1.2, ±0.6, and ±0.24 V transmembrane biases that induced a statistically significant number of ion permeations, required to make statistically significant observations of the ionic selectivity. The resulting cumulative and average currents are shown in Figs. 11 and 12 (solid squares); the currents of K⁺ and Cl⁻ species are given in Table 2.

The change of the protonation states of His-144 was observed to increase the total ionic current at transmembrane biases of 1.2, 0.6, and −0.24 V (Fig. 11) and decrease the total current at 0.24 V. The ratio of the total currents at ±240 mV dropped from 1.75 to 0.71 (see Fig. 12) indicating a rectification of the current reduced by the protonation of His-144. In the simulations carried out at −1.2 and −0.6 V biases, the current dropped by more then a half after ∼2.5 ns (∼5 ns at −0.6 V), when one of the strands comprising the β-barrel peeled off from the trans end of the channel, partially blocking the pore entrance. In all simulations but at −0.24 V, the protonation of His-144 increased the ratio of Cl⁻ to K⁺ currents (Table 2); at a −0.24 V bias, the currents were too noisy to draw a statistically sound conclusion. Results of these simulations suggest that the protonation states of the seven His-144 affect the ion conductance; the changes introduced by the protonation agree, overall, with the changes observed experimentally on lowering the pH. We note, however, that the simulated reduction of the total current upon protonation of His-144 at +0.24 V may indicate that, in addition to His-144, other side chains make a contribution to the observed pH-dependence of the ion conductance.

The changes in ion conductance parallel the changes in the electrostatic potential induced by the protonation of His-144. In Fig. 14, we present the average profile of the electrostatic potential at 1.2 (squares) and −1.2 (circles) V bias, simulated with the pH 8.0 (black symbols) and the pH 4.5 (red symbols) structures. At −1.2V, the introduction of the seven positive charges on His-144 resulted in rising the energy barrier by 100 mV in the second half of the stem (0 < z < 30). At 1.2 V, the introduction of the charges shifted the curve downward, marginally reducing the barrier. The difference between the averaged electrostatic profiles at ±1.2 V biases originates from the asymmetric response of the protein structure to the direction of the applied electric field.

CONCLUSIONS

Through large-scale MD simulations, we investigated the permeability of the α-hemolysin channel in its native environment, a lipid bilayer. Applying external electric fields, we measured the current/voltage dependence and found the results of our simulations in excellent agreement with experiment. Analyzing trajectories of all water molecules inside the transmembrane pore, we computed the osmotic permeability of α-hemolysin for water and found the obtained value in agreement with experiment as well. By averaging the instantaneous snapshots of the electrostatic field over long (>10 ns) MD trajectories, we determined the average distribution of the electrostatic potential at different voltage biases.

At all times, the transmembrane pore of α-hemolysin was found fully occupied by water. Submerged in a lipid bilayer, the stem part of the protein was observed to undergo structural fluctuations that altered geometry of its cross section, but did not influence the total ionic current. We found that the most probable cross section of the stem is an ellipse, having one of the seven preferable (by the α-hemolysin stoichiometry) orientations, the latter alternating on a timescale of several nanoseconds.

Our MD simulations revealed that water can permeate through the seven side channels of α-hemolysin as well as in, out, and within the cavity bounded by the rim and stem domains of the protein and the lipid bilayer, i.e., the rim-step crevice. Furthermore, we found that these water channels connect the cis compartment to seven histidine residues (His-144) located in the rim-stem crevice, which implies that the pH of the cis compartment can affect the protonation states of these residues. Changing the protonation states of seven His-144 from neutral to positively charged was observed to increase the ion conductance at both positive and negative biases, diminish the current rectification, and increase the selectivity for Cl⁻, which agrees with the changes of the ion conductance observed experimentally when lowering pH from 8.0 to 4.5. Therefore, we propose that the seven His-144 residues, arranged in a circle around the β-barrel stem, comprise the pH sensor that gates the conductance and selectivity of the α-hemolysin channel. Our study, however, does not exclude that, in addition to His-144, some other residues, in particular Asp and Glu, may alter their protonation states when changing the solution pH, and thereby also contribute to the observed changes of the ion conductance.

This study demonstrates that, with currently available computational resources, large-scale MD simulations can predict with quantitative accuracy ionic currents through transmembrane channels induced by external electric fields. The resolution of the method is defined by the timescale of the simulations, which should be sufficiently long to collect a statistically significant number of ion permeations. The method performs particularly well for membrane channels of high conductance, for high salt conditions, and for large (100 mV and higher) transmembrane biases. From 100 ns simulations, one can expect to resolve a current difference of 1 pA, which makes this method highly suitable for rational design of stochastic sensors, once structures are known with atomic precision.

α-Hemolysin has been adopted in groundbreaking studies (Kasianowicz et al., 1996; Akenson et al., 1999; Meller et al., 2000; Howorka et al., 2001) for single molecule electrical recordings of DNA strands with the aim to develop a device for DNA sequencing (for a recent review, see (Meller, 2003)). Large-scale, long time simulations carried out here for investigations of ion conduction can be extended to simulate the transport of DNA through α-hemolysin, assisting in the interpretation of electrical recordings and improvement of measurement conditions for DNA sequencing. Indeed, simulations have demonstrated their potential in designing DNA sequencing devices in the case of synthetic channels (Aksimentiev et al., 2004; Heng et al., 2004).