Numerical Investigation of Sequence Dependence in Homologous Recognition: Evidence for Homology Traps

Abstract

During the initial phase of RecA-mediated recombination, known as the search for homology, a single-stranded DNA coated by RecA protein and a homologous double-stranded DNA have to perfectly align and pair. We designed a model for the homology search between short molecules, and performed Monte Carlo Metropolis computer simulations of the process. The central features of our model are 1), the assumption that duplex DNA longitudinal thermal fluctuations are instrumental in the binding; and 2), the explicit consideration of the nucleotide sequence. According to our results, recognition undergoes a first slow nucleation step over a few basepairs, followed by a quick extension of the pairing to adjacent bases. The formation of the three-stranded complex tends to be curbed by heterologies but also by another possible obstacle: the presence of partially homologous stretches, such as mono- or polynucleotide repeats. Actually, repeated sequences are observed to trap the molecules in unproductive configurations. We investigate the dependence of the phenomenon on various energy parameters. This mechanism of homology trapping could have a strong biological relevance in the light of the genomic instability experimentally known to be triggered by repeated sequences.

INTRODUCTION

Homologous recombination is a vital biological phenomenon, which is in particular involved in the repair of DNA lesions. It consists in an exchange of genetic material between homologous DNA molecules. The whole reaction can be performed in vitro with a single enzyme, RecA protein from Escherichia coli (Kuzminov, 1999). The successive steps of the paradigmatic three-strand reaction are: 1), the polymerization of RecA monomers on single-stranded DNA (ssDNA) to form a nucleofilament; 2), the search for homology between the filament and neighboring double-stranded DNA (dsDNA) molecules, leading to the alignment and pairing of the filament with its homologous partner; and 3), strand exchange between the two entities.

The homology search process is complex. Firstly, recognition relies on interactions between ssDNA and dsDNA bases, either via triple-helix non-Watson-Crick bonding (Hsieh et al., 1990; Bertucat et al., 1999) or via rotation of bases and direct establishment of new Watson-Crick bonds (Adzuma, 1992; Nishinaka et al., 1998). Since homology has to be tested simultaneously over a few bases, it is necessary to overcome geometric incompatibility between duplex DNA and RecA-bound ssDNA, the latter being overextended by a 1.5 factor (Egelman and Stasiak, 1986). Secondly, sequence-independent attraction between nucleofilaments and naked DNA has been demonstrated. Although this nonspecific interaction does not promote long-range sliding of the substrates relative to each other (Adzuma, 1998), it is responsible under some experimental conditions for the formation of nucleofilament-DNA networks, which are thought to be instrumental in the homology search process (Tsang et al., 1985).

A few attempts have already been made to provide a physical description of the homology search process. Large scale dynamics of the molecules involved in the search for homology have been numerically modeled by Patel and Edwards (2004). Klapstein et al. (2004) have studied the theoretical implications of the incompatible interbase spacing and of the remarkable stiffness of the filament. In some of our previous work, we have described the search for homology as a two-scale problem (Dutreix et al., 2003): 1), on a global scale, an initial contact between homologous partners is achieved by mere diffusion, biased by the polymeric nature of the ligand and substrate, and by the nonspecific interactions between them; and 2), on a local scale, the homologous partners are thought to have temporarily and locally aligned axes, and to be free to one-dimensionally diffuse over a short distance. We also assume that, for a homology recognition nucleus to be formed over a few bases, the dsDNA has to be partially stretched by thermal fluctuations, so that its interbase spacing becomes compatible with that of the filament. An analytical study of our model, relying on a first-passage time analysis, has been proposed (Dorfman et al., 2004). The agreement with experimental data is good, and the analysis also predicts new dependencies; for example, on the fluid viscosity.

The aim of the present article is to focus on the local part of the model, and to use basic Monte Carlo Metropolis simulations to explicitly take into account the role of sequence on homologous recognition. To the best of our knowledge, this has not been attempted before. We begin with describing the model and the algorithm; then we study sequence effects such as heterologies or sequence repeats and propose the notion of homology traps, which might be crucial in the recognition process; we finally examine the robustness of our results relative to the choice of parameters and also suggest how the model can be made further sophisticated, in order to test the local mechanism of homologous recognition in more detail.

DESCRIPTION OF THE MODEL

The Monte Carlo Metropolis technique is widely used to study complex physical systems (Binder and Heermann, 2002). Its primary application regards the computation of the equilibrium characteristics of a system. However, with due precaution, it can also be employed to simulate dynamical effects. This is the case in our own simulations, since we are looking at the kinetics of homologous pairing between a single nucleofilament and a single duplex DNA. It is important to point out that we will not try to directly relate the computed kinetics to a real recognition time, but will instead make relative comparisons between simulation results under various conditions and thus merely derive qualitative conclusions about some features or parameters, whose effect cannot always be experimentally tested.

Fundamental assumptions

1. An ssDNA perfectly covered by RecA and a homologous duplex DNA have been brought into contact before the beginning of the simulation. Their axes are straight (because we limit ourselves to a size ∼20–30 basepairs, that is much less than the persistence length) and are assumed to be aligned owing to nonspecific attractive interactions. The only authorized diffusive movement during the contact time is thus a one-dimensional random walk of one molecule relative to the other.

2. The possibility of cofactor hydrolysis is not taken into account in our study. The experimental equivalent would be a reaction with adenosine 5′-(γ-thio)-triphosphate as a nonhydrolysable substitute for adenosine triphosphate (ATP). Homology recognition is known to occur in such reactions (Honigberg et al., 1985).

3. Because the ssDNA inside the filament is firmly held by the protein scaffold, it is supposed to have a constant and uniform interbase spacing equal to 1.5 times that of canonical B-DNA. On the other hand, the dsDNA is subject to local compression or overextension due to longitudinal thermal fluctuations.

4. During the short-range one-dimensional diffusion process, every basepair of the duplex is free to establish (or to break) a bond with the closest base of the filament. We make no hypothesis about the physical phenomenon involved, either triplex interaction or exchange of Watson-Crick bonding. The fact that all basepairs are free to interact with the bases inside the filament at a given time amounts to neglecting helical incompatibility between the molecules. This is readily justified by the shortness of the molecules that we are dealing with: coiling the duplex inside the filament helix over slightly more than one turn (∼18.6 ssDNA bases) must typically arise from attractive interactions. If we were studying molecules hundreds of bases long, intertwining would be highly disfavored during the homology search; therefore, we would have to consider that only a periodic fraction of the duplex is in efficient contact with the ssDNA at a given time. Even in this case, the general relevance of the present study would still hold.

5. The energy involved in dsDNA-ssDNA bonding depends on several factors, namely, whether the bases are homologous or not; how good the longitudinal alignment between the interacting bases is; and what the local extension state of the dsDNA is. To be more precise, we assume that the duplex has to be locally stretched by thermal fluctuations for the bonding to the filament to be favorable. This is probably our strongest hypothesis. It was inspired by the work of Léger et al. (1998), who experimentally and numerically studied the interaction between dsDNA and RecA monomers, and who demonstrated a good agreement between experiment and theory under the similar assumption that dsDNA has to be thermally or mechanically stretched for RecA to bind to it.

The state of the system is essentially described by extension variables and binding variables. At every time-step in the Monte Carlo procedure, we update one variable: one of the first set of variables at odd dates and one of the second set at even dates. Indeed, we assume that the frequency of each type of event is the same, because the amplitude of the molecular motions involved is of the same order of magnitude (typically the size of the canonical spacing between basepairs).

Extension variables: semicontinuous description of dsDNA

The dsDNA is divided into N sites. Each site i represents one basepair and its neighborhood and is characterized by a variable l_i describing how extended it is (Fig. 1). In a basic Ising model such as the one used by Léger et al. (1998), l_i could take only two values (stretched and nonstretched), but this approach would be unsatisfactory for homologous recognition. Our own model is semicontinuous insofar as l_i belongs to the finite set of values {0.7, 0.8, 0.9,… 1.8, 1.9}. The value l_i = 1 corresponds to the canonical extension a = 0.34 nm, whereas l_i = 1.5 is the same base spacing as in the filament. The range of possible extension states, 0.7a–1.9a, is in accordance with the probability distribution for local stretching described by Léger et al. (1998). The upper limit is given by the full stretching of the backbone, whereas the lower one represents a slight compression relative to the mean canonical equilibrium spacing a.

FIGURE 1.

Representation of a three-site dsDNA and its homologous three-site filament during the simulations. Each rectangle stands for one base (or basepair) with its neighborhood. All filament sites always keep the same 1.5 size, whereas the dsDNA sites' lengths can change (variables l_i). Variable r indicates the relative position of the filament to the DNA. Variables n_i indicate which DNA site is bound to which filament site. (A) State of the system at time-step t (no bond between the filament and the DNA). (B–D) Possible state of the system at time-step t + 1. (B) Update of the l_i's, example of a length exchange between sites 1 and 2. (C) Update of the l_i's, example of a length exchange between site 1 and the thermal bath. (D) The n_i update, example of the formation of a bond between DNA site 1 and filament site 2.

Updating the extension variables is conducted by picking an integer i ∈ {0, …N} at random. If i > 0 and i < N, length is exchanged between adjacent sites i and i + 1 in the following way: if l_i becomes l_i + Δl, then l_i+1 becomes l_i+1 – Δl (Fig. 1 B). At any rate Δl is a multiple of 0.1, taken at random under the condition that the new values of l_i and l_i+1 remain bound by 0.7 and 1.9. The extremities of the molecule are particular cases; if i = 0 (respectively, i = N), length is exchanged between site 1 (respectively, site N) and the thermal bath. This is the only way for the dsDNA to grow or shrink in a global manner (Fig. 1 C).

The simulation of the longitudinal diffusion of the dsDNA relative to the filament directly arises from updating the l_i. Knowing exactly which dsDNA site is opposite which ssDNA site at every time-step stems from the l_i values as well as from that of an additional variable r, which gives the position of one end of the dsDNA relative to one end of the filament. The r-variable is automatically updated when site 1 exchanges length with the thermal bath (Fig. 1 C).

Binding variables

Another set of variables n_i (i = 1, …, N) describes the binding to the filament. If site i on the dsDNA is not bound to the filament, then n_i = 0. Otherwise, site i is bound to a site j on the filament (j = 1, …, N), and we have n_i = j. The first step in the updating of binding variables is choosing a site i at random. If n_i ≠ 0, it becomes n_i = 0 (breaking of a bond). If n_i = 0, a short algorithm tells us which site j of the filament is just opposite site i of the duplex, and we impose n_i = j (formation of a bond, as can be seen on Fig. 1 D). If there is no filament site opposite site i of the duplex, we keep n_i = 0.

Computing the energy

The core of the simulation is summarized as

1. At time-step t, the system is in a state 1 characterized by variables l₁, …l_N, n₁, …n_N, r, and by the energy E₁.

2. At time-step t + 1, a single variable update is made: either one of the n_i or one of the (l_i,l_i+1) couples (or l₁ or l_N alone). Updating l₁ alone implies updating r as well. This yields a new state 2 with an energy E₂.

3. E₁ and E₂ are compared. If E₂ < E₁, the system goes to state 2 at time t + 1. Otherwise, the system goes to state 2 with the probability 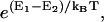and remains in state 1 with the complementary probability (k_BT being the thermal energy).

The essential issue is thus determining the dependence of the energy on all the variables. In this respect, we propose the following energetic calculation (in units of k_BT),

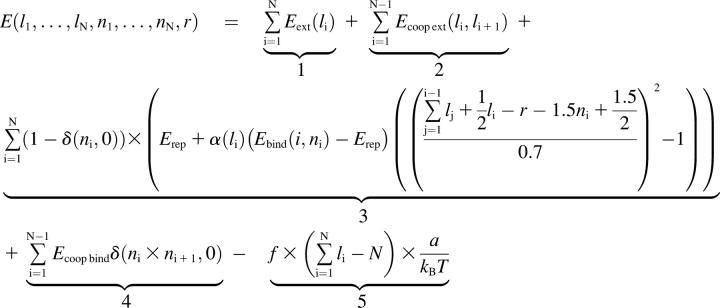, (1)

where δ is the Kronecker notation. The meaning of each term is explained below:

1. Energy associated with the extension of the DNA. The reference is E_ext(1) = 0, corresponding to the canonical form of the duplex. Every site i with l_i ≠ 1 represents an energy cost. We assimilate the extension 1.7 to the metastable stretched S-state (Cluzel et al., 1996; Smith et al., 1996). Therefore we know that E_ext(1.7) = 3.75, using the value derived by Cizeau and Viovy (1997). All the other extension values have to be guessed. We only impose that the energy profile should exhibit two local wells—one at extension 1 and the other at extension 1.7.

2. Energy cost related to the cooperative nature of DNA extension. Every frontier between sites with different extensions has to be penalized because of the enthalpic cost of a local structural distortion. For instance, it was computed by Cizeau and Viovy (1997) that in the B → S transition, every B/S frontier has an approximate cost of 3.6 k_BT. For consistency reasons, we therefore assume that E_coop ext(l_i, l_i+1) = 3.6 if |l_i − l_i+1| = 0.7. On the other hand, it is clear that E_coop ext(l_i, l_i+1) = 0 if l_i = l_i+1. Other possible values are extrapolated in a reasonable way by fitting a parabolic profile:

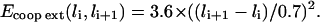
3. Energy related to the filament binding. The central component is E_bind(i, n_i), which will take up the value E_hom if site i on the duplex is homologous to site n_i on the filament, and E_het if the sites are heterologous. The quadratic factor at the end of the term is an energy penalty imposed when one dsDNA site tends to slide away from the ssDNA site to which it is bound. It makes sure that bound sites essentially remain in register (thus avoiding the nonsensical configuration of a bond maintained between remote sites), while still allowing for a certain flexibility. For example, this factor is 1 if the sites are perfectly aligned; 0 if their centers are shifted by 0.7a (approximately one-half the filament site size); and <0 if they are even more displaced. Of course the definition of this term is ad hoc but all potentials can be considered quadratic in a first approximation. Another factor, named α(l_i), ensures that there is a penalty for each bond when the duplex site is in an extension state far from the optimal 1.5 value. We decide to define α(l_i) as a parabolic factor: 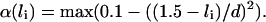We thus introduce a new parameter d which specifies how flexible the binding is, relative to the 1.5 optimal extension. We have worked with typical values of d in the 0.25–0.45 range. Finally, E_rep is a penalty for every binding, which is compensated only if close-to-optimal conditions are combined: homology, proper alignment of the sites, and extension close to 1.5. The value E_rep can be regarded as an entropy cost. There was already an equivalent of this parameter (noted h) in the study by Léger et al. (1998).

4. Cooperativity cost for the binding: we choose to penalize every frontier between bound and unbound sites of the duplex for the same molecular reason as the extension cooperativity cost.

5. Work done by an optional external force f exerted on the duplex, for example in a single-molecule experiment. The value a is the canonical interbase spacing (equal to 0.34 nm). If we want to mimic recombination in a test-tube, we set f to 0.

A few comments

This simple algorithm is implemented in C language. We first test the validity of our model by analyzing the one-dimensional diffusive motion of the dsDNA in the absence of any interaction with the filament (which amounts to getting rid of the n_i variables and of energy terms 3 and 4). The mean-square distance covered by the molecule varies linearly with the number of time-steps, which is consistent with the requirement of a diffusive process. We then plot the mean equilibrium contour length of the dsDNA versus an applied external force. Changing the E_ext energy profile alters the force/extension curve: in practice the shape of the B (or S) well is related to the low (or high) force part of the curve, whereas the position and height of the energy barrier between the B and S wells is linked to the transition plateau. We finally choose an energy profile which gives the closest curve relative to the experimental result of Cluzel et al. (1996). The correspondence between relative extension and energy cost is then the following: 0.7:4.5; 0.8:2; 0.9:0.75; 1:0; 1.1:0.75; 1.2:3; 1.3:6; 1.4:5.25; 1.5:4.5; 1.6:4; 1.7:3.75; 1.8:4.5; and 1.9:7.

Once the diffusion part of the model has been validated, true simulations of homologous pairing can be performed. We initialize the process by picking at random a position of partial contact between the dsDNA and the filament: −1.5N ≤ r ≤ l_N. All the n_i values are initially set to 0 (dsDNA unbound) and all the l_i values are set to 1. In practice, equilibrium of the dsDNA length is reached long before any binding takes place. If the duplex DNA and the filament lose contact because of diffusion (r > l_N or r < −1.5N), we reinitialize the system by picking a new r position. We keep track of the average number of such reinitializations and find that it shows little variation for the different simulations described here. Therefore, it has not been included in the results, although of course, if we wanted to relate our simulated kinetics to real-time kinetics, we would have to take into account the additional three-dimensional diffusion time required to make two molecules into contact again after each separation. We will now discuss the main results of the simulations, before justifying our choices of energy parameters and studying their respective effect.

RESULTS

Typical homologous recognition

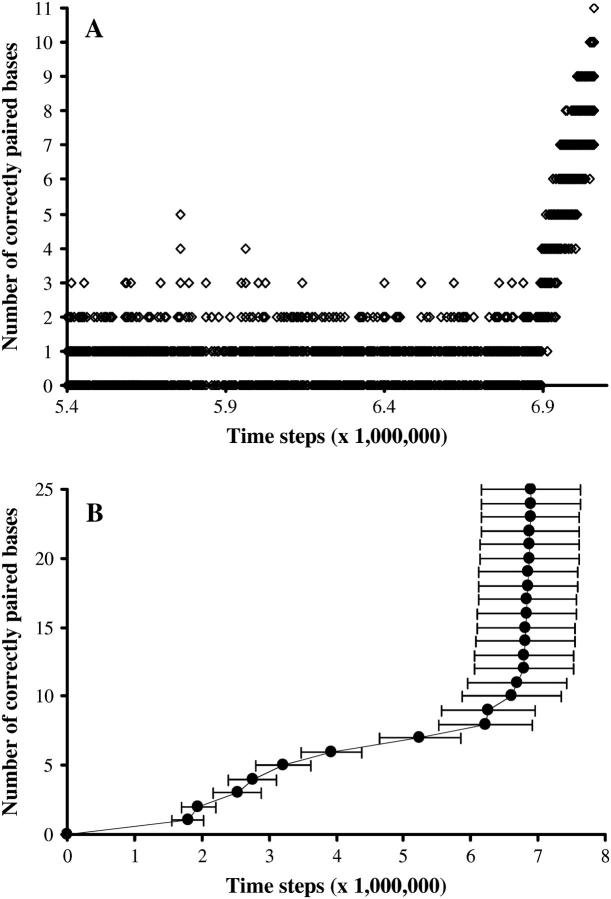
The process of homologous recognition is monitored by recording how many bases are correctly paired. Correct pairing does not mean that the paired bases are homologous, but rather that pairing occurs in correct register (site #1 of the DNA to site #1 of the filament, etc.). Wrong-matching (site #1 of the DNA to site #2 of the filament, for instance) does not appear in our presentation of the results, although it can happen in the course of the simulation. The simulation ends when all bases are correctly paired. For example, in Fig. 2 A, we monitor how many bases are correctly paired during one simulation, starting when the first good pairing occurs. It is blatant that the process is highly reversible: correct pairing is done and undone (the number of correct pairing oscillating in the example between 0 and 2, or 5 at the most) until the nucleus of correct pairing is stable enough. The rest of the basepairing then occurs in a ziplike fashion, quickly as compared to the nucleation time. At this point the system acquires irreversibility, even though pairing always remains reversible on a local timescale. When all N bases are correctly paired, the amount of correct basepairing typically fluctuates between N and N−1, and the system spends at least 90% of the time in the fully paired configuration. That is why we consider in what follows that the N^th correct basepairing is equivalent to complete homologous recognition.

FIGURE 2.

Typical progression of homologous recognition. (A) Evolution of the number of correctly paired bases versus time for one particular simulation. Only changes in the number of correctly paired bases are plotted. Random sequence, N = 11, E_hom = −5.5, E_het = −1.5, E_rep = 2, E_coopbind = 2, and d = 0.35. (B) Average first time of correct basepairing. One-hundred simulations, random sequence, N = 25, E_hom = −5.5, E_het = −1.5, E_rep = 2, E_coopbind = 2, and d = 0.25.

Our model contains two cooperative effects: one for the DNA stretching (E_coopext), the other for binding to the filament (E_coopbind). Therefore creating one frontier between a paired domain and an unpaired one is very unfavorable. This is why: 1), the progression of correct basepairing is almost always observed to happen on adjacent sites, and not in a scattered way; and 2), nucleation of the recognition almost always happens at one end of the molecules (which implies creating one frontier) rather that anywhere else (which implies creating two frontiers). This effect would probably be less pronounced if we dealt with longer molecules than in this study.

To be able to statistically compare simulated recognition times for various energy sequences or parameters, we generally repeat the simulation 100 times and compute average values. We then plot the mean first time (x axis) at which a certain number of bases are correctly paired (y axis). Fig. 2 B is a typical example of such a plot, for a random sequence and standard energy values. Error bars (computed from the standard deviation) are typically 10–15% of the mean value. They are omitted in subsequent figures for reasons of clarity.

Effect of substitutions

So far we have only worked with perfectly homologous molecules. If we now examine the case of one or several substitutions, results are significantly altered.

1. If a limited number of bases are heterologous, homology recognition takes place all the same, but it is delayed.

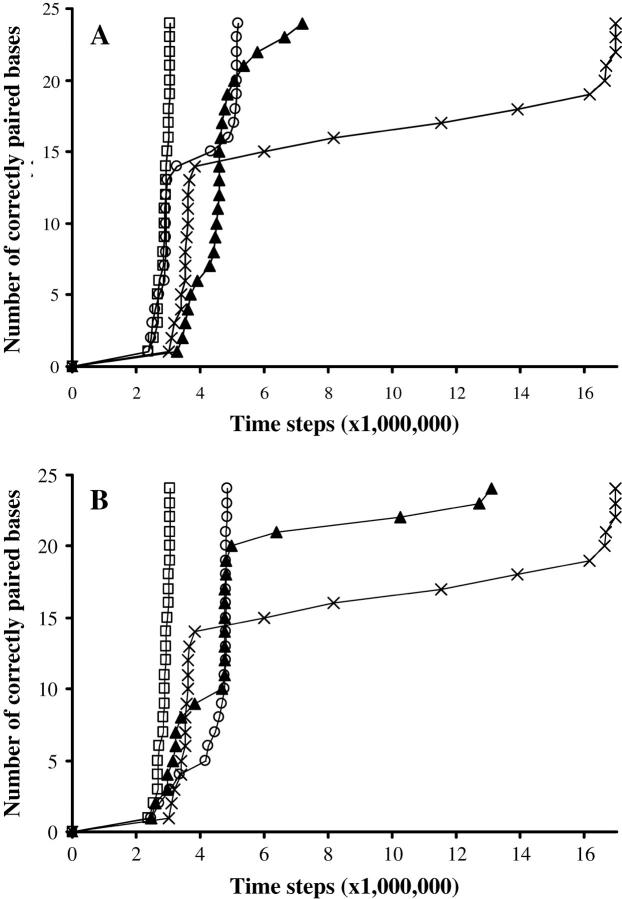
2. The more substitutions there are, the greater the delay (Fig. 3 A).

3. Adjacent substitutions are a bigger obstacle than scattered substitutions (Fig. 3 A).

4. The substitutions position acts on the delay. Central substitutions are the most unfavorable (Fig. 3 B).

FIGURE 3.

Effect of substitutions. (A) Effect of the number of substitutions. Symbol key: □, random sequence with no substitution; ○, two adjacent substitutions in a central position; ×, three adjacent substitutions in a central position; ▴, eight non-adjacent substitutions scattered along the molecule. (B) Effect of the position of substitutions. Symbol key: □, random sequence with no substitution; ○, three adjacent substitutions at one extremity; ×, three adjacent substitutions in the center; ▴, three adjacent substitutions at one-quarter of the end of the molecule. Data for A and B: 100 simulations per curve; N = 24, E_hom = – 5.5, E_het = −1.5, E_rep = 2, E_coopbind = 2, and d = 0.45.

In our model, heterologous bases can be correctly paired, but the energy gain from the binding is weaker (E_het versus E_hom) so that binding is globally unfavorable. In practice, if one or several substitutions are present at one end of the molecule, nucleation can only happen on the other end. This divides the number of possible configurations by 2, and thus doubles the total nucleation time (Fig. 3 B). Besides, when the zipping process finally gets to the substitutions at the heterologous end from the homologous end, the last few bases are not stably paired. As for internal substitutions, they result in a transient arrest when the heterologous area is reached. This arrest time increases exponentially when there are several adjacent substitutions (Fig. 3 A). During the stop, heterologous pairing is done and undone: it is not stable until the next few homologous bases are paired. The crossing of the heterologous barrier seems unidirectional in our model (because of cooperativity costs). When substitutions are present in a neither central nor extremal position, the stopping time is divided into two separate delays, because the heterologous area is at a different distance from the nucleation point depending on which extremity nucleates, and the result is a statistical average of both cases.

It is noteworthy that recombination in the absence of ATP hydrolysis, which is mimicked in the present simulations, was experimentally demonstrated to be able to cross substitutions (Bucka and Stasiak, 2001). In contrast, hydrolysis of the cofactor seems to be an absolute requirement for the traversal of heterologous inserts or deletions during strand exchange (Rosselli and Stasiak, 1991; Bucka and Stasiak, 2001), which is thought to involve more complex events such as dsDNA melting via the generation of torsional stress. Similarly, in our simulations, a heterologous insertion or deletion cannot be overcome, because it is almost impossible for the two molecules to be simultaneously in register on both sides of the insertion or deletion. Indeed, we deal with short DNA sequences and do not take into account the possibility of transversal deformations such as those involved in bulging; but even if we allow bulging in a straightforward improvement of the model, it can be assumed that the cost of such a deformation will be far greater than all the other energy terms. Therefore, correctly addressing the problem of heterology bypass in future work will imply taking into account the topological properties of the dsDNA-filament system and the possibility of ATP hydrolysis.

Effect of sequence repeats and notion of homology traps

Strikingly, our numerical simulations also show a dependence of the recognition time on the sequence even when the two substrates are perfectly homologous, and even though we do not introduce any dependence of the pairing energy on basepair nature. A particularly dramatic effect is observed when a single, two, or several nucleotides are repeated in a row. For reasons of clarity we have investigated the consequences of having 1,2,…n sequence repeats relative to an “unambiguous sequence” (Fig. 4). By “unambiguous”, we mean a fictitious set of letters such as ABCDEF…, designed to avoid the fortuitous repetitions that occur when only four letters (ATGC) are used. This artificial configuration, only possible with simulations, enables us to specifically test sequence features one at a time, even if the effect of repeats described below is qualitatively similar with realistic ATGC sequences.

FIGURE 4.

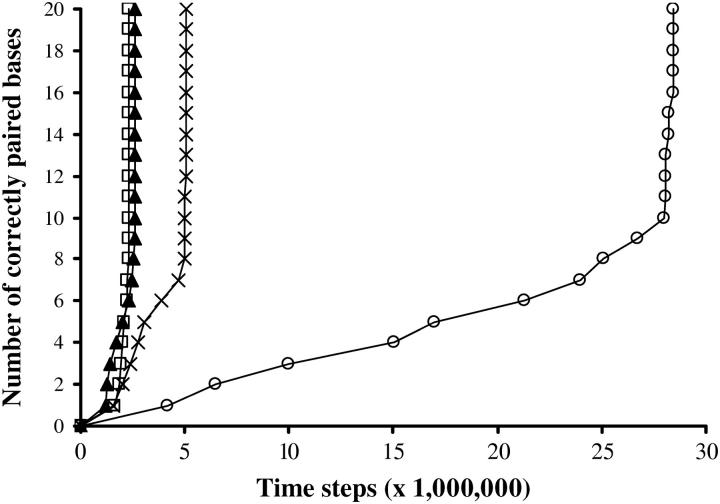
Effect of sequence repeats. Symbol key: □, unambiguous sequence; ▴, six dinucleotide repeats; ×, seven dinucleotide repeats; ○, eight dinucleotide repeats. The repeats are always positioned at one end of the molecule. One-hundred simulations per curve, N = 20, E_hom = −5.5, E_het = −1.5, E_rep = 2, E_coopbind = 2, and d = 0.45.

It is observed that when the size of the repeated region is greater than a certain threshold, homologous recognition is considerably delayed. The reason for this delay is that sequence repeats favor homology traps. Homology traps are pairing events between the substrates in a wrong pairing frame. If a sufficient number of homologous bases are paired in a different alignment from the real homologous one, a rather stable binding has to be broken before the homology search can further progress. The longer the region of wrong homology, the greater the delay. Such homology traps are particularly frequent in the presence of repeated sequences. For instance, with a dinucleotide-repeated sequence such as AGAGAG…, the correct pairing competes with a pairing shifted by two (or four or more) bases. The rise in the nucleation time is thus related to rearrangements from metastable configurations. Noticeably, this delay seems to primarily depend on the size of the repetition zone, and not on whether the repeated pattern is a mono-, di-, or trinucleotide.

The effect of repeated sequences has been investigated in vitro (Dutreix, 1997) and in vivo (Gendrel et al., 2000). The (GT)_n and (CA)_n sequences were demonstrated to have a harmful impact on homologous recombination: joint molecule formation between 39-bp-long fully homologous DNAs is strongly inhibited by a sequence of seven repeats in their middle (Dutreix, 1997). This was then interpreted as RecA having such a strong affinity for these sequences that the nucleofilament is too stable to perform strand exchange. Our numerical results enable us to suggest a complementary explanation: GT and CA repeats probably lead to homology trapping, thus preventing the realignment required for true homologous recognition. The experimental dependence of homologous recombination hindrance on the type of bases that are repeated could be attributed to different values of energy release upon pairing (different values of E_hom). Besides, the concept of homology traps could be essential in RecA-mediated recombination: indeed, post-pairing and ATP-hydrolysis-related rearrangements of the pairing frame have been evidenced (Sen et al., 2000; Navadgi et al., 2002). This property of RecA has not been taken into account here but it hints that homology traps are potentially deleterious to homology recognition and have to be reversed.

Effect of an external force

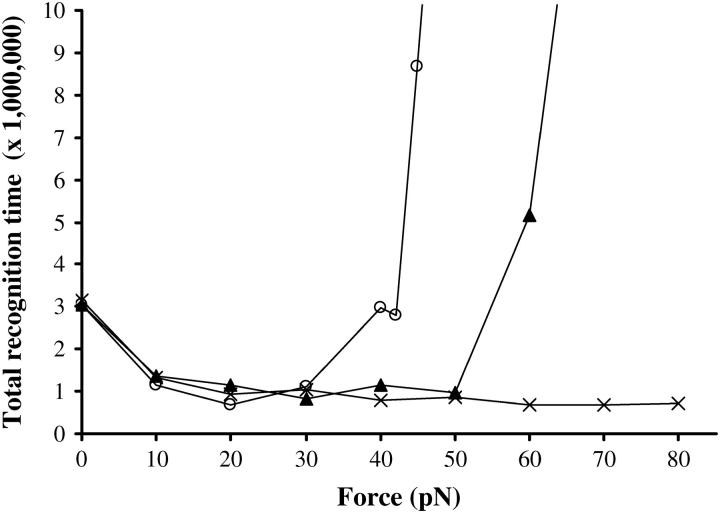
So far we have set f (in Eq. 1) to zero, which means that we mimic bulk recombination experiments. Let us now study the effect of the external force f by plotting the total recognition time (time required to properly align and pair all homologous bases) versus f. One can see on Fig. 5 that stretching the duplex DNA favors homologous recognition at moderate forces (typically by a factor of 3 between 0 and 20 pN). This is qualitatively similar to what was observed with the polymerization of RecA (Léger et al., 1998): indeed, stretching the dsDNA favors the 1−1.5 extension transition. However, above a certain force threshold, homologous recognition is dramatically poisoned, which is a completely unexpected effect in comparison with RecA polymerization. Interestingly, this deleterious effect of the external force is only observed with realistic ATGC sequences and not with the fictitious unambiguous sequence. It implies that the great delay at higher forces is related to homology traps. Actually, stretching the dsDNA facilitates not only the correct pairing but wrong pairings between partially homologous stretches as well. This is also the reason why the value of the force threshold depends on the sequence; for instance, if dinucleotide repeats are present, the unfavorable force threshold is lowered because homology trapping is easier (40 pN instead of 60 pN in the example of Fig. 5). It is important to note that data become statistically very dispersed beyond the force threshold. The average delay is attributable to some molecules remaining stuck in wrong configurations for a very long time, whereas others still achieve recognition more quickly than at 0 pN.

FIGURE 5.

Effect of an external stretching force. Symbol key: ×, unambiguous sequence; ▴, AGTCGATGCTTACCA sequence; ○, AGAGAGATCTTACCA sequence (with partial repetitions). One-hundred simulations per dot, N = 15, E_hom = −5.5, E_het = −1.5, E_rep = 2, E_coopbind = 2, and d = 0.25.

Klapstein et al. (2004) have recently proposed that the incompatible interbase spacing between the filament and the dsDNA should statistically facilitate the initiation of recognition. Our comparison of the kinetics at 0 and 60 pN (the geometric incompatibility being mostly overcome by dsDNA stretching in the latter case) enables us to make the complementary remark that another advantage of this structure consists in the prevention of homology trapping owing to high activation barriers.

ROLE OF THE PARAMETERS

We will now focus on the binding parameters, giving the reasons for our choices and explaining how these parameters affect the reported results.

Effect of E_hom

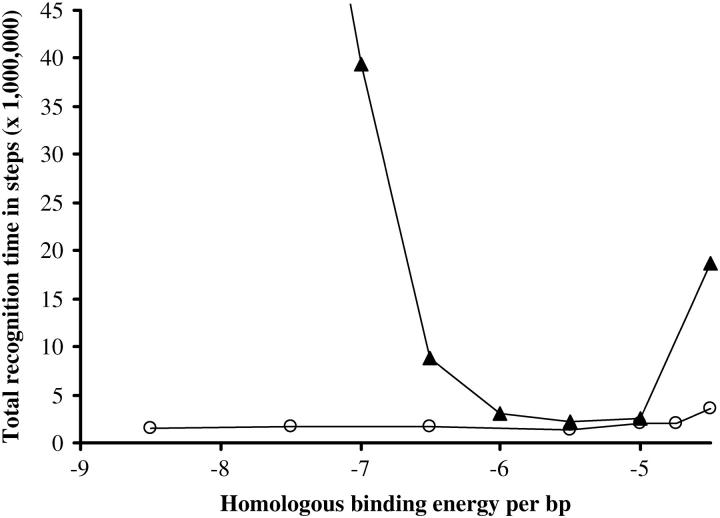
E_hom is the energy per basepair released upon optimal pairing. There is no experimental estimation of this fundamental parameter in the literature. Nevertheless, unpublished microcalorimetry measurements suggest an average energy gain of 1 k_BT per basepair upon synaptic complex formation (M. Takahashi, personal communication). This would correspond to E_hom = −E_ext(l = 1.5) −1 = −5.5, which is our usual choice. Nevertheless, we can also plot the total recognition time versus different values of E_hom (Fig. 6). It is then observed that although the choice of E_hom seems unimportant for unambiguous sequences, it has a dramatic effect for realistic random ATGC sequences. A low value of |E_hom| is obviously an obstacle to homologous recognition because pairing is not favorable enough, but on the other hand a strong value of |E_hom| is deleterious as well, because homology trapping is facilitated on homologous but misaligned bases. Interestingly, the optimal range is −6 < E_hom < −5, which turns out to correspond to experimentally suggested data.

FIGURE 6.

Effect of the E_hom parameter. Symbol key: ○, unambiguous sequence; ▴, random sequence with four letters. One-hundred simulations per dot, N = 20, E_het = −1.5, E_rep = 2, E_coopbind = 2, and d = 0.25.

Effect of E_het

E_het is the optimal energy gain upon heterologous binding. We must have E_het > E_hom and presumably E_het > −E_ext(l = 1.5) to ensure that incorporating a substitution during synaptic complex extension is unfavorable (this incorporation can become favorable afterwards if it enables the binding of further homologous bases). We have generally chosen E_het = −1.5, which is consistent with the range in the heterology-related energy cost computed by Malkov and Camerini-Otero (1998) owing to kinetic experiments. If E_het varies around this value, little effect is observed on a random sequence (except when E_het gets close to E_hom, which is unfavorable because homology is poorly discriminated). On the other hand, a sequence with substitutions requires more and more time for recognition with increasing E_het, because incorporating heterologous bases becomes more costly. The E_het parameter is thus closely related to the number of substitutions that can be tolerated in the synapsis.

Effect of E_coopbind and E_rep

The E_coopbind term (cooperative cost for binding to the filament) has been arbitrarily set to 2 in our simulations. Nevertheless, this parameter is qualitatively unessential: the total recognition time increases smoothly with increasing E_coopbind independently of the sequence. As for E_rep (barrier to binding), it has very little effect in the 0–2 range for most sequences. However, when there is a delay in the recognition time due to the sequence (because of substitutions or of sequence repeats), the delay is worsened if E_rep is big (typically by a factor of 3–4 between E_rep = 0 and E_rep = 2, data not shown). The value E_rep = 2 usually taken in our simulations lies in a reasonable range, and a slight mistake would not significantly alter the results, just like for E_coopbind.

Effect of d

The d parameter (which can take any value > 0) is an arbitrary and convenient way to account for how the system tolerates any deviation in the binding relative to the 1.5 filament periodicity. If d is small, the dsDNA must perfectly adjust to the filament structure for the binding to be probable, whereas the binding to the filament is flexible relative to the dsDNA interbase spacing if d is big. Data on the dynamical molecular structure of the synapsis would be required to correctly define parameter d. In the absence of such information, using a 0.25–0.45 range in d in our simulations seemed a reasonable compromise between a very flexible and a very rigid structure.

The d parameter does have a significant impact on the homology recognition process. For a random sequence, the optimal value of d lies at ∼0.45 (Table 1, top). At lower d, binding is unlikely because of the lesser tolerance toward deviations from the 1.5 extension. Higher values of d also have a dramatically negative effect, although not for unambiguous sequences: actually, facilitating the binding by increasing the longitudinal flexibility probably results in higher chances of getting stuck in homology traps. Interestingly, the choice of d is even more crucial for an abnormal sequence, such as one with substitutions or with repeats (Table 1, bottom). Considerable differences are observed in the 0.25–0.45 range. A low value of d is an impediment to the recognition of sequences with substitutions, and a high value has a strongly negative impact on repeated sequences. In the former case the binding has to be easy enough for the substitutions to be incorporated, whereas in the latter situation an easy binding worsens homology trapping. For example, if d = 0.45, the recognition time is significantly delayed when at least three or four substitutions are present, but it is strongly affected by as few as two substitutions if d = 0.25. Conversely, a sequence with eight dinucleotide repeats is difficult to recognize if d = 0.45, whereas if d = 0.25, such a dramatic effect would only be seen with more than nine dinucleotide repeats.

TABLE 1.

Effect of the parameter d

d	Unambiguous	Random
0.15	17	18
0.25	4.6	4.9
0.45	2.3	2
0.75	1.3	2.8
1.15	1.1	86
d	Two substitutions	8 × GT
0.25	6.3	1.1
0.35	3.2	2.8
0.45	1.6	12

(Top) Total recognition time (×10⁶) for an unambiguous sequence and for a realistic random sequence, for different values of d. (Bottom) Ratio of the total recognition time for a sequence with two substitutions (respectively, a sequence with eight dinucleotide repeats) to the total recognition time for an unambiguous sequence, for different values of d. One-hundred simulations per value, N = 20, E_hom = −5.5, E_het = −1.5, E_rep = 2, and E_coopbind = 2.

A modular model

The number of parameters in our model is probably its major weakness, but may also be its primary strength. Admittedly we do not precisely know the value of all these parameters, but some of them have been observed to have little if any qualitative influence on our results (E_coopbind, E_rep), and we have experimental (even if preliminary) arguments for the choice of the others (E_hom, E_het). The least characterized parameter is d, but we have studied its influence in detail. Furthermore, our model is rather modular, insofar as it can be conveniently modified for better accuracy; it is therefore intended as a foundation for further development. For instance, E_hom can be replaced by four different values depending on whether the base is A,T,G, or C; the same applies to E_het, since the heterologous binding cost depends on the sequence (Malkov and Camerini-Otero, 1998). The binding can also easily be divided into two steps, like in the experimental kinetic studies by Bazemore et al. (1997). This would, for example, enable us to account for a putative mechanism of homology testing by 1), triplex-bond formation and then 2), base-flipping. Other refinements of the model could include different extension/energy profiles according to the sequence, because the dsDNA stretching could very well be heterogeneous to preserve as much base-stacking as possible (see molecular modeling by Bertucat et al., 1999, for instance). Different binding parameters according to the position of the base (1, 2, or 3) relative to a RecA monomer could also be introduced, to test a recent proposition by Volodin and Camerini-Otero (2002).

CONCLUSION

The present work aims at developing a numerical model of homologous recognition at a ∼20-bp scale, with sensitivity to molecular details. The model is based on short-range sliding of a dsDNA relative to a homologous filament, and of longitudinal breathing of the dsDNA enabling its binding to the filament. Our model yields good agreement with commonly accepted features of the homology recognition process, such as a nucleation of the recognition over a few bases followed by the rapid extension of the synaptic complex, with transient stops in the process when heterologous bases are incorporated. But our results also suggest that the possibility of partial homology in a wrong pairing frame should be an essential factor in the process. What we call homology trapping occurs preferentially on sequence repeats and is characterized by a severe delay in the simulated recognition kinetics; in real experiments, it can be postulated that a homology-trapping delay can sometimes prevent recognition from taking place at all, because metastable trapped complexes make some molecules ineffective on experimental timescale. Since repeated sequences are known to be a major cause of genomic instability in vivo and are thought to be involved in cancer and hereditary diseases (Karran and Bignami, 1994; Debrauwere et al., 1997), this concept clearly deserves much attention. The homology trapping effect is also reflected in the sensitivity of the recognition time toward the parameters that define the binding (E_hom, d): therefore, it stems from our results that the recognition mechanism must have an activation barrier that is 1), low enough to allow binding and 2), high enough to avoid untimely homology traps. Of course in biologically relevant experiments, a reaction model based on adenosine 5′-(γ-thio)-triphosphate is not satisfactory, and the possibility of cofactor hydrolysis (notably associated with RecA depolymerization) has to be taken into account. This property is necessary in some forms of strand exchange (Kuzminov, 1999) and seems to permit partial correction of homology trapping (Sen et al., 2000; Navadgi et al., 2002). The possibility of ATP hydrolysis could be included into future calculations.

More generally, we have proposed several ways to improve this flexible model and to specify the parameters, in the hope that it will ultimately enable us to make kinetic predictions. In the meantime, we have already predicted an original effect of the external force; this external force could be exerted on the dsDNA by a tweezer-like device (Léger et al., 1998; Fulconis et al., 2004). The verification of this effect would also confirm the preponderance of homology trapping and would encourage one to look more closely at how RecA deals with homology traps once a metastable synapsis is formed.