Effect of Cell Electroporation on the Conductivity of a Cell Suspension

Abstract

An increased permeability of a cell membrane during the application of high-voltage pulses results in increased transmembrane transport of molecules that otherwise cannot enter the cell. Increased permeability of a cell membrane is accompanied by increased membrane conductivity; thus, by measuring electric conductivity the extent of permeabilized tissue could be monitored in real time. In this article the effect of cell electroporation caused by high-voltage pulses on the conductivity of a cell suspension was studied by current-voltage measurements during and impedance measurement before and after the pulse application. At the same time the percentage of permeabilized and survived cells was determined and the extent of osmotic swelling measured. For a train of eight pulses a transient increase in conductivity of a cell suspension was obtained above permeabilization threshold in low- and high-conductive medium with complete relaxation in <1 s. Total conductivity changes and impedance measurements showed substantial changes in conductivity due to the ion efflux in low-conductive medium and colloid-osmotic swelling in both media. Our results show that by measuring electric conductivity during the pulses we can detect limit permeabilization threshold but not directly permeabilization level, whereas impedance measurements in seconds after the pulse application are not suitable.

INTRODUCTION

A cell membrane represents a barrier to the transport of the majority of water-soluble molecules due to the hydrophobic nature of the inner part of the lipid bilayer. When a strong electric field is applied the cell membrane becomes more permeable thus enabling entrance of various molecules, which can be used as a method for introducing certain drugs or genes into the cell. The process was named electroporation because it is believed that pores are formed in the membrane due to the induced transmembrane voltage above some critical voltage (between 0.2 and 1 V), but the term electropermeabilization is used as well to stress that increased membrane permeability is observed (Neumann and Rosenheck, 1972; Zimmermann, 1982; Neumann et al., 1989; Tsong, 1991; Weaver and Chizmadzhev, 1996). After application of electric pulses the membrane completely reseals for proper selection of pulse parameters. The process of resealing takes several minutes thus allowing transport of molecules from the exterior into the cell. When the electric field is too high, for a given duration and number of pulses, physiological changes of the cell become too large to be repaired; a cell either loses too much of its content or it swells too much, which ultimately leads to cell death.

In the last decade it was shown that electroporation can be successfully used on patients, as a part of electrochemotherapy (Okino and Mohri, 1987; Mir et al., 1991; Jaroszeski et al., 1997; Mir, 2000; Serša et al., 2000) where electric pulses are used to increase locally the uptake of cytostatic drugs. In parallel it was shown that electroporation can be successfully used also for gene transfection (Wong and Neumann, 1982; Neumann et al., 1982, 1989; Sukharev et al., 1992). Electric field mediated gene transfection uses locally delivered electric pulses to transfer DNA into the cell. In contrast to more frequently used viral transfection, which has been proved to have severe side effects in some cases of in vivo gene therapy on animals and humans, electroporation presents a safer alternative method, as it does not use viral vectors (Ferber, 2001; Nebeker, 2002). Although being already an established method for in vitro gene transfection, electroporation is currently being extensively studied on animal models in vivo (Jaroszeski et al., 1999; Mir, 2000).

Until now the rate of permeabilization, survival of cells, and related efficiency of the electropermeabilization could be determined only after the application of pulses by various time-consuming methods. However, the possibility of monitoring the extent of permeabilized tissue in real time is of great importance for practical clinical use of electrochemotherapy or gene therapy. Under an assumption that the increased conductivity, which is observed in single cells, cell pellets, and cell suspensions, correlates with the extent of permeabilization, measuring electrical properties could enable observation of cell permeabilization (Kinosita and Tsong, 1977a,b, 1979; Abidor et al., 1993, 1994). Nevertheless, the complex structure of a tissue makes the interpretation of such measurements difficult. For these reasons it is important to verify this hypothesis on a dense suspension of cells, which represent a more controllable and homogeneous sample than tissue.

Only a few studies have been performed to assess changes of the electrical properties of cells in suspensions or pellets due to electroporation. The first measurements of the electrical properties were done on erythrocytes 20 years ago (Kinosita and Tsong, 1977a,b, 1979). Increased conductivity was observed above the threshold electric field, which after the pulse returned to its initial value. On a longer timescale, however, conductivity of a cell suspension was increased due to the ion efflux. The observed increase in conductivity correlated with the hemolysis of the cells. These observations were confirmed on pellets of different cell lines by Abidor and co-workers as well (Abidor et al., 1993, 1994), where a similar nonlinear current voltage relationship and fast resealing after the pulse was observed. In another study (Hibino et al., 1991, 1993) a decrease of the induced transmembrane voltage was detected on a part of the cell indicating increased membrane permeability for ions in that region of the membrane. Using microsecond and nanosecond pulses also increased conductivity was observed (Garner et al., 2004). Recently it was suggested (Davalos et al., 2000, 2002; Pliquett et al., 2004) that measurement of conductivity could enable online observation and control of tissue electroporation.

In this article we present measurements of electrical conductivity of a dense cell suspension in typical electroporation experiments. Conductivity of cells in a suspension was measured by current-voltage measurements during and impedance measurement before and after the application of high-voltage pulses. In parallel we determined the percentage of permeabilized and survived cells, and extent of osmotic swelling. The effect of different parameters (e.g., cell volume fraction, number of pulse, medium conductivity,…) on the conductivity of a cell suspension was studied and measured changes were compared to theoretical estimates. Previous studies focused on experiments with one or two pulses at most, however, for more efficient permeabilization several pulses have been proved to be more successful (Kotnik et al., 2000; Canatella et al., 2001). Thus, our interest was to also determine conductivity changes during a train of successive pulses. We analyzed how conductivity changes are related to the percentage of permeabilized cells in view of possible application of such measurements for online monitor of cell electroporation. Finally, we discuss how our observations agree with the current theoretical models of electroporation and which processes might contribute to the observed increase of bulk conductivity of a cell suspension.

MATERIALS AND METHODS

Current-voltage and impedance measurements

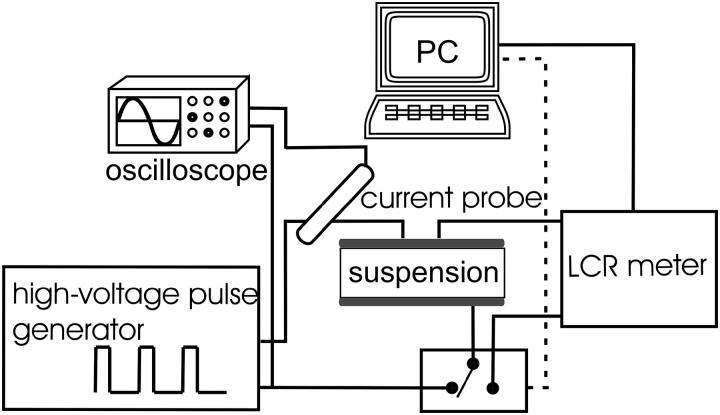
The experimental setup for current-voltage and impedance measurements is shown in Fig. 1. To generate high-voltage square pulses a high-voltage generator (prototype developed at the Laboratory of Biocybernetics, Faculty of Electrical Engineering, University of Ljubljana) was used. Impedance amplitude |Z| and phase angle-ϕ before and after pulses were measured with impedance meter (HP4274A, Houston, TX). For every sample first impedance was measured after which the system switched electrodes to the high-voltage pulse generator and pulses were delivered. The second impedance measurement was carried out 2–3 s after the train of pulses and the third measurement 10 s after the second measurement. Impedance was measured at 10 different frequencies from 100 Hz to 100 kHz and altogether lasted 4 s.

FIGURE 1.

A schematic diagram of the system for electroporation and current-voltage and impedance measurements. The cell suspension (100 μl) was placed between the electrodes. First, impedance was measured then the system switched electrodes to the high-voltage pulse generator and pulses were delivered. Two to three seconds after the pulses, impedance was measured for the second time and after another 10 s for the third time. For each pulse application, voltage, and current were traced on oscilloscope and stored for further analysis.

During the pulses the electric current was measured with a current probe (LeCroy AP015, New York, NY) and both current and voltage were measured and stored on the oscilloscope (LeCroy 9310 C Dual, 400 MHz). Pulse amplitudes were varied to produce applied electric field E₀ between 0.4 and 1.8 kV/cm. We used a train of eight square pulses of 100-μs duration with 1 Hz repetition frequency except where stated otherwise. The memory segmentation function was used to obtain high time resolution during the pulses and only 100 μs after the pulses were recorded. Parallel aluminum plate electrodes (Eppendorf cuvettes) with 2-mm distances between the electrodes when the whole range of amplitude were used and 4-mm distances in experiments where two volume fractions of cells were used. For every set of parameters a reference measurement on medium with no cells was also performed.

Cells and medium

Mouse melanoma cell line, B16F1, was used in experiments. Cells were grown in Eagle's minimum essential medium supplemented with 10% fetal bovine serum (Sigma-Aldrich Chemie GmbH, Deisenhofen, Germany) at 37°C in a humidified 5% CO₂ atmosphere in the incubator (WTB Binder, Labortechnik GmbH, Seelbach, Germany). For all experiments the cell suspension was prepared from confluent cultures with 0.05% trypsin solution containing 0.02% EDTA (Sigma-Aldrich Chemie GmbH). From the obtained cell suspension trypsin and growth medium were removed by centrifugation at 1000 rpm at 4°C (Sigma-Aldrich Chemie GmbH) and the resulting pellet was resuspended in medium and again centrifuged. Two media were used for electroporation: a high-conductive medium Spiner's modification of Eagle's minimum essential medium (SMEM) (Life Technologies, Paisey, UK) having conductivity σ₀ (25°C) = 1.58 S/m that does not contain calcium and a low-conductive medium that contained phosphate buffer with 250 mM sucrose, PB σ₀ (25°C) = 0.127 S/m. Cell suspensions having cell volume fractions f = 0.15 (5 × 10⁷ cells/ml) and f = 0.3 (1 × 10⁸ cells/ml) were used in the experiments.

Permeabilization and viability experiments

Cell permeabilization was determined by the uptake of the cytostatic drug bleomycin and cell survival by the cell ability to survive the application of electric pulses. It was shown that bleomycin at 5 nM external concentration penetrates only the permeabilized cells thus it can be used as an indicator of membrane permeabilization. The method is described in detail by Kotnik and co-workers (Kotnik et al., 2000). A 100-μl droplet of a cell suspension was placed between electrodes. Bleomicyn was added (5 nM external concentration) immediately after pulse application (never >60 s after the end of pulse application) to determine permeabilization. We used two amplitudes of the applied electric pulses, under permeabilization threshold (0.4 kV/cm) and above the threshold (0.94 kV/cm) for cells suspended in SMEM medium, and one amplitude for PB medium (0.94 kV/cm) for which two different volume fractions were used. For each pulse amplitude, a train of eight rectangular pulses with duration of 100 μs and repetition frequency 1 Hz was applied and a control consisting of cells that were not exposed to an electric field was prepared. All cells were incubated at room temperature for 30 min to allow resealing of membrane and were plated at a concentration of 250 cells per petri dish for clonogenic assay. Colonies were grown in the same conditions as described above for cell culturing and after five days colonies were fixed with methanol (Merck KGaA, Darmstadt, Germany) and stained with crystal violet (Sigma-Aldrich Chemie GmbH). Visible colonies were counted and results were normalized to the control (cells with added 5 nM bleomycin not exposed to electric field). The percentage of survived colonies was subtracted from 100 percent to obtain the percentage of bleomycin uptake. Three different sample data were pooled together to obtain average and standard deviation. Each experiment was repeated twice on two separate days. Cell survival was determined as described above for the cell permeabilization but without addition of bleomycin. Results were expressed as a percentage of the cell survival.

Both results of permeabilization and survival were compared to the results obtained with the same procedure in similar conditions but with lower cell density (2 × 10⁷/ml) obtained from our previous study. Results are plotted against the local electric field E rather than applied electric field E₀ = U/d because for a high density of cells the local field experienced by each cell is smaller than the applied field due to the interaction between the cells (Susil et al., 1998; Canatella et al., 2001; Pavlin et al., 2002a). The scaling factor E/E₀ was taken from our previous study (Pavlin et al., 2002a), where the decrease of the field (and induced transmembrane voltage) due to the neighboring cells was calculated to be 1% for f = 0.05 and 9% for f = 0.3.

Measurements of cells swelling

In separate experiments we exposed cells to pulses (E₀ = 0.4, 0.95, 1.43 kV/cm) in an observation chamber under the inverted phase contrast microscope (Zeiss 200, Axiovert, Jena, Germany). As in other measurements a train of eight 100-μs pulses with 1-Hz repetition frequency was used. The images were recorded (MetaMorph imaging system, Visitron, Puchheim, Germany) during the train of pulses and after the pulses up to 600 s after the first pulse. Three experiments for each, SMEM and PB medium, were made on three different days. For every parameter the area of five cells was measured from which an average was obtained. From this the changes in cells volume fraction was determined.

Theoretical analysis: calculation of the conductivity of a suspension of permeabilized cells

For theoretical analysis we used an analytical model that relates the change in the membrane conductivity with the change of the effective conductivity of a cell suspension (Pavlin and Miklavčič, 2003). The induced transmembrane voltage for a nonpermeabilized spherical cell exposed to the external electrical field E can be derived from the Laplace equation. Except in very low-conductive medium, the solution can be approximated with

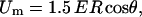(1)

where we assume that the cell membrane is almost nonconductive compared to the external medium. R is the cell radius and θ is the angle between direction of the electric field and the point vector on the membrane.

When the induced transmembrane voltage exceeds the threshold voltage, the part of the cell membrane where U_m exceeds U_c is permeabilized. The permeabilized part of the cell membrane can be therefore defined by the critical angle θ_c, where 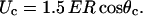This permeabilized part of the cell membrane is in the model described by the increased membrane conductivity σ_m, whereas other parts of the cell membrane have zero conductivity. The potential around such permeabilized cell oriented parallel to the electric field is calculated with the Laplace equation and by using a dipole approximation the equivalent conductivity σ_p of a single cell is calculated. From this, using the Maxwell equation (Maxwell, 1873; Pavlin et al., 2002b)

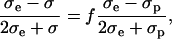(2)

the effective conductivity σ of a suspension of permeabilized cells is obtained, where f is the volume fraction of the cells and σ_e the conductivity of the external medium. The model takes into account the anisotropic nature of permeabilization, i.e., that only part of the membrane is permeabilized, and incorporates this in the calculation of the effective conductivity. The model allows calculation of the change of the effective conductivity (σ − σ₀), which depends on different parameters: the cell volume fraction f, average membrane conductivity of the permeabilized area σ_m, critical angle of permeabilized area θ_c, and conductivities of the external medium and cytoplasm, σ_e and σ_i, respectively. A more detailed description of the model is described in our previous article (Pavlin and Miklavčič, 2003).

RESULTS

In the presented study we performed experiments where conductivity of a cell suspension was measured in parallel with the extent of cell permeabilization and cell survival. We used low-conductive medium typically used in in vitro conditions and high-conductive medium that is more representative for in vivo conditions. In addition, different volume fractions and pulse repetition frequencies were used to establish their effect on the conductivity changes.

Measured data were analyzed in terms of “instant” conductivity σ(t) = I(t)/U(t) d/S, the ratio between current and voltage at a given time point, where d is the distance between the electrodes, and S the surface of the sample volume at the electrodes. We obtained time-dependent conductivity of cell suspension σ for a train of eight 100-μs pulses and applied electric field between 0.4 and 1.8 kV/cm, as shown in Fig. 2. Because our goal was to determine the difference in the conductivity of permeabilized and nonpermeabilized cells, only the difference in the initial and final level was analyzed and not the dynamic behavior. The initial value of conductivity at the start of each pulse 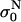was determined 3 μs after the start of the pulse, so that transient effects were not taken into account. The conductivity at the end of each pulse σ^N was determined and from this the change in the conductivity during the N^th pulse was obtained: Δσ^N = σ^N − 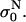With σ₀ we denote the initial conductivity at the start of the first pulse σ₀ =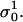

FIGURE 2.

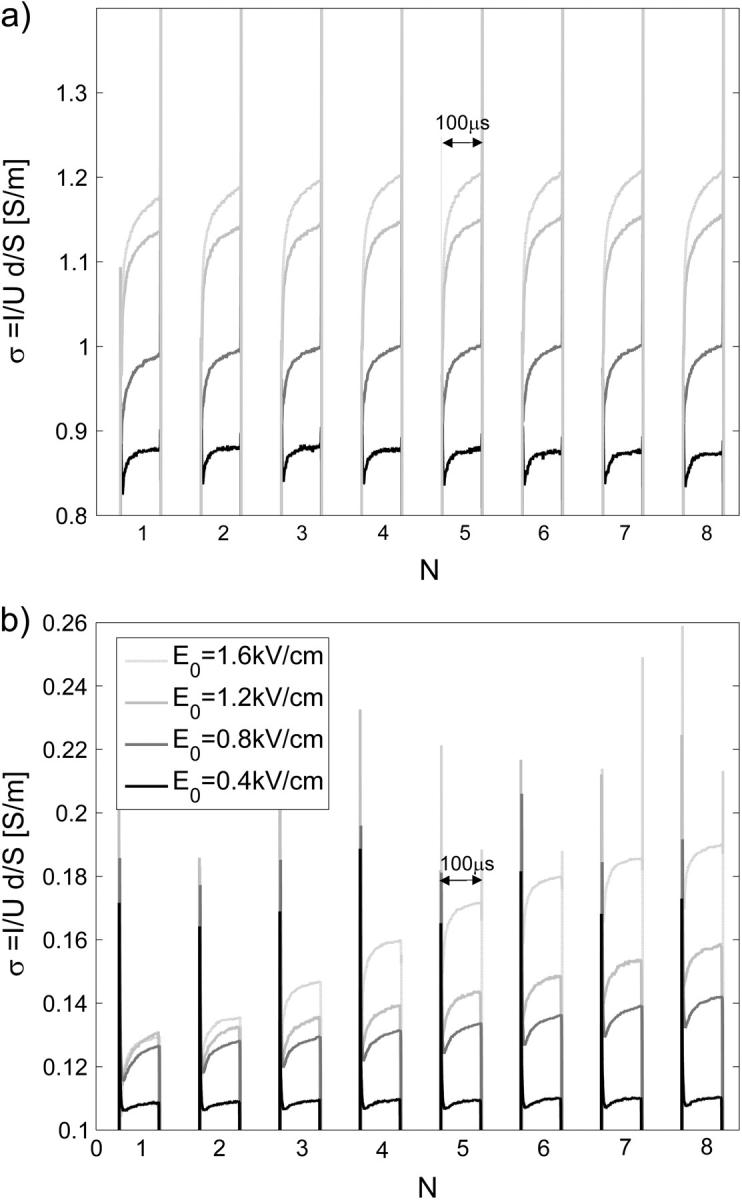
Measured time-dependent conductivity σ(t) = I(t)/U(t) d/S during a train of eight 100-μs pulses, 1-Hz repetition frequency for (a) cells in high-conductive SMEM medium and (b) cells in low-conductive PB medium for different applied electric fields E₀ = U/d. The memory segmentation function of the oscilloscope was used to obtain high time resolution during the pulses, and only 100 μs after the pulse were recorded. Legend in panel b applies also to panel a.

Fig. 3 represents conductivity changes Δσ¹/σ₀ during the first 100-μs pulse for cells in SMEM medium (a) and cells in PB medium (b) for E₀ = U/d = [0.4–1.8] kV/cm, electrode distance was 2 mm. In analysis all data are represented for the local electric field E obtained from the applied electric field E₀ by taking into account the decrease of the electric field due to the neighboring cells.

FIGURE 3.

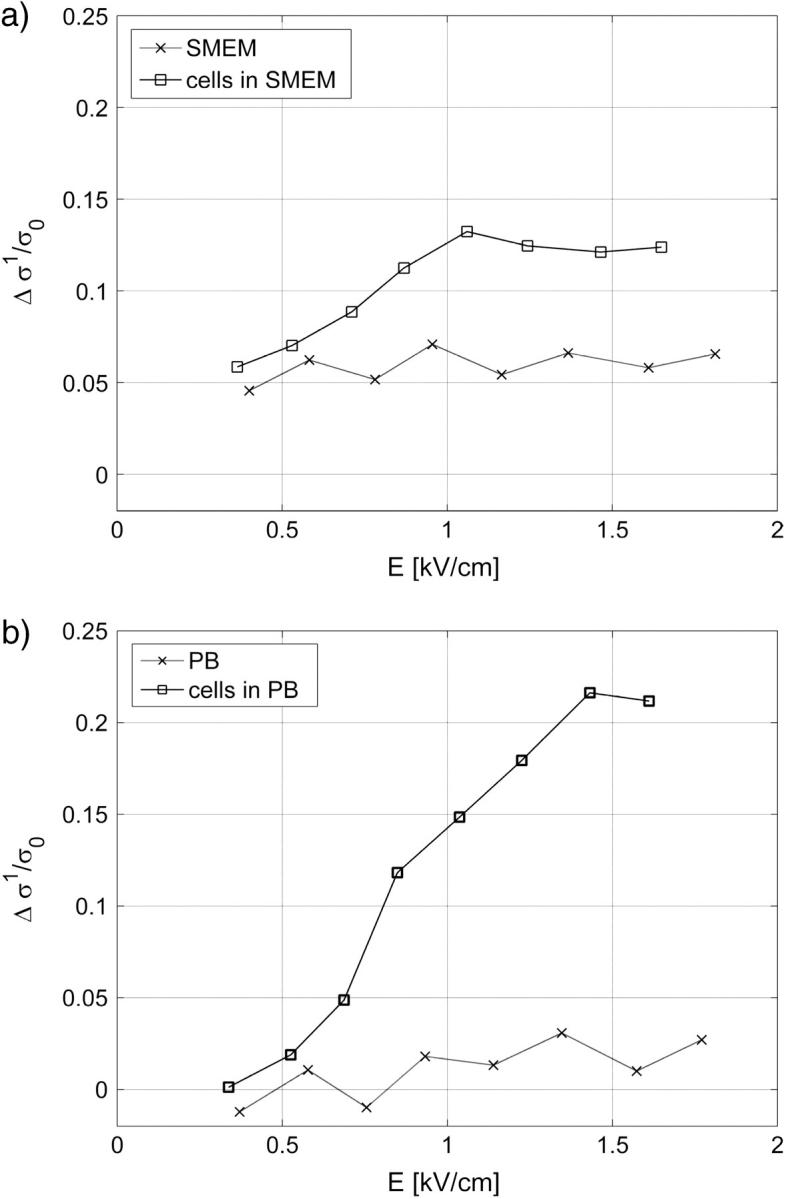
Conductivity change after the first pulse of the train of 8 × 100-μs pulses Δσ¹ normalized to initial conductivity in (a) cells in SMEM medium and (b) cells in PB medium, cells in medium (solid line), reference measurement on medium without the cells (dotted line). The results are shown for local electric field E, where E/E₀ = 0.91 (f = 0.3).

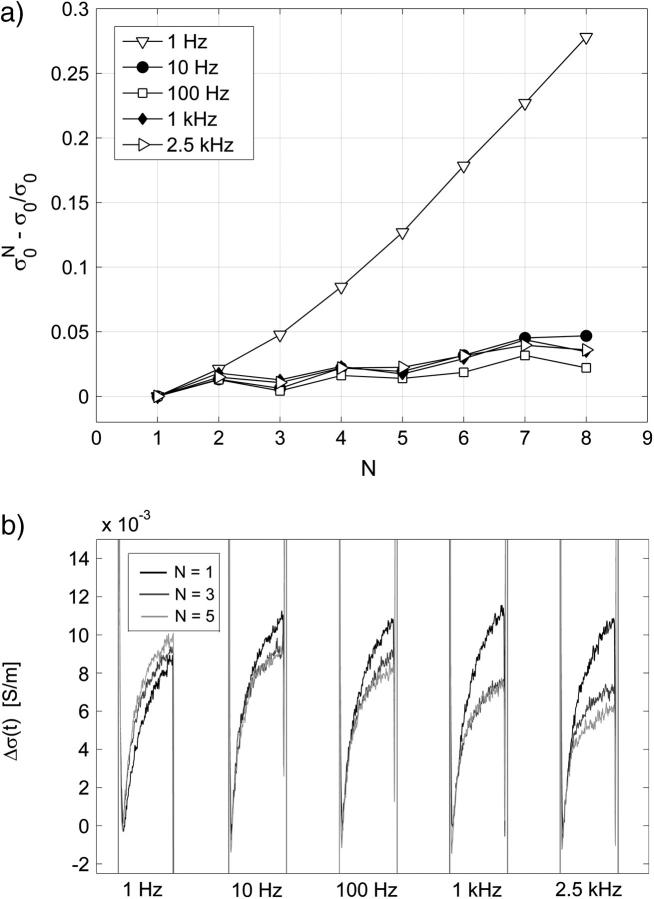
For cells in both media, an increase in conductivity change during first pulse Δσ¹/σ₀ is observed for E above 0.5 kV/cm, which reaches the maximum (12%) around 1 kV/cm in SMEM medium and at 1.4 kV/cm (25%) in PB medium. Very similar field dependence is obtained for all pulses in both media, where a dramatic increase in conductivity is observed above 0.5 kV/cm. The reference measurements in pure SMEM and PB media show constant Δσ¹/σ₀ that can be attributed to electrode processes and Joule heating. Conductivity changes Δσ^N/σ₀ during consecutive pulses in PB (see Fig. 8 b) and SMEM media are approximately constant at 1-Hz repetition frequency and even when a train of 24 pulses was applied, the increase in the conductivity during the pulses surprisingly remained constant.

FIGURE 8.

Effect of the repetition frequency on the conductivity changes in PB medium. Pulses 8 × 100 μs with repetition frequencies from 1 Hz to 2.5 kHz were used, E = 0.84 kV/cm. (a) Relative change of the initial level of the conductivity 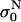is shown. (b) The time-dependent conductivity changes Δσ(t) of the first, third, and fifth pulse with respect to the first pulse (all initial levels are set to zero) are compared for different frequencies.

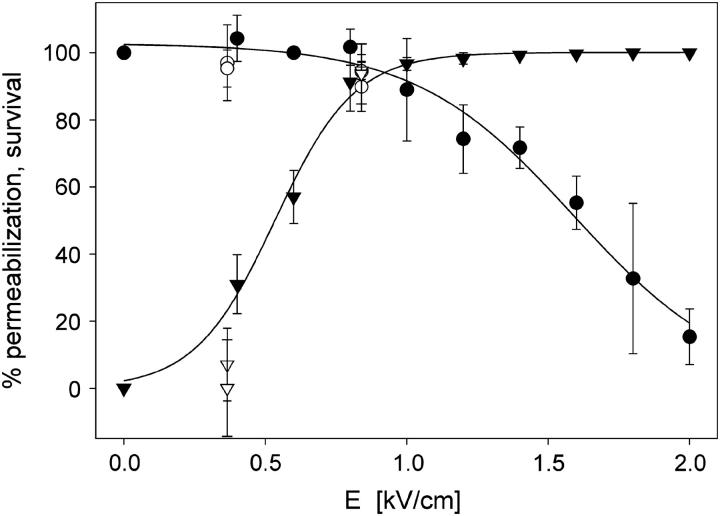
In Fig. 4 percentage of permeabilized and survived cells in SMEM medium after application of 8 × 100 μs pulses (E = 0.84 kV/cm) is shown. Results in dense suspensions (f = 0.3) are compared to previous measurements performed using the same experimental protocol but with lower cell density (f = 0.05). We can see good agreement with the permeabilization curve for a lower density of cells. The permeabilization curve for PB medium is similar to the curve for SMEM medium because we have shown previously that permeabilization curves for SMEM and PB medium are similar (Pucihar et al., 2001). Similar agreement of measurements for high density with results for lower density of cells was obtained also for PB medium where at E = 0.84 kV/cm 92% of permeabilization is achieved with survival being 100%.

FIGURE 4.

Permeabilization (▾) and survival rate (•) of B16F1 cells in SMEM medium for electroporation experiments with 8 × 100-μs pulses, 1-Hz repetition frequency (lines show fitted sigmoid function). Experiments where high density of cells f = 0.3 (open symbols) are compared with the permeabilization and survival curves obtained in experiments with lower cell density f = 0.05 (solid symbols).

Comparing Figs. 3 and 4 it can be seen that transient conductivity changes Δσ¹/σ₀ increase above 0.5 kV/cm agrees with permeabilization curve shown in Fig. 4. Percentage of permeabilized cells reaches maximum at 1 kV/cm similarly as conductivity changes in SMEM, whereas in PB medium maximum conductivity increase is obtained at 1.4 kV/cm.

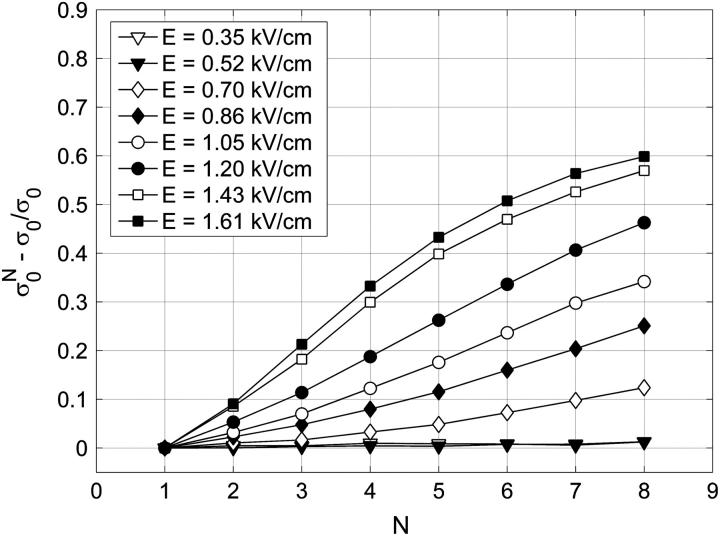
In Fig. 5 relative changes of the initial level of conductivity 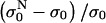in PB medium for consecutive pulses are shown. It can be seen that the initial level starts to increase again for E > 0.5 kV/cm, which can be explained with the efflux of ions (mostly K⁺ ions) from the cytoplasm into the medium through membrane pores due to the concentration gradient, indicating that the cell membrane is permeabilized above 0.5 kV/cm. In high-conductive SMEM medium the increase of the initial conductivity is solely due to Joule heating as almost the same values are obtained for medium alone (results not shown). For higher electric fields the efflux of ions in PB increases up to 1.4 kV/cm where it reaches maximum, similarly as transient conductivity changes during a single pulse. Up to E = 1.0 kV/cm the conductivity increases approximately linearly with time but starts to reach saturation level at higher electric field due to a decrease of the concentration gradient of the ions. This is expected because the total duration of the train of eight pulses at 1 Hz is 7 s and the time constant for diffusion of ions is few seconds. In Appendix B we theoretically analyzed the efflux of ions through the permeabilized membrane and obtained an exponential rise to a maximum. Deviation from this behavior is due to different simplifications of the model and statistical variation of cell sizes that are consequently permeabilized above different critical electric fields.

FIGURE 5.

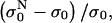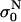The relative change of the initial level of conductivity in PB medium for consecutive pulses: where is the initial level at the start of the N^th pulse is shown.

Another interesting parameter is the total conductivity change Δσ_tot = σ⁸ − σ₀, which we define as the difference between the final conductivity at the end of the eight pulse and the initial conductivity. In Fig. 6 the total conductivity changes after the application of a train of eight 100-μs pulses are presented for the same experiments as shown in Fig. 3. For the low-conductive medium a steady increase of the total conductivity change is observed above 0.5 kV/cm, corresponding to both ion efflux from the cell interior and the increased conductivity. The conductivity changes in low-conductive medium without cells are negligible.

FIGURE 6.

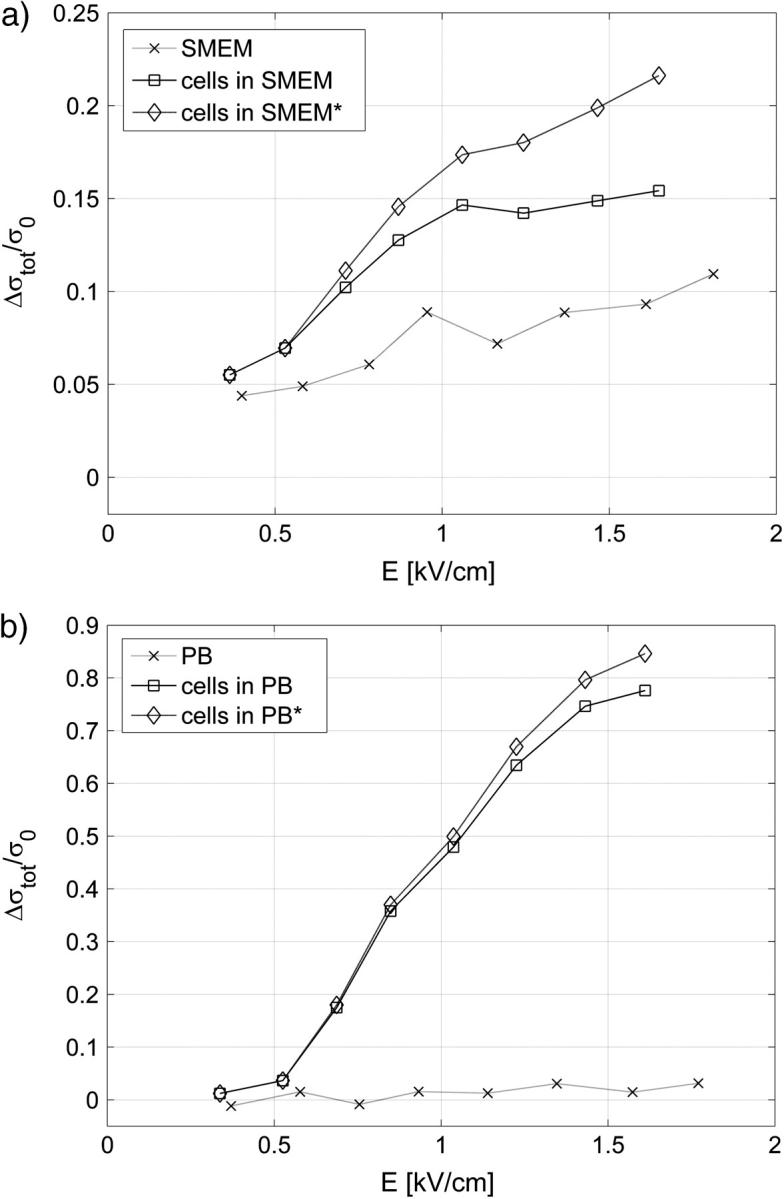
The total conductivity change Δσ_tot = σ⁸ − σ₀ after the application of 8 × 100-μs pulses (same experiment as in Fig. 3) in (a) cells in SMEM medium and (b) cells in PB medium, cells in medium (solid line), reference measurement (dotted line) on pure medium (×). Note the difference in scale between panels a and b. In Fig. 6 a measured total conductivity change (□) and total conductivity change corrected for the increased cell size due to the colloid-osmotic swelling (⋄) Δσ′_tot/σ₀ = Δσ_tot/σ₀ − Δσ_swell/σ₀ is shown.

In contrast, in high-conductive medium the difference between the total change in conductivity for cells in a suspension and the total conductivity change for pure medium is less pronounced. This can be attributed to substantial Joule heating during 8 × 100-μs pulses, which can be calculated theoretically when neglecting the heat dissipation:

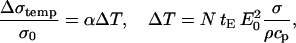(3)

where T is temperature of the suspension, α is constant of the conductivity temperature dependence, t_E is length of the pulse, ρ the density, c_p specific heat capacity of the suspension, and N number of pulses. The above equation gives for α = 0.017/°C (SMEM medium) a temperature increase of ∼3°C after eight pulses for E₀ = 1 kV/cm. From this theoretical calculation of the conductivity change due to Joule heating for 8×100-μs pulses gives 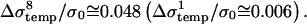But during a single 100-μs pulse in pure medium a change of Δσ¹/σ₀ ≅ 0.04 is observed (see Fig. 3 a), which is evidently not only due to Joule heating but also due to some other effects (electrode processes, anomalous heating), which has been observed by other authors (Pliquett et al., 1996).

Another important process that significantly affects mainly the results obtained in high-conductive medium (because the total changes are smaller) is colloid-osmotic swelling of cells, which increases the effective volume fraction of the cells and consequently decreases the conductivity (see Fig. 7). In Fig. 6 a we compare the total conductivity changes (open squares) and total conductivity changes corrected for the increased cell size due to the colloid-osmotic swelling (*) Δσ′_tot/σ₀ = Δσ_tot/σ₀ − Δσ_swell/σ₀. We can see that when the increase in cell size is taken into account the total change after the eight pulses shows a similar strong increase above the threshold field as in the low-conductive medium.

FIGURE 7.

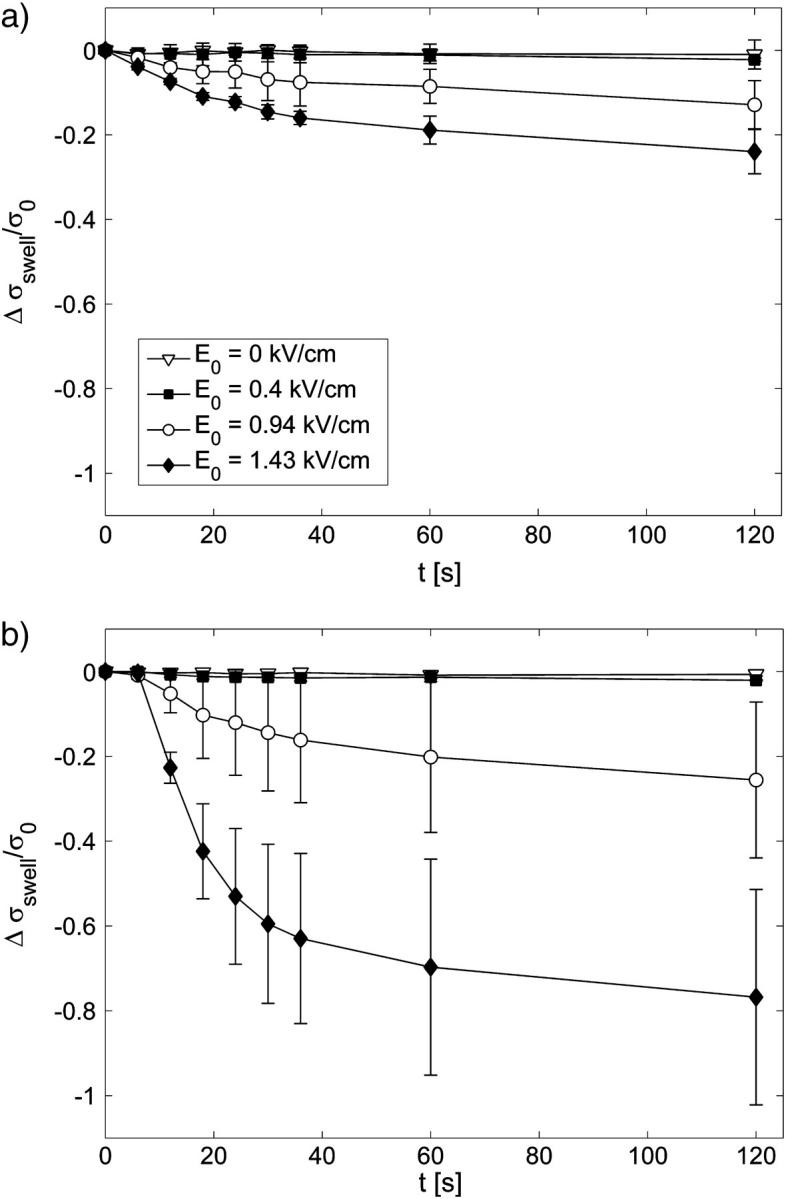
The effect of colloid-osmotic swelling on the bulk conductivity for different applied electric field strengths E₀ and control (E₀ = 0 kV/cm); time t = 0 s, start of the first pulse; t = 7 s, end of the pulsation. The changes of cells volume fractions due to the increased cell sizes were transformed into the conductivity change Δσ_swell/σ₀ in (a) SMEM and (b) PB medium.

Measurements of colloid-osmotic swelling

It was shown in several experiments that cells swell during electroporation and consequently a drop in the conductivity of the cell suspensions and pellets after the pulses was observed (Kinosita and Tsong, 1977b; Abidor et al., 1993, 1994). Swelling of permeabilized cells is caused due to the difference in the permeabilities of ions and larger molecules (macromolecules) inside the cell, which results in an osmotic pressure that drives water into the cells and leads to cell swelling.

To determine the dynamics and the extent of cell swelling for our experimental conditions we made additional experiments where images of cells during and after pulse application were recorded. The results of the measurements of the cell sizes during and after the pulses are shown in Fig.7 where the changes in the volume fraction were transformed into changes of conductivity Δσ_swell / σ₀(Δf) according to Eq. 2. The corrected curve in Fig. 6 a was obtained by extracting the Δσ_swell / σ₀ due to cell swelling at t = 7 s, which corresponds to the time point at the end of the eight pulse.

The time constant of colloid-osmotic swelling is a few tens of seconds; this is in agreement with the time constant for efflux of ions, which is between 10 and 20 s (see Fig. 5).

Impedance measurements

From impedance measurements before and after application of pulses, the change of the real part of the impedance was calculated. From the impedance spectrum only the results at 100-kHz frequency were used due to the large scattering of data at lower frequencies. From the real part of the impedance we calculated bulk conductivity: σ = 1/Re(Z) d/S. For each sample we present values of the conductivity change Δσ/σ₀ at the two time points: t₁ = 14 s and t₂ = 28 s after the first pulse.

Impedance measurements in all experiments showed reproducibly decrease in conductivity in SMEM medium above permeabilization threshold and increase in conductivity in PB medium. Results of the experiments with the 8 × 100-μs pulses for E = 0.35–1.6 kV/cm are given in Table 1. We can observe steady increase in conductivity in PB medium for higher fields whereas in SMEM medium conductivity is decreased after the pulses. We can explain these values by considering all the effects that contribute to post-pulse conductivity: efflux of ions in PB medium, Joule heating in SMEM medium, and osmotic swelling: Δσ_imp/σ₀ = Δσ_efflux/σ₀ + Δσ_swell/σ₀ + Δσ_temp/σ₀. For example, in PB medium at 1 kV/cm is Δσ_imp/σ₀ (14 s) = 0.47, which can be obtained from extrapolating the values of the initial conductivity changes from Fig. 5 at t = 7 s (N = 8) to t = 14 s, which gives approximately Δσ_efflux/σ₀ + Δσ_swell/σ₀ ≅ 0.5. Here the first term efflux of ions dominates because from Fig. 7 b we obtain Δσ_swell/σ₀ (14 s) ≅ −0.05. At higher fields osmotic swelling drastically decreases conductivity up to −0.4, however, the efflux of ions in PB is so large that after the pulse Δσ_imp/σ₀ (14 s) increases up to +0.7, which is also the saturation level of the changes of the initial level. On the other hand in SMEM medium there is no net efflux of ions, therefore, mostly osmotic swelling contributes to reducing of bulk conductivity, which results in negative values of Δσ_imp/σ₀; e.g., at 1 kV/cm we obtain Δσ_imp/σ₀ (28 s) = −0.04, which can be explained by contributions of cell swelling Δσ_swell/σ₀ ≅ −0.07 (see Fig. 7 a) and Joule heating Δσ_temp/σ₀ ≅ +0.035 whereas efflux of ions in high-conductive SMEM medium is negligible.

TABLE 1.

The changes of the real part of the impedance 14 and 28 s after the first pulse transformed into the conductivity change Δσ_imp/σ₀ for cells in SMEM and PB medium

Δσimp/σ0	E = 0.35 kV/cm	E = 0.52 kV/cm	E = 0.7 kV/cm	E = 0.86 kV/cm	E = 1.05 kV/cm	E = 1.2 kV/cm	E = 1.43 kV/cm	E = 1.61 kV/cm
SMEM t1 = 14 s	−0.002	−0.025	−0.010	−0.0136	−0.026	−0.030	−0.023	−0.032
SMEM t2 = 28 s	0.000	−0.061	−0.017	−0.022	−0.040	−0.043	−0.033	−0.042
PB t1 = 14 s	0.010	0.027	0.24	0.40	0.47	0.58	0.66	0.70
PB t2 = 28 s	0.015	0.041	0.33	0.48	0.54	0.63	0.70	0.73

The effect of the repetition frequency on the measured increase in conductivity

Fig. 8 summarizes the effect of the repetition frequency on the conductivity changes in low-conductive PB medium. In Fig. 8 a the initial level of conductivity is shown for consecutive pulses and it can be seen that for frequencies above 10 Hz (100-ms pause between the pulses) very small changes of the initial level are obtained, which agrees with previous observation that the diffusion time constant is around a few seconds. In Fig. 8 b absolute changes of conductivity Δσ(t) during the first, third, and the fifth pulse are compared for different frequencies.

We can observe that for 1 Hz the consecutive pulses are almost identical and that relaxation of the conductivity is complete in one second, however, for higher frequencies each consecutive pulse is smaller than the previous pulse and the time course of the second part of the pulse is different. This indicates that relaxation in milliseconds after the pulse is not complete and that the conductivity does not relax to its initial level but constantly increases. In SMEM medium (results not shown) we also obtained complete relaxation at 1 Hz and difference in pulse shapes for consecutive pulses at 1 kHz. The initial level of conductivity increased between the pulses almost twice as in pure medium at 1 kHz, whereas at 1 Hz no difference between pure medium and cells was observed, which similarly as in PB medium shows that time constant of conductivity relaxation is in the millisecond range.

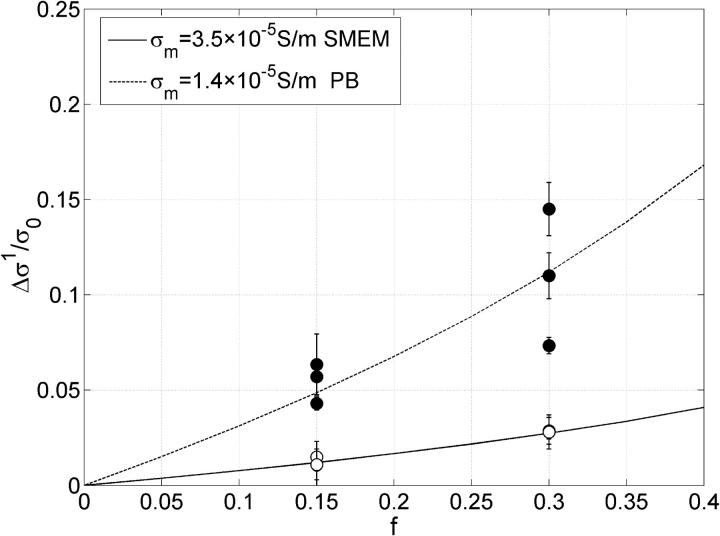
In Fig. 9 changes of conductivity after the first pulse Δσ¹ for two volume fractions are shown at E = 0.84 kV/cm, electrode distance was 4 mm. The measured values for cells in SMEM medium are corrected for the changes in the medium alone. The lines represent results of the theoretical model described in the Materials and Methods section. Membrane conductivity was fitted to the measured data in high- and low-conductive medium to obtain the equivalent conductivity σ_p = 0.0495 and 0.0209 S/m, respectively. Then the dependence of the relative changes on the electric field were obtained from finite elements models of permeabilized cells for different critical angles and by this a scaling factor was determined between equivalent conductivity σ_p when θ_c = 54° (at 0.84 kV/cm) and σ′_p when θ_c = 90°. From the equivalent conductivity σ′_p [0.053 S/m, 0.0226 S/m] of a single cell σ_m for θ_c = 90° can be obtained from the Pauly-Schwan equation:

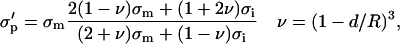(4)

where R is the cell radius and d the thickness of the membrane. In this way we obtained average membrane conductivity of the permeabilized part to be σ_m = 3.5 × 10⁻⁵ S/m (SMEM) and σ_m = 1.4 × 10⁻⁵ S/m (PB).

FIGURE 9.

Absolute change in conductivity during the first pulse Δσ¹ is shown. Each error bar represents three sample data pooled together, obtained for a train of eight 100-μs pulses of 0.84 kV/cm in SMEM medium (○) and PB medium (•). The conductivity changes in pure SMEM medium were subtracted from the measured value obtained for cells in SMEM. The lines represent values of the theoretical model (see the Materials and Methods section) where membrane conductivity was fitted to obtain the best agreement with measured data.

Under the assumption that that the number and size of the pores remain constant for different electric field strengths, the average membrane conductivity of the permeabilized area σ_m does not depend on E. Therefore, E governs only the area of the permeabilized surface given by (Schwister and Deuticke, 1985)

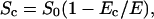(5)

and by this the dependency of the cell equivalent conductivity on E.

In Fig. 10 the theoretical curve of the dependency of the conductivity increase due to the increased surface of permeabilized area for different E is shown where the critical angle θ_c is defined by the applied electric field and the critical voltage U_c. We numerically calculated the equivalent conductivity of a single cell σ_p (θ_c) and the bulk conductivity of a suspension of permeabilized cells for different critical angles as described in our previous work (Pavlin and Miklavčič, 2003) and in Materials and Methods. From this field-dependent conductivity changes Δσ/σ₀ (E) were calculated for constant membrane conductivity or taking into account the nonohmic behavior of the conductivity inside the pore using Eq. A.7, as shown in Fig. 10. Values of membrane conductivity were obtained from fitted values of our experimental data shown in Fig. 9. Critical electric field strength in both media was set to 0.5 kV/cm according to our experimental results (see Figs. 3 and 4).

FIGURE 10.

The theoretical curve of the dependency of the conductivity increase on the electric field due to the increased permeabilized surface area according to the theoretical model (see Appendix). Field-dependent conductivity change calculated theoretically for high conductive medium (squares) and low conductive medium (circles), f = 0.3, under an assumption of constant membrane conductivity of the permeabilized area (solid line) or *taking into account the nonohmic behavior of the conductivity inside the pore using Eq. A.7 (dashed line) is shown. Values for membrane conductivity σ_m were chosen as obtained from experiments shown in Fig. 9 at E = 0.84 kV/cm), threshold electric field in both cases was set to 0.5 kV/cm according to our experimental results.

DISCUSSION

The aim of our study was to analyze the effect of high-voltage pulses on the electrical properties of cells in a suspension and to analyze how these changes correspond to the level of membrane permeabilization. We performed current and voltage measurements during the train of eight high-voltage pulses and impedance measurements before and after the application of pulses in a dense suspension of cells. At the same time we determined the percentage of permeabilized cells and cell survival. In additional experiments the extent of colloid-osmotic swelling was also determined.

We observed a transient increase in conductivity during electric pulses for electric fields above 0.5 kV/cm (U_m = 450 mV) both in low- and high-conductive medium after which the pulse conductivity relaxed almost to the initial level. Our results are in agreement with the results of other groups obtained on single cells (Chernomordik et al., 1987; Ryttsen et al., 2000), cell suspensions (Kinosita and Tsong, 1977a,b; 1979), and cell pellets (Abidor et al., 1993; 1994) where also a transient increase in conductivity above a threshold electric field was observed. The threshold electric field at which the increased conductivity is observed in our experiments corresponds to the permeabilization threshold for the uptake of molecules for both media for several pulses. We obtained similar results for dense and dilute suspensions for permeabilization and survival, in agreement with Canatella et al. (2001) where it has been shown that the cell density itself does influence permeabilization only by affecting the local electric field. For tissue electroporation in general, however, there are several effects that contribute to nonhomogeneous molecules uptake due to differences in cell state, solute concentration, and local electric field (Canatella et al., 2004).

The saturation of the conductivity in high-conductive medium, which is reached at the same electric field (around 1 kV/cm) as the permeabilization level (see Figs. 3 and 4) for eight pulses, agrees with the theoretical model where the field strength determines the permeabilized area and the membrane conductivity is assumed to be constant or having conductivity of the pore dependent on the electric field (see Appendix A) as shown in Fig. 10. In low-conductive medium maximum increase in conductivity is reached at higher electric field as permeabilization (and as described by the theoretical model) indicating that conductivity of permeabilized area is also increased due to increase in number or size of the pores, as has been suggested in some theoretical descriptions of pore evolution during the electric pulses (Chernomordik et al., 1987; Glaser et al., 1988). The changes of the initial level of conductivity obtained in the low-conductive medium (see Fig. 5) clearly show an increase of the overall level of the conductivity above 0.5 kV/cm, as well as saturation of conductivity increase at 1.4 kV/cm indicating that permeable structures in the membrane are present, which enable ions to leak from the cytoplasm into the external medium.

When analyzing the total increase in conductivity after the eight pulses (see Fig. 6) and the impedance several seconds after the pulses, we obtained that the change in conductivity consists of several contributions: i), a transient increase in conductivity during each pulse, which is observed above the threshold electric field and drops back to the initial level in less than a second; ii), a decrease in conductivity caused by colloid-osmotic swelling due to osmotic imbalance when the cell membrane is permeabilized, which is again observed only above the threshold field; swelling decreases the relative conductivity for a few percent in seconds after the application of pulses and up to 80% on the order of minutes; iii), increase in conductivity due to Joule heating by a few percent in high-conductive medium; and iv), efflux of ions from the cell interior, which is observed in low-conductive medium above the threshold electric field. All these contributions have to be taken into account when measuring the conductivity in cell suspensions as well as in tissue, where except for the efflux of ions, both the Joule heating and swelling of cells could affect the results considerably. Altogether our experiments on cell suspensions indicate that only measurements during the pulses or very shortly after the pulses relate to permeabilization, whereas impedance measurements several seconds later detect predominantly other effects. Because of higher density of cells in tissue and consequently lesser cell swelling due to cell-cell contacts (Abidor et al., 1993; 1994) the impedance measurements in tissue could give more information compared to measurements in cell suspensions.

Fitting the measured values of the conductivity changes to our theoretical model gives us an approximate membrane conductivity at the end of the 100-μs pulse σ_m = [1.4–3.5] × 10⁻⁵ S/m, which is smaller than the membrane conductivity determined on sea urchin eggs σ_m = [1–4] × 10⁻⁴ S/m (Hibino et al., 1991) or a magnitude lower than the values obtained on erythrocytes by Kinosita and Tsong (1977a, 1979) (σ_m = 5 × 10⁻⁴ −5 × 10⁻³ S/m). This discrepancy can be explained by different experimental procedures and differences between the cell types. Comparison of theoretical curves in Fig. 10 and permeabilization dependence on the electric field suggest that electric field affects mostly the surface of the permeabilized area and consequently increased conductivity as well as fraction of permeabilized cells. Of course, the surface area of the permeabilized part of the cell membrane depend on the number as well as on the size of the pores, which both are time dependent. But in this article we limited our analysis only on the change of the conductivity and surface area of pores at the end of one pulse. A complementary theoretical analysis of the conductivity changes caused by membrane electroporation on CHO cell pellets was published recently (Schmeer et al., 2004). Authors analyze also the dynamic behavior and the size of the pores and obtain similarly that the conductivity changes during the pulses are transient whereas the conductivity increase between the pulses in a low conductive medium is due to the ion efflux.

In Appendix A, we estimate the fraction of surface area of the pores f_p = S_por/S₀ from obtained membrane conductivity that gives us f_p ≈ 10⁻⁵–10⁻⁴. This is substantially less than the values obtained on sea urchin eggs (Hibino et al., 1991) f_p ≈ 10⁻⁴–10⁻³ and CHO cells f_p ≈ 10⁻⁴ (Neumann et al., 1998) or values that were obtained by electrooptical measurements on vesicles f_p ≈ 10⁻⁴ (Tönsing et al., 1997). We further estimated fraction of pores from ion efflux between the pulses in low-conductive medium (see Appendix B) and obtained f_p ≈ 10⁻⁷–10⁻⁶ that is approximately two orders of magnitude lower than the fraction of pores calculated from the membrane conductivity during the pulses.

Our results are in agreement with fast relaxation of the conductivity and with results of other authors (Kinosita and Tsong, 1977a, 1979; Hibino et al., 1991, 1993) where the conductivity of the membrane dropped for an order of magnitude in the millisecond range. The results support the hypothesis of the existence of two types of pores: short-lived pores, which are created during the pulse and transiently increase conductivity, and long-lived pores that contribute to increased permeability for ions and molecules in minutes after the pulses.

The results obtained in both low-conductive and high-conductive medium show that the conductivity changes during each pulse do not “remember” previous pulses for 1-Hz repetition frequency, similarly as observed by other authors on planar bilayer membranes (Chernomordik et al., 1987; Macek-Lebar et al., 2002a) and cells (Chernomordik et al., 1987; Kinosita and Tsong, 1979), where for a 1-s pause between the pulses the second pulse started from the same level as the first one. When repetition frequency is increased above 1 kHz, relaxation is not complete and the initial level of conductivity for consecutive pulses increases. This is in agreement with the results of other authors where at 1-kHz repetition frequency the second pulse started from much higher level (Chernomordik et al., 1987; Kinosita and Tsong, 1979), except for slightly faster relaxation in our experiments. It is also interesting to note that even after application of three series of 24 pulses of 1 Hz in low-conducting medium the dynamic behavior and conductivity change during each pulse remained the same.

One possible explanation for fast relaxation of conductivity is that the number and diameter of short-lived conductive pores is decreased to a level where their contribution to the conductivity is negligible, whereas some of them are still present and can later participate in formation of the long-lived transport pores that have long resealing time and are large enough to facilitate transport of molecules. Only a few long-lived pores could suffice for a substantial uptake of molecules, however, their contribution to the increase in conductivity would be negligible; e.g., from our data for the efflux of ions the membrane conductivity 10⁻⁶ S/m gives an increase in conductivity on the order of 0.1%, which is not measurable, but the corresponding fraction of pores gives approximately N = 100 pores having a radius of 1 nm (from the literature approximately the size of a hydrophilic metastable pore) and large enough for the transport of molecules of a few kilodaltons such as bleomycine (1.5 kDa).

This is in accordance with the theoretical predictions of the electroporation theory that the size distribution of the pores is changed after the pulse (Weaver and Chizmadzhev, 1996) due to the resealing of smaller pores while a small number of larger long-lived pores remain in the membrane. Long-lived permeable state of the cell membrane is not yet fully explained even though several hypotheses exist such as existence of metastable hydrophilic pores (Weaver and Chizmadzhev, 1996; Neumann et al., 1989; Smith et al., 2004; Leontiadou et al., 2004), coalescence of pores (Sugar and Neumann, 1984), or presence of small defects in the lipid bilayer (Teissie and Ramos, 1998). Also specific cell structures could be important for the creation of long-lived permeable structures and could lead to difference in resealing dynamics between lipid bilayers and cells like involvement of cytoskeletal network (Rols and Teissie, 1992; Teissie and Rols, 1994), membrane proteins (Weaver and Chizmadzhev, 1996), or anisotropic inclusions in the membrane (Fošnarič et al., 2003; Kandušer et al., 2003).

Another possible explanation of the fast relaxation of conductivity could be, that only a smaller part of the increased conductivity can be attributed to the conductive pores and that the larger part is a result of some related process (e.g., release of bound charges in the vicinity of a pore due to the very strong local electric field) with relaxation around 1 ms. This process remains, however, to be identified and explained.

When analyzing if transient conductivity changes reflect the level of permeabilization we identified the major discrepancy between permeabilization and conductivity changes when a train of pulses was analyzed, which has not been studied in previous reports. Our results indicate that the increase in conductivity is observed above the threshold electric field for permeabilization. This on one hand suggests that permeabilization could be detected with measurements of conductivity. On the other hand, almost identical transient conductivity changes for consecutive pulses are observed, indicating that the conductivity increase is not necessarily related to the formation of the long-lived “transport” pores. The results further show that conductivity changes and the conductivity threshold do not depend on number of pulses, in contrast to cell permeabilization (detected usually as a transport of certain molecules), which depends on the duration and the number of pulses (Rols and Teissie, 1990; Kotnik et al., 2000; Canatella et al., 2001; Macek-Lebar et al., 2002b). This can be partially explained by the fact that electric current depends on different ion properties (mobility, concentration, and charge) and is governed by the electric field, whereas for small and especially noncharged molecules transport is governed mostly by diffusion (Puc et al., 2003). Hence, increased conductivity and permeabilization are not necessarily directly linked. It was also shown (Rols and Teissie, 1990) that when the number of pulses (or pulse duration) is increased, the threshold level reaches a certain limit threshold that cannot be decreased any further. So it is possible that with conductivity measurements we actually detect this limit threshold, which then explains why the conductivity threshold is equal for one or several pulses.

To summarize, conductivity measurements during the pulses give information about increased membrane permeability whereas impedance measurements several seconds after pulse application are not suitable due to fast relaxation of conductivity changes, colloid-osmotic swelling, and ions leakage. By measuring electric conductivity we can detect limit permeabilization threshold above which the electroporation process (uptake) occurs. However, conductivity changes are similar for a single or several pulses in contrast to considerable increase in permeabilization for several pulses, thus the transient conductivity changes, i.e., short-lived pores are related to permeabilization (long-lived pores) only indirectly and the relationship between the transient pores and long-lived permeable structures in the membrane remains to be explained. So, our results suggest that conductivity measurements can be used to optimize the voltage but not to control cell permeabilization in vitro in general, e.g., varying all pulse parameters. For application of conductivity measurements for online monitoring of cell electroporation relationship between permeabilization for a single and several pulses should be known, which is feasible because usually a certain protocol is chosen with constant number of pulses, and only the electric field is varied to achieve optimum efficiency. In such case the use of conductivity measurements for online control of the electroporation could be readily applied.

Appendix A: CALCULATION OF THE FRACTION OF SURFACE AREA OF PORES

Here we present the estimation of the fraction of the surface area of pores in the cell membrane from the increased membrane conductivity (similar derivation was first presented by Hibino). We assume that the specific conductance of the permeabilized area of a cell is approximately the sum of the conductance of N_p pores having radius r_p:

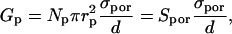(A.1)

where we neglect the very small conductance of nonpermeabilized cell membrane, S_por represents the surface of all conducting pores. On the other hand this conductance is equal to the average membrane conductance of the permeabilized area as obtained from our measurement and from the theoretical model:

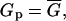(A.2)

thus

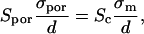(A.3)

where S_c represents the total permeabilized surface of one cell (the area exposed to above-threshold transmembrane voltage), which is described by Eq. 5 and σ_m the average membrane conductivity of permeabilized area as defined in the theoretical model.

Conductance of the pore in a 1:1 electrolyte is given by (Glaser et al., 1988)

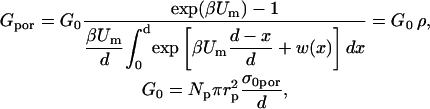(A.4)

where β = e / kT and w(x) = W(x) / kT where e is the electron charge, U_m is the transmembrane voltage, and W(x) the energy of an ion inside the pore due to the interactions of the ion with the pore walls (Parsegian, 1969; Glaser et al., 1988). Parameter ρ is a scaling factor, which reduces the conductivity of the ions inside the pores (σ_por), compared to the bulk approximation σ_0por ≈ (σ_e + σ_i)/2 in the limit of very large pores when interactions are negligible. For a trapezoid shape of w(x) we obtain from Eq. A.4 that when the transmembrane voltage is small nβU_m ≪ w₀

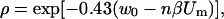(A.5)

and when the transmembrane voltage is large, e.g., for βU_m ≫ w₀ (U_m ≫ 25mV) we get

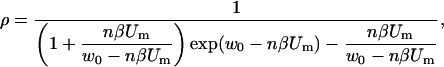(A.6)

where n is the relative size of the entrance region of the pore, and was estimated to be ∼0.15 (Glaser et al., 1988). W₀ is the energy of an ion inside center of a pore and was estimated to be a few kT (Glaser et al., 1988). Thus, the fraction of pores f_p of the total membrane surface is approximately:

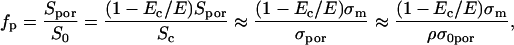(A.7)

where ρ is obtained from Eq. A.4. To estimate fraction of pores in our case for the membrane conductivity σ_m = [1.4–3.5] × 10⁻⁵ at E = 0.84 kV/cm we can use approximation Eq. A.6 because U_m ≫ 450 mV. Inserting values of parameters (see Table 2) into Eq. A.7 (1 − E_c / E) = 0.404 and Eq. A.6 w₀ = 2.5–5 we obtain for fraction of pores after 100-μs pulse being f_p = 10⁻⁵–10⁻⁴.

TABLE 2.

Values of used parameters

n	e/kT	σi	Um	R	d
0.15	40 V−1	0.5 S/m	900 mV	9.5 μm	5 nm
E	Ec	w0	ρ	σm	D
0.84 kV/cm	0.5 kV/cm	2.5–5	0.22–0.57	1.4–3.5 × 10−5 S/m	2.5 × 10−5 cm2/s

APPENDIX B: EFFLUX OF IONS

From the efflux of ions in the low conductivity medium (see Fig. 5) the fraction of the surface area of pores can be estimated. Here we assume that all conductivity increase on the order of seconds can be attributed to the efflux of ions (also some other process could be involved). Because by far the largest concentration difference between internal and external concentration is for K⁺ ions (c_e ≈ 0 mM, c_i = 142 mM) only this ion will be considered in the following analysis and their contribution to the external conductivity.

The diffusion of ions through the membrane is governed by Nernst-Planck equation

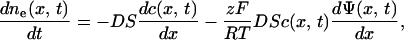(A.8)

where n_e is the number of mol in the external medium, D is the diffusion constant (2 × 10⁻⁵ cm²/s), c the molar concentration, S the total transport surface S = N S_por of N permeabilized cells, and Ψ the electric potential. In general D and S depend on time, electric field strength, and number of pulses, but here we will assume that they are approximately constant. The diffusion of ions is a slow process compared to the duration of the electric pulses, thus we can assume that the major contribution to efflux of ions occurs without the presence of the electric field. When there is no external electric field present, ΔΨ is small (around 20 mV) because only the imbalance of the electric charges due to concentration gradient contributes (i.e., the reversal potential); therefore, the second term in Eq. A.8 can be neglected. By replacing the concentration gradient with (c_e − c_i)/d we obtain:

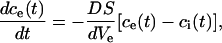(A.9)

where V_e represent the external volume. In the above equation, we neglect spatial changes of the concentration and assume that they are approximately constant. We further neglect the volume fraction changes during the pulses and by taking into account that the sum of ions inside and outside remains constant, the equation further simplifies:

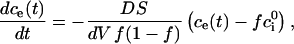(A.10)

where 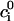is the initial internal concentration of K⁺ ions. Solution of the above equation is an exponential increase to maximum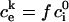

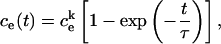(A.11)

with a time constant

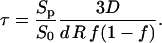(A.12)

From the time constant τ the fraction of pores can be estimated:

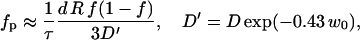(A.13)

where we again take into account that the effective diffusion constant D′ of K⁺ ions inside the pore differs from that in bulk. From Fig. 5 we obtain that for E = 0.84 kV/cm the time constant for conductivity changes is ≈ 22 s. Using Eq. A.12 for w₀ = 2.5–5 we obtain for diffusion time constants being between 8 s (E = 1.6 kV/cm) and 42 s (E = 0.7 kV/cm) fraction of the pores in PB medium f_p = 10⁻⁷–10⁻⁶.