Significance and statistical errors in the analysis of DNA microarray data

Abstract

DNA microarrays are important devices for high throughput measurements of gene expression, but no rational foundation has been established for understanding the sources of within-chip statistical error. We designed a specialized chip and protocol to investigate the distribution and magnitude of within-chip errors and discovered that, as expected from theoretical expectations, measurement errors follow a Lorentzian-like distribution, which explains the widely observed but unexplained ill-reproducibility in microarray data. Using this specially designed chip, we examined a data set of repeated measurements to extract estimates of the distribution and magnitude of statistical errors in DNA microarray measurements. Using the common “ratio of medians” method, we find that the measurements follow a Lorentzian-like distribution, which is problematic for subsequent analysis. We show that a method of analysis dubbed ”median of ratios“ yields a more Gaussian-like distribution of errors. Finally, we show that the bootstrap algorithm can be used to extract the best estimates of the error in the measurement. Quantifying the statistical error in such measurements has important applications for estimating significance levels, clustering algorithms, and process optimization.

Any measurement is only an estimate of a physical value, but to be useful the measurement should be accompanied by an estimate of the error. The error in a single measurement can be estimated by examining a histogram of many independently repeated measurements. Typically, a histogram of many measurements will form a normal (i.e., Gaussian) distribution whose mean value is taken as the best estimate of the true value. The standard deviation of this distribution is an estimate of the error in a single measurement.

The measurement of ratios poses special statistical problems. The distribution of the ratio x/y of two Gaussian random variables x and y is not necessarily Gaussian. In the case of noisy measurements, where the standard deviation is a significant fraction of the measured value, the distribution of the ratio approaches a Lorentzian or Cauchy distribution (1). In the case of non-noisy measurement, where the standard deviation is a small fraction of the mean, the distribution of the ratio will follow a Gaussian distribution. Loosely speaking, Lorentzian distributions have longer tails than Gaussian distributions. This means that points sampled from a Lorentzian distribution will have more frequent “outliers” than points sampled from a similar Gaussian distribution. The mean, standard deviation, and higher moments of the Lorentzian distribution are undefined. The measurement of ratios can give wide tails and nonsensical error estimates unless the data are handled properly. Thus, one needs to turn to other statistical tools for measurement and error estimates rather than the mean and standard error in the mean.

To examine the statistical reliability of measurements from DNA microarrays, we examined microarrays with multiply repeated spots and looked at differences in the measured values. We analyzed data from experiments that measure a large number (1,152) of mRNAs four different times on a single slide. When the ratio measurements are extracted using one common method [the ratio of medians (2)], the distribution of deviations follow a Lorentzian-like distribution rather than a normal (Gaussian) distribution. When we re-analyzed the data by using a modified algorithm (median of ratios), the distribution became more Gaussian-like and we obtained more consistent results.

We describe a method for estimating the error in the measured ratio by using the bootstrap method (3). The bootstrap is an algorithm used to estimate confidence intervals of an arbitrary parameter estimated from a population of measurements. It does this by repeatedly randomly sampling from the population and calculating the parameter of interest. We evaluated this method of error estimation by comparing the actual differences in multiple measurements of the ratio (the median of the ratios) to the estimated error for a single measurement. There is good agreement between the two, leading us to conclude that the bootstrap can give reliable error estimates.

Methods

A test slide was constructed containing 100 spots representing cDNA cloned from mouse glycerol-3-phosphate dehydrogenase (G3PDH). The series of spots were from a single preparation of cDNA. Arrays were hybridized to mRNA from C2C12 and 10T1/2 cell lines. Results are shown in Fig. 1; all 100 points are represented.

Figure 1.

Repeated measurements using a DNA microarray of the level of glycerol-3-phosphate dehydrogenase (G3PDH) in C2C12 myoblast cells and 10T1/2 fibroblasts (100 measurements). There is a large variation in the “quality” of each individual spot, but the ratio is consistent.

A 4,608 spot DNA microarray representing 1,152 mouse genes each repeated four times was constructed. mRNA was extracted from a whole adult mouse liver (Cy5) and a C2C12 mouse myoblast cell line (Cy3) and hybridized to the microarray. The slide was scanned and spots were grouped by the cDNA clone they represent.

The commonly used measure of signal is the log₂ transform of the ratio of medians. The ratio of medians is defined as “the ratio of the median intensities of each feature for each wavelength, with the median background subtracted.” We found that the median of ratios, defined as “the median of pixel-by-pixel ratios of pixel intensities, with the median background subtracted,” provided a more consistent measurement.

A scatter plot, presented in Fig. 2, was constructed by taking all possible pairs of measurements and plotting them against each other. Points which had background values greater than foreground values in either the Cy3 or Cy5 channel were excluded from the analysis. The ratios were transformed by taking the log₂ and normalized. Values are reported in Fig. 2. Numbers were extracted from the image by using genepix software (Axon Instruments, Foster City, CA).

Figure 2.

A scatter plot of the data collected from the 4 × 1,152 dataset. Each point represents a pair of different measurements of the same physical value. Ideally, all points should fall on the diagonal line indicating exact reproducibility. The extent to which points are spread from the line gives an indication of the statistical errors in the measurements. Both sets of data arise from the same slide and scan. For each gene, there are as many as 12 points plotted on this graph. The plotted points are intrinsically symmetric across the diagonal line because a pair of points is plotted as both (x, y) and (y, x). (a) Numbers are extracted from the image by using the median of ratios method. (b) Numbers are extracted with the ratio of medians method.

We used a computer algorithm to calculate the bootstrap median and confidence levels in the median. The bootstrap algorithm works as follows. A list of measured ratios, one from each pixel in a spot, was compiled. A new list was created by sampling (with replacement) from this list. The median value of the new list was computed and recorded on a list of medians. This procedure was repeated as many times as there were pixels in the spot. The mean and 90% confidence interval in the mean was computed from the list of medians. In the bootstrap algorithm, these represent the best estimate of the median and 90% confidence level of the estimate. This is reported in Table 1 and shown graphically in Fig. 3.

Table 1.

An example of using the bootstrap algorithm for error estimation

Accession	Cy3	Cy5	Measurement
			1	2	3	4
W14393	2,700	2,100	1.15  ± 0.11	1.37  ± 0.14	1.21  ± 0.05	1.30  ± 0.06
W09867	2,900	50	54  ± 8	68  ± 14	69  ± 11	55  ± 6
W34179	150	35	3.8  ± 1.8	2.9  ± 1.9	3.2  ± 0.9	3.3  ± 0.8

Data from three different genes each spotted four times onto a single slide is shown (represented by the Genbank accession identifier of the sequence). For each gene, an approximate background subtracted Cy3 and Cy5 level is shown in relative fluorescence units. In addition, the median value of the pixel-by-pixel ratio and standard error (90% confidence interval) of the median as reported by the bootstrap algorithm is given for each of the four different spots. The genes were chosen to represent a “bright yellow” (bright in both channels, W14393), “bright green” (bright in a single channel, W09867), and a dim spot (W34179). The calculation of errors for each spot is independent of the other three. The spread in the four measurements for each gene is consistent with the error, demonstrating the utility of the algorithm. 

Figure 3.

Repeated measurements of three different genes with bootstrap error bars. The line indicates the mean value of the four measurements for each gene. The error bars indicate 90% confidence intervals in the median value of the pixels in the spot. The error bars are estimated by using the bootstrap on the population of pixels. The average coefficient of variation for the measurements was approximately W14393:7%, W09867:15%, and W34179:40%. More precise measurements of the ratio can be made on abundant transcripts.

Results

The Efficiency of Hybridization on DNA Spots Varies Over a Wide Range.

This has been known since the first paper on spotted DNA microarrays (4, 5); we reproduce it here to show the magnitude of the variation. The wide variation requires the use of an internal control on each DNA spot. The control and sample are labeled with different fluorophores and the ratio of intensities between the sample and control is reported. As is shown in Fig. 1, the ratio between the two measurements is considerably more consistent than the absolute intensity of either one.

Measurements Extracted from Images of DNA Microarrays by Using the Commonly Accepted Methods (Ratio of Medians) Follow a Lorentzian-Like Distribution.

Our measurements on 1,152 different genes repeated four times show that the measured values follow a Lorentzian-like distribution. Measurements extracted using the ratio of means algorithm give similar results. This indicates that approximately one in five of the genes that appear to have significant changes in expression level do not; they are statistical outliers that are an artifact of the data analysis method.

Measurements Extracted from Images by Using the Median of Pixel-by-Pixel Ratios Follow a Gaussian-Like Distribution.

By examining a population of pixel-by-pixel ratio measurements at each spot and selecting the median of the population, the distribution of deviations follows a Gaussian distribution, with a significantly smaller width (see Fig. 4).

Figure 4.

A histogram of distances to the diagonal line from Fig. 2 (differences from repeated DNA microarray measurements). The curves are fit to log Gaussian, Eq. 4 (taller curve for the median of ratios), and log Lorentzian, Eq. 2 (wider curve for the ratio of medians), functions. Both curves were extracted from the same experimental data. There is an excess of points at 0 in the ratios of medians curve due to digitization of the measurements. The fit to the median of ratios curve is substantially under estimating the data at the transition from the base to the peak. The median of ratios has 3% of the points outside the range of −1 to 1, and 1.2% of the points outside the range of −1.2 to 1.2, whereas the ratio of median curve has 24% and 18% outside of the same ranges.

The Error on an Individual Spot Can Be Estimated by Using the Bootstrap Algorithm on the Ratios of Individual Pixels Within a Spot.

Confidence levels (90%) in the median for each spot were estimated using the bootstrap algorithm. These errors agreed well with the observed spread in measurements across different spots that contained the same DNA (see Fig. 3).

Discussion

DNA microarray measurements are typically made in two colors (using the fluorophores Cy3 and Cy5), where one color corresponds to a control and the other is the value of interest. For technical reasons (2), the measured value is reported as the ratio of the two channels, usually the logarithm (base 2, by convention) of the ratio. By taking the logarithm, equal changes in up/down concentrations are represented by equal numerical values.

The distribution of the ratio x/y of two correlated normal random variables has been solved (1). It is a function of five parameters: the means x̄, ȳ, standard deviations σ_x, σ_y of both the numerator and denominator, and the correlation coefficient ρ between the numerator and denominator. In the limit that the standard deviations are much greater than the means, σ_x ≫ x̄ and σ_y ≫ ȳ the distribution is exactly equal to a Lorentzian distribution. (For instance, when x and y are normally distributed and x̄ = 0 and ȳ = 0, the distribution of x/y is exactly Lorentzian.)

The experimental distributions we examined were found to approximately follow the log-transformed Lorentz distribution, as expected for a ratio of two noisy measurements. The Lorentz distribution can be written as,

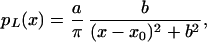1

and the log transformed equivalent of the Lorentz distribution is obtained by using the fundamental law of probabilities

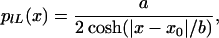2

where a is a normalization constant that only depends on the total number of points measured and b is the half width at half maximum of the curve, a measure of the width of the distribution or overall reproducibility of the experiment. We observed the Lorentz distribution in data taken in our laboratory and analyzed with the ratio of medians.

In DNA microarray experiments, the experimental quantity of interest is the ratio. More accurate measurements can be obtained by making a large number of independent measurements of the ratio and computing the median of the measurements. Because the measurements are drawn from a Lorentzian-like distribution whose mean is undefined, the median is the appropriate measure of the central value. Computing the mean value and/or the standard deviation of the population will result in meaningless values, because the determination of the values will be dominated by the outliers of the measurements and will not be reproducible.

Independent measurements of the ratio can be made by repeated spotting of the same DNAs, but this takes up valuable area on the chip. If the dominant source of variation in the relative values occurs within a spot (as well as between spots), then a single spot can be subdivided into smaller independent areas (pixels), and the ratio for each one of these pixels could be computed (median of ratios). The median and standard error of the median can be calculated from this population of pixels within a single spot.

When we reanalyzed the data by using the “median of ratios” algorithm, we found the data followed the Gaussian distribution,

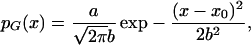3

and its log transformed equivalent,

4

We also used this method to estimate errors for the 4 × 1,152 slide, and found that the spread in the measured values of the spots are consistent with the calculated errors (Table 1, Fig. 3). An important technical requirement to use this approach is the ability to have good registration (at the level of much less than a single pixel) between the images in the two different colors. This method is robust, in the sense that it is not dependent on the underlying data following any particular statistical distribution.

Larger spots give more accurate measurements than smaller spots when using the median of ratios. The standard error in the median is roughly inversely proportional to the square root of the number of independent measurements, as would be true for any measurement with a Gaussian distribution. A large spot that has twice the diameter of a small spot will have four times the number of pixels when using the same scanner resolution. The error in the measurement will be about one half as large in the larger spot compared with the smaller spot. This follows from general statistical principles, where the standard error in a measurement is proportional to the square root of the number of independent measurements made. This result has obvious implications for tradeoffs in measurement accuracy versus array density, and should be considered during array and reader design.

Many methods of analyzing-large scale expression patterns rely on quantitative measurements of transcript levels to “cluster” different genes into groups (6, 7). Many clustering algorithms use a maximum likelihood estimator that should be chosen to reflect the statistics of the underlying data. It is crucial to understand the distribution of the measured data when choosing such an estimator, especially if that distribution has long tails. Finally, an error measurement of transcript levels provides a parameter that can be used with clustering algorithms to estimate confidence levels for membership of a transcript in a cluster.

Some methods of analyzing large scale expression patterns do not rely on measurements of quantitative levels of expression, but rather on whether the transcript is absent/present (8) or whether the expression level of a gene is significantly higher or lower in two different populations of cells. In these cases, there are more sensitive ways to assess the significance of the signal than by measuring the ratios with error bars. One such method is to compute a P value corresponding to the hypothesis that the mean values of the spots represent identical or distinct expression levels (9).

Experimental errors can be classified as two different types: random and systematic. We have examined the random error in a single DNA microarray experiment. The goal here is to quantify the statistical random errors inherent in the experiment and provide a quantitative measure of quality so that experimental systematic errors can be evaluated and optimized.

Conclusion

We have outlined a method of obtaining reliable error estimates for spotted DNA microarray measurements. Ratios accompanied by error estimates will allow more meaningful interpretations of single chip data, better comparisons of data across multiple experiments, and more consistent results from clustering algorithms.