Abstract
In the attempt to understand human variation and the genetic basis of complex disease, a tremendous number of single nucleotide polymorphisms (SNPs) have been discovered and deposited into NCBI's dbSNP public database. More than 2.7 million SNPs in the database have genotype information. This data provides an invaluable resource for understanding the structure of human variation and the design of genetic association studies. The genotypes deposited to dbSNP are unphased, and thus, the haplotype information is unknown. We applied the phasing method HAP to obtain the haplotype information, block partitions, and tag SNPs for all publicly available genotype data and deposited this information into the dbSNP database. We also deposited the orthologous chimpanzee reference sequence for each predicted haplotype block computed using the UCSC BLASTZ alignments of human and chimpanzee. Using dbSNP, researchers can now easily perform analyses using multiple genotype data sets from the same genomic regions. Dense and sparse genotype data sets from the same region were combined to show that the number of common haplotypes is significantly underestimated in whole genome data sets, while the predicted haplotypes over the common SNPs are consistent between studies. To validate the accuracy of the predictions, we benchmarked HAP's running time and phasing accuracy against PHASE. Although HAP is slightly less accurate than PHASE, HAP is over 1000 times faster than PHASE, making it suitable for application to the entire set of genotypes in dbSNP.
Many risk factors for human disease are accounted for by variation in DNA sequence (Carlson et al. 2004). The most common type of human sequence variation consists of differences in individual base pairs termed single nucleotide polymorphisms (SNPs) (Wang et al. 1998; Cargill et al. 1999; Halushka et al. 1999). It has been estimated that there are about 7.1 million common biallelic SNPs with a minimum minor allele frequency of 5%. These SNPs appear, on average, once every 450 bp (Kruglyak and Nickerson 2001). In recent years, a tremendous number of single nucleotide polymorphisms (SNPs) have been discovered and deposited into NCBI's dbSNP public database. Today, dbSNP contains information for over 10 million human SNPs with over 5 million of them validated. More recently, a significant amount of genotype data has been deposited as well. More than 2.7 million human SNPs in the database have genotype information. This data resource consists of 286,757,371 genotypes over 3285 individuals split into 417 data sets. The database contains two whole-genome human variation maps, one deposited by the HAPMAP project (The International HapMap Consortium 2003) and the other deposited by Perlegen Sciences (Hinds et al. 2005). The database also contains a significant amount of sequenced gene data from the Environmental Genome Project (Livingston et al. 2004) and the SeattleSNPs (Crawford et al. 2004) project in addition to many other smaller data sets. This data is an invaluable resource for understanding the haplotype structure of human variation and the design of effective genetic association studies for understanding the genetic basis of complex diseases. Each data set has different properties in terms of the number of individuals genotyped, average SNP density, genome coverage, and types of genomic regions covered. Analysis of multiple data sets with different properties genotyped over the same region in the human genome can reduce the bias of any inferences to the specific properties of a data set.
Alleles of SNPs that are physically located in close proximity to each other on a chromosome are often correlated (i.e., in “linkage disequilibrium”) with each other. Thus, within most short regions, there is limited genetic variability, and only a small number of allele sequences (haplotypes) exist in a population. In a typical region or “block of limited diversity,” three or four common haplotypes often account for at least 80% of the sequence variation in a population (Daly et al. 2001; Patil et al. 2001; Gabriel et al. 2002). The haplotype structure of a given region depends on evolutionary and population genetic factors such as mutation and recombination rates, selection, and population history.
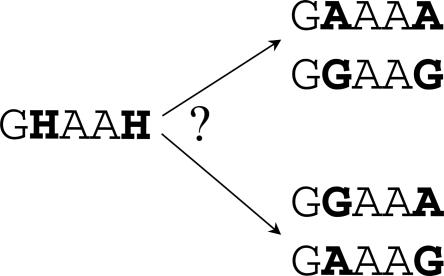
Obtaining the haplotypes and partitioning the region into blocks of limited diversity are the first steps for many types of analysis of human variation. However, since humans are diploid, haplotype (or phase) information is not immediately available. Therefore, the construction of haplotypes from the diploid genotype information (i.e., phasing the genotypes) requires statistical inference or the financially prohibitive collection of extended pedigrees. Consider, for example, two SNPs lying on the same chromosome, both with alleles A and G. If both SNPs are observed as heterozygous, it is unclear whether one chromosome contains allele A at both loci and the other chromosome contains allele G in both loci, or whether one chromosome contains allele A at the first locus and allele G at the second locus and the other chromosome contains alleles G and A, respectively (Fig. 1). In order to overcome this problem, many computer programs have been designed to estimate and assign phase from diploid genotype data (Stephens et al. 2001; Niu et al. 2002; Halperin and Eskin 2004). In order to compute the full set of haplotypes for dbSNP, we used HAP (Halperin and Eskin 2004), a phasing program that determines haplotypes by exploiting the correlation between SNPs in physical proximity due to linkage disequilibrium using a genealogy based model (perfect phylogeny) (Hudson 1991). HAP is able to process up to 40,000 SNPs at a time, allowing for phasing and partitioning into blocks the 286 million genotypes in the dbSNP database in less than 24 h on a 30-CPU cluster. We benchmark both the accuracy and running time of HAP using mother-father-child pedigrees from the HAPMAP data and compare with the PHASE phasing method (Stephens et al. 2001). The error rate of HAP is about 0.81% (estimated for the CEU population of the HAPMAP), which is slightly less accurate than PHASE. However, our benchmarks show that PHASE is several orders of magnitude slower than HAP, and therefore, it appears that applying PHASE to the entire database is computationally infeasible.
Figure 1.
A genotype for five SNPs (left) and two possible phasings of the genotype into pairs of haplotypes (right) demonstrating the inherent ambiguity of haplotype phasing. Each SNP has possible bases of “A” and “G”. “A” and “G” positions in the genotype represent homozygous genotypes at a particular SNP, and an “H” position represents a heterozygous genotype at a particular SNP. From only the observed data, it is impossible to determine which haplotype phasing is correct.
Since many of the data sets were originally mapped to different human genome builds, reconciling the original data sets and mapping them to a common genome build is a very time-consuming task. One of the main contributions of this study is the organization of the data sets in a way that corrects for errors in the strand and physical location annotations of the SNPs submitted to dbSNP. Through dbSNP, researchers can easily access all public genotype and haplotype data in their regions of interest. For example, researchers interested in the ABO gene can easily obtain haplotype and genotype data from data sets including the HAPMAP, Perlegen, and SeattleSNPs. By comparing multiple data sets, we perform a preliminary analysis to estimate the significance of the effect of SNP density on the inferred haplotype and block structure in a short region. By combining high-density data from Seattle SNPs and the Perlegen data sets in the same individuals, we show how the numbers of haplotypes in the blocks defined by the Perlegen data set are underestimated by a factor of 3.6. These differences illustrate the advantage of examining multiple data sets when inferring human variation structure.
We also infer the chimpanzee reference sequence corresponding to each human haplotype block by mapping all of the SNPs typed to the UCSC BLASTZ alignment of the human and chimpanzee genomes. We use this data to compute how often the reference sequence matches a common haplotype in the Perlegen whole-genome data set. These sequences are also available for download from dbSNP.
The haplotype and genotype data in dbSNP is a valuable resource for researchers planning to perform genetic association studies. Using the multiple data sets, the researchers can obtain a clearer picture of the haplotype structure and make more informed choices on which SNPs to genotype in a planned association study. The haplotypes, block partitions, and tag SNPs discussed in this study have been deposited into dbSNP (accession nos. phs3.1, vs:3:4136.1–vs:3:835194.1, sh:3:142355.1–sh:3: 5247813.1) and can be accessed at http://www.ncbi.nlm.nih.gov/projects/SNP/.
Results
Data description
The human portion of the dbSNP database contains 286,757,371 total genotypes from 3285 individuals over 2.7 million SNPs partitioned into 417 data sets. A total of 835 of the individuals have genotypes from two or more data sets. The CEPH families, for example, were used in several different genotyping studies.
Two whole-genome data sets compose 94.2% of the genotypes, i.e., the HAPMAP data set that contains 159,862,776 genotypes taken from four populations consisting of a total of 270 individuals over 954,302 SNPs, and the Perlegen data sets that consist of 110,385,051 genotypes taken from three populations consisting of a total of 71 individuals over 1,576,578 SNPs. In addition to these data sets, there are an additional 16,509,544 genotypes from other data sets. dbSNP contains a significant amount of genotypes derived from sequenced data, including the SeattleSNPs (PGA/UW) data and the Environmental Genome Project (EGP) sequenced genes. The Seattle SNPs consists of 573,194 genotypes of 48 individuals taken from two populations, in which 15,981 SNPs were genotyped in a total of 177 sequenced genes. The Environmental Genome Project (EGP) sequenced genes contains 3,184,170 genotypes over 37,737 SNPs in a total of 304 sequenced genes in 90 individuals. The 48 individuals in SeattleSNPs are the same individuals as the ones genotyped for the Perlegen data. Some of these data sets contain a much larger number of individuals, such as the SNP Consortium (TSC) Celera CEPH data set containing 691 individuals and a data set from Perlegen containing 655 individuals from Mexico City. Others data sets contain many populations, such as the TSC data set containing 17 populations. Table 1 summarizes the contents of the largest 10 data sets contained in dbSNP.
Table 1.
Summary of genotype data contained in dbSNP
| Data set | Genotypes | SNPs | Populations | Individuals | Average SNP density | Reference |
|---|---|---|---|---|---|---|
| HAPMAP | 159,862,776 | 954,302 | 4 | 270 | 3149 | (International HapMap Consortium 2003) |
| PERLEGEN | 110,385,051 | 1,576,578 | 3 | 71 | 1938 | (Hinds et al. 2005) |
| Affymetrix | 6,189,466 | 125,778 | 6 | 116 | 24,029 | (Kennedy et al. 2003) |
| TSC | 4,932,382 | 19,048 | 17 | 1963 | 312,754 | (International SNP Map Working Group 2001) |
| EGP | 3,184,170 | 37,737 | 1 | 90 | 72,443 | (Livingston et al. 2004) |
| PGA/UW | 573,194 | 15,981 | 2 | 47 | 153,861 | (Crawford et al. 2004) |
| IIPGA | 176,162 | 3801 | 3 | 47 | 430,361 | (Innate Immunity PGA, http://innateimmunity.net/) |
| NIHPDR | 159,549 | 1982 | 1a | 448 | 1,419,125 | (Collins et al. 1998) |
| WICVAR | 33,240 | 1462 | 1 | 130 | 2,011,277 | |
| HG_BONN | 24,522 | 320 | 1 | 143 | 5,284,550 | (Freudenberg-Hua et al. 2003) |
The NIHPDR data contains a single mixed population.
Since many of the original data sets were released at different times, the data sets were mapped to different human genome builds, and the genome positions listed for the SNPs are not necessarily compatible between different data sets. In dbSNP, each genotype is mapped to the human genome, consistent with the latest available build providing a common mapping of SNPs across data sets. Each genotype data set in dbSNP contains references to the dbSNP identifier for each genotyped SNP. Any strand or mapping errors corrected for a SNP are propagated to all genotype data sets containing that SNP.
Since many of the data sets contain information on the same SNP for the same individual, we can measure the amount of discrepancy in the genotype calls between the data sets. In particular, 996,553 of the recorded SNPs contain information from two individuals or more, corresponding to a total of 19,719,200 specific SNPs in individuals that have information from at least two data sets. We consider the set of SNPs in individuals with information from two or more data sets where at least two of the genotype calls are not missing. Within this set, 33,076 SNPs have at least one individual with different genotype calls from different data sets. A total of 216,625 (1.1%) specific SNPs in individuals contain differing genotype calls.
We applied HAP to all of the genotypes in dbSNP by phasing each data set separately. Whenever available in dbSNP, we used the mother-father-child pedigree to increase the accuracy of the phasing. The haplotypes were partitioned into blocks of limited diversity so that five haplotypes covered at least 80% of the total number of haplotypes. A set of tag SNPs was chosen to minimize the number of SNPs needed to distinguish between the common haplotypes of each block (Zhang et al. 2002). The full phasing of dbSNP, partitioning all of the haplotypes in blocks of limited diversity, and determining a set of tag SNPs took under 24 h on a 30-CPU cluster. Table 2 summarizes the block partitions and the number of tag SNPs for each data set.
Table 2.
Summary of block partitions and tag SNPs for the largest six data sets in dbSNP
| Data set | Population | Number of genotypes | Number of SNPs | Number of individuals | Number of blocks | Number of tag SNPs | Avg. block length (kb) | Number tag SNPs per kb |
|---|---|---|---|---|---|---|---|---|
| HAPMAP | CEU | 84,727,965 | 954,302 | 90 | 73,986 | 179,351 | 30.7 | 0.079 |
| HAPMAP | HCB | 18,443,054 | 411,568 | 45 | 41,381 | 94,583 | 40.2 | 0.057 |
| HAPMAP | JPT | 18,030,239 | 411,627 | 44 | 20,671 | 31,466 | 41.8 | 0.054 |
| HAPMAP | YRI | 38,661,518 | 431,505 | 90 | 67,111 | 157,287 | 21.5 | 0.109 |
| PERLEGEN | Afr | 35,568,060 | 1,569,392 | 23 | 235,139 | 569,182 | 9.1 | 0.267 |
| PERLEGEN | Asi | 37,417,872 | 1,572,384 | 24 | 86,636 | 211,972 | 26.9 | 0.090 |
| PERLEGEN | Eur | 37,399,120 | 1,570,560 | 24 | 109,212 | 274,153 | 21.8 | 0.115 |
| Affymetrix | Afr | 885,135 | 125,776 | 20 | 24,526 | 40,050 | 44.1 | 0.037 |
| Affymetrix | Cau | 1,534,726 | 125,778 | 20 | 27,561 | 47,957 | 37.2 | 0.047 |
| Affymetrix | Asi | 884,091 | 125,772 | 20 | 20,671 | 31,466 | 54.5 | 0.028 |
| Affymetrix | CEPH | 50 | 30 | 3 | 18,453 | 26,018 | 62.9 | 0.022 |
| Affymetrix | PDpanel | 2,869,641 | 125,776 | 24 | 35,048 | 67,154 | 26.11 | 0.073 |
| Affymetrix | APE | 15,823 | 9027 | 2 | 6253 | 6262 | 5.9 | 0.170 |
| TSC | ALL | 4,932,382 | 19,048 | 1963 | 31,886 | 46,789 | 21.8 | 0.075 |
| EGP | ALL | 3,184,170 | 37,737 | 90 | 3847 | 6643 | 2.9 | 0.590 |
| PGA/UW | Afr | 363,643 | 15,981 | 24 | 2833 | 5375 | 1.26 | 1.503 |
| PGA/UW | Eur | 209,551 | 9525 | 23 | 1086 | 2378 | 3.6 | 0.359 |
Within dbSNP, the complete set of genotypes mapped to the correct positions in the genome are available for download along with the haplotypes, block partitions, and tag SNPs resulting from this study. The data is available in multiple formats including XML, allowing the data in dbSNP to be easily integrated into other databases.
Haplotype coverage
The combined set of haplotypes in dbSNP provides a significant amount of coverage of the genome. We measure coverage by two criteria, i.e., minimum gap length and depth. A region is considered covered by a data set at a minimum gap length if the inter-SNP distances are below the minimum gap length. The depth of a data set is defined as the number of individuals for whom haplotypes are available in the region. Given a depth value and a minimum gap value, the coverage is the percentage of the genome covered by haplotypes with the minimum number of individuals and with a minimum gap between SNPs.
The coverage of the HAPMAP and Perlegen data as well as the combined two data sets is shown in Table 3. As can be seen from the table, the HAPMAP and Perlegen data sets provide excellent coverage for minimum gap lengths of 10 kb and more, but they give poor coverage for minimum gap lengths of 1 and 5 kb—for a minimum gap length of 5 kb, they only cover about 50% of the genome. When the two data sets are combined with the remaining data sets of dbSNP, the coverage significantly increases for the minimum gap lengths of 1 or 5 kb. In addition, the remaining data in dbSNP provides higher coverage of the genome at higher depths, since the Perlegen data set has 71 individuals and the HAPMAP data has 270 individuals. The coverage of the haplotypes in dbSNP is summarized in Table 4.
Table 3.
Coverage of whole genome data sets in dbSNP
|
Minimum gap
|
|||||
|---|---|---|---|---|---|
| Data set | 1 kb | 5 kb | 10 kb | 20 kb | 50 kb |
| HAPMAP | 3.56% | 54.50% | 85.13% | 89.52% | 90.46% |
| PERLEGEN | 10.79% | 48.69% | 63.06% | 78.07% | 88.24% |
| Combined | 15.12% | 72.70% | 87.51% | 90.02% | 90.84% |
The Perlegen data set contains 71 individuals and the HAPMAP contains 270 individuals.
Table 4.
Coverage of combined data sets in dbSNP
|
Minimum gap
|
|||||
|---|---|---|---|---|---|
| Depth | 1 kb | 5 kb | 10 kb | 20 kb | 50 kb |
| 1 | 15.62% | 73.02% | 87.60% | 90.09% | 90.89% |
| 10 | 15.61% | 73.01% | 87.60% | 90.08% | 90.88% |
| 50 | 15.48% | 72.68% | 87.22% | 89.70% | 90.48% |
| 100 | 4.73% | 28.84% | 36.49% | 37.49% | 37.73% |
| 200 | 3.23% | 20.75% | 26.67% | 27.37% | 27.51% |
| 300 | 1.36% | 8.51% | 10.53% | 10.72% | 10.75% |
| 350 | 0.62% | 4.11% | 5.14% | 5.23% | 5.26% |
Haplotype structure and genotype density
We observe that the number of blocks and tag SNPs in the high-density sequence data is much higher than in the corresponding HAPMAP or Perlegen data sets. This shows that there is a considerable amount of information loss when the data is sampled every 5 kb, such as in the HAPMAP data set. We examined 41 blocks in the Perlegen data set that overlapped with SNPs typed in the Seattle data set. Figure 2 shows an example of such a region. There are 91 common haplotypes over the Seattle individuals on these SNPs. We then added in the additional Seattle SNPs typed on the blocks and re-examined the haplotypes for each individual. From the 91 original common haplotypes, 369 haplotypes were found with 72 common ones. On average, 1.2 common haplotypes were created for every original common haplotype, and 30 of the original haplotypes were split into only rare haplotypes. One may hypothesize that this is due to the rare SNPs in the Seattle data. However, we performed the same analysis using only Seattle SNPs with a minor allele frequency of 10% or greater. The 91 original haplotypes were split into 330 haplotypes with 73 common ones. On average, each original common haplotype was split into 1.16 new common haplotypes, and 28 common haplotypes were split into only rare haplotypes when the Seattle SNPs were added. The haplotype blocks and common haplotypes found by examining only the Perlegen data are significantly different from those found over the same individuals in the Seattle data. This type of analysis allows us to measure how much common variation is missed in the whole-genome data sets and demonstrates the utility of the analysis of multiple genotype data sets.
Figure 2.
A region of chromosome 6 from position 161122860–161124861 showing the comparison of the Perlegen whole-genome data set with the SeattleSNPs data set in build 123 of dbSNP containing SNPs rs783145, rs4252128, rs4252129, rs4252130, rs4252131, rs4252132, rs4252133, rs4252134, rs4252135, rs4252136, and rs4252137. The first, second and eleventh SNPs are contained in the Perlegen data and are in bold. The Perlegen haplotypes over these SNPs that occur in the population are ACG, GCG, ACA, and GTG. When SNPs contained in the SeattleSNPs data set are added to the Perlegen SNPs, many more haplotypes emerge. For example, the first Perlegen haplotype gets split into two common haplotypes and three rare haplotypes in the SeattleSNPs data set. “I” and “D” represent insertion and deletion polymorphisms in the SeattleSNPs data set.
Chimpanzee reference alleles
We used the BLASTZ alignments of the human and chimpanzee genomes from the UCSC Genome Browser to determine the chimpanzee reference allele corresponding to each human SNP. For each human haplotype block found, we examined the chimpanzee allele corresponding to each SNP in the human haplotype block. These chimpanzee reference allele sequences can serve as outgroups or starting points in determining human haplotype phylogeny. We examine the relation between the common haplotypes and the chimpanzee reference alleles. For each block in the Perlegen data, we compare each common haplotype with the chimpanzee reference alleles. We observe that in 73.4% of the blocks, the chimpanzee reference allele matches a haplotype from the Perlegen data set with frequency >5%.
Haplotype accuracy benchmarks
Since the haplotypes are obtained by statistical inference, a natural concern is that the results of analysis of this data may be biased due to errors in the inference. The accuracy of HAP has previously been tested on various regions of the genome (Eskin et al. 2003; Halperin and Eskin 2004) and it has proven to phase correctly 97% of the heterozygous SNPs, which is comparable in accuracy to other established methods. We performed a large-scale benchmarking of HAP over data collected in the HAPMAP project to obtain an estimate of the error rate for phasing unrelated individuals. The error rate for phasing related individuals has been shown to be very low in a recent benchmarking study performed by the HAPMAP analysis group (J. Marchini, D. Cutler, N. Patterson, M. Stephens, E. Eskin, E. Halperin, S. Lin, S. Qin, G. Abecassis, H. Munro, et al., in prep.). We use mother-father-child pedigree information to measure the inference of haplotypes over the parents treating them as unrelated and then compare these predictions to what can be inferred from the pedigrees. The error rate of HAP for unrelated individuals is only 0.81% in the CEU population from the HAPMAP project, which is on the order of the amount of missing genotypes in the region. In addition, the haplotypes inferred from the whole-genome variation data sets are consistent with the haplotypes inferred from the high-density data sets obtained from resequencing studies. The accuracy and consistency of the haplotypes appear to minimize this concern.
HAP error estimation
In order to benchmark the accuracy of the predicted phase, we considered 5000 SNPs obtained from the HAPMAP CEPH data. This set consisted of 50 randomly chosen regions containing 100 SNPs. The data set contains 30 mother-father-child trios from families in Utah with European ancestry. We used the trios to resolve haplotypes for heterozygous SNPs whenever Mendelian genetics determines the phase. We then phased only the 60 parents, excluding the children from each of the trios, thus resulting in a set of 60 unrelated individuals. Among 300,000 genotypes in the parents, 82,314 (27.4%) are heterozygous and 65,463 (21.8%) can be resolved into haplotypes using the trio information. The predictions for the parents' genotypes treating them as unrelated are then compared with the haplotypes resolved using trios.
We evaluated the benchmark on both HAP and the widely used phasing algorithm PHASE (Stephens et al. 2001). We also measured the discrepancies between the predictions of PHASE and HAP. We used PHASE 2.1.0 with its default option, and the default parameters of HAP.
Our results show that PHASE and HAP give identical results in 98.6% of the genotypes and 95.0% of heterozygous SNPs. We measured the accuracy of the results using the switch error rate. The switch error rate measures the proportion of heterozygous positions for which the phase is erroneously inferred relative to the previous heterozygous position. In terms of switch error rate, PHASE and HAP show 2.38% and 3.70% of switch error rates, respectively. When compared with the total number of genotypes, these switch errors occur in only 0.52% and 0.81% of genotypes, respectively, and these are comparable to the rate of missing SNPs in these regions, which is 1.14%. We performed the same benchmark for the African (YRI) population in the HAPMAP data and observed overall error rates of 2.22% and 1.37% for HAP and PHASE, respectively. This increase in error rate in African populations relative to European populations is consistent with the benchmark performed by the HAPMAP analysis group (J. Marchini, D. Cutler, N. Patterson, M. Stephens, E. Eskin, E. Halperin, S. Lin, S. Qin, G. Abecassis, H. Munro, et al., in prep.).
As opposed to the accuracy of the phase prediction, the running time of HAP and PHASE differs considerably. In Table 5 we provide the summary of the running times of HAP and PHASE on 10 randomly selected regions in chromosome 19 with different numbers of SNPs. From these experiments it is not clear how long it would take for PHASE to predict the haplotypes for the database, because of the high variance in running time and the fact that it does not appear that PHASE scales linearly with the number of SNPs. As can be seen from Table 5, the running time of HAP is several orders of magnitude faster than PHASE in most cases. Extrapolating from these results, by assuming that the PHASE algorithm is run with 100 SNPs sequentially on a single CPU, it would take PHASE at least 75,000 h to phase the whole dbSNP database. In the benchmark performed by the HAPMAP analysis group, HAP was able to phase unrelated individuals over 1000 times faster than PHASE (J. Marchini, D. Cutler, N. Patterson, M. Stephens, E. Eskin, E. Halperin, S. Lin, S. Qin, G. Abecassis, H. Munro, et al., in prep.).
Table 5.
Comparison of running time in seconds between HAP and PHASE
|
Mean
|
Standard deviation
|
Minimum
|
Maximum
|
|||||
|---|---|---|---|---|---|---|---|---|
| Number of SNPs | HAP | PHASE | HAP | PHASE | HAP | PHASE | HAP | PHASE |
| 10 | 0.06 | 19.12 | 0.03 | 8.88 | 0.03 | 12.08 | 0.10 | 37.74 |
| 20 | 0.56 | 109.71 | 0.30 | 68.78 | 0.23 | 46.24 | 1.08 | 237.78 |
| 30 | 1.10 | 327.55 | 0.55 | 257.59 | 0.54 | 99.76 | 2.24 | 887.82 |
| 40 | 1.53 | 833.99 | 0.61 | 831.93 | 0.80 | 165.57 | 2.58 | 2906.84 |
| 50 | 1.99 | 1643.49 | 0.75 | 1454.08 | 1.02 | 581.80 | 3.32 | 5013.80 |
| 60 | 2.45 | 3719.40 | 0.83 | 4352.68 | 1.19 | 915.95 | 3.74 | 14554.47 |
| 70 | 3.02 | 5931.03 | 0.91 | 5680.70 | 1.56 | 1212.59 | 4.48 | 18593.30 |
| 80 | 3.43 | 8071.75 | 1.00 | 7495.58 | 1.74 | 1774.35 | 5.12 | 26016.98 |
| 90 | 3.82 | 10585.10 | 1.10 | 9307.13 | 1.90 | 2167.37 | 5.72 | 32363.89 |
| 100 | 4.42 | 13409.43 | 1.25 | 12113.96 | 2.16 | 2634.38 | 6.53 | 40183.36 |
| 110 | 4.86 | 16082.93 | 1.21 | 12598.09 | 2.66 | 6127.91 | 6.83 | 44603.33 |
| 120 | 5.25 | 20283.20 | 1.20 | 14935.60 | 3.31 | 7756.14 | 7.14 | 54431.03 |
| 130 | 5.70 | 25249.62 | 1.35 | 18740.87 | 3.73 | 9636.97 | 8.09 | 63775.21 |
| 140 | 6.16 | 30643.41 | 1.39 | 18292.52 | 4.19 | 12226.41 | 8.53 | 69463.15 |
| 150 | 6.63 | 35768.83 | 1.46 | 20482.31 | 4.79 | 14280.62 | 9.05 | 74459.95 |
| 160 | 7.05 | 42161.60 | 1.49 | 23714.27 | 5.29 | 19106.80 | 9.73 | 91346.27 |
| 170 | 7.53 | 51597.25 | 1.59 | 30670.41 | 5.44 | 20676.32 | 10.4 | 113281.51 |
| 180 | 8.09 | 63743.02 | 1.72 | 37621.29 | 5.72 | 31889.18 | 11.08 | 138096.67 |
The running time is measured by running both methods from 10 different positions in chromosome 19, with different length of genotypes. Intel Xeon 3.20 GHz CPU is used in the measurement.
Haplotype consistency analysis
We measure the robustness of the haplotype inference by comparing the haplotypes inferred over the same SNPs in the same individuals from different data sets. We considered regions where resequenced genes are available from the SeattleSNPs (Crawford et al. 2004) and compared the haplotypes and blocks inferred from these data sets with the haplotypes and blocks inferred from the HAPMAP and Perlegen data. The European population was used for comparison because there is a corresponding population in each data set and there are overlapping individuals in the data sets. The HAPMAP data contain genotypes for 1545 SNPs that are present in the SeattleSNPs data. The Perlegen data contains 2426 such SNPs. The predicted haplotypes over the HAPMAP data and the SeattleSNPs (PGA) data differ by 679 switches and the Perlegen data and PGA data differ by 11,071 switches. These differences correspond to switch differences of 0.4% and 2.4%, respectively. These switch distances are comparable to the amount of genotype calls that differ between these data sets. Between the HAPMAP and the PGA data, there are 17,424 (3.5%) genotype calls in 602 SNPs that differ in the two data sets. Between the Perlegen and PGA data, there are 179,906 (3.8%) genotype calls in 6758 SNPs that differ.
Discussion
Understanding the structure of common variation is an important step that will give insights into designing effective strategies for genetic association analysis. Our analyses show that the use of a combination of the various data sets of dbSNP increases the coverage of the genome considerably for high-density markers. Furthermore, we show that when the density of the sampled SNPs increases, the block partition and the set of tag SNPs changes considerably, providing evidence that multiple data sets can provide a more accurate picture of the structure of human variation in a region. These findings suggest that the design of genetic association studies in these regions can benefit from analysis of multiple data sets.
However, several methodological challenges remain regarding how to most effectively use multiple data sets to understand the structure of human variation and design genetic association studies. dbSNP allows researchers to easily access multiple data sets for a genomic region and provide an invaluable resource for researchers to both address these methodological challenges as well as design effective genetic association studies.
The haplotype resource of dbSNP will provide immediate access to the haplotypes, block partitions, and tag SNPs for all of the publicly available data sets. In addition, as the amount of data in dbSNP grows, new haplotypes will be computed with every dbSNP build, which will provide haplotype information for newly deposited data shortly after it is deposited. dbSNP can be accessed at http://www.ncbi.nlm.nih.gov/projects/SNP/.
Methods
HAP phasing of genome-wide data
We used the HAP algorithm in order to phase the dbSNP data sets. HAP was run on a 30-CPU cluster consisting of 15 2GB RAM Nodes dual Intel Xeon 3.96 GHz processors.
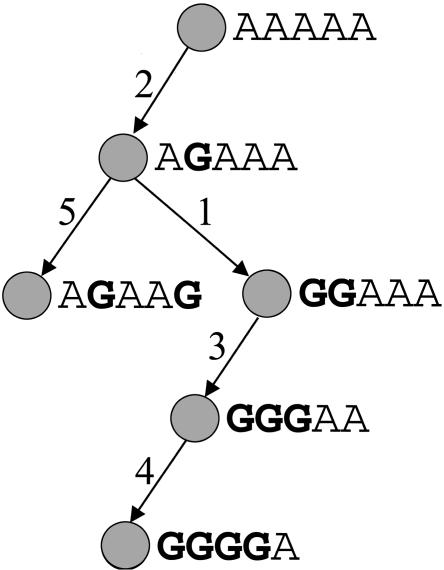
The HAP algorithm assumes that a perfect phylogeny tree can describe the ancestral history of the haplotypes. A perfect phylogeny tree is a genealogy tree with no recombinations and no recurrent mutations (see Fig. 3). HAP considers all phases that result in a set of haplotypes that are almost consistent with a perfect phylogeny. HAP then efficiently enumerates over all such phases, and gives a score to each phase according to the likelihood of the solution under the assumption that the haplotypes were randomly picked from the population. HAP then chooses the phase with the highest score. In order to phase a long region, HAP applies the perfect phylogeny model in a sliding window to short overlapping regions. These overlapping predictions are then combined using a dynamic programming-based tiling algorithm that chooses the optimal phase for the long region that is most consistent with the overlapping predictions of phase in the short regions. We considered all tiles of length 10–12 when constructing the haplotypes.
Figure 3.
A perfect phylogeny model consists of a tree where each vertex corresponds to a haplotype and each edge corresponds to a mutation in one of the positions of the haplotype. An edge is labeled with the position of the mutation. The tree fits the perfect phylogeny model if there are no recurrent mutations and no obligate recombination events. A set of haplotypes fits the perfect phylogeny model if it satisfies the four gamete test, that is, at most three allele combinations are observed for any pair of marker positions.
HAP is capable of phasing data sets up to 40,000 SNPs. The computational bottleneck is the size of the data structure necessary to perform the tiling. Since we only phased one chromosome at a time, the vast majority of the data in dbSNP was smaller than this limit. For some of the chromosomes in the HAPMAP and Perlegen data, we had to split the data set into two to four regions in order to perform phasing. We partitioned the data sets within a gap of at least 50 kb between SNPs. Similarly, when computing block partitions, we only considered blocks that do not span a gap in SNPs >50 kb.
Partition into blocks of limited diversity
We applied the dynamic programming-based algorithm as described in Zhang et al. (2002) to partition the inferred haplotypes into blocks of limited diversity. Their algorithm is based on the minimization of the number of tag SNPs so that the common haplotypes of each block could be distinguished by the tag SNPs. We consider as possible blocks regions where the common haplotypes (>5% frequency) account for >80% of the variation in a population. We only consider SNPs with a minor allele frequency >5%. We partitioned the haplotypes into candidate blocks, where the partition minimizes the total number of SNPs that are necessary to distinguish between the common haplotypes in the blocks. HAP implements the Zhang et al. (2002) approach in a very efficient manner that can allow for partitioning of whole-genome data sets. In order to compute the number of representative SNPs in a block, we apply a branch and bound algorithm that significantly reduces the computational time compared with the traditional exhaustive approach.
Extension of HAP to trios
We extended the phasing algorithm HAP (Halperin and Eskin 2004) in order to allow it to cope with genotypes typed from mother-father-child trios. Within a short region, the extension of HAP to trios must take into account the fact that the haplotypes of the children are copies of the haplotypes of the parents. We assume that there are no recombinations or mutations between the parents and the children in the trios. This allows us to first unambiguously resolve the phase of the trios in many of the positions. For the remaining positions we use HAP in order to enumerate overall possible phases. This results in a set of haplotypes that are almost consistent with a perfect phylogeny. In that enumeration we exclude the solutions that contradict Mendelian heredity within a trio. For each such solution we give the likelihood score, which is the probability to observe the parents' haplotypes in our sample. We pick the solution with maximum likelihood as a candidate solution. In order to further improve the solution, we use a local search algorithm. The local search algorithm starts from the solution given by HAP, and it repeatedly changes the phase of one of the trios to a different possible phase and checks whether the likelihood function has increased. If it has increased, we use the new solution as the candidate solution and repeat this procedure. If no local change can be applied in order to increase the likelihood, we stop and use the solution as a putative solution for this region. The resulting algorithm is very efficient and running times are comparable to the running time of HAP over unrelated individuals (J. Marchini, D. Cutler, N. Patterson, M. Stephens, E. Eskin, E. Halperin, S. Lin, S. Qin, G. Abecassis, H. Munro, et al., in prep.).
Acknowledgments
E.E. is supported by the California Institute for Telecommunications and Information Technology, Calit2. Computational resources for performing the phasing and block partition were provided by Calit2 and the National Biomedical Computational Resource, NBCR (Grant no. P41 RR08605 NCRR, NIH). This research was supported in part by the Intramural Research Program of the NIH, National Library of Medicine.
[The sequence data from this study have been submitted to dbSNP under accession nos. phs3.1, vs:3:4136.1–vs:3:835194.1, sh:3:142355.1–sh:3:5247813.1]
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.4297805. Freely available online through the Genome Research Immediate Open Access option.
References
- Cargill, M., Altshuler, D., Ireland, J., Sklar, P., Ardlie, K., Patil, N., Shaw, N., Lane, C.R., Lim, EP., Kalyanaraman, N., et al. 1999. Characterization of single-nucleotide polymorphisms in coding regions of human genes. Nat. Genet. 22: 231–238. [DOI] [PubMed] [Google Scholar]
- Carlson, C.S., Eberle, M.A., Kruglyak, L., and Nickerson, D.A. 2004. Mapping complex disease loci in whole-genome association studies. Nature 429: 446–452. [DOI] [PubMed] [Google Scholar]
- Collins, F.S., Brooks, L.D., and Chakravarti, A. 1998. A DNA polymorphism discovery resource for research on human genetic variation. Genome Res. 8: 1229–1231. [DOI] [PubMed] [Google Scholar]
- Crawford, D.C., Carlson, C.S., Rieder, M.J., Carrington, D.P., Yi, Q., Smith, J.D., Eberle, M.A., Kruglyak, L., and Nickerson, D.A. 2004. Haplotype diversity across 100 candidate genes for inflammation, lipid metabolism, and blood pressure regulation in two populations. Am. J. Hum. Genet. 74: 610–622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daly, M.J., Rioux, J.D., Schaffner, S.F., Hudson, T.J., and Lander, E.S. 2001. High-resolution haplotype structure in the human genome. Nat. Genet. 29: 229–232. [DOI] [PubMed] [Google Scholar]
- Eskin, E., Halperin, E., and Karp, R.M. 2003. Efficient reconstruction of haplotype structure via perfect phylogeny. J. Bioinform. Comput. Biol. 1: 1–20. [DOI] [PubMed] [Google Scholar]
- Freudenberg-Hua, Y., Freudenberg, J., Kluck, N., Cichon, S., Propping, P., and Nothen, M.M. 2003. Single nucleotide variation analysis in 65 candidate genes for CNS disorders in a representative sample of the European population. Genome Res. 13: 2271–2276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabriel, G.B., Schaffner, S.F., Nguyen, H., Moore, J.M., Roy, J., Blumenstiel, B., Higgins, J., DeFelice, M., Lochner, A., Faggart, M., et al. 2002. The structure of haplotype blocks in the human genome. Science 296: 2225–2229. [DOI] [PubMed] [Google Scholar]
- Halperin, E. and Eskin, E. 2004. Haplotype reconstruction from genotype data using imperfect phylogeny. Bioinformatics 20: 1842–1849. [DOI] [PubMed] [Google Scholar]
- Halushka, M.K., Fan, J.B., Bentley, K., Hsie, L., Shen, N., Weder, A., Cooper, R., Lipshutz, R., and Chakravarti, A. 1999. Patterns of single-nucleotide polymorphisms in candidate genes for blood-pressure homeostasis. Nat. Genet. 22: 239–247. [DOI] [PubMed] [Google Scholar]
- Hinds, D.A., Stuve, L.L., Nilsen, G.B., Halperin, E., Eskin, E., Ballinger, D.G., Frazer, K.A., and Cox, D.R. 2005. Whole genome patterns of common DNA variation in diverse human populations. Science 307: 1072–1079. [DOI] [PubMed] [Google Scholar]
- Hudson, R.R. 1991. Gene genealogies and the coalescent process. Oxford Surveys in Evol. Biol. 7: 1–44. [Google Scholar]
- The International HapMap Consortium. 2003. The International HapMap Project. Nature 426: 789–796. [DOI] [PubMed] [Google Scholar]
- The International SNP Map Working Group. 2001. A map of human genome sequence variation containing 1.4 million SNPs. Nature 409: 928–933. [DOI] [PubMed] [Google Scholar]
- Kennedy, G.C., Matsuzaki, H., Dong, S., Liu, W.M., Huang, J., Liu, G., Su, X., Cao, M., Chen, W., Zhang, J., et al. 2003. Large-scale genotyping of complex DNA. Nat. Biotechnol. 10: 1233–1237. [DOI] [PubMed] [Google Scholar]
- Kruglyak, L. and Nickerson, D.A. 2001. Variation is the spice of life. Nat. Genet. 27: 234–236. [DOI] [PubMed] [Google Scholar]
- Livingston, R.J., von Niederhausern, A., Jegga, A.G., Crawford, D.C., Carlson, C.S., Rieder, M.J., Gowrisankar, S., Aronow, B.J., and Nickerson, D.A. 2004. Patterns of sequence variation across 213 environmental response genes. Genome Res. 14: 1821–1831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niu, T., Qin, S., Xu, X., and Liu, J. 2002. Bayesian haplotype inference for multiple linked single nucleotide polymorphisms. Am. J. Hum. Genet. 70: 157–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patil, N., Berno, A.J., Hinds, D.A., Barrett, W.A., Doshi, J.M., Hacker, C.R., Kautzer, C.R., Lee, D.H., Marjoribanks, C., McDonough, D.P., et al. 2001. Blocks of limited haplotype diversity revealed by high-resolution scanning of human chromosome 21. Science 294: 1719–1723. [DOI] [PubMed] [Google Scholar]
- Stephens, M., Smith, N., and Donnelly, P. 2001. A new statistical method for haplotype reconstruction from population data. Am. J. Hum. Genet. 68: 978–989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, D.G., Fan, J.B., Siao, C.J., Berno, A., Young, P., Sapolsky, R., Ghandour, G., Perkins, N., Winchester, E., Spencer, J., et al. 1998. Large-scale identification, mapping, and genotyping of single-nucleotide polymorphisms in the human genome. Science 280: 1077–1082. [DOI] [PubMed] [Google Scholar]
- Zhang, K., Deng, M., Chen, T., Waterman, M.S., and Sun, F. 2002. A dynamic programming algorithm for haplotype block partitioning. Proc. Nat. Acad. Sci. 99: 7335–7339. [DOI] [PMC free article] [PubMed] [Google Scholar]
Web site references
- http://www.ncbi.nlm.nih.gov/projects/SNP; dbSNP
- http://innateimmunity.net/; Innate Immunity PGA. NHLBI program in genomic applications.