Structure and energy of a DNA dodecamer under tensile load

Abstract

In the last decade, methods to study single DNA molecules under tensile load have been developed. These experiments measure the force required to stretch and melt the double helix and provide insights into the structural stability of DNA. However, it is not easy to directly relate the shape of the force curve to the structural changes that occur in the double helix under tensile load. Here, state-of-the-art computer simulations of short DNA sequences are preformed to provide an atomistic description of the stretching of the DNA double helix. These calculations show that for extensions larger that ∼25% the DNA undergoes a structural transformation and a few base pairs are lost from both the terminal and central part of the helix. This locally melted DNA duplex is stable and can be extended up to ∼50–60% of the equilibrium length at a constant force. It is concluded that melting under tension cannot be modeled as a simple two-state process. Finally, the important role of the cantilever stiffness in determining the shape of the force–extension curve and the most probable rupture force is discussed.

INTRODUCTION

With the development of atomic force microscopy (AFM), single DNA molecule pulling experiments have become very popular [for a review see Ref. (1)]. In these experiments a DNA strand is attached between a solid support and a force-recording device, which can either be an atomic force microscope cantilever or an optical or magnetic tweezer. The distance between the two extremities of the DNA molecule is varied and the force required to stretch the double helix is recorded. It is observed that the force required to stretch long DNA tracts reaches a plateau at ∼70 pN and then remains constant (2,3). This behavior has been attributed to the formation of a new overstretched form of DNA (S-DNA) (2) with ∼38 bases per right-handed turn and a helical pitch of 22 nm (4). When the helix is further elongated to about twice the original length the force sharply increases and a melting transition is observed at a load between 35 and 300 pN, where the actual value depends on the sequence composition and loading rate (5,6). For short DNA sequences, the measurement is more complex due to the possibility of interactions between the DNA molecule, the force-recording device and the solid surface, as well as the influence of the geometry of attachment and cantilever properties on the recorded force. For these reasons, values ranging from 20 to 450 pN have been measured (7–12) for the melting of short (<20 nucleobases) DNA oligomers. The force required for the melting of short DNA oligomers is proportional to the logarithm of the loading rate and, at 27°C, varies from 20 pN for loading rates of ∼100 pN s⁻¹ to 50 pN for loading rates of ∼1 × 10⁶ pN s⁻¹ (8,10,11). A transition to an overstretched DNA helix at 120 ± 70 pN has also been observed during stretching of DNA 14mers (13); the force required to melt the 14mer in this experiment was 0.4 nN. The structure of overstretched DNA has not been fully characterized yet. Rouzina and Bloomfield (14–16) have proposed that the B–S transition corresponds to force-induced melting of the double helix, though their proposal is still the subject of debate (17). Molecular mechanics calculations (18) and molecular dynamics (MD) simulations of a DNA dodecamer pulled from the 3′-termini suggested that the S-form has a ladder structure where base pairing is retained, but the nucleobases are tilted with respect to the axis of the helix and base stacking is interstrand, rather than intrastrand (19). The calculated force required for the B–S transition in an (ACTG)₃–(CATG)₃ dodecamer was 80 pN, while the calculated melting force is 1200 pN (19). This value is significantly larger than values observed experimentally (11). The difference between the calculated and the expected melting force might be ascribed to the approximate treatment of the solvent–DNA interactions that in this work were modeled implicitly with a distance-dependent dielectric constant (20). In an early study by MacKerrel and Lee (9), where solvent and counterions were modeled explicitly, the calculated force required to melt an (ACTG)₃–(CATG)₃ dodecamer by pulling at the 5′-termini was found to be 130 ± 25 pN and complete melting was observed at an extension of 6 nm. The stability of the ladder S-DNA structure has been questioned by a recent MD simulation of DNA stretching (21) where the entropic contributions to the stability of an overstretched d(CGCAAAAAAGCG) duplex were analyzed and it was concluded that the ladder structure is unstable towards melting already at extensions of 1.5–2.0 nm.

In the last 5 years, considerable progress has been made towards more reliable computer simulations of DNA (22). The widely used CHARMM and the AMBER force fields have been refined to better reproduce the properties of DNA in solution (23) and efficient methods to describe long-range electrostatic interactions have been developed (24,25). Here we take full advantage of the latest developments, and of the increased available computational power, to perform a number of state-of-the-art MD simulations of pulling of a DNA dodecamer. Calculations were performed using explicit solvent and counterions with a Particle Mesh Ewald (PME) method (26) to account for the long-range electrostatic interactions. This computational setup has been shown to be required in order to obtain reliable MD simulations of DNA in solution (25). The results of the simulations allow the reinterpretation of some of the experimental data available on the stretching of short DNA sequences. At variance with the earlier calculations (18,19) these simulations predict a sequence-dependent conformational transition at 25% extension characterized by partial fraying of the double strand and formation of internal denaturation bubbles (9,21). This newly formed structure is stable towards further denaturation up to an extension of at least 50% and might be involved in the B–S transition observed in long DNA pulling experiments. Finally, it is discussed how the force profile and rupture force measured in an AFM pulling experiment can be influenced by the cantilever stiffness. This observation might explain why very different forces have been reported in the literature for the melting of short DNA nucleotides.

METHODS

All the atomistic calculations described in this work were performed using the Amber 8.0 (27) suite of programs and the Amber 2003 force field (28). The following DNA molecules were studied in this work: 12 poly(dA)_n–poly(dT)_n DNA strands, with n ranging from 3 to 14; 12 poly(dC)_n–poly(dG)_n DNA strands, with n ranging from 3 to 14; and the d(ACTG)₃–d(CAGT)₃ dodecamer. Starting structures for the DNA double helix were generated with the program nucgen; the Arnott B-DNA form (29) was chosen as starting conformation for all the sequences investigated. The DNA strands were terminated with a hydroxyl group at the 3′- and 5′-termini. The DNA double strands were immersed in a periodic box of TIP3P water (30), the size of the box was chosen such that the minimum distance between the periodic images was 2.4 nm in the x and y direction and 6.0 nm in the z direction. For the d(ACTG)₃–d(CAGT)₃ dodecamer simulation, this corresponds to a box size of ∼5 × 5 × 11 nm. The negative charge of the DNA double strands was neutralized with 22 Na⁺ counterions, corresponding to a Na⁺ concentration of ∼0.13 M. The counterions were placed in the regions of largest negative potential with the program Xleap. MD simulations were performed with the pmemd program. A cut-off of 0.9 nm was used for the Lennard–Jones interactions and the real space part of the electrostatic interactions. The PME method (26,31) was used to describe the reciprocal space part of electrostatic interactions. This computational setup is expected to provide reliable MD simulations of DNA tracts in solution on the nanosecond time scale (23,32,33). The time step for the MD simulation was 1.5 fs; constant pressure and temperature conditions (NPT) were obtained by coupling the system to a Berendsen thermostat (34) and barostat with relaxation times of 2.0 and 3.0 ps, respectively. The water molecules and the counterion positions were relaxed with 0.3 ns of MD simulation where the position of the DNA molecules was kept fixed. Subsequently each system was equilibrated by performing 1.8 ns of NPT MD simulation at 300 K.

Simulations of AFM pulling at constant rate

NPT MD simulations of DNA stretching were performed by connecting the 5′-terminal hydroxyl group to a harmonic spring. The force constant of the spring was 1390 pN nm⁻¹ and the equilibrium distance for the spring was taken as the distance between the 5′-termini of the two DNA strands at the end of the equilibration. During the MD simulation the equilibrium distance of the spring was increased at a rate of 1.0 nm ns⁻¹. The total simulation time was 3 ns for each poly(dA)–poly(dA)-poly(dT) or poly(dC)-poly(dG) sequence investi-gated. For the d(ACTG)₃–d(CATG)₃ dodecamer, three pulling simulations (pull_a, pull_b and pull_c) at pulling rates of 0.3, 0.3 and 0.12 nm ns⁻¹ were performed. Starting structures were obtained performing 1.2, 1.8 and 1.8 ns of equilibration for simulation pull_a, pull_b and pull_c, respectively. Simulations pull_a and pull_b were carried out until the separation of the DNA strands was observed; while simulation pull_c was carried out up to an extension of 9.4 nm, where the extension is defined as the distance between the 5′-termini of the DNA strands. The total simulation time was 24, 24 and 48 ns for simulation pull_a, pull_b and pull_c, respectively. In all the simulations, sampling of the force and energies was performed after every 0.15 ps of MD simulation. The potential energy surface along the pulling reaction coordinate was calculated as the logarithmic average of the three simulations, according to the Jarzynski inequality (35,36), while forces were calculated as the derivative of the free energy surface (FES).

Umbrella sampling simulations

Umbrella sampling simulations were performed for the d(ACTG)₃–d(CAGT)₃ dodecamer at increasing DNA extension. Five simulations were performed (u1–u5) with a restraining harmonic potential of 695, 139, 139, 139 and 695 pN nm⁻¹ for simulations u1, u2, u3, u4 and u5, respectively. In simulation u1, 2.4 ns of MD simulation at a fixed restraint distance of 3.7 nm was initially performed. Subsequently, the restraint distance was gradually increased by 0.2 nm in 0.3 ns of MD simulation and the process was repeated 24 times up to a restraint distance of 8.1 nm. For each of simulations u2, u3, u4 and u5, 30 umbrella sampling simulations of 2.4 ns each were performed with restraint distances ranging from 3.7 to 9.7 nm. Starting structures for each umbrella sampling were conformations taken at 0.2 nm intervals from the pulling simulations pull_a, pull_b, pull_c and pull_b, respectively. The last 1.5 ns of each 2.4 ns simulation were collected for data analysis. The total combined simulation time for the umbrella sampling calculations was 345 ns. The distance histograms of the five simulations were combined to reconstruct the FES according to the weighted histogram analysis method (37) as implemented in the WHAM program by Alan Grossfield (38). Forces were calculated as the derivative of the FES.

Energetic analysis

The energy G of a molecule in solution can be decomposed as described in Ref. (39).

$$G=E^{\text{int}}+G^{\text{sol}}+T{S}^{\text{int}}$$

where G^sol is the free energy of solvation, E^int is the internal energy and S^int is the conformational entropy of the molecule. The average internal energy of the duplex can be directly obtained from an MD simulation, while an upper bound to the internal entropy can be calculated from the covariance matrix of atomic positional fluctuations (40). The free energy of solvation is not directly accessible from an MD simulation in explicit solvent, but can be calculated with an implicit solvation model as the generalized Born (GB) approximation (41). Thirty-five MD simulations of 4.5 ns each were performed duplex at extensions ranging from 3.7 to 10.7 nm. In these simulations the GB approximation was used to represent solvation. The last 4 ns of each trajectory were used to calculate the internal energy E^int, solvation G^sol and entropic S^int contributions to the duplex free energy at increasing values of extension. The error on the solvation and internal energy was calculated for each extension as the SD of block averages calculated over 150 ps intervals and ranges between 2 and 4 kcal mol⁻¹. The internal entropy in the limit of infinite sampling S_∞ is estimated from S(t) values calculated for time frames of different lengths t using the empirical relationship (21,39) given below.

$$S\left(t\right)=S_{\infty }-\left(\frac{\alpha }{t^n}\right),$$

where S_∞, α are parameters in the fitting and n is equal to 2/3 (39). To estimate the error on the internal entropy in the limit of infinite sampling, the results of several simulations should be compared. A 26.4 ns simulation at constant extension of 6.1 nm was performed. This simulation was subdivided into four trajectories of 6.6 ns each and the error was calculated as the SD between the S_∞ values calculated for the four trajectories. The estimated error on the internal entropy contribution TS^int is 10 kcal mol⁻¹ at 298 K.

Simulation of the tip motion during an AFM experiment

The equation of motion for the tip was integrated using a velocity Verlet algorithm and a time step of 0.5 ns. Calculations were performed with a tip of mass 1.5 × 10⁻¹¹ kg, the mass of a tip of resonance frequency 13 kHz and a spring constant of 20 pN nm⁻¹, which represent typical values for tips used in AFM pulling experiments (8,10,13). Pulling speeds ranging between 5 and 5000 nm s⁻¹ were used (8,10). The viscous friction coefficient was 0.5 × 10⁻³ pN s nm⁻¹ (42). An analytical expression for the potential of mean force (PMF) V₀(x,ϕ) (kJ mol⁻¹) of the DNA molecule along the pulling coordinate x (bound and overstretched states) was obtained by integration of a third-degree polynomial fitting of the force profile obtained from the umbrella sampling simulation u5. Coefficients of the fittings were 0.138483 pN nm⁻³, −17.5736 pN nm⁻², 746.791 pN nm⁻¹, −10612.6 pN and 0.042471 pN nm⁻³, −21.956 pN nm⁻², 1346.842 pN nm⁻¹, −27544 pN for the bound and overstretched state, respectively. The unbound state was modeled as a state of constant energy V₀(x) = 20 kcal mol⁻¹, roughly corresponding to the thermal stability of the d(ACTG)₃–d(CAGT)₃ duplex (43). The energy minimum of the overstretched state was set to 5 kcal mol⁻¹, consistently with the loss of ∼3 out of 12 bp in the overstretched conformation (Figure 2). Starting conditions for the simulations were x = 3.9 nm and a random starting velocity selected with a Boltzmann probability for T = 298 K.

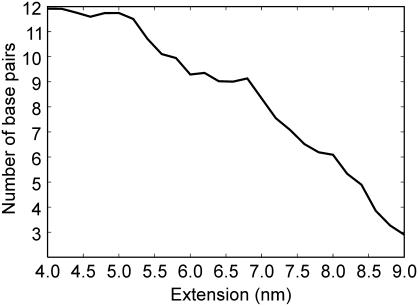
Figure 2.

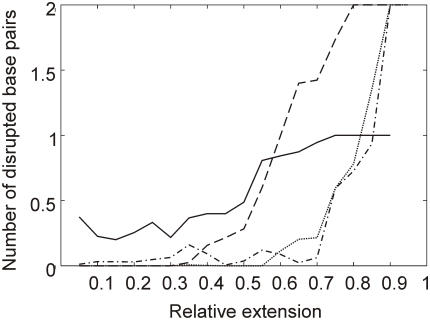
Number of Watson–Crick base pairs as a function of the d(ACTG)₃–(CAGT)₃ extension (nm). The presence of a base pair is assumed when the N₁–N₃ distance for A:T or G:C is <0.4 nm. The values reported here are averages over all the conformations sampled in the umbrella sampling and AFM pulling simulations.

RESULTS

Free energy surface of the d(ACTG)₃–d(CAGT)₃ dodecamer under tensile load

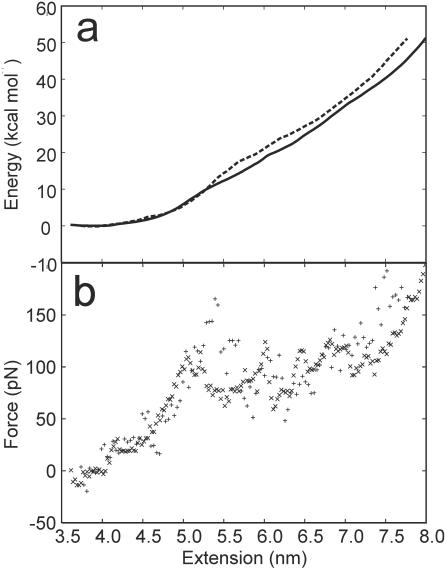
Three simulated AFM pulling experiments were performed by connecting the 5′-termini of the DNA duplex to a harmonic spring and increasing the equilibrium distance for the spring at a constant rate. The Jarzynski inequality (35,36) was used to reconstruct the unperturbed FES from the force versus extension profiles obtained from the three pulling simulations. The same FES was also reconstructed using distance histograms (37) calculated from five umbrella sampling simulations. The two free energy profiles are reported in Figure 1a together with the forces calculated as the derivative of the free energy with respect to the reaction coordinate. Even in these relatively long MD simulations, the DNA molecule is extended at a much faster rate than in any real AFM experiments. This might prevent the double helix to relax on the thermodynamically most stable state at each extension value. For this reason, the calculated FES provides an upper bound to the FES that would be obtained in the limit of an infinitely slow relaxation. Comparison of the two independent free energy profiles allows to estimate the convergence of the simulations with respect to the sampling of the space of conformations. Overlapping FESs are obtained up to an extension of ∼5.5 nm, indicating that up to that extension the sampling is sufficient to obtain a converged FES. For larger extensions the free energy calculated from the umbrella sampling simulations is slightly smaller than those calculated from the Jarzynski inequality. This suggests that, after this extension, incomplete sampling can be an issue. The larger sampling performed in the umbrella sampling simulations allows further relaxation of the system and provides a better estimate of the FES. Assuming that the entropy loss when a double helix is formed from two immobilized single strands is negligible, the estimated stability of a constrained (ACTG)₃–(CAGT)₃ dodecamer in 1 M NaCl at 25°C is 19.4 kcal mol⁻¹ (44) (Figure 1a). This value is approached in the umbrella sampling simulation at 6.0 nm of extension. We conclude that in the calculations, the dodecamer is thermodynamically stable up to an extension of ∼6.0 nm.

Figure 1.

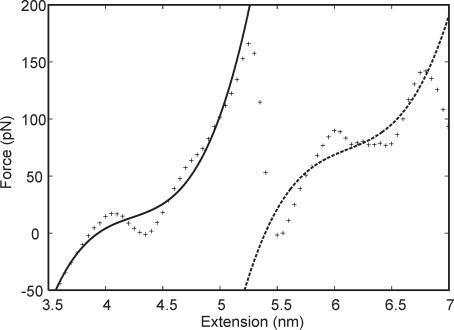
(a) Plot of the PMF (kcal mol⁻¹) versus extension (nm) as determined by a weighted histogram analysis of the five umbrella sampling simulations (solid line), or from the three AFM pulling simulations using the Jarzynski equality (dashed line). (b) Plot of the force (pN) versus extension (nm). Forces have been obtained as the derivative of the PMF calculated from the umbrella sampling (cross) or the pulling simulations (plus).

The force profiles show that as the dodecamer is slightly displaced from the equilibrium length of 3.8 nm, it behaves as a harmonic spring of force constant ∼0.1 nN nm⁻¹. As the length approaches 5.0 nm, a plateau is reached and the helix can be further extended up to 7.5 nm at an almost constant force of 80 pN (Figure 1b). For extensions that exceed 7.5 nm, the force required to further stretch the duplex increases until the helix–coil transition occurs. An analysis of the number of Watson–Crick pairings present in the helix as a function of the extension allows the identification of three different regimes (Figure 2): (i) from 3.8 to 5 nm, where the helix can be stretched without disrupting any base pairing, (ii) from 5.5 to 6.5 nm, where 2–3 bp are lost, and the double helix can be stretched at an almost constant force, and (iii) after 7 nm any further extension leads to an increase of the force and a loss of base pairing. The limit of the thermodynamic stability (extension >6.0 nm) is located in the constant force region, after the transition to a partially melted helix. Unfortunately, owing to limitations in the time scale accessible by MD simulations, it is not possible to determine the kinetic barrier to the duplex separation in the overstretched state. In the MD simulations, complete separation is observed only for extensions larger than 9.0 nm.

Enthalpic and entropic contributions to the dimer stability

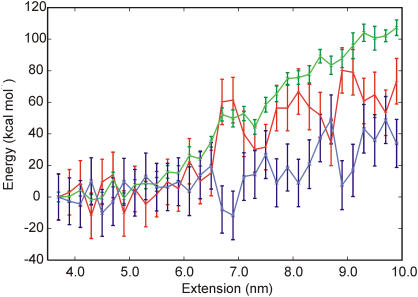
Harris et al. (39) introduced an empirical approach to estimate the entropy contribution to the free energy in the limit of infinite sampling. This method has been recently applied to the stretching of the d(GCGAAAAAACGC) duplex (21). In this work it was shown that it is not possible to stretch the d(GCGAAAAAACGC) duplex over 1–2 nm without disrupting some of the base pair interactions. Interestingly, it was also found that at extensions >2 nm the overstretched DNA becomes thermodynamically more stable than the unrestrained double helix (21). The free energy profiles calculated from the AFM pulling and umbrella sampling simulations (Figure 1) do not indicate any increase in the stability of the double helix upon extension. However, there is the possibility that the duplex is thermodynamically unstable towards melting, but the relatively short time scale of the simulation does not allow for the dissociation to occur fully. In order to provide an estimate of the stability of the double helix under tensile load in the limit of infinite sampling, the scheme suggested by Harris et al. (21) to calculate relative free energies was applied to the DNA duplex at increasing values of extension. According to this scheme, a GB approximation (41) is used to calculate the internal duplex energy and the free energy of solvation, while the internal entropy of the double helix is calculated from the mass-weighted covariance matrix within a harmonic approximation (40). In Figure 3 the energy versus extension profile calculated with this method is shown. The energy profile is compatible with the profile calculated from the umbrella sampling simulations up to an extension of 6.5 nm, where a sudden increase in the internal entropy of the helix leads to a substantial stabilization of the overstretched DNA. Such a stabilization is not observed in the profile calculated from the AFM pulling and umbrella sampling simulations, again suggesting that for extensions larger than 6.5 nm the sampling could be incomplete. The relative charge in the overall duplex stability is the result of the sum of two large contributions: the internal plus solvation and the entropic contribution. While the error on the former is not large (∼3 kcal mol⁻¹), the error on the entropic contribution is significant (∼14 kcal mol⁻¹) and prevents a more quantitative comparison. The main reason for this fact should be ascribed to the very slow convergence of the absolute entropy with respect to the simulation time when multiple states can be populated (45). It should also be pointed out that the use of the harmonic approximation provides an upper bound to the real entropy of the system (40). For a system of Lennard–Jones particles and for the ideal gas the harmonic approximation overestimates the entropy by ∼5 and ∼20%, respectively (45). An error of 5% in the internal entropy a DNA dodecamer corresponds to ∼150 cal mol⁻¹ K⁻¹. Although error cancellations might improve the quality of the data in favorable cases, relative free energies calculated with this methodology should be treated with caution.

Figure 3.

DNA energy as a function of extension. The DNA energy (blue) was obtained as the sum of the internal energy, solvation free energy and conformational entropy. The internal plus solvation energies (green) were calculated with the GB/SA approximation (41). The internal entropy contribution TS_∞ (red) was calculated from the mass-weighted covariance matrix using a harmonic approximation (40).

In conclusion, the energy versus extension profiles obtained from AFM pulling and umbrella sampling simulations and calculated with the method of Harris et al. (39) provide a consistent picture of the duplex stretching up to an extension of 6.0–6.5 nm, where the duplex appears to become unstable and begins sampling a larger number of conformations. This is in line with the observation that in the umbrella sampling simulations base pairs are reversibly broken and reformed only up to an extension of ∼6.5 nm; after this limit any rupture of a base pair contact is irreversible.

Structure and melting pathway of a DNA double helix under tensile load

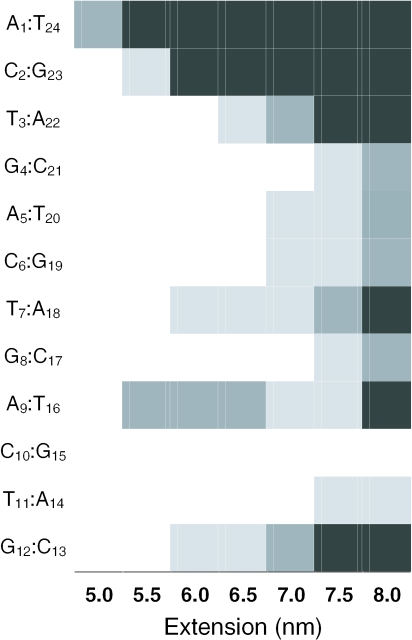
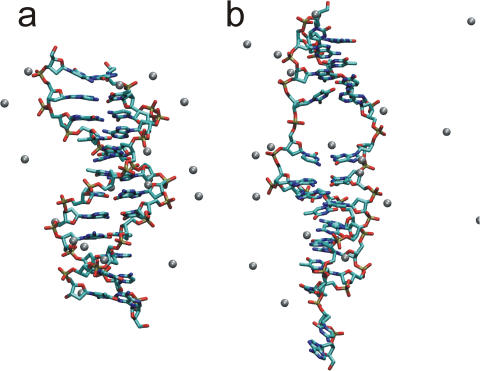
Early calculations in implicit solvent (19) have suggested that DNA under tension undergoes a structural transition to a ladder-like form called S-DNA which is responsible for the force plateau observed experimentally for extensions larger than 30–60% the equilibrium length of the DNA duplex. A force plateau for extensions larger than 5 nm, roughly corresponding to a displacement of 25% from the equilibrium distance, is indeed observed in the present calculations. However, this plateau is produced by the rupture of a few Watson–Crick base pairs (Figure 2) and consequent disruption of the helix structure; S-DNA has not been observed in any of the simulations performed here. The probability of dissociation at different helix extensions has been calculated for each base pair as an average over all the simulations performed (Figure 4). The duplex can be stretched without loss of any base pairs up to 5 nm (Figure 5a), where the A₁ : T₂₄ base pair becomes unstable towards melting and in all simulations it is lost for extensions >5.5 nm. Subsequently, between 5.5 and 6.0 nm, the terminal C : G pairs (C₂ : G₂₃ or G₁₂ : C₁₃) and two of the internal A : T pairs (T₇ : A₁₈ and A₉ : T₁₆) are destabilized. The loss of one or two out of these four contacts is sufficient to stabilize the remaining base pairs and to extend the duplex up to 7 nm at a constant force. The loss of an internal base pair allows a large relaxation of the phosphate backbone that leads to local opening of the minor groove and a substantial (50%) unwinding of the helix (Figure 5b). In most of the simulations, this relaxation appears to be stabilized by a Na⁺ ion localized in the denaturation bubble that is formed upon opening of one of the internal base pairs (Figure 5b).

Figure 4.

Rupture probability as a function of extension (nm) for each base pair of the d(ACTG)₃–(CAGT)₃ dodecamer. Probabilities are indicated in white (40%), light gray (60%), dark gray (80%) and black (>80%). The presence of a base pair is assumed when the N₁–N₃ distance for A:T or G:C is <0.4 nm. The values reported here are averages over all the conformations sampled in the umbrella sampling and AFM pulling simulations.

Figure 5.

Umbrella sampling simulation of d(ACTG)₃–(CAGT)₃. Structures obtained from simulation u4 at 5.0 nm (a) and 6.5 nm (b) of extension. The bond of the DNA molecules are represented as sticks colored according to the atoms participating in a bond (carbon—cyan, oxygen—red, nitrogen—blue, phosphorous—green). The Na⁺ counterions are represented as balls. Water molecules and hydrogen atoms are not shown for the sake of clarity.

Any extension over 7 nm produces a number of further melting events and leads to the progressive separation of the double helix. This reaction pathway for the ‘mechanically induced’ helix to coil transition can be compared with the pathway for the thermally induced helix to coil transition as determined from NMR experiments. In these experiments it is found that at low salt concentration (0.01 M NaCl) the helix to coil transition approaches a two-state process and melting of the double helices begins at the ends of the duplex and then propagates into the core (46,47). However, in 0.1 M NaCl an intermediate state, characterized by structural changes in the internal A : T base pairs, is also observed (46). The mechanical pathway determined here in 0.13 M Na⁺ is remarkably similar to the thermal pathway determined in 0.1 N NaCl, as in both cases the helix to coil transition cannot be described as a two steps process but involves the formation of an intermediate state with structural rearrangements in the core of the helix.

Structural properties of short poly(dA)–poly(dT) and poly(dC)–poly(dG) DNA tracts under tensile load

The sequence dependence of the DNA helix stability under tensile load was further investigated by performing pulling MD simulations of poly(dA)_n–poly(dT)_n and poly(dC)_n–poly(dG)_n DNA molecules of increasing length. For each of the two DNA types, 12 sequences of length ranging from 3 to 14 bp were stretched. In each experiment, the 5′-termini of the two strands were linked to a harmonic spring and the equilibrium position of the spring was increased by 3.0 nm at a rate of 1.0 nm ns⁻¹. The relative extension at which the poly(dA)–poly(dT) and poly(dC)–poly(dG) terminal and the internal base pairs starts to open is reported in Figure 6. The plot clearly shows that A : T base pairs have a tendency to open earlier than C : G base pairs, consistent with the results of the d(ACTG)₃–d(CAGT)₃ calculations and with the lower thermodynamic stability of A : T pairs with respect to G : C pairs (43). At variance with the thermal melting pathway, for G : C base pairs there is not a well-defined tendency for the terminal base pairs to open much earlier than the internal ones. In conclusion, Figure 6 shows that in mixed sequences there might be a preference for the opening of internal A : T base pairs with respect to terminal C : G. However, it should be noted that the location of the most unstable steps is also expected to be determined by the overall DNA sequence composition. This might explain why in the d(ACTG)₃–d(CAGT)₃ dodecamer A₉ : T₁₆ appears to be significantly less stable than the other internal A : T pairs (Figure 4).

Figure 6.

AFM pulling simulations of d(A)_n–d(T)_n and d(C)_n–d(G)_n. Number of broken Watson–Crick base pairs as a function of extension for the terminal A:T base pairs (solid line), the internal A:T base pairs (dashed line), the terminal C:G base pairs (dotted line) and the internal C:G base pairs (dashed-dotted line).

Influence of cantilever stiffness on the rupture force

Very different values for the rupture force of a short (10–30 bases) DNA double helix have been reported in the literature. Rupture forces obtained for short DNA sequences can be broadly subdivided in two categories: (i) values >100 pN, usually obtained with stiff cantilevers (7,9,13) and (ii) values <100 pN, usually obtained with soft cantilevers (8,10–12). An influence of the cantilever stiffness on the rupture force is expected, in particular if the energy surface is characterized by multiple states and the possibility of rebinding is allowed (48). The MD simulations performed here suggest that the DNA under tensile load can be described as a three-state system with a bound, an overstretched and an unbound state. The influence of the cantilever stiffness on rupture force measurements has been investigated by performing numerical simulations of the tip motion during an AFM pulling experiment. These simulations include the effect of the temperature, the cantilever stiffness and the viscous drag. In a typical AFM pulling experiment, one strand of the DNA duplex is attached with some linker molecule to a surface, while the complementary strand is connected to an AFM tip (1). The tip is attached to a flexible cantilever that is retracted at a constant rate v. Following previous works, we assume that the cantilever can be represented by an harmonic spring of effective spring constant k which includes contributions arising from the presence of non-polymer extensible linker molecules (48,49). The potential for the DNA-cantilever system is given below (50).

$$V\left(x,t\right)=V_0\left(x\right)+\frac{k}{2}{\left(x-vt\right)}^2,$$ 1

where x is the position of the tip. The corresponding 1D Langevin equation of motion for the tip is given as follows (51):

$$m\frac{{\partial }^{2}x}{\partial t^2}=\frac{\partial V_0\left(x\right)}{\partial x}+kx-kvt+\eta \frac{\partial x}{\partial t}+{\xi }_x\left(t\right),$$ 2

where m is the mass of the tip, V₀(x) is the PMF of the DNA helix along the pulling coordinate x calculated from the MD simulations, η is the viscous drag coefficient (42) and ξ_x is a random force that represents the effect of thermal fluctuations (51). The DNA helix is described as a three-state system with a bound, an overstretched and an unbound state:

$$V\left(x,t,\varphi \right)=V_0\left(x,\varphi \right)+\frac{k}{2}{\left(x-vt\right)}^2.$$ 3

Hopping between the states ϕ_i and ϕ_j occurs according to the rate (52):

$$k_{i\to j}=A{\text{e}}^{-\Delta E_{ij}/k_{b}T},$$

where the rate of hopping k_i→j depends on the energy difference ΔE_ij(x) between the two states i and j and A is the rate of hopping between state of the same energy.

Force–displacement profiles were calculated from numerical integration of Equation 2 using a velocity Verlet algorithm. Simulations were performed with two cantilevers of different stiffness (20 and 200 pN nm⁻¹) and loading rates varying from 83 to 83000 pN s⁻¹. Typical loading rates applied in AFM pulling experiments range between 100 and 10000 pN s⁻¹. The energy profiles for the bound and overstretched states were obtained from a polynomial fit of the first and second part of the force profile calculated from the umbrella sampling simulation u5 (Figure 7). Two force–displacement curves obtained with cantilevers of 20 and 200 pN nm⁻¹ at the same loading rate of 8300 pN s⁻¹ are reported in Figure 8a. While the stiffest cantilever follows the PMF surface up to the detachment, the softer cantilever ‘snaps’ at the first maximum in the energy surface. This is due to the large elastic energy that is accumulated in the soft cantilever and that is released when the first transition state is reached (also see Appendix 1). The distance traveled by the tip after snapping depends on the force constant of the cantilever and, for forces of a few tens of pN, may vary between few angstroms for a stiff cantilever and few nanometers for a soft cantilever. Therefore, if more than one transition state is present, a soft cantilever does not sample uniformly the potential energy surface, but hops between equilibrium states. It is possible that during the snapping motion the molecule attached to the tip is rapidly overstretched to a high-energy elongated conformation without the possibility to relax before rupture (48). This will occur in particular if the snapping motion is much larger than the value of thermal fluctuations, as in the case of a small molecule pulled with a soft cantilever.

Figure 7.

Two-state model representation of the DNA double helix under tensile load. An analytical expression for the force required to stretch the bound (solid line) and the overstretched (dashed line) states was obtained by fitting to a third-degree polynomial the forces calculated from the umbrella sampling simulation u5 (crosses) at low (from 3.5 to 5.0 nm) and moderate (from 5.5 to 6.8 nm) extensions, respectively.

Figure 8.

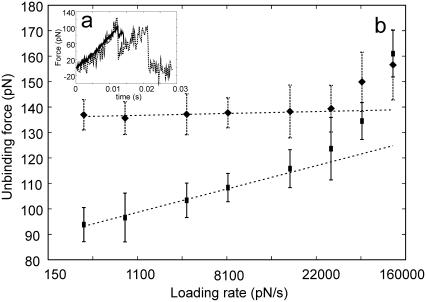
Numerical simulation of an AFM pulling experiment. (a) Force versus time plots for experiments performed with a soft (20 pN nm⁻¹—solid line) and a stiff (200 pN nm⁻¹—dashed line) cantilever. The loading rate in both experiments is 1000 pN s⁻¹. (b) Loading rate dependence of the most probable rupture force for experiments performed with a soft (20 pN nm⁻¹—squares) and a stiff (200 pN nm⁻¹—diamonds) cantilever. Averages and SDs for each data point were calculated from the result of 30 numerical experiments performed with different initial velocities.

Figure 8b shows a comparison of the rupture forces calculated from numerical simulations at loading rates ranging from 83 to 83000 pN s⁻¹. Over a large range of loading rates the rupture force for the stiff cantilever is constant, while the rupture force calculated for the softer cantilever is linearly dependent on the logarithm of the loading rate. The two forces eventually match at very high loading rates. This is the typical behavior of a system with more than one energy barrier where rebinding is allowed (48). This model is consistent with the observation that for stiffer cantilevers a higher force (7,9,13), independent of the loading rate (7), is required to separate the duplex, while for softer cantilevers the unbinding force is lower and linearly dependent on the logarithm of the loading rate (8,10,11).

Finally, some confusion might arise from the definition of loading rate, which in the literature is sometimes defined as kv. As pointed out by several authors and demonstrated in Appendix 1, the loading rate is in fact a function of the PMF (8,10,48,53). It approaches kv only in the limit of very fast pulling with a very soft cantilever. This result prevents the direct comparison of data obtained with cantilevers of different stiffness (53), unless the functional form of the stretch modulus of the system is known (Appendix 1).

DISCUSSION

The overall picture that emerges from the umbrella sampling and AFM pulling simulations of the d(ACTG)₃–d(CAGT)₃ dodecamers is very similar (Figure 1a and b). In both cases a first conformational transition is observed at a force of <100 pN and an extension of 25%. During this transition between two and three terminal, internal base pairs are lost and a locally melted double helix is formed. This event is associated with a 50% unwinding of the helix and severe distortion of the phosphate backbone (Figure 5b). This locally melted DNA conformation is stable up to an extension of ∼50% and can be stretched at an almost constant force (∼80 pN). After 60% of extension the force required to stretch the duplex increases and any extension is associated with the loss of base pairs. Calculation of the PMF for the DNA-cantilever system suggests that soft cantilevers are likely to ‘snap’ at the barrier for the first conformational transition at 25% extension, while experiments performed with a more rigid cantilever may also probe the second barrier at 50–60% of extension. Furthermore, it is shown that experiments performed at the same loading rate with cantilevers of different stiffness can give very different results in terms of rupture force and force–extension curves. These findings may provide an interpretation for the large spectrum of rupture forces measured in different dynamic force spectroscopy experiments where forces ranging from tens to hundreds of pN are required to melt short DNA duplexes in different experiments (7–10,12,13).

In the d(ACTG)₃–d(CAGT)₃ simulations, melting of non-terminal base pairs has been invariably observed for extensions exceeding 6.0 nm. This is not completely unexpected, as melting in a central position allows for the largest degree of unwinding and conformational flexibility. Opening of central base pairs was also observed in previous simulations by Harris et al. (21) and MacKerrel and Lee (9). Interestingly, in the d(CGCAAAAAAGCG)–d(GCGTTTTTTCGC) sequence simulated by Harris et al. (21) there is no terminal A : T base pair and in the simulations the central A : T base pairs invariably open before the terminal C : G. This observation is completely consistent with the results of the AFM pulling calculations of poly(dA)–poly(dT) and poly(dC)–poly(dG), indicating that A : T internal base pairs are destabilized at lower extensions with respect to terminal C : G pairs. The observation that under tensile load some internal base pairs can dissociate earlier than the terminal base pairs also suggests why in a recent work (12) the stability of C : G base pairs was found to be essentially the same as those of A : T pairs. In this work, the assignment of a rupture force to the loss of a specific base pair was based on the assumption that base pair opening proceeds sequentially from the termini to the center of the helix (12). If this assumption is incorrect, then it is likely that A : T rupture events have been assigned to C : G base pairs and vice versa. The net result would be that very similar average forces are calculated for the rupture of an A : T and a C : G base pair.

In summary, this work provides a detailed description of the structure and energy of a DNA dodecamer under tensile load and allows the interpretation of the experimental results in terms of the formation of a locally melted DNA double strand at 25% extension. This intermediate form can be stretched at constant force and is stable up to at least 50% extension.

The MD simulation results suggest that for a dodecamer the so-called B–S transition is in fact partial melting of the helix. This interpretation is also consistent with several observations coming from experiments performed on long DNA tracts, namely (i) the B–S transition has properties similar to a melting transition (14–16), (ii) unwinding greatly reduces the force at which the B–S transition occurs (4), and (iii) S-DNA is formed at an extension of ∼10–20% and can be stretched up to ∼80% before melting occurs. (17). However, it is not clear if the results obtained for a dodecamer are relevant at all for the interpretation of data obtained from stretching of much longer sequences and further studies are needed to investigate this issue.

Finally, our calculations indicate that a limited stretching and free energy change are required to locally open the double helix. The opening can occur at the termini or in the central part of the duplex, and there are strong indications that the position of the opening can be sequence-dependent. We therefore suggest that the mechanism of locally melting a DNA double helix with applied tension might have some biological relevance as it provides a pathway to open the double helix in a specific position with a relatively low effort.

APPENDIX

Loading rate and potential energy as a function of cantilever stiffness

Here, an analytical expression for the total energy of the DNA-tip system and of the loading rate is derived. If thermal fluctuations are neglected, the position of the tip in the first part of the pulling can be derived analytically from Equation 1 assuming a quasi-equilibrium condition:

$$\begin{array}{c}\frac{\partial V\left(x,t\right)}{\partial x}=\frac{\partial V_0\left(x\right)}{\partial x}+k\left(x-vt\right)=0\\ x\left(t\right)=-\frac{1}{k}\frac{\partial V_0\left(x\right)}{\partial x}+vt.\end{array}$$ 4

In this regime the PMF of the system V_eq(x) is not time-dependent:

$$V_{eq}\left(x\right)=V_0\left(x\right)+\frac{1}{2k}{\left(\frac{\partial V_0\left(x\right)}{\partial x}\right)}^2,$$ 5

where [(1/2k))(∂V₀(x)/∂x)²] is the difference between V_eq(x) and V₀(x) and represents the elastic energy accumulated in the cantilever during the equilibrium pulling. Note that this difference is inversely proportional to the spring constant of the cantilever. When the first local maxima of the force is crossed, this elastic energy is released as the tip starts traveling towards the cantilever at high speed, until a new equilibrium position is found.

The loading rate r_f is defined as follows:

$$r_f=\frac{\partial \left(x\left(t\right)-vt\right)}{\partial t}.$$ 6

This equation immediately shows that the approximation r_f = kv is only valid if x(t) is negligible. In the quasi-equilibrium regime it is possible to derive r_f analytically by substituting Equation 4 into Equation 6:

$$r_f=kv\cdot \frac{{\partial }^2{V}_0\left(x\right)}{\partial x^2}\cdot \frac{1}{k+\frac{{\partial }^2{V}_0\left(x\right)}{\partial x^2}}$$ 7

The equation above shows that r_f ≈ kv only when k ≪ [∂²V₀(x)/∂x²]. This is clearly not the case for most of single biomolecule AFM pulling experiments where the stretch modulus of the molecule is usually comparable with the force constant of the cantilever. For these reasons, very different behaviors can be observed for cantilevers of different spring constant, even if the same loading rate kv is applied.