Inhibitory control by an integral feedback signal in prefrontal cortex: A model of discrimination between sequential stimuli

Abstract

The prefrontal cortex (PFC) is known to be critical for inhibitory control of behavior, but the underlying mechanisms are unclear. Here, we propose that inhibitory control can be instantiated by an integral signal derived from working memory, another key function of the PFC. Specifically, we assume that an integrator converts excitatory input into a graded mnemonic activity that provides an inhibitory signal (integral feedback control) to upstream afferent neurons. We demonstrate this scenario in a neuronal-network model for a temporal discrimination task. The task requires the working memory of the vibrational frequency (f1) of an initial stimulus (stimulus 1), followed by comparison of the frequency (f2) of a second stimulus (stimulus 2) with the stored f1 and a binary decision (f2 > f1 or f2 < f1). The integral feedback signal generated by stimulus 1 gates the later inputs based on the amplitude difference (f2 – f1). The feedback control signal enables a subset of neurons to reverse their tuning to f1 between stimulus 1 and stimulus 2, when they become tuned to the difference, f2 – f1. These neurons maintain a lower firing rate during the delay compared with their peak rate during stimulus 1. A second subset of neurons, tuned to f1 during the delay, reaches a rate during stimulus 2 that depends on the maximum of f1 and f2. Our work suggests a circuit mechanism for discrimination across time and predicts neuronal behavior that can be tested experimentally.

Flexible behavior depends on the brain's ability to integrate information from ongoing sensory stimuli across time, in which the prefrontal cortex (PFC) plays a critical role (1). If the earlier information is recent, it can be held in working memory and used later for processing ongoing input. Everyday examples include understanding speech, where the beginning of a sentence must be held in mind while the end of the sentence is being heard, or selecting the best fruit in a store by observing sequentially an array of fruits one item at a time. To investigate the neural mechanisms underlying such behaviors, a commonly used laboratory paradigm is delayed discrimination (2, 3), which is amenable to rigorous behavioral analysis and neurophysiological investigation.

In a series of experiments in which the monkey performs a vibrotactile discrimination task (4–9), Romo and colleagues have analyzed neuronal activity in sensory, memory, and motor areas (somatosensory cortex, PFC, premotor cortex, and motor cortex) of macaque monkeys. The task requires a discrimination between the vibrational frequencies f1 and f2 of two stimuli separated by a delay of 3–6 s. The stimuli are vibrations on a fingertip, at a frequency in the range of 10–40 Hz. Neurons in the primary somatosensory cortex are active during the stimuli, with a firing rate that increases monotonically with vibrational frequency (10). After stimulus 2, at a frequency f2, the monkey must decide whether f2 is higher or lower than the vibrational frequency f1 of stimulus 1 and press one of two levers accordingly. An essential computation required to perform this task is a subtraction between the two stimulus strengths. That is, a neuron whose activity correlates with the decision of whether f2 > f1 should be tuned to the difference, f2 – f1 (in a set of trials where f2 – f1 is fixed).

Vibrational frequency is an analog quantity encoded during the delay by graded persistent neural activity. Neurons observed to maintain stimulus-dependent activity across the delay have firing rates that monotonically increase or decrease as a function of stimulus frequency. Models describing such monotonically tuned persistent activity are akin to models of a neural integrator, such as the one in the oculomotor system used to maintain fixation of gaze (11). An integrator can be continuous, in which case it is subject to noise-driven drift and requires fine tuning, or discrete and robust (12). In either case, the essence of an integrator is summation of consecutive inputs from the same afferent pathway, in contrast to the subtraction (or division) of two consecutive inputs that is necessary for discrimination to occur. Therefore, it is unclear how a single circuit can perform both the temporal integration needed during stimulus 1 and the delay and the computation needed during stimulus 2.

Machens et al. (13) have recently published an ingenious model to perform the task. Their model has the advantage of amplitude-dependent encoding of the stimulus rather than only encoding the integral of amplitude over time. In their model, the subtraction between consecutive stimuli is posited to be achieved by a gating mechanism for the afferent stimuli, such that stimulus 2 reaches the mnemonic part of the circuitry with opposite sign of tuning to stimulus 1. Whether such a switching of the input line occurs during the task remains an open question.

In this article, we propose an alternative scenario, in which integral feedback control (14–18) performs a subtraction across time. Integral feedback control has been suggested to underlie many important biological processes (19, 20), such as adaptation (16), regulation (15, 17, 21), and fine-tuning of parameters to a critical point (18). Integral feedback control is an inhibitory, top-down process. The integrator, which stores the short-term memory of an afferent signal, sends inhibition back to upstream targets. The neurons that encode such a short-term memory are found in the PFC (4, 22, 23), which is known to be important for flexible behavior in general (24) and, in particular, for inhibitory control (25, 26). Recently, excitatory projections from neurons in the PFC have been found to target inhibitory neurons in upstream cortical areas (27), suggesting an anatomical substrate for inhibitory control. In this article, we propose a function of integral feedback control within the PFC to solve the sequential discrimination task.

Materials and Methods

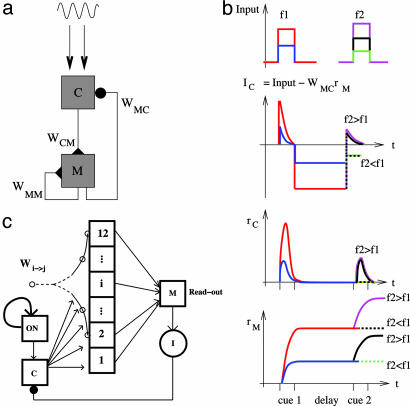
Integral Feedback Control. Inspired by Romo's data (4), we modeled the working-memory circuitry as an integrator (11, 12, 28–30). The key idea here is that memory (M) neurons inhibit their inputs (31) (Fig. 1a) to provide integral feedback control (14, 16). Specifically, comparison (C) neurons receive stimulus-dependent input and excite M neurons in the integrator. M neurons store the stimulus as working memory and send inhibitory feedback to the C neurons.

Fig. 1.

Basic model of discrimination through integral feedback control. (a) The C neurons are quiescent unless excited by external input. The M neurons are integrators of the activity of the C neurons. The key component is the inhibition of the C neurons by the M neurons, which produce the integral feedback control. All connections are local, because all neurons in the circuit are within the PFC. (b Top) Stimulus 1, at frequency f1, (blue, low; red, high) is followed after a delay by stimulus 2, at frequency f2, (green, very low f2 or black, moderate f2 after low f1; black, moderate f2 or magenta, very high f2 after high f1). (b Middle) C neurons respond during stimulus 1, at a rate that increases with stimulus strength. During the delay, the C neurons are quiescent and inhibited by M neuron activity. The inhibition by M neurons means that the C neurons can respond to stimulus 2 only when it is stronger than stimulus 1 (f2 > f1). Importantly, the response to moderate f2 (black) is present after low f1 (blue) but absent after high f1 (red). (b Bottom) M neurons integrate the activity of C neurons and so exhibit constant, persistent activity during the delay when the C neurons are quiescent. During stimulus 2, the activity of M neurons further increases if the C neurons respond (solid line when f2 > f1, dashed line when f2 < f1). (c) Twelve excitatory subpopulations (connected squares) constitute an integrator (labeled M in a) that is capable of persistent activity at a number of graded levels (see Fig. 3e). Tuned recurrent excitation is strongest within a subpopulation and decreases exponentially to other subpopulations. A range of excitability is generated [from 1 (most excitable population) to 12 (least excitable)] by including a range of leak conductances across the network. An extra excitatory population (ON square) is bistable and feeds stimulus-independent input to C neurons after stimulus 1. The readout cell excites a group of interneurons (labeled I) which provide the necessary inhibitory feedback to the C neurons.

We first use a linear firing-rate model to analyze the behavior of the two groups of neurons, coupled as shown in Fig. 1a. We note here that the network behavior does not depend on the linearities in either the feed-forward or feed-back connections, but linearity simplifies the analysis. When the average firing rate of the population of C neurons is r_C and that of M neurons is r_M, then

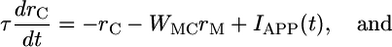[1]

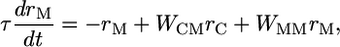[2]

where I_APP is the transient stimulus-dependent current from somatosensory neurons to C neurons, W_MC is the strength of inhibitory connection from M to C neurons, and W_CM and W_MM are the strength of excitatory feed-forward and recurrent connections to M neurons. The key for the M neurons to act as an integrator is to set W_MM = 1, so that Eq. 2 becomes: τdr_M/dt = W_CMr_C. Such a requirement on W_MM is an example of the fine tuning of parameters necessary to create a continuous integrator (11). In the full model, we use a more robust, discrete integrator (12, 32), but the analysis is made more tractable for the present purpose with a continuous linear integrator (see Appendix).

Network Simulations. We simulate the model by using a network of interconnected leaky integrate-and-fire neurons. The network architecture is shown schematically in Fig. 1c. Subpopulations of identical neurons, all receiving independent background-noise input but common network input, form five components of the network.

Comparison. C neurons each receive separate Poisson-spike trains at a rate proportional to the vibrational frequency (f1 or f2), representing input from the secondary somatosensory cortex. Following the standard experimental scheme, f2 = f1 + 8 Hz or f2 = f1 – 8 Hz.

ON. The stimuli also excite a group of “ON” cells (see Fig. 1c), which have strong, saturating recurrent excitation. The ON cells fire during the task but are not tuned to f1. Such untuned, task-dependent cells are observed and, in our network, provide extra excitation to the C neurons during the task.

Memory. The memory network is based on a published model (30), with the simplification of containing only positively monotonic excitatory neurons. The M neurons are connected as 12 bistable populations with a range of excitabilities to form a discrete integrator (12). The number of active subpopulations after the input represents a memory that is a discrete approximation of the temporal integral of the input. We adjusted strengths of excitatory cross-connections so that, with n active populations, the input required to activate the n + 1th population (the threshold in Fig. 3e) is approximately constant for all n. This input threshold for M neurons sets an activity threshold θ for C neurons (dashed line in Fig. 2b) that must be surpassed to produce integration.

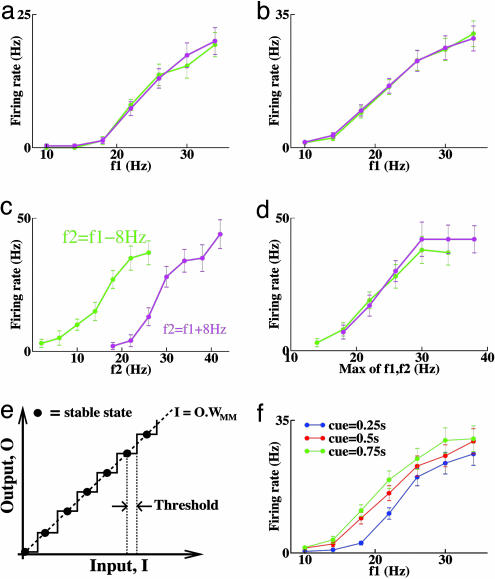
Fig. 3.

Activity of memory cell in the model. (a) Average firing rates during stimulus 1. Magenta, f2 > f1; green, f2 < f1. Standard error is indicated. (b) Average firing rates during the delay (same symbols as a). (c) Average firing rate during the first 200 ms of stimulus 2 (same symbols as a). (d) Average firing rate during the last 100 ms (final steady state) of stimulus 2 plotted against the greater of f1 or f2 (same symbols as a). (e) Schematic input–output relationship for the discrete memory network, showing a set of discrete stable states along the line where the recurrent feedback input = W_MM× output (filled circles). Any external input must exceed a threshold (distance from the stable state to the next step jump) to affect the memory cells. (f) When the duration of stimulus 1 is varied, memory activity shifts slightly.

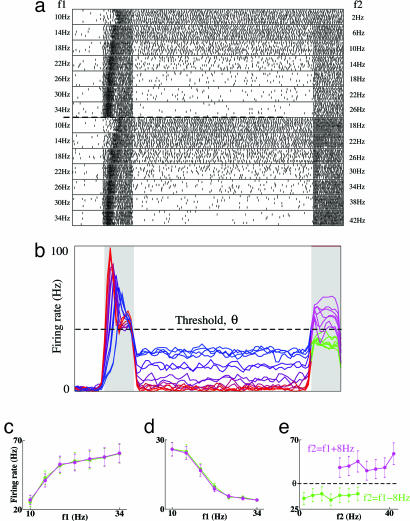
Fig. 2.

Reversal of tuning response between stimulus 1 and the delay for C neurons. (a) Rastergram of spikes produced in a group of 10 trials for each stimulus pair, for f2 = f1 – 8 Hz (Upper) and f2 = f1 + 8 Hz (Lower). (b) Histogram, indicating rate averaged over 10 trials for each stimulus pair as a function of time. Purple color range indicates magnitude of stimulus 1 from f1 = 10 Hz (blue) through f1 = 34 Hz (red). During stimulus 2, magenta, f2 > f1; green, f2 < f1. Data are smoothed with 150-ms Gaussian kernel. (c) Average firing rates for the first 300 ms of stimulus 1 (positively monotonic). Magenta, f2 > f1; green, f2 < f1. Standard error is indicated. (d) Average firing rates during the delay (negatively monotonic, same symbols as c). (e) Average firing rate during the first 200 ms of stimulus 2 (same symbols as c).

Readout. The 12 bistable subpopulations excite a population of readout cells whose firing rates encode the memory.

Inhibition. A single interneuron population receives input from the readout cells and inhibits the C neurons with a strength approximately proportional to memory-readout activity.

Our purpose here is to investigate how a discrete integrator affects the integral feedback-control model and not to address the mechanisms needed to create such an integrator, which could arise from single cell properties (33, 32) and from strong recurrent feedback between cells (12).

All spiking-network simulations were carried out by using GNU-compiled C++ code, running on dual Athlon processors (Microway, Plymouth, MA). We also used the program xppaut to test the feasibility of the concept by using linear firing-rate models. See Supporting Information, which is published on the PNAS web site, for full details of the simulation and access to all codes.

Results

Mechanism of Integral Feedback Control. We summarize here how integral feedback control can lead to discrimination and leave the full details to the Appendix. The rate r_C of the input-receiving C neurons and the rate r_M of the M neurons follow Eqs. 1 and 2.

Initially, we assume the neurons are quiescent, r_C = 0, and r_M = 0. C neurons are excited by stimulus 1 and, in turn, activate the M neurons: dr_C/dt > 0, because I_APP(t) > r_C + W_MCr_M and dr_M/dt > 0, because W_CMr_C > 0. The M neurons integrate their inputs and store a memory of the amplitude of stimulus 1. That memory is reflected in the amount of inhibition fed back to the C neurons (W_MCr_M > 0). The M neurons fire at a gradually increasing rate, integrating the activity of the C neurons over time, until the C neurons are silenced. Therefore, the amount of inhibition increases to reach the precise value needed to silence the C neurons in the presence of stimulus 1. That is, when the system reaches a steady state during stimulus 1: dr_M/dt = 0, hence r_C = 0; to reach r_C = 0, then W_MCr_M = I_APP must be true. During the delay, when the stimulus is absent, the C neurons remain silent (I_APP = 0 < W_MCr_M). During stimulus 2, the inhibition is still present, so the C neurons cannot fire unless the stimulus I_APP(t₂) is strong enough to overcome the inhibition. That is, dr_C/dt > 0 only when I_APP(t₂) > W_MCr_M = I_APP(t₁). Because the inhibition exactly matches the strength of stimulus 1, the C neurons fire only when stimulus 2 is stronger than stimulus 1 (see Fig. 1b). Hence, the essence of discrimination is achieved.

The system is robust, because changes in the weights affect the stable rates of M neurons during the delay but do not affect the steady-state condition that the persistent inhibitory feedback exactly cancels the excitation from stimulus 1. However, two conditions are necessary to ensure such a matching of inhibitory feedback to the stimulus current. First, the steady state should be reached before the stimulus is removed, so the time constant of the system should be shorter than the stimulus duration T. Second, the system should not be susceptible to oscillations. The two requirements can be fulfilled over a broad range of synaptic weights when the neuronal time constant is significantly shorter than the stimulus duration τ ≪ T. Because a typical stimulus duration is 0.5 s, the network can be robust when feed-forward connections are mediated primarily by α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptors rather than NMDA receptors.

Simulation Results: Discrete Integrator. The network with a discrete integrator can maintain a memory of stimulus 1 and perform the discrimination (Figs. 2 and 3).

The C neuron we show in Fig. 2 is tuned positively monotonically during stimulus 1: The greater the vibrational frequency f1, the greater its initial firing rate. Similarly, because C neurons provide input to M neurons, the greater f1, the greater the activity of M neurons by the end of the stimulus. In the discrete network, M neurons integrate only input that is above a threshold, so C neurons must fire above a threshold rate θ (≈40 Hz in our example) to activate the memory network. During a stimulus that produces activity >θ in the C neurons, the M neurons increase their rate and, so, inhibit the C neurons. Once the activity of C neurons is inhibited <θ, the M neurons no longer receive enough input to increase their rate further. Hence, a steady state is reached with C neuron activity decreased to θ, whereas M neurons fire persistently at a rate that is tuned positively monotonically to f1.

Once the excitatory stimulus to the C neurons ends, the rate drops further, <θ (Fig. 2 b and d). So, during the delay, C neurons fire at a rate lower than during stimulus 1. M neurons remain tuned positively monotonically to f1 (Fig. 3b) and continue to provide feedback inhibition to C neurons. Hence, a C neuron receives more inhibition if it fired more during stimulus 1, so the slope of its tuning curve switches sign between stimulus 1 and delay (Fig. 2 c and d). When θ is low and the feedback inhibition from M neurons is high, then the C neurons may be silenced and untuned in the delay (as with a continuous integrator). However, in our network, we chose a relatively high value of θ (40 Hz), so the C neuron delay activity never reaches 0, but is tuned negatively monotonically to f1. So, a notable feature of our network is a switch in sign of the tuning of C neurons, as their activity first responds to f1 but later is determined by feedback inhibition from M neurons.

During stimulus 2, the network generates a response based on the difference (f2 – f1). Strong inhibition from M neurons limits the range of activity of C neurons during stimulus 2 compared with stimulus 1. When f2 < f1, the C neuron is not silent (as in the linear-rate model with a continuous integrator), but its activity remains <θ. Feedback inhibition reduced the rate of C neurons to θ when they were excited by f1, so excitation with f2 < f1 is insufficient for the rate to reach θ, because the feedback inhibition persists. In contrast, when f2 > f1, the C neurons receive greater excitation during stimulus 2 than they did during stimulus 1, leading to a rate >θ. In this case, M neurons are further excited by above-threshold firing of C cells, eventually inhibiting the C neurons back down to θ again. The activity of C neurons is significantly greater when f2 > f1 than when f2 < f1 (Fig. 2e); hence, activity of C neurons can serve to produce a motor output.

If we use alternate stimuli with half the magnitude of difference between f1 and f2 such that f2 = f1 ± 4 Hz, the curves for f2 > f1 and f2 < f1 are similar to Fig. 2e but only about half as far apart (data not shown). This proportionate change in difference is because the peak response during stimulus 2 increases approximately linearly with f2 – f1. In contrast to C neurons, which are tuned to the constant difference f2 – f1, rates of M neurons do vary across stimulus pairs (Fig. 3c), because their steady-state firing rate is tuned to the maximum of f1 and f2 (see Fig. 3d and Appendix).

We used a discrete integrator in the spiking-network model for two reasons. First, a continuous integrator does require fine tuning of parameters, whereas a discrete integrator is more robust to parameter changes (11, 12). Second, a continuous integrator integrates noise (34), so, in our network, the inhibitory feedback from a continuous integrator silences any spontaneous activity in the C neurons. However, cells observed in the PFC typically do fire at significant rates in the absence of stimulus presentation.

A discrete integrator has a set of stable activities (see Fig. 3e) that must be sufficient in number to encode all stimulus values. The activity changes from one stable state to the next only when the input exceeds a threshold (distance to the next step in Fig. 3e). So, the network does not integrate, and then silence, all input activity. In our model, thresholds for further integration are approximately equal for all stable states of the memory network. For optimal performance, inhibitory feedback from the integrator should increase linearly with the excitatory input to the integrator. So, significant variation of thresholds is detrimental, because the integrator would increase activity more rapidly in some ranges than others. However, the precise value of a constant integration threshold does not affect the circuit's ability to perform discrimination. Indeed, we have run simulations with θ = 20 Hz instead of 40 Hz, and the network behavior remains the same (data not shown).

Reducing stimulus duration from 500 ms to 250 ms reduces the activity of M neurons, whereas increasing duration to 750 ms increases their activity slightly (Fig. 3f). The increase in activity after 500 ms is driven by noise-induced, upward transitions in the discrete integrator with near-threshold input. By 1 s of stimulus duration, input is reduced far enough below threshold to prevent further change.

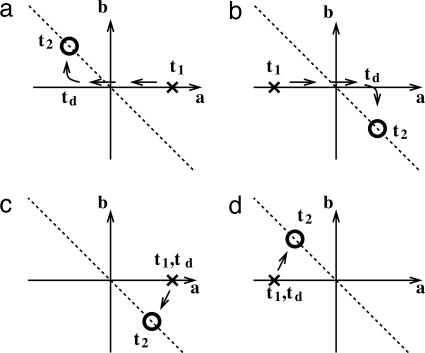
Experimental Comparison. Cells involved in the discrimination are tuned to the difference in frequencies, f2 – f1, during stimulus 2. The firing rate r(t) can be written as r(t) = a(t)f1 + b(t)f2 + c(t), where a(t), b(t), and c(t) are coefficients that vary with time t (6, 5). Cells tuned to the difference f2 – f1 during stimulus 2 have a =–b and fall on the diagonal dashed lines of Fig. 4. When such cells are also tuned during stimulus 1, then initially they have a(t) ≠ 0 and will lie on the x axis in Fig. 4. So, neurons that are input-dependent during stimulus 1 (crosses in Fig. 4) then discriminatory during stimulus 2 (circles in Fig. 4) can fall into the four categories depicted in Fig. 4 a–d. Our model is consistent with cells that flip their tuning to f1 and produce the tuning behavior seen in Fig. 4 a and b. The reversal of tuning of C neurons to f1 is apparent early in the delay when a discrete integrator with a sufficiently high threshold is used (Fig. 3e). Experimental observation of a sign-flip in tuning after stimulus-offset would be a strong indication of feedback control from a discrete integrator. When a continuous integrator is used, C neurons are silent during the delay, so the sign switch to f1 appears only during stimulus 2.

Fig. 4.

Schematic figure, showing tuning as a function of two stimuli. We assume the firing rate of a neuron is given by r(t) = a(t)f1 + b(t)f2 + c(t), where the coefficients a and b represent the tuning to f1 and f2, respectively (5). Crosses represent the tuning during stimulus 1, [they must lie on the x axis, because neurons cannot have any tuning to f2 (so b = 0) before stimulus 2]. Circles represent the tuning during stimulus 2. The diagonal dashed line is the line for discriminatory response, where firing rate is proportional to the difference between f2 and f1. Neurons that are both tuned to f1 during stimulus 1 and are discriminatory during stimulus 2 behave according to one of the four a–d. (a and b) Representation of the behavior of C neurons in our network. (c and d) Representation of the behavior of neurons in an alternative network (13) with a switch at the input stage.

The behavior of our model is to be contrasted to the proposal of Machens et al. (13) that the necessary sign-flip in tuning occurs in the afferent connections, so that stimulus 2 has an opposite effect on the network to the first (a sign-flip for f2 apparent only during stimulus 2). Such circuitry would lead to the behavior of Fig. 4 c and d. To understand the mechanism of sequential discrimination, it will be important to assess whether neurons observed in the experiment more often show a sign-flip in f1 (Fig. 4 a and b) or f2 (Fig. 4 c and d).

Discussion

The method of integral feedback control leads to a discrimination in the amplitude of two inputs that are separated in time. Whereas this mechanism uses an integrator to store the memory of stimulus 1, the inhibitory feedback affects the encoding of that stimulus. Importantly, instead of encoding the product of amplitude and time, as occurs with a straightforward integration of the stimulus, integral feedback control leads to delay activity that depends only on the amplitude of the stimulus, so long as a minimal duration is reached (35). Increasing the duration of f1 in our simulations leads to just a small increase in memory activity (see Fig. 3f), in agreement with the small increase in perceived value of f1 seen in psychophysical data (9). In both our model and in the psychophysics, reducing the stimulus duration to <500 ms has a stronger (opposite) effect than increasing duration. This result is understandable, because the input to the integrator decays exponentially at longer times (Eq. 3), so increasing duration has a diminishing effect.

A continuous integrator would integrate noise and perform a random walk during the delay (34). Because the variance of a random walk increases (linearly) with time, errors in performance would increase with length of delay. Psychophysical data suggest length of delay does matter but, perhaps, for behavioral reasons (35).

In contrast, a discrete integrator integrates only when the neurons providing it input reach a finite level of activity (their activation threshold θ; Fig. 2b). We use such a discrete integrator because it does not integrate spontaneous activity. A constant excitatory input can “switch on” the integrator, allowing it to respond sensitively to other inputs (reducing θ), whereas a constant inhibition can make the integrator insensitive to other excitatory input (increasing θ). So, in addition to providing robustness to noise, an integration threshold permits gating of inputs to the graded memory store.

In our model, θ (≈40 Hz) separates the values of the firing rate of C neurons across different epochs of the task (Fig. 2b). During stimulus 1, the C neurons must fire at a rate >θ to activate the memory network. By the end of stimulus 1, the rate is reduced to ≈θ. During the delay, the C neurons are inhibited <θ and so must fire at a lower rate than during stimulus 1 (Fig. 2 c and d). During stimulus 2, the C neurons fire more than during the delay but exceed θ only when f2 > f1 (Fig. 2e). This type of behavior can be tested for experimentally. The continuous network leads to equivalent results, except it has θ = 0 Hz, so any effects of inhibition are not observable as a firing rate <θ.

The basic connection strengths that carry out the discrimination (W_CM and W_MC in the model), and even the shape of the input–output curves corresponding to those synapses, are very robust to variations. Our model explains some observations in the experimental data, such as cells that switch the sign of their tuning to f1 after stimulus 1 and cells whose firing rates rise and drop rapidly before the end of the stimulus. On the other hand, our model does not capture ramping activities observed during the mnemonic delay period (4), which require additional mechanisms to be elucidated in the future.

Integral feedback control requires inhibition of excitatory afferent neurons and so is functionally similar to top-down inhibitory control (26). Although the neurons we model are all located in the PFC, recent work demonstrates projections from neurons in the PFC to inhibitory neurons in upstream circuits (27). This finding supports the role of the PFC in top-down inhibitory control (26). Our model circuitry resembles inhibitory control, because any response to stimulus 2 is inhibited by the memory of stimulus 1. Stimulus 2 is able to cause activity in downstream neurons only when stimulus 2 produces a greater input current than did stimulus 1. The integral feedback-control circuit combines working memory with a computation based on inhibitory control, thus unifying two cognitive roles of the PFC to solve one task.

C neurons in our circuit are most active when f2 > f1. In order for a monkey to respond when f2 < f1, the neuronal circuitry would use neurons that are oppositely tuned to the vibrational stimulus. In the experimental data, neurons are observed in the secondary (but not primary) somatosensory cortex that fire at higher rates for lower stimulus frequencies. These neurons provide such oppositely tuned input to a second subset of neurons in the PFC. The consecutive inputs I₁ and I₂ (see Appendix) to negatively monotonically tuned neurons in the PFC are negatively tuned to the stimulus frequencies (i.e., dI₁/df1 = dI₂/df2 < 0). In our model, C neurons with such oppositely tuned input would respond only to f2 < f1 (see Fig. 5).

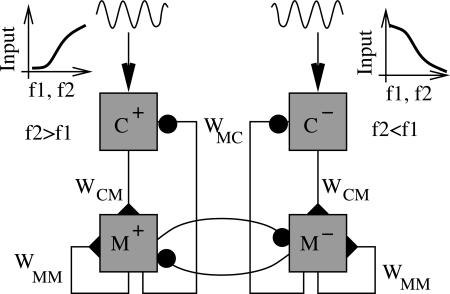
Fig. 5.

Combined network for full response. Oppositely tuned inputs from secondary somatosensory cortex feed forward to two separate, parallel circuits that function by integral feedback control. The circuit that receives input from the positively monotonic neurons (Left) signals when f2 > f1 (Fig. 4a), whereas the circuit that receives input from negatively monotonic neurons (Right) signals when f2 < f1 (Fig. 4b). Cross-inhibition between the two sets of M neurons (M⁺ and M^–) can stabilize memory activity (30) and account for the negative noise correlation between cell types (13).

Our model of integral feedback control can use the two sets of oppositely tuned neurons in parallel, with one set providing a response for the decision f2 > f1 and the other set responding in the opposite case (Fig. 5). Instead of comparing the activity of C neurons with a fixed level (Fig. 2 b and e), discrimination is based on which of the two sets of C neurons has greater activity. Whereas the working memory network may be stabilized by cross-connections between the two sets, the process of discrimination does not require any such interaction. Rather, cross-inhibition is necessary at the response stage, when the decision is made (36). Our network requires inhibition to reset the integrator during the decision/response stage. In the model of Machens et al. (13), the oppositely tuned neurons are essential to the subtraction process involved in discrimination. In that model, the push–pull response to stimulus 1 is switched at the input stage to a pull–push response to stimulus 2. Thus, a reversal of tuning in the inputs causes a subtraction (rather than addition) of successive stimuli. In that model, the M neurons are also those most essentially correlated with the decision. In our model, the strongest correlation with the decision occurs in the neurons that project to the M neurons. The model of Machens et al. (13) has the advantage that strong cross-inhibition between memory cells allows firing rates to covary slowly in time during the delay (strong temporal variation is seen in real data) (4) without loss of memory. Our model has the advantage that no extra switch in sign is needed at the input stage.

Because the subtraction occurs at different points in the network of the two models, their neuronal tuning curves differ as a function of time. Considering neurons that are tuned positively monotonically to stimulus 1, integral feedback control would suggest the sequence +f1, –f1 (or 0), f2 – f1 for the sequence of tuning during stimulus 1, delay, stimulus 2 (Fig. 4a). The model of Machens et al. (13) leads to +f1, +f1, f1 – f2 for the same three epochs (Fig. 4c). Hence, comparison of neuronal-tuning curves across all epochs can help distinguish between different candidate mechanisms underlying this delayed-discrimination task. Experimental evidence does not unambiguously favor either model.

To conclude, although we focused on a specific circuit for the sequential discrimination task, the principle of integral feedback control, demonstrated here, is more general. Our work suggests a specific scenario through which the prefrontal cortex uses working memory to inhibit and gate upstream neural circuits.

Appendix

Analysis of Firing-Rate Model. We solve the coupled Eqs. 1 and 2, assuming no activity in the neurons before stimulus 1 (r_M = 0, r_C = 0 for t < 0), and I_APP(t) = I₁ during stimulus 1. We find

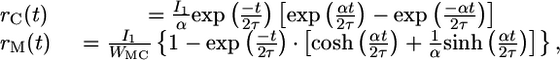[3]

where 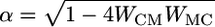. The system approaches a steady state, with r_C = 0 and r_M = I₁/W_MC for t ≫ τ/(1 – Re[α]). Hence, when the stimulus duration is long enough, the system will maintain persistent activity that perfectly suppresses the stimulus. The requirement of a sufficiently long stimulus duration can be expressed as a criterion on the product of the connection strengths, 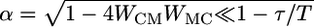, where T, the stimulus duration, should be significantly greater than the neuronal time constant τ. In this case, we have the criterion for the synaptic weights: W_CMW_MC ≫ τ/(2T). Note that, when the synaptic weights are strong, such that 4W_CMW_MC > 1, then α is imaginary, and the solution is oscillating. In this case, r_C will reach 0 more quickly, and the integration will end prematurely, because negative values of rate will be cut off. The rate of the M neuron will actually be higher than the equilibrium value above, essentially because it does not integrate a negative rate. So, in short, for the system to behave correctly in the discrimination task, we have a second criterion, W_CMW_MC < 0.25. The criteria on the product of connection strengths give a large range of values where strengths can be varied without loss of function. Given a feed-forward time constant τ = 10 ms and a stimulus duration of 0.5 s, we have an operational range of 0.02 ≪ W_CMW_MC < 0.25, indicating that the network is robust.

Assuming stimulus 1 is robustly encoded such that r_M ≈ I₁/W_MC during the delay, the response to stimulus 2 when I_APP(t) = I₂ is 0 when I₂ < I₁. In contrast, the response follows

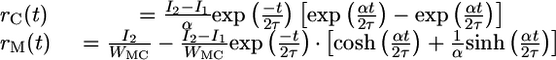[4]

when I₂ > I₁. Hence, the firing rate of the C neurons is proportional to the difference between the consecutive input currents, I₂ – I₁, and discrimination is achieved. The M neurons reach a rate proportional to the greater of I₁ or I₂.