Abstract
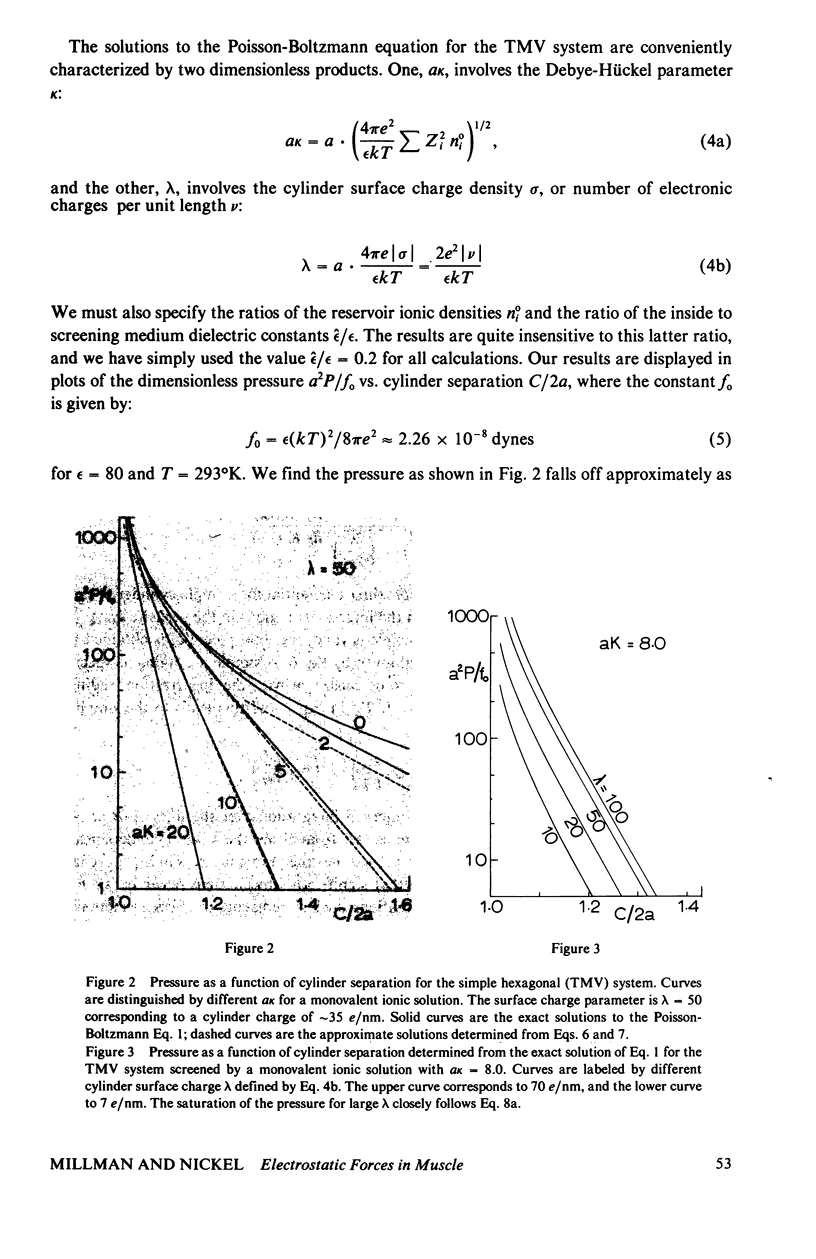
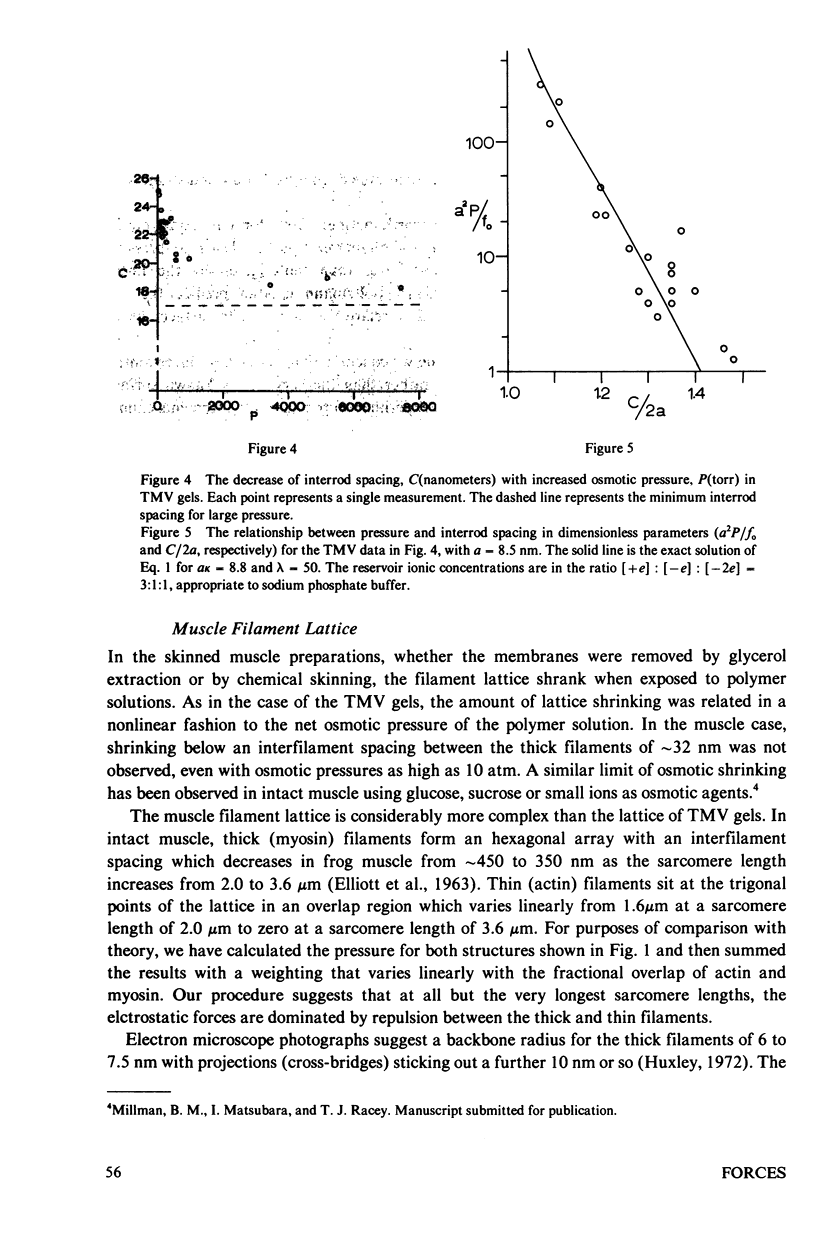
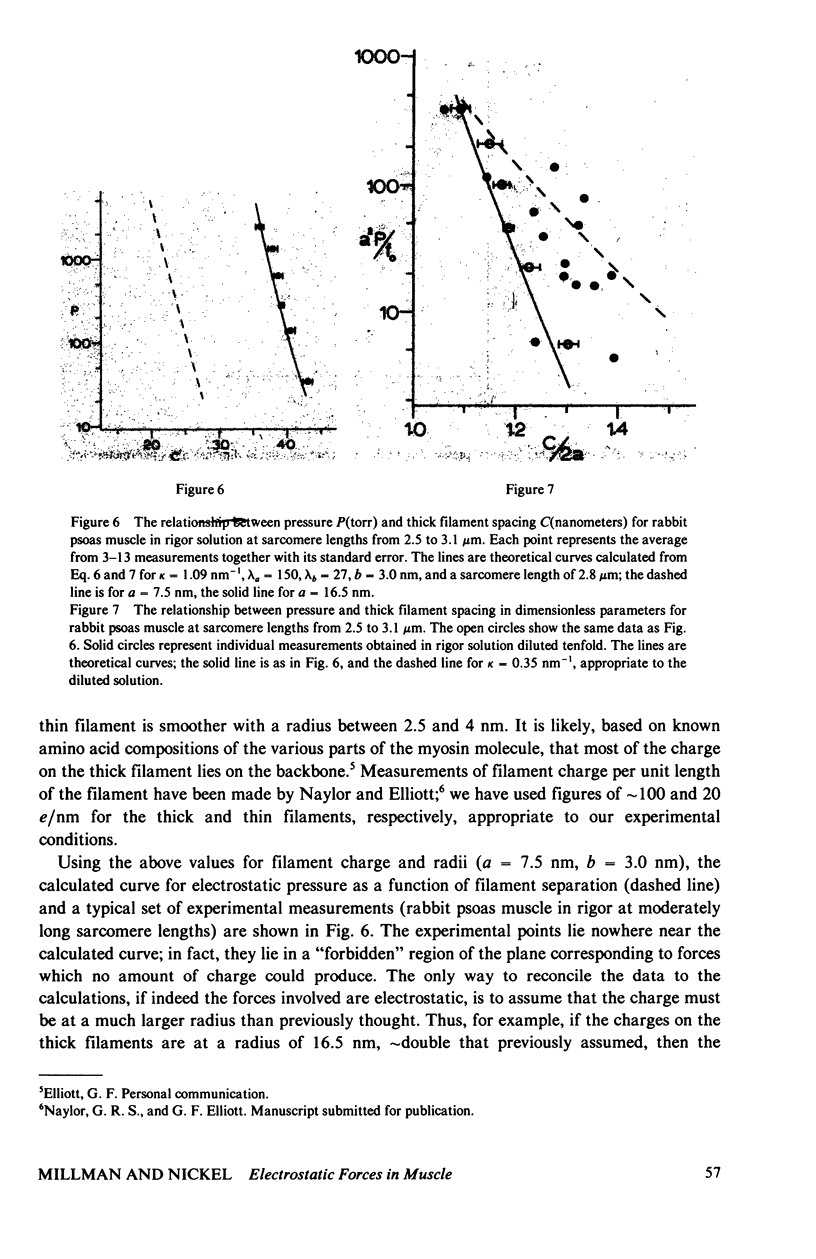
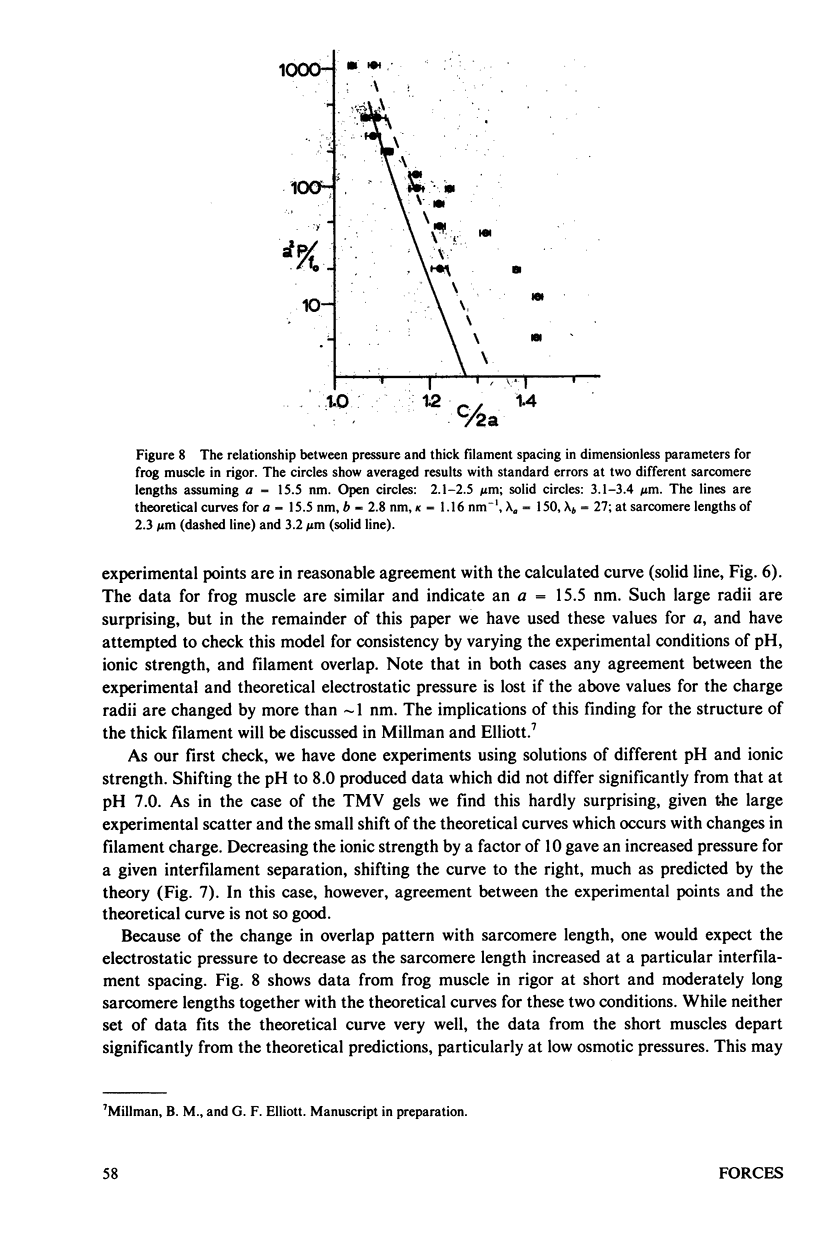
Repulsive pressure has been measured as a function of lattice spacing in gels of tobacco mosaic virus (TMV) and in the filament lattice of vertebrate striated muscle. External pressures up to ten atm have been applied to these lattices by an osmotic stress method. Numerical solutions to the Poisson-Boltzmann equation in hexagonal lattices have been obtained and compared to the TMV and muscle data. The theoretical curves using values for k calculated from the ionic strength give a good fit to experimental data from TMV gels, and an approximate fit to that from the muscle lattice, provided that a charge radius for the muscle thick filaments of approximately 16 nm is assumed. Variations in ionic strength, sarcomere length and state of the muscle give results which agree qualitatively with the theory, though a good fit between experiment and theory in the muscle case will clearly require consideration of other types of forces. We conclude that Poisson-Boltzmann theory can provide a good first approximation to the long-range electrostatic forces operating in such biological gel systems.
Full text
PDF







Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Brenner S. L., McQuarrie D. A. Force balances in systems of cylindrical polyelectrolytes. Biophys J. 1973 Apr;13(4):301–331. doi: 10.1016/S0006-3495(73)85987-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenner S. L., Parsegian V. A. A physical method for deriving the electrostatic interaction between rod-like polyions at all mutual angles. Biophys J. 1974 Apr;14(4):327–334. doi: 10.1016/S0006-3495(74)85919-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elliott G. F. Force-balances and stability in hexagonally-packed polyelectrolyte systems. J Theor Biol. 1968 Oct;21(1):71–87. doi: 10.1016/0022-5193(68)90060-x. [DOI] [PubMed] [Google Scholar]
- Huxley H. E., Brown W. The low-angle x-ray diagram of vertebrate striated muscle and its behaviour during contraction and rigor. J Mol Biol. 1967 Dec 14;30(2):383–434. doi: 10.1016/s0022-2836(67)80046-9. [DOI] [PubMed] [Google Scholar]
- LeNeveu D. M., Rand R. P., Parsegian V. A. Measurement of forces between lecithin bilayers. Nature. 1976 Feb 19;259(5544):601–603. doi: 10.1038/259601a0. [DOI] [PubMed] [Google Scholar]
- Magid A., Reedy M. K. X-ray diffraction observations of chemically skinned frog skeletal muscle processed by an improved method. Biophys J. 1980 Apr;30(1):27–40. doi: 10.1016/S0006-3495(80)85074-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsubara I., Elliott G. F. X-ray diffraction studies on skinned single fibres of frog skeletal muscle. J Mol Biol. 1972 Dec 30;72(3):657–669. doi: 10.1016/0022-2836(72)90183-0. [DOI] [PubMed] [Google Scholar]
- Parsegian V. A., Brenner S. L. The role of long range forces in ordered arrays of tobacco mosaic virus. Nature. 1976 Feb 26;259(5545):632–635. doi: 10.1038/259632a0. [DOI] [PubMed] [Google Scholar]
- Rome E. Light and X-ray diffraction studies of the filament lattice of glycerol-extracted rabbit psoas muscle. J Mol Biol. 1967 Aug 14;27(3):591–602. doi: 10.1016/0022-2836(67)90061-7. [DOI] [PubMed] [Google Scholar]
- Schoenberg M. Geometrical factors influencing muscle force development. II. Radial forces. Biophys J. 1980 Apr;30(1):69–77. doi: 10.1016/S0006-3495(80)85077-6. [DOI] [PMC free article] [PubMed] [Google Scholar]


