Abstract
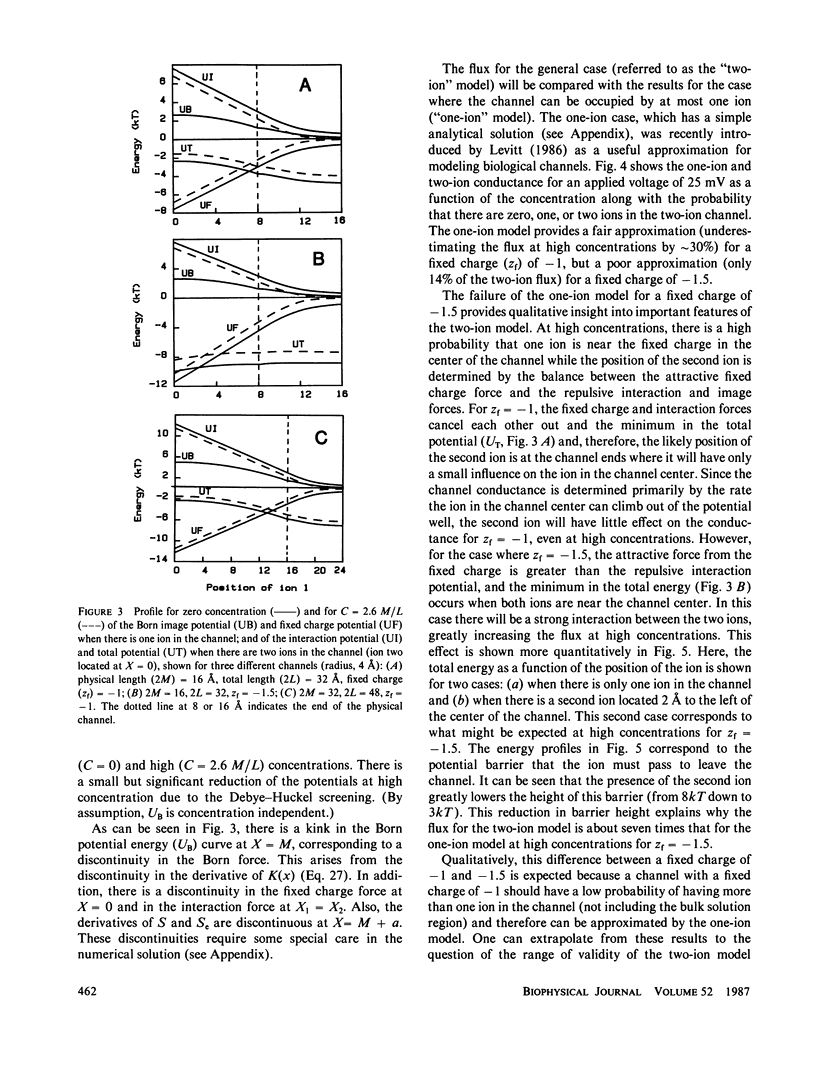
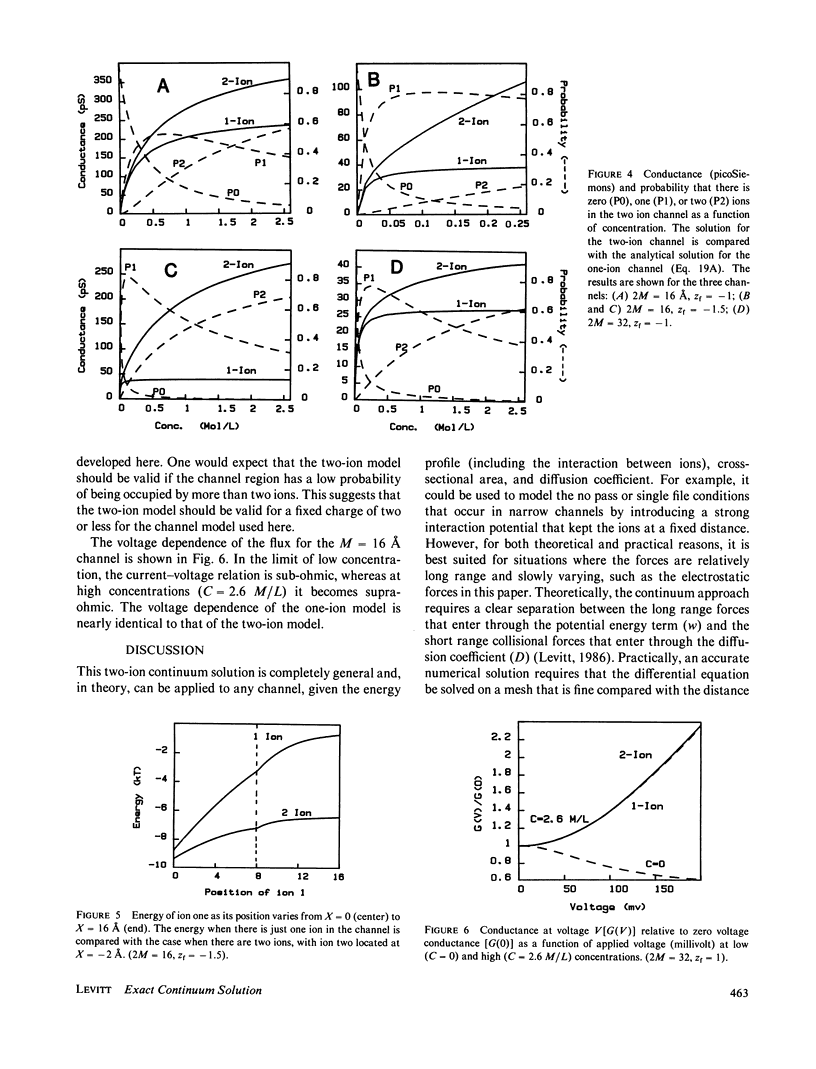
The classical Nernst-Planck continuum equation is extended to the case where the channel can be occupied simultaneously by two ions. A two-dimensional partial differential equation is derived to describe the steady-state channel. This differential equation is of the form of the generalized Laplace equation, but it has the novel feature that the boundary conditions are periodic. The finite difference solution takes approximately 8 s on a large computer. The equations are solved for the special case of a cylindrical channel with a fixed charge in the center. It is assumed that the forces on the ions result entirely from the sum of the Born image potential, the fixed charge potential, the interaction potential between the two ions, and the applied voltage. Approximate simple analytical expressions are derived for these potential terms, based on the assumption that the electric field perpendicular to the channel wall is zero. The potentials include the contribution from a diffuse charge (Debye-Huckel) reaction field in the bulk solution for the monovalent cation flux was obtained for channels with a radius of 4 A and lengths of 16 and 32 A and a fixed charge valence of -1 and -1.5. For these channels, a significant fraction (up to 90%) of the total resistance is contributed by the bulk solution and results were obtained for the case where the "channel" included 8 A of bulk solution at each channel end. These results for the two-ion channel were compared with the analytical solution for a one-ion channel. The one-ion channel is a fair approximation to the two-ion channel for a fixed charge of -1, underestimating the flux at high concentrations by approximately 30%. However, for a fixed charge of -1.5, the one-ion model is a poor approximation, with the two-ion flux about seven times that of the one-ion model at high concentrations. The absolute conductance and concentration dependence of these channels (with a fixed charge of -1) mimic the behavior of the large conductance K+ channel and the acetylcholine receptor channel.
Full text
PDF









Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Brisson A., Unwin P. N. Quaternary structure of the acetylcholine receptor. Nature. 1985 Jun 6;315(6019):474–477. doi: 10.1038/315474a0. [DOI] [PubMed] [Google Scholar]
- Dani J. A., Eisenman G. Monovalent and divalent cation permeation in acetylcholine receptor channels. Ion transport related to structure. J Gen Physiol. 1987 Jun;89(6):959–983. doi: 10.1085/jgp.89.6.959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan P. C. Electrostatic modeling of ion pores. Energy barriers and electric field profiles. Biophys J. 1982 Aug;39(2):157–164. doi: 10.1016/S0006-3495(82)84503-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latorre R., Miller C. Conduction and selectivity in potassium channels. J Membr Biol. 1983;71(1-2):11–30. doi: 10.1007/BF01870671. [DOI] [PubMed] [Google Scholar]
- Levitt D. G. Comparison of Nernst-Planck and reaction rate models for multiply occupied channels. Biophys J. 1982 Mar;37(3):575–587. [PMC free article] [PubMed] [Google Scholar]
- Levitt D. G. Electrostatic calculations for an ion channel. I. Energy and potential profiles and interactions between ions. Biophys J. 1978 May;22(2):209–219. doi: 10.1016/S0006-3495(78)85485-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt D. G. Interpretation of biological ion channel flux data--reaction-rate versus continuum theory. Annu Rev Biophys Biophys Chem. 1986;15:29–57. doi: 10.1146/annurev.bb.15.060186.000333. [DOI] [PubMed] [Google Scholar]
- Levitt D. G. Strong electrolyte continuum theory solution for equilibrium profiles, diffusion limitation, and conductance in charged ion channels. Biophys J. 1985 Jul;48(1):19–31. doi: 10.1016/S0006-3495(85)83757-7. [DOI] [PMC free article] [PubMed] [Google Scholar]


